| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Однородная деформация
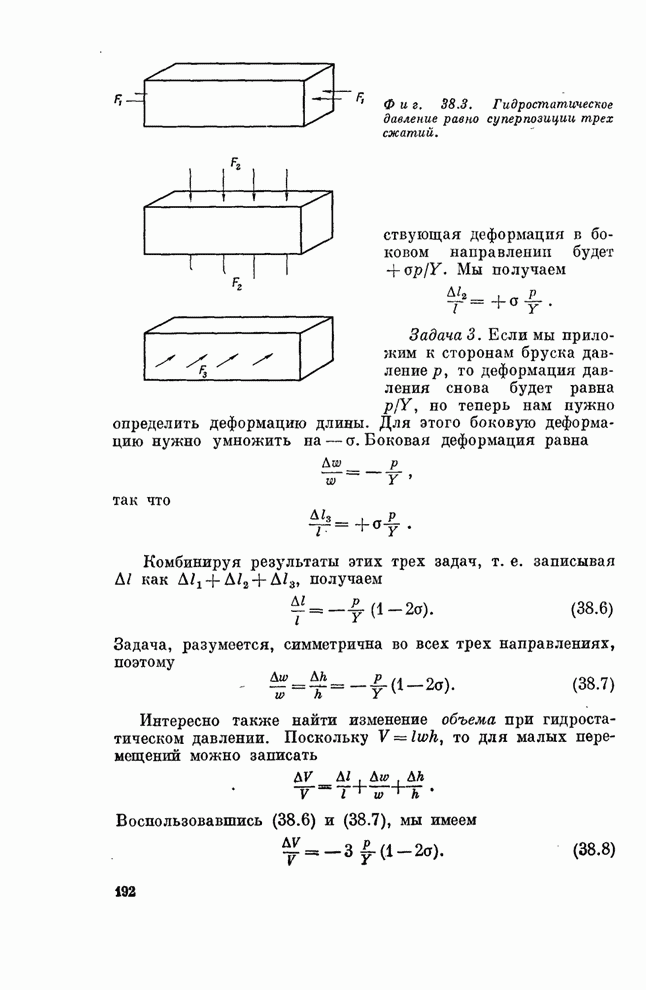
В качестве первого примера посмотрим, что происходит с прямоугольным бруском при однородном гидростатическом сжатии. Давайте поместим брусок в резервуар с водой. При этом возникнет сила, действующая на каждую грань бруска и пропорциональная его площади (фиг. 38.2). Поскольку гидростатическое давление однородно, то напряжение (сила на единичную площадь) на каждой грани бруска будет одним и тем же. Прежде всего найдем изменение длины бруска. Его можно рассматривать как сумму изменений длин, которые происходили бы в трех независимых задачах, изображенных на фиг. 38.3.

Фиг. 38.2. Брусок под действием равномерного гидростатического давления.

Фиг. 38.3. Гидростатическое давление равно суперпозиции трех сжатий.
Задача
1. Если мы приложим к концам бруска давление ![]() , то деформация сжатия будет
отрицательна и равна
, то деформация сжатия будет
отрицательна и равна ![]() :
:
![]() .
.
Задача
2. Если мы надавим на горизонтальные грани бруска, то деформация по высоте
будет равна ![]() ,
а соответствующая деформация в боковом направлении будет
,
а соответствующая деформация в боковом направлении будет ![]() . Мы получаем
. Мы получаем
![]() .
.
Задача
3. Если мы приложим к сторонам бруска давление ![]() , то деформация давления снова будет
равна
, то деформация давления снова будет
равна ![]() ,
но теперь нам нужно определить деформацию длины. Для этого боковую деформацию
нужно умножить на
,
но теперь нам нужно определить деформацию длины. Для этого боковую деформацию
нужно умножить на ![]() . Боковая деформация равна
. Боковая деформация равна
![]() ,
,
так что
![]() .
.
Комбинируя
результаты этих трех задач, т. е. записывая ![]() как
как ![]() , получаем
, получаем
![]() . (38.6)
. (38.6)
Задача, разумеется, симметрична во всех трех направлениях, поэтому
![]() . (38.7)
. (38.7)
Интересно
также найти изменение объема при гидростатическом давлении. Поскольку ![]() , то для малых
перемещений можно записать
, то для малых
перемещений можно записать
![]() .
.
Воспользовавшись (38.6) и (38.7), мы имеем
![]() . (38.8)
. (38.8)
Имеются
любители называть ![]() объемной деформацией и писать
объемной деформацией и писать
![]() .
.
Объемное
напряжение ![]() (гидростатическое
давление) пропорционально вызванной им объемной деформации - снова закон Гука.
Коэффициент
(гидростатическое
давление) пропорционально вызванной им объемной деформации - снова закон Гука.
Коэффициент ![]() называется
объемным модулем и связан с другими постоянными выражением
называется
объемным модулем и связан с другими постоянными выражением
![]() . (38.9)
. (38.9)
Поскольку
коэффициент ![]() представляет
некоторый практический интерес, то во многих справочниках вместо
представляет
некоторый практический интерес, то во многих справочниках вместо ![]() и
и ![]() приводятся
приводятся ![]() и
и ![]() . Но если вам
нужно знать
. Но если вам
нужно знать ![]() ,
то вы всегда можете получить это значение из формулы (38.9). Из этой формулы
видно также, что коэффициент Пуассона
,
то вы всегда можете получить это значение из формулы (38.9). Из этой формулы
видно также, что коэффициент Пуассона ![]() должен быть меньше 1/2. Если бы это
было не так, то объемный модуль
должен быть меньше 1/2. Если бы это
было не так, то объемный модуль ![]() был бы отрицательным и материал при
увеличении давления расширялся бы. Это позволило бы добывать механическую
энергию из любого кубика, т. е. это означало бы, что кубик находится в неустойчивом
равновесии. Если бы он начал расширяться, то расширение продолжалось бы само по
себе с высвобождением энергии.
был бы отрицательным и материал при
увеличении давления расширялся бы. Это позволило бы добывать механическую
энергию из любого кубика, т. е. это означало бы, что кубик находится в неустойчивом
равновесии. Если бы он начал расширяться, то расширение продолжалось бы само по
себе с высвобождением энергии.
Посмотрим,
что получится, если мы приложим к чему-то «косое» напряжение. Под косым, или
скалывающим, напряжением мы подразумеваем такое воздействие, как показано на
фиг. 38.4. В качестве предварительной задачи посмотрим, какова будет деформация
кубика под действием сил, показанных на фиг. 38.5. Снова можно разделить эту
задачу на две: вертикальное давление и горизонтальное растяжение. Обозначая
через ![]() площадь
грани кубика, мы получаем для изменения горизонтальной длины
площадь
грани кубика, мы получаем для изменения горизонтальной длины
![]() . (38.11)
. (38.11)

Фиг. 38.4. Однородный сдвиг.

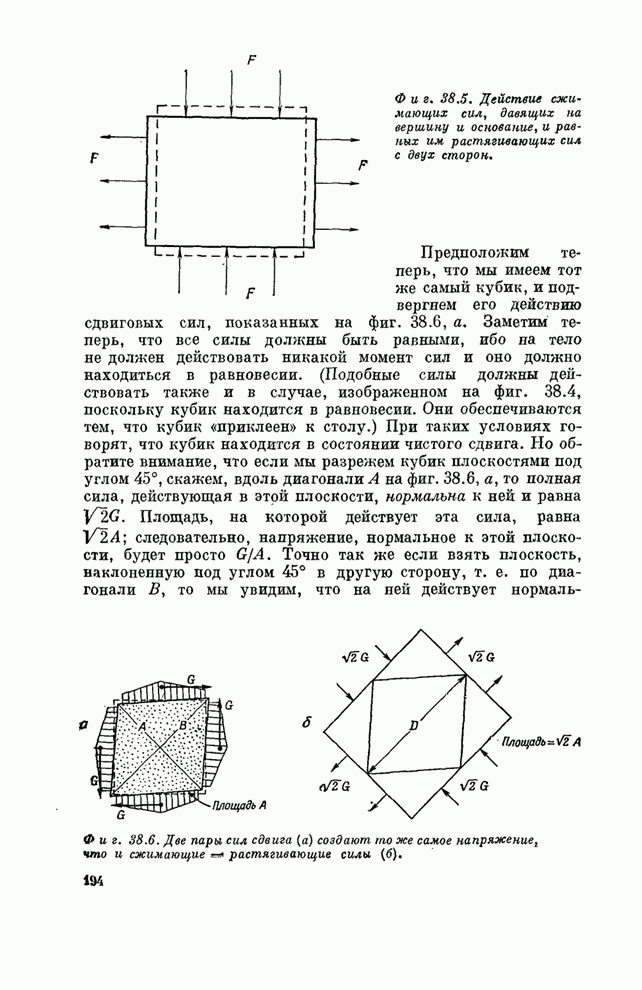
Фиг. 38.5. Действие сжимающих сил, давящих на вершину и основание, и равных им растягивающих сил с двух сторон.
Изменение же высоты по вертикали равно просто тому же выражению с обратным знаком.
Предположим
теперь, что мы имеем тот же самый кубик, и подвергнем его действию сдвиговых
сил, показанных на фиг. 38.6,а. Заметим теперь, что все силы должны быть
равными, ибо на тело не должен действовать никакой момент сил и оно должно
находиться в равновесии. (Подобные силы должны действовать также и в случае,
изображенном на фиг. 38.4, поскольку кубик находится в равновесии. Они обеспечиваются
тем, что кубик «приклеен» к столу.) При таких условиях говорят, что кубик
находится в состоянии чистого сдвига. Но обратите внимание, что если мы
разрежем кубик плоскостями под углом 45°, скажем, вдоль диагонали ![]() на фиг. 38.6,а,
то полная сила, действующая в этой плоскости, нормальна к ней и равна
на фиг. 38.6,а,
то полная сила, действующая в этой плоскости, нормальна к ней и равна ![]() . Площадь, на
которой действует эта сила, равна
. Площадь, на
которой действует эта сила, равна ![]() ; следовательно, напряжение,
нормальное к этой плоскости, будет просто
; следовательно, напряжение,
нормальное к этой плоскости, будет просто ![]() . Точно так же если взять плоскость,
наклоненную под углом 45° в другую сторону, т. е. по диагонали
. Точно так же если взять плоскость,
наклоненную под углом 45° в другую сторону, т. е. по диагонали ![]() , то мы увидим,
что на ней действует нормальное сдавливающее напряжение, равное
, то мы увидим,
что на ней действует нормальное сдавливающее напряжение, равное ![]() . Из этого ясно,
что напряжение при «чистом сжатии» эквивалентно комбинации растягивающего и
сжимающего напряжений, направленных под прямым углом друг к другу и под углом
45° к первоначальным граням кубика. Внутренние напряжения и деформации будут такими
же, как и в большом кубике материала под действием сил, показанных на фиг.
38.6,б. Но эту задачу мы уже решили. Изменение длины диагонали задается
уравнением (38.10):
. Из этого ясно,
что напряжение при «чистом сжатии» эквивалентно комбинации растягивающего и
сжимающего напряжений, направленных под прямым углом друг к другу и под углом
45° к первоначальным граням кубика. Внутренние напряжения и деформации будут такими
же, как и в большом кубике материала под действием сил, показанных на фиг.
38.6,б. Но эту задачу мы уже решили. Изменение длины диагонали задается
уравнением (38.10):
![]() . (38.11)
. (38.11)
(Одна диагональ сокращается, а другая удлиняется.)

Фиг. 38.6. Две пары сил сдвига (а) создают то же самое напряжение, что и сжимающие - растягивающие силы (б).
Часто
деформацию сдвига удобно описывать с помощью угла «искажения» кубика ![]() , показанного на
фиг. 38.7. Из геометрии фигуры вы видите, что горизонтальный сдвиг
, показанного на
фиг. 38.7. Из геометрии фигуры вы видите, что горизонтальный сдвиг ![]() верхнего края
равен
верхнего края
равен ![]() ,
так что
,
так что
![]() . (38.12)
. (38.12)
Напряжение
сдвига ![]() определяется
как отношение тангенциальной силы, действующей на грань, к площади грани
определяется
как отношение тангенциальной силы, действующей на грань, к площади грани ![]() . Воспользовавшись
уравнением (38.11), мы из (38.12) получаем
. Воспользовавшись
уравнением (38.11), мы из (38.12) получаем
![]() .
.

Фиг. 38.7. Напряжение сдвига ![]() равно
равно ![]() .
.
Или, если написать это в форме
![]() (38.13)
(38.13)
Коэффициент
пропорциональности ![]() называется модулем сдвига (или
иногда коэффициентом жесткости). Вот как он выражается через
называется модулем сдвига (или
иногда коэффициентом жесткости). Вот как он выражается через ![]() и
и ![]() :
:
![]() . (38.14)
. (38.14)
Кстати,
модуль сдвига должен быть положительным, иначе мы бы могли получить энергию от
самопроизвольного сдвига кубика. Из уравнения (38.14) очевидно, что постоянная ![]() должна быть
больше
должна быть
больше ![]() .
Теперь мы знаем, что
.
Теперь мы знаем, что ![]() заключена между
заключена между ![]() и 1/2, но на практике,
однако, она всегда больше нуля. В качестве последнего примера состояний
подобного типа, когда напряженность постоянна по всему материалу, давайте
рассмотрим задачу о бруске, который растягивается и в то же время закреплен
таким образом, что боковое сокращение невозможно. (Технически немного легче
сжимать брусок и сдерживать бока его от «распирания», но в сущности - это та же
самая задача.) Что при этом происходит? На брусок должны действовать боковые
силы, которые препятствуют изменению его толщины, - силы, которых мы не знаем
непосредственно, но которые следует вычислить. Эта задача того же самого сорта,
что мы решали, но только с немного другой алгеброй. Представьте себе силы,
действующие на все три стороны, как это показано на фиг. 38.8. Мы вычислим
изменение размеров и подберем такие поперечные силы, чтобы ширина и высота
оставались постоянными. Следуя обычным рассуждениям, мы получаем для трех
напряжений
и 1/2, но на практике,
однако, она всегда больше нуля. В качестве последнего примера состояний
подобного типа, когда напряженность постоянна по всему материалу, давайте
рассмотрим задачу о бруске, который растягивается и в то же время закреплен
таким образом, что боковое сокращение невозможно. (Технически немного легче
сжимать брусок и сдерживать бока его от «распирания», но в сущности - это та же
самая задача.) Что при этом происходит? На брусок должны действовать боковые
силы, которые препятствуют изменению его толщины, - силы, которых мы не знаем
непосредственно, но которые следует вычислить. Эта задача того же самого сорта,
что мы решали, но только с немного другой алгеброй. Представьте себе силы,
действующие на все три стороны, как это показано на фиг. 38.8. Мы вычислим
изменение размеров и подберем такие поперечные силы, чтобы ширина и высота
оставались постоянными. Следуя обычным рассуждениям, мы получаем для трех
напряжений
 , (38.15)
, (38.15)
 , (38.16)
, (38.16)
 . (38.17)
. (38.17)

Фиг. 38.8. Растяжение без сокращения бокового размера.
Но
поскольку по условию ![]() и
и ![]() равны нулю, то уравнения (38.16) и
(38.17) дают два соотношения, связывающие
равны нулю, то уравнения (38.16) и
(38.17) дают два соотношения, связывающие ![]() и
и ![]() с
с ![]() . Совместно решая их, найдем
. Совместно решая их, найдем
 , (38.18)
, (38.18)
а подставляя (38.18) в (38.15), получаем
 . (38.19)
. (38.19)
Это
соотношение вы часто можете встретить «перевернутым» и с преобразованным
квадратичным полиномом по ![]() , т. е.
, т. е.
![]() . (38.20)
. (38.20)
Когда
вы удерживаете бока, модуль Юнга умножается на некоторую сложную функцию ![]() . Из уравнения
(38.19) можно сразу же увидеть, что множитель перед
. Из уравнения
(38.19) можно сразу же увидеть, что множитель перед ![]() всегда больше единицы.
Растянуть брусок, когда его бока удерживаются, гораздо труднее. Это означает
также, что брусок становится жестче, когда его боковые стороны закреплены,
нежели когда они свободны.
всегда больше единицы.
Растянуть брусок, когда его бока удерживаются, гораздо труднее. Это означает
также, что брусок становится жестче, когда его боковые стороны закреплены,
нежели когда они свободны.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
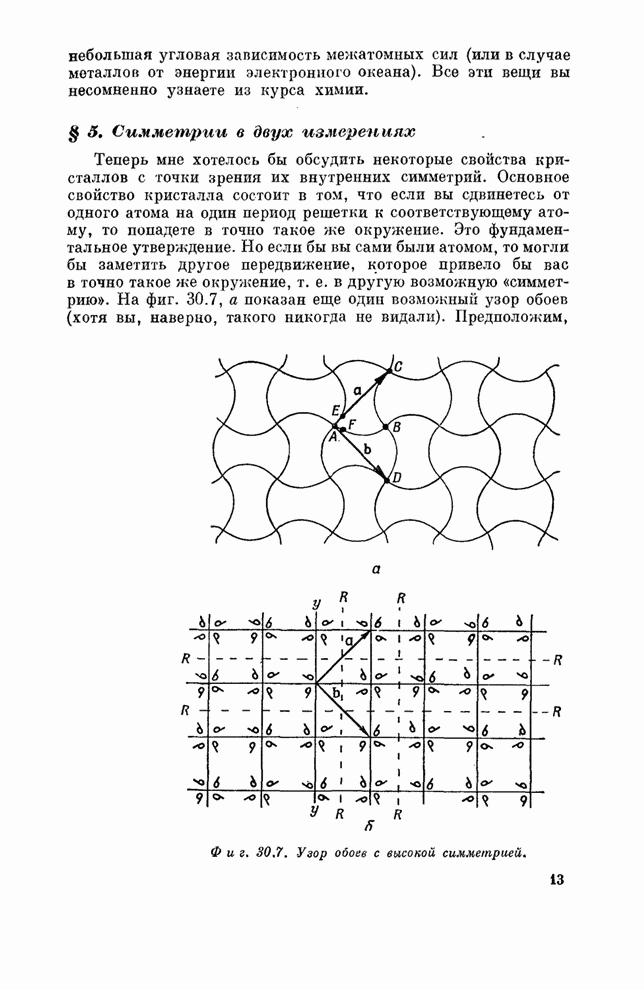
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
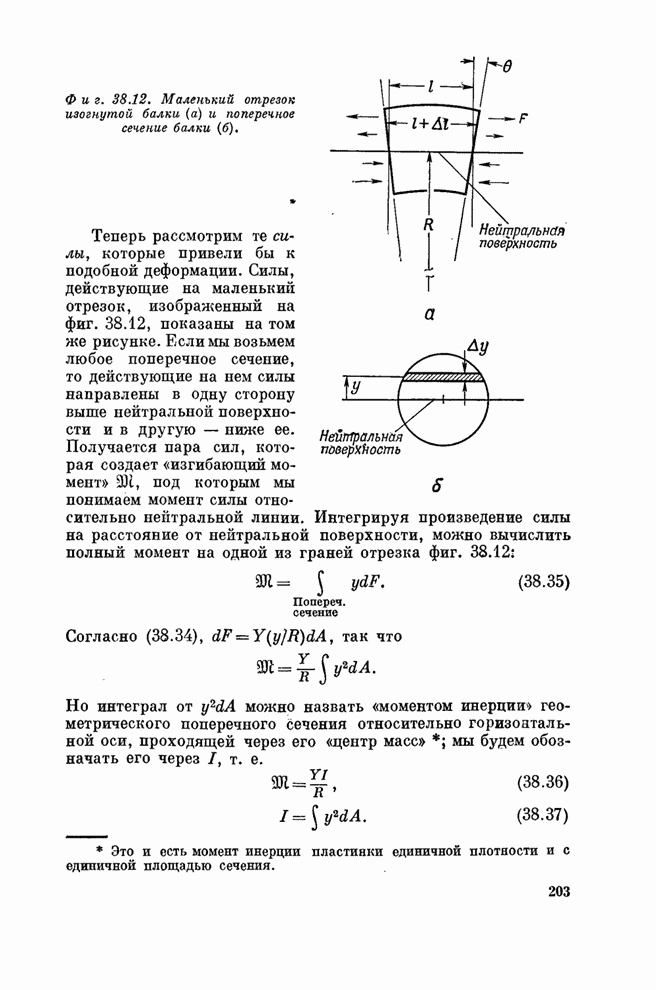
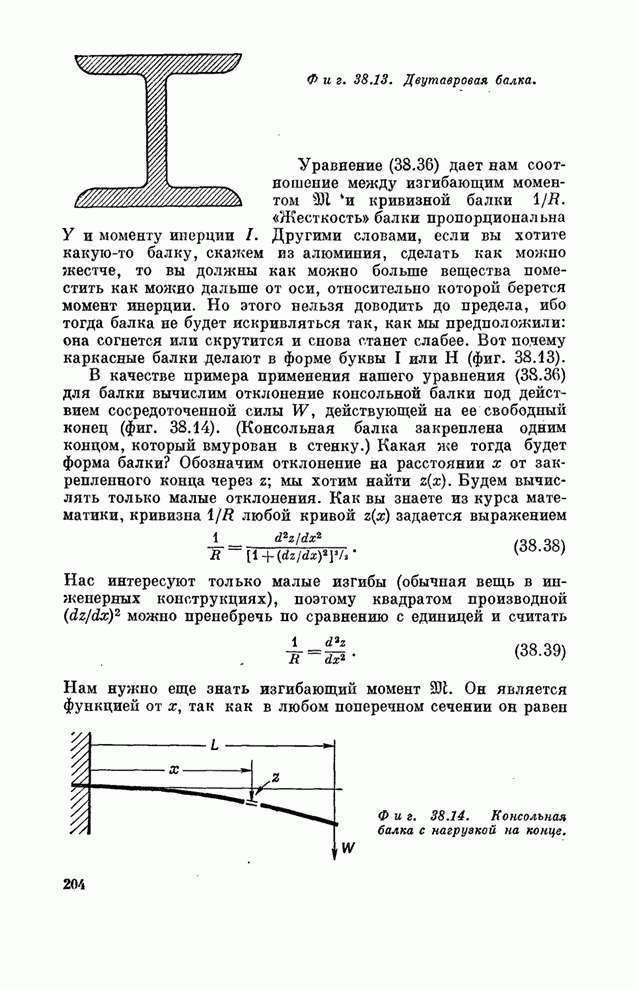
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
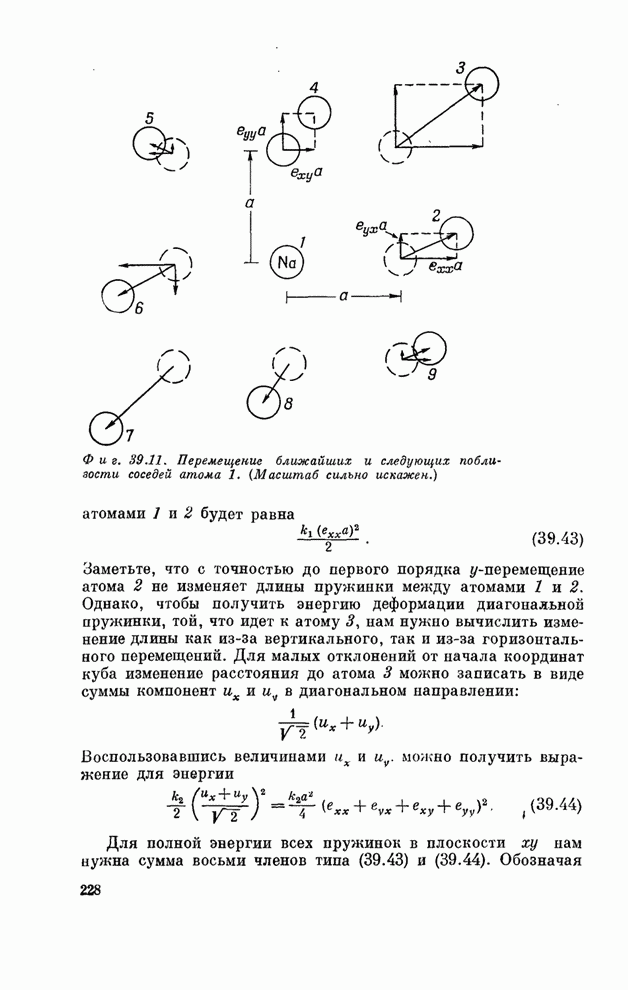
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)