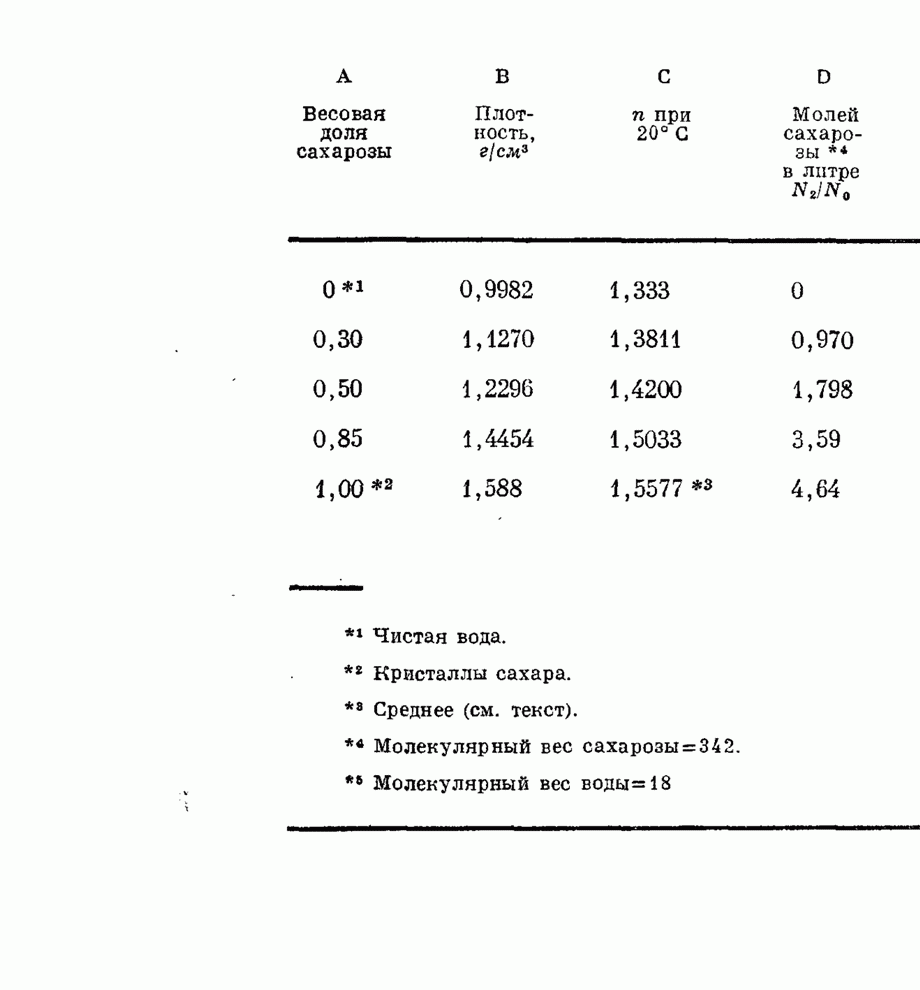
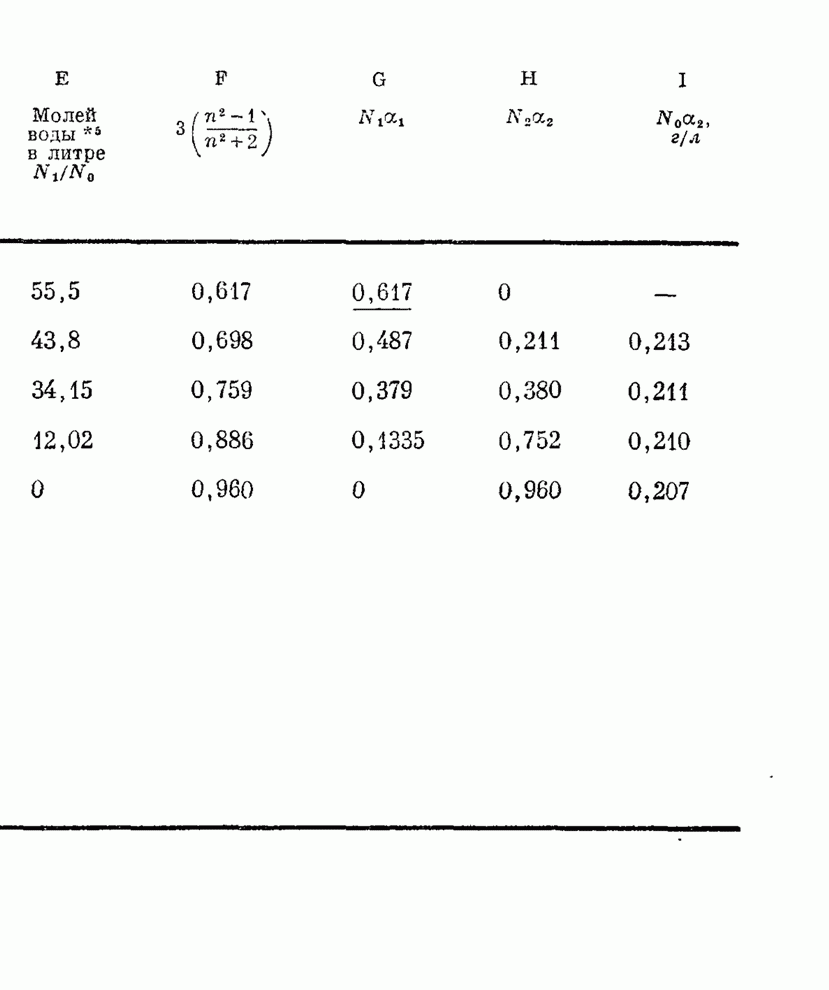
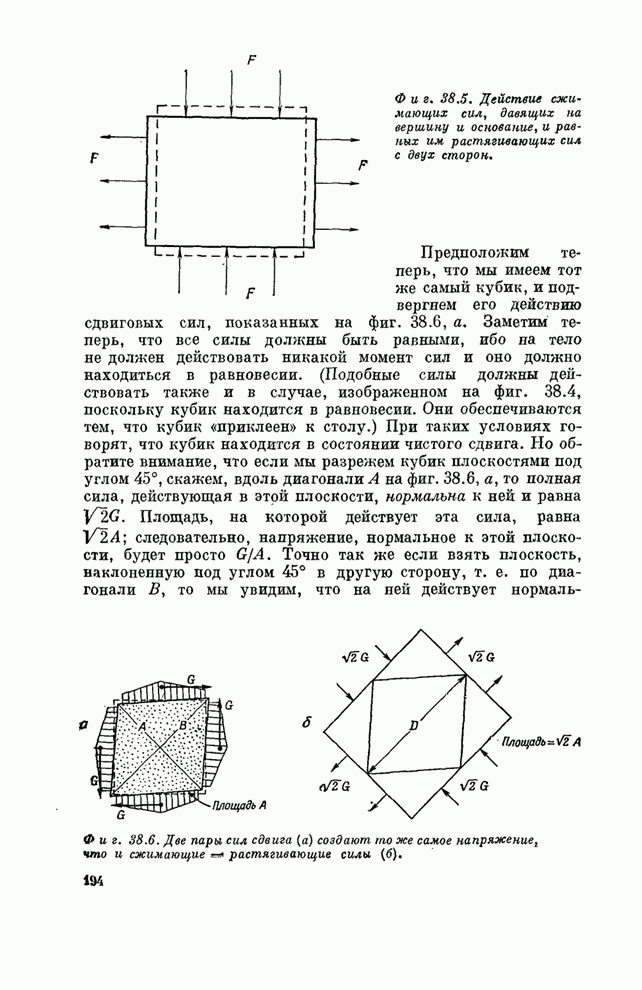
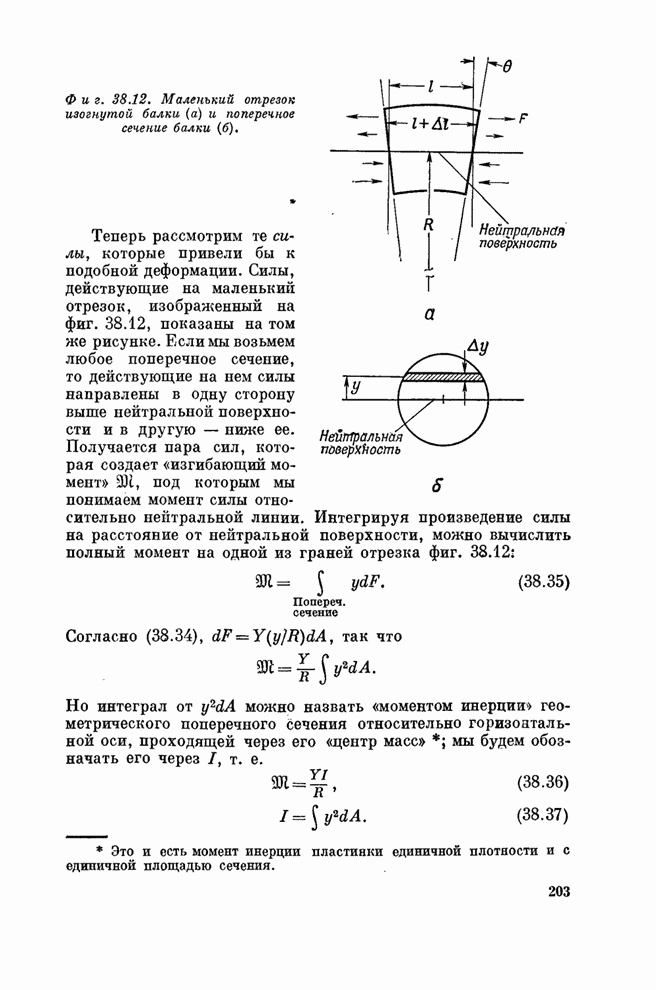
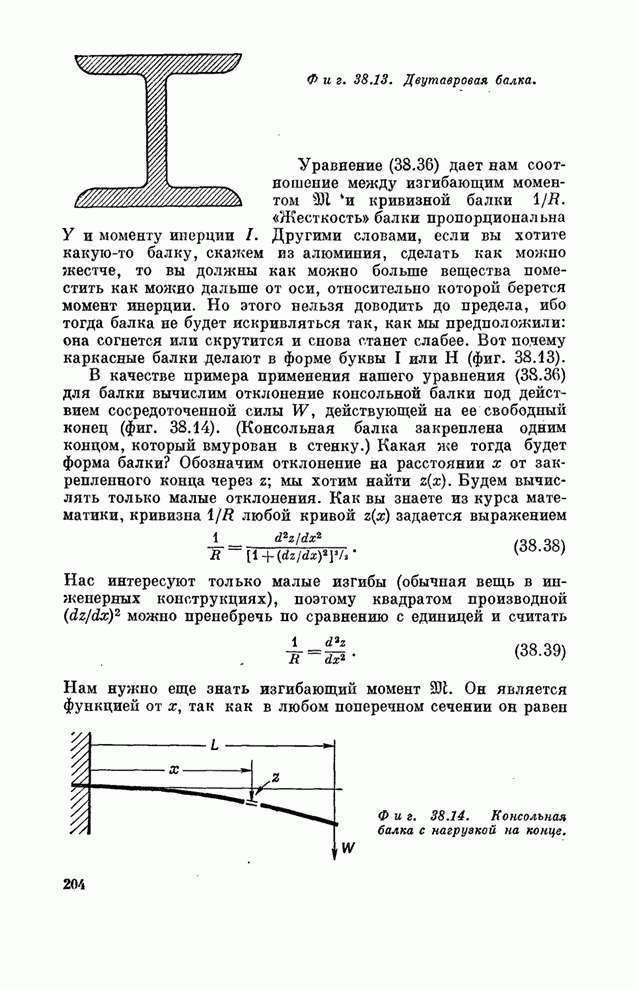
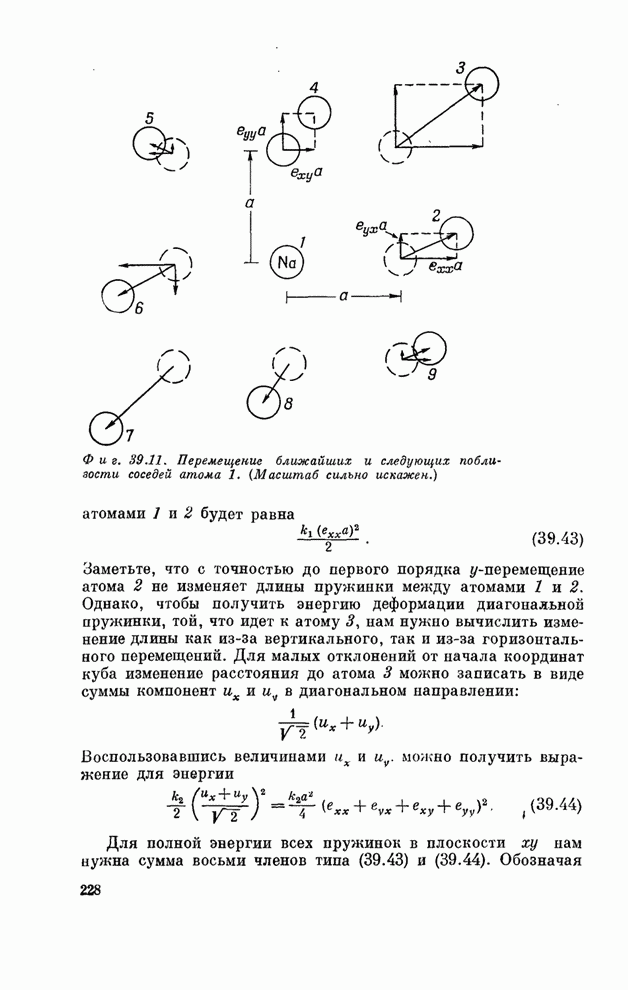
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Число Рейнольдса
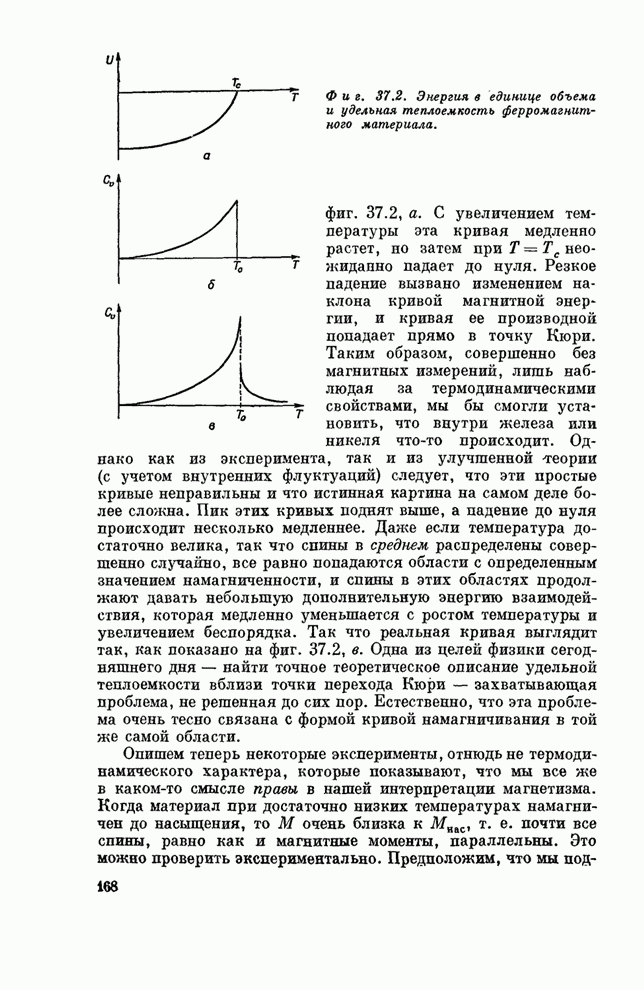
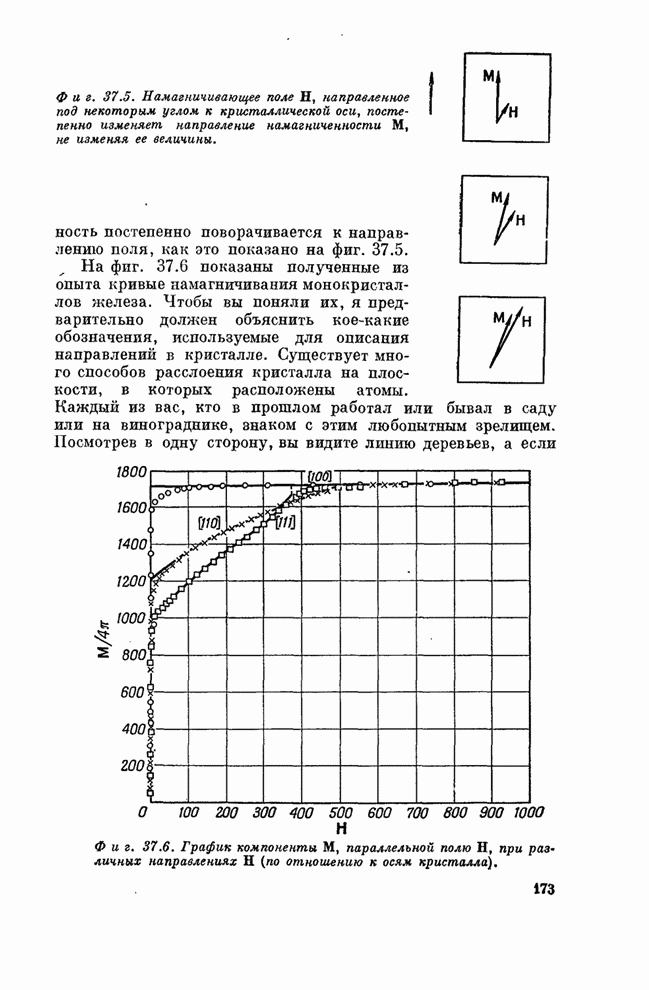
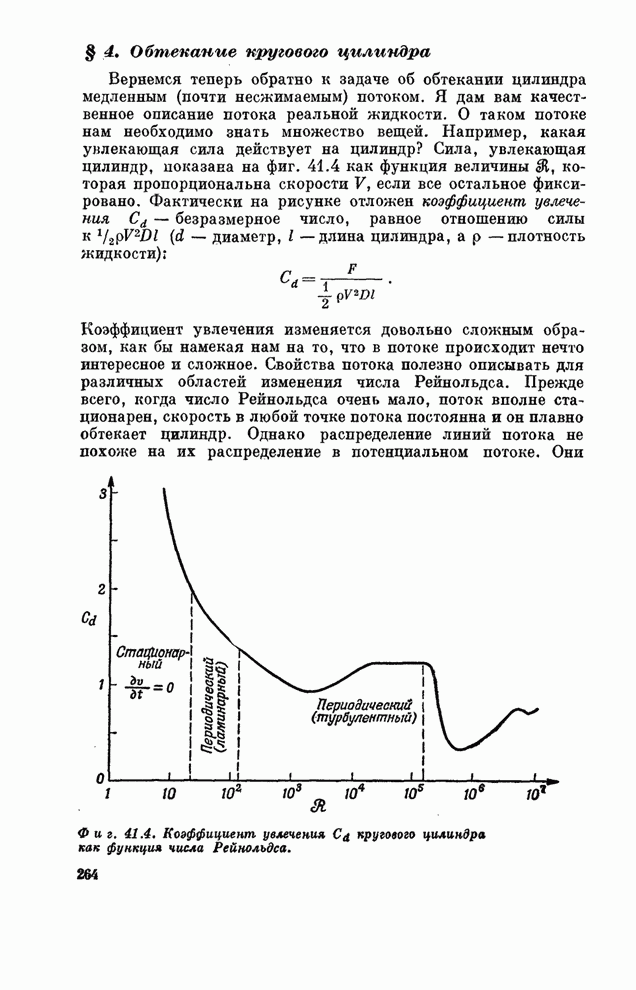
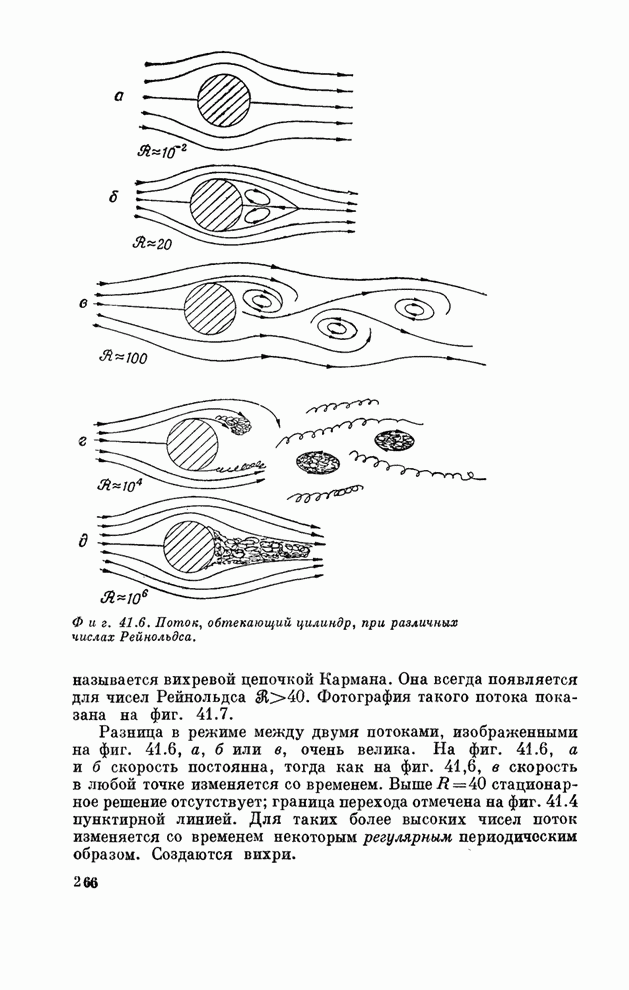
Посмотрим теперь, - как изменяется течение жидкости из-за нового члена с вязкостью. Рассмотрим несколько подробнее две задачи. Первая - обтекание жидкостью цилиндра; эту задачу мы пытались решить в предыдущей главе, используя теорию невязкой жидкости. Оказывается, что сегодня возможно найти решение вязких уравнений только для некоторых специальных случаев. Так что кое-что из того, что я расскажу вам, основано на экспериментальных измерениях, считая, конечно, что экспериментальная модель удовлетворяла уравнению (41.17).
Математически
задача состоит в следующем: мы хотим найти решение для потока несжимаемой
вязкой жидкости вблизи длинного цилиндра диаметром ![]() . Поток должен определяться
уравнением (41.17) и
. Поток должен определяться
уравнением (41.17) и
![]() (41.18)
(41.18)
с
условием, что скорость на больших расстояниях равна некоторой постоянной ![]() (параллельной оси
(параллельной оси
![]() ), а на
поверхности цилиндра равна нулю. Так что
), а на
поверхности цилиндра равна нулю. Так что
![]() (41.19)
(41.19)
при
![]() .
.
Это полностью определяет математическую задачу.
Если
вы вглядитесь в эти выражения, то увидите, что в задаче есть четыре различных
параметра: ![]() ,
,
![]() ,
, ![]() и
и ![]() . Можно подумать,
что нам придется иметь дело с целой серией решений для разных
. Можно подумать,
что нам придется иметь дело с целой серией решений для разных ![]() , разных
, разных ![]() и т. д. Вовсе
нет. Все возможные различные решения соответствуют разным значениям одного
параметра. Такова наиболее важная общая вещь, которую мы можем сказать о вязком
потоке. А чтобы понять, почему это так, заметьте сначала, что вязкость и
плотность появляются в виде отношения
и т. д. Вовсе
нет. Все возможные различные решения соответствуют разным значениям одного
параметра. Такова наиболее важная общая вещь, которую мы можем сказать о вязком
потоке. А чтобы понять, почему это так, заметьте сначала, что вязкость и
плотность появляются в виде отношения ![]() , т. е. удельной вязкости. Это
уменьшает число независимых параметров до трех. Предположим теперь, что все
расстояния мы измеряем в единицах той единственной длины, которая появляется в
задаче: диаметра цилиндра
, т. е. удельной вязкости. Это
уменьшает число независимых параметров до трех. Предположим теперь, что все
расстояния мы измеряем в единицах той единственной длины, которая появляется в
задаче: диаметра цилиндра ![]() , т. е. вместо
, т. е. вместо ![]() ,
, ![]() ,
, ![]() мы вводим новые переменные
мы вводим новые переменные
![]() ,
, ![]() ,
, ![]() , причем
, причем
![]() .
.
При
этом параметр ![]() из
(41.19) исчезает. Точно так же если будем измерять все скорости в единицах
из
(41.19) исчезает. Точно так же если будем измерять все скорости в единицах ![]() , т. е. если мы
положим
, т. е. если мы
положим ![]() ,
то избавимся от
,
то избавимся от ![]() ,
a
,
a ![]() на
больших расстояниях будет просто равно единице. Поскольку мы фиксировали наши
единицы длины и скорости, то единицей времени теперь должно быть
на
больших расстояниях будет просто равно единице. Поскольку мы фиксировали наши
единицы длины и скорости, то единицей времени теперь должно быть ![]() , так что мы
должны сделать подстановку:
, так что мы
должны сделать подстановку:
![]() . (41.20)
. (41.20)
В
наших новых переменных производные в уравнении (41.18) тоже изменятся: так, ![]() перейдет в
перейдет в ![]() и т. д., так что
уравнение (41.18) превратится в
и т. д., так что
уравнение (41.18) превратится в
![]() . (41.21)
. (41.21)
А наше основное уравнение (41.17) перейдет в
![]() .
.
Все
постоянные при этом собираются в один множитель, который мы, следуя традиции,
обозначим через ![]() :
:
![]() . (41.22)
. (41.22)
Если теперь мы просто запомним, что все наши уравнения должны выписываться для величин, измеряемых в новых единицах, то все штрихи можно опустить. Тогда уравнения для потока примут вид
![]() (41.23)
(41.23)
и
![]() ,
,
с условиями
![]()
для
![]() (41.24)
(41.24)
и
![]()
для
![]() .
.
Что
все это значит? Если, например, мы решили задачу для потока с одной скоростью ![]() и некоторого
цилиндра диаметром
и некоторого
цилиндра диаметром ![]() , а затем интересуемся обтеканием
цилиндра другого диаметра
, а затем интересуемся обтеканием
цилиндра другого диаметра ![]() другой жидкостью, то поток будет
одним и тем же при такой скорости
другой жидкостью, то поток будет
одним и тем же при такой скорости ![]() , которая отвечает тому же самому
числу Рейнольдса, т. е. когда
, которая отвечает тому же самому
числу Рейнольдса, т. е. когда
![]() . (41.25)
. (41.25)
В
любых случаях, когда числа Рейнольдса одинаковы, поток при выборе надлежащего
масштаба ![]() ,
,
![]() ,
, ![]() и
и ![]() будет «выглядеть»
одинаково. Это очень важное утверждение, ибо оно означает, что мы можем
определить поведение потока воздуха при обтекании крыла самолета, не строя
самого самолета и не испытывая его. Вместо этого мы можем сделать модель и
провести измерения, используя скорость, которая дает то же самое число
Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений
над маленькой моделью самолета в аэродинамической трубе или результаты,
полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это
можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В
противном случае войдет новая величина - скорость звука. При этом различные
модели будут действительно соответствовать друг другу только тогда, когда отношение
будет «выглядеть»
одинаково. Это очень важное утверждение, ибо оно означает, что мы можем
определить поведение потока воздуха при обтекании крыла самолета, не строя
самого самолета и не испытывая его. Вместо этого мы можем сделать модель и
провести измерения, используя скорость, которая дает то же самое число
Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений
над маленькой моделью самолета в аэродинамической трубе или результаты,
полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это
можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В
противном случае войдет новая величина - скорость звука. При этом различные
модели будут действительно соответствовать друг другу только тогда, когда отношение
![]() к
скорости звука тоже приблизительно одинаково. Отношение скорости
к
скорости звука тоже приблизительно одинаково. Отношение скорости ![]() к скорости звука
называется числом Маха. Таким образом, для скоростей, близких к скорости звука
или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха
и число Рейнольдса в обеих ситуациях одинаковы.
к скорости звука
называется числом Маха. Таким образом, для скоростей, близких к скорости звука
или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха
и число Рейнольдса в обеих ситуациях одинаковы.
| << Предыдущий параграф | Следующий параграф >> |
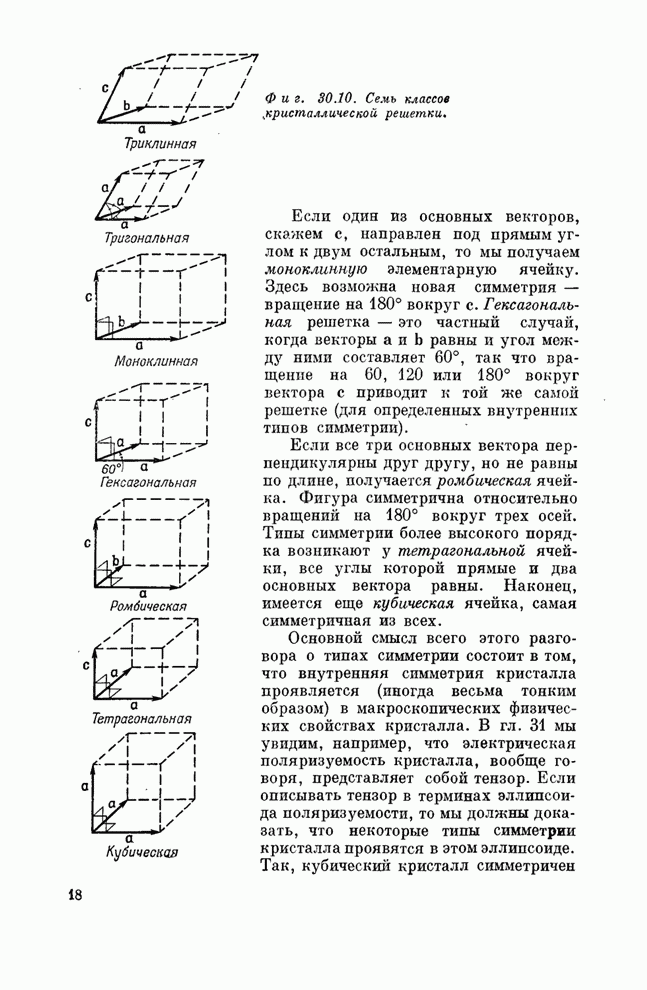
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
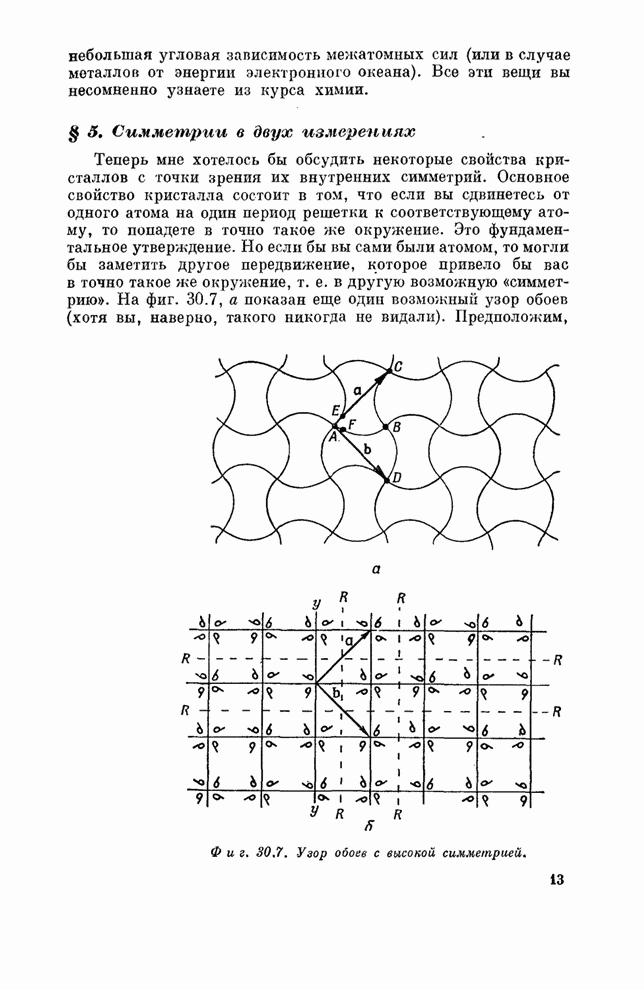
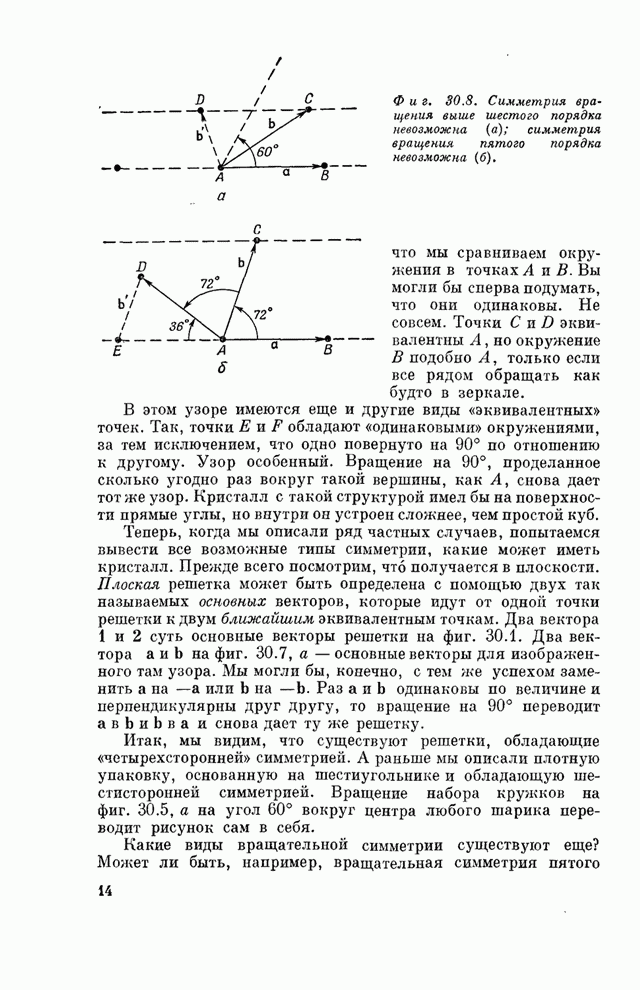
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
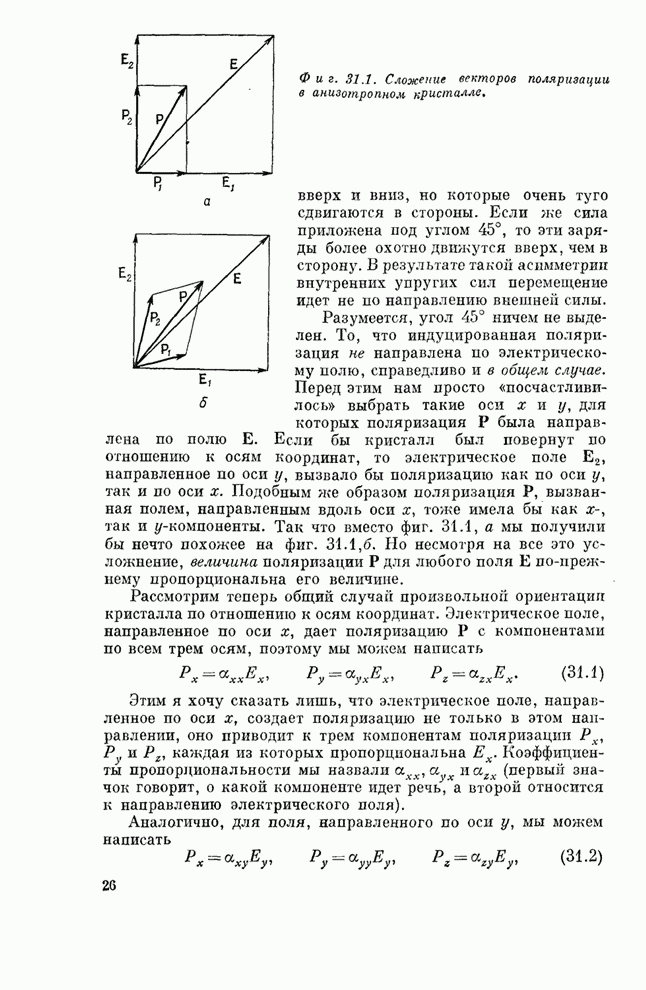
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
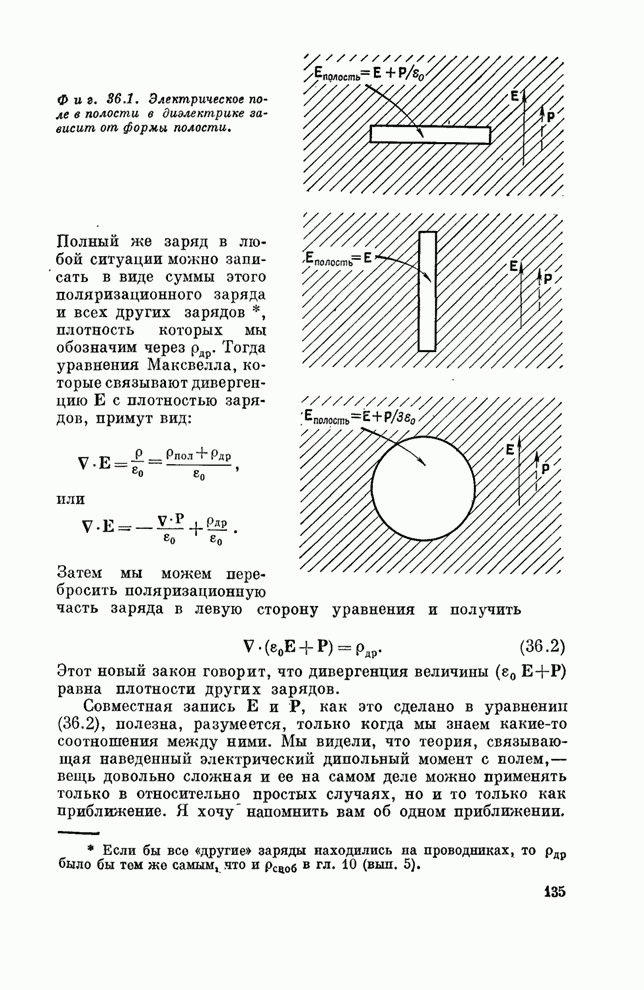
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
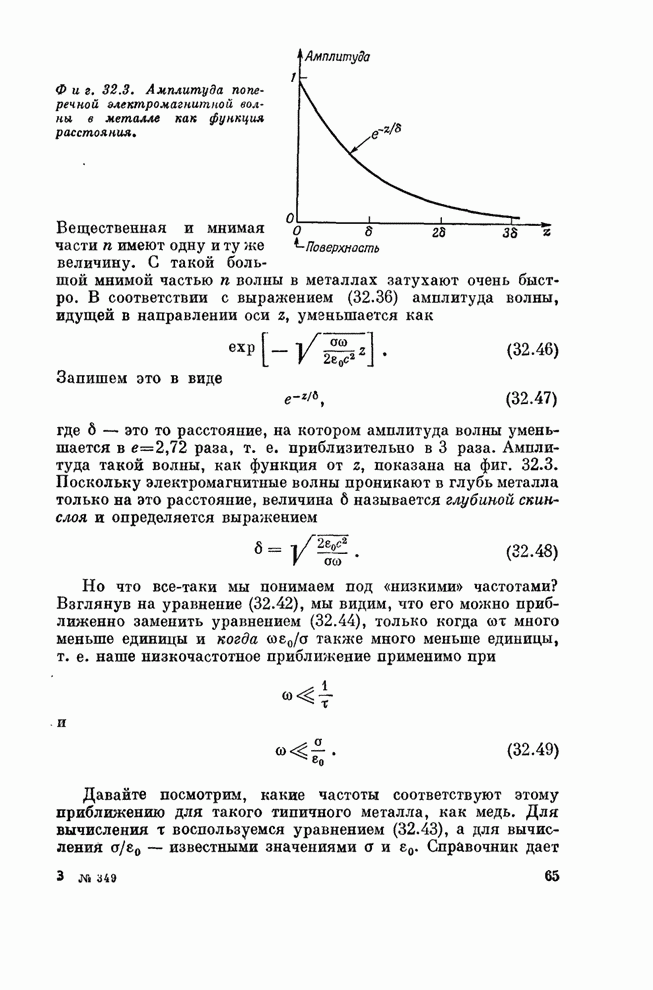
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
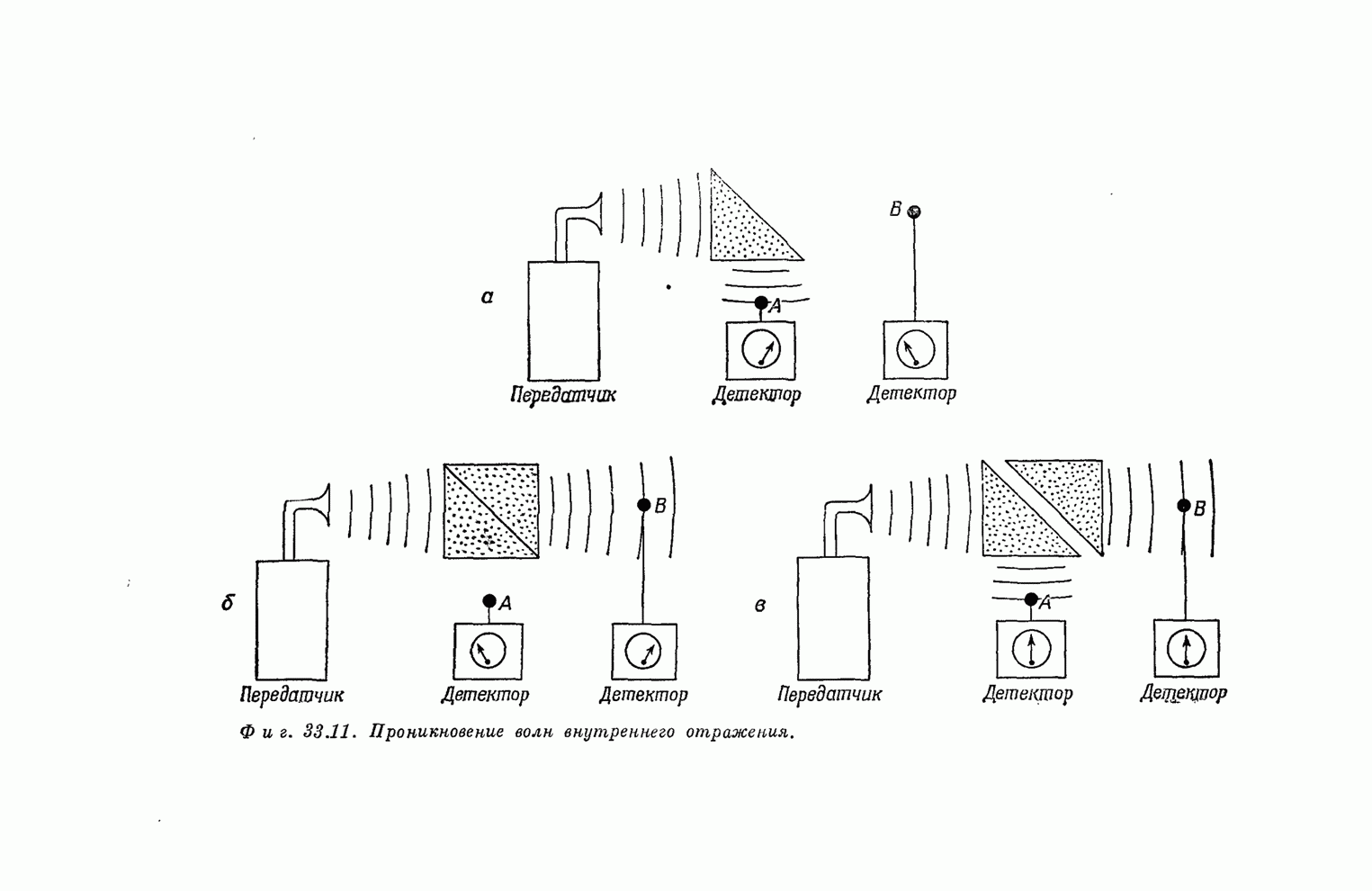
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
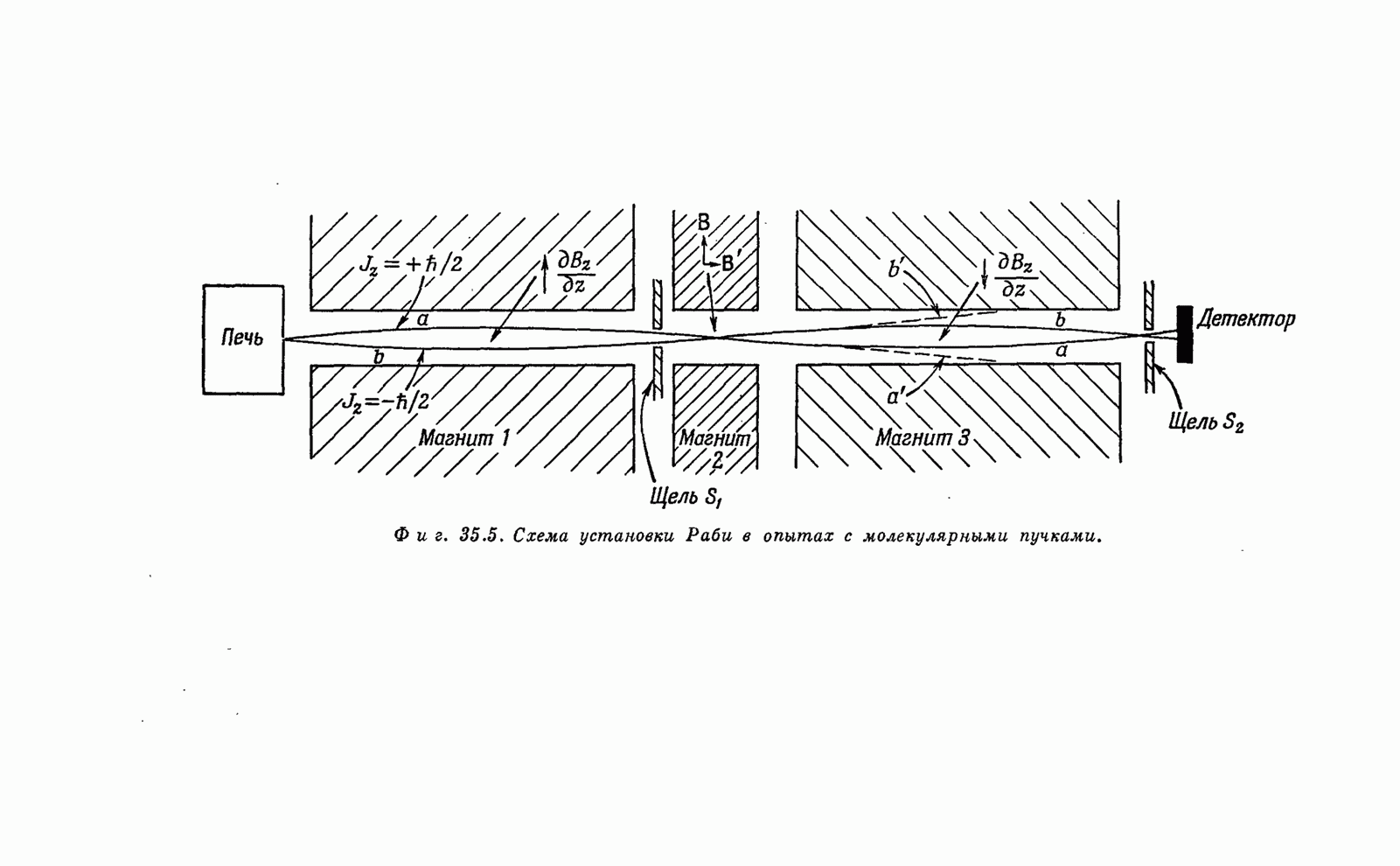
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
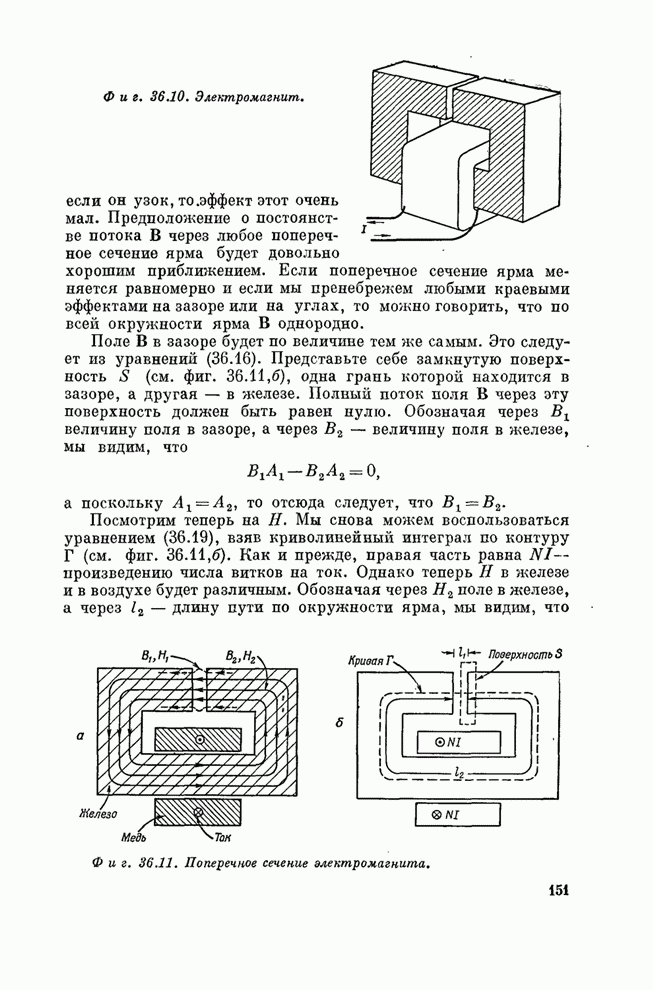
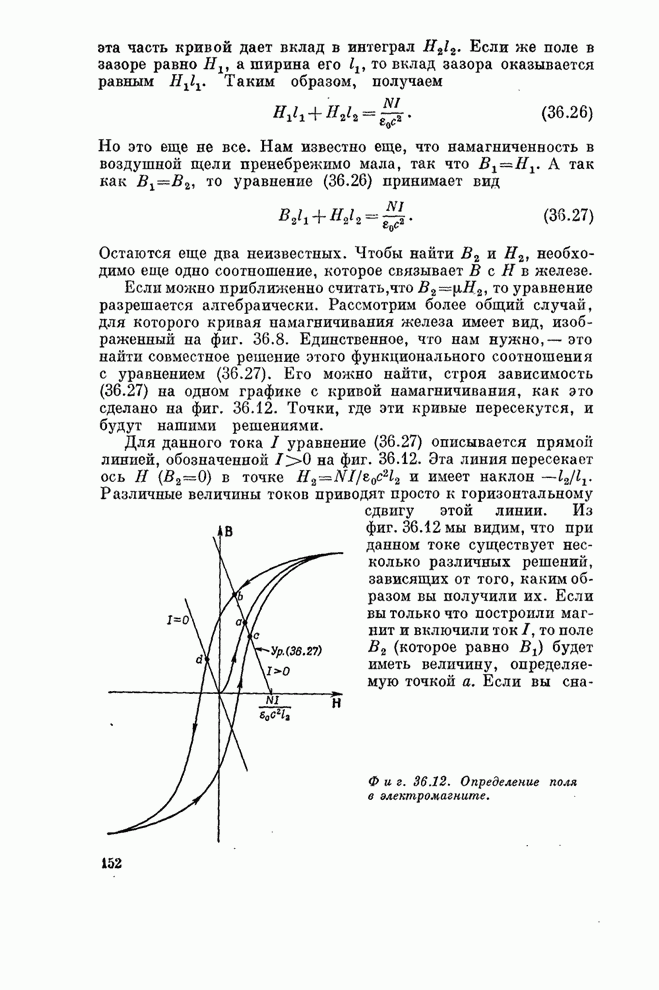
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
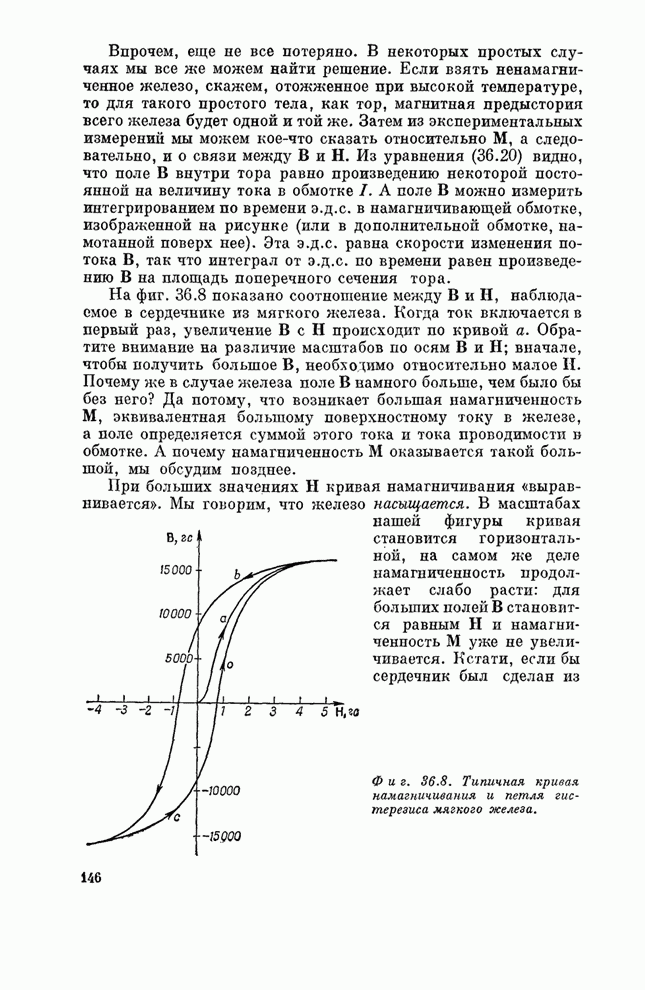
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
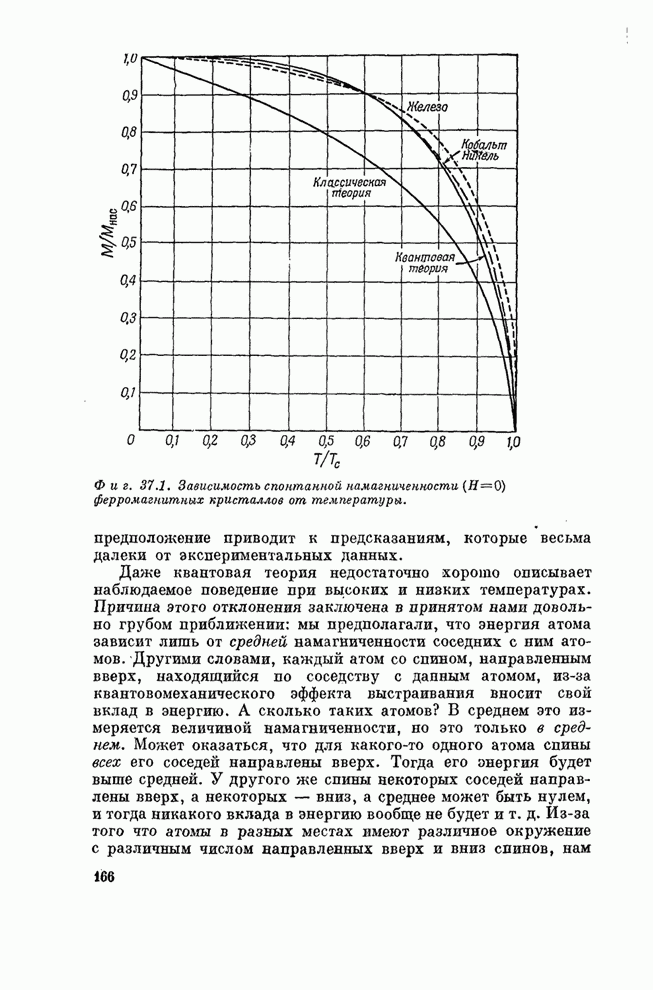
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
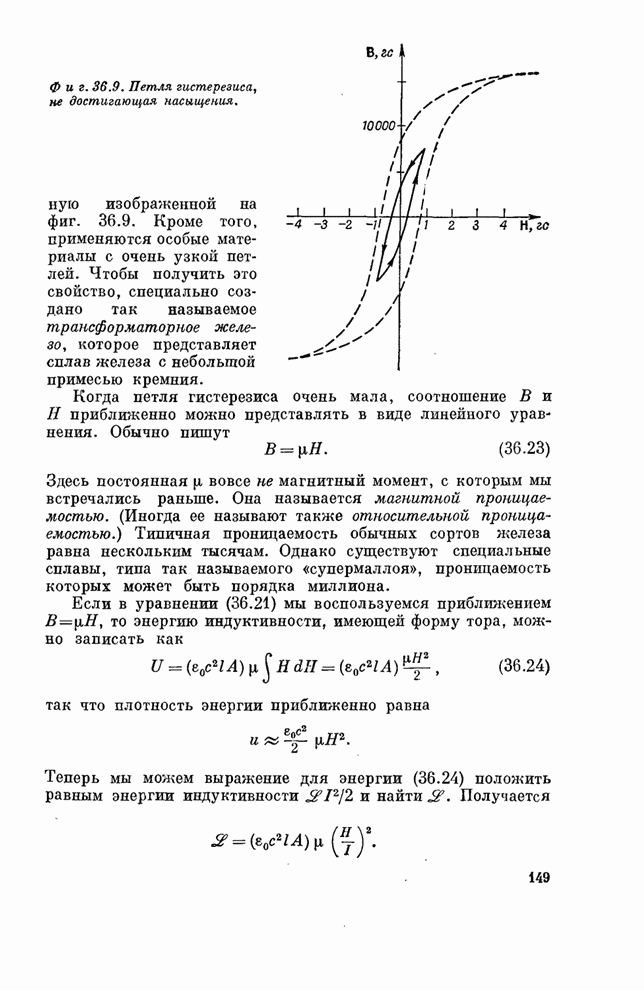
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)