| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 3. Волны в диэлектрике
Теперь
нам предстоит выяснить, какого сорта электромагнитные волны могут существовать
в диэлектрическом веществе, где других зарядов, кроме тех, что связаны в атомах,
нет. Таким образом, мы возьмем ![]() и
и ![]() . При этом уравнения Максвелла примут
такой вид:
. При этом уравнения Максвелла примут
такой вид:
 (32.19)
(32.19)
Мы можем решить эти уравнения, как делали это прежде. Начнем с применения к уравнению (32.19в) операции ротора:
![]() .
.
Используя затем векторное тождество
![]()
и
подставляя выражение для ![]() из (32.196), получаем
из (32.196), получаем
 .
.
Используя
уравнение (32.19а) для ![]() , находим
, находим
 . (32.20)
. (32.20)
Таким
образом, вместо волнового уравнения мы теперь получили, что даламбертиан ![]() равен двум
членам, содержащим поляризацию
равен двум
членам, содержащим поляризацию ![]() .
.
Однако
![]() зависит
от
зависит
от ![]() ,
поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем
ограничиваться изотропными диэлектриками, т. е.
,
поэтому уравнение (32.20) все еще допускает волновые решения. Сейчас мы будем
ограничиваться изотропными диэлектриками, т. е. ![]() всегда будет иметь то же
направление, что и
всегда будет иметь то же
направление, что и ![]() . Попробуем найти решение для волны,
движущейся в направлении оси
. Попробуем найти решение для волны,
движущейся в направлении оси ![]() . Электрическое поле при этом будет
изменяться как
. Электрическое поле при этом будет
изменяться как ![]() .
Предположим также, что волна поляризована в направлении оси
.
Предположим также, что волна поляризована в направлении оси ![]() , т. е. что электрическое
поле имеет только
, т. е. что электрическое
поле имеет только ![]() -компоненту. Все это записывается
следующим образом:
-компоненту. Все это записывается
следующим образом:
![]() . (32.21)
. (32.21)
Вы
знаете, что любая функция от ![]() представляет волну, бегущую со
скоростью
представляет волну, бегущую со
скоростью ![]() .
Показатель экспоненты в выражении (32.21) можно переписать в виде
.
Показатель экспоненты в выражении (32.21) можно переписать в виде
![]() ,
,
так что выражение (32.21) представляет волну, фазовая скорость которой равна
![]() .
.
В
гл. 31 (вып. 3) показатель преломления ![]() определялся нами из формулы
определялся нами из формулы
![]() .
.
С учетом этой формулы (32.21) приобретает вид
![]() .
.
Таким
образом, показатель ![]() можно определить, если мы найдем ту
величину
можно определить, если мы найдем ту
величину ![]() ,
которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим
уравнениям поля, и затем воспользуемся соотношением
,
которая необходима, чтобы выражение (32.21) удовлетворяло соответствующим
уравнениям поля, и затем воспользуемся соотношением
![]() . (32.22)
. (32.22)
В
изотропном материале поляризация будет иметь только ![]() -компоненту; кроме того,
-компоненту; кроме того, ![]() не изменяется с
изменением координаты
не изменяется с
изменением координаты ![]() , поэтому
, поэтому ![]() и мы сразу же избавляемся
от первого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш
диэлектрик «линейным», поэтому
и мы сразу же избавляемся
от первого члена в правой стороне уравнения (32.20). Вдобавок мы считаем наш
диэлектрик «линейным», поэтому ![]() будет изменяться как
будет изменяться как ![]() и
и ![]() . Лапласиан же в
уравнении (32.20) превращается просто в
. Лапласиан же в
уравнении (32.20) превращается просто в ![]() , так что в результате получаем
, так что в результате получаем
 . (32.23)
. (32.23)
Теперь
на минуту предположим, что раз ![]() изменяется синусоидально, то
изменяется синусоидально, то ![]() можно считать
пропорциональной
можно считать
пропорциональной ![]() , как в уравнении (32.5). (Позднее мы
вернемся к этому предположению и обсудим его.) Таким образом, пишем
, как в уравнении (32.5). (Позднее мы
вернемся к этому предположению и обсудим его.) Таким образом, пишем
![]() .
.
При
этом ![]() выпадает
из уравнения (32.23), и мы находим
выпадает
из уравнения (32.23), и мы находим
![]() . (32.24)
. (32.24)
Мы
получили, что волна вида (32.21) с волновым числом ![]() , задаваемым уравнением
(32.24), будет удовлетворять уравнениям поля. Использование же выражения
(32.22) для показателя
, задаваемым уравнением
(32.24), будет удовлетворять уравнениям поля. Использование же выражения
(32.22) для показателя ![]() дает
дает
![]() . (32.25)
. (32.25)
Сравним эту формулу с тем, что получилось у нас для показателя преломления газа (гл. 31, вып. 3).Там мы нашли уравнение (31.19), которое тогда имело вид
 . (32.26)
. (32.26)
Формула
(32.25) после подстановки ![]() из (32.6) дает
из (32.6) дает
 . (32.27)
. (32.27)
Что
здесь нового? Во-первых, появился новый член ![]() , возникший в результате учета
поглощения энергии в осцилляторах. Во-вторых, слева вместо
, возникший в результате учета
поглощения энергии в осцилляторах. Во-вторых, слева вместо ![]() теперь стоит
теперь стоит ![]() и, кроме того,
отсутствует дополнительный множитель 1/2. Но заметьте, что если значение
и, кроме того,
отсутствует дополнительный множитель 1/2. Но заметьте, что если значение ![]() достаточно мало,
так что
достаточно мало,
так что ![]() близок
к единице (как это имеет место в газе), то выражение (32.27) говорит, что
близок
к единице (как это имеет место в газе), то выражение (32.27) говорит, что ![]() равен единице
плюс некое малое число, т. е.
равен единице
плюс некое малое число, т. е. ![]() . При этом условии мы можем написать,
что
. При этом условии мы можем написать,
что ![]() , и
оба выражения оказываются эквивалентными. Таким образом, наш новый метод дает
для газа тот же самый, найденный нами ранее результат.
, и
оба выражения оказываются эквивалентными. Таким образом, наш новый метод дает
для газа тот же самый, найденный нами ранее результат.
Теперь
можно надеяться, что выражение (32.27) должно давать показатель преломления и
для плотных материалов. Но по некоторым причинам оно нуждается в модификации.
Во-первых, при выводе этого уравнения предполагалось, что поляризованное поле,
действующее на каждый из атомов, - это поле ![]() . Однако такое предположение неверно,
поскольку в плотном материале существуют и другие поля, создаваемые соседними
атомами, которые могут быть сравнимы с
. Однако такое предположение неверно,
поскольку в плотном материале существуют и другие поля, создаваемые соседними
атомами, которые могут быть сравнимы с ![]() . Аналогичную задачу мы уже
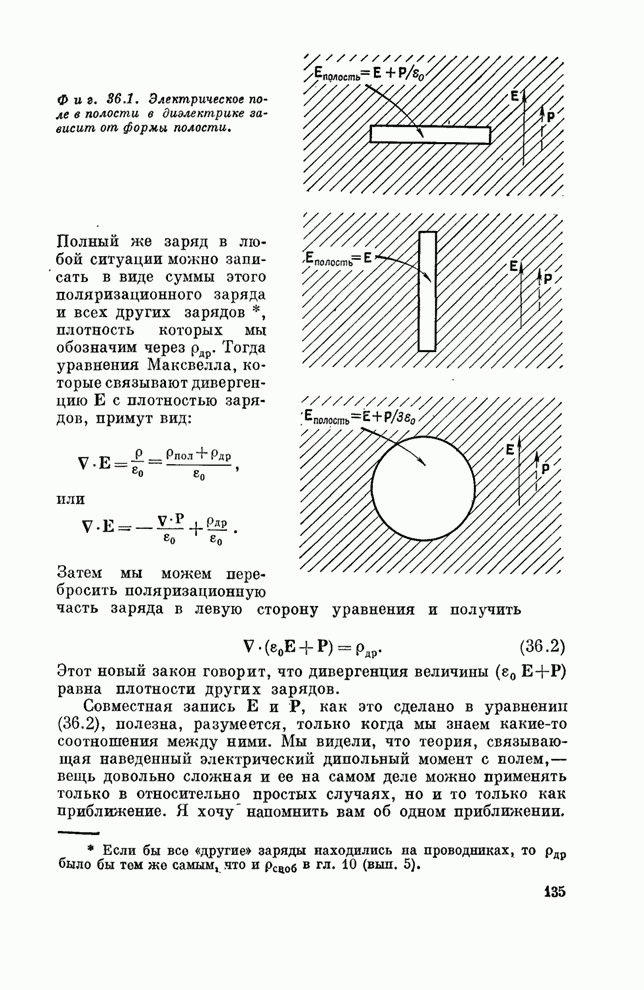
рассматривали при изучении статических полей в диэлектрике (см. гл. 11, вып.
5). Вы, вероятно, помните, что мы нашли поле, действующее на отдельный атом;
представив его сидящим в сферической полости в окружающем диэлектрике. Поле в
такой полости (мы назвали его локальным) увеличивается по сравнению со средним
полем
. Аналогичную задачу мы уже
рассматривали при изучении статических полей в диэлектрике (см. гл. 11, вып.
5). Вы, вероятно, помните, что мы нашли поле, действующее на отдельный атом;
представив его сидящим в сферической полости в окружающем диэлектрике. Поле в
такой полости (мы назвали его локальным) увеличивается по сравнению со средним
полем ![]() на
величину
на
величину ![]() .
(Не забудьте, однако, что этот результат, строго говоря, справедлив только для
изотропного материала, а также в случае кубического кристалла.)
.
(Не забудьте, однако, что этот результат, строго говоря, справедлив только для
изотропного материала, а также в случае кубического кристалла.)
Те же рассуждения верны и для электрического поля в волне, но до тех пор, пока длина ее много больше расстояния между атомами. При таком ограничении
![]() . (32.28)
. (32.28)
Именно
это локальное поле следует использовать вместо ![]() в (32.8), т. е. это выражение должно
быть переписано следующим образом:
в (32.8), т. е. это выражение должно
быть переписано следующим образом:
![]() . (32.29)
. (32.29)
Подставляя
теперь ![]() из
формулы (32.28), находим
из
формулы (32.28), находим
 ,
,
или
![]() . (32.30)
. (32.30)
Иными
словами, ![]() для
плотного материала все еще пропорциональна
для
плотного материала все еще пропорциональна ![]() (для синусоидального поля). Однако
константа пропорциональности будет уже
(для синусоидального поля). Однако
константа пропорциональности будет уже ![]() , а не
, а не ![]() , как раньше. Таким образом, нам
нужно поправить формулу (32.25):
, как раньше. Таким образом, нам
нужно поправить формулу (32.25):
![]() . (32.31)
. (32.31)
Более удобно переписать это в виде
![]() , (32.32)
, (32.32)
который алгебраически эквивалентен прежнему. Это и есть известная формула Клаузиуса-Моссотти.
В
плотном материале возникает и другое усложнение. Поскольку атомы расположены
слишком тесно, они сильно взаимодействуют друг с другом. Поэтому внутренние
гармоники осцилляции изменяются. Собственные частоты атомных осцилляций
размазываются этими взаимодействиями и обычно весьма сильно подавляются ими, а
коэффициент трения становится очень большим. Таким образом, все ![]() и
и ![]() твердого вещества
будут другими, чем для свободных атомов. С этой оговоркой мы все-таки можем
представлять
твердого вещества
будут другими, чем для свободных атомов. С этой оговоркой мы все-таки можем
представлять ![]() ,
по крайней мере приближенно, уравнением (32.7), так что
,
по крайней мере приближенно, уравнением (32.7), так что
 . (32.33)
. (32.33)
Наконец,
последнее усложнение. Если плотный материал представляет собой смесь нескольких
компонент, то каждая из них дает свой вклад в поляризацию. Полная ![]() будет суммой
вкладов различных компонент смеси [за исключением неточности приближения
локального поля в упорядоченных кристаллах, т. е. выражения (32.28) - эффекты,
которые мы обсуждали при разборе сегнетоэлектриков]. Обозначая через
будет суммой
вкладов различных компонент смеси [за исключением неточности приближения
локального поля в упорядоченных кристаллах, т. е. выражения (32.28) - эффекты,
которые мы обсуждали при разборе сегнетоэлектриков]. Обозначая через ![]() число атомов
каждой компоненты в единице объема, мы должны заменить формулу (32.32)
следующей:
число атомов
каждой компоненты в единице объема, мы должны заменить формулу (32.32)
следующей:
 , (32.34)
, (32.34)
где
каждая ![]() будет
определяться выражением типа (32.7). Выражение (32.34) завершает нашу теорию
показателя преломления. Величина
будет
определяться выражением типа (32.7). Выражение (32.34) завершает нашу теорию
показателя преломления. Величина ![]() задается комплексной функцией
частоты, каковой является средняя атомная поляризуемость
задается комплексной функцией
частоты, каковой является средняя атомная поляризуемость ![]() . Точное вычисление
. Точное вычисление ![]() (т. е. нахождение
(т. е. нахождение
![]() ,
, ![]() и
и ![]() ) для плотного
вещества - одна из труднейших задач квантовой механики. Это было сделано только
для нескольких особенно простых веществ.
) для плотного
вещества - одна из труднейших задач квантовой механики. Это было сделано только
для нескольких особенно простых веществ.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
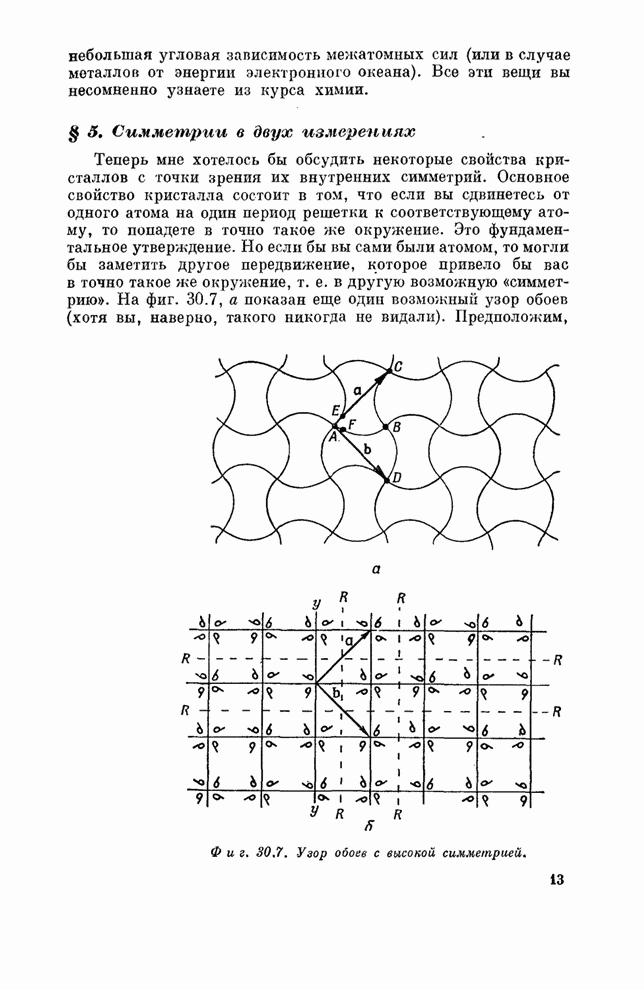
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
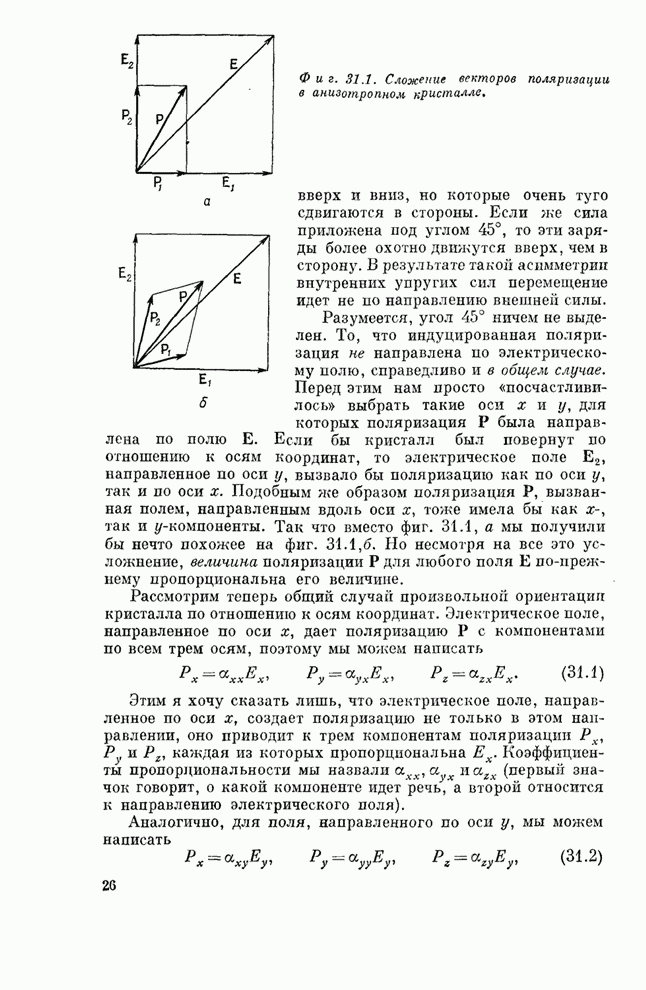
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)