| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Момент количества движения в квантовой механике
Я
уже приводил вам соотношение между магнитным моментом и моментом количества
движения. Очень хорошо. Но что означает магнитный момент и момент количества
движения в квантовой механике? Оказывается, что для полной уверенности в том,
что они означают в квантовой механике, лучше определять вещи, подобные
магнитному моменту, через другие понятия, такие, как энергия. Магнитный момент
легко определить через энергию, ибо энергия магнитного момента в магнитном поле
равна в классической теории ![]() . Следовательно, в квантовой механике
необходимо принять следующее определение. Если мы вычисляем энергию системы в
магнитном поле и видим, что она пропорциональна напряженности (для малых
полей), то коэффициент пропорциональности мы будем называть магнитным моментом
в направлении поля. (Нам сейчас в нашей работе не требуется особой элегантности
и мы можем продолжать думать о магнитном моменте в обычном, т. е. в каком-то
отношении классическом смысле.)
. Следовательно, в квантовой механике
необходимо принять следующее определение. Если мы вычисляем энергию системы в
магнитном поле и видим, что она пропорциональна напряженности (для малых
полей), то коэффициент пропорциональности мы будем называть магнитным моментом
в направлении поля. (Нам сейчас в нашей работе не требуется особой элегантности
и мы можем продолжать думать о магнитном моменте в обычном, т. е. в каком-то
отношении классическом смысле.)
Теперь мне бы хотелось обсудить понятие момента количества движения в квантовой механике, или, вернее, характеристики того, что в квантовой механике называется моментом количества движения. Видите ли, при переходе к законам нового рода нельзя предполагать, что каждое слово будет в точности означать то же, что и раньше. Подумав, вы можете сказать: «Постойте, а ведь я знаю, что такое момент количества движения. Это штука, которую измеряет момент силы». Но что такое момент силы? В квантовой механике у нас должно быть новое определение старых величин. Поэтому законно было бы назвать ее каким-то другим именем, вроде «углоквантового момента», или чем-то в этом духе, и уж это был бы момент количества движения «по-квантовомеханически». Однако если в квантовой механике мы можем найти величину, которая, когда система становится достаточно большой, идентична нашему старому понятию момента количества движения, то никакой пользы от изобретения новых слов нет. Ее тоже можно называть моментом количества движения. В этом понимании та странная вещь, которую мы собираемся описать, и есть момент количества движения. Это характеристика, в которой мы для больших систем узнаем момент количества движения классической механики.
Прежде всего возьмем систему с сохраняющимся моментом количества движения наподобие атома в пустом пространстве. Такая система (подобно Земле, вращающейся вокруг собственной оси) может крутиться вокруг любой оси, какую бы нам ни вздумалось выбрать. Для данной величины спина возможно много различных «состояний» с одной и той же энергией, причем каждое из них соответствует какому-то направлению оси момента количества движения. Таким образом, в классической механике с данным моментом количества движения связано бесконечное число возможных состояний с одной и той же энергией.
Однако
в квантовой механике, как оказывается, происходит несколько странных вещей.
Во-первых, число состояний, в которых может находиться такая система,
ограниченно – их можно перечислить. Для маленькой системы это число довольно
мало, но если система велика, конечное число становится очень и очень большим.
Во-вторых, мы не можем описывать «состояния» заданием направления момента
количества движения, а можем только задавать его компоненту в некотором
направлении, скажем в направлении оси ![]() . Классически объект с данным полным
моментом количества движения
. Классически объект с данным полным
моментом количества движения ![]() может в качестве
может в качестве ![]() -компоненты иметь любую
величину между
-компоненты иметь любую
величину между ![]() и
и
![]() . Но в
квантовой механике
. Но в
квантовой механике ![]() -компонента момента количества
движения может принимать только определенные дискретные значения. Любая данная
система, в частности атом или ядро или что-то другое, с заданной энергией имеет
характерное число
-компонента момента количества
движения может принимать только определенные дискретные значения. Любая данная
система, в частности атом или ядро или что-то другое, с заданной энергией имеет
характерное число ![]() , а ее
, а ее ![]() -компонента момента количества
движения может принимать только одно из значений:
-компонента момента количества
движения может принимать только одно из значений:
![]() . (34.23)
. (34.23)
Наибольшая
величина ![]() -компоненты
равна произведению
-компоненты
равна произведению ![]() на
на ![]() , следующая на
, следующая на ![]() меньше и т. д. до
меньше и т. д. до ![]() . Число
. Число ![]() называется
«спином системы». (Некоторые называют его «квантовым числом полного момента
количества движения», а мы будем называть его попросту «спином».)
называется
«спином системы». (Некоторые называют его «квантовым числом полного момента
количества движения», а мы будем называть его попросту «спином».)
Вас,
вероятно, волнует, не будет ли все сказанное нами верно только для некоторой
особой оси ![]() ?
Это не так. Для системы со спином
?
Это не так. Для системы со спином ![]() компонента момента количества движения
по любой оси может принимать только одно из значений (34.23). Хотя все это
выглядит довольно невероятно, я еще раз прошу вас мне поверить. Позднее мы еще
вернемся к этому пункту и обсудим его. Вам, наверно, будет приятно услышать,
что
компонента момента количества движения
по любой оси может принимать только одно из значений (34.23). Хотя все это
выглядит довольно невероятно, я еще раз прошу вас мне поверить. Позднее мы еще
вернемся к этому пункту и обсудим его. Вам, наверно, будет приятно услышать,
что ![]() -компонента
пробегает набор значений от некоторого числа до минус то же самое число, так
что нам, к счастью, не приходится гадать, какое же направление оси
-компонента
пробегает набор значений от некоторого числа до минус то же самое число, так
что нам, к счастью, не приходится гадать, какое же направление оси ![]() положительное.
(Конечно, если бы я сказал, что он пробегает значения от
положительное.
(Конечно, если бы я сказал, что он пробегает значения от ![]() до минус какое-то другое
число, это было бы крайне подозрительно, ибо тогда мы были бы лишены
возможности направить ось
до минус какое-то другое
число, это было бы крайне подозрительно, ибо тогда мы были бы лишены
возможности направить ось ![]() в другую сторону.)
в другую сторону.)
Но
если ![]() -компонента
момента количества движения изменяется на целое число от
-компонента
момента количества движения изменяется на целое число от ![]() до
до ![]() , то не должно ли само
, то не должно ли само ![]() тоже быть целым
числом? Нет! Не совсем так, целым должно быть удвоенное
тоже быть целым
числом? Нет! Не совсем так, целым должно быть удвоенное ![]() , т. е.
, т. е. ![]() . Иначе говоря, целым
должна быть лишь разность между
. Иначе говоря, целым
должна быть лишь разность между ![]() и
и ![]() . Таким образом, спин
. Таким образом, спин ![]() , вообще говоря,
может быть либо целым, либо полуцелым в зависимости от того, будет ли
, вообще говоря,
может быть либо целым, либо полуцелым в зависимости от того, будет ли ![]() нечетным или
четным. Возьмем, к примеру, ядро типа лития, спин которого равен
нечетным или
четным. Возьмем, к примеру, ядро типа лития, спин которого равен ![]() . При этом момент
количества движения относительно оси
. При этом момент
количества движения относительно оси ![]() принимает в единицах
принимает в единицах ![]() одно из следующих
значений:
одно из следующих
значений:
![]() .
.
Так
что если ядро находится в пустом пространстве в отсутствие внешних полей, то у
него имеются четыре возможных состояния, каждое с одной и той же энергией. Для
системы со спином 2 ![]() -компонента момента количества
движения принимает в единицах
-компонента момента количества
движения принимает в единицах ![]() только следующие значения:
только следующие значения:
![]() .
.
Если
вы подсчитаете, сколько возможно состояний для данного спина ![]() , то их получится
, то их получится ![]() . Другими словами,
если вы скажете мне, какова энергия системы и ее спин
. Другими словами,
если вы скажете мне, какова энергия системы и ее спин ![]() , то число состояний с этой
же энергией в точности будет равно
, то число состояний с этой
же энергией в точности будет равно ![]() , причем каждое из них соответствует
одной из различных величин
, причем каждое из них соответствует
одной из различных величин ![]() -компоненты момента количества
движения.
-компоненты момента количества
движения.
Мне
хотелось бы прибавить еще один факт. Если вы случайно выберете некоторый атом с
известным ![]() и
измерите его
и
измерите его ![]() -компоненту
момента количества движения, то сможете получить какое-то одно из возможных
значений, причем каждое из них равновероятно. Любое состояние может
характеризоваться только одним из возможных значений, но каждое из них столь же
хорошо, как и любое другое. Каждое из них имеет в мире один и тот же вес (мы
предполагаем, что никакой предварительной «сортировки» не было).
-компоненту
момента количества движения, то сможете получить какое-то одно из возможных
значений, причем каждое из них равновероятно. Любое состояние может
характеризоваться только одним из возможных значений, но каждое из них столь же
хорошо, как и любое другое. Каждое из них имеет в мире один и тот же вес (мы
предполагаем, что никакой предварительной «сортировки» не было).
Кстати,
этот факт имеет простой классический аналог. Представьте, что тот же самый
вопрос вас интересует с классической точки зрения: какова вероятность какого-то
определенного значения ![]() -компоненты момента количества
движения, если из набора систем, имеющих один и тот же момент количества
движения, вы наугад выбрали одну? Ответ: любое из значений от максимального до
минимального равновероятно (в чем вы можете легко убедиться сами). Этот
классический результат соответствует равной вероятности любой из
-компоненты момента количества
движения, если из набора систем, имеющих один и тот же момент количества
движения, вы наугад выбрали одну? Ответ: любое из значений от максимального до
минимального равновероятно (в чем вы можете легко убедиться сами). Этот
классический результат соответствует равной вероятности любой из ![]() возможностей в
квантовой механике.
возможностей в
квантовой механике.
Из
того, что у нас было до сих пор, можно получить другое интересное и в каком-то
смысле удивительное заключение. В некоторых классических расчетах в
окончательном результате появлялась величина, равная квадрату момента
количества движения ![]() , другими словами,
, другими словами, ![]() . И вот
оказывается, что правильную квантовомеханическую формулу можно угадать с
помощью классических вычислений и следующего простого правила: замените
. И вот
оказывается, что правильную квантовомеханическую формулу можно угадать с
помощью классических вычислений и следующего простого правила: замените ![]() на
на ![]() . Этим правилом
часто пользуются, и обычно оно дает верный результат, однако не всегда. Чтобы
показать вам, почему это правило может хорошо работать, я приведу следующее
рассуждение.
. Этим правилом
часто пользуются, и обычно оно дает верный результат, однако не всегда. Чтобы
показать вам, почему это правило может хорошо работать, я приведу следующее
рассуждение.
Скалярное
произведение ![]() можно
записать как
можно
записать как
![]() .
.
Поскольку
это скаляр, то он должен оставаться одним и тем же для любой ориентации спина.
Предположим, что мы случайно выбрали образец какой-либо атомной системы и
произвели измерения либо величины ![]() , либо
, либо ![]() , либо
, либо ![]() - среднее значение любой из них
должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества
перед любым другим.) Следовательно, среднее значение
- среднее значение любой из них
должно быть тем же самым. (Ни одно из направлений не имеет особого преимущества
перед любым другим.) Следовательно, среднее значение ![]() равно просто утроенной
средней величине любой компоненты, скажем
равно просто утроенной
средней величине любой компоненты, скажем ![]() :
:
![]() .
.
Но
поскольку ![]() при
любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной
при
любой ориентации одно и то же, его среднее, разумеется, будет постоянной величиной
![]() . (34.24)
. (34.24)
Если
же мы теперь скажем, что то же самое уравнение будет использоваться и в
квантовой механике, то можем легко найти ![]() . Нам просто нужно взять сумму
. Нам просто нужно взять сумму ![]() возможных значений
и поделить ее на число всех значений:
возможных значений
и поделить ее на число всех значений:
 . (34.25)
. (34.25)
Вот что получается для системы со спином 3/2:
 .
.
Отсюда мы заключаем, что
![]() .
.
На вашу долю остается доказать, что соотношение (34.25) вместе с (34.24) дает в результате
![]() . (34.26)
. (34.26)
Хотя
в рамках классической физики мы бы думали, что наибольшее возможное значение ![]() -компоненты
-компоненты ![]() равно просто абсолютной
величине
равно просто абсолютной
величине ![]() ,
именно
,
именно ![]() ,
в квантовой механике максимальное значение
,
в квантовой механике максимальное значение ![]() всегда немного меньше его, ибо
всегда немного меньше его, ибо ![]() всегда меньше
всегда меньше ![]() . Момент
количества движения никогда не направлен «полностью вдоль оси
. Момент
количества движения никогда не направлен «полностью вдоль оси ![]() ».
».
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
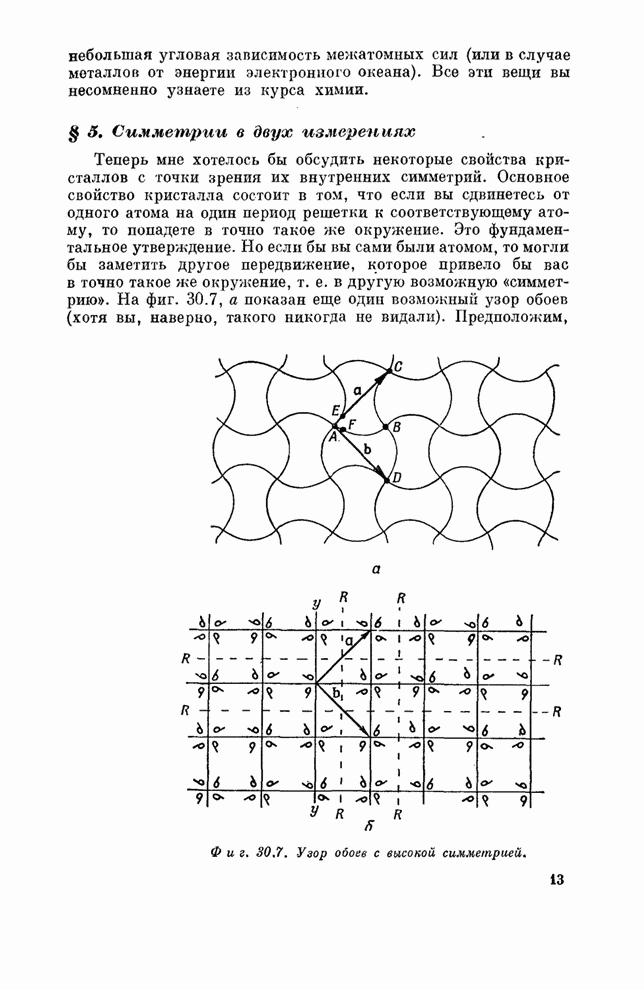
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
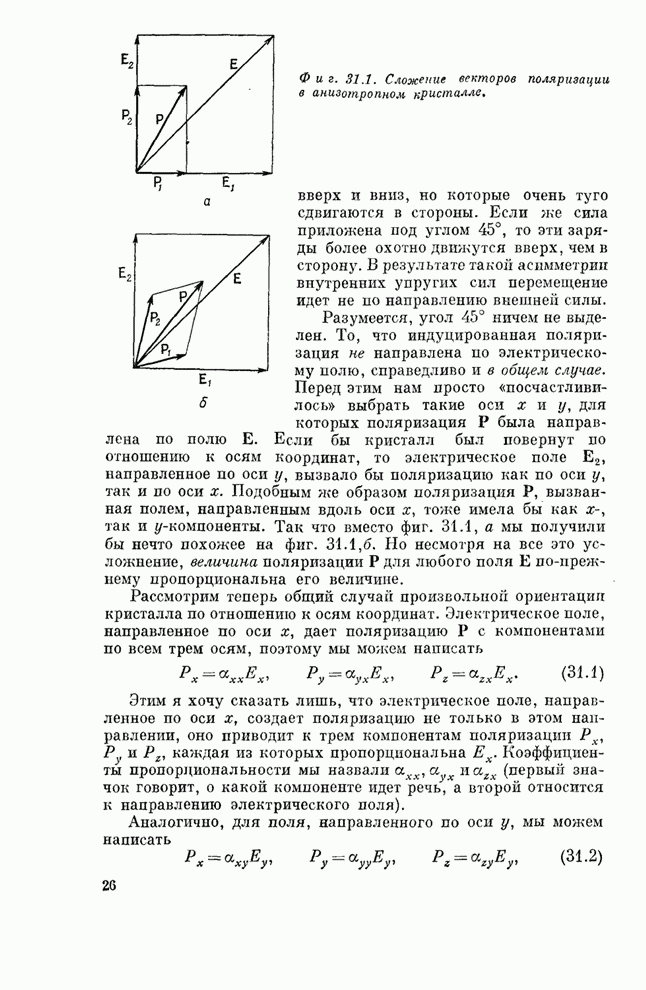
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)