| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Парамагнетизм
Теперь мне бы хотелось описать явление парамагнетизма вещества. Предположим, имеется вещество, в составе которого имеются атомы, обладающие постоянным магнитным моментом, например кристаллы медного купороса. В этих кристаллах содержатся ионы меди, у которых электроны на внутренних оболочках имеют суммарный момент количества движения и магнитный момент, не равные нулю. Таким образом, ионы меди будут источником постоянного магнитного момента молекул купороса. Буквально несколько слов о том, какие атомы имеют постоянный магнитный момент, а какие - нет. Любой атом, у которого число электронов нечетно, подобно натрию, например, будет иметь магнитный момент. На незаполненной оболочке натрия имеется один электрон. Этот электрон и определяет спин и магнитный момент атома. Однако обычно при образовании соединения этот дополнительный электрон на внешней оболочке спаривается с другим электроном, направление спина которого в точности противоположно, так что все моменты количества движения и магнитные моменты валентных электронов в точности компенсируют друг друга. Вот почему молекулы, вообще говоря, не обладают магнитным моментом. Конечно, если у вас есть газ атомов натрия, то там такой компенсации не происходит. Точно так же если у вас есть то, что в химии называется «свободным радикалом», т. е. объект с нечетным числом валентных электронов, то связи оказываются неполностью насыщенными и появляется ненулевой момент количества движения.
У подавляющего большинства материалов полный магнитный момент появляется только тогда, когда там присутствуют атомы с незаполненной внутренней электронной оболочкой. Благодаря этому они могут иметь суммарный момент количества движения и магнитный момент. Такие атомы принадлежат к «переходным элементам» периодической таблицы Менделеева, например: хром, марганец, железо, никель, кобальт, палладий и платина - элементы как раз такого сорта. Кроме того, все редкоземельные элементы имеют незаполненную внутреннюю оболочку, а следовательно, и постоянные магнитные моменты. Правда, встречаются еще странные вещества (к числу их относятся жидкий кислород и окись азота), которые, оказывается, тоже обладают магнитным моментом, но объяснить причины этих странностей я предоставляю химикам.
Предположим теперь, что у нас есть ящик, наполненный молекулами или атомами с постоянным магнитным моментом, скажем газ, жидкость или кристалл. Нам хочется знать, что получится, если мы поместим его во внешнее магнитное поле. В отсутствие магнитного поля атомы сбиваются тепловым движением и их магнитные моменты распределяются по всем направлениям. Но когда действует магнитное поле, оно выстраивает эти маленькие магнитики, так что магнитных моментов, направленных по полю, становится больше, чем направленных против него. Материал «намагничивается».
Намагниченность
![]() материала
мы определяем как полный магнитный момент единицы объема, под которым мы
понимаем векторную сумму всех атомных магнитных моментов единицы объема. Если
среднее число атомов в единице объема равно
материала
мы определяем как полный магнитный момент единицы объема, под которым мы
понимаем векторную сумму всех атомных магнитных моментов единицы объема. Если
среднее число атомов в единице объема равно ![]() , а их средний момент равен
, а их средний момент равен ![]() , то
, то ![]() можно записать
как произведение
можно записать
как произведение ![]() на средний магнитный момент:
на средний магнитный момент:
![]() . (35.8)
. (35.8)
Это
определение ![]() аналогично
определению электрической поляризации
аналогично
определению электрической поляризации ![]() , данному в гл. 10 (вып. 5).
, данному в гл. 10 (вып. 5).
Классическая
теория парамагнетизма, как вы уже убедились в гл. 11 (вып. 5), в точности
аналогична теории диэлектрической проницаемости. Предполагается, что магнитный
момент ![]() каждого
из атомов всегда имеет одну и ту же величину, но может быть направлен в любую
сторону. Магнитная энергия в поле
каждого
из атомов всегда имеет одну и ту же величину, но может быть направлен в любую
сторону. Магнитная энергия в поле ![]() равна
равна ![]() , где
, где ![]() - угол между моментом и полем.
Согласно статистической физике, относительная вероятность угла равна
- угол между моментом и полем.
Согласно статистической физике, относительная вероятность угла равна ![]() , так что угол 0° более
вероятен, чем угол
, так что угол 0° более
вероятен, чем угол ![]() . Следуя в точности по пути,
проделанному нами в гл. 11, § 3 (вып. 5), мы обнаружим, что для слабых
магнитных полей
. Следуя в точности по пути,
проделанному нами в гл. 11, § 3 (вып. 5), мы обнаружим, что для слабых
магнитных полей ![]() направлена
параллельно
направлена
параллельно ![]() и
имеет величину
и
имеет величину
![]() . (35.9)
. (35.9)
[См.
выражение (11.20), вып. 5.] Эта приближенная формула верна, только когда
отношение ![]() много
меньше единицы.
много
меньше единицы.
Мы
нашли, что намагниченность, т. е. магнитный момент единицы объема,
пропорциональна магнитному полю. Это явление и называется парамагнетизмом. Вы
увидите, что эффект сильнее проявляется при низких температурах и слабее при
высоких. При помещении вещества в магнитное поле возникающий в нем магнитный
момент в случае слабых полей пропорционален величине поля. Отношение ![]() к
к ![]() (для слабых
полей) называется магнитной восприимчивостью.
(для слабых
полей) называется магнитной восприимчивостью.
Рассмотрим
теперь парамагнетизм с точки зрения квантовой механики. Обратимся сначала к
атомам со спином 1/2. Если в отсутствие магнитного поля атомы обладают вполне
определенной энергией, то в магнитном поле энергия изменится; возможны два
значения энергии для разных значений ![]() . Для
. Для ![]() магнитное поле изменяет энергию на
величину
магнитное поле изменяет энергию на
величину
![]() . (35.10)
. (35.10)
(Для
атомов сдвиг энергии ![]() положителен, ибо заряд электрона
отрицателен.) Для
положителен, ибо заряд электрона
отрицателен.) Для ![]() энергия изменяется на величину
энергия изменяется на величину
![]() . (35.11)
. (35.11)
Для сокращения записи обозначим
![]() ; (35.12)
; (35.12)
тогда
![]() . (35.13)
. (35.13)
Совершенно
ясен и смысл ![]() ;
;
![]() равно
равно ![]() -компоненте
магнитного момента для спина, направленного вверх, а
-компоненте
магнитного момента для спина, направленного вверх, а ![]() равно
равно ![]() -компоненте магнитного
момента в случае спина, направленного вниз.
-компоненте магнитного
момента в случае спина, направленного вниз.
Статистическая механика говорит нам, что вероятность нахождения атома в каком-то состоянии пропорциональна
![]() .
.
В отсутствие магнитного поля энергия обоих состояний одна и та же, поэтому в случае равновесия в магнитном поле вероятности пропорциональны
![]() . (35.14)
. (35.14)
Число же атомов в единице объема со спином, направленным вверх, равно
![]() , (35.15)
, (35.15)
а со спином, направленным вниз,
![]() . (35.16)
. (35.16)
Постоянная
![]() должна
определяться из условия
должна
определяться из условия
![]() , (35.17)
, (35.17)
т.е. равна полному числу атомов в единице объема. Таким образом, мы получаем
![]() . (35.18)
. (35.18)
Однако
нас интересует средний магнитный момент в направлении оси ![]() . Каждый атом со спином,
направленным вверх, дает в этот момент вклад, равный
. Каждый атом со спином,
направленным вверх, дает в этот момент вклад, равный ![]() , а со спином, направленным
вниз,
, а со спином, направленным
вниз, ![]() ,
так что средний момент будет
,
так что средний момент будет
![]() . (35.19)
. (35.19)
Тогда
![]() -
магнитный момент единицы объема - будет равен
-
магнитный момент единицы объема - будет равен ![]() . Воспользовавшись выражениями
(35.15)-(35.17), получим
. Воспользовавшись выражениями
(35.15)-(35.17), получим
![]() . (35.20)
. (35.20)
Это
и есть квантовомеханическая формула для ![]() в случае атомов со спином
в случае атомов со спином ![]() . К счастью, ее
можно записать более коротко через гиперболический тангенс:
. К счастью, ее
можно записать более коротко через гиперболический тангенс:
![]() . (35.21)
. (35.21)
График
зависимости ![]() от
от
![]() приведен
на фиг. 35.7. Когда поле
приведен
на фиг. 35.7. Когда поле ![]() становится очень большим,
гиперболический тангенс приближается к единице, а
становится очень большим,
гиперболический тангенс приближается к единице, а ![]() - к своему предельному значению
- к своему предельному значению ![]() . Таким образом,
при сильных полях происходит насыщение. Нетрудно понять, почему так получается
- ведь при достаточно больших полях все магнитные моменты выстраиваются в одном
и том же направлении. Другими словами, при насыщении все атомы находятся в состоянии
со спинами, направленными вниз, и каждый из них дает вклад в магнитный момент,
равный
. Таким образом,
при сильных полях происходит насыщение. Нетрудно понять, почему так получается
- ведь при достаточно больших полях все магнитные моменты выстраиваются в одном
и том же направлении. Другими словами, при насыщении все атомы находятся в состоянии
со спинами, направленными вниз, и каждый из них дает вклад в магнитный момент,
равный ![]() .
.

Фиг. 35.7. Изменение
намагниченности парамагнетика при изменении напряженности магнитного поля ![]() .
.
Обычно
при комнатной температуре и полях, которые можно получить (порядка 10 000 гс),
отношение ![]() равно
приблизительно 0,02. Чтобы наблюдать насыщение, необходимо спуститься до очень
низких температур. Для комнатной и более высоких температур обычно можно
равно
приблизительно 0,02. Чтобы наблюдать насыщение, необходимо спуститься до очень
низких температур. Для комнатной и более высоких температур обычно можно ![]() заменить на
заменить на ![]() и написать
и написать
![]() . (35.22)
. (35.22)
Точно
так же, как и в классической теории, намагниченность ![]() оказывается
пропорциональной полю
оказывается
пропорциональной полю ![]() . Даже формула оказывается той же
самой, за исключением того, что в ней, по-видимому, где-то потерян множитель 1/3.
Но нам еще нужно связать
. Даже формула оказывается той же
самой, за исключением того, что в ней, по-видимому, где-то потерян множитель 1/3.
Но нам еще нужно связать ![]() в квантовомеханической формуле с
величиной
в квантовомеханической формуле с
величиной ![]() ,
которая появилась в классическом результате, в выражении (35.9).
,
которая появилась в классическом результате, в выражении (35.9).
В
классической формуле у нас появилось ![]() - квадрат вектора магнитного
момента, или
- квадрат вектора магнитного
момента, или
![]() . (35.23)
. (35.23)
В
предыдущей главе я уже говорил, что очень часто правильный ответ можно получить
из классических вычислений с заменой ![]() на
на ![]() . В нашем частном примере
. В нашем частном примере ![]() , так что
, так что
![]() .
.
Подставляя
этот результат вместо ![]() в (35.23), получаем
в (35.23), получаем
![]() ,
,
или,
вводя величину ![]() ,
определенную соотношением (35.12), получаем
,
определенную соотношением (35.12), получаем
![]() .
.
Подставляя
это вместо ![]() в
классическое выражение (35.9), мы действительно воспроизведем истинный
квантовомеханический результат - формулу (35.22).
в
классическое выражение (35.9), мы действительно воспроизведем истинный
квантовомеханический результат - формулу (35.22).
Квантовая
теория парамагнетизма легко распространяется на атомы с любым спином ![]() . При этом для
намагниченности в слабом поле получим
. При этом для
намагниченности в слабом поле получим
![]() , (35.24)
, (35.24)
где
![]() (35.25)
(35.25)
представляет комбинацию постоянных с размерностью магнитного момента. Моменты большинства атомов приблизительно равны этой величине. Она называется магнетоном Бора. Спиновый магнитный момент электрона почти в точности равен магнетону Бора.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
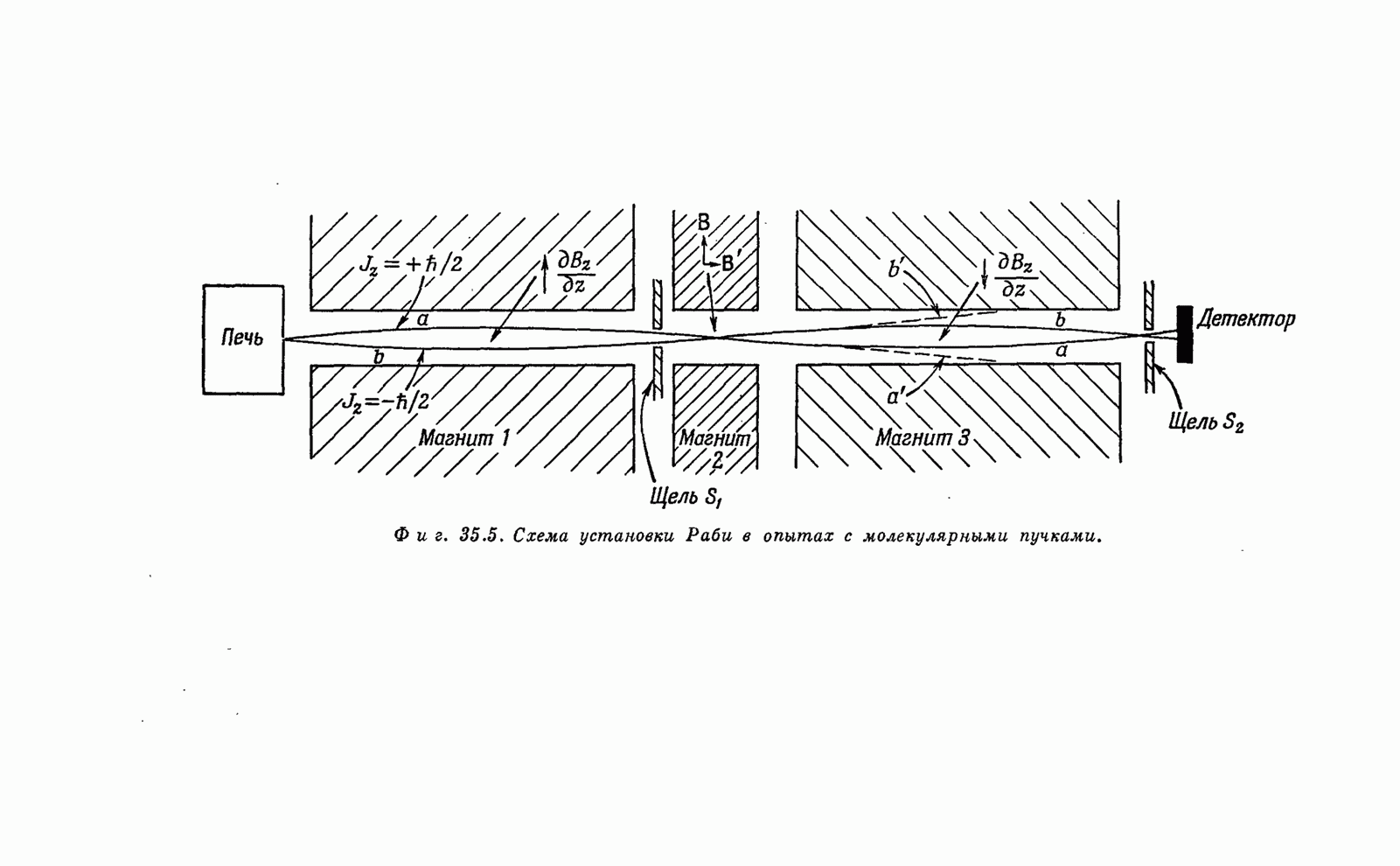
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)