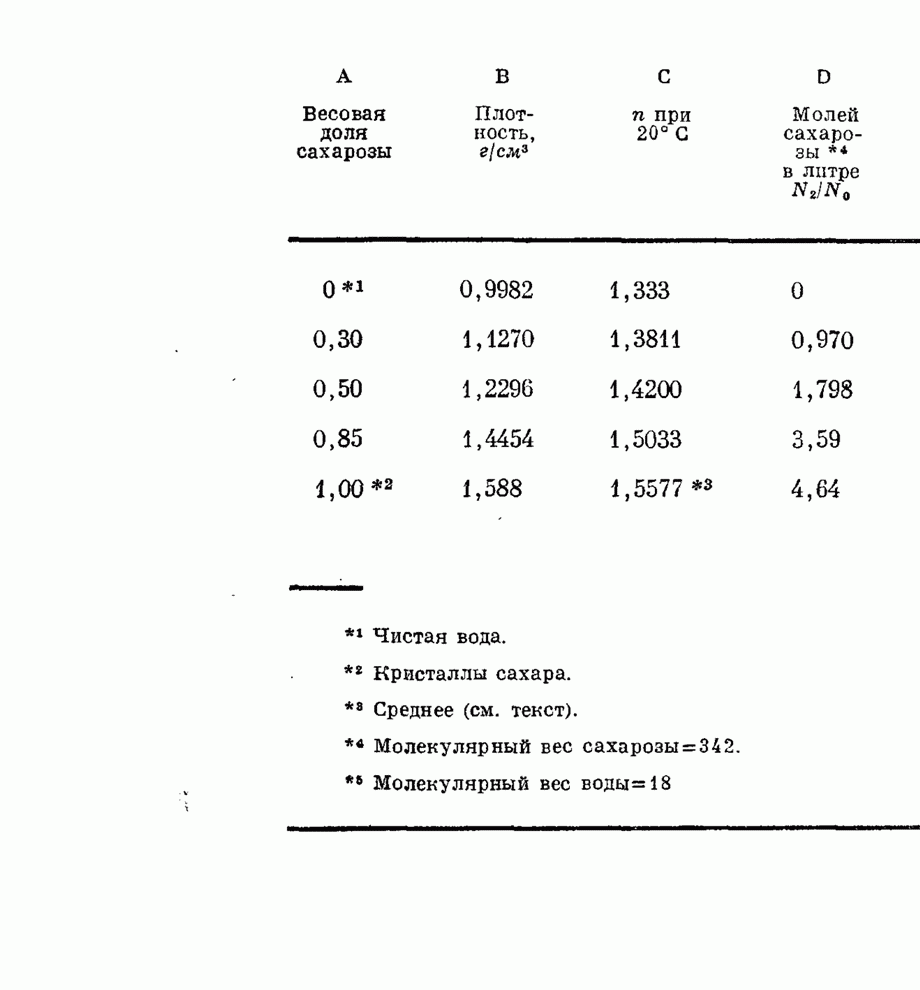
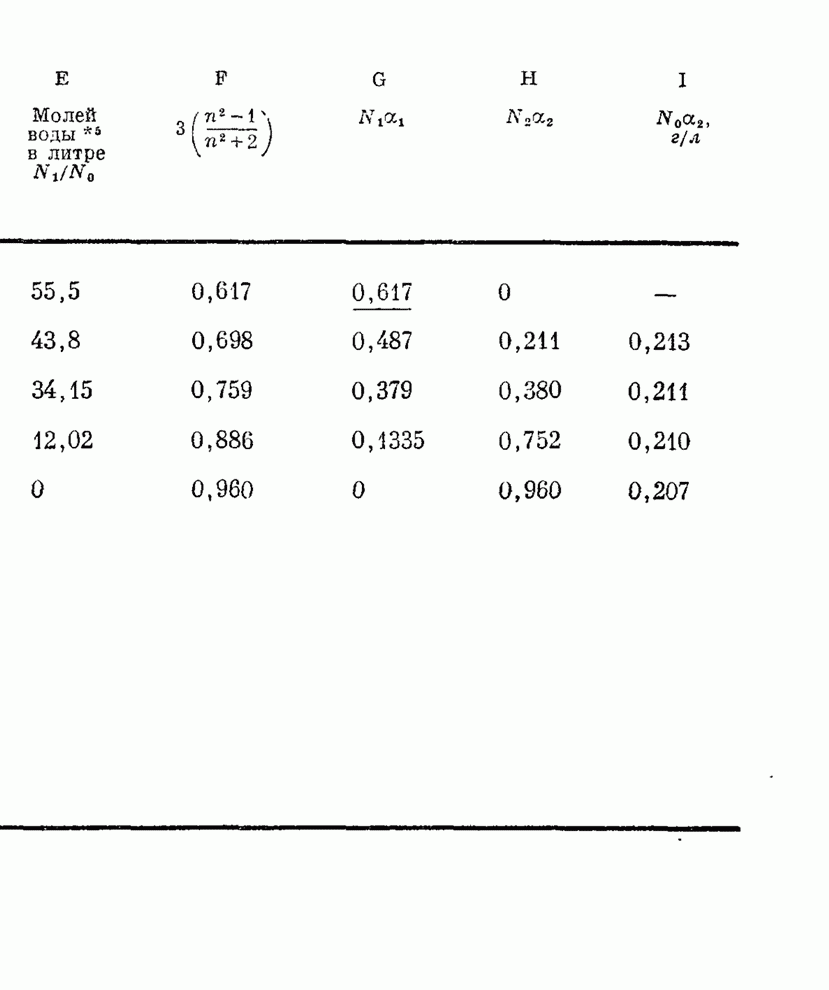
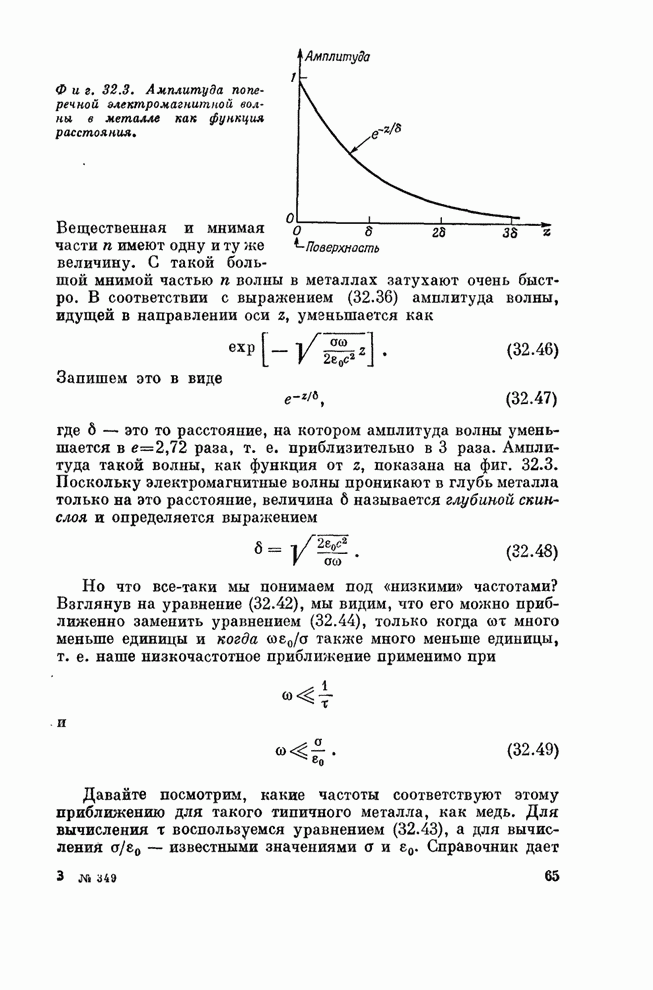
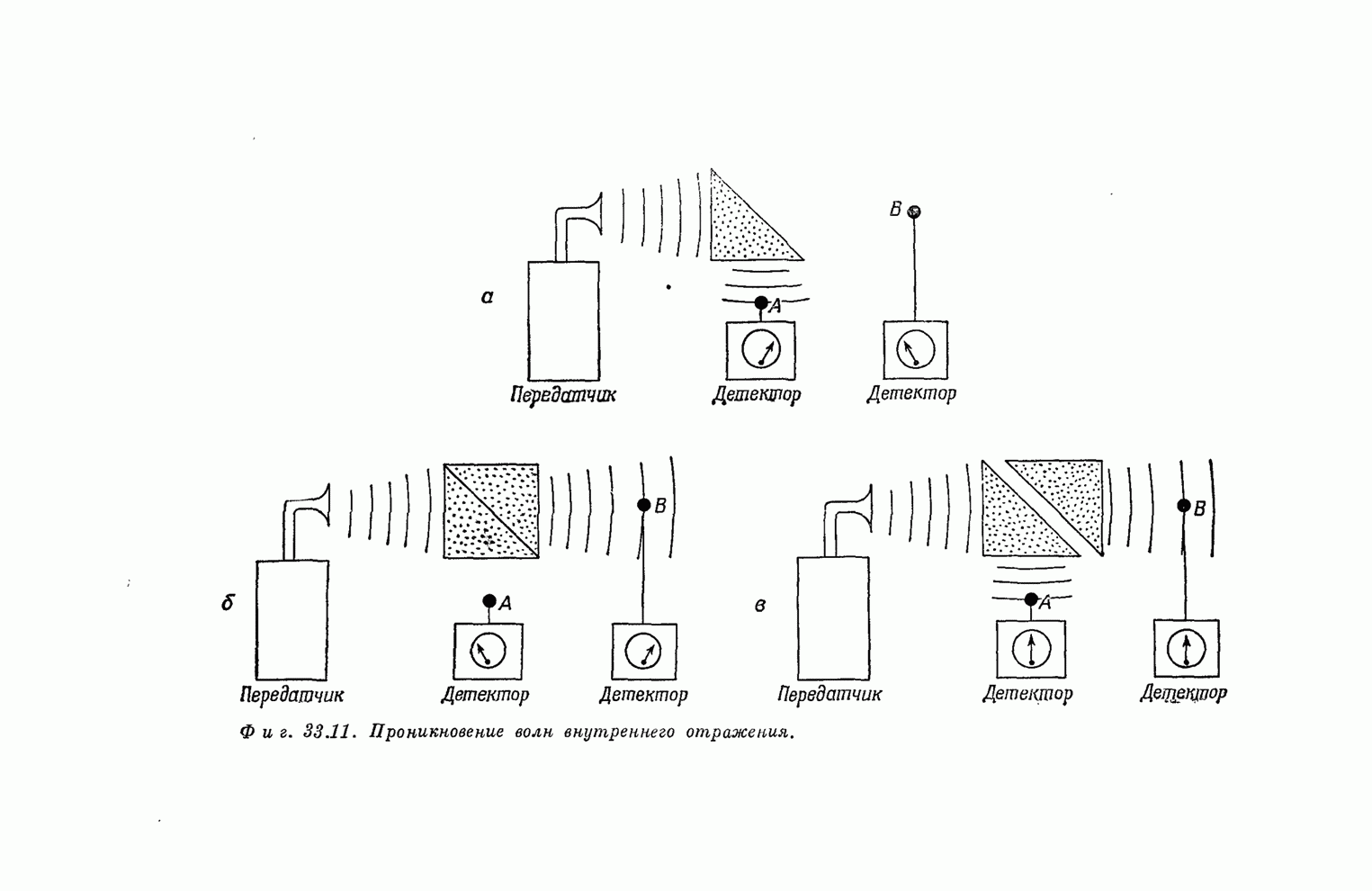
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. Поле 
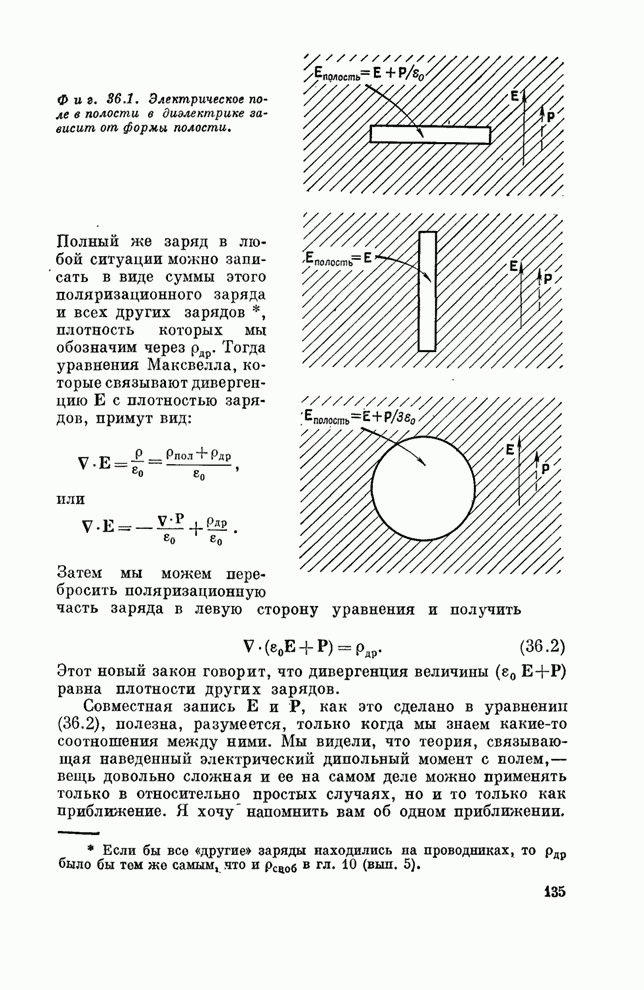
Теперь можно подставить выражение для тока (36.10) в уравнение Максвелла. Мы получаем
![]() .
.
Слагаемое
с ![]() можно
перенести в левую часть:
можно
перенести в левую часть:
 . (36.11)
. (36.11)
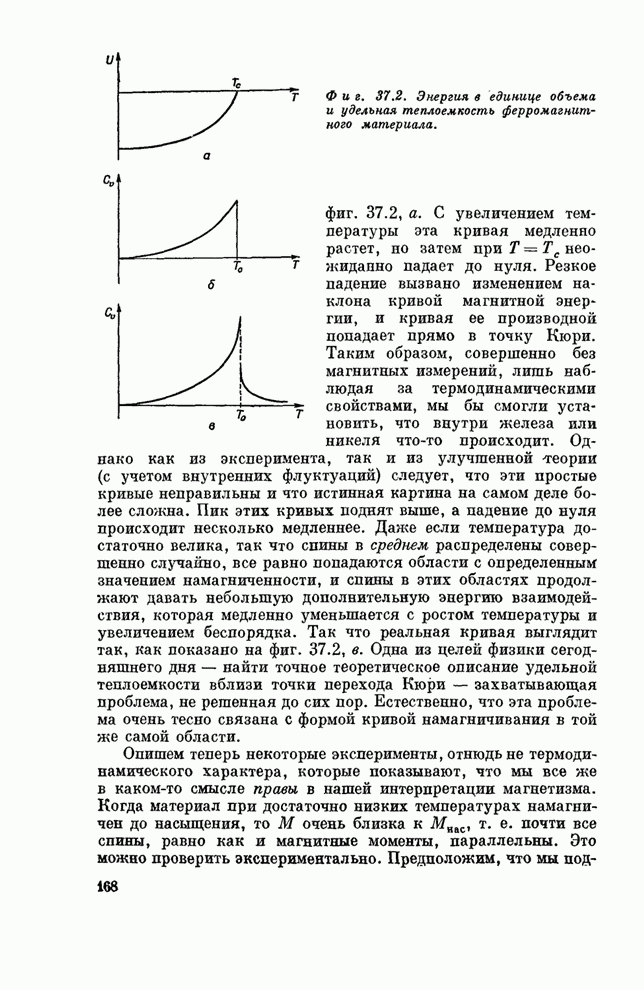
Как
мы уже отмечали в гл. 32, иногда удобно записывать ![]() как новое векторное поле
как новое векторное поле ![]() . Точно так же
удобно
. Точно так же
удобно ![]() записывать
в виде единого векторного поля. Такое поле мы обозначим через
записывать
в виде единого векторного поля. Такое поле мы обозначим через ![]() , т. е.
, т. е.
![]() . (36.12)
. (36.12)
После этого уравнение (36.11) принимает вид
![]() . (36.13)
. (36.13)
Выглядит
оно просто, но вся его сложность теперь скрыта в буквах ![]() и
и ![]() .
.
Хочу
предостеречь вас. Большинство людей, которые применяют систему СИ, пользуются
другим определением ![]() . Называя свое поле через
. Называя свое поле через ![]() (они, конечно, не
пишут штриха), они определяют его как
(они, конечно, не
пишут штриха), они определяют его как
![]() . (36.14)
. (36.14)
(Кроме
того, величину ![]() они
обычно записывают в виде
они
обычно записывают в виде ![]() , так что появляется еще одна
постоянная, за которой все время нужно следить!) При таком определении уравнение
(36.13) будет выглядеть еще проще:
, так что появляется еще одна
постоянная, за которой все время нужно следить!) При таком определении уравнение
(36.13) будет выглядеть еще проще:
![]() . (36.15)
. (36.15)
Но
трудность здесь заключается в том, что такое определение, во-первых, не
согласуется с определением, принятым теми, кто не пользуется системой СИ, и,
во-вторых, поля ![]() и
и
![]() измеряются
в различных единицах. Я думаю, что
измеряются
в различных единицах. Я думаю, что ![]() удобнее измерять в тех же единицах,
что и
удобнее измерять в тех же единицах,
что и ![]() ,
а не в единицах
,
а не в единицах ![]() ,
как
,
как ![]() . Но
если вы собираетесь стать инженером и проектировать трансформаторы, магниты и т.
п., то будьте внимательны. Вы столкнетесь со множеством книг, где в качестве
определения
. Но
если вы собираетесь стать инженером и проектировать трансформаторы, магниты и т.
п., то будьте внимательны. Вы столкнетесь со множеством книг, где в качестве
определения ![]() используется
уравнение (36.14), а не (36.12), а в других книгах, особенно в справочниках о
магнитных материалах, связь между
используется
уравнение (36.14), а не (36.12), а в других книгах, особенно в справочниках о
магнитных материалах, связь между ![]() и
и ![]() такая же, как и у нас. Нужно быть
внимательным и понимать, какое где использовано соглашение.
такая же, как и у нас. Нужно быть
внимательным и понимать, какое где использовано соглашение.
Одна
из примет, указывающих нам на соглашение, - это единицы измерения. Напомним,
что в системе СИ величина ![]() , а следовательно, и наше
, а следовательно, и наше ![]() измеряются в
единицах
измеряются в
единицах ![]()
![]() .Магнитный же
момент (т. е. произведение тока на площадь) в той же системе СИ измеряется в
единицах
.Магнитный же
момент (т. е. произведение тока на площадь) в той же системе СИ измеряется в
единицах ![]() .
Тогда намагниченность
.
Тогда намагниченность ![]() имеет размерность а/м. Размерность
имеет размерность а/м. Размерность ![]() та же, что и
размерность
та же, что и
размерность ![]() .
Нетрудно видеть, что это согласуется с уравнением (36.15), поскольку
.
Нетрудно видеть, что это согласуется с уравнением (36.15), поскольку ![]() имеет размерность
обратной длины.
имеет размерность
обратной длины.
Те,
кто работает с электромагнитами, привыкли измерять поле ![]() (определенное как
(определенное как ![]() ) в
ампер-витках/метр, имея при этом в виду витки провода в обмотке. Но «виток»
ведь фактически величина безразмерная, и она не должна вас смущать. Поскольку
наше
) в
ампер-витках/метр, имея при этом в виду витки провода в обмотке. Но «виток»
ведь фактически величина безразмерная, и она не должна вас смущать. Поскольку
наше ![]() равно
равно
![]() , то,
если вы пользуетесь системой СИ,
, то,
если вы пользуетесь системой СИ, ![]() (в вб/м) равно произведению
(в вб/м) равно произведению ![]() на
на ![]() (в а/м). Может быть,
более удобно помнить, что
(в а/м). Может быть,
более удобно помнить, что ![]() (в гс) равно
(в гс) равно ![]() (в а/м).
(в а/м).
Здесь
есть еще одна ужасная вещь. Многие люди, использующие наше определение ![]() , решили назвать
единицы измерения
, решили назвать
единицы измерения ![]() и
и ![]() по-разному. И даже несмотря на
одинаковую размерность, они называют единицу
по-разному. И даже несмотря на
одинаковую размерность, они называют единицу ![]() гауссом, а единицу
гауссом, а единицу ![]() - эрстедом
(конечно, в честь Гаусса и Эрстеда). Таким образом, во многих книгах вы найдете
графики зависимости
- эрстедом
(конечно, в честь Гаусса и Эрстеда). Таким образом, во многих книгах вы найдете
графики зависимости ![]() в гауссах от
в гауссах от ![]() в эрстедах. На самом деле
это одна и та же единица, равная
в эрстедах. На самом деле
это одна и та же единица, равная ![]() единиц СИ. Эту неразбериху в
магнитных единицах мы увековечили в табл. 36.1.
единиц СИ. Эту неразбериху в
магнитных единицах мы увековечили в табл. 36.1.
Таблица 36.1 ЕДИНИЦЫ МАГНИТНЫХ ВЕЛИЧИН
|
Полезные соотношения
|
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
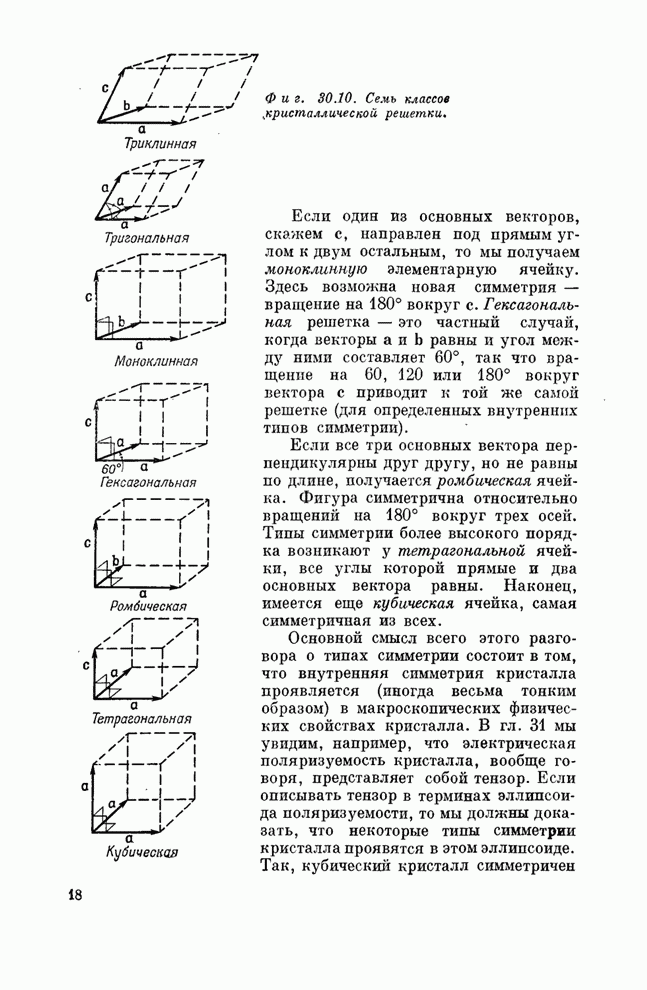
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
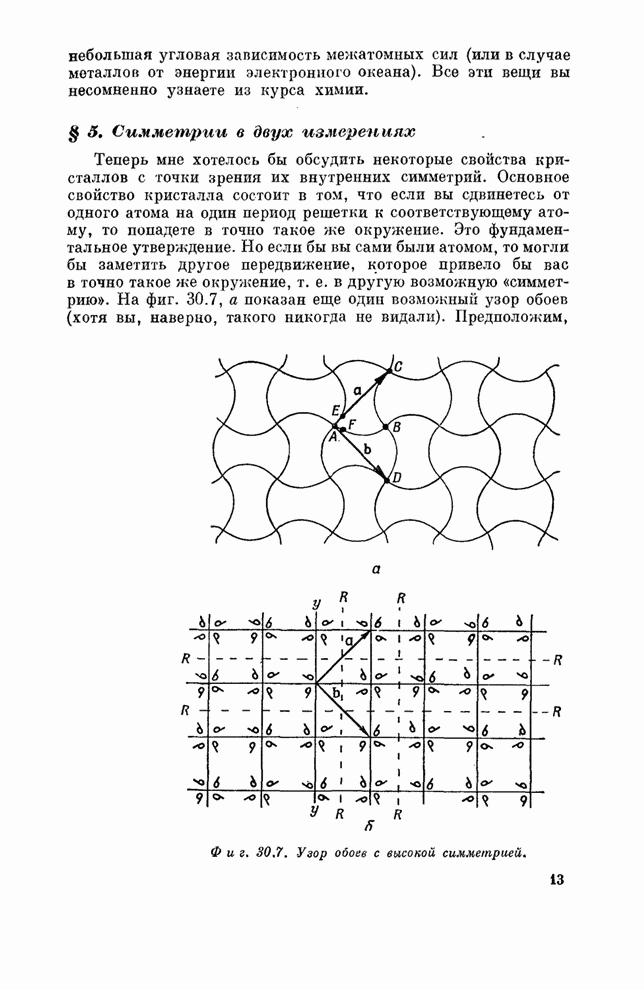
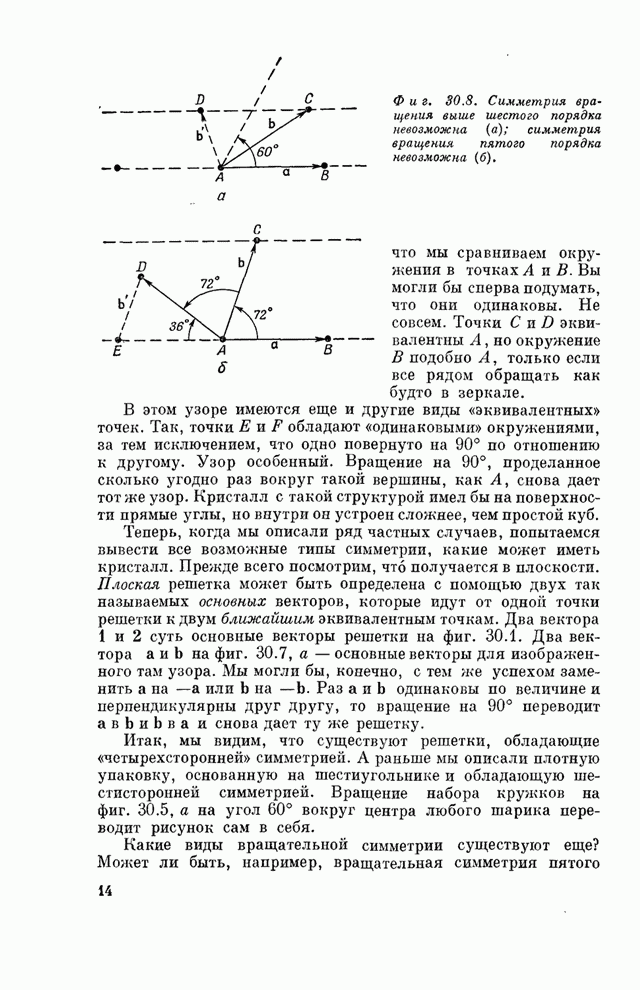
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
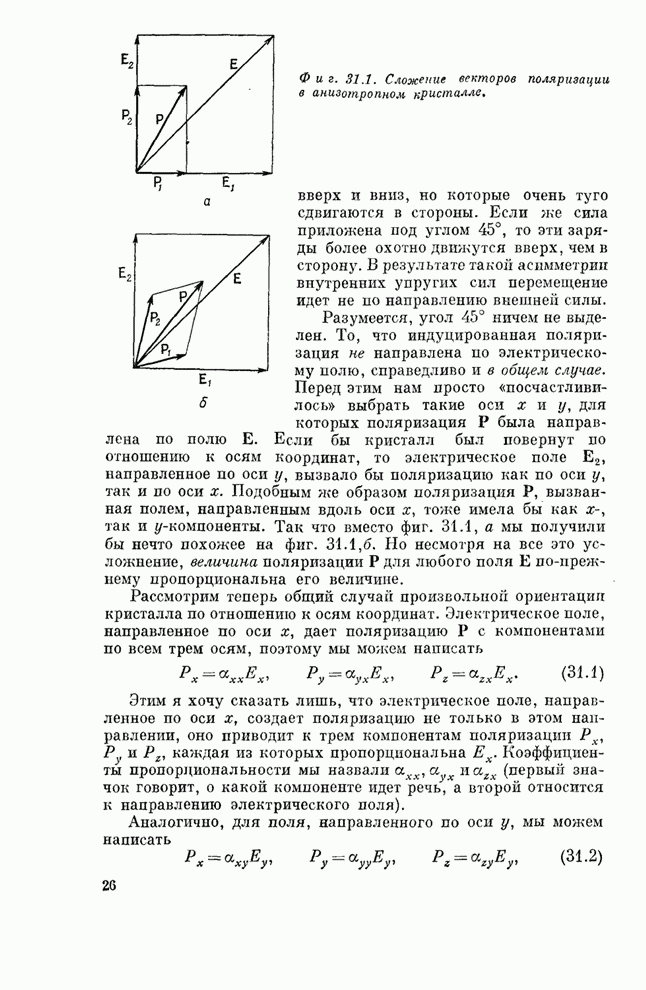
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
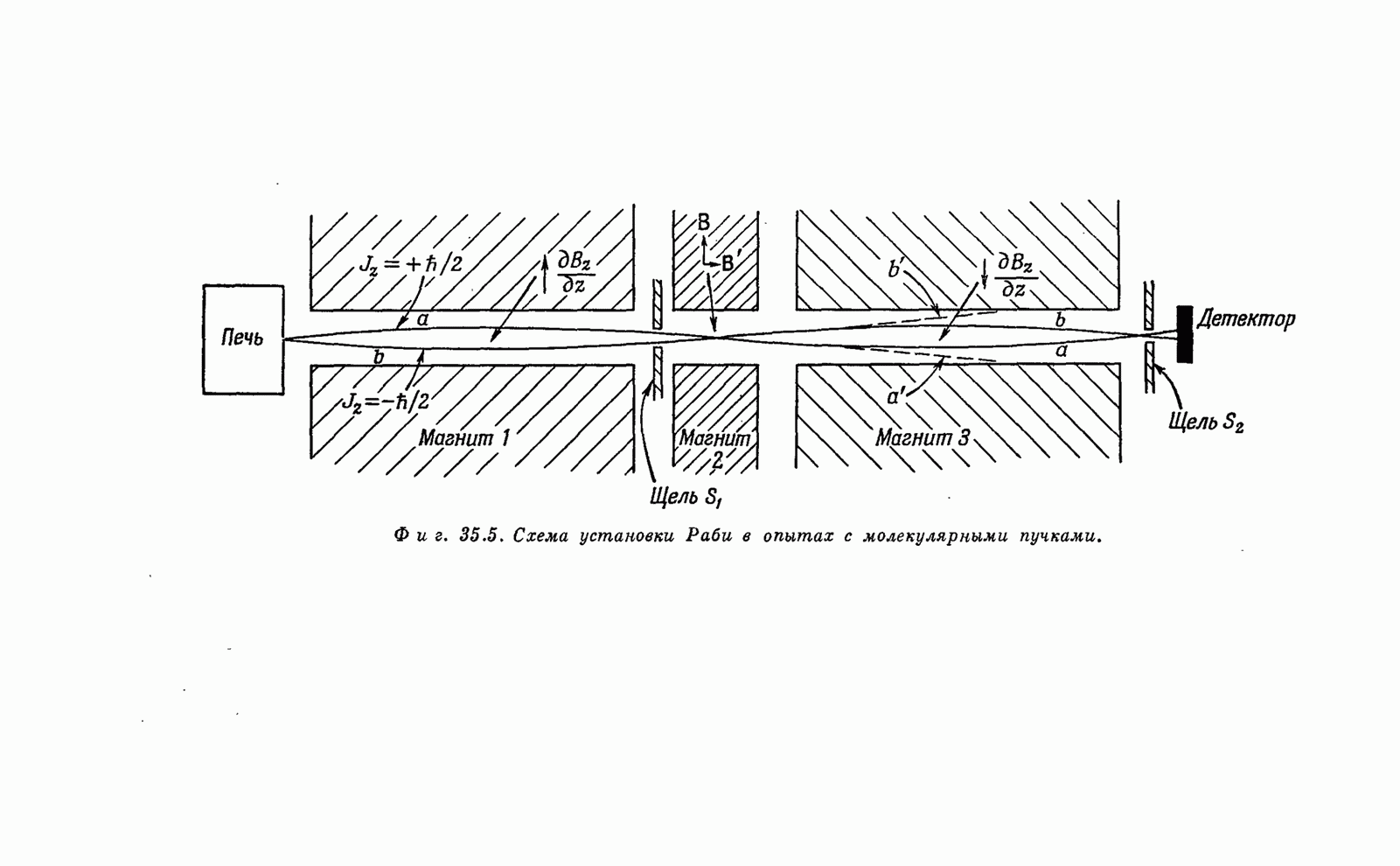
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
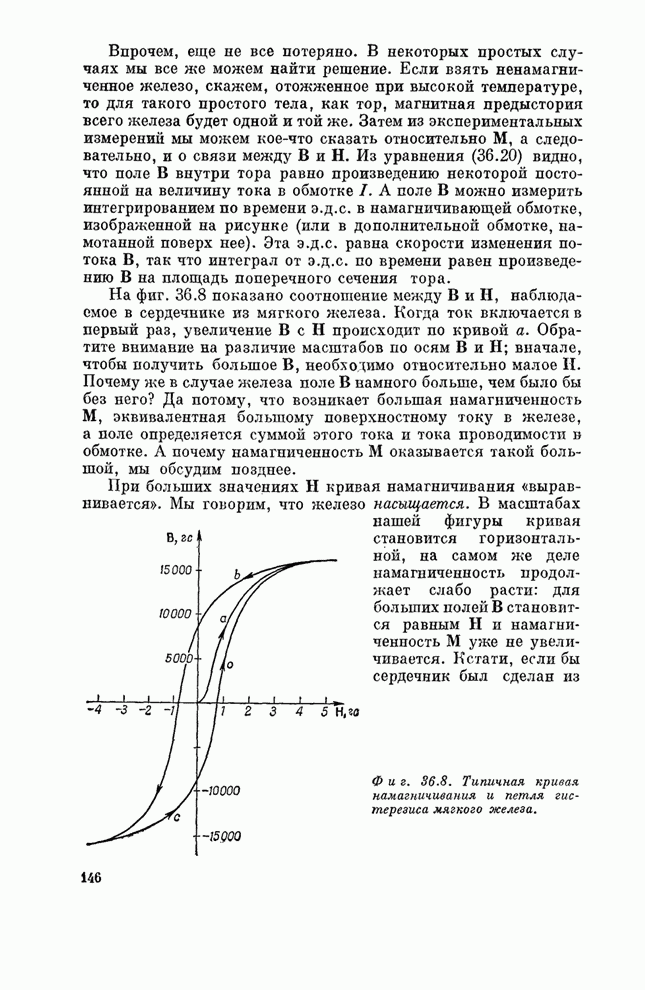
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
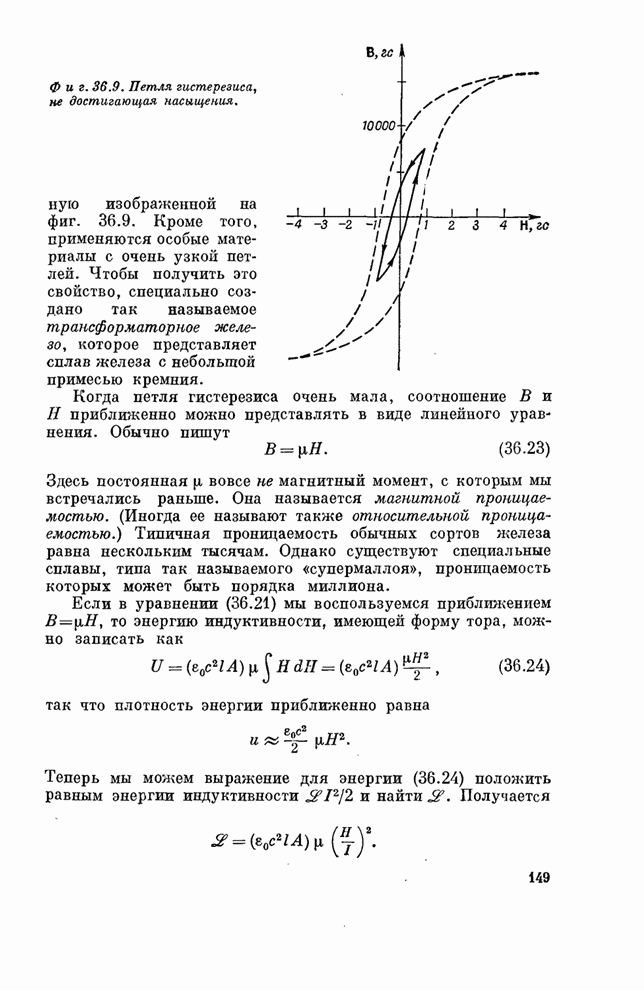
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
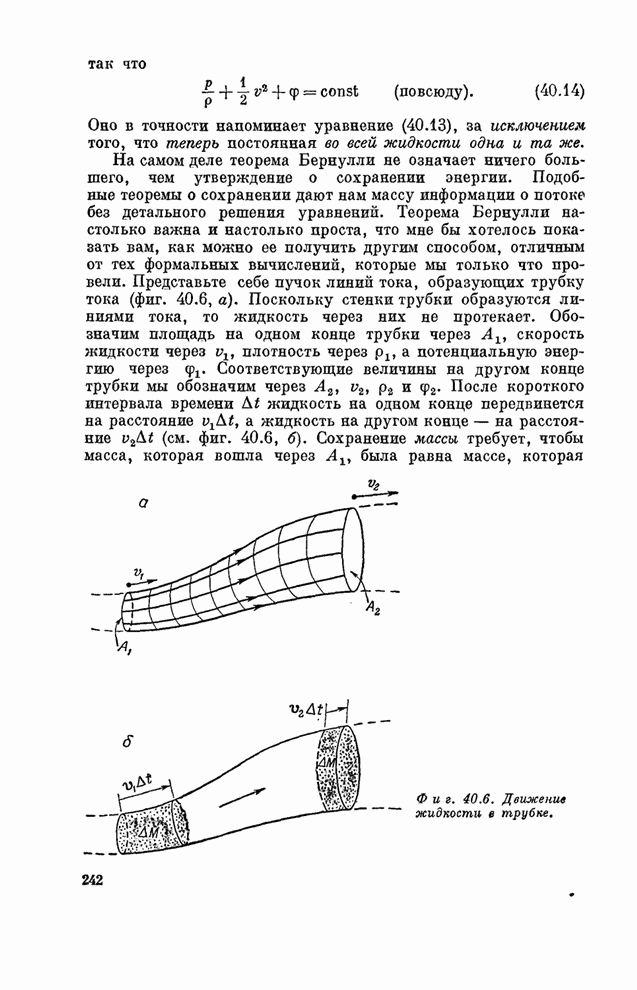
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
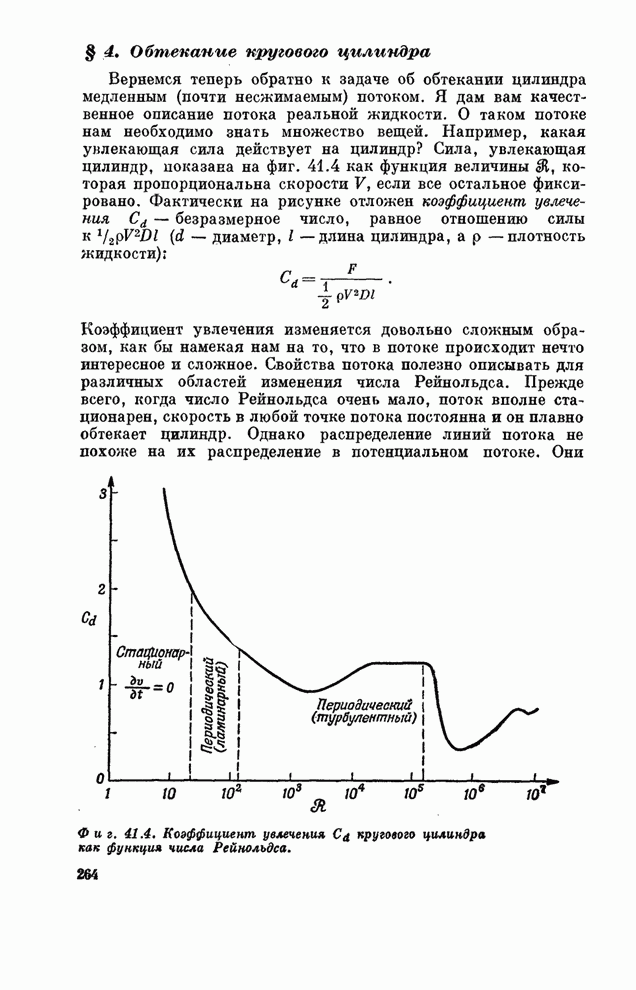
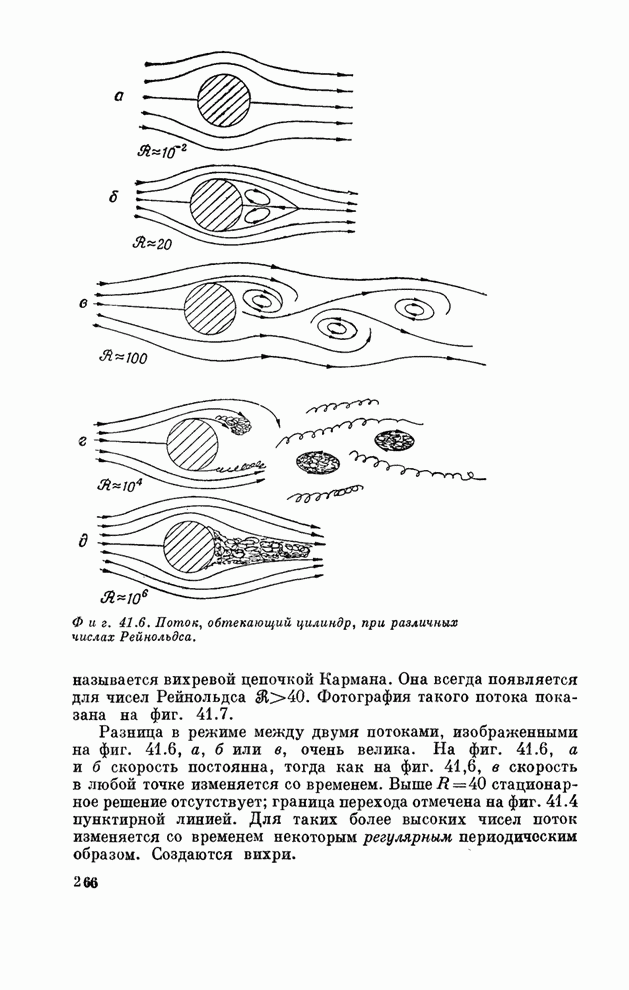
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)