| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Продольный изгиб
Теперь воспользуемся нашей теорией, чтобы понять, что происходит при продольном изгибе бруска, опоры или стержня. Рассмотрим то, что изображено на фиг. 38.16. Здесь стержень, обычно прямой, удерживается в согнутом виде двумя противоположными силами, давящими на его концы. Найдем форму стержня и величину сил, действующих на концы.

Фиг. 38.16. Продольно изогнутая балка.
Пусть
отклонение стержня от прямой линии между концами будет ![]() , где
, где ![]() – расстояние от одного
конца. Изгибающий момент
– расстояние от одного
конца. Изгибающий момент ![]() в точке
в точке ![]() на рисунке равен силе
на рисунке равен силе ![]() , умноженной на
плечо, перпендикулярное направлению
, умноженной на
плечо, перпендикулярное направлению ![]() :
:
![]() . (38.43)
. (38.43)
Воспользовавшись выражением для момента (38.36), имеем
![]() . (38.44)
. (38.44)
При
малых отклонениях можно считать ![]() (отрицательный знак выбран потому,
что кривизна направлена вниз). Отсюда
(отрицательный знак выбран потому,
что кривизна направлена вниз). Отсюда
![]() , (38.45)
, (38.45)
т.
е. появилось дифференциальное уравнение для синуса. Таким образом, для малых
отклонений кривая такого продольно изогнутого стержня представляет синусоиду.
«Длина волны» ![]() этой
синусоиды в два раза больше расстояния
этой
синусоиды в два раза больше расстояния ![]() между концами. Если изгиб невелик,
она просто равна удвоенной длине неизогнутого стержня. Таким образом,
получается кривая
между концами. Если изгиб невелик,
она просто равна удвоенной длине неизогнутого стержня. Таким образом,
получается кривая
![]() .
.
Беря вторую производную, находим
![]() .
.
Сравнивая это с (38.45), видим, что сила равна
![]() . (38.46)
. (38.46)
Для
малого продольного изгиба сила не зависит от перемещения ![]() !
!
Физически
же получается вот что. Если сила ![]() меньше определяемой уравнением
(38.46), то никакого продольного изгиба не происходит. Но если она хоть немного
больше этой силы, то балка внезапно и очень сильно согнется, т. е. под
действием сил, превышающих критическую величину
меньше определяемой уравнением
(38.46), то никакого продольного изгиба не происходит. Но если она хоть немного
больше этой силы, то балка внезапно и очень сильно согнется, т. е. под
действием сил, превышающих критическую величину ![]() (часто называемую «силой Эйлера»),
балка будет «гнуться». Если на втором этаже здания разместить такой груз, что
нагрузка на поддерживающие колонны превысит силу Эйлера, то здание рухнет.
Другая область, где очень важны продольно изгибающие силы, - это космические
ракеты. С одной стороны, ракета должна выдерживать свой вес на стартовой
площадке и вынести напряжения во время ускорения, а с другой - очень важно
свести вес всей конструкции до минимума, чтобы полезная нагрузка и полезная
мощность двигателей были как можно больше.
(часто называемую «силой Эйлера»),
балка будет «гнуться». Если на втором этаже здания разместить такой груз, что
нагрузка на поддерживающие колонны превысит силу Эйлера, то здание рухнет.
Другая область, где очень важны продольно изгибающие силы, - это космические
ракеты. С одной стороны, ракета должна выдерживать свой вес на стартовой
площадке и вынести напряжения во время ускорения, а с другой - очень важно
свести вес всей конструкции до минимума, чтобы полезная нагрузка и полезная
мощность двигателей были как можно больше.
Фактически
превышение силы Эйлера вовсе не означает, что после этого балка полностью
разрушится. Когда отклонение становится большим, сила благодаря члену ![]() в уравнении
(38.38), которым мы пренебрегли, будет на самом деле больше вычисленной. Чтобы
найти силы при большом продольном изгибании стержня, мы должны вернуться к
точному уравнению (38.44), которое получалось до использования приближенной
связи между
в уравнении
(38.38), которым мы пренебрегли, будет на самом деле больше вычисленной. Чтобы
найти силы при большом продольном изгибании стержня, мы должны вернуться к
точному уравнению (38.44), которое получалось до использования приближенной
связи между ![]() и
и
![]() .
.
Уравнение
(38.44) имеет довольно простые геометрические свойства. Решается оно немного
сложнее, но зато гораздо интереснее. Вместо того чтобы описывать кривую через ![]() и
и ![]() , можно
воспользоваться двумя новыми переменными:
, можно
воспользоваться двумя новыми переменными: ![]() - расстоянием вдоль кривой и
- расстоянием вдоль кривой и ![]() - наклоном
касательной к кривой (фиг. 38.17.) Тогда кривизна будет равна скорости
изменения угла с расстоянием
- наклоном
касательной к кривой (фиг. 38.17.) Тогда кривизна будет равна скорости
изменения угла с расстоянием
![]() .
.
Поэтому точное уравнение (38.44) можно записать в виде
![]() .
.
После
взятия производной этого уравнения по ![]() и замены
и замены ![]() на
на ![]() получим
получим
![]() . (38.47)
. (38.47)
[Если
углы ![]() малы,
то мы снова приходим к уравнению (38.45), стало быть здесь все в порядке.]
малы,
то мы снова приходим к уравнению (38.45), стало быть здесь все в порядке.]

Фиг. 38.17. Координаты кривой
продольно изогнутой балки ![]() и
и ![]() .
.
Не
знаю, можете ли вы еще удивляться, но уравнение (38.47) получилось в точности
таким же, как и для колебаний маятника с большой амплитудой (разумеется, с
заменой ![]() другой
постоянной). Еще раньше, в гл. 9 (вып. 1), мы узнали, как находить решение
такого уравнения численным методом. В ответе вы получите очаровательную кривую.
На фиг. 38.18 показаны три кривые для разных значений постоянной
другой
постоянной). Еще раньше, в гл. 9 (вып. 1), мы узнали, как находить решение
такого уравнения численным методом. В ответе вы получите очаровательную кривую.
На фиг. 38.18 показаны три кривые для разных значений постоянной ![]() .
.

Фиг. 38.18. Формы продольно изогнутого стержня.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
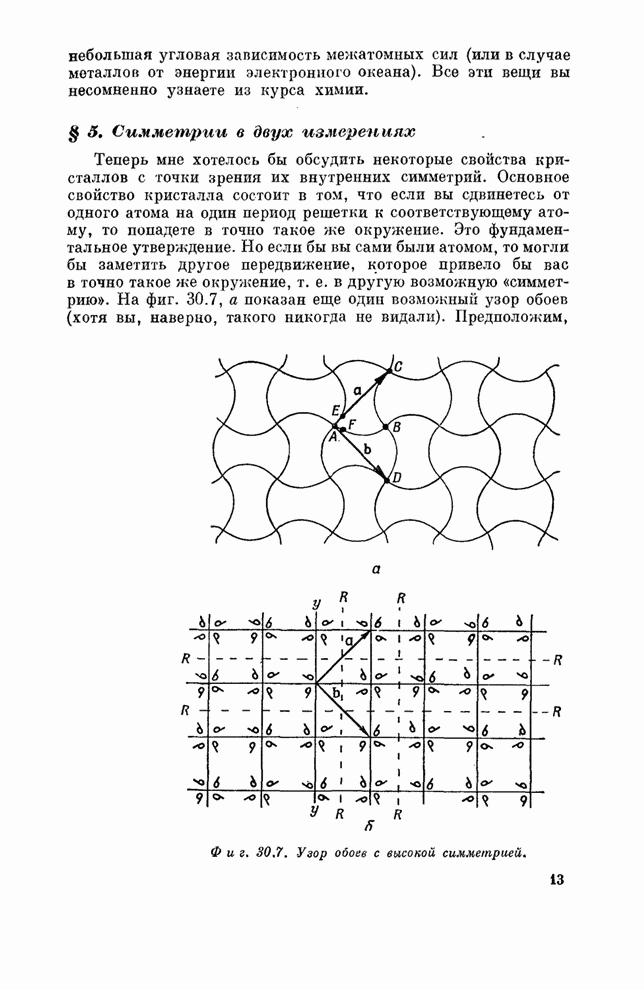
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
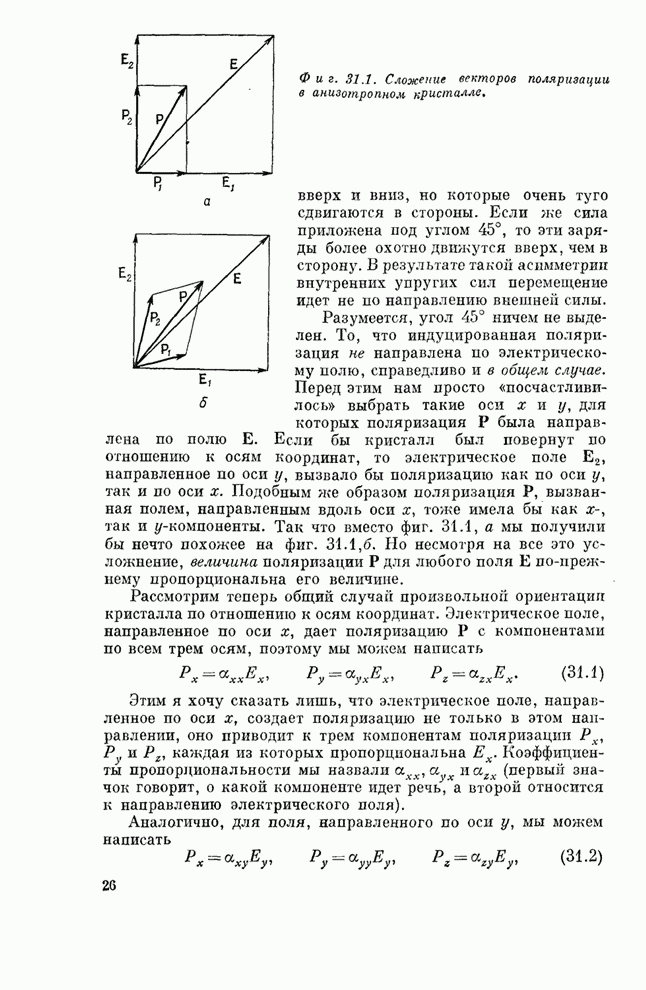
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
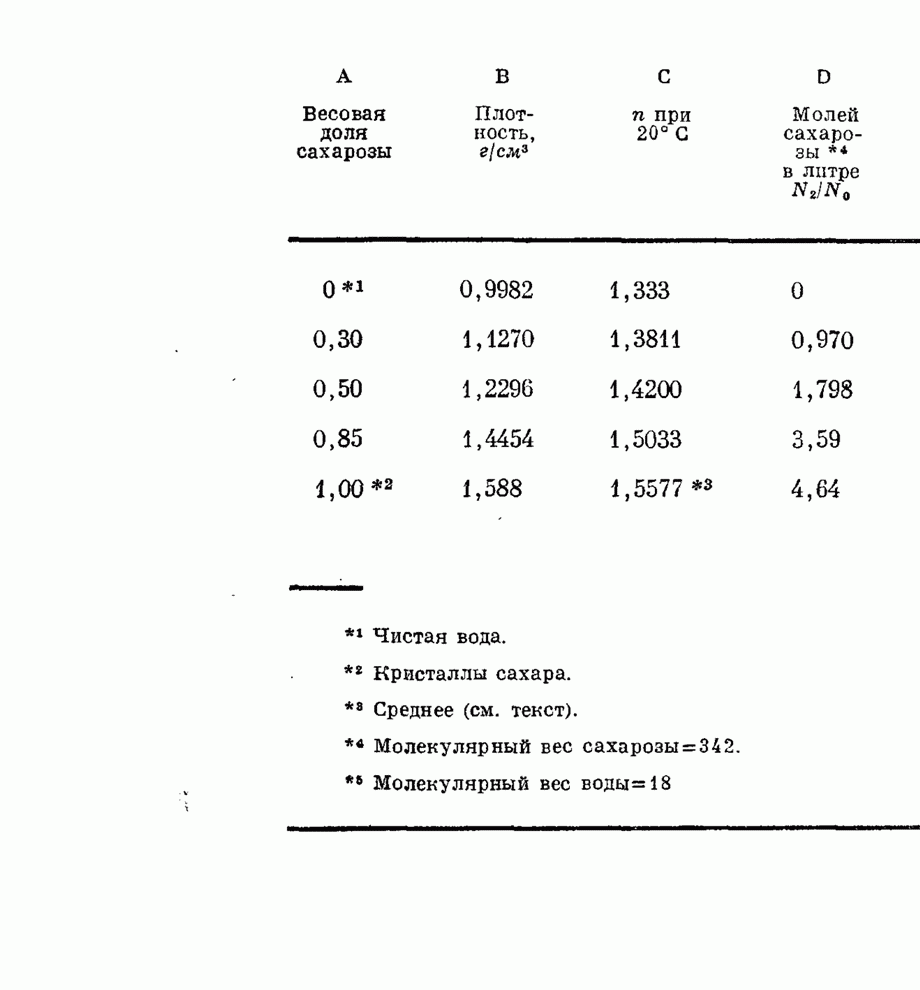
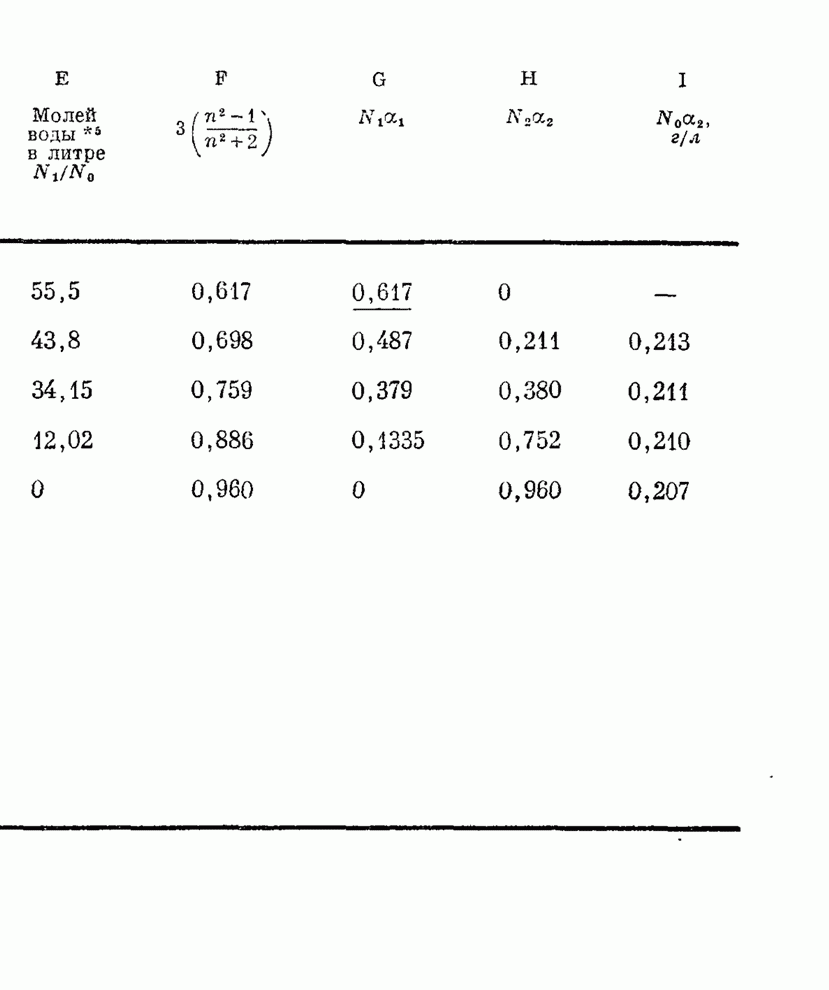
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
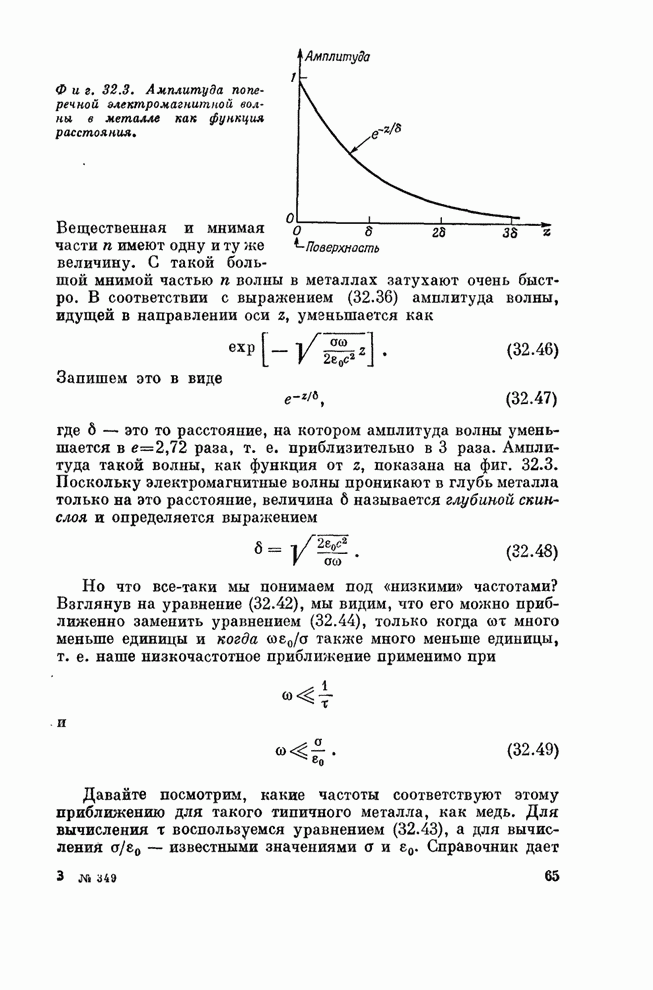
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
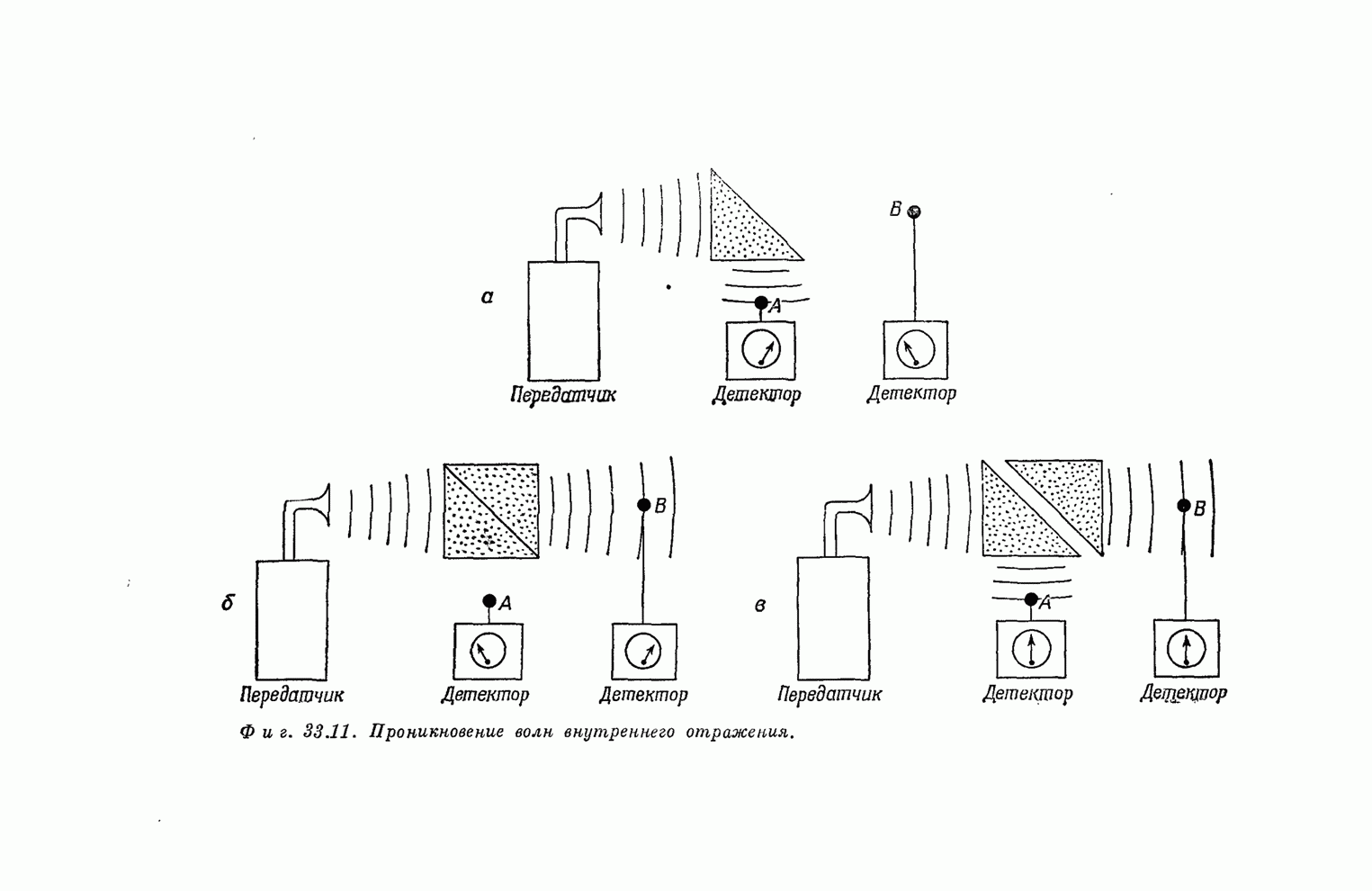
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
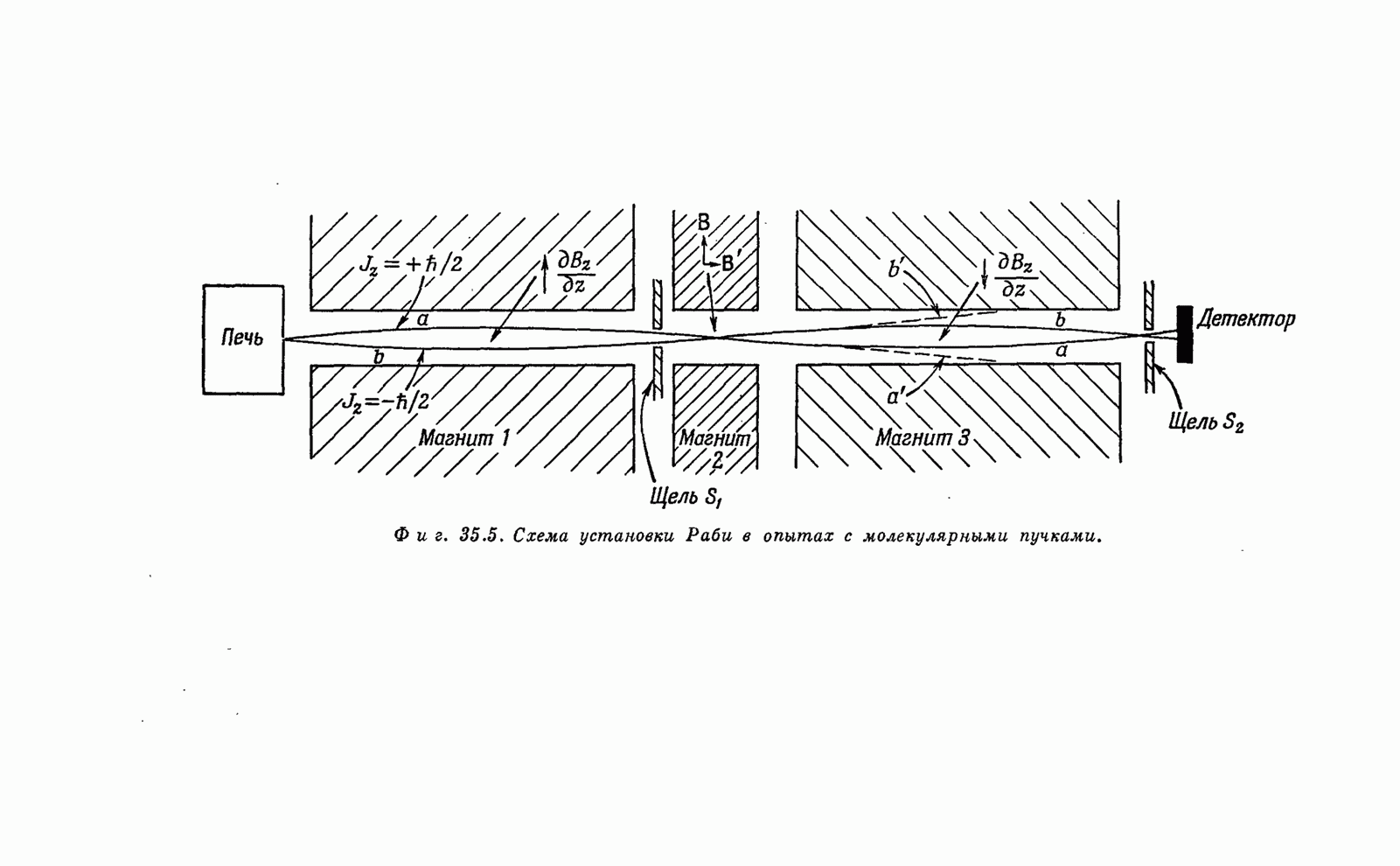
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
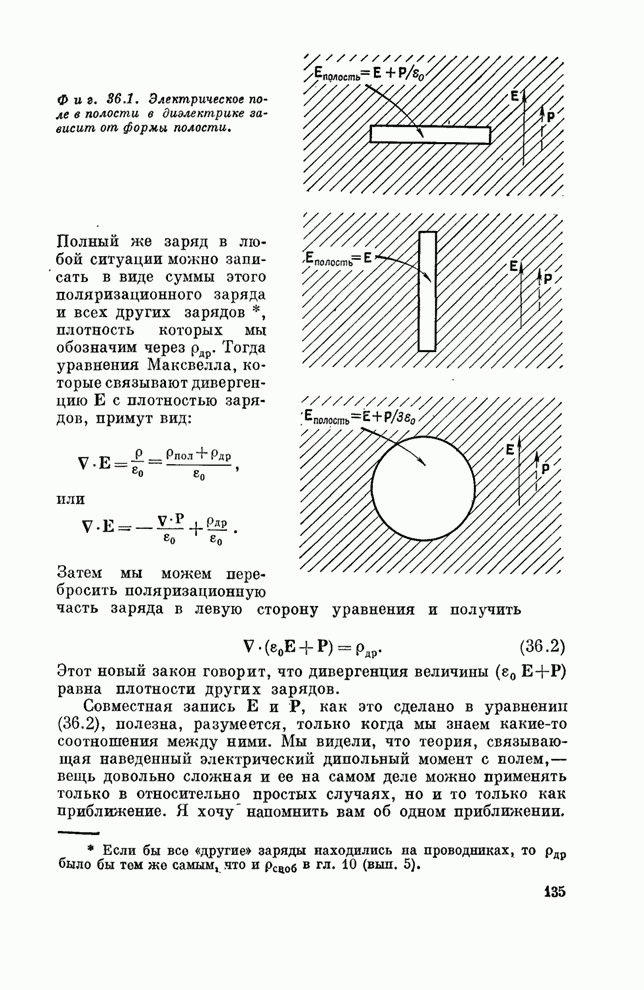
- § 1. Токи намагничивания
- § 2. Поле
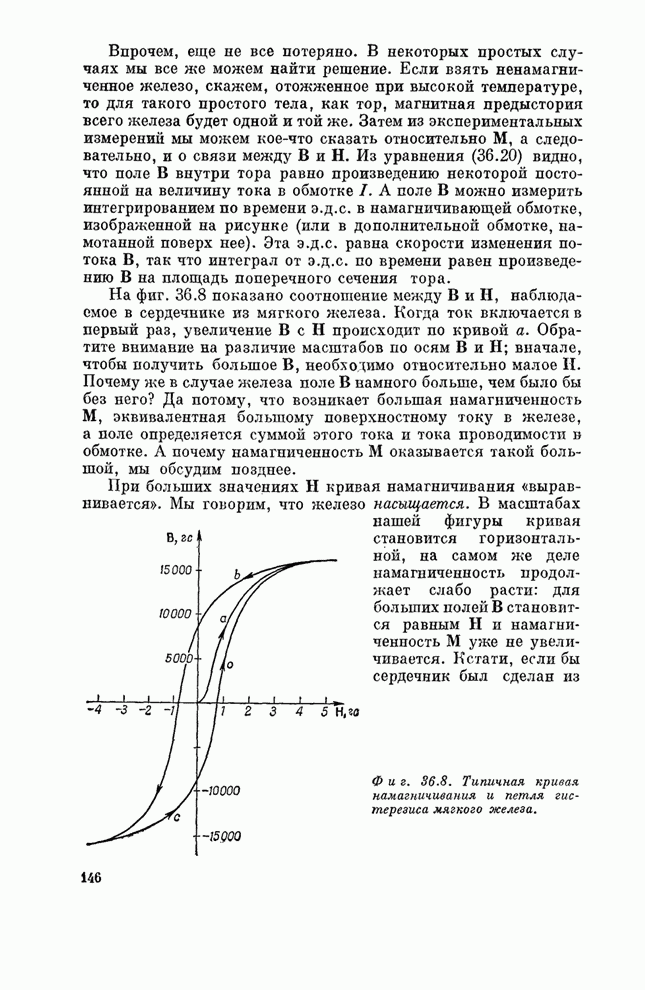
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
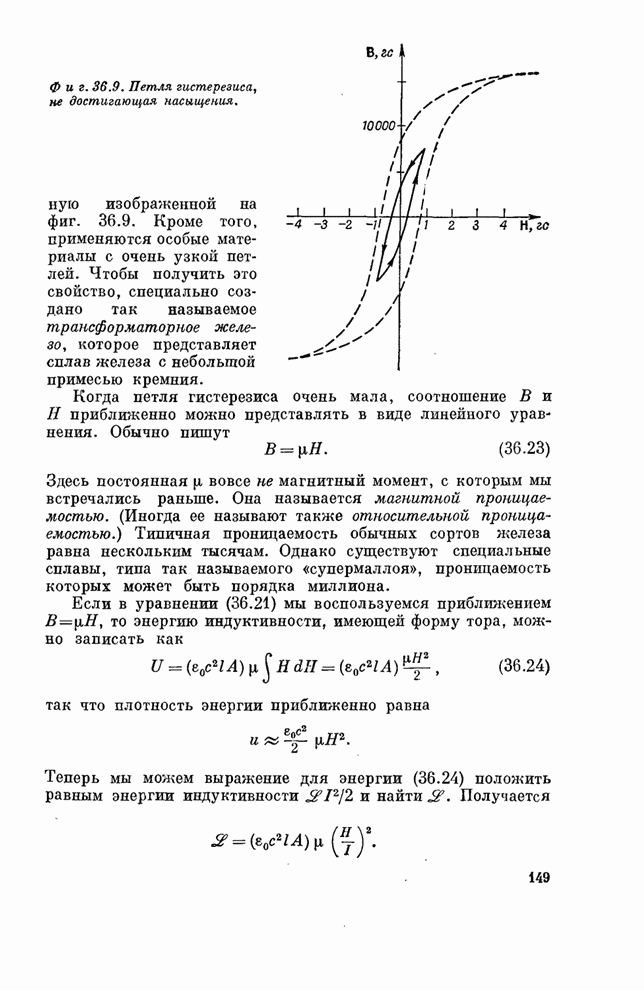
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)