| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Неупругое поведение
Во
всем, что до сих пор говорилось, мы предполагали, что напряжение
пропорционально деформации, а это вообще-то неверно. На фиг. 39.8 приведена
типичная диаграмма напряжение-деформация упругого материала. Для малых
деформаций напряжение пропорционально деформации. Однако после некоторой точки
зависимость напряжения от деформации начинает отклоняться от прямой линии. Для
многих материалов, которые мы назовем «хрупкими», разрушение наступает, когда
деформация несколько превысит ту точку, где кривая начинает загибаться. В общем
же случае в диаграмме напряжение-деформация есть и другие усложнения. Например,
когда вы деформируете предмет, существующие большие напряжения могут затем
медленно уменьшиться со временем. Если вы достигнете высоких напряжений, однако
ниже точки разрыва, а затем будете уменьшать деформацию, то напряжения будут
возвращаться назад уже по другой кривой. Возникает небольшой гистерезисный
эффект (наподобие того, что мы видели в связи между ![]() и
и ![]() в магнитных материалах).
в магнитных материалах).

Фиг. 39.8. Типичная диаграмма напряжение-деформация для больших деформаций.
Напряжения, при которых происходит разрушение, сильно изменяются от материала к материалу. Некоторые материалы разрушаются при максимальном растягивающем напряжении. Другие же разрушаются при определенной величине напряжения сдвига. Скажем, мел гораздо слабее противостоит растяжению, чем сдвигу. Если вы потянете за концы палочки мела, то она сломается перпендикулярно направлению приложенной силы (фиг. 39.9, справа). Ведь мел - это только спрессованные частички, которые легко растаскиваются в стороны, поэтому он ломается перпендикулярно приложенной силе. А в отношении сдвига этот материал гораздо крепче, так как в этом случае частицы мешают друг другу. Вспомните теперь, что когда мы скручиваем стержень, то в любом его поперечном сечении возникают сдвиги. Мы показали, кроме того, что сдвиг эквивалентен комбинации растяжения и сжатия под углом 45°. По этой причине при скручивании кусочек мела разломится по сложной поверхности, которая расположена под углом 45° к образующим. На фиг. 39.9 (слева) приведена фотография куска мела, сломанного таким способом. Мел ломается там, где напряжения максимальны.

Фиг. 39.9. Сломанный кусочек мела:
Справа - растягиванием за концы; слева - скручиванием.
Есть и другие материалы, которые ведут себя очень странным и сложным образом. Чем сложнее материал, тем причудливей его поведение. Если мы возьмем лист сарана, скомкаем его и бросим на стол, то постепенно он расправится и примет свою первоначальную плоскую форму. На первый взгляд кажется соблазнительным считать, что здесь основную роль играет именно упругость. Но простой подсчет покажет, что она слишком слаба (на несколько порядков слабее), чтобы как-то влиять на этот эффект. Оказывается, что здесь соревнуются два механизма: «нечто» внутри материала «помнит» первоначальную форму и «пытается» вернуться к старому виду, а «нечто» другое «предпочитает» новую форму и сопротивляется возврату к старой,
Я не хочу вдаваться в подробности и описывать тот механизм, который играет роль в поведении скомканного листа сарана, но получить представление о том, как такие эффекты происходят, вы можете на следующей модели. Представьте себе материал, изготовленный из длинных гибких, но крепких нитей вперемешку с пустотелыми ячейками, заполненными вязкой жидкостью. Представьте также, что между каждой ячейкой и соседними с ней имеются узкие проходы, по которым жидкость может медленно проникать из одной ячейки в другую. Если мы скомкаем лист такого материала, то длинные нити деформируются, жидкость из одной ячейки будет выжиматься и переходить в другие ячейки, которые оказались растянутыми. Когда же мы отпускаем лист, то длинные нити будут стремиться вернуться к своей первоначальной форме. Однако, чтобы сделать это, они должны заставить жидкость возвратиться на свое прежнее место, что происходит довольно медленно из-за ее вязкости. Силы, которые мы прилагаем, комкая лист, гораздо больше сил, развиваемых нитями. Скомкать лист можно очень быстро, а вот вернуться к прежнему виду он сможет гораздо медленнее. Несомненно, что здесь основную роль играет комбинация больших, жестких молекул и более мелких, но более подвижных. Этот механизм согласуется также с тем фактом, что материал быстрее принимает свою первоначальную форму, если он нагрет, и медленнее в холодном состоянии: тепло увеличивает подвижность (уменьшает вязкость) мелких молекул.
Хотя
мы обсуждали, как происходит нарушение закона Гука, но, по-видимому, наиболее
удивительно все же не нарушение этого закона при больших деформациях, а его универсальность.
Некоторое понятие о том, почему так происходит, вы можете получить,
рассматривая энергию деформации материала. Утверждение о том, что напряжение
пропорционально деформации, равносильно утверждению, что энергия деформации
изменяется как квадрат напряжения. Предположим, что мы скрутили стержень на
малый угол ![]() Если
справедлив закон Гука, то энергия деформации должна быть пропорциональна
квадрату
Если
справедлив закон Гука, то энергия деформации должна быть пропорциональна
квадрату ![]() .
Предположим, что энергия является некоторой произвольной функцией угла. Мы
можем записать ее в виде разложения Тэйлора около нуля:
.
Предположим, что энергия является некоторой произвольной функцией угла. Мы
можем записать ее в виде разложения Тэйлора около нуля:
![]() . (39.40)
. (39.40)
Момент
силы ![]() представляет
производную
представляет
производную ![]() по
углу, поэтому
по
углу, поэтому
![]() . (39.41)
. (39.41)
Если
теперь отсчитывать угол от положения равновесия, то первое слагаемое будет
равно нулю. Таким образом, первое оставшееся слагаемое пропорционально ![]() и при достаточно
малых углах оно будет превосходить слагаемое с
и при достаточно
малых углах оно будет превосходить слагаемое с ![]() . [На самом деле, внутренне материалы
в достаточной мере симметричны, так что
. [На самом деле, внутренне материалы
в достаточной мере симметричны, так что ![]() ; слагаемое с
; слагаемое с ![]() оказывается нулем, а
отклонение от линейности происходит только из-за слагаемого с
оказывается нулем, а
отклонение от линейности происходит только из-за слагаемого с ![]() . Однако нет
причин, по которым это было бы верно для растяжения и сжатия.] Единственно, что
мы не объяснили, - почему материалы обычно разрушаются вскоре после того, как
становятся существенными члены высшего порядка.
. Однако нет
причин, по которым это было бы верно для растяжения и сжатия.] Единственно, что
мы не объяснили, - почему материалы обычно разрушаются вскоре после того, как
становятся существенными члены высшего порядка.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
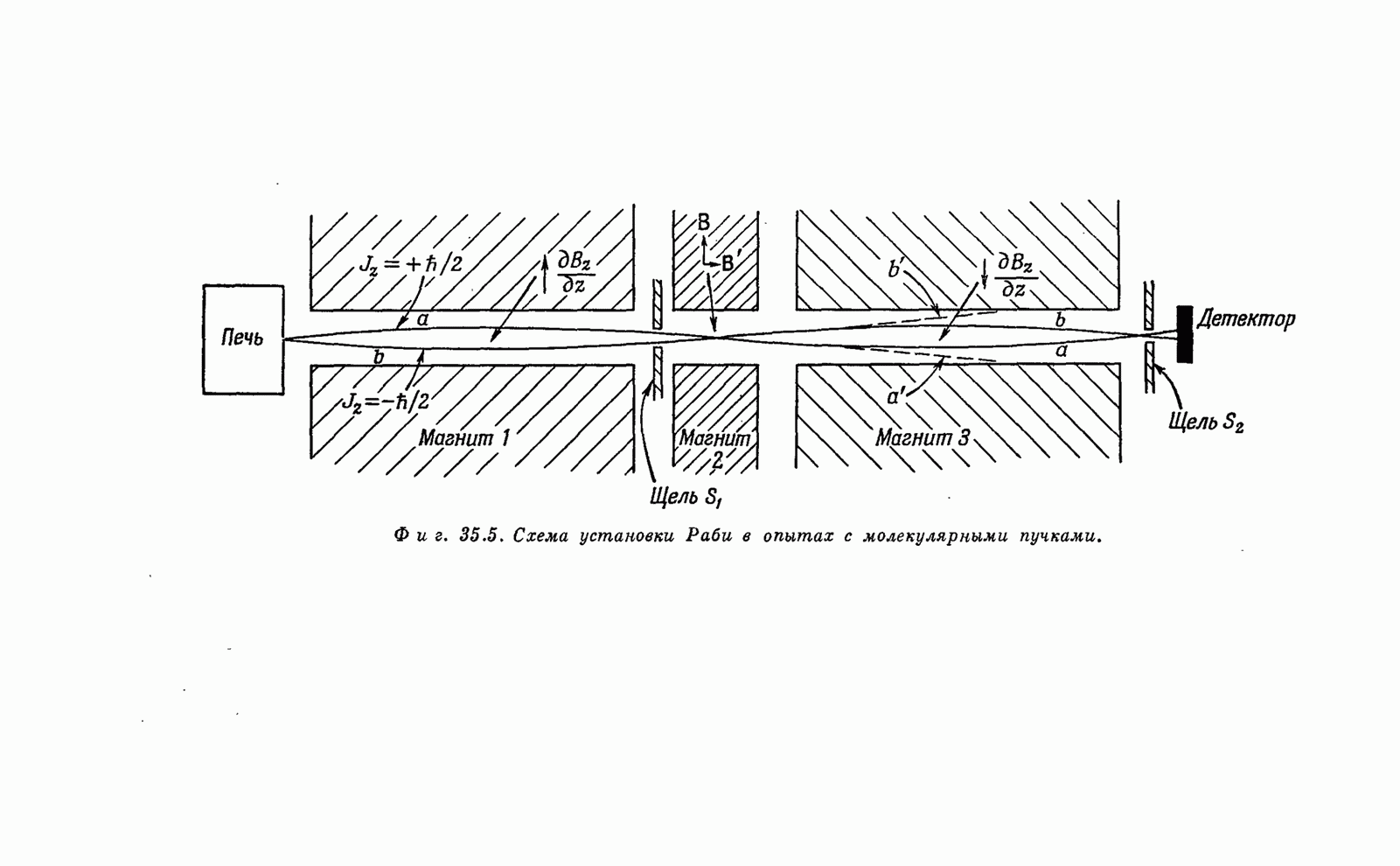
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)