| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. Магнитная энергия атомов
Теперь я снова хочу поговорить о магнитном моменте. Я уже говорил, что в квантовой механике магнитный момент атомной системы может быть связан с моментом количества движения соотношением (34.6):
![]() , (34.27)
, (34.27)
где
![]() -
заряд, a
-
заряд, a ![]() -
масса электрона.
-
масса электрона.
Атомные магнитики, будучи помещены во внешнее магнитное поле, приобретут дополнительную магнитную энергию, которая зависит от компоненты их магнитного момента в направлении поля. Мы знаем, что
![]() . (34.28)
. (34.28)
Выбирая
ось ![]() вдоль
направления поля
вдоль
направления поля ![]() , получаем
, получаем
![]() . (34.29)
. (34.29)
А используя уравнение (34.27), находим
![]() .
.
Согласно
квантовой механике, величина ![]() может принимать только такие
значения:
может принимать только такие
значения: ![]() .
Поэтому магнитная энергия атомной системы не произвольна, допустимы только
некоторые ее значения. Например, максимальная величина энергии равна
.
Поэтому магнитная энергия атомной системы не произвольна, допустимы только
некоторые ее значения. Например, максимальная величина энергии равна
![]() .
.
Величину
![]() обычно
называют «магнетоном Бора» и обозначают через
обычно
называют «магнетоном Бора» и обозначают через ![]() :
:
![]() .
.
Возможные значения магнитной энергии будут следующими:
![]() ,
,
где
![]() принимает
одно из следующих значений:
принимает
одно из следующих значений: ![]() .
.
Другими
словами, энергия атомной системы, помещенной в магнитное поле, изменяется на
величину, пропорциональную полю и компоненте ![]() . Мы говорим, что энергия атомной
магнитной системы «расщепляется магнитным полем на
. Мы говорим, что энергия атомной
магнитной системы «расщепляется магнитным полем на ![]() уровня». Например, атомы
со спином
уровня». Например, атомы
со спином ![]() ,
энергия которых вне магнитного поля равна
,
энергия которых вне магнитного поля равна ![]() , в магнитном поле будут иметь четыре
возможных значения энергии. Эти энергии можно изобразить на диаграмме энергетических
уровней наподобие фиг. 34.5. Однако энергия каждого атома в данном поле
, в магнитном поле будут иметь четыре
возможных значения энергии. Эти энергии можно изобразить на диаграмме энергетических
уровней наподобие фиг. 34.5. Однако энергия каждого атома в данном поле ![]() принимает только
одно из четырех возможных значений. Именно это говорит квантовая механика о
поведении атомной системы в магнитном поле.
принимает только
одно из четырех возможных значений. Именно это говорит квантовая механика о
поведении атомной системы в магнитном поле.

Фиг. 34.5. Возможные магнитные
энергии атомной системы со спином 3/2 в магнитном поле ![]() .
.
Простейшая
«атомная» система - отдельный электрон. Спин электрона равен 1/2, поэтому у
него возможны два состояния: ![]() и
и ![]() . Для спинового магнитного момента
отдельного покоящегося электрона (у которого отсутствует орбитальное движение)
. Для спинового магнитного момента
отдельного покоящегося электрона (у которого отсутствует орбитальное движение) ![]() , так что
магнитная энергия будет
, так что
магнитная энергия будет ![]() . На фиг. 34.6 показаны возможные
энергии электрона в магнитном поле. Грубо говоря, спин электрона направлен либо
«вверх» (по магнитному полю), либо «вниз» (против поля).
. На фиг. 34.6 показаны возможные
энергии электрона в магнитном поле. Грубо говоря, спин электрона направлен либо
«вверх» (по магнитному полю), либо «вниз» (против поля).

Фиг. 34.6. Два возможных энергетических
состояния электрона в магнитном поле ![]() .
.
У
системы с более высоким спином число состояний тоже больше. Поэтому мы можем в
зависимости от величины ![]() говорить о спине, направленном
«вверх» или «вниз» или под некоторым «углом».
говорить о спине, направленном
«вверх» или «вниз» или под некоторым «углом».
Эти результаты квантовой механики мы будем использовать при обсуждении магнитных свойств материалов в следующей главе.
| << Предыдущий параграф | Следующий параграф >> |
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
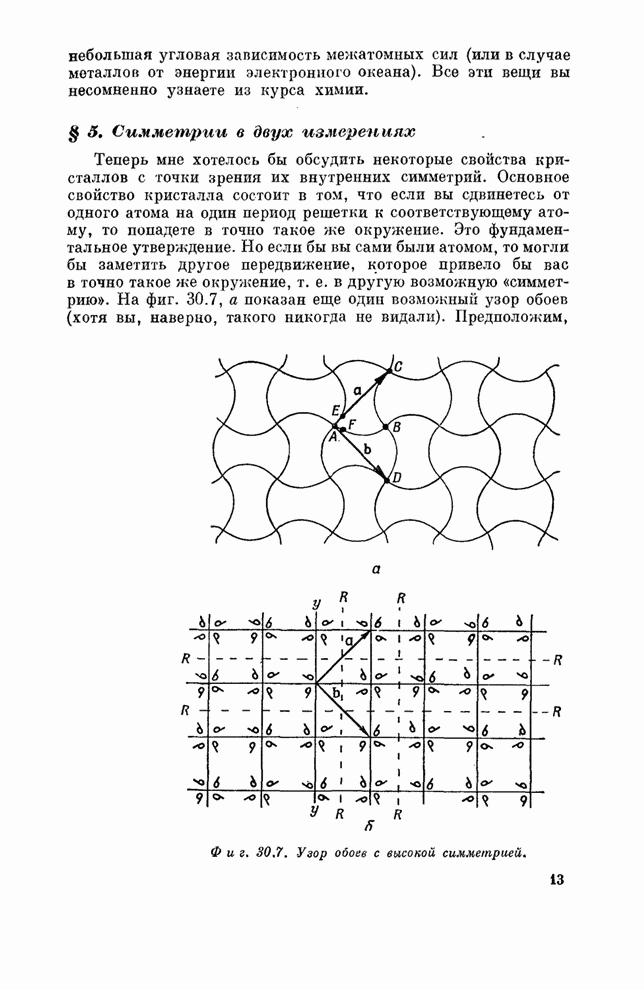
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
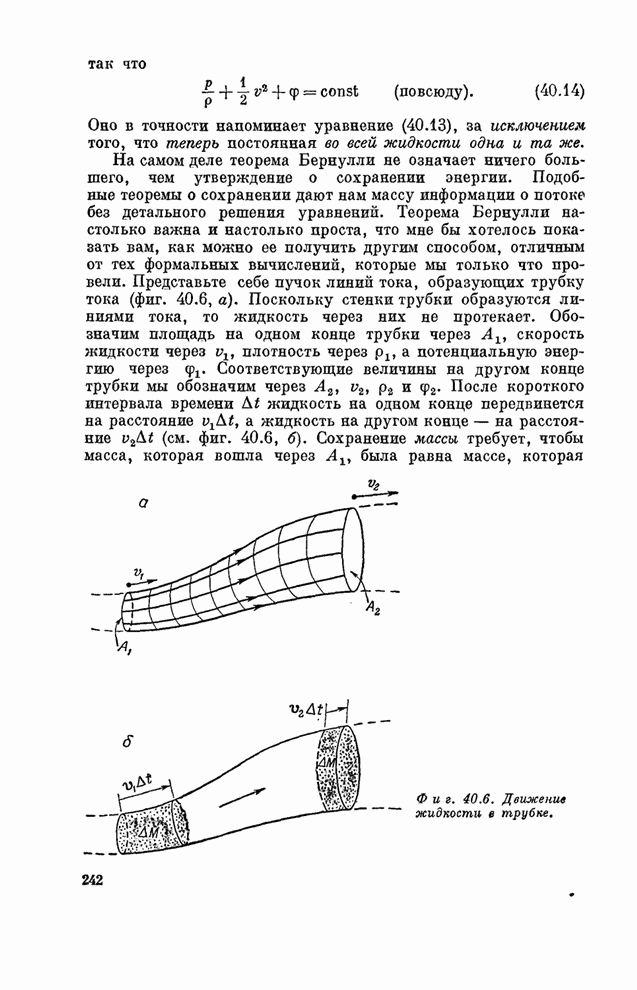
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
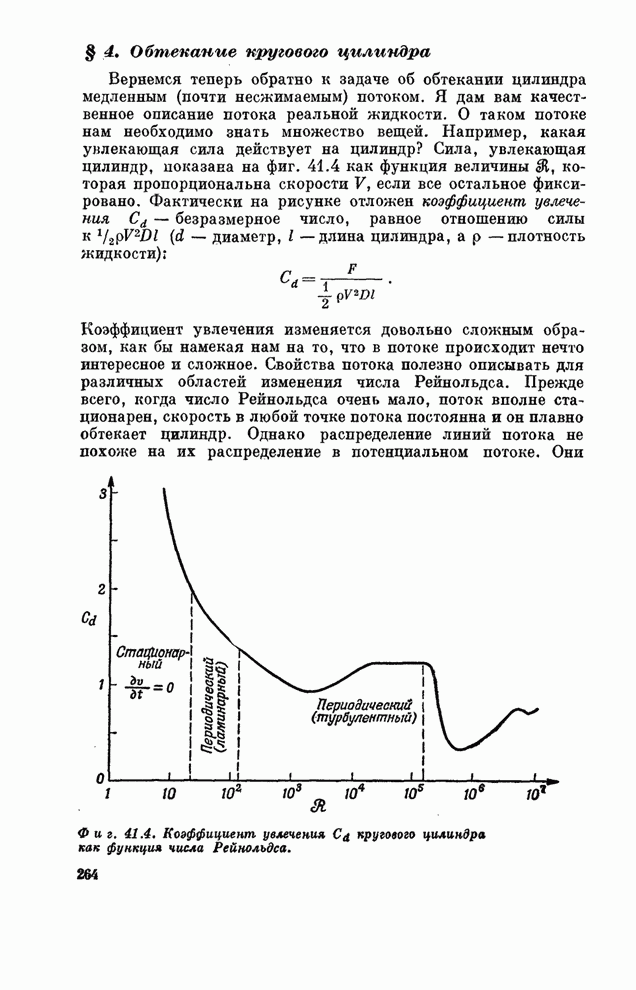
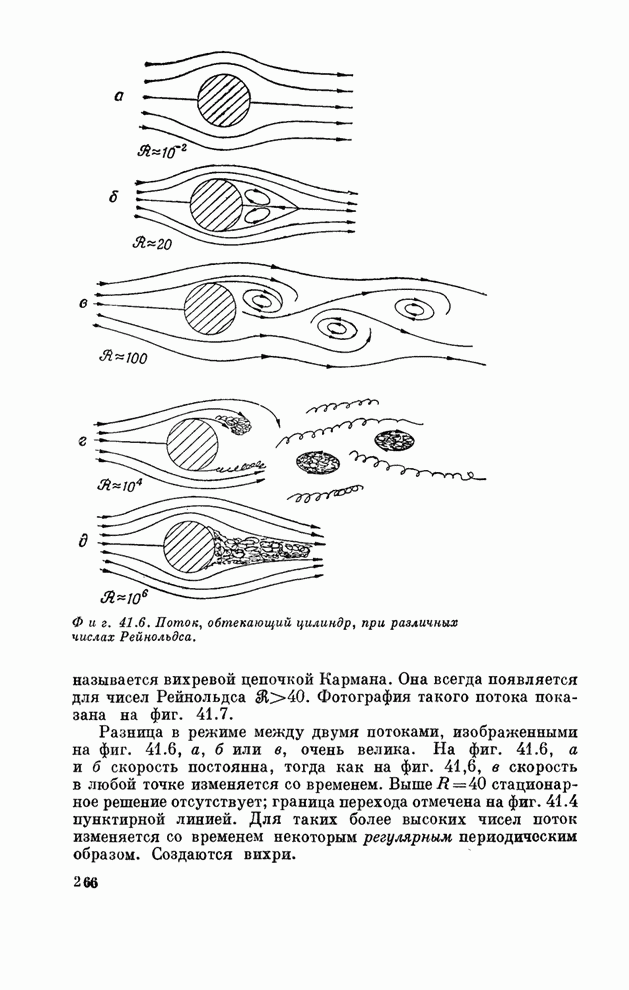
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)