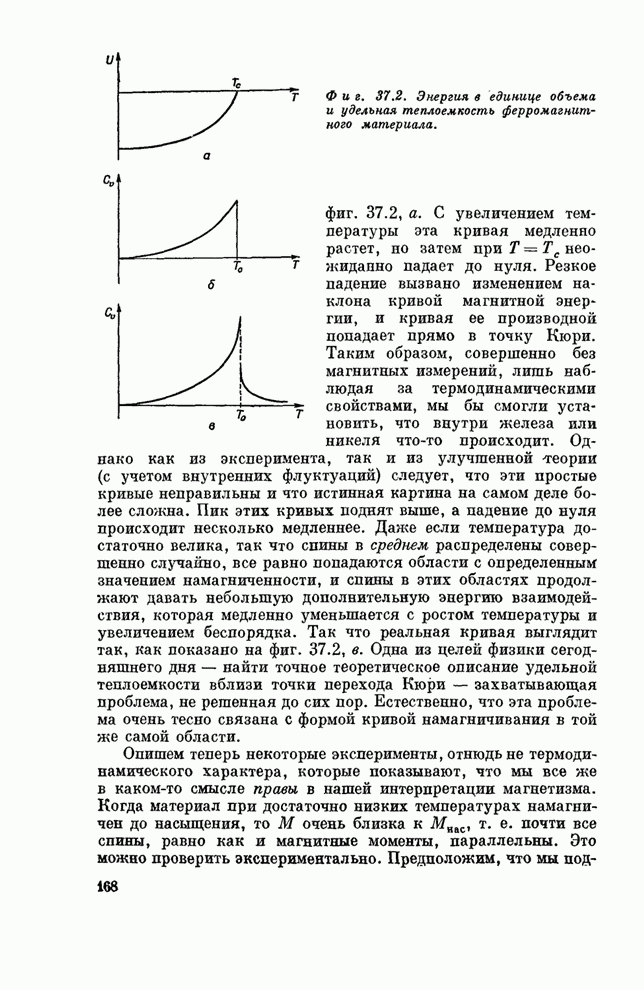
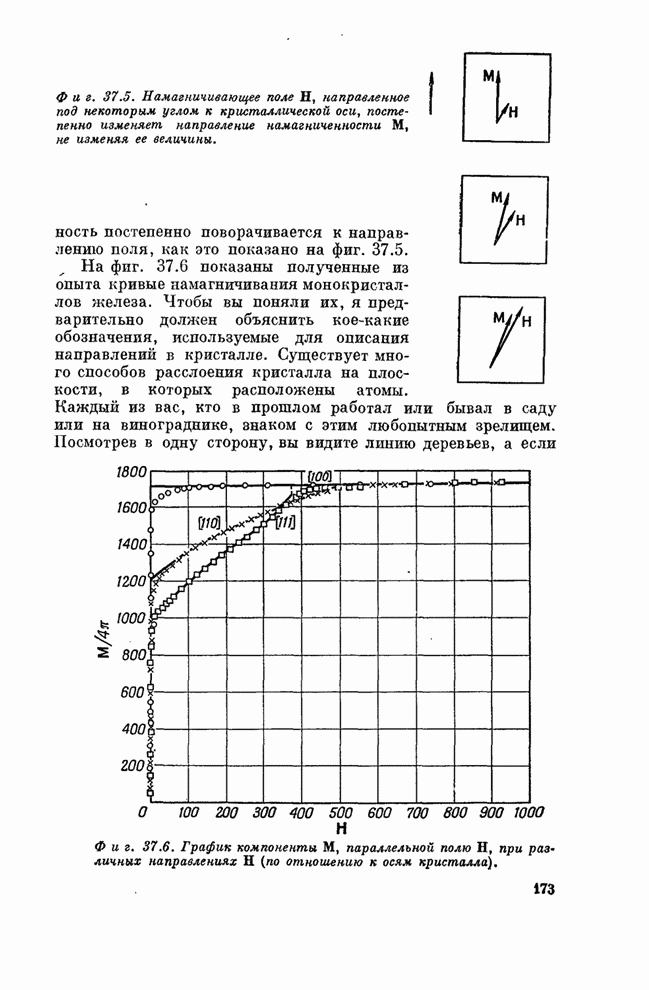
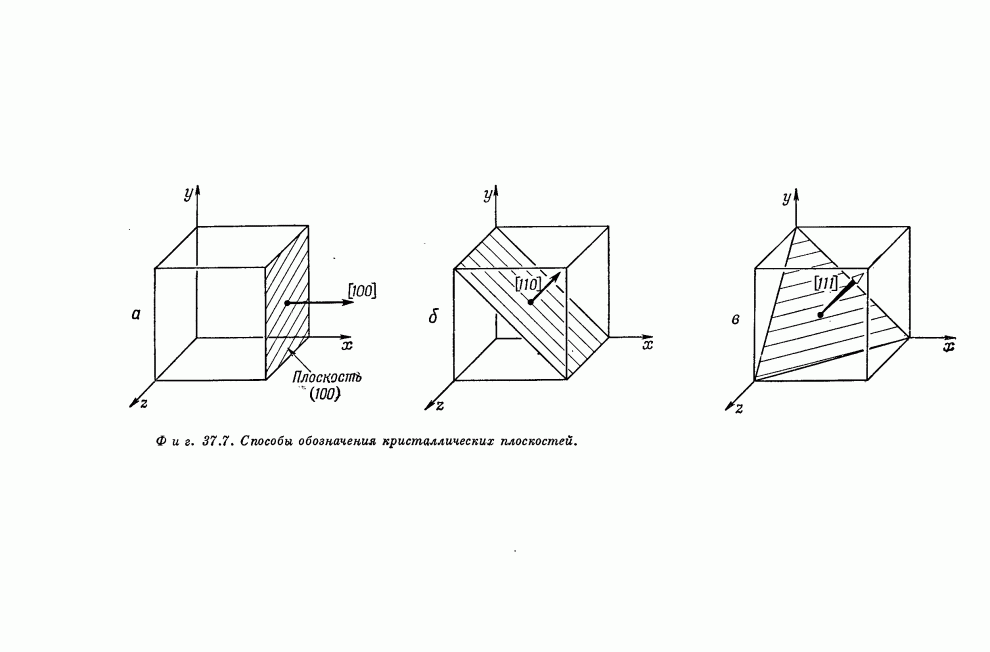
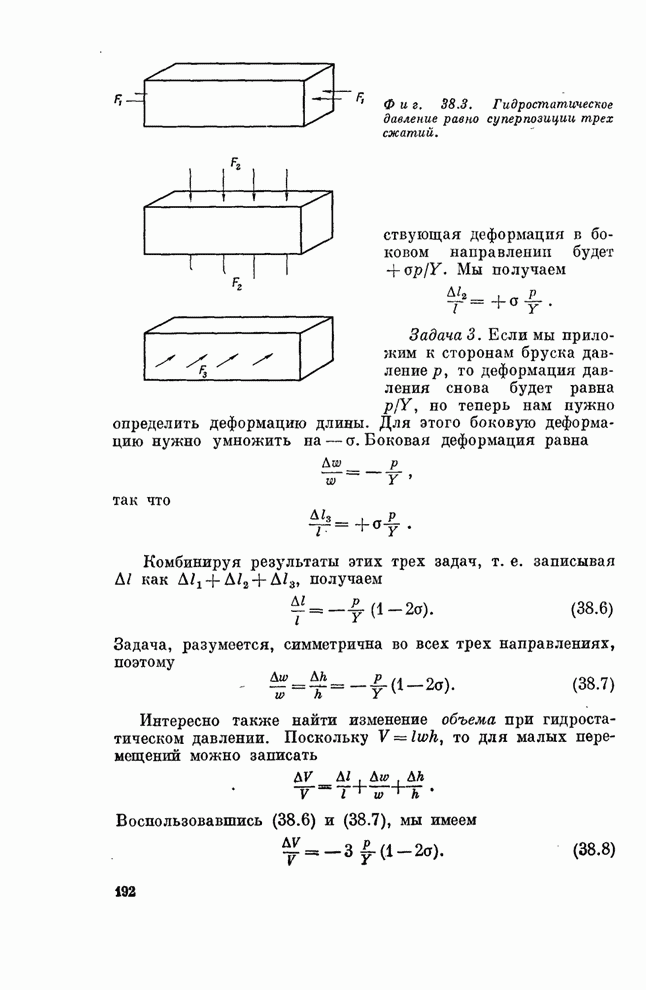
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Отраженная и преломленная волны
Теперь мы готовы применить наши граничные условия к волнам, перечисленным в § 2, где мы получили:
![]() , (33.32)
, (33.32)
![]() , (33.33)
, (33.33)
![]() , (33.34)
, (33.34)
![]() , (33.35)
, (33.35)
![]() , (33.36)
, (33.36)
![]() . (33.37)
. (33.37)
Нами
получены еще кое-какие сведения: вектор ![]() перпендикулярен для каждой волны
вектору распространения
перпендикулярен для каждой волны
вектору распространения ![]() .
.
Полученный
результат будет зависеть от направления вектора ![]() («поляризации») в падающей волне.
Анализ сильно упростится, если мы рассмотрим отдельно случай, когда вектор
(«поляризации») в падающей волне.
Анализ сильно упростится, если мы рассмотрим отдельно случай, когда вектор ![]() параллелен
«плоскости падения» (т. е. плоскости
параллелен
«плоскости падения» (т. е. плоскости ![]() ), и случай, когда он перпендикулярен
к ней. Волна с любой другой поляризацией будет просто линейной комбинацией этих
волн. Другими словами, отраженные и преломленные интенсивности для различных
поляризаций будут разными и легче всего отобрать два простейших случая и
отдельно рассмотреть их.
), и случай, когда он перпендикулярен
к ней. Волна с любой другой поляризацией будет просто линейной комбинацией этих
волн. Другими словами, отраженные и преломленные интенсивности для различных
поляризаций будут разными и легче всего отобрать два простейших случая и
отдельно рассмотреть их.
Я
подробно проанализирую случай падающей волны, перпендикулярной к плоскости
падения, а потом просто опишу вам, что получается в других случаях. Я немного
жульничаю, рассматривая простейший пример, однако в обоих случаях принцип один
и тот же. Итак, мы считаем, что вектор ![]() имеет только
имеет только ![]() -компоненту, а поскольку
все векторы
-компоненту, а поскольку
все векторы ![]() смотрят
в одном и том же направлении, векторный значок можно опустить.
смотрят
в одном и том же направлении, векторный значок можно опустить.
Оба
материала изотропны, поэтому вынужденные колебания зарядов в материале будут
происходить в направлении оси ![]() и
и ![]() полей
полей ![]() в преломленной и отраженной волнах
тоже будет только одна
в преломленной и отраженной волнах
тоже будет только одна ![]() -компонента. Таким образом, для всех
волн
-компонента. Таким образом, для всех
волн ![]() и
и ![]() ,
, ![]() и
и ![]() равны нулю.
Направления векторов
равны нулю.
Направления векторов ![]() и
и ![]() в этих волнах показаны на фиг. 33.6.
(Здесь мы изменили нашему первоначальному намерению все получить из уравнений.
Этот результат также можно было бы получить из граничных условий, однако,
используя физические аргументы, мы избежали больших алгебраических выкладок.
Когда у вас будет свободное время, посмотрите, можно ли его действительно
вывести из уравнений. Он, разумеется, согласуется с уравнениями; просто мы не
доказали, что отсутствуют другие возможности.)
в этих волнах показаны на фиг. 33.6.
(Здесь мы изменили нашему первоначальному намерению все получить из уравнений.
Этот результат также можно было бы получить из граничных условий, однако,
используя физические аргументы, мы избежали больших алгебраических выкладок.
Когда у вас будет свободное время, посмотрите, можно ли его действительно
вывести из уравнений. Он, разумеется, согласуется с уравнениями; просто мы не
доказали, что отсутствуют другие возможности.)

Фиг. 33.6. Поляризации отраженной
и преломленной волн, когда поле ![]() в падающей волне перпендикулярно к
плоскости падения.
в падающей волне перпендикулярно к
плоскости падения.
Теперь
наши граничные условия [уравнения (33.26)-(33.31)] должны дать соотношения
между компонентами ![]() и
и ![]() в областях 1 и 2. В области 2 у нас
есть только одна преломленная волна, а вот в области 1 - их две. Какую же из
них нам взять? Поля в области 1 будут, разумеется, суперпозицией полей падающей
и отраженной волн. (Поскольку каждое удовлетворяет уравнениям Максвелла, то им
удовлетворяет и сумма.) Поэтому, когда мы используем граничные условия, нужно
помнить, что
в областях 1 и 2. В области 2 у нас
есть только одна преломленная волна, а вот в области 1 - их две. Какую же из
них нам взять? Поля в области 1 будут, разумеется, суперпозицией полей падающей
и отраженной волн. (Поскольку каждое удовлетворяет уравнениям Максвелла, то им
удовлетворяет и сумма.) Поэтому, когда мы используем граничные условия, нужно
помнить, что
![]()
и
аналогично для ![]() .
.
Для
поляризаций, которыми мы сейчас занимаемся, уравнения (33.26) и (33.28) не дают
никакой новой информации, и только уравнение (33.27) поможет нам. Оно говорит,
что на границе, т. е. при ![]() :
:
![]() .
.
Таким образом, мы получаем уравнение
![]() , (33.38)
, (33.38)
которое
должно выполняться для любого ![]() и любого
и любого ![]() . Возьмем сначала
. Возьмем сначала ![]() . Для этого
значения уравнение (33.38) превращается в
. Для этого
значения уравнение (33.38) превращается в
![]() ,
,
согласно которому два осциллирующих члена равны третьему. Это может произойти, только когда частоты всех осцилляций одинаковы. (Невозможно, сложив три или какое-то другое число подобных членов с различными частотами, получить для любого момента времени в результате нуль.) Итак,
![]() , (33.39)
, (33.39)
как это и было нам всегда известно, т. е. частоты преломленной и отраженной волн те же самые, что и падающей.
Если бы мы предположили это с самого начала, то несомненно избежали бы многих трудностей, но мне хотелось показать вам, что тот же самый результат можно получить и из уравнений. А вот когда перед вами будет стоять реальная задача, лучше всего пускать в оборот сразу все, что вы знаете. Это избавит вас от лишних хлопот.
По
определению абсолютная величина ![]() задается равенством
задается равенством ![]() , поэтому
, поэтому
 . (33.40)
. (33.40)
А
теперь обратимся к уравнению (33.38) для ![]() . Используя снова те же рассуждения,
что и прежде, но на сей раз основываясь на том, что уравнения должны быть
справедливы при всех значениях
. Используя снова те же рассуждения,
что и прежде, но на сей раз основываясь на том, что уравнения должны быть
справедливы при всех значениях ![]() , мы получаем
, мы получаем
![]() . (33.41)
. (33.41)
Из
формулы (33.40) ![]() ,
так что
,
так что
![]() .
.
Комбинируя это с (33.41), находим
![]() ,
,
или
![]() . Знак
плюс не имеет никакого смысла; он не дает нам никакой отраженной волны, а лишь
другую падающую волну, и с самого начала мы говорили, что будем решать задачу с
единственной падающей волной, так что
. Знак
плюс не имеет никакого смысла; он не дает нам никакой отраженной волны, а лишь
другую падающую волну, и с самого начала мы говорили, что будем решать задачу с
единственной падающей волной, так что
![]() . (33.42)
. (33.42)
Два соотношения (33.41) и (33.42) говорят нам, что угол отражения равен углу падения, как это и ожидалось (см, фиг. 33.3). Итак, в отраженной волне
![]() . (33.43)
. (33.43)
Для преломленной волны мы уже получали
![]()
и
 . (33.44)
. (33.44)
Их можно решить и в результате получить
 . (33.45)
. (33.45)
Предположим
на мгновение, что ![]() и
и ![]() - вещественные числа (т. е. что
мнимая часть показателей очень мала). Тогда все
- вещественные числа (т. е. что
мнимая часть показателей очень мала). Тогда все ![]() тоже будут вещественными и из фиг.
33.3 мы видим, что
тоже будут вещественными и из фиг.
33.3 мы видим, что
![]() . (33.46)
. (33.46)
Но ввиду уравнения (33.44) мы получаем
![]() , (33.47)
, (33.47)
т. е. уже известный нам закон Снелла для преломления. Если же показатель преломления не вещественный, то волновые числа оказываются комплексными и нам следует воспользоваться
(33.45).
[Конечно, мы могли бы определить углы ![]() и
и ![]() из (33.46), и тогда закон Снелла
(33.47) был бы верен и в общем случае. Однако при этом углы тоже стали бы
комплексными числами и, следовательно, потеряли бы свою геометрическую
интерпретацию как углы. Уж лучше описывать поведение волн соответствующими
комплексными величинами
из (33.46), и тогда закон Снелла
(33.47) был бы верен и в общем случае. Однако при этом углы тоже стали бы
комплексными числами и, следовательно, потеряли бы свою геометрическую
интерпретацию как углы. Уж лучше описывать поведение волн соответствующими
комплексными величинами ![]() или
или ![]() .]
.]
До
сих пор мы не обнаружили ничего нового. Мы доставили себе только простенькое
развлечение, выводя очевидные вещи из сложного математического механизма. А
сейчас мы готовы найти амплитуды волн, которые нам еще не известны. Используя
результаты для всех ![]() и
и ![]() , мы можем сократить экспоненциальный
множитель в (33.38) и получить
, мы можем сократить экспоненциальный
множитель в (33.38) и получить
![]() . (33.48)
. (33.48)
Но
поскольку мы не знаем ни ![]() , ни
, ни ![]() , то необходимо еще одно соотношение.
Нужно использовать еще одно граничное условие. Уравнения для
, то необходимо еще одно соотношение.
Нужно использовать еще одно граничное условие. Уравнения для ![]() и
и ![]() не помогут, ибо
все
не помогут, ибо
все ![]() имеют
только одну
имеют
только одну ![]() -компоненту.
Так что мы должны воспользоваться условием на
-компоненту.
Так что мы должны воспользоваться условием на ![]() . Попробуем взять (33.29):
. Попробуем взять (33.29):
![]() .
.
Согласно условиям (33.35)-(33.37),
![]() .
.
Вспоминая,
что ![]() и
и ![]() , получаем
, получаем
![]() .
.
Но это снова уравнение (33.48)! Мы напрасно потратили время и получили то, что уже давно нам известно.
Можно
было бы обратиться к (33.30) ![]() , но у вектора
, но у вектора ![]() отсутствует
отсутствует ![]() -компонента!
Осталось только одно условие - (33.31)
-компонента!
Осталось только одно условие - (33.31) ![]() . Для наших трех волн
. Для наших трех волн
![]() . (33.49)
. (33.49)
Подставляя
вместо ![]() ,
,
![]() и
и ![]() волновые
выражения при
волновые
выражения при ![]() (ибо
дело происходит на границе), мы получаем следующее граничное условие:
(ибо
дело происходит на границе), мы получаем следующее граничное условие:
![]() .
.
Учитывая
равенство всех ![]() и
и
![]() , снова
приходим к условию
, снова
приходим к условию
![]() . (33.50)
. (33.50)
Это
дает нам уравнение для величины ![]() , отличное от (33.48). Получившиеся
два уравнения можно решить относительно
, отличное от (33.48). Получившиеся
два уравнения можно решить относительно ![]() и
и ![]() . Вспоминая, что
. Вспоминая, что ![]() получаем
получаем
![]() , (33.51)
, (33.51)
![]() . (33.52)
. (33.52)
Вместе
с (33.45) или (33.46) для ![]() эти формулы дают нам все, что мы
хотели узнать. Следствия полученного результата мы обсудим в следующем
параграфе.
эти формулы дают нам все, что мы
хотели узнать. Следствия полученного результата мы обсудим в следующем
параграфе.
Если
взять поляризованную волну с вектором ![]() , параллельным плоскости падения, то
, параллельным плоскости падения, то ![]() , как это видно из
фиг. 33.7, будет иметь как
, как это видно из
фиг. 33.7, будет иметь как ![]() -, так и
-, так и ![]() -компоненту. Вся алгебра
при этом будет менее хитрая, но более сложная. (Можно, правда, несколько
уменьшить работу в этом случае, выражая все через магнитное поле, которое
целиком направлено по оси
-компоненту. Вся алгебра
при этом будет менее хитрая, но более сложная. (Можно, правда, несколько
уменьшить работу в этом случае, выражая все через магнитное поле, которое
целиком направлено по оси ![]() .) При этом мы найдем
.) При этом мы найдем
 (33.53)
(33.53)
и
![]() . (33.54)
. (33.54)

Фиг. 33.7. Поляризации волн, когда
поле ![]() в
падающей волне параллельно плоскости падения.
в
падающей волне параллельно плоскости падения.
Давайте
посмотрим, будет ли наш результат согласовываться с тем, что мы получали
раньше. Выражение (33.3) мы вывели в вып. 3, когда находили отношение
интенсивностей отраженной и падающей волн. Однако тогда мы рассматривали только
вещественный показатель преломления. Для вещественного показателя (или
вещественных ![]() )
можно записать:
)
можно записать:

Подставляя это в уравнение (33.51), получаем
![]() , (33.55)
, (33.55)
что
нисколько не похоже на уравнение (33.3). Если, однако, мы воспользуемся законом
Снелла и избавимся от всех ![]() , то сходство будет восстановлено.
Подставляя
, то сходство будет восстановлено.
Подставляя ![]() и
умножая числитель и знаменатель на
и
умножая числитель и знаменатель на ![]() , получаем
, получаем
![]() .
.
Обратите
внимание, что в числителе и знаменателе стоят просто синусы ![]() и
и ![]() , поэтому
, поэтому
![]() . (33.56)
. (33.56)
Поскольку
амплитуды ![]() и
и
![]() измеряются
в том же самом материале, интенсивности пропорциональны квадратам электрических
полей и мы получаем тот же результат, что и раньше. Подобным же образом формула
(33.53) тоже аналогична формуле (33.4).
измеряются
в том же самом материале, интенсивности пропорциональны квадратам электрических
полей и мы получаем тот же результат, что и раньше. Подобным же образом формула
(33.53) тоже аналогична формуле (33.4).
Для
волн, падающих перпендикулярно, ![]() и
и ![]() . Формула (33.56) выглядит как 0/0,
от чего нам пользы мало. Однако мы можем вернуться назад к формуле (33.55),
согласно которой
. Формула (33.56) выглядит как 0/0,
от чего нам пользы мало. Однако мы можем вернуться назад к формуле (33.55),
согласно которой
 . (33.57)
. (33.57)
Этот результат, естественно, применим для «любой» поляризации, поскольку для перпендикулярного луча нет никакой особой «плоскости падения».
| << Предыдущий параграф | Следующий параграф >> |
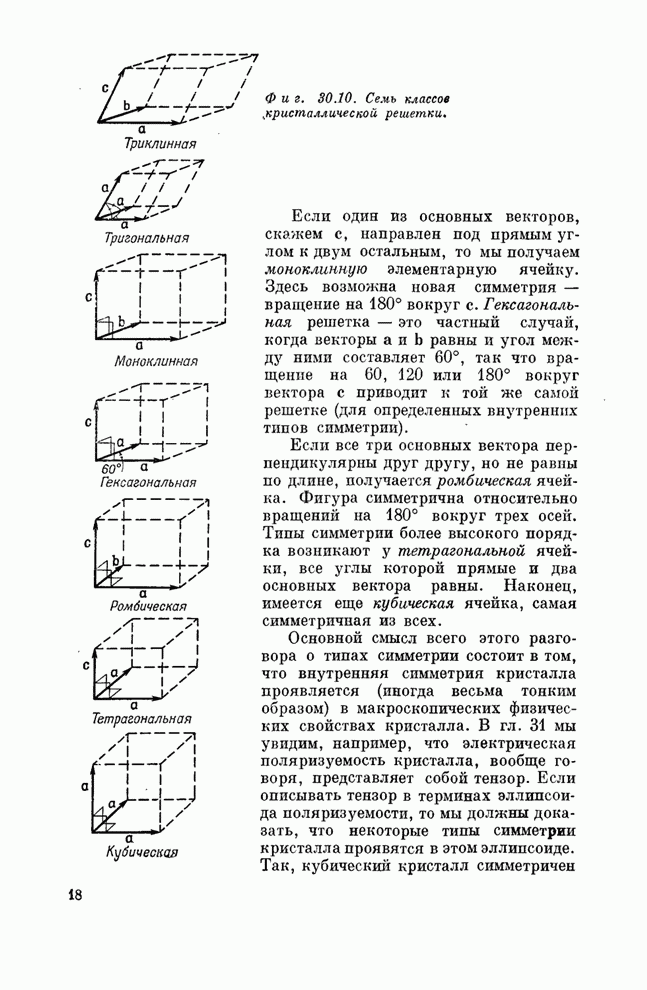
- Глава 30. ВНУТРЕННЯЯ ГЕОМЕТРИЯ КРИСТАЛЛОВ
- § 1. Внутренняя геометрия кристаллов
- § 2. Химические связи в кристаллах
- § 3. Рост кристаллов
- § 4. Кристаллические решетки
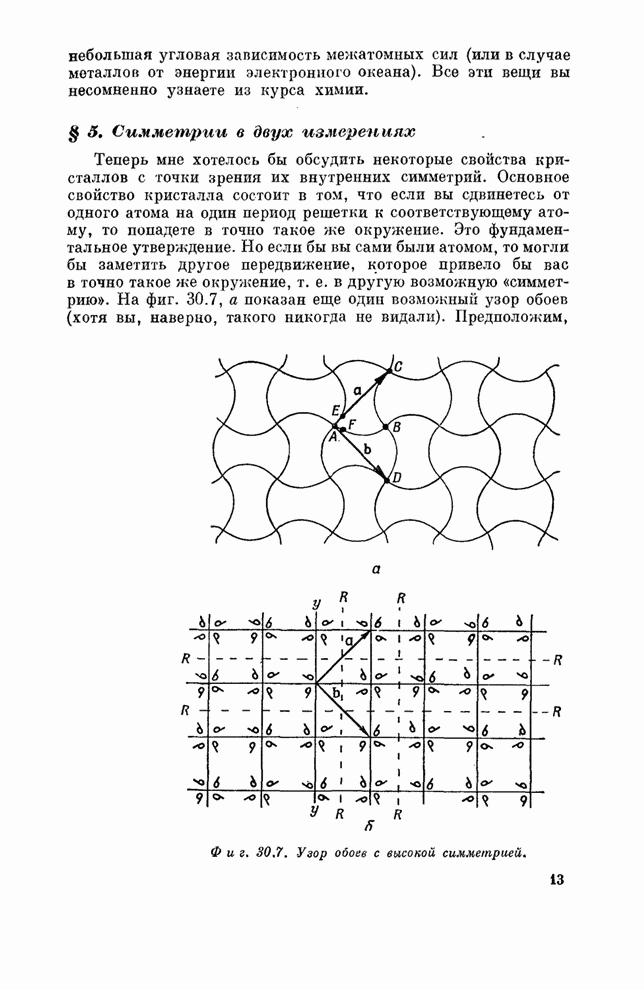
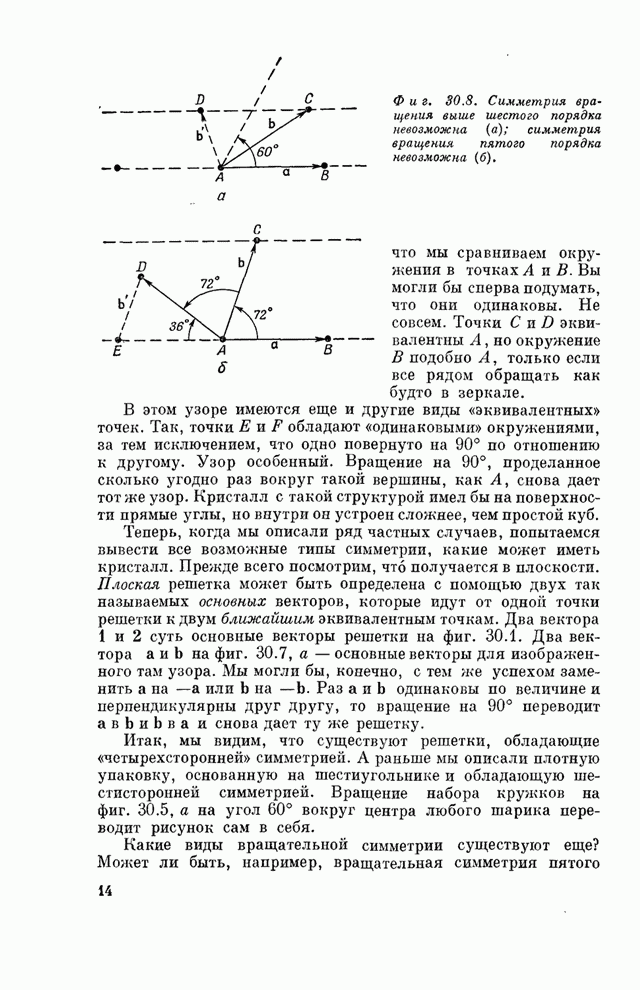
- § 5. Симметрии в двух измерениях
- § 6. Симметрии в трех измерениях
- § 7. Прочность металлов
- § 8. Дислокации и рост кристаллов
- § 9. Модель кристалла по Брэггу и Наю
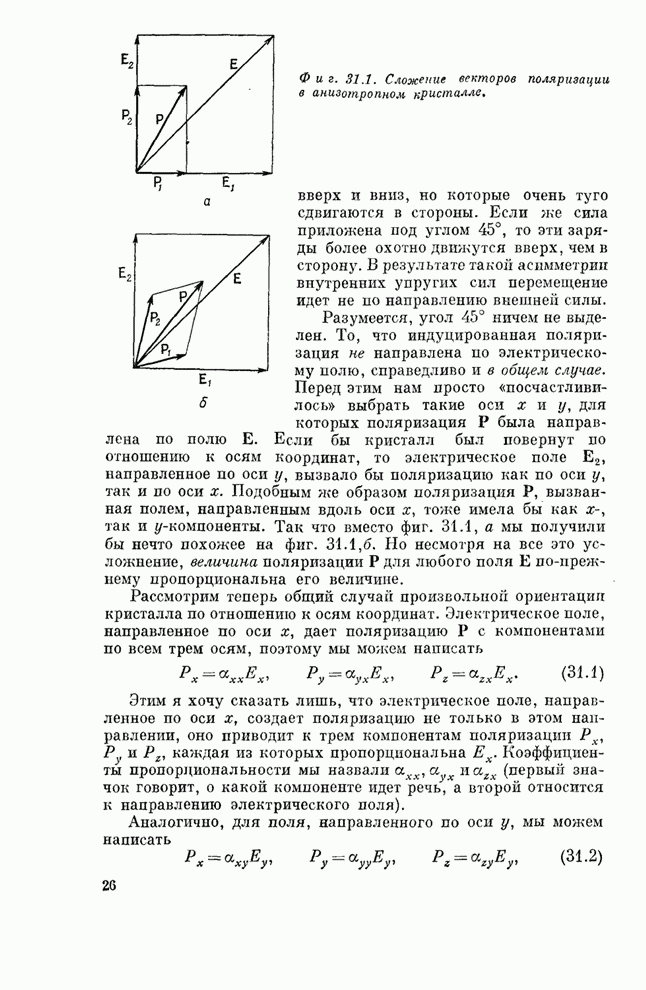
- Главa 31. ТЕНЗОРЫ
- § 1. Тензор поляризуемости
- § 2. Преобразование компонент тензора
- § 3. Эллипсоид энергии
- § 4. Другие тензоры; тензор инерции
- § 5. Векторное произведение
- § 6. Тензор напряжений
- § 7. Тензоры высших рангов
- § 8. Четырехмерный тензор электромагнитного импульса
- Глава 32. ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ ПЛОТНОГО ВЕЩЕСТВА
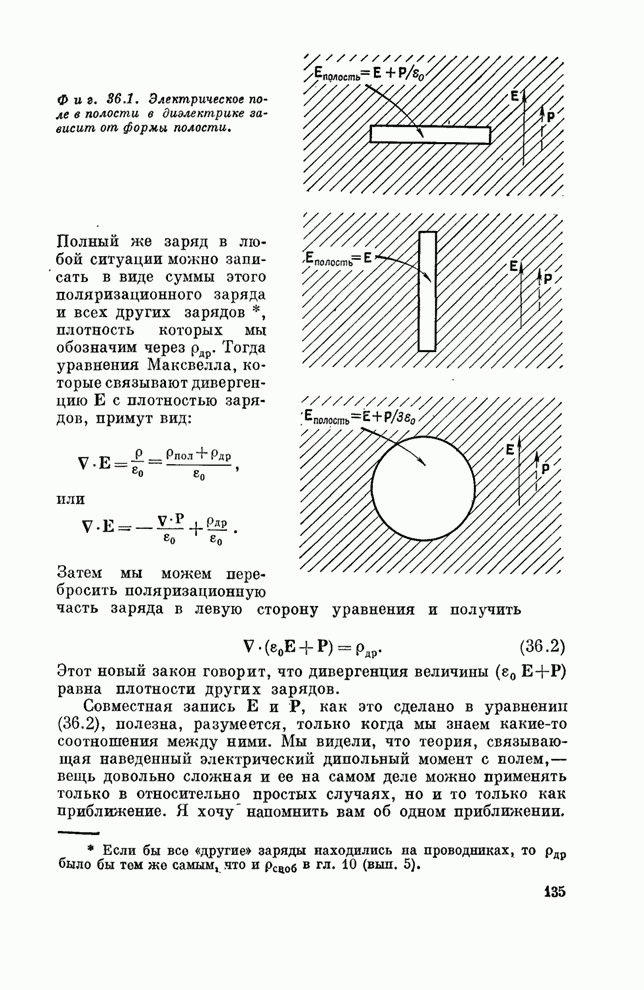
- § 1. Поляризация вещества
- § 2. Уравнения Максвелла в диэлектрике
- § 3. Волны в диэлектрике
- § 4. Комплексный показатель преломления
- § 5. Показатель преломления смеси
- § 6. Волны в металлах
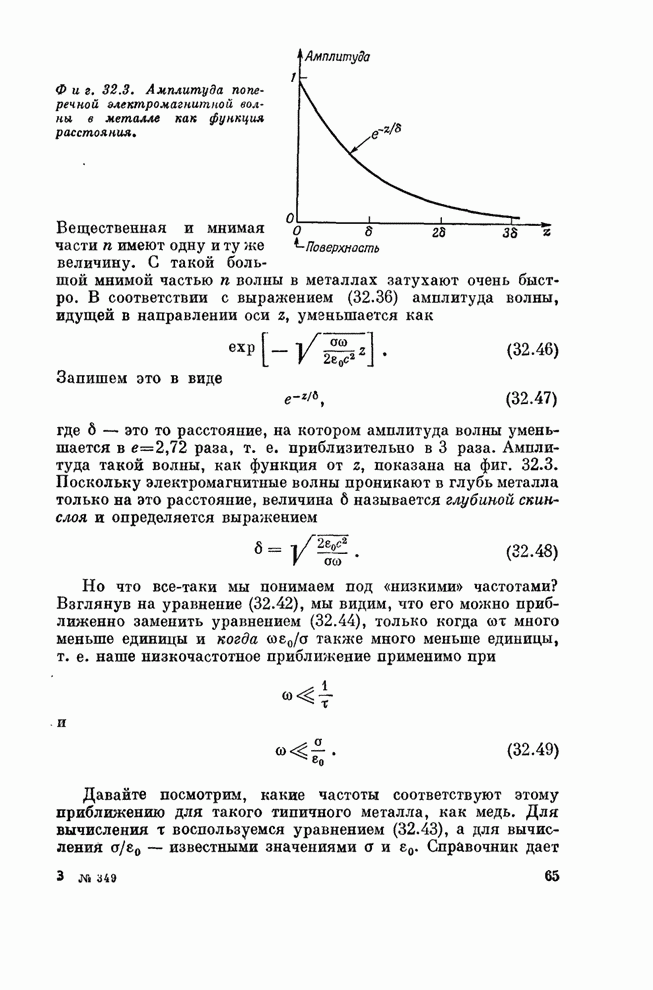
- § 7. Низкочастотное и высокочастотное приближения; глубина скин-слоя и плазменная частота
- Глава 33. ОТРАЖЕНИЕ ОТ ПОВЕРХНОСТИ
- § 1. Отражение и преломление света
- § 2. Волны в плотных материалах
- § 3. Граничные условия
- § 4. Отраженная и преломленная волны
- § 5. Отражение от металлов
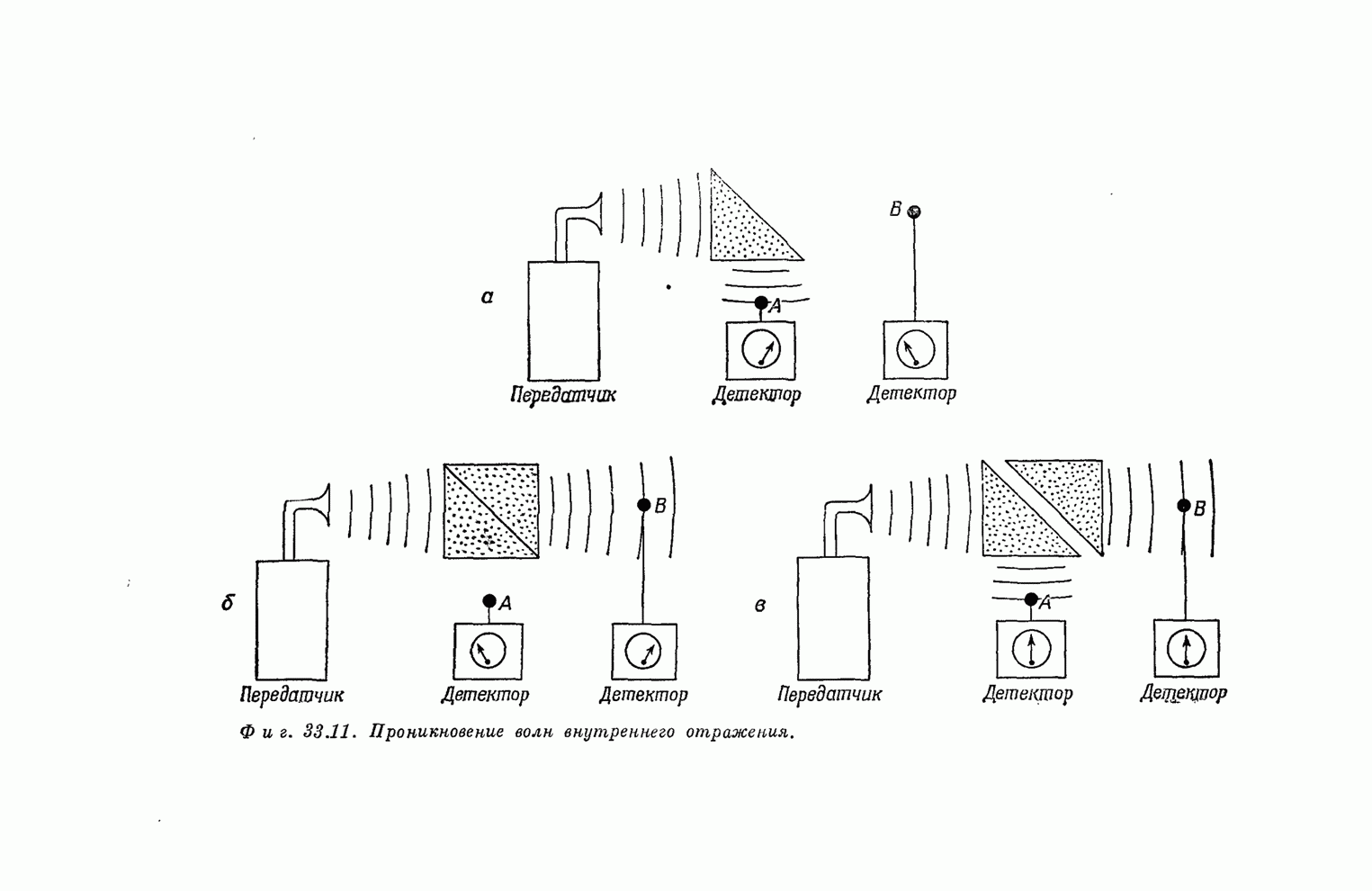
- § 6. Полное внутреннее отражение
- Глава 34. МАГНЕТИЗМ ВЕЩЕСТВА
- § 1. Диамагнетизм и парамагнетизм
- § 2. Магнитные моменты и момент количества движения
- § 3. Прецессия атомных магнитиков
- § 4. Диамагнетизм
- § 5. Теорема Лармора
- § 6. В классической физике нет ни диамагнетизма, ни парамагнетизма
- § 7. Момент количества движения в квантовой механике
- § 8. Магнитная энергия атомов
- Глава 35. ПАРАМАГНЕТИЗМ И МАГНИТНЫЙ РЕЗОНАНС
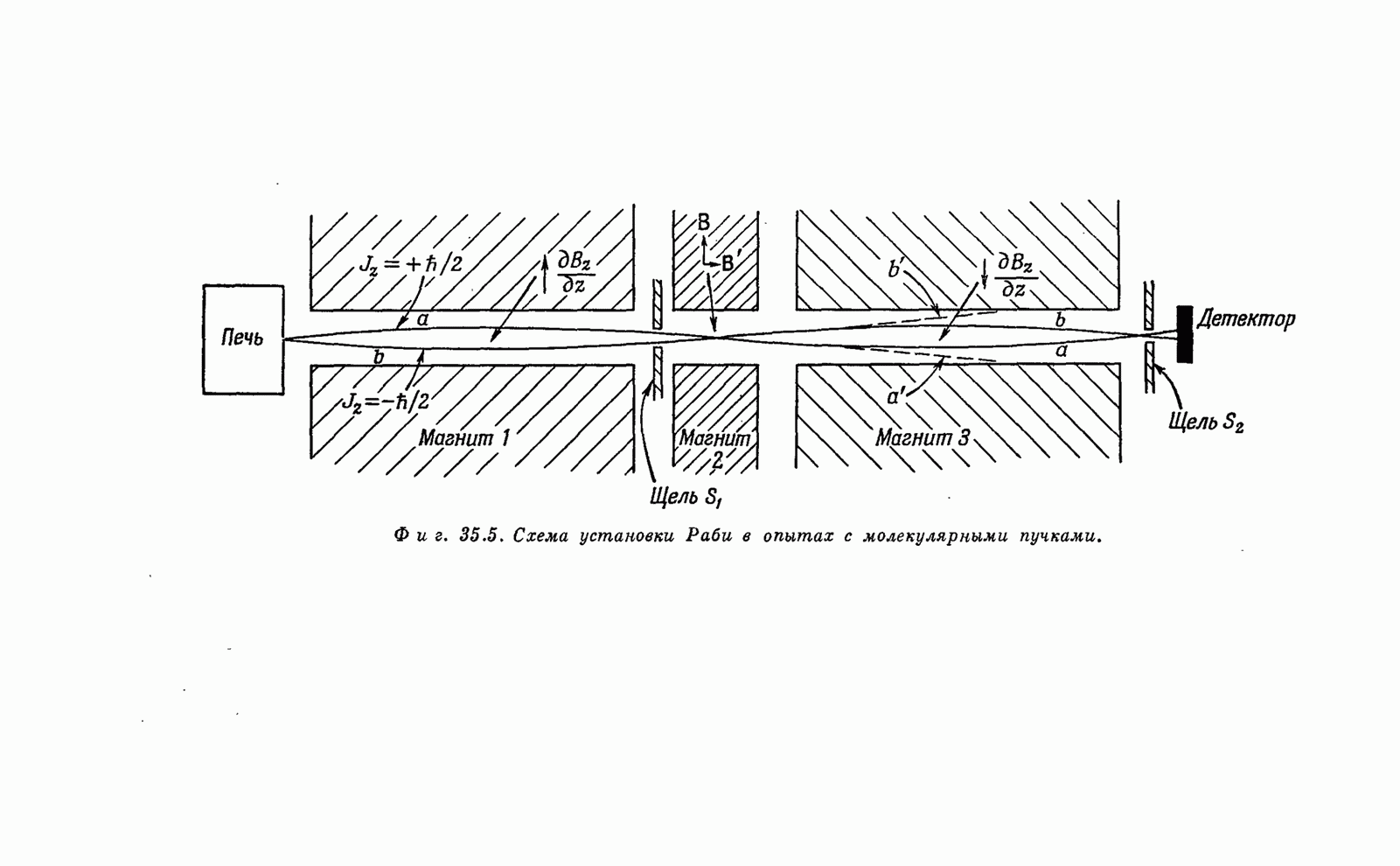
- § 1. Квантованные магнитные состояния
- § 2. Опыт Штерна-Герлаха
- § 3. Метод молекулярных пучков Раби
- § 4. Парамагнетизм
- § 5. Охлаждение адиабатическим размагничиванием
- § 6. Ядерный магнитный резонанс
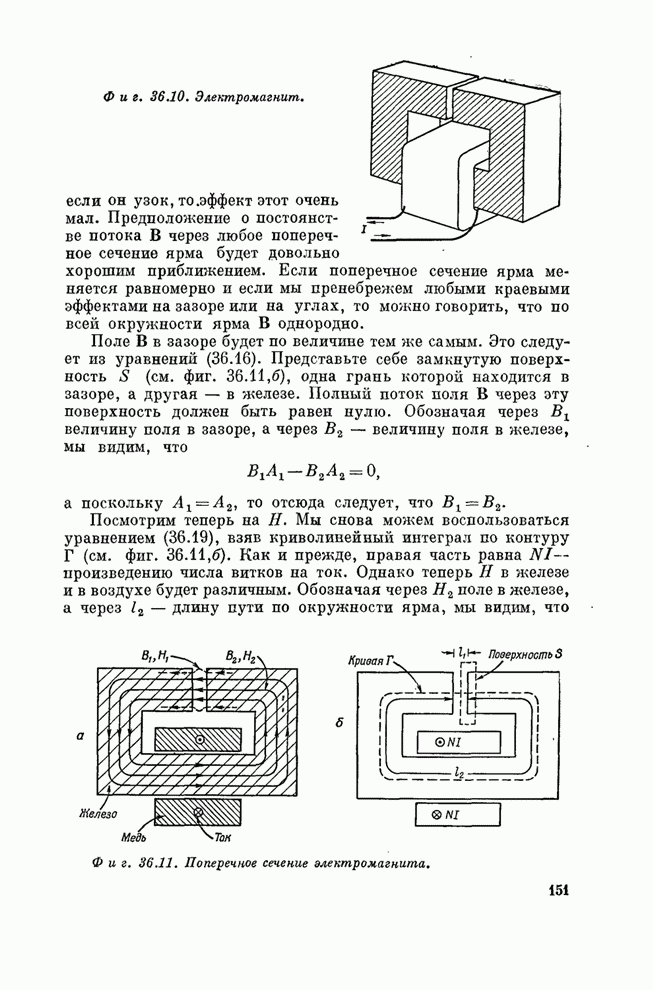
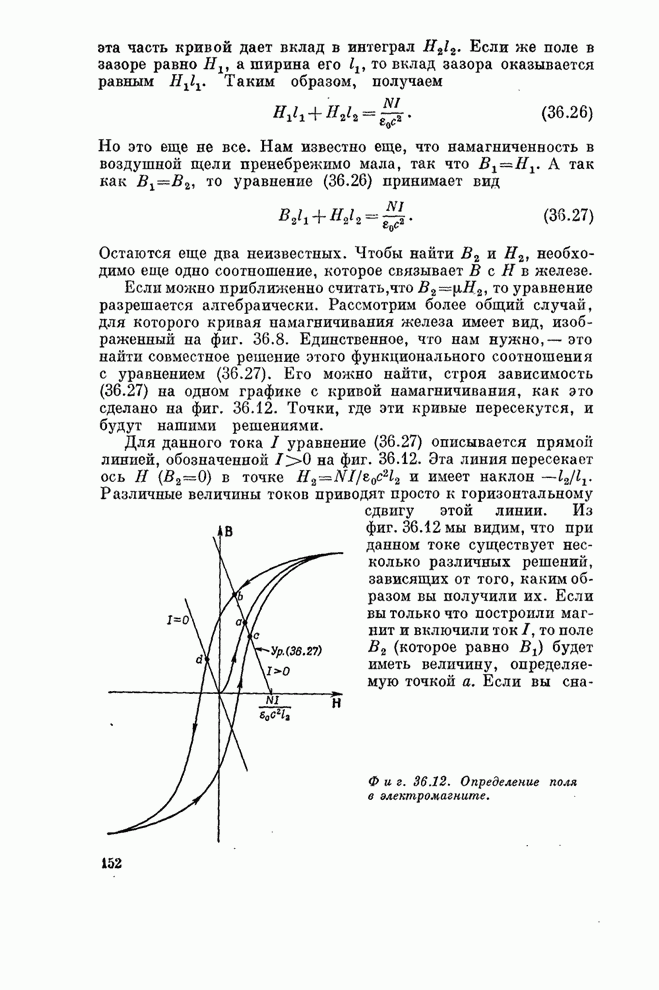
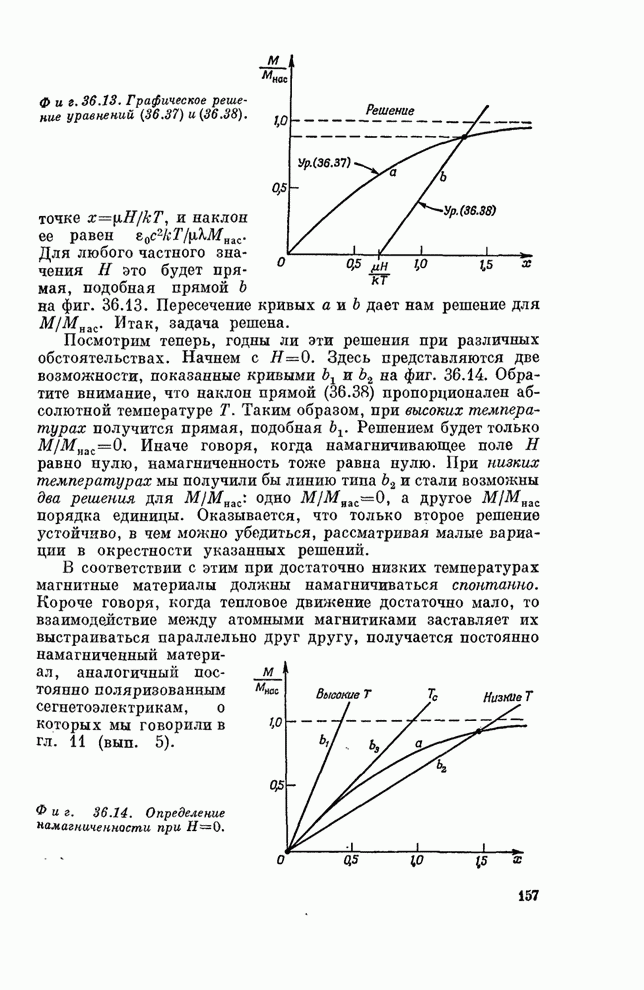
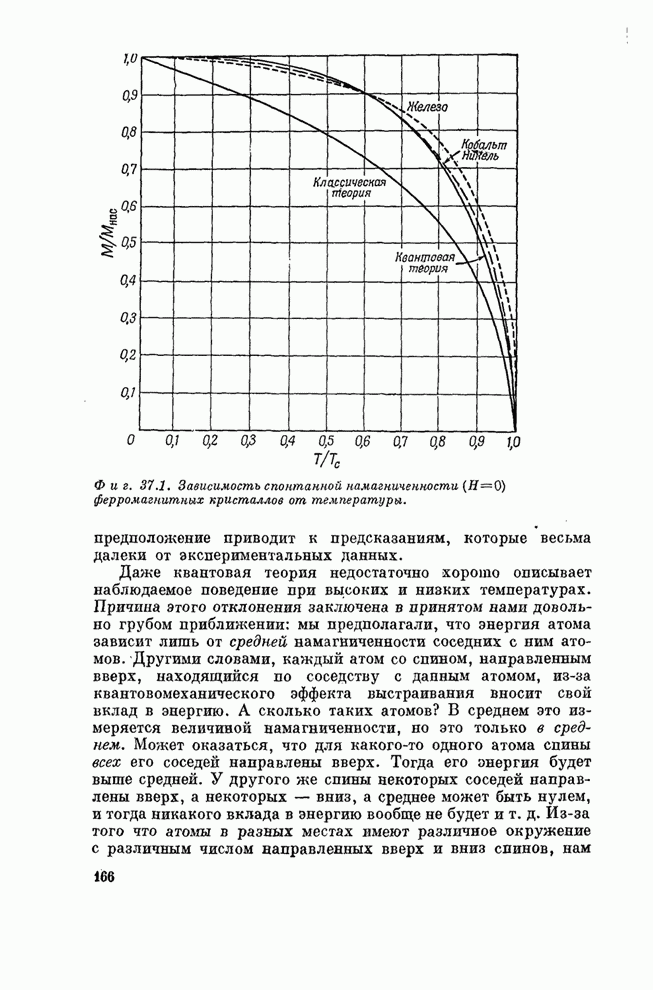
- Глава 36. ФЕРРОМАГНЕТИЗМ
- § 1. Токи намагничивания
- § 2. Поле
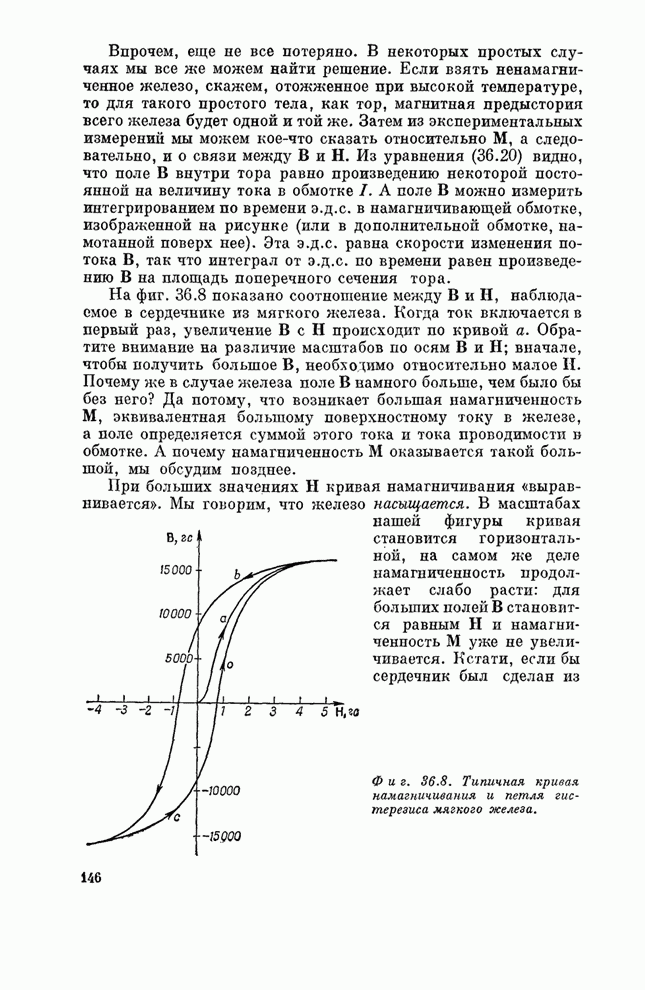
- § 3. Кривая намагничивания
- § 4. Индуктивность с железным сердечником
- § 5. Электромагниты
- § 6. Спонтанная намагниченность
- Глава 37. МАГНИТНЫЕ МАТЕРИАЛЫ
- § 1. Сущность ферромагнетизма
- § 2. Термодинамические свойства
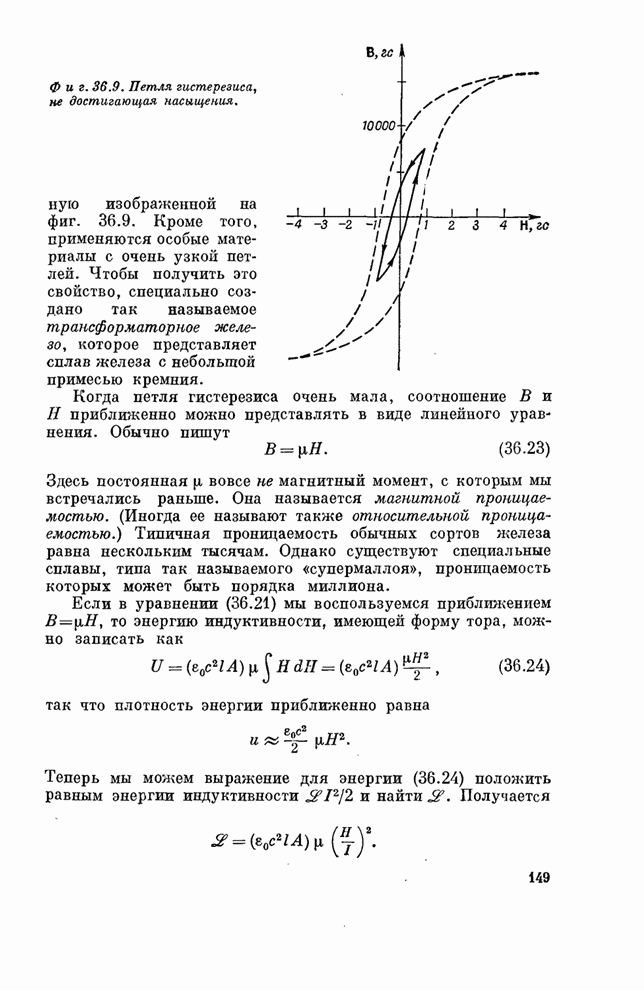
- § 3. Петля гистерезиса
- § 4. Ферромагнитные материалы
- § 5. Необычные магнитные материалы
- Глава 38. УПРУГОСТЬ
- § 1. Закон Гука
- § 2. Однородная деформация
- § 3. Кручение стержня; волны сдвига
- § 4. Изгибание балки
- § 5. Продольный изгиб
- Глава 39. УПРУГИЕ МАТЕРИАЛЫ
- § 1. Тензор деформации
- § 2. Тензор упругости
- § 3. Движения в упругом теле
- § 4. Неупругое поведение
- § 5. Вычисление упругих постоянных
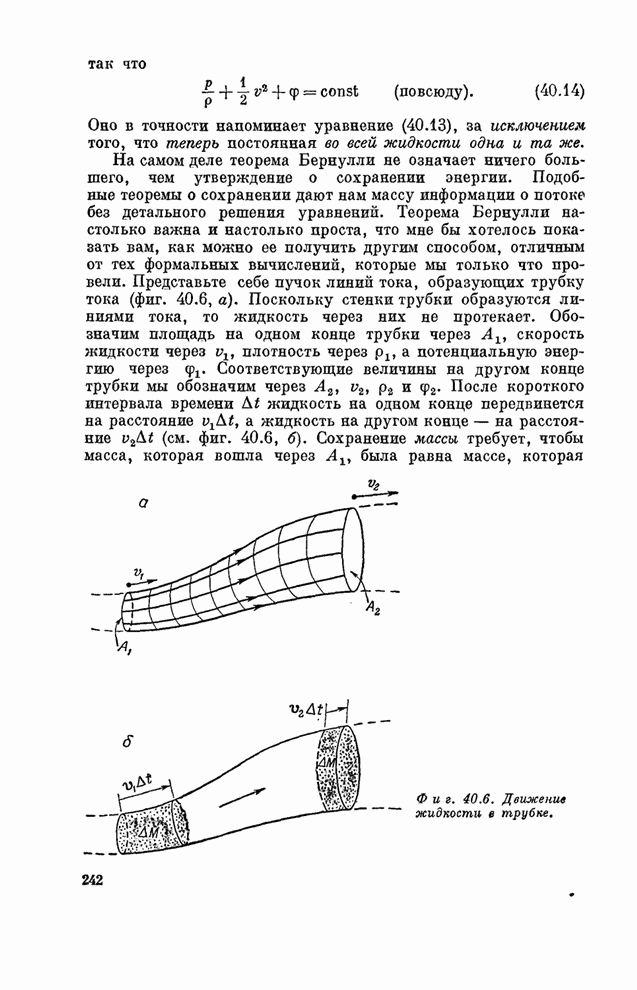
- Глава 40. ТЕЧЕНИЕ «СУХОЙ» ВОДЫ
- § 1. Гидростатика
- § 2. Уравнение движения
- § 3. Стационарный поток; теорема Бернулли
- § 4. Циркуляция
- § 5. Вихревые линии
- Глава 41. ТЕЧЕНИЕ «МОКРОЙ» ВОДЫ
- § 1. Вязкость
- § 2. Вязкий поток
- § 3. Число Рейнольдса
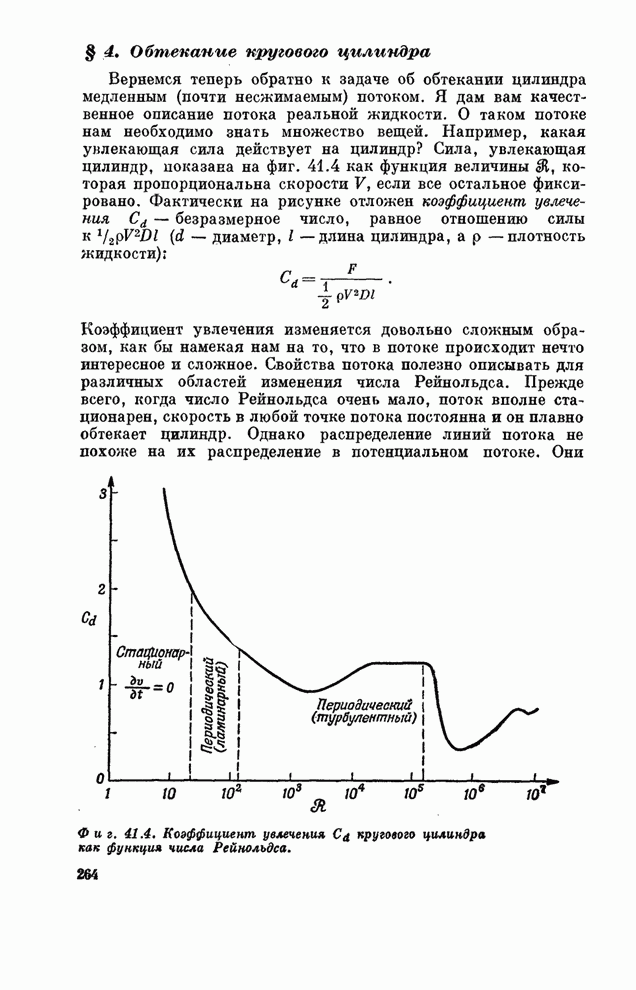
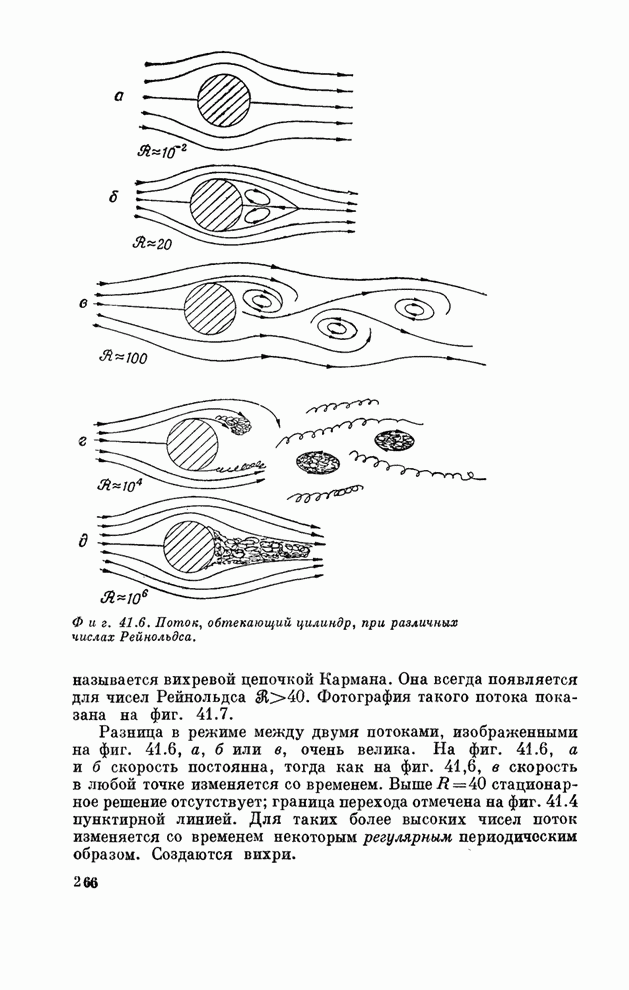
- § 4. Обтекание кругового цилиндра
- § 5. Предел нулевой вязкости
- § 6. Поток Куеттэ
- ПРИЛОЖЕНИЕ (к главе 30)