| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
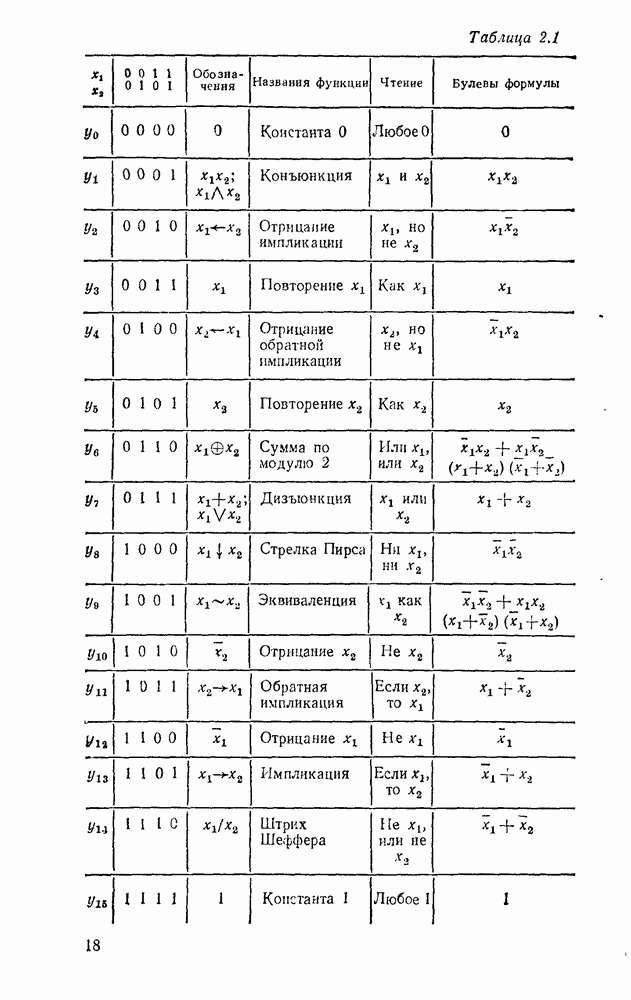
Как видно из табл. 2.1, все функции попарно связаны между собой посредством отрицания, т. е.  .
.
Отсюда следуют зависимости  для функции одной переменной
для функции одной переменной  (двойное отрицание) и для функций двух переменных:
(двойное отрицание) и для функций двух переменных:

Из этих зависимостей следует, что любую функцию двух переменных, включая константы, можно выразить в аналитической форме через совокупность шести функций, содержащей отрицание и любую из каждой пары  Например, такую совокупность наряду с константой 0 и отрицанием
Например, такую совокупность наряду с константой 0 и отрицанием  могут составлять функции: конъюнкция
могут составлять функции: конъюнкция  , дизъюнкция
, дизъюнкция  , импликация
, импликация  и эквиваленция
и эквиваленция  . Все они используются в исчислении высказываний. Рассматривая буквы переменных как некоторые высказывания, которые могут быть истинными или ложными, можно образовывать сложные высказывания с помощью сентенционалышх связок, соответствующих функциям этих переменных.
. Все они используются в исчислении высказываний. Рассматривая буквы переменных как некоторые высказывания, которые могут быть истинными или ложными, можно образовывать сложные высказывания с помощью сентенционалышх связок, соответствующих функциям этих переменных.
При этом отрицанию соответствует связка не, конъюнкции — и, дизъюнкции — или, импликации — если, то и эквиваленцни — если и только если.
Дежду тем выбранная совокупность шести функций является избыточной. С помощью таблицы соответствия можно показать, что импликация и эквнваленция выражаются через остальные функции этой совокупности:  .
.

Приняв во внимание, что  , можно сократить комплект элементарных функций до трех: отрицания
, можно сократить комплект элементарных функций до трех: отрицания  , конъюнкции
, конъюнкции  и дизъюнкции
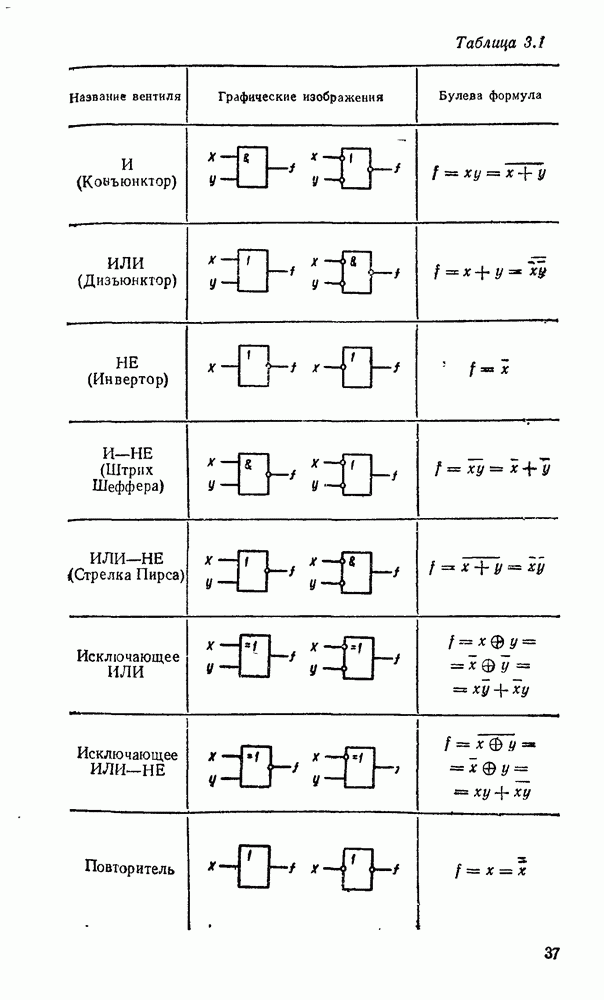
и дизъюнкции  . Совокупность этих функций положена в основу булевой алгебры, которая преимущественно используется при математическом моделировании цифровых систем (в последней колонке табл. 2.1 приведены выражения через булевы функции). Но и этот комплект не является необходимым с точки зрения функциональной полноты. Из соотношений
. Совокупность этих функций положена в основу булевой алгебры, которая преимущественно используется при математическом моделировании цифровых систем (в последней колонке табл. 2.1 приведены выражения через булевы функции). Но и этот комплект не является необходимым с точки зрения функциональной полноты. Из соотношений  , в справедливости которых также можно убедиться с помощью таблицы соответствия, следует, что все функции выражаются через отрицание и конъюнкцию или через отрицание и дизъюнкцию. Более того, для записи любой функции достаточно одной из двух элементарных функций — стрелки Пирса или штриха Шеффера. Это вытекает из соотношений:
, в справедливости которых также можно убедиться с помощью таблицы соответствия, следует, что все функции выражаются через отрицание и конъюнкцию или через отрицание и дизъюнкцию. Более того, для записи любой функции достаточно одной из двух элементарных функций — стрелки Пирса или штриха Шеффера. Это вытекает из соотношений:  которые доказываются аналогично.
которые доказываются аналогично.
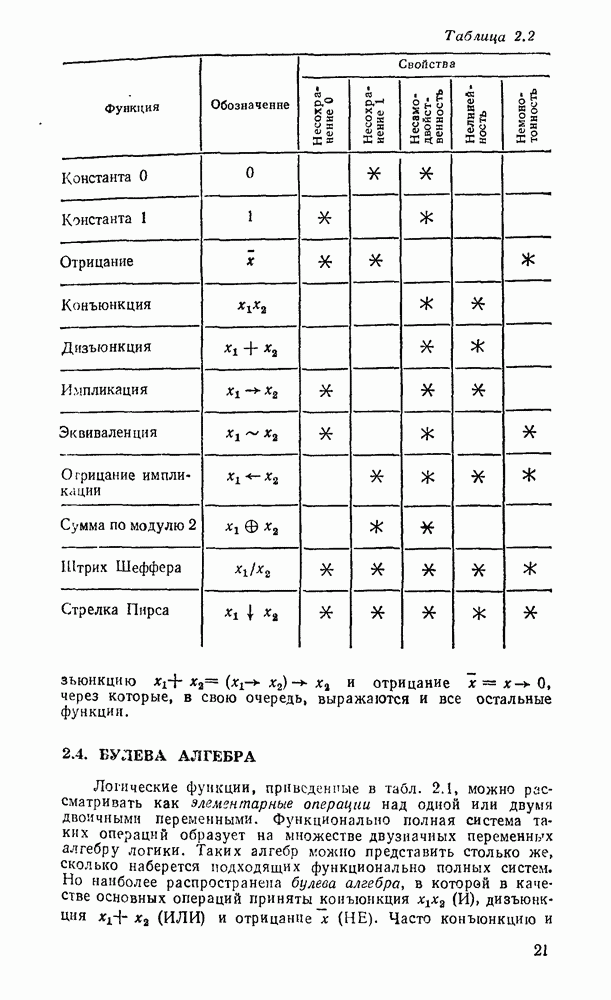
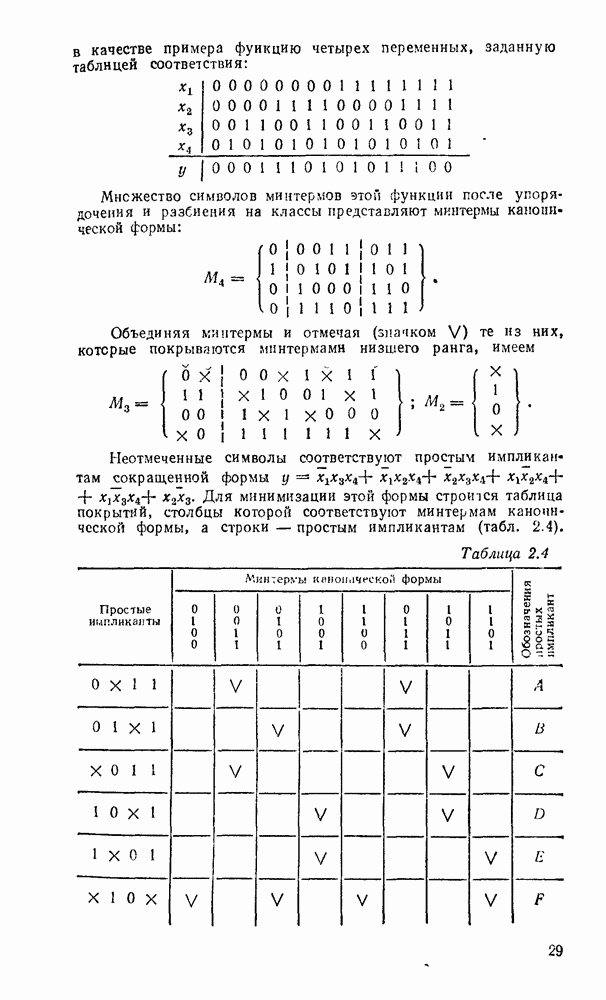
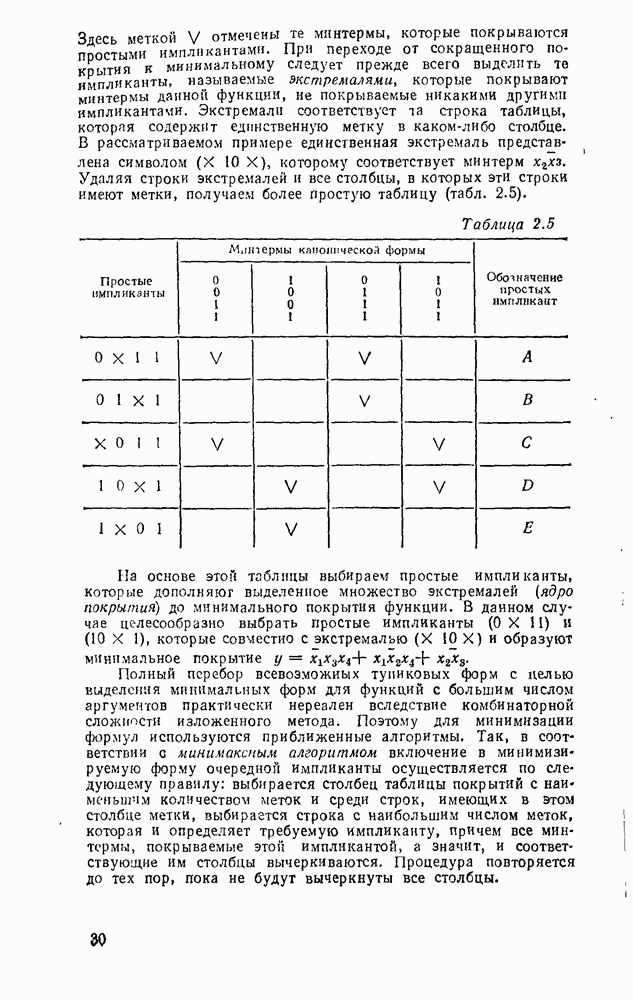
Система функций, суперпозицией которых может быть представлена любая функция из некоторого множества логических функций, называется функционально полной. Если в такой системе допускаются константы 0 и 1, то ее называют ослабленпо функционально полной. Система функций является минимально полной, если удаление из нее любой функции превращает эту систему в неполную. Необходимое и достаточное условие функциональной полноты состоит в том, что выбранные функции должны в совокупности обладать всеми свойствами, приведенными в табл. 2.2 (звездочкой отмечены свойства, которыми обладает данная функция).
Как видно из табл. 2.2, рассмотренные выше системы функций удовлетворяют условию функциональной полноты. Выбргн любую элементарную функцию и дополнив ее одной или несколькими функциями так, чтобы они вместе образовали функционально полную систему, можно выразить через них  другие функции. Например, выбрав импликацию вместе с константой 0 (можно было бы вместо константы 0 взять отрицание, сумму по модулю 2 или отрицание импликации), выразим дизъюнкцию
другие функции. Например, выбрав импликацию вместе с константой 0 (можно было бы вместо константы 0 взять отрицание, сумму по модулю 2 или отрицание импликации), выразим дизъюнкцию  и отрицание
и отрицание  , через которые, в свою очередь, выражаются и все остальные функции.
, через которые, в свою очередь, выражаются и все остальные функции.
Таблица 2.2

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
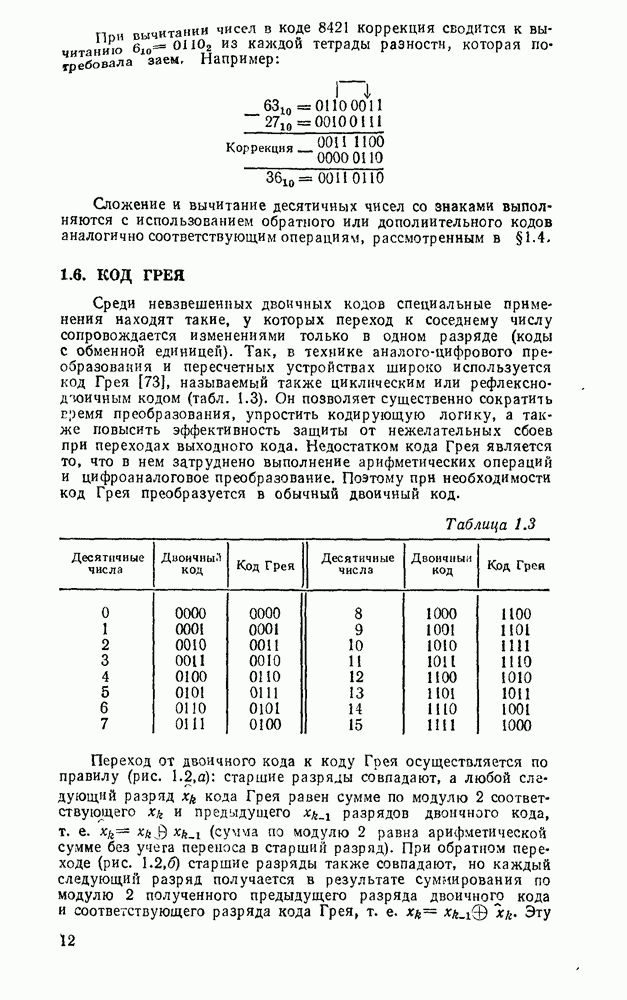
- 1.6. КОД ГРЕЯ
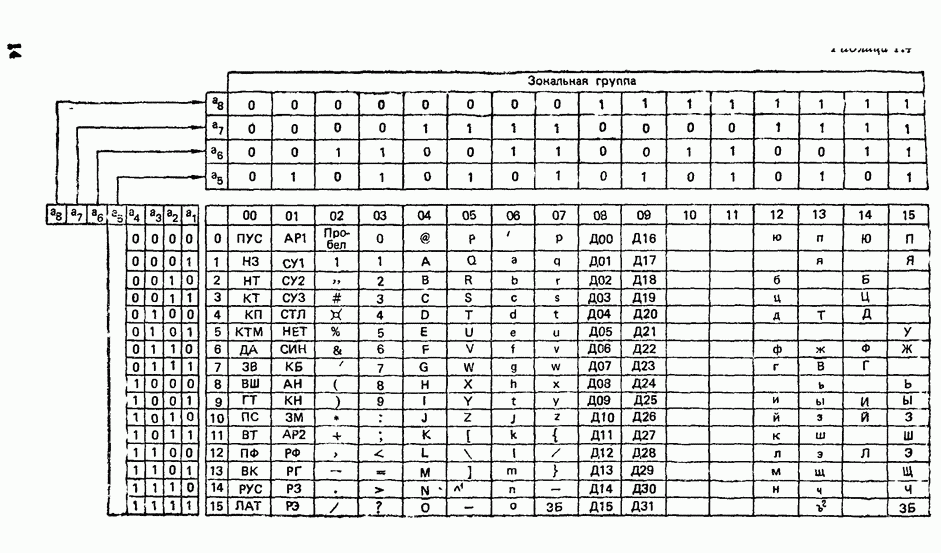
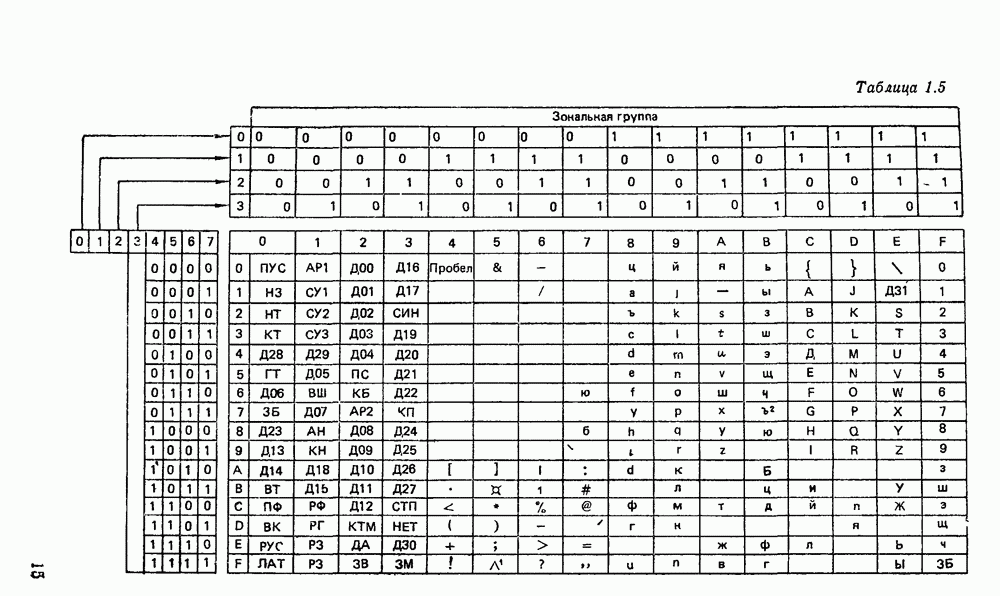
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
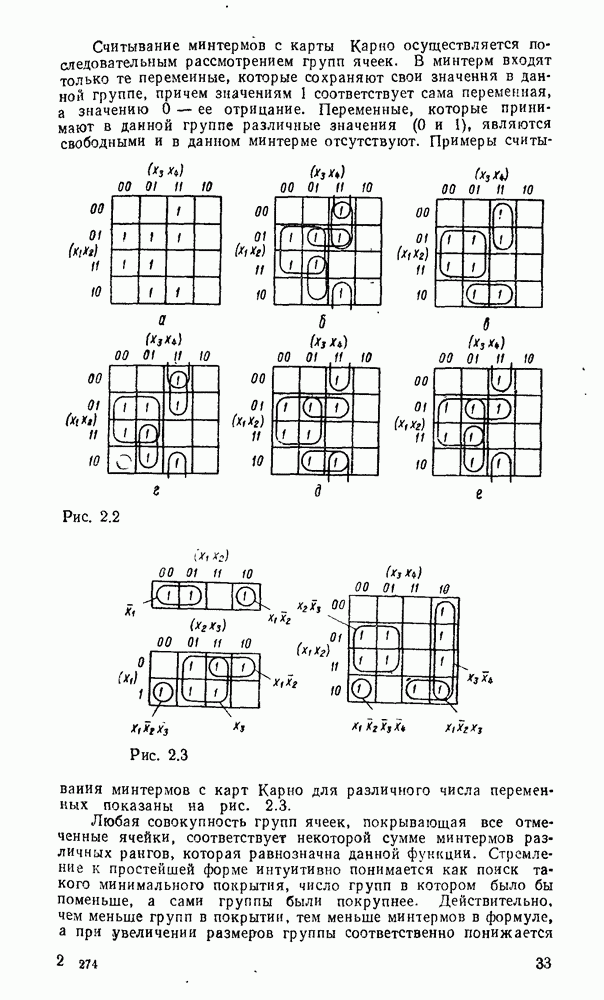
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
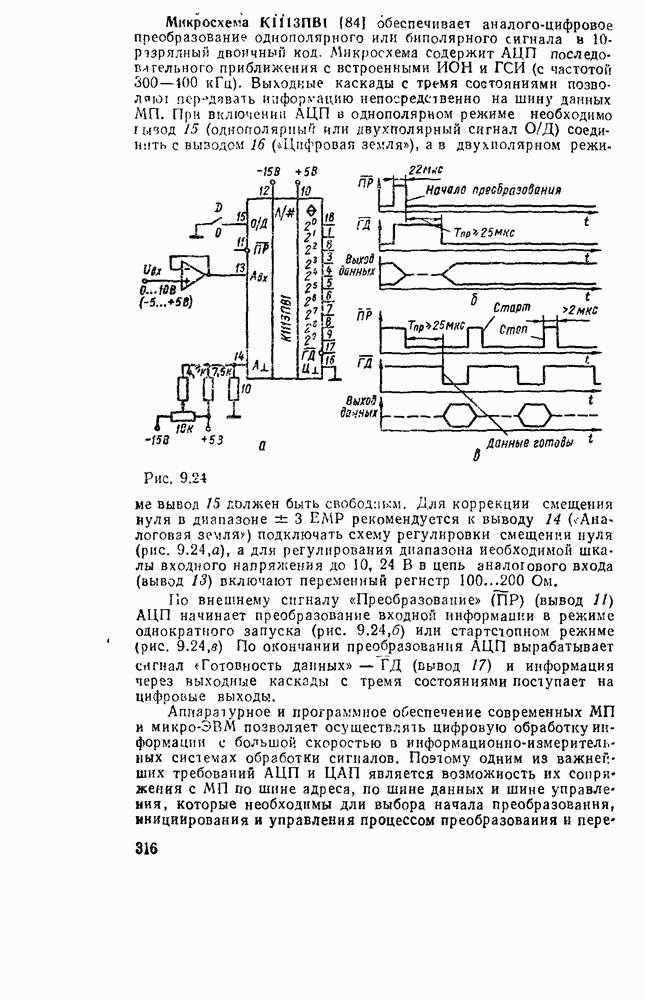
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
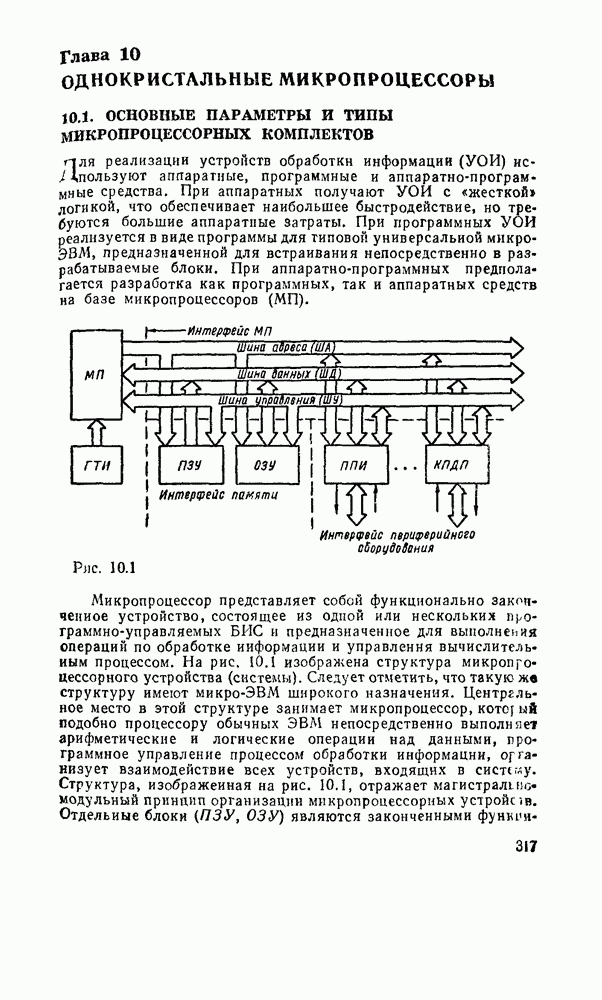
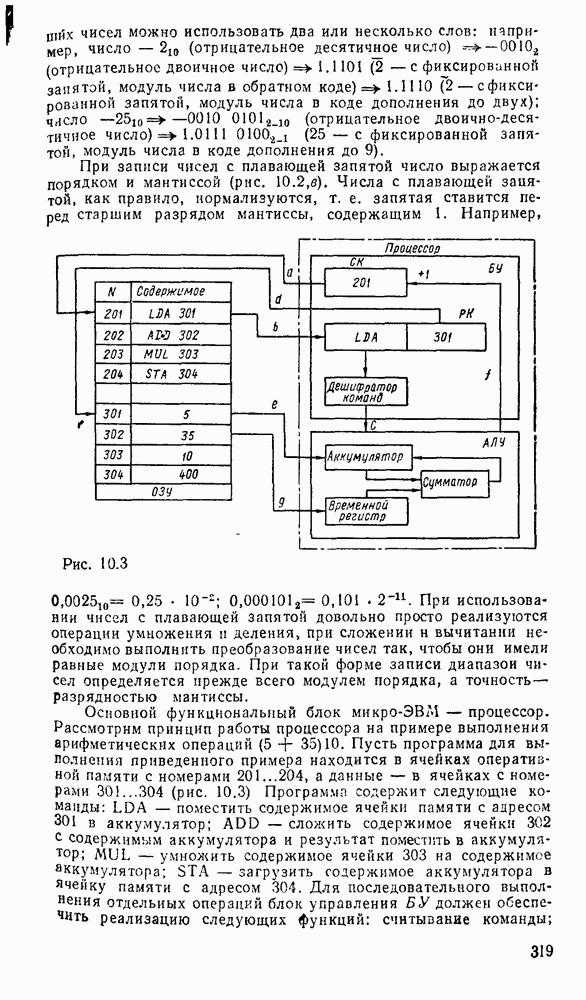
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
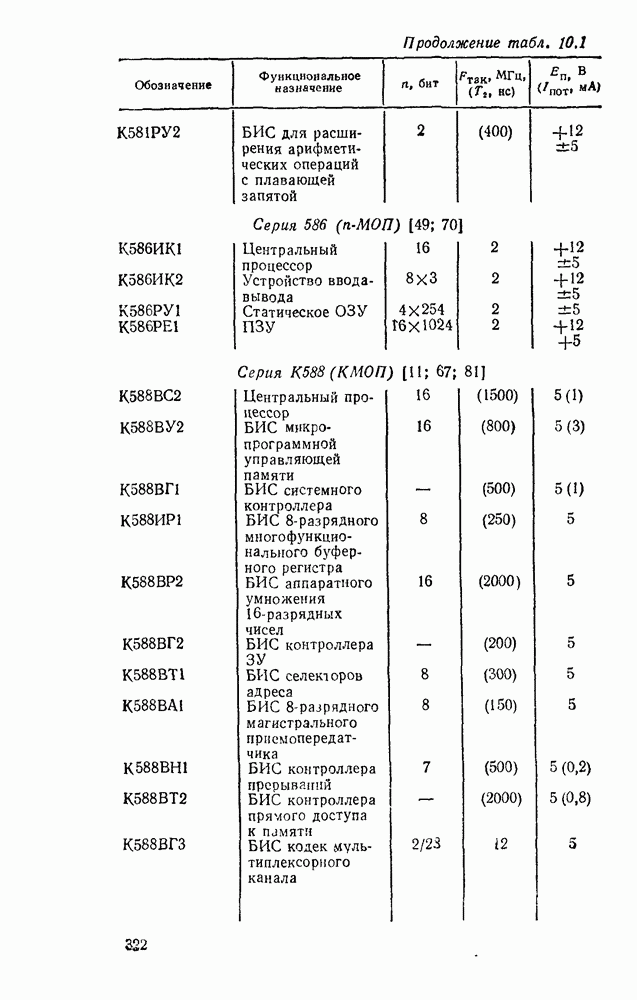
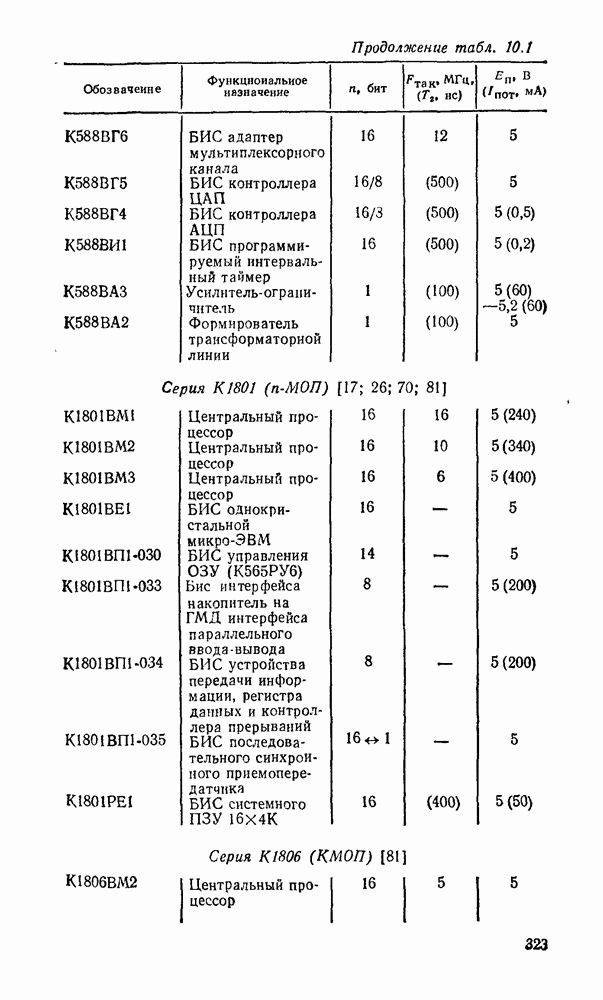
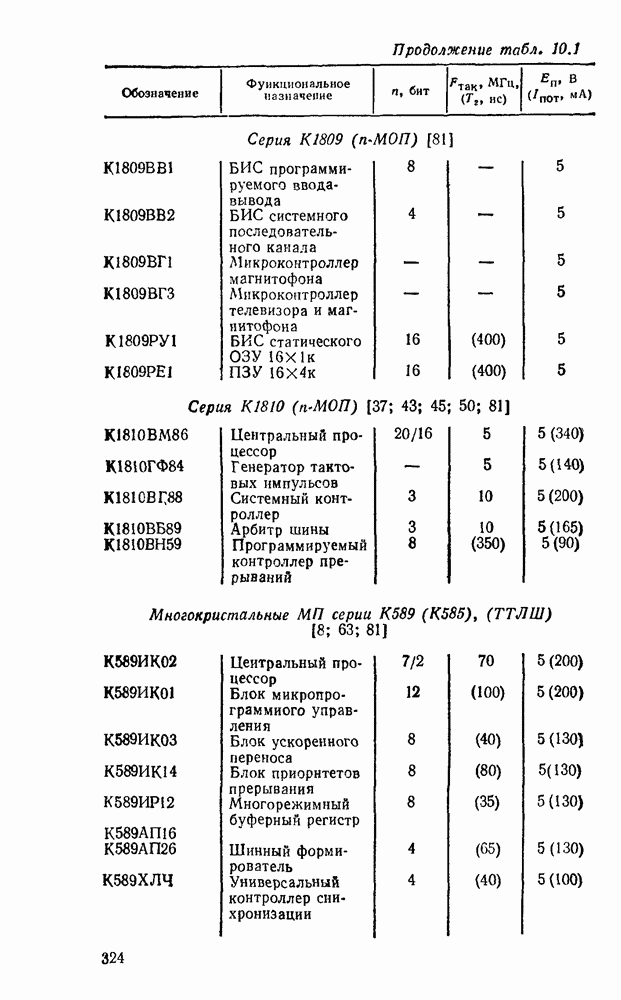
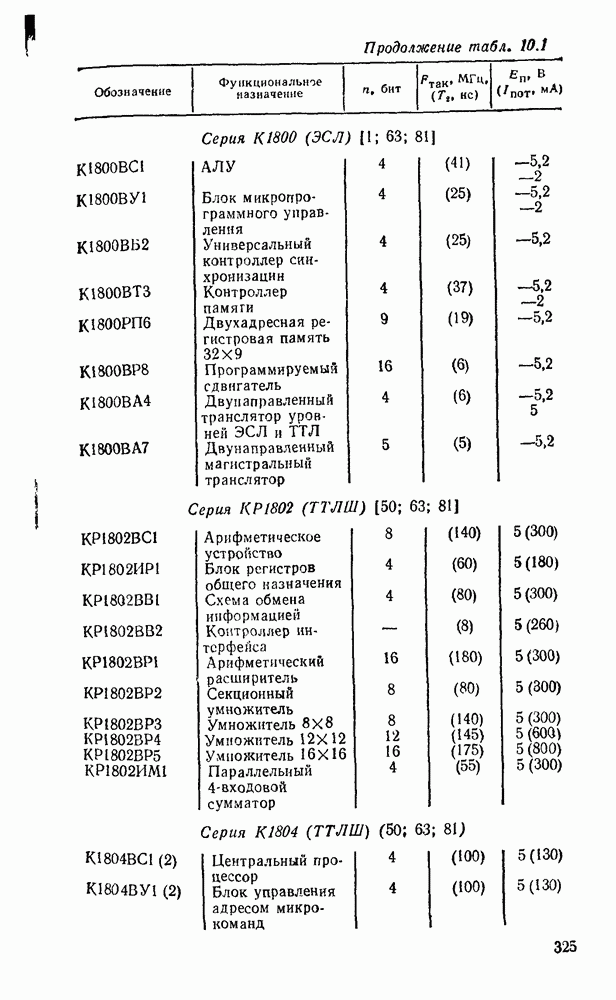
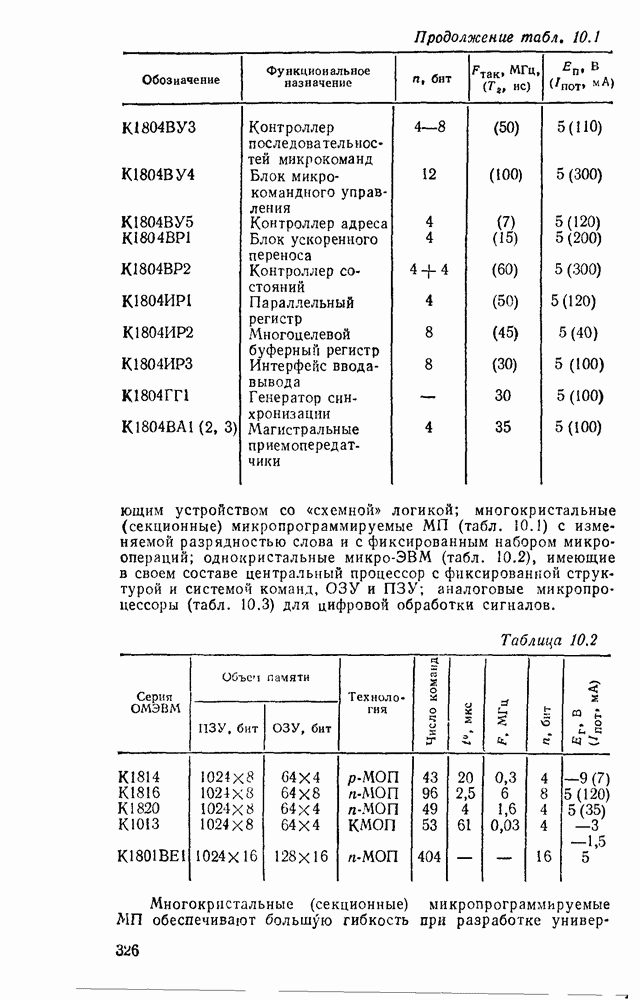
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
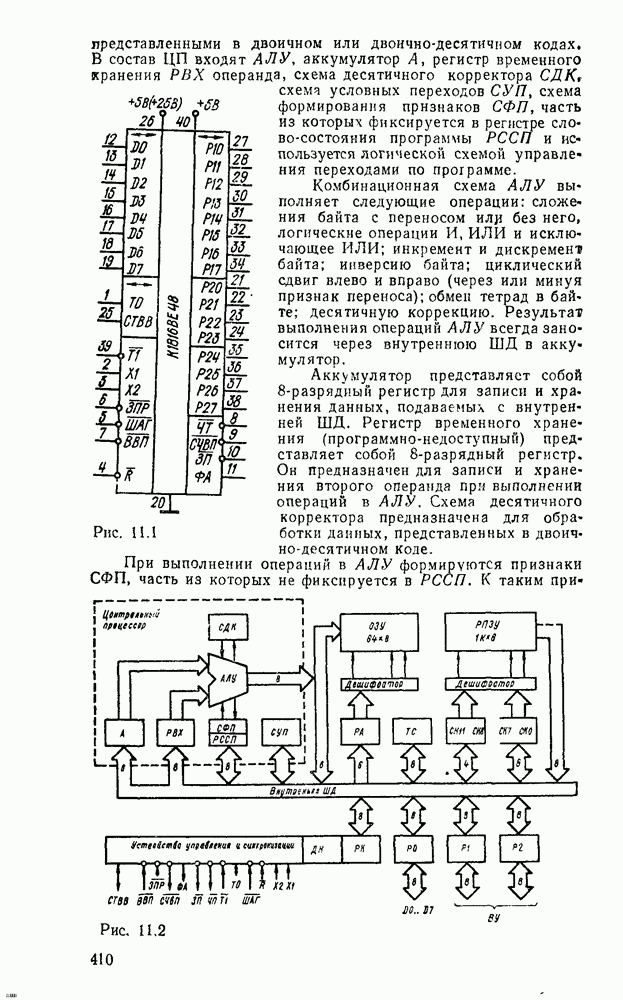
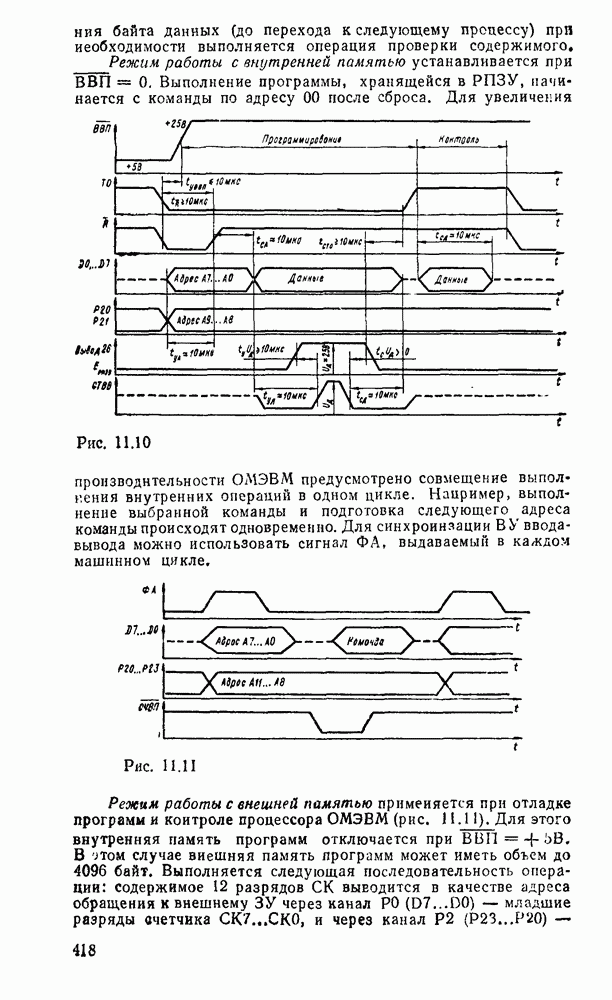
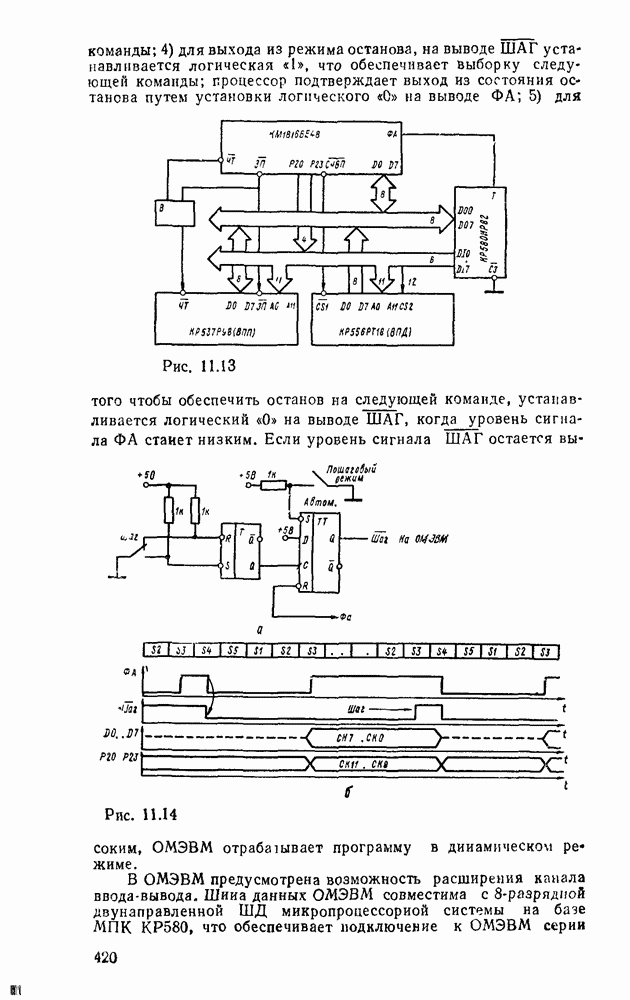
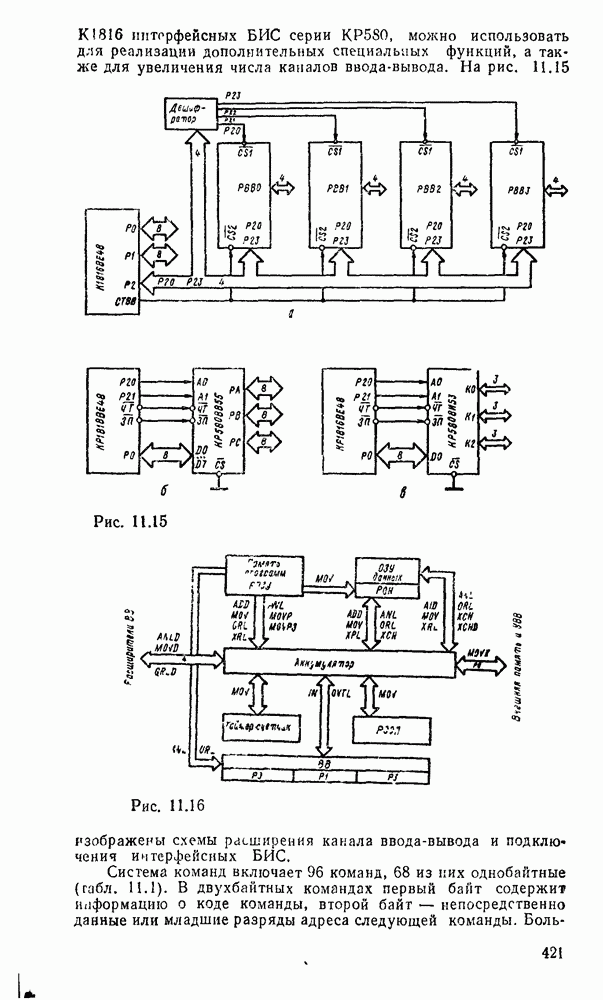
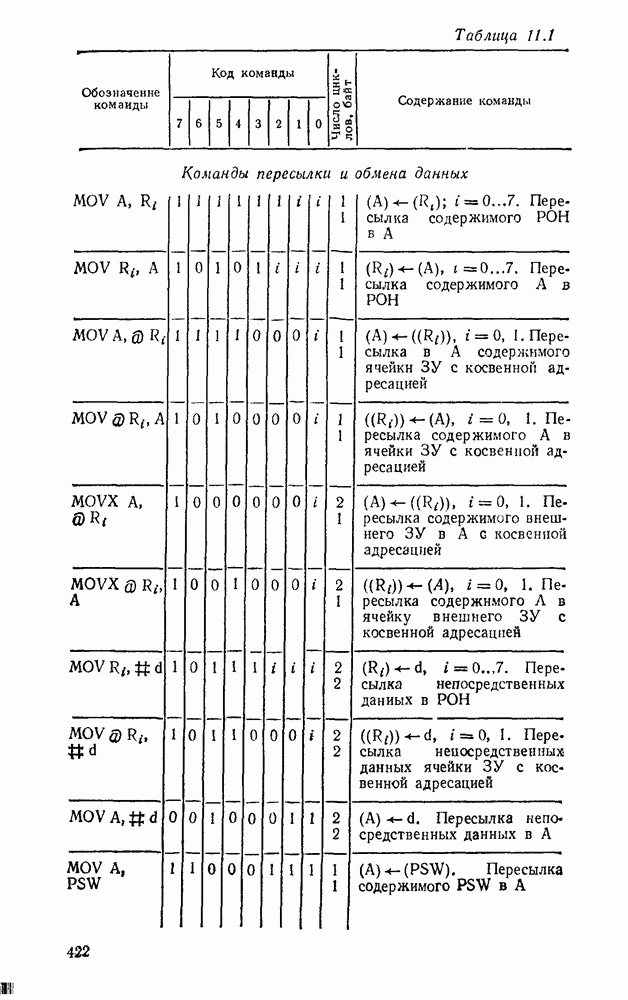
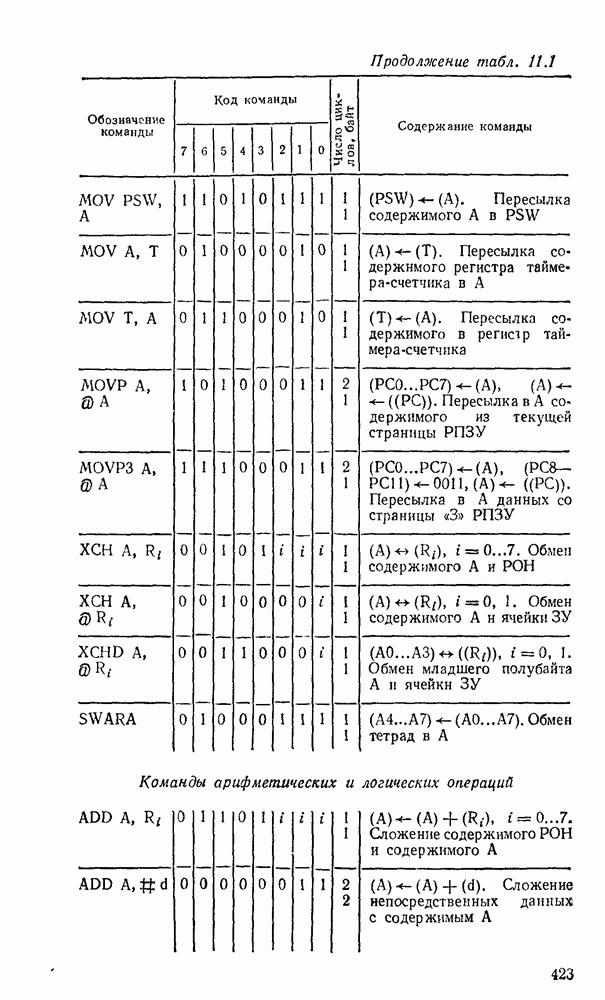
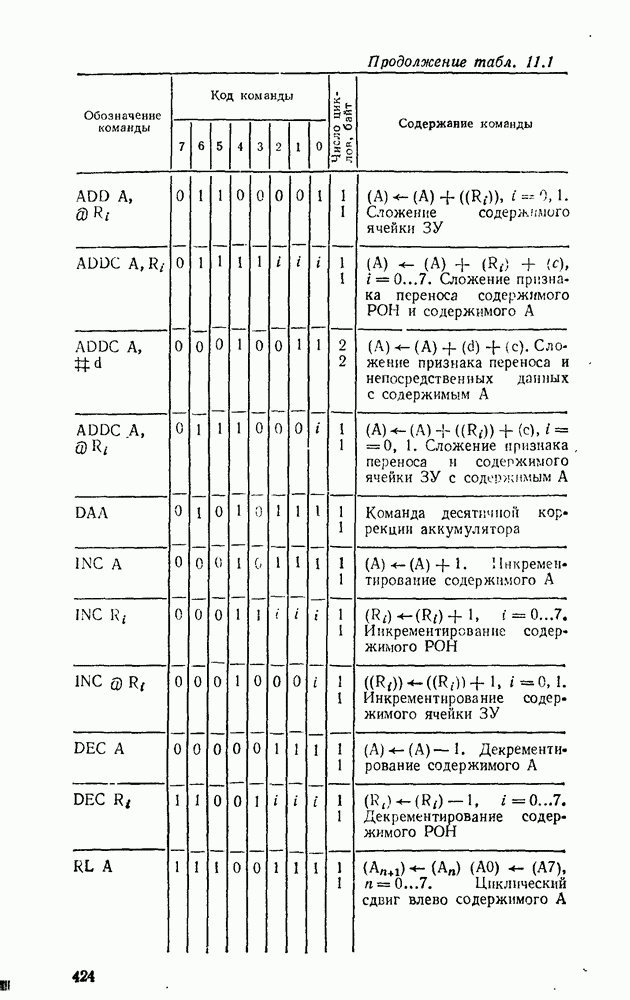
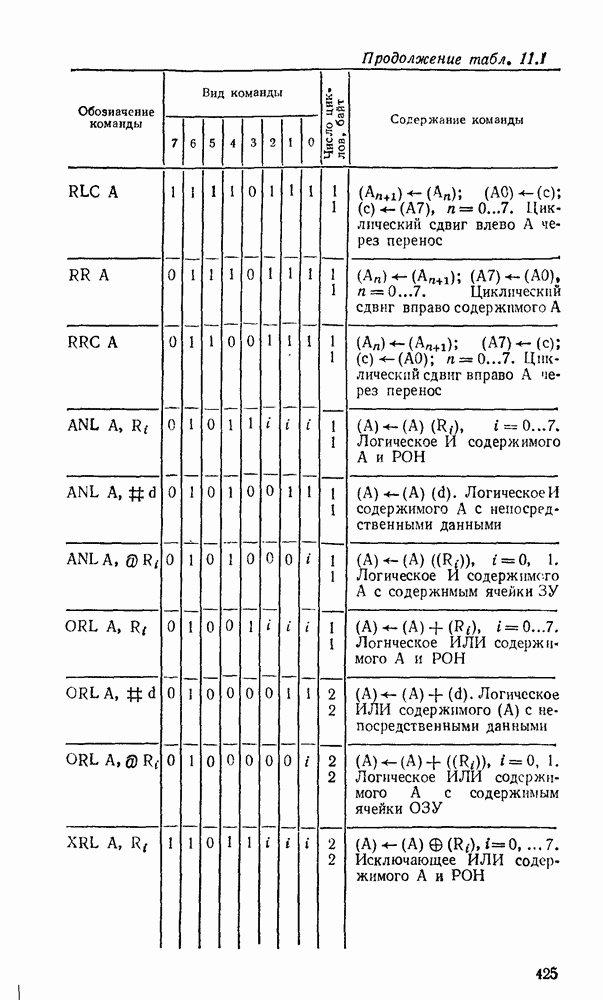
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ