| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.3. МАШИННОЕ СЛОВО
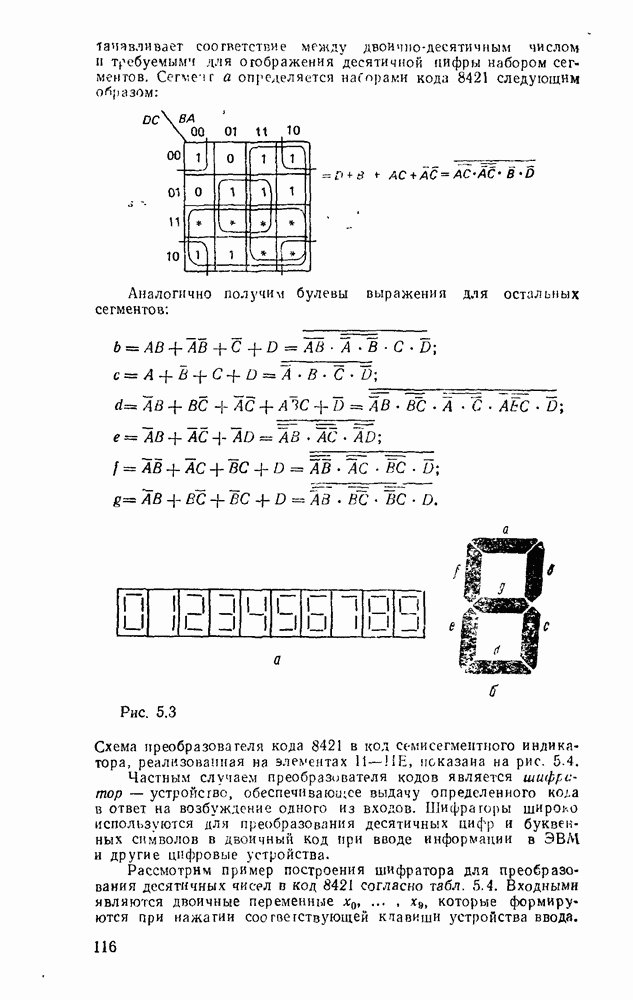
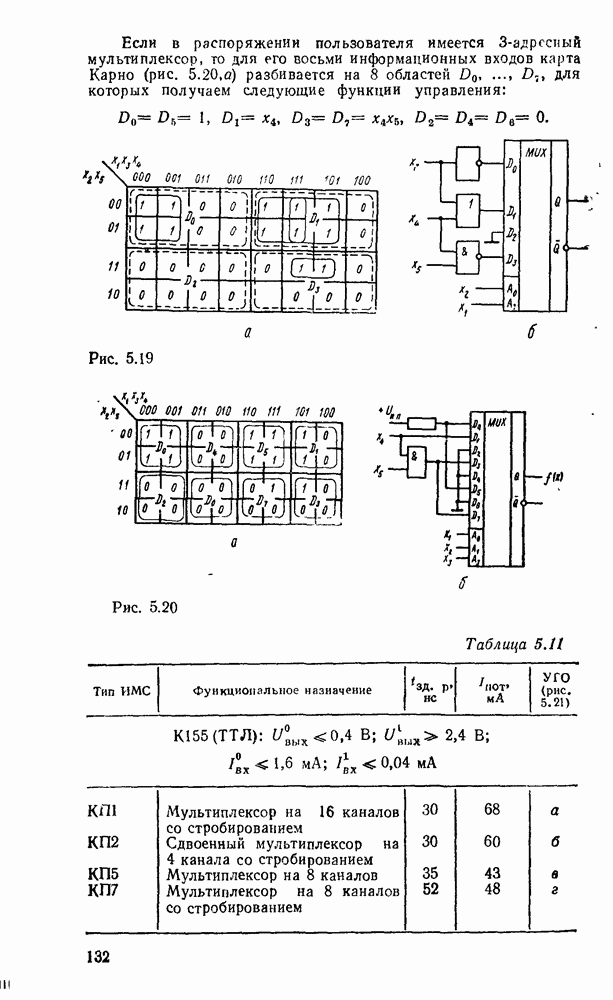
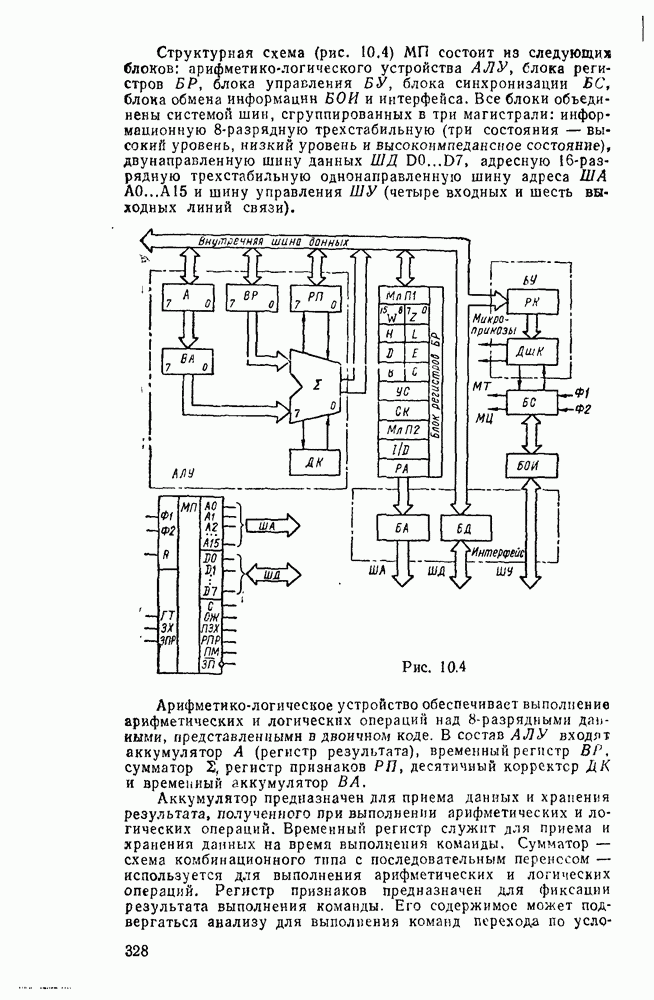
Сигналы, играющие роль носителей информации, представляются в цифровых системах последовательностями бит (или байт), которые объединяются в слова. Длнна слова может быть любой» обычно в диапазоне от 4 до 128 бит. Численное выражение слова понимается как значение соответствующей переменной. Цифровые сигналы могут представляться в двух формах: с фиксированной или с плавающей запятой.
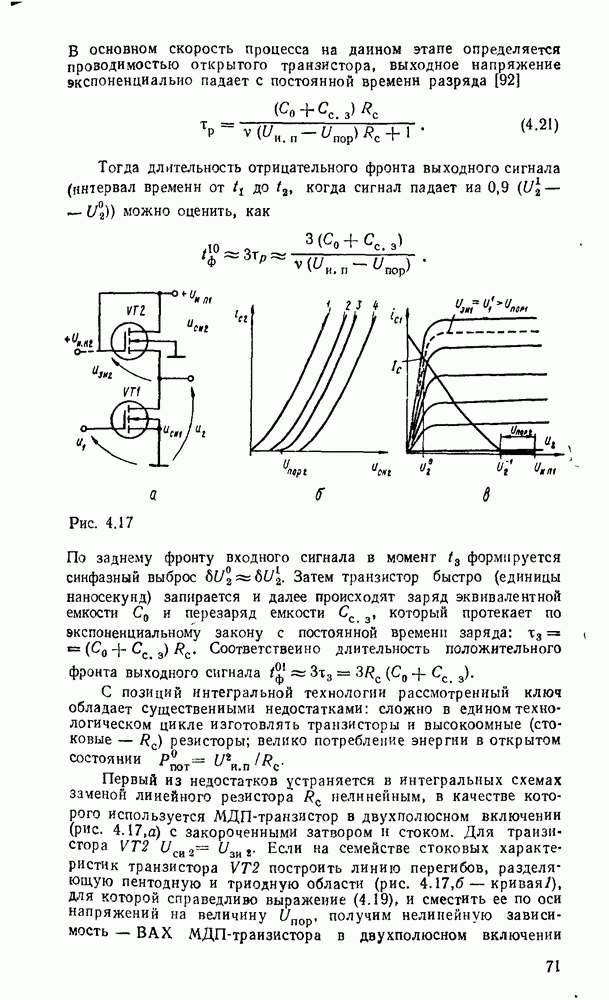
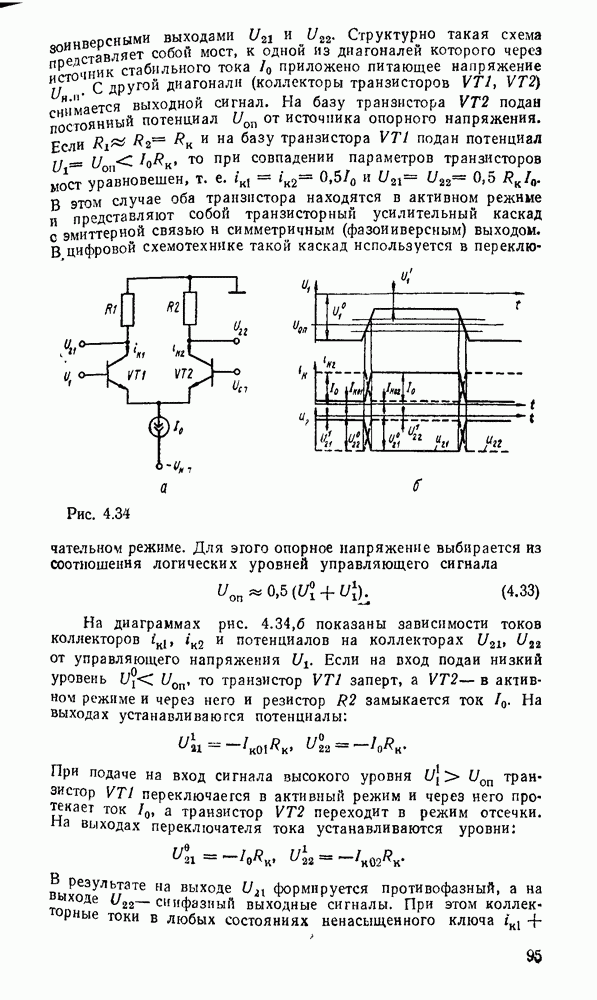
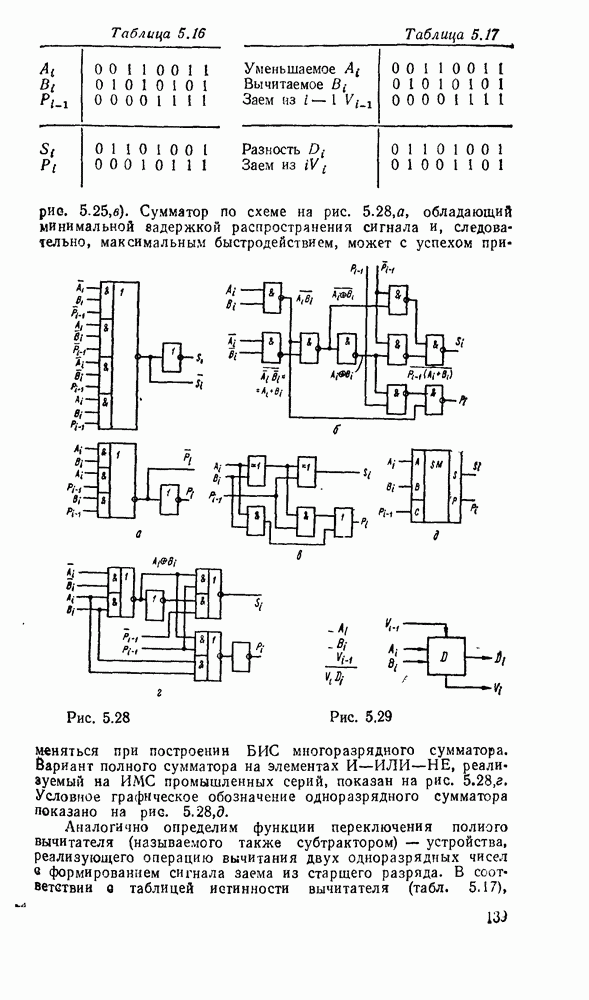
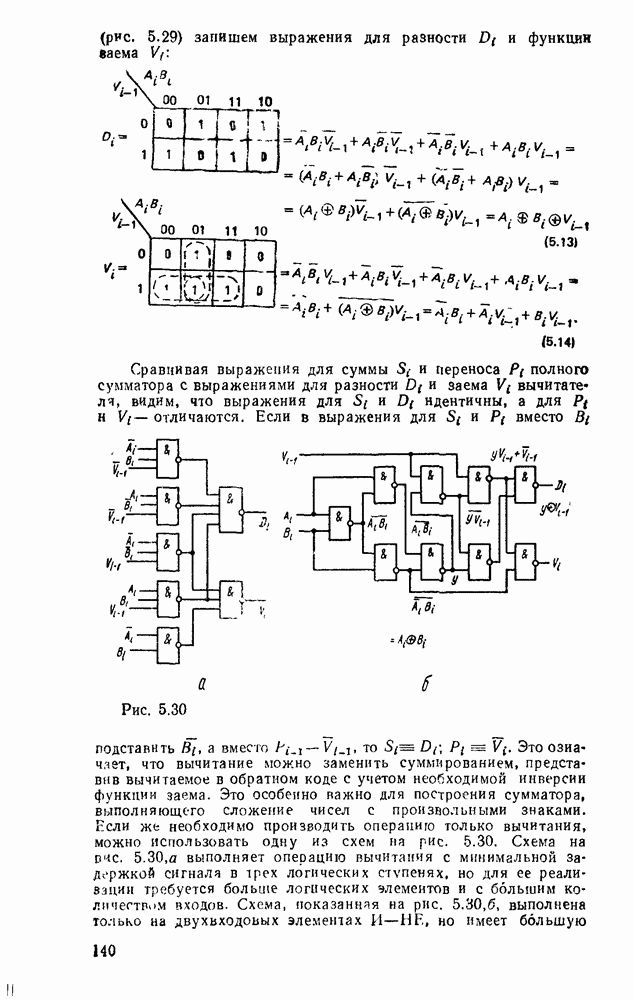
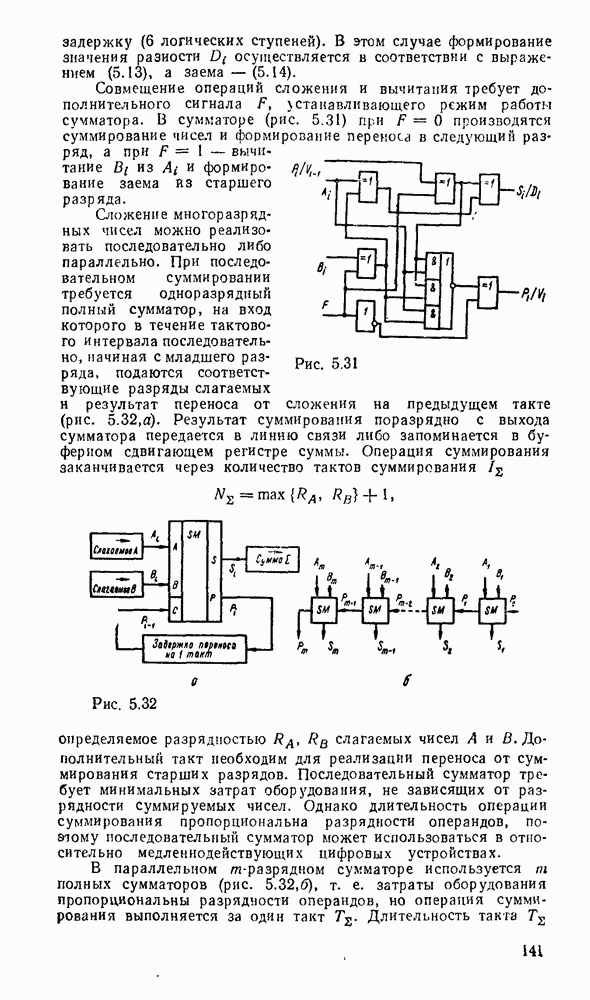
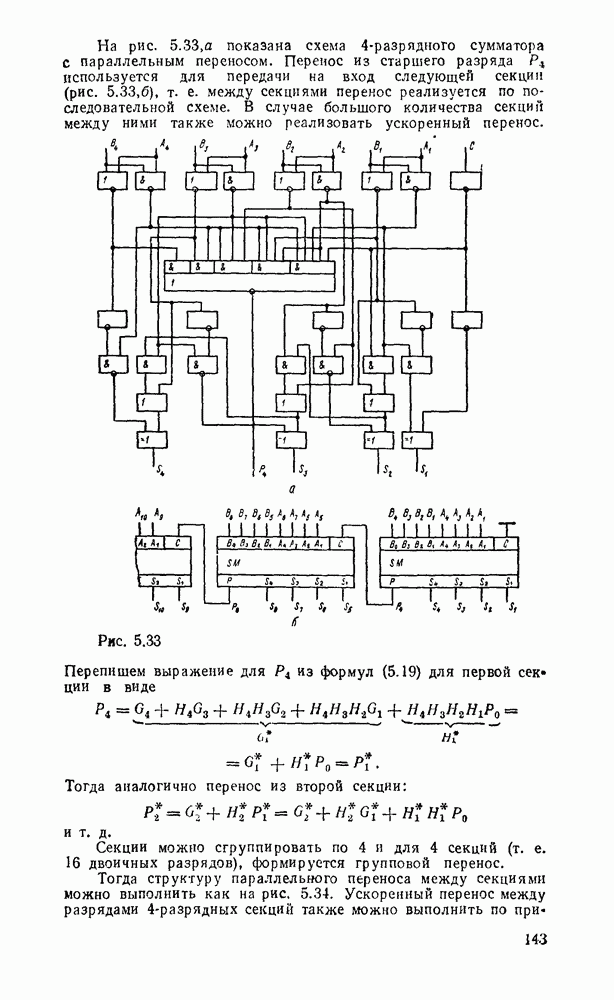
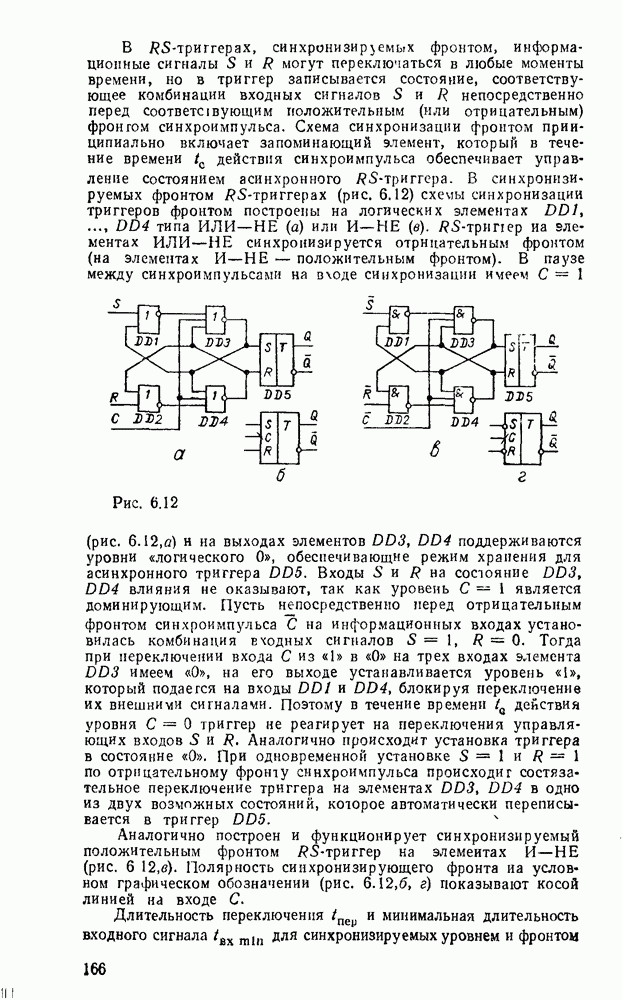
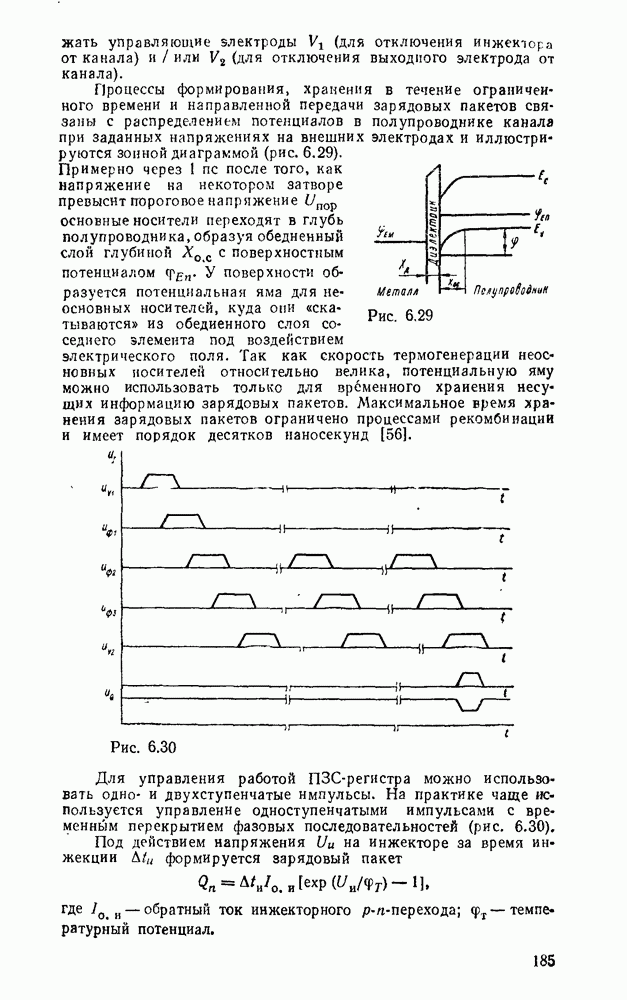
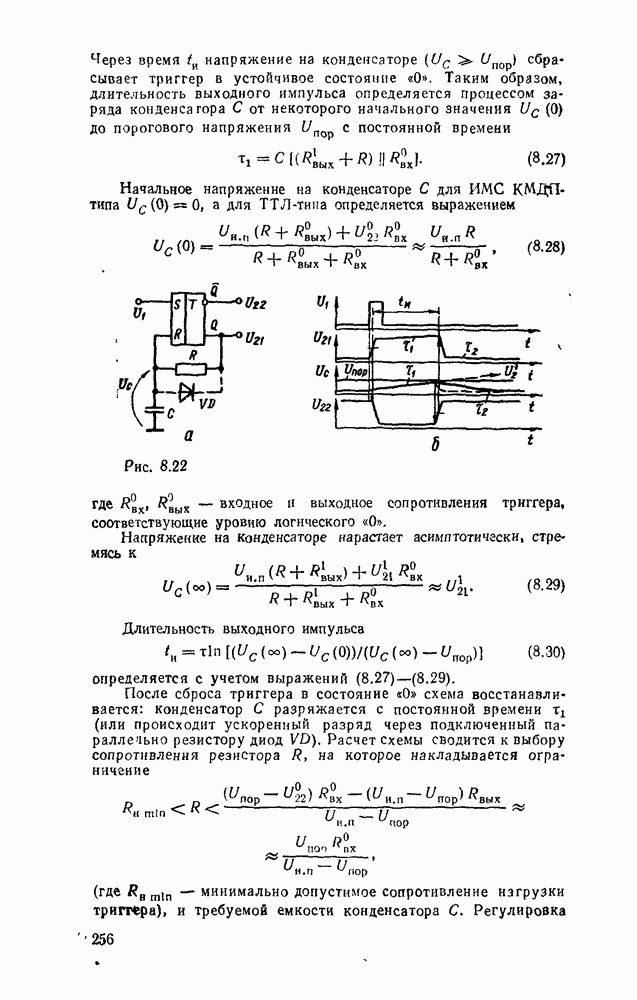
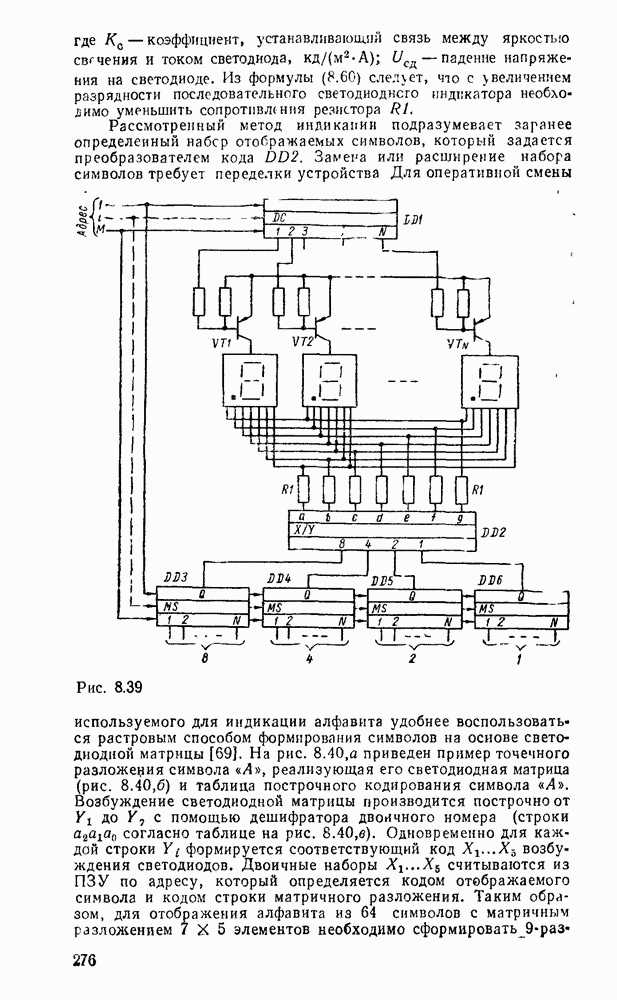
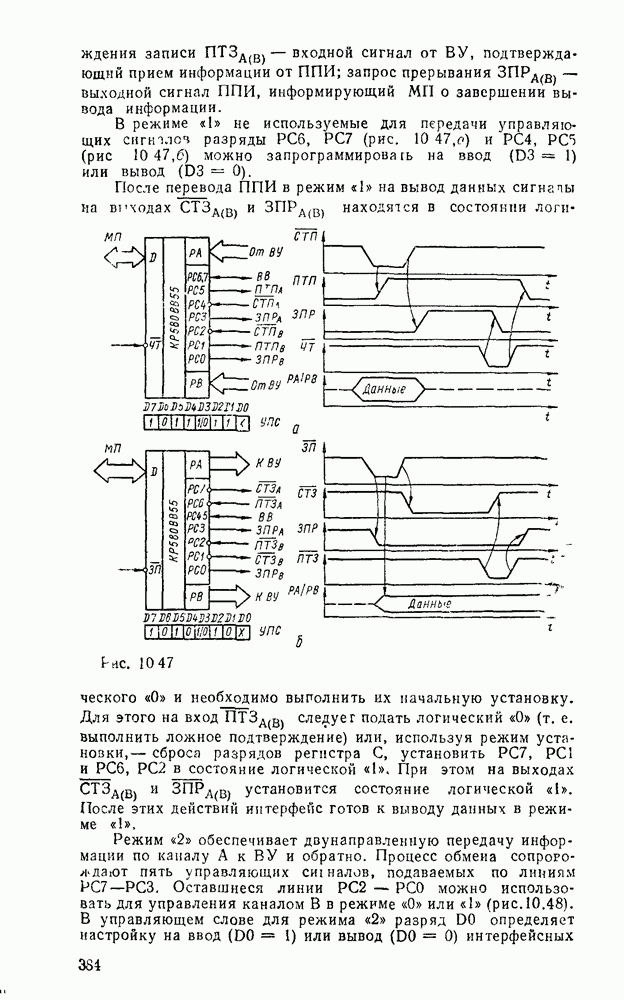
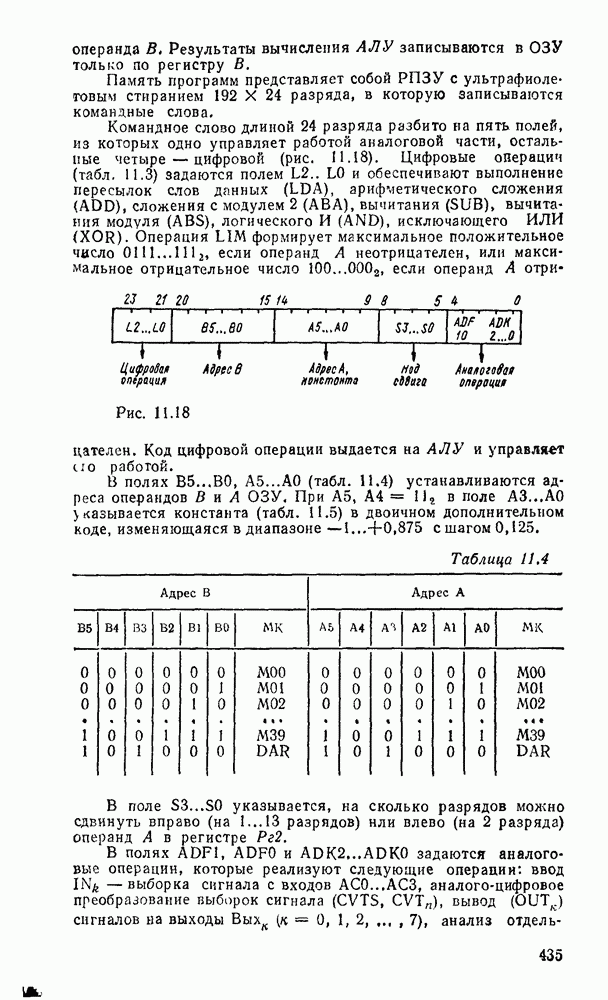
При представлении числа в форме с фиксированной запятой  -разрядное слоро разбивается на три части. Пергый бит используется для знака (0 для положительных чисел и 1 для отрицательных). Остальные разряды распределяются между целей и дробной частями числа с жестким положением места разделения, т. е. указанием количества отводимых разрядов (рис. 1.1,а).
-разрядное слоро разбивается на три части. Пергый бит используется для знака (0 для положительных чисел и 1 для отрицательных). Остальные разряды распределяются между целей и дробной частями числа с жестким положением места разделения, т. е. указанием количества отводимых разрядов (рис. 1.1,а).

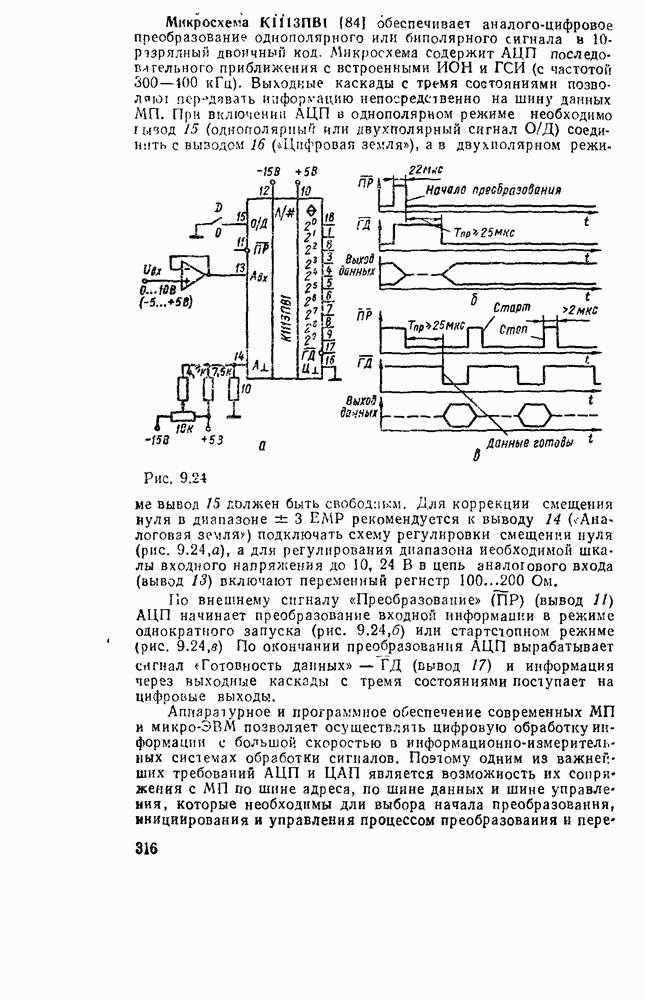
Рис. 1.1.
Если для дробной части выделено  бит, то наибольшее по абсолютной величине число не может превосходить
бит, то наибольшее по абсолютной величине число не может превосходить  . Ограниченность диапазона представляемых чисел и жесткое расположение фиксированной запятой — основные недостатки этого способа, которые могут привести к потере точности при выполнении арифметических операций вследствие переполнения.
. Ограниченность диапазона представляемых чисел и жесткое расположение фиксированной запятой — основные недостатки этого способа, которые могут привести к потере точности при выполнении арифметических операций вследствие переполнения.
Более удобной является форма с плавающей запятой. Она основана на соотношении  , где М — мантисса и Е — порядок числа N. Величины М и Е могут быть как положительными, так и
, где М — мантисса и Е — порядок числа N. Величины М и Е могут быть как положительными, так и  , но М всегда дробное число, меньше единицы, а Е — целое число. Тем не менее обе эти величины представляются как целые числа и для каждого из них (включая знаки) отводится в слове определенное количество разрядов (рис.
, но М всегда дробное число, меньше единицы, а Е — целое число. Тем не менее обе эти величины представляются как целые числа и для каждого из них (включая знаки) отводится в слове определенное количество разрядов (рис.  ). При этом разрядность мантиссы влияет на точность, а разрядность порядка на диапазон представляешь
). При этом разрядность мантиссы влияет на точность, а разрядность порядка на диапазон представляешь  чисел.
чисел.
Сдвиг мантиссы на один разряд влево увеличивает, а вправо — уменьшает ее вдвое. Чтобы такие сдвиги не влияли на значение числа, необходимо соответственно уменьшить и увеличить порядок на единицу. Сдвиг мантиссы влево допустим только при наличии старшего нулевого разряда. Если же старший разряд равен 1, то это соответствует максимально возможному значен)  данной мантиссы, которое лежит в диапазоне
данной мантиссы, которое лежит в диапазоне  Числа с таким представлением мантиссы называют нормализованными, и они чаще всего используются в вычислительных системах.
Числа с таким представлением мантиссы называют нормализованными, и они чаще всего используются в вычислительных системах.
Процесс нормализации состоит в сдвиге числа на необходимое количество разрядов влево или вправо с соответствующим уменьшением или увеличением порядка.
Если мантисса и порядок нормализованного числа занимают соответственно  и q разрядов, то минимальное и максимальное значения (в десятичной записи)
и q разрядов, то минимальное и максимальное значения (в десятичной записи)

что определяет диапазон представления чисел  . В этом отношении форма с плавающей запятой предпочтительна.
. В этом отношении форма с плавающей запятой предпочтительна.
При сложении чисел с плавающей запятой необходимо сначала выравнять показатели слагаемых, для чего мантисса одного из них сдвигается на число разрядов, равное разности показателей. Умножение сводится к определению произведения  и суммы показателей.
и суммы показателей.  операции выполняются над целыми числами, а результат обычно (хотя и не всегда) нормализуется.
операции выполняются над целыми числами, а результат обычно (хотя и не всегда) нормализуется.
Машинное слово не обязательно должно иметь структуру, показанную на рис. 1.1. Используются и другие варианты расположения мантиссы и порядка, а также их знаков. Но слово, как правило, содержит целое число байт. Числа в форме с плавающей запятой для повышения точности могут представляться двумя последовательными словами.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
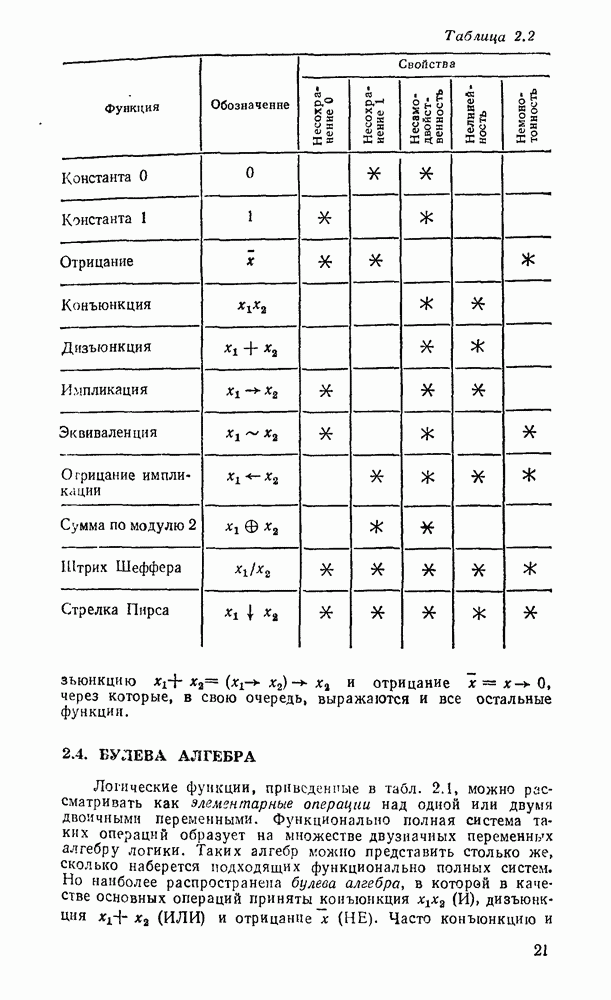
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
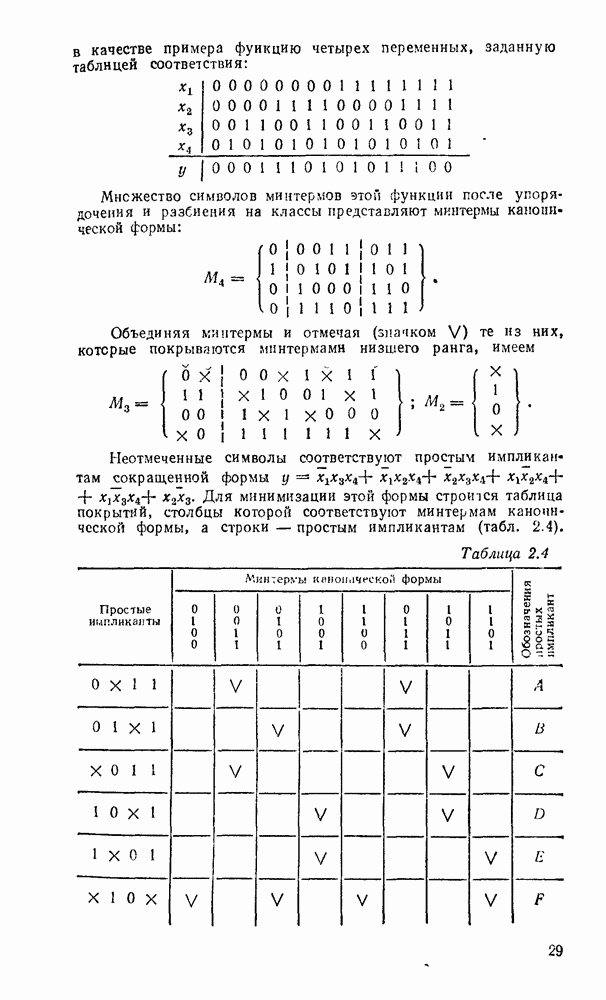
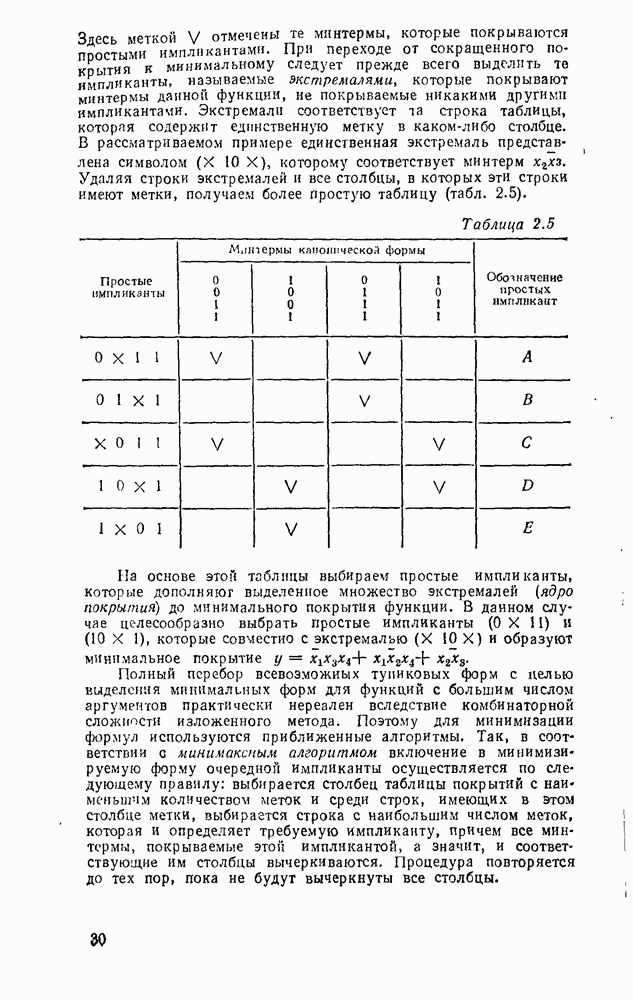
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
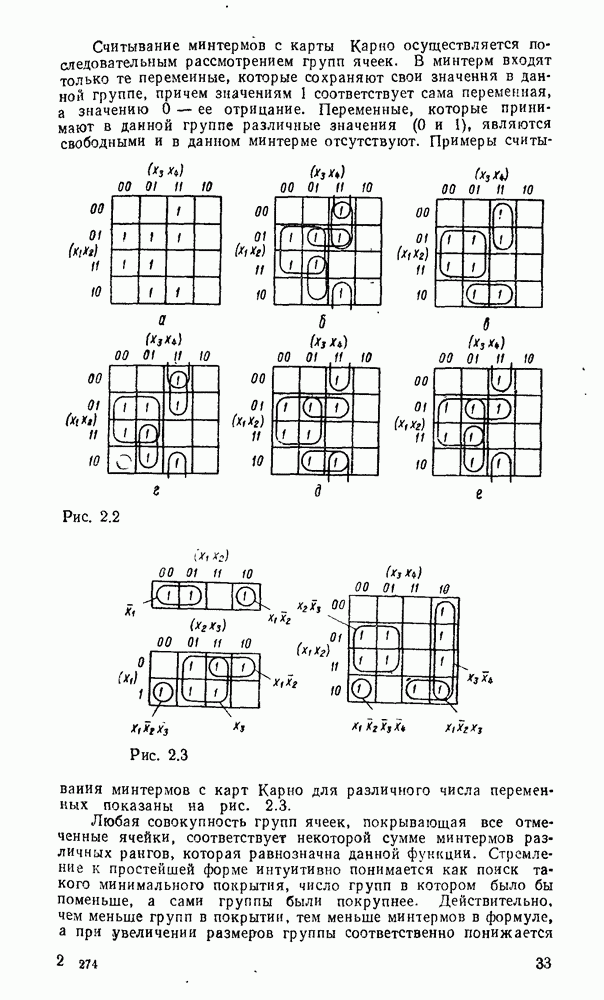
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
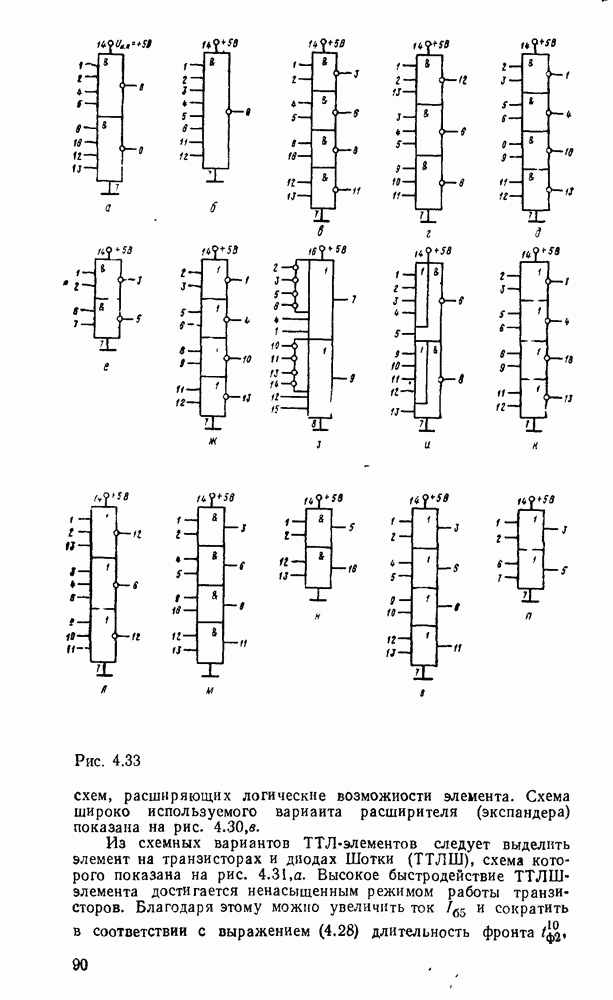
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
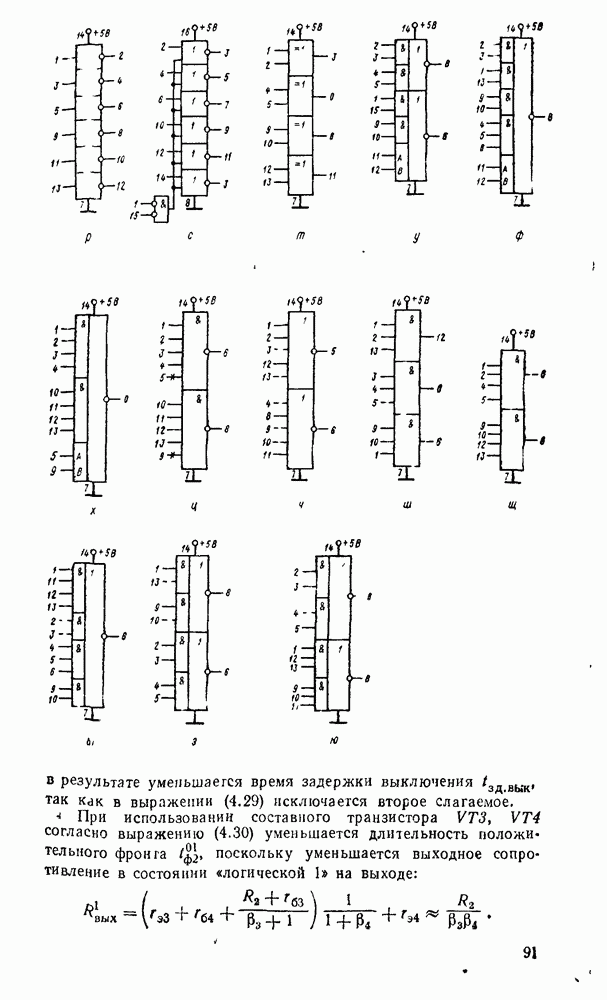
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
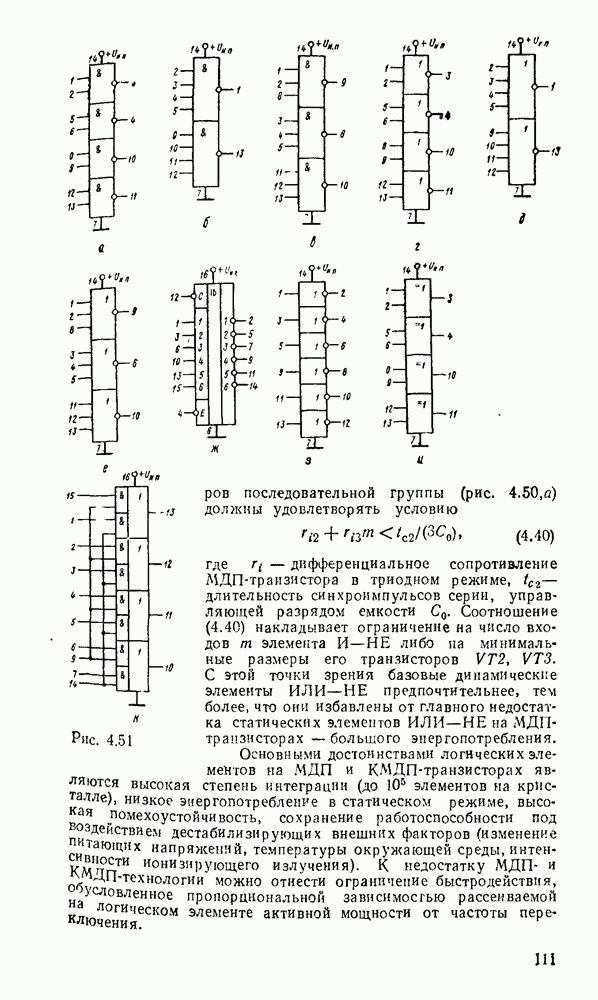
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
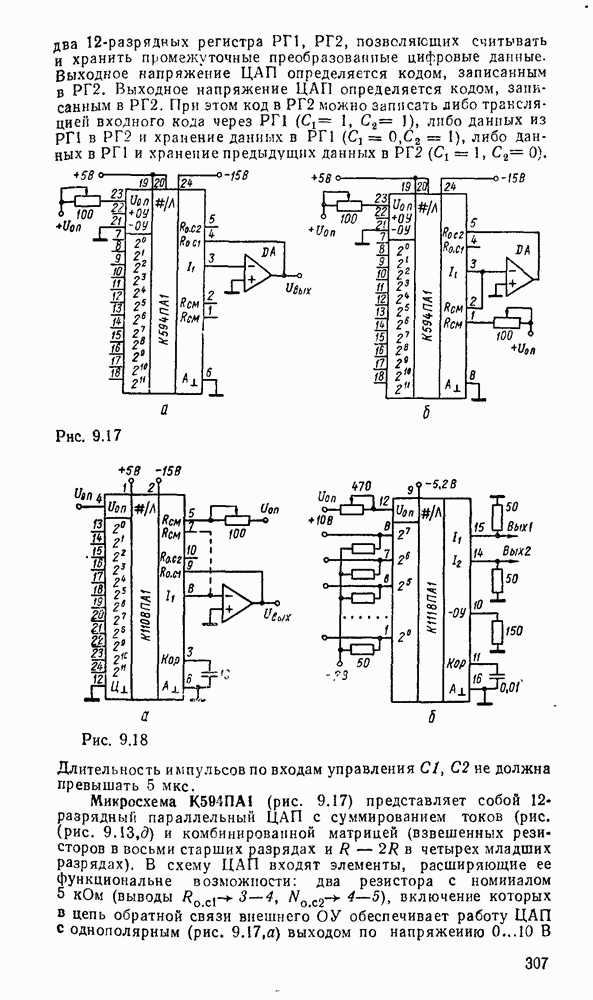
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
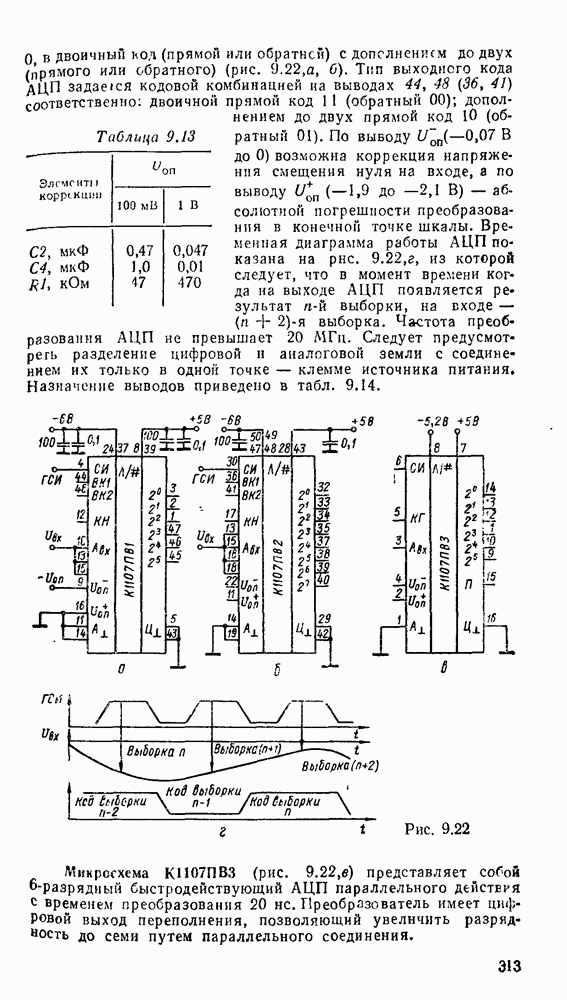
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
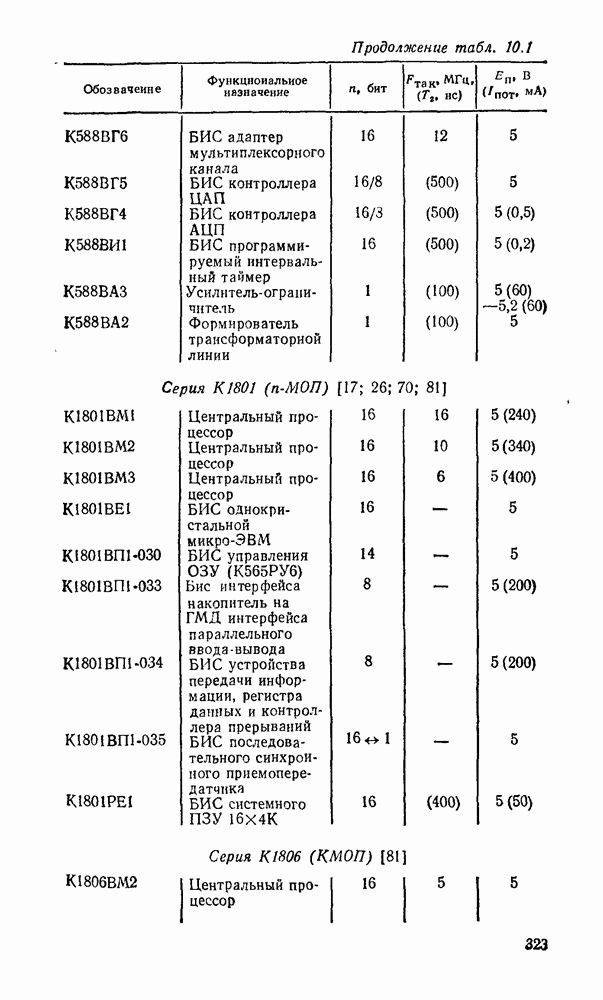
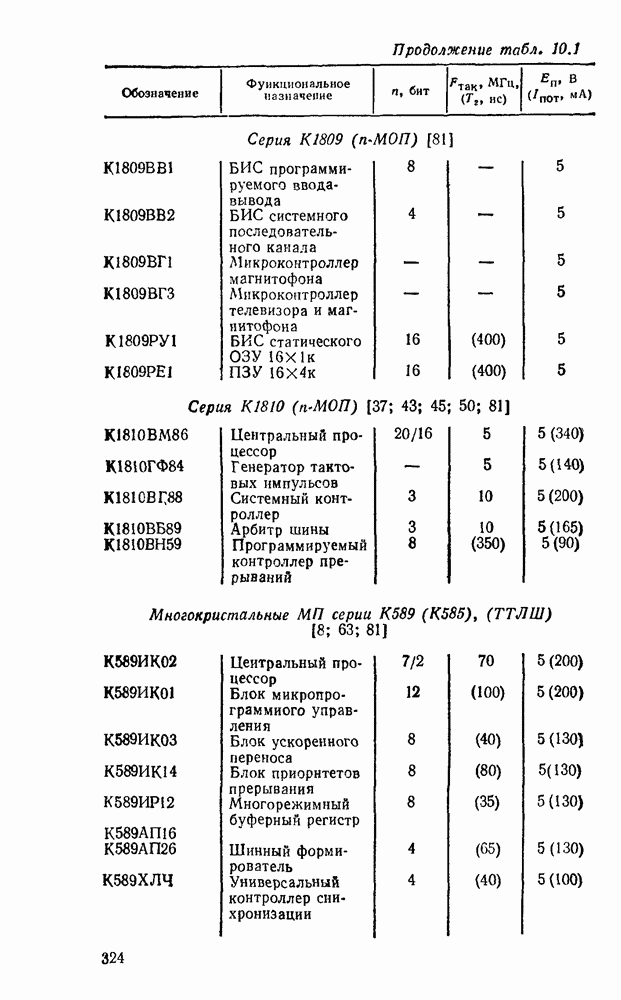
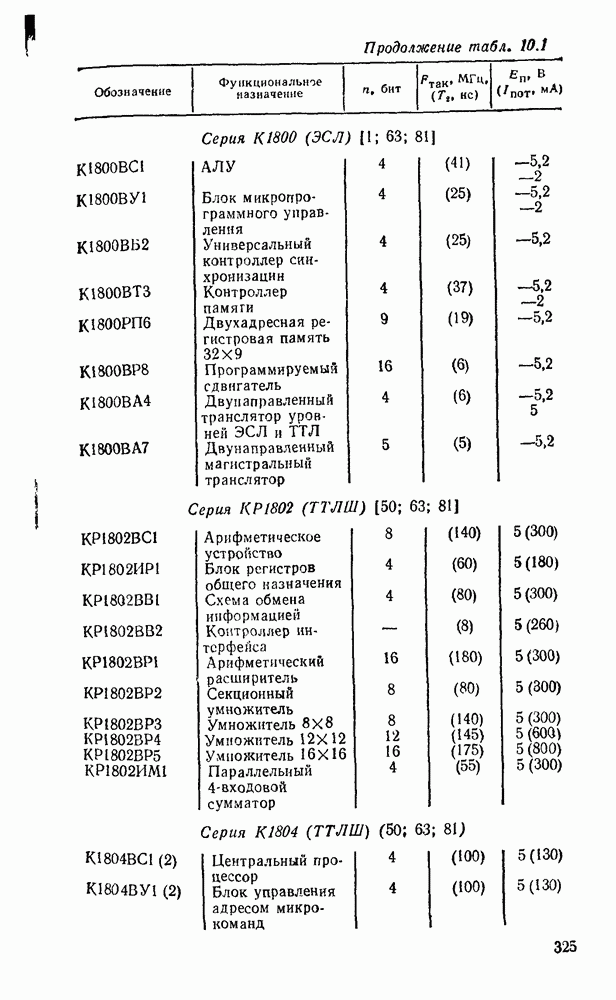
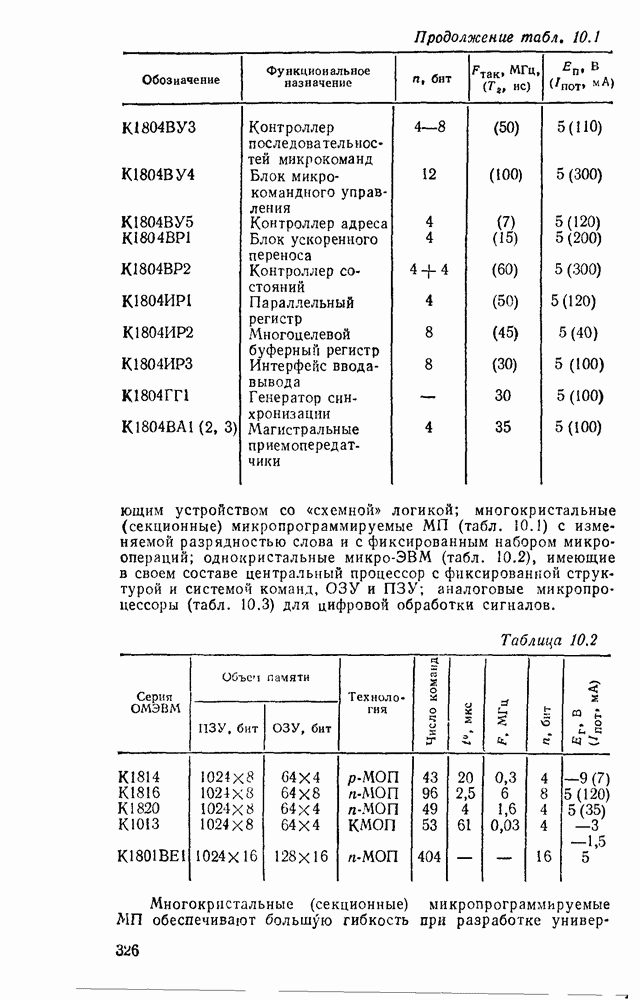
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
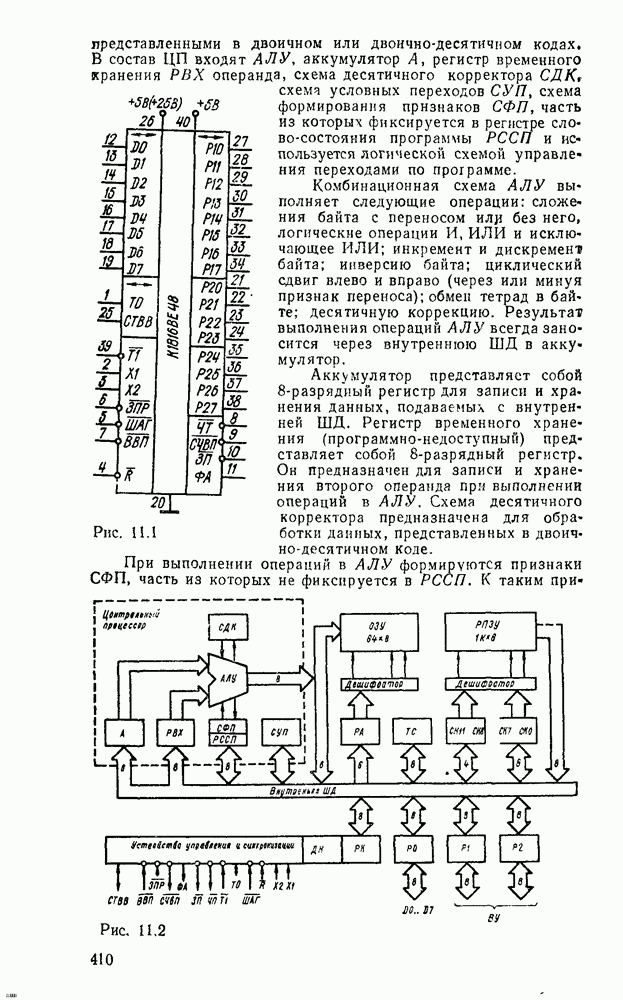
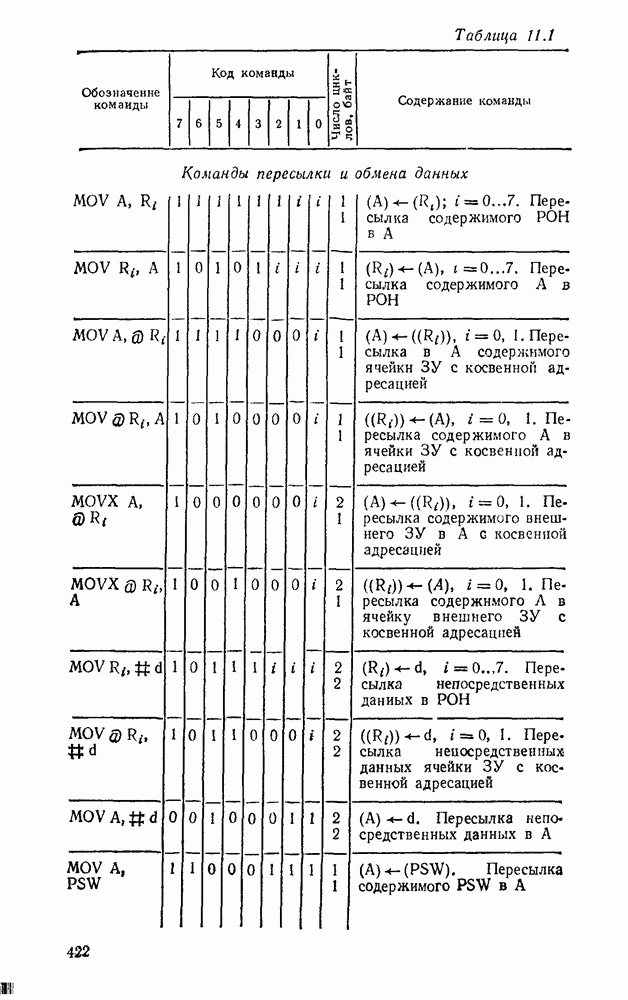
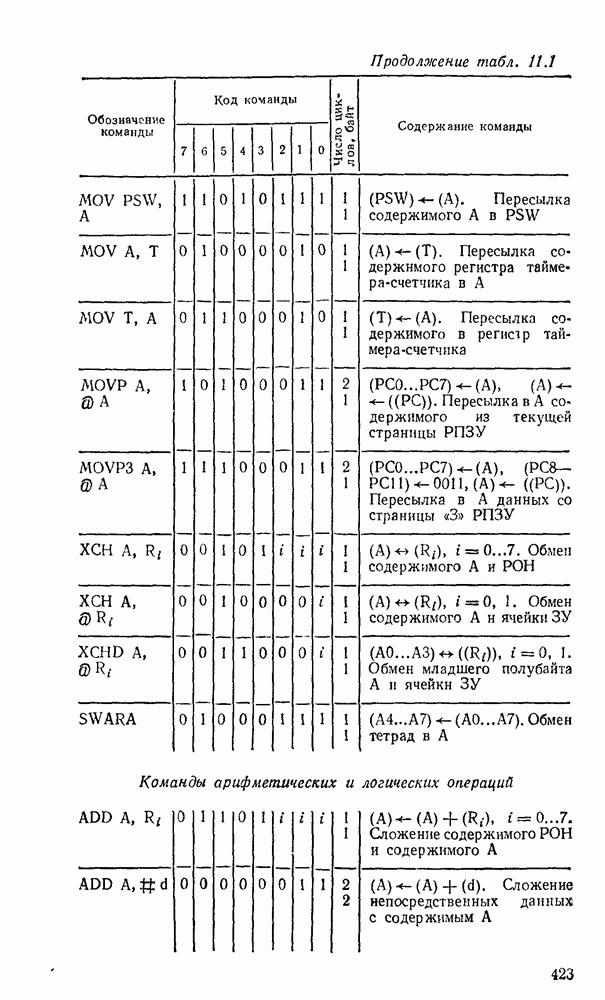
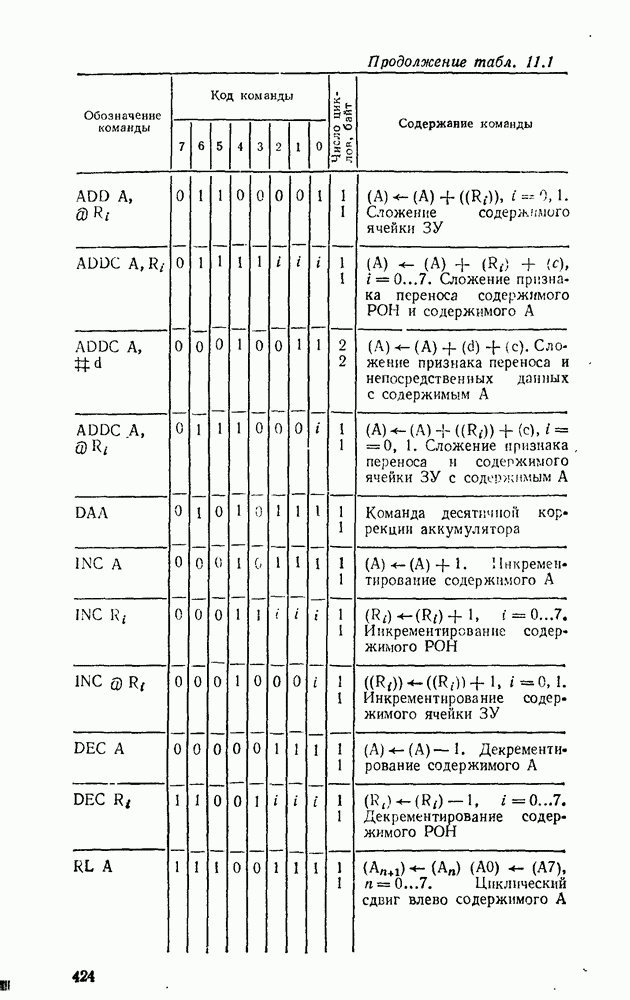
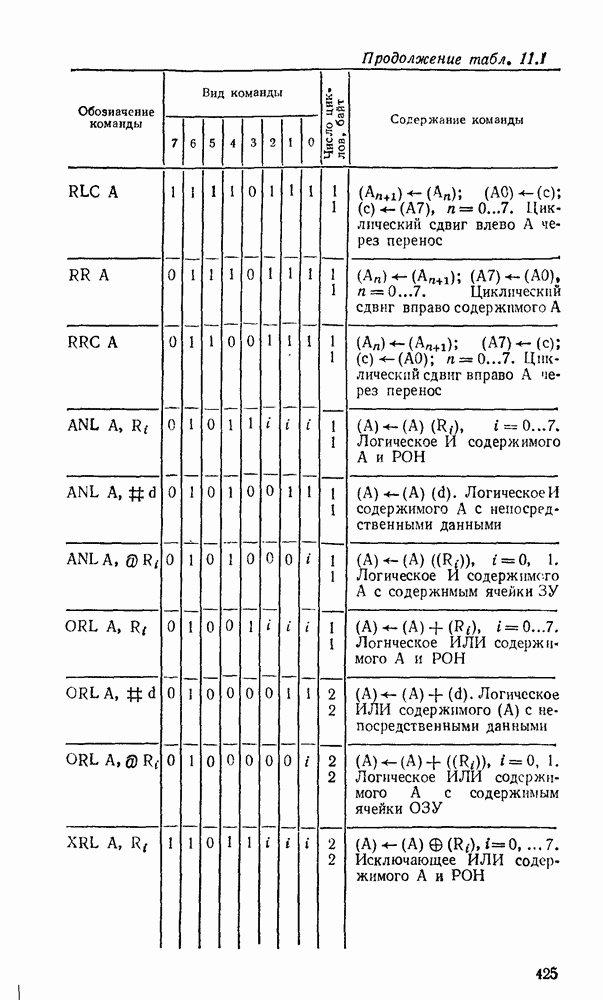
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ