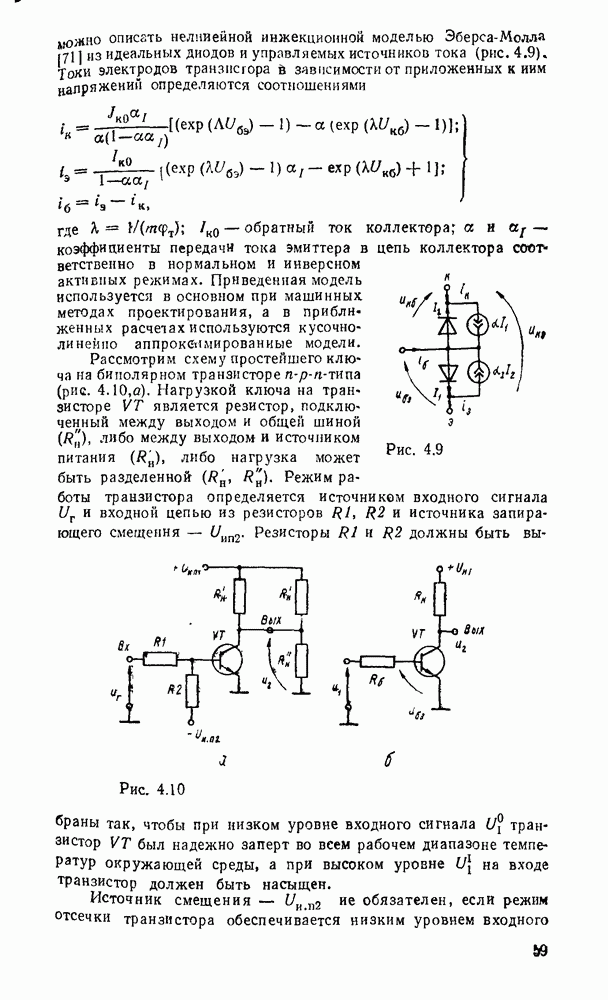
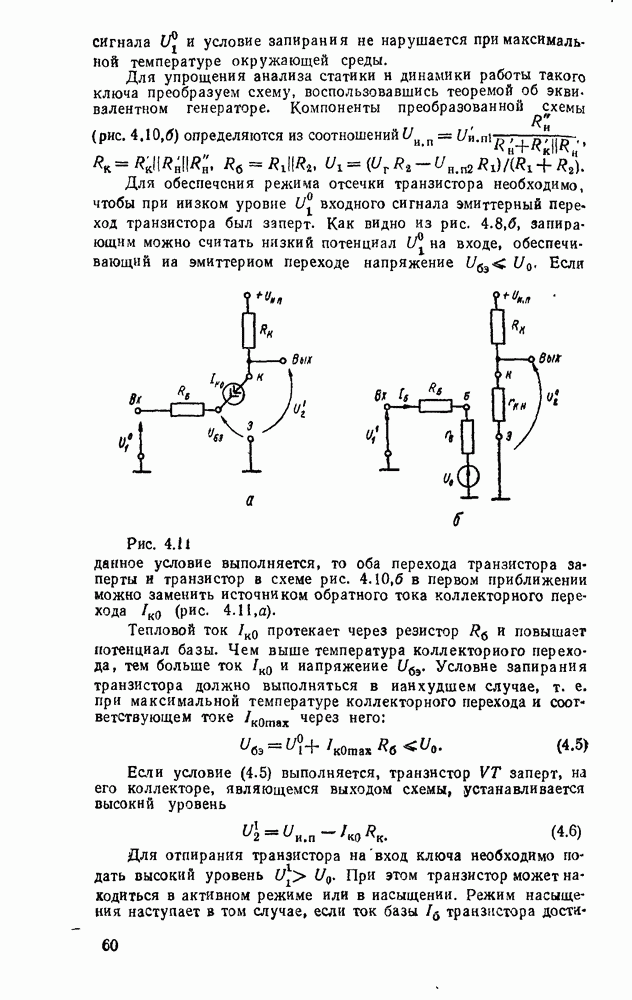
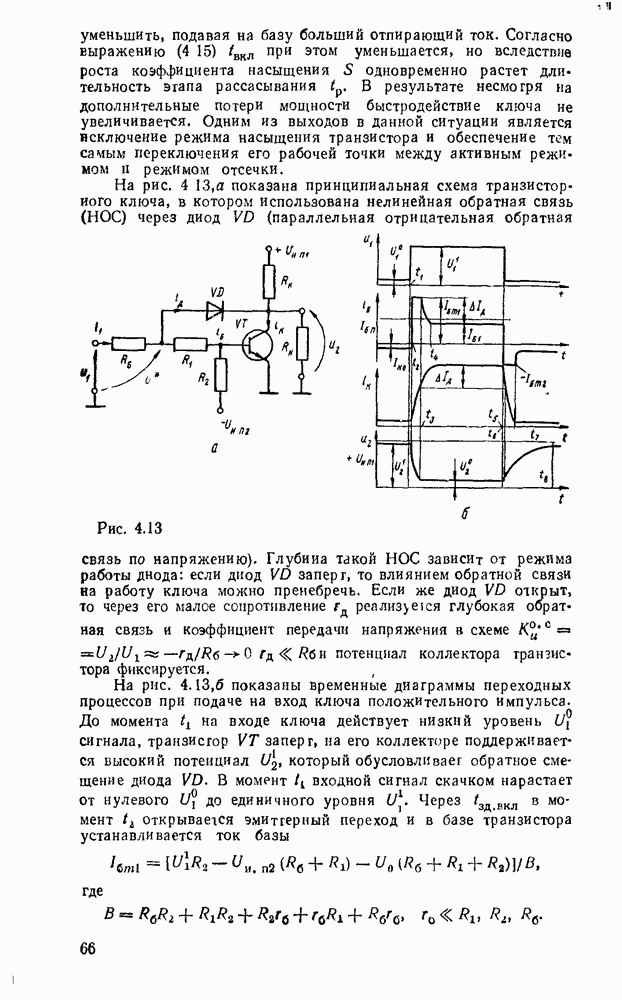
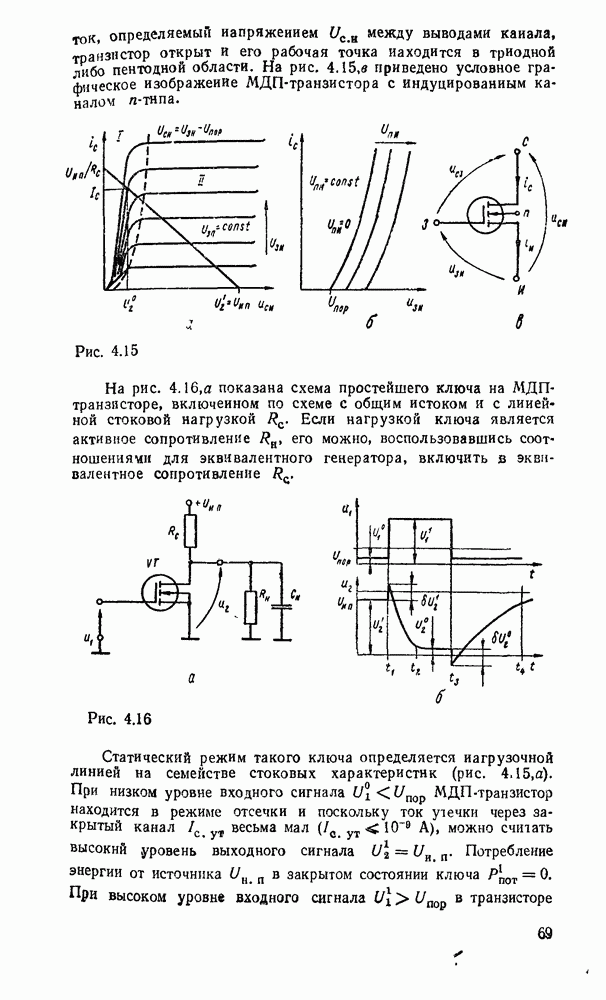
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
 узлы комбинационного типа характеризуй
узлы комбинационного типа характеризуй  однозначным соответствием выходных сигналов допустимым комбинациям сигналов на входе и не зависят от последовательности их смены. Для построения комбинационного функционального узла должны быть заданы все множество кодов (слов) и соответствующий нм набор выходных кодов либо система уравнений, описывающая зависимость каждого разряда выходного кода
однозначным соответствием выходных сигналов допустимым комбинациям сигналов на входе и не зависят от последовательности их смены. Для построения комбинационного функционального узла должны быть заданы все множество кодов (слов) и соответствующий нм набор выходных кодов либо система уравнений, описывающая зависимость каждого разряда выходного кода  независимых входных переменных. Комбинационные схемы строятся либо на основе логических элементов, либо на основе постоянных запоминающих устройств (ПЗУ), в которые записывается таблица преобразования входных слов в выходные К комбинационным функциональным узлам относятся преобразователи кодов, (частным случаем которых являются шифраторы и дешифраторы), мультиплексоры, демультиплексоры, устройства сдвига чисел, комбинационные сумматоры, цифровые компараторы и др.
независимых входных переменных. Комбинационные схемы строятся либо на основе логических элементов, либо на основе постоянных запоминающих устройств (ПЗУ), в которые записывается таблица преобразования входных слов в выходные К комбинационным функциональным узлам относятся преобразователи кодов, (частным случаем которых являются шифраторы и дешифраторы), мультиплексоры, демультиплексоры, устройства сдвига чисел, комбинационные сумматоры, цифровые компараторы и др.
Преобразователи кодов предназначены для перевода  из одной формы представления в другую.
из одной формы представления в другую.
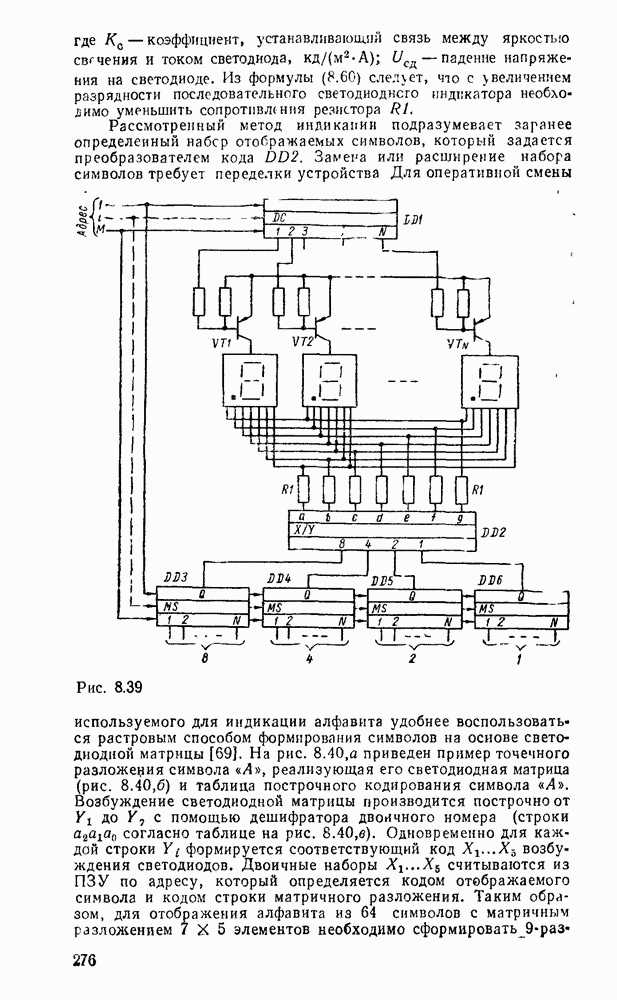
Например, при вводе информации в ЭВМ необходимо преобразовывать десятичные числа в двоичные, а при выводе информации на индикаюры или печатающее устройство — двоичные или двоично-десятичные коды в коды управления знакогенератором, светодиодными или жидкокриааллическими индикаторными панелями, механизмом печати.
Таблица 5.1

Таблица 5.2

Отправным пунктом для построения преобразователя кодов является таблица соответствия, в которой записывается потный набор входных и соответствующий ьабор выходных слов. Если входные и выходные слова записаны двоичными символами, то сишез преобразователя кода сводится к нахождению для каждого разряда выходного слова булевой функции, устанавливающей связь данного разряда с входными наборачя двоичных переменных. Нахождение такой связи и минимизация булевого выражения осуществляйся с помощью карт Карно (диаграмм Вейча). На заключительном этапе полученная функция преобразуется к виду, удобному для реализации в заданном (выбранном) элементном базисе.
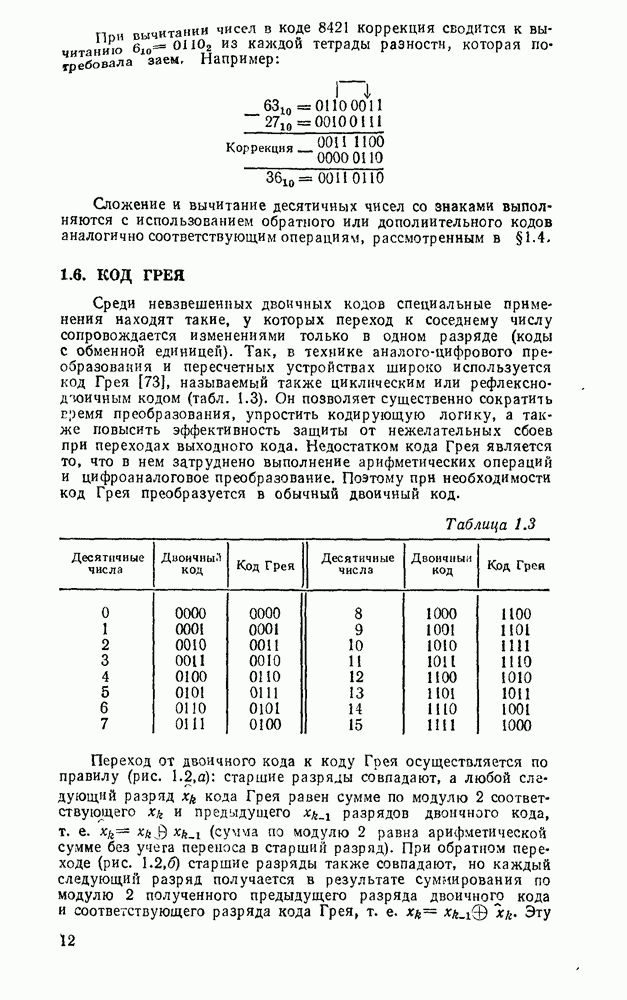
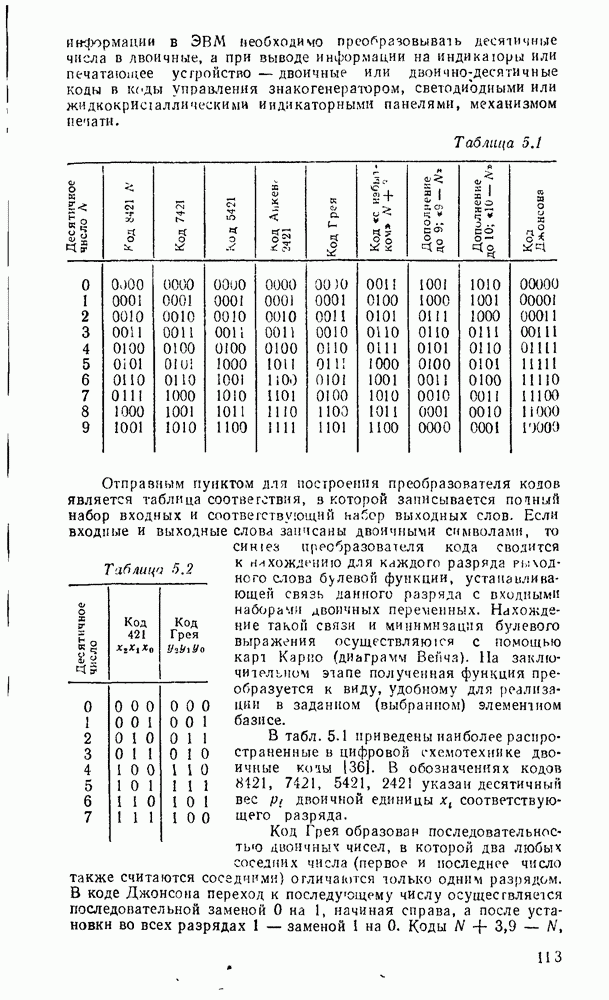
В табл. 5.1 приведены наиболее распространенные в цифровой схемотехнике двоичные коды [36]. В обозначениях кодов 8121, 7421, 5421, 2421 указан десятичный вес  двоичной единицы соответствующего разряда.
двоичной единицы соответствующего разряда.
Код Грея образован последовательностью двоичных чисел, в которой два любых соседних числа (первое и последнее число также считаются соседними) отличаются только одним разрядом. В коде Джонсона переход к последующему числу осуществляется последовательной заменой 0 на 1, начиная справа, а после установки во всех разрядах 1 — заменой 1 на 0.
Коды  , используютси в арифметических устройствах для выполнения операций сложения и вычитания двоично-десятичных чисел.
, используютси в арифметических устройствах для выполнения операций сложения и вычитания двоично-десятичных чисел.
Пусть необходимо построить преобразователь двоичного кода 421 в  -разрядный код Грея. Запишем таблицу соответствия (табл. 5.2).
-разрядный код Грея. Запишем таблицу соответствия (табл. 5.2).
Каждый разряд  получаемого на выходе кода является независимой функцией входных наборов
получаемого на выходе кода является независимой функцией входных наборов  , которою необходимо найти и минимизировать.
, которою необходимо найти и минимизировать.

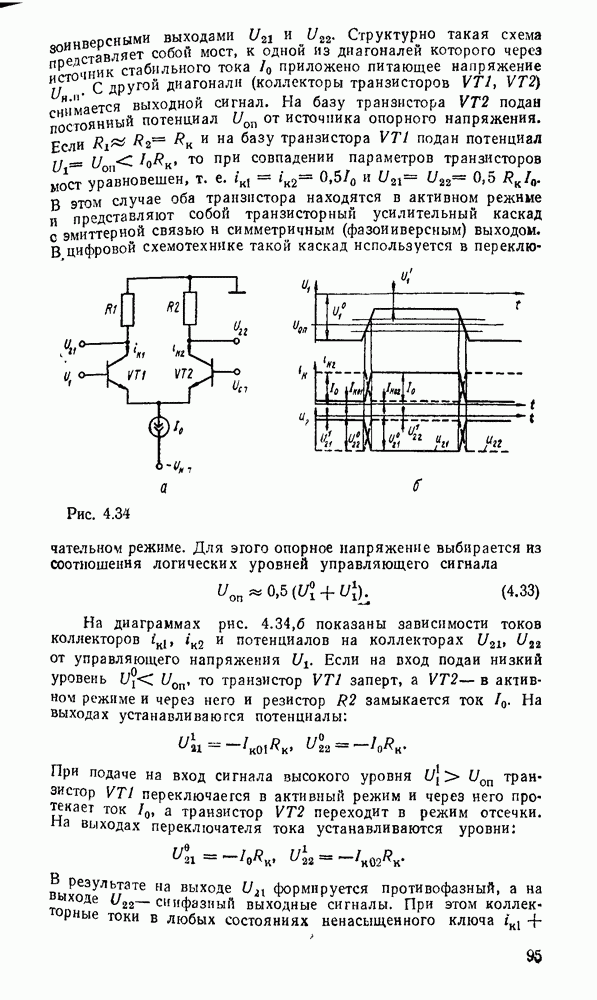
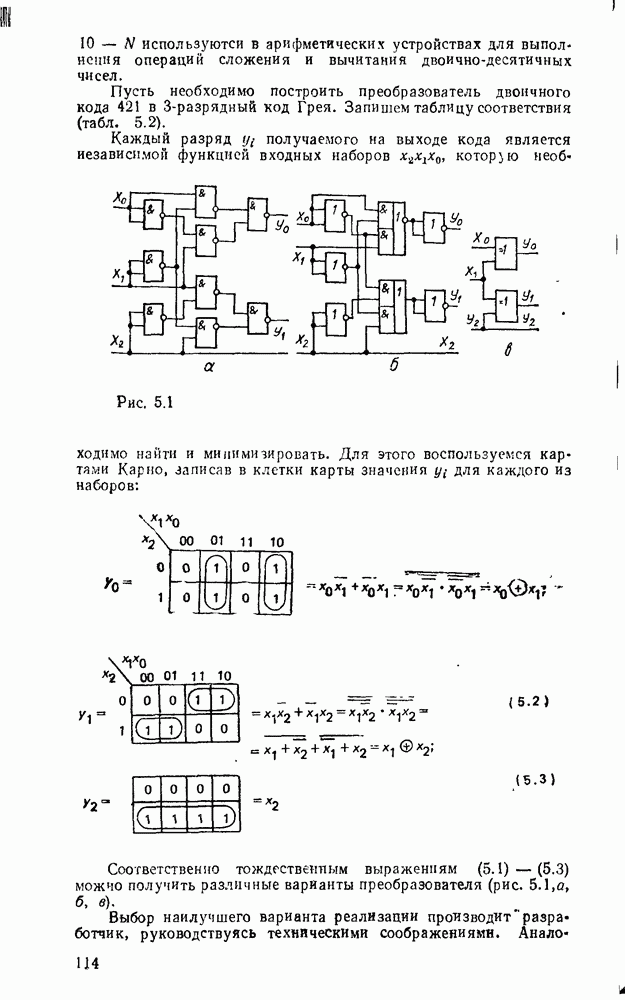
Рис. 5.1.
Для этого воспользуемся картами Карно, записав в клетки карты значения для каждого из наборов:

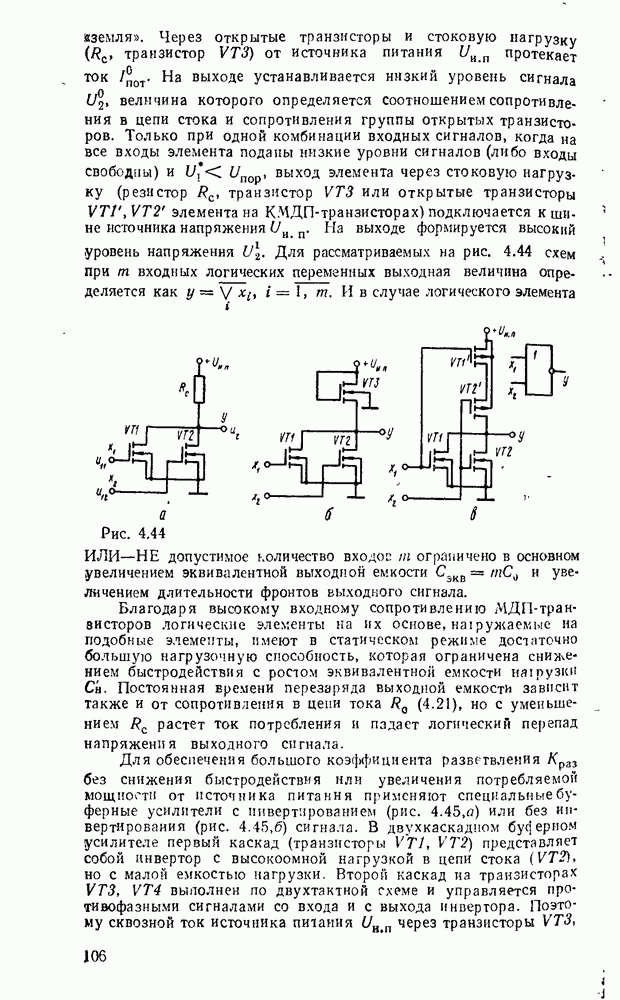
Соответственно тождественным выражениям (5.1) — (5.3) можчо получить различные варианты преобразователя (рис.  , б, в).
, б, в).
Выбор наилучшего варианта реализации производит разработчик, руководствуясь техническими соображениями.
Аналогично, используя ту же табл. 5.2, можно выполнить обратное греобразование кода Грея в код 421:

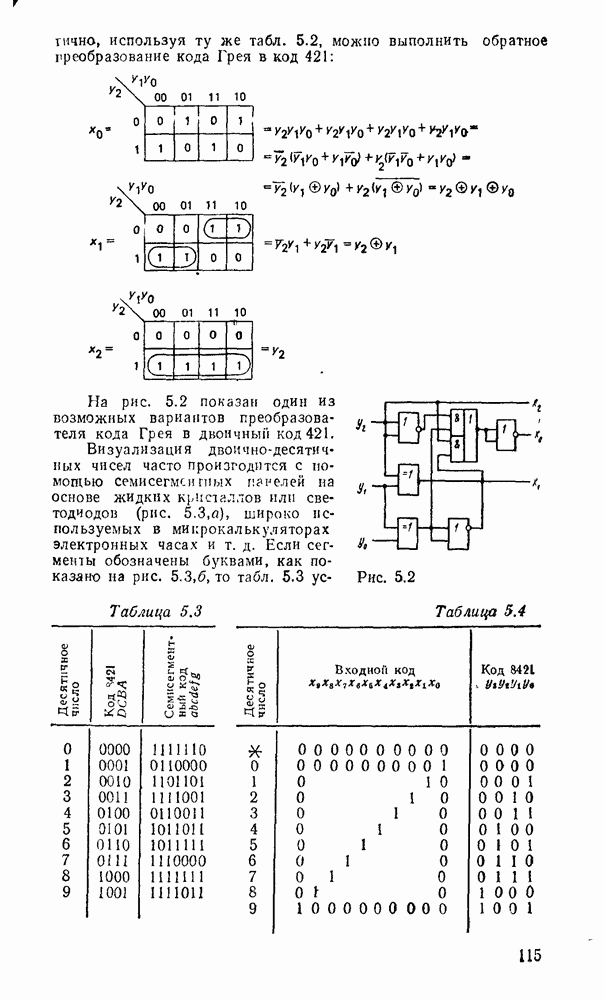
На рис. 5.2 показан один из возможных вариантов преобразователя кода Грея в двоичный код 421.
Визуализация двоично-десятичных чисел часто произгодится с помощью семисегмсн гпых панелей на основе жидких кристаллов или светодиодов (рис. 5.3,а), широко используемых в микрокалькуляторах электронных часах и т. д. Если сегменты обозначены буквами, как показано на рис.  , то табл. 5.3. устанавливает соответствие между двоично-десятичным числом и требуемым для отображения десятичной цифры набором сегментов.
, то табл. 5.3. устанавливает соответствие между двоично-десятичным числом и требуемым для отображения десятичной цифры набором сегментов.

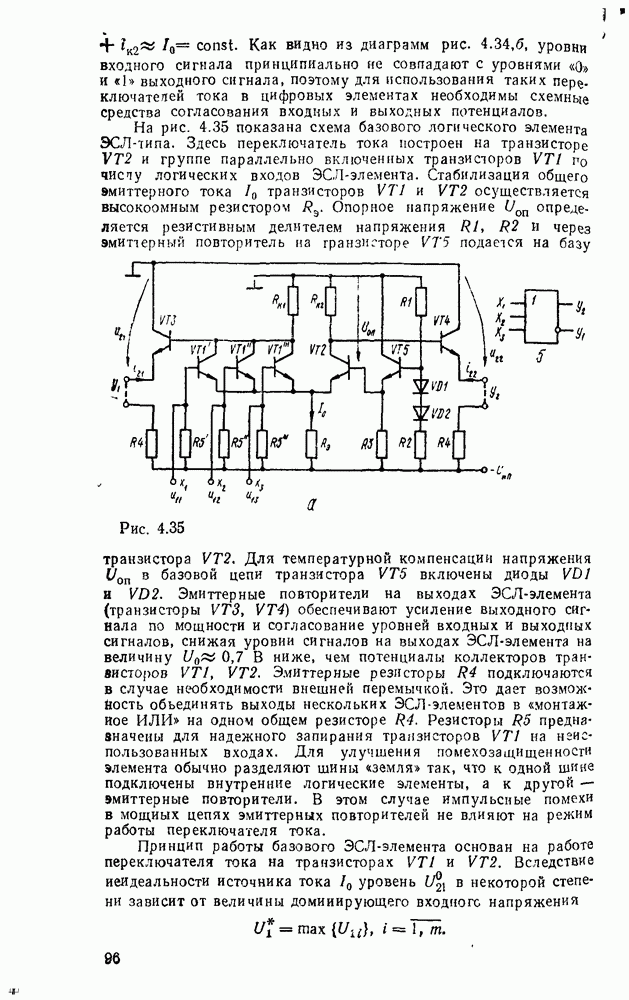
Рис. 5.2.
Таблица 5.3

Таблица 5.4

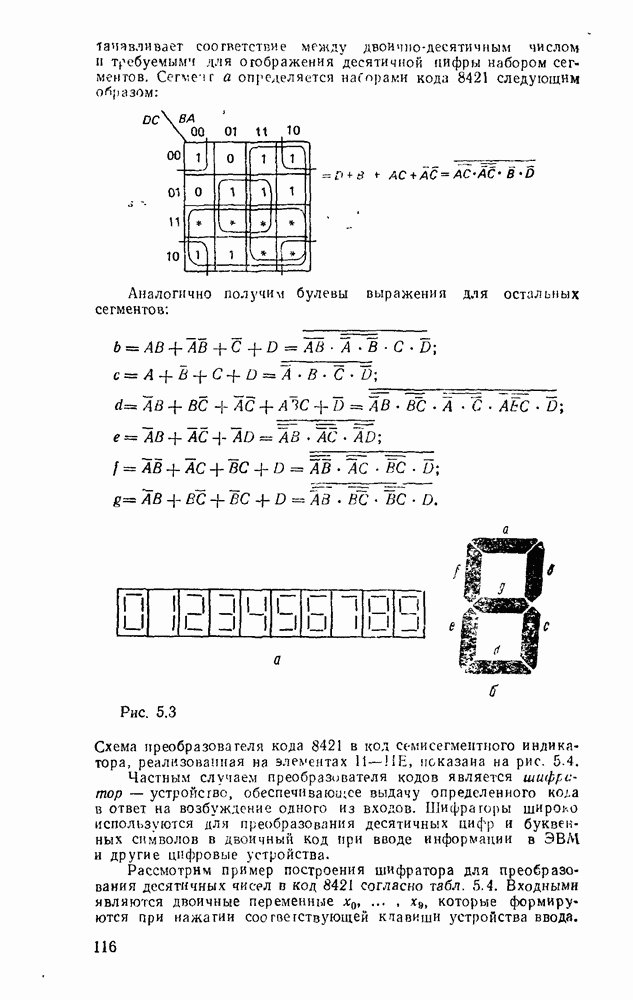
Сегмент а определяется наборами кода 8421 следующим образом:

Аналогично получим булевы выражения для остальных сегментов:


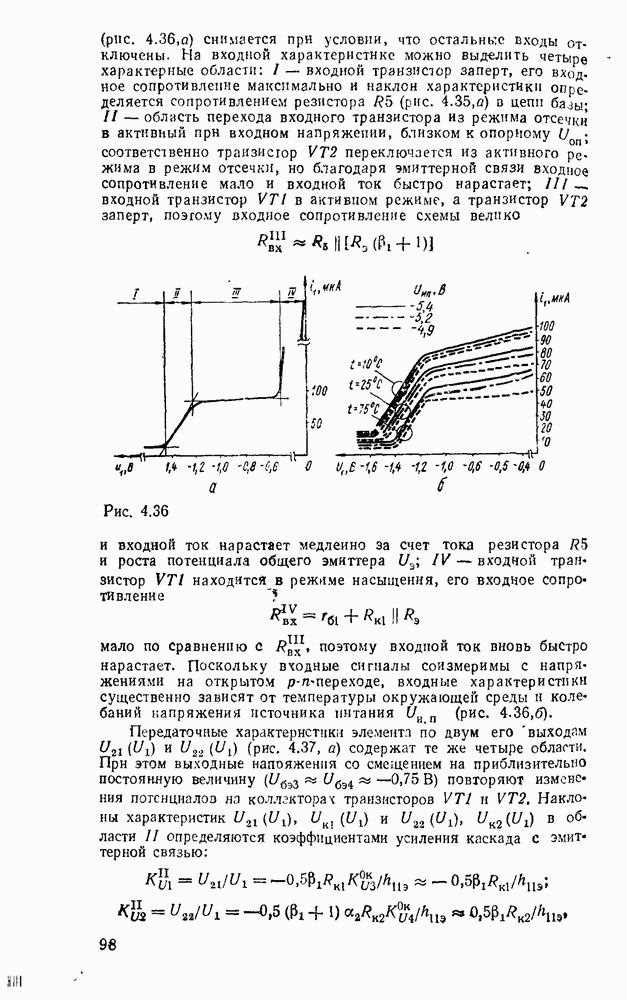
Рис. 5.3.
Схема преобразователя кода 8421 в код семисегментного индикатора, реализованная на элементах  , показана на рис. 5.4.
, показана на рис. 5.4.
Частным случаем преобразователя кодов является шифратор — устройство, обеспечивающее выдачу определенного кола в ответ на возбуждение одного из входов. Шифраторы широко используются для преобразования десятичных цифр и буквенных символов в двоичный код при вводе информации в ЭВМ и другие цифровые устройства.
Рассмотрим пример построения шифратора для преобразования десятичных чисел в код 8421 согласно табл. 5.4. Входными являются двоичные переменные  , которые формируются при нажатии соответствующей клавиши устройства ввода.
, которые формируются при нажатии соответствующей клавиши устройства ввода.
Переменные являются независимыми и позволяют построить  входных комбинаций, но если налагается ограничение, запрещающее нажатие двух и более клавиш, то из 1042 остается 11 допустимых входных комбинаций. Соответствующий данному ограничению входной код называют кодом «1 из
входных комбинаций, но если налагается ограничение, запрещающее нажатие двух и более клавиш, то из 1042 остается 11 допустимых входных комбинаций. Соответствующий данному ограничению входной код называют кодом «1 из  » или унитарным. В табл. 5.4 нажатой клавише соответствует «югическая 1», я ненажатой — «логический 0». Две первых входных комбинации порождают один и тот же двоичный код 0000. Отличие между ними состоит в том, что при нажатии клавиши «0», как и при вводе других цифр, в устройстве должна формироваться команда ввода и запоминания очередной десятичной цифры.
» или унитарным. В табл. 5.4 нажатой клавише соответствует «югическая 1», я ненажатой — «логический 0». Две первых входных комбинации порождают один и тот же двоичный код 0000. Отличие между ними состоит в том, что при нажатии клавиши «0», как и при вводе других цифр, в устройстве должна формироваться команда ввода и запоминания очередной десятичной цифры.

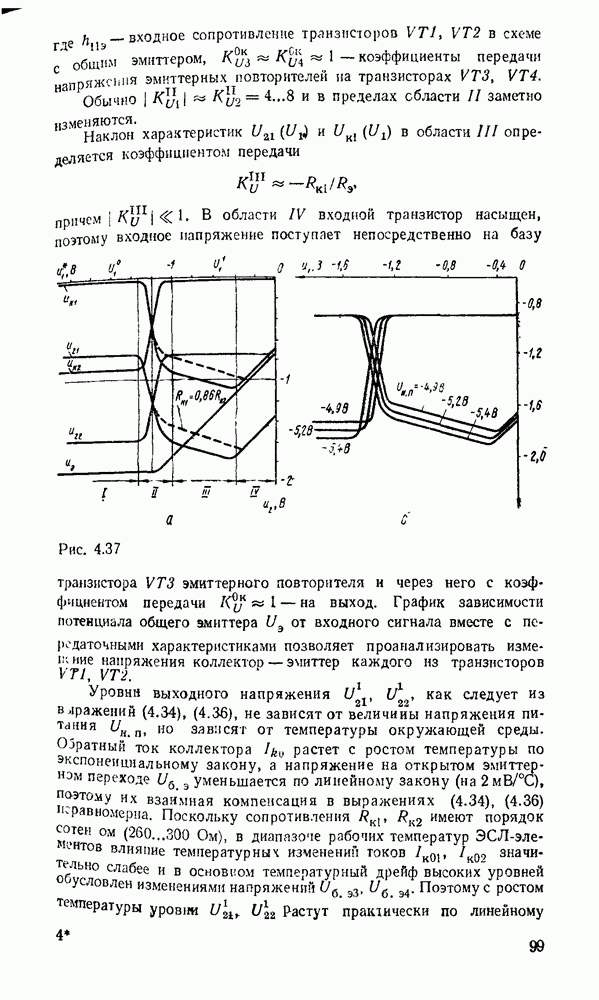
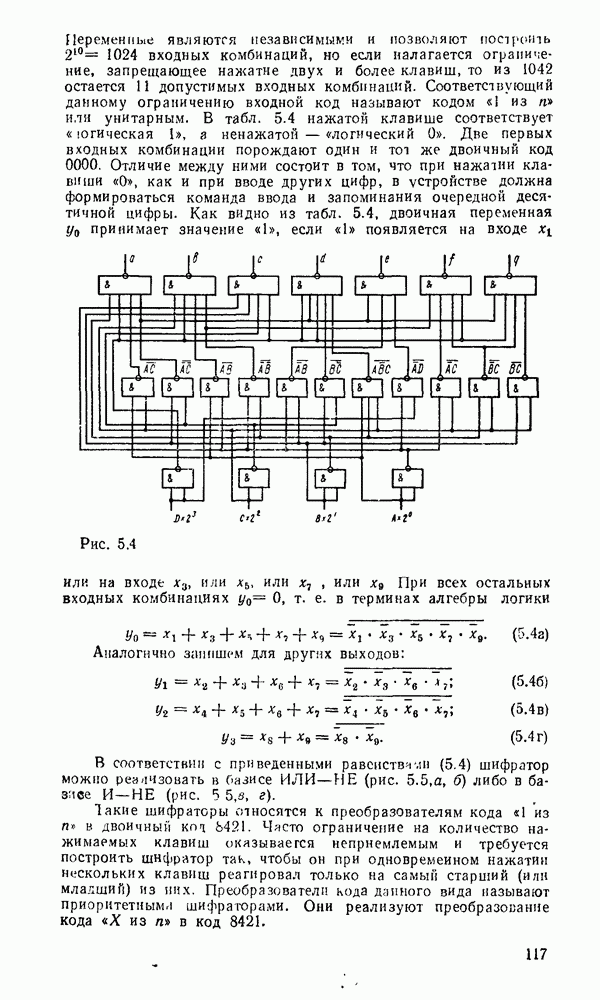
Рис. 5.4.
Как видно из табл. 5.4, двоичная переменная  принимает значение «1», если «1» появляется на входе
принимает значение «1», если «1» появляется на входе  или на входе
или на входе  , или
, или  , или
, или  , или
, или  . При всех остальных входных комбинациях
. При всех остальных входных комбинациях  т. е. в терминах алгебры логики
т. е. в терминах алгебры логики

Аналогично запишем для других выходов:

В соответствии с приведенными равеиствччн (5.4) шифратор можно реализовать в базисе ИЛИ—НЕ (рис. 5.5,а, б) либо в базисе  (рис. 5 5,а, г).
(рис. 5 5,а, г).
Такие шифраторы относятся к преобразователям кода «1 из  » в двоичный кол
» в двоичный кол  . Часто ограничение на количество нажимаемых клавиш оказывается неприемлемым и требуется построить шифратор так, чтобы он при одновременном нажатии нескольких клавиш реагировал только на самый старший (или младший) из них. Преобразователи кода данного вида называют приоритетными шифраторами. Они реализуют преобразование кода
. Часто ограничение на количество нажимаемых клавиш оказывается неприемлемым и требуется построить шифратор так, чтобы он при одновременном нажатии нескольких клавиш реагировал только на самый старший (или младший) из них. Преобразователи кода данного вида называют приоритетными шифраторами. Они реализуют преобразование кода  из
из  в код 8421.
в код 8421.
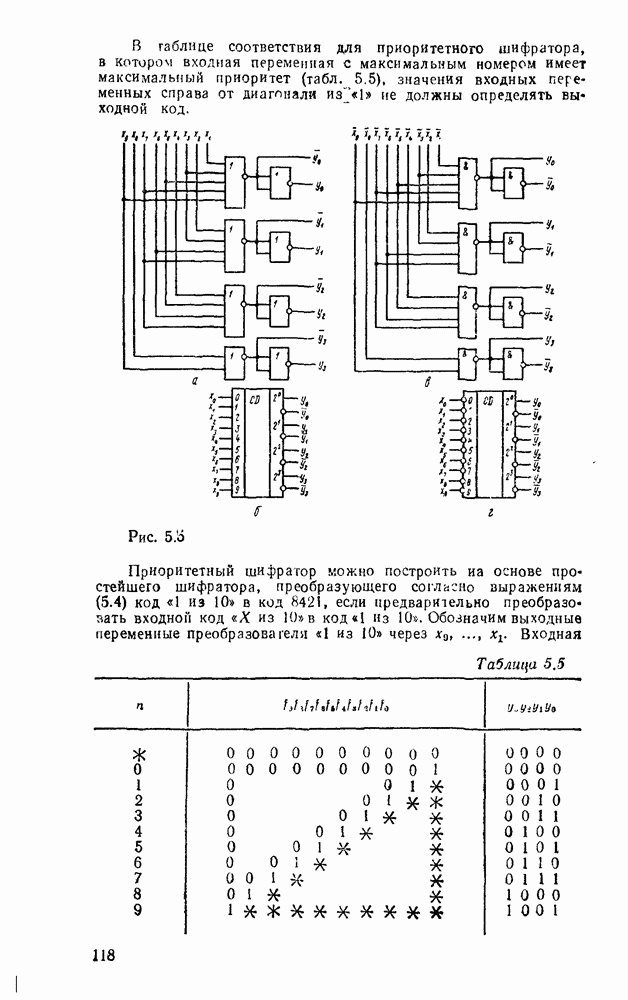
В таблице соответствия для приоритетного шифратора, в котором входная переменная с максимальным номером имеет максимальный приоритет (табл. 5.5), значения входных переменных справа от диагонали из «1» не должны определять выходной код.

Рис. 5.5.
Приоритетный шифратор можно построить на основе простейшего шифратора, преобразующего согласно выражениям (5.4) код «1 из 10» в код 8421, если предварительно преобразовать входной код «X из 10» в  Обозначим выходные переменные преобразователя «1 из 10» через
Обозначим выходные переменные преобразователя «1 из 10» через  .
.
Таблица 5.5

Входная переменная  имеет максимальный приоритет, поэтому не зависит от других входных переменных:
имеет максимальный приоритет, поэтому не зависит от других входных переменных:  . Любая другая выходная переменная
. Любая другая выходная переменная  принимает значение «1», если
принимает значение «1», если  при условии, что ни на один из «старших» входов
при условии, что ни на один из «старших» входов  9 не подана «логическая 1», т. е.
9 не подана «логическая 1», т. е.

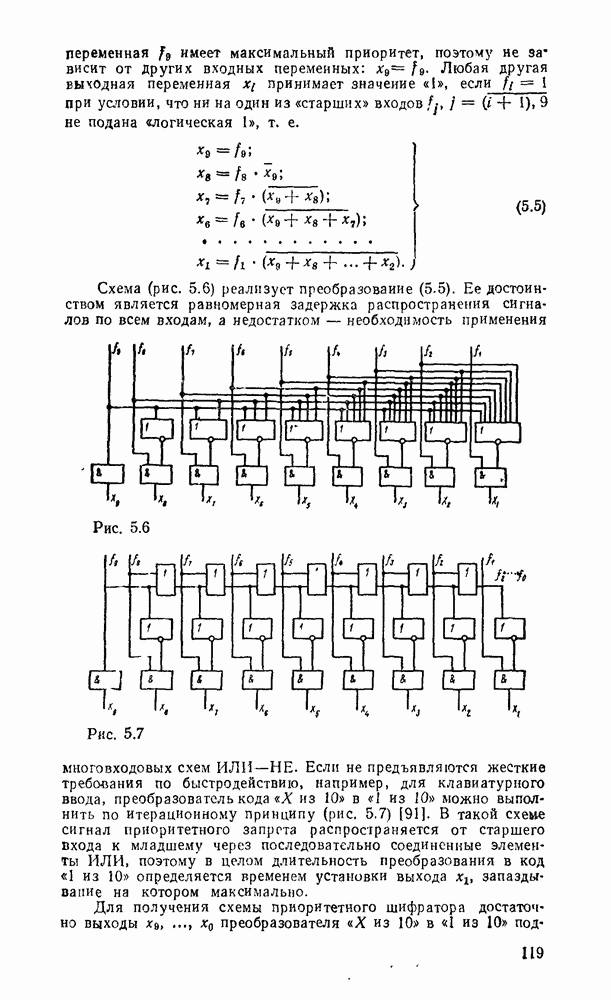
Схема (рис. 5.6) реализует преобразование (5.5). Ее достоинством является равномерная задержка распространения сигналов по всем входам, а недостатком — необходимость применения многовходовых схем ИЛИ—НЕ.

Рис. 5.6.

Рис. 5.7.
Если не предъявляются жесткие требования по быстродействию, например, для клавиатурного ввода, преобразователь кода «А из 10» в «1 из 10» можно выполнить по итерационному принципу (рис. 5.7) [91]. В такой схеме сигнал приоритетного запрета распространяется от старшего входа к младшему через последовательно соединенные элементы ИЛИ, поэтому в целом длительность преобразования в код «1 из 10» определяется временем установки выхода  , запаздывание на котором максимально.
, запаздывание на котором максимально.
Для получения схемы приоритетного шифратора достаточно выходы  преобразователя «X из 10» в «1 из 10» подключить к соответствующим входам преобразователя кода "1 из 10" в код 8421.
преобразователя «X из 10» в «1 из 10» подключить к соответствующим входам преобразователя кода "1 из 10" в код 8421.
Обратное преобразование двоичного кода в кол « 1 из  » выполняют преобразователи кода, называемые дешифраторами. Наиболее широко дешифраторы используются в устройствах вывода информации из ЭВМ и других цифровых устройств на внешние устройства визуализации и документирования алфавитно-цифровой информации. Для этого нужно подать сигнал на 1 из
» выполняют преобразователи кода, называемые дешифраторами. Наиболее широко дешифраторы используются в устройствах вывода информации из ЭВМ и других цифровых устройств на внешние устройства визуализации и документирования алфавитно-цифровой информации. Для этого нужно подать сигнал на 1 из  , например, катодов газоразрядного индикатора или элементов выборки символов печатающего устройства
, например, катодов газоразрядного индикатора или элементов выборки символов печатающего устройства
Таблица 5.6

Таблица 5.7

Синтез структуры дешифратора, как и любого другого преобразователя кодов, начинается с записи таблицы соответствия входных и выходных кодов. Пусть необходимо преобразовать двоичный код 21 в код «1 из 4» Тогда табл 5 6 пол ноет но определяет значения выходов для всех входных наборов. Далее следует для каждой выходной функции составить карту Карно и получить ее минимизированное выражение. В рассматриваемом примере это бессмысленно, так как для каждой функции  карта Карно содержит только одну "1", поэтому соответствующий ей минтерм и является минимальной формой. Тогда на основании табл. 5.6 напишем:
карта Карно содержит только одну "1", поэтому соответствующий ей минтерм и является минимальной формой. Тогда на основании табл. 5.6 напишем:

Выражения (5.6) уожио реализовать в элементном базисе  (рис
(рис  либо базисе ИЛИ—НЕ (рис 5 8,в)
либо базисе ИЛИ—НЕ (рис 5 8,в)
Если число входов  и число выходов «дешифратора связаны соотношением
и число выходов «дешифратора связаны соотношением  . то выходы определены для всех двоичных наборов и дешифратор называется полным [97] В случае
. то выходы определены для всех двоичных наборов и дешифратор называется полным [97] В случае  дешифратор
дешифратор  неполным. Пример неполного дешифратора — преобразователь двоичного кода 8421 в код «1 из 10» согласно табл. 5.7.
неполным. Пример неполного дешифратора — преобразователь двоичного кода 8421 в код «1 из 10» согласно табл. 5.7.
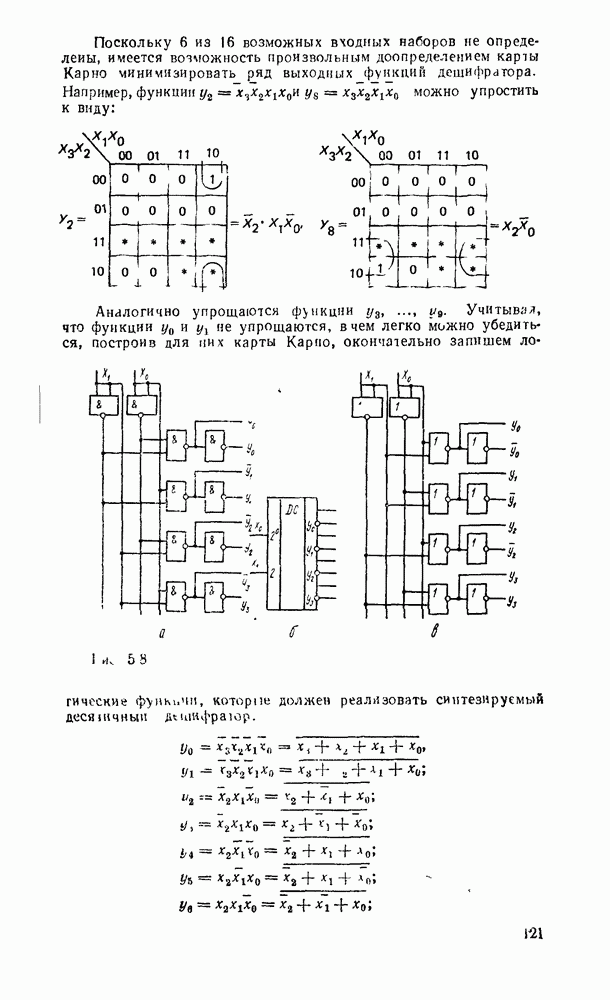
Поскольку 6 из 16 возможных входных наборов не определены, имеется возможность произвольным доопределением карты Карно минимизировать ряд выходных функций дешифратора. Например, функции  можно упростить к виду:
можно упростить к виду:


Рис. 5.8.
Аналогично упрощаются функции  . Учитывая, что функции
. Учитывая, что функции  не упрощаются, в чем легко можно убедиться, построив для них карты Карно, окончательно запишем логические функции, которые должен реализовать синтезируемый десятичный дешифратор:
не упрощаются, в чем легко можно убедиться, построив для них карты Карно, окончательно запишем логические функции, которые должен реализовать синтезируемый десятичный дешифратор:


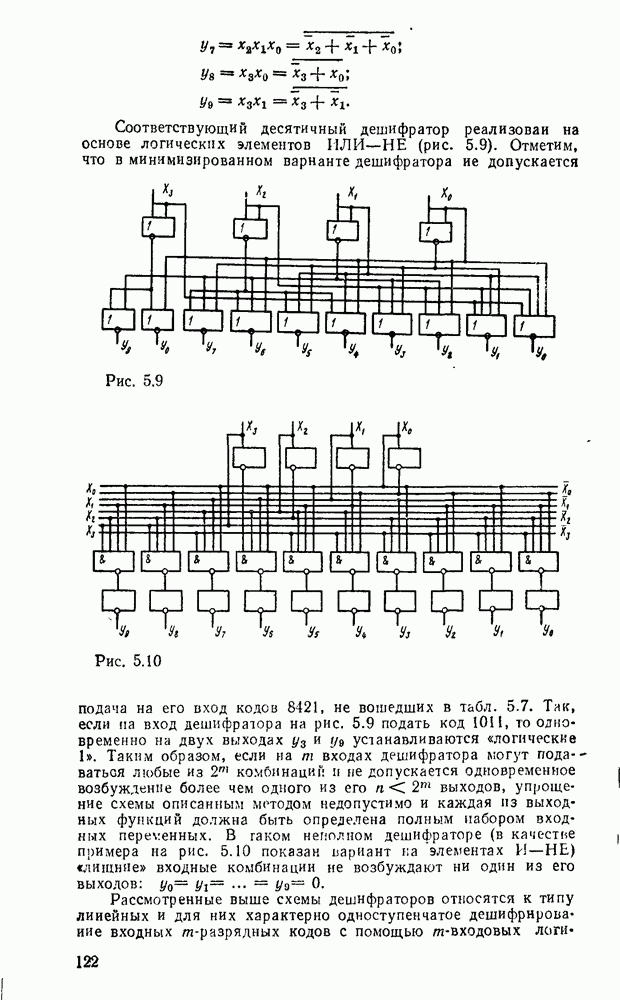
Соответствующий десятичный дешифратор реализован на основе логических элементов ИЛИ—НЕ (рис. 5.9). Отметим, что в минимизированном варианте дешифратора не допускается подача на его вход кодов 8421, не вошедших в табл. 5.7.

Рис. 5.9.

Рис. 5.10.
Так, если на вход дешифратора на рис. 5.9 подать код 1011, то одновременно на двух выходах  устанавливаются «логические 1». Таким образом, если на
устанавливаются «логические 1». Таким образом, если на  входах дешифратора могут подаваться любые из
входах дешифратора могут подаваться любые из  комбинации и не допускается одновременное возбуждение более чем одного из его
комбинации и не допускается одновременное возбуждение более чем одного из его  выходов, упрощение схемы описанным методом недопустимо и каждая из выходных функций должна быть определена полным набором входных переменных. В гаком неполном дешифраторе (в качестве примера на рис. 5.10 показан вариант на элементах
выходов, упрощение схемы описанным методом недопустимо и каждая из выходных функций должна быть определена полным набором входных переменных. В гаком неполном дешифраторе (в качестве примера на рис. 5.10 показан вариант на элементах  ) «лишние» входные комбинации не возбуждают ни один из его выходов:
) «лишние» входные комбинации не возбуждают ни один из его выходов: 
Рассмотренные выше схемы дешифраторов относятся к типу линейных и для них характерно одноступенчатое дешифрирование входных  -разрядных кодов с помощью
-разрядных кодов с помощью  -входовых логических элементов.
-входовых логических элементов.
Линейные дешифраторы обеспечивают преобразование кода с минимальной задержкой и используются в наиболее быстродействующих цифровых схемах. Однако с ростом разрядности входного кода  быстро нарастает нагрузка каждого из входов и количество корпусов ИМС для реализации дешифратора. Линейная структура обычно используется для построения дешифраторов при
быстро нарастает нагрузка каждого из входов и количество корпусов ИМС для реализации дешифратора. Линейная структура обычно используется для построения дешифраторов при  .
.
Если число входов  , то с целью уменьшения количества корпусов ИМС дешифраторы выполняются по многоступенчатой схеме.
, то с целью уменьшения количества корпусов ИМС дешифраторы выполняются по многоступенчатой схеме.

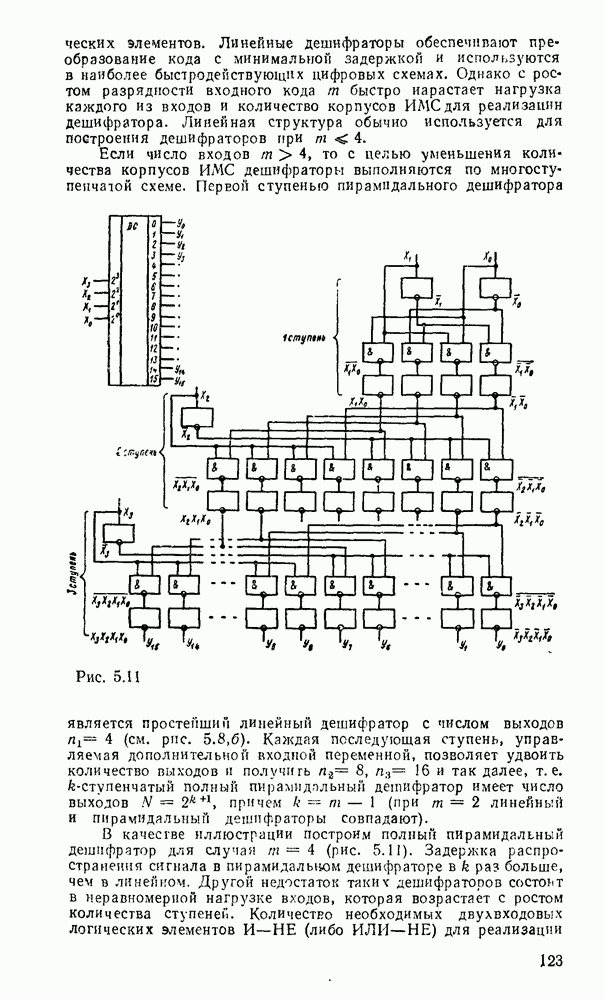
Рис. 5.11.
Первой ступенью пирамидального дешифратора является простейший линейный дешифратор с числом выходов  (см. рис. 5.8,б). Каждая последующая ступень, управляемая дополнительной входной переменной, позволяет удвоить количество выходов и получнгь
(см. рис. 5.8,б). Каждая последующая ступень, управляемая дополнительной входной переменной, позволяет удвоить количество выходов и получнгь  и так далее, т. е.
и так далее, т. е.  -ступенчатый полный пирамидальный дешифратор имеет число выходов
-ступенчатый полный пирамидальный дешифратор имеет число выходов  , причем
, причем  (при
(при  линейный и пирамидальный дешифраторы совпадают).
линейный и пирамидальный дешифраторы совпадают).
В качестве иллюстрации построим полный пирамидальный дешифратор для случая  (рис. 5.11). Задержка распространения сигнала в пирамидальном дешифраторе в k раз больше, чем в линейном. Другой недостаток таких дешифраторов состоит в неравномерной нагрузке входов, которая возрастает с ростом количества ступеней.
(рис. 5.11). Задержка распространения сигнала в пирамидальном дешифраторе в k раз больше, чем в линейном. Другой недостаток таких дешифраторов состоит в неравномерной нагрузке входов, которая возрастает с ростом количества ступеней.

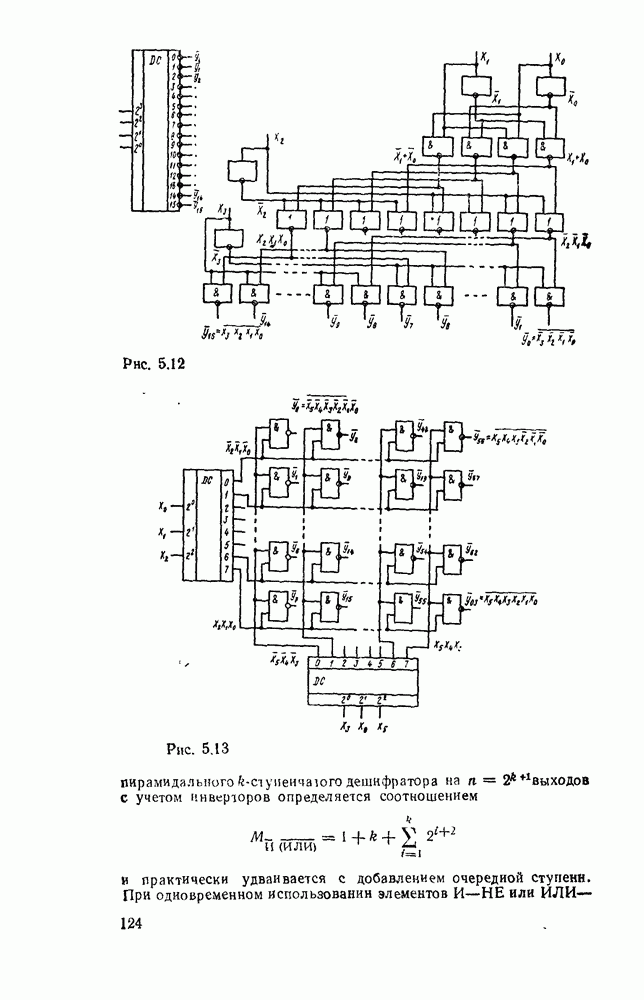
Рис. 5.12.

Рис. 5.13.
Количество необходимых двухвходовых логических элементов  (либо ИЛИ—НЕ) для реализации пирамидального
(либо ИЛИ—НЕ) для реализации пирамидального  -ступенчатого дешифратора на
-ступенчатого дешифратора на  выходов с учетом инверторов определяется соотношением
выходов с учетом инверторов определяется соотношением

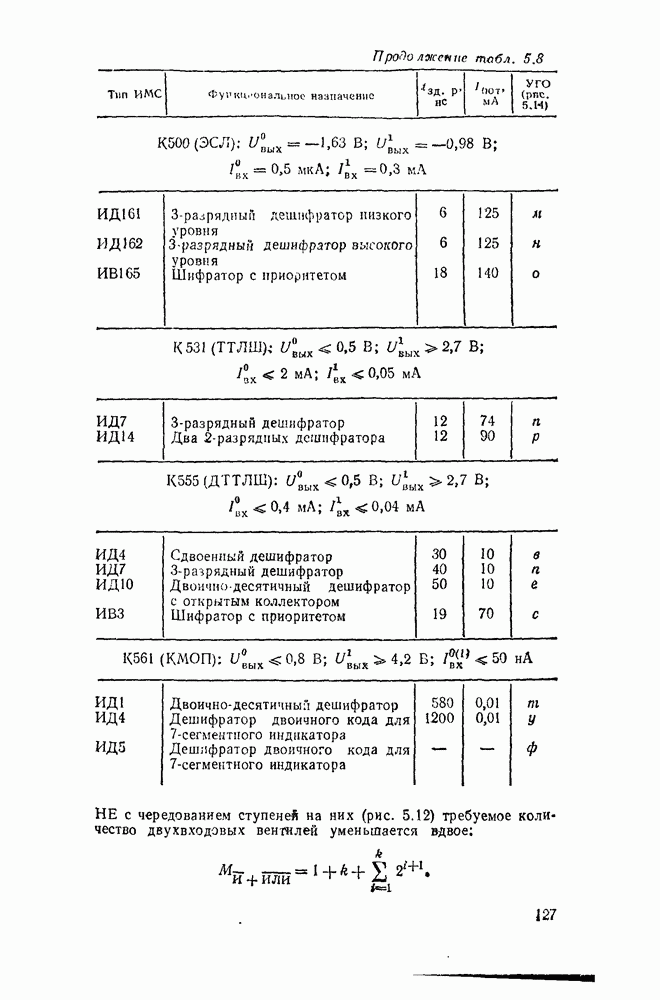
и практически удваивается с добавлением очередной ступени. При одновременном использовании элементов  или ИЛИ—НЕ с чередованием ступеней на них (рис. 5.12) требуемое количество двухвходовых вентилей уменьшается вдвое:
или ИЛИ—НЕ с чередованием ступеней на них (рис. 5.12) требуемое количество двухвходовых вентилей уменьшается вдвое:
Рисунок (см. оригинал.)
Рисунок и таблица 5.8. (см. оригинал.)
Таблица 5.8. (продолжение)
(см. оригинал.)
НЕ с чередованием ступеней на них (рис. 5.12) требуемое количество двухвходовых вентилей уменьшается вдвое:

В случае если число входов  полные дешифраторы целесообойзно строить но матричной структуре. При четном
полные дешифраторы целесообойзно строить но матричной структуре. При четном  количество строк и столбцов матрицы равно
количество строк и столбцов матрицы равно  и матрица выходных вентилей получается квадратной. При нечетном
и матрица выходных вентилей получается квадратной. При нечетном  входные переменные разделяют на
входные переменные разделяют на  . В обоих случаях для выбора строк и столбцов (рис. 5.13), в узлах которых подключаются двухвходовые вентили, используются линейные или пирамидальные дешифраторы. Такого типа дешифраторы называют прямоугольными.
. В обоих случаях для выбора строк и столбцов (рис. 5.13), в узлах которых подключаются двухвходовые вентили, используются линейные или пирамидальные дешифраторы. Такого типа дешифраторы называют прямоугольными.
Таким образом, прямоугольный дешифратор содержит две ступени независимо от величины  и обеспечивает высокое быстродействие. Для реализации прямоугольного дешифратора с линейным дешифратором в его первой стугепи необходимо
и обеспечивает высокое быстродействие. Для реализации прямоугольного дешифратора с линейным дешифратором в его первой стугепи необходимо  элементов при четном
элементов при четном  элементов при
элементов при  нечетном. В прямоугольном дешифраторе на рис. 5.13 выходы являются инверсными, т. е. на всех его пыходач, кроме одного, определяемого входным кодом, уианавлнпаются «логические
нечетном. В прямоугольном дешифраторе на рис. 5.13 выходы являются инверсными, т. е. на всех его пыходач, кроме одного, определяемого входным кодом, уианавлнпаются «логические  и лишь на одном выходе — «логический 0» На основе комбинации любого из дешифраторов с
и лишь на одном выходе — «логический 0» На основе комбинации любого из дешифраторов с  выходами
выходами  -входного шифратора можно помтроить преобразователь исходного кода в заданный. Для этого достаточно соответствующим образом соединить выходы дешифратора со входами шифратора.
-входного шифратора можно помтроить преобразователь исходного кода в заданный. Для этого достаточно соответствующим образом соединить выходы дешифратора со входами шифратора.
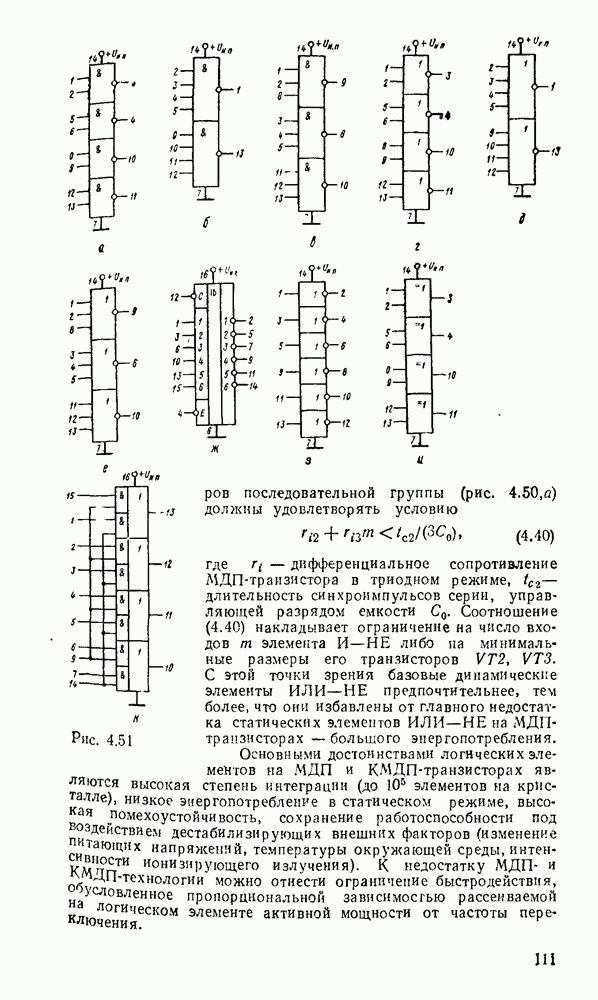
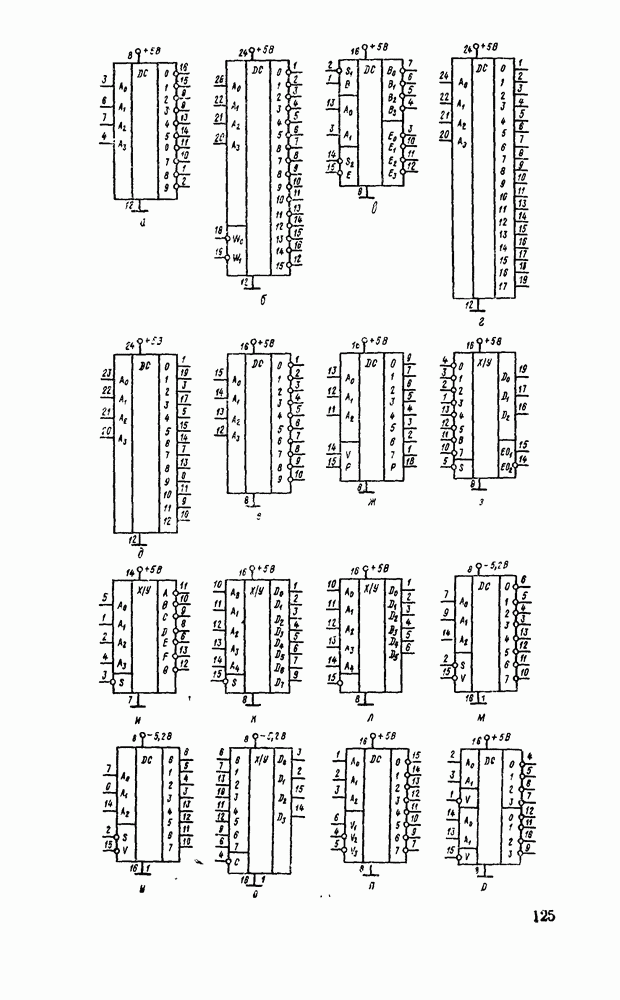
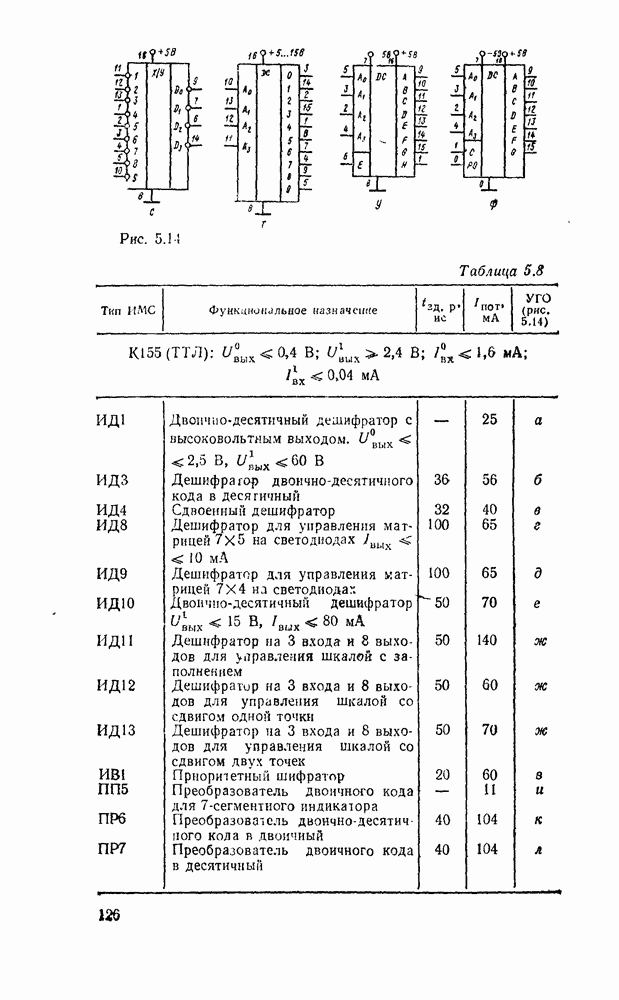
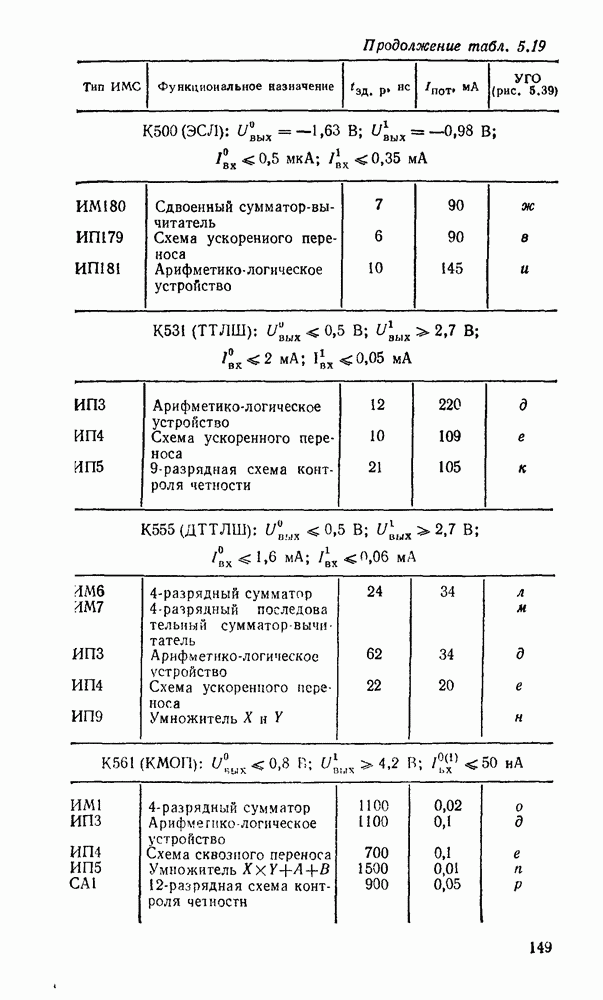
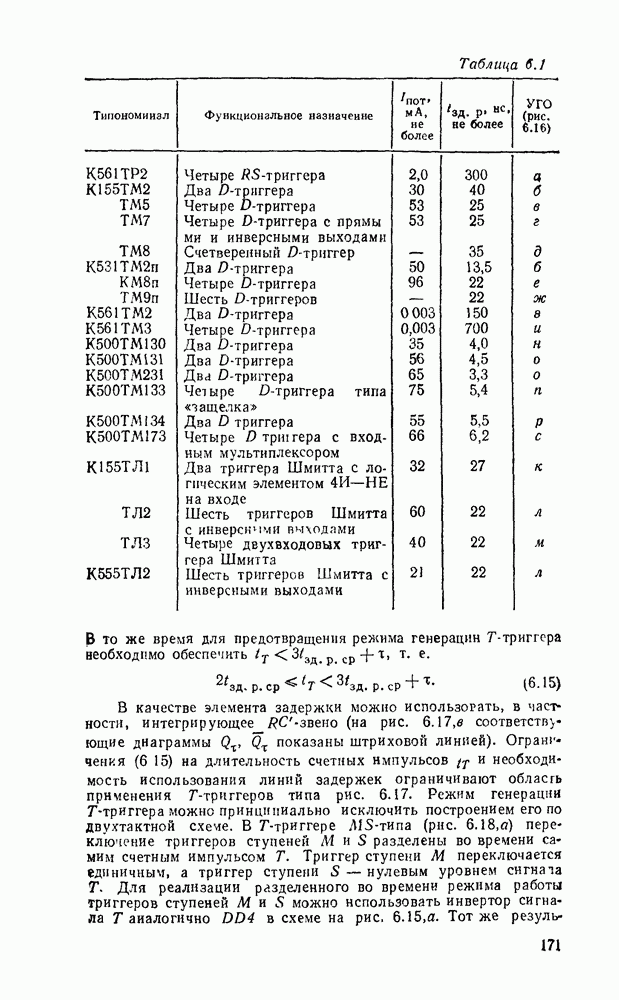
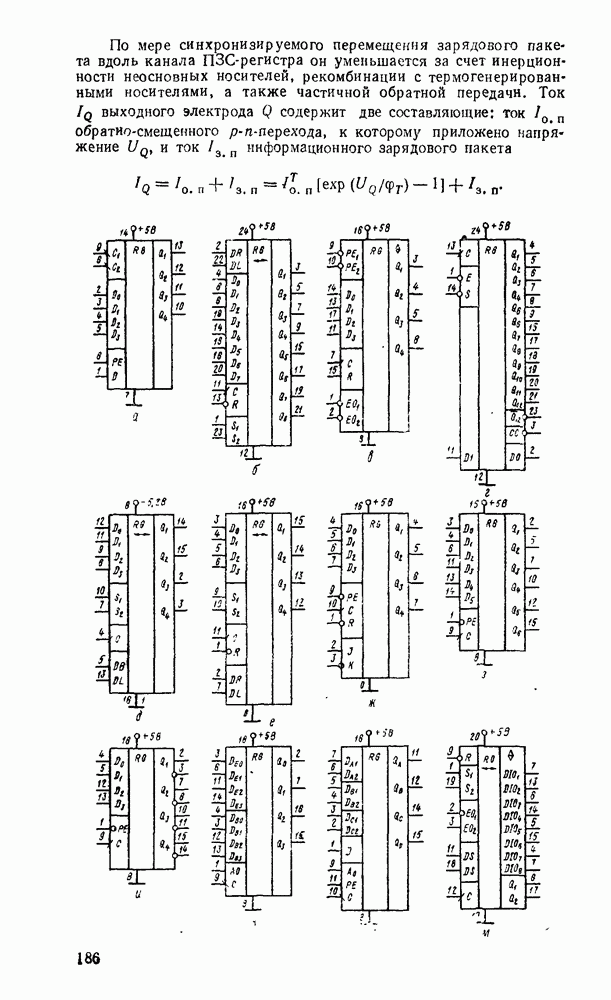
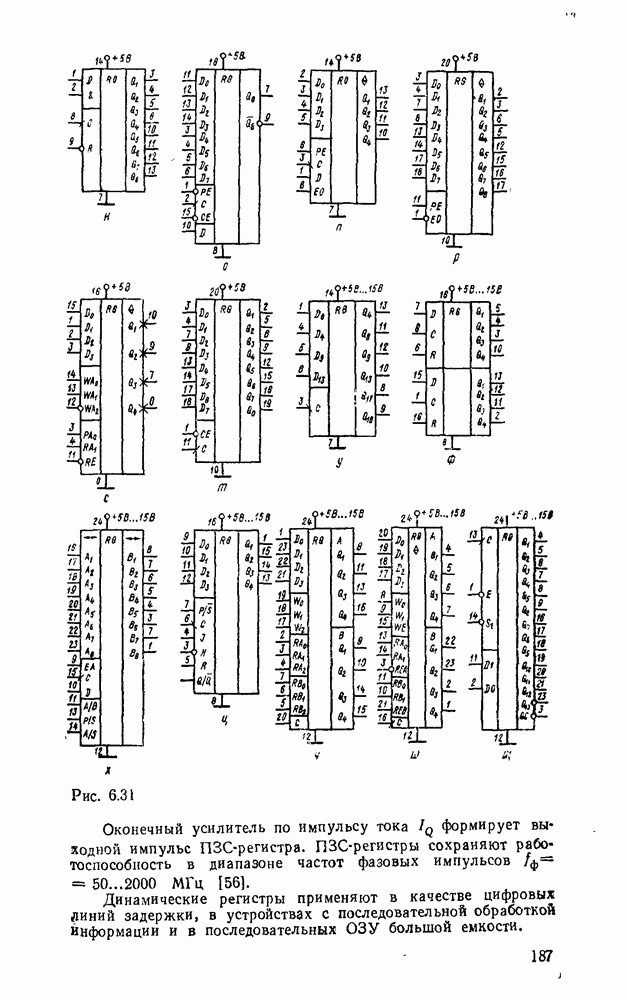
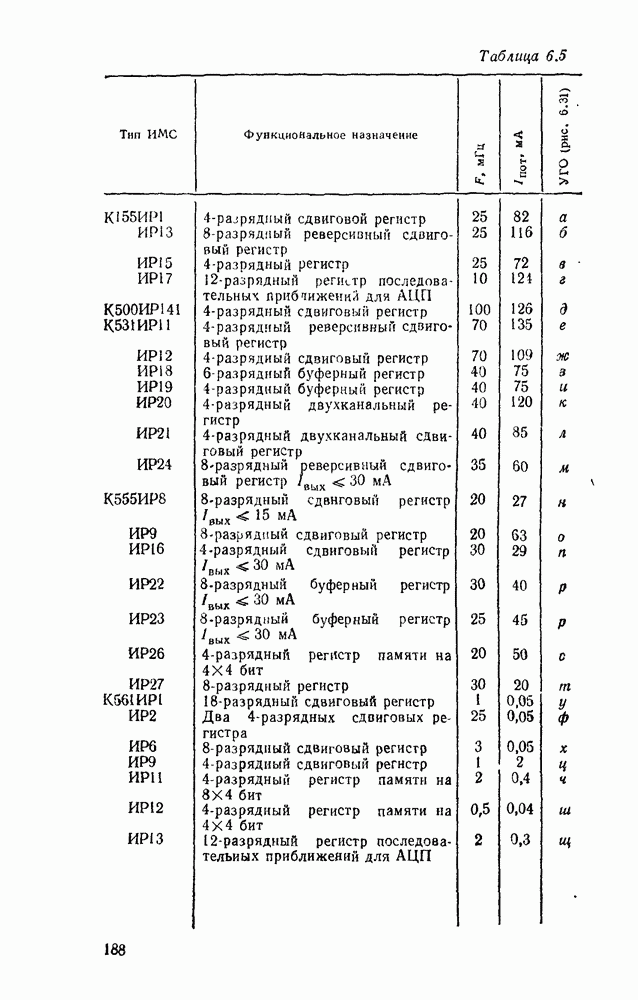
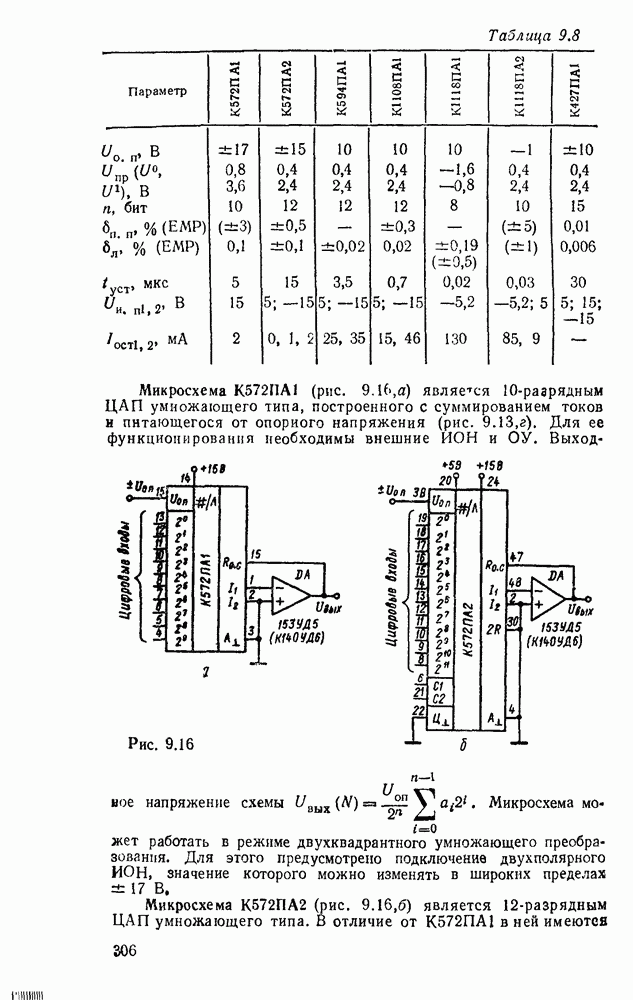
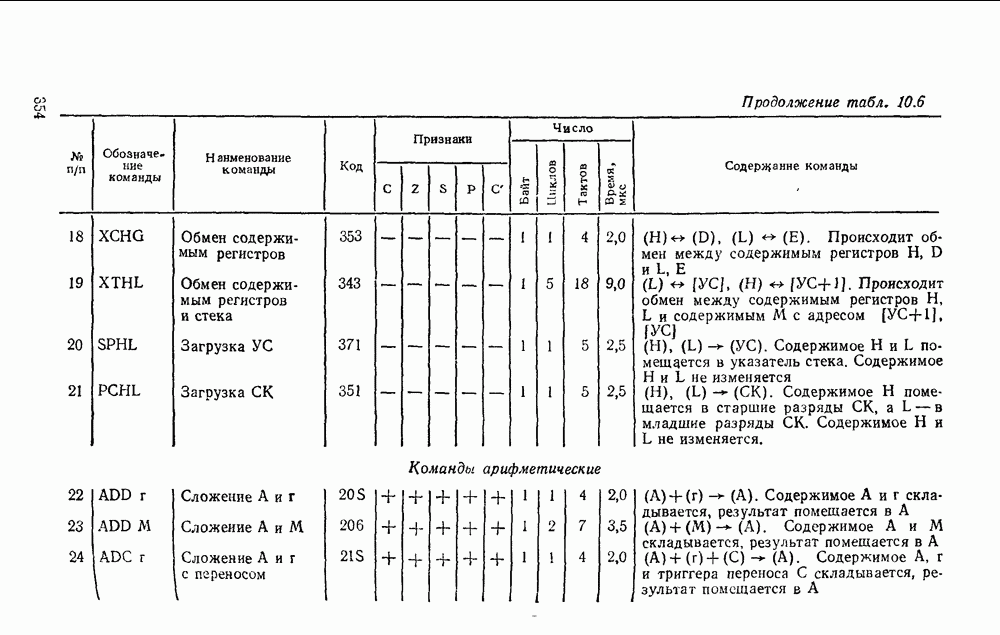
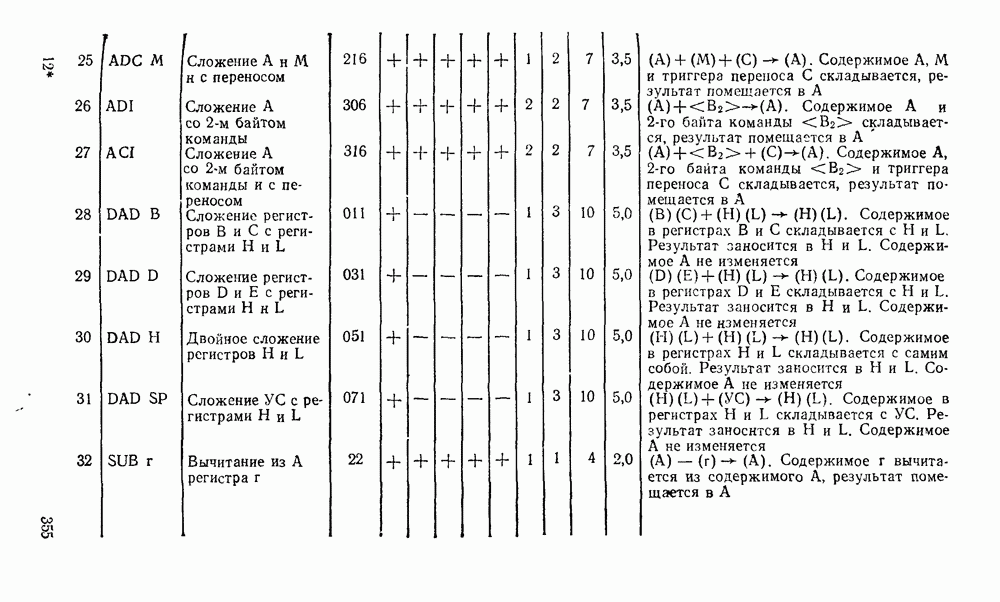
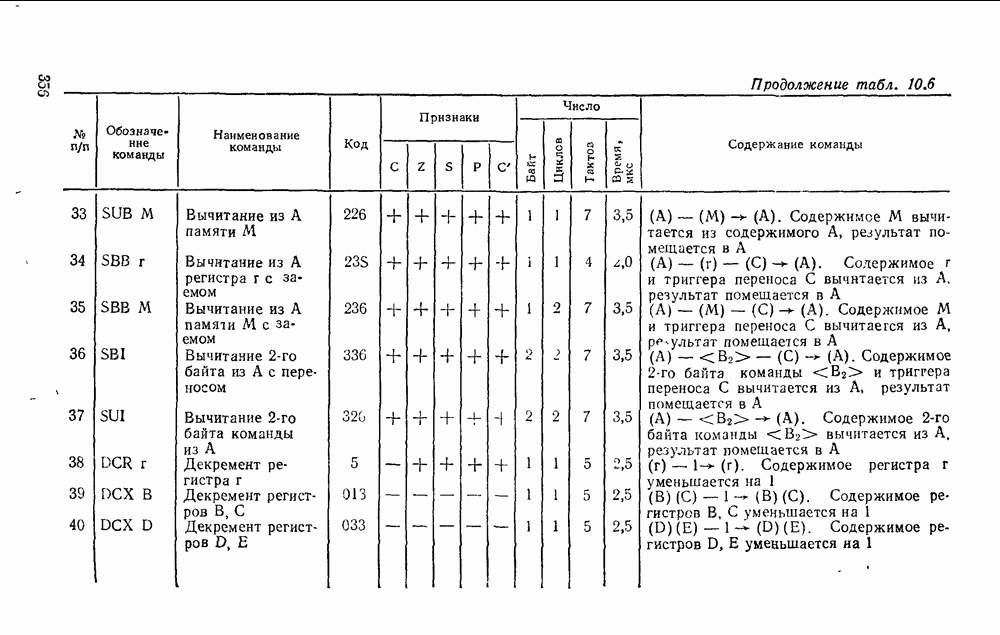
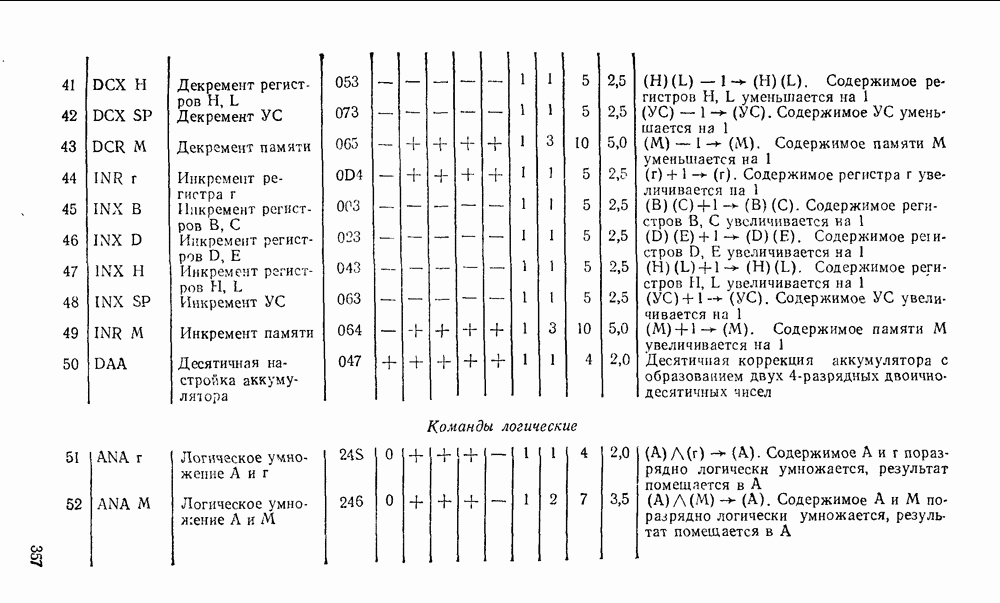
В табл. 5 8 приведены параметры шифраторов и дешифраторов наиболее широко применяемых серий ИМС. На рис. 5.11 показано функциональное назначение выводов ИМС из табл. 5.8.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
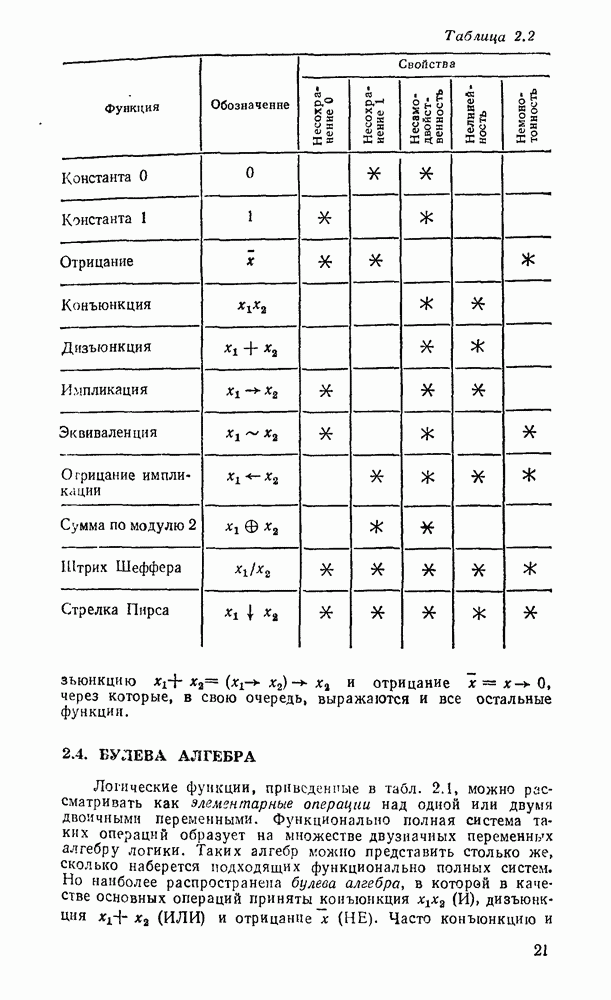
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
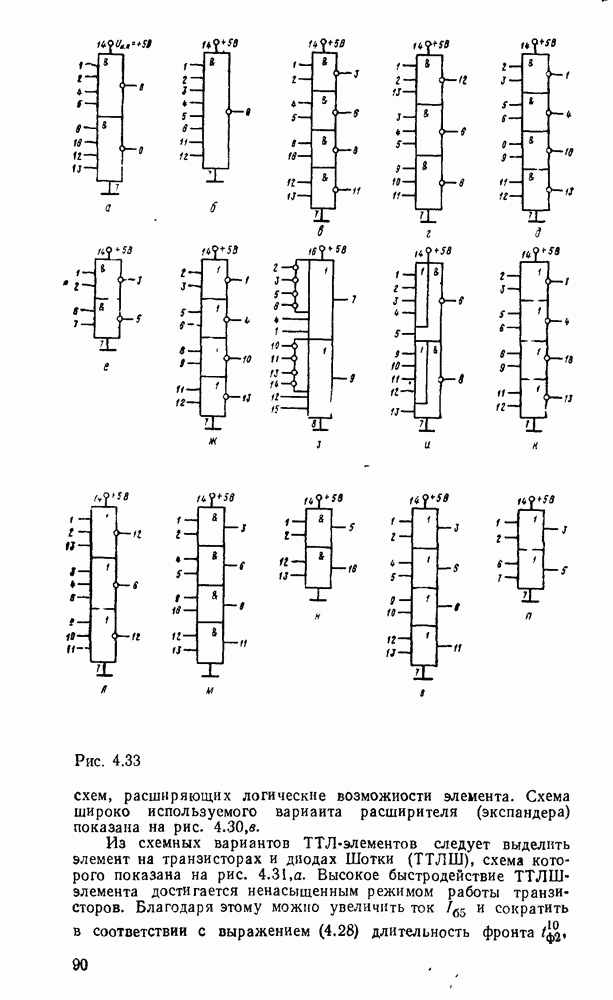
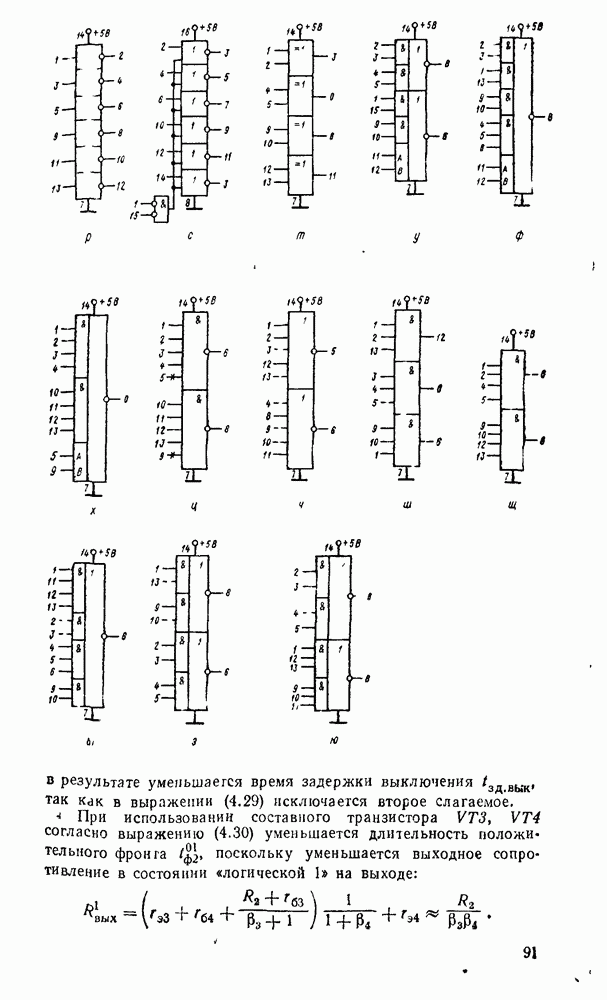
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
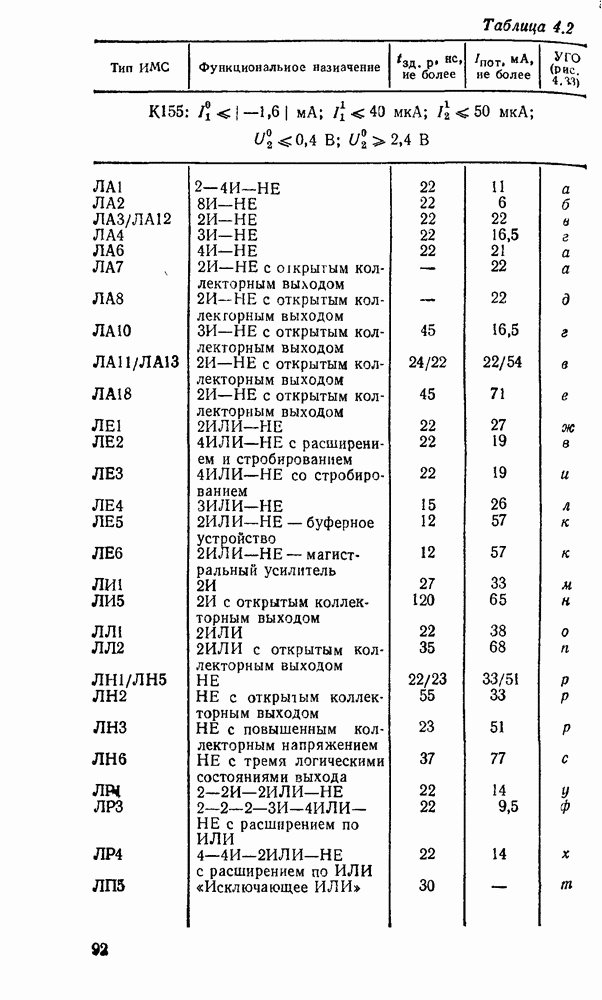
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
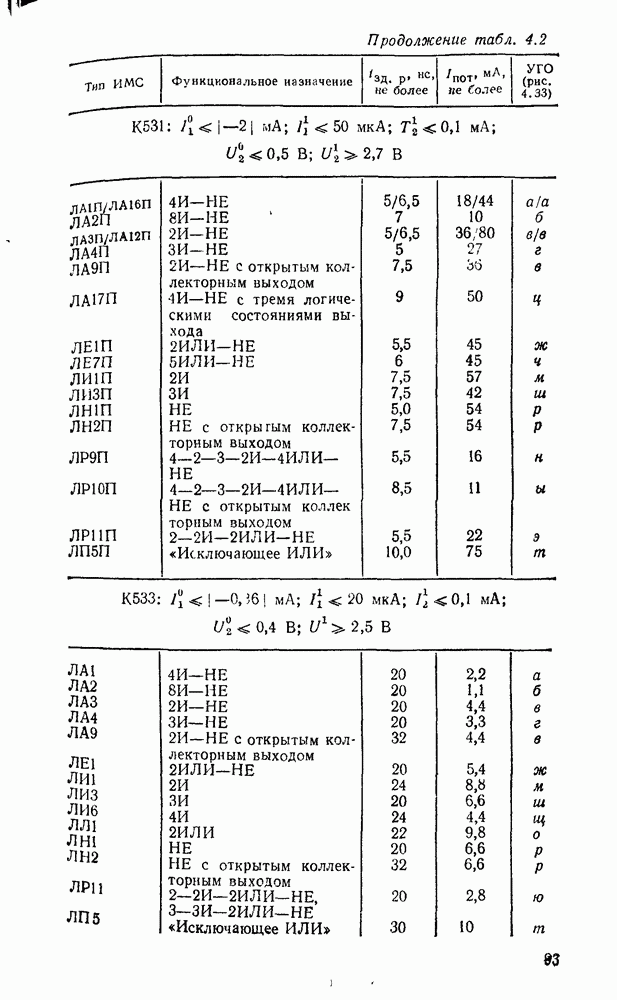
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
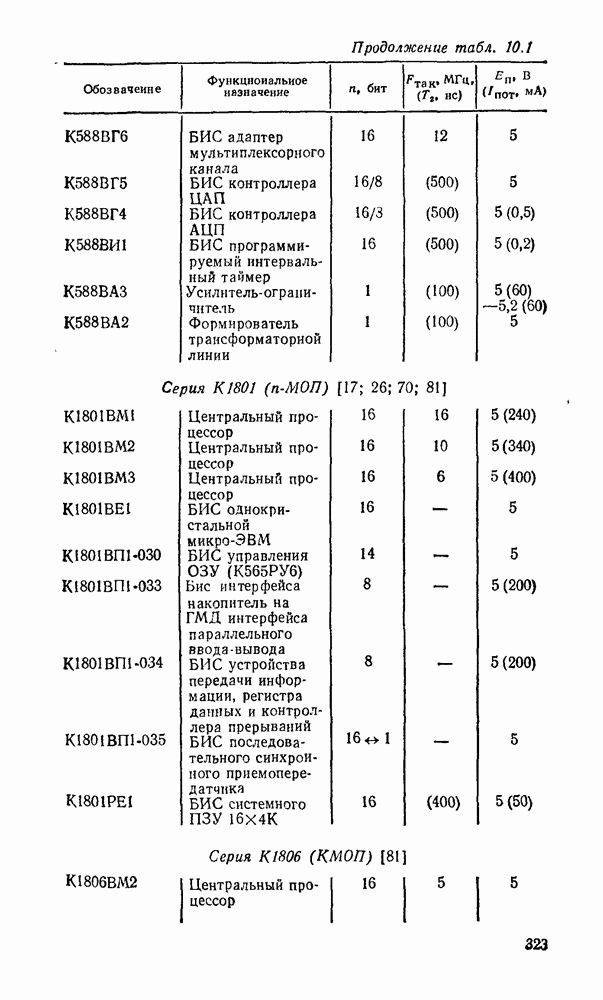
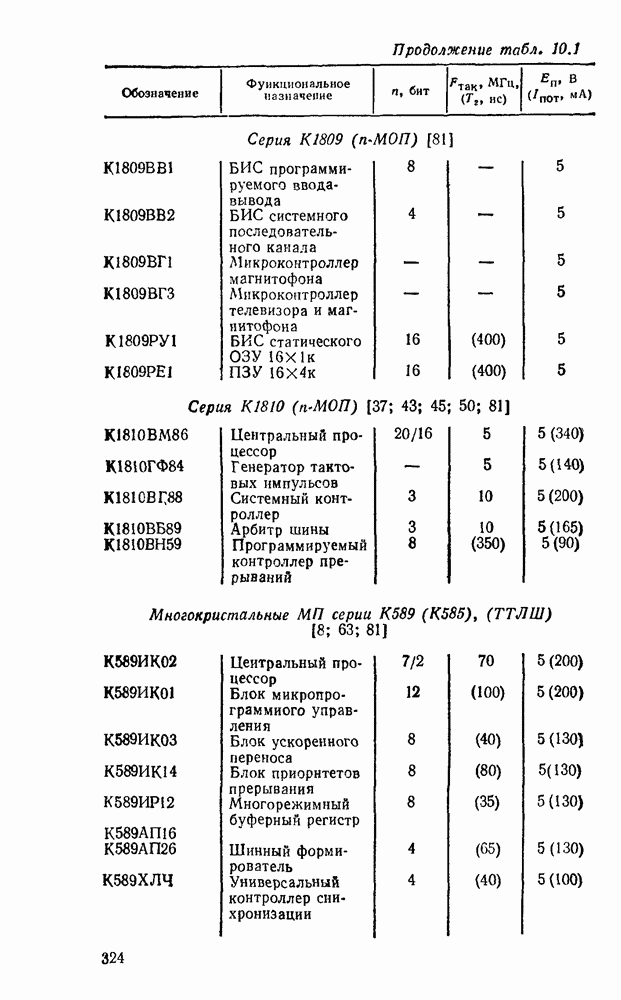
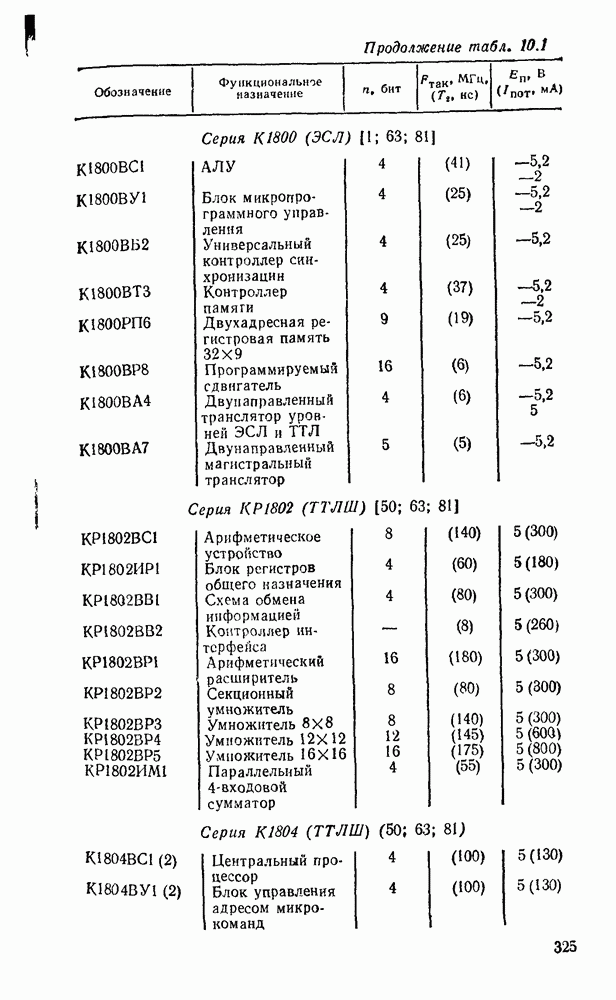
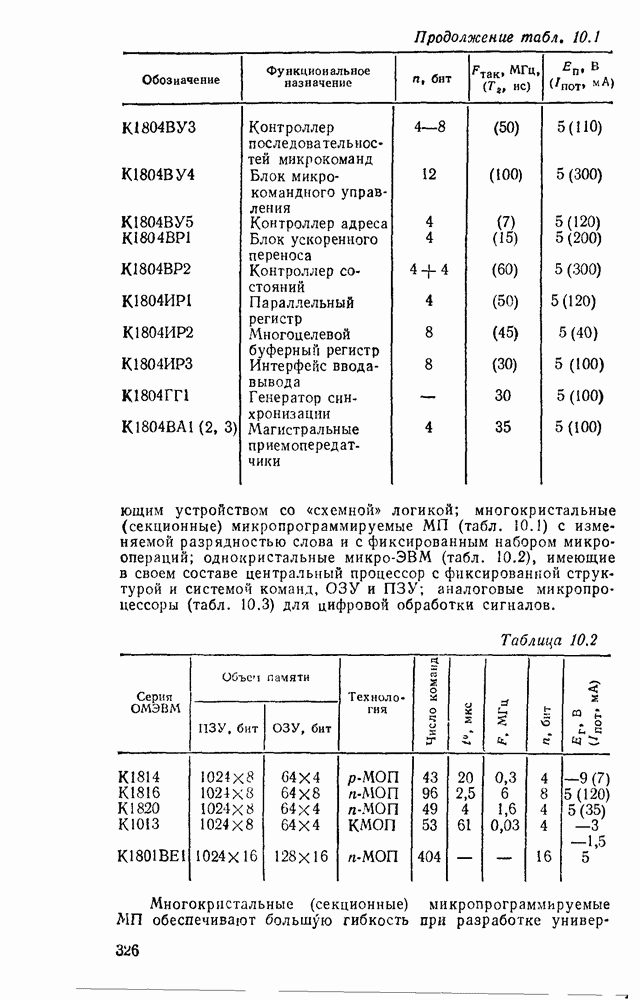
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
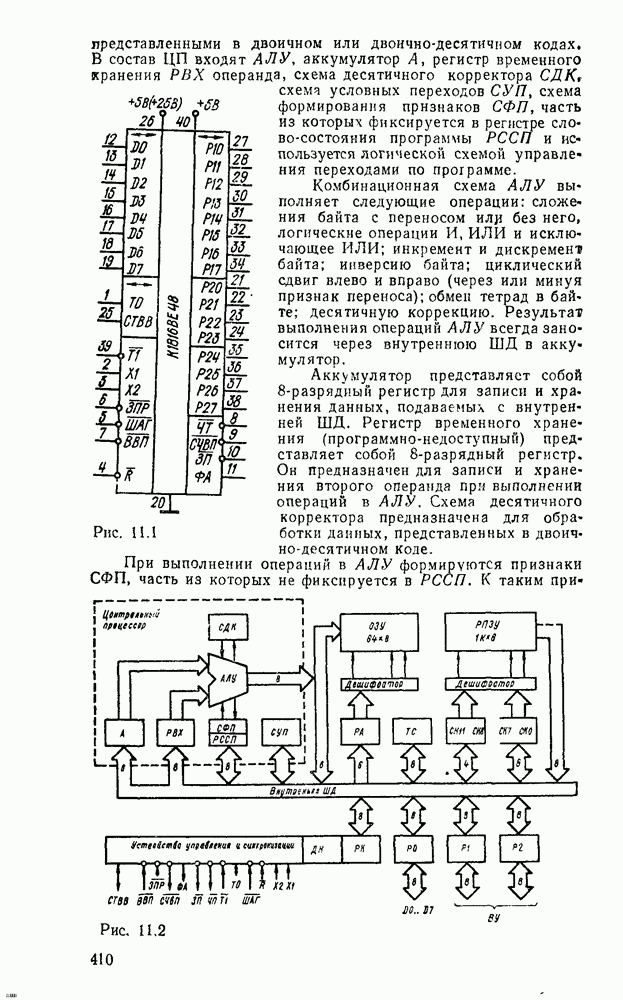
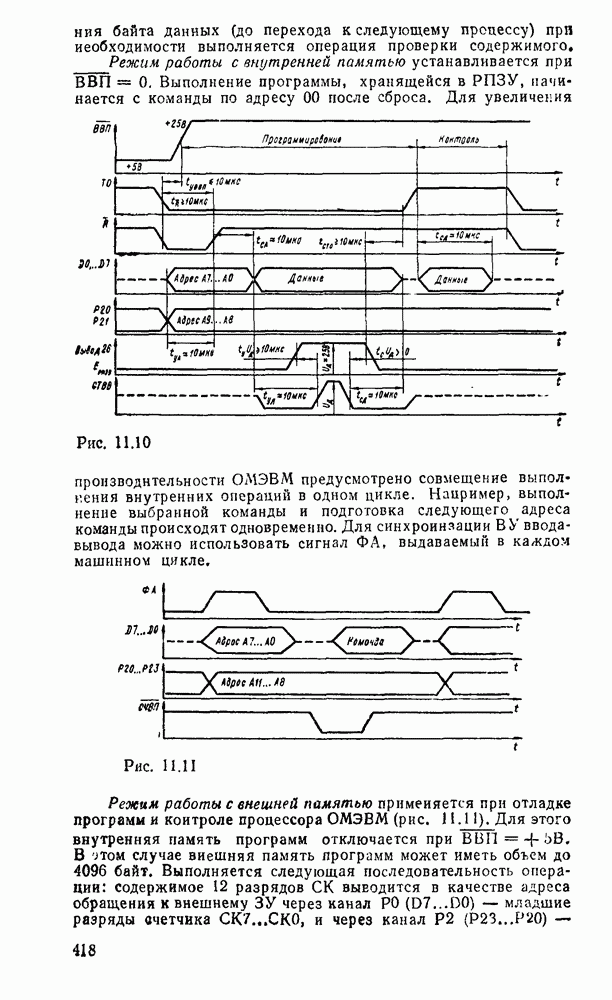
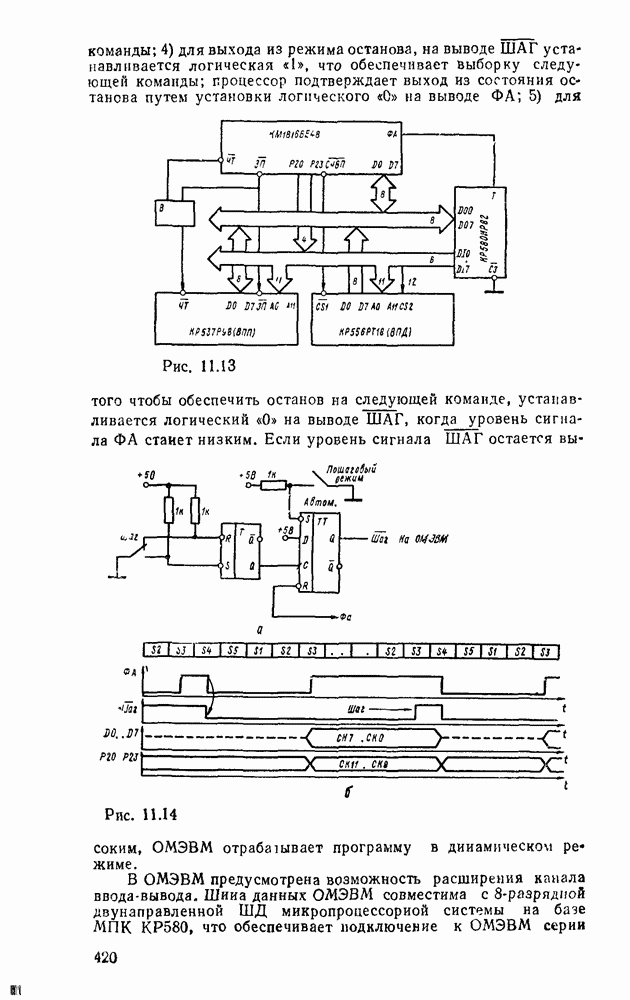
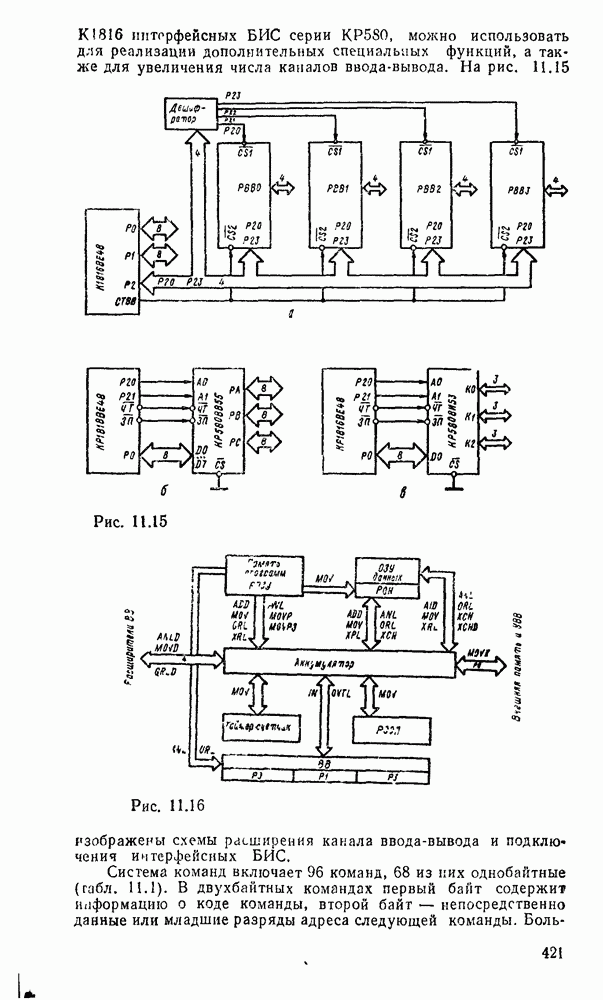
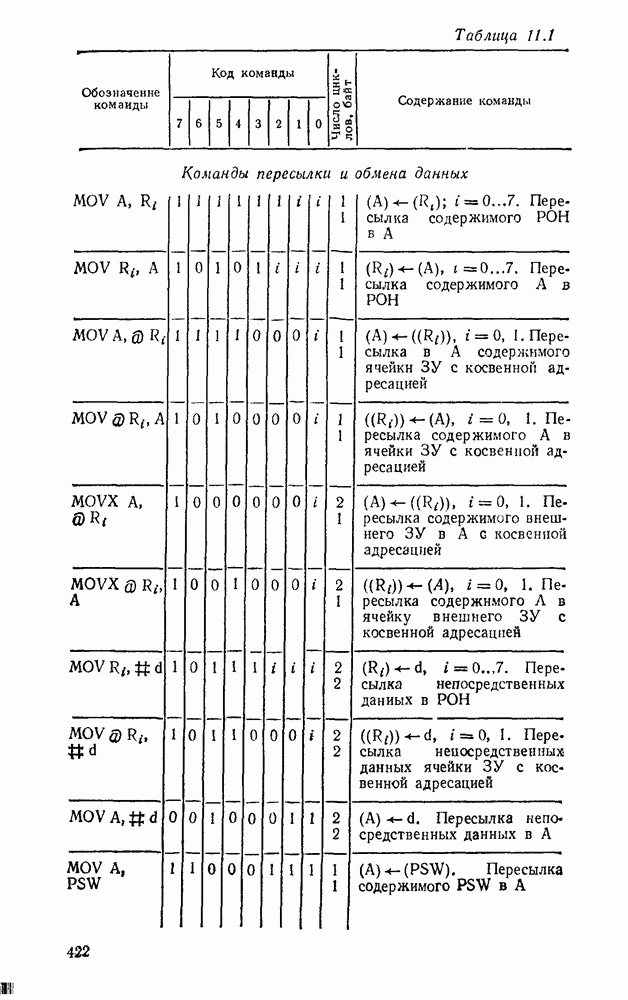
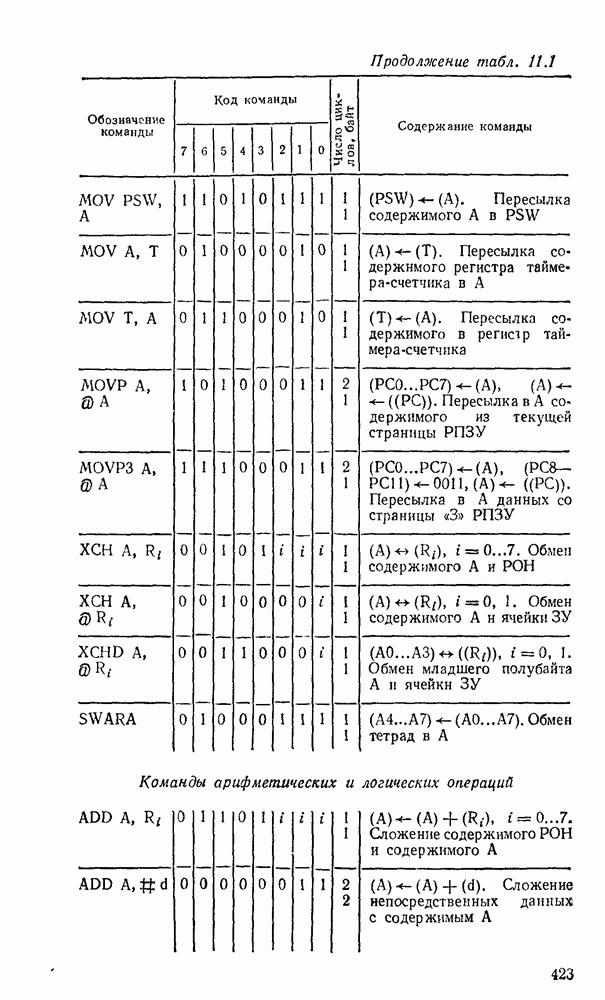
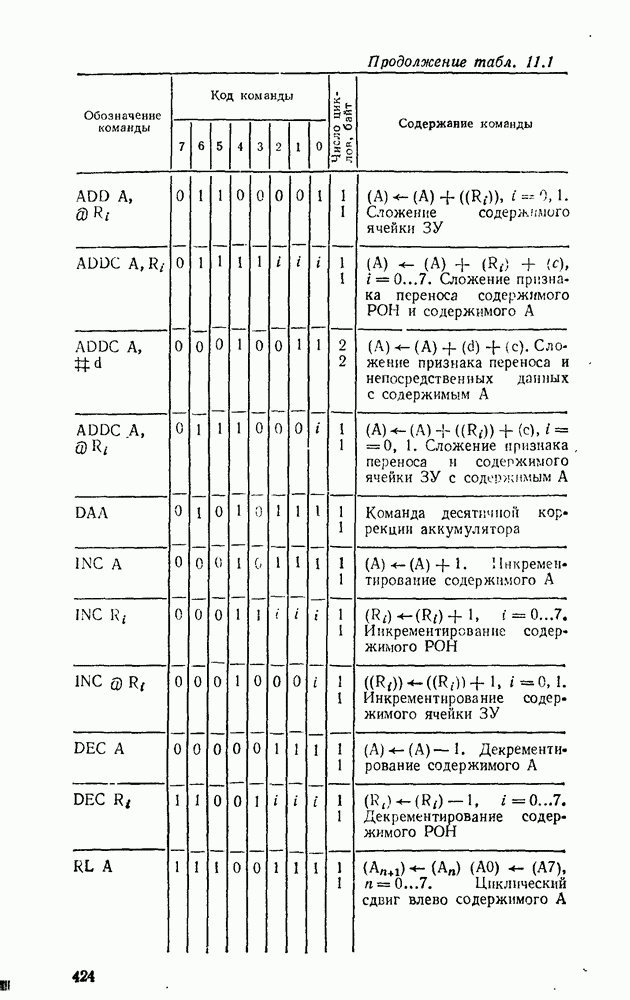
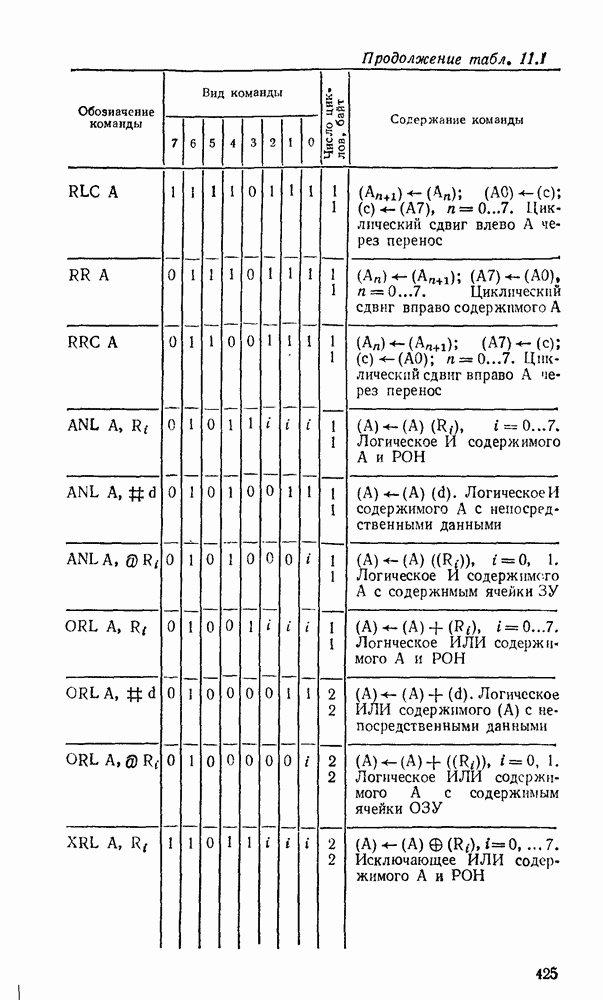
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
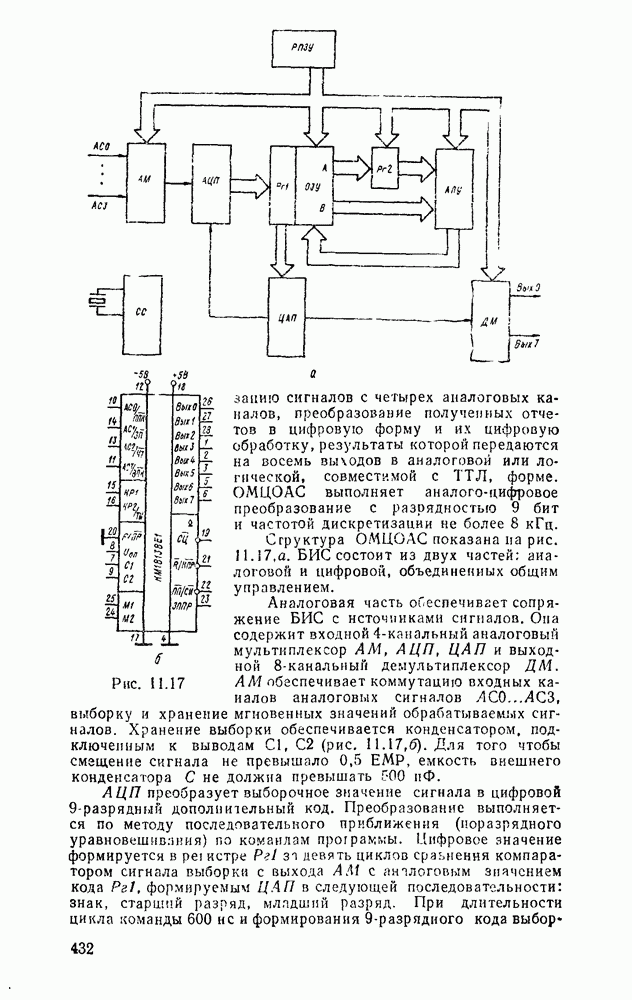
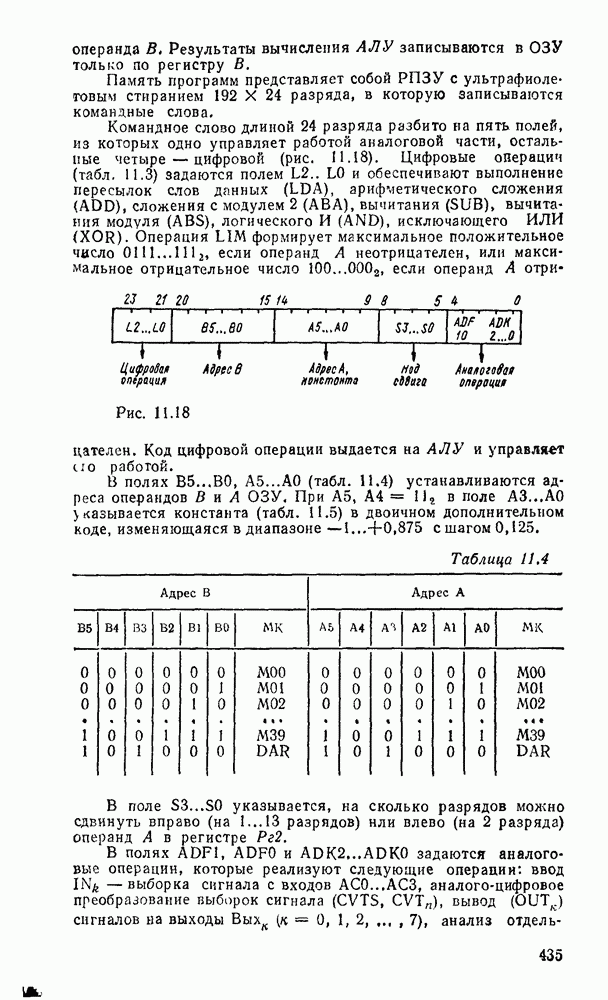
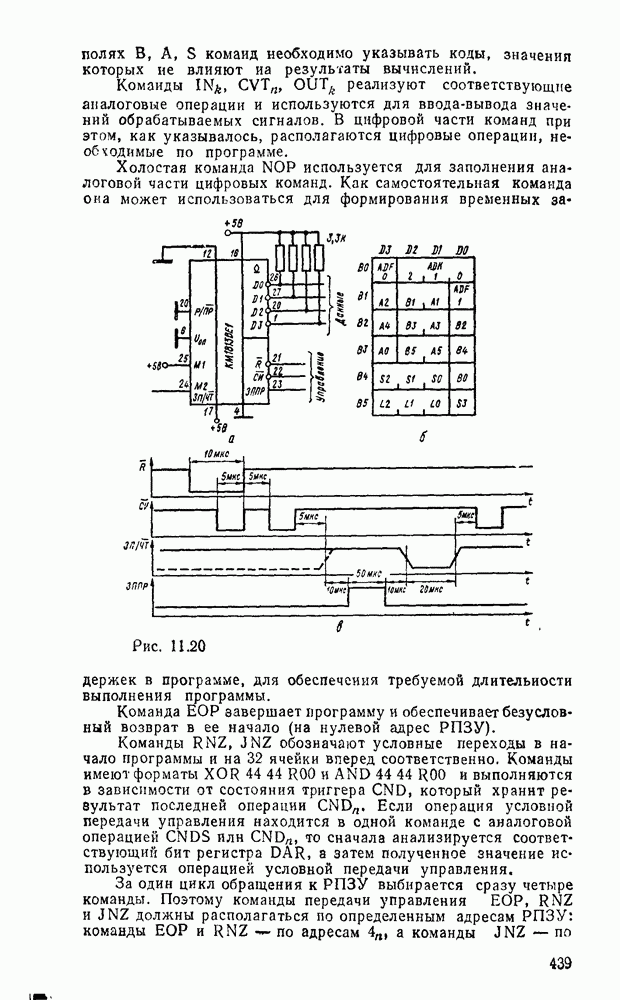
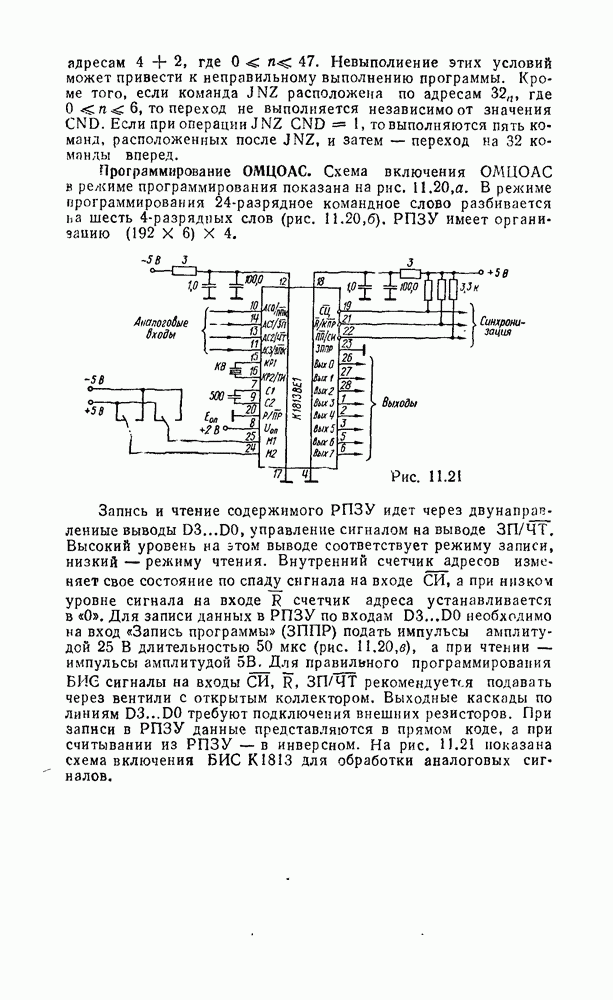
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ