| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
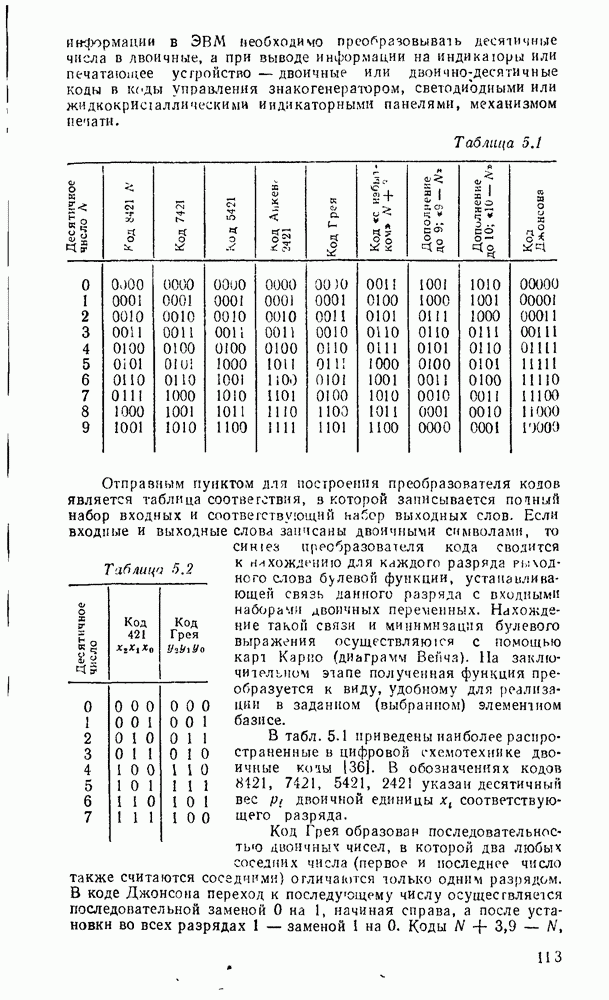
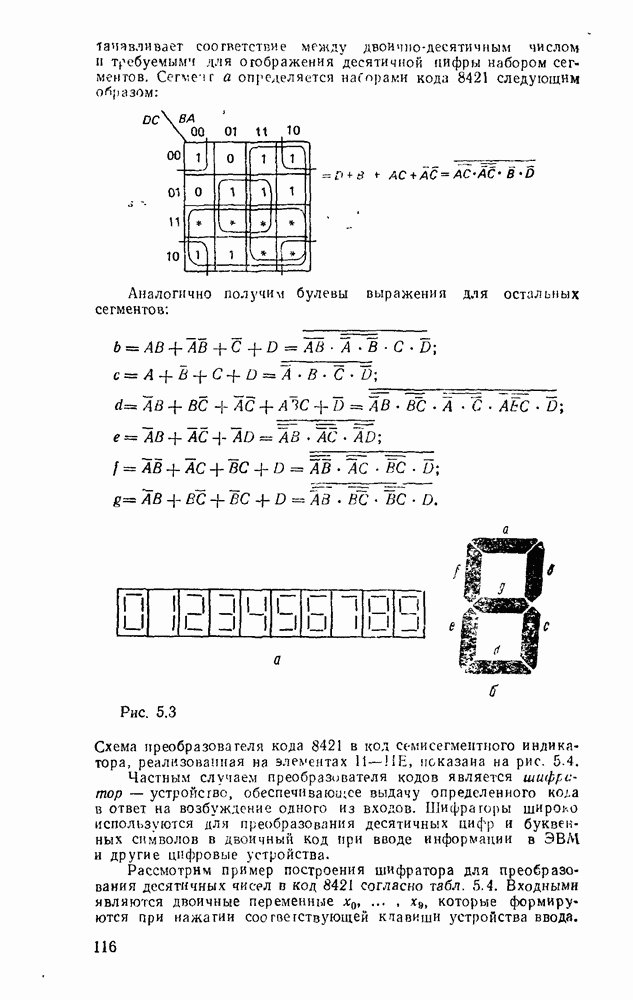
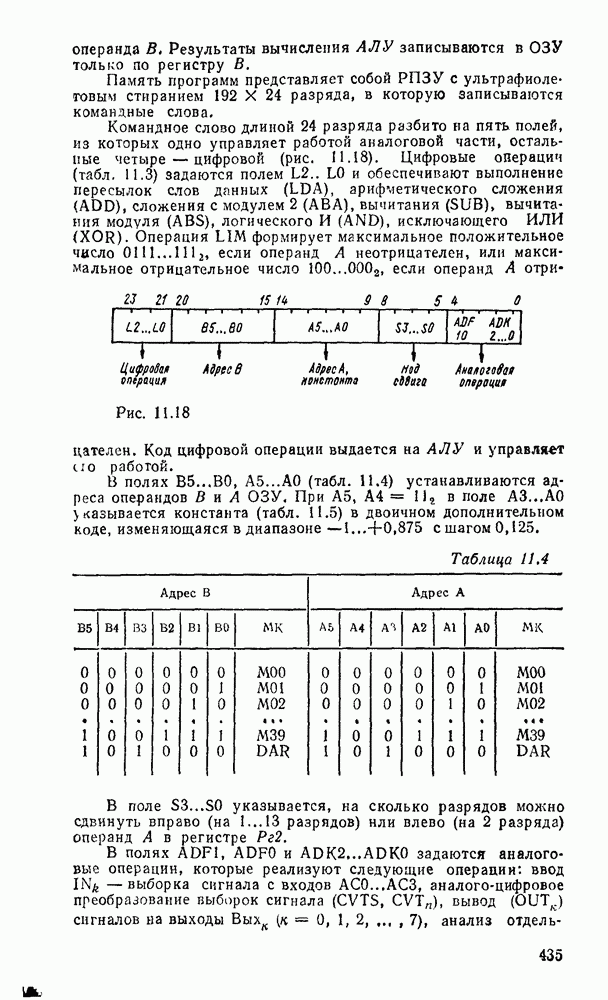
Для представления информации в десятичной системе счисления и выполнения операций над десятичными числами в цифровых устройствах используется двоично-десятичное кодирование [18], при котором каждая десятичная цифра представляется группой двоичных цифр. Число битов в таких группах строго фиксируется  должно быть не менее четырех) с сохранением всех левых нулевых разрядов. В практике используется несколько разновидностей двоично-десятичных кодов (табл. 1.2), сохраняющих свое значение благодаря полезным специфическим особенностям.
должно быть не менее четырех) с сохранением всех левых нулевых разрядов. В практике используется несколько разновидностей двоично-десятичных кодов (табл. 1.2), сохраняющих свое значение благодаря полезным специфическим особенностям.
Таблица 1.2

Наиболее естественным и популярным считается упоминавшийся (см. гл. 1.2) код прямого замещения, в котором каждая цифра десятичного числа заменяется соответствующим четырехразрядным двоичным числом. Его другое название код 8421 отражает значение весовых множителей, приписываемых соответствующим битам в кодирующей группе, в связи с чем  называется также взвешенным кодом. Удобства этого кода проявляются при машинном переводе из десятичной системы в двоичную и обратно, а также при суммировании на обычных двоичных сумматорах благодаря его аддитивности (сумма кодов двух цифр представляет код суммы).
называется также взвешенным кодом. Удобства этого кода проявляются при машинном переводе из десятичной системы в двоичную и обратно, а также при суммировании на обычных двоичных сумматорах благодаря его аддитивности (сумма кодов двух цифр представляет код суммы).
Избыточность тетрады, допускающей 16 кодовых комбинаций, позволяет создавать и другие варианты двоично-десятичных кодов с использованием четверки битов на десятичный разряд.
Одни из них код 2421 также взвешенный, но старший разряд имеет вес не 8, а 2. Его положительная особенность состоит в том, что замена в кодирующей тетраде нулей на единицы, а единиц на нули превращает каждую десятичную цифру 
т. е. получается обратный код. Для превращения его в дополнительный код достаточно прибавить единицу. Коды с таким свойством называют самодополнительными. Они применяются при выполнении арифметических операций над десятичными числами в обратном или дополнительном коде.
Самодополнительным является и код с избытком 3, который получается прибавлением  к каждой цифре кода прямого замещения. Как и код 2421, он удобен для выполнения операций над десятичными числами. При этом легко определяется перенос, так как сумма двух слагаемых, каждое из которых берется с избытком 3, получится с избытком 6, что исключает лишние кодовые комбинации (для получения правильного кода суммы из полученного результата вычитается 3). Но этот код в отличие от кодов 8421 и 2421 не является взвешенным, вследствие чего мало удобен для преобразования чисел из одной системы в другую.
к каждой цифре кода прямого замещения. Как и код 2421, он удобен для выполнения операций над десятичными числами. При этом легко определяется перенос, так как сумма двух слагаемых, каждое из которых берется с избытком 3, получится с избытком 6, что исключает лишние кодовые комбинации (для получения правильного кода суммы из полученного результата вычитается 3). Но этот код в отличие от кодов 8421 и 2421 не является взвешенным, вследствие чего мало удобен для преобразования чисел из одной системы в другую.
Используются также двоично-десятичные коды, в которых кодирующие тетрады дополняются избыточными битами с тем, чтобы использовать эту избыточность для придания кодам специфических свойств, служащих для обнаружения ошибок и тем самым для повышения надежности вычислительных систем.
Так, в коде 2 из 5 каждая десятичная цифра представляется пятью разрядами, из которых два и только два содержат единицы. Если появится ошибка в одном из двоичных разрядов, т. е. если нуль превратится в единицу или единица превратится в нуль, то общее число единиц окажется больше или меньше двух, что можно обнаружить простым их подсчетом. Другой способ обнаружения одиночной ошибки основан на использовании бита, которым дополняется какой-либо код, для контроля четности. Значение дополнительного бита выбирается таким, чтобы общее число единиц в кодирующей группе всегда было четным или нечетным (в зависимости от принятого правила контроля). Рассмотренные способы обнаруживают одиночные ошибки, точнее, нечетное количество ошибок, по не реагируют на двойные и вообще четное количество ошибок. Существуют более сложные способы построения корректирующих кодов, используемых в технике связи, но в обычных вычислительных системах из-за громоздкости они не применяются.
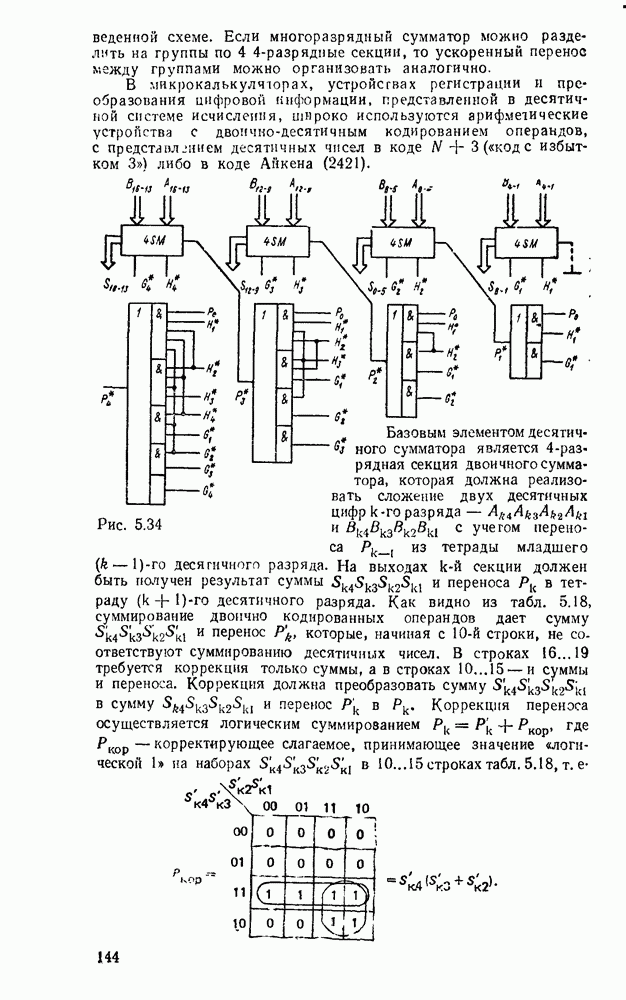
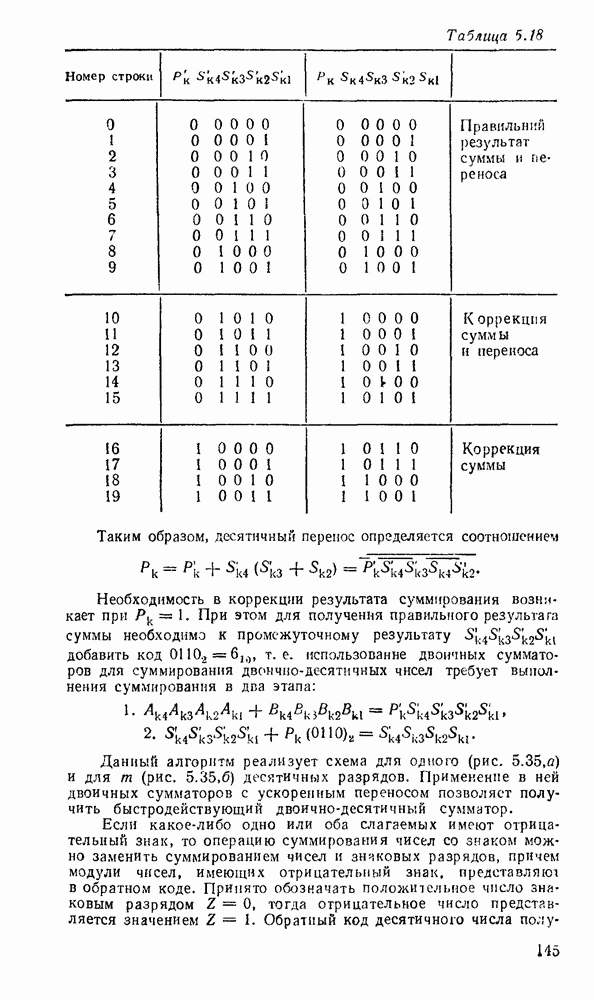
Операции над десятичными числами выполняются с помощью несколько дополненной двоичной арифметики. Так, при сложении двух чисел в коде прямого замещения 8421 необходимо добавить корректирующее слагаемое  0110а к каждой тетраде, в которой в процессе суммирования получена недопустимая цифра (1010, 1011, 1100, 1101, 1110) или возник перенос в следующую тетраду. Например:
0110а к каждой тетраде, в которой в процессе суммирования получена недопустимая цифра (1010, 1011, 1100, 1101, 1110) или возник перенос в следующую тетраду. Например:

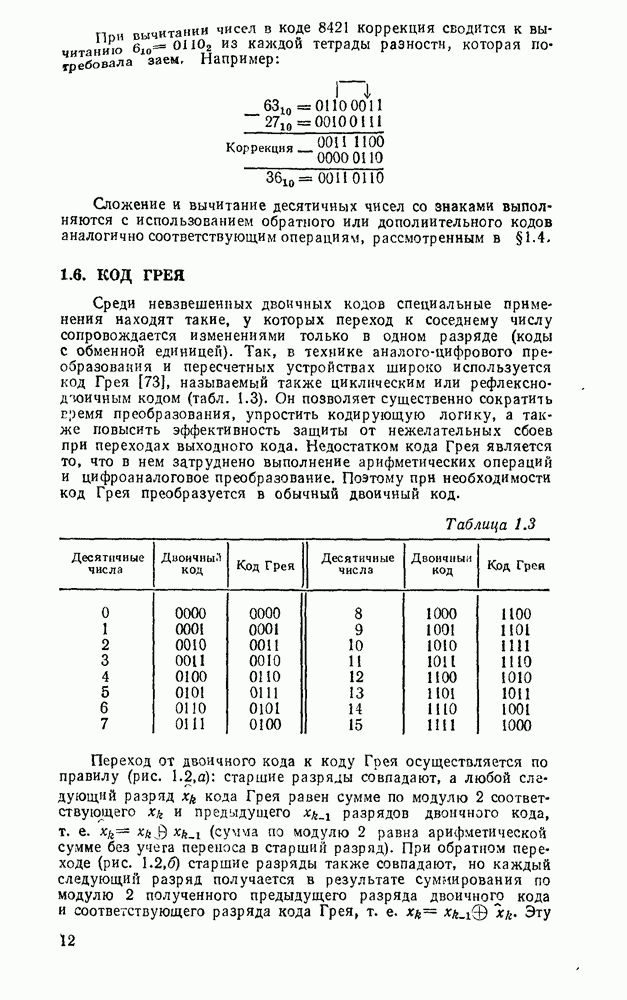
При вычитании чисел в коде 8421 коррекция сводится к вычитанию  , из каждой тетрады разности, которая потребовала заем. Например:
, из каждой тетрады разности, которая потребовала заем. Например:

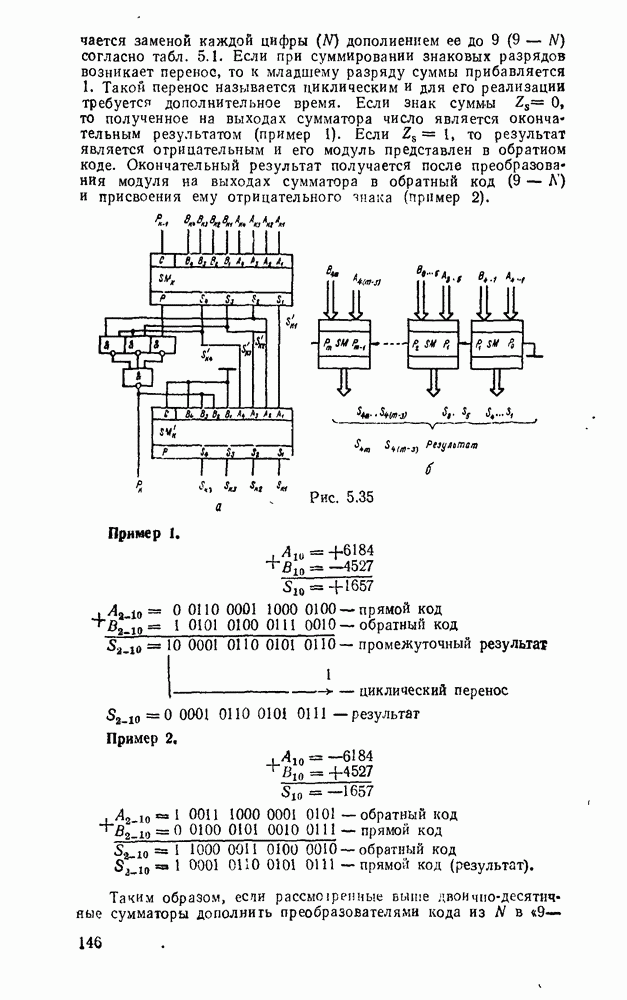
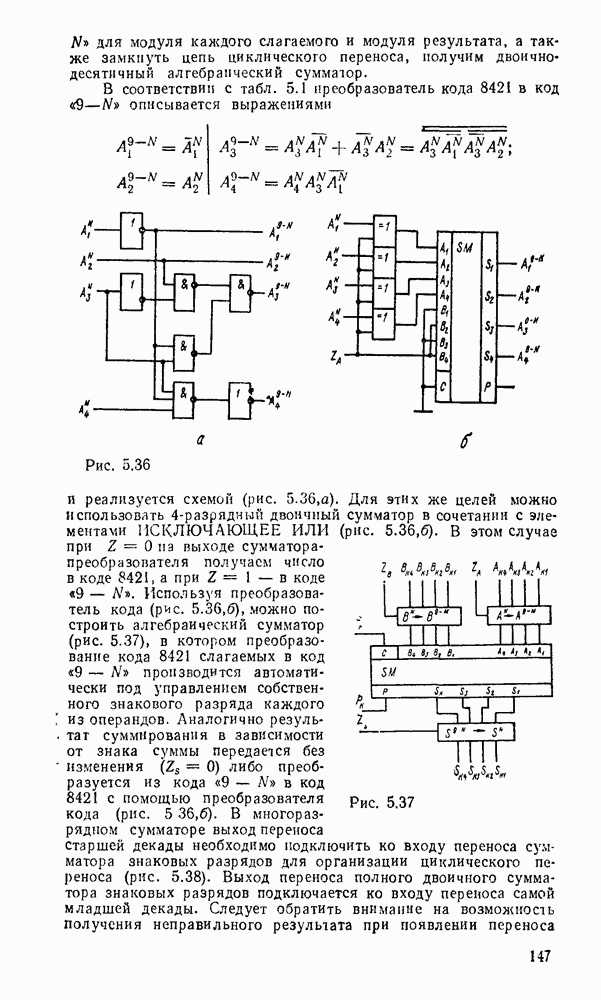
Сложение и вычитание десятичных чисел со знаками выполняются с использованием обратного или дополнительного кодов аналогично соответствующим операциям, рассмотренным в §1.4.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
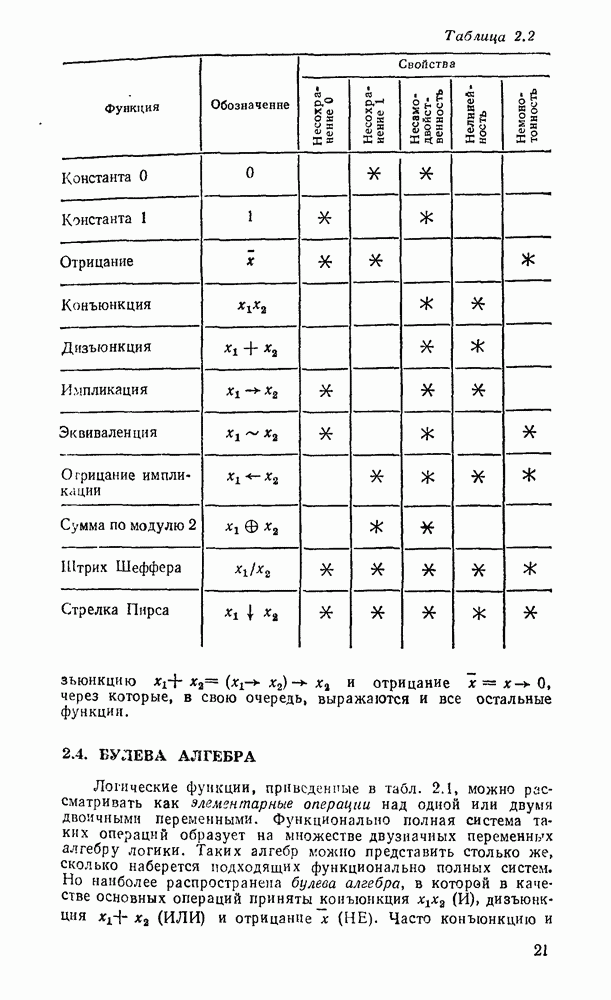
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
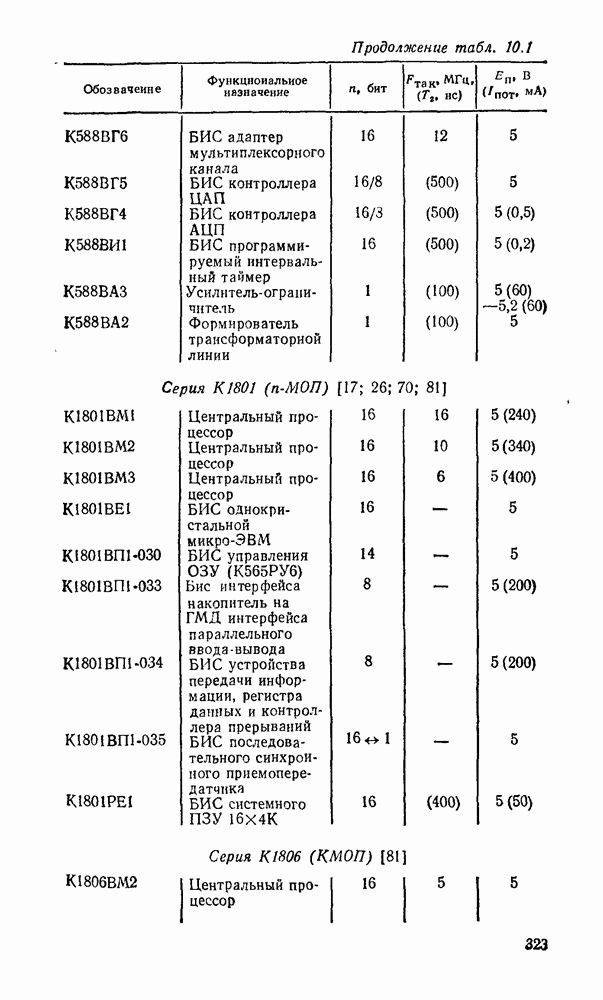
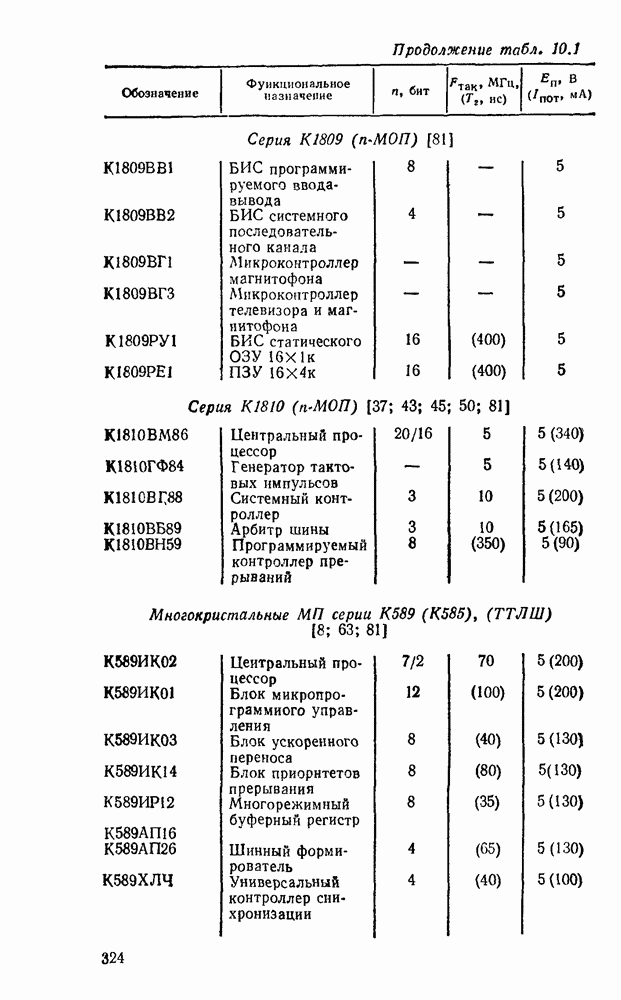
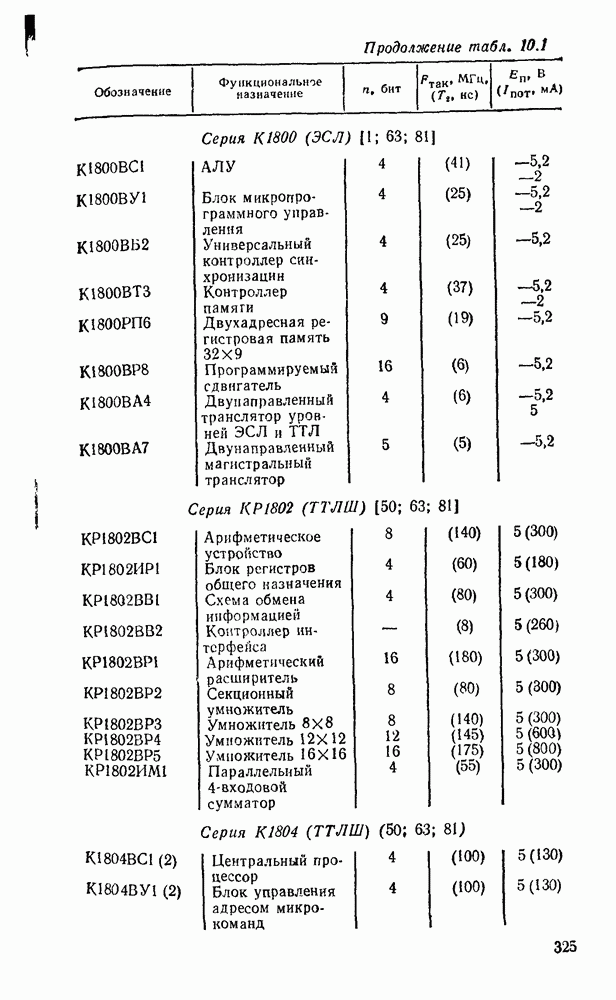
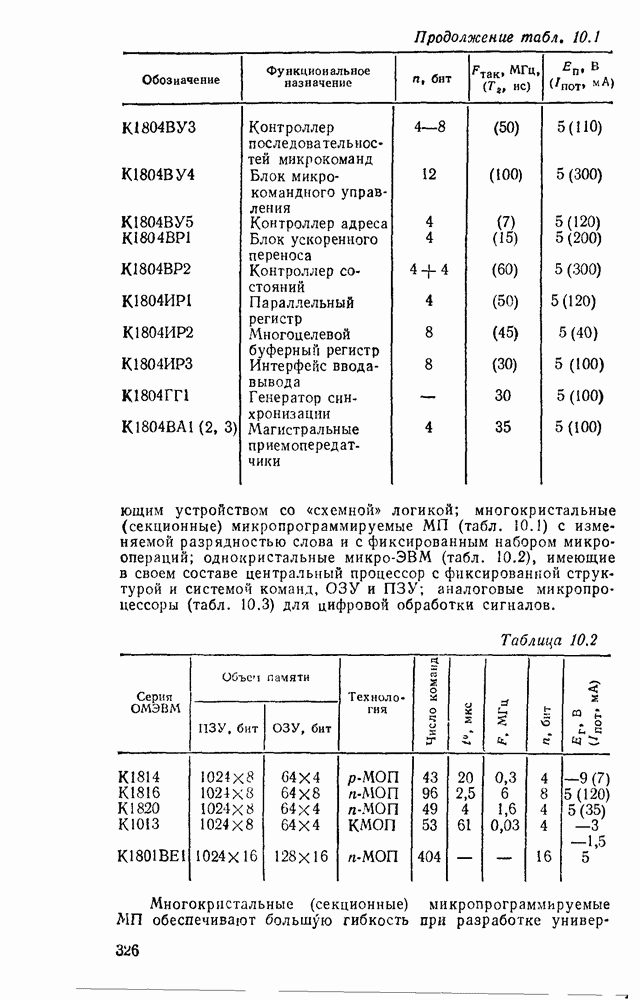
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
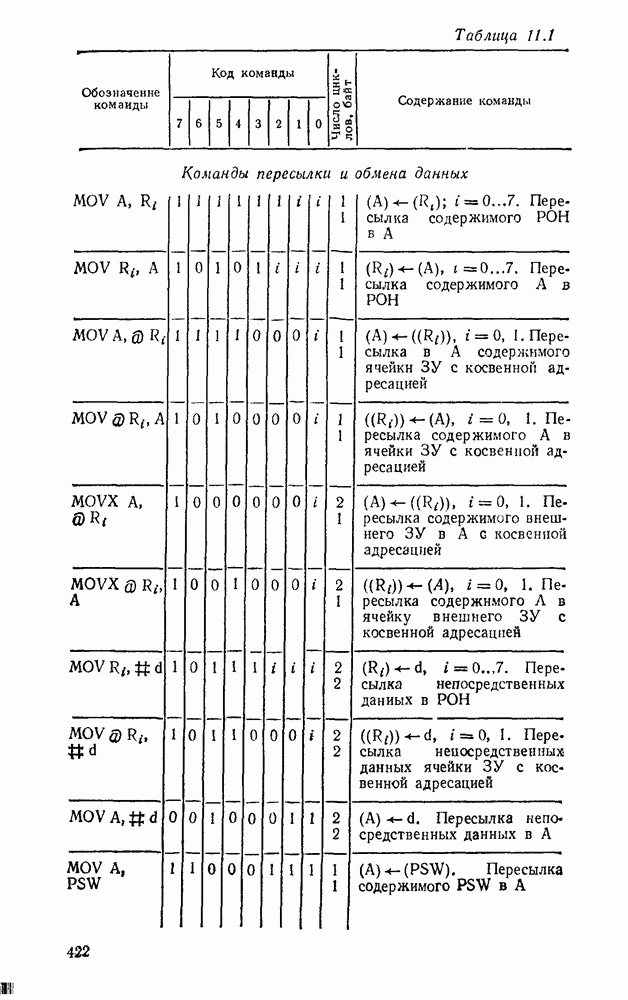
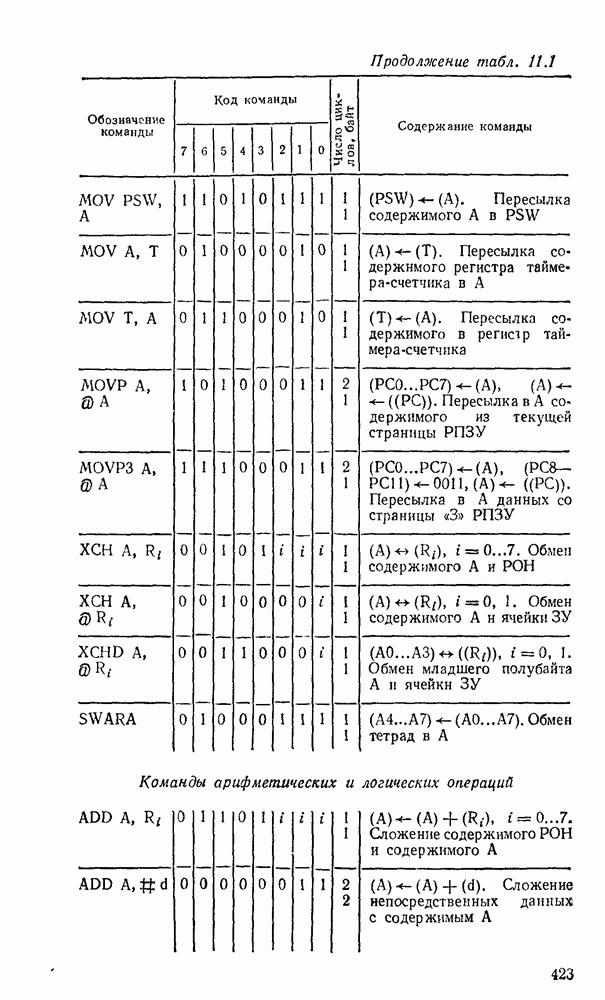
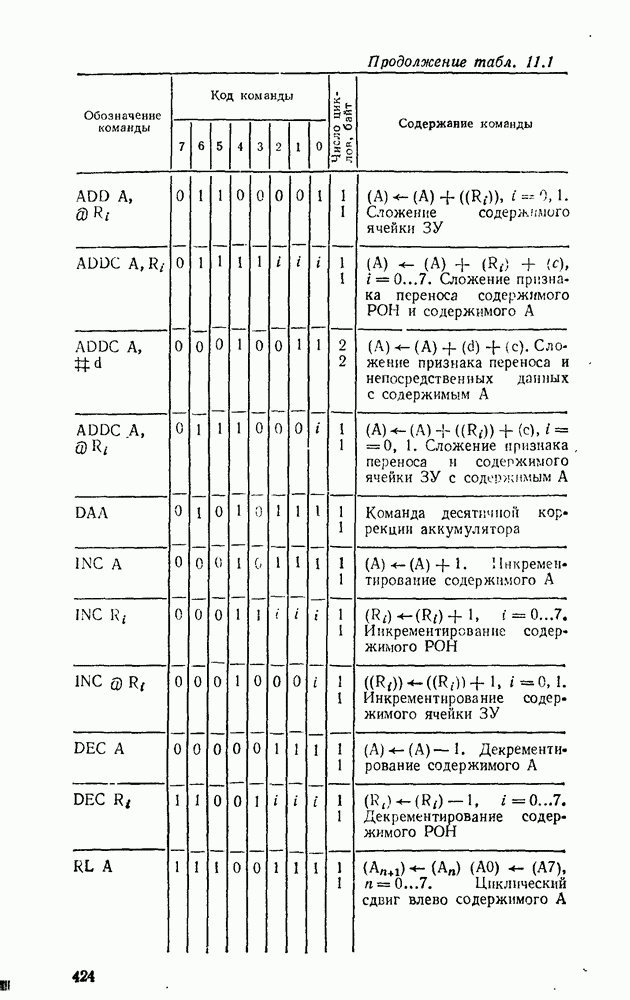
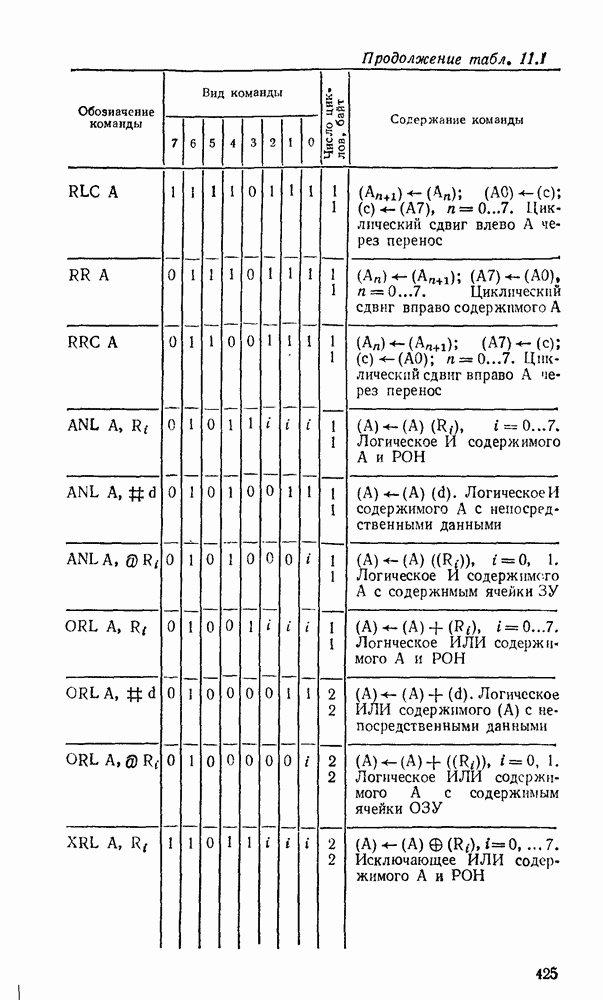
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ