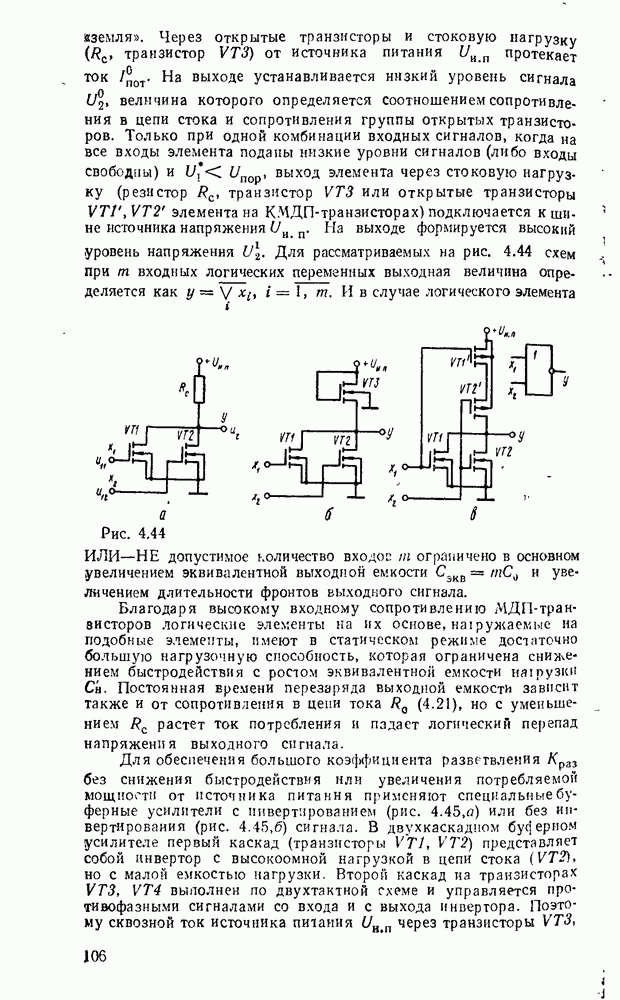
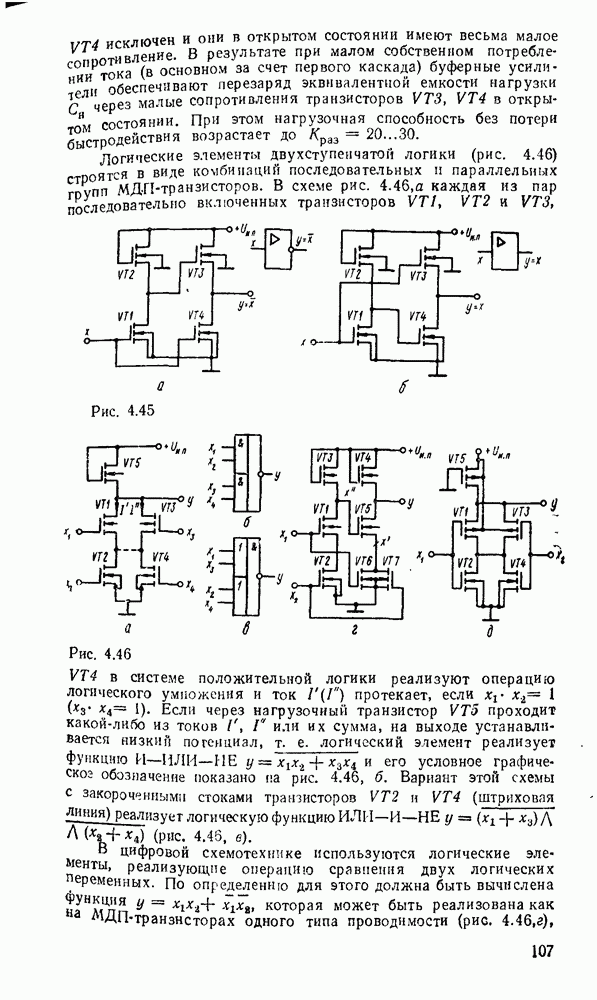
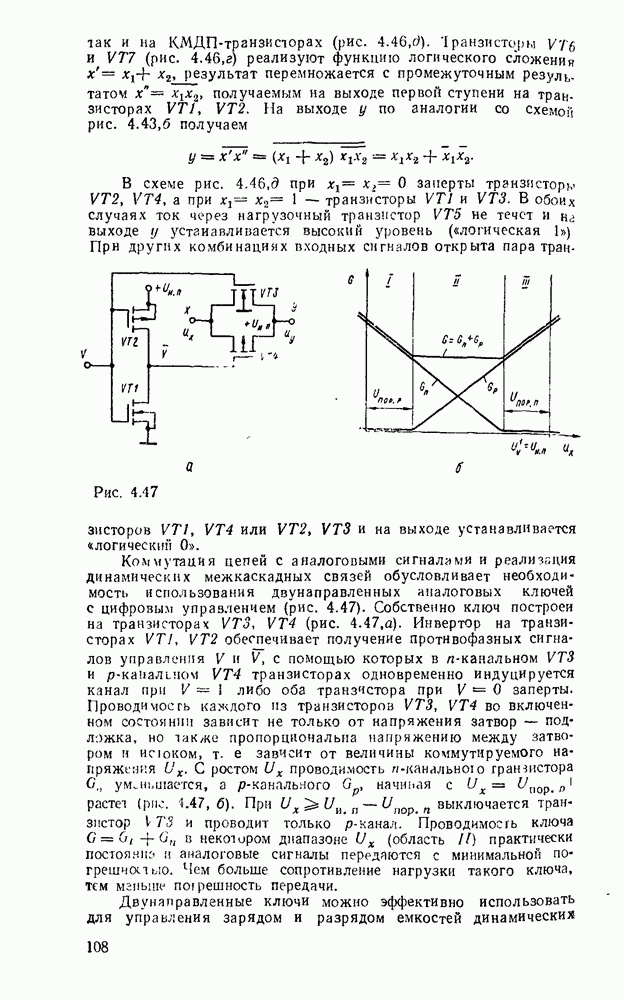
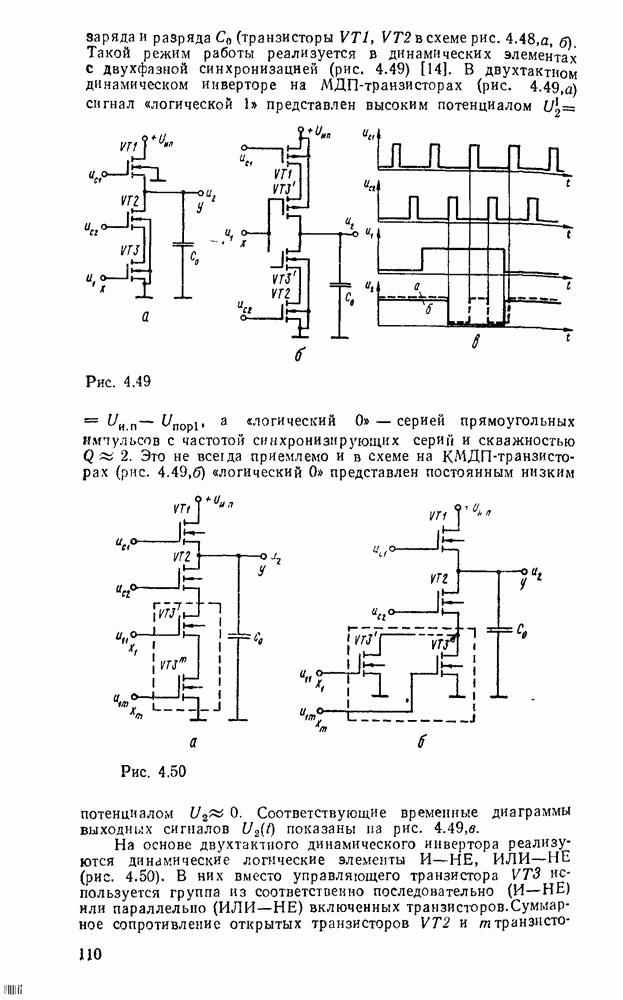
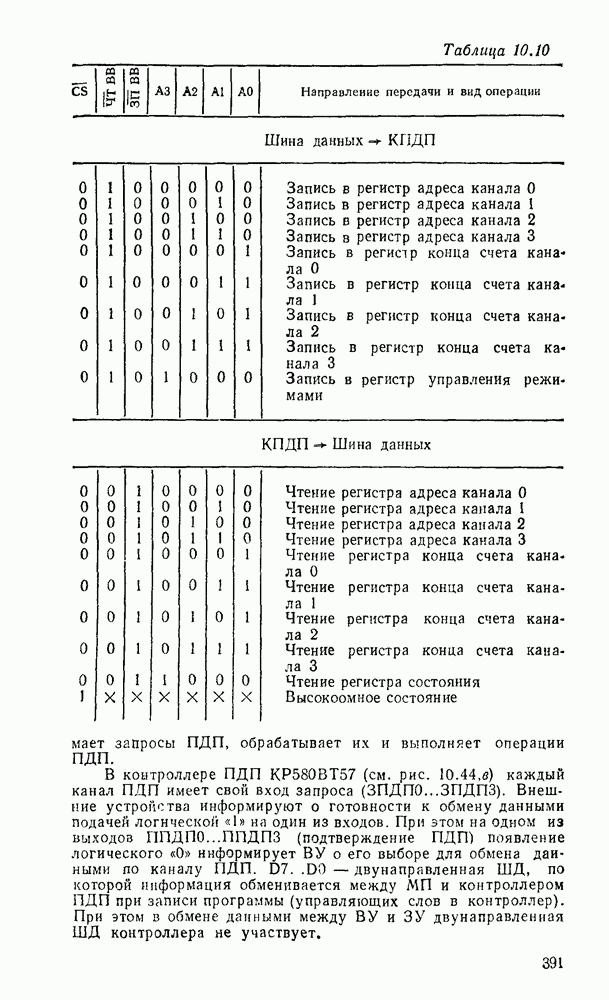
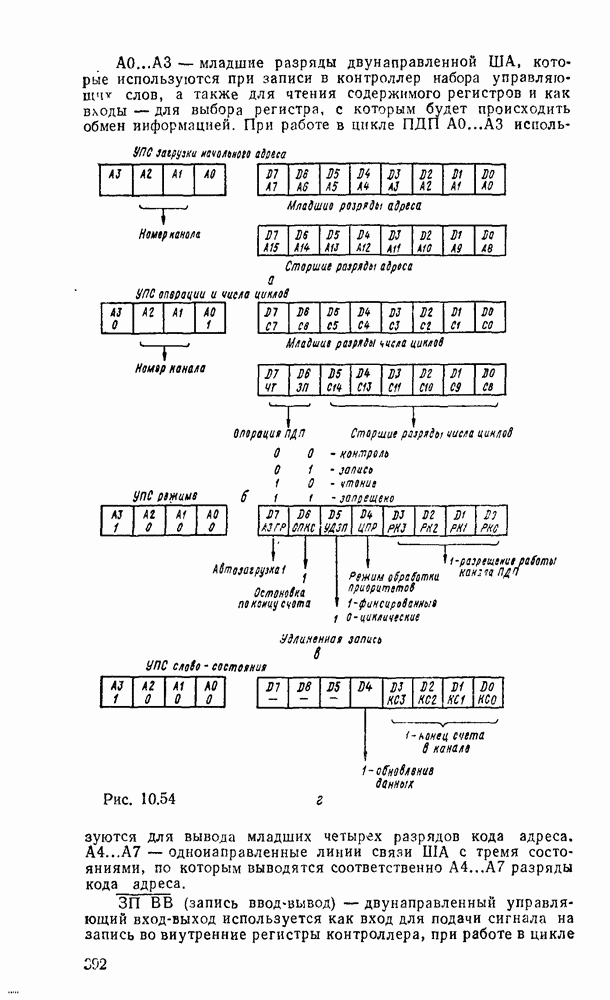
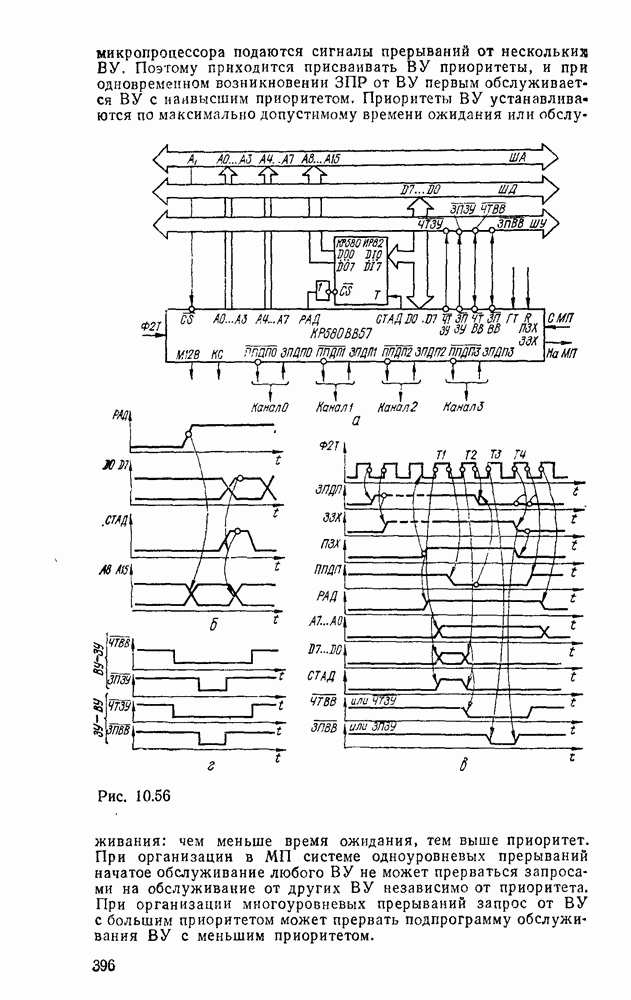
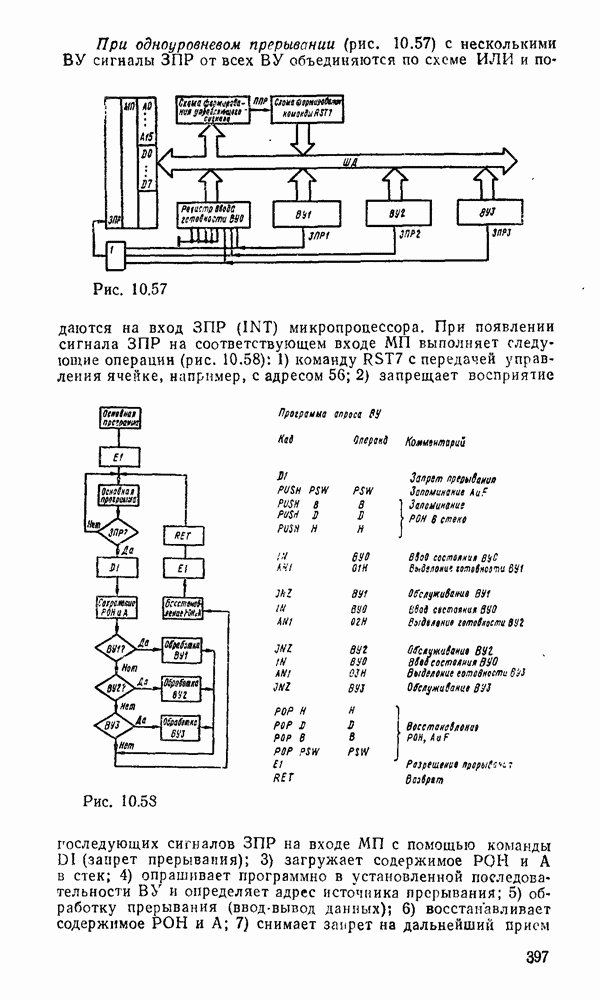
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
Этот метод включает в себя два этапа — преобразование исходной функции к сокращенной форме с помощью операции склеивания и получение минимальной формы путем исключения избыточных простых импликант.
Преобразование булевых формул путем склеивания удобно выполнять в символическом виде, где минтермы записываются в столбик словами длины  , буквы которых соответствуют всем переменным данной функции. Входящие в минтерм переменные называются связанными и предстарляются значениями, при которых минтерм равен единице (1 для
, буквы которых соответствуют всем переменным данной функции. Входящие в минтерм переменные называются связанными и предстарляются значениями, при которых минтерм равен единице (1 для  и 0 для
и 0 для  ). Не входящие в миитерм переменные являются свободными и обозначаются через X. Минтермы
). Не входящие в миитерм переменные являются свободными и обозначаются через X. Минтермы  ранга канонической формы представляются просто наборами значений переменных, на которых функция равна единице.
ранга канонической формы представляются просто наборами значений переменных, на которых функция равна единице.
При склеивании пары минтермов  ранга, отличающихся только значениями переменной
ранга, отличающихся только значениями переменной  появляется минтерм
появляется минтерм  ранга
ранга  который входит в
который входит в  сомножителя в исходные мингермы, т. е.
сомножителя в исходные мингермы, т. е.  . При этом представляющий его символ получается замещением в символе склеиваемого минтерма значения переменной
. При этом представляющий его символ получается замещением в символе склеиваемого минтерма значения переменной  на X. Аналогично склеивание пары минтермов
на X. Аналогично склеивание пары минтермов  ранга приводит к появлению минтерма
ранга приводит к появлению минтерма  ранга с двуми свободными переменными и т. д. Принято говорить, что склеиваемые минтермы покрываются результирующими минтермами более низкого порядка.
ранга с двуми свободными переменными и т. д. Принято говорить, что склеиваемые минтермы покрываются результирующими минтермами более низкого порядка.
Чтобы уменьшить количество сравниваемых пар, целесообразно разбить множество минтермов на классы, в каждом из которых содержатся символы с одинаковым числом единиц (или нулей), и упорядочить эти классы по возрастающему (или убывающему) числу единиц. Так как объединяться могут только такие минтермы, символы которых содержат точно на одну больше или на одну меньше единиц, то достаточно ограничиться попарным сравнением символов соседних классов.
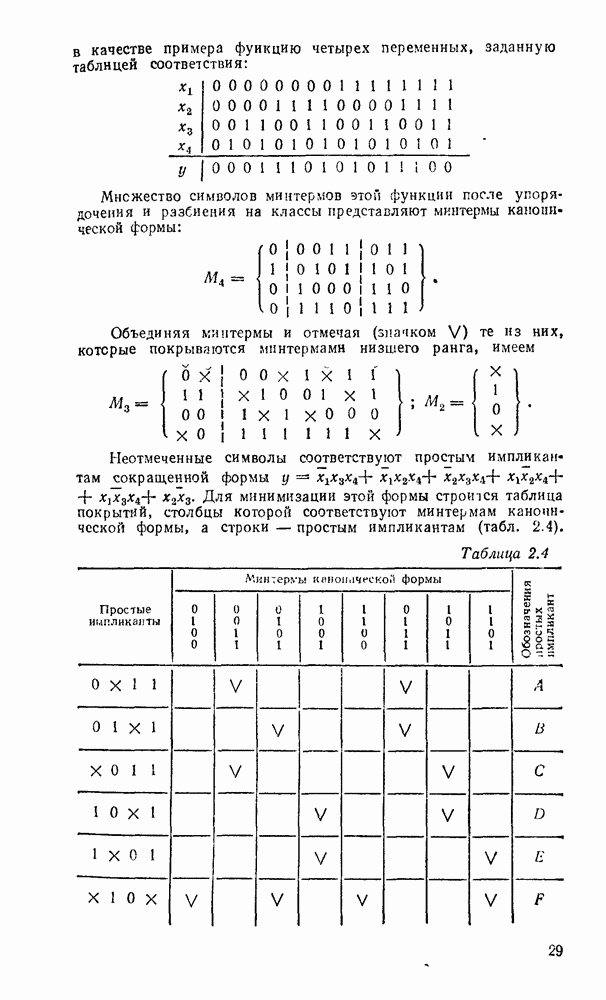
Рассмотрим в качестве примера функцию четырех переменных, заданную таблицей соответствия:

Множество символов минтермов этой функции после упорядочения и разбиения на классы представляют минтермы канонической формы:

Объединяя минтермы и отмечая (значком V) те из них, которые покрываются мннтермамн низшего ранга, имеем

Неотмеченные символы соответствуют простым импликантам сокращенной формы  . Для минимизации этой формы строится таблица покрытий, столбцы которой соответствуют минтермам канонической формы, а строки — простым импликантам (табл. 2.4).
. Для минимизации этой формы строится таблица покрытий, столбцы которой соответствуют минтермам канонической формы, а строки — простым импликантам (табл. 2.4).
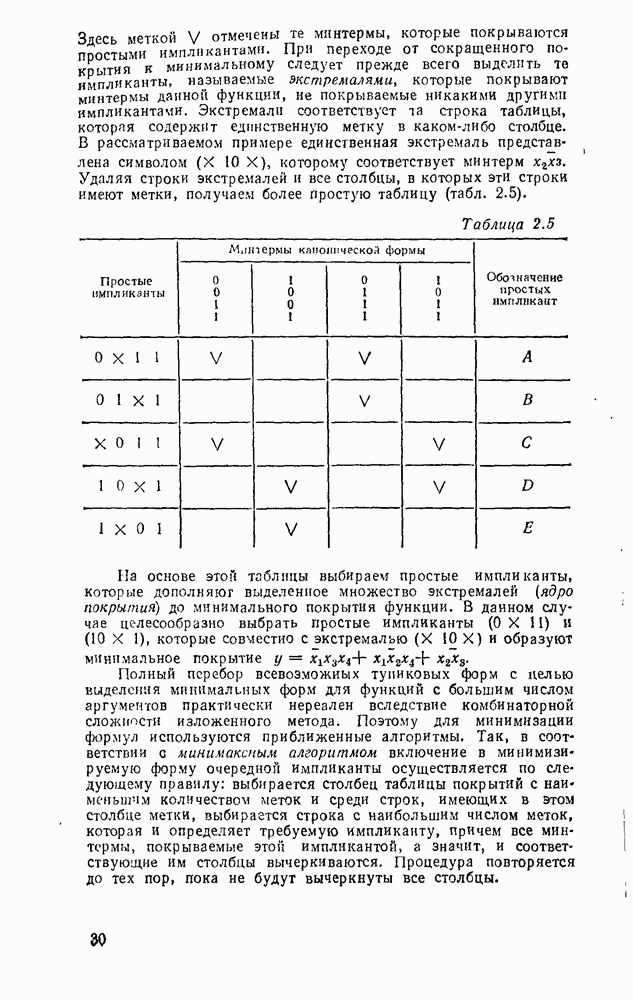
Таблица 2.4

Здесь меткой V отмечены те минтермы, которые покрываются простыми имплнкантами. При переходе от сокращенного покрытия к минимальному следует прежде всего выделить те импликанты, называемые экстремалями, которые покрывают минтермы данной функции, не покрываемые никакими другими импликантами. Экстремали соответствует та строка таблицы, которая содержит единственную метку в каком-либо столбце. В рассматриваемом примере единственная экстремаль представлена символом (X 10 X), которому соответствует минтерм  . Удаляя строки экстремалей и все столбцы, в которых эти строки имеют метки, получаем более простую таблицу (табл. 2.5).
. Удаляя строки экстремалей и все столбцы, в которых эти строки имеют метки, получаем более простую таблицу (табл. 2.5).
Таблица 2.5

На основе этой таблицы выбираем простые импликанты, которые дополняют выделенное множество экстремалей (ядро покрытия) до минимального покрытия функции. В данном случае целесообразно выбрать простые импликанты (ОХ 11) и (10 X 1), которые совместно с экстремалью (X 10 X) и образуют минимальное покрытие  .
.
Полный перебор всевозможных тупиковых форм с целью выделения минимальных форм для функций с большим числом аргументов практически нереален вследствие комбинаторной сложности изложенного метода. Поэтому для минимизации формул используются приближенные алгоритмы. Так, в соответствии с минимаксным алгоритмом включение в минимизируемую форму очередной импликанты осуществляется по следующему правилу: выбирается столбец таблицы покрытий с наименьшим количеством меток и среди строк, имеющих в этом столбце метки, выбирается строка с наибольшим числом меток, которая и определяет требуемую импликанту, причем все минтермы, покрываемые этой импликантой, а значит, и соответствующие им столбцы вычеркиваются. Процедура повторяется до тех пор, пока не будут вычеркнуты все столбцы.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
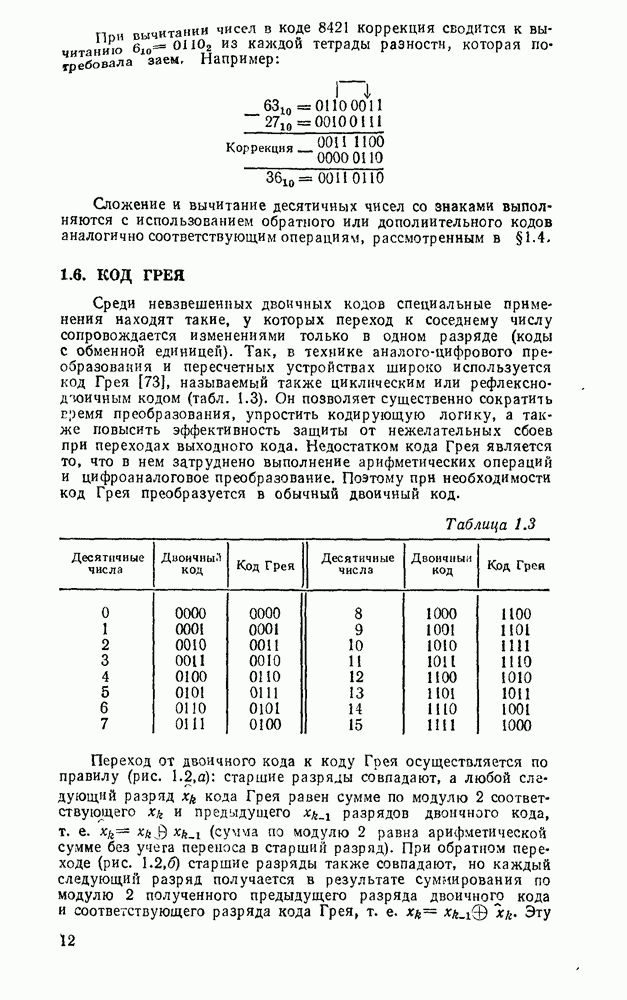
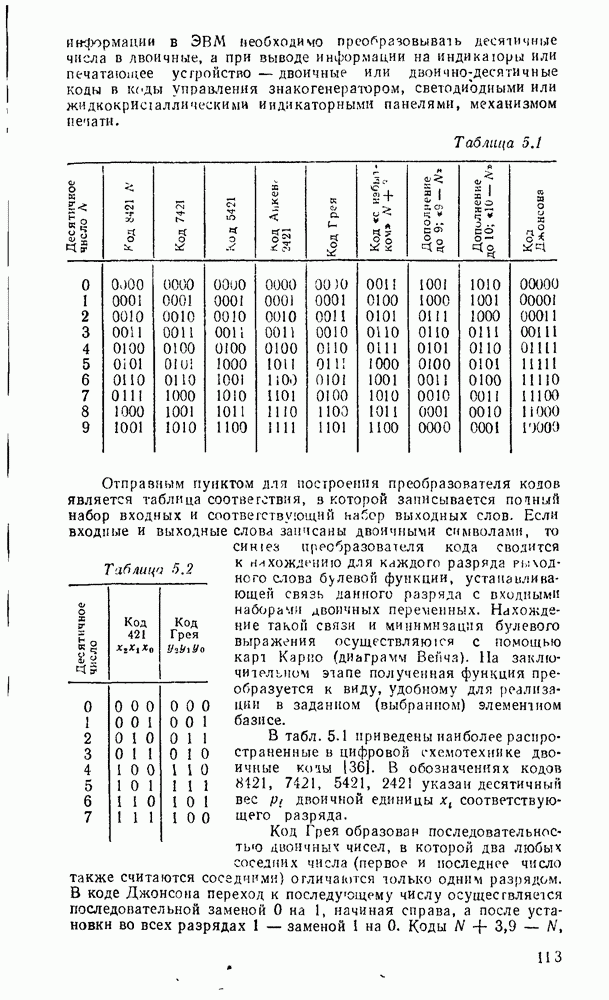
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
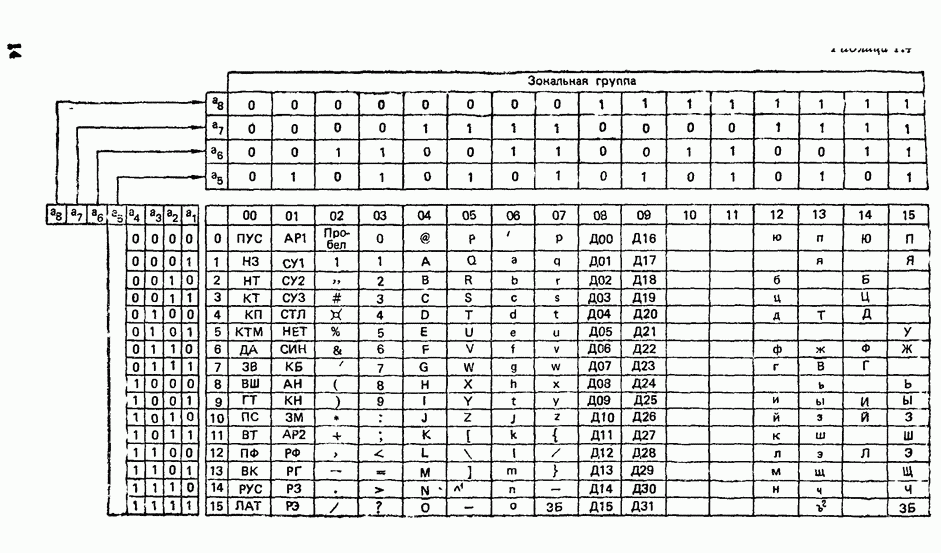
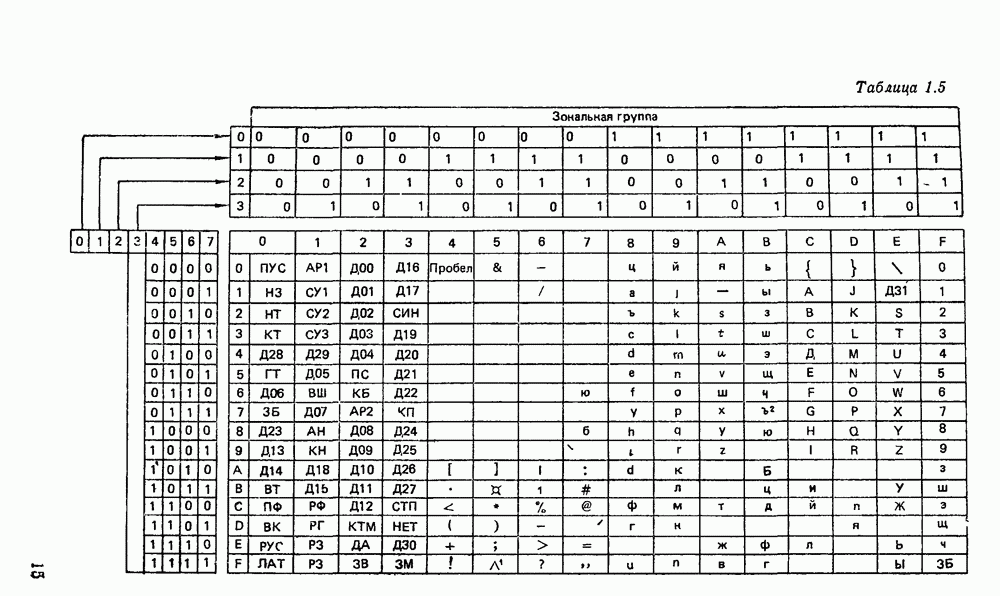
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
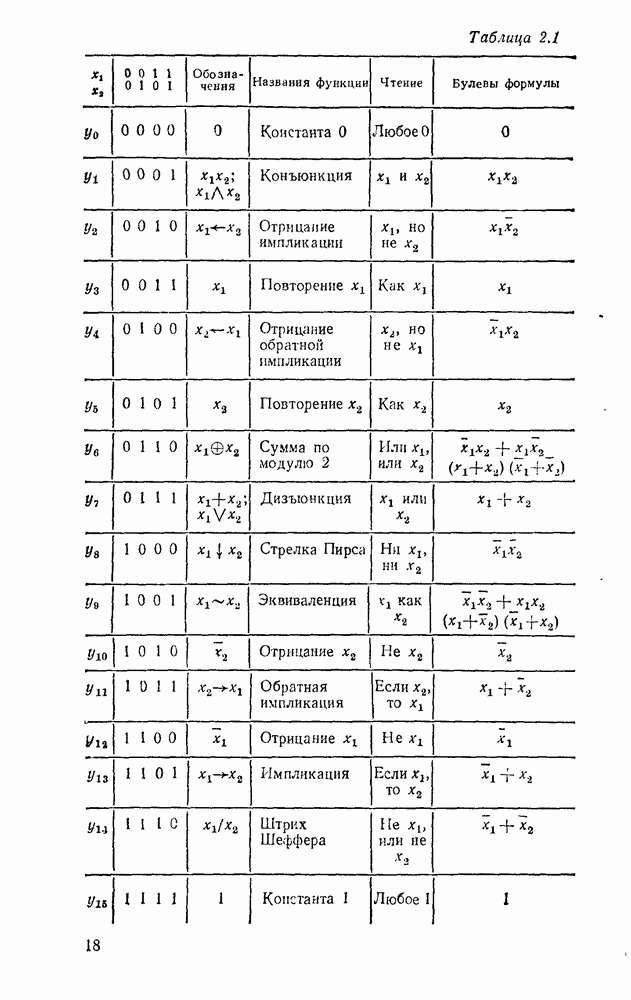
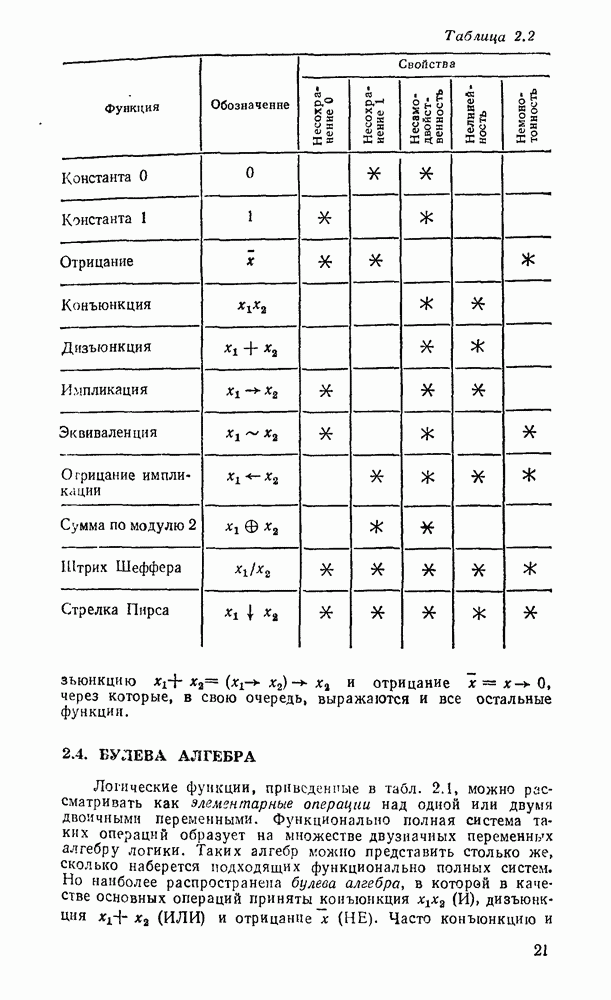
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
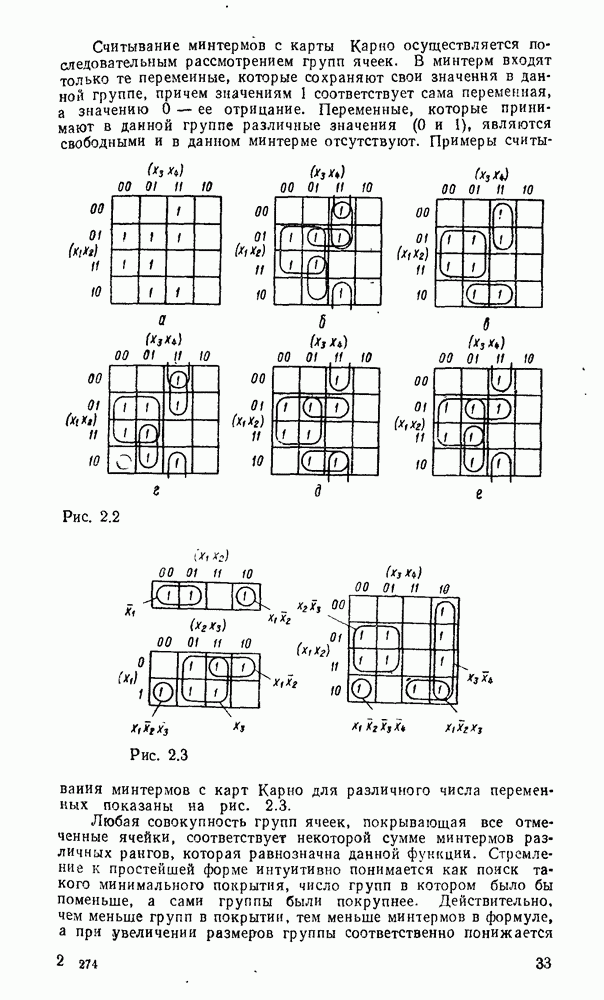
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
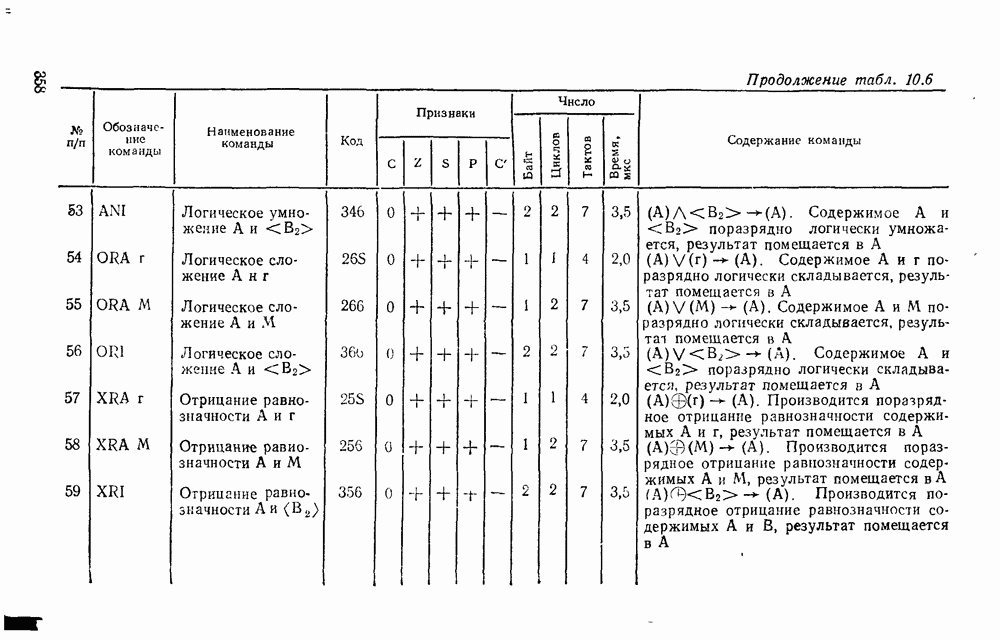
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
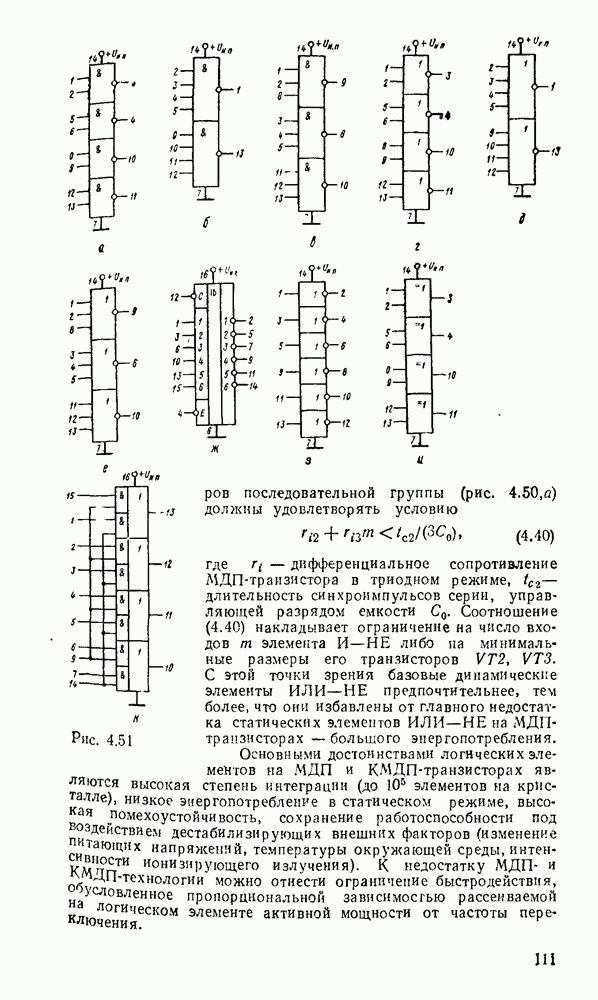
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
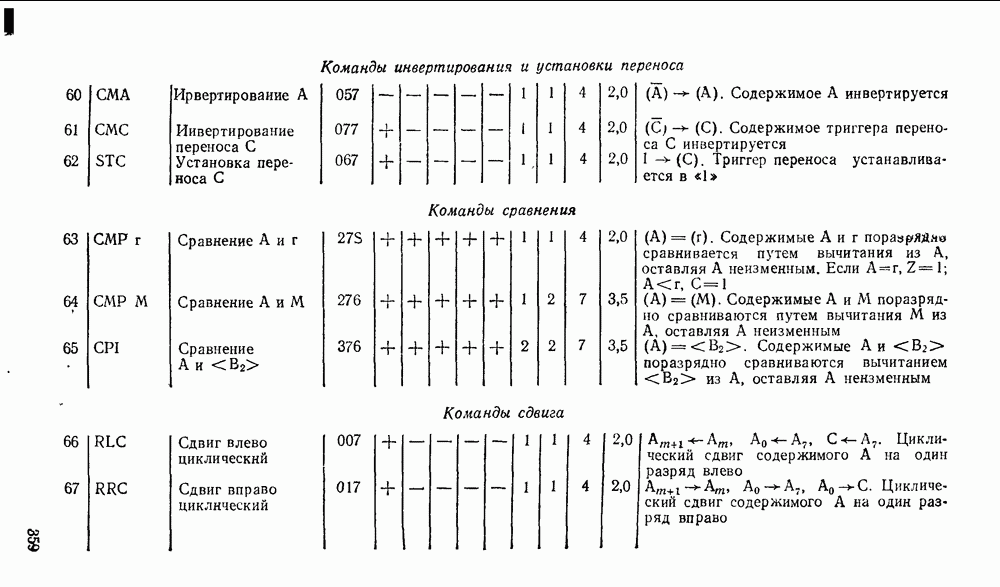
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
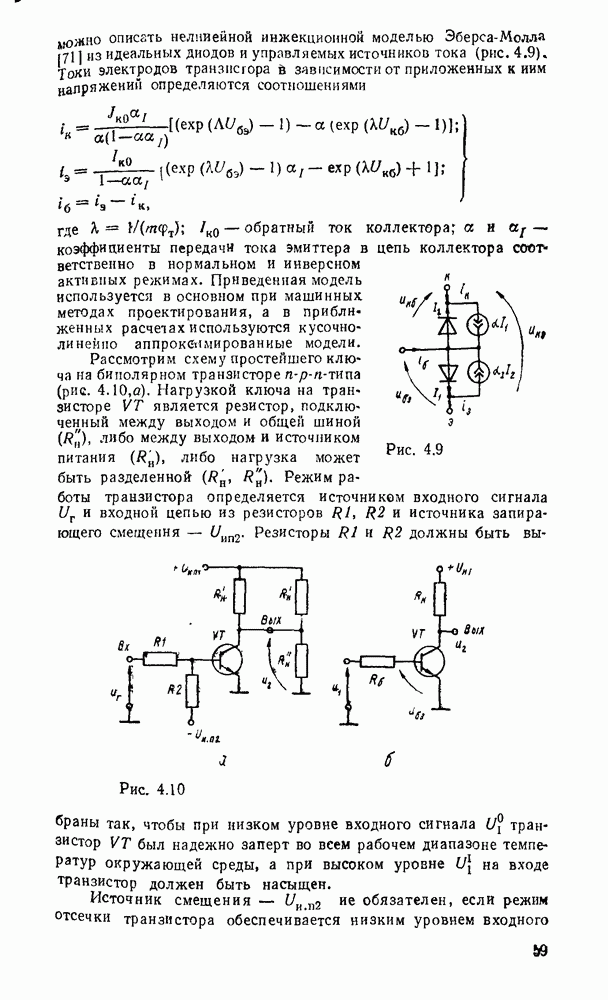
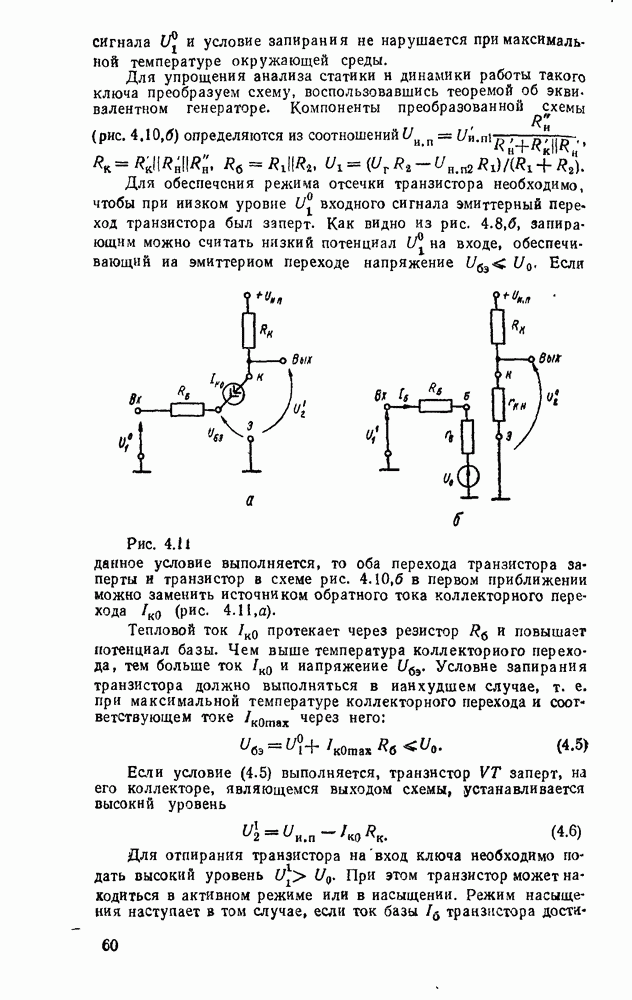
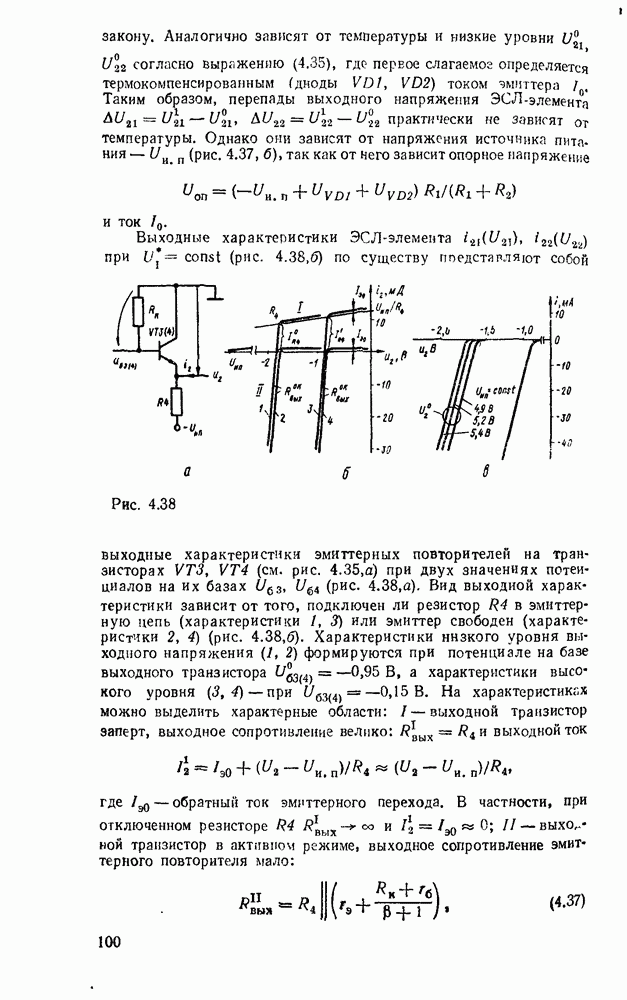
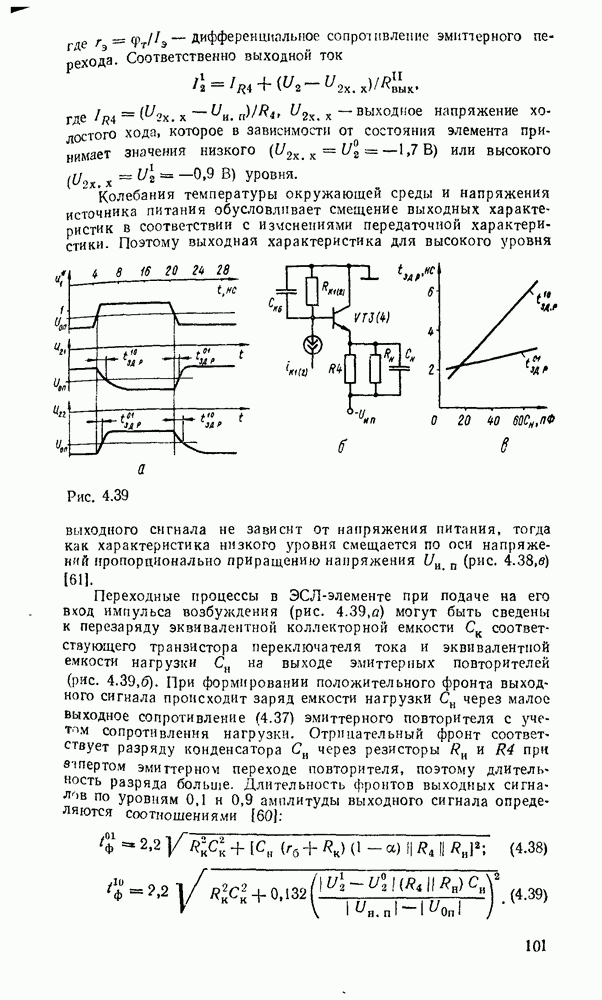
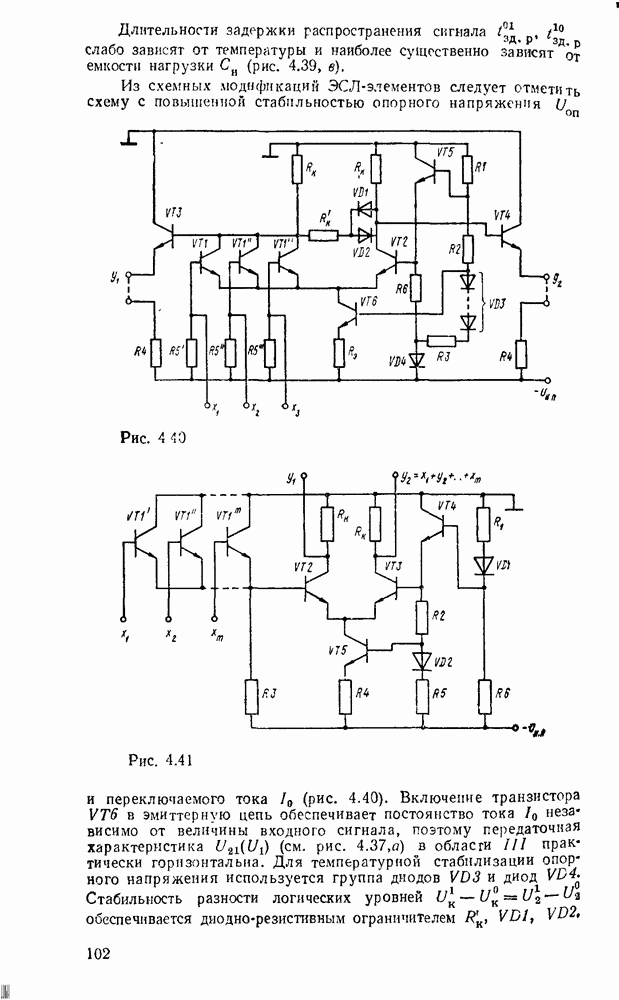
- Электронные ключи на биполярных транзисторах.
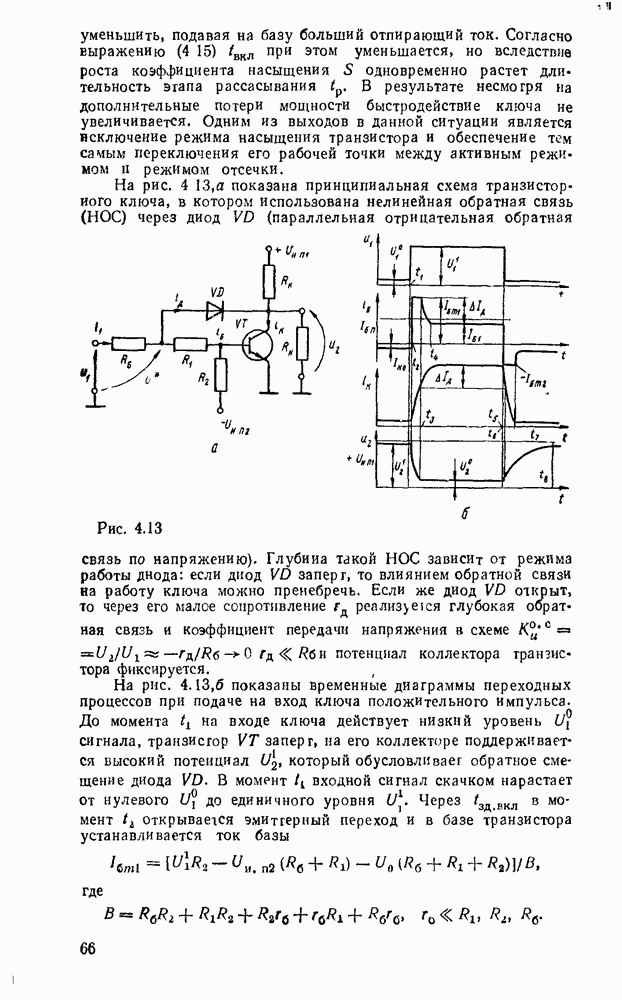
- Ключ на биполярном транзисторе с нелинейной обратной связью.
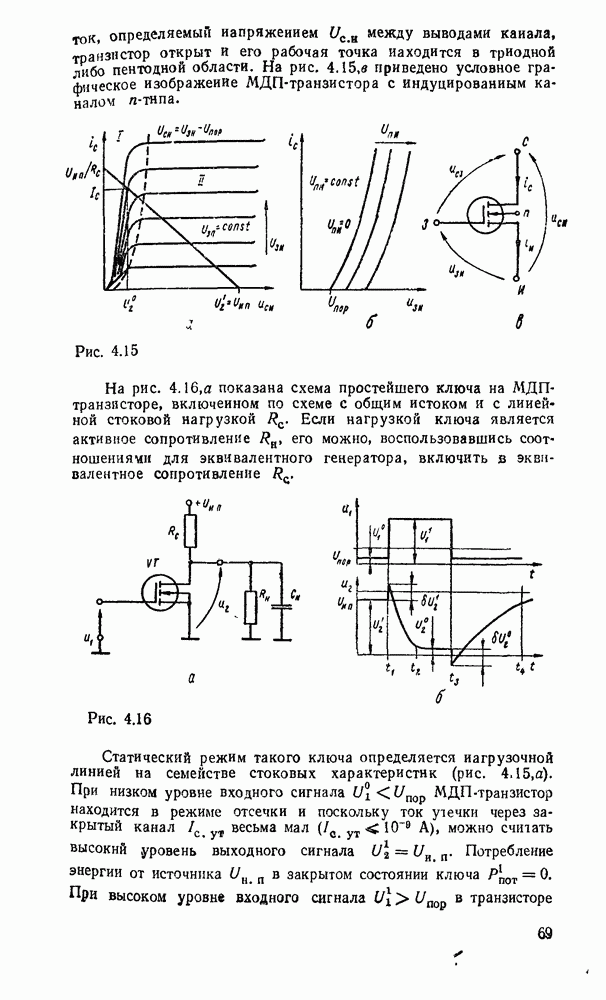
- Электронные ключи на полезых транзисторах.
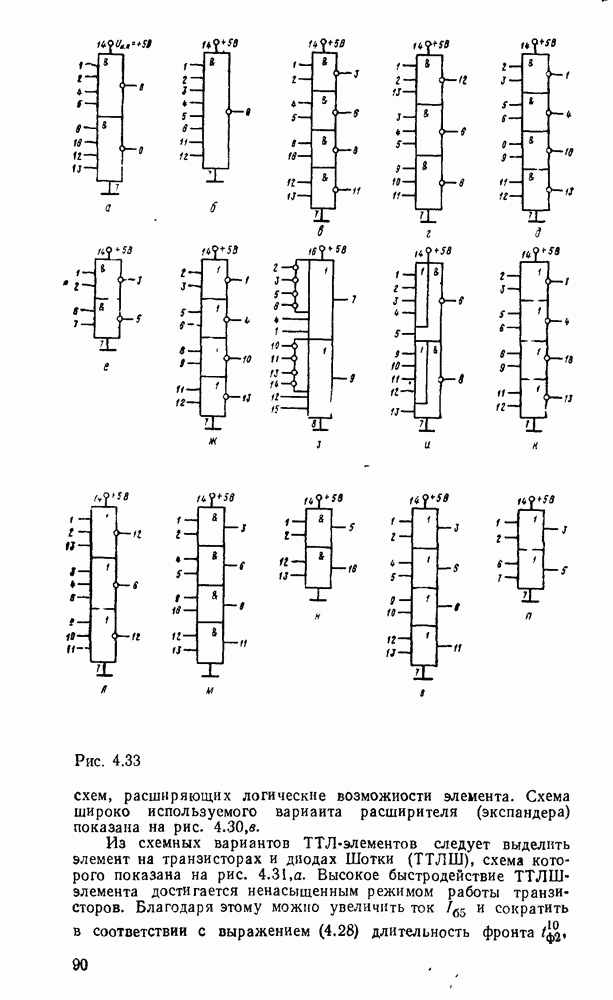
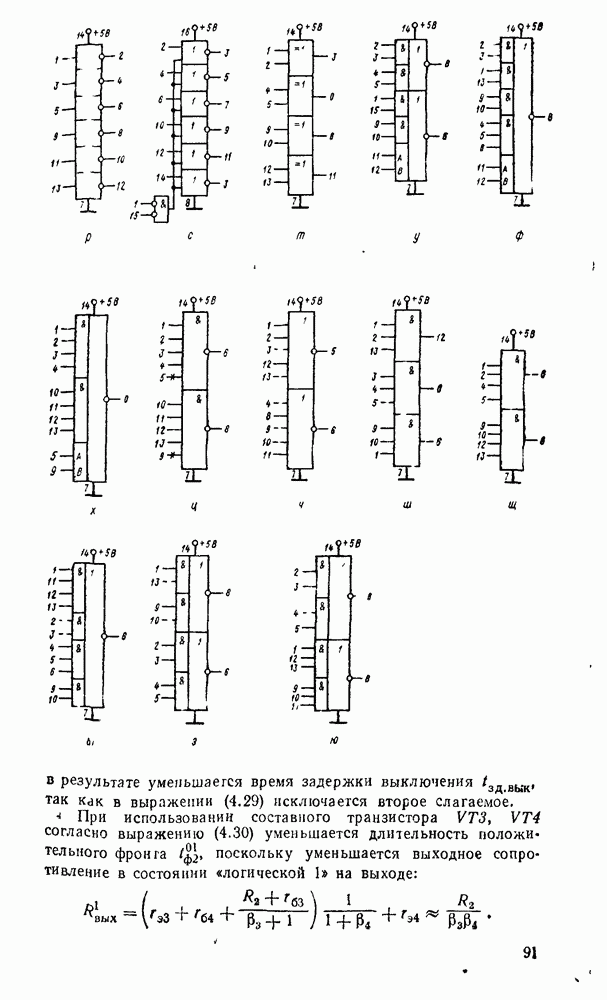
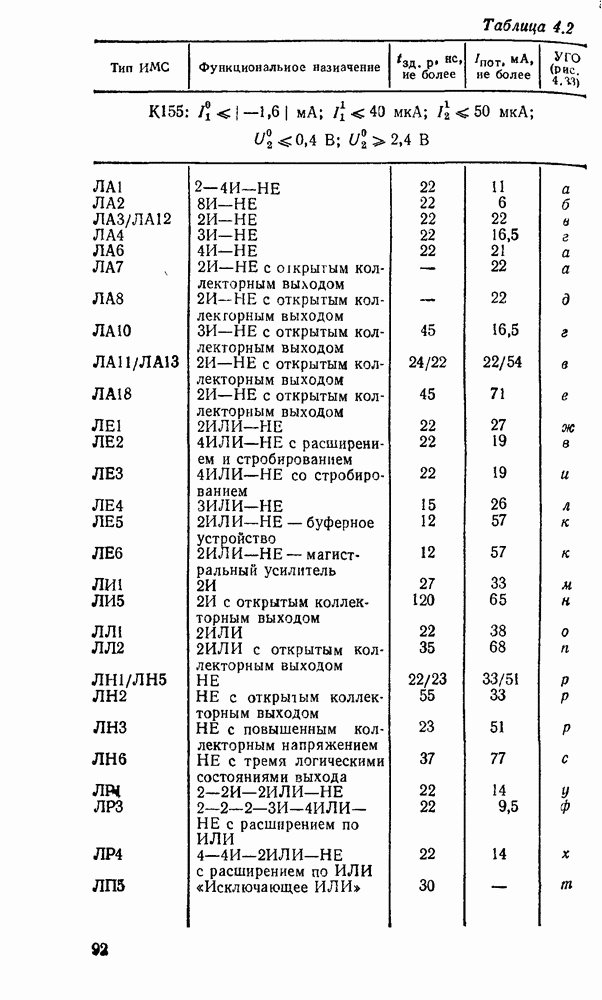
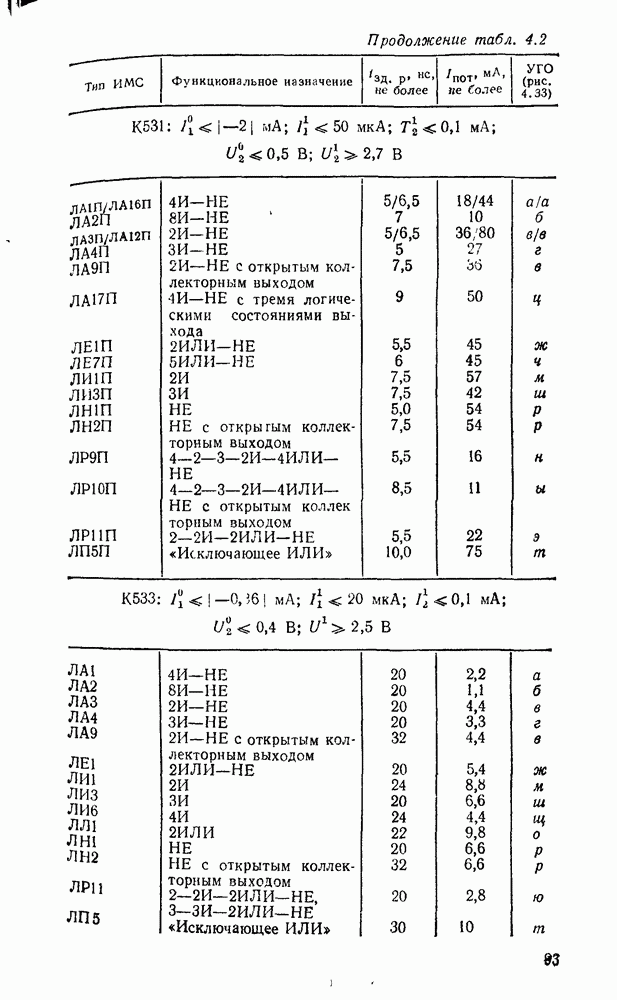
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
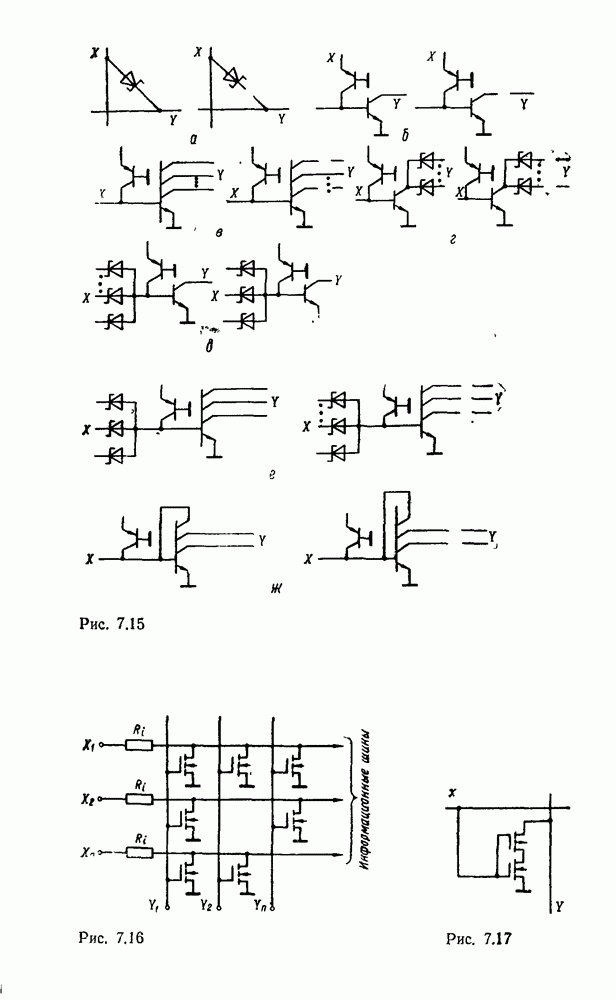
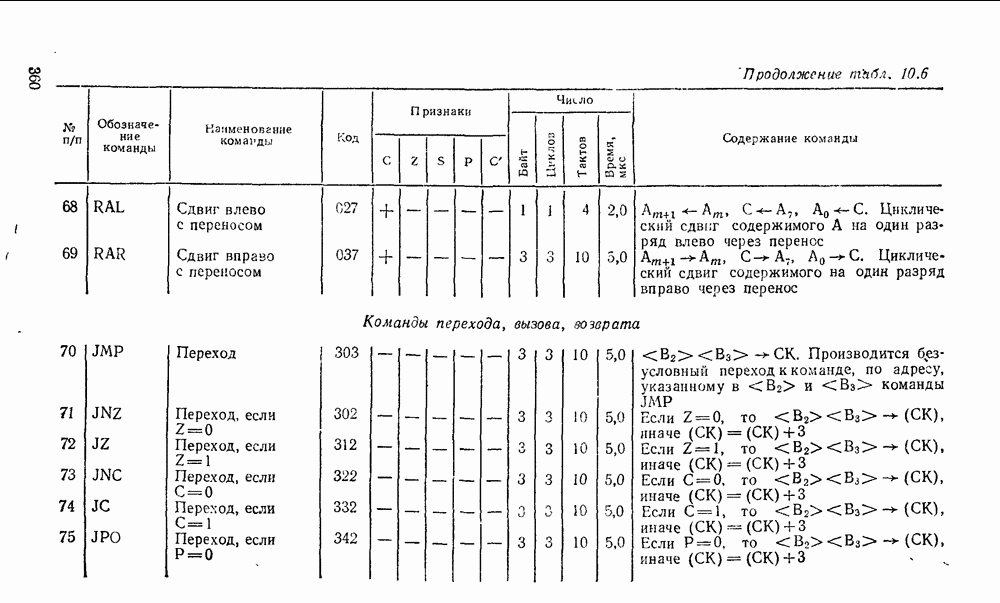
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
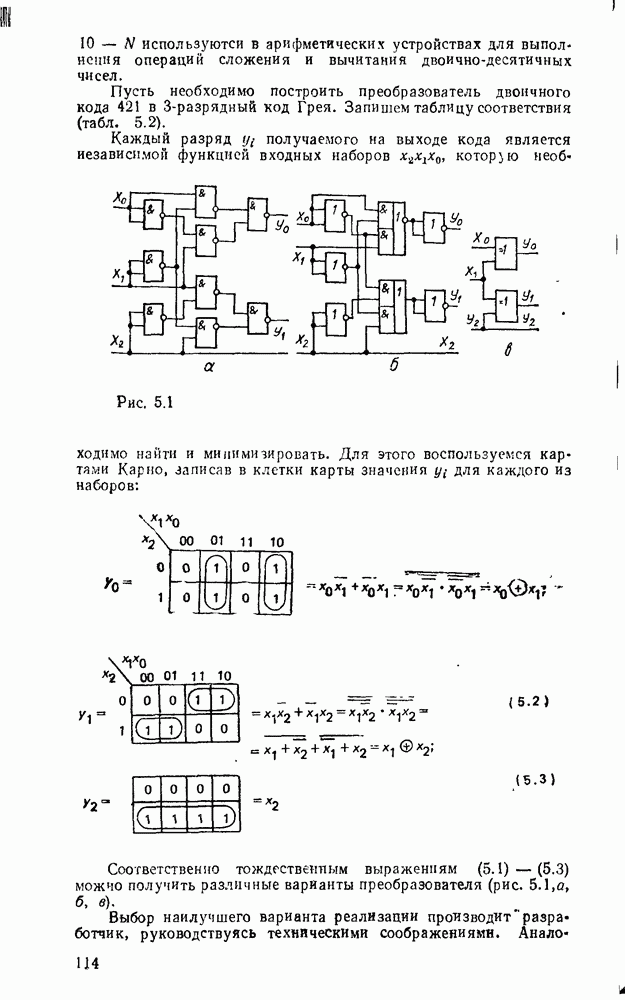
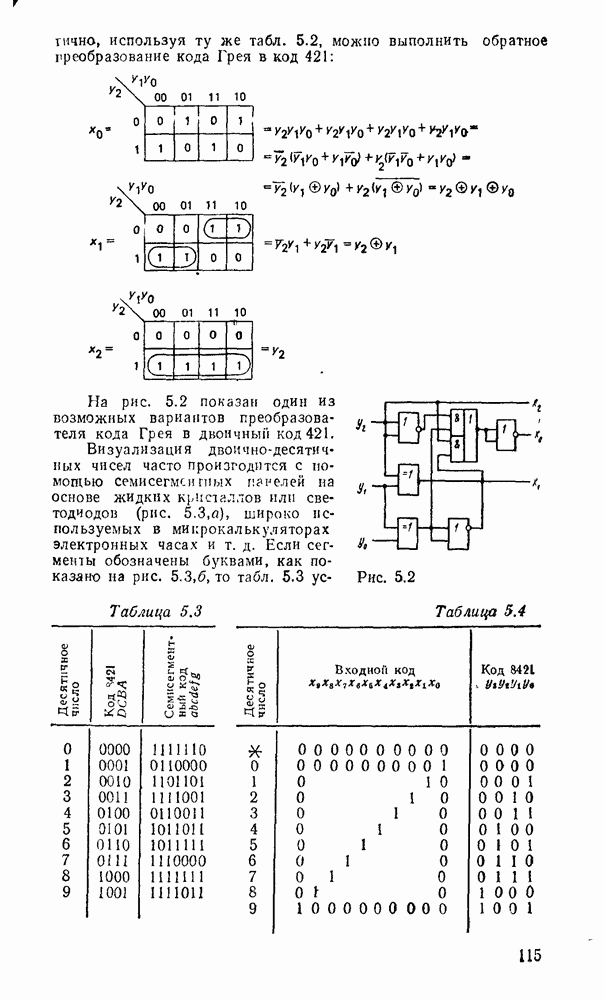
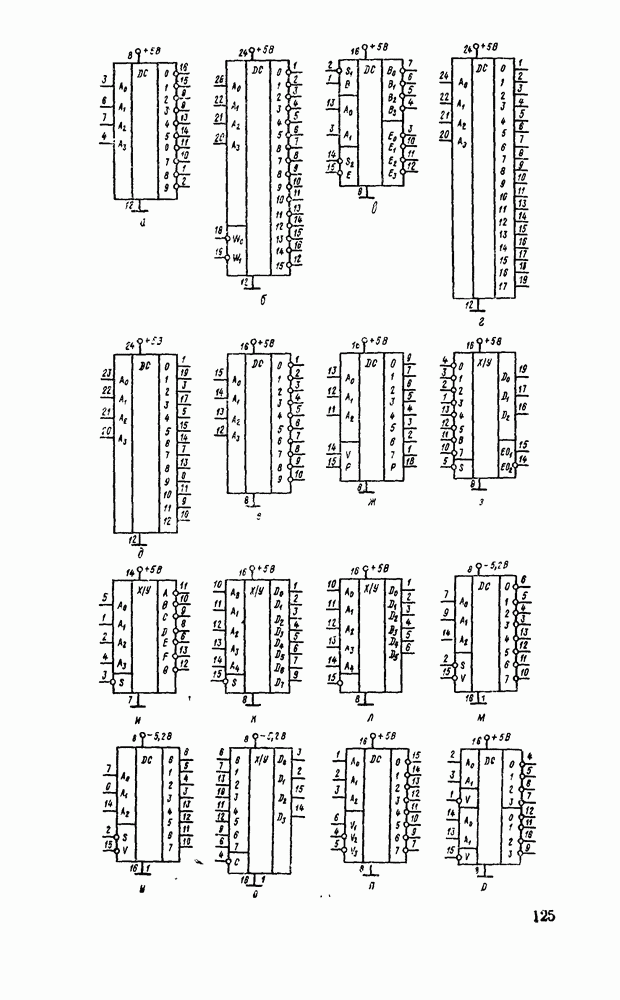
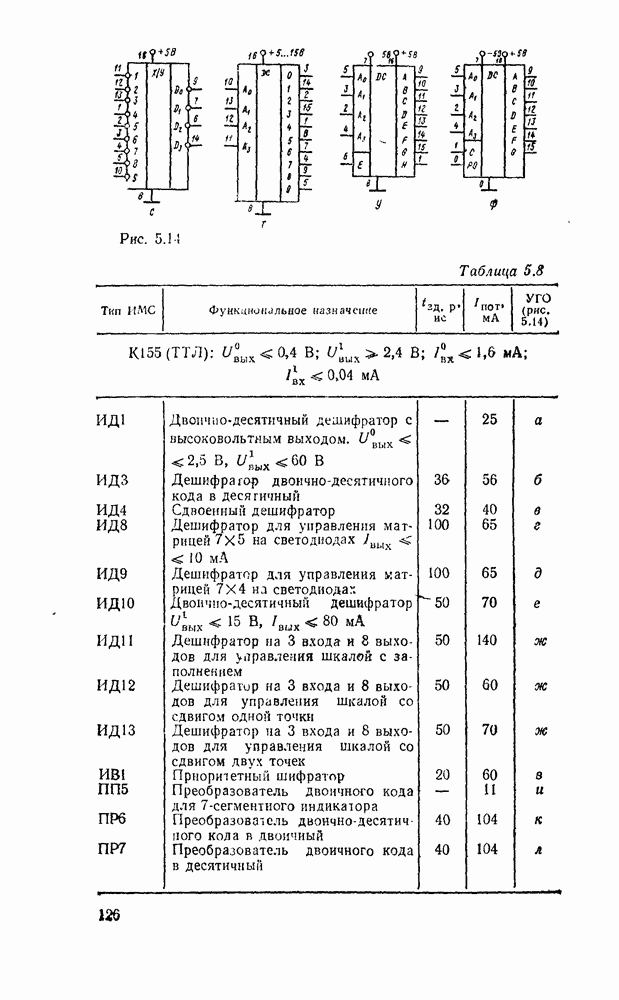
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
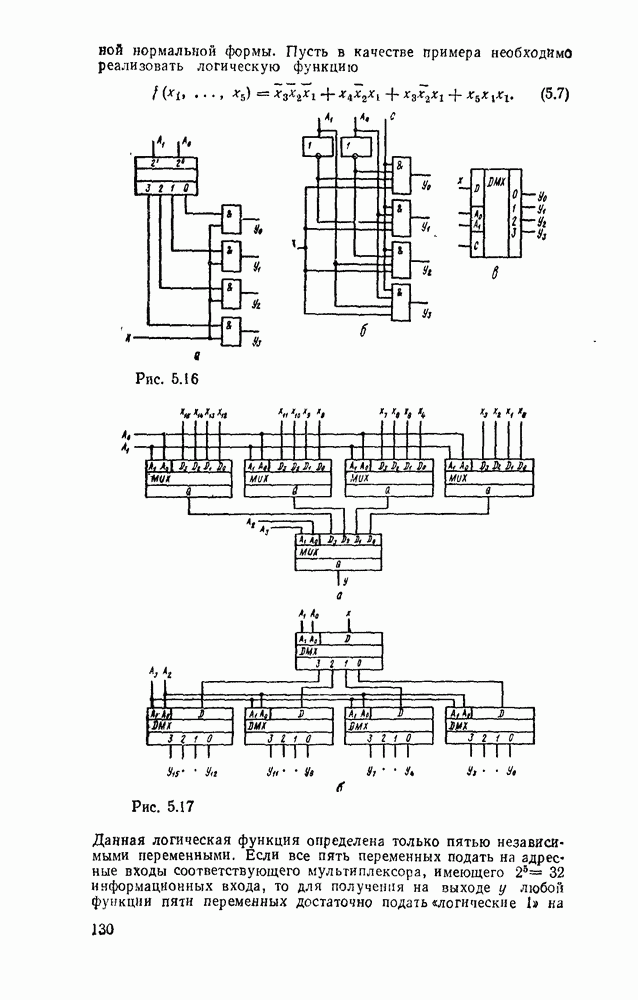
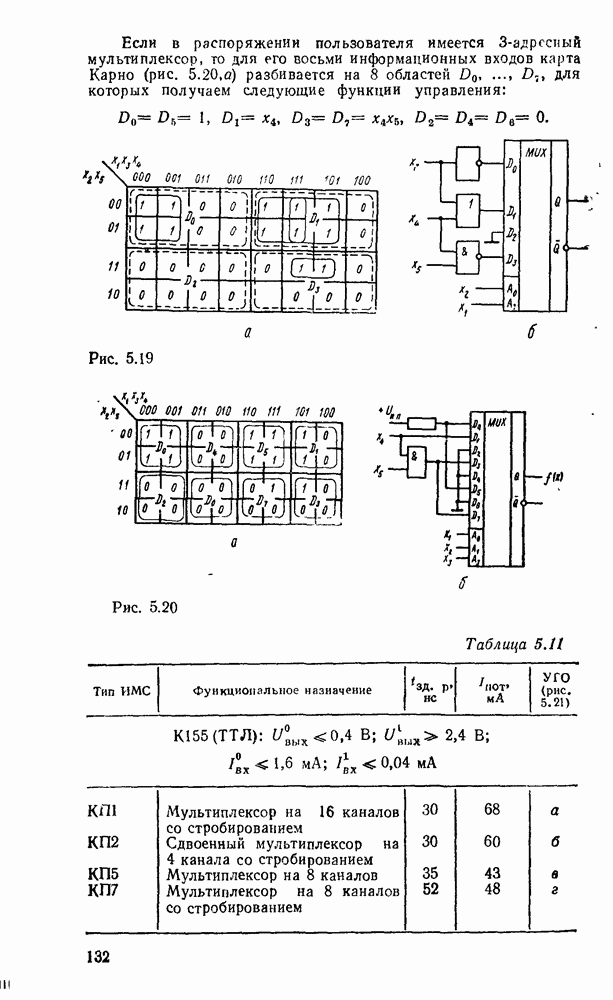
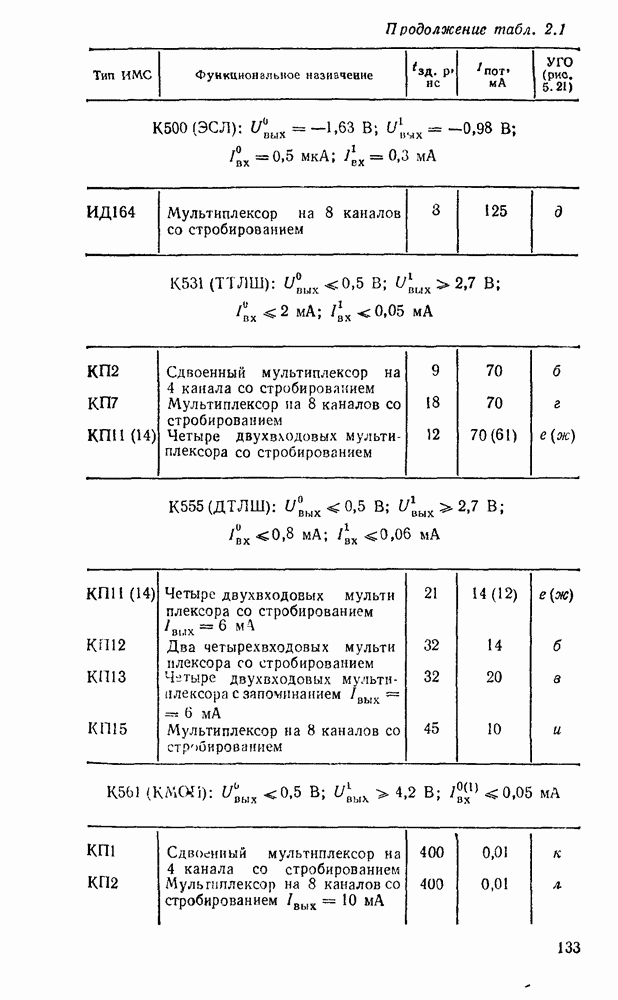
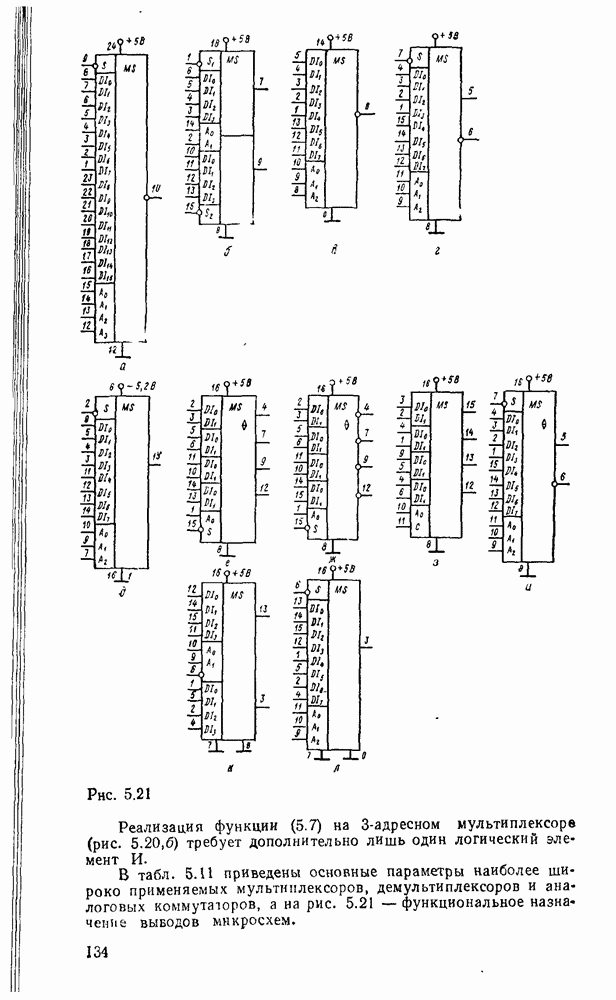
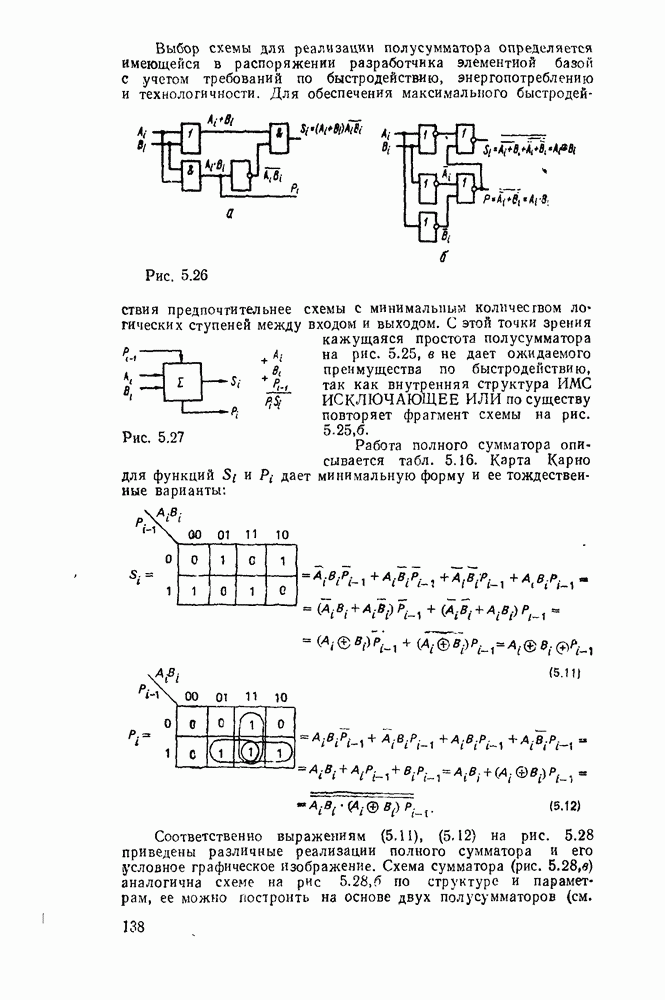
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
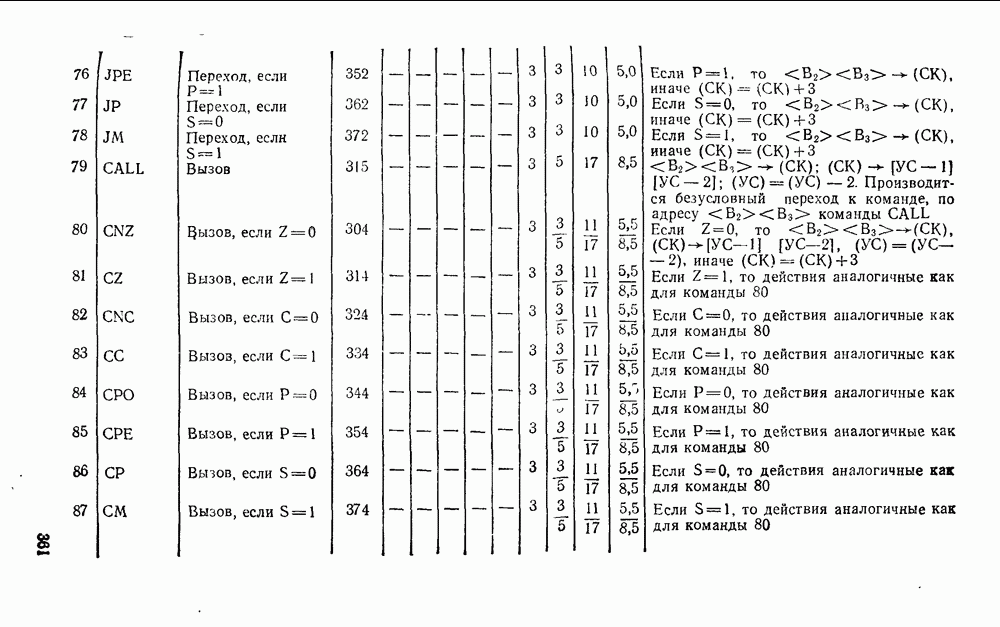
- 6.2. РЕГИСТРЫ
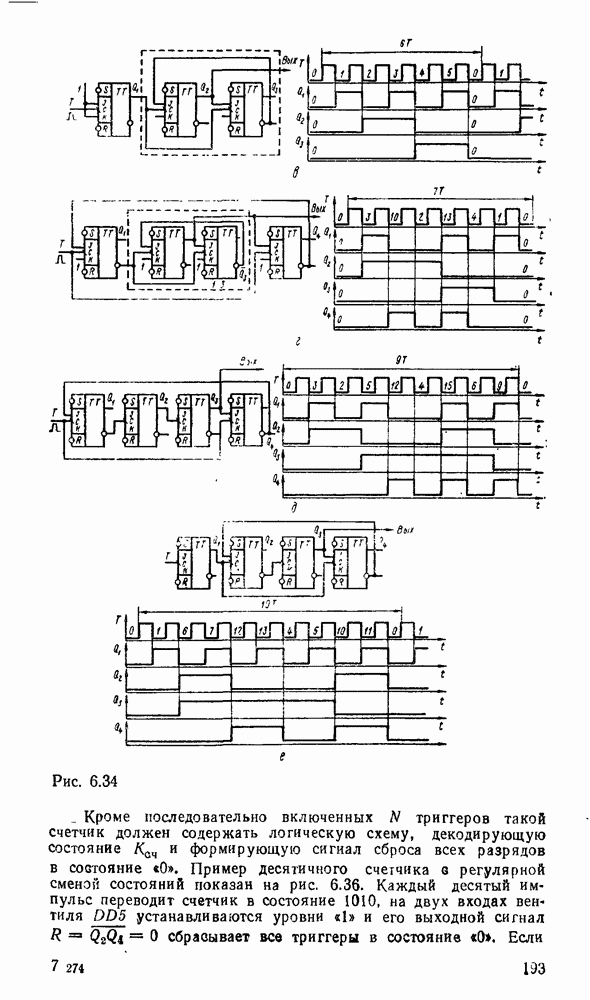
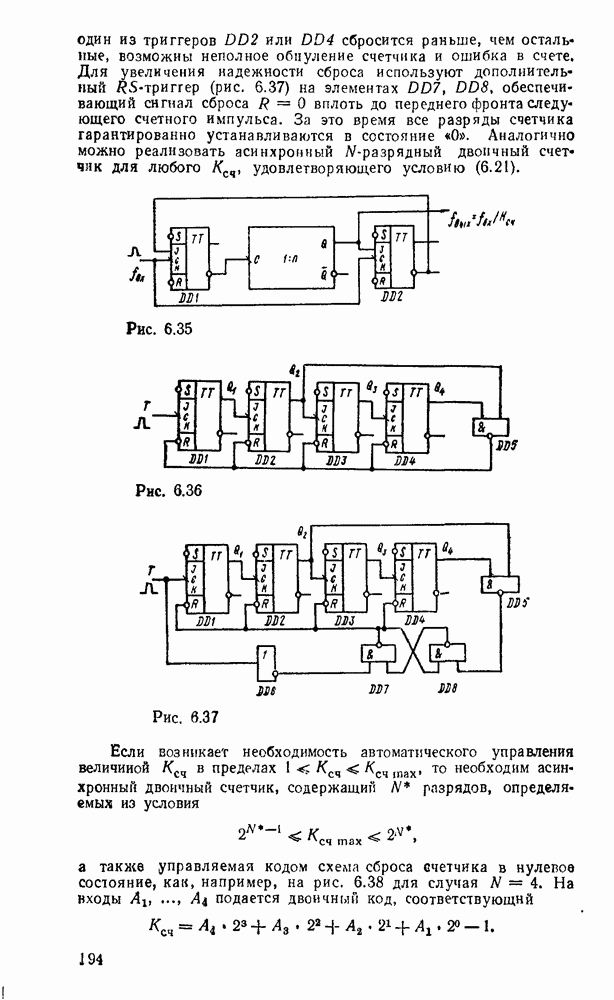
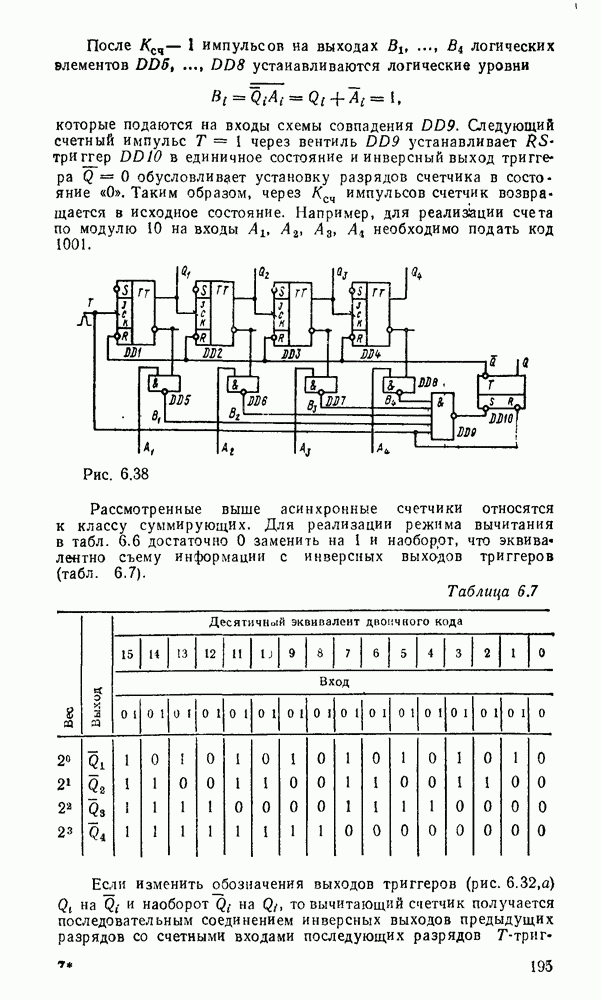
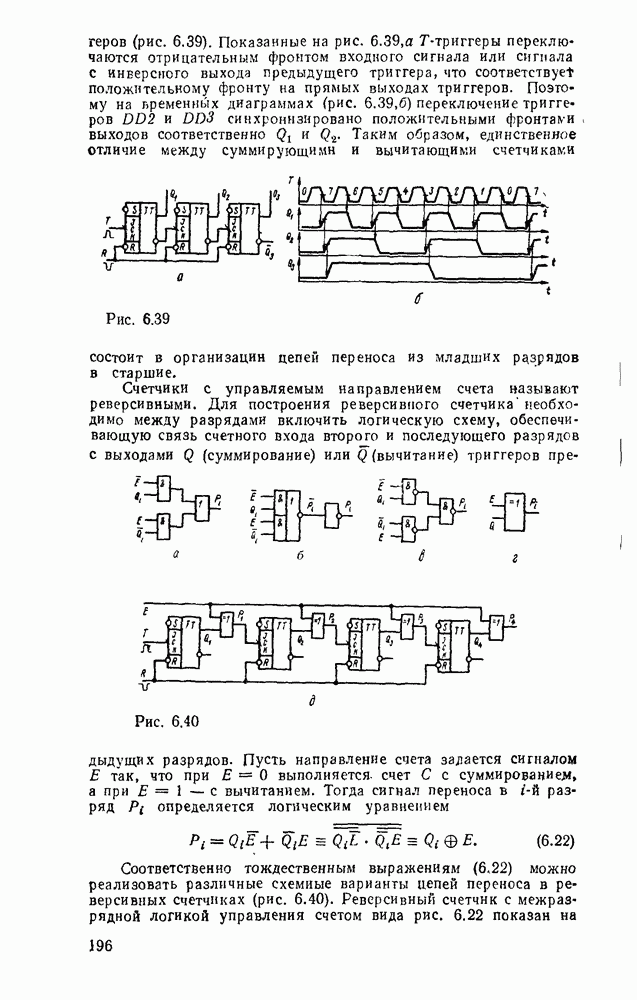
- 6.3. СЧЕТЧИКИ
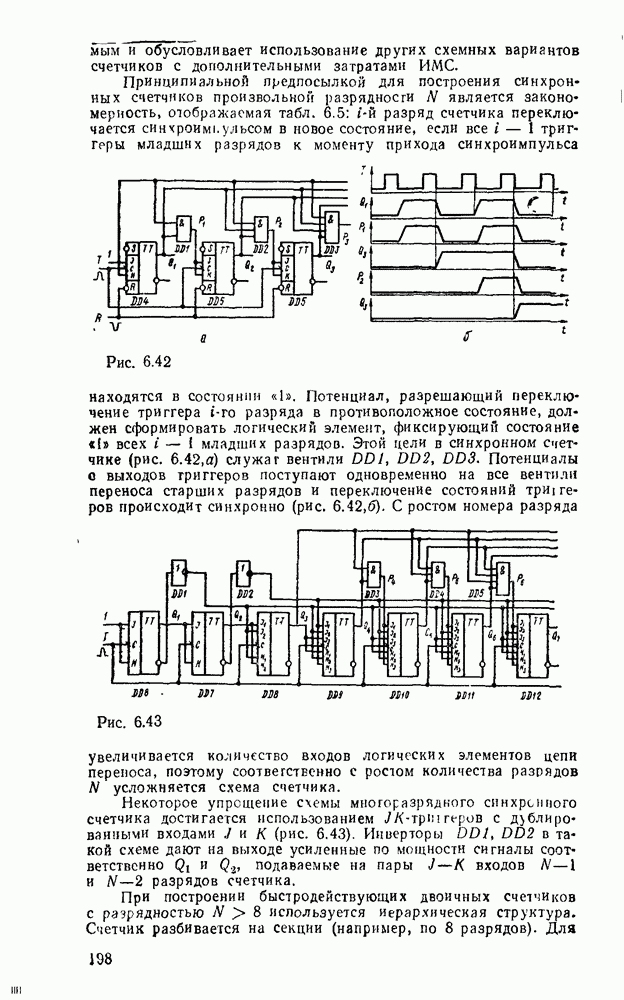
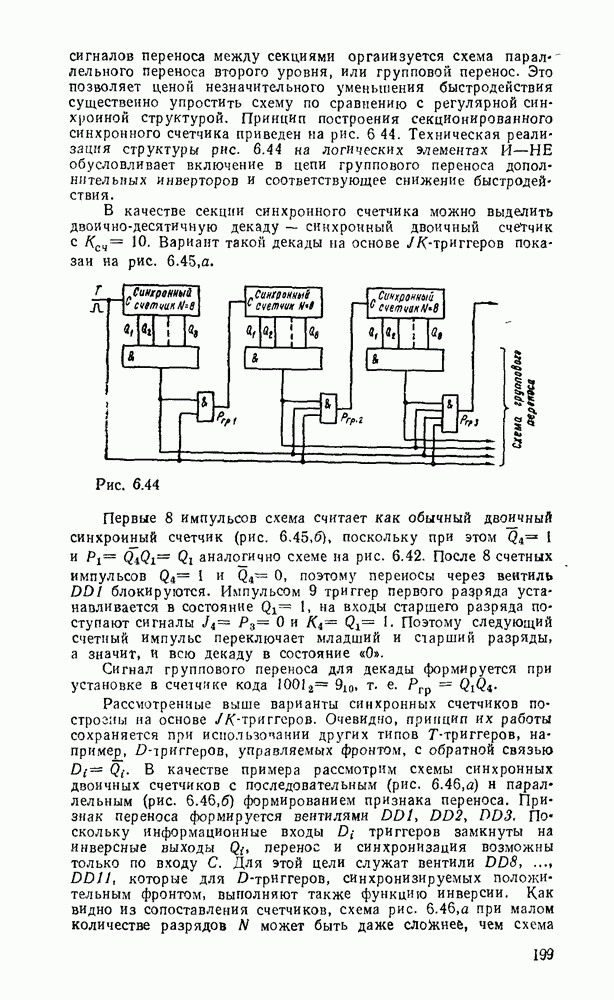
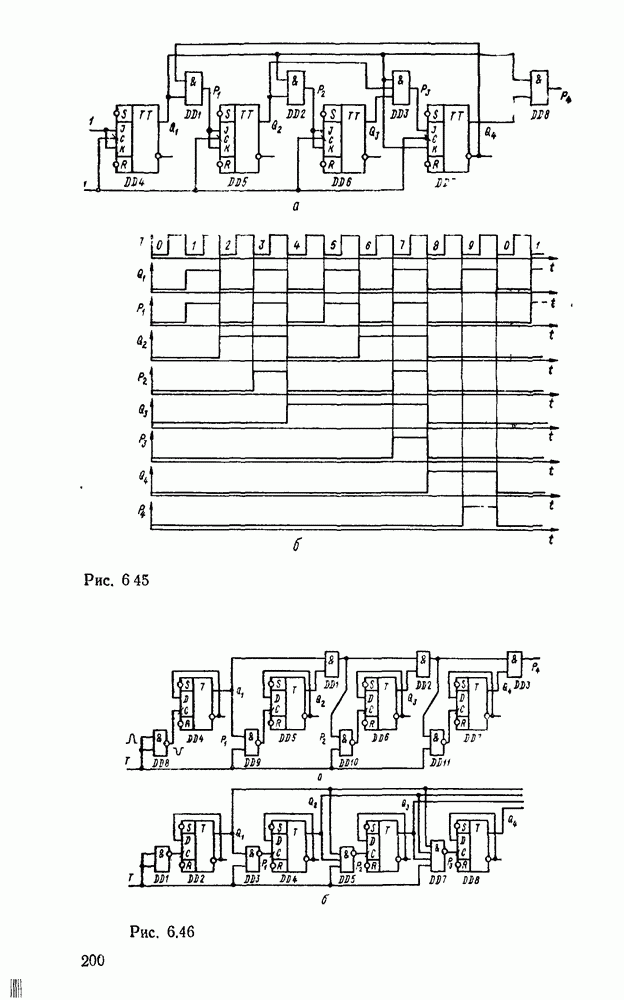
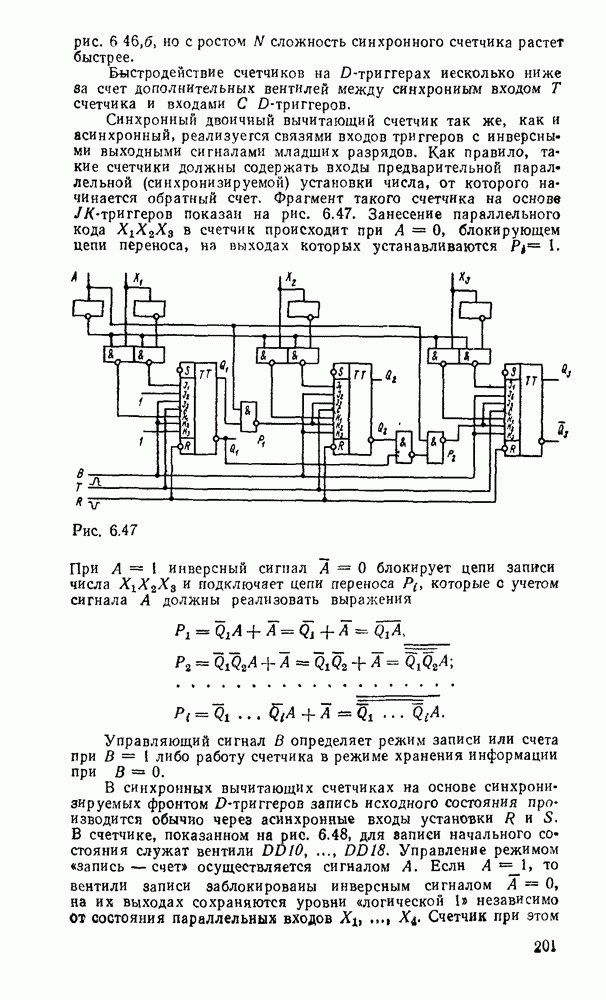
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
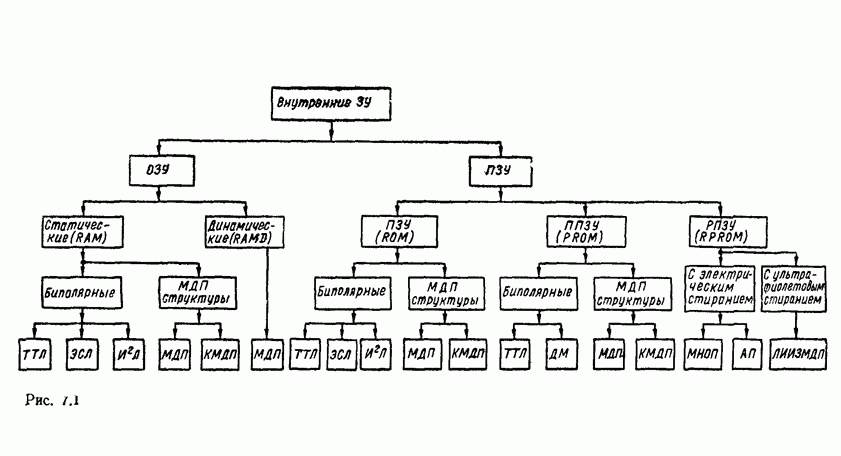
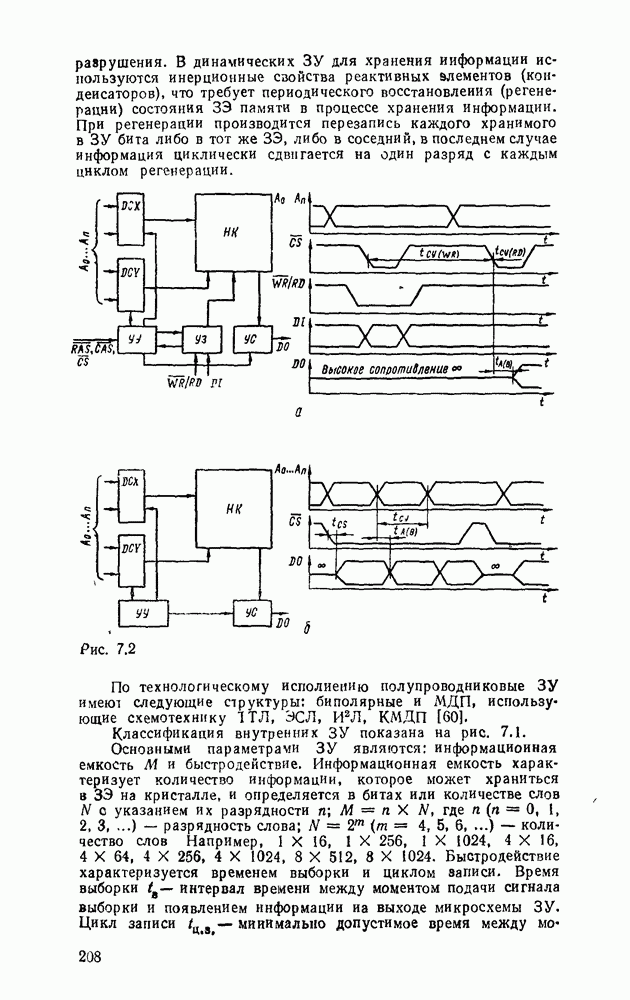
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
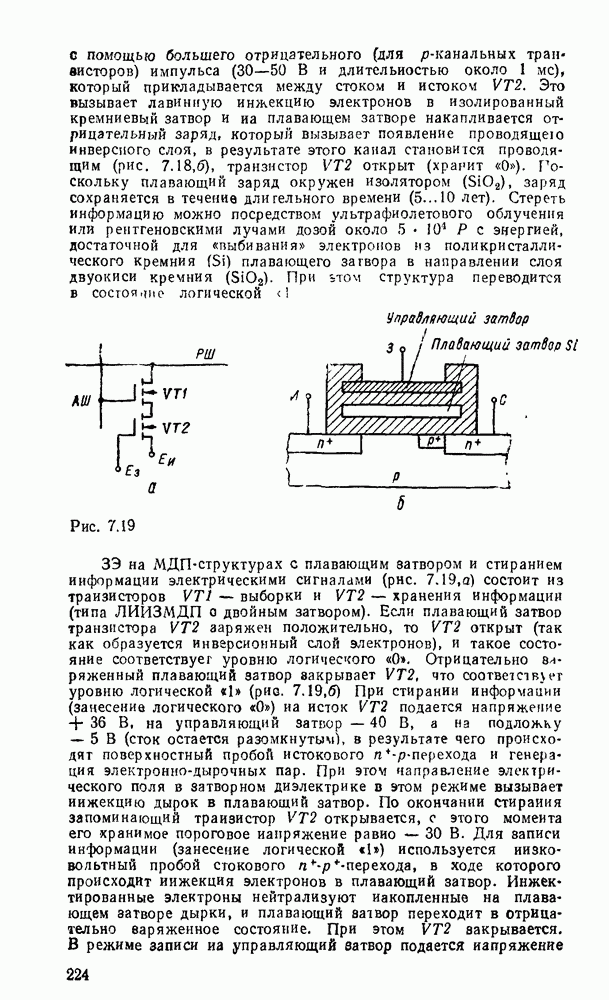
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
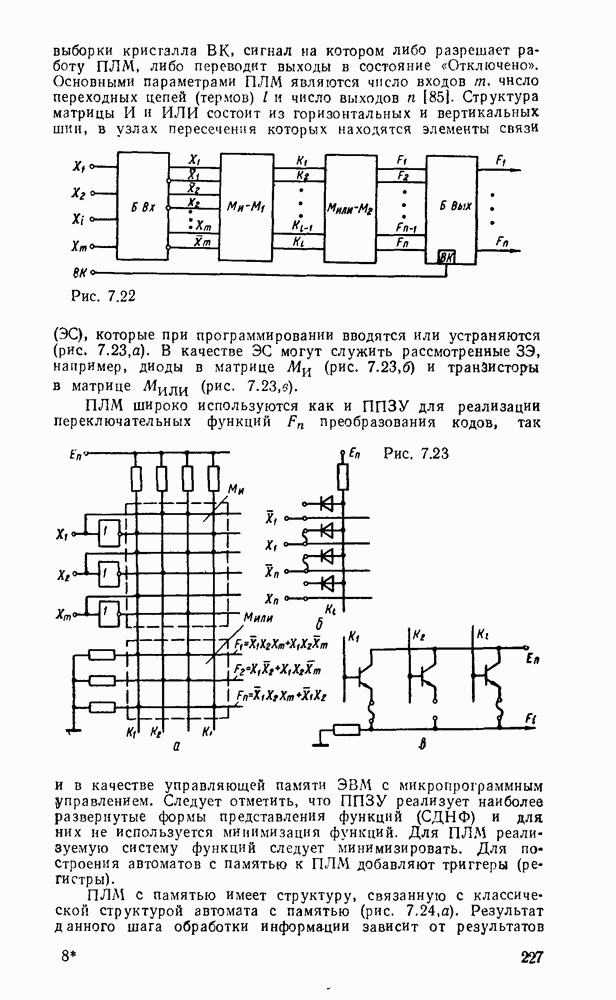
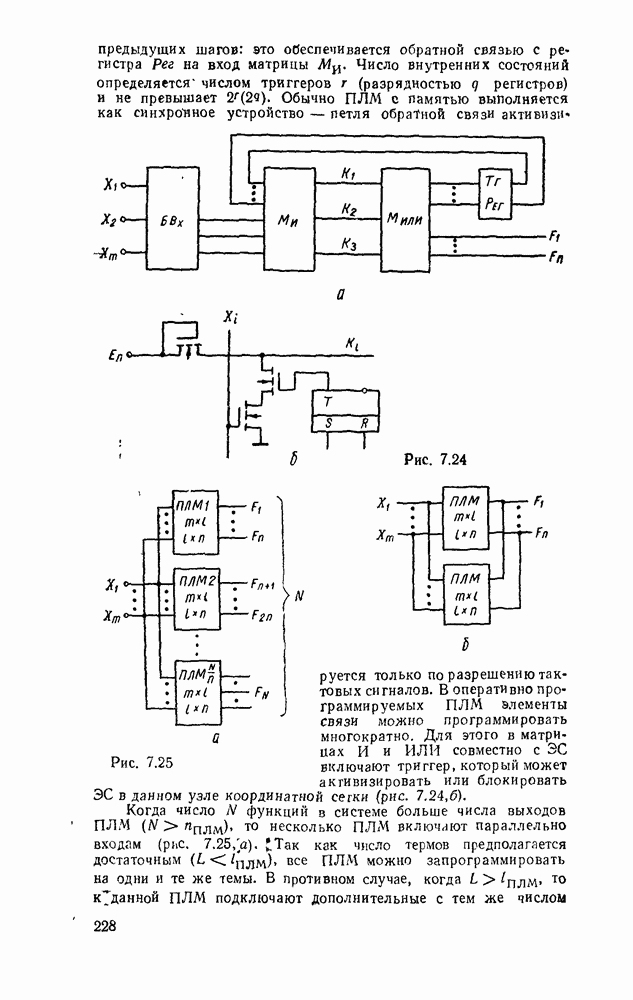
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
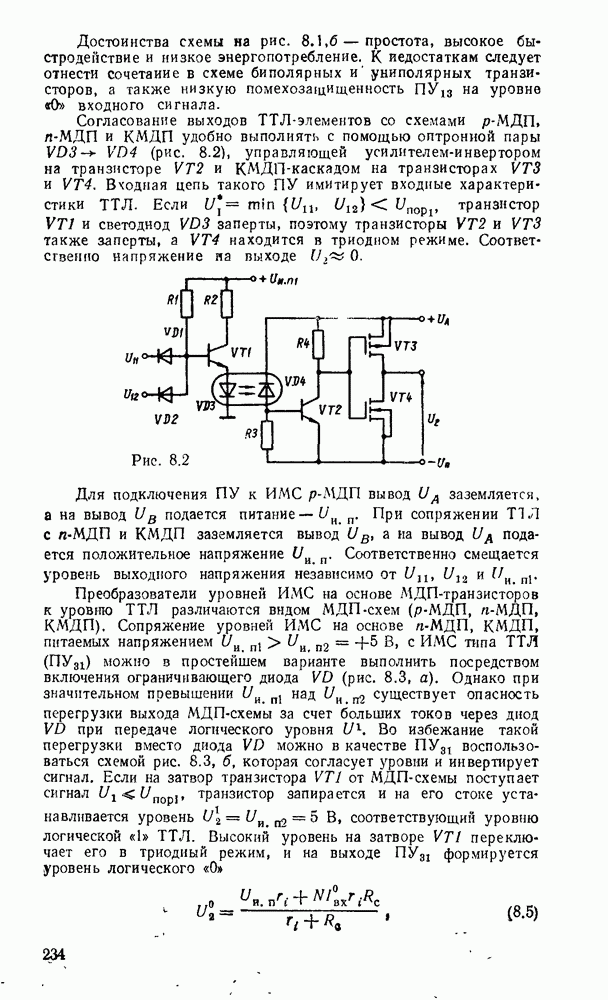
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
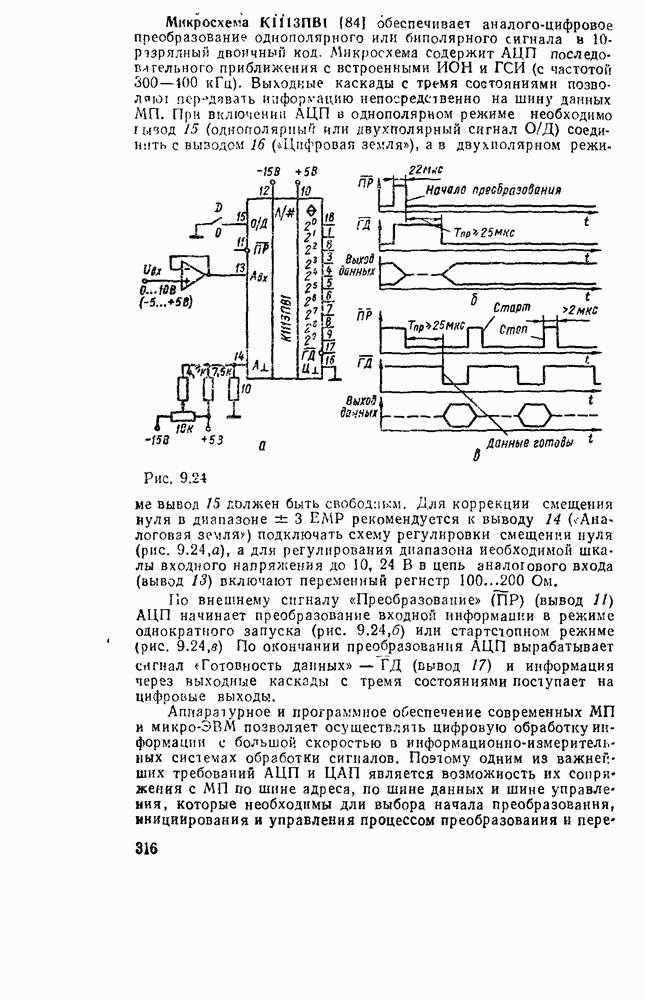
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
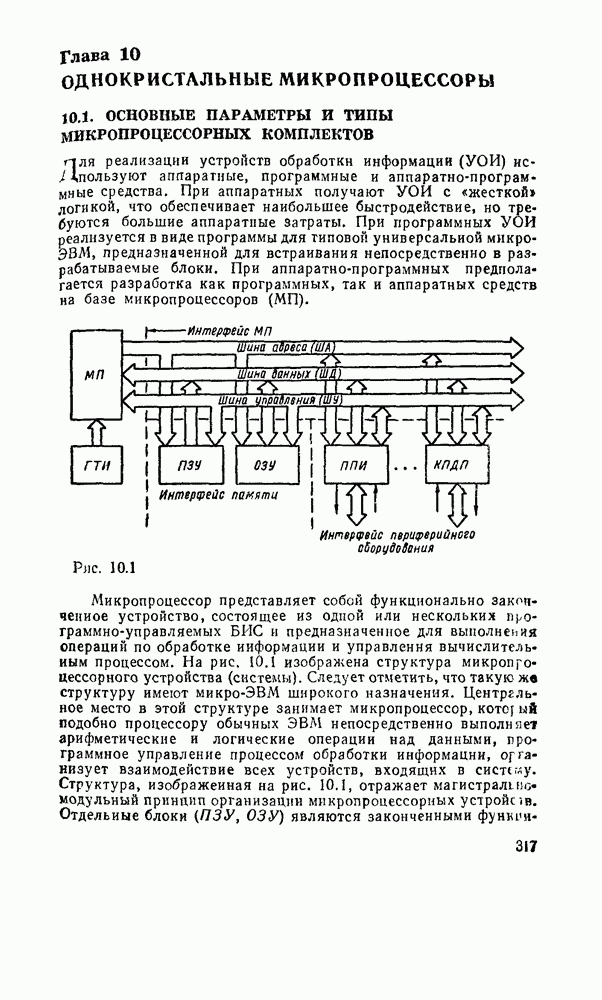
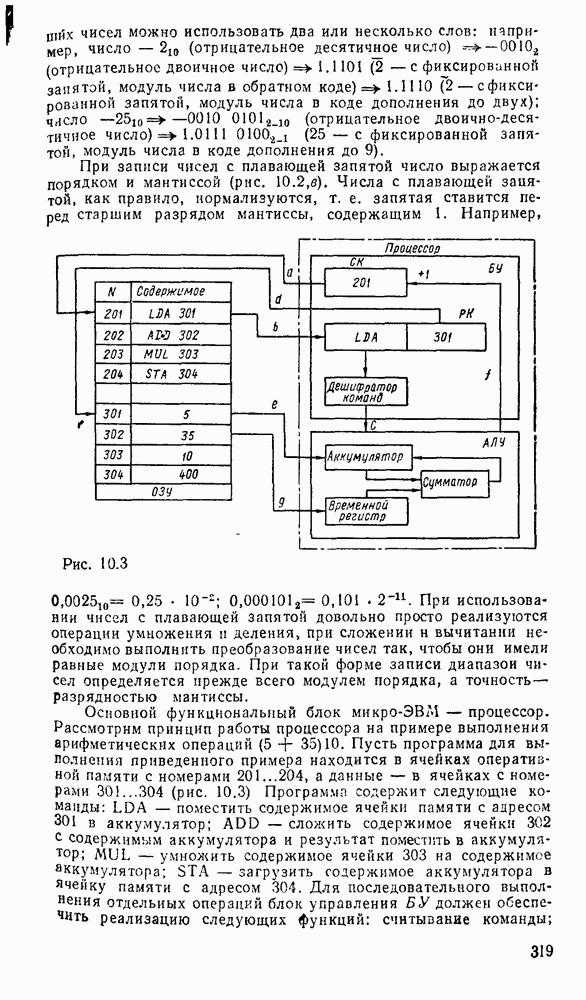
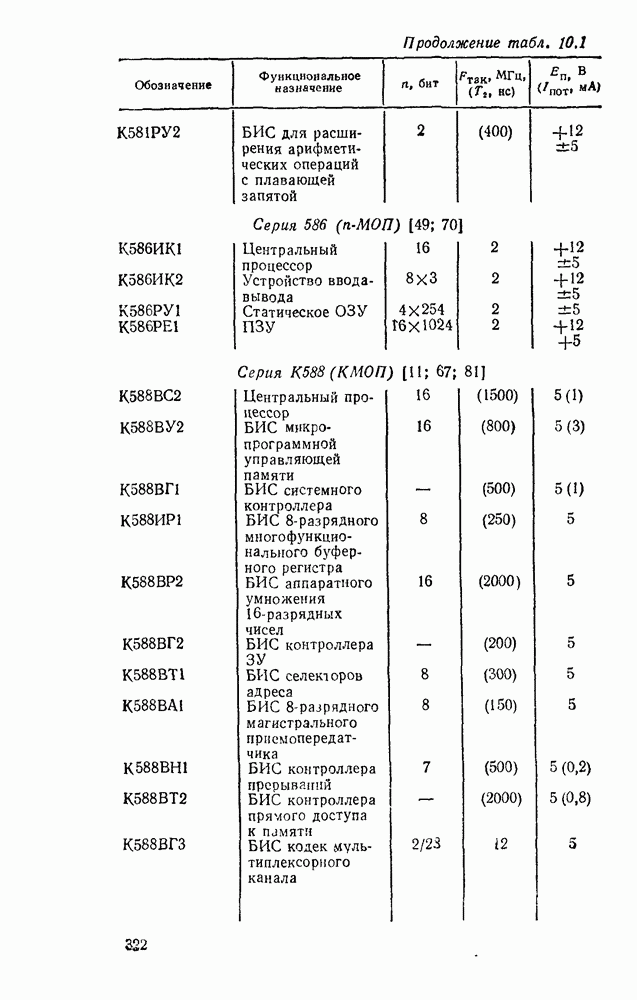
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
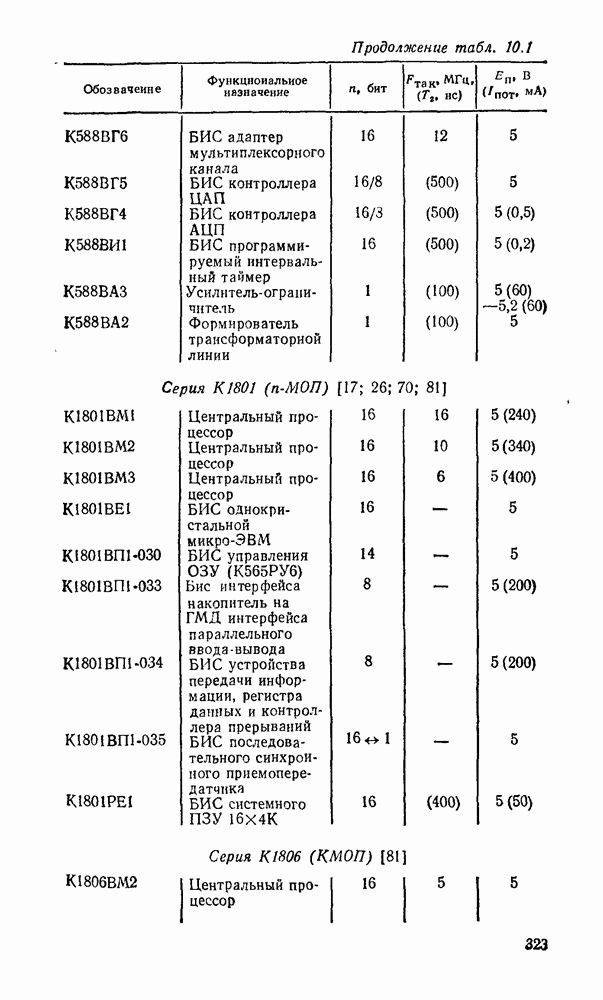
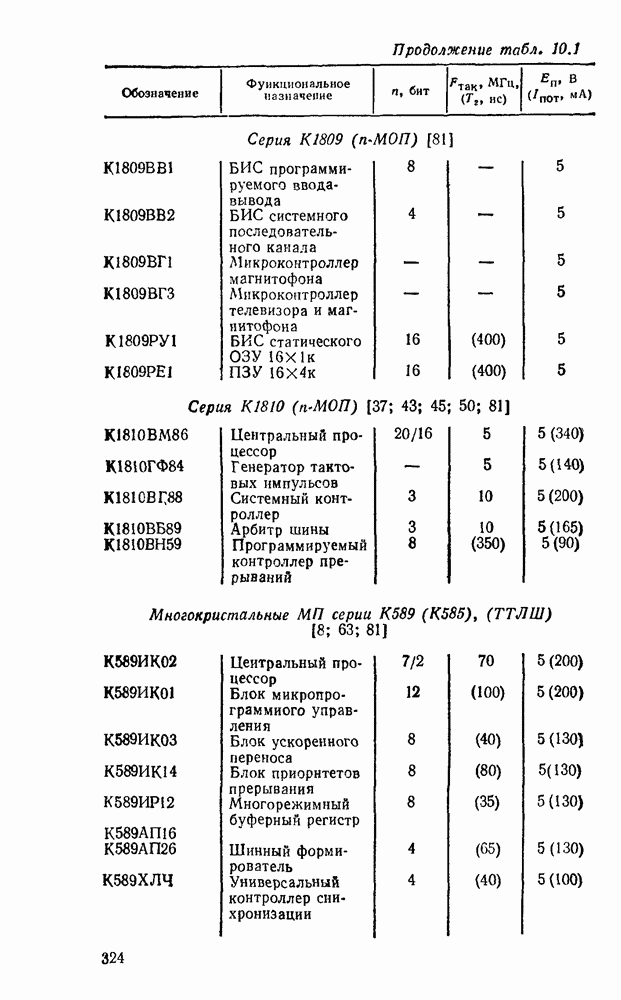
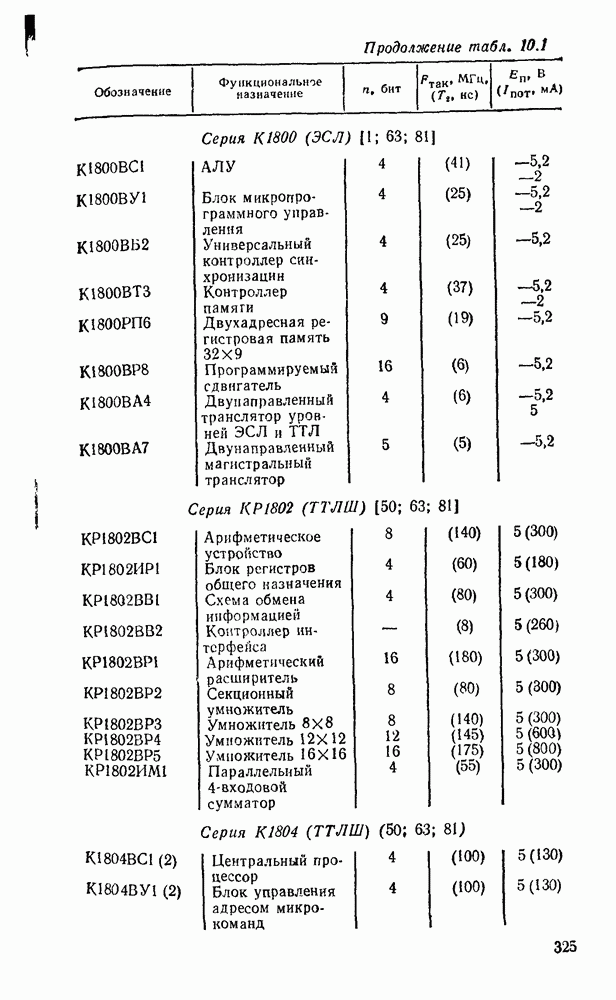
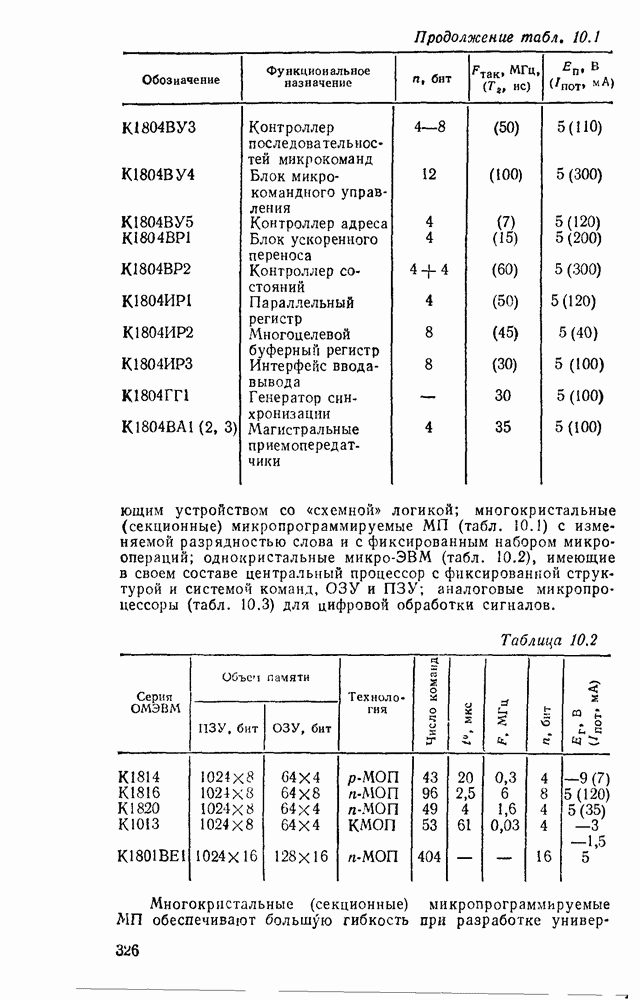
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
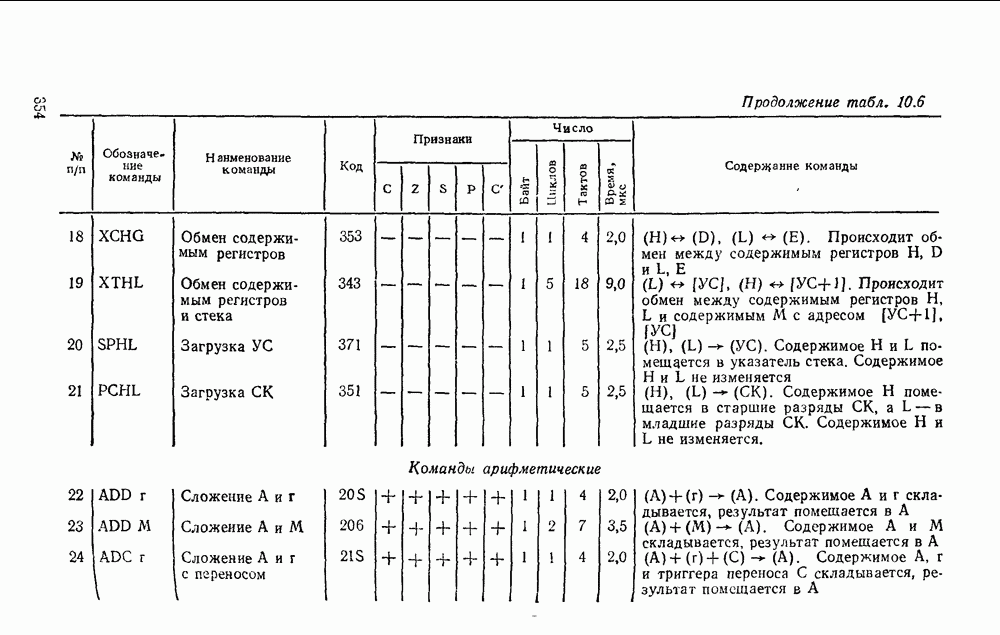
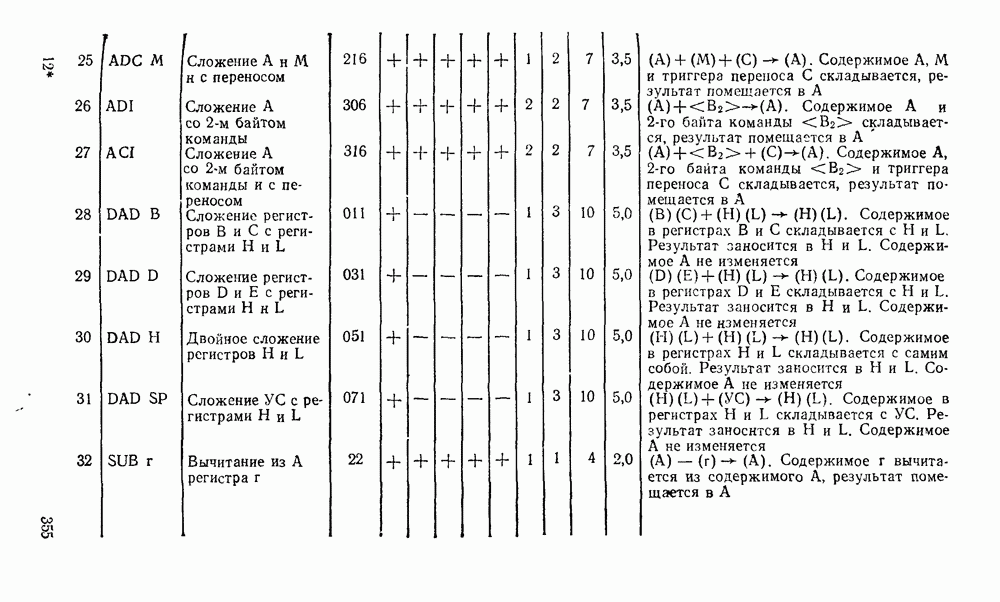
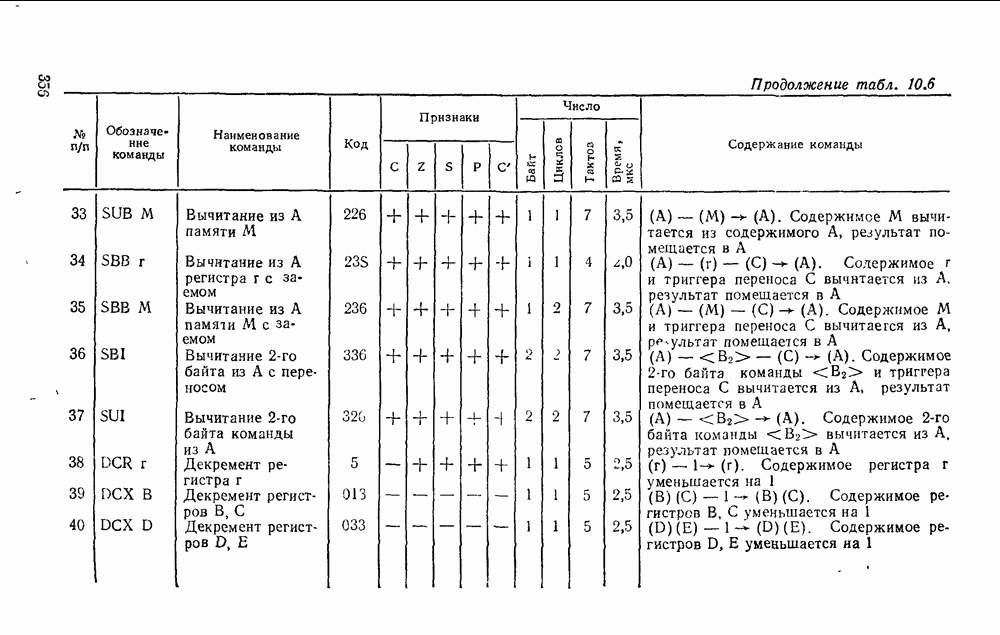
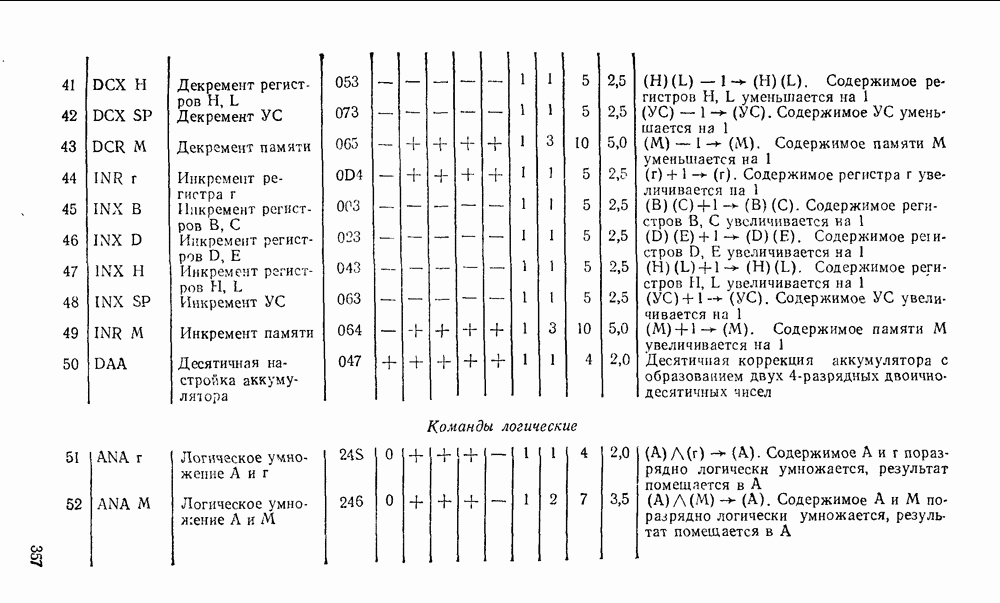
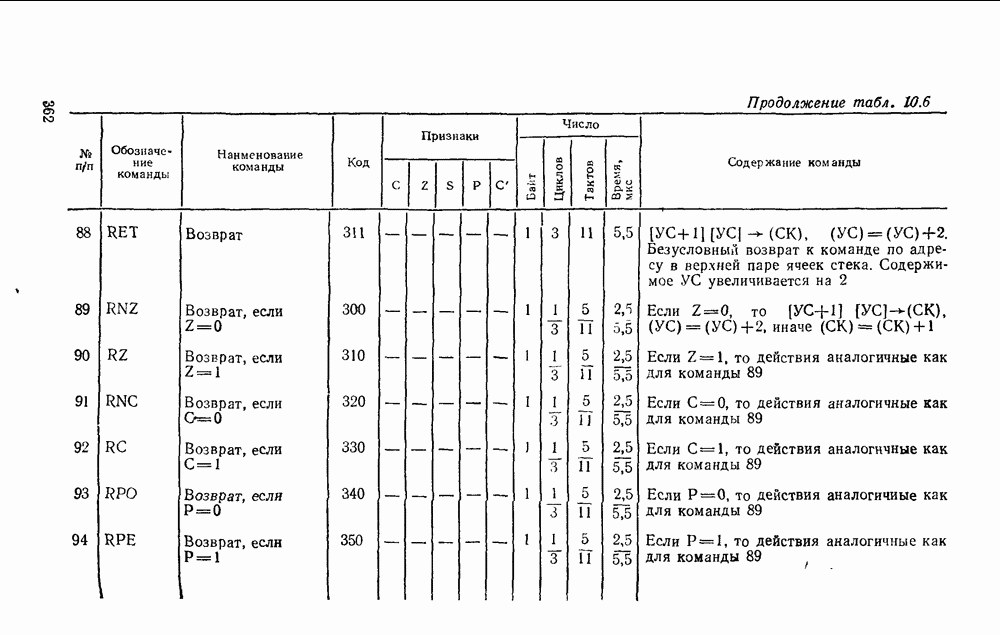
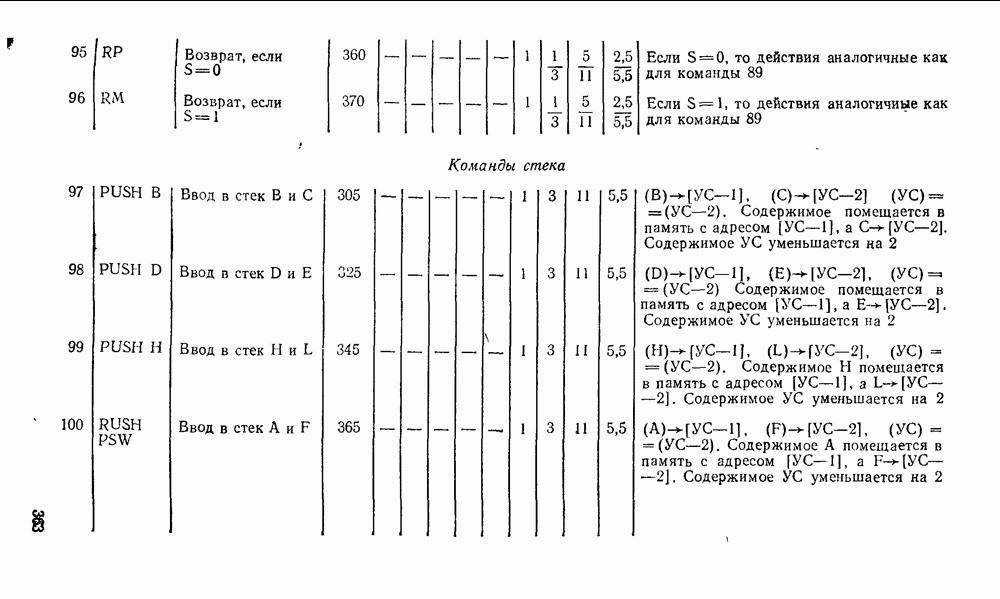
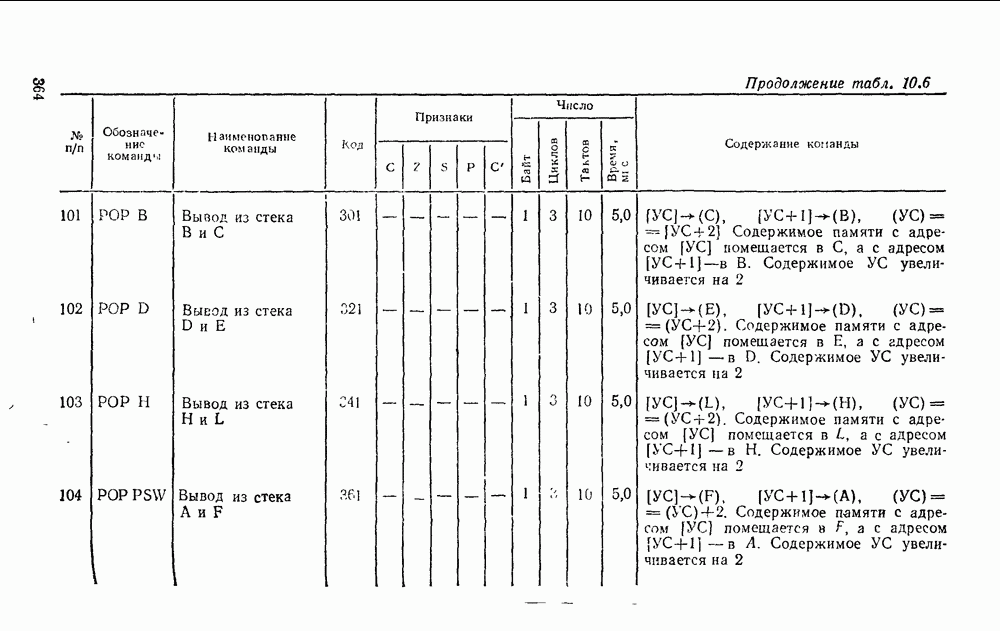
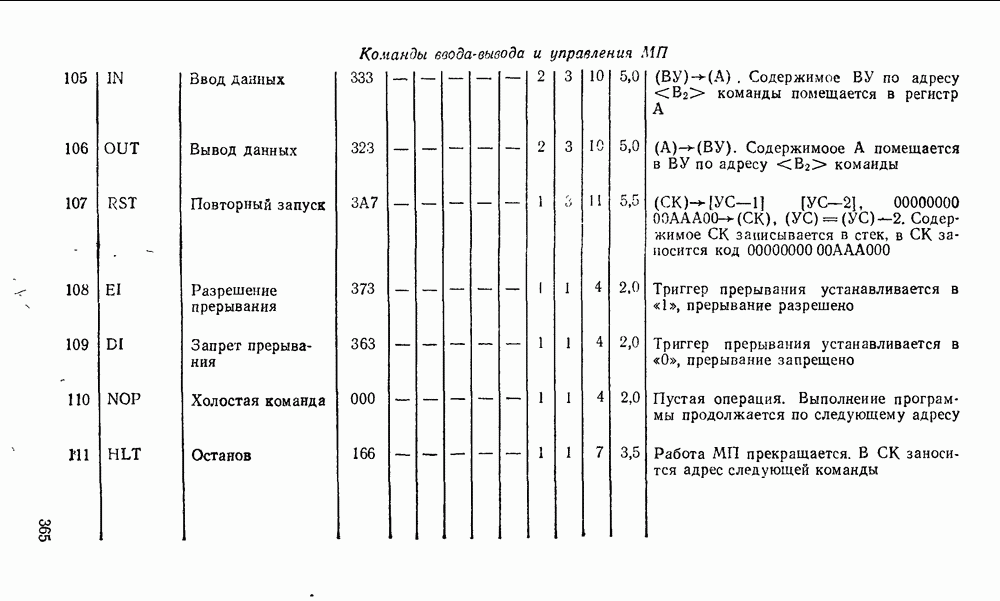
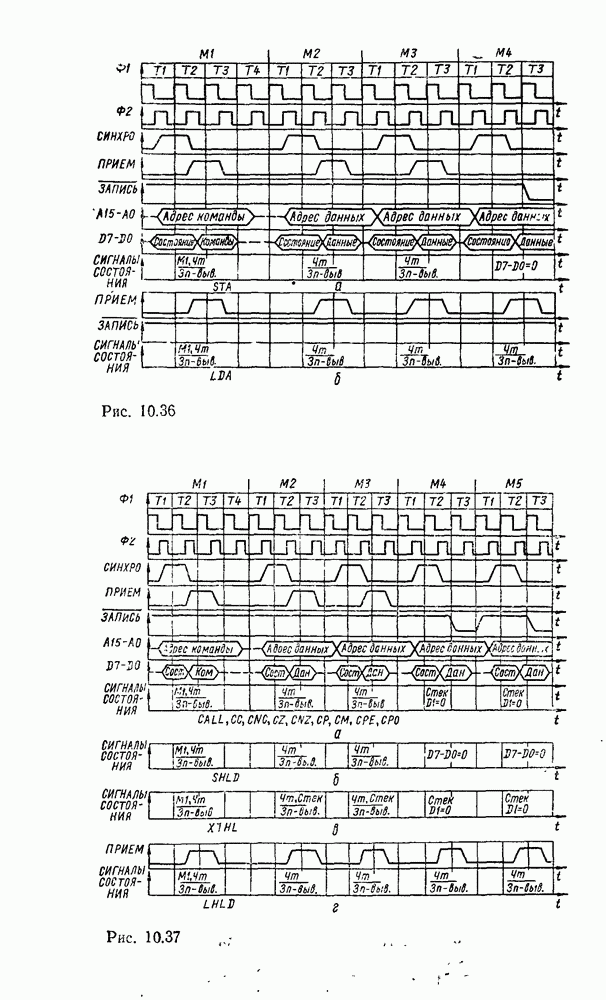
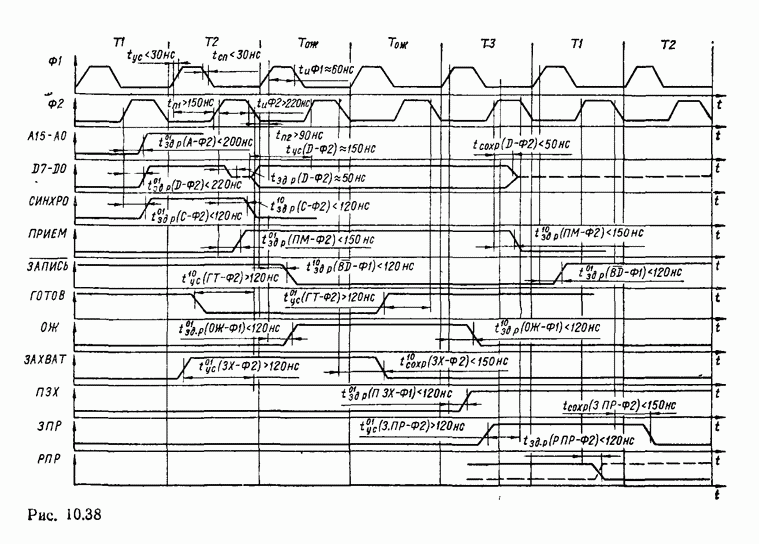
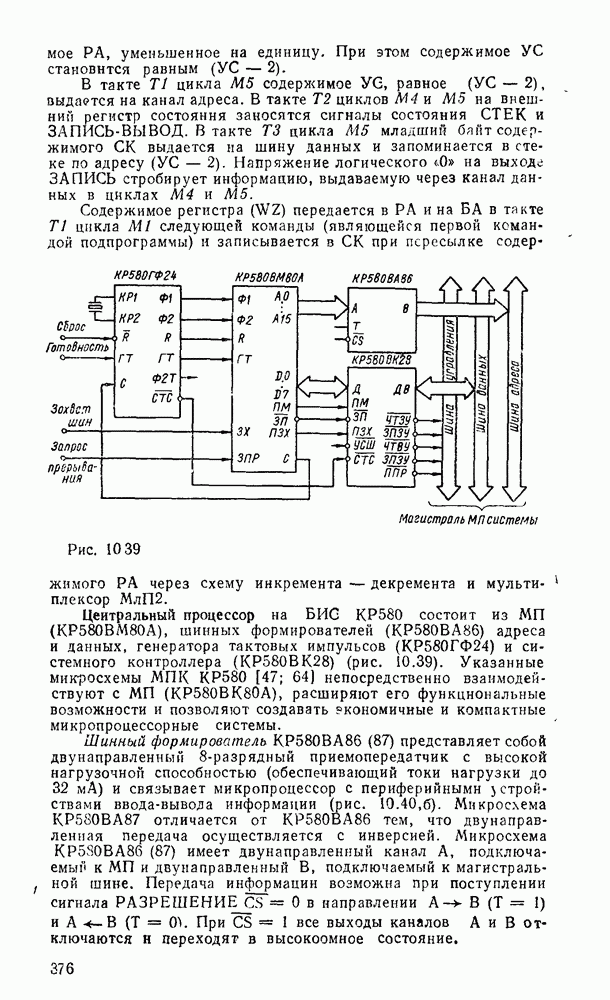
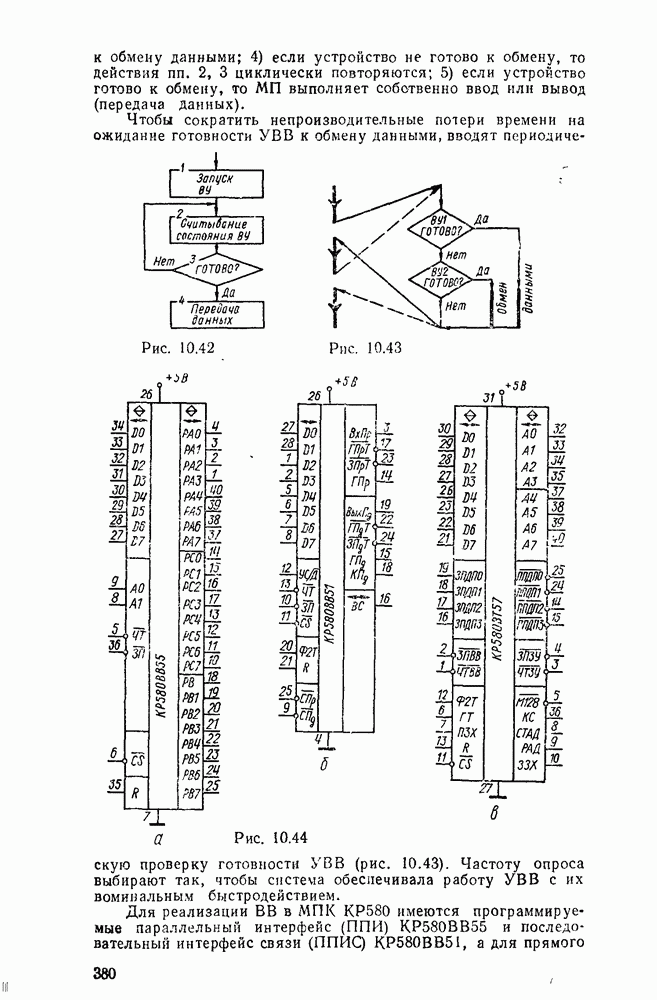
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
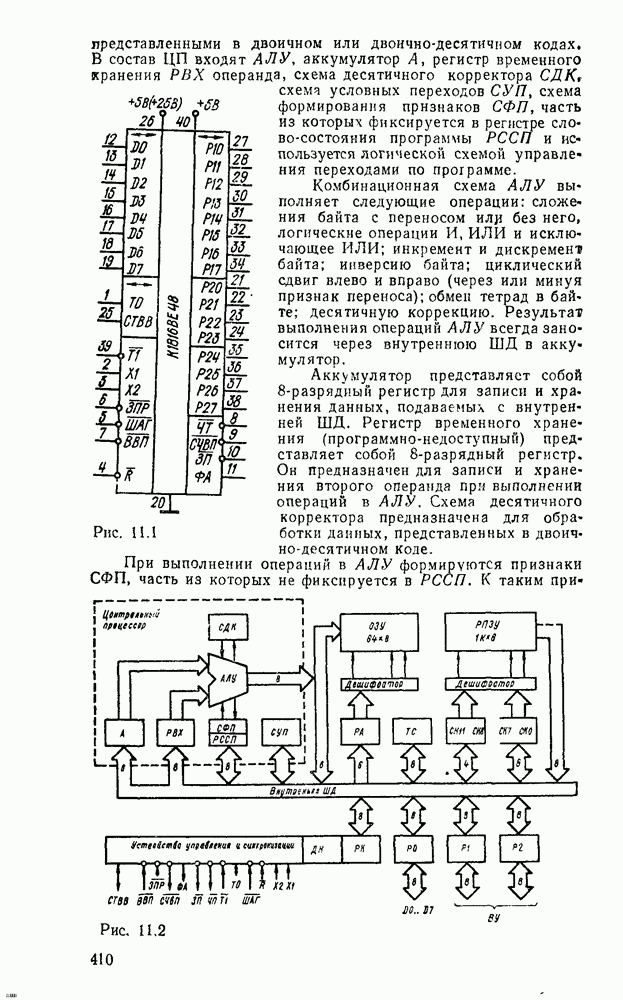
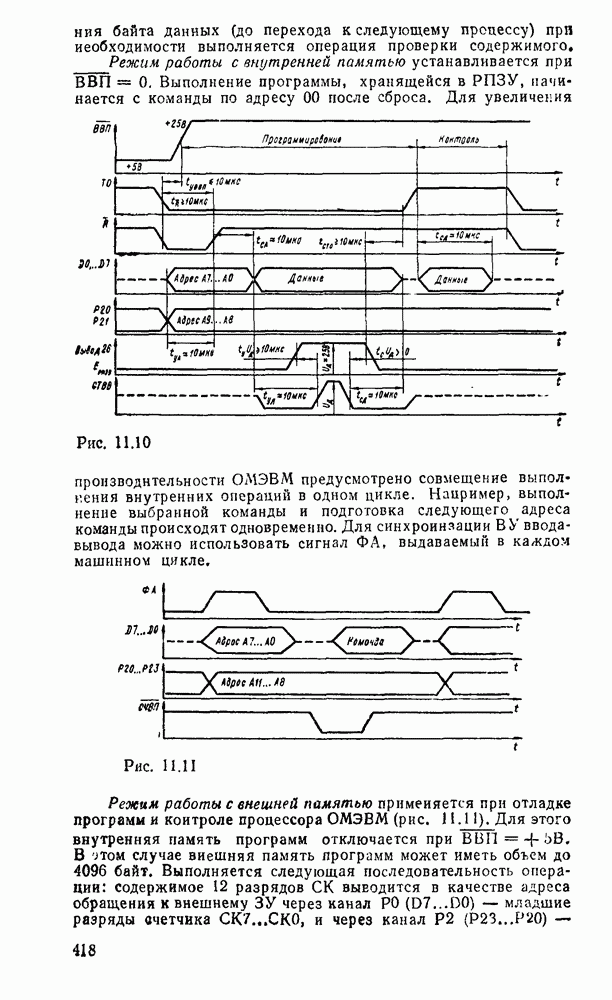
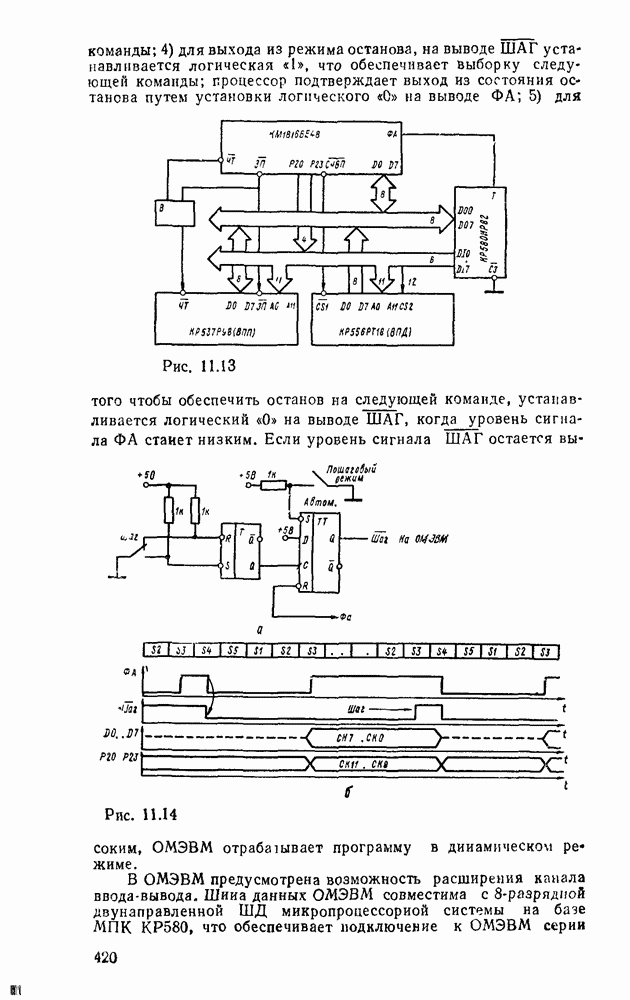
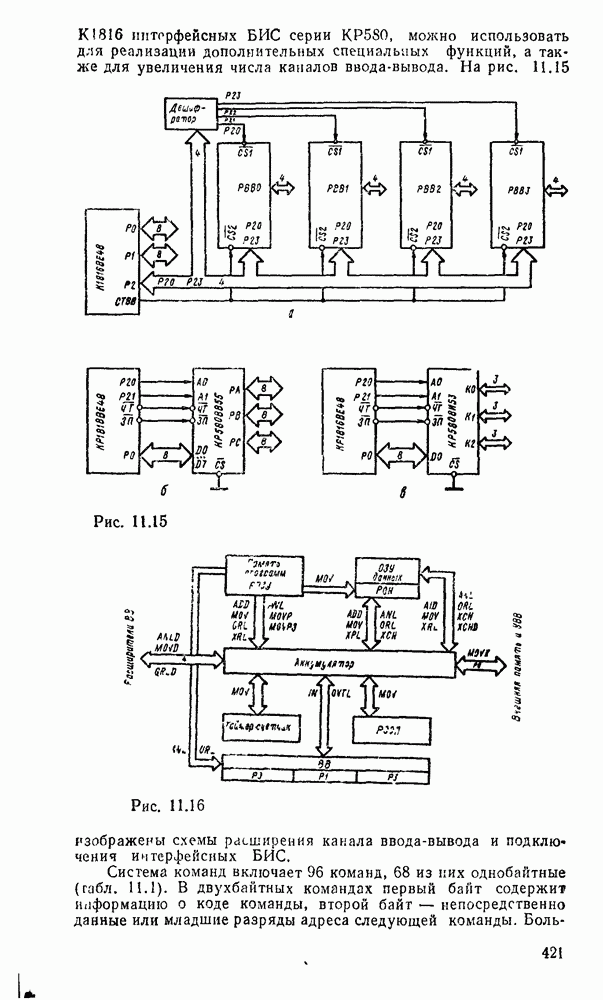
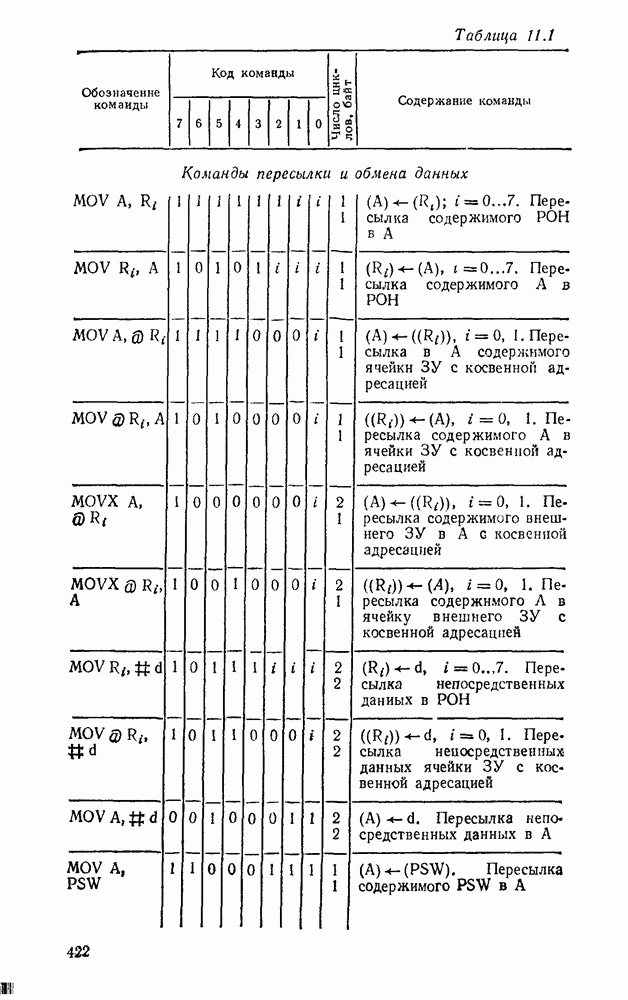
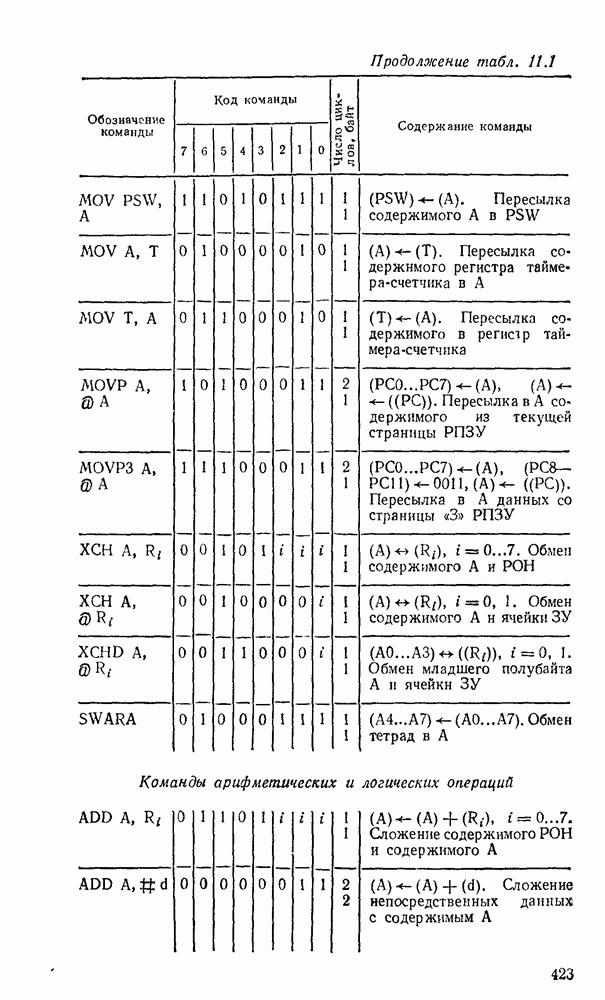
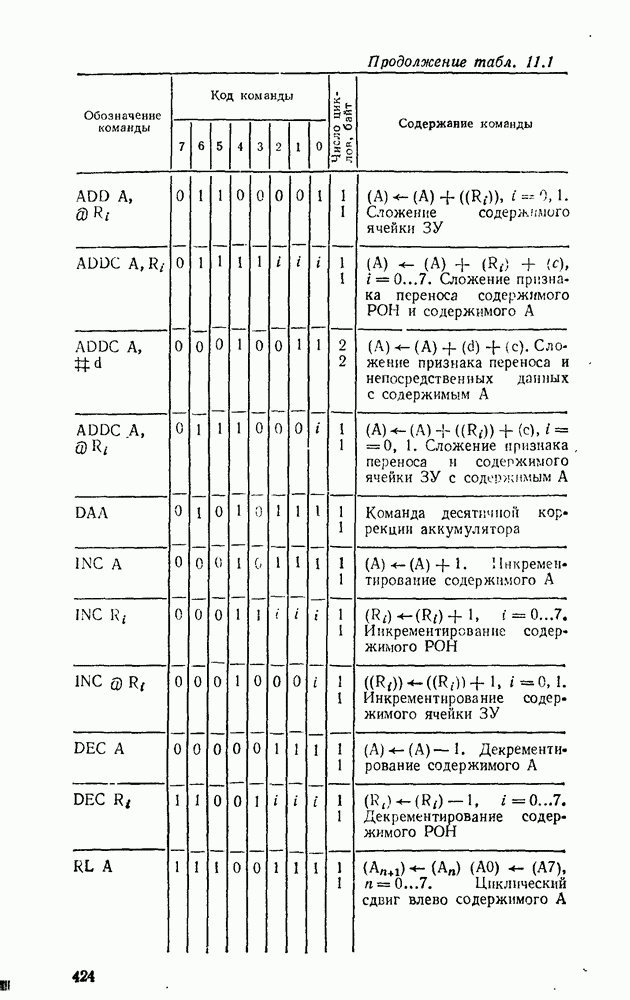
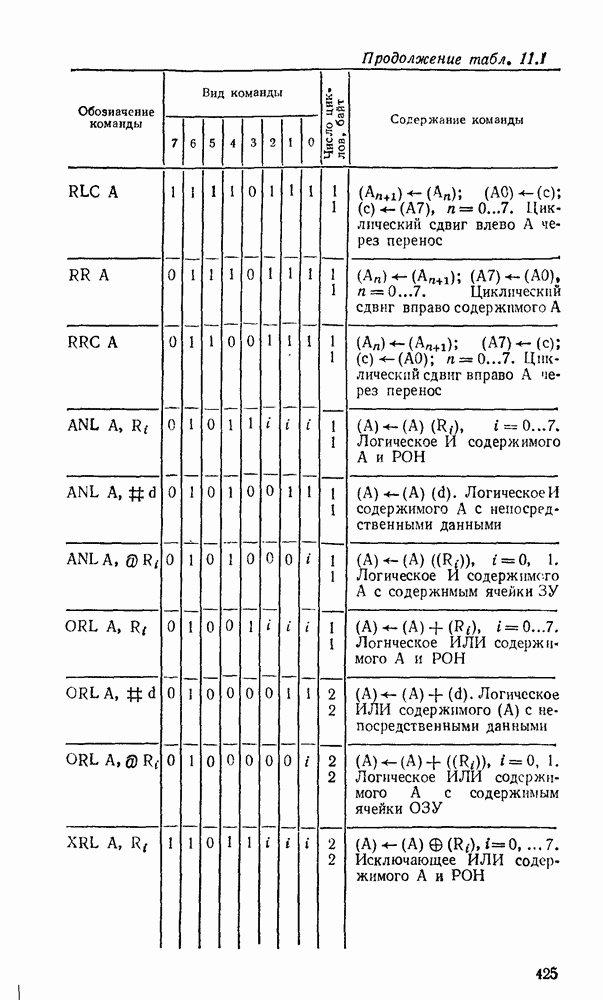
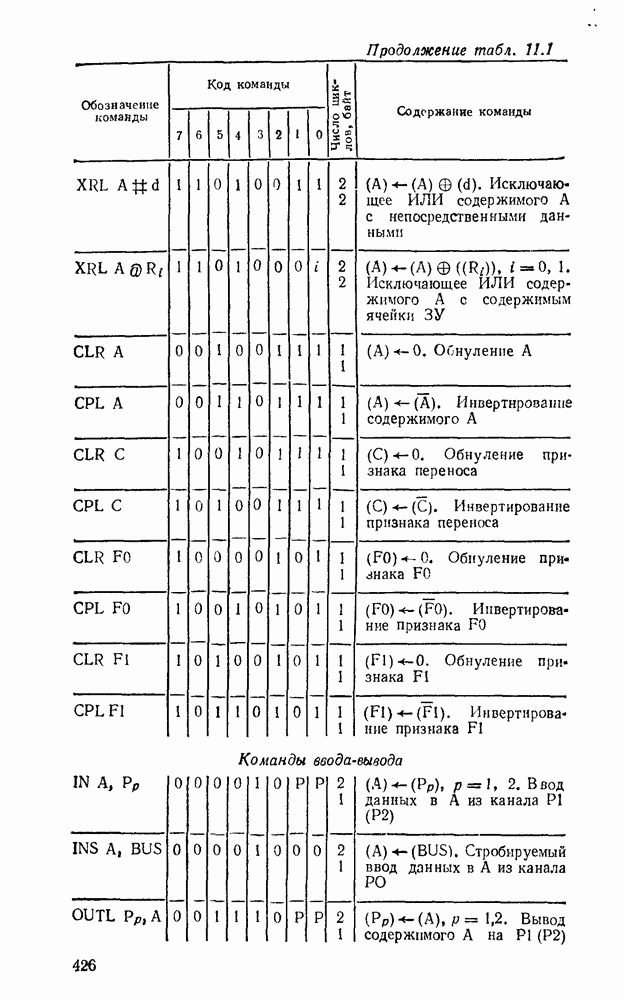
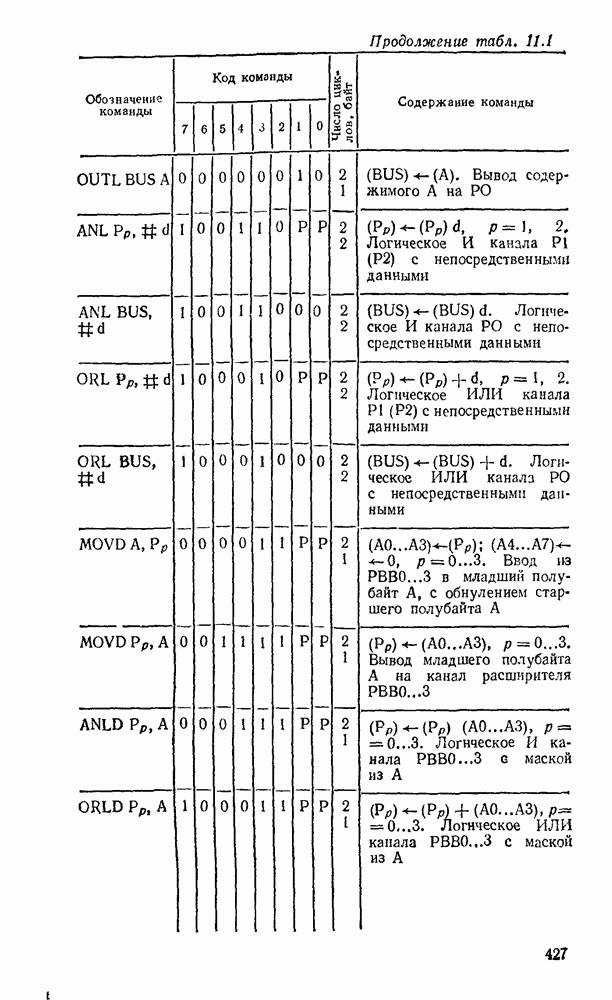
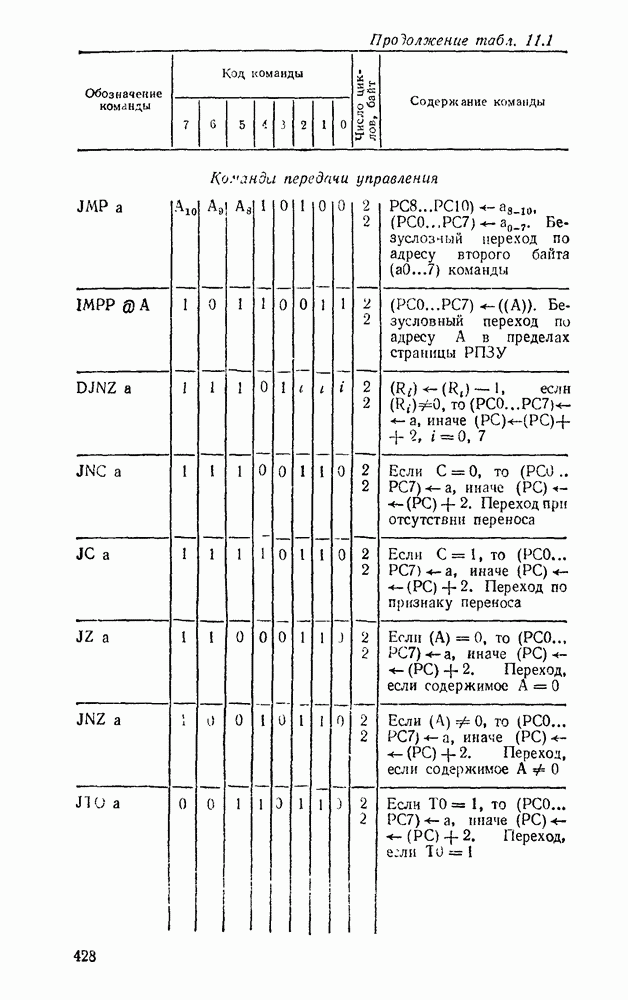
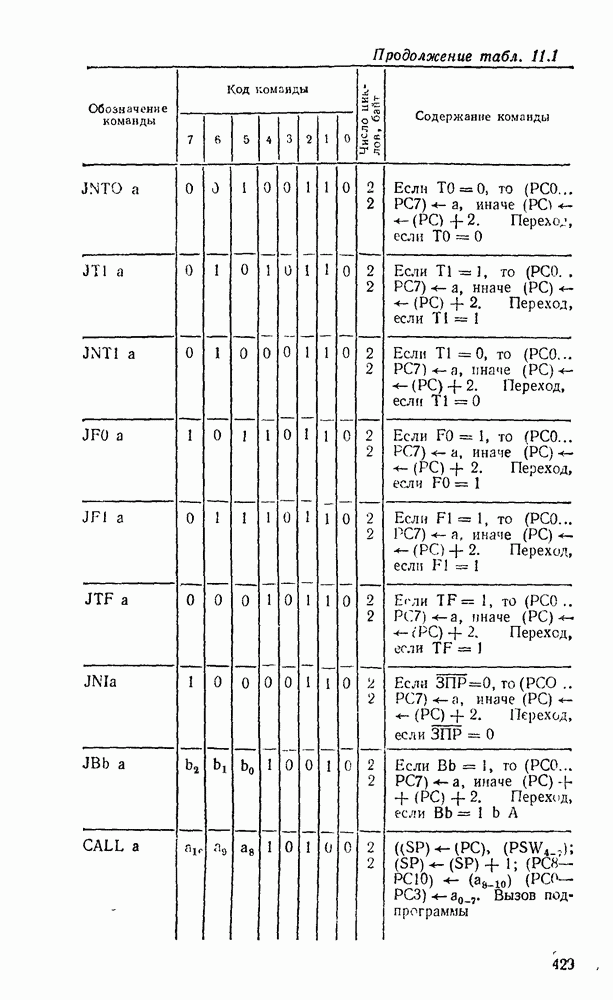
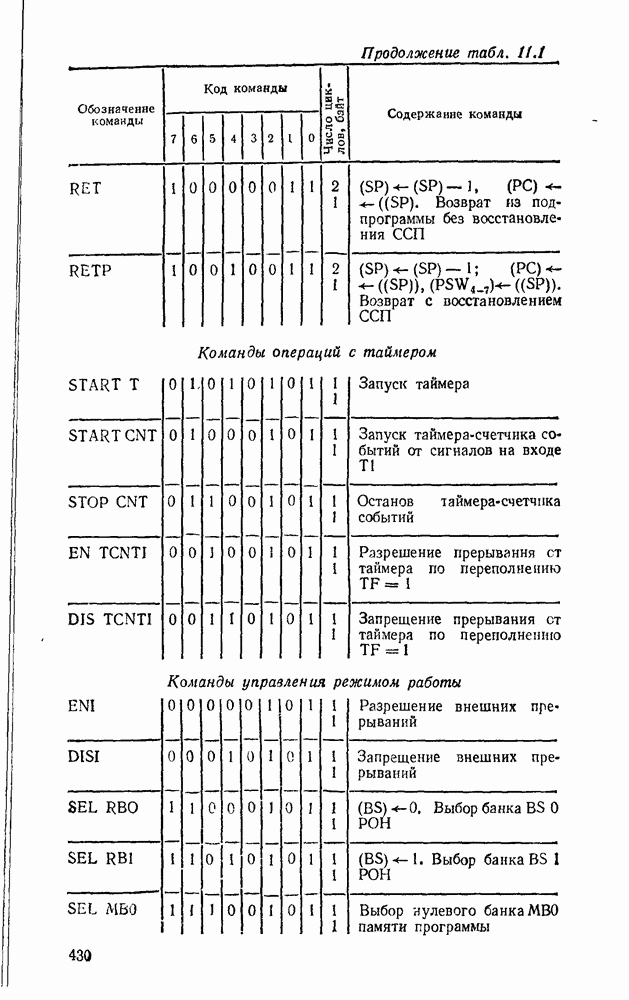
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
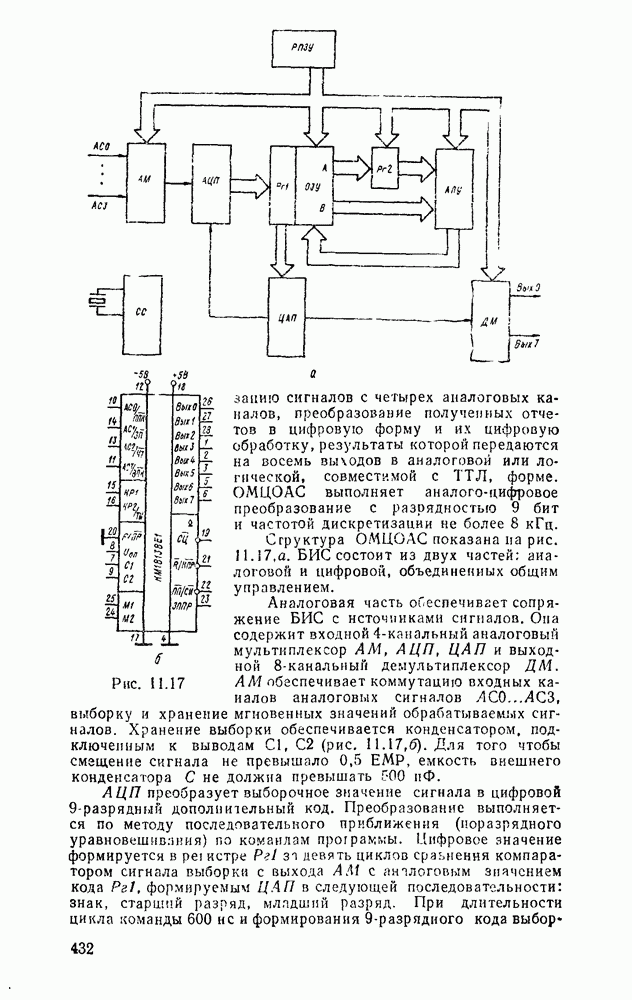
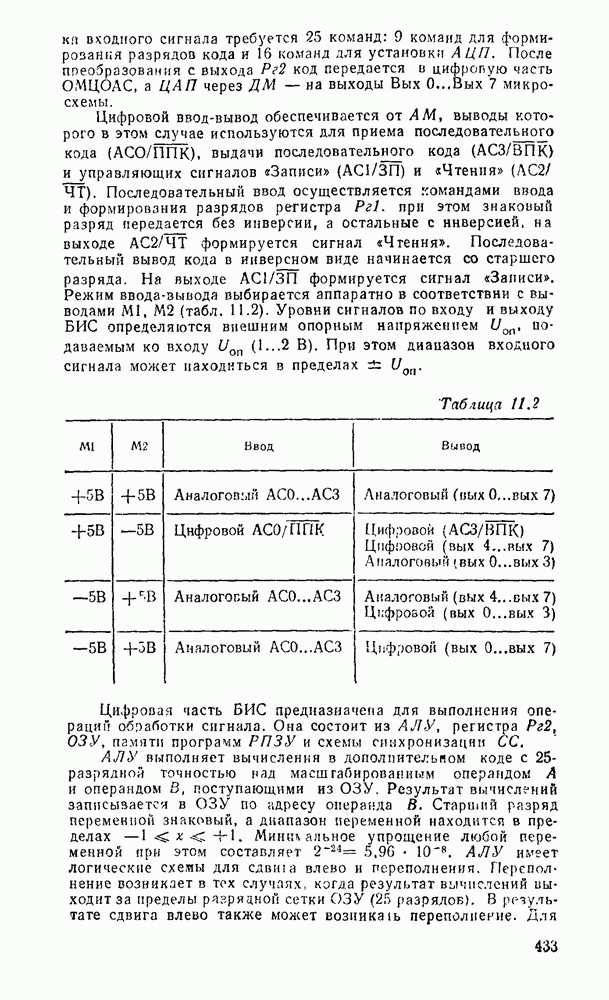
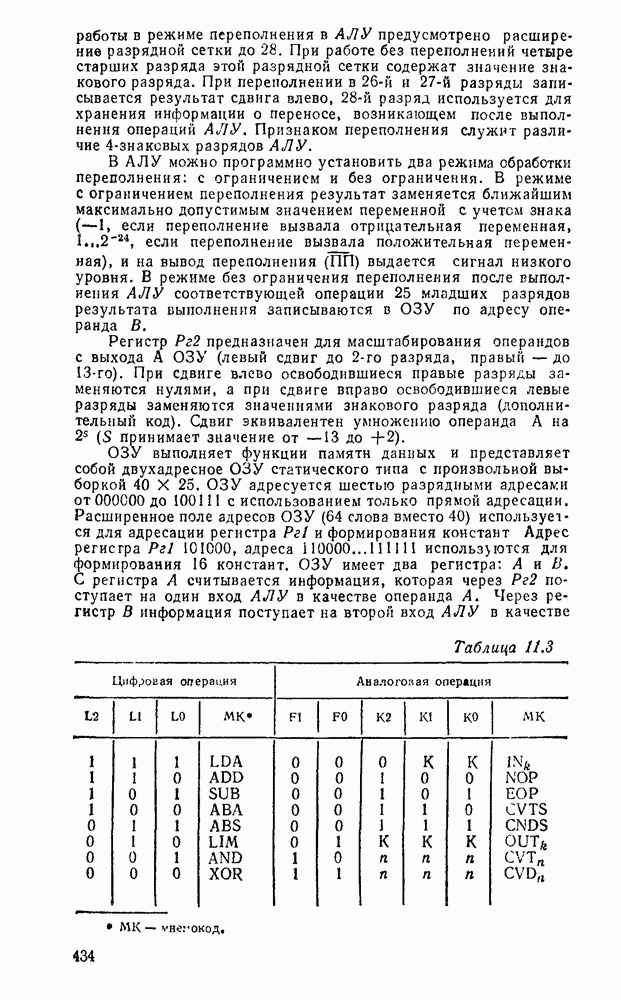
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ