| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5. СТАНДАРТНЫЕ ФОРМЫ
Два способа представления булевой функции — с помощью логической формулы и таблицы соответствия — взаимно связаны между собой в том смысле, что имеется возможность переходить от одного способа к другому. Построение таблицы соответствия по логической формуле рассмотрено ранее. Обратная задача — запись логической формулы по данной таблице соответ» ствия решается на основе стандартных форм.
В совершенной дизъюнктивной нормальной форме, называемой также канонической суммой минтермов или стандартной суммой произведений, каждому набору значений переменных, при котором функция равна единице, соответствует свой минтерм.
Он выражается как логическое произведение всех переменных, причем те переменные, которые в данном наборе имеют значение нуль, входят в произведение с отрицанием, а имеющие значение единица — без отрицания. Дизъюнкция (сумма) минтермов, построенных для всех наборов с единичными значениями функции, и является канонической суммой минтермов, соответствующей заданной таблице истинности.
Другая стандартная форма, дуальная рассмотренной выше, называется совершенной конъюнктивной нормальной формой. В технической литературе ее также называют каноническим произведением макстермов или стандартным произведением  . В этой форме макстермы соответствуют тем наборам значений переменных, на
. В этой форме макстермы соответствуют тем наборам значений переменных, на  равна нулю. Каждый макстерм представляет собой логическую сумму всех переменных, причем те переменные, которые на данном наборе имеют значение единицы, входят в сумму с отрицанием, а имеющие значение нуль — без отрицания. Конъюнкция (произведение) макстермов, построенных для всех наборов с нулевыми значениями функции, и является соответствующим каноническим произведением макстермов.
равна нулю. Каждый макстерм представляет собой логическую сумму всех переменных, причем те переменные, которые на данном наборе имеют значение единицы, входят в сумму с отрицанием, а имеющие значение нуль — без отрицания. Конъюнкция (произведение) макстермов, построенных для всех наборов с нулевыми значениями функции, и является соответствующим каноническим произведением макстермов.
Следующий пример иллюстрирует запись стандартных форм по заданной таблице соответствия


Если булева функция задана логической формулой, то ее можно привести к стандартной форме последовательностью эквивалентных преобразований, основанных на свойствах булевой алгебры. Сначала с помощью теорем  Моргана исходное выражение приводится к такому виду, чтобы знаки отрицания относились только к отдельным переменным. Затем на основе свойств дистрибутивности осуществляется преобразование к одной из форм — сумме произведений или произведению сумм. На
Моргана исходное выражение приводится к такому виду, чтобы знаки отрицания относились только к отдельным переменным. Затем на основе свойств дистрибутивности осуществляется преобразование к одной из форм — сумме произведений или произведению сумм. На  этапе используются свойства
этапе используются свойства  для введения недостающих переменных в минтермы и макстермы, а также свойства идемпотентности
для введения недостающих переменных в минтермы и макстермы, а также свойства идемпотентности  для исключения повторяющихся слагаемых и сомножителей. Например,
для исключения повторяющихся слагаемых и сомножителей. Например,  предварительно преобразуется к виду
предварительно преобразуется к виду  , после чего имеем:
, после чего имеем:  (каноническая сумма минтермов) или
(каноническая сумма минтермов) или  (каноническое произведение макстермов).
(каноническое произведение макстермов).
Соответствующая таблица истинности имеет вид

В качестве стандартных рассматриваются также нормальные формы, минтермы (или макстермы) которых в отличие от совершенных нормальных (канонических) форм не обязательно должны содержать все переменные данной функции. В зависимости от числа k входящих в них переменных они называются минтермами (или макстермами)  ранга. Данная функция представляется единственной канонической формой, но соответствующих ей эквивалентных нормальных форм может быть различное количество. Поиск среди них минимальных форм является одной из главных задач синтеза логических схем.
ранга. Данная функция представляется единственной канонической формой, но соответствующих ей эквивалентных нормальных форм может быть различное количество. Поиск среди них минимальных форм является одной из главных задач синтеза логических схем.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
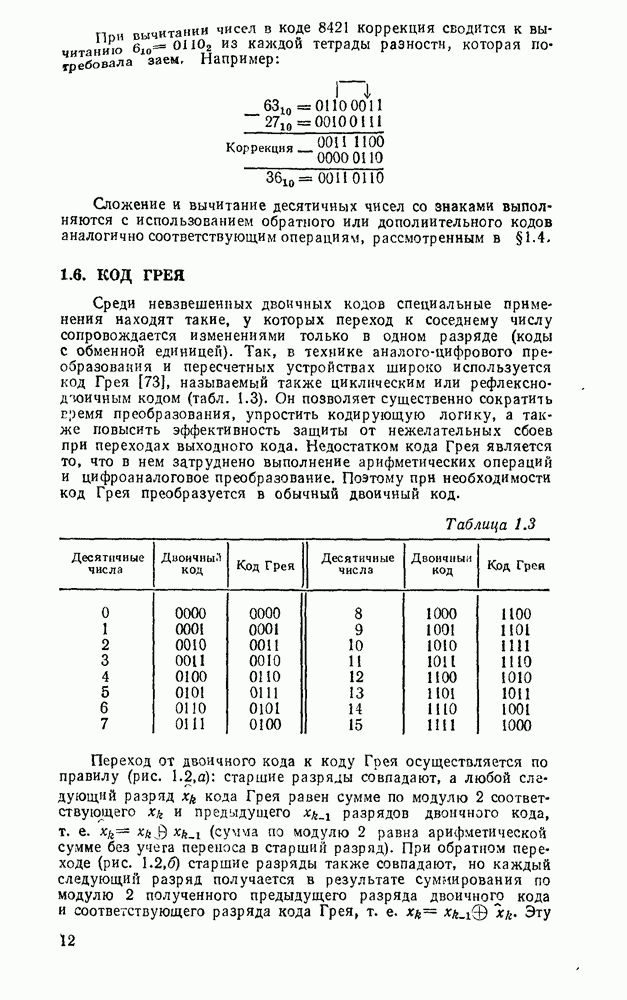
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
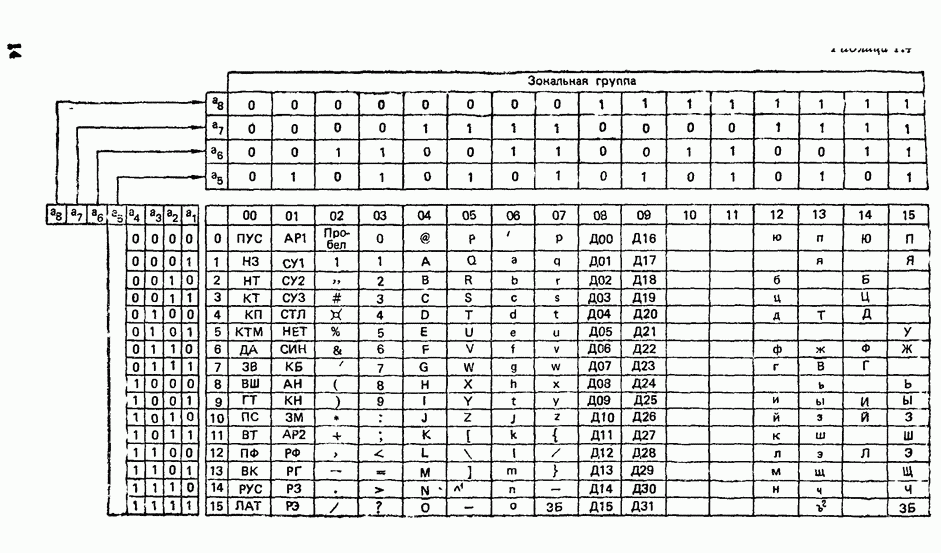
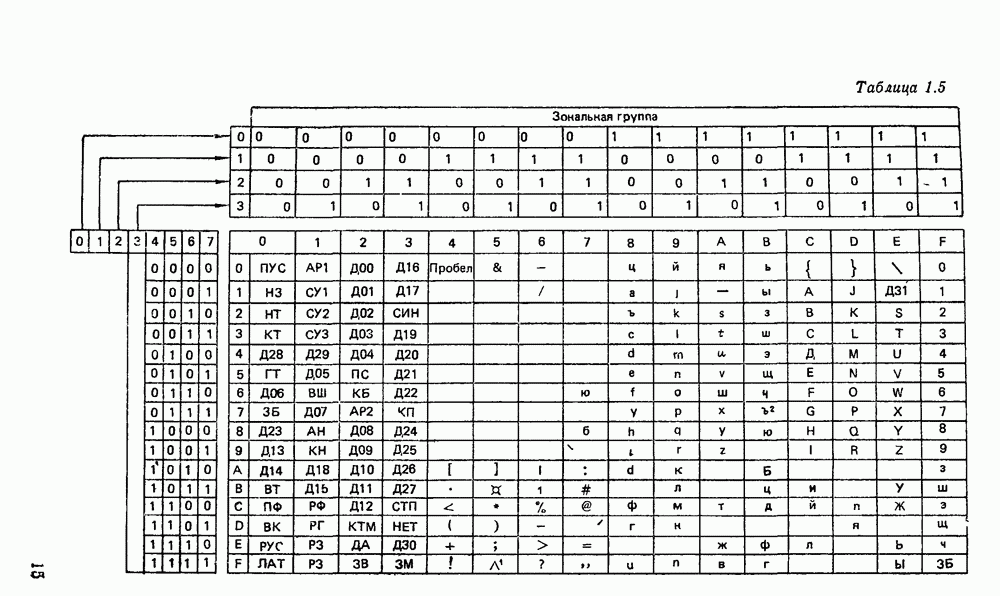
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
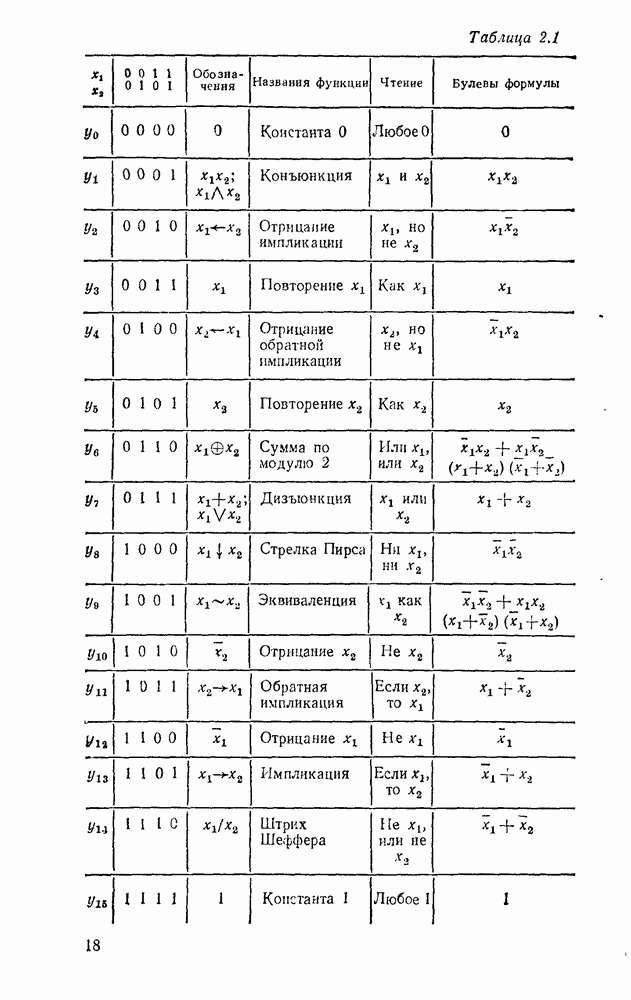
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
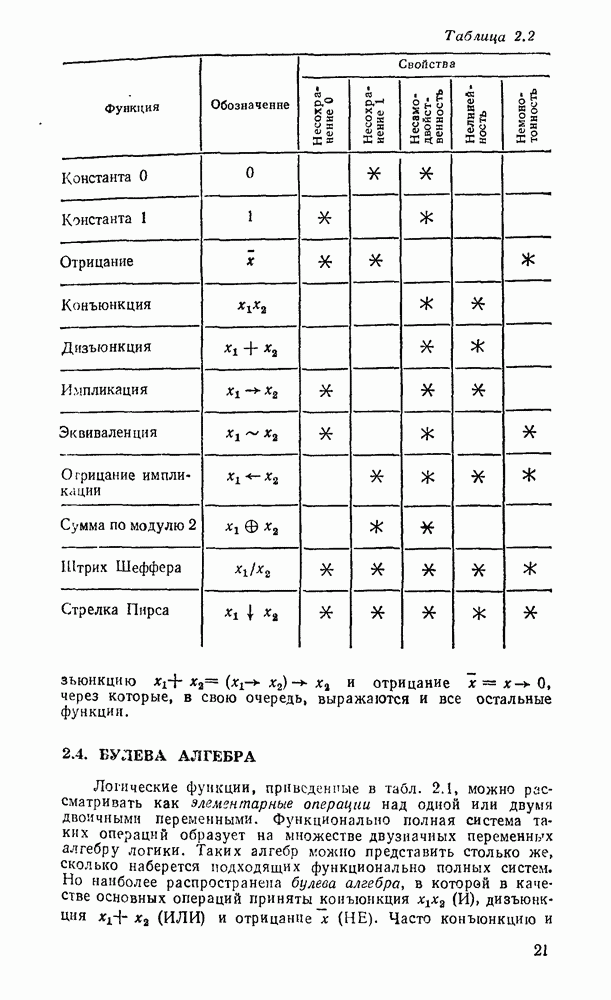
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
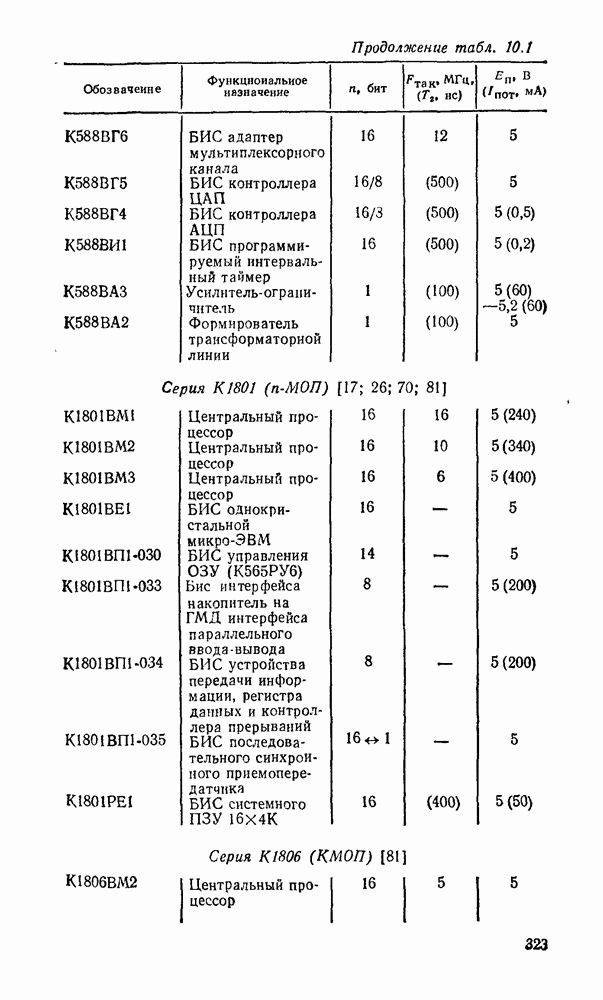
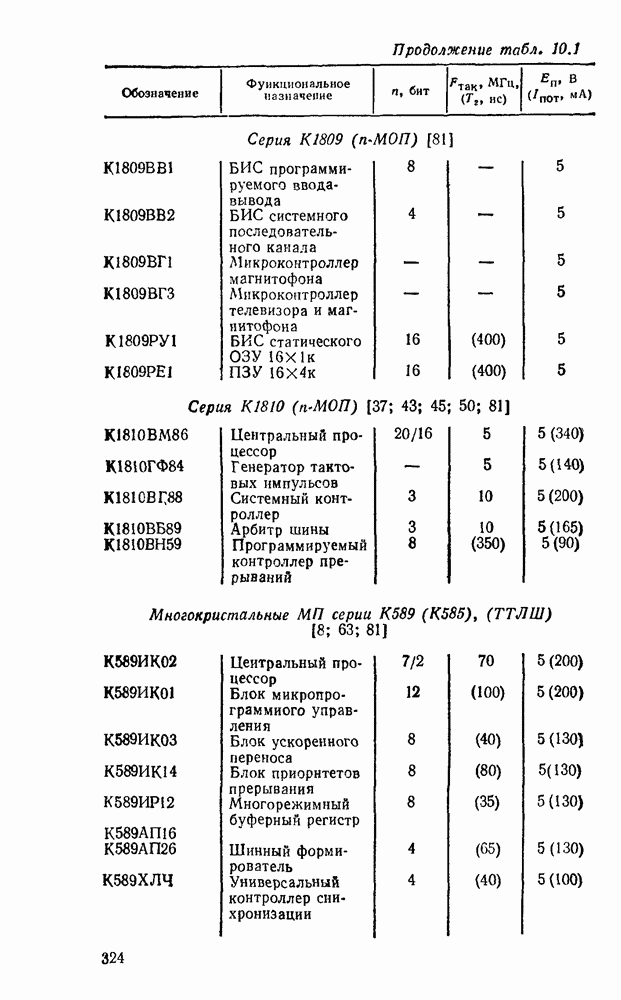
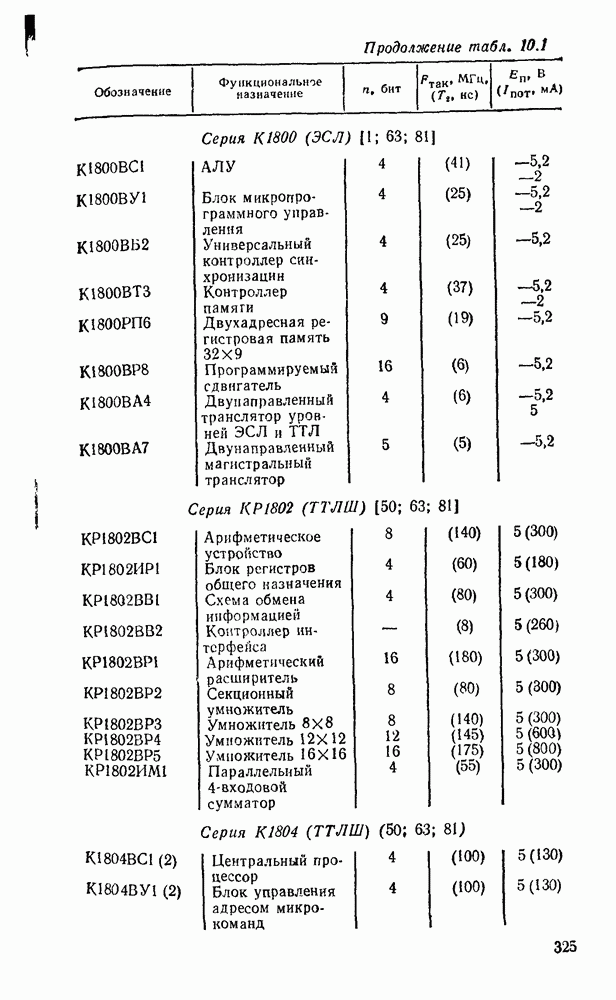
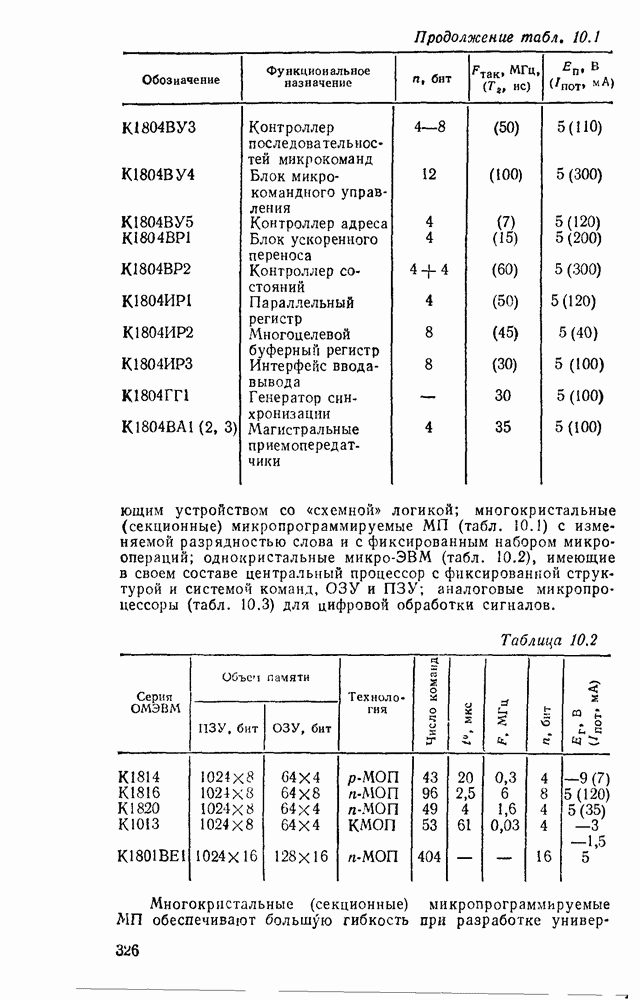
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
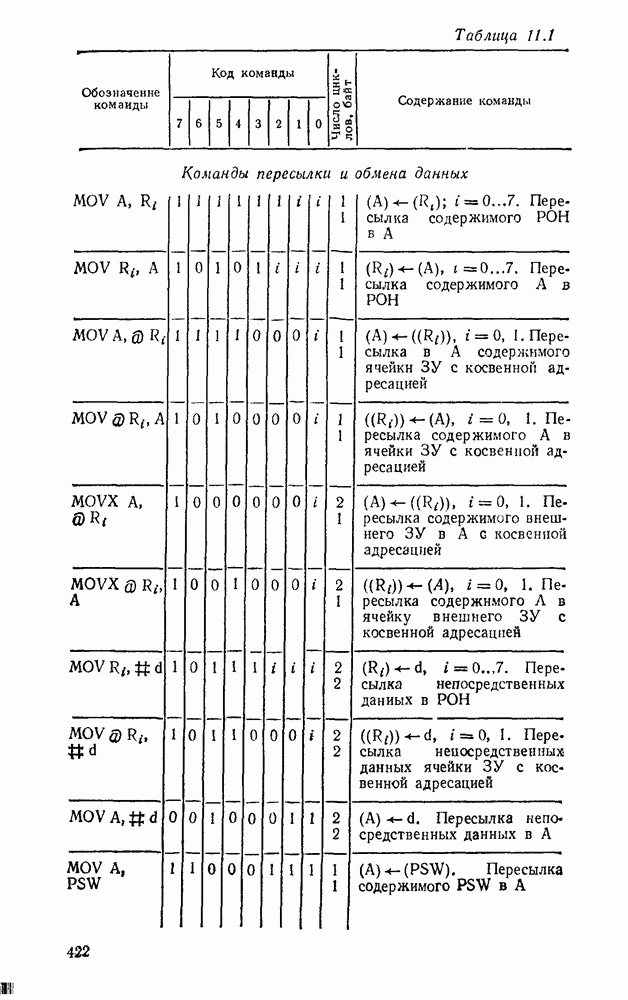
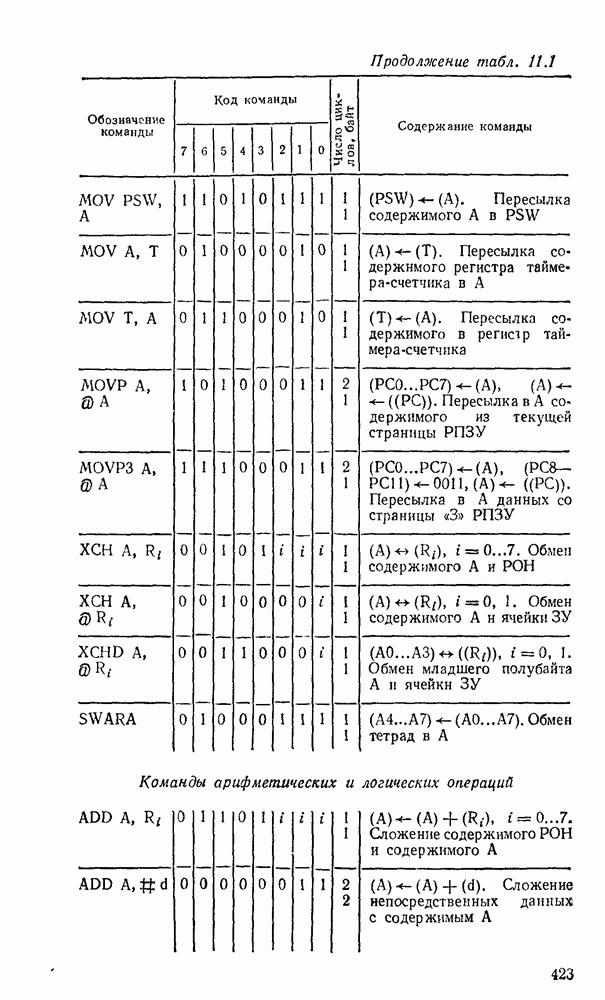
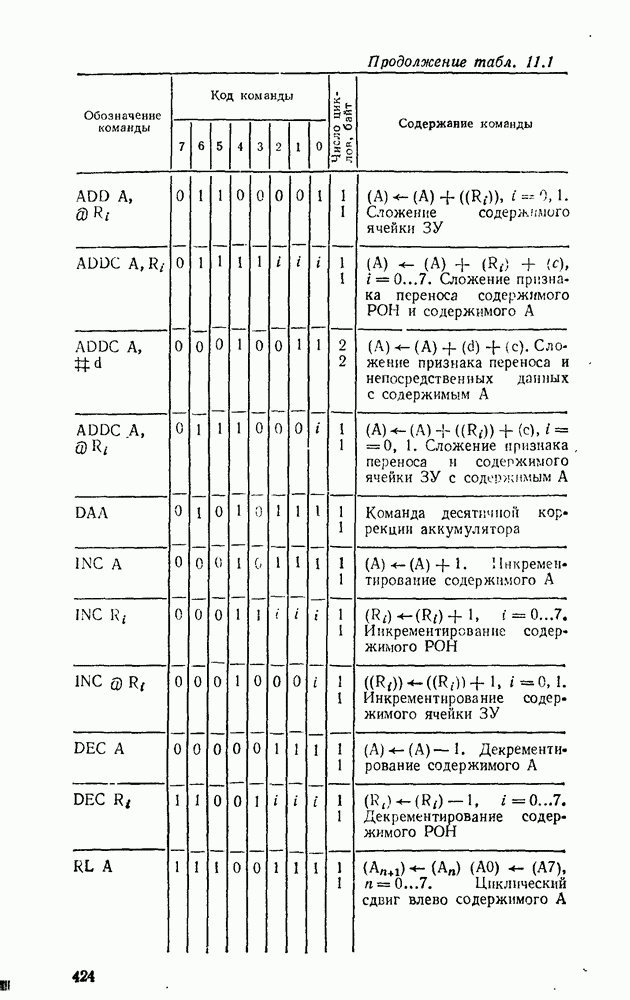
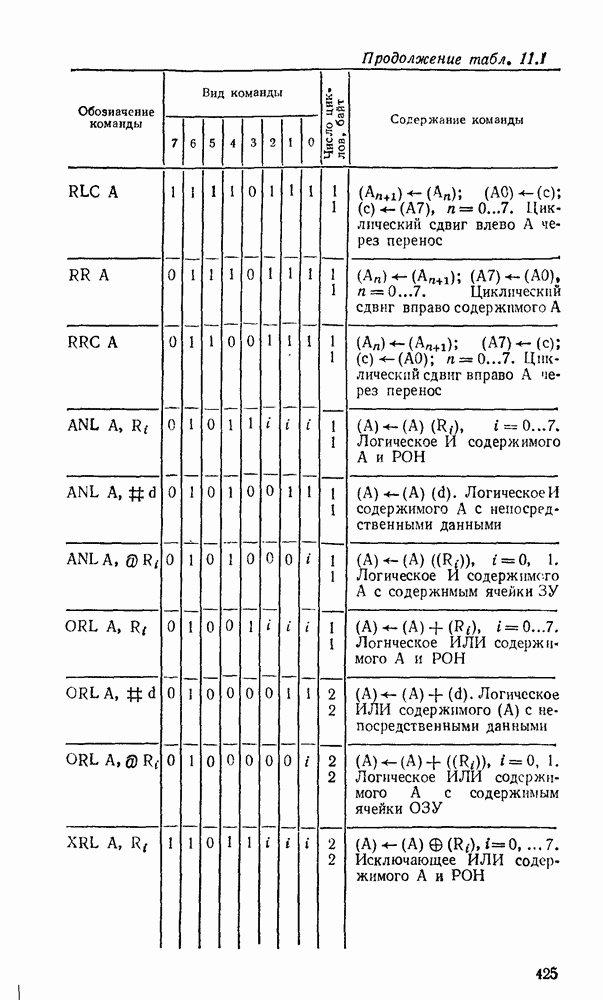
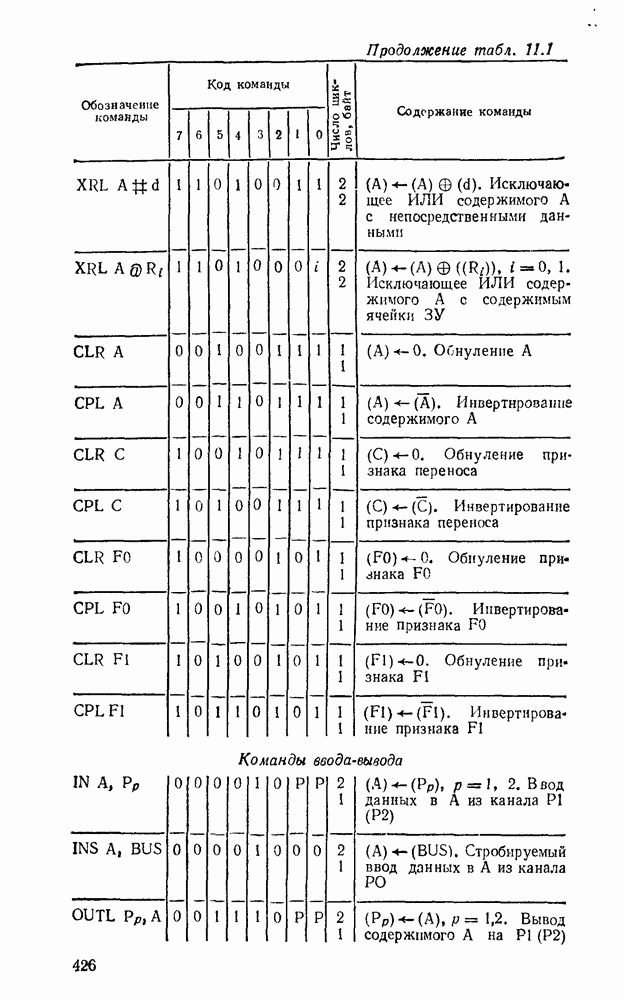
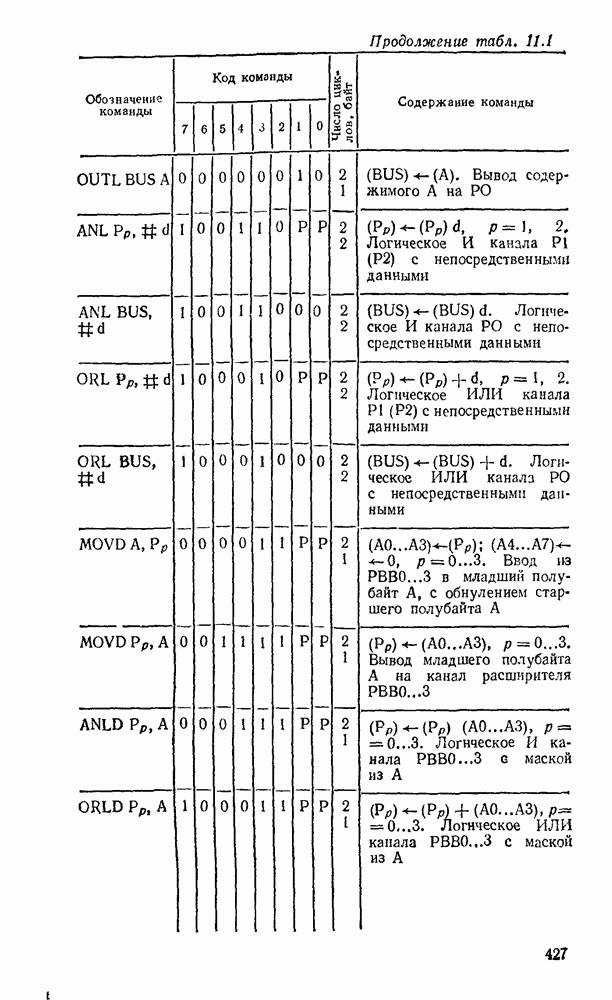
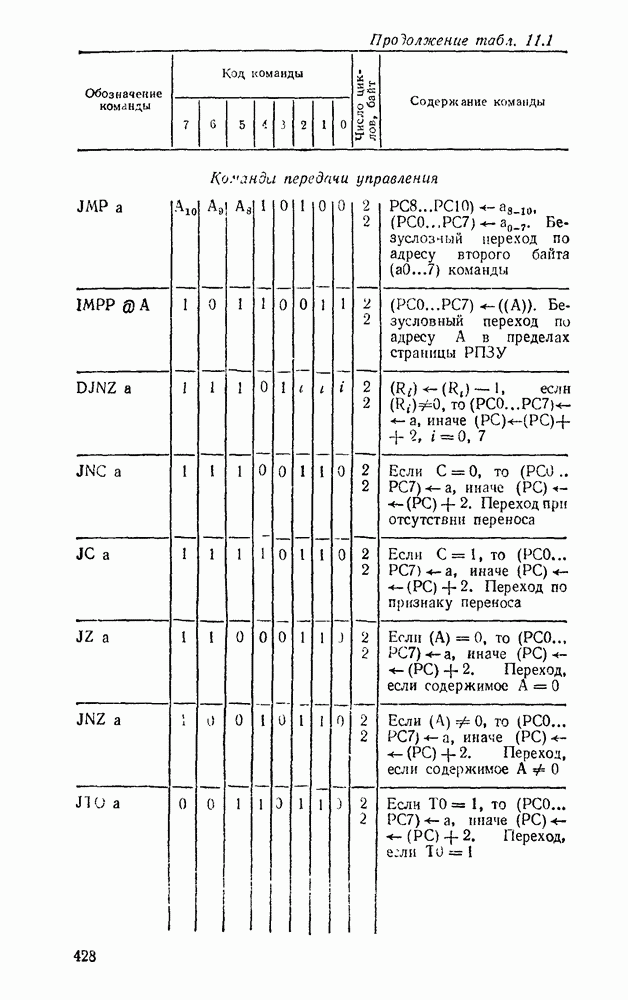
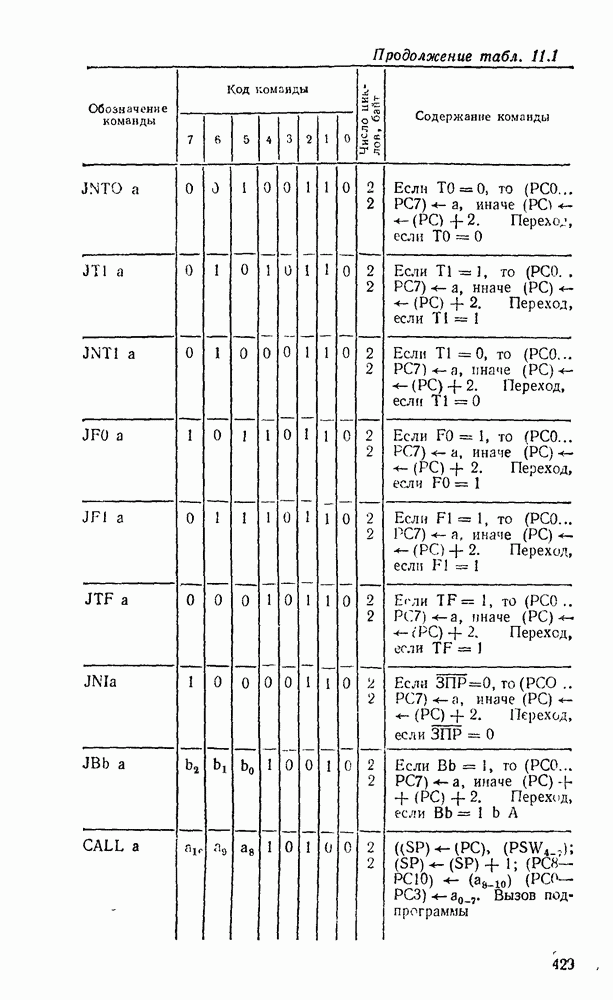
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
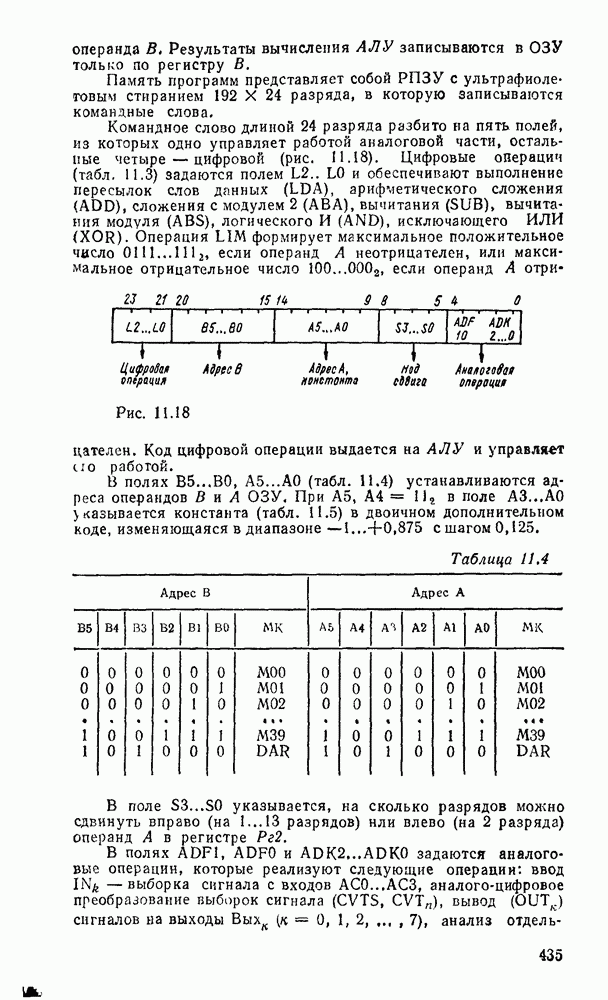
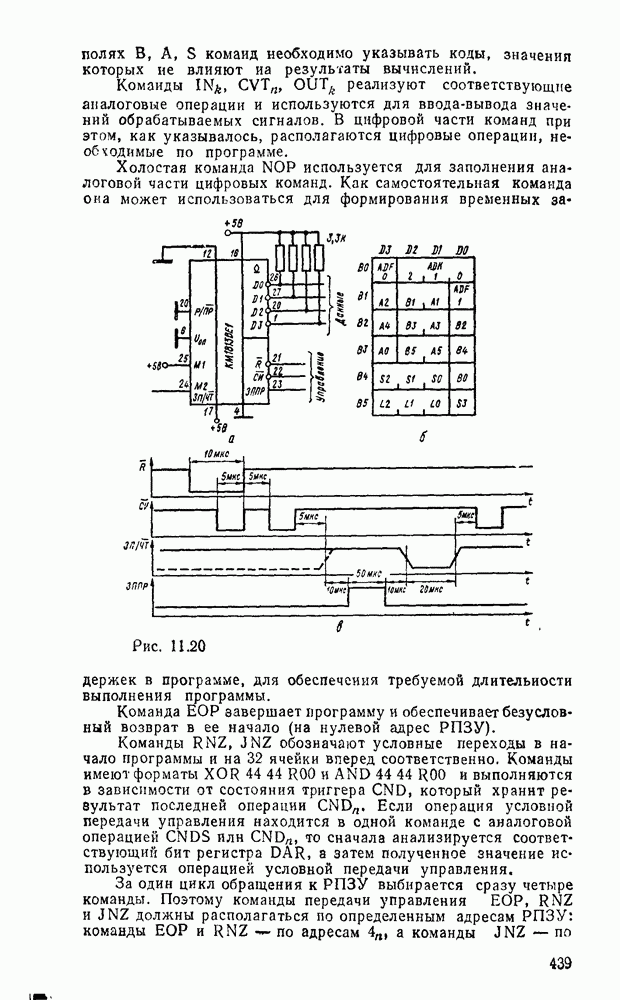
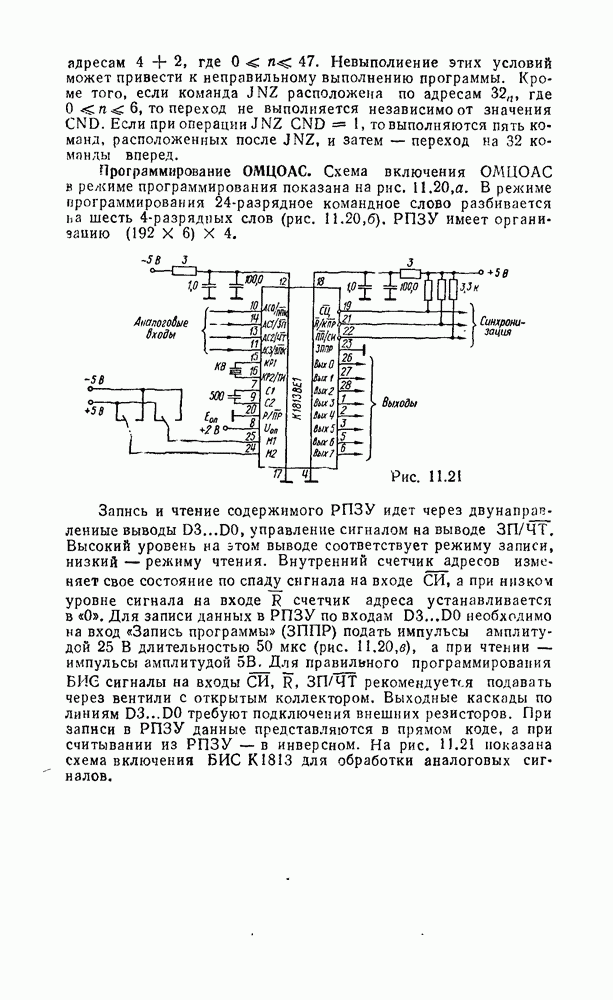
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ