| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
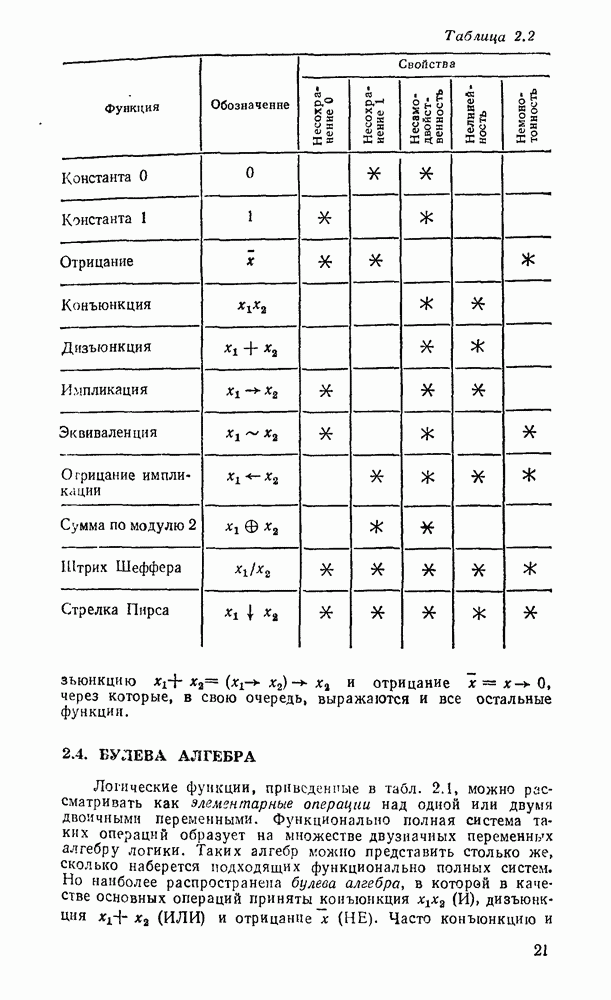
Основные свойства булевой алгебры позволяют осуществлять эквивалентные преобразования формул для их упрощения или приведения к требуемому виду, а также для доказательства логических правил и теорем. Иллюстрацией преобразования булевых выражений может служить, например, доказательство свойства выявления (см. табл.  .
.
Здесь использованы последовательно свойства  и
и  и
и  (штрихами отмечены соответственно
(штрихами отмечены соответственно  и вторая формы). Как видно, в выражении
и вторая формы). Как видно, в выражении  дополнительный член,
дополнительный член,  представляет собой произведение переменных (или формул) при
представляет собой произведение переменных (или формул) при  в порождающих членах
в порождающих членах  и невлияет на значение этого выражения при условии, что порождающие члены присутствуют.
и невлияет на значение этого выражения при условии, что порождающие члены присутствуют.
Процесс упрощения сводится к последовательному применению тех или иных общих свойств с тем, чтобы уменьшить общее количество вхождений в формулу переменных и символов логических операции. Между тем далеко не очевидно, какое из свойств наиболее целесообразно использовать на каждом шаге, поэтому работа с формулами на интуитивном уровне подобна блужданию в лабиринте. Этому процессу можно придать целенаправленный характер, если воспользоваться свойствами склеивания, поглощения и выявления, представив предварительно исходное выражение в нормальной форме. В дальнейшем преобразования выполняются в дизъюнктивной нормальной форме (сумме минтермов), а соответствующие правила для конъюнктивной нормальной формы (произведения макстермов) можно получить на основе принципа дуальности.
Склеивание  можно понимать любое выражение) позволяет заменить два минтерма, отличающихся вхождением только одной переменной (с отрицанием и без него), одним миптермом более низкого ранга.
можно понимать любое выражение) позволяет заменить два минтерма, отличающихся вхождением только одной переменной (с отрицанием и без него), одним миптермом более низкого ранга.
Пусть, например, функция задана в виде каиоиической суммы минтермов:  и применяя операцию склеивания,
и применяя операцию склеивания,  при другом варианте группирования получим
при другом варианте группирования получим 
Последующие упрощения основаны на свойствах поглощения и выявления. Поглощение  , если под
, если под  и у понимать не только переменные, но и любые булевы выражения, позволяет исключить все минтермы, в которые в качестве сомножителя входит некоторый другой минтерм более низкого ранга. Наряду с этим дополнительный член, который вводится на основе свойства выявления, можно использовать для поглощения и/или замещения других членов (минтермов). Эта операция, называемая обобщенным склеиванием, всегда возможна, если исходная формула наряду с порождающими членами содержит минтермы, в которые в качестве сомножителя входит дополнительный член, например:
и у понимать не только переменные, но и любые булевы выражения, позволяет исключить все минтермы, в которые в качестве сомножителя входит некоторый другой минтерм более низкого ранга. Наряду с этим дополнительный член, который вводится на основе свойства выявления, можно использовать для поглощения и/или замещения других членов (минтермов). Эта операция, называемая обобщенным склеиванием, всегда возможна, если исходная формула наряду с порождающими членами содержит минтермы, в которые в качестве сомножителя входит дополнительный член, например:

Здесь дополнительный член поглотил  , после чего удаляется как не влияющий на значение полученного выражения. В случаях, когда дополнительный член поглощает один из порождающих членов, его удалять нельзя и, следовательно, происходит замещение этого порождающего члена. Например:
, после чего удаляется как не влияющий на значение полученного выражения. В случаях, когда дополнительный член поглощает один из порождающих членов, его удалять нельзя и, следовательно, происходит замещение этого порождающего члена. Например:

Здесь дополнительный член поглощает минтерм  и замещает породивший его минтерм
и замещает породивший его минтерм  . Заметим, что это выражение можно было бы упростить и без введения дополнительного члена с помощью поглощения и замещения:
. Заметим, что это выражение можно было бы упростить и без введения дополнительного члена с помощью поглощения и замещения:  .
.
Применяя изложенную процедуру к рассматриваемому примеру для первого варианта группирования  получаем
получаем  или
или  . Аналогично второй вариант
. Аналогично второй вариант  упрощается к виду
упрощается к виду  что повторяет уже полученный результат для первого варианта. Таким образом, исходная формула преобразуется к двум формам, которые в данном случае являются и минимальными. К такому же результату можно было бы прийти, применяя только простое склеивание, если в исходном выражении повторить минтерм
что повторяет уже полученный результат для первого варианта. Таким образом, исходная формула преобразуется к двум формам, которые в данном случае являются и минимальными. К такому же результату можно было бы прийти, применяя только простое склеивание, если в исходном выражении повторить минтерм  , или
, или  , о чем, конечно, не так просто догадаться в самом начале преобразования. Следует заметить, что с применением обобщенного склеивания можно упрощать формулы, заданные в любой форме, а не обязательно в канонической. В то же время эта операция не проходит, если порождающие члены содержат различное вхождение (с отрицанием и без него) не одной, а двух или больше переменных.
, о чем, конечно, не так просто догадаться в самом начале преобразования. Следует заметить, что с применением обобщенного склеивания можно упрощать формулы, заданные в любой форме, а не обязательно в канонической. В то же время эта операция не проходит, если порождающие члены содержат различное вхождение (с отрицанием и без него) не одной, а двух или больше переменных.
Например,  , так как при этом дополнительный член
, так как при этом дополнительный член  обращается в тождественный нуль.
обращается в тождественный нуль.
Хотя в рассмотренном примере получены минимальные формы, в общем случае процедура склеивания минтермов не гарантирует этого. Она обеспечивает лишь преобразование к сокращенной форме, минтермы которой называют простыми импликантами. Так как склеиваемые минтермы покрываются минтермом низшего ранга, сокращенная форма не содержит таких импликант, которые целиком покрываются какой-либо одной импликантой. В то же время среди простых импликант могут быть такие, которые покрываются совокупностями других импликант и, следовательно, являются избыточными. После удаления избыточных импликант приходим к тупиковым формам, среди которых находятся и минимальные формы. Следует заметить, что для данной функции существует единственная сокращенная форма, в то время как тупиковых и минимальных форм может быть несколько. Для минимизации булевых формул разработан ряд методов, среди которых наиболее известны алгоритм Квайна—Мак-Класки и графический метод, основанный на картах Карно.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
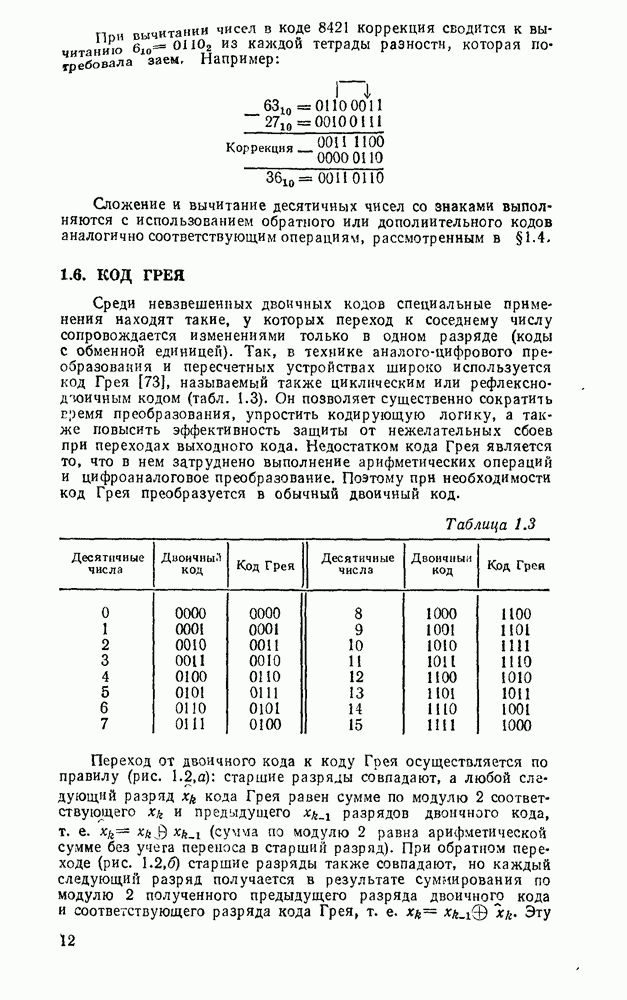
- 1.6. КОД ГРЕЯ
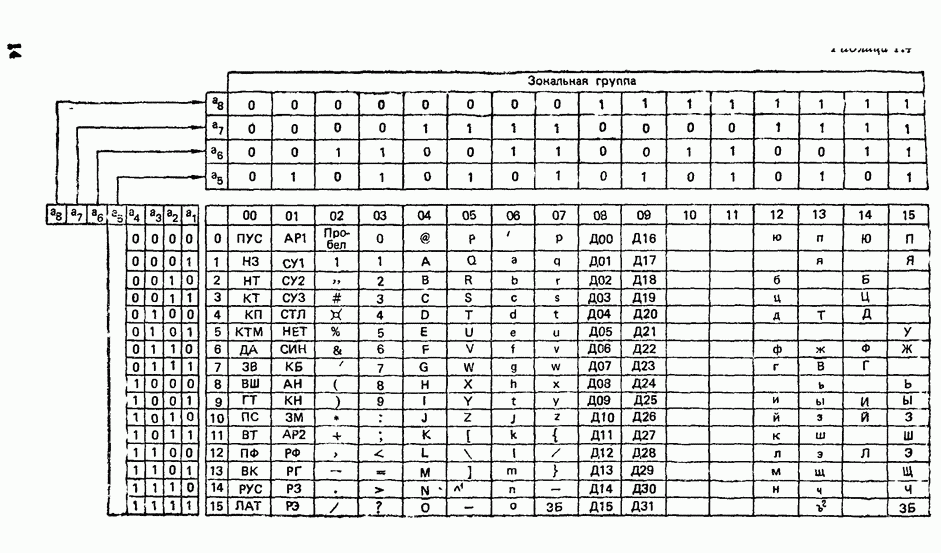
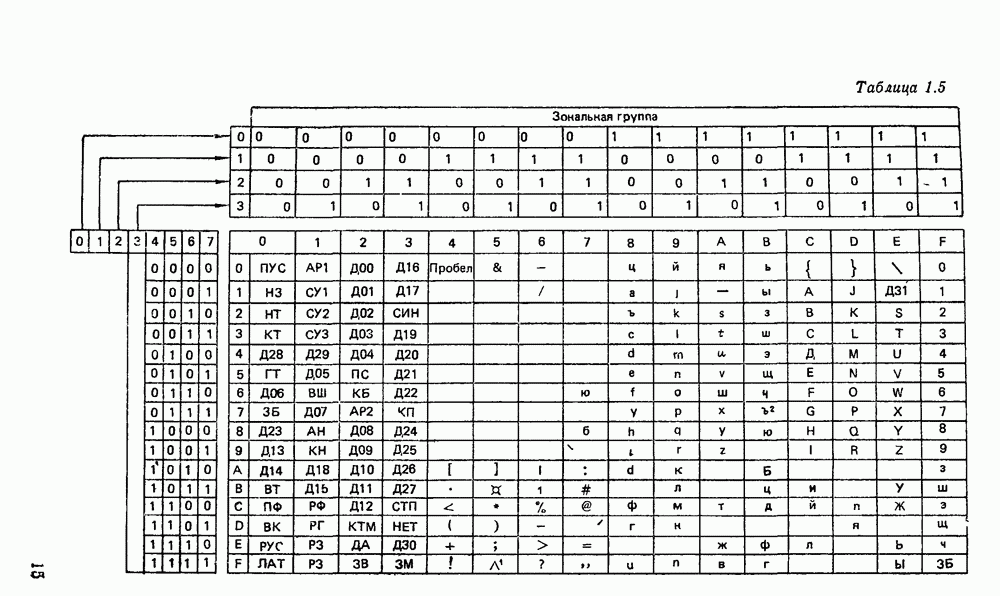
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
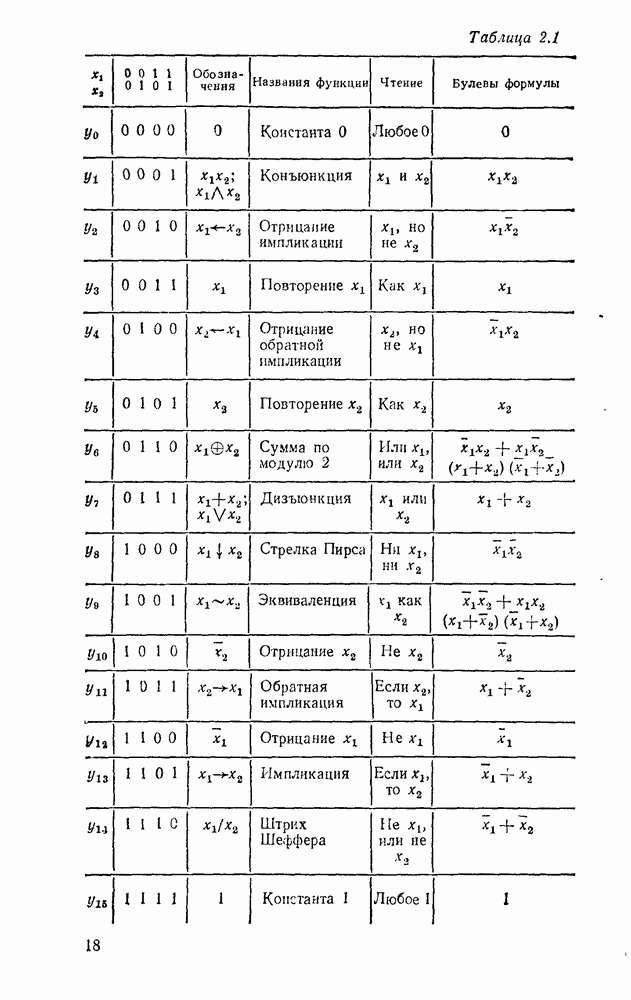
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
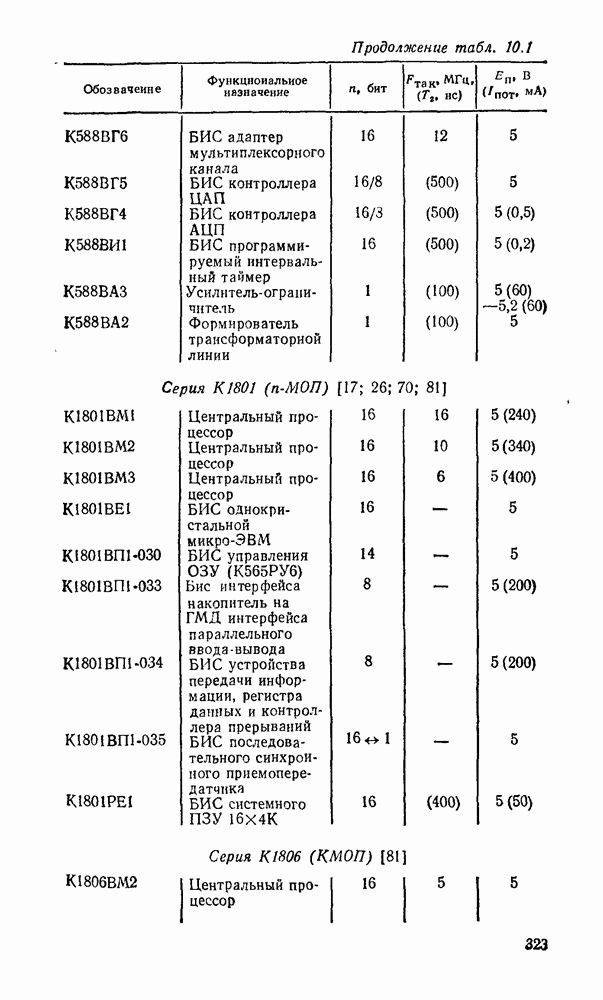
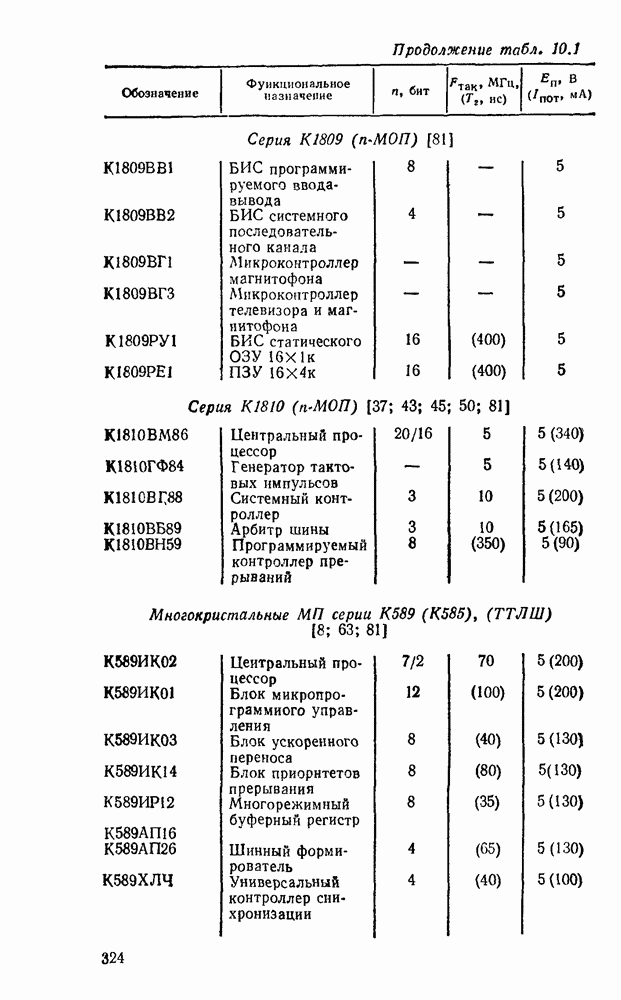
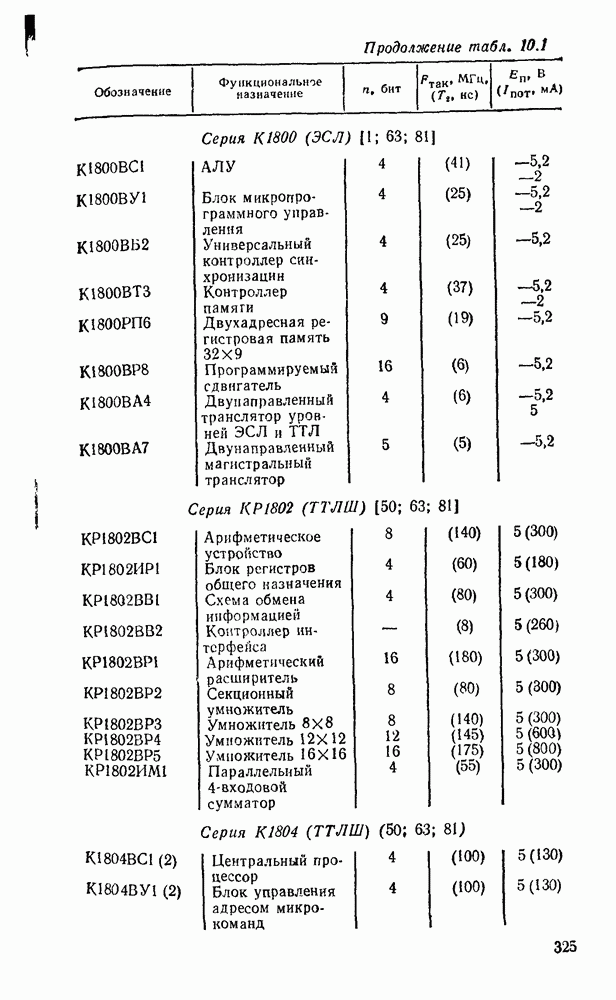
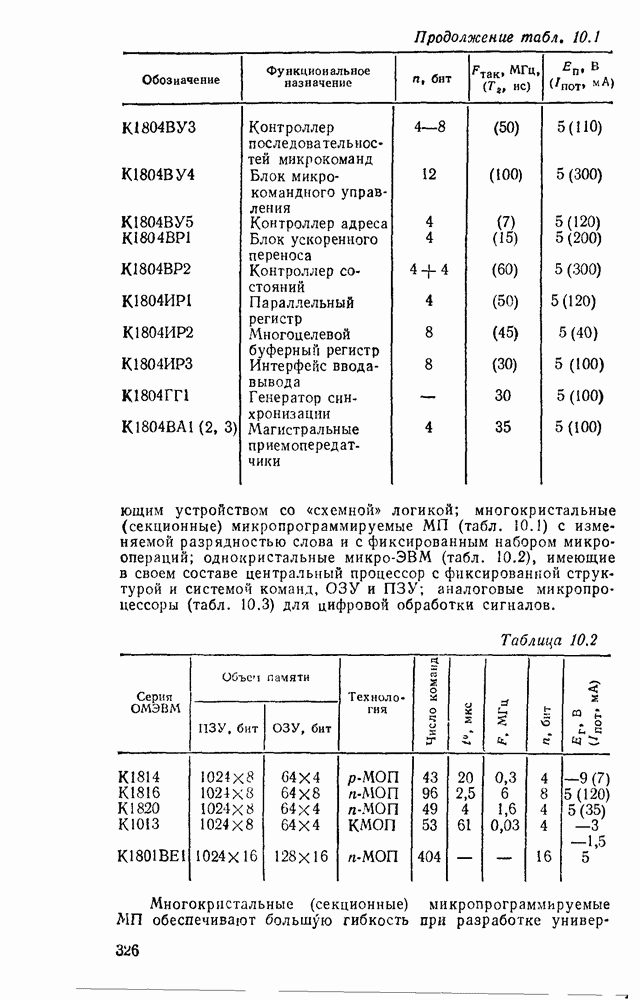
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
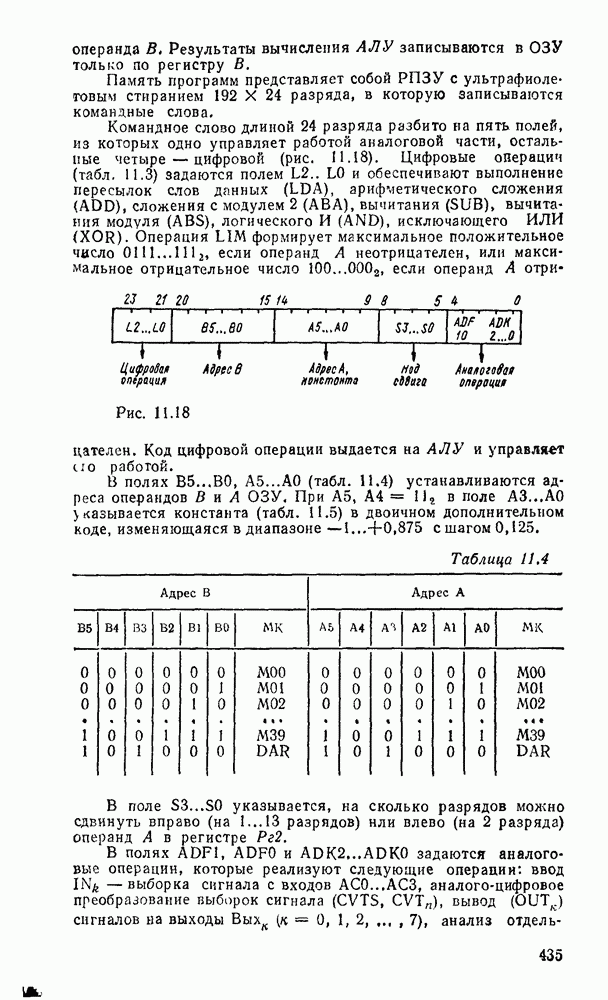
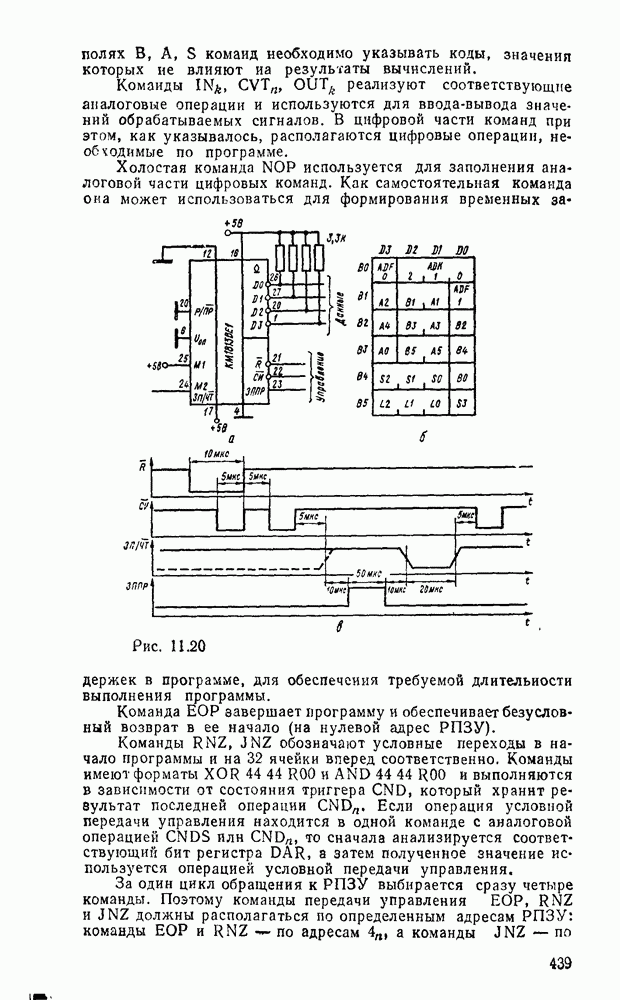
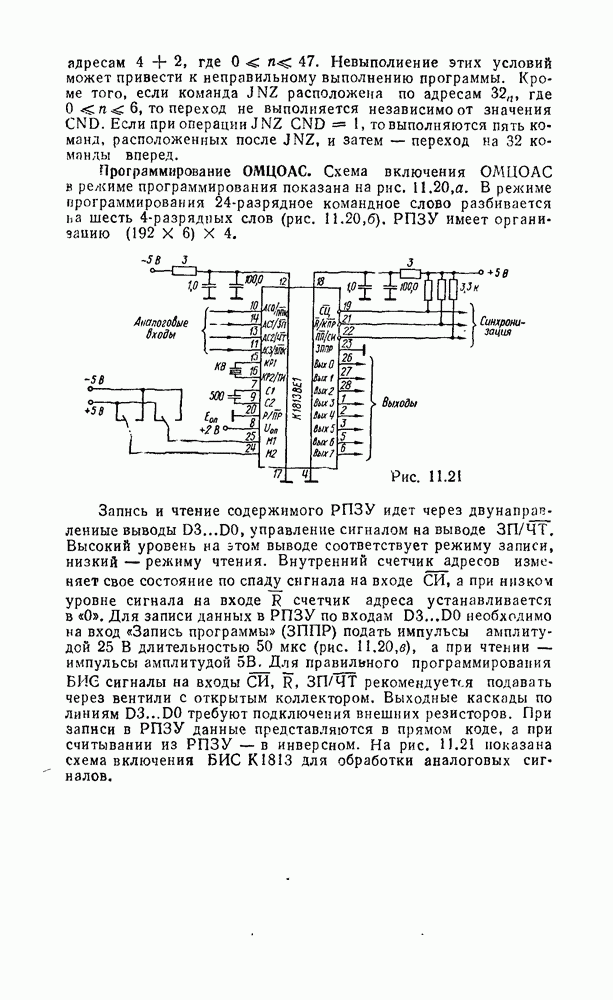
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ