| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
Множество функций  переменных можно представить с помощью таблицы соответствия, столбцы которой отводятся для
переменных можно представить с помощью таблицы соответствия, столбцы которой отводятся для  слов длины
слов длины  , а строки — для
, а строки — для  функций. При этом номера столбцов определяются расположенными над ними
функций. При этом номера столбцов определяются расположенными над ними  -разрядными двоичными числами, которые читаются по вертикали сверху вниз. Номера функций отождествляются с
-разрядными двоичными числами, которые читаются по вертикали сверху вниз. Номера функций отождествляются с  -разрядными двоичными числами, записанными в соответствующих строках таблицы. Таблицу соответствия часто называют также таблицей истинности. Таблица соответствия для булевых функций одной переменной
-разрядными двоичными числами, записанными в соответствующих строках таблицы. Таблицу соответствия часто называют также таблицей истинности. Таблица соответствия для булевых функций одной переменной  имеет вид (справа указаны обозначения функций)
имеет вид (справа указаны обозначения функций)

Функции  представляют собой константы (соответственно тождественный нуль и тождественную единицу), так как они не изменяют своих значений при изменении аргумента. Функция
представляют собой константы (соответственно тождественный нуль и тождественную единицу), так как они не изменяют своих значений при изменении аргумента. Функция  — это повторение, так как ее значения просто совпадают со значениями переменной
— это повторение, так как ее значения просто совпадают со значениями переменной  . Единственной нетривиальной функцией является
. Единственной нетривиальной функцией является  , называемая отрицанием или инверсией (читается «не
, называемая отрицанием или инверсией (читается «не  ). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
). Она равна 1, когда аргумент принимает значение 0, и равна 0 при аргументе 1.
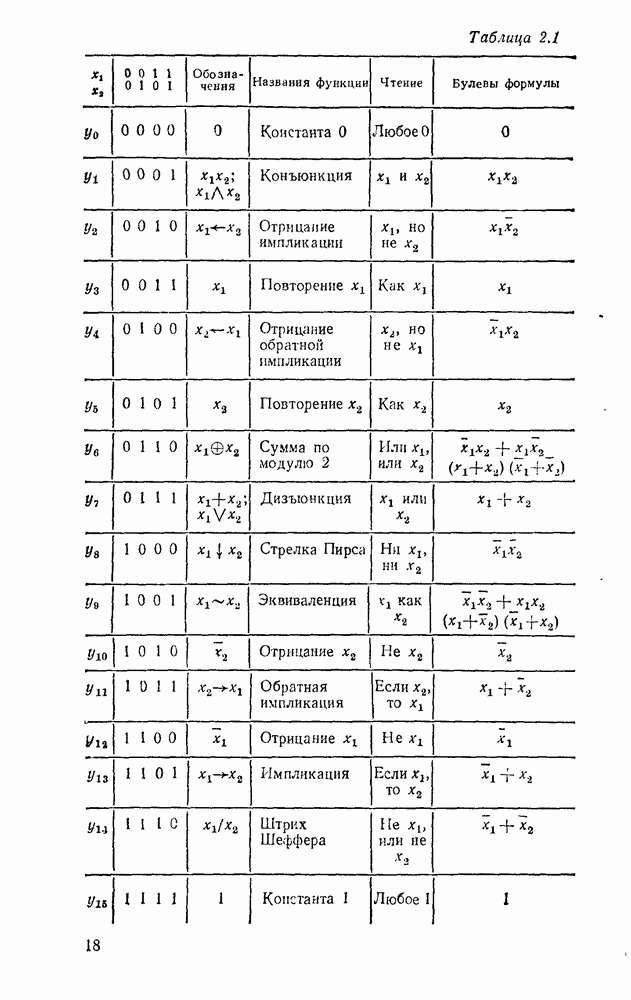
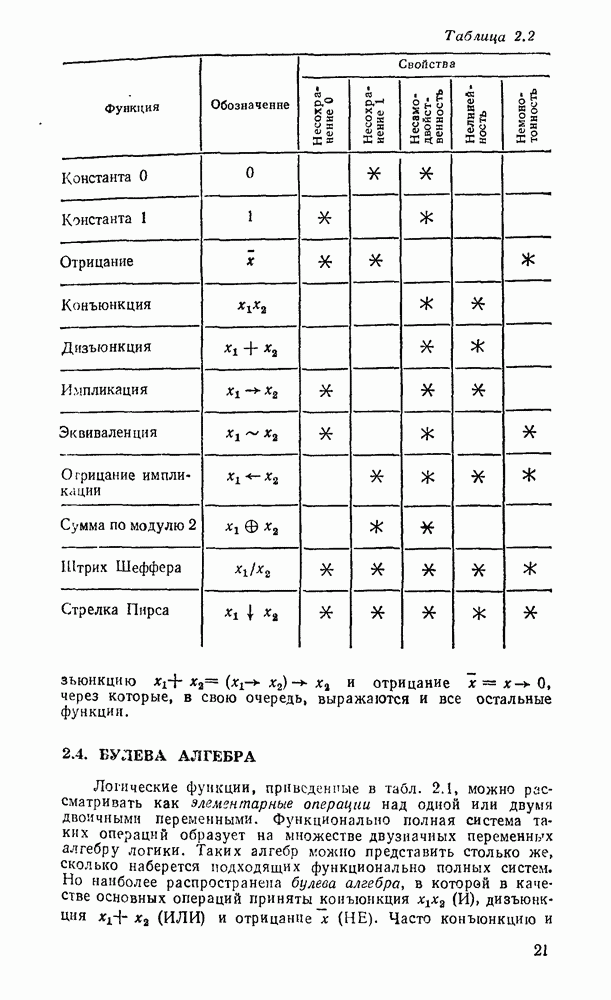
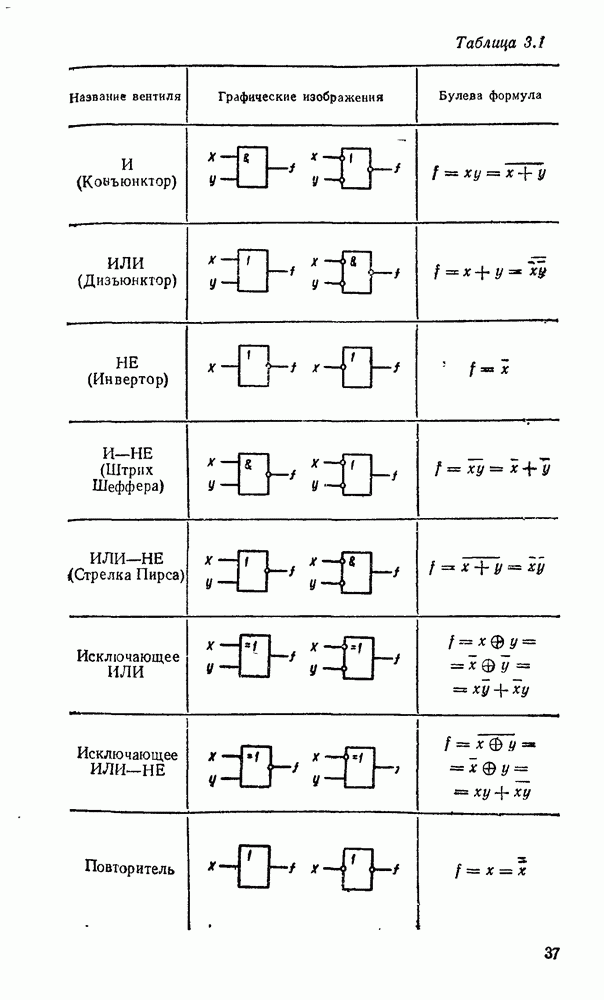
Всевозможные 16 функций двух переменных приведены в табл. 2.1, где указаны наиболее употребительные обозначения и названия. Шесть из приведенных функций не зависят или от  . или от
. или от  , или от обоих вместе. Это константы
, или от обоих вместе. Это константы  повторения
повторения  и отрицания
и отрицания  , являющиеся функциями одной из переменных
, являющиеся функциями одной из переменных  или
или  .
.
Таблица 2.1
(см. оригинал)
Среди остальных 10 функций две  отличаются от соответствующих им функций
отличаются от соответствующих им функций  лишь порядком расположения аргументов. Поэтому из 16 булевых функций двух переменных оригинальными являются только восемь:
лишь порядком расположения аргументов. Поэтому из 16 булевых функций двух переменных оригинальными являются только восемь:  . Можно также заметить, что среди булевых функций некоторого числа переменных содержатся всевозможные функции меньшего числа переменных, которые называются вырожденными функциями. Так, среди функций одной переменной имеются две вырожденные — константы 0 и 1, которые можно рассматривать как функции от нуля переменных. Функции двух переменных содержат те же константы и четыре функции одной переменной и т. д.
. Можно также заметить, что среди булевых функций некоторого числа переменных содержатся всевозможные функции меньшего числа переменных, которые называются вырожденными функциями. Так, среди функций одной переменной имеются две вырожденные — константы 0 и 1, которые можно рассматривать как функции от нуля переменных. Функции двух переменных содержат те же константы и четыре функции одной переменной и т. д.
Функции от любого числа переменных можно получить с помошью суперпозиции, т. е. замещения переменных некоторыми функциями. Например, подставляя в  вместо а дизъюнкцию
вместо а дизъюнкцию  и вместо b импликацию
и вместо b импликацию  , а затем вместо с отрицание
, а затем вместо с отрицание  , получаем
, получаем  . Таблица соответствия для этой функции трех переменных
. Таблица соответствия для этой функции трех переменных  записывается на основе таблиц элементарных функций (табл. 2.1):
записывается на основе таблиц элементарных функций (табл. 2.1):

Если во всех наборах значений аргументов функция равна О или 1, то она вырождается в соответствующую константу и называется тождественным нулем или тождественной единицей.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
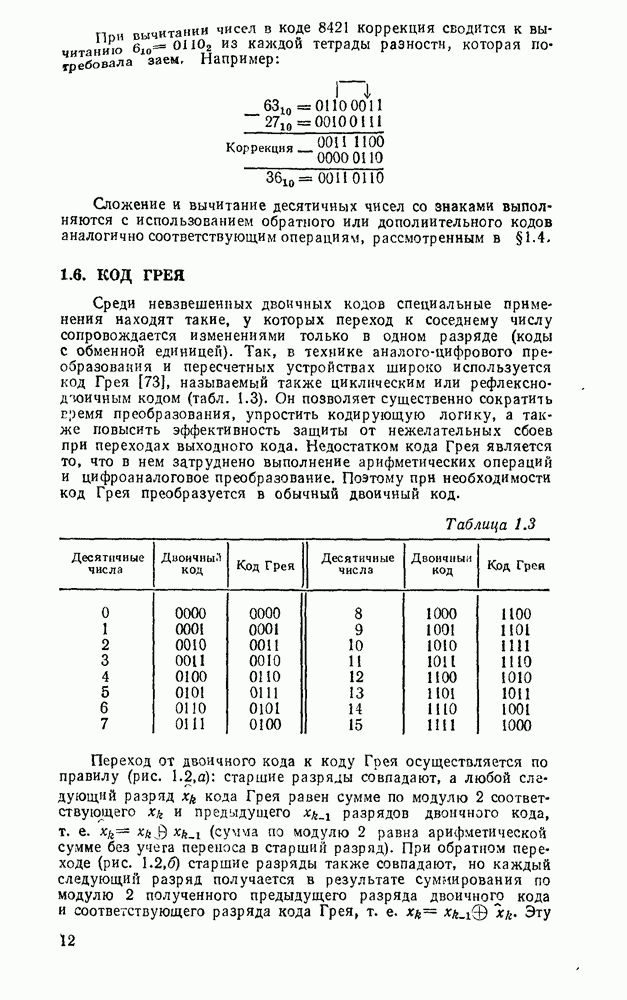
- 1.6. КОД ГРЕЯ
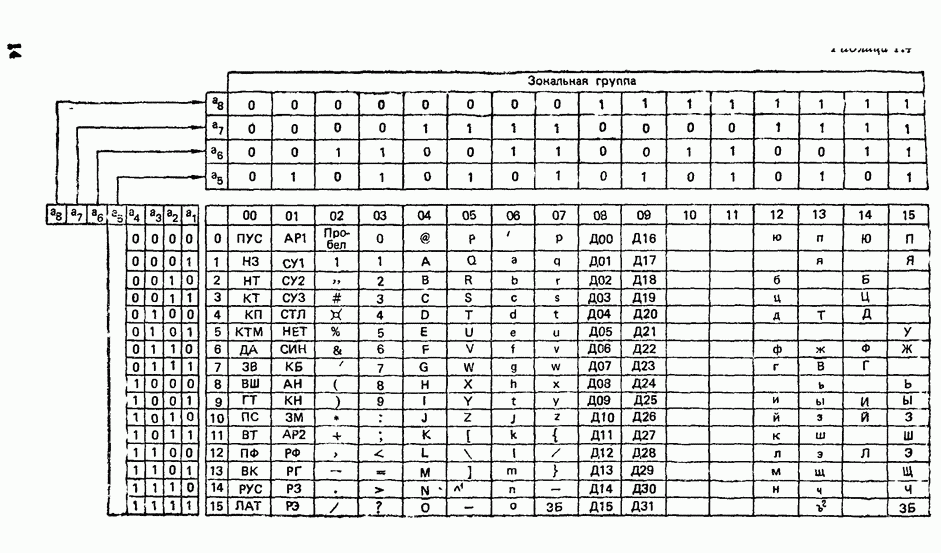
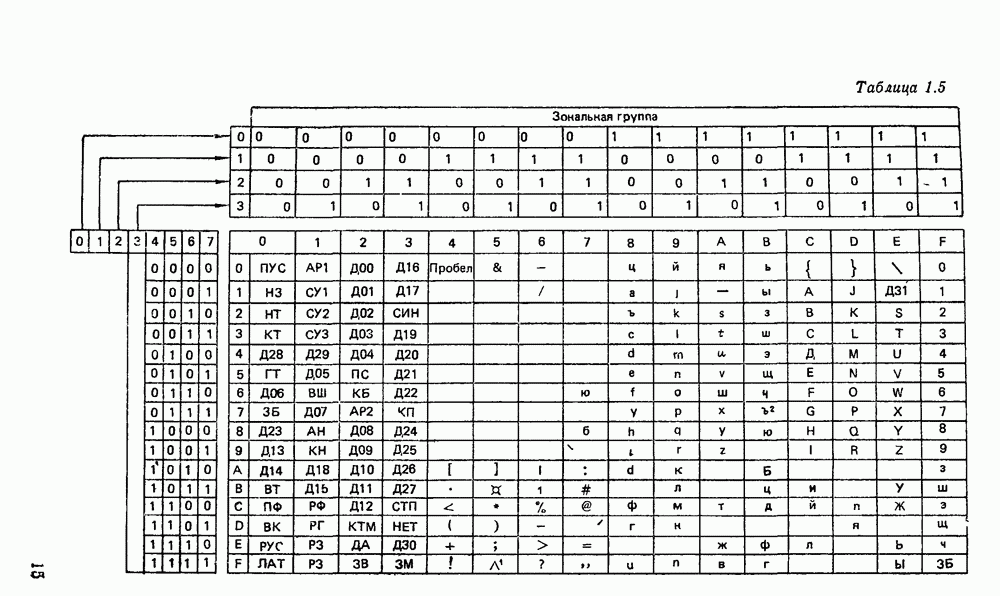
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
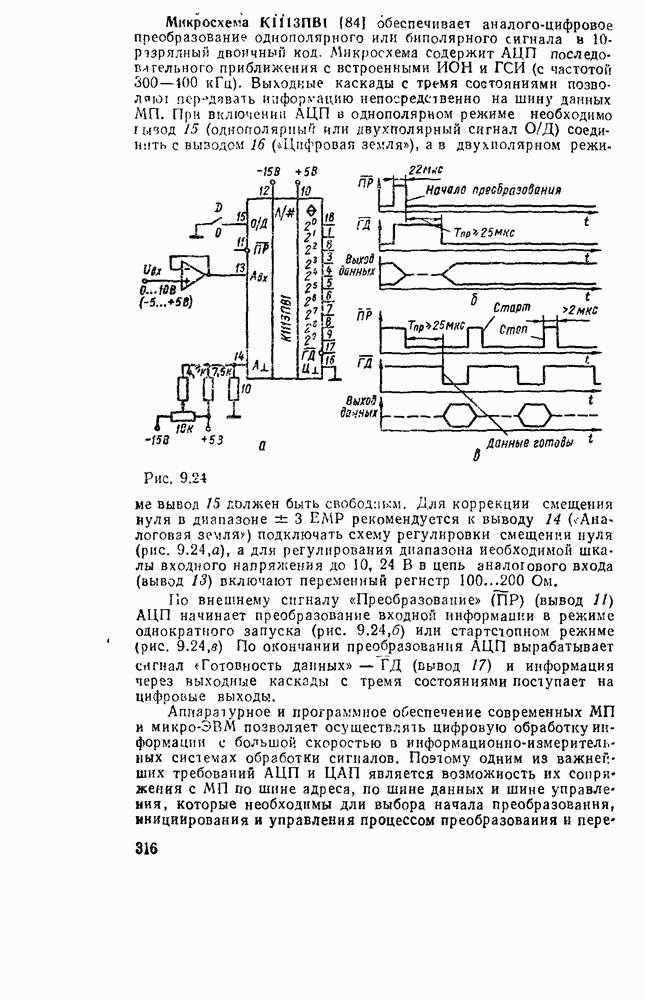
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
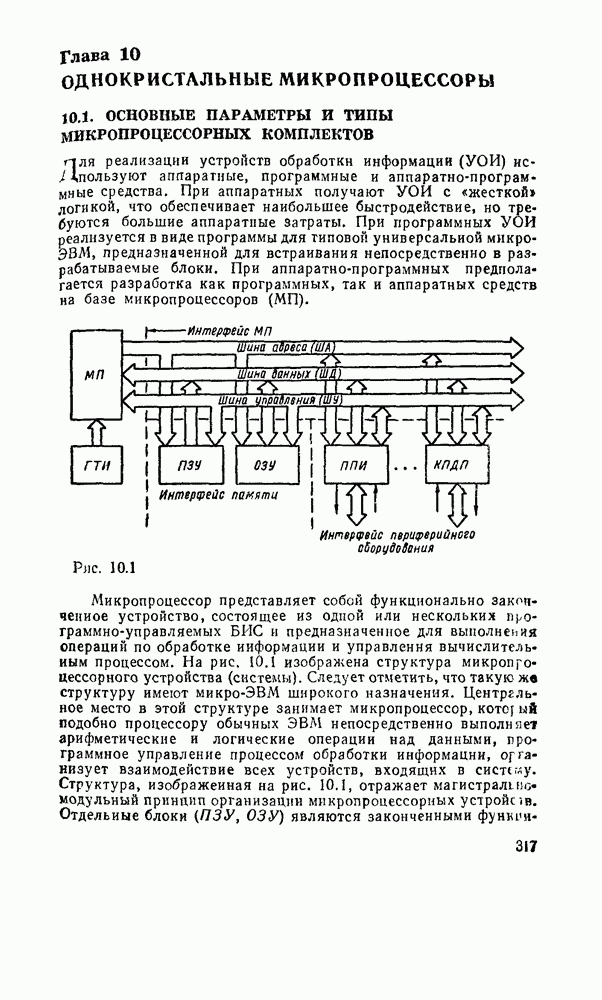
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
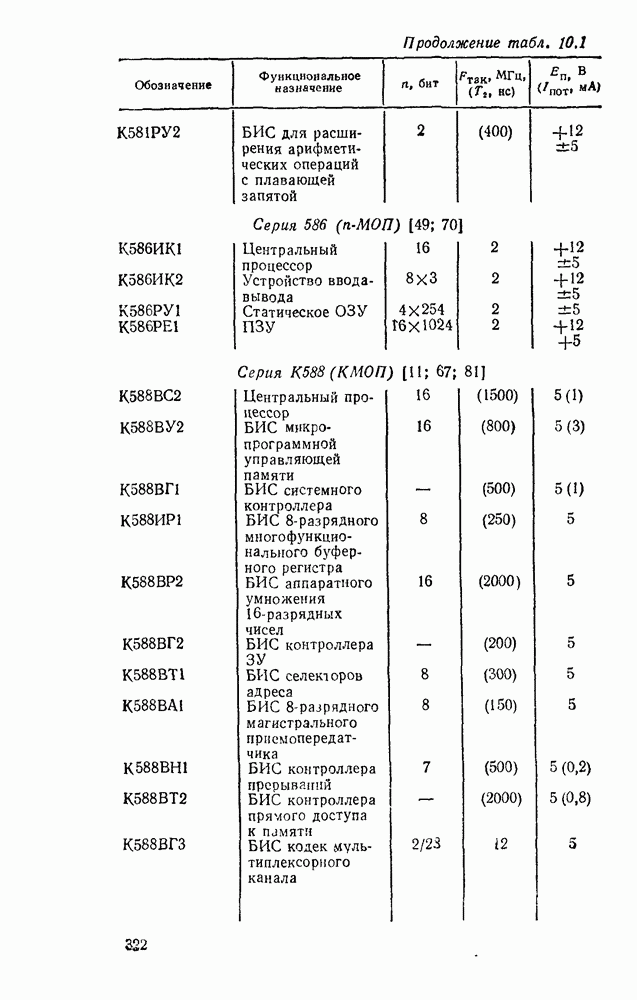
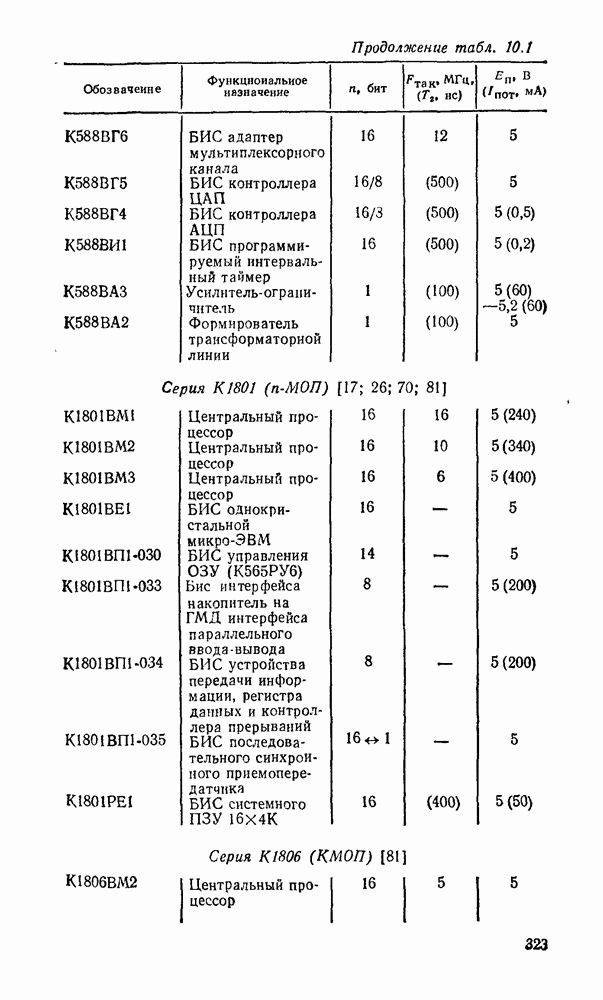
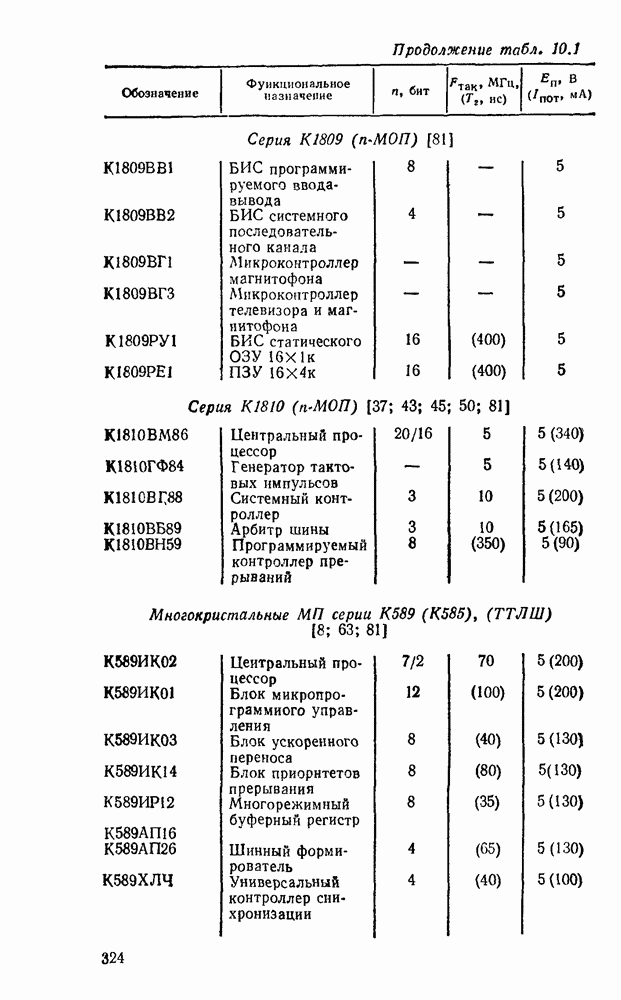
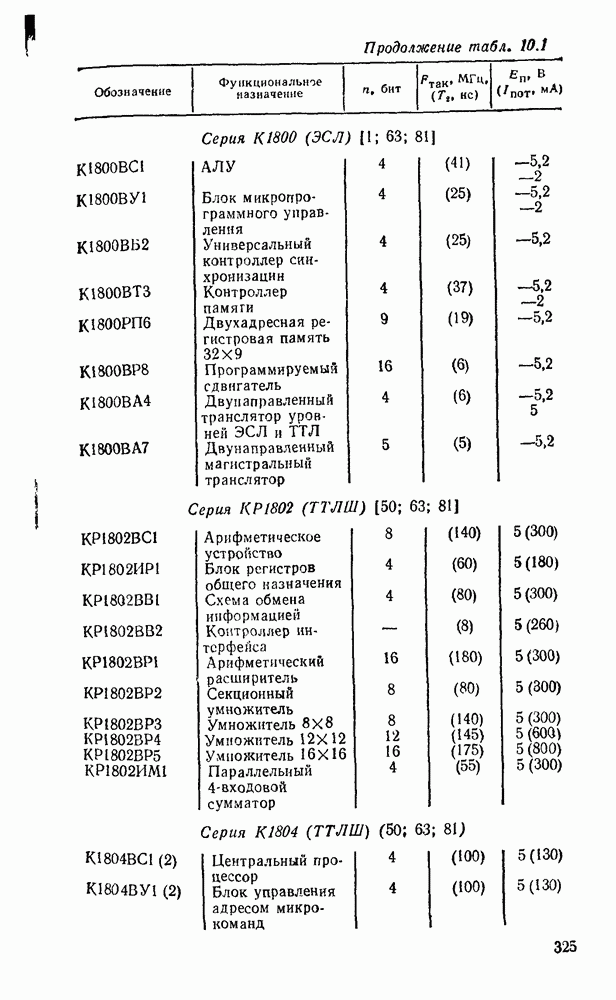
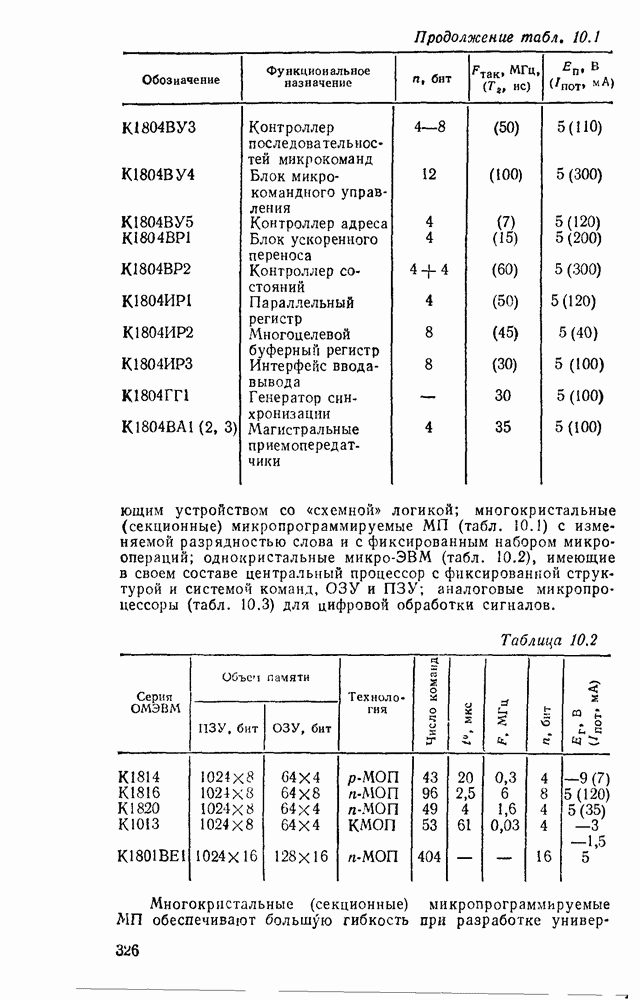
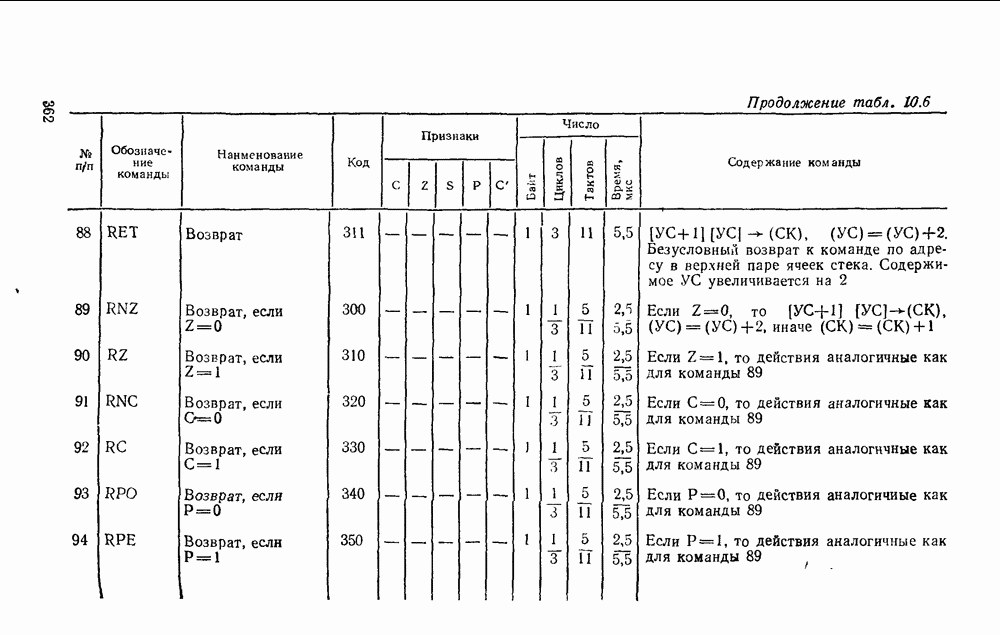
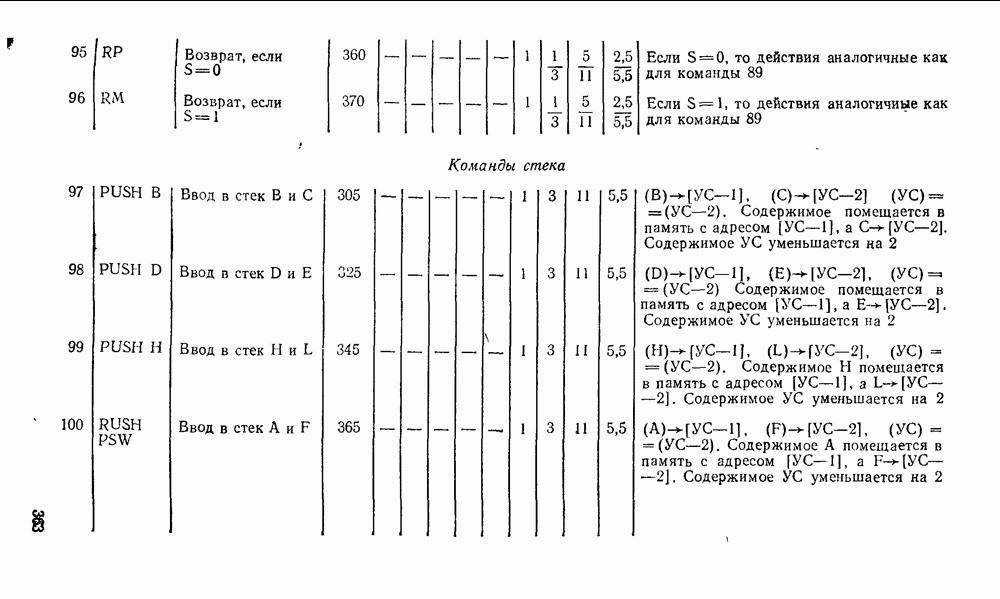
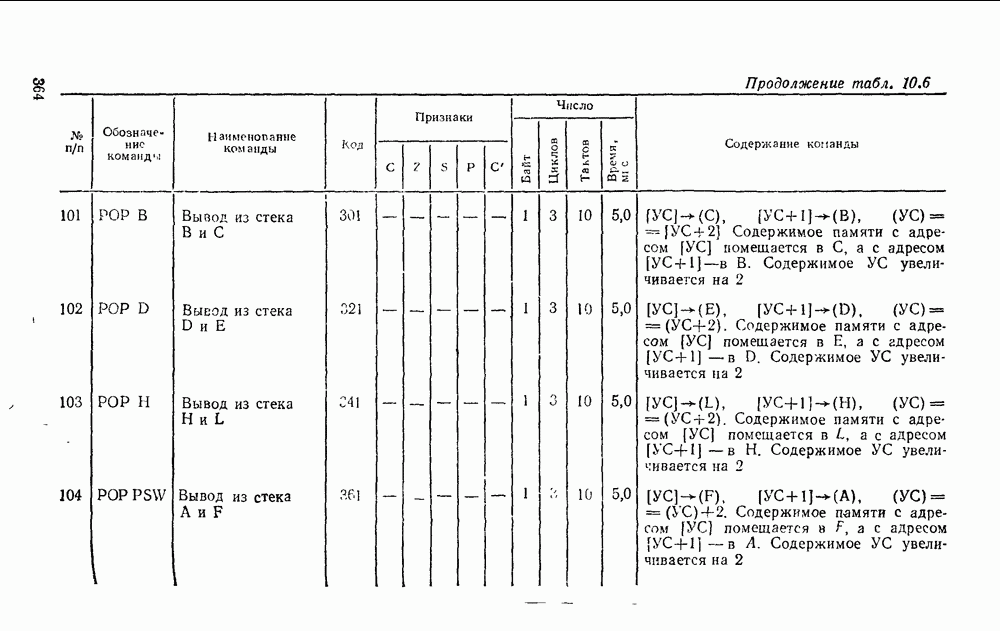
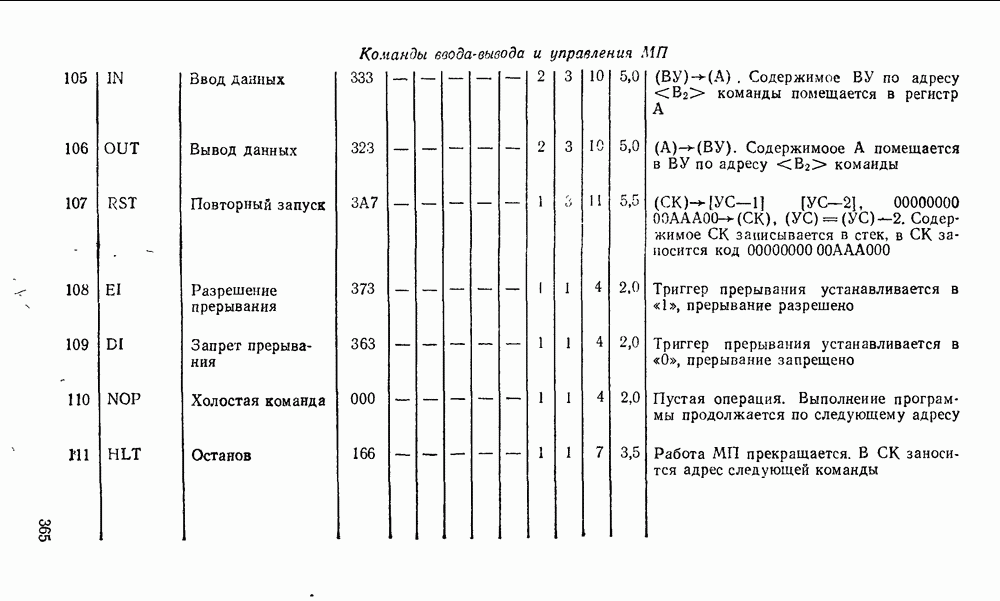
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
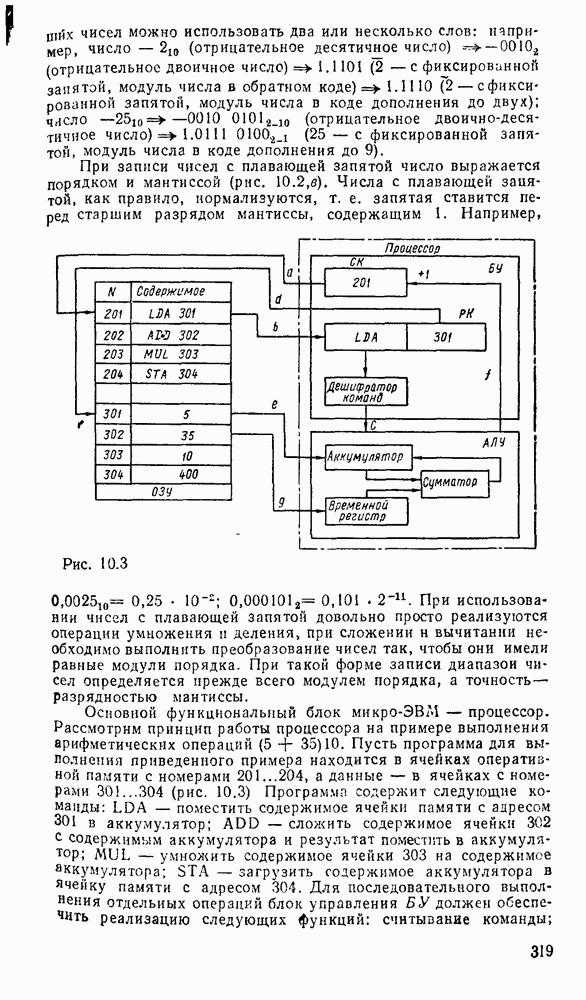
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
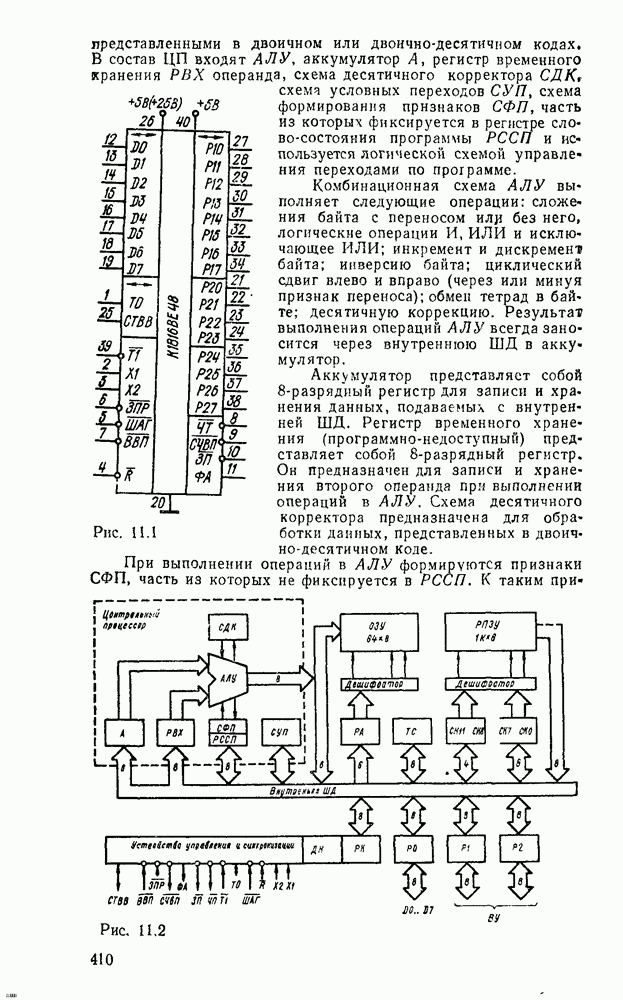
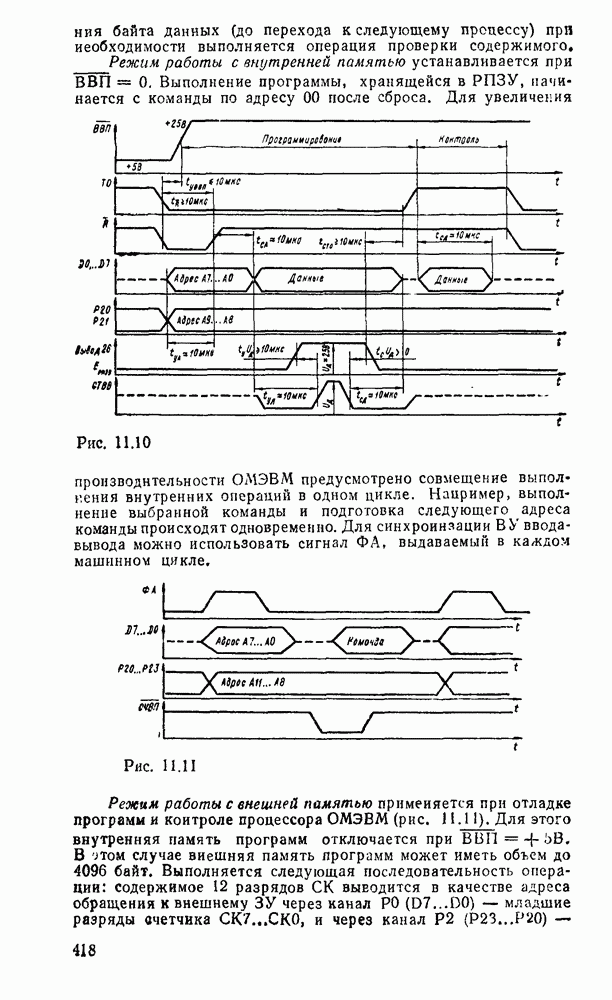
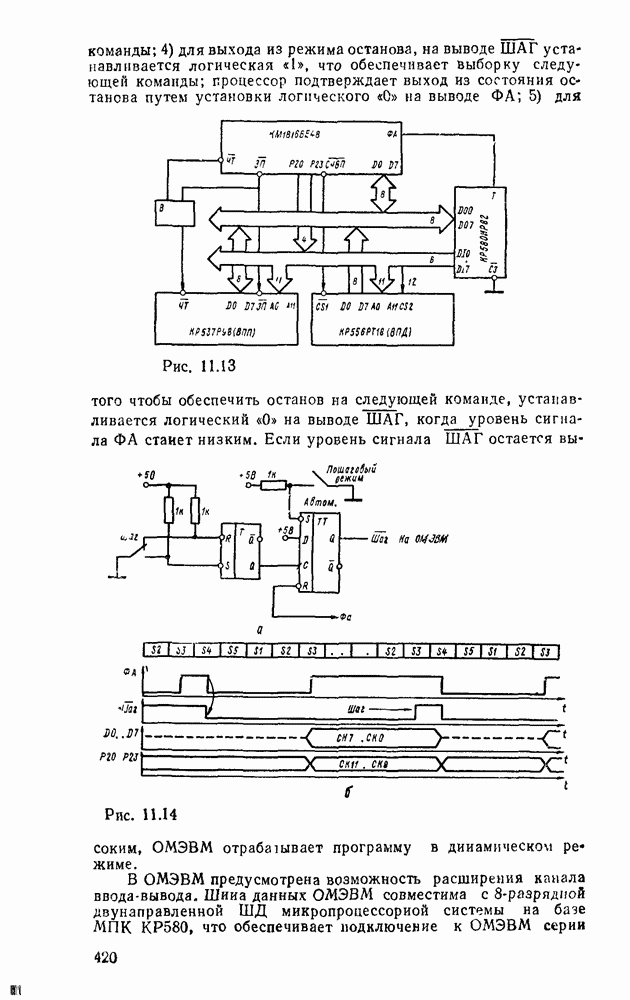
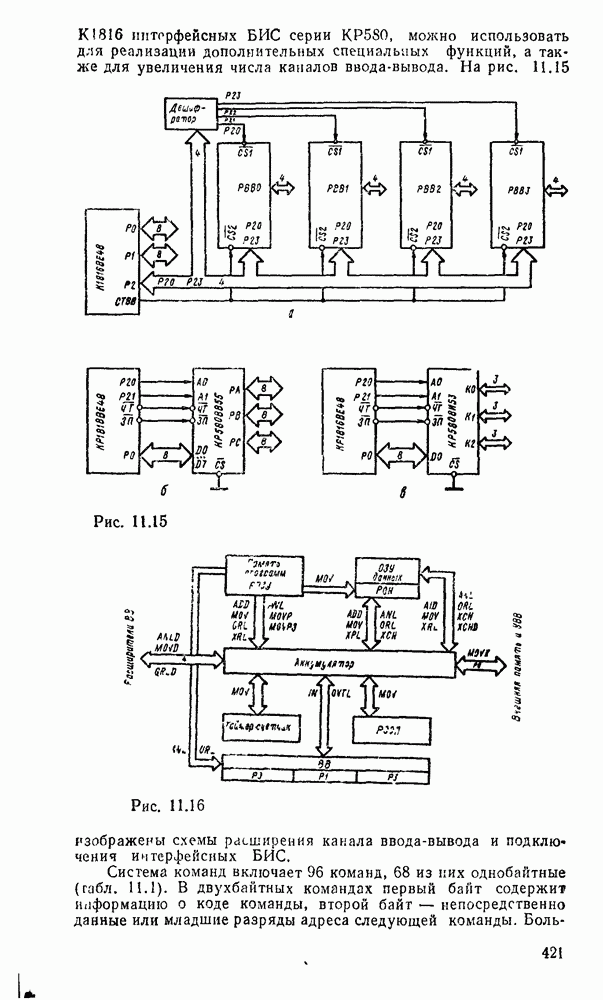
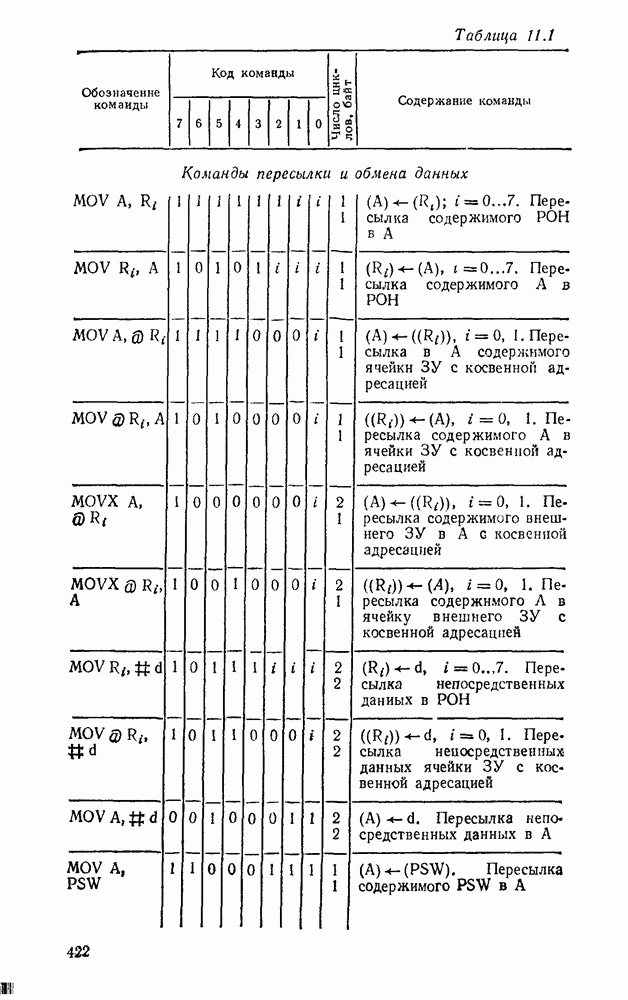
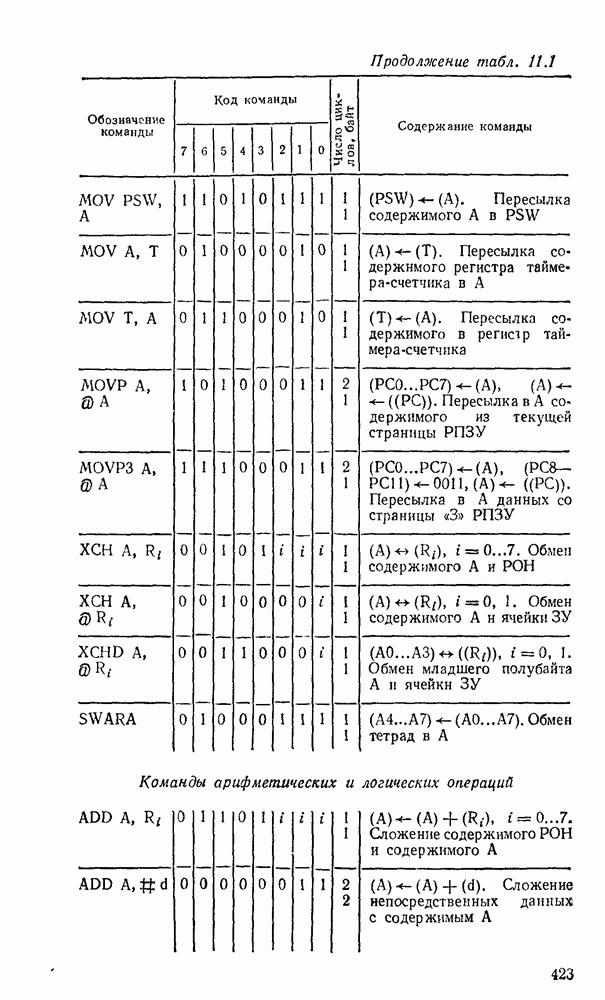
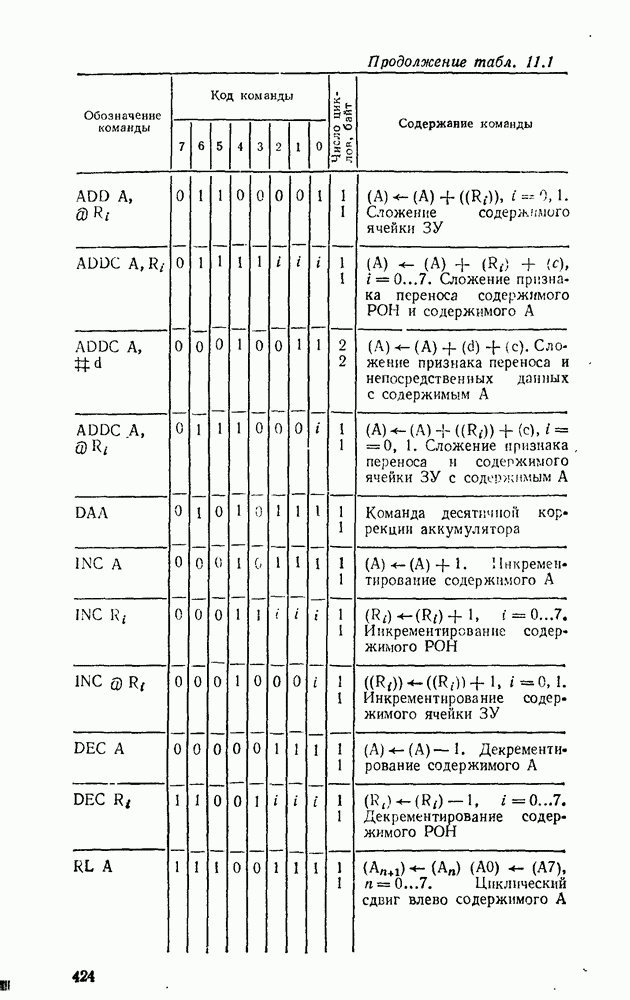
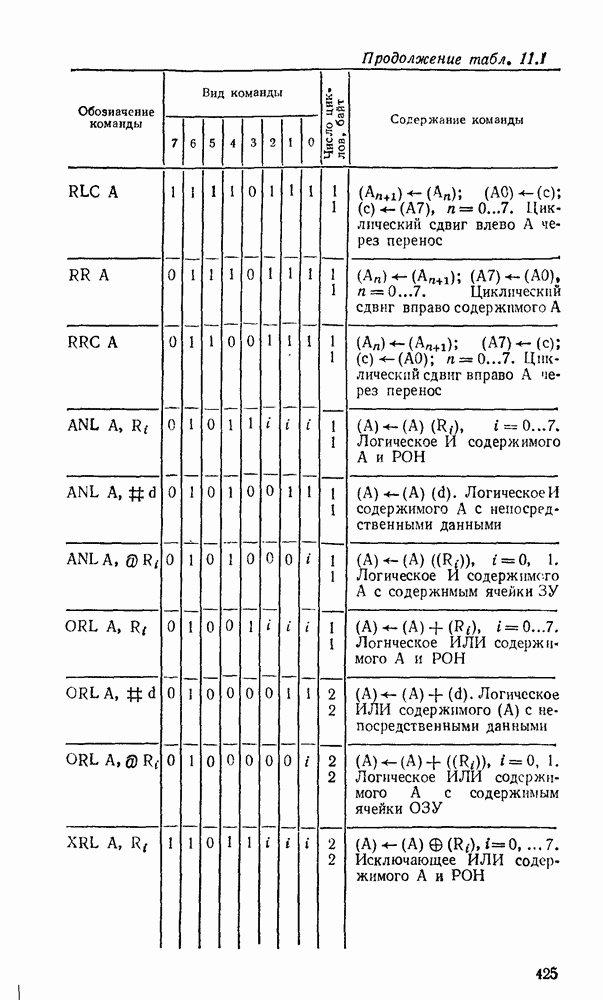
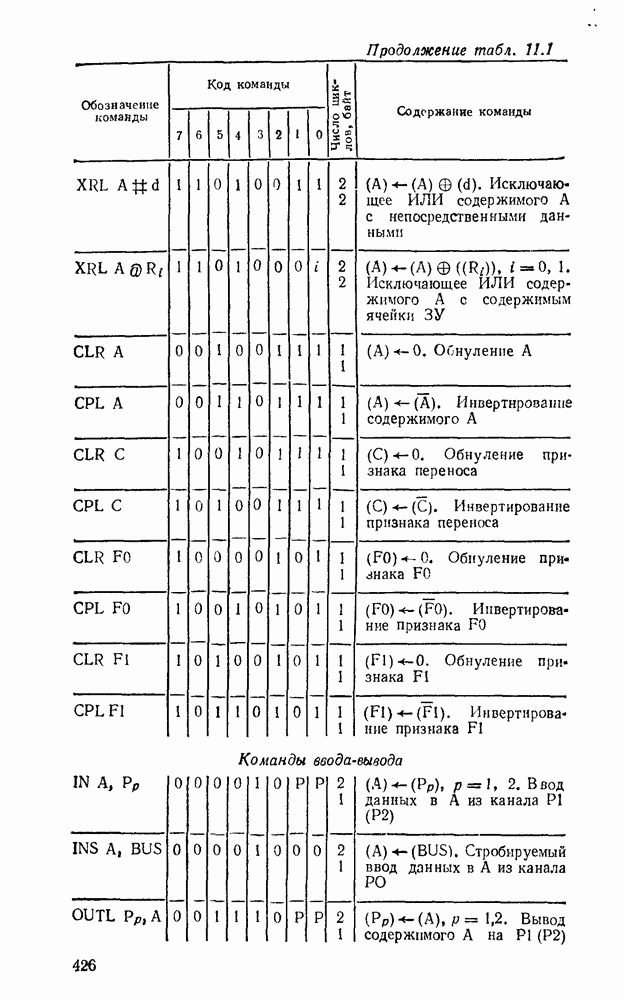
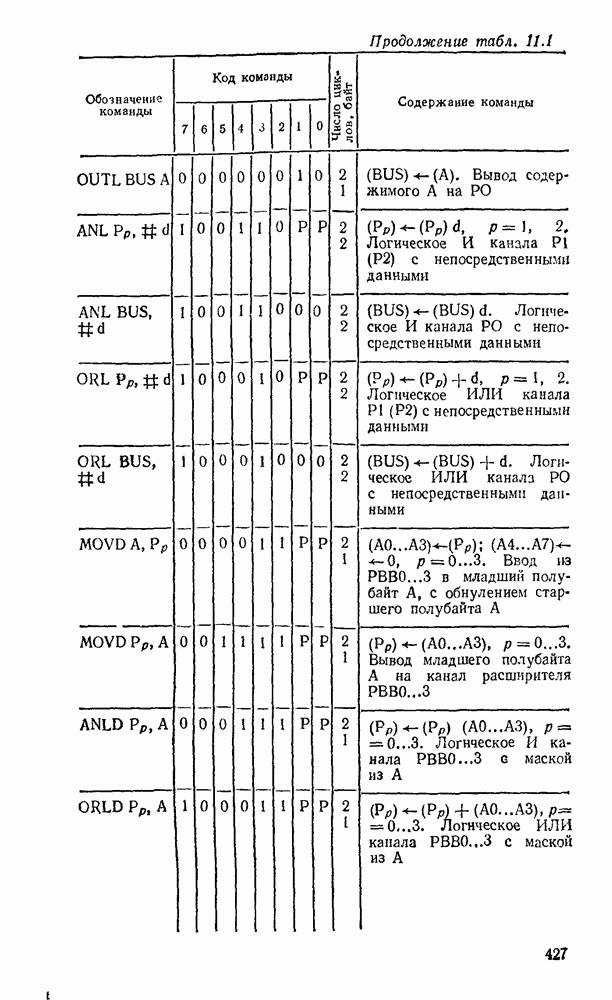
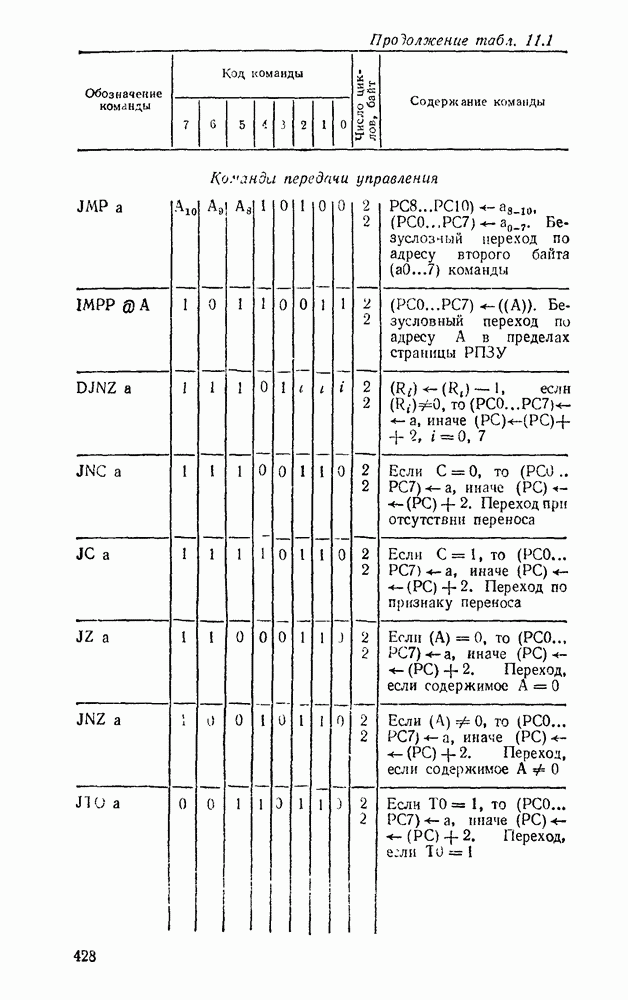
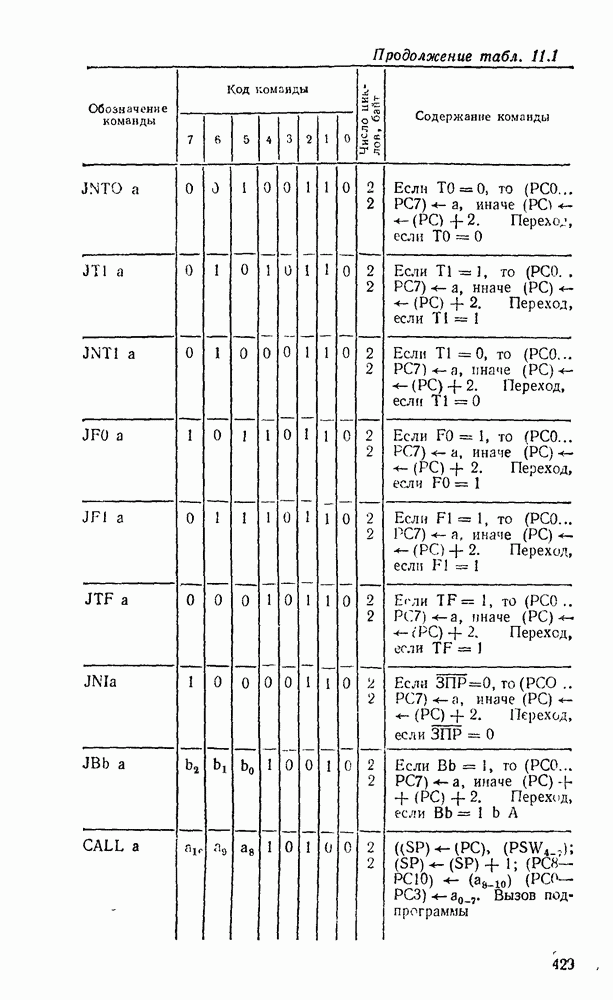
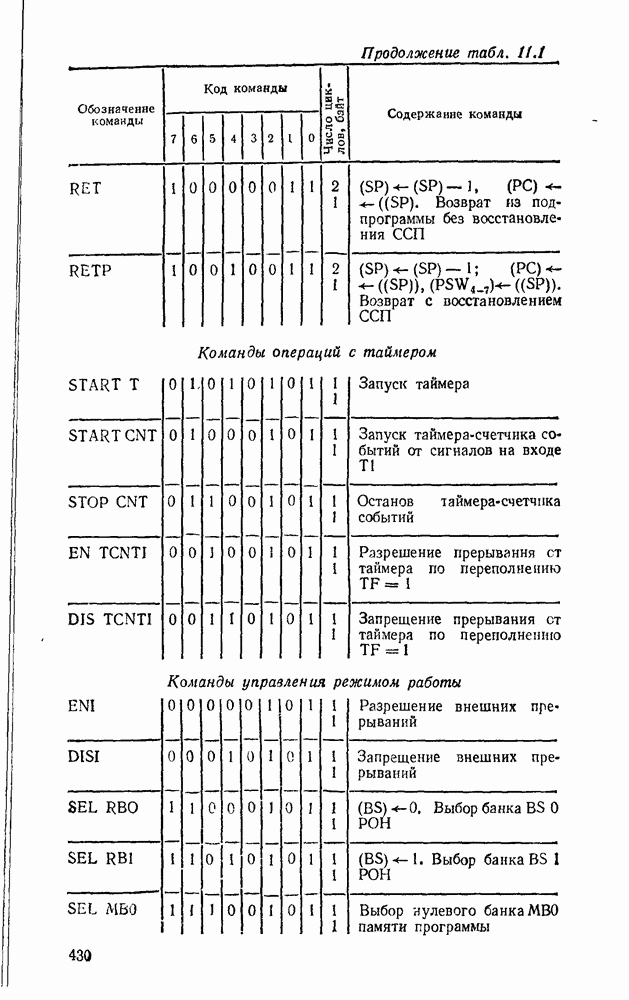
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
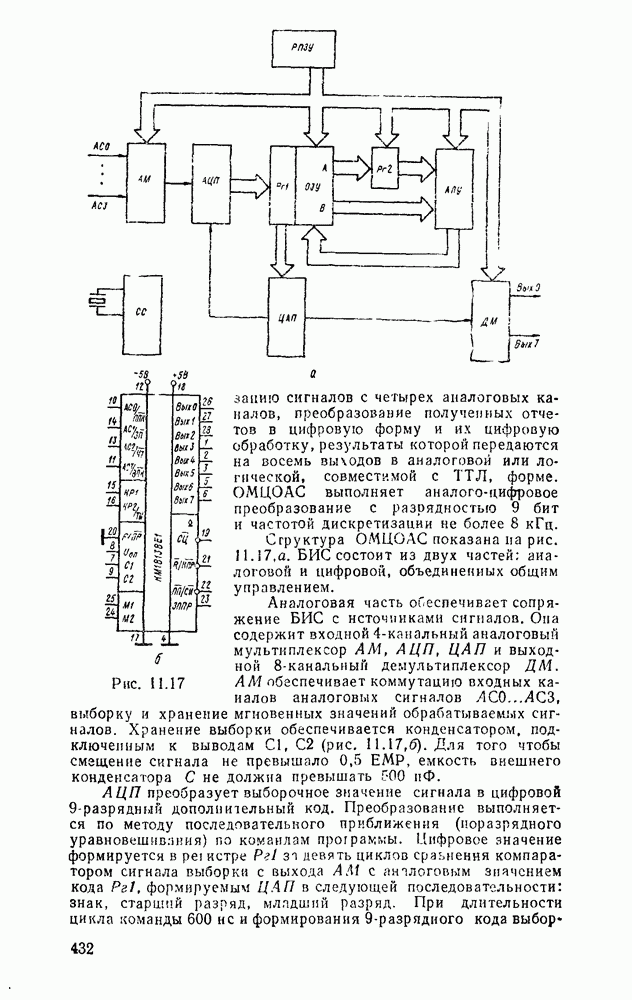
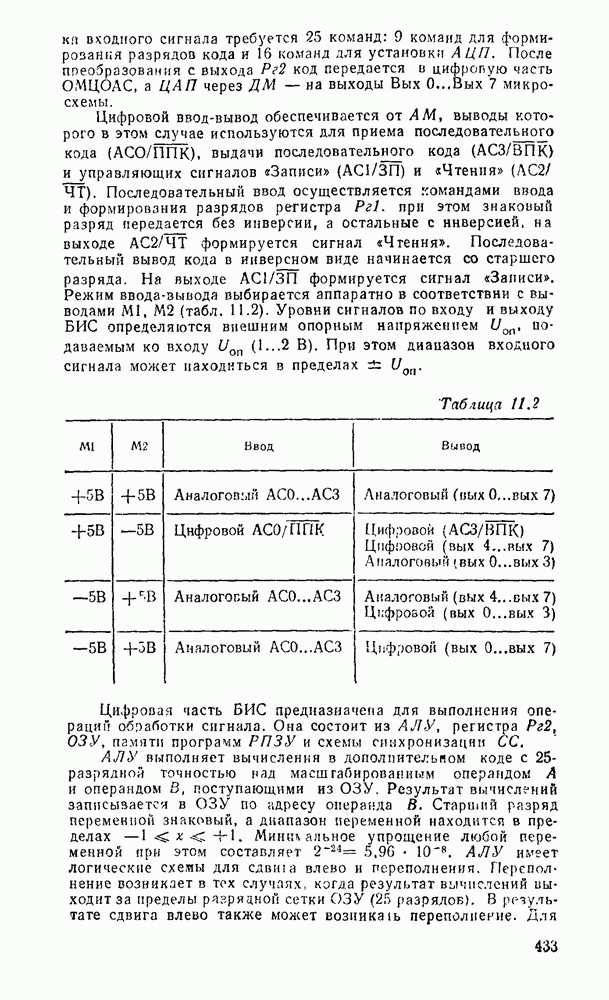
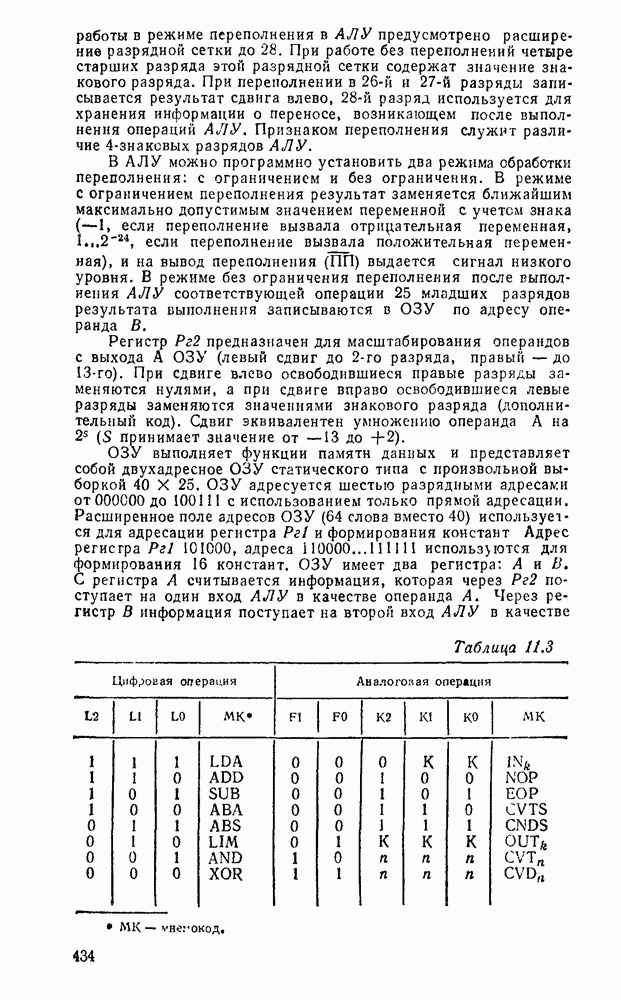
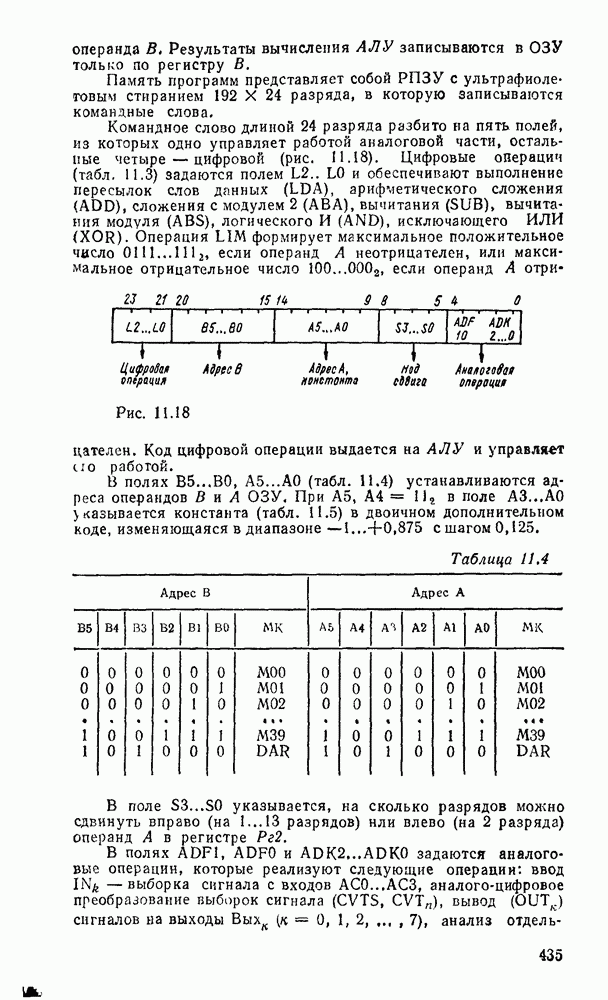
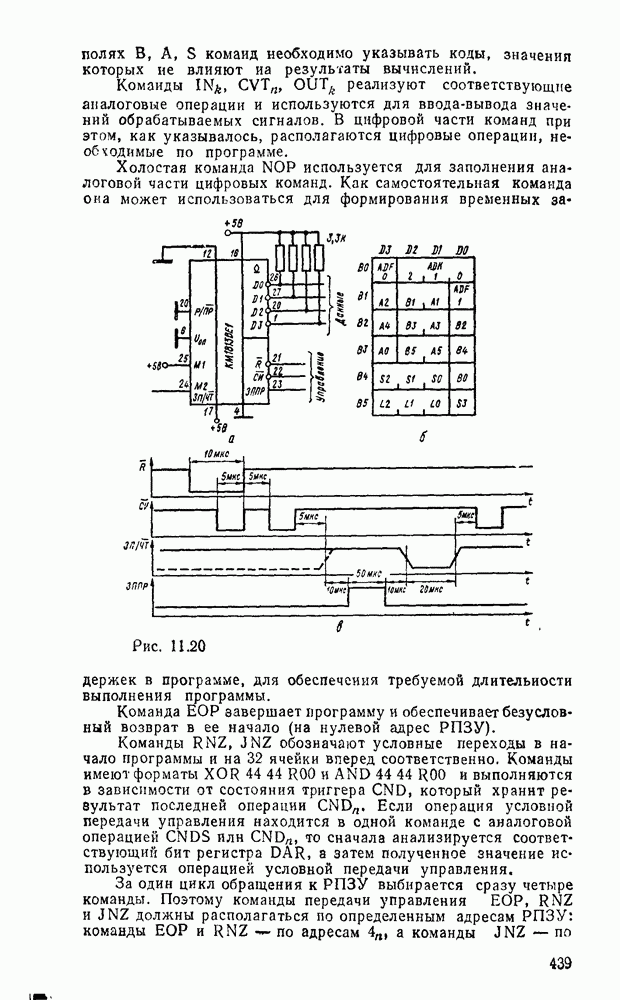
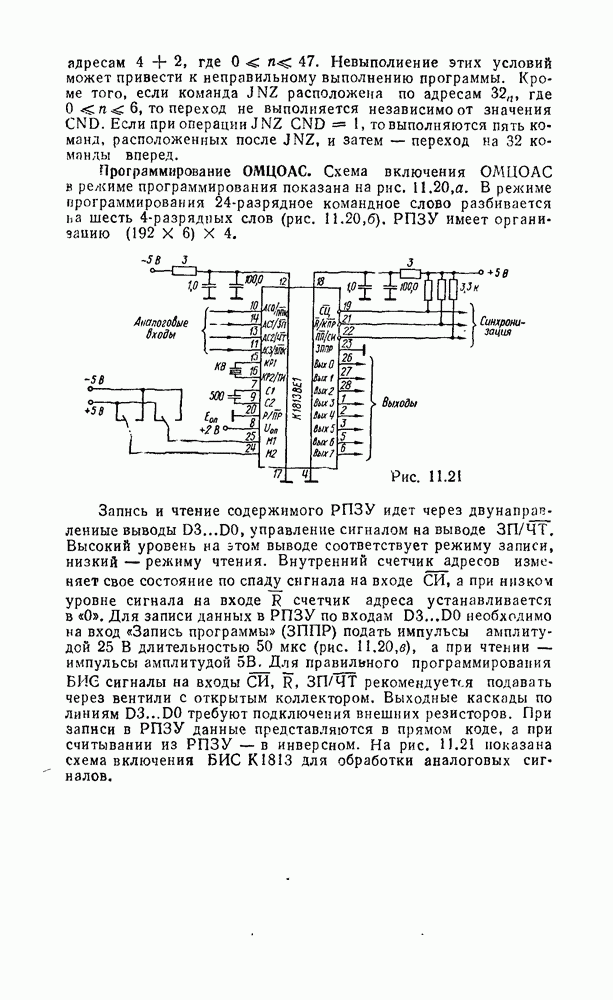
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ