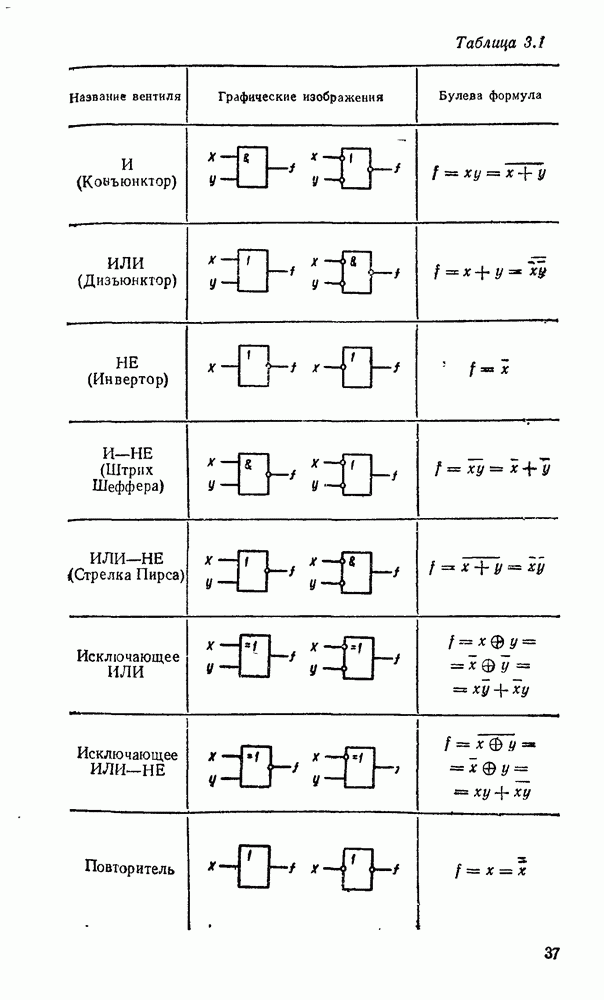
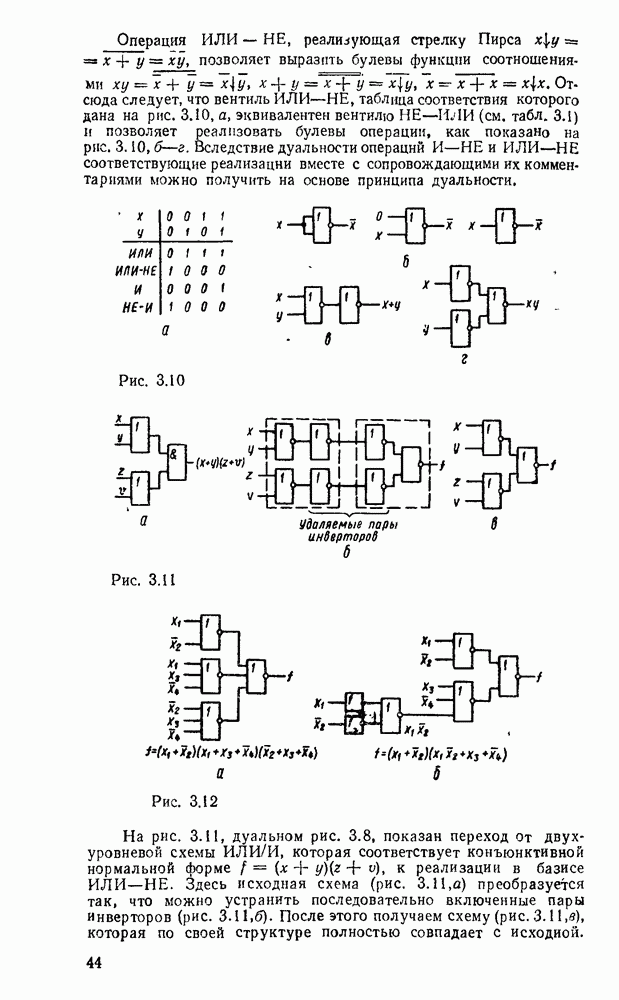
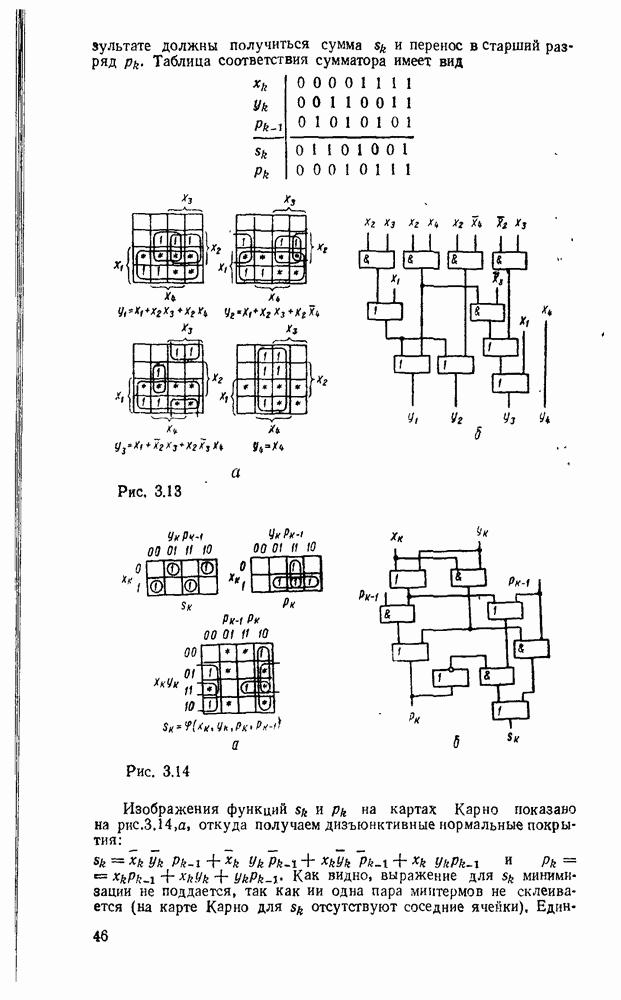
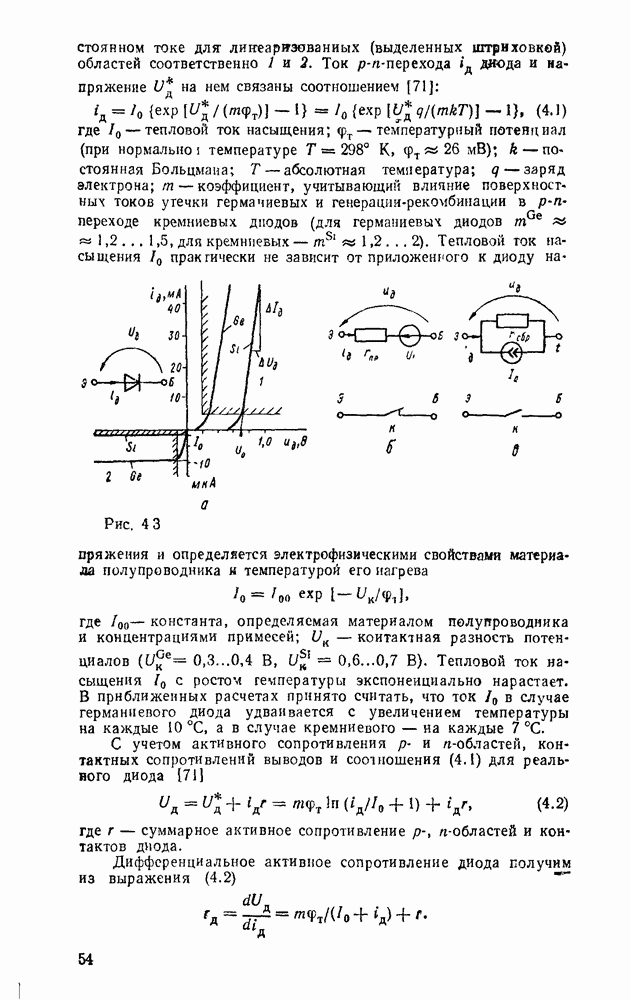
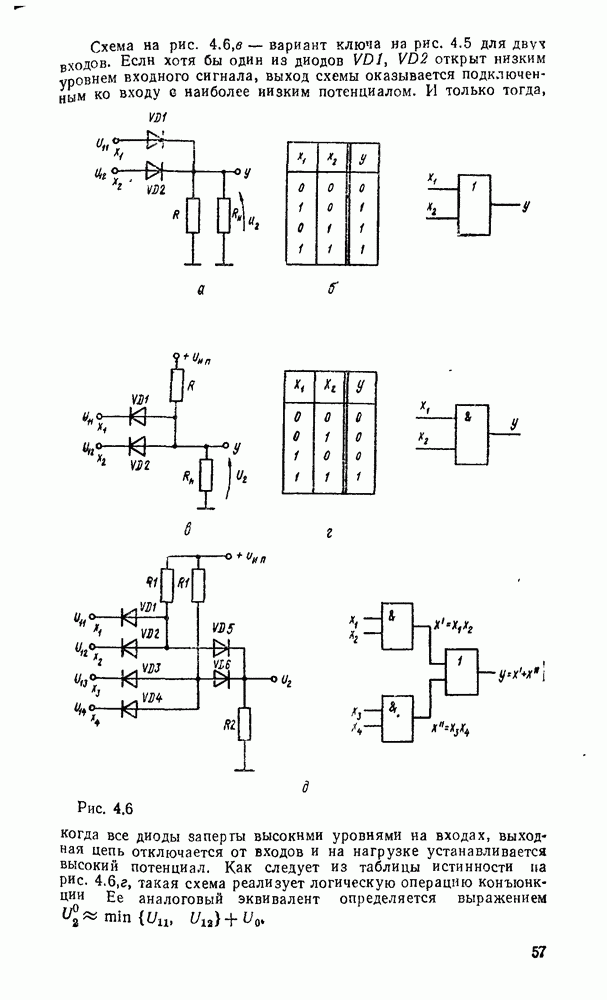
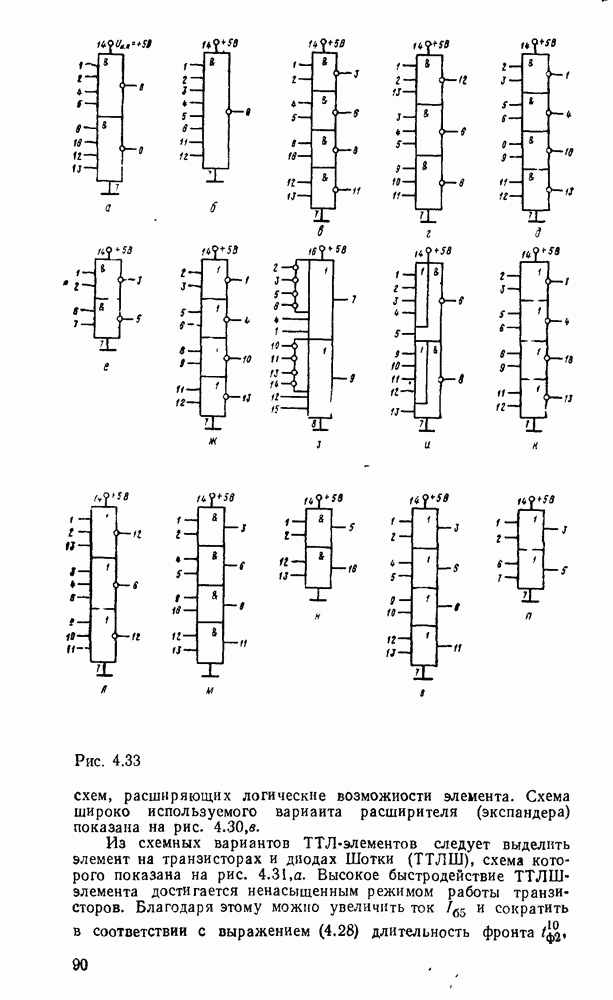
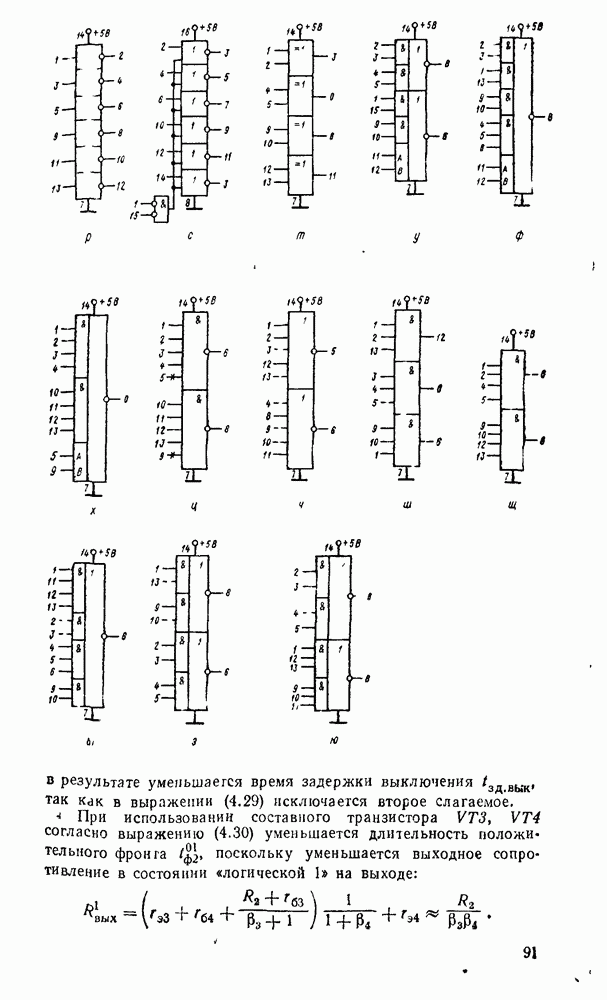
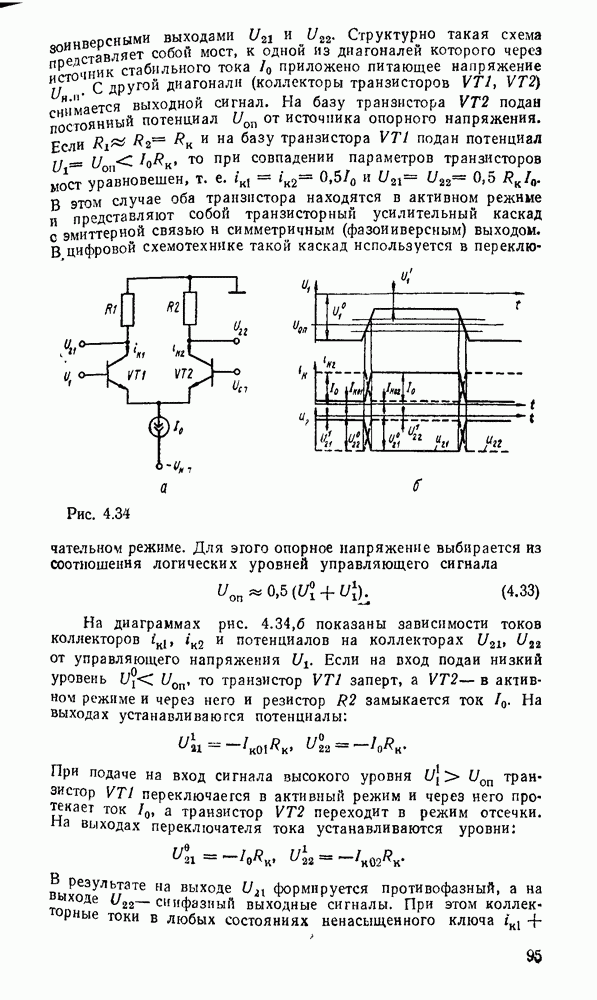
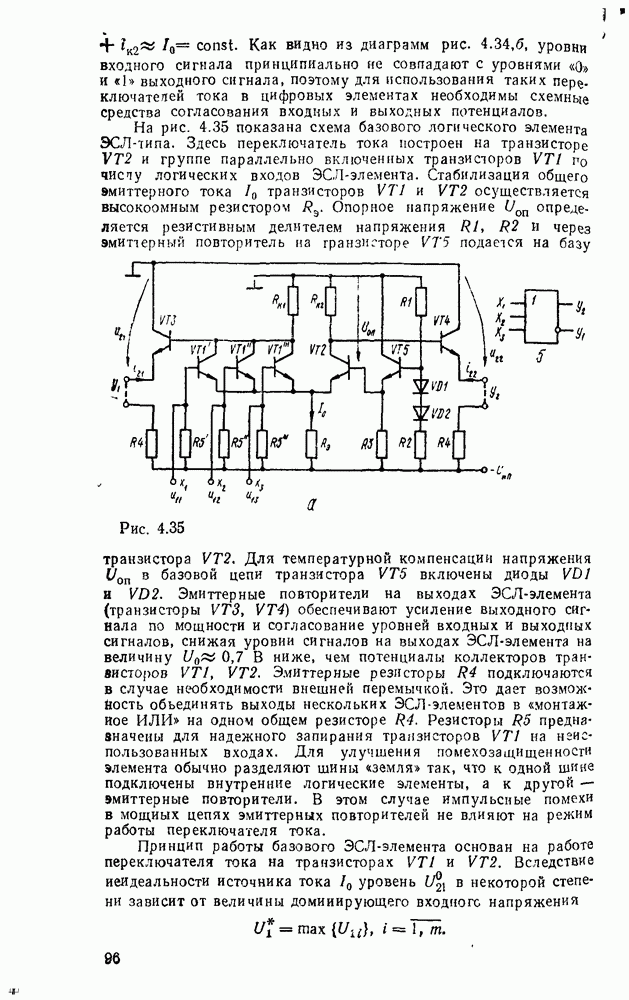
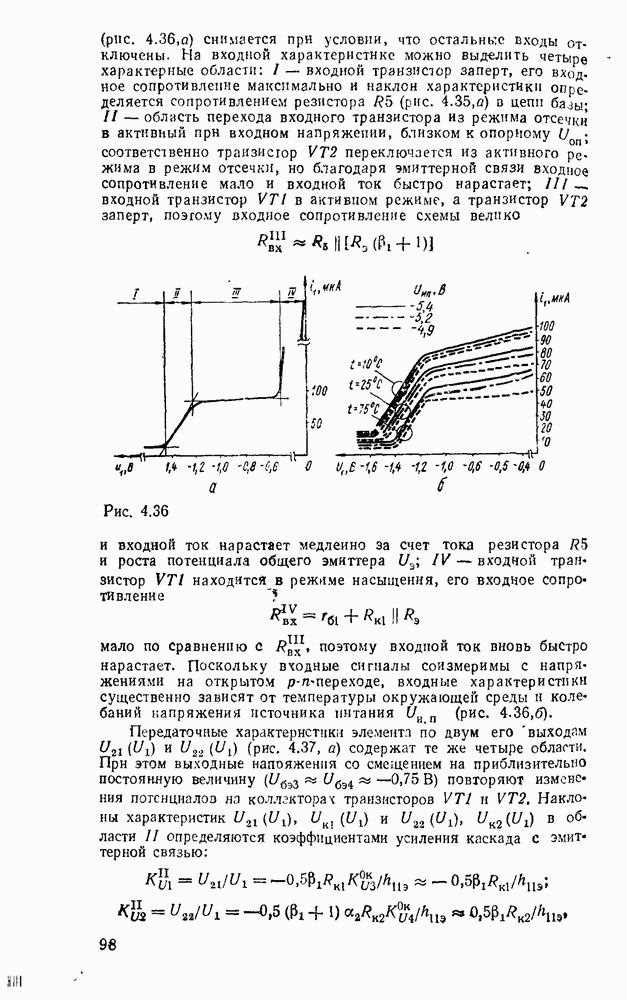
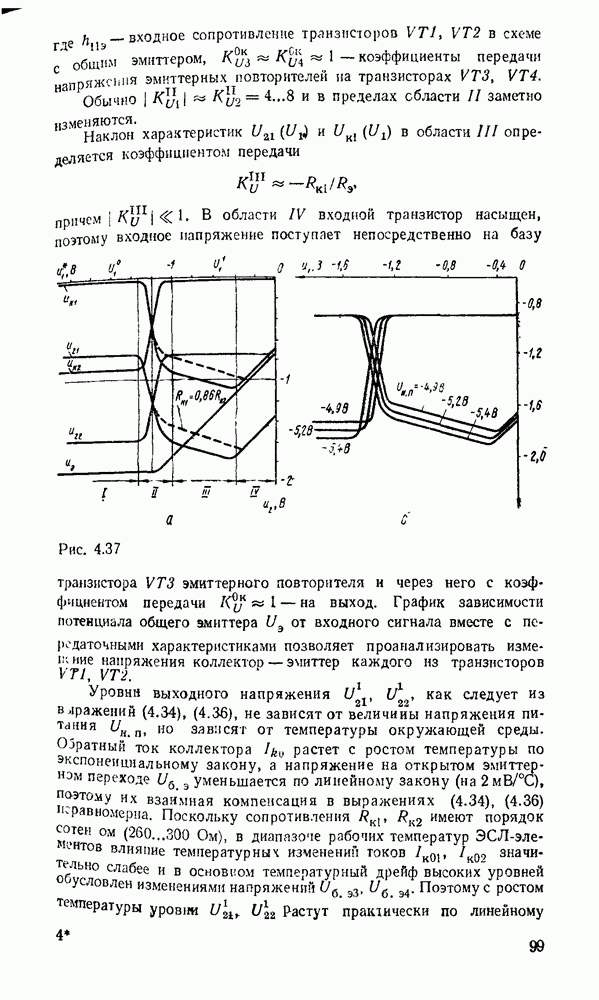
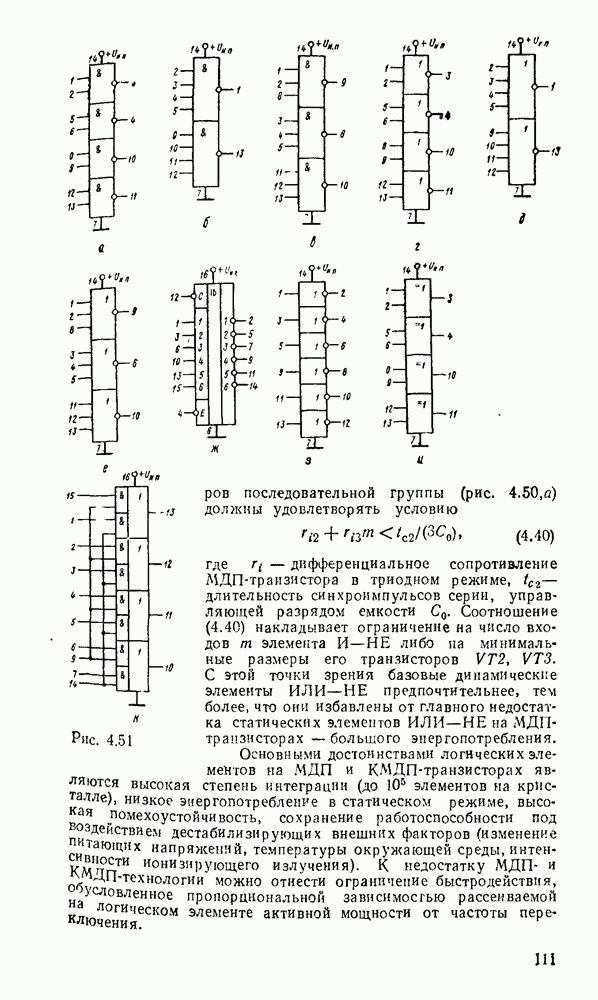
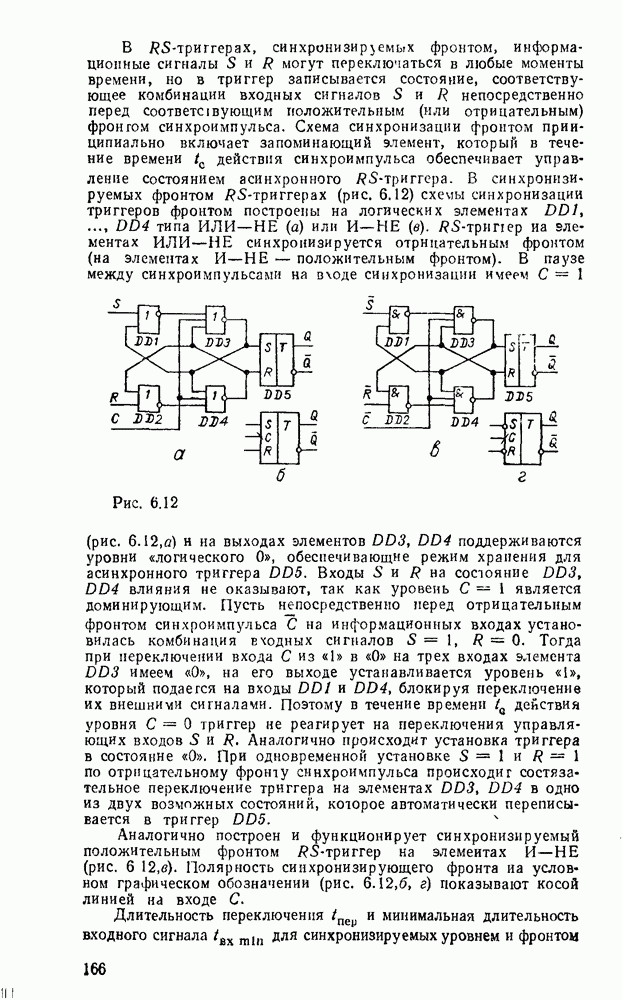
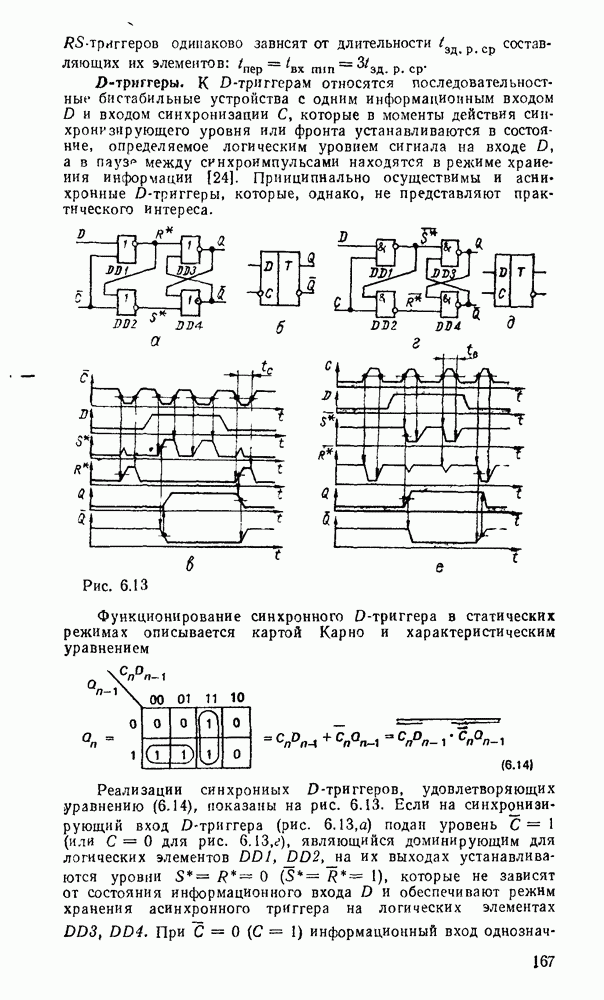
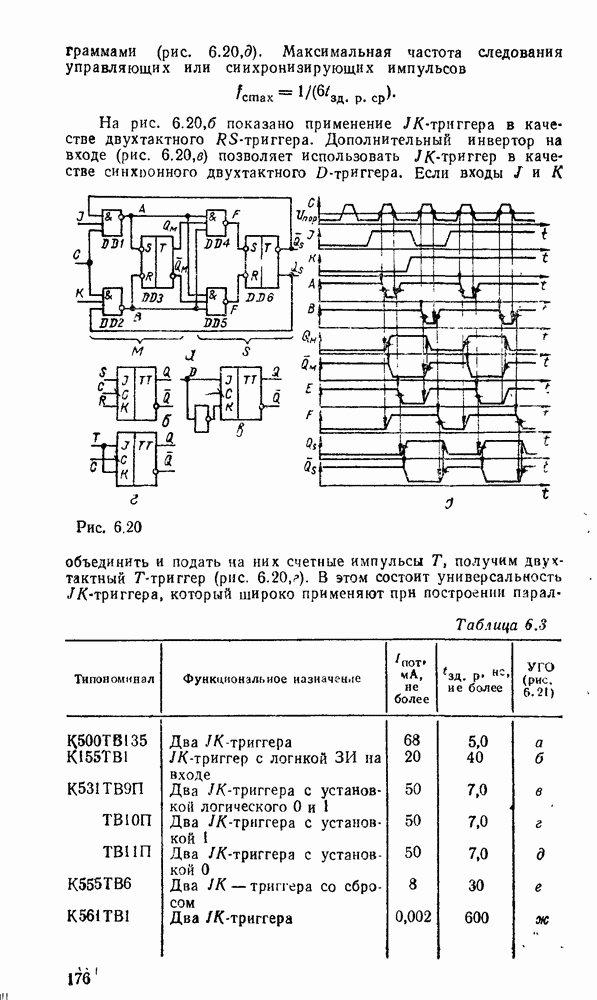
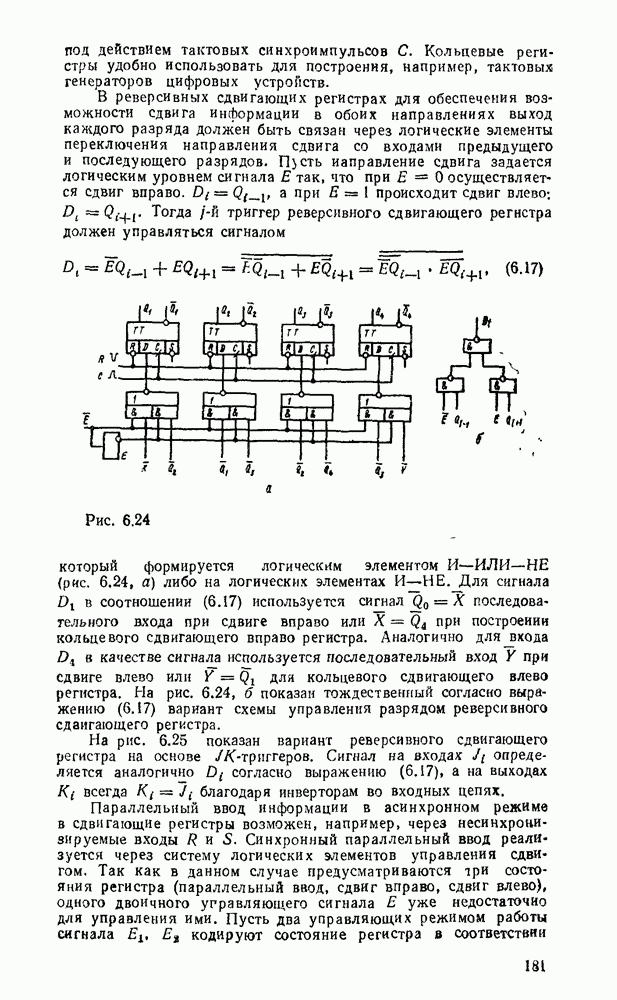
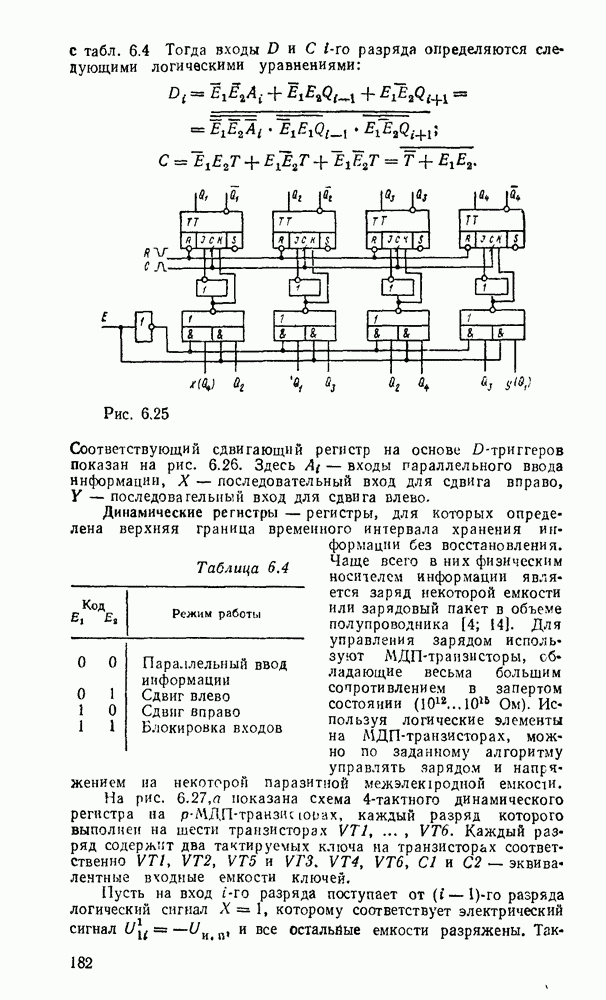
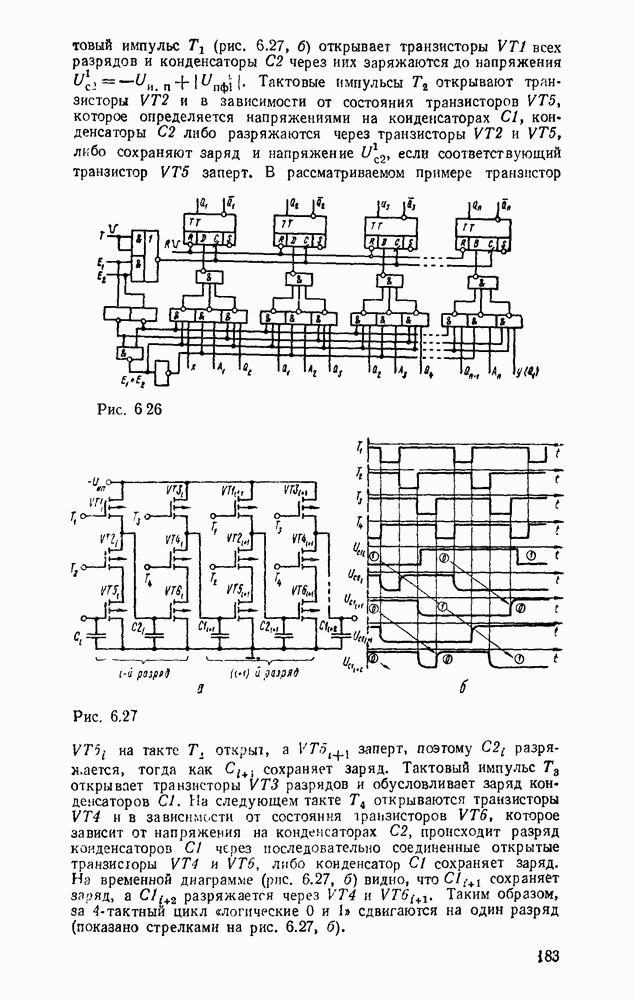
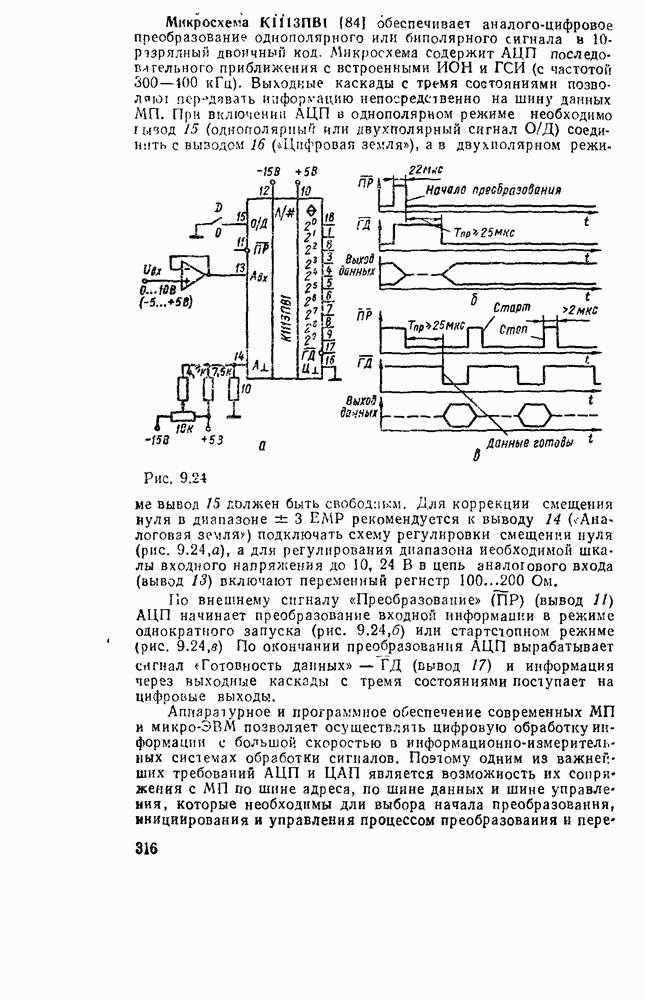
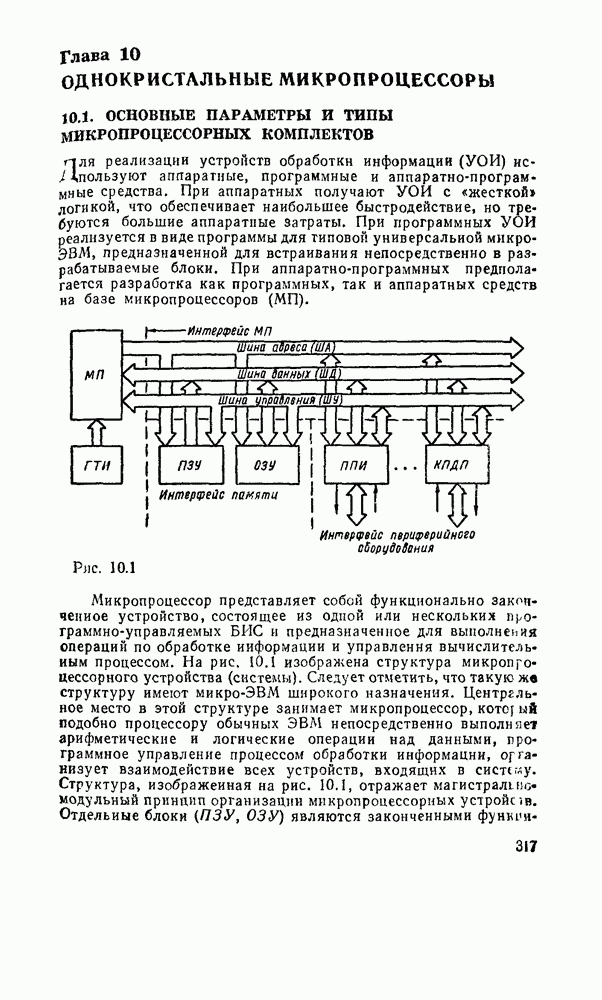
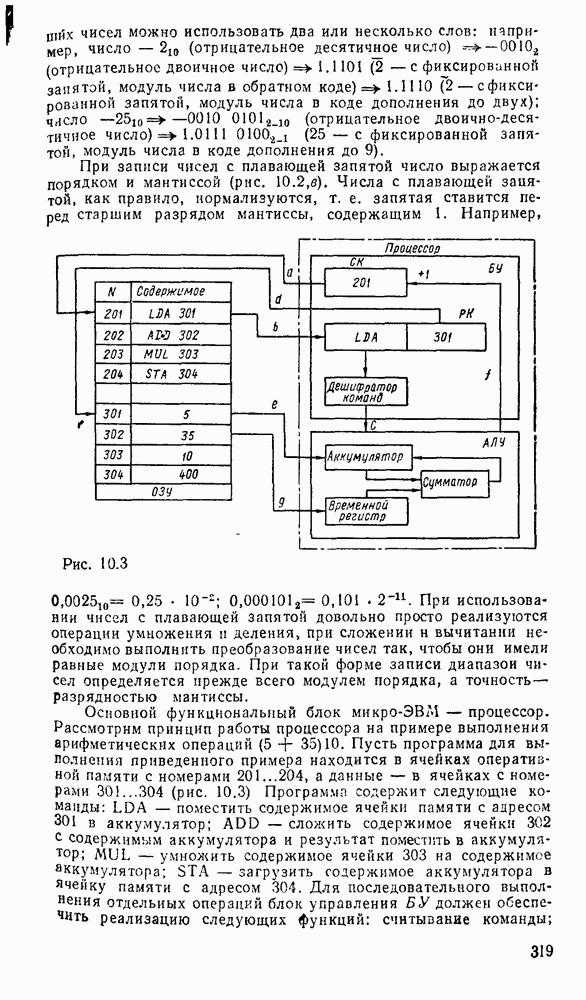
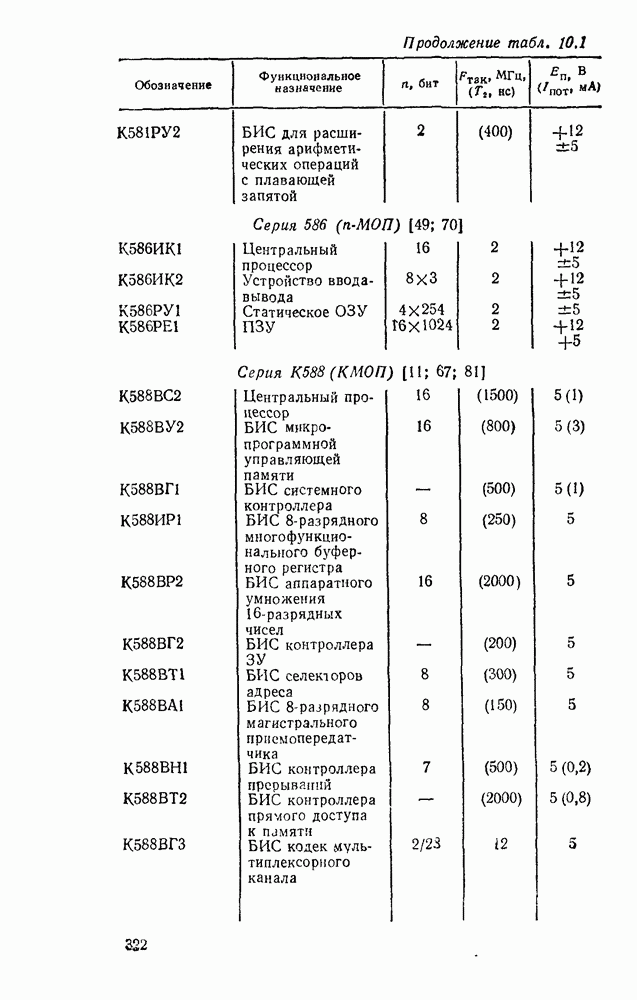
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
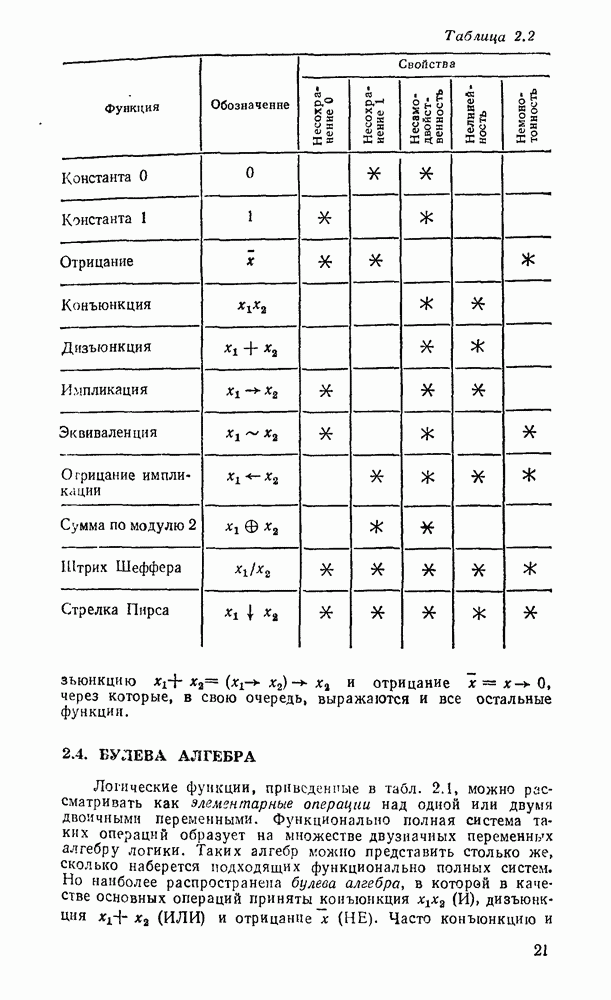
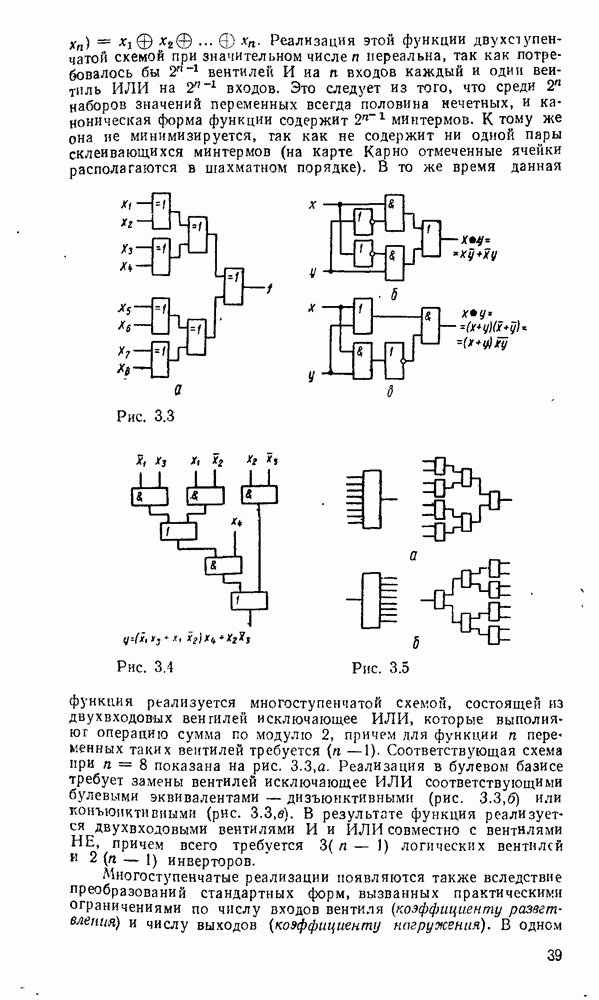
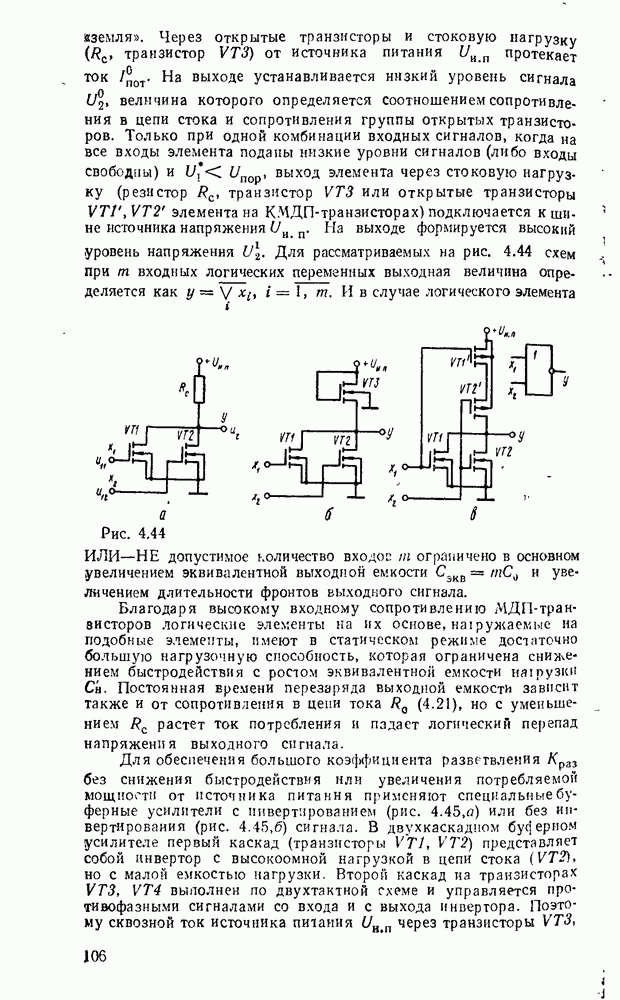
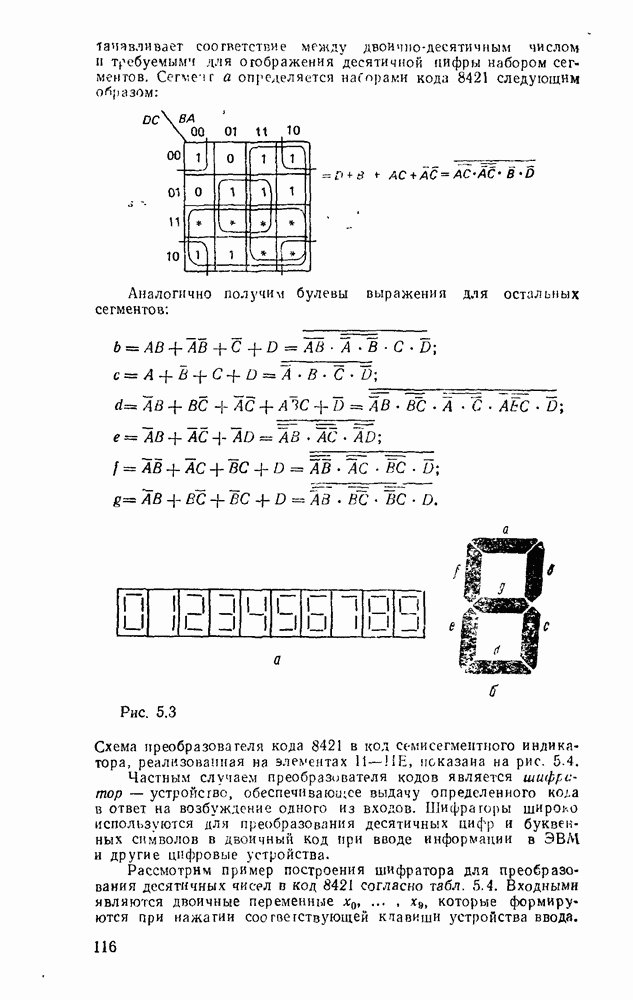
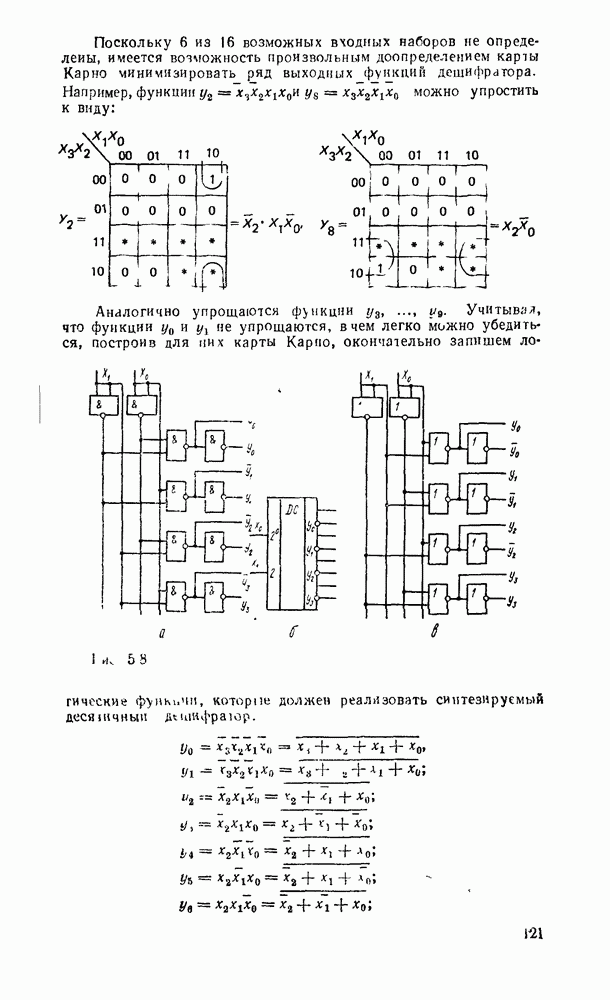
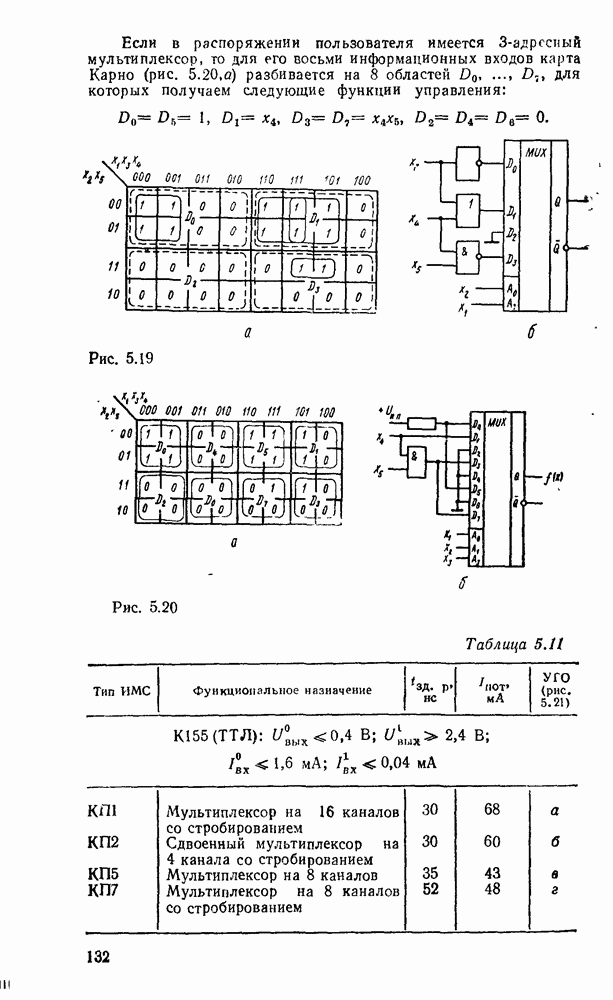
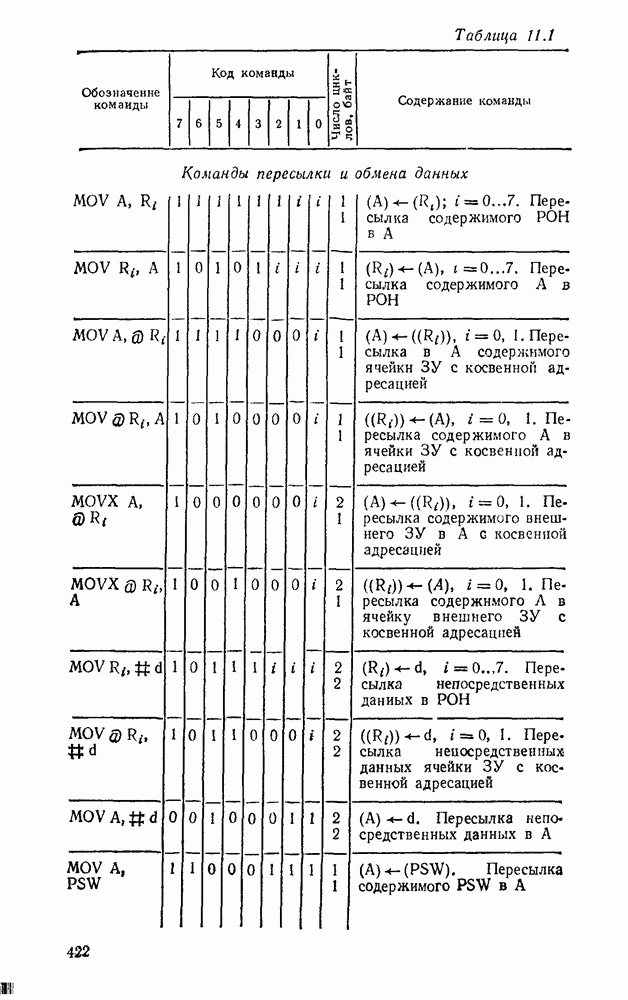
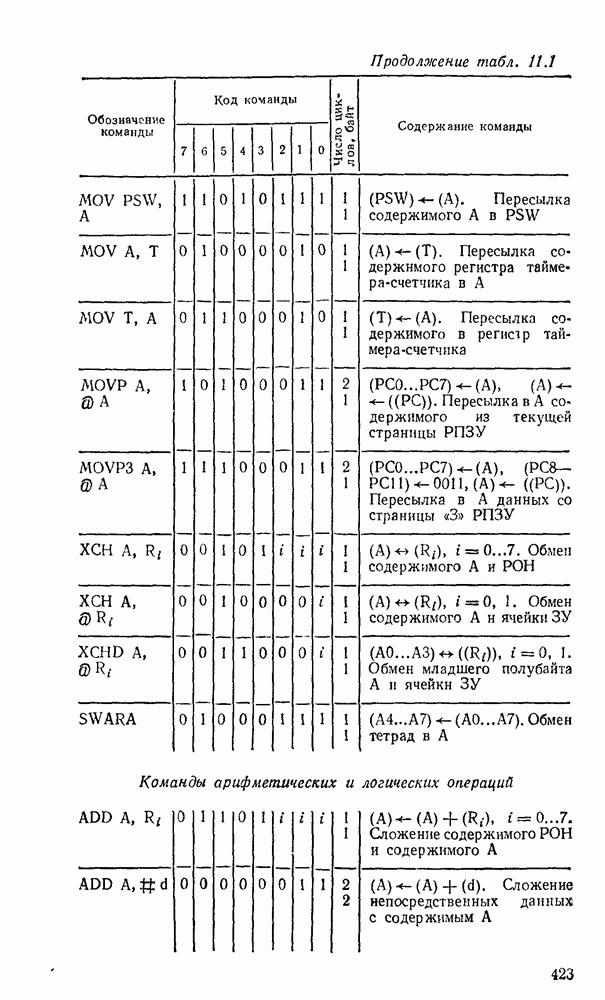
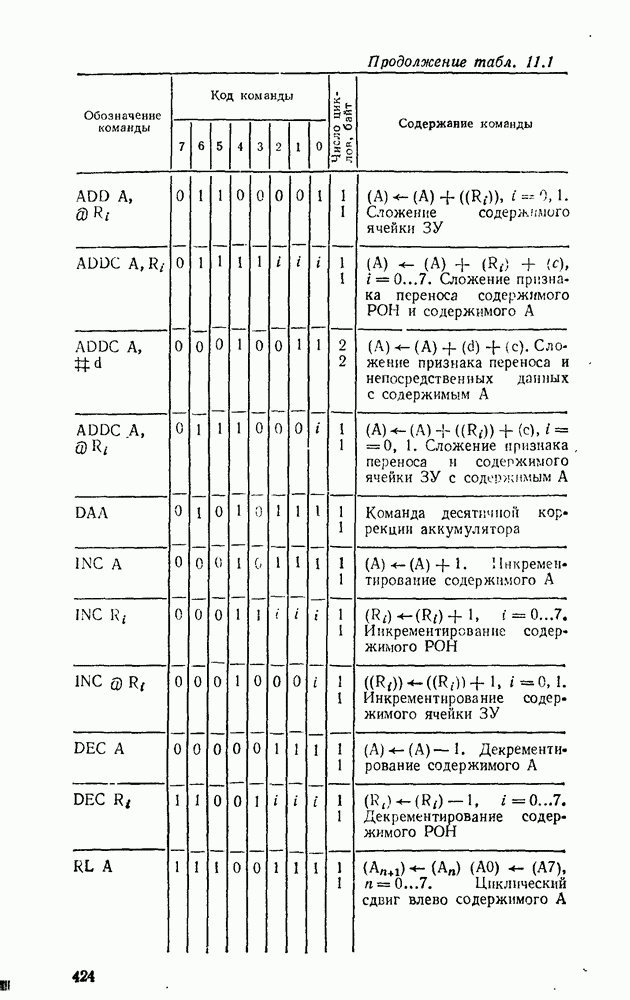
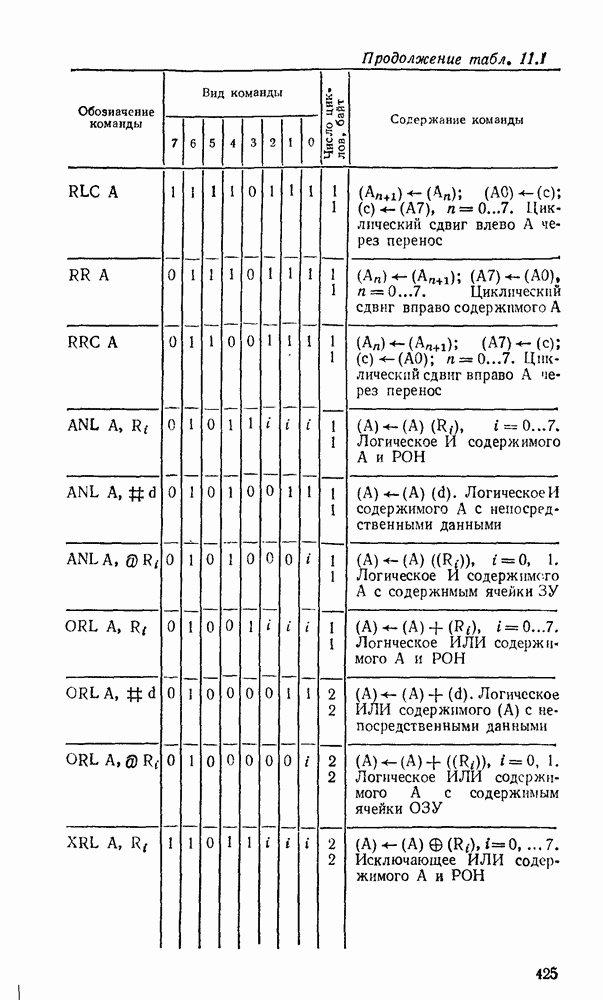
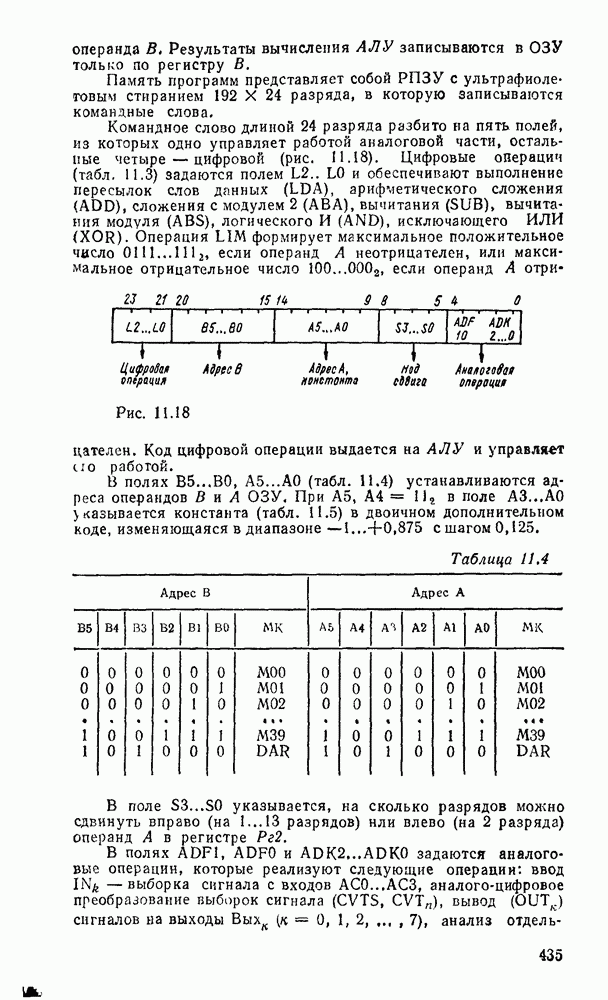
5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
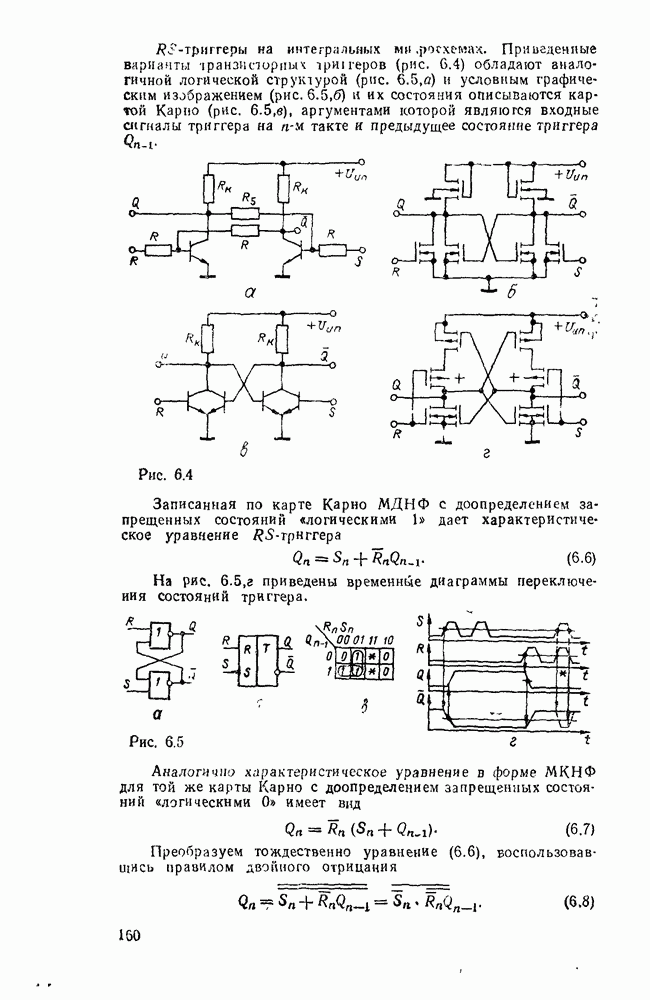
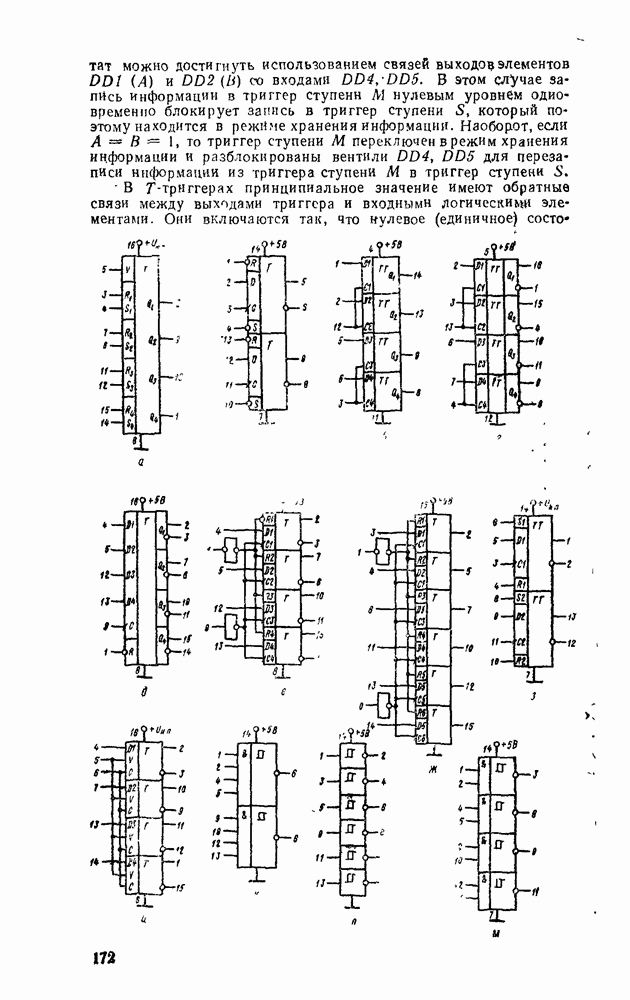
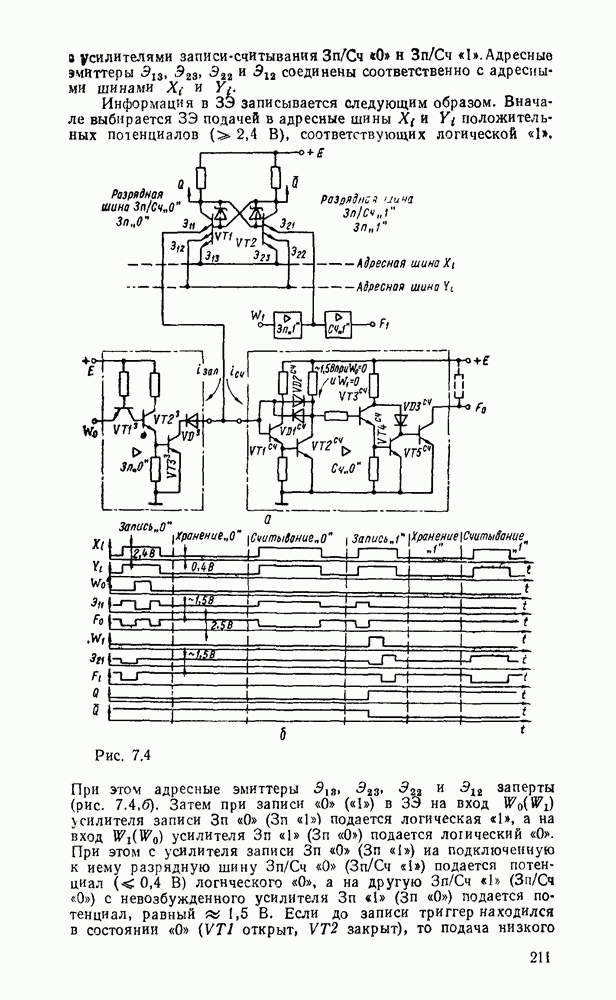
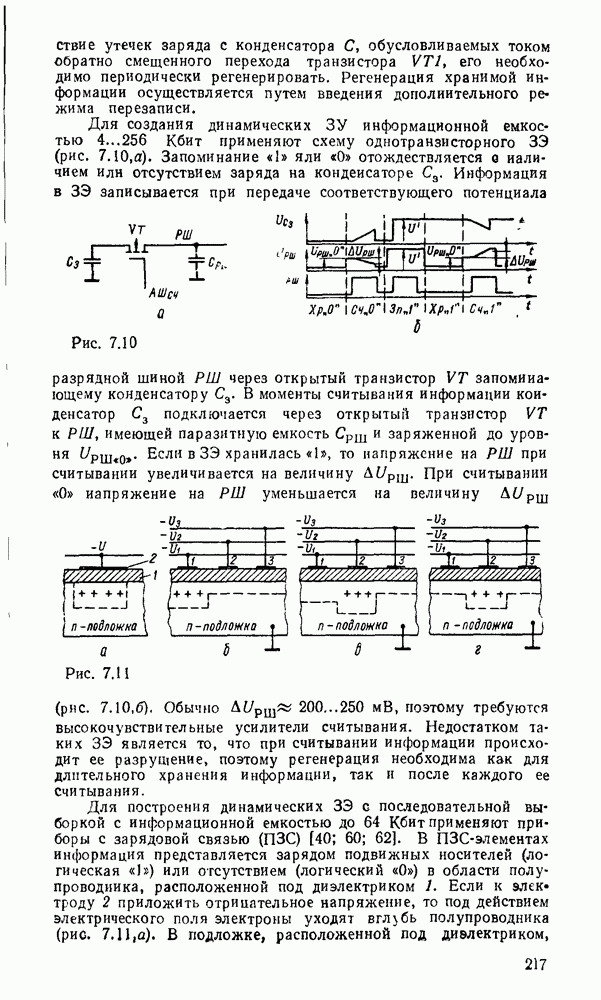
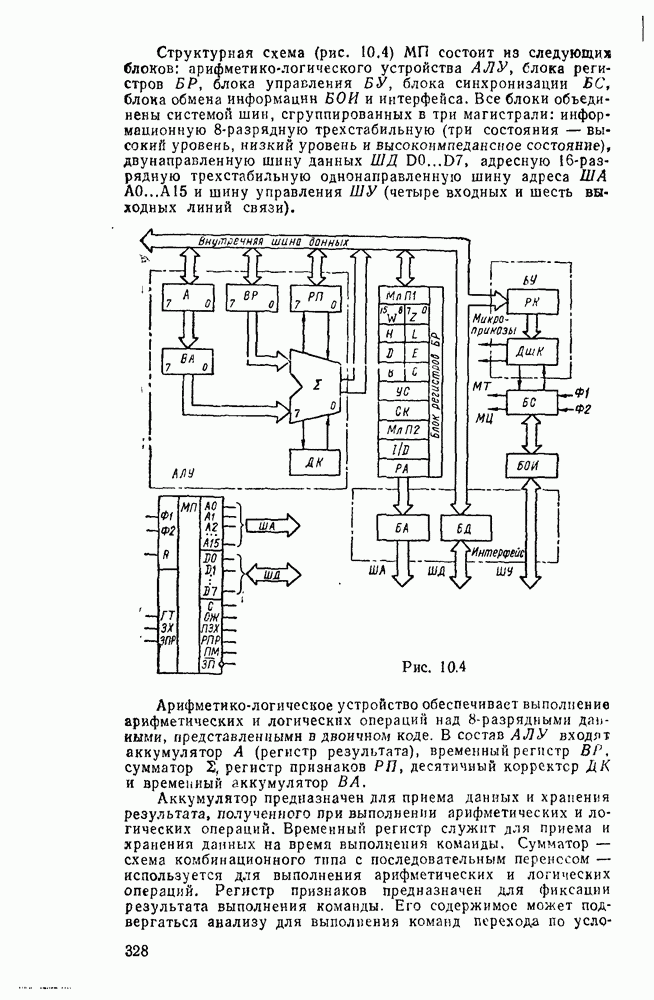
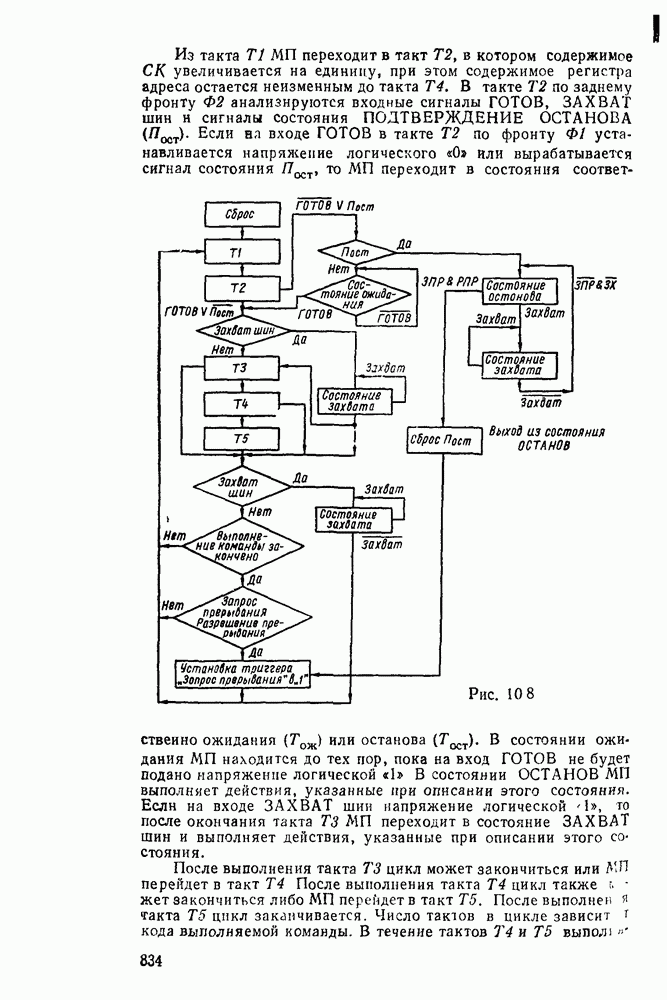
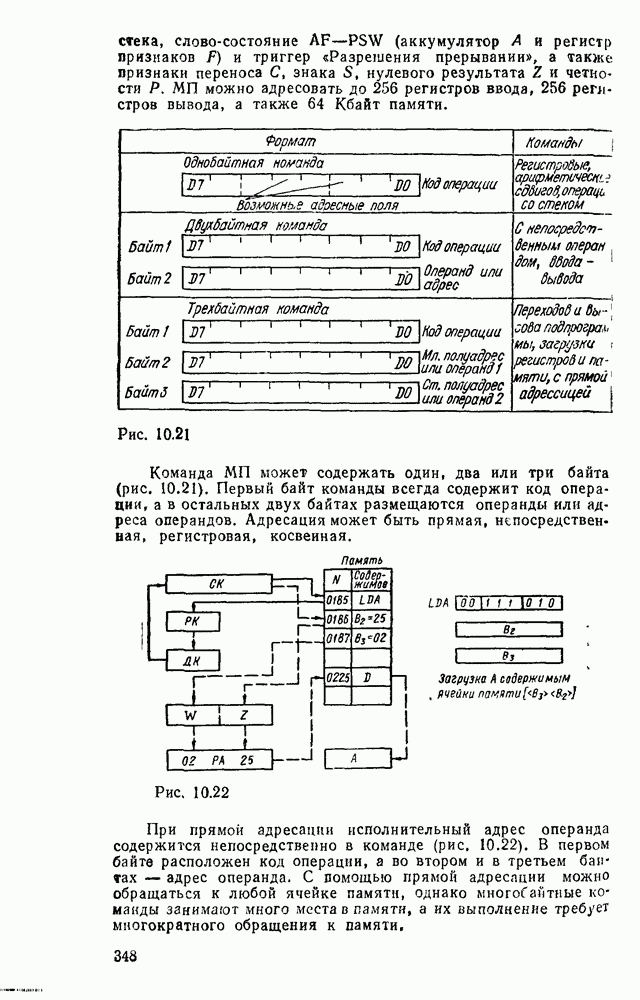
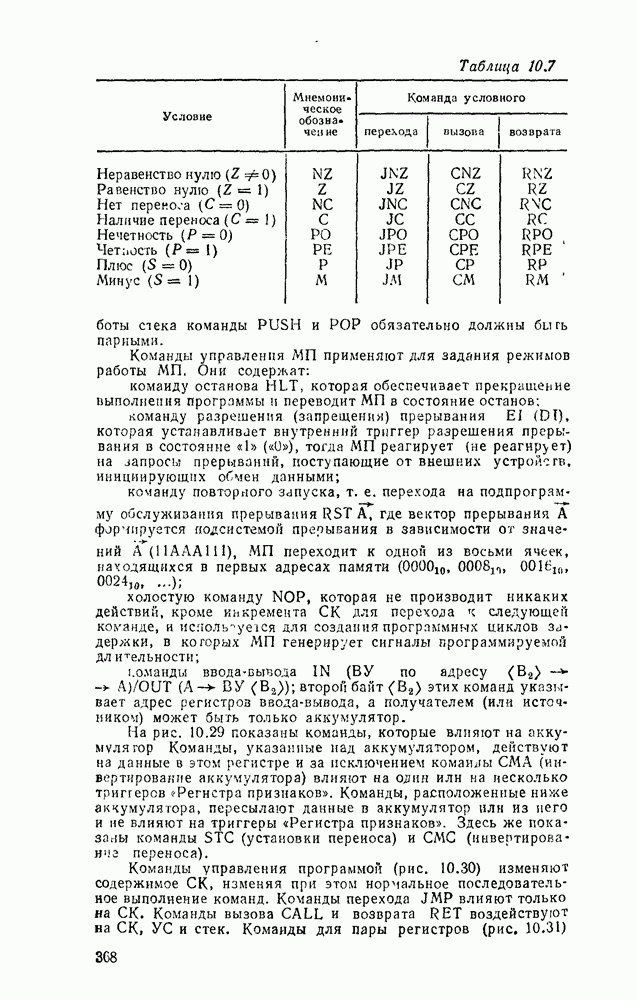
Сумматор — устройство, предназначенное для выполнения операций сложения и вычитания над многоразрядными числами (операндами). Многоразрядный сумматор состоит из одноразрядных, реализующих сложение одноразрядных чисел.

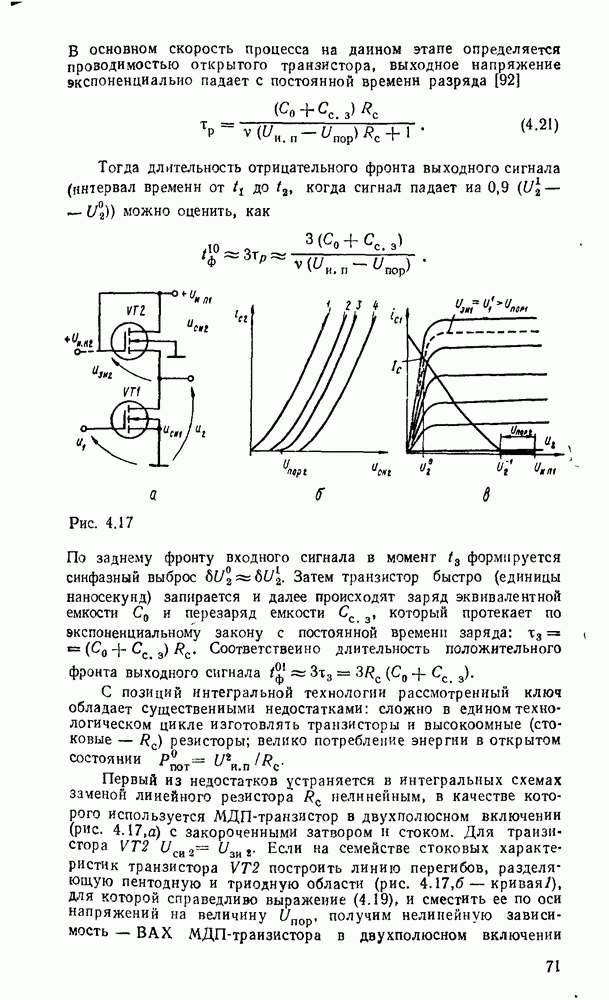
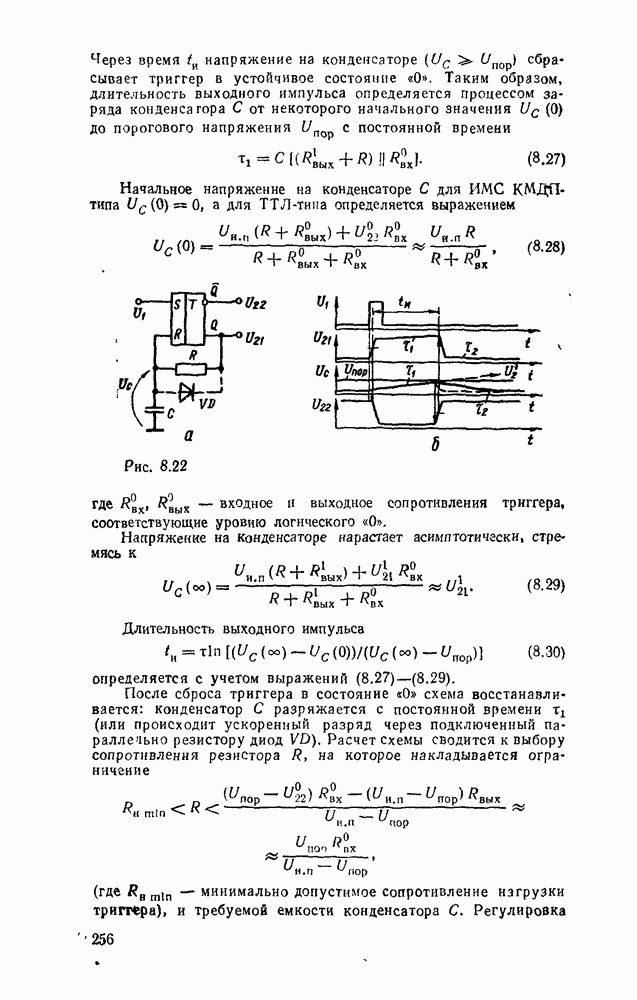
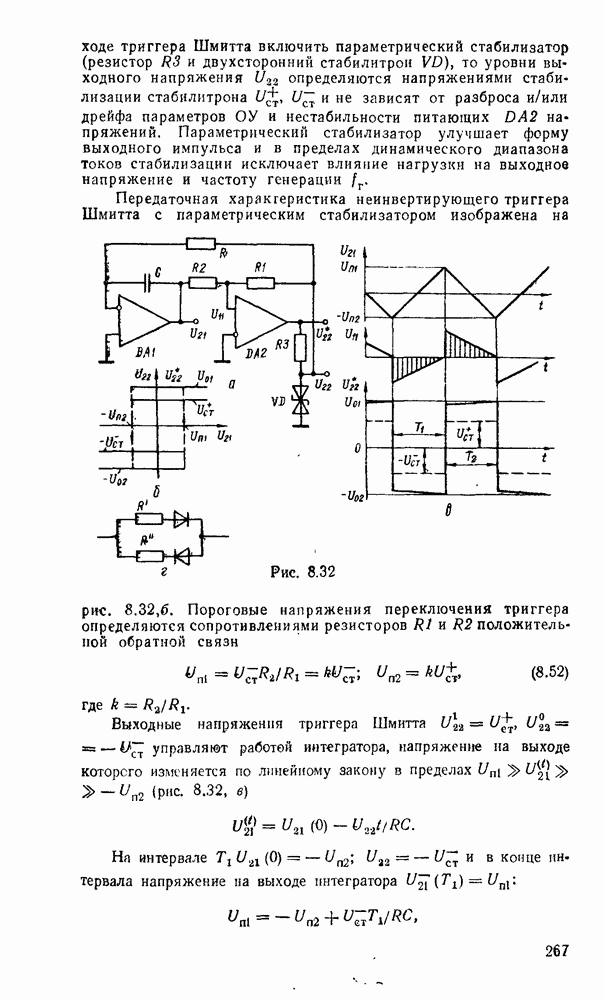
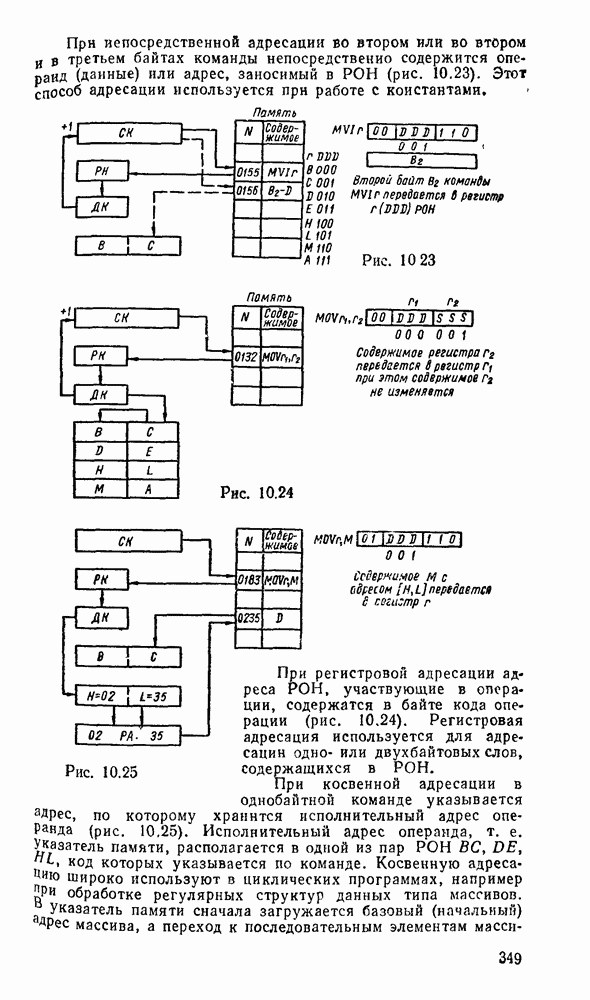
Рис. 5.25.
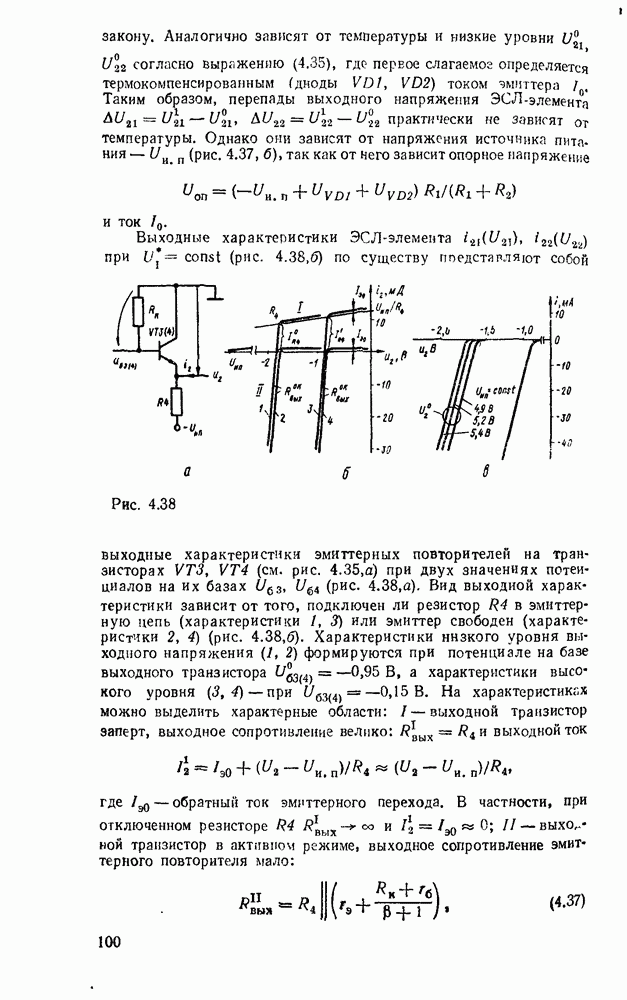
Одноразрядный сумматор, на вход которого поступают два одноразрядных числа  , а на выходе формируются также одноразрядные числа суммы и переноса
, а на выходе формируются также одноразрядные числа суммы и переноса  , называют полусумматором
, называют полусумматором  . Если одноразрядный сумматор реализует сложение трех одноразрядных чисел
. Если одноразрядный сумматор реализует сложение трех одноразрядных чисел  (перенос из младшего разряда), то такой сумматор называют полным. В многоразрядном сумматоре только самый младший разряд можно выполнить по схеме полусумматора, а остальные разряды выполняют функции полного сумматора. Ниже рассмотрены слемы сумматоров для двоично кодированных чисел
(перенос из младшего разряда), то такой сумматор называют полным. В многоразрядном сумматоре только самый младший разряд можно выполнить по схеме полусумматора, а остальные разряды выполняют функции полного сумматора. Ниже рассмотрены слемы сумматоров для двоично кодированных чисел  .
.
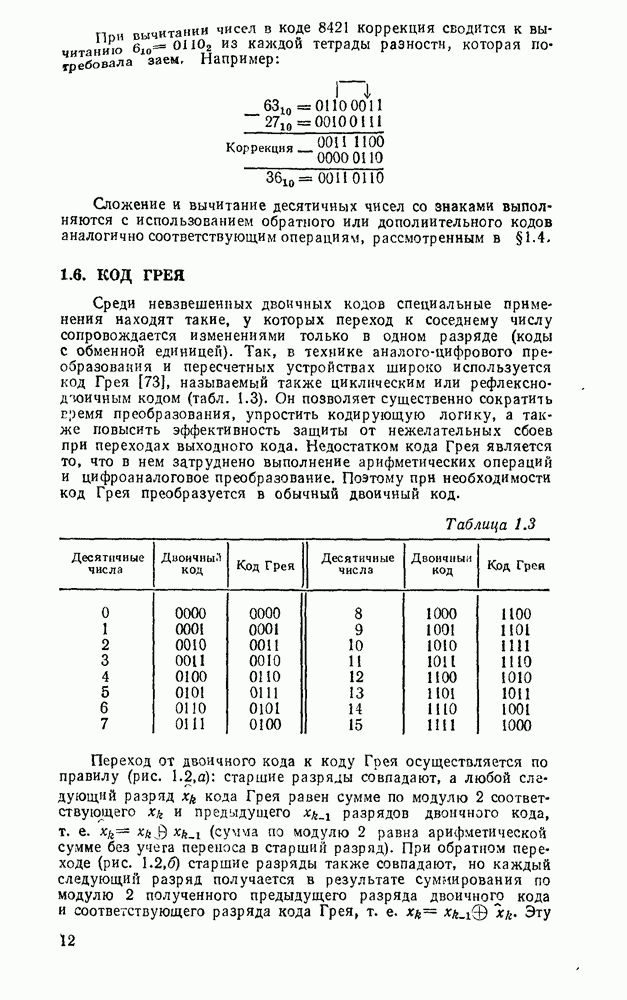
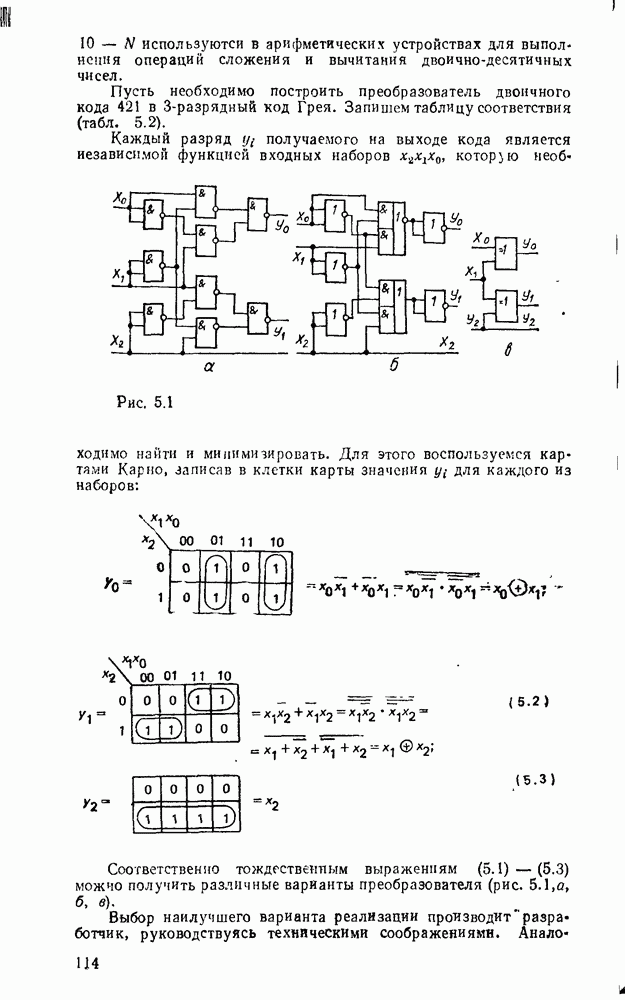
Таблица истинности для полусумматора (табл. 5.15) позволяет записать функцию вычисления суммы  и переноса единицы переполнения
и переноса единицы переполнения  в старший разряд:
в старший разряд:

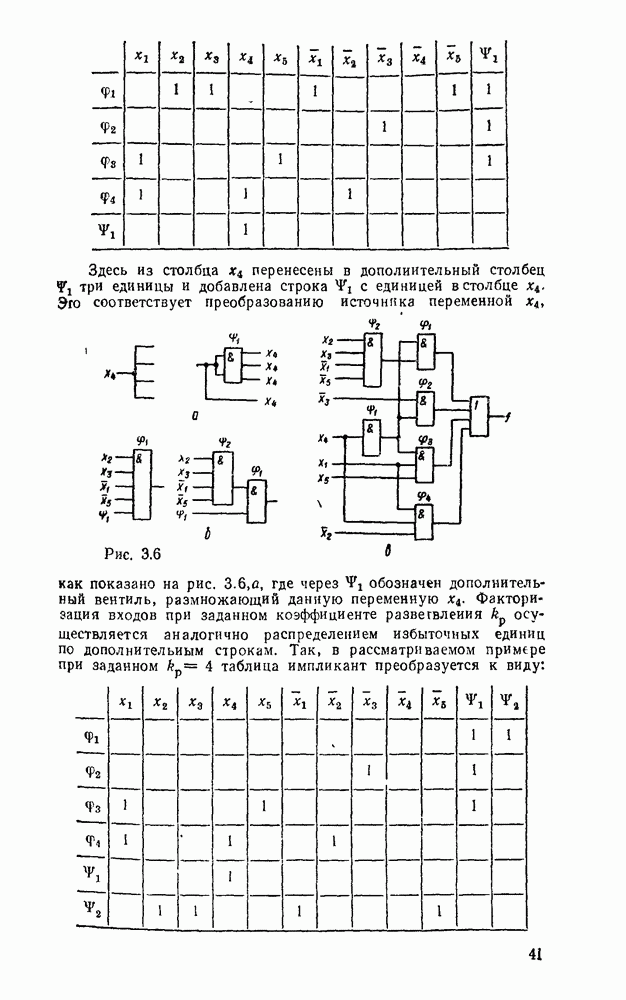
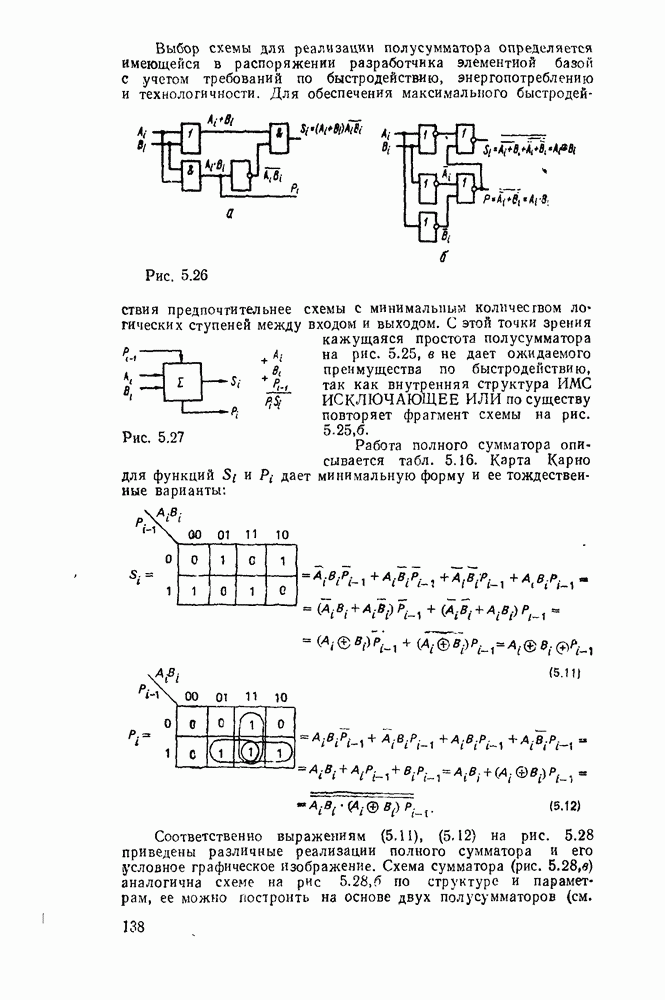
Согласно выражениям (5.10) полусумматор можно реализовать в базнсе элементов  , ИЛИ—НЕ либо на основе логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ и конъюнктора (рис. 5.25,в). Возможны другие реализации полусумматора на основании тождественных преобразований (5.10)
, ИЛИ—НЕ либо на основе логического элемента ИСКЛЮЧАЮЩЕЕ ИЛИ и конъюнктора (рис. 5.25,в). Возможны другие реализации полусумматора на основании тождественных преобразований (5.10)

Соответствующие реализации показаны на рис.  .
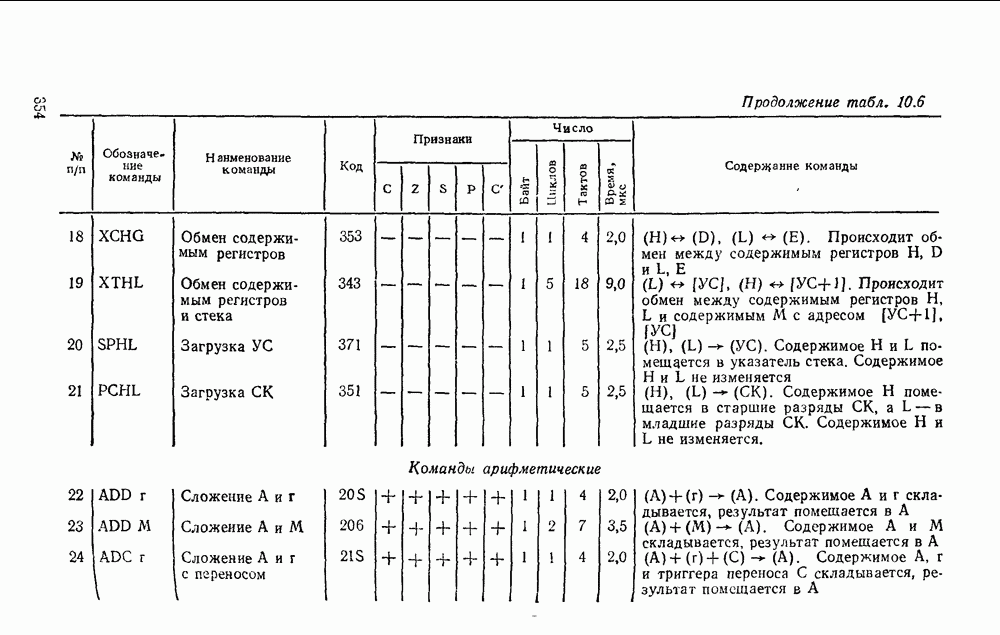
.
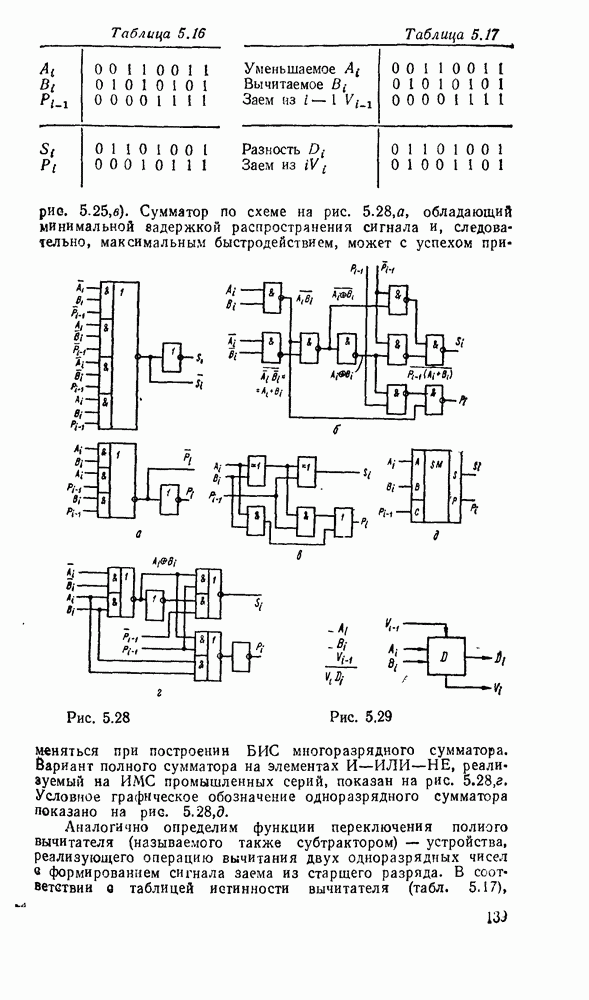
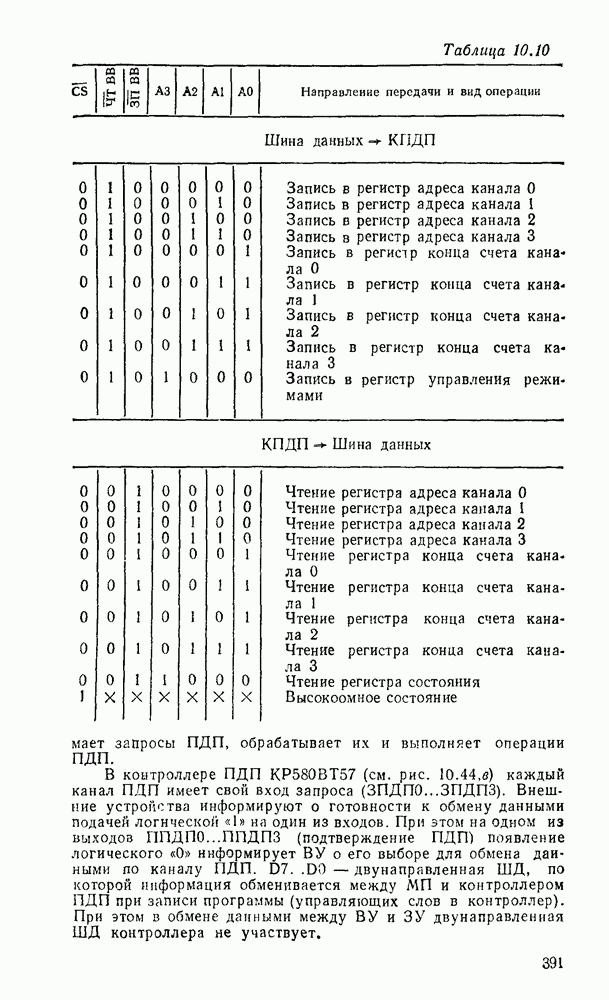
Таблица 5.15

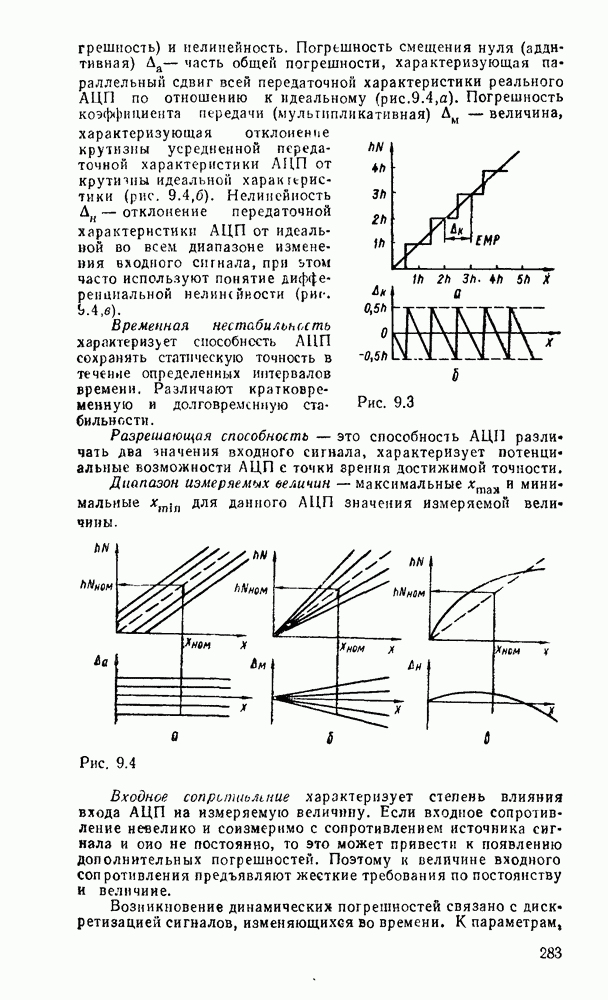
Выбор схемы для реализации полусумматора определяется имеющейся в распоряжении разработчика элементной базой с учетом требований по быстродействию, энергопотреблению и технологичности.

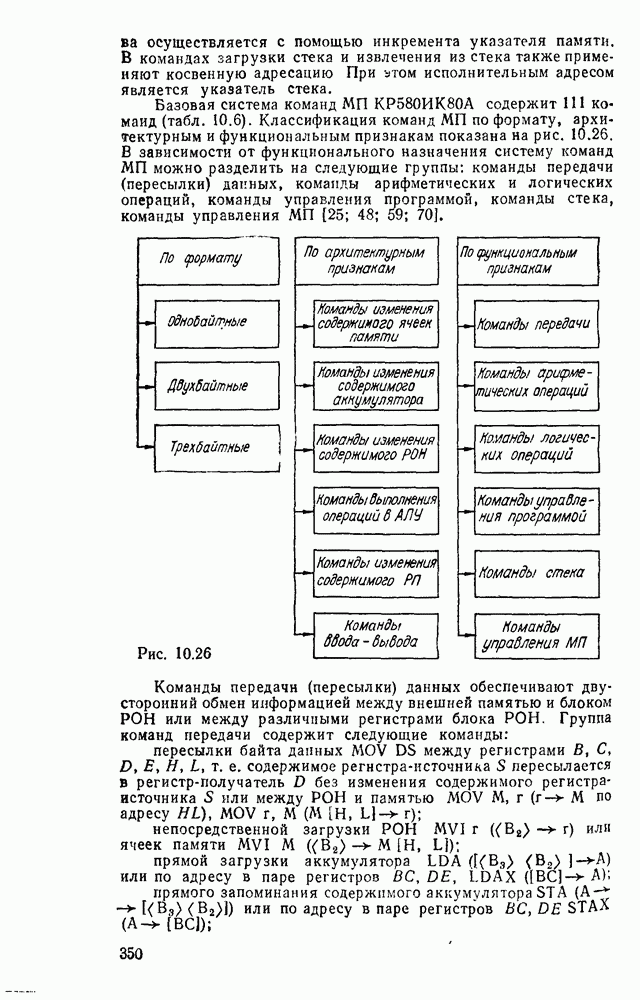
Рис. 5.26.
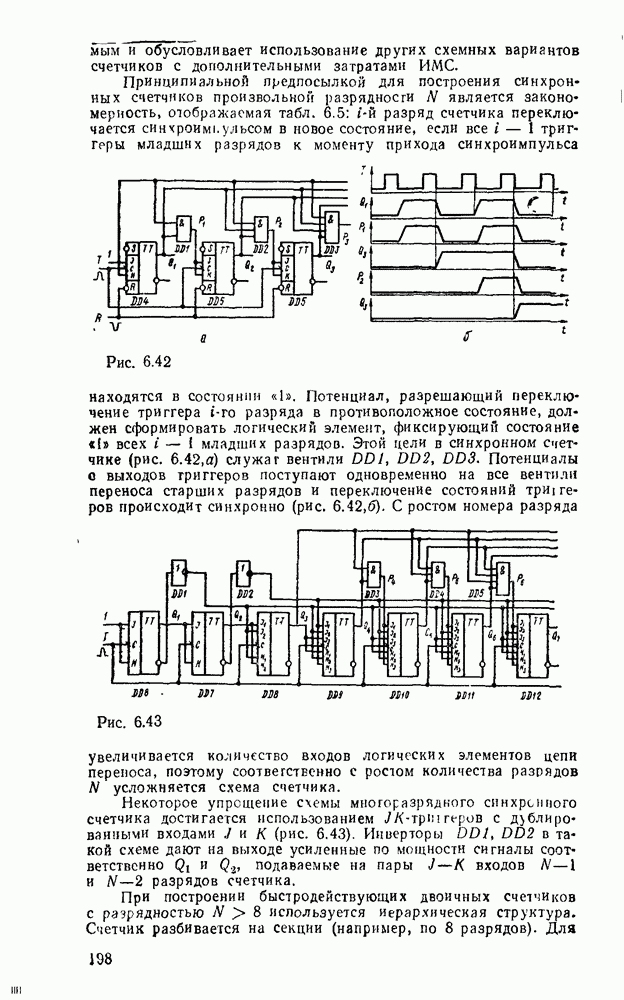
Для обеспечения максимального быстродействия предпочтительнее схемы с минимальным количеством логических ступеней между входом и выходом. С этой точки зрения кажущаяся простота полусумматора на рис. 5.25, в не дает ожидаемого преимущества по быстродействию, так как внутренняя структура ИМС ИСКЛЮЧАЮЩЕЕ ИЛИ по существу повторяет фрагмент схемы на рис.  .
.

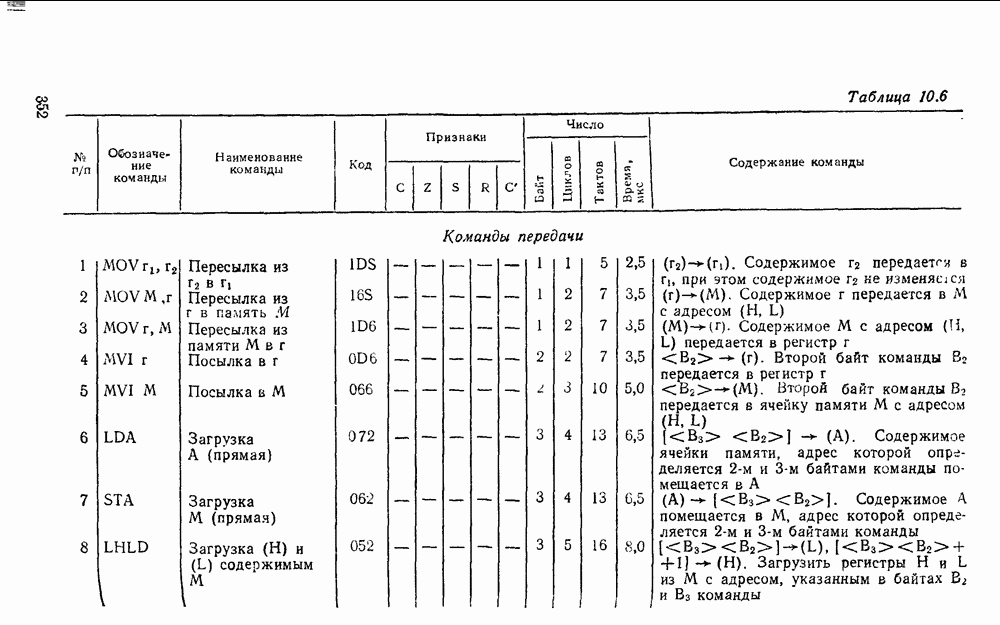
Рис. 5.27.
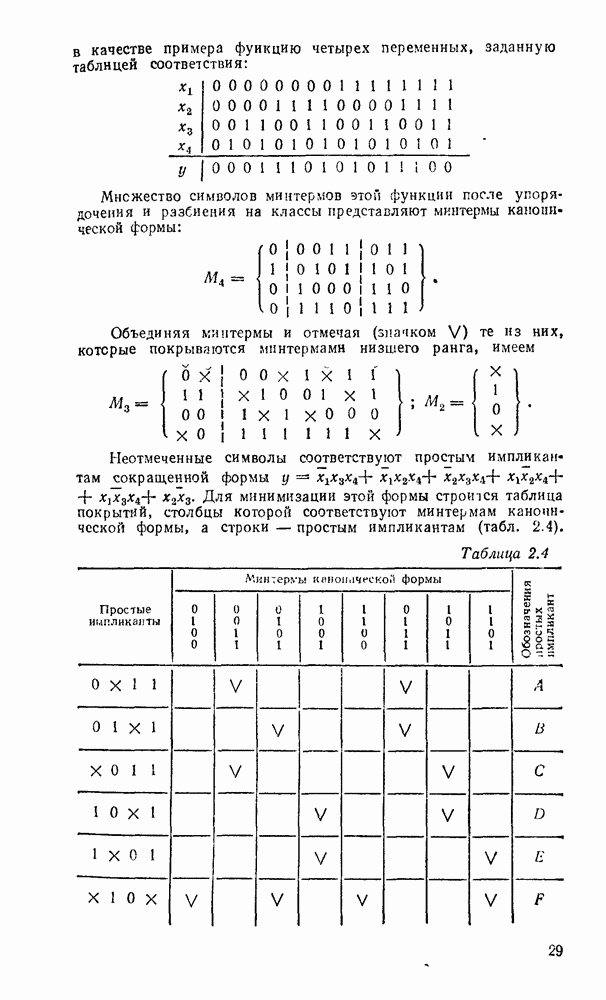
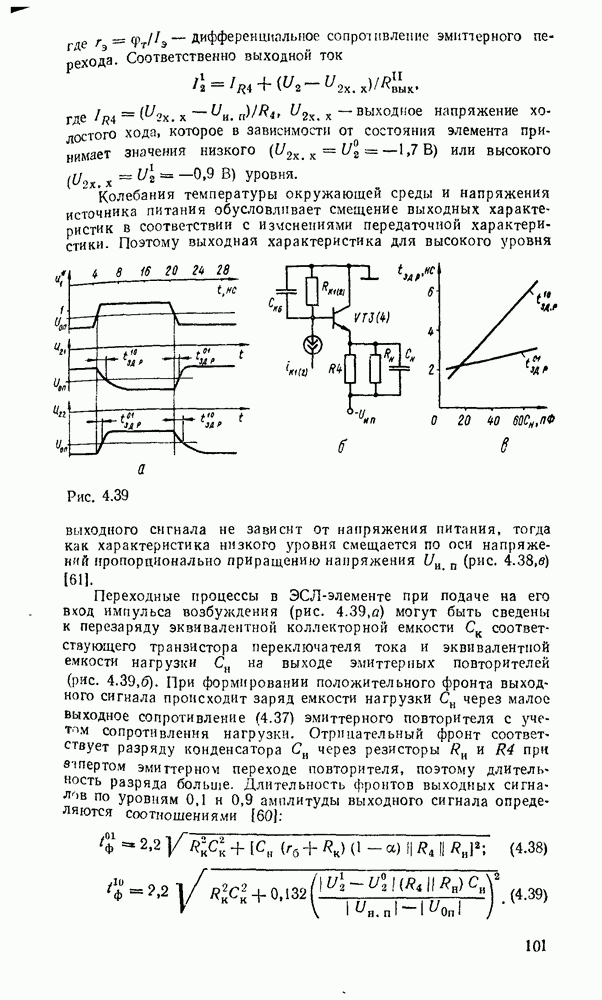
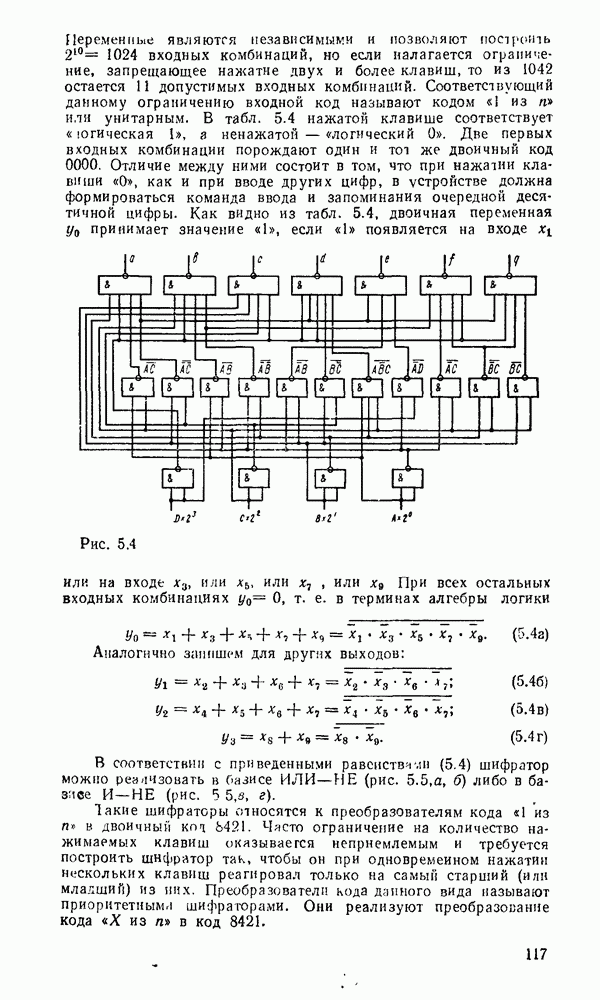
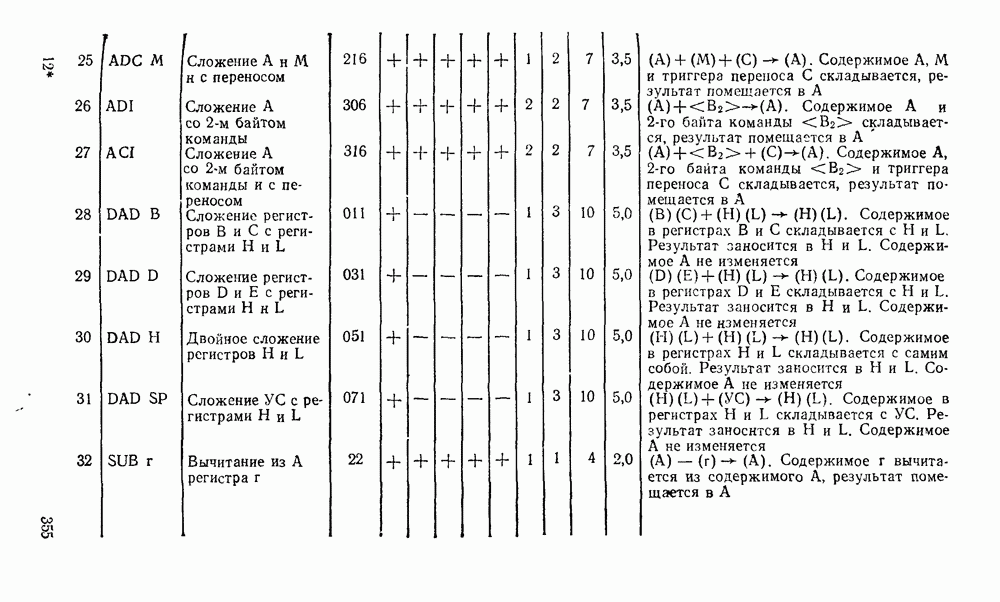
Работа полного сумматора описывается табл. 5.16. Карта Карно для функций  дает минимальную форму и ее тождественные варианты:
дает минимальную форму и ее тождественные варианты:

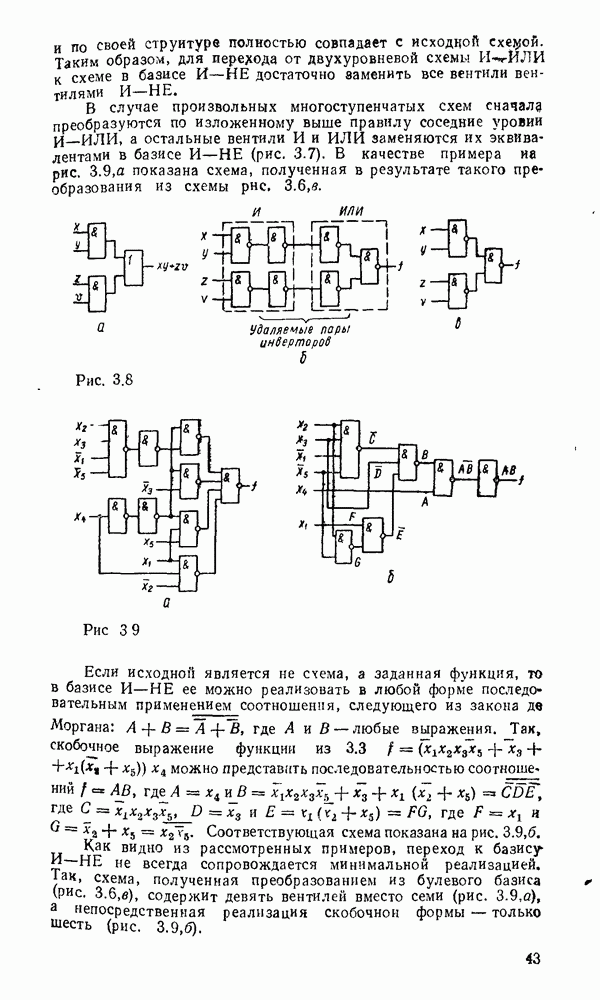
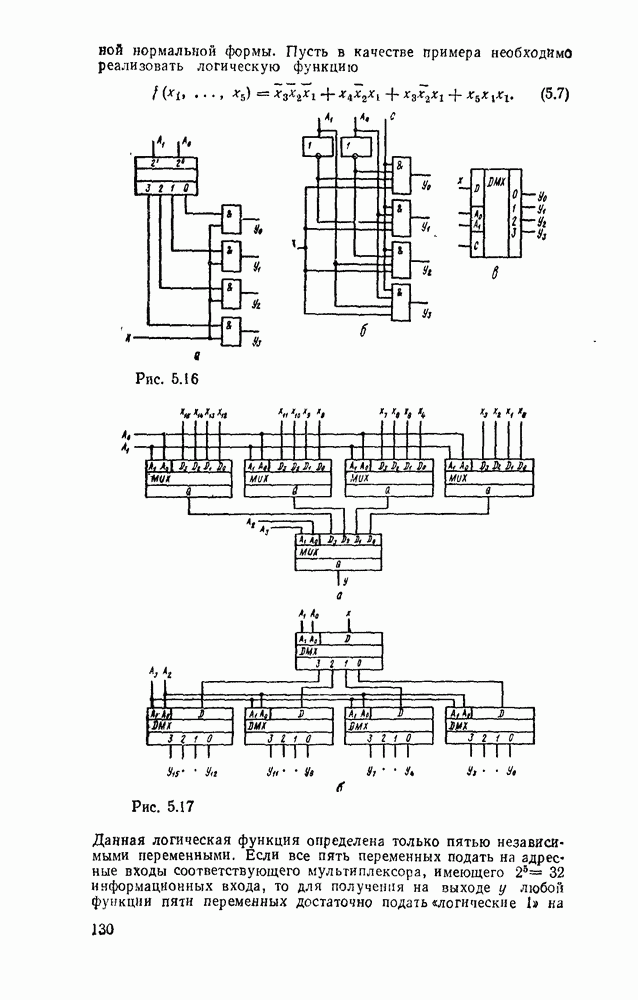
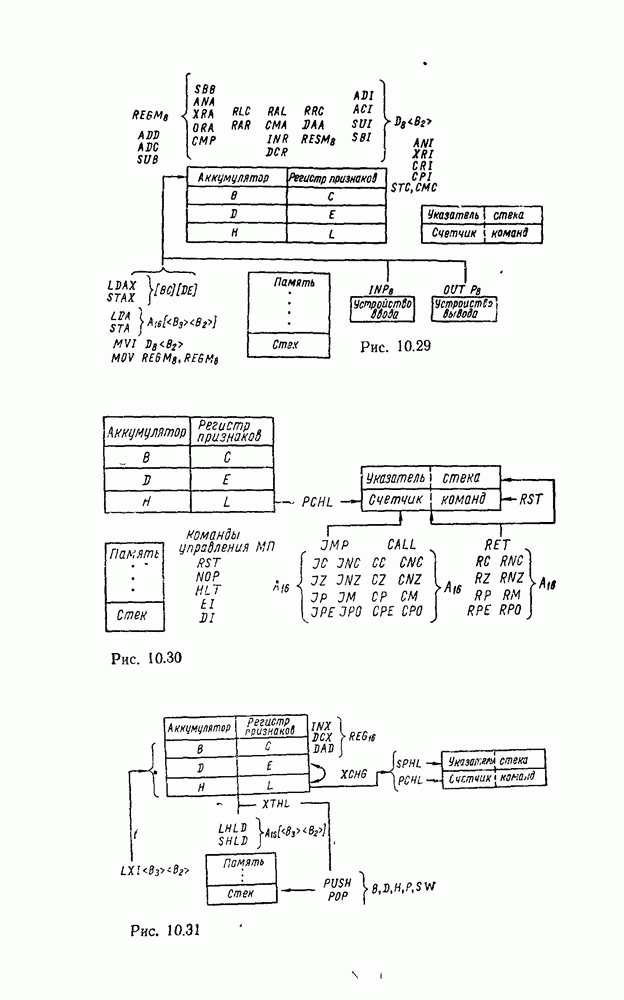
Соответственно выражениям (5.11),  на рис. 5.28 приведены различные реализации полного сумматора и его условное графическое изображение. Схема сумматора (рис. 5.28,в) аналогична схеме на рис
на рис. 5.28 приведены различные реализации полного сумматора и его условное графическое изображение. Схема сумматора (рис. 5.28,в) аналогична схеме на рис  по структуре и параметрам, ее можно построить на основе двух полусумматоров (см. рис. 5.25, в).
по структуре и параметрам, ее можно построить на основе двух полусумматоров (см. рис. 5.25, в).
Таблица 5.16

Таблица 5.17

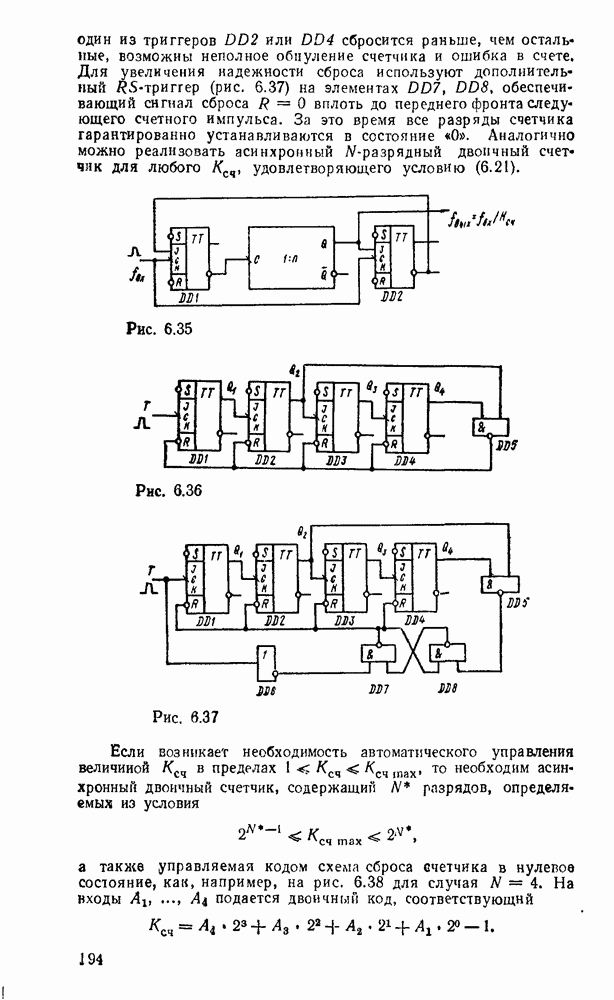
Сумматор по схеме на рис. 5.28,а, обладающий минимальной еадержкой распространения сигнала и, следовательно, максимальным быстродействием, может с успехом применяться при построении БИС многоразрядного сумматора.


Рис. 5.28.

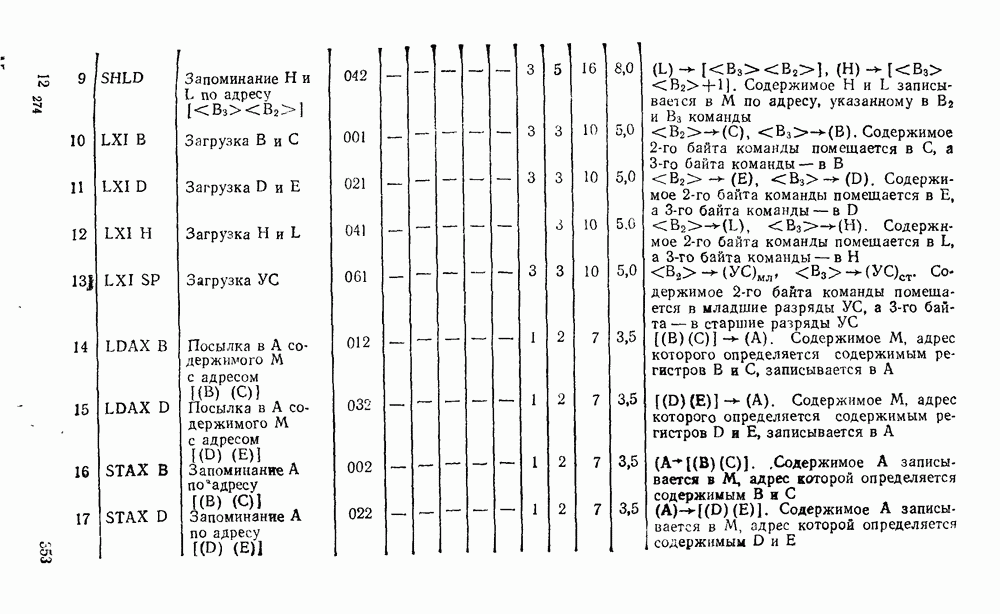
Рис. 5.29.
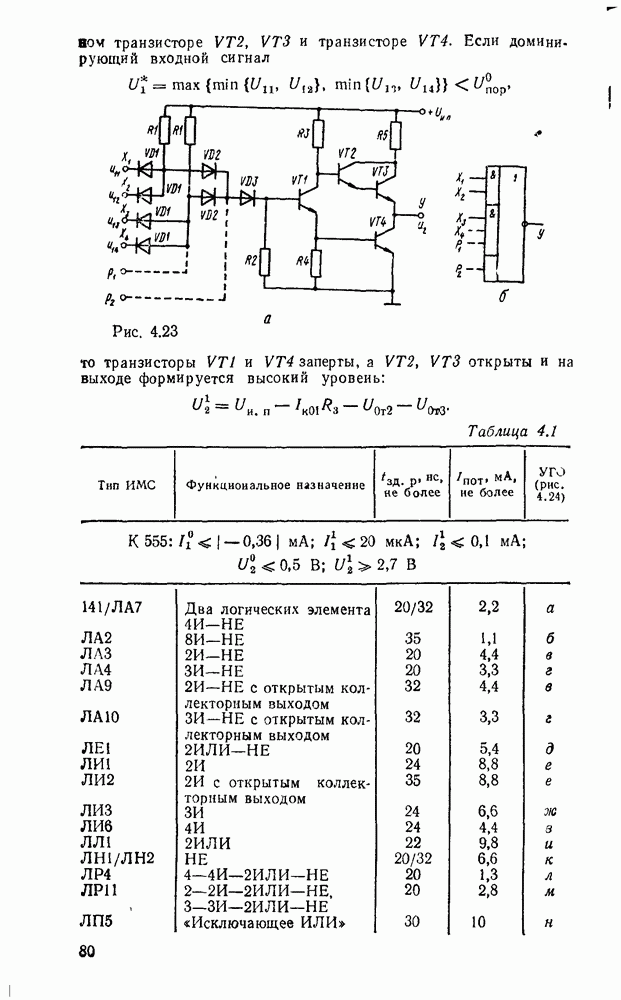
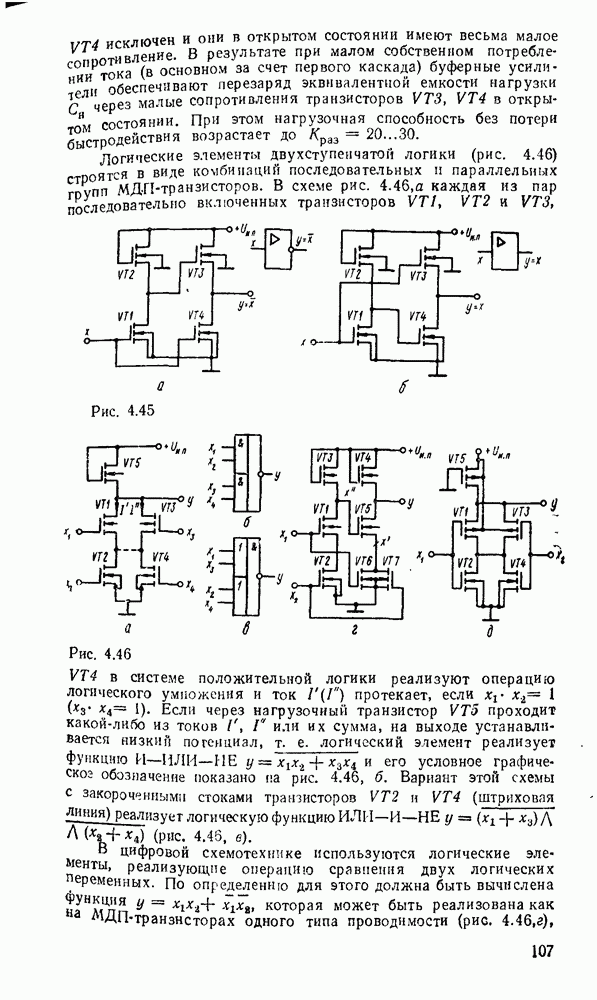
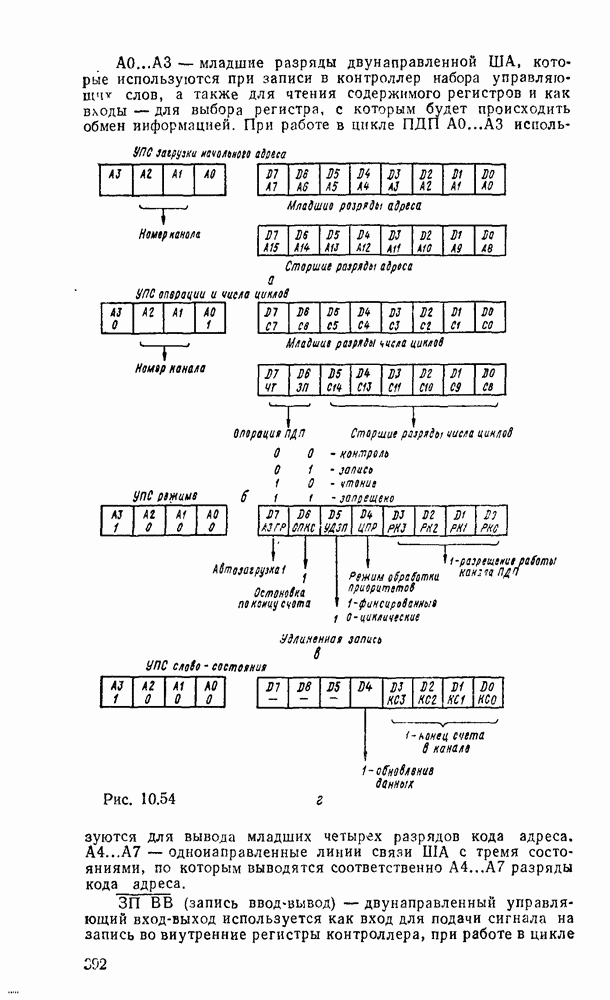
Вариант полного сумматора на элементах И—ИЛИ—НЕ, реализуемый на ИМС промышленных серий, показан на рис. 5.28,г. Условное графическое обозначение одноразрядного сумматора показано на  .
.
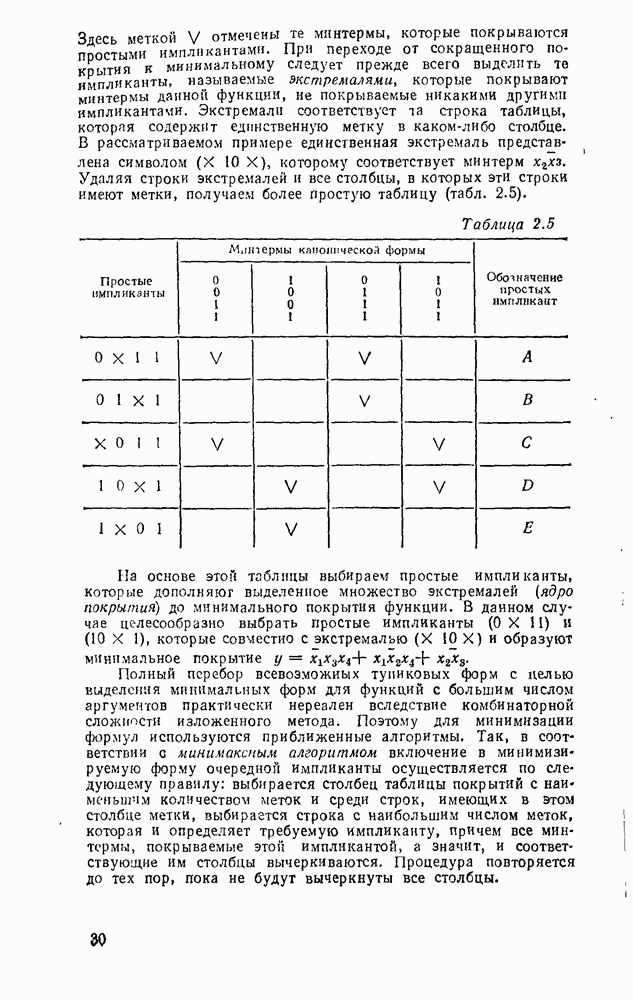
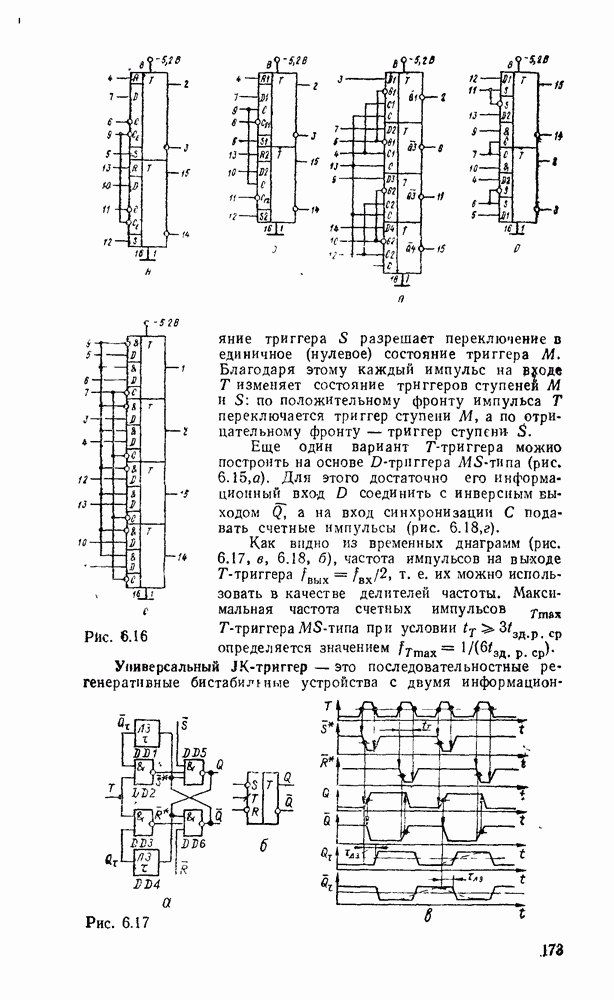
Аналогично определим функции переключения полного вычитателя (называемого также субтрактором) — устройства, реализующего операцию вычитания двух одноразрядных чисел в формированием сигнала заема из старшего разряда.
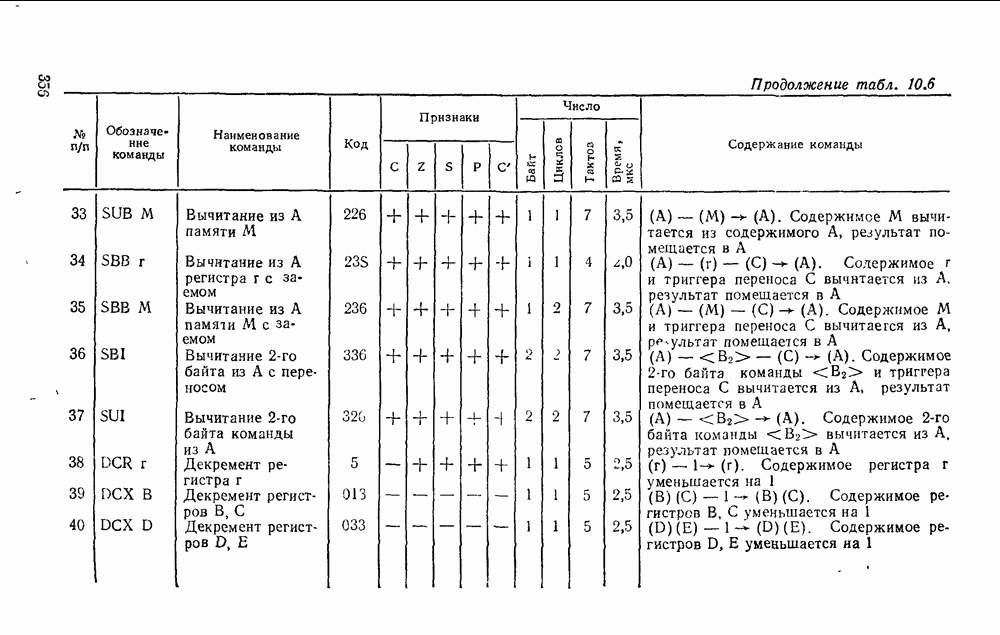
В соответствии в таблицей истинности вычитателя (табл. 5.17), (рис. 5.29) запишем выражения для разности  и функции заема
и функции заема  :
:

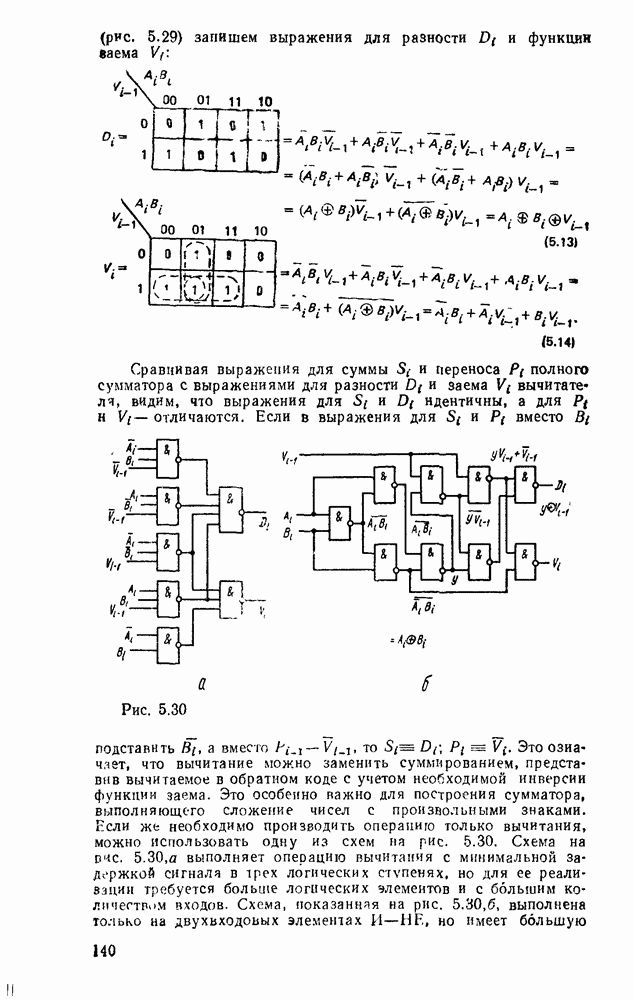
Сравнивая выражения для суммы  и переноса
и переноса  полного сумматора с выражениями для разности
полного сумматора с выражениями для разности  и заема
и заема  вычитателя, видим, что выражения для S; и
вычитателя, видим, что выражения для S; и  идентичны, а для
идентичны, а для  отличаются.
отличаются.

Рис. 5.30.
Если в выражения для  вместо
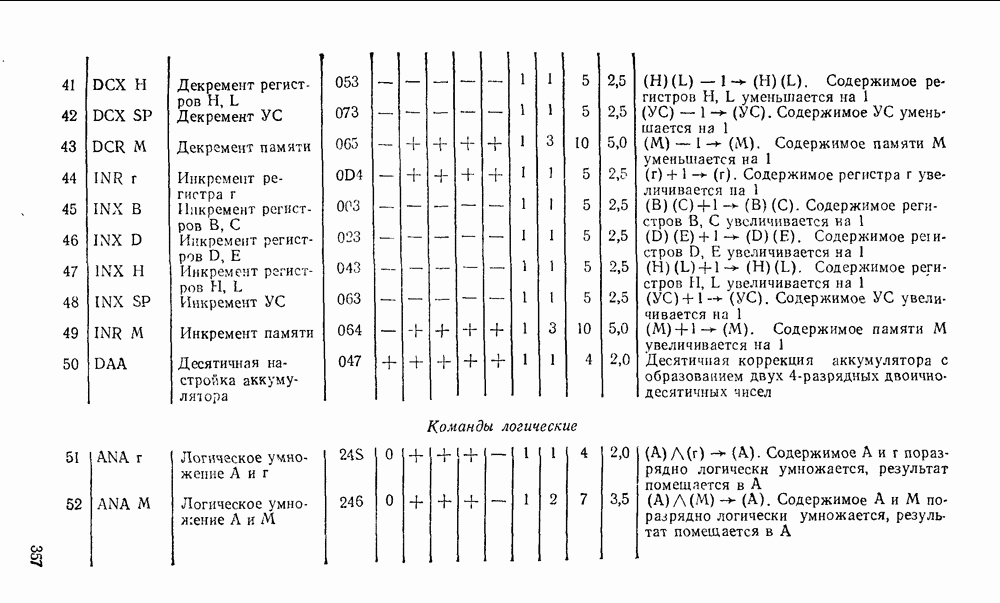
вместо  подставить
подставить  , а вместо
, а вместо  , то
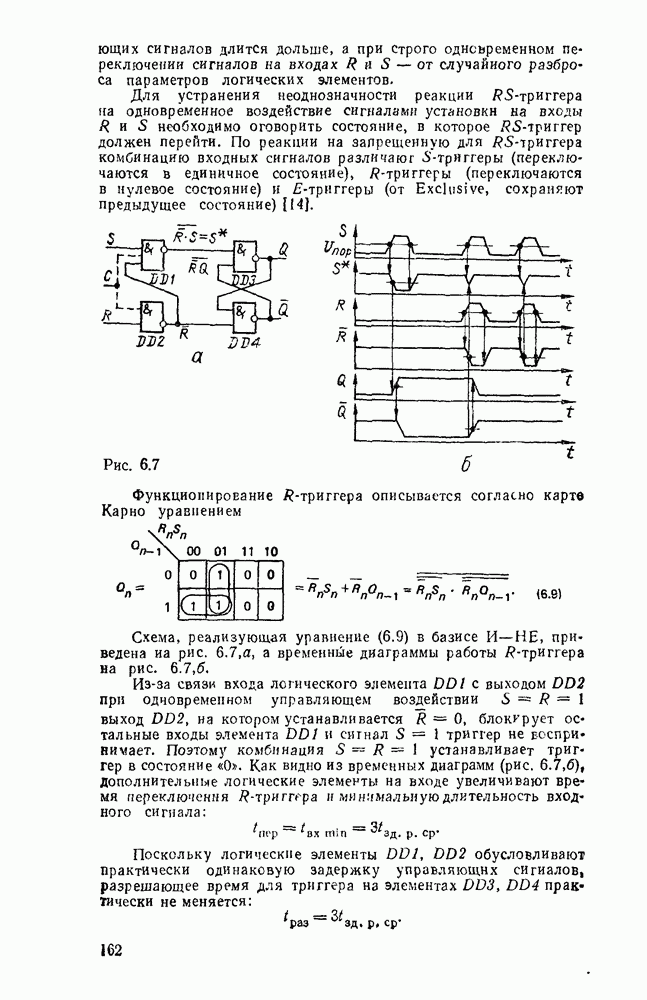
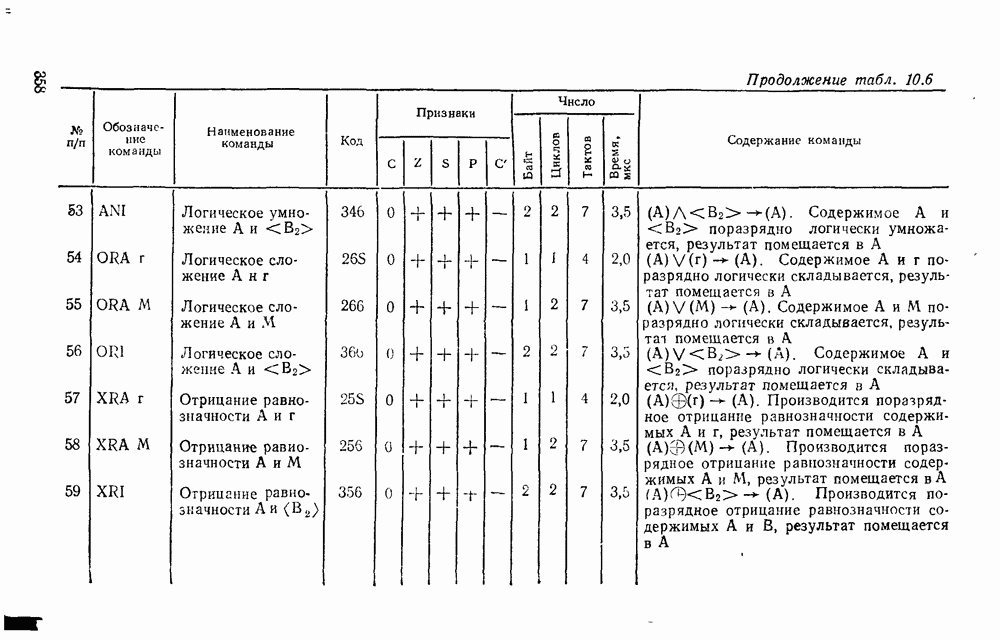
, то  означает, что вычитание можно заменить суммированием, представив вычитаемое в обратном коде с учетом необходимой инверсии функции заема. Это особенно иажно для построения сумматора, выполняющего сложение чисел с произвольными знаками. Если же необходимо производить операцию только вычитания, можно использовать одну из схем на рис. 5.30. Схема на
означает, что вычитание можно заменить суммированием, представив вычитаемое в обратном коде с учетом необходимой инверсии функции заема. Это особенно иажно для построения сумматора, выполняющего сложение чисел с произвольными знаками. Если же необходимо производить операцию только вычитания, можно использовать одну из схем на рис. 5.30. Схема на  . 5.30,а выполняет операцию вычитания с минимальной задержкой сигнала в трех логических ступенях, но для ее реализации требуется больше логических элементов и с большим количеств входов. Схема, показанная на рис.
. 5.30,а выполняет операцию вычитания с минимальной задержкой сигнала в трех логических ступенях, но для ее реализации требуется больше логических элементов и с большим количеств входов. Схема, показанная на рис.  , выполнена только на двухвходоьых элементах
, выполнена только на двухвходоьых элементах  , но имеет большую задержку (6 логических ступеней).
, но имеет большую задержку (6 логических ступеней).
В этом случае формирование значения разности  осуществляется в соответствии с выражением (5.13), а заема — (5.14).
осуществляется в соответствии с выражением (5.13), а заема — (5.14).
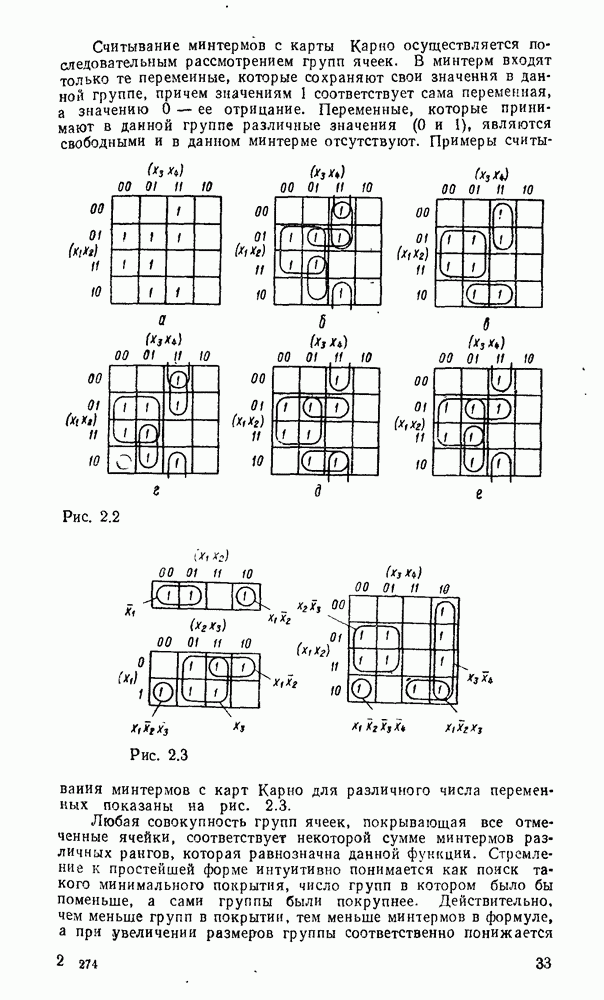
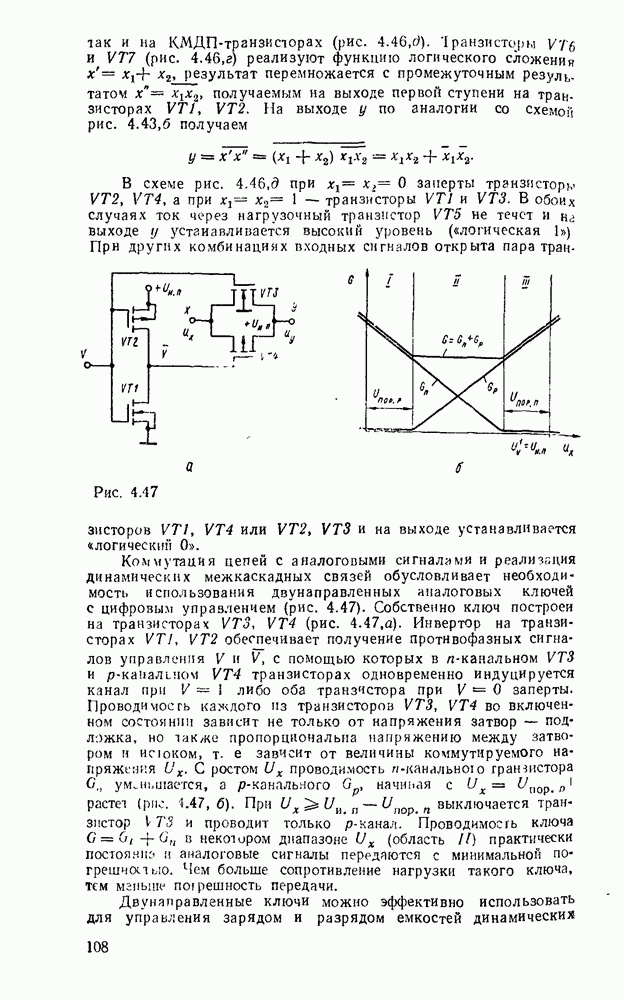
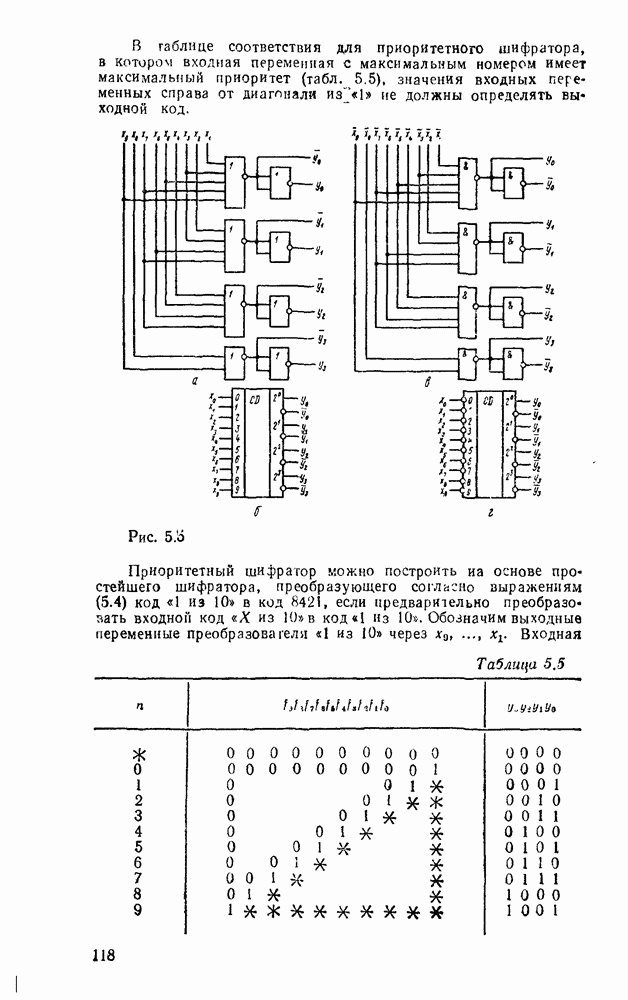
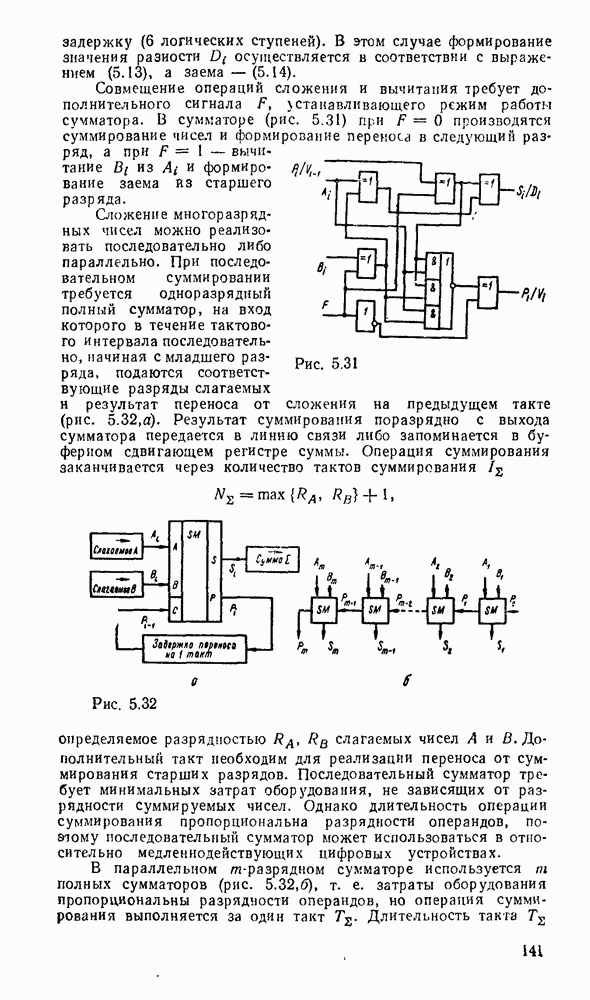
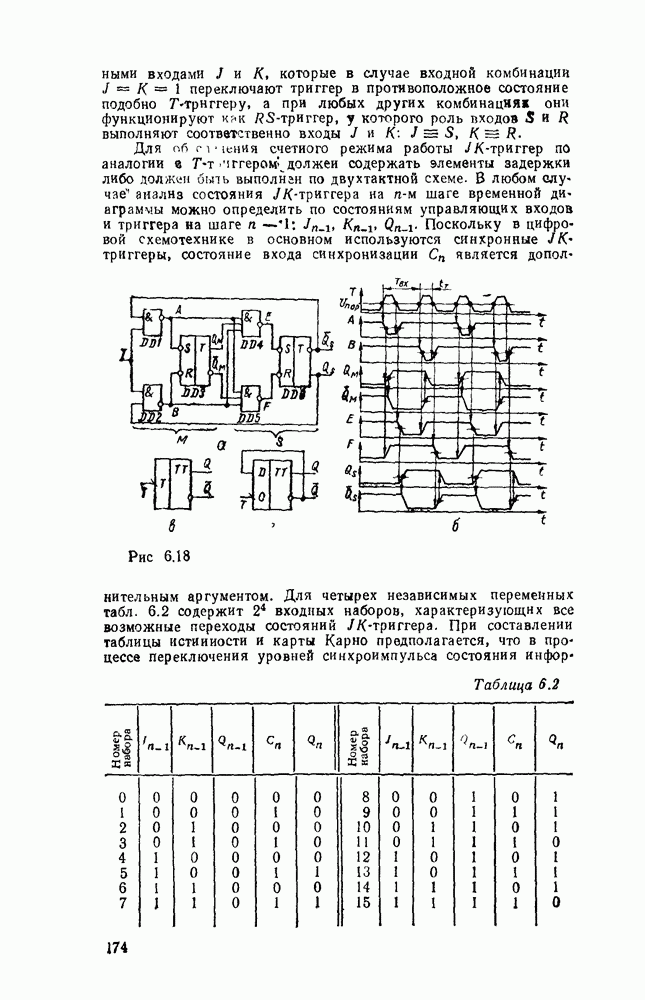
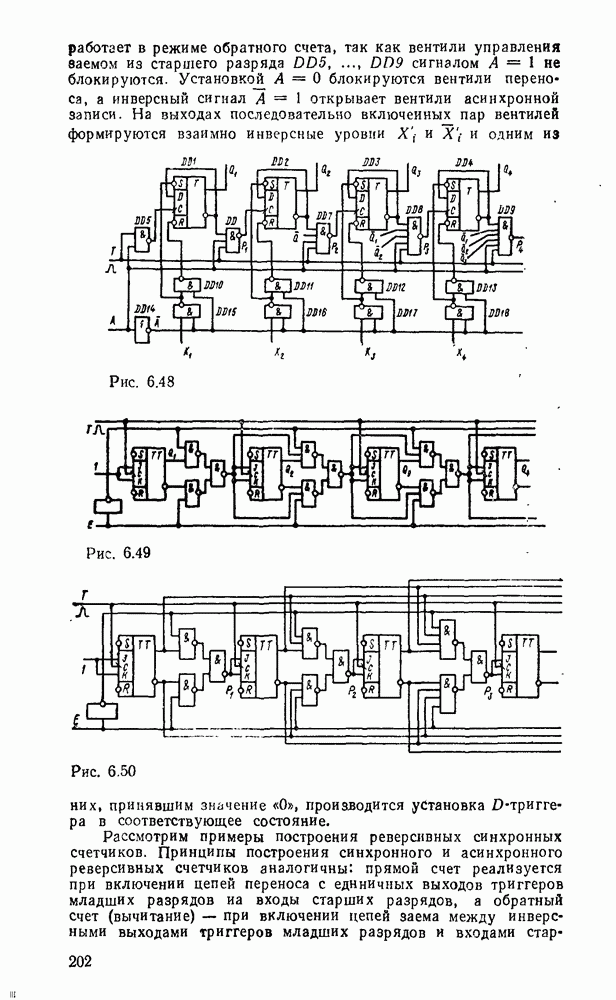
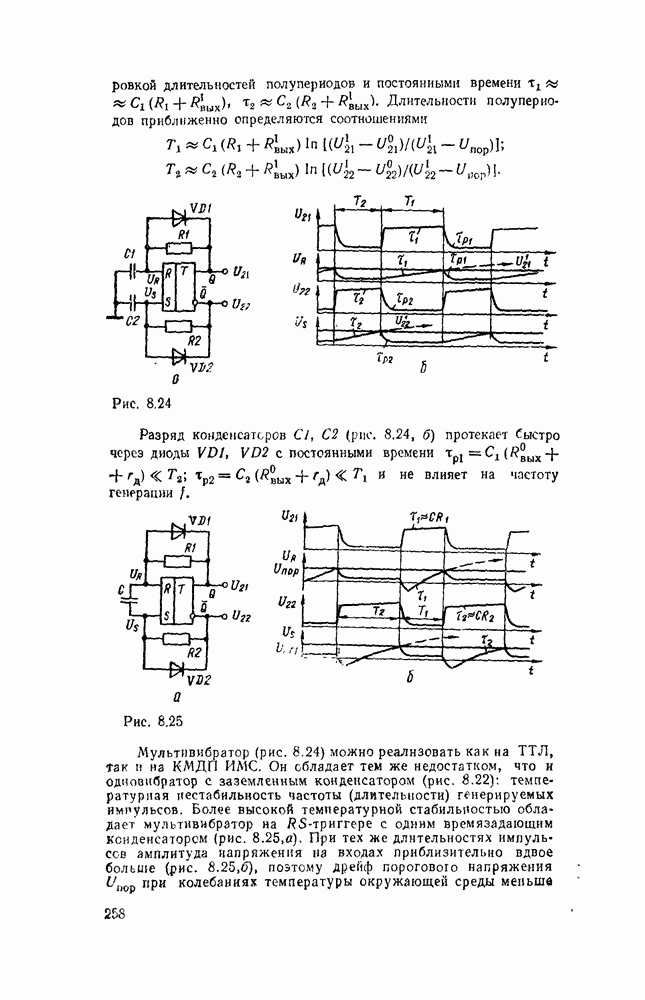
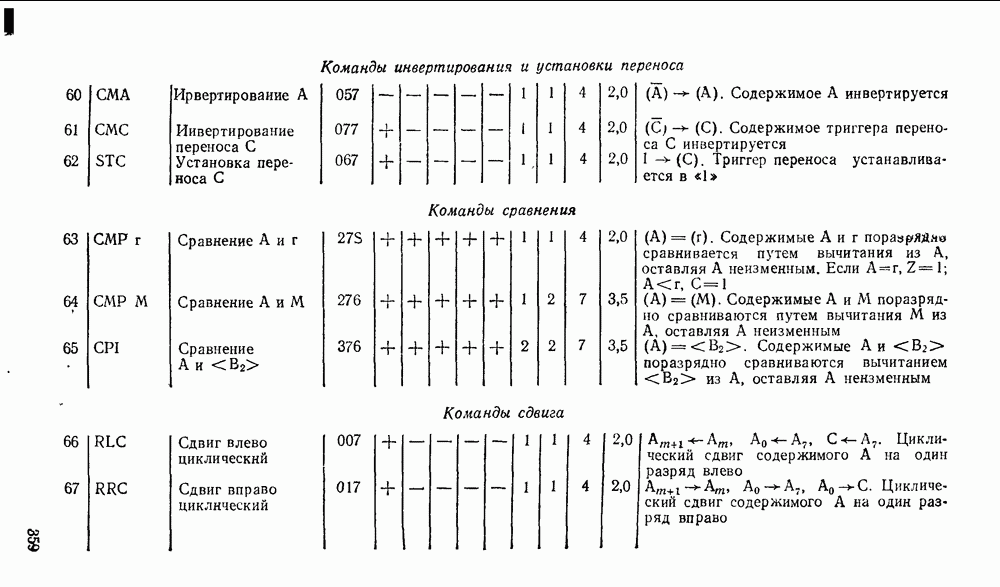
Совмещение операций сложения и вычитания требует дополнительного сигнала F, хстанавливающего режим работы сумматора. В сумматоре (рис. 5.31) при  производятся суммирование чисел и формирование переноса в следующий разряд, а при
производятся суммирование чисел и формирование переноса в следующий разряд, а при  — вычитание
— вычитание  из
из  и формирование заема из старшего разряда.
и формирование заема из старшего разряда.

Рис. 5.31.
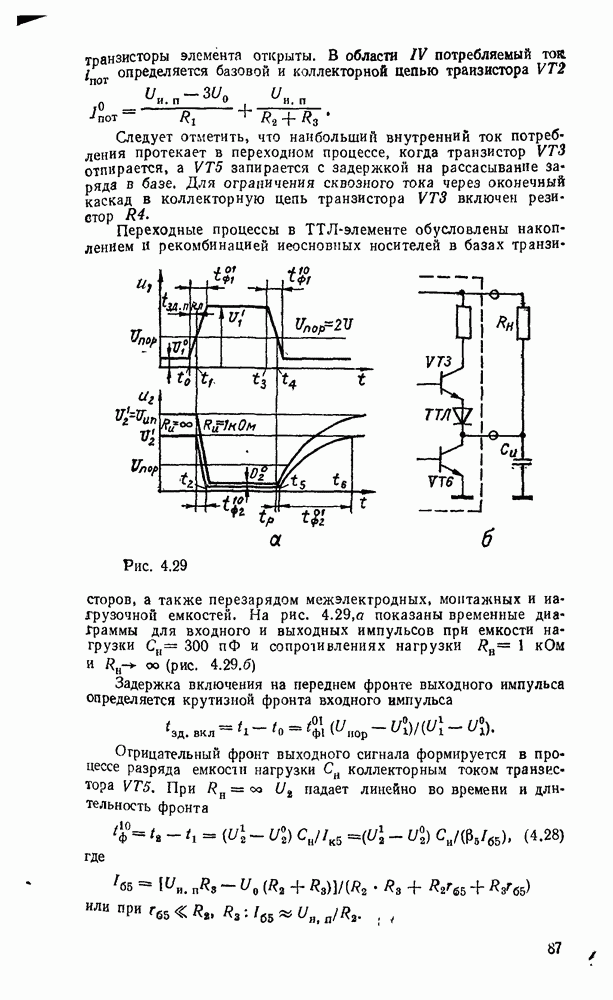
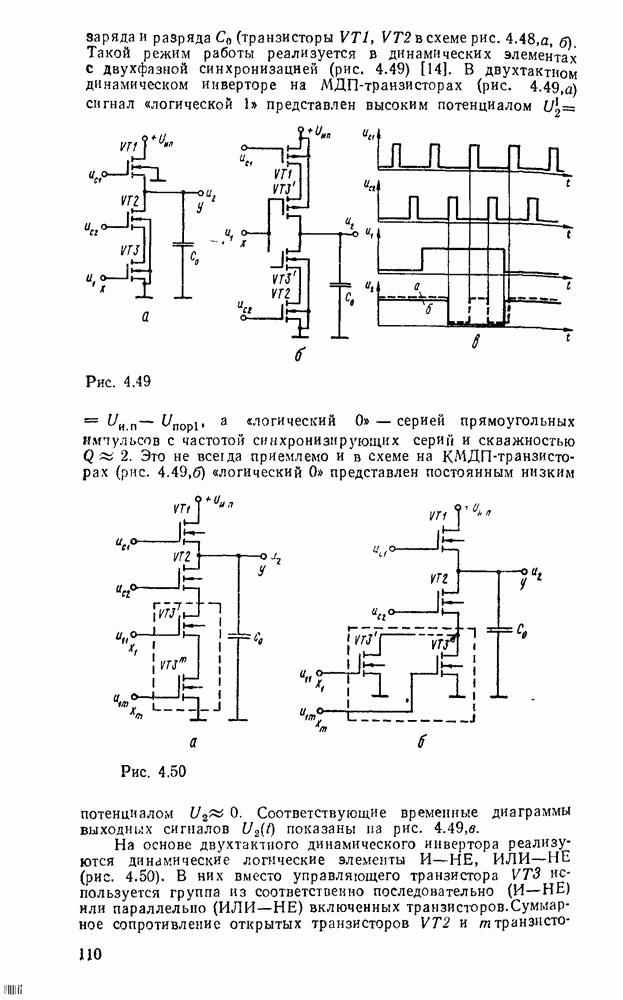
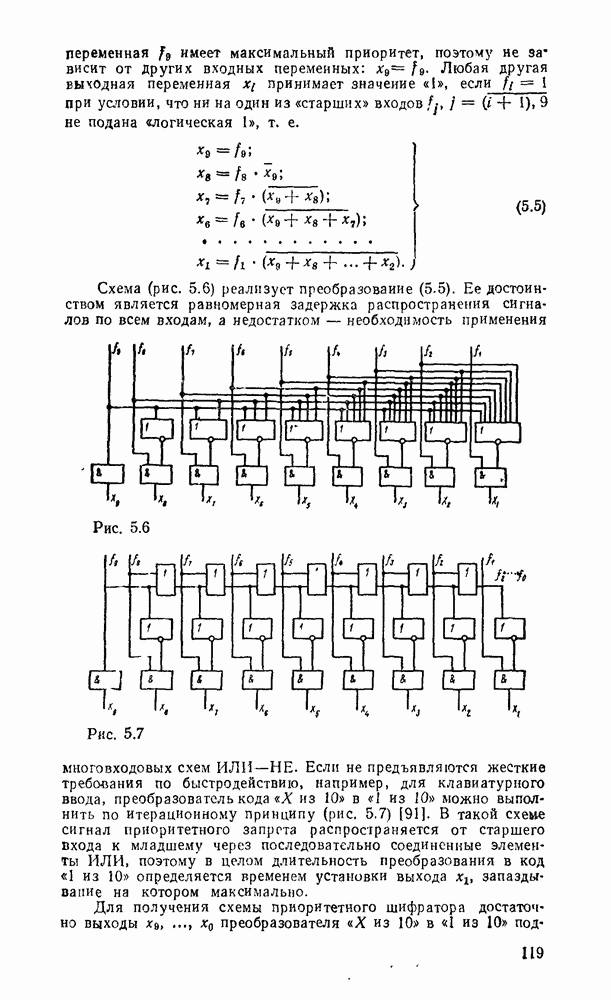
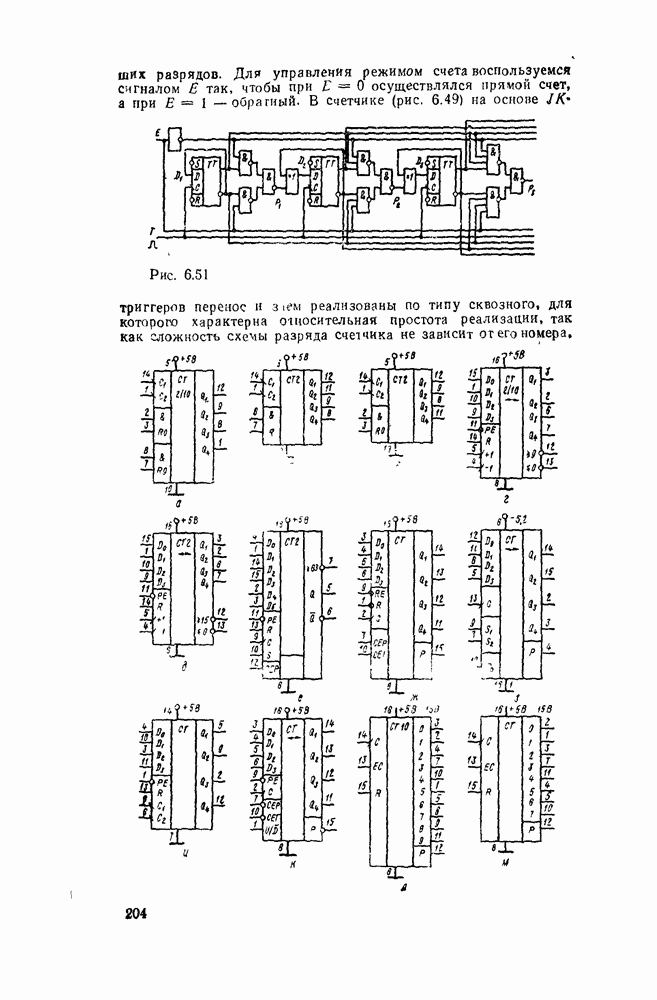
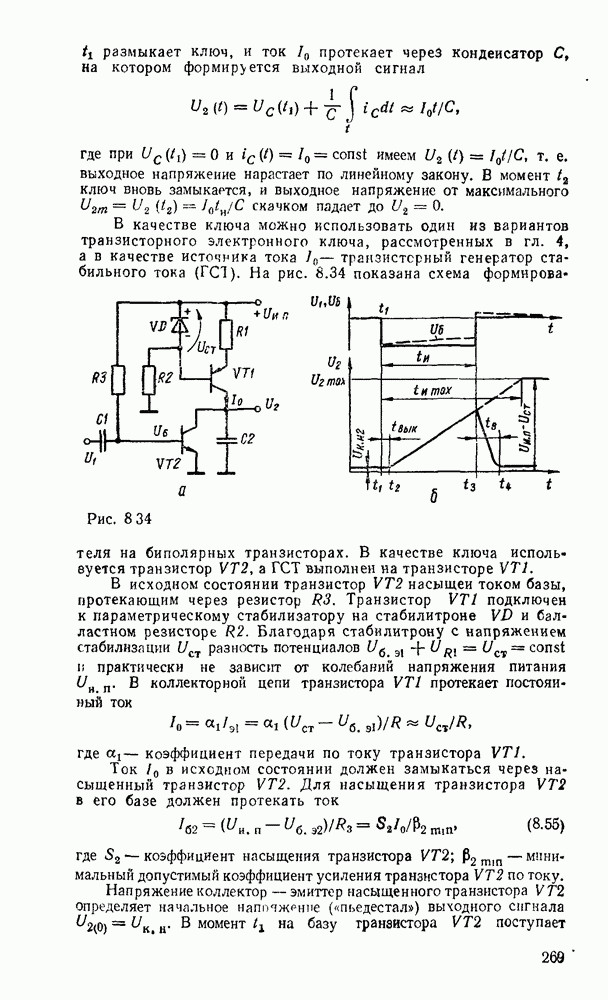
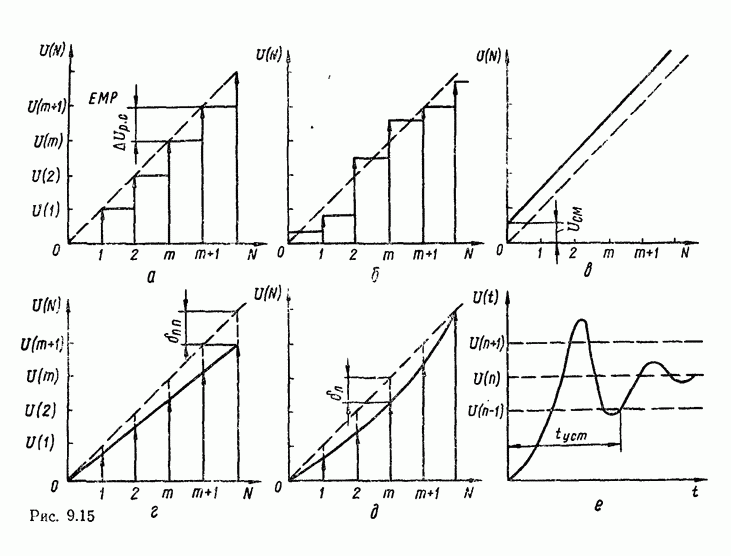
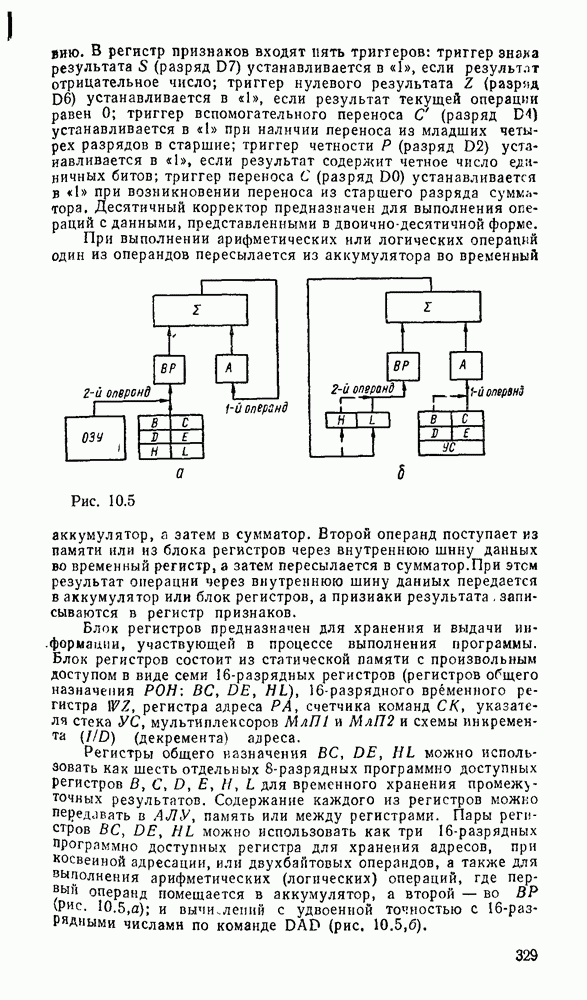
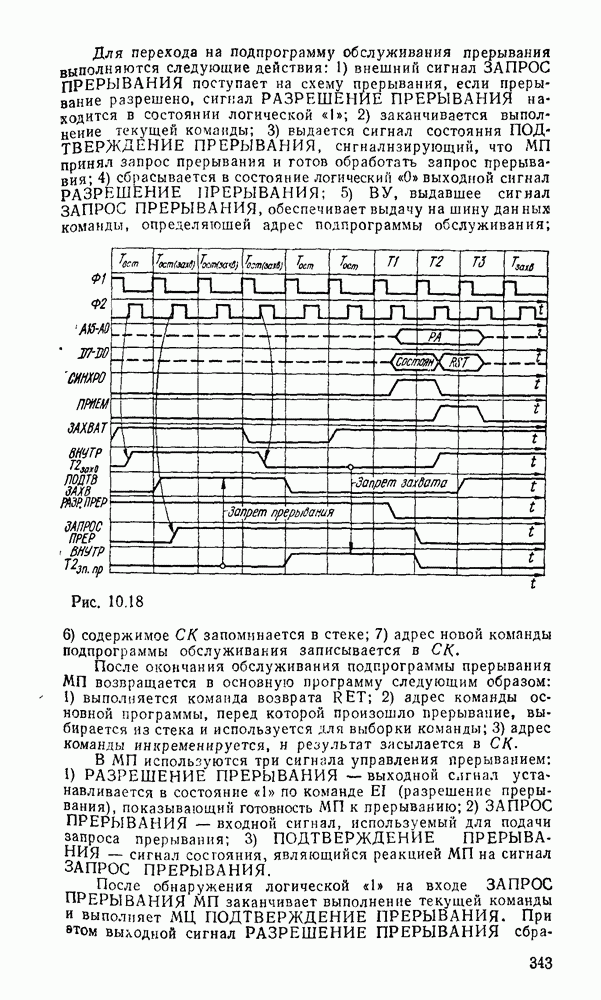
Сложение многоразрядных чисел можно реализовать последовательно либо параллельно. При последовательном суммировании требуется одноразрядный полный сумматор, на вход которого в течение тактового интервала последовательно, начиная с младшего разряда, подаются соответствующие разряды слагаемых и результат переноса от сложения на предыдущем такте (рис. 5.32,а). Результат суммирования поразрядно с выхода сумматора передается в линию связи либо запоминается в буферном сдвигающем регистре суммы.


Рис. 5.32.
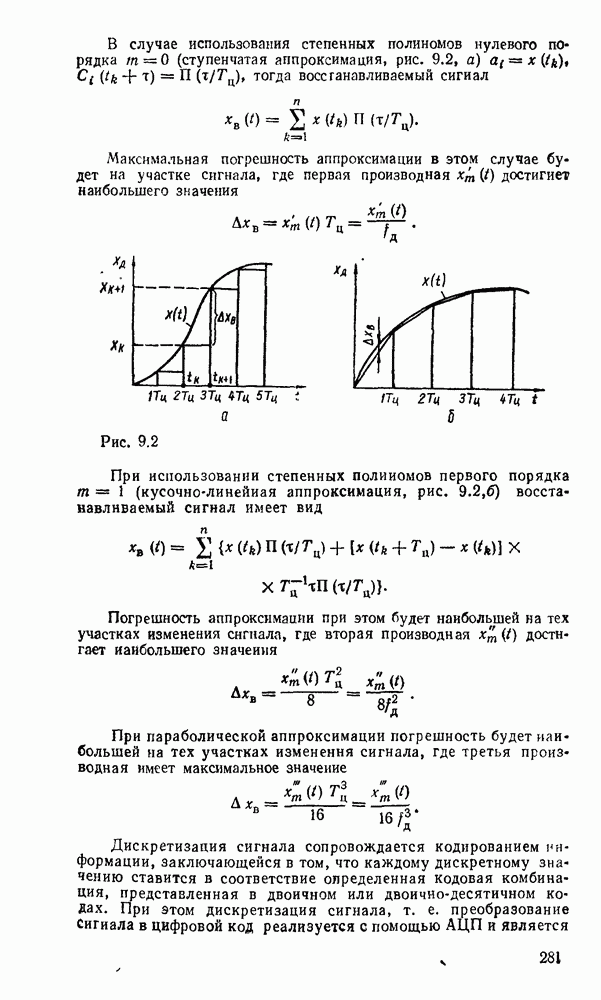
Операция суммирования заканчивается через количество тактов суммирования  определяемое разрядностью
определяемое разрядностью  слагаемых чисел А и В. Дополнительный такт необходим для реализации переноса от суммирования старших разрядов. Последовательный сумматор требует минимальных затрат оборудования, не зависящих от разрядности суммируемых чисел. Однако длительность операции суммирования пропорциональна разрядности операндов, поэтому последовательный сумматор может использоваться в относительно медленнодействующих цифровых устройствах.
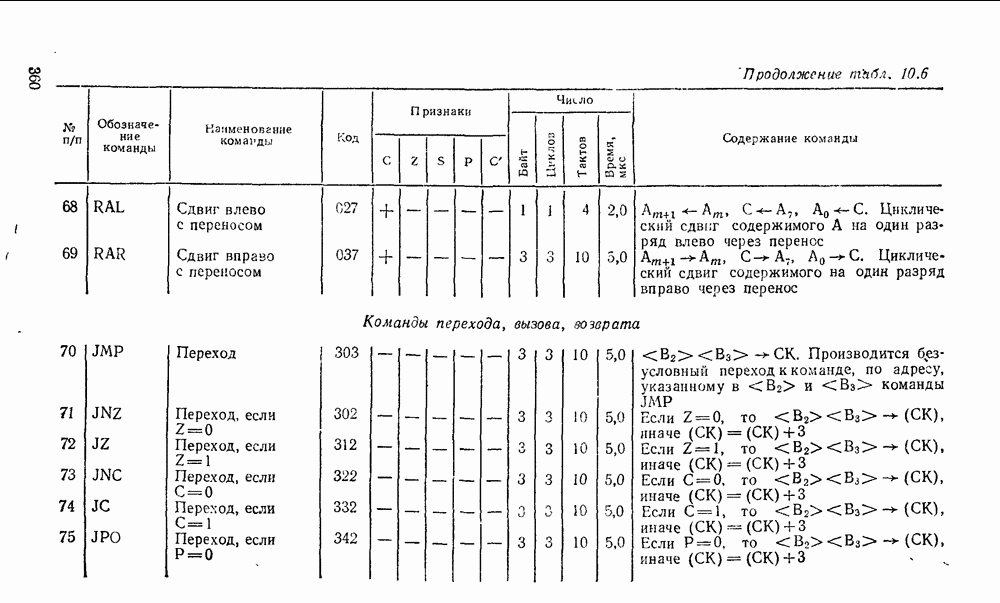
слагаемых чисел А и В. Дополнительный такт необходим для реализации переноса от суммирования старших разрядов. Последовательный сумматор требует минимальных затрат оборудования, не зависящих от разрядности суммируемых чисел. Однако длительность операции суммирования пропорциональна разрядности операндов, поэтому последовательный сумматор может использоваться в относительно медленнодействующих цифровых устройствах.
В параллельном  -разрядном сумматоре используется
-разрядном сумматоре используется  полных сумматоров (рис.
полных сумматоров (рис.  ), т. е. затраты оборудования пропорциональны разрядности операндов, но операция суммирования выполняется за один такт
), т. е. затраты оборудования пропорциональны разрядности операндов, но операция суммирования выполняется за один такт  .
.
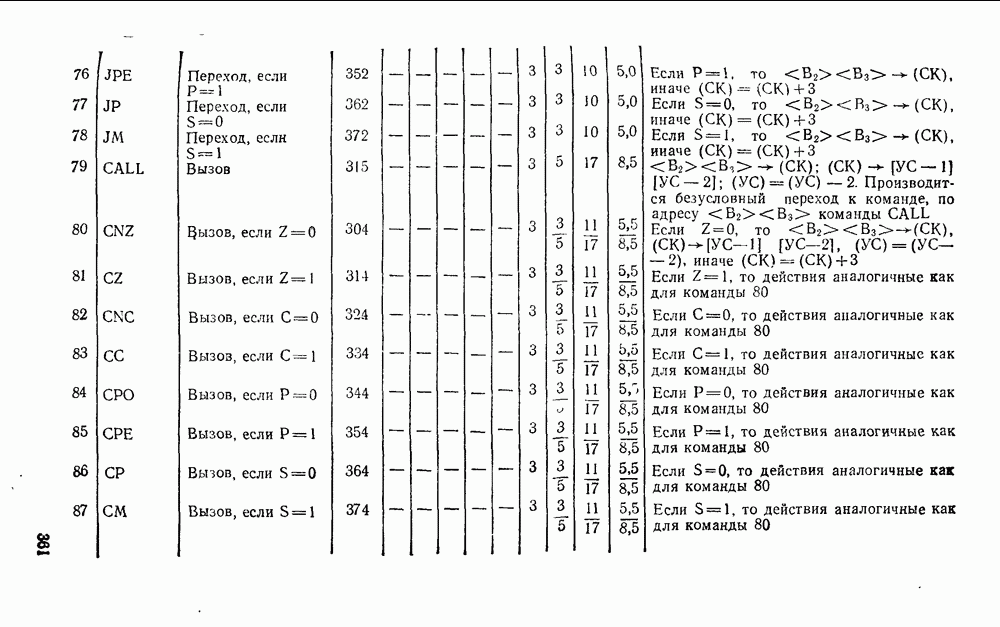
Длительность такта  и сложность реализации параллельного сумматора зависят от способа реализации переносов. В простейшем случае выходы и входы цепей переноса соединяются последовательно (рис.
и сложность реализации параллельного сумматора зависят от способа реализации переносов. В простейшем случае выходы и входы цепей переноса соединяются последовательно (рис.  ) и длительность такта пропорциональна количеству разрядов сумматора и времени реализации переноса в одном разряде
) и длительность такта пропорциональна количеству разрядов сумматора и времени реализации переноса в одном разряде  :
:

где длительность суммирования в одноразрядном сумматоре. При большом количестве разрядов и последовательной реализации переноса длительность суммирования (5.15) оказывается недопустимо большой. Увеличение быстродействия параллельного сумматора достигается за счет одновременного формирования сигналов переноса во всех его  разрядах. Для этого в сумматор включается специальная схема ускоренного переноса, аргументами которой являются промежуточные переменные полного сумматора.
разрядах. Для этого в сумматор включается специальная схема ускоренного переноса, аргументами которой являются промежуточные переменные полного сумматора.
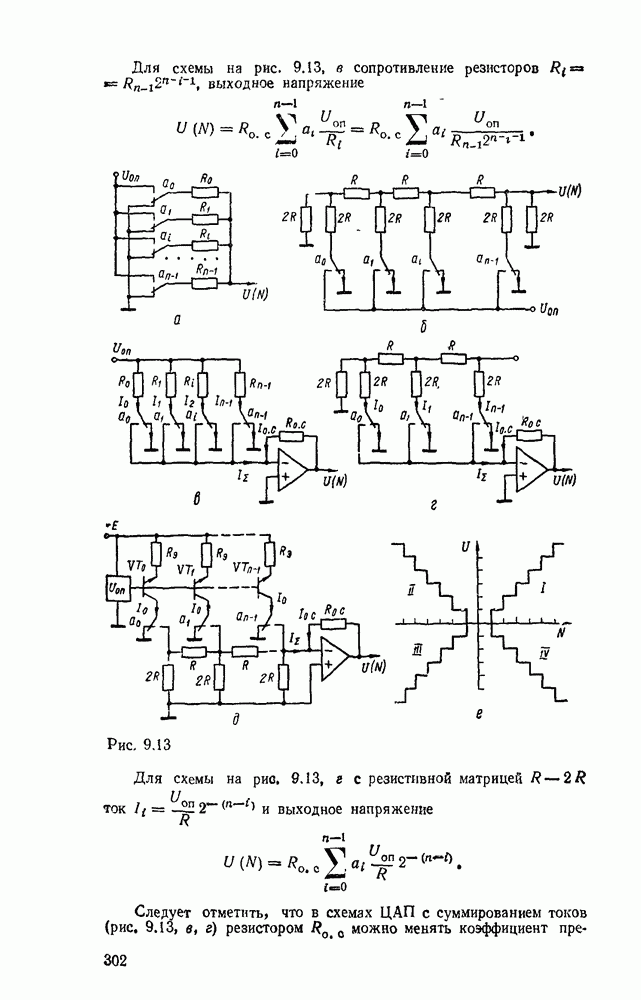
Для построения схемы параллельного переноса введем обозначения  и перепишем соотношения (5.11) и (5.12) в виде
и перепишем соотношения (5.11) и (5.12) в виде

На основании выражения (5.16) результат суммирования на выходах многорядного сумматора:

где  — возможный перенос при каскадном соединении сумматоров (для самой младшей секции
— возможный перенос при каскадном соединении сумматоров (для самой младшей секции  ),
),  определяются выражением (5.17):
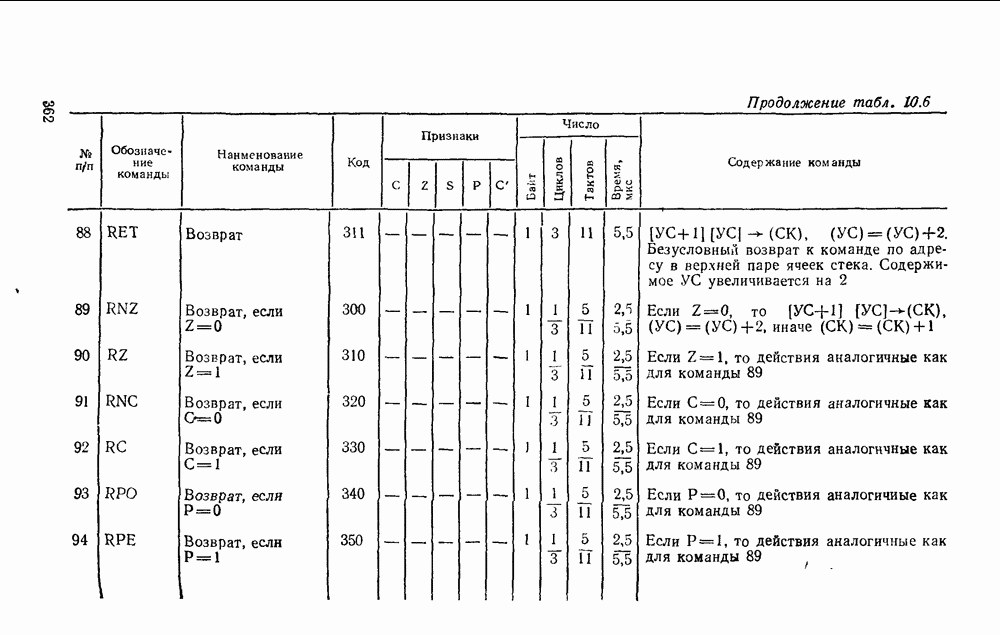
определяются выражением (5.17):

Из выражения (5.19) видно, что схема параллельного переноса тем сложнее, чем старше разряд сумматора, но в любом разряде длительности операции переноса  одинаковы и определяются задержкой сигнала в четырех логических ступенях
одинаковы и определяются задержкой сигнала в четырех логических ступенях  . Тогда сигнал суммы, который запаздывает по отношению к сигналу переноса, как видно из выражения (5.18), формируется с задержкой
. Тогда сигнал суммы, который запаздывает по отношению к сигналу переноса, как видно из выражения (5.18), формируется с задержкой  .
.
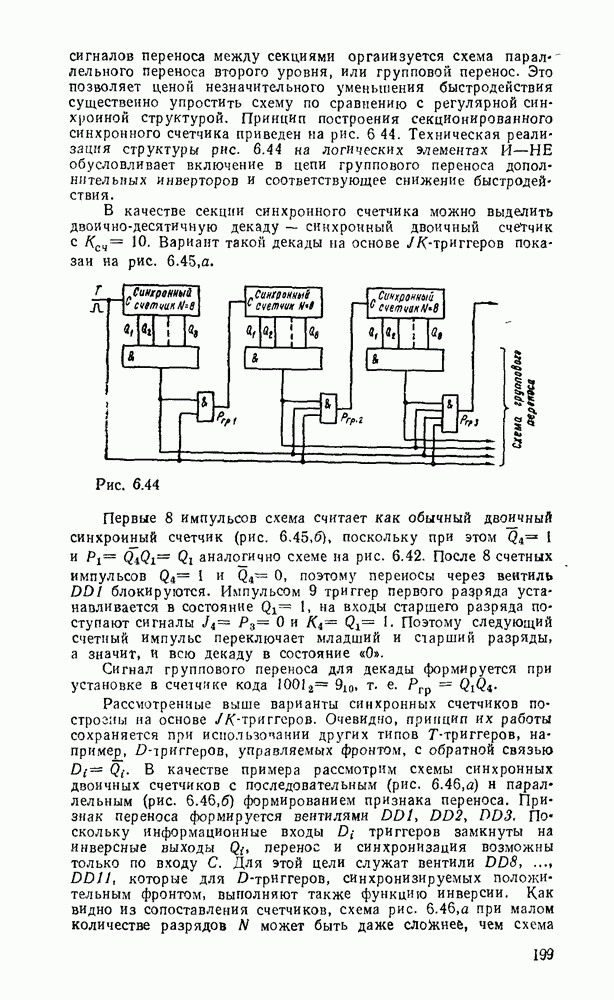
Поскольку сложность схемы параллельного переноса быстро нарастает с увеличением номера разряда сумматора, часто многоразрядные сумматоры разбивают на секции, внутри которых реализуется параллельный перенос, а между секциями перенос реализуется либо последовательно, либо по алгоритму, описываемому соотношениями вида (5.19),
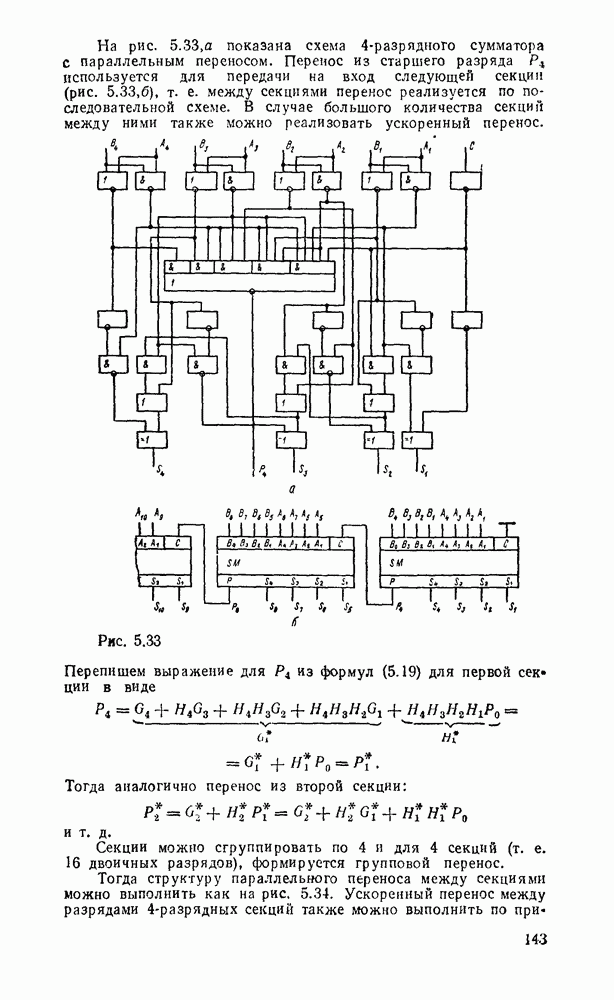
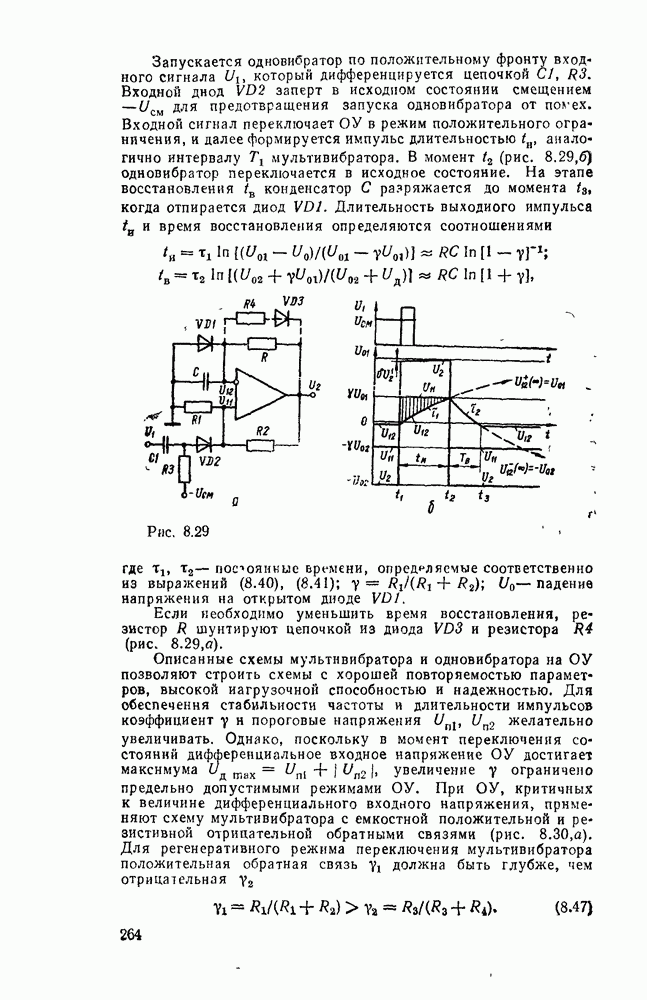
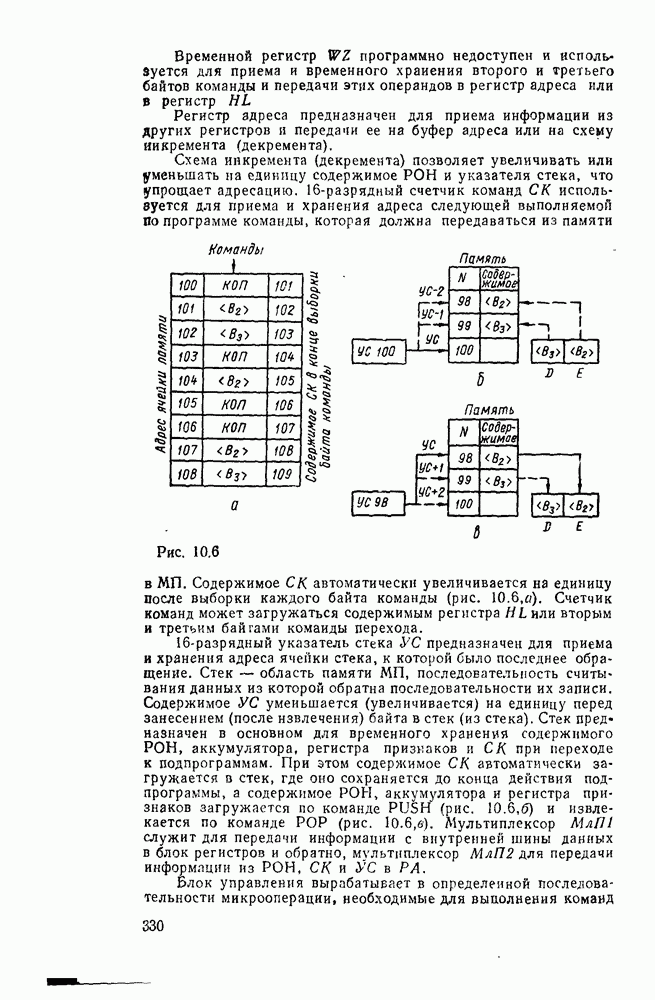
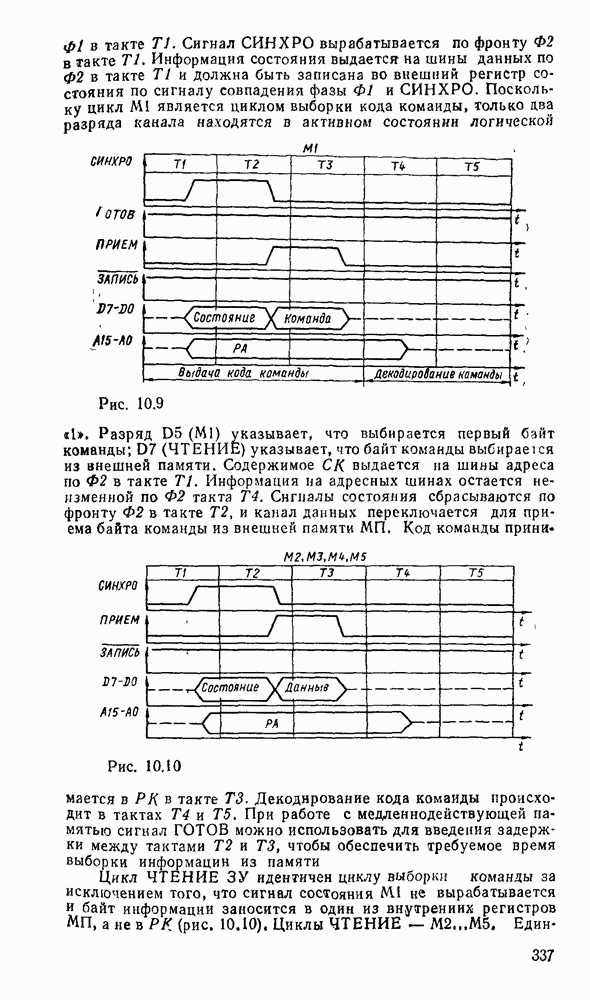
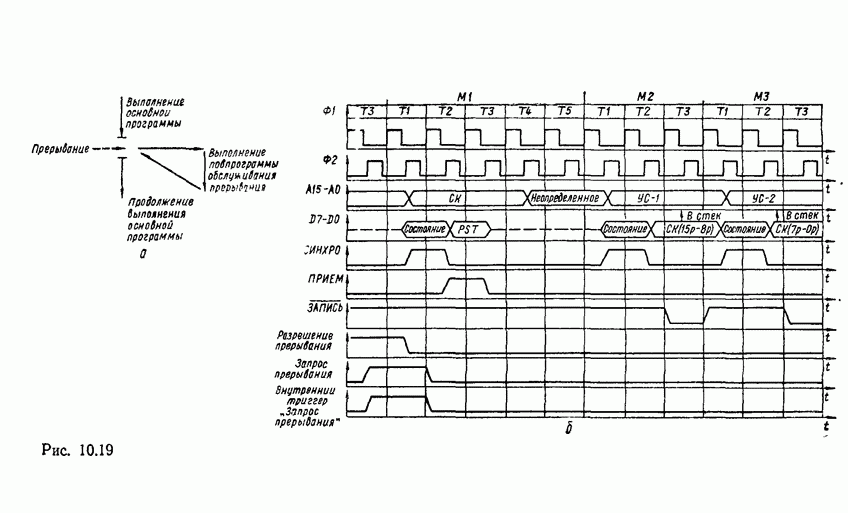
На рис. 5.33, а показана схема  -разрядного сумматора с параллельным переносом. Перенос из старшего разряда
-разрядного сумматора с параллельным переносом. Перенос из старшего разряда  используется для передачи на вход следующей секции (рис.
используется для передачи на вход следующей секции (рис.  ), т. е. между секциями перенос реализуется по последовательной схеме. В случае большого количества секций между ними также можно реализовать ускоренный перенос.
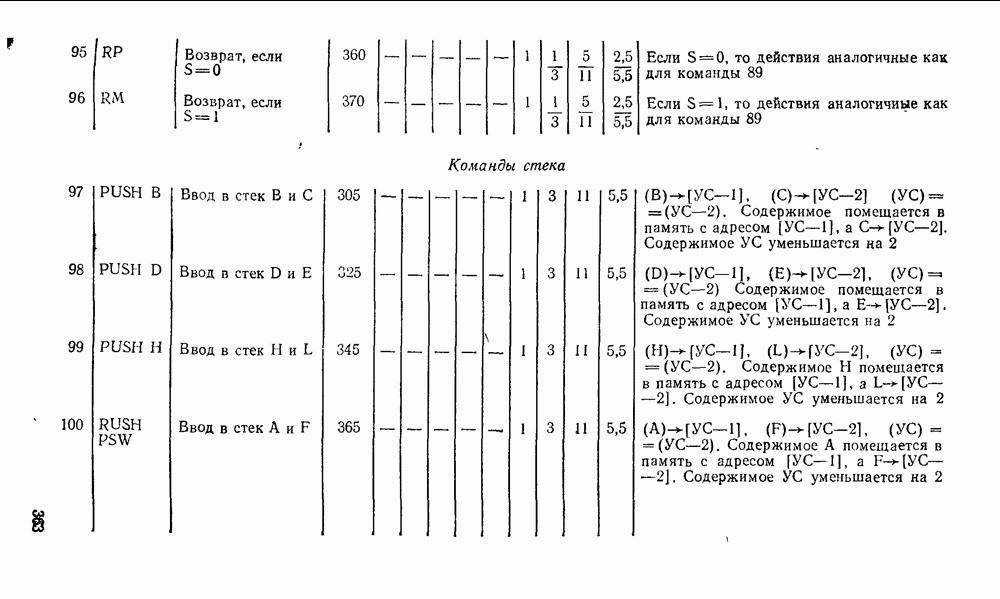
), т. е. между секциями перенос реализуется по последовательной схеме. В случае большого количества секций между ними также можно реализовать ускоренный перенос.

Рис. 5.33.
Перепишем выражение для  из формул (5.19) для первой секции в виде
из формул (5.19) для первой секции в виде

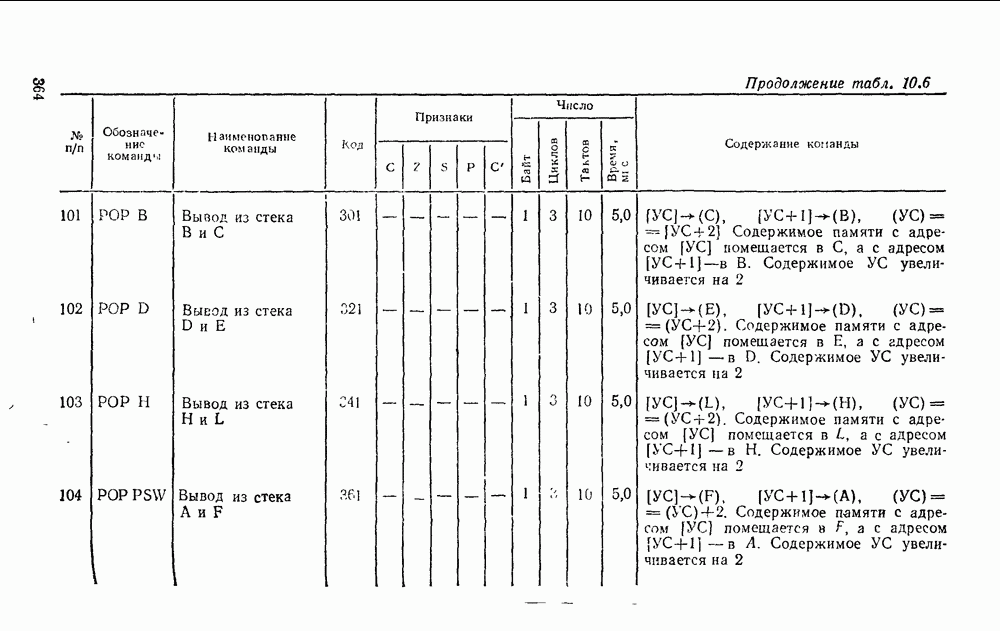
Тогда аналогично перенос из второй секции:

Секции можно сгруппировать по 4 и для 4 секций (т. е. 16 двоичных разрядов), формируется групповой перенос.
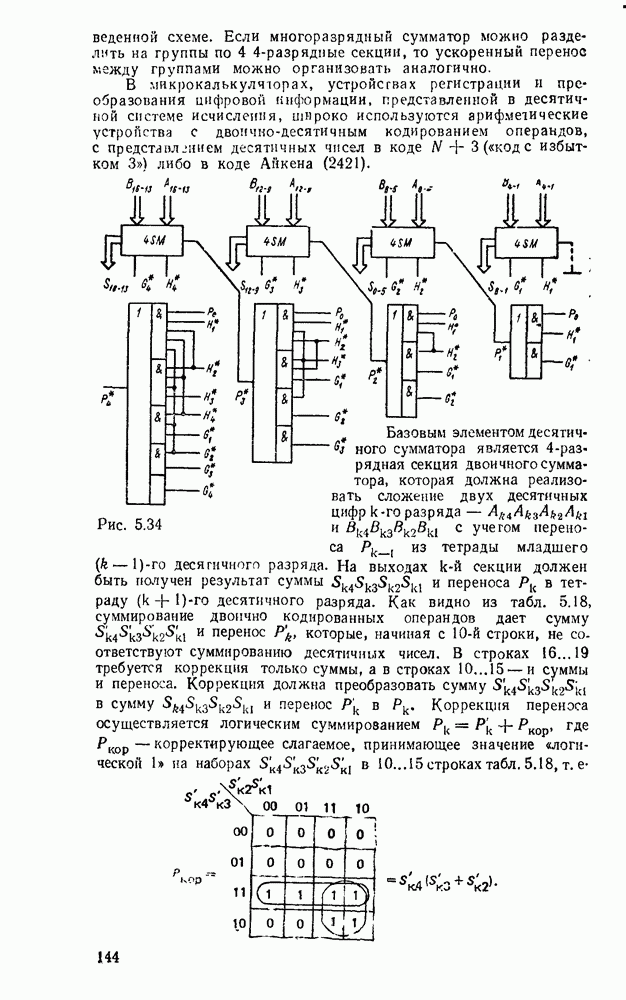
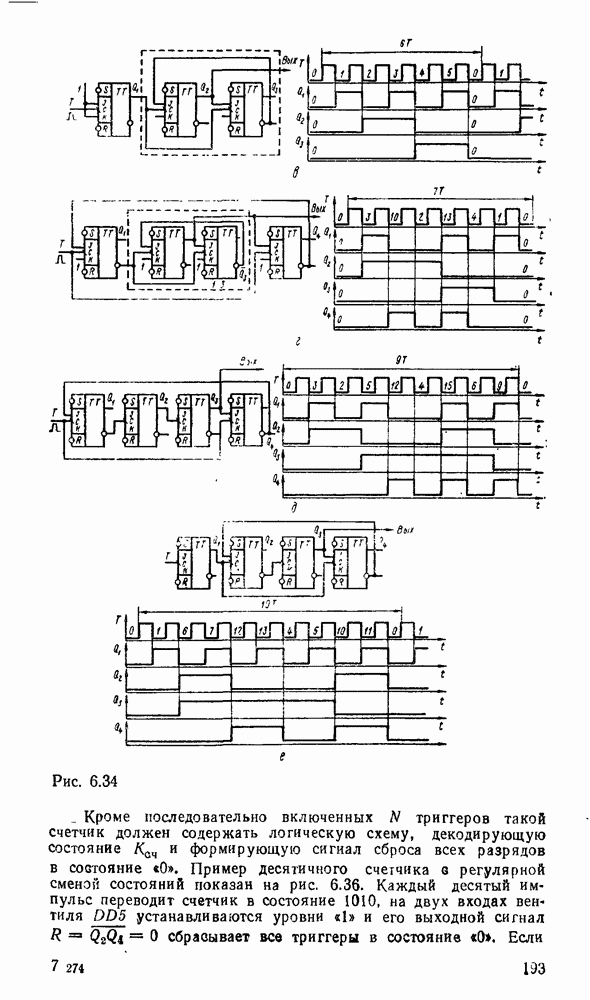
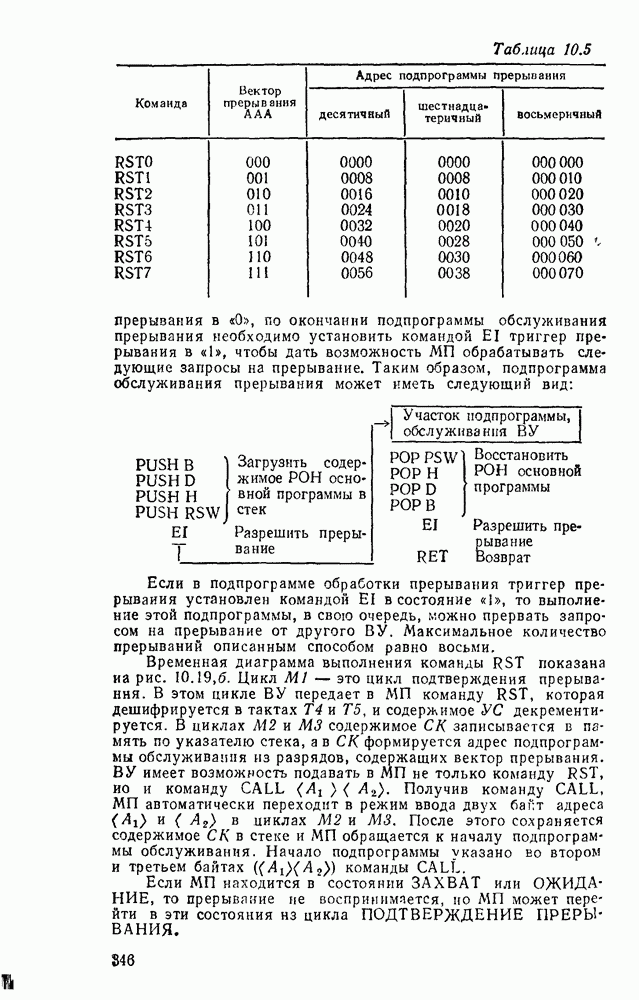
Тогда структуру параллельного переноса между секциями можно выполнить как на рис. 5.34. Ускоренный перенос между разрядами  -разрядных секций также можно выполнить по приведенной схеме.
-разрядных секций также можно выполнить по приведенной схеме.
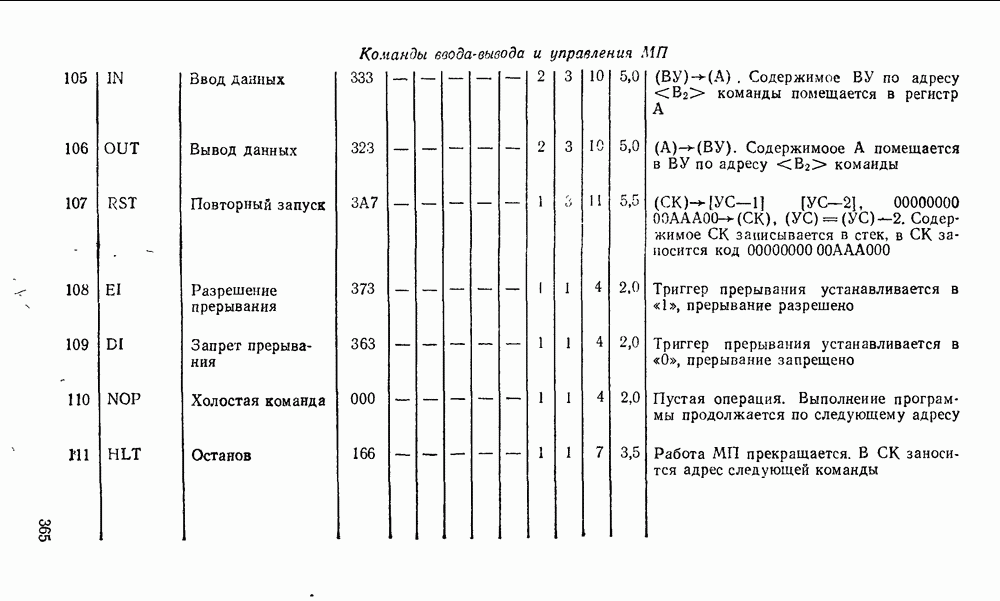
Если многоразрядный сумматор можно разделить на группы по  секции, то ускоренный перенос между группами можно организовать аналогично.
секции, то ускоренный перенос между группами можно организовать аналогично.
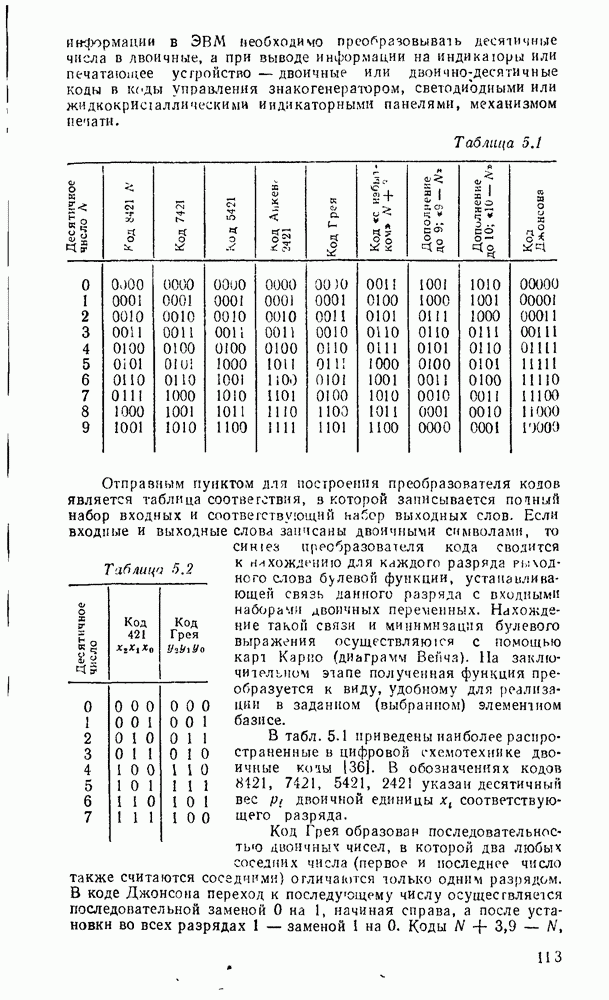
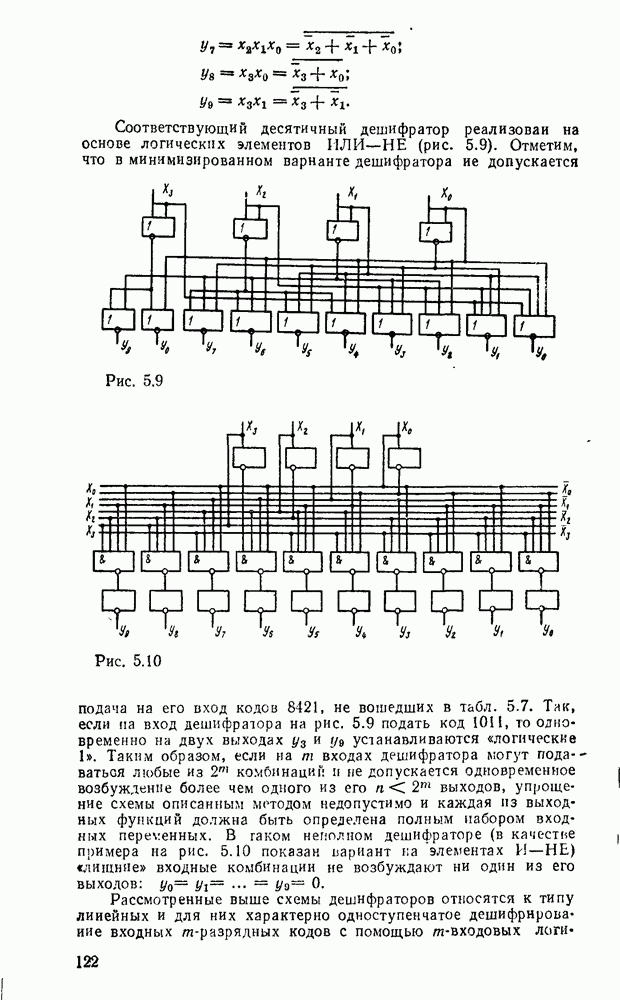
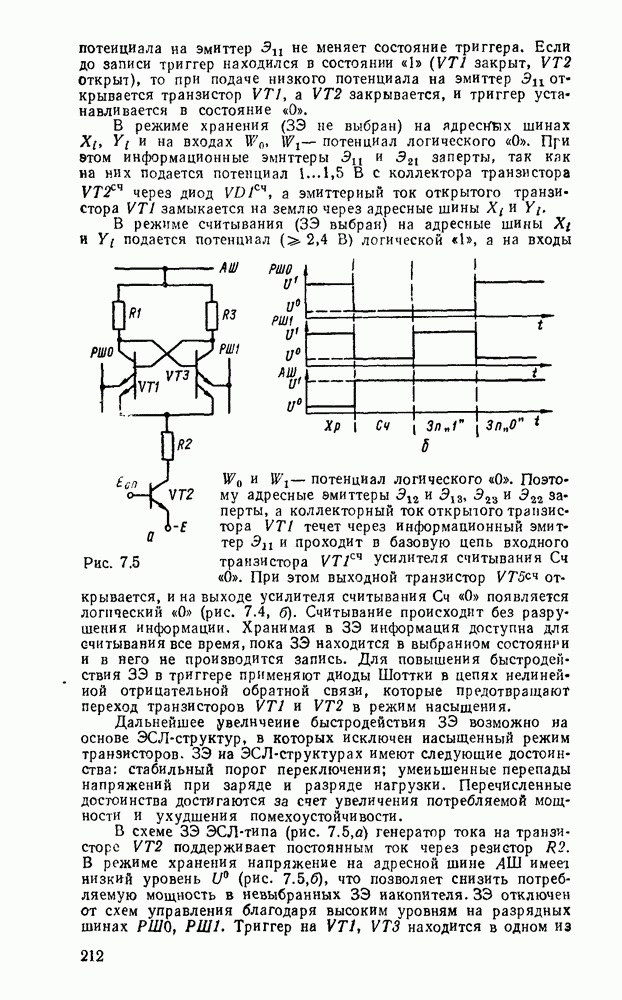
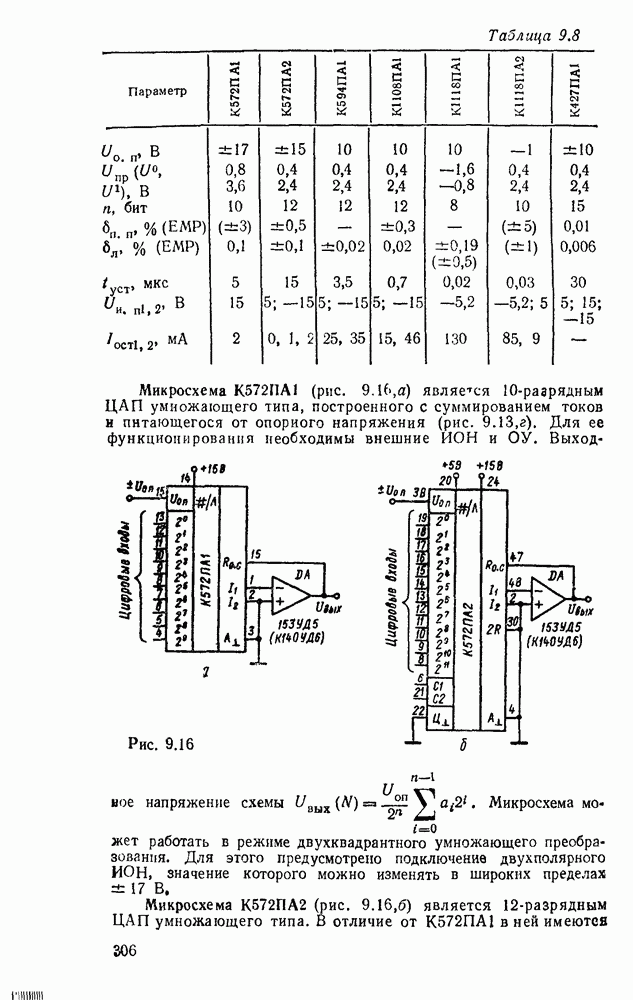
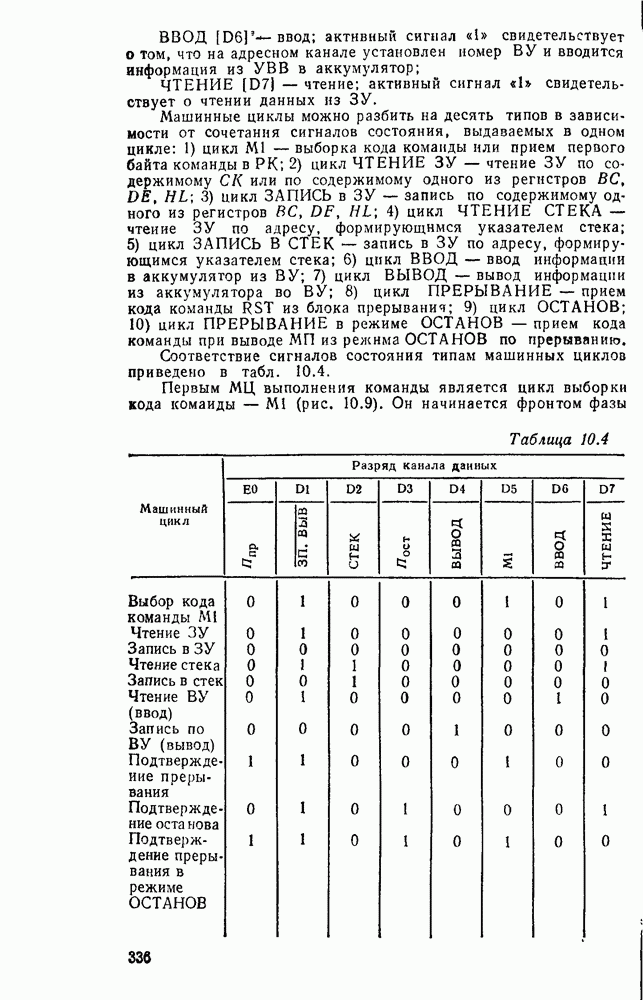
В микрокалькуляторах, устройствах регистрации и преобразования цифровой информации, представленной в десятичной системе исчисления, широко используются арифметические устройства с двоично-десятичным кодированием операндов, с представл лшем десятичных чисел в коде  («код с избытком
(«код с избытком  ) либо в коде Айкена (2421).
) либо в коде Айкена (2421).

Рис. 5.34.
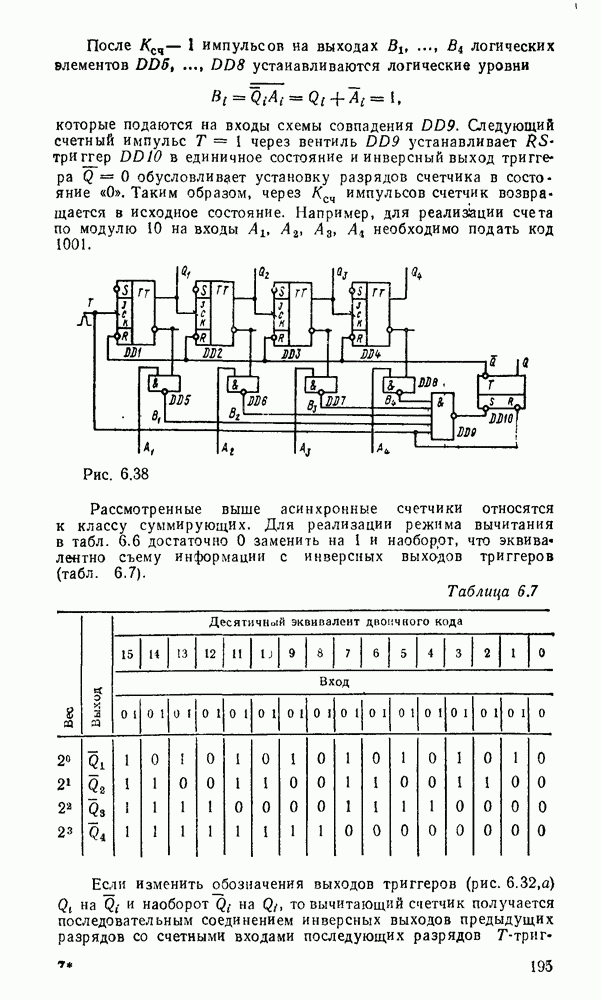
Базовым элементом десятичного сумматора является  -раз-рядная секция двоичного сумматора, которая должна реализовать сложение двух десятичных цифр
-раз-рядная секция двоичного сумматора, которая должна реализовать сложение двух десятичных цифр  разряда —
разряда —  с учетом переноса
с учетом переноса  , из тетрады младшего
, из тетрады младшего  десятичного разряда. На выходах
десятичного разряда. На выходах  секции должен быть получен результат суммы
секции должен быть получен результат суммы  и переноса
и переноса  в тетраду
в тетраду  десятичного разряда. Как видно из табл. 5.18, суммирование двончно кодированных операндов дает сумму и перенос
десятичного разряда. Как видно из табл. 5.18, суммирование двончно кодированных операндов дает сумму и перенос  , которые, начиная с
, которые, начиная с  строки, не соответствуют суммированию десятичных чисел. В строках
строки, не соответствуют суммированию десятичных чисел. В строках  требуется коррекция только суммы, а в строках
требуется коррекция только суммы, а в строках  и суммы и переноса. Коррекция должна преобразовать сумму
и суммы и переноса. Коррекция должна преобразовать сумму  в сумму
в сумму  и перенос
и перенос  . Коррекция переноса осуществляется логическим суммированием
. Коррекция переноса осуществляется логическим суммированием  , где Ркор — корректирующее слагаемое, принимающее значение «логической 1» на наборах
, где Ркор — корректирующее слагаемое, принимающее значение «логической 1» на наборах  строках табл. 5.18, т. е.
строках табл. 5.18, т. е.

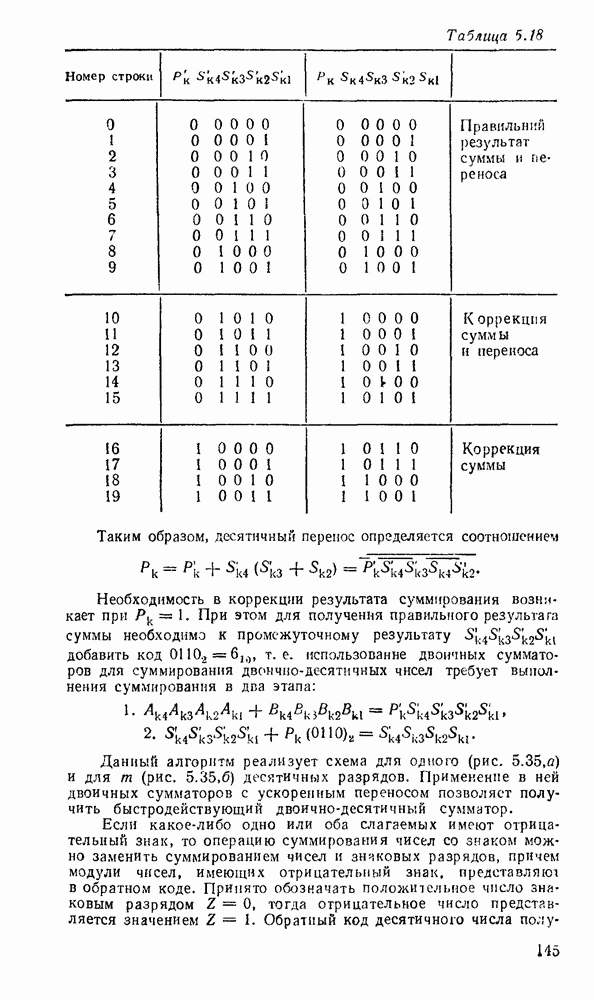
Таблица 5.18

Таким образом, десятичный перенос определяется соотношением

Необходимость в коррекции результата суммирования возникает при  . При этом для получения правильного результата суммы необходимо к промежуточному результату добавить код 0110а
. При этом для получения правильного результата суммы необходимо к промежуточному результату добавить код 0110а  т. е. использование двоичных сумматоров для суммирования двоично-десятичных чисел требует выполнения суммирования в два этапа:
т. е. использование двоичных сумматоров для суммирования двоично-десятичных чисел требует выполнения суммирования в два этапа:

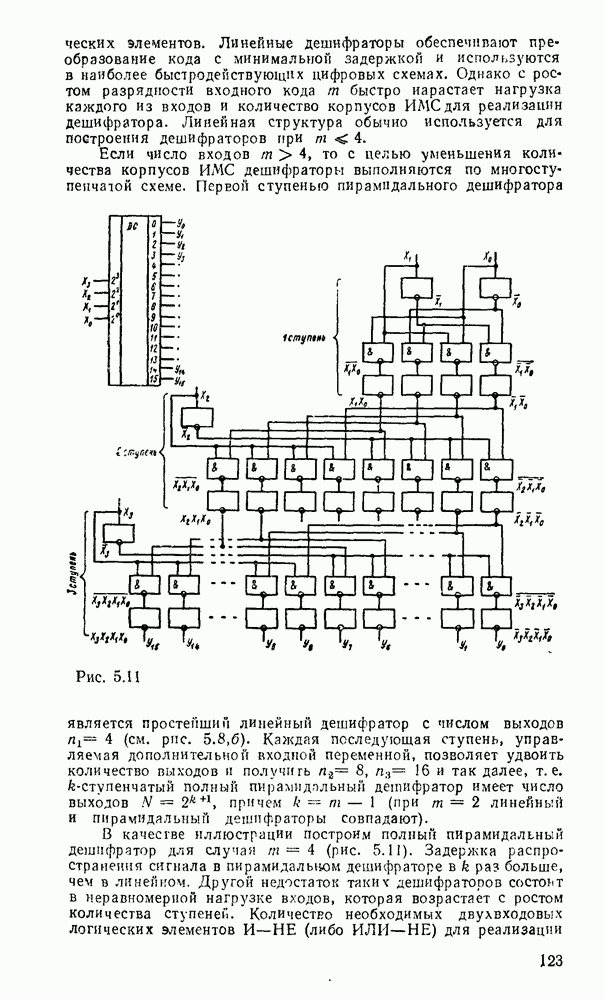
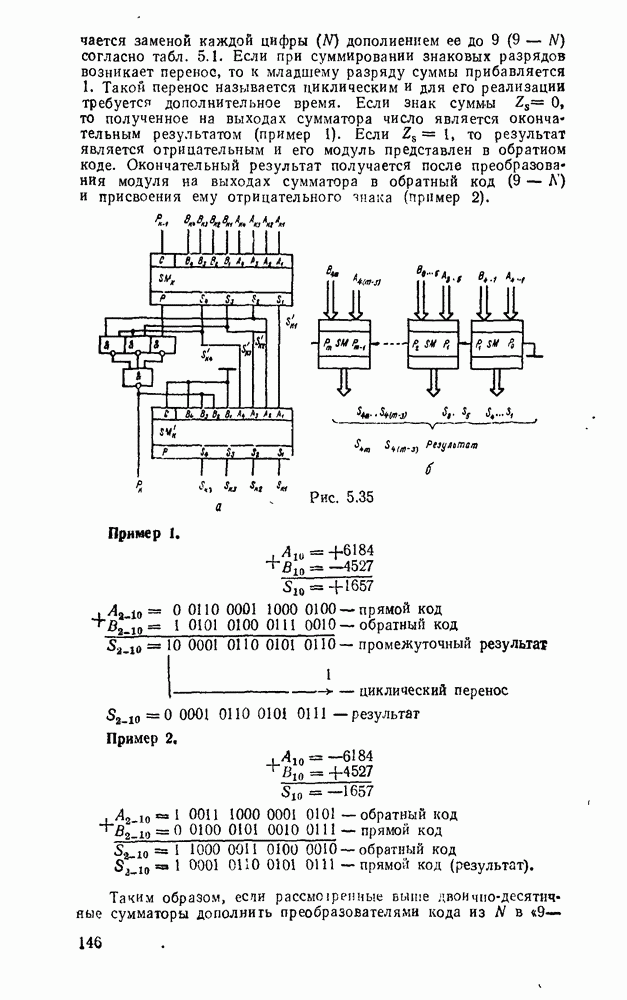
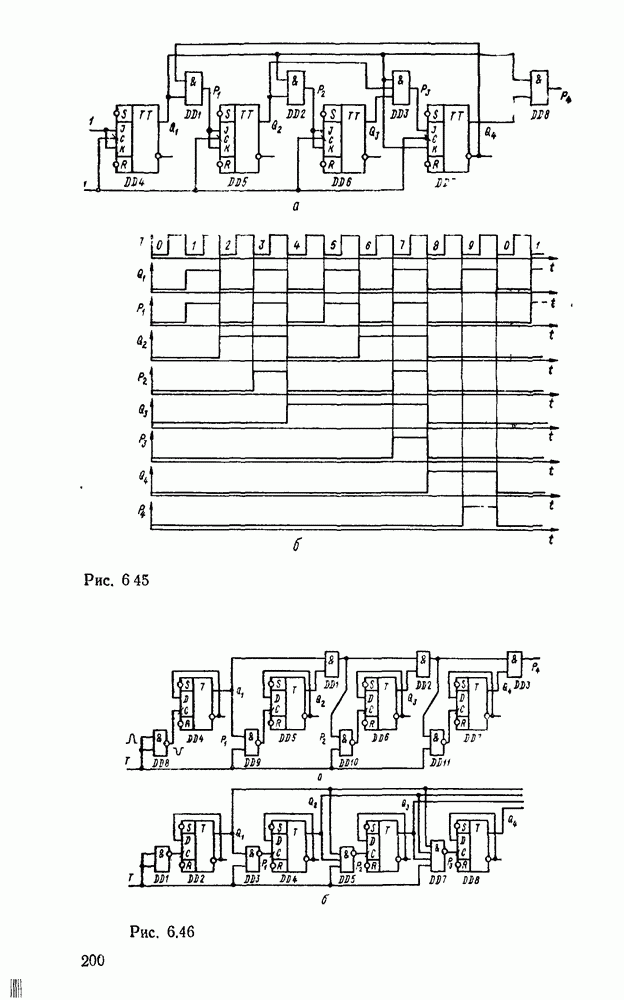
Данный алгоритм реализует схема для одного (рис. 5.35,а) и для  (рис.
(рис.  ) десятичных разрядов. Применение в ней двоичных сумматоров с ускоренным переносом позволяет получить быстродействующий двоично-десятичный сумматор.
) десятичных разрядов. Применение в ней двоичных сумматоров с ускоренным переносом позволяет получить быстродействующий двоично-десятичный сумматор.
Если какое-либо одно или оба слагаемых имеют отрицательный знак, то операцию суммирования чисел со знаком можно заменить суммированием чисел и знаковых разрядов, причем модули чисел, имеющих отрицательный знак, представляют в обратном коде. Принято обозначать положительное число знаковым разрядом  , тогда отрицательное число представляется значением
, тогда отрицательное число представляется значением  .
.
Обратный код десятичного числа получается заменой каждой цифры (N) дополнением ее до 9(9 — N) согласно табл. 5.1. Если при суммировании знаковых разрядов возникает перенос, то к младшему разряду суммы прибавляется 1. Такой перенос называется циклическим и для его реализации требуется дополнительное время. Если знак суммы  , то полученное на выходах сумматора число является окончательным результатом (пример 1). Если
, то полученное на выходах сумматора число является окончательным результатом (пример 1). Если  , то результат является отрицательным и его модуль представлен в обратном коде. Окончательный результат получается после преобразования модуля на выходах сумматора в обратный код (
, то результат является отрицательным и его модуль представлен в обратном коде. Окончательный результат получается после преобразования модуля на выходах сумматора в обратный код ( ) и присвоения ему отрицательного знака (пример 2).
) и присвоения ему отрицательного знака (пример 2).

Рис. 5.35.
Пример 1.

Пример 2.

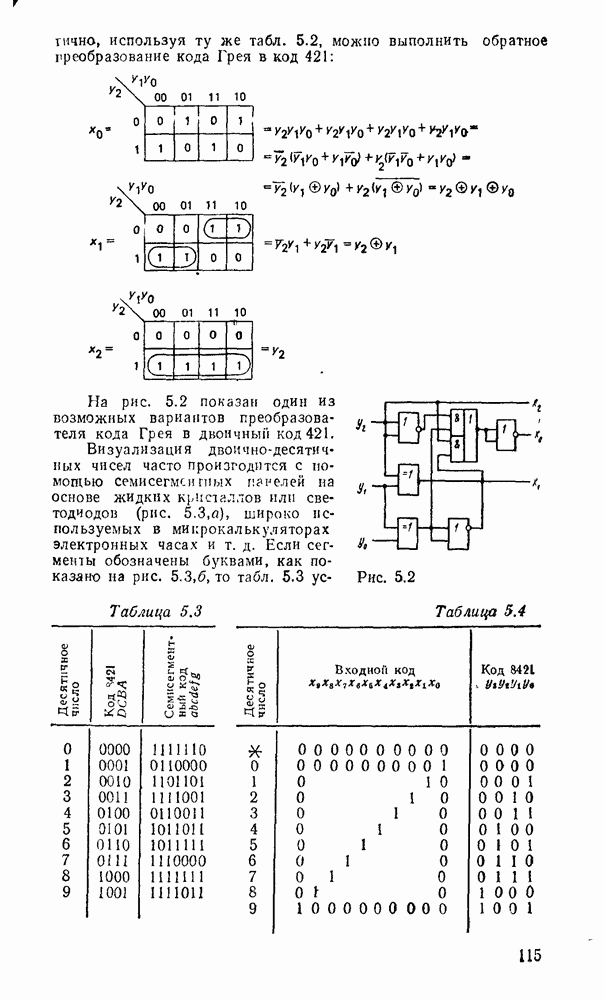
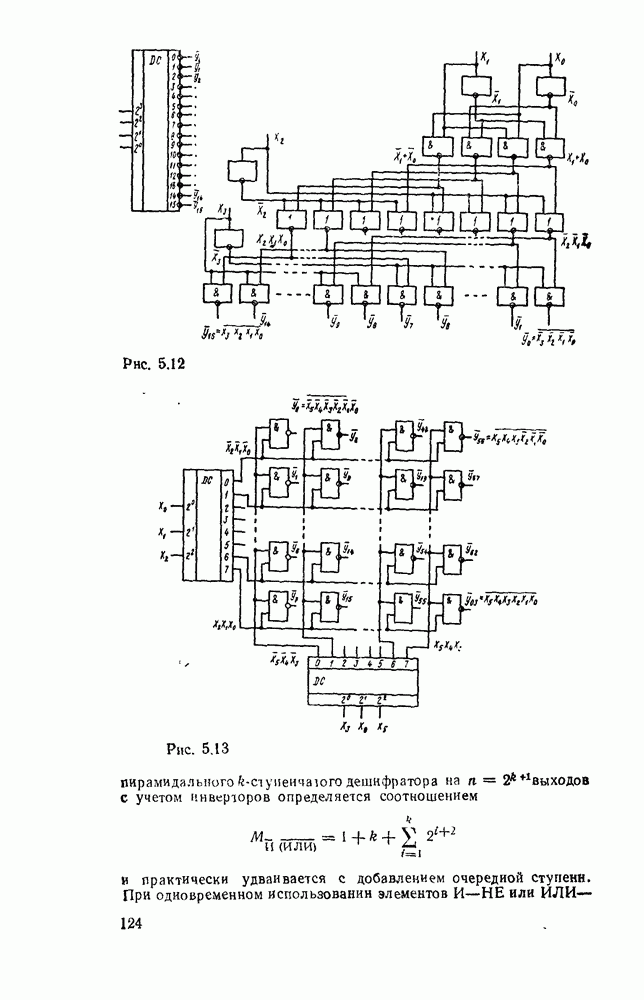
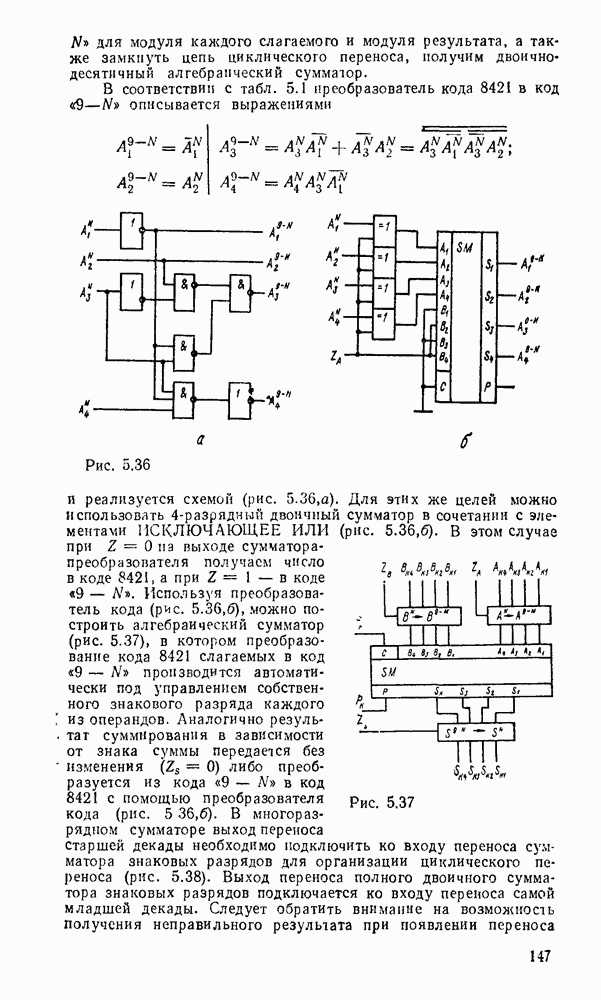
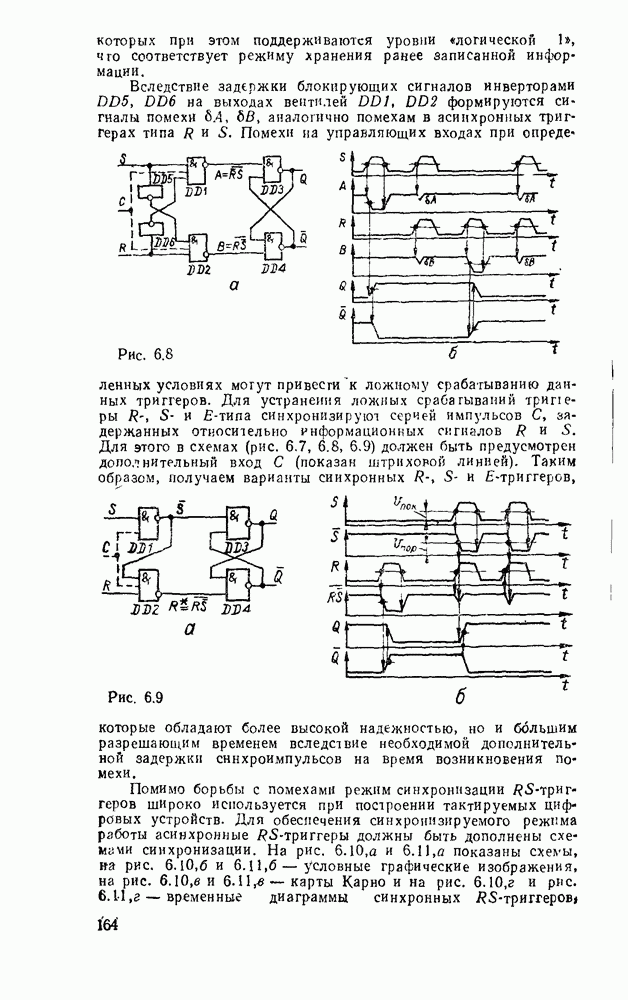
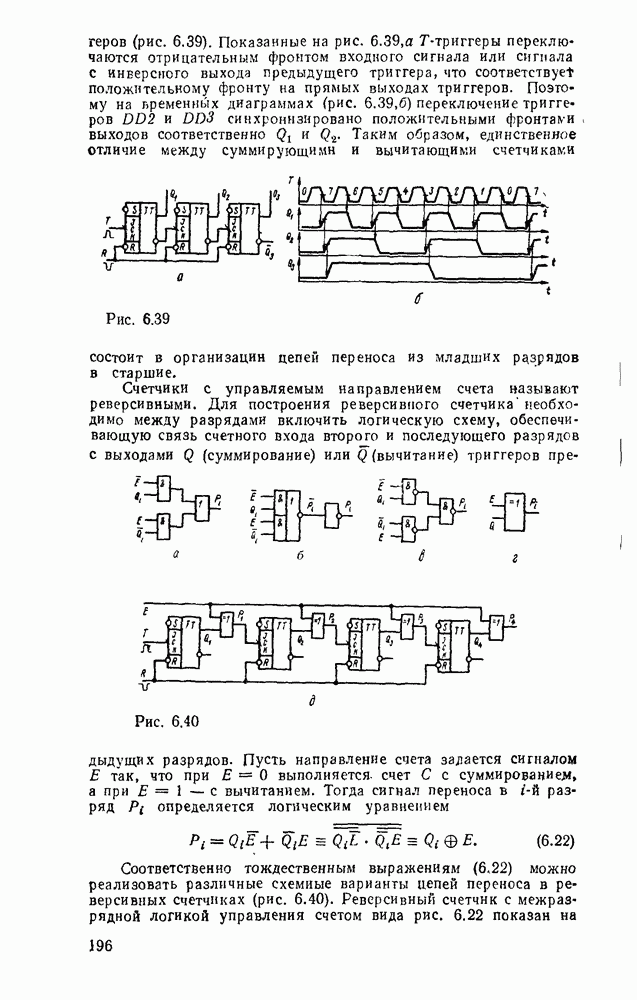
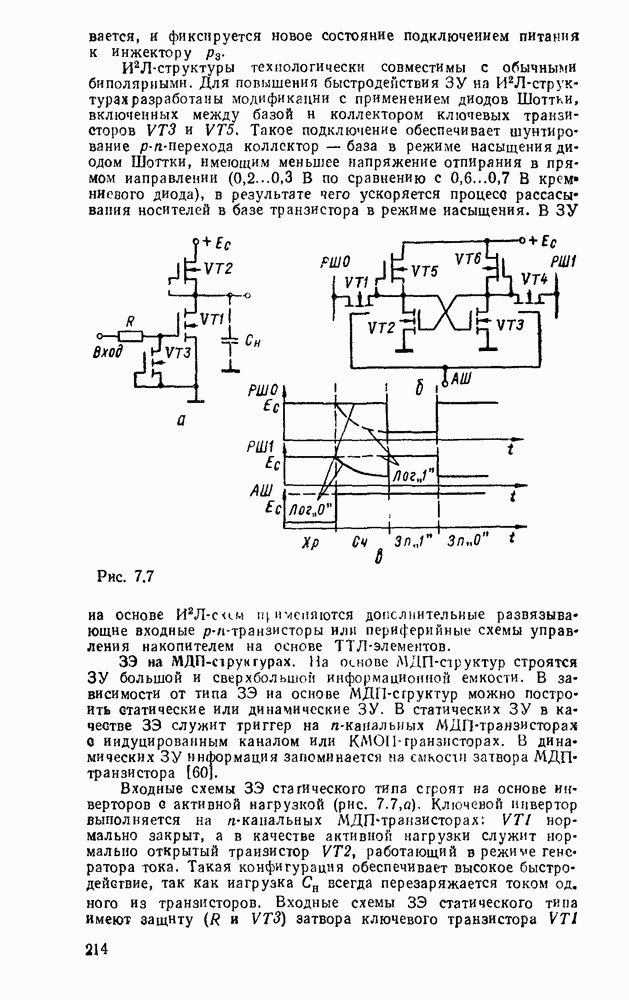
Таким образом, есчи рассмешенные выше двоично-десятичные сумматоры дополнить преобразователями кода из N в  для модуля каждого слагаемого и модуля результата, а также замкнуть цепь циклического переноса, иолучим двоичнодесятичный алгебраический сумматор.
для модуля каждого слагаемого и модуля результата, а также замкнуть цепь циклического переноса, иолучим двоичнодесятичный алгебраический сумматор.
В соответствии с табл. 5.1 преобразователь кода 8421 в код  описывается выражениями
описывается выражениями


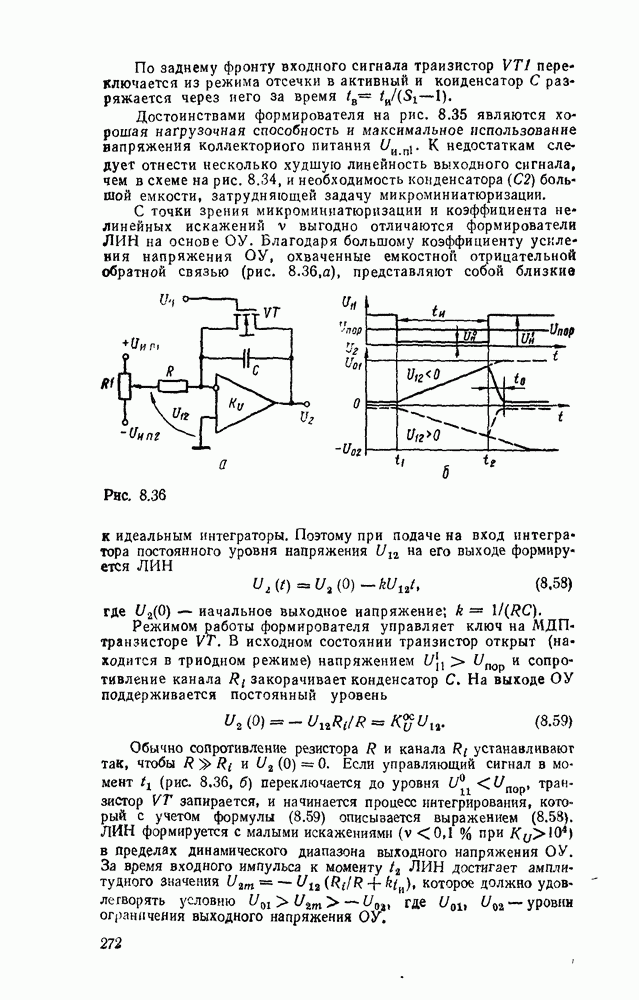
Рис. 5.36.

Рис. 5.37.
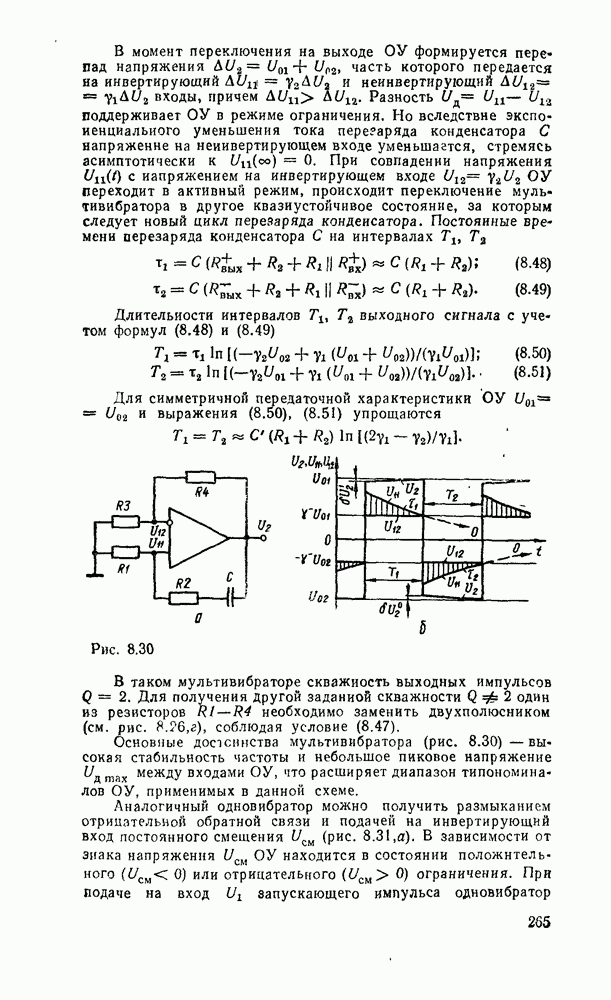
и реализуется схемой (рис. 5.36,а). Для этих же целей можно использовать  -разрядный двоичный сумматор в сочетании с элементами ИСКЛЮЧАЮЩЕЕ ИЛИ (рис.
-разрядный двоичный сумматор в сочетании с элементами ИСКЛЮЧАЮЩЕЕ ИЛИ (рис.  ). В этом случае при
). В этом случае при  на выходе сумматора-преобразователя получаем число в коде 8421, а при
на выходе сумматора-преобразователя получаем число в коде 8421, а при  — в коде
— в коде  . Используя преобразователь кода (рис.
. Используя преобразователь кода (рис.  ), можно построить алгебраический сумматор (рис. 5.37), в котором преобразование кода 8421 слагаемых в код
), можно построить алгебраический сумматор (рис. 5.37), в котором преобразование кода 8421 слагаемых в код  производится автоматически под управлением собственного знакового разряда каждого из операндов. Аналогично результат суммирования в зависимости от знака суммы передается без изменения
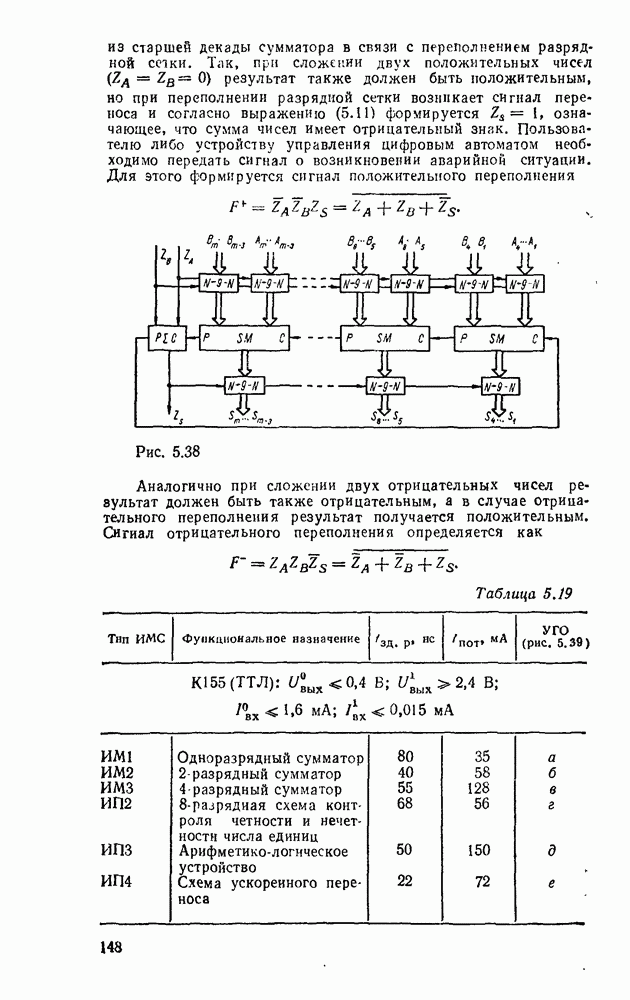
производится автоматически под управлением собственного знакового разряда каждого из операндов. Аналогично результат суммирования в зависимости от знака суммы передается без изменения  либо преобразуется из кода «9 — N» в код 8421 с помощью преобразователя кода (рис. 5 36,б). В многоразрядном сумматоре выход переноса старшей декады необходимо подключить ко входу переноса сумматора знаковых разрядов для организации циклического переноса (рис. 5.38). Выход переноса полного двоичного сумматора знаковых разрядов подключается ко входу переноса самой младшей декады. Следует обратить внимание на возможность получения неправильного результата при появлении переноса из старшей декады сумматора в связи с переполнением разрядной сетки.
либо преобразуется из кода «9 — N» в код 8421 с помощью преобразователя кода (рис. 5 36,б). В многоразрядном сумматоре выход переноса старшей декады необходимо подключить ко входу переноса сумматора знаковых разрядов для организации циклического переноса (рис. 5.38). Выход переноса полного двоичного сумматора знаковых разрядов подключается ко входу переноса самой младшей декады. Следует обратить внимание на возможность получения неправильного результата при появлении переноса из старшей декады сумматора в связи с переполнением разрядной сетки.
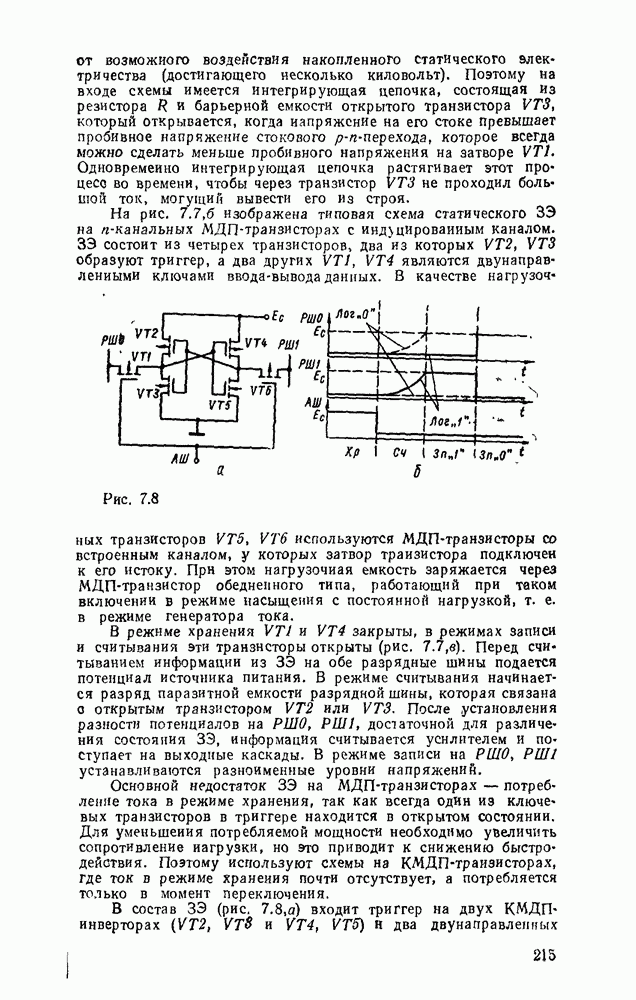
Так, при сложении двух положительных чисел  результат также должен быть положительным, но при переполнении разрядной сетки возникает сигнал переноса и согласно выражению (5.11) формируется — 1, означающее, что сумма чисел имеет отрицательный знак. Пользователю либо устройству управления цифровым автоматом необходимо передать сигнал о возникновении аварийной ситуации. Для этого формируется сигнал положительного переполнения
результат также должен быть положительным, но при переполнении разрядной сетки возникает сигнал переноса и согласно выражению (5.11) формируется — 1, означающее, что сумма чисел имеет отрицательный знак. Пользователю либо устройству управления цифровым автоматом необходимо передать сигнал о возникновении аварийной ситуации. Для этого формируется сигнал положительного переполнения


Рис. 5.38.
Аналогично при сложении двух отрицательных чисел результат должен быть также отрицательным, а в случае отрицательного переполнения результат получается положительным. Сигнал отрицательного переполнения определяется как

Таблица 5.19

Таблица 5.19 (продолжение)
(см. оригинал)
Тогда общий сигнал переполнения определяется выражением

Схема, реализующая функцию (5.20), может входить в состав ИМС сумматора либо должна  собрана дополнительно.
собрана дополнительно.
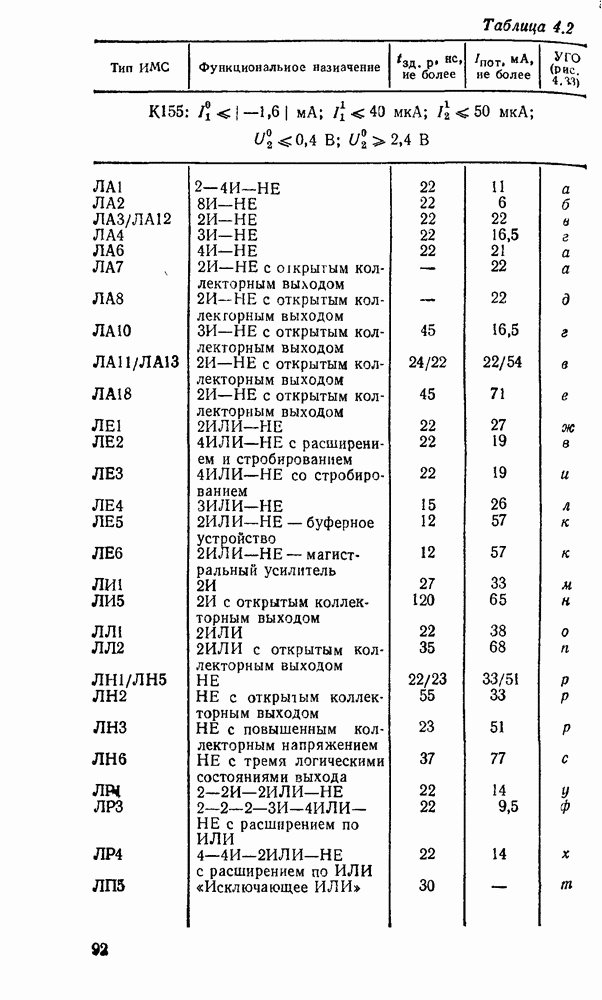
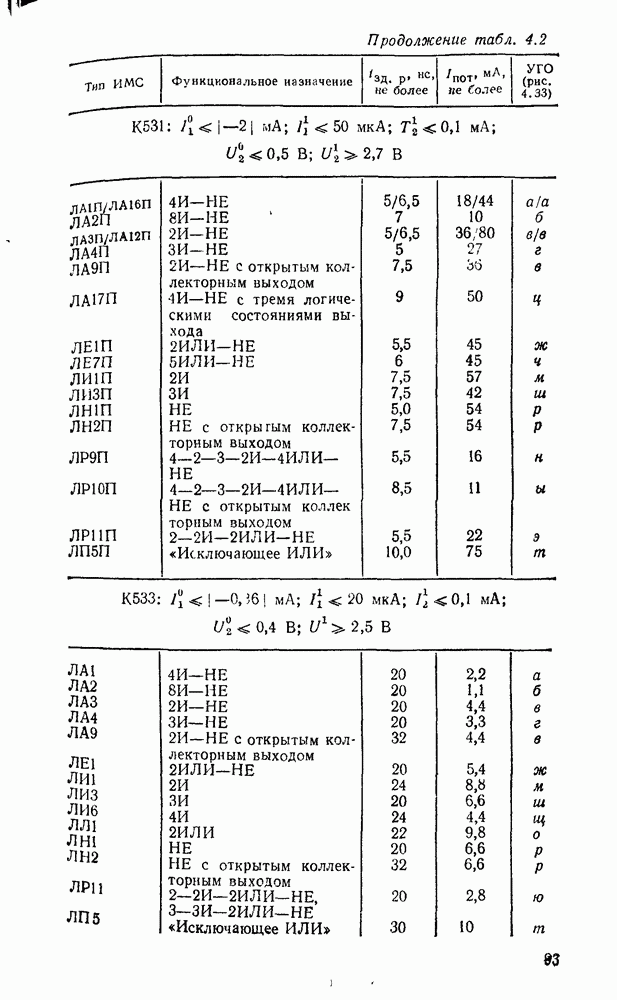
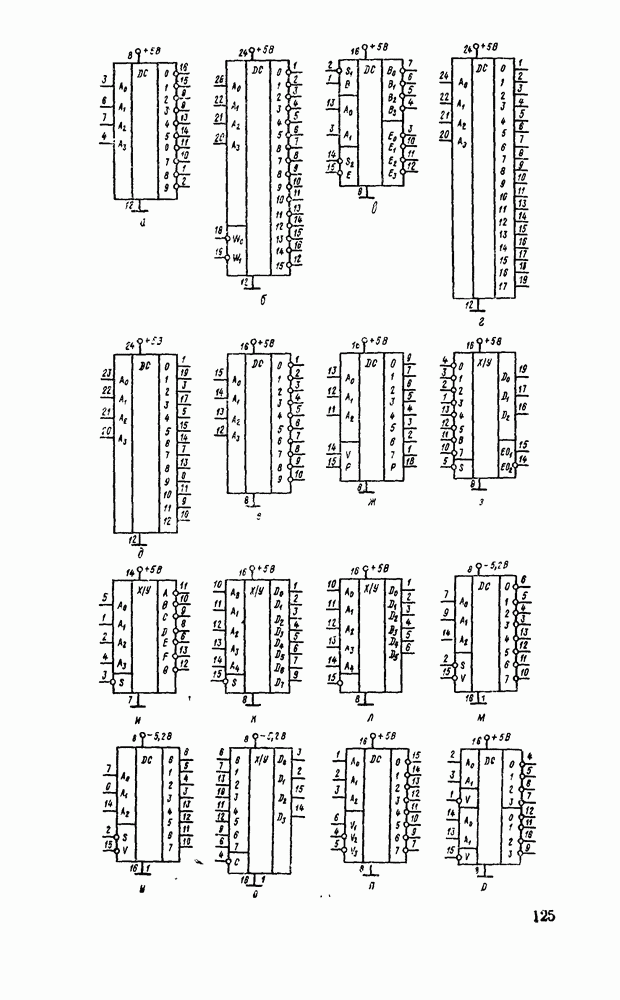
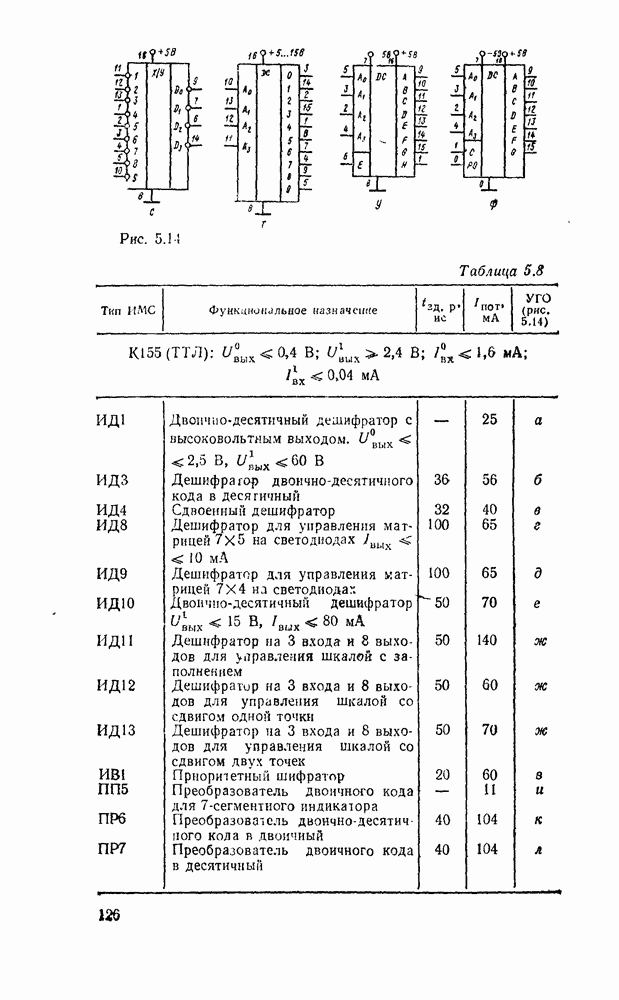
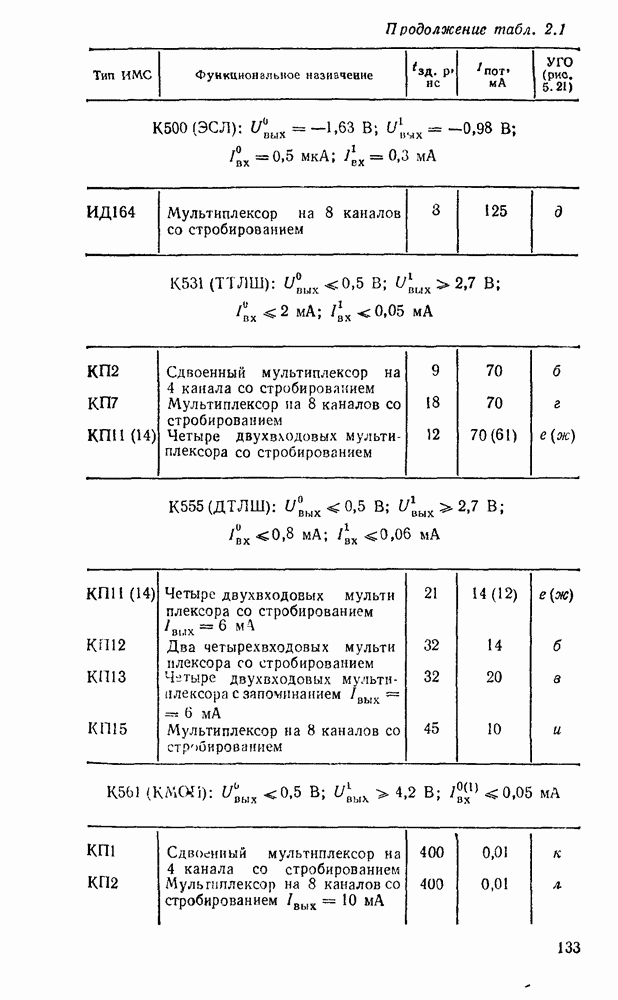
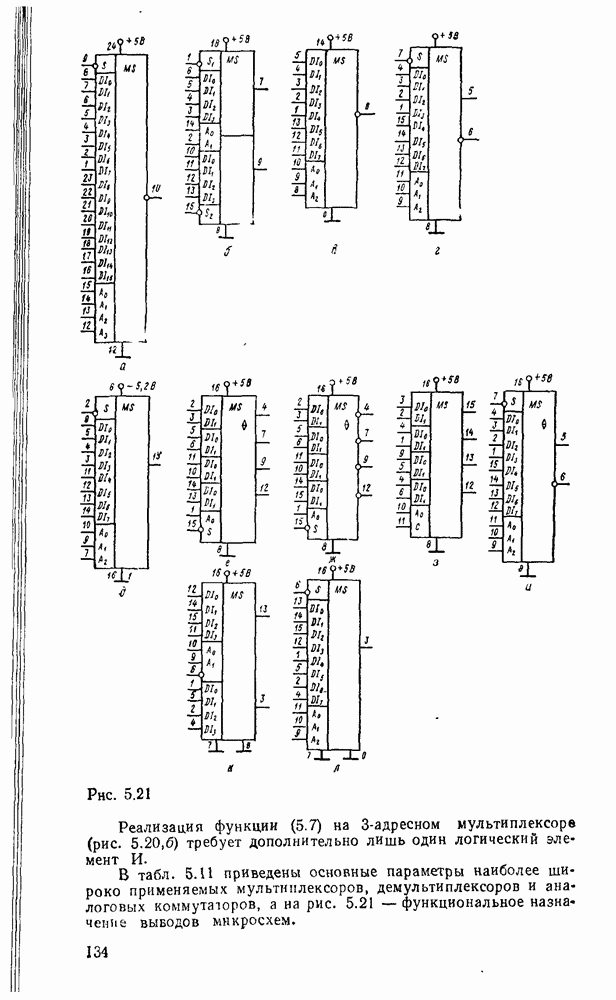
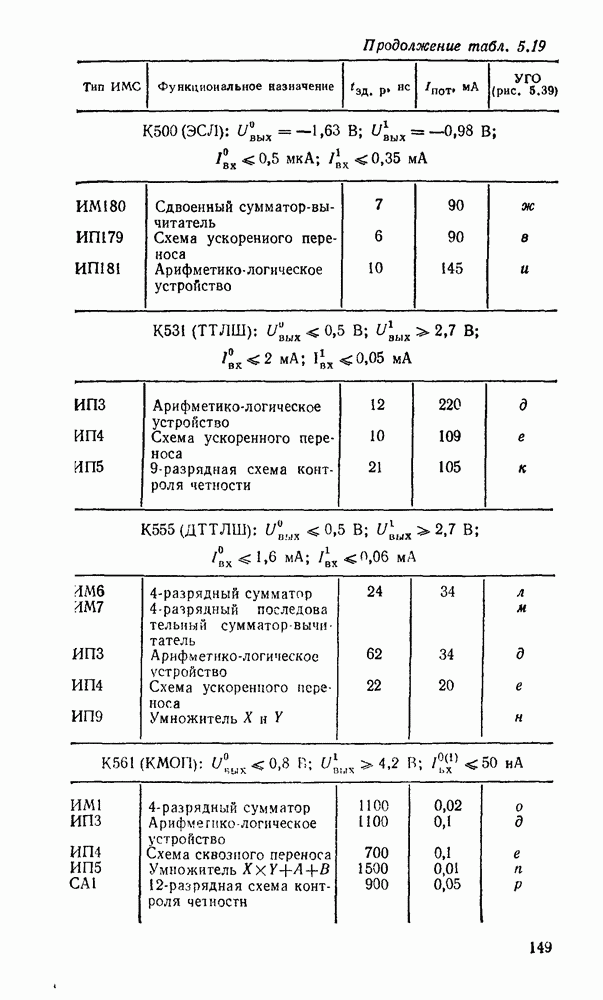
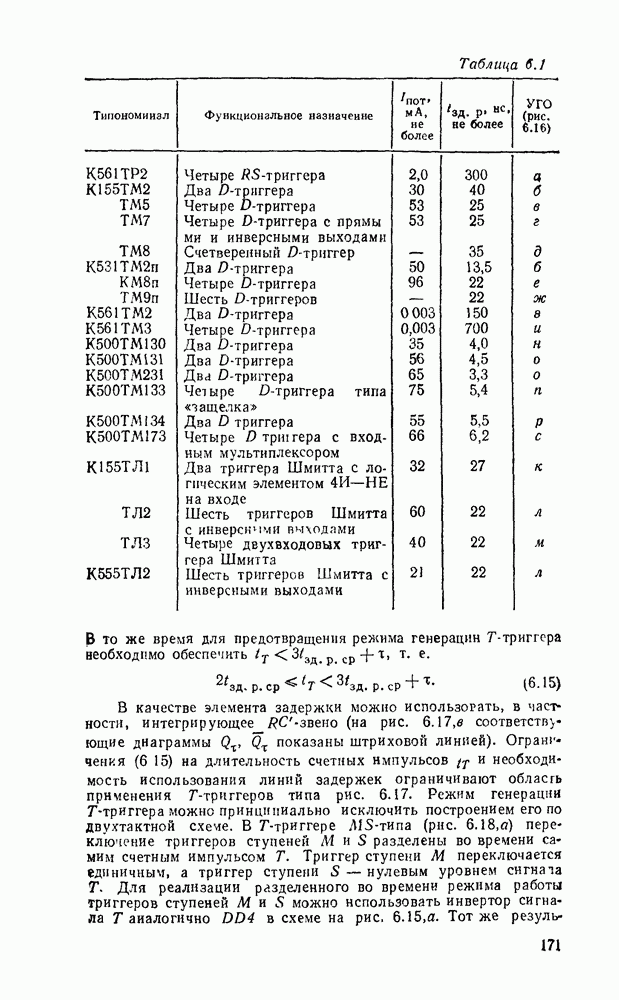
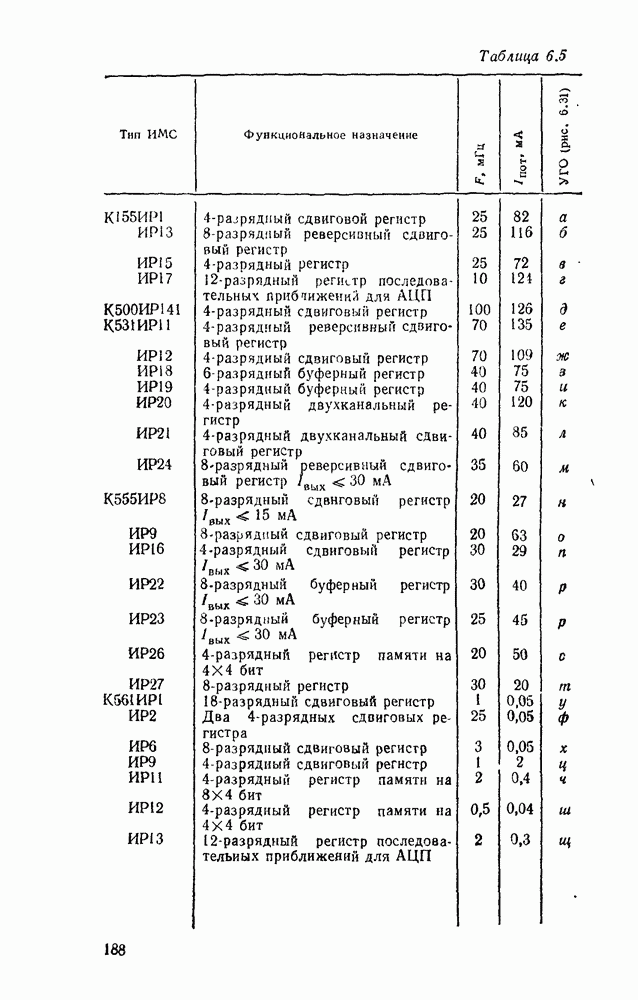
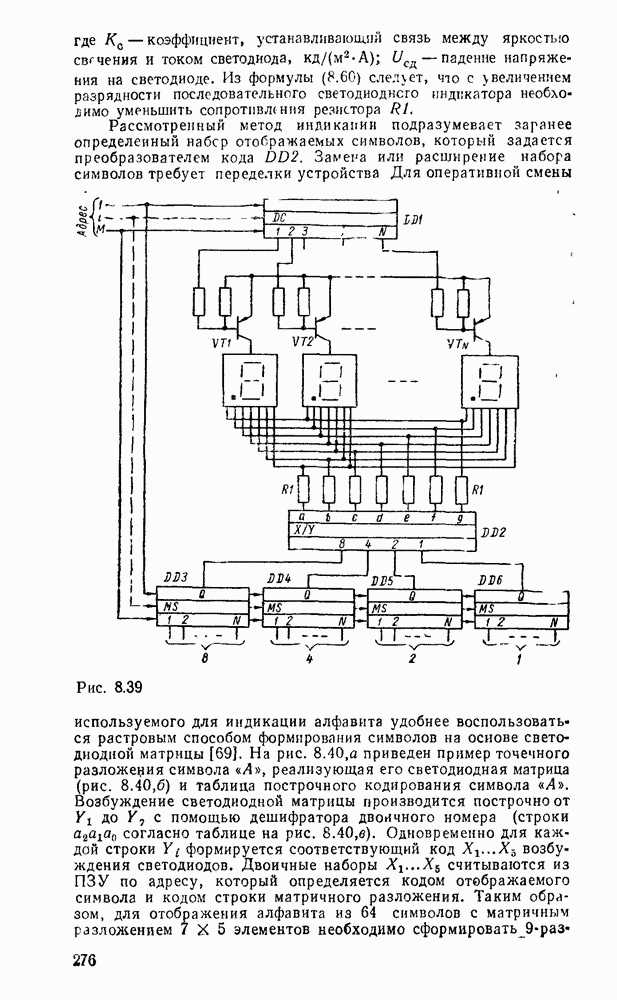
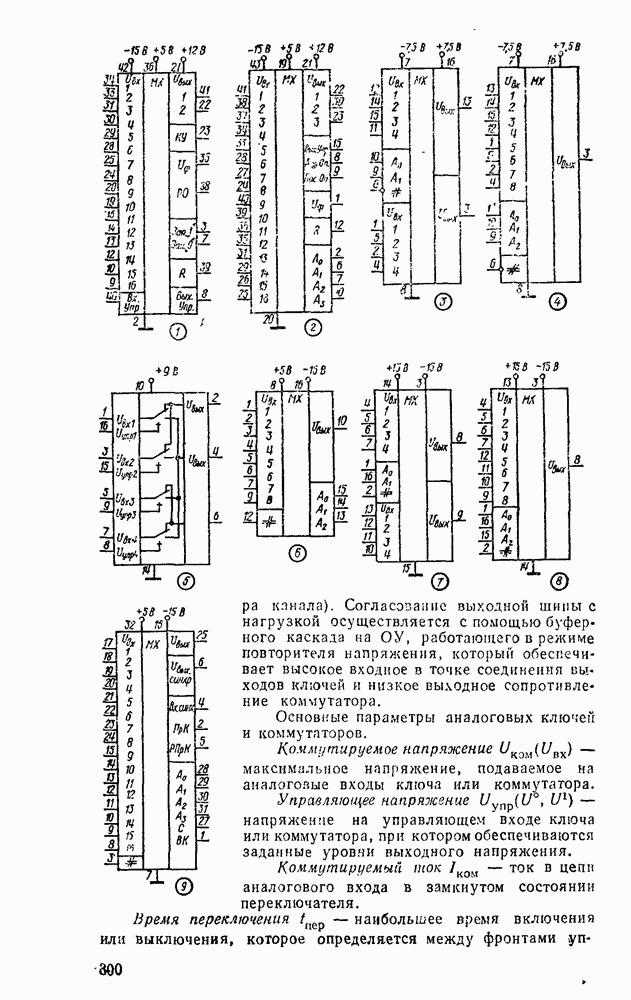
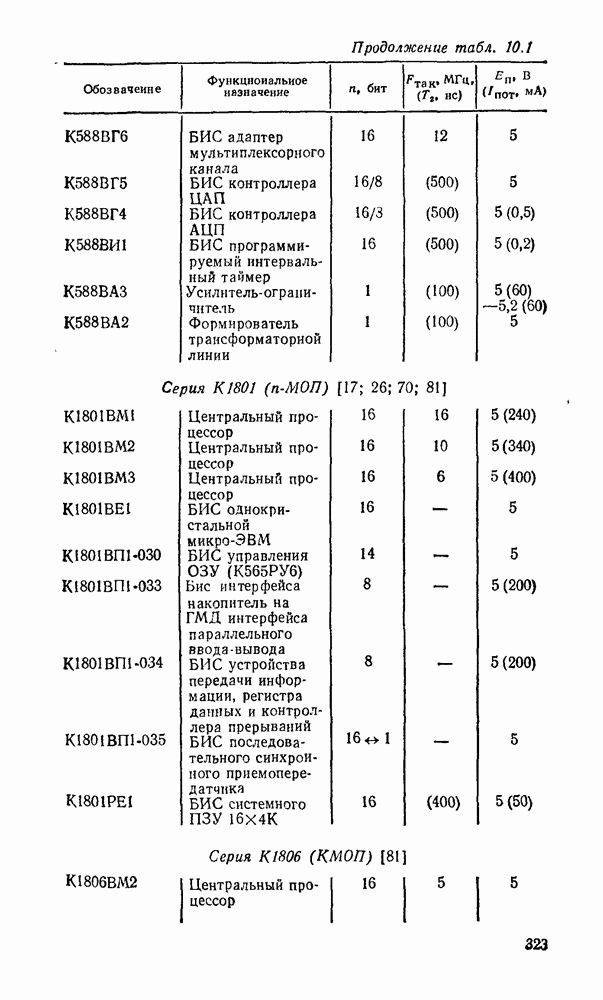
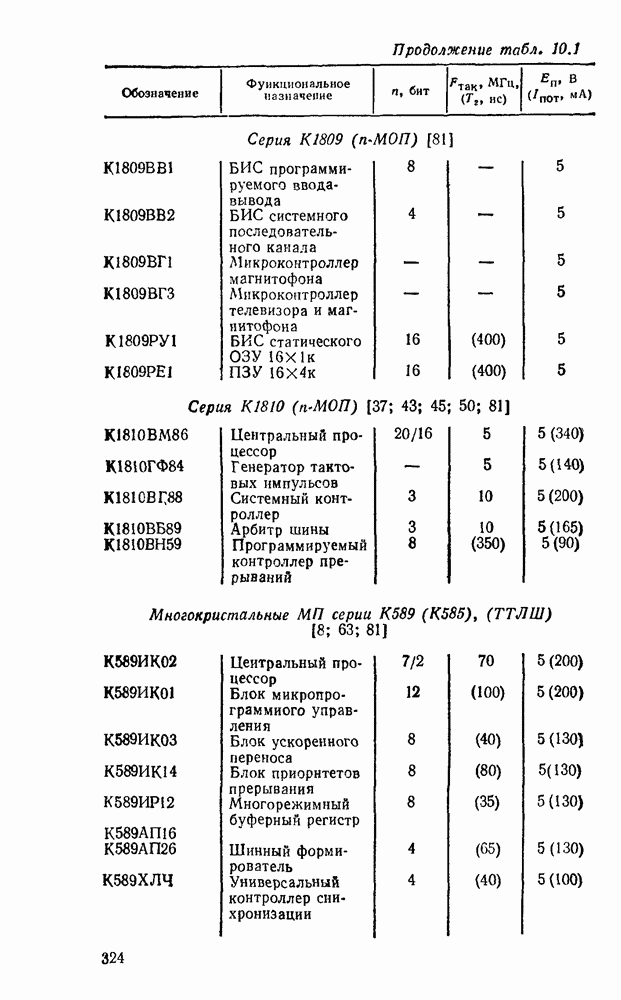
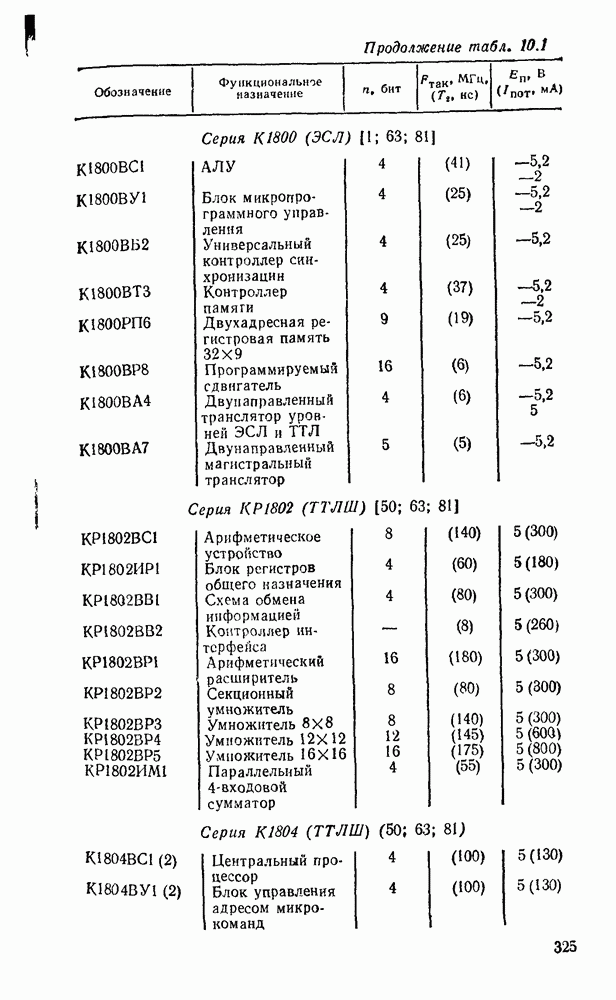
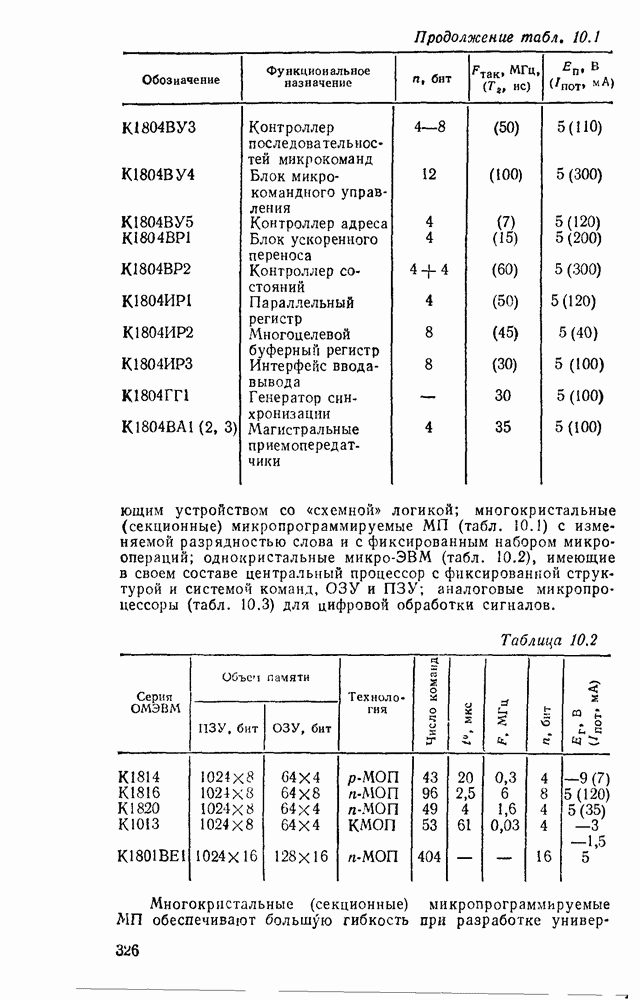
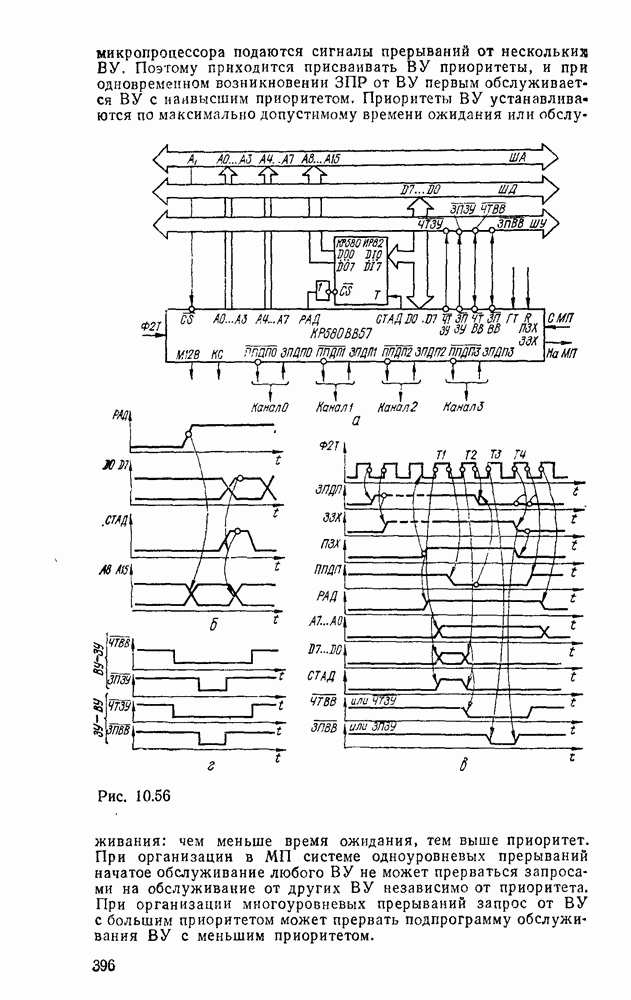
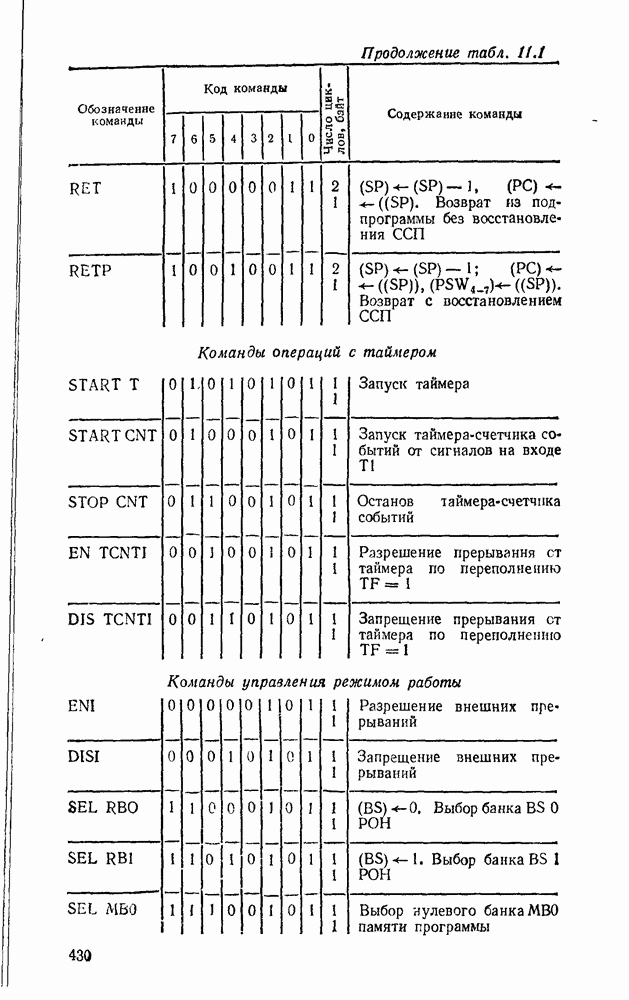
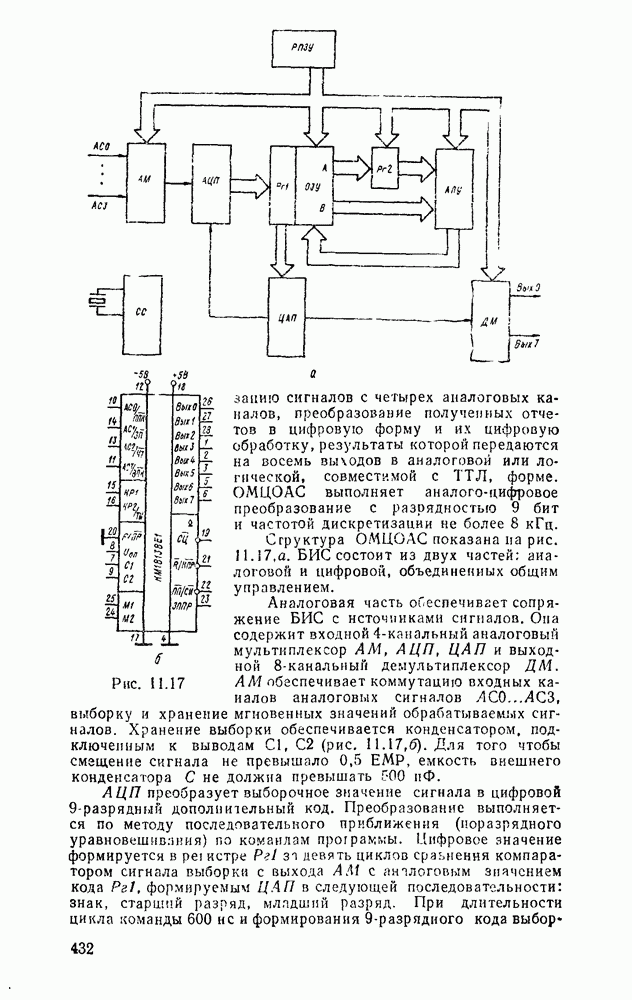
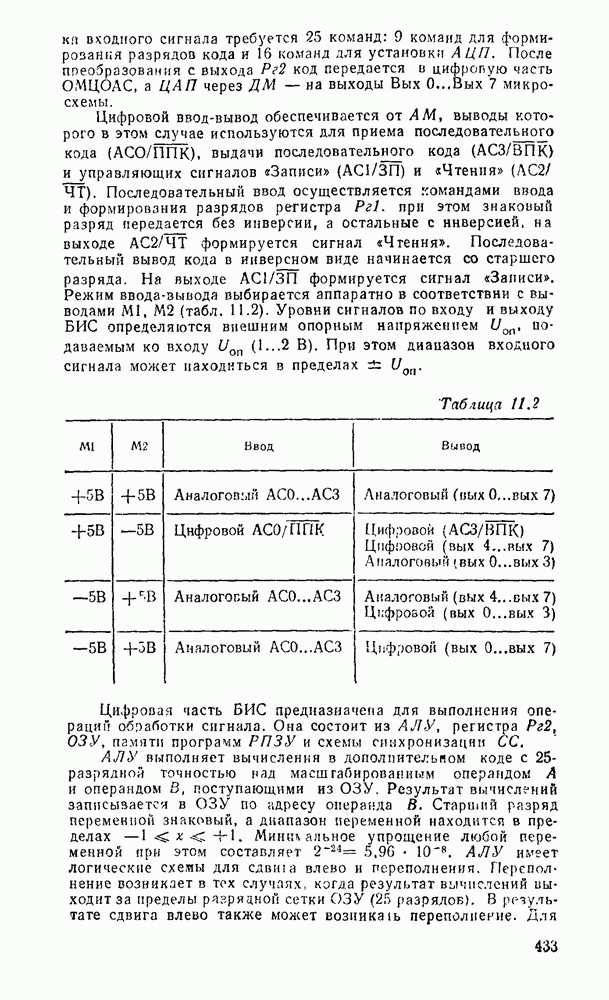
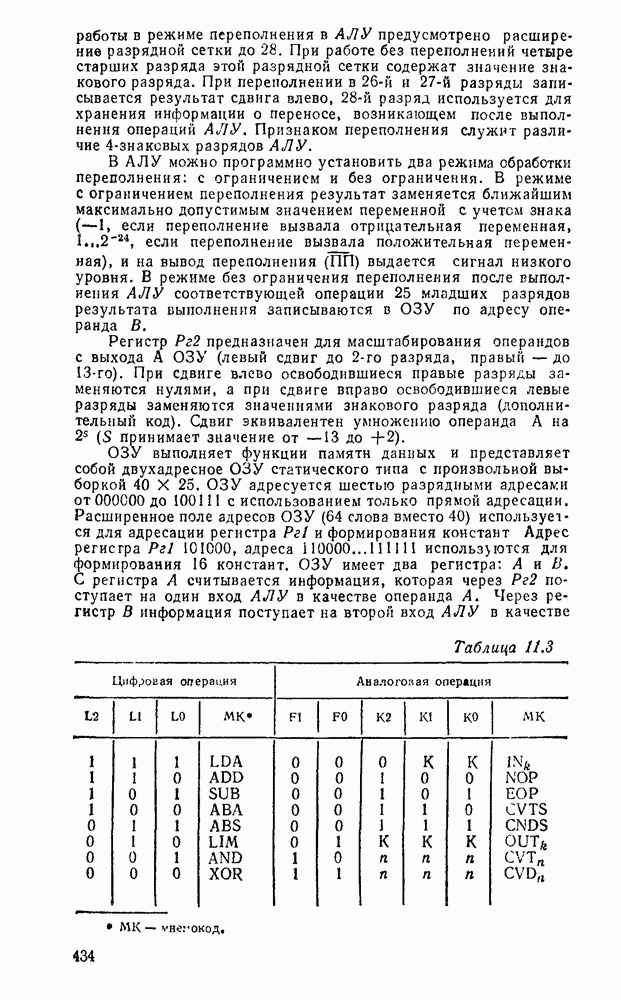
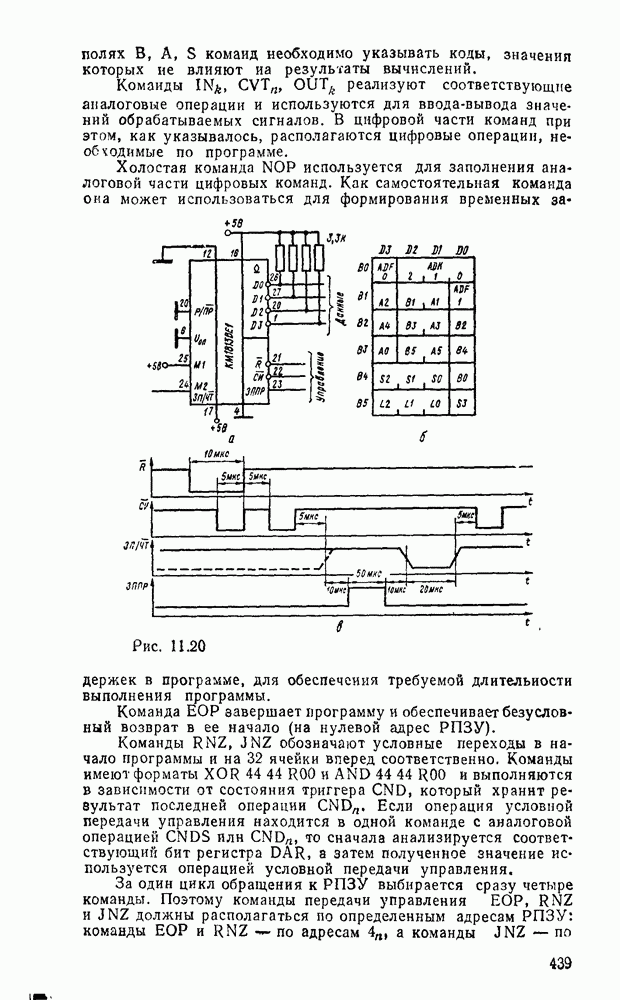
В табл. 5.19 приведены параметры сумматора наиболее широко используемых серий ИМС, а на рис. 5.39 показано функциональное назначение выводов ИМС из табл. 5.19.
Комбинационные сумматоры благодаря высокому быстродействию применяют в различных устройствах обработки цифровой информации.


Рис. 5.39.
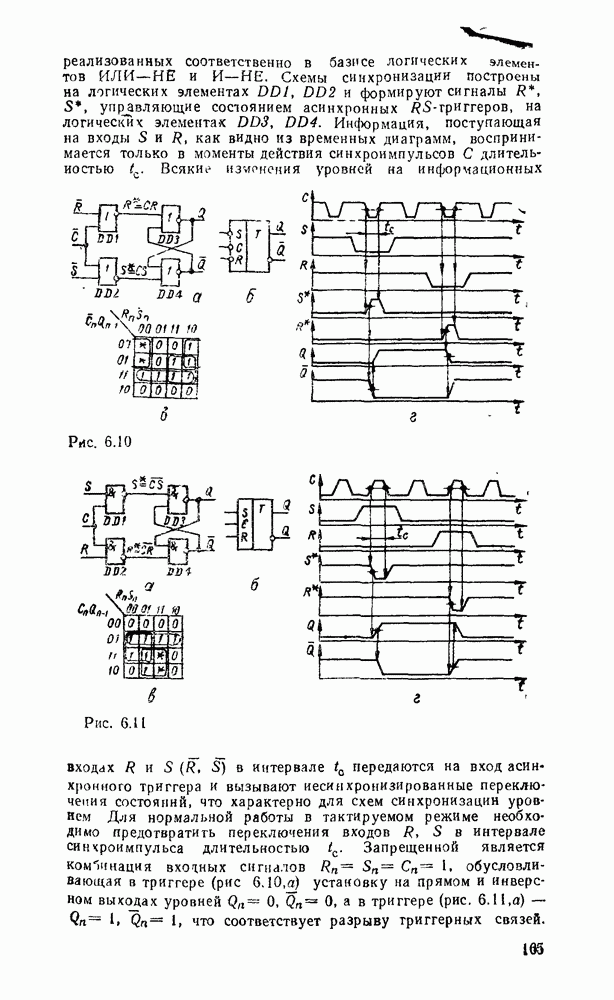
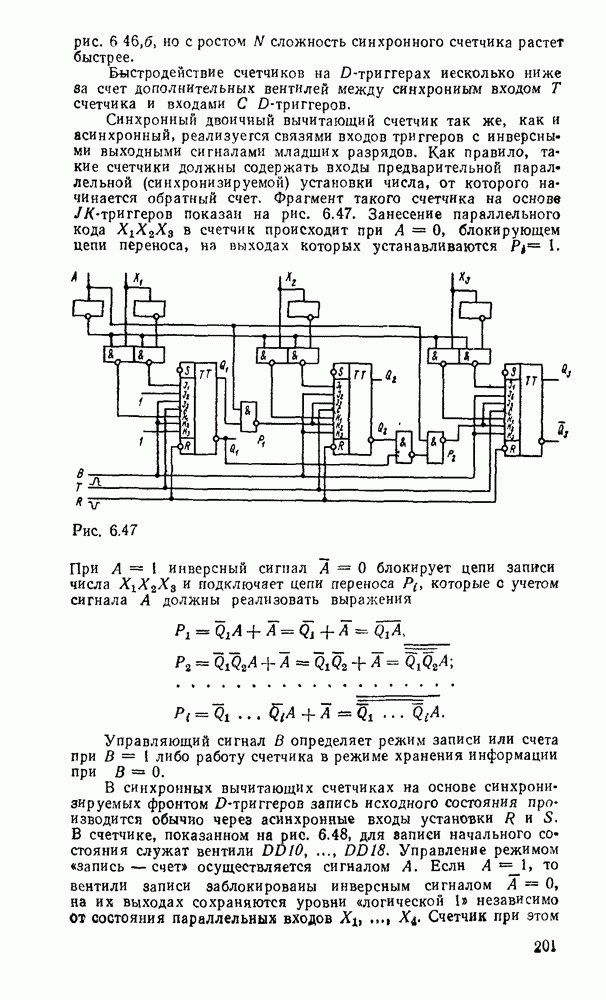
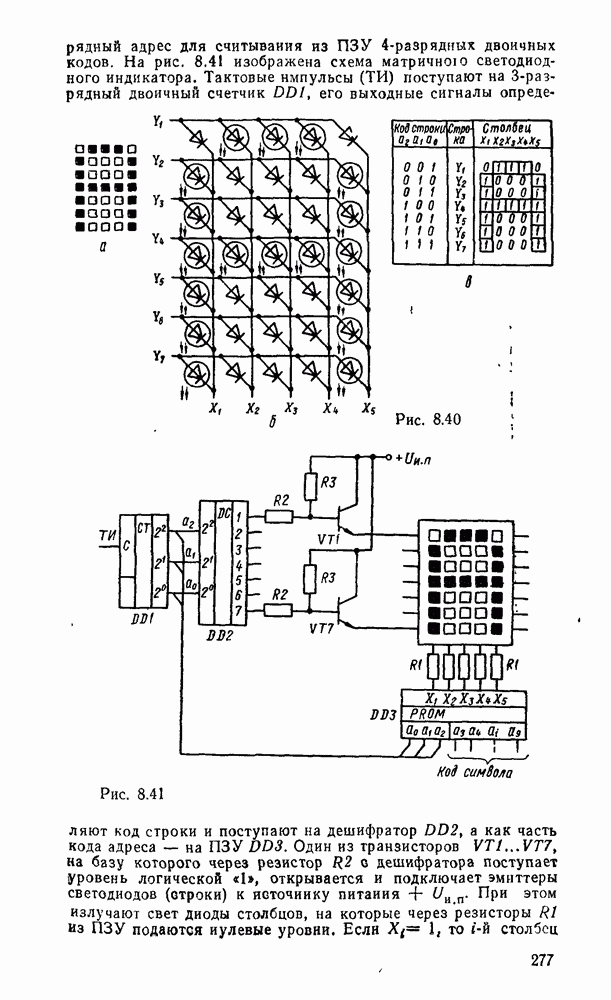
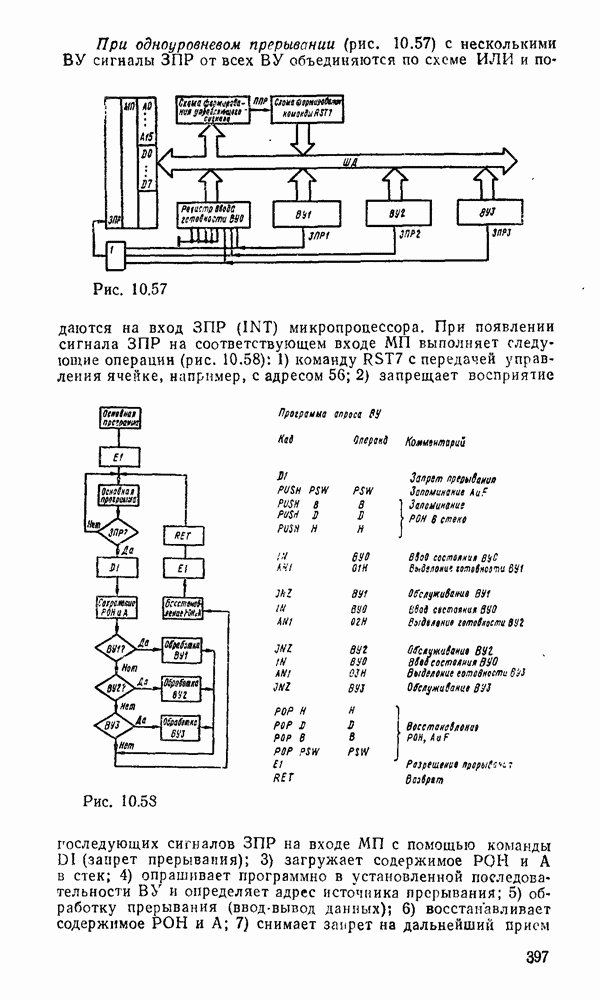
В частности, на их основе строятся устройства перемножения чисел. Для перемножения двух чисел А и В можно просто число А сложить с самим собой В раз. Это можио выполнить комбинационными сумматорами, но гораздо быстрее и экономичнее простое суммирование заменить суммированием со сдвигом. Как видно из примера, частные произведения однозначно определяются множимым и очередным битом множителя. Частное  произведение либо равно множителю, если
произведение либо равно множителю, если  , либо оно равно нулю, если
, либо оно равно нулю, если  Каждое последующее частное произведение сдвинуто на один разряд по отношению к
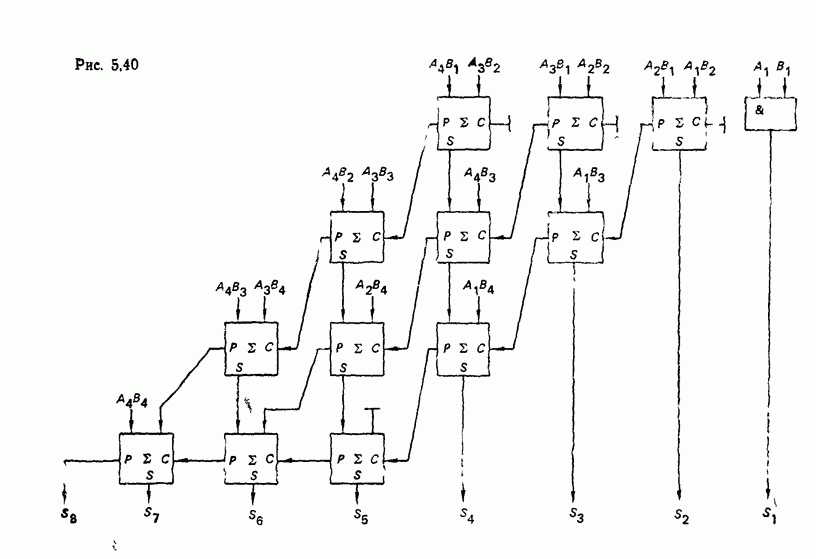
Каждое последующее частное произведение сдвинуто на один разряд по отношению к  Окончательное произведение получается последовательным суммированием частных произведений. Функциональная схема, реализующая данный алгоритм на основе полных комбинационных сумматоров, показана на рис. 5.40. Операнды полных сумматоров
Окончательное произведение получается последовательным суммированием частных произведений. Функциональная схема, реализующая данный алгоритм на основе полных комбинационных сумматоров, показана на рис. 5.40. Операнды полных сумматоров  получают с помощью
получают с помощью  -входовых схем И аналогично
-входовых схем И аналогично 
Пример 3.

Основное достоинство комбинационного перемножителя — высокое быстродействие (длительность умножения  -разрядных двоичных чисел — менее 100 нс), которое не связано с тактовой синхронизацией устройства, а определяется лишь задержками сигналов в логических элементах.
-разрядных двоичных чисел — менее 100 нс), которое не связано с тактовой синхронизацией устройства, а определяется лишь задержками сигналов в логических элементах.
Рис. 5.40
(см. оригинал)
Высокое быстродействие достигается ценой значительных аппаратурных аатрат: для реализации перемножителя  -разрядного множимого и
-разрядного множимого и  -разрядного множителя требуется
-разрядного множителя требуется  логических элементов
логических элементов  и
и  полных одноразрядных сумматоров.
полных одноразрядных сумматоров.
Комбинационные перемножители эффективно можно использовать при построении цифровых фильтров, для выполнения необходимых вычислений быстрого преобразования Фурье, в микропроцессорных системах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
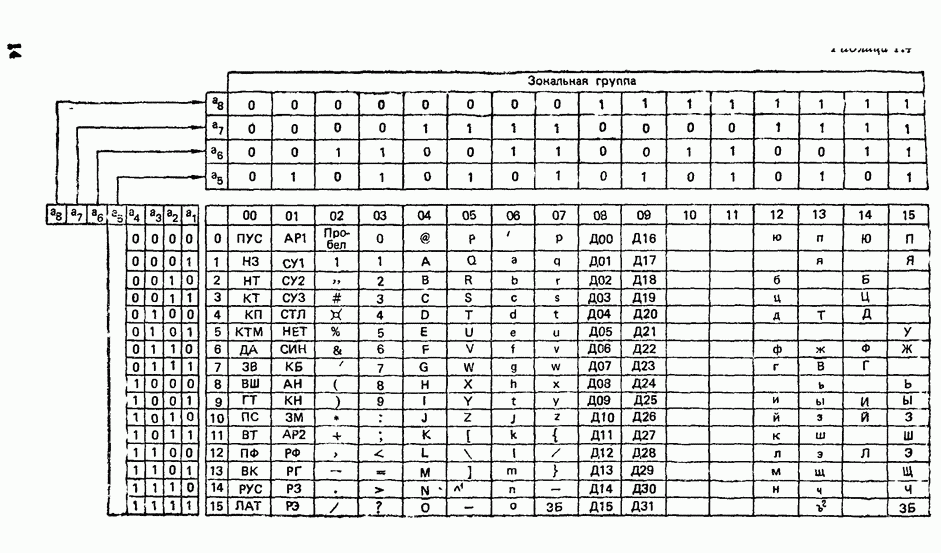
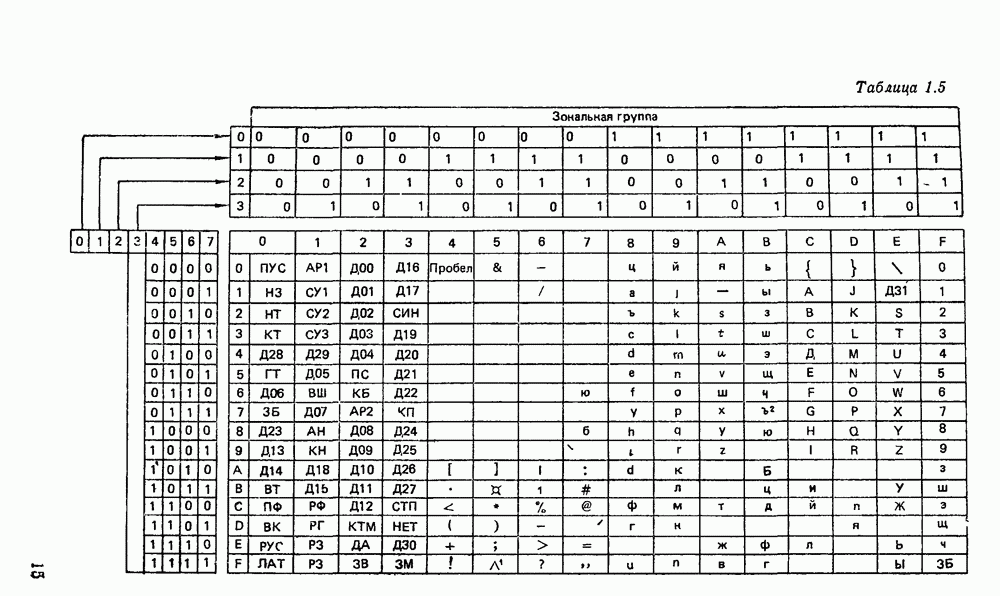
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
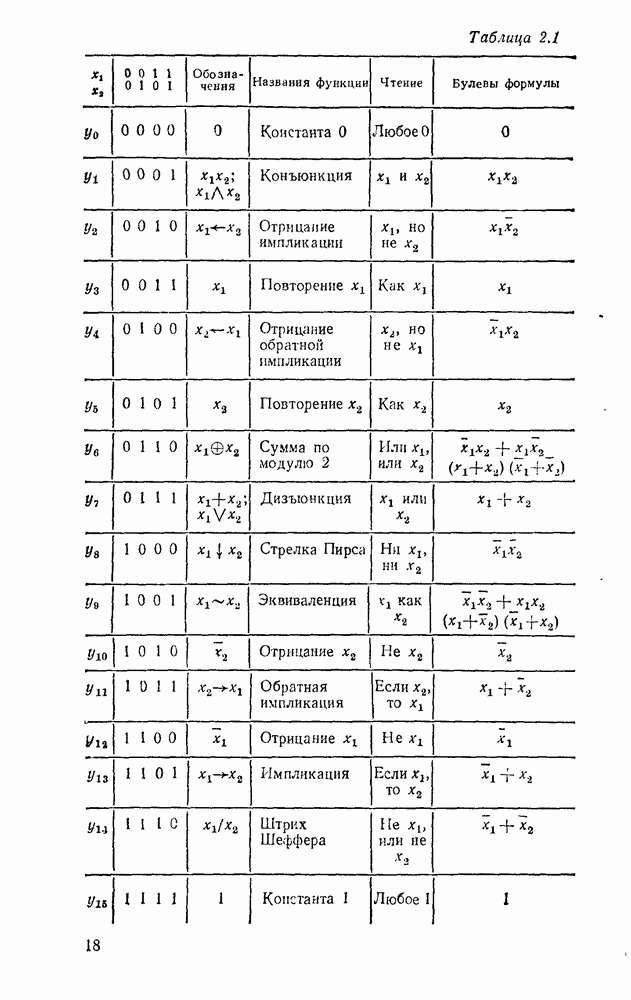
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
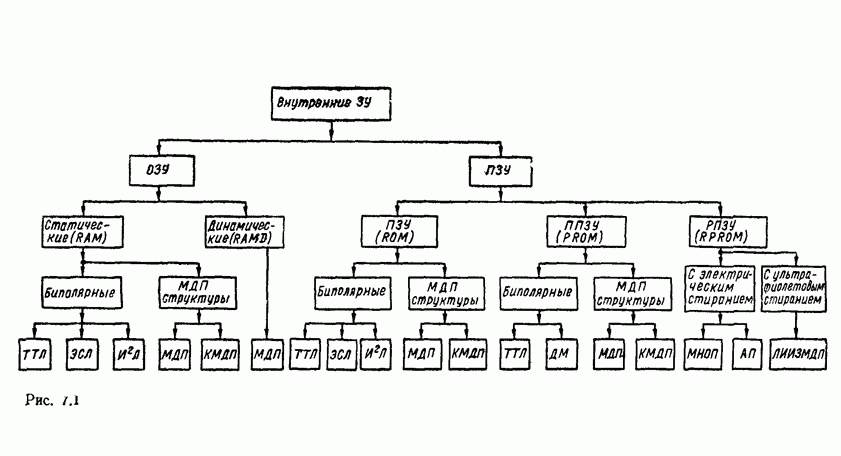
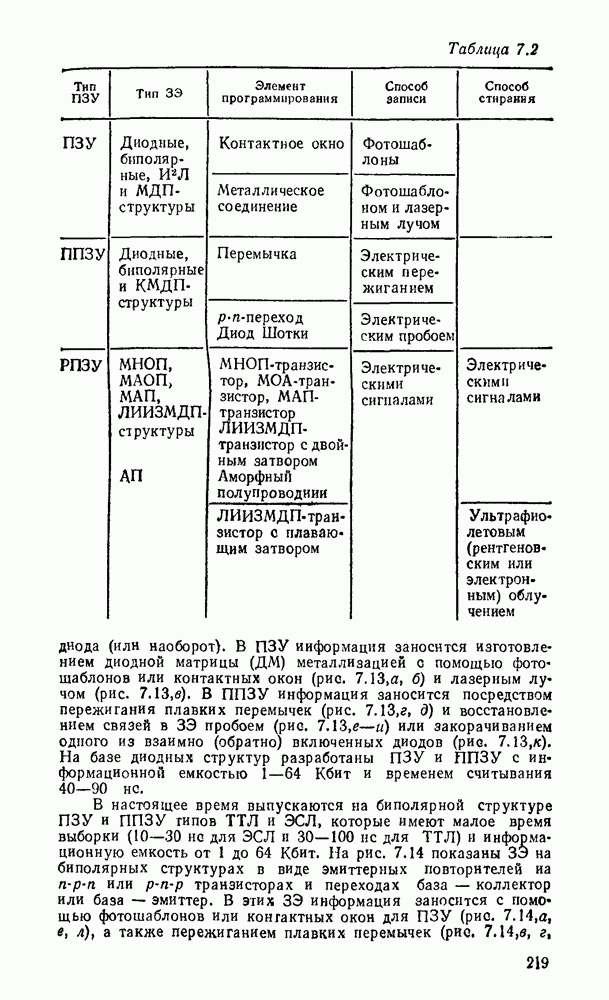
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
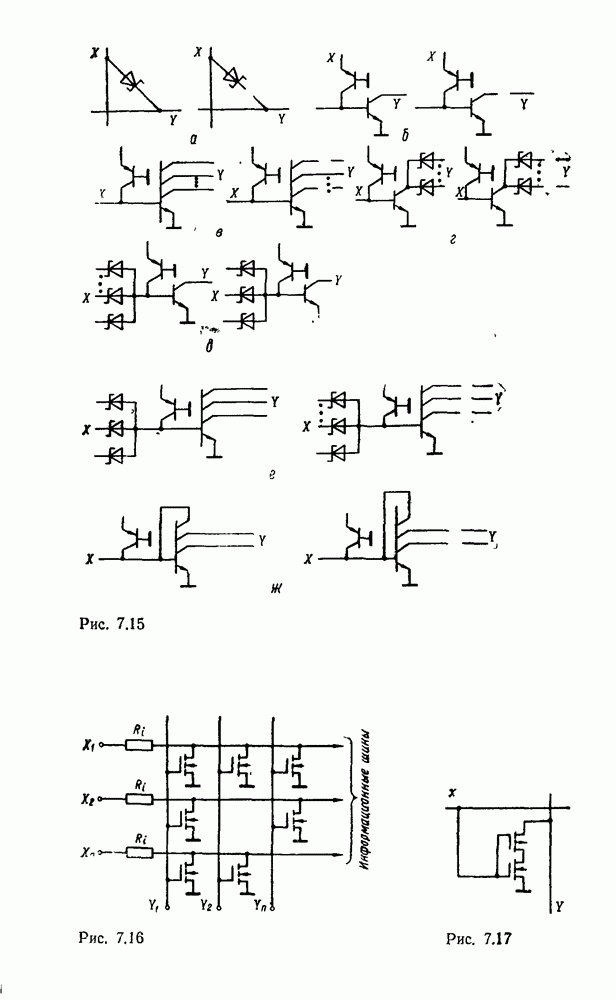
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
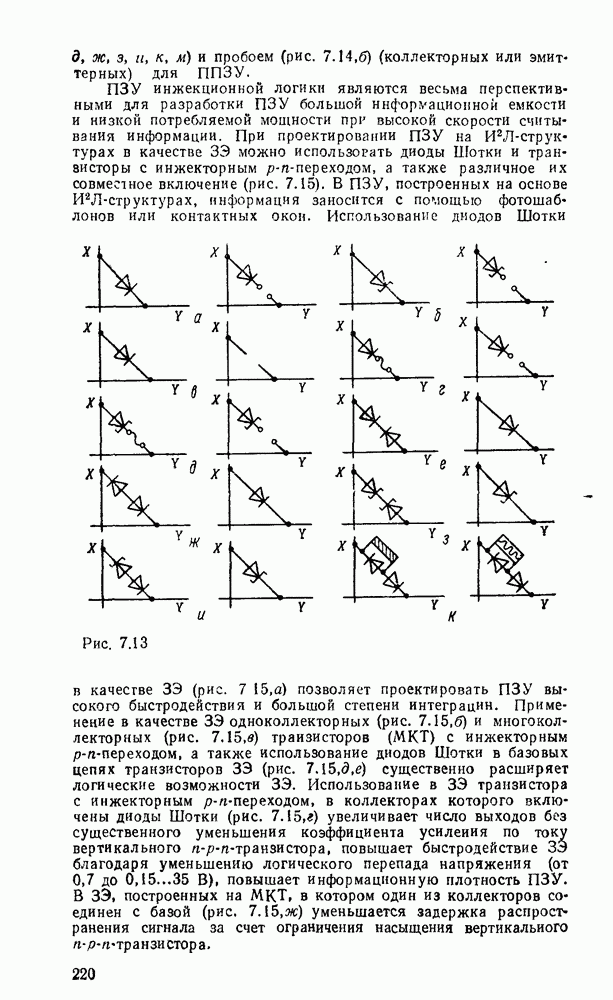
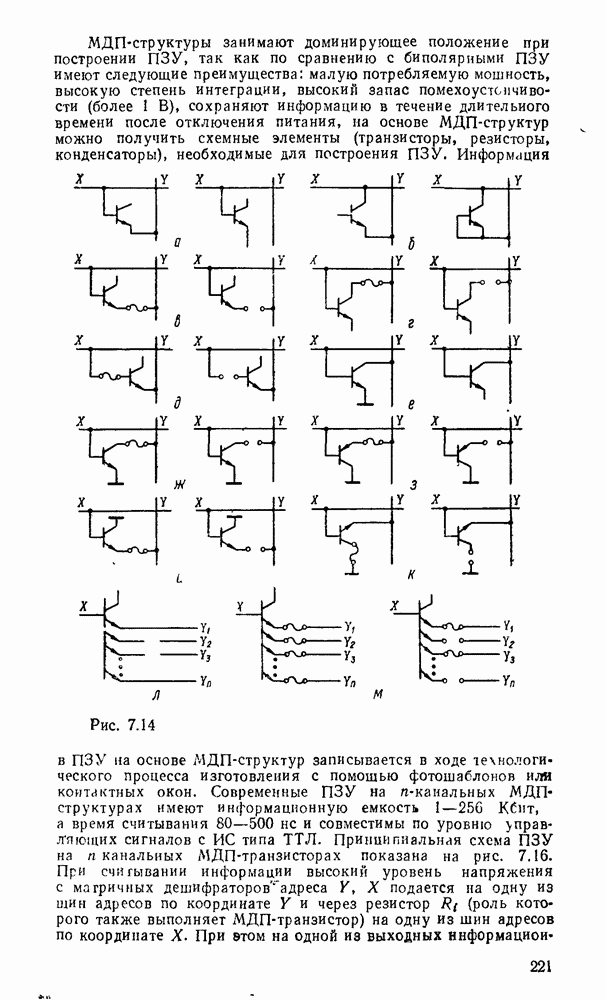
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
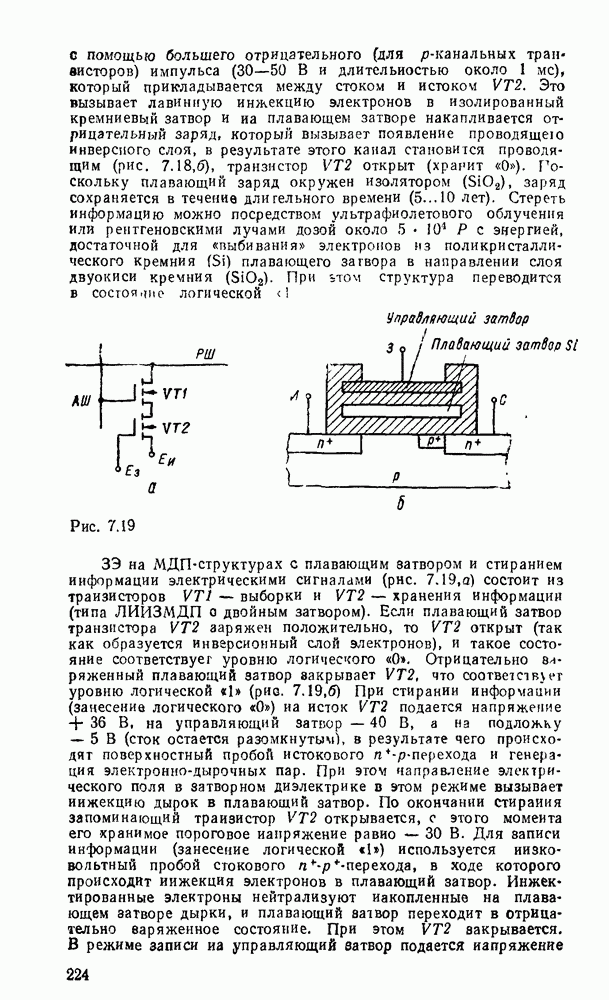
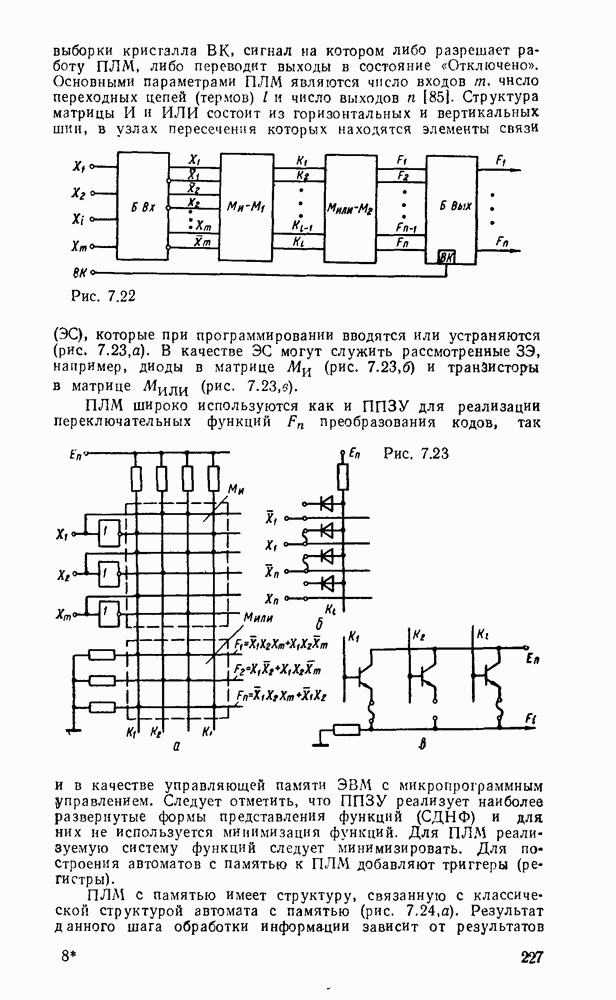
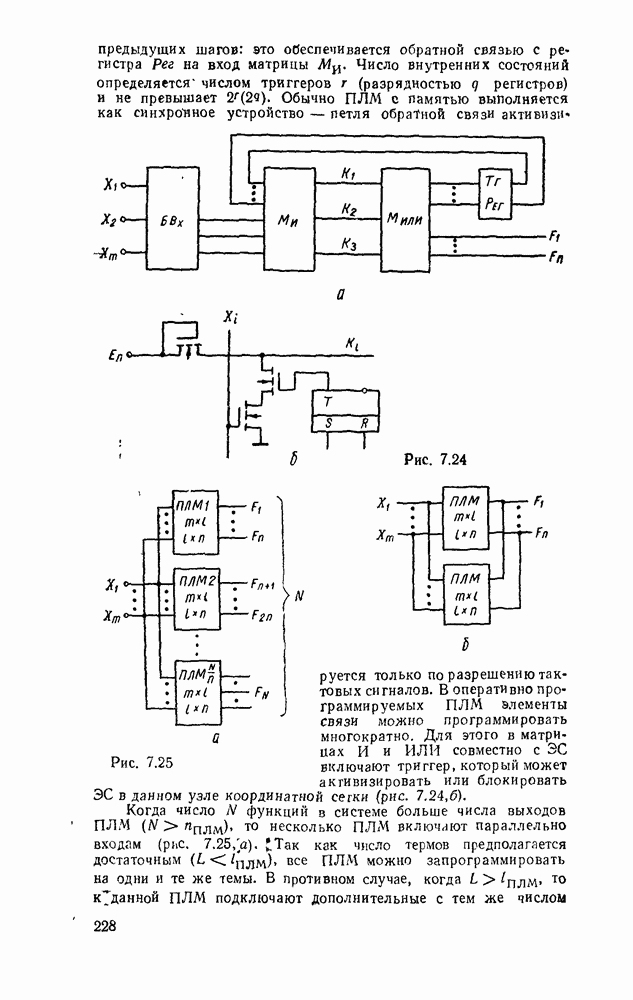
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
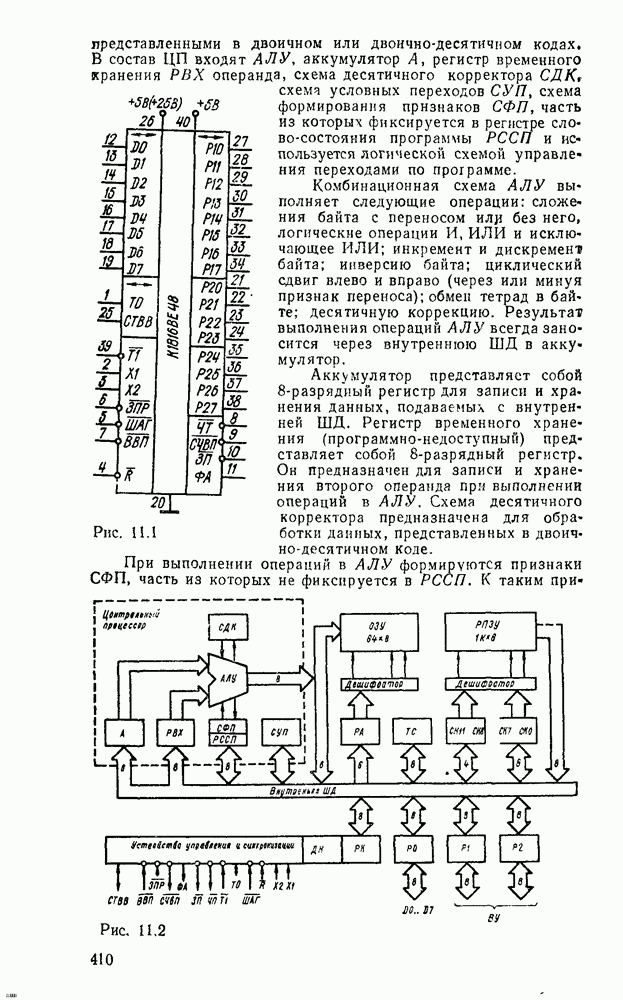
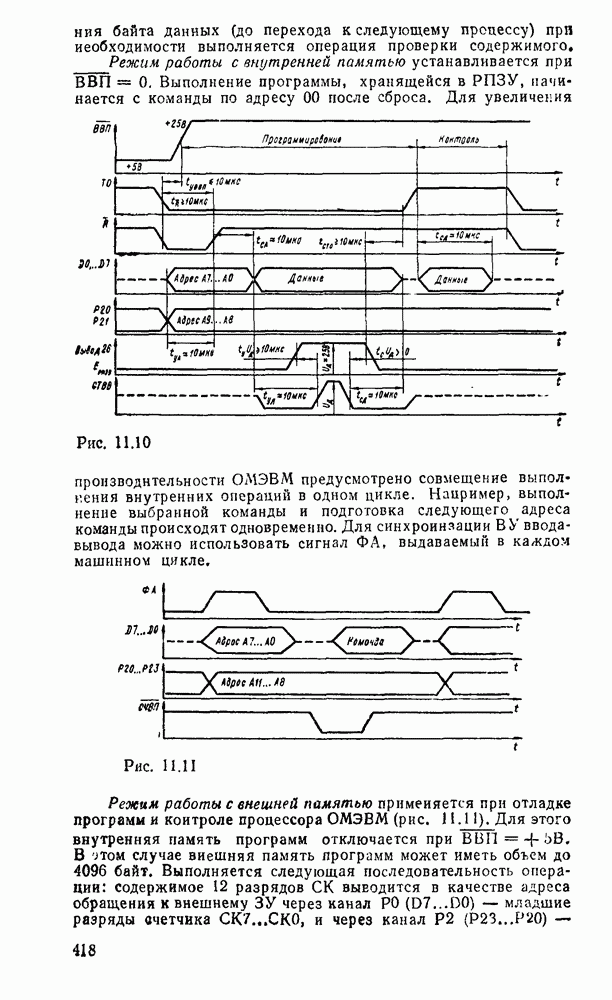
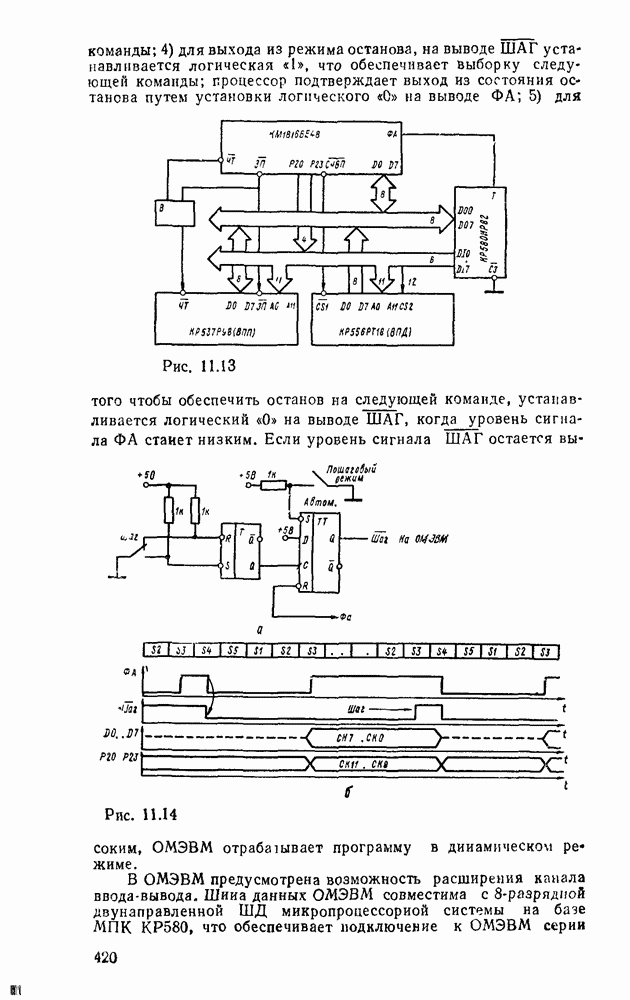
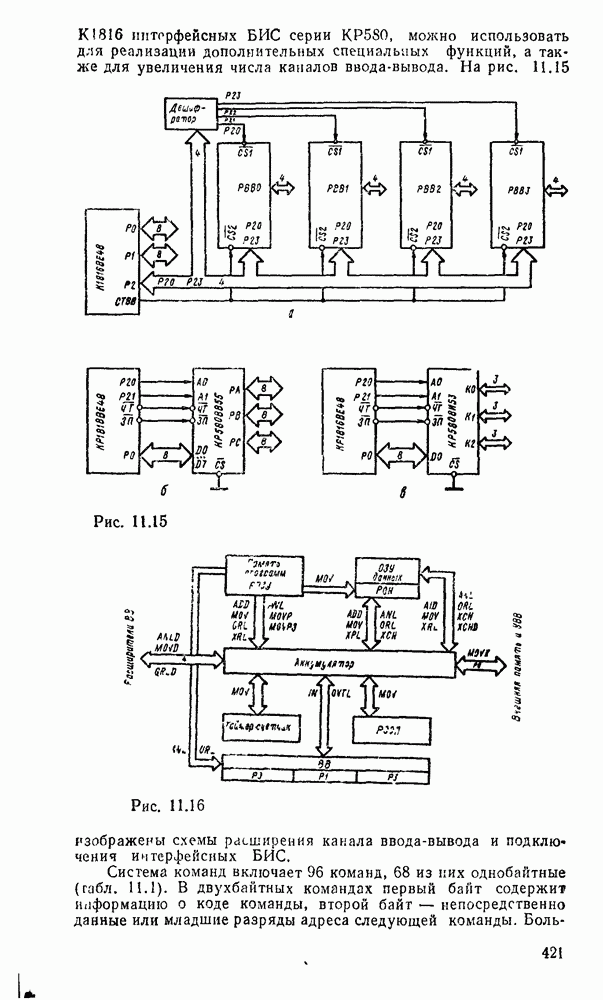
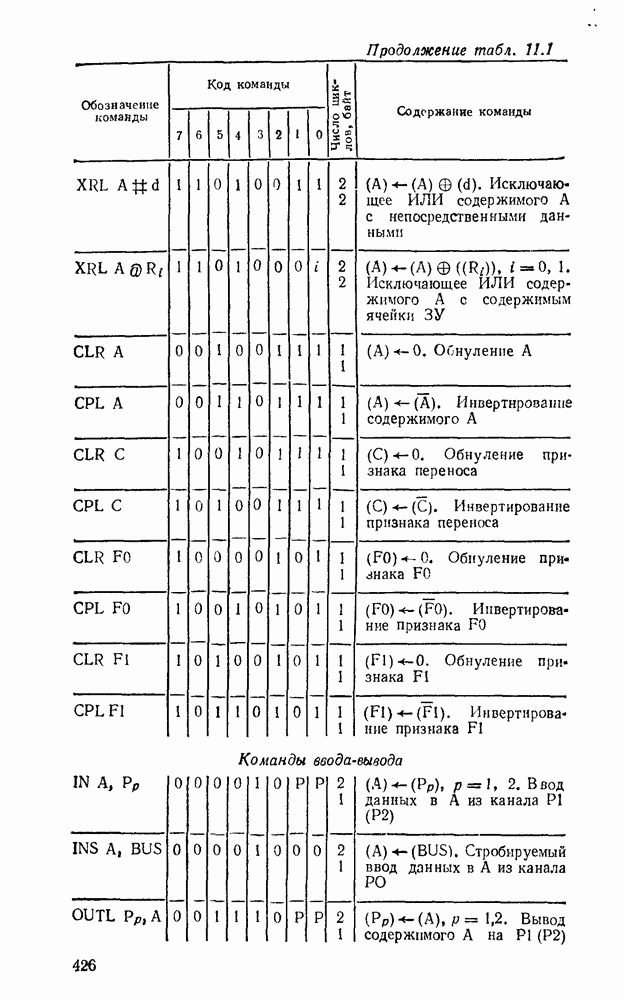
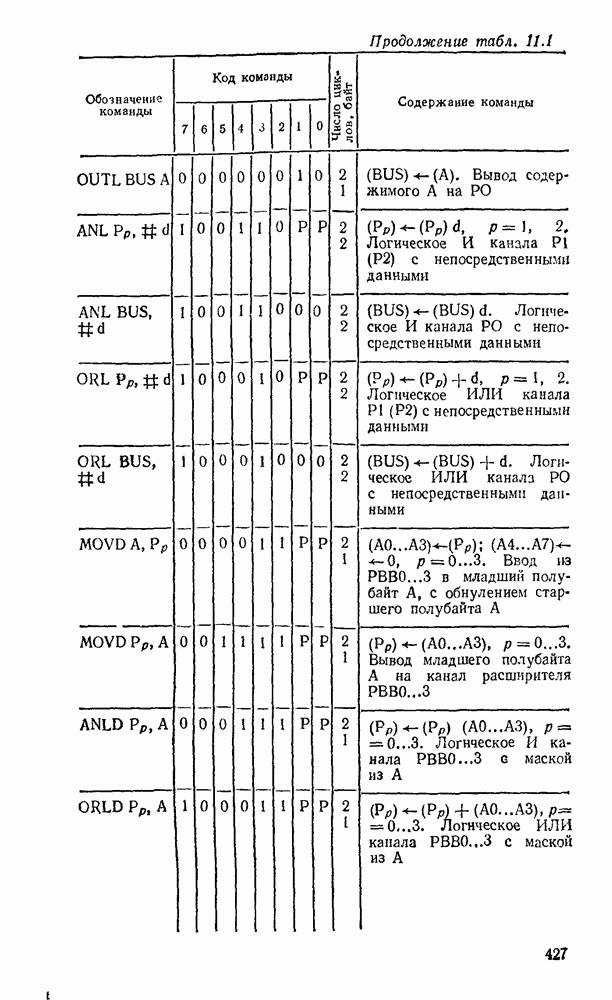
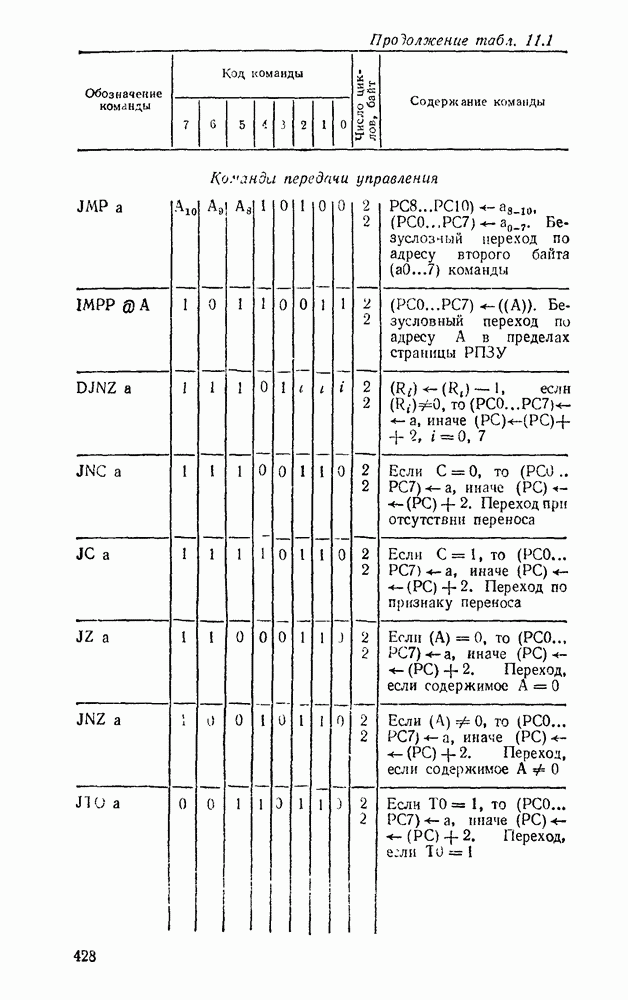
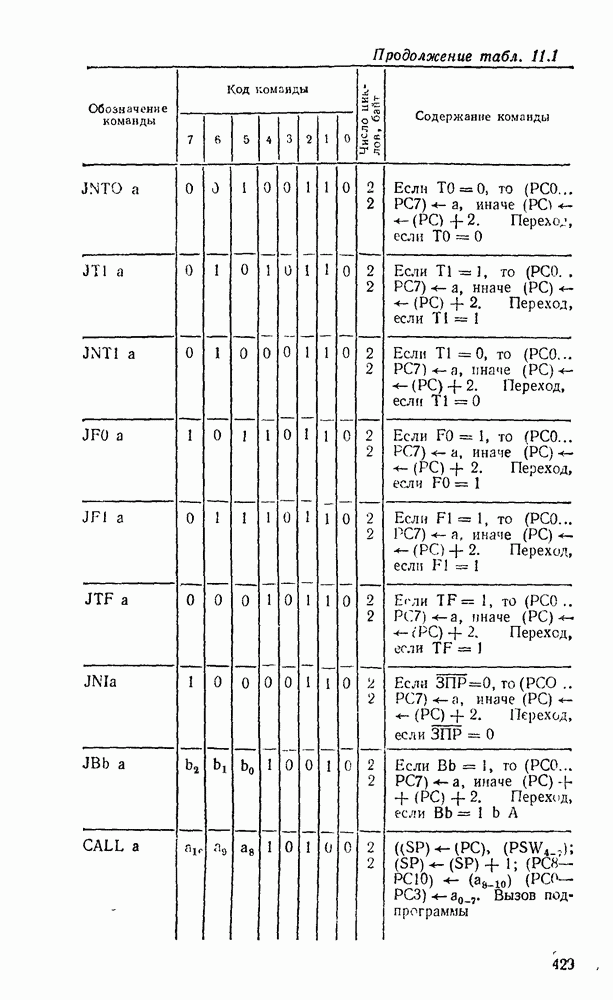
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ