| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.4. БУЛЕВА АЛГЕБРА
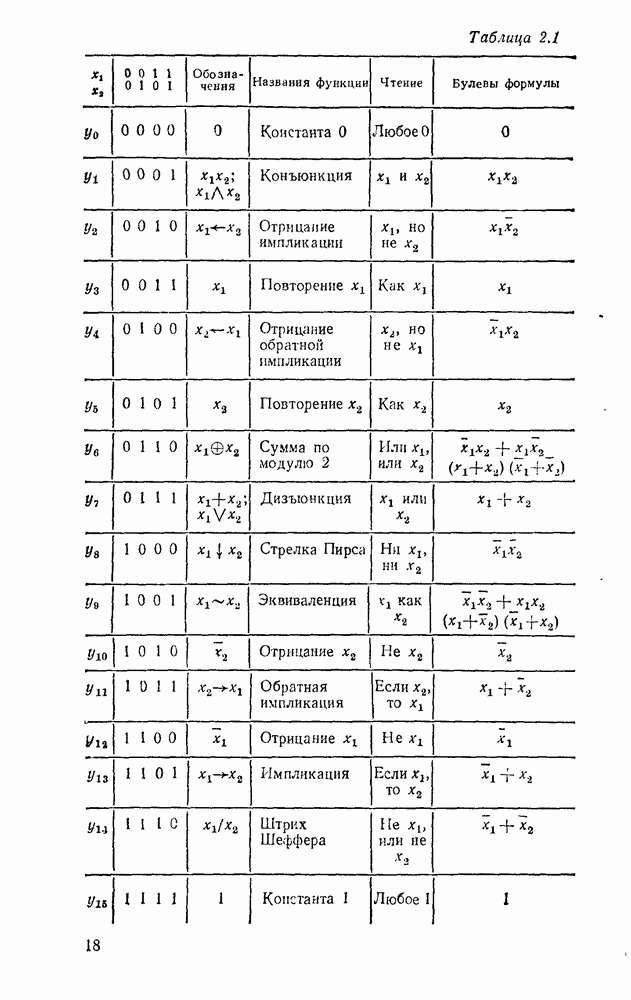
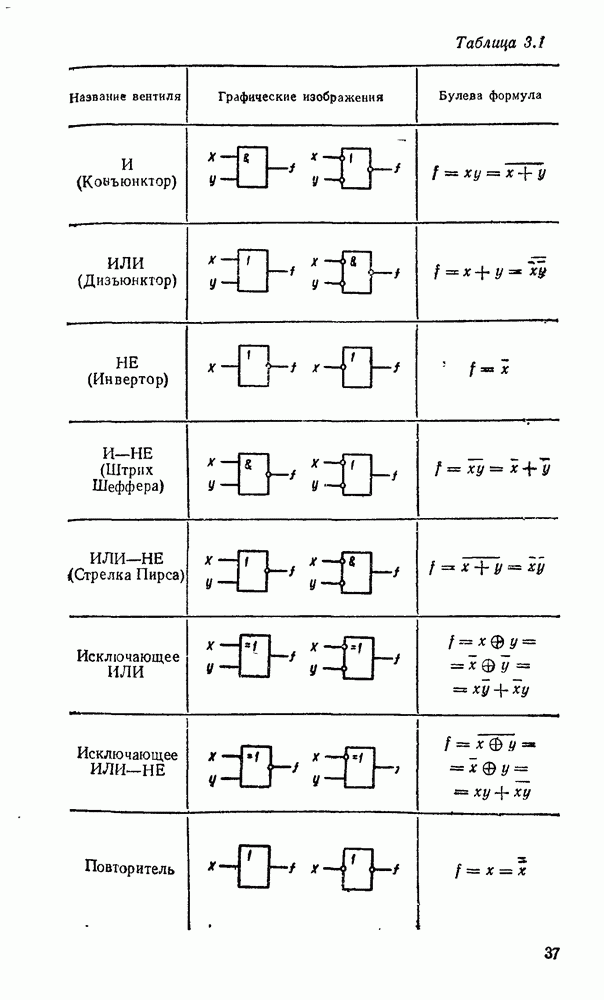
Логические функции, приведенные в табл. 2.1, можно рассматривать как элементарные операции над одной или двумя двоичными переменными. Функционально полная система таких операций образует на множестве двузначных переменных алгебру логики. Таких алгебр можно представить столько же, сколько наберется подходящих функционально полных систем. Но наиболее распространена булева алгебра, в которой в качестве основных операций приняты конъюнкция  (И), дизъюнкция
(И), дизъюнкция  (ИЛИ) и отрицание
(ИЛИ) и отрицание  (НЕ).
(НЕ).
Часто конъюнкцию и дизъюнкцию называют соответственно логическим произведением я суммой, а отрицание — инверсией. Используются также и  -гие варианты обозначений: для конъюнкции
-гие варианты обозначений: для конъюнкции  , для дизъюнкции
, для дизъюнкции  и Для отрицания
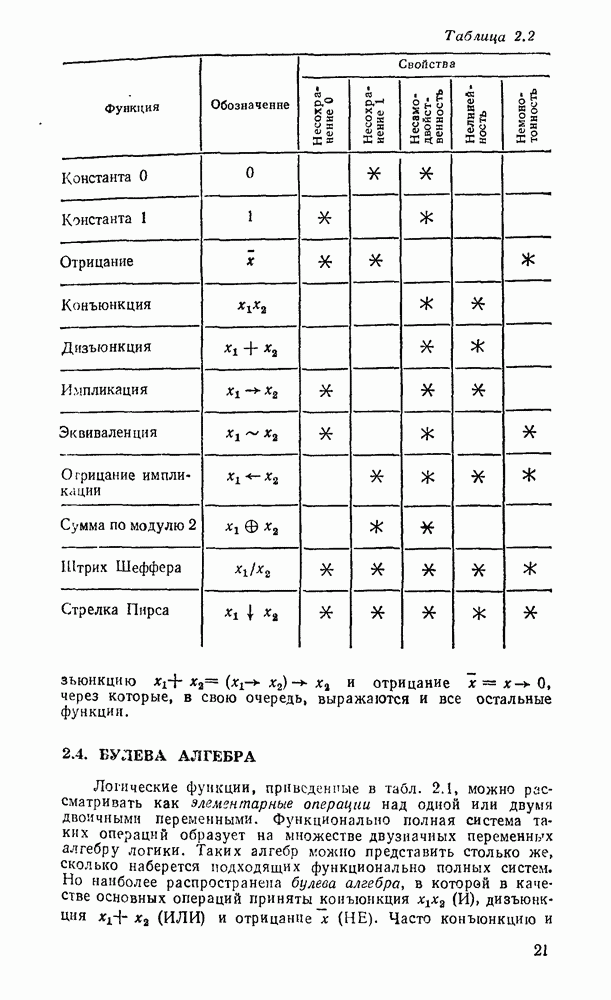
и Для отрицания  . Чтобы избежать в сложных формулах лишних скобок, которые появляются при суперпозиции функций, установлен жесткий порядок выполнения операций — конъюнкция предшествует дизъюнкции. Свойства булевых операций И, ИЛИ, НЕ определяются таблицами соответствующих функций (см. табл. 2.1) и могут быть представлены в виде
. Чтобы избежать в сложных формулах лишних скобок, которые появляются при суперпозиции функций, установлен жесткий порядок выполнения операций — конъюнкция предшествует дизъюнкции. Свойства булевых операций И, ИЛИ, НЕ определяются таблицами соответствующих функций (см. табл. 2.1) и могут быть представлены в виде

Здесь использована другая форма таблицы соответствия, в которой всевозможные комбинации значений переменных записываются по строкам, а для значений функции при этих комбинациях отводится столбец. Использование той или ииой формы в конкретных случаях обусловлено удобством, а часто и просто привычкой.
Из приведенных определений булевых операций вытекают основные свойства булевой алгебры (табл. 2.3), которые можно доказывать методом совершенной индукции, т. е. проверкой для всех возможных комбинаций значений переменных. Любые свойства булевой алгебры можно также доказать аналитически без обращения к таблицам соответствия на основе первых пяти свойств, которые играют при эгом роль аксиом. Например, идемпотентность дизъюнкции доказывается следующими преобразованиями:  . Следует подчеркнуть, что знак равенства в формулах алгебры логики не имеет количественного смысла и означает равносильность функций в левой и правой частях. Две функции считаются равносильными, если при любых значениях аргументов они принимают одинаковые значения.
. Следует подчеркнуть, что знак равенства в формулах алгебры логики не имеет количественного смысла и означает равносильность функций в левой и правой частях. Две функции считаются равносильными, если при любых значениях аргументов они принимают одинаковые значения.
Свойства булевой алгебры используются для преобразования и упрощения логических формул, а также для доказательства теоретических положений. Коммутативность и ассоциативность позволяют выполнять операции И и ИЛИ, группируя переменные в любом порядке. Первая форма дистрибутивности указывает на допустимость вынесения общего множителя за скобки, как в обычной алгебре. Но вторая форма в обычной алгебре аналога не имеет, что является одним из основных отличий ее от алгебры логики. Свойства отрицания подчеркивают взаимодополнительную природу логических переменных. Повторы переменной и константы позволяют избавляться от постоянных слагаемых и множителей или при необходимости вводить их. Двойное отрицание не изменяет переменную, что можно рассматривать как пустую операцию. На основе идемпотентности можно удалять повторяющиеся переменные, вследствие чего в булевой алгебре не имеют смысла показатели степени и числовые коэффициенты, что также существенно отличает ее от обычной алгебры. Законы  Моргана позволяют свести отрицание сложного выражения к отрицанию отдельных переменных.
Моргана позволяют свести отрицание сложного выражения к отрицанию отдельных переменных.
Таблица 2.3
(см. оригинал)
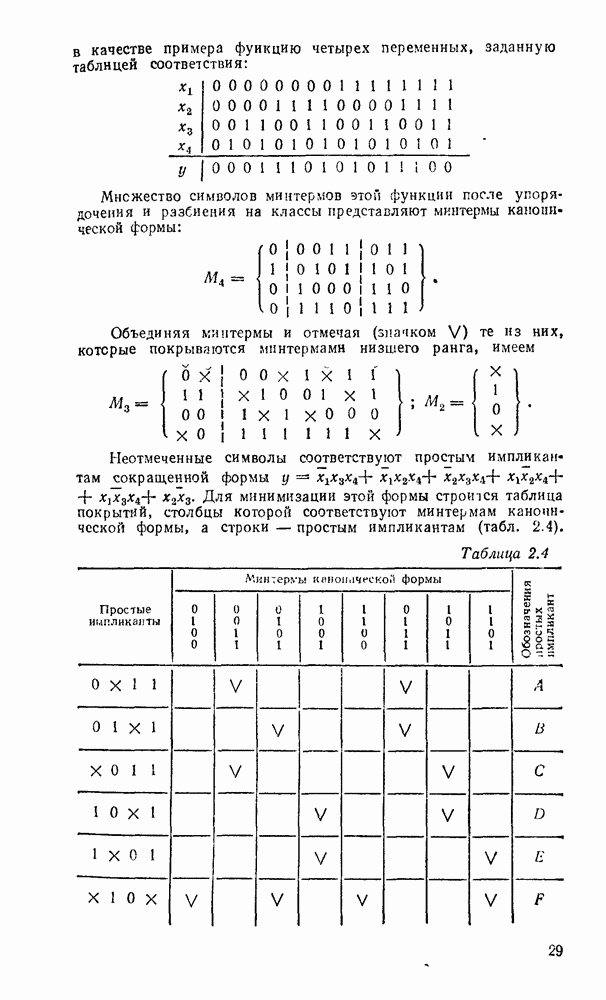
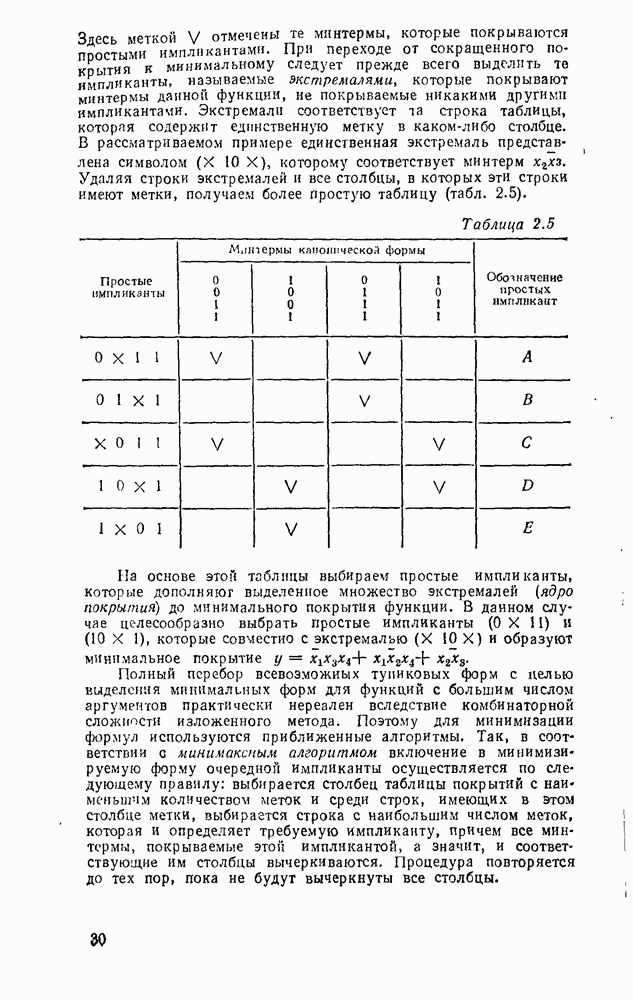
Последние четыре свойства (склеивание, поглощение, замещение и выявление) полезны при различных преобразованиях и упрощениях булевых формул.
Приведенные в табл. 2.3 пары свойств характеризуются специфической симметрией, выражающей принцип дуальности алгебры логики. В каждой паре одна форма получается из другой взаимной заменой операций И и ИЛИ, а также констант О и 1. В связи с этим операции И и ИЛИ, как и константы 0 и 1, называются дуальными. Вообще замена в любой формуле алгебры логики каждой операции и константы на дуальные приводит к дуальной формуле. Формула или функция, равносильная своей дуальной, называется автодуальной (как, например, двойное отрицание).
С принципом дуальности непосредственно связано обобщение законов  Моргана на любое число переменных. Если функция
Моргана на любое число переменных. Если функция  дуальная функции
дуальная функции  , то
, то

откуда следует, что отрицание некоторой функции можно определить заменой в дуальной функции каждой переменной ее отрицанием. Пусть, например, задана функция  . Дуальная ей
. Дуальная ей  и, следовательно,
и, следовательно,  .
.
Из выражения (2.1) также следует, что дуальная функция выражается как отрицание исходной функции, в которой каждая переменная замещена ее отрицанием:

 позволяет построить таблицу соответствия дуальной функции заменой значений исходной функции и всех переменных на противоположные (0 на 1 и 1 на 0). Так, для приведенного выше примера
позволяет построить таблицу соответствия дуальной функции заменой значений исходной функции и всех переменных на противоположные (0 на 1 и 1 на 0). Так, для приведенного выше примера

Как видно, для получения таблицы соответствия дуальной функции достаточно отрицание исходной функции записать в обратном порядке.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
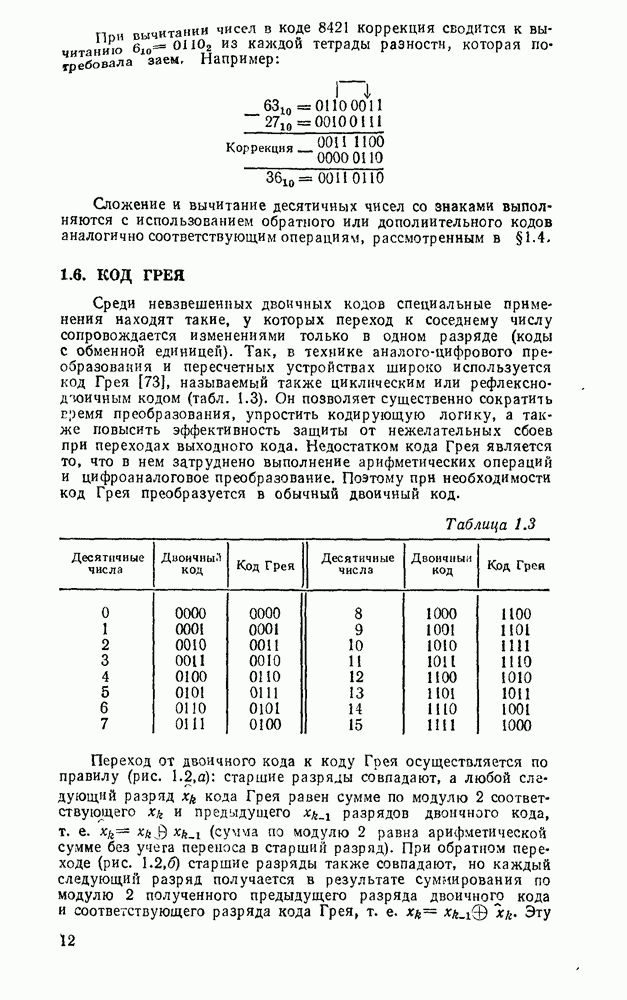
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
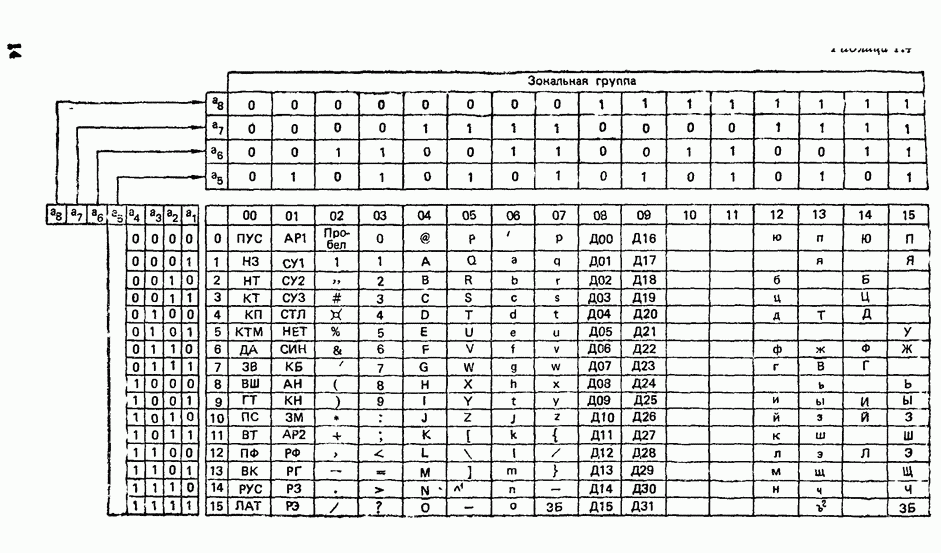
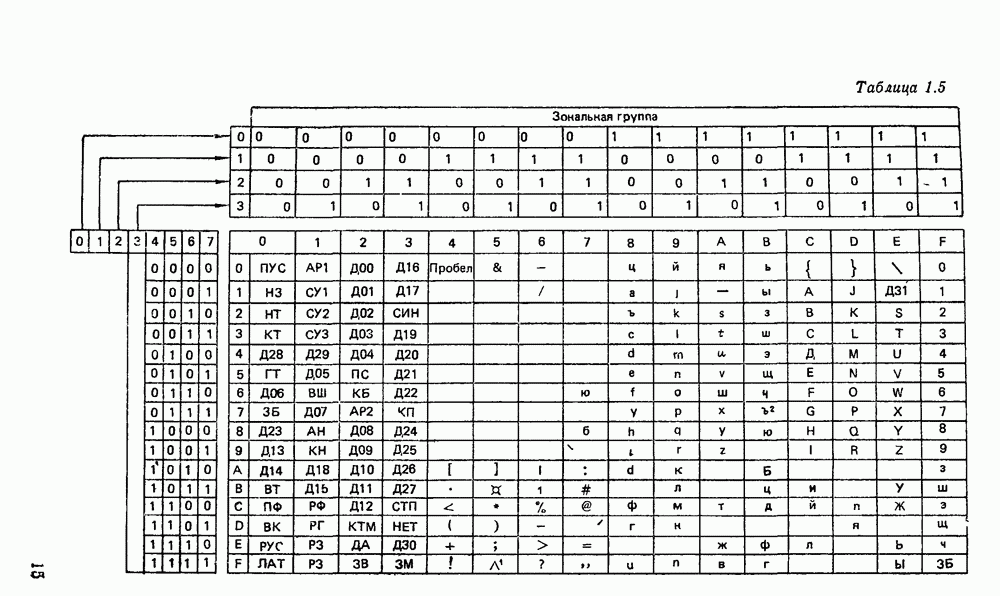
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
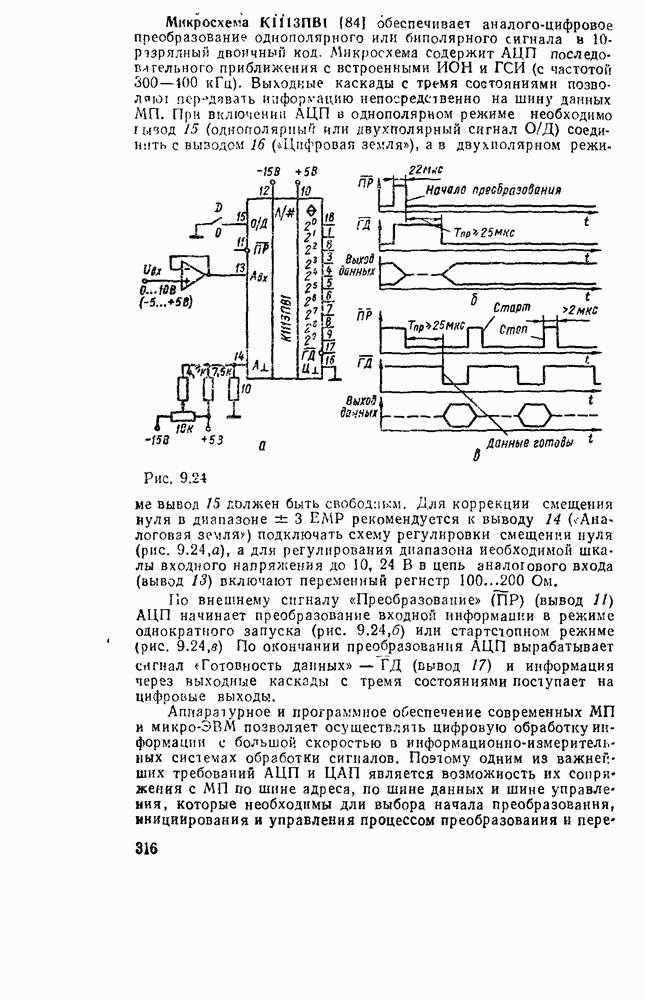
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
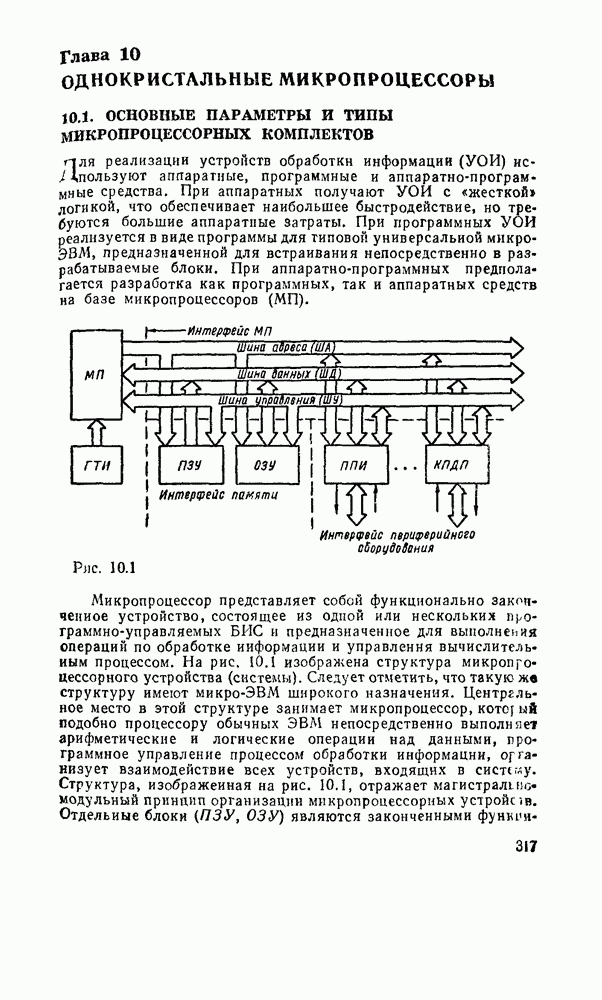
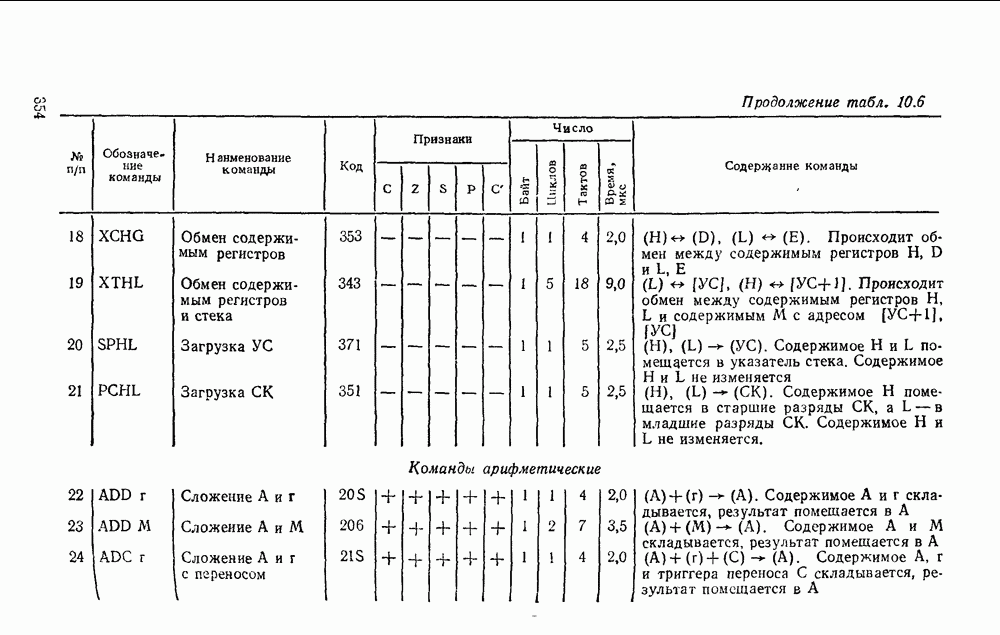
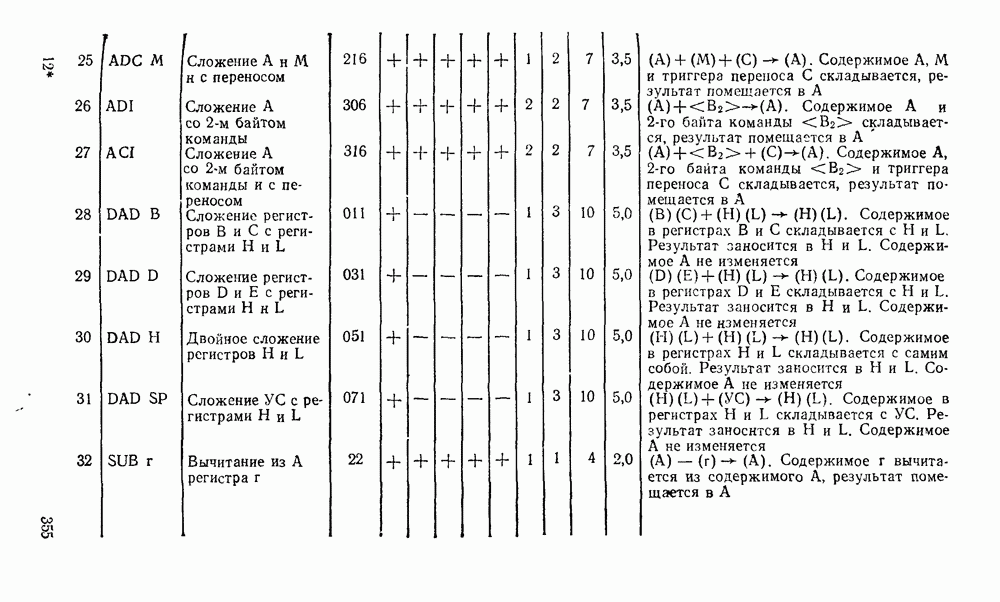
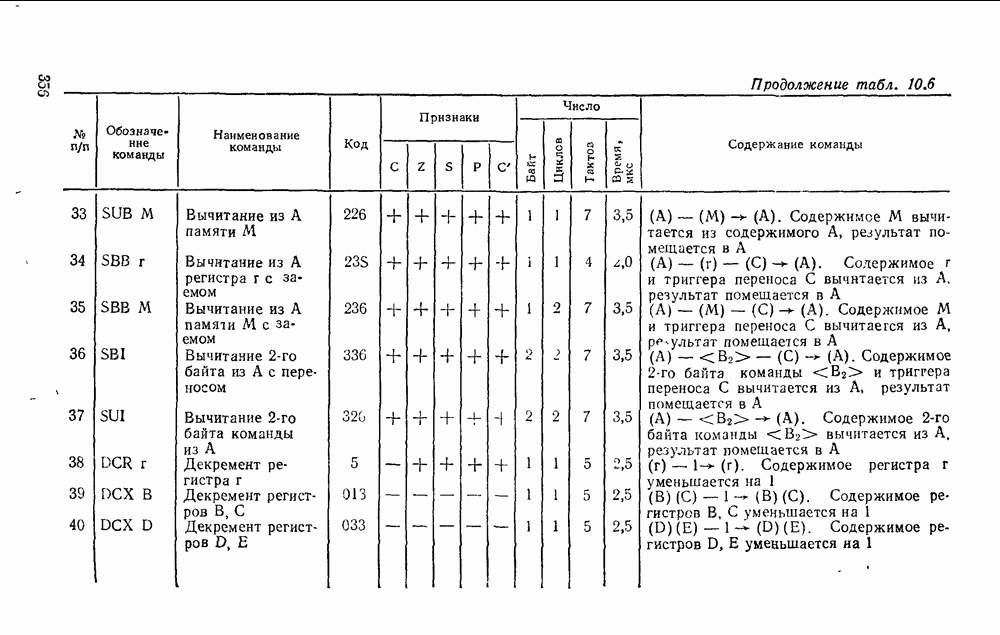
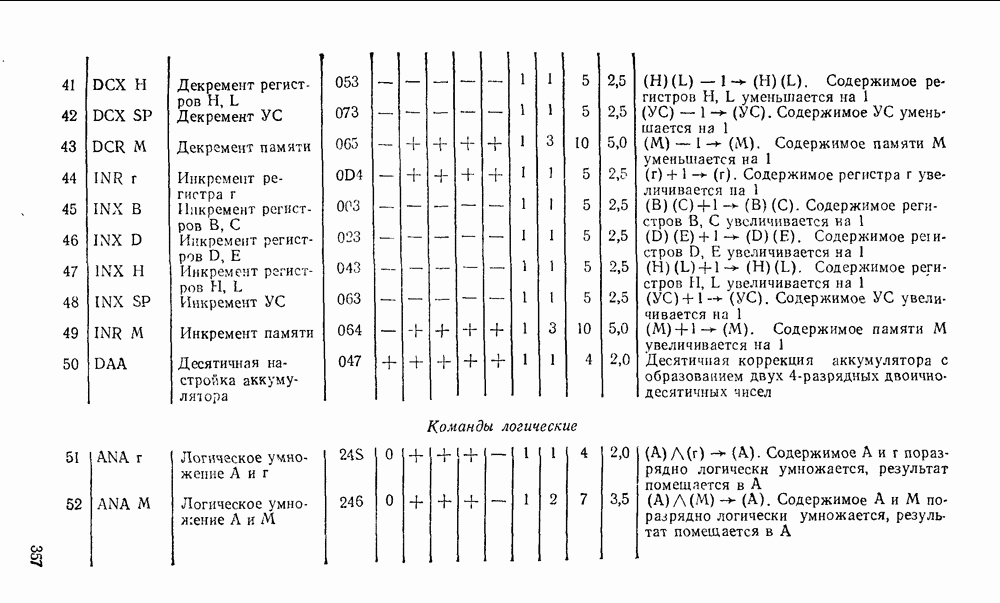
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
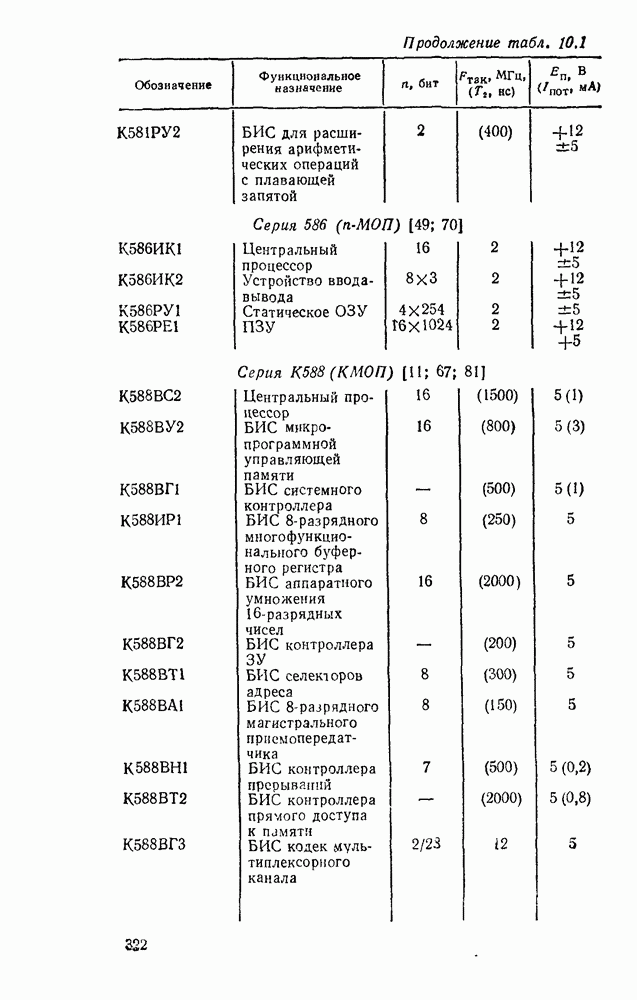
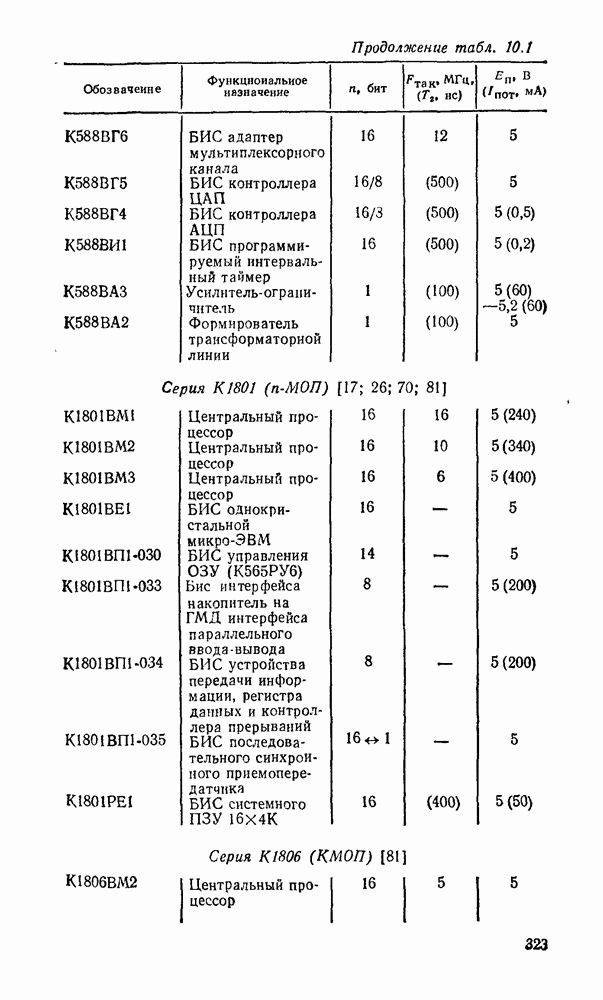
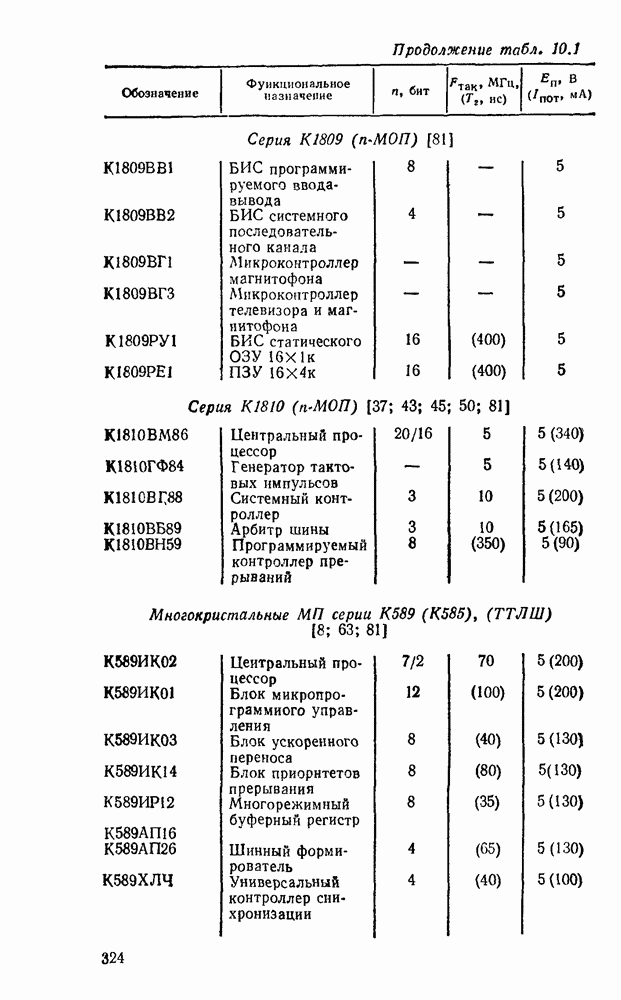
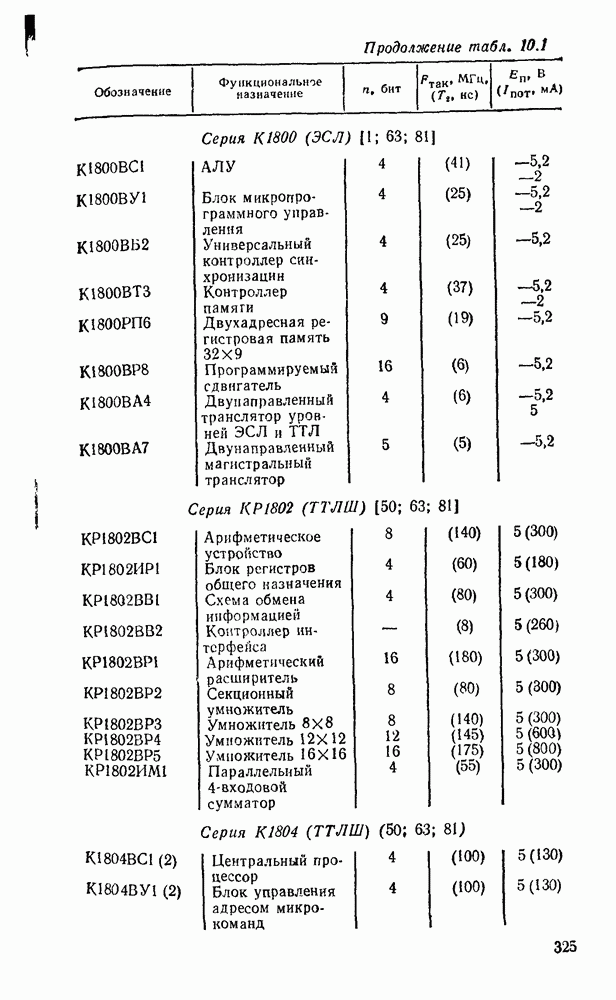
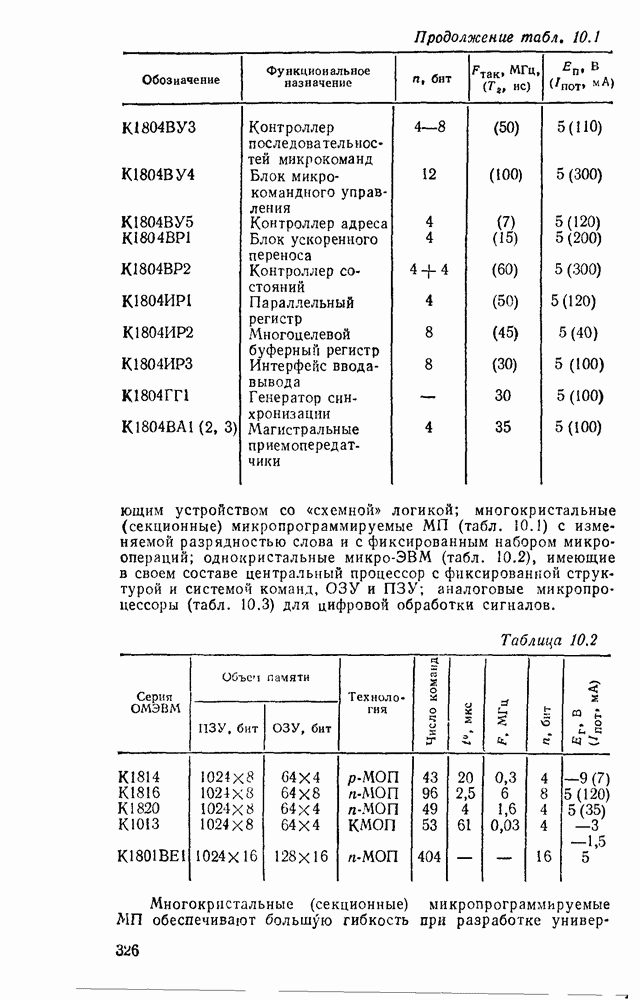
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
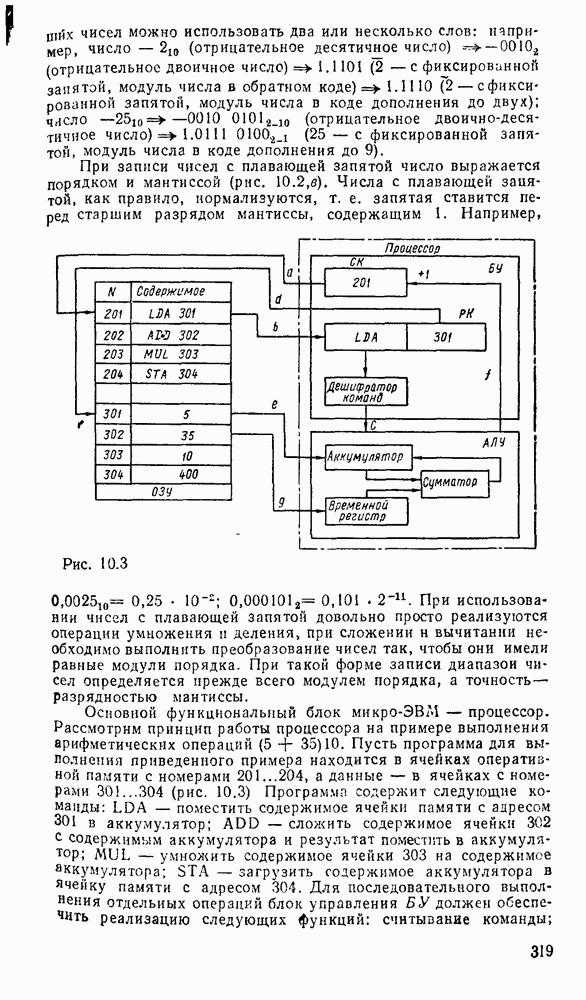
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
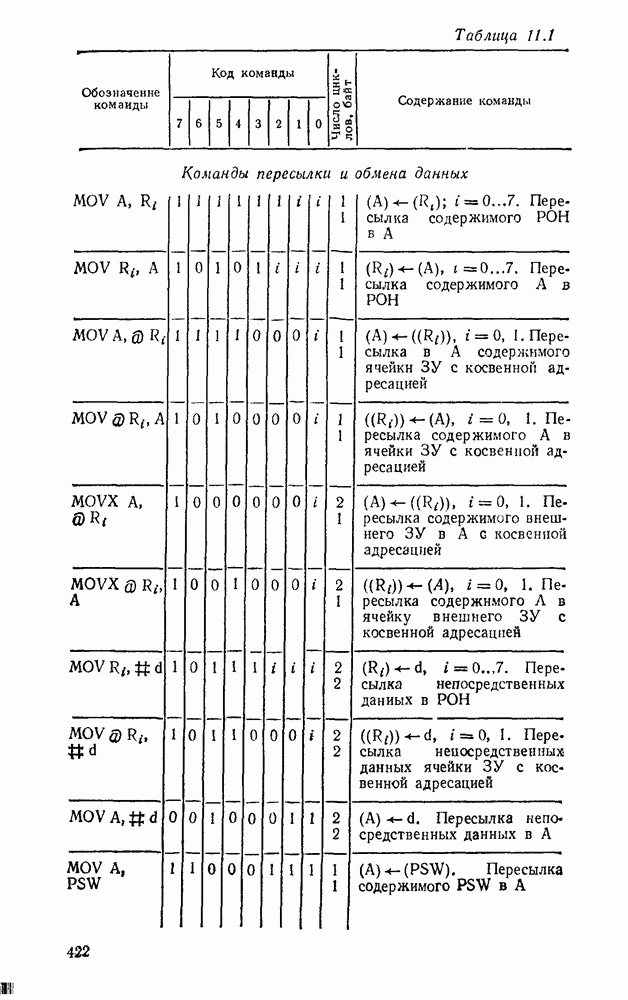
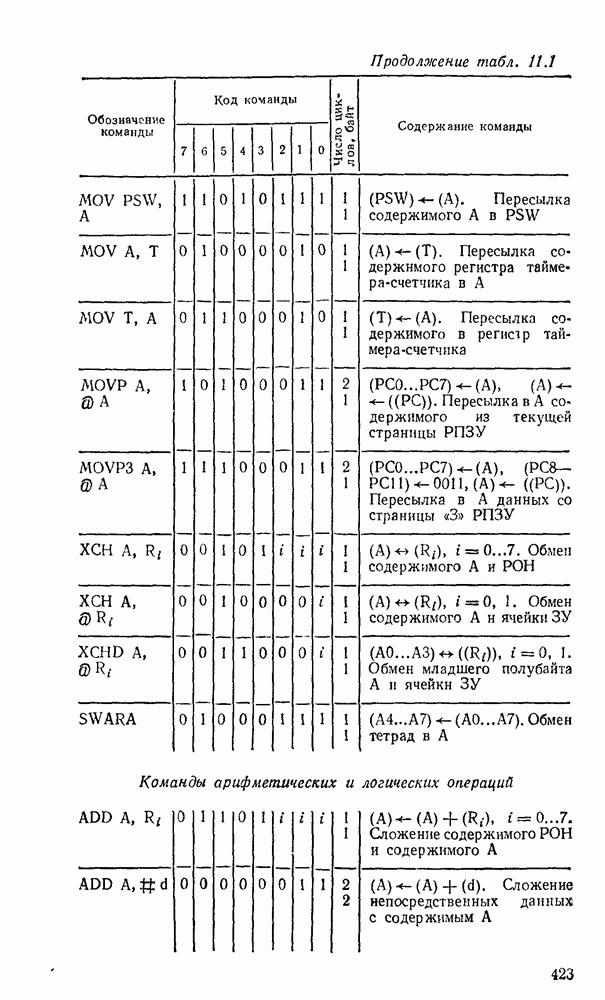
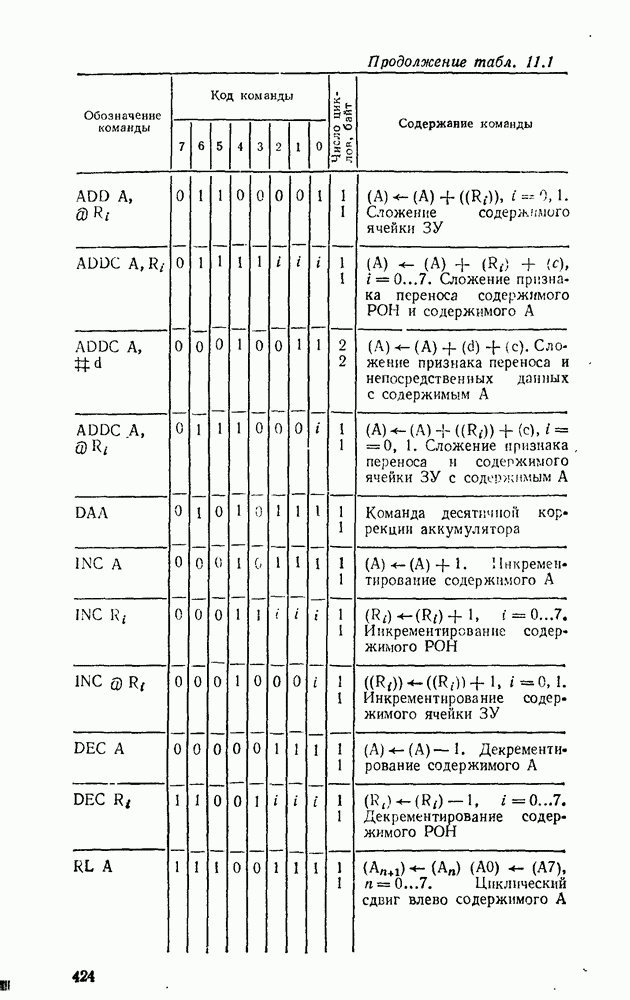
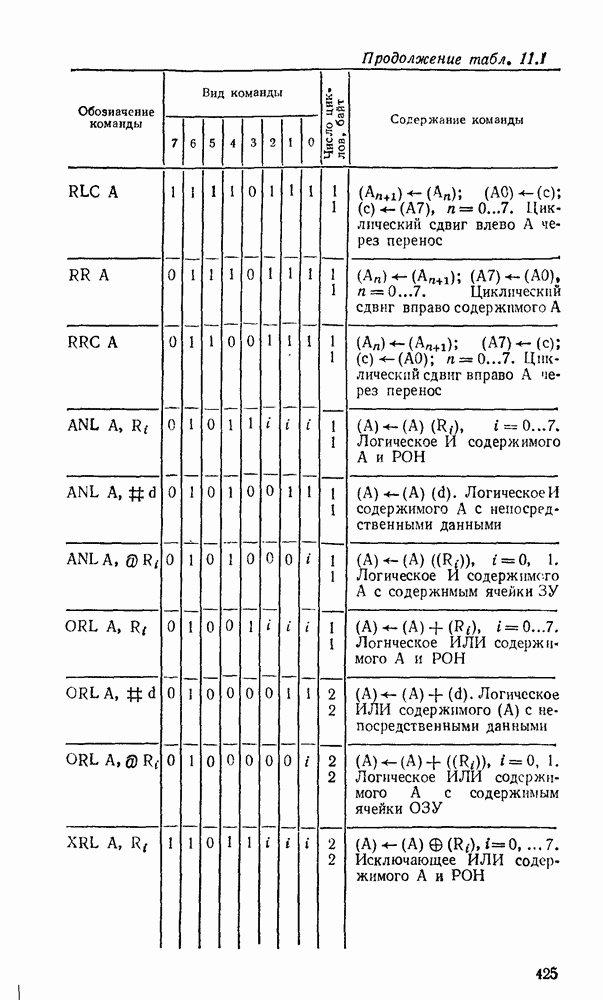
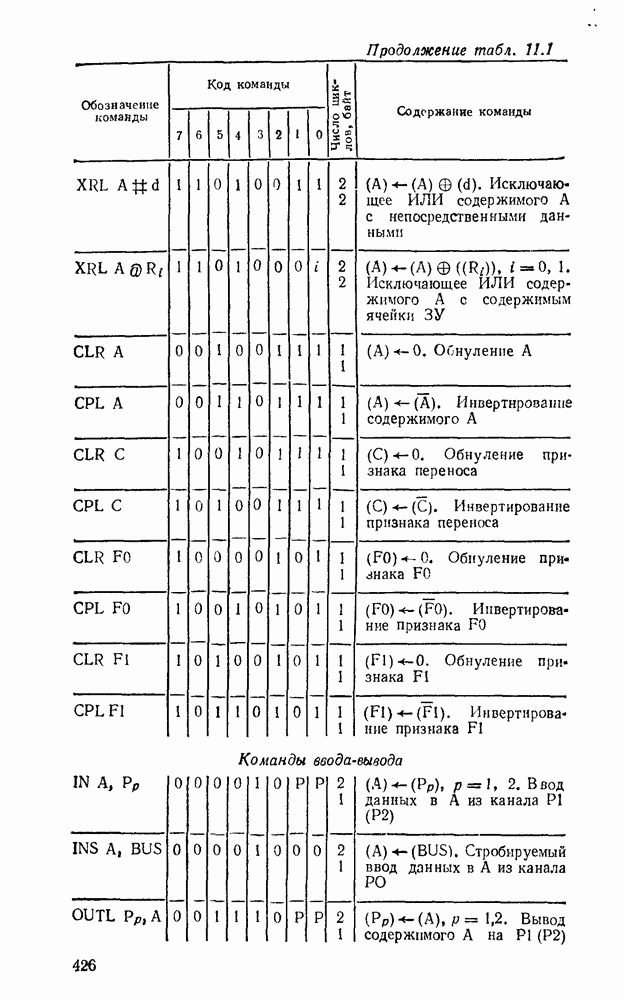
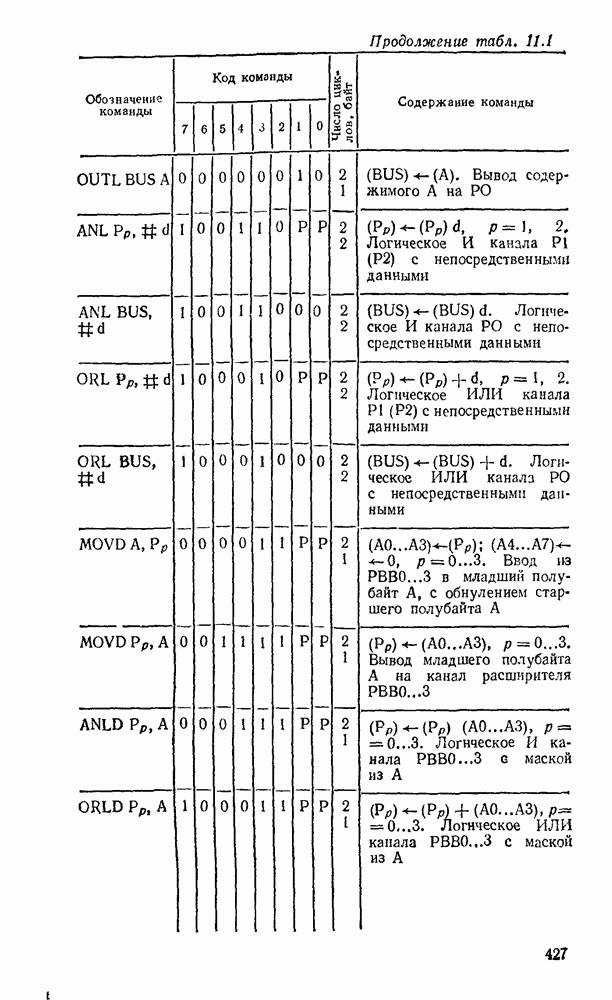
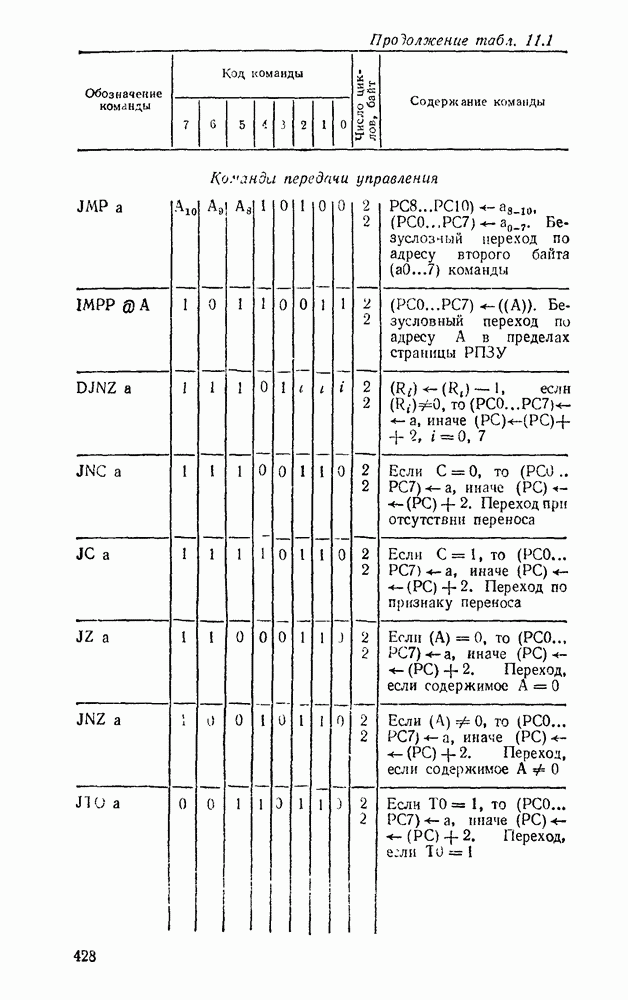
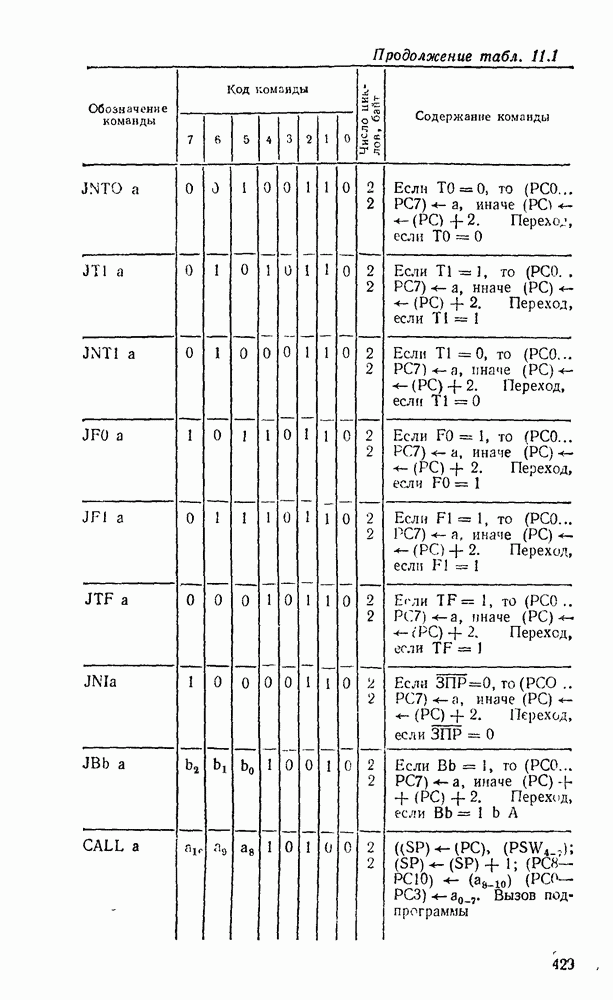
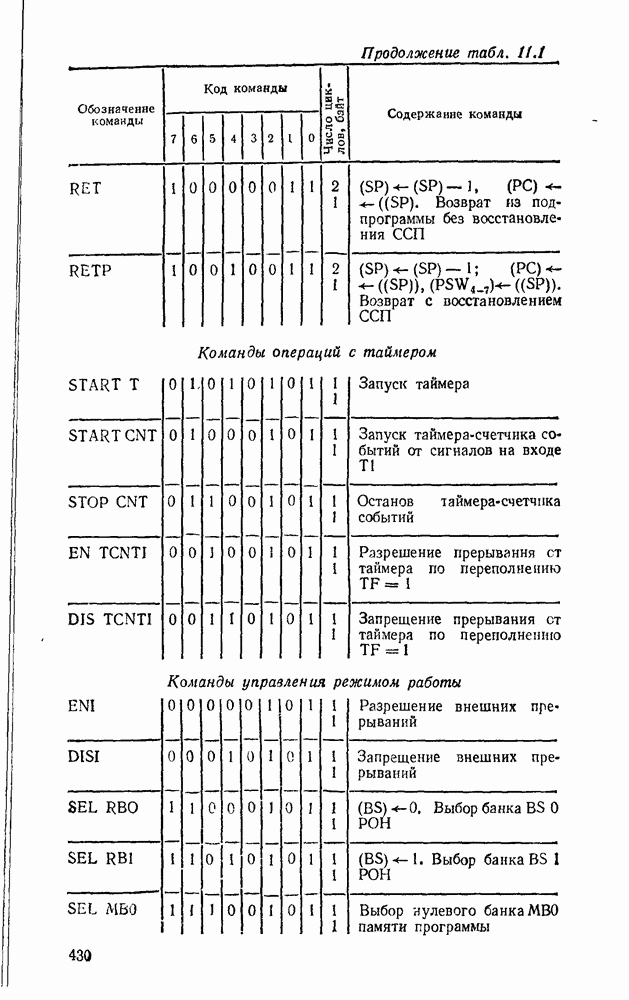
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
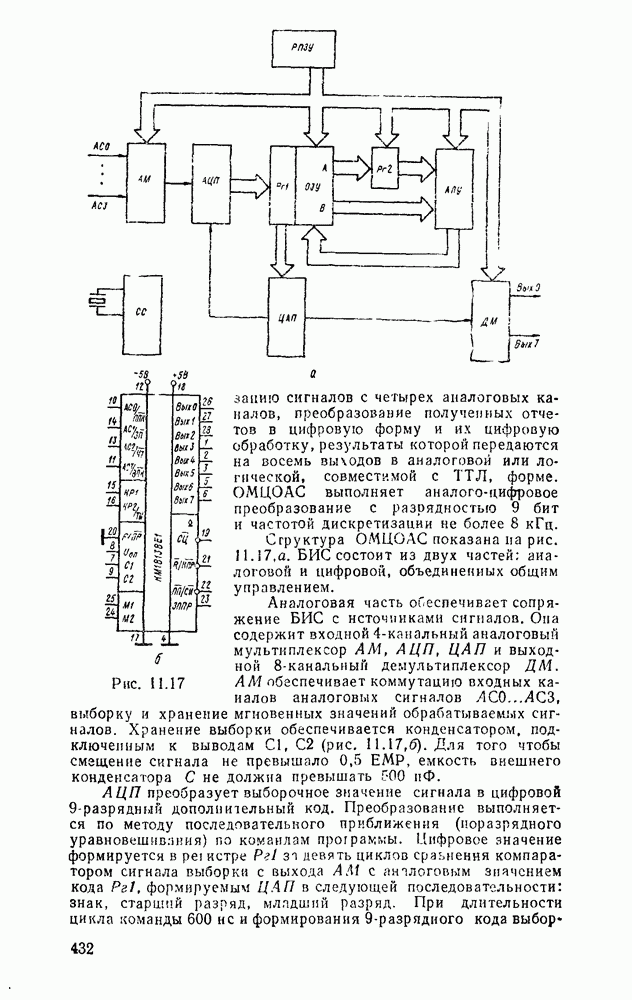
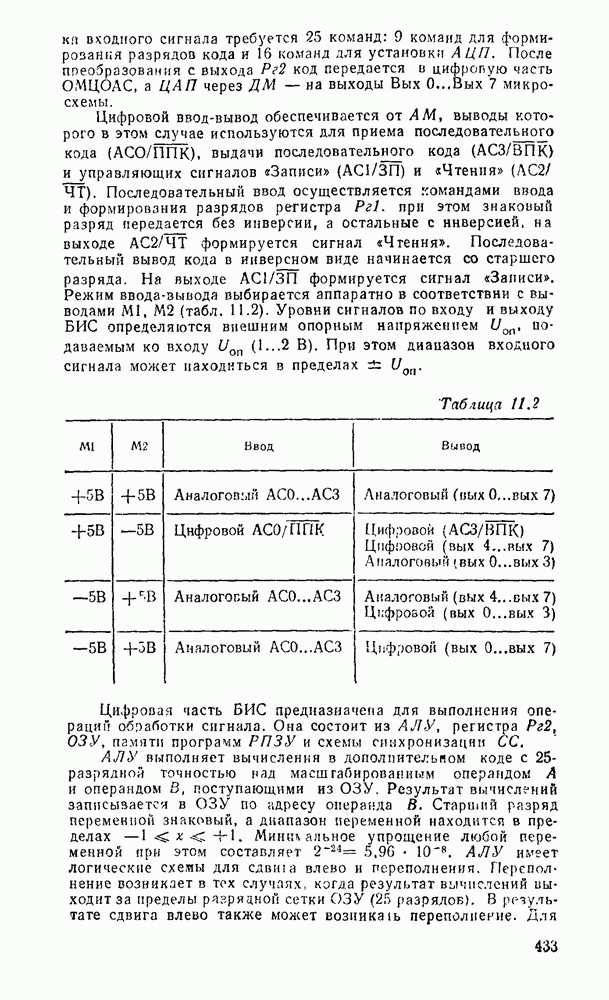
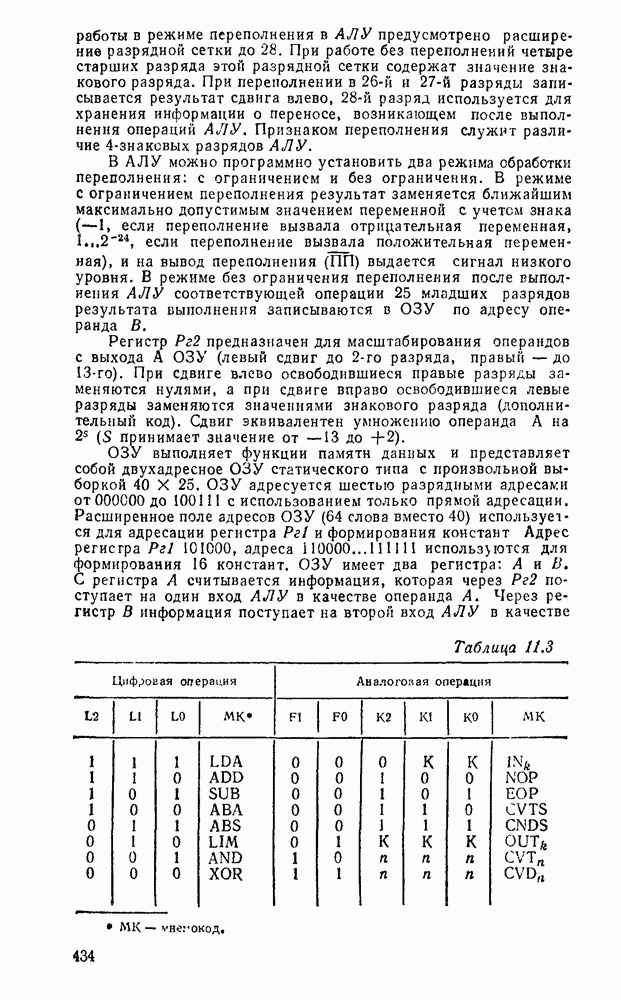
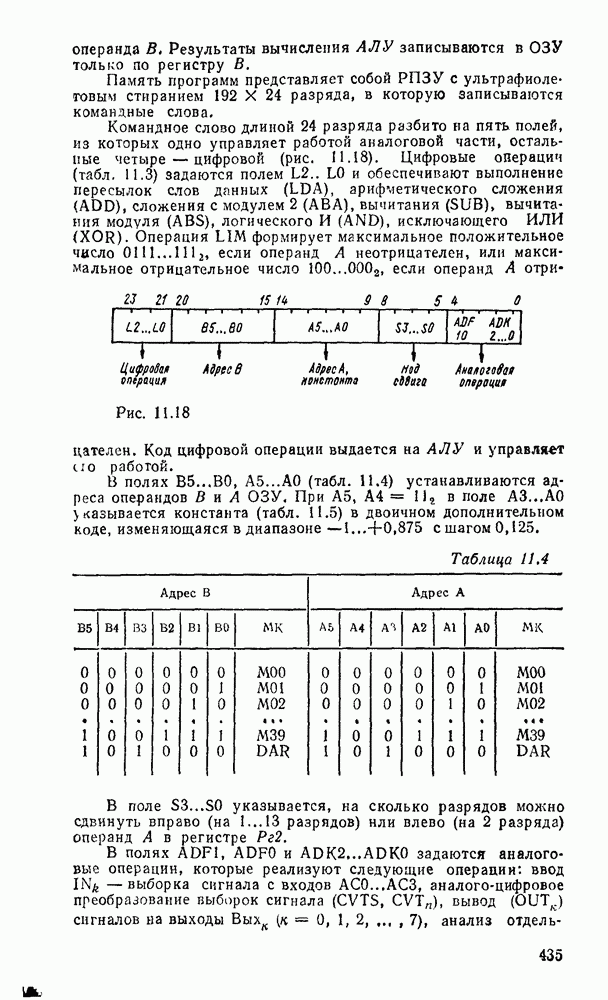
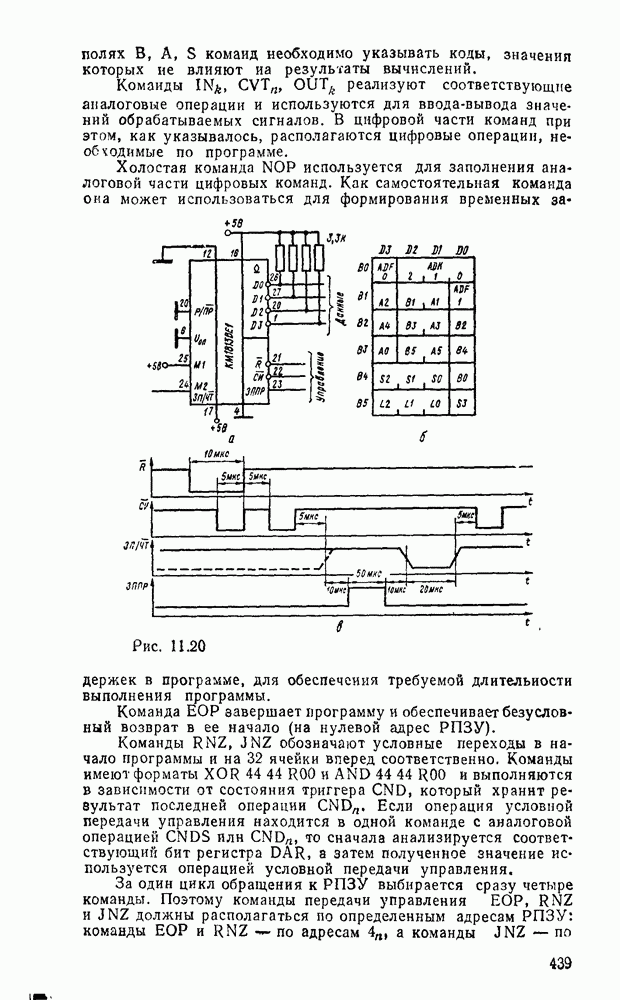
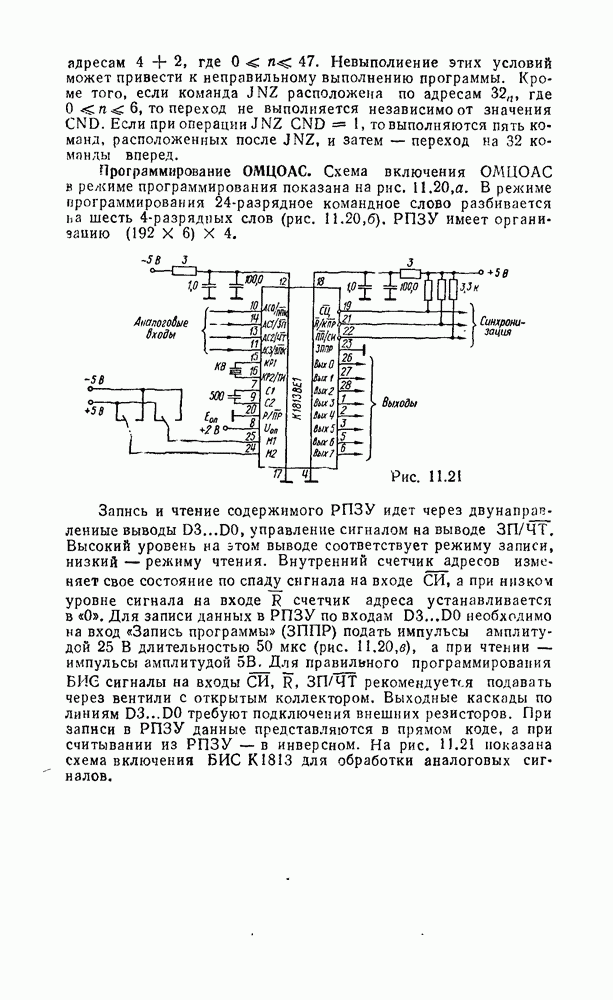
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ