| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 1. ЧИСЛА И КОДЫ
1.1. СИСТЕМЫ СЧИСЛЕНИЯ
В дискретной технике вся информация независимо от ее характера представляется в числовой форме, причем используются только позиционные системы счисления. В этих системах любое целое неотрицательное  - разрядное число записывается в виде последовательности
- разрядное число записывается в виде последовательности  цифр
цифр  Число а различных символов (0, 1, 2, а — 1), принятых для представления цифр, определяет основание системы счисления. Вклад цифры в изображаемое число зависит как от этого основания, так и от занимаемой ею позиции (разряда) в последовательности цифр. Цифра
Число а различных символов (0, 1, 2, а — 1), принятых для представления цифр, определяет основание системы счисления. Вклад цифры в изображаемое число зависит как от этого основания, так и от занимаемой ею позиции (разряда) в последовательности цифр. Цифра  входит с весом
входит с весом  и означает
и означает  , а вся последовательность цифр
, а вся последовательность цифр  . выражаете системе счисления с основанием а число
. выражаете системе счисления с основанием а число

Привычная десятичная система  использует цифры
использует цифры  так, что, например:
так, что, например:  . В вычислительной технике преимущественное значение получила двоичная система счисления
. В вычислительной технике преимущественное значение получила двоичная система счисления  , для которой достаточно двух цифр 0 и 1. Двоичный разряд представляет собой наименьшее количество информации, называемое битом. Последовательность двоичных цифр
, для которой достаточно двух цифр 0 и 1. Двоичный разряд представляет собой наименьшее количество информации, называемое битом. Последовательность двоичных цифр  служит записью двоичного числа
служит записью двоичного числа

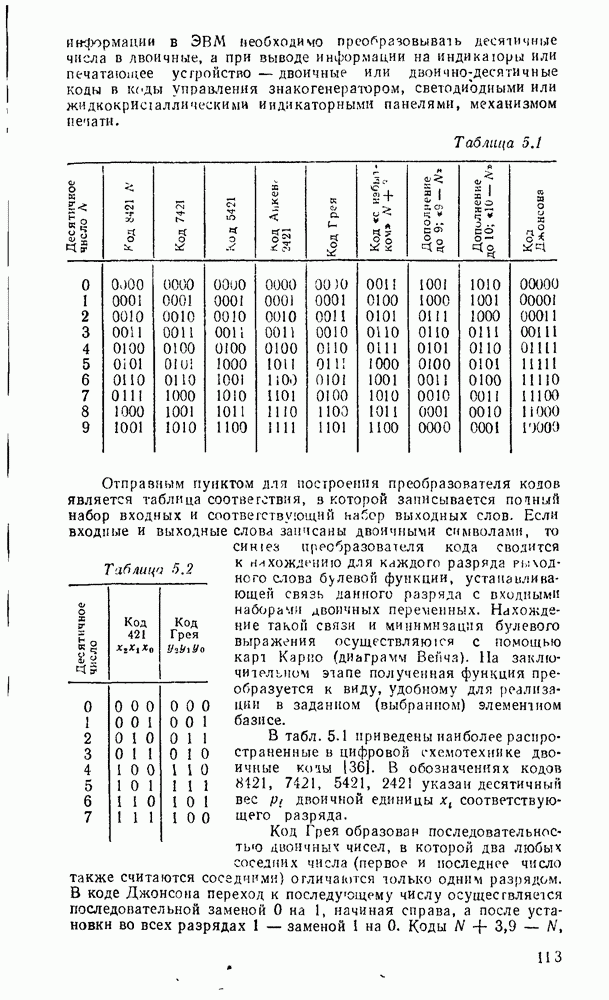
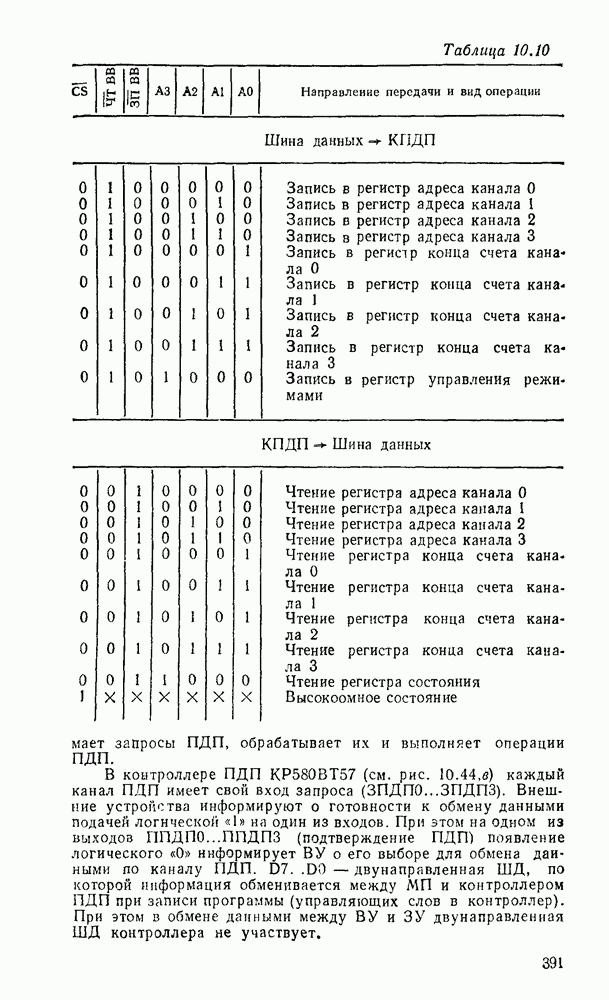
Среди других систем счисления чаще всего используются восьмеричная и шестнадцатеричная. В восьмеричной системе, цифры изображаются теми же символами, что и в десятичной, а в шестнадцатеричной системе к ним добавляется еще шесть символов А, В, С, D, Е, F, которые соответствуют десятичным числам 10, 11, 12, 13, 14, 15. Запись первых 32 чисел в системах счисления с основанием 2, 8 и 16 показаны в табл. 1.1. Если требуется указать основание системы счисления, запись числа сопровождается десятичным индексом. Например:

Отсюда видно, что для преобразования числа из любой системы счисления в десятичную достаточно вычислить значение соответствующего многочлена, подставив в него десятичные значения разрядов и основания системы счисления. Вычисления удобно выполнять по схеме Горнера, основанной на представлении многочлена (1.1) в виде

Таблица 1.1

т. е. цифра  старшего разряда переводимого числа умножается на основание а исходной системы счисления и результат суммируется со следующей цифрой, затем этот процесс повторяется, пока не дойдет до цифры младшего разряда. Например, преобразование восьмеричного числа в десятичное по этой схеме представляется следующим образом:
старшего разряда переводимого числа умножается на основание а исходной системы счисления и результат суммируется со следующей цифрой, затем этот процесс повторяется, пока не дойдет до цифры младшего разряда. Например, преобразование восьмеричного числа в десятичное по этой схеме представляется следующим образом:

Наибольшее десятичное число, которое можно представить  -разрядным числом в системе счисления с основанием а, равно
-разрядным числом в системе счисления с основанием а, равно  При этом для представления
При этом для представления  чисел необходимо по а различных цифр на каждый разряд, т. е. всего
чисел необходимо по а различных цифр на каждый разряд, т. е. всего  цифр. В то же время количество чисел, которые можно представить в системе счисления с основанием а, располагая q цифрами, выражается функцией
цифр. В то же время количество чисел, которые можно представить в системе счисления с основанием а, располагая q цифрами, выражается функцией  . Она достигает максимума при равенстве а основанию натуральных логарифмов
. Она достигает максимума при равенстве а основанию натуральных логарифмов  что указывает на троичную систему как наиболее экономичную. В свое время этот вывод служил одним из оснований для построения троичных вычислительных машин, но с развитием интегральной технологии он потерял свое значение. В вычислительной технике доминирующую роль по-прежнему играет двоичная система благодаря таким ее преимуществам как удобство технической реализации, простота арифметических и логических операций и др. Между тем в информационно-измерительной технике применяются также многозначные элементы и структуры, с помощью которых осуществляются различные операции в десятичной и других системах счисления [52, 53].
что указывает на троичную систему как наиболее экономичную. В свое время этот вывод служил одним из оснований для построения троичных вычислительных машин, но с развитием интегральной технологии он потерял свое значение. В вычислительной технике доминирующую роль по-прежнему играет двоичная система благодаря таким ее преимуществам как удобство технической реализации, простота арифметических и логических операций и др. Между тем в информационно-измерительной технике применяются также многозначные элементы и структуры, с помощью которых осуществляются различные операции в десятичной и других системах счисления [52, 53].
В общем случае, когда число имеет дробную часть, последняя отделяется от целой части разделительным символом — точкой или запятой:

что соответствует числу:

Выражение любого числа в десятичной системе сводится к вычислению его многочленного представления, например:

Арифметические операции над  в любой системе счисления выполняются по тем же правилам, что и в десятичной системе.
в любой системе счисления выполняются по тем же правилам, что и в десятичной системе.
1.2. ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
Чаще всего приходится переводить десятичные числа в двоичные и обратно, что можно выполнить с помощью универсального алгоритма, применяемого раздельно для целой и дробной частей. Перевод целой части десятичного числа в двоичную систему сводится к записи в обратном порядке остатков (0 или 1), получаемых при делении исходного числа и каждого последующего частного на два. Дробная часть получается из целых частей (0 или 1) при ее последовательном умножении на два, причем такое умножение продолжается до тех пор, пока дробная часть обратится в нуль или получится требуемое количество знаков после разделительной точкч. Покажем, например, что  :
:

Обратное преобразование двоичного числа в десятичное можно выполнить аналогично с тем различием, что делить и умножать нужно на 10 в двоичной системе, т. е. на 10102.
Так, соотношение  получается следующим образом:
получается следующим образом:

Как видно, при использовании этого алгоритма цифры десятичного эквивалента двоичного числа выражаются первоначально в двоичной системе. Отводя для каждого десятичного разряда четыре двоичных разряда (тетраду), получим двоично-десятичную запись числа:

Такое представление чисел удобно при обработке в вычислительных машинах информации, характеризующейся большим количеством исходных данных и результатов в десятичной системе счисления.
Проще всего переводятся в двоичные числа восьмеричные и шестнадцатеричные, основания которых представляют собой целые степени двойки, т. е.  . Для этого достаточно каждый разряд восьмеричного числа представить тройкой (триадой), а шестнадцатеричного — четверкой (тетрадой) двоичных разрядов. Например:
. Для этого достаточно каждый разряд восьмеричного числа представить тройкой (триадой), а шестнадцатеричного — четверкой (тетрадой) двоичных разрядов. Например:

Обратный перевод двоичного числа в восьмеричное или шестнадцатеричное выполняется его разбиением на блоки (триады или тетрады) влево и вправо от разделительного символа. Недостающие разряды в крайнем левом и правом блоках дополняются нулями. Затем каждая триада заменяется восьмеричным, а каждая тетрада шестнадцатеричным числом. Например:

Восьмеричное и шестнадцатеричное представления двоичных чисел повсеместно используются для более компактной записи при программировании и вводе программ в вычислительные машины. В частности, шестнадцатеричная система удобна для представления укрупненной единицы информации — байта, равного 8 битам, для чего достаточно двузначного шестнадцатеричного числа.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
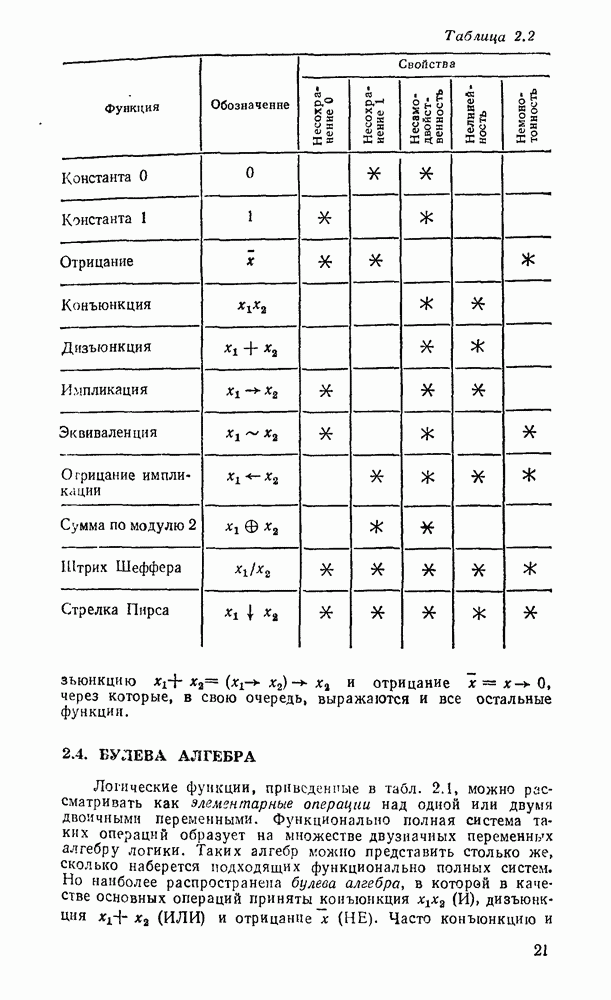
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
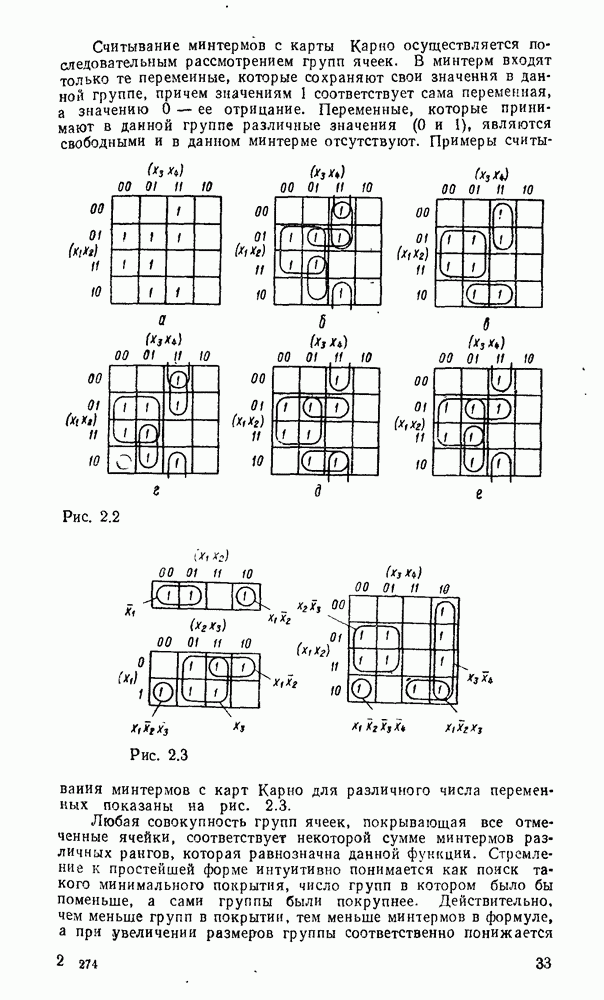
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
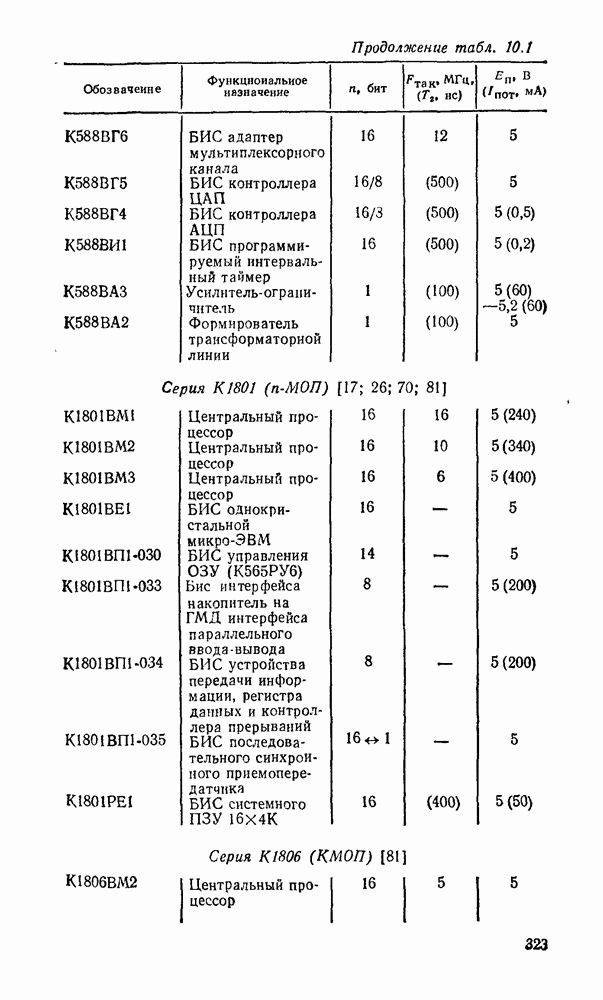
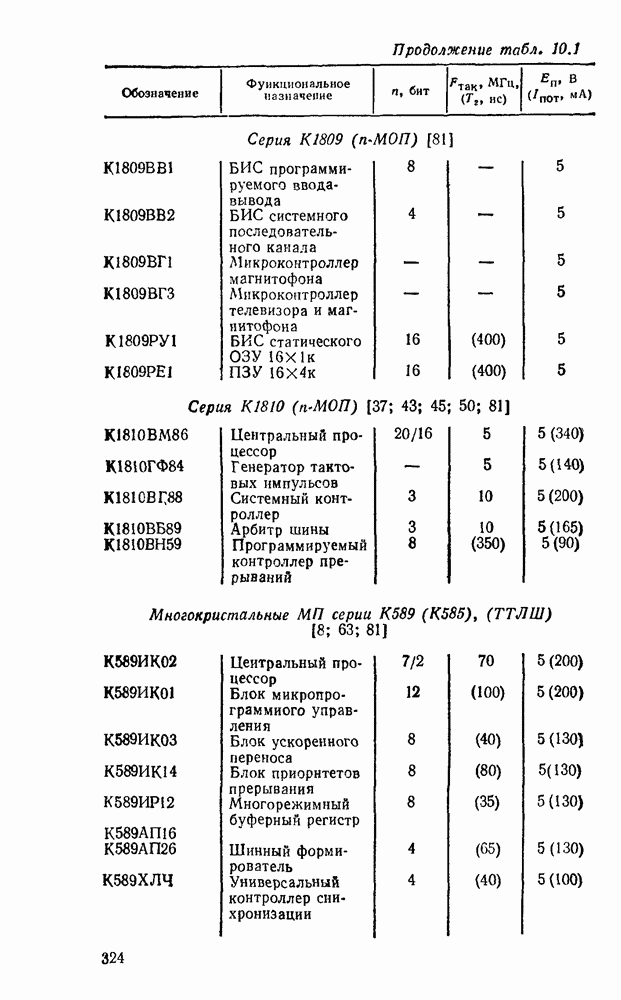
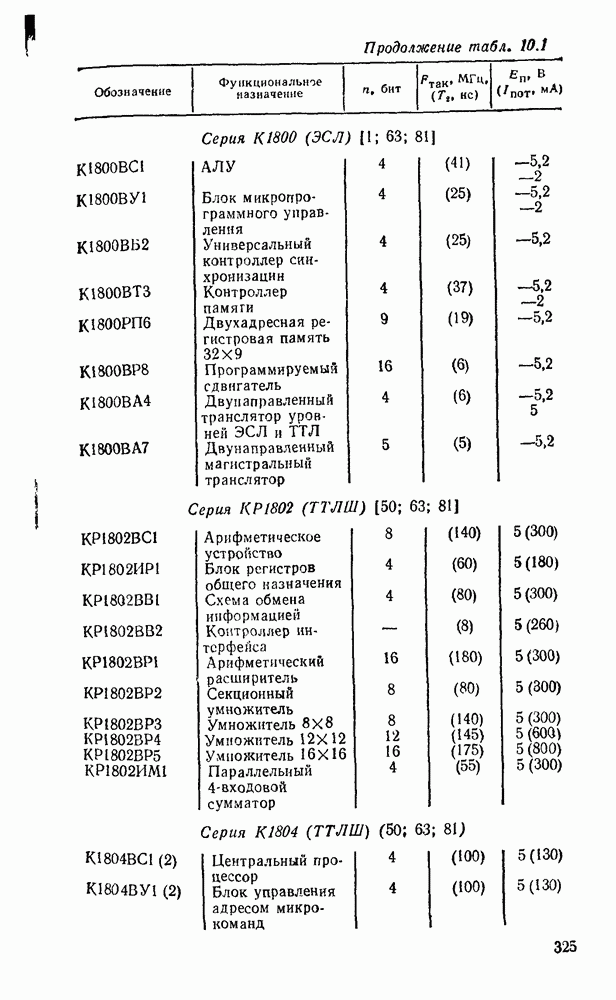
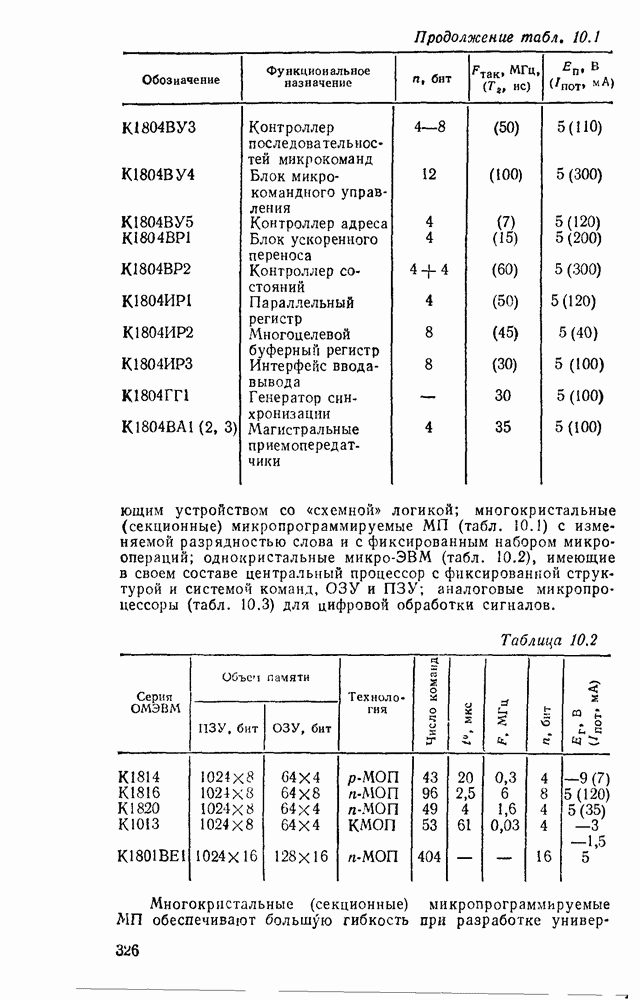
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
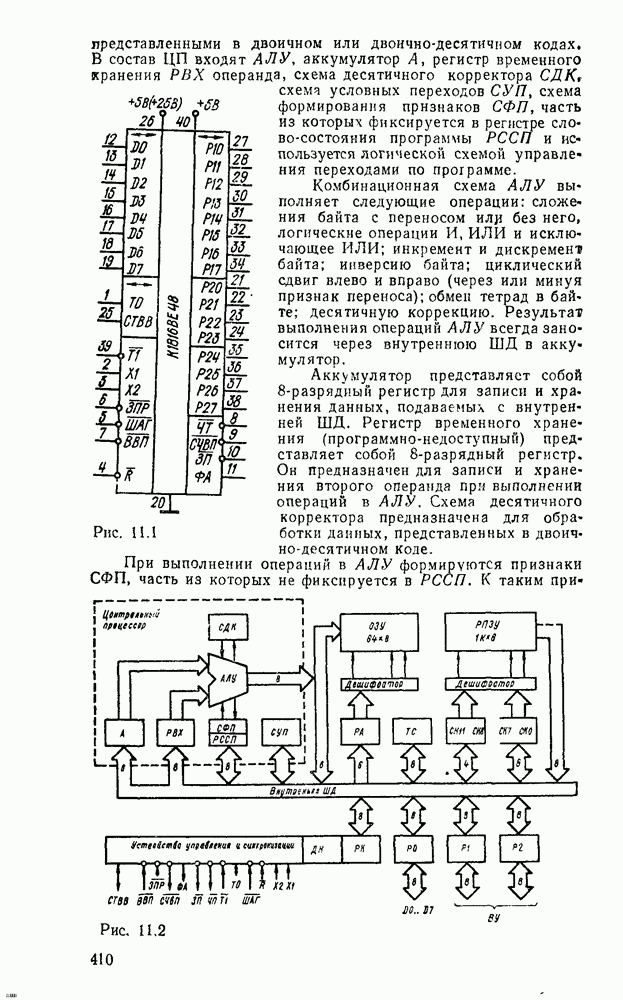
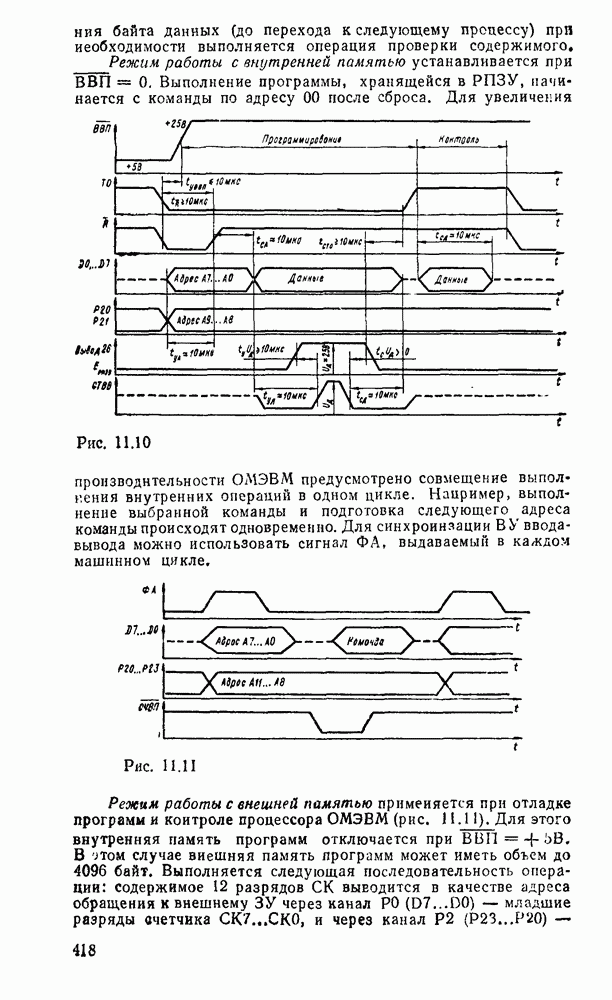
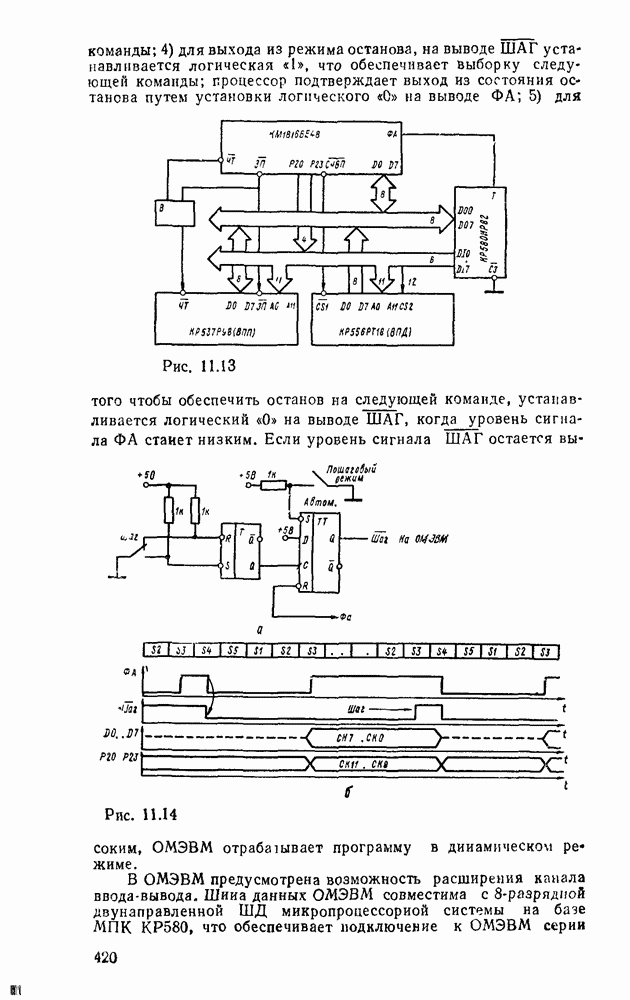
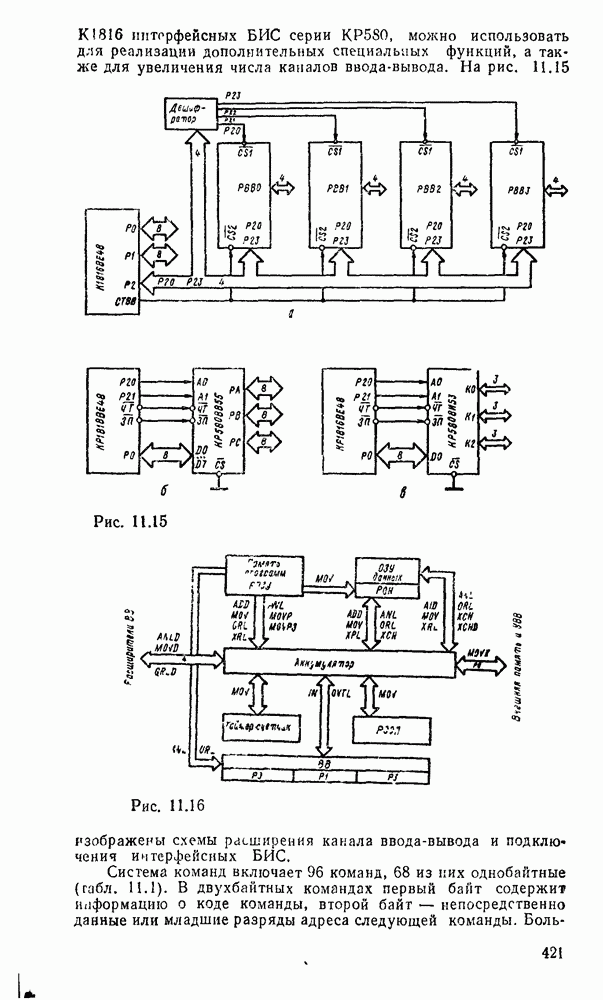
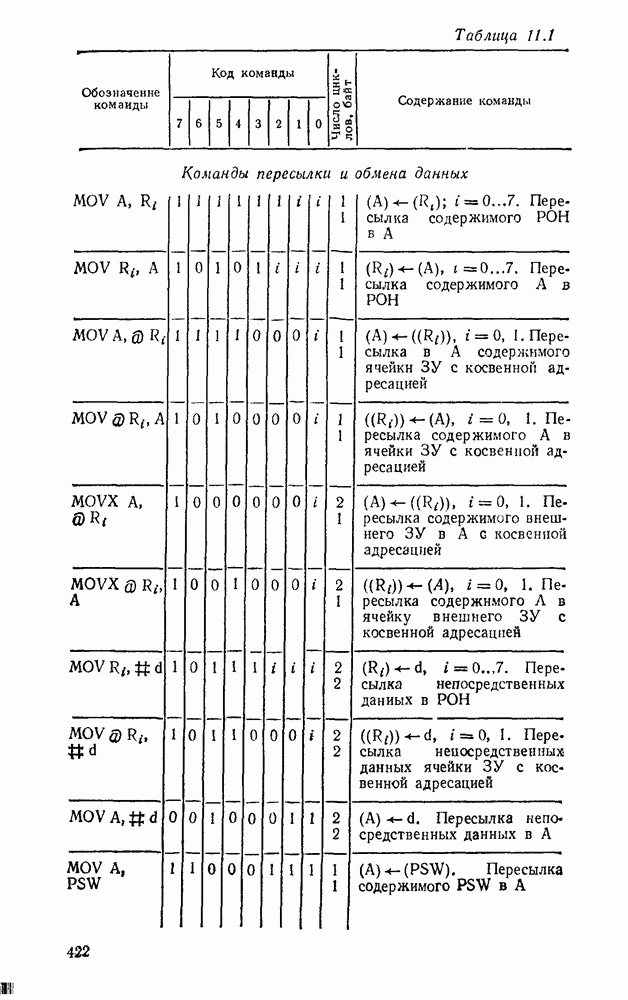
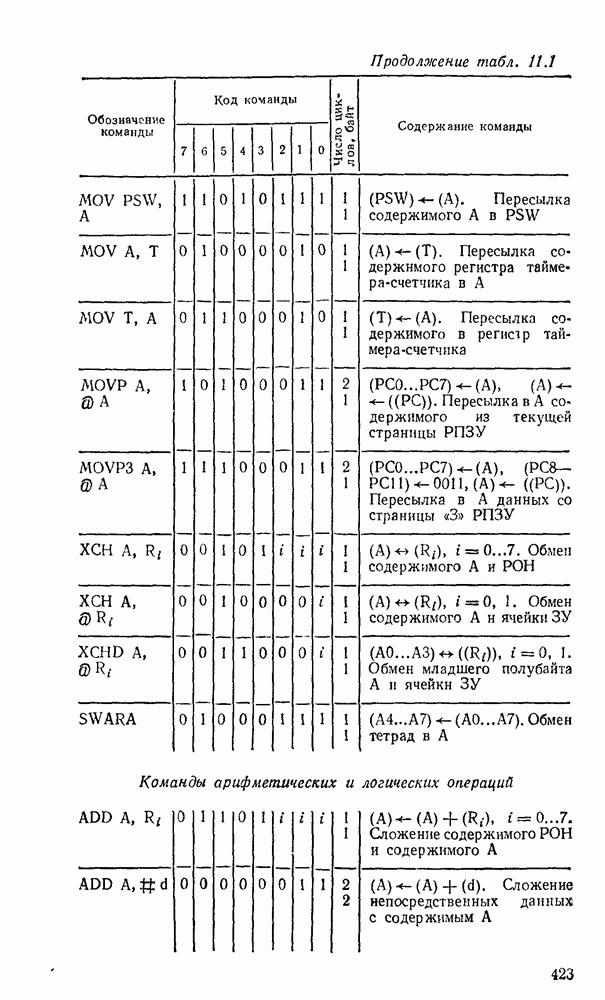
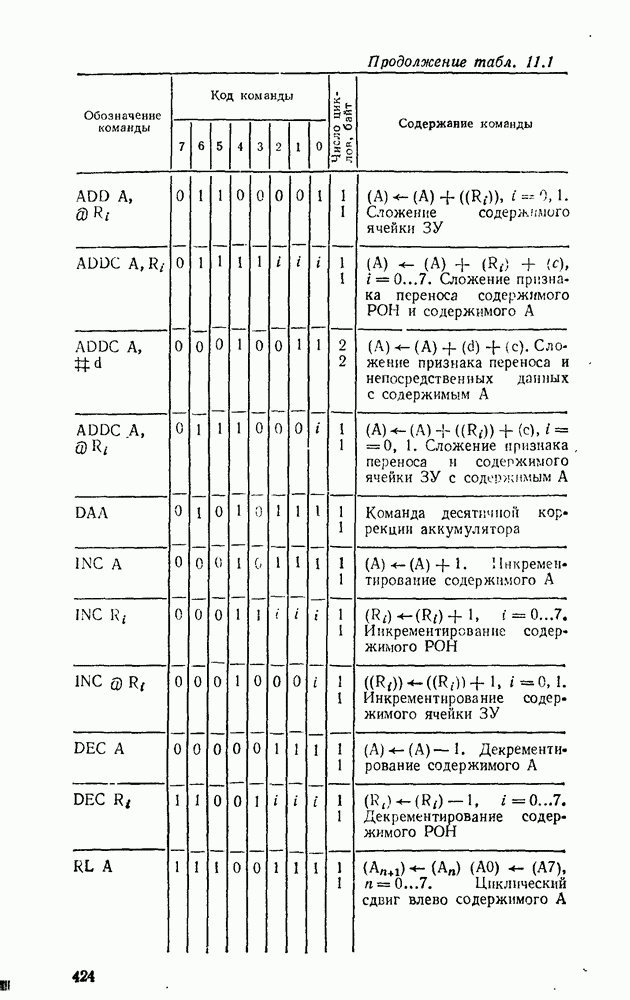
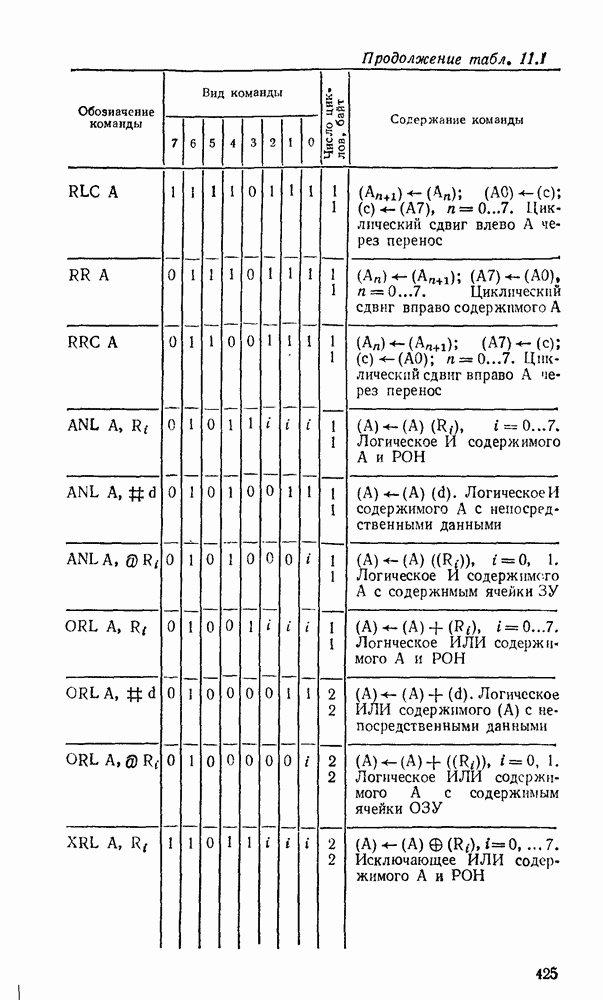
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
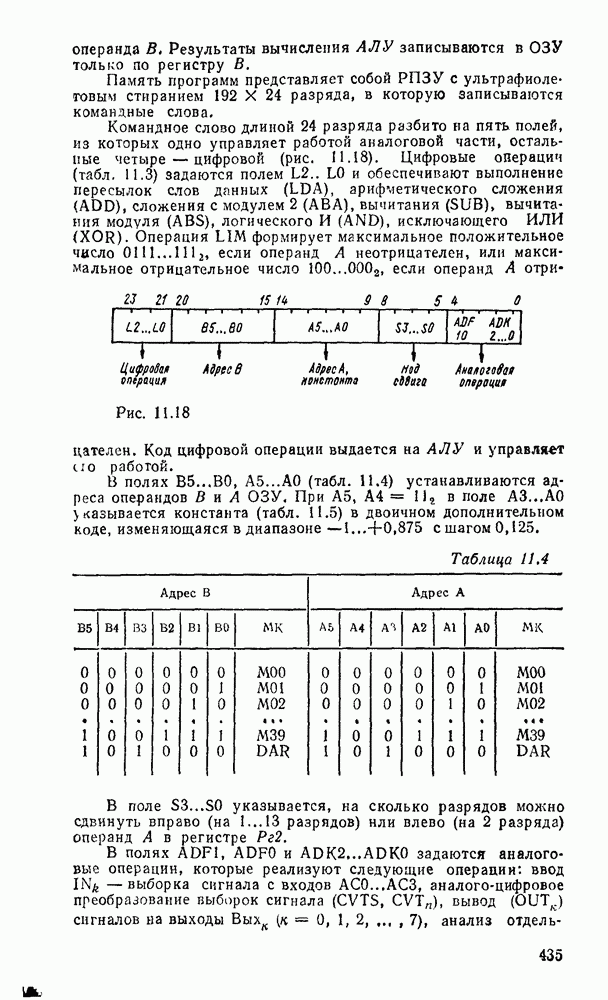
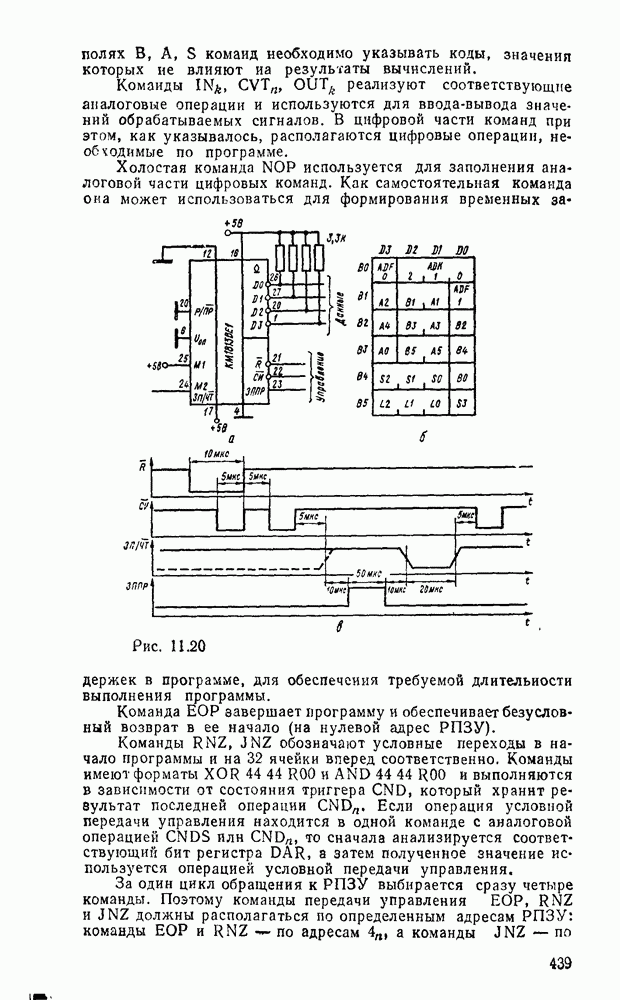
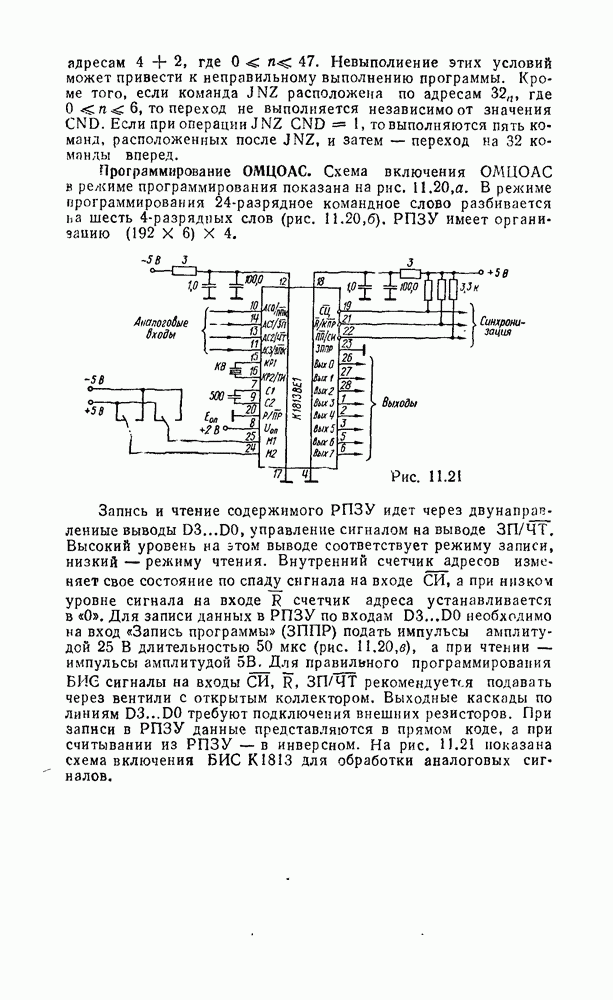
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ