| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 2. АЛГЕБРА ЛОГИКИ
2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
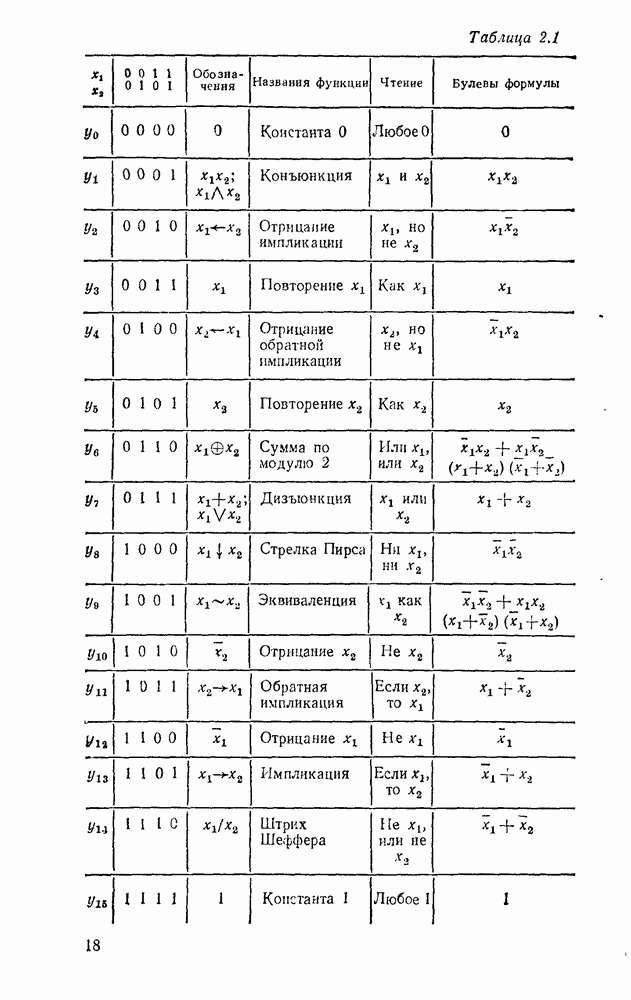
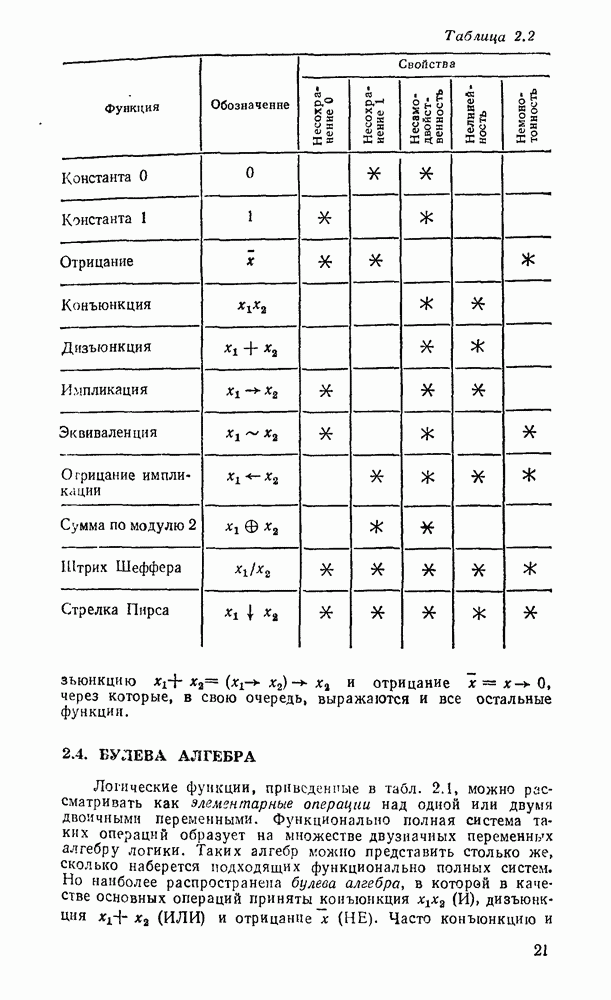
Вследствие того что сигналы в цифровых системах представляются двоичными кодами, математическое моделирование таких систем основано на использовании двузначной логики (29; 68; 801, в которой переменные могут принимать только одно из двух значений. Эти значения соответствуют двум возможным состояниям реальных объектов (истинное или ложное высказывание, высокое или низкое напряжение, наличие или отсутствие данного признака и т. п.). Они обозначаются цифрами 0 и 1, буквами Л (ложно) и И (истинно) или вообще любыми двумя различающимися символами. В технических приложениях обычно используются цифровые обозначения, которые естественным образом связаны с двоичными кодами.
В общем случае логические переменные могут принимать одно из k значений ( -значная логика). Перечень всех k символов, соответствующих области значений, называют алфавитом, а сами символы — буквами этого алфавита. Логические функции могут зависеть от одной, двух и вообще любого числа переменных (аргументов). Областью определения
-значная логика). Перечень всех k символов, соответствующих области значений, называют алфавитом, а сами символы — буквами этого алфавита. Логические функции могут зависеть от одной, двух и вообще любого числа переменных (аргументов). Областью определения  -значной функции от
-значной функции от  переменных
переменных  служит множество наборов
служит множество наборов  , являющихся словами длины
, являющихся словами длины  , где каждый из аргументов замещается буквами
, где каждый из аргументов замещается буквами  -ичного алфавита.
-ичного алфавита.
Так как количество всевозможных слов длины  в
в  -ичном алфавите равно количеству различных
-ичном алфавите равно количеству различных  -разрядных чисел с основанием k, т. е.
-разрядных чисел с основанием k, т. е.  , а каждому такому слову можно сопоставить одно из к значений, то общее количество
, а каждому такому слову можно сопоставить одно из к значений, то общее количество  -значных функций от
-значных функций от  переменных выражается числом
переменных выражается числом  Многозначная логика располагает собственным аппаратом и используется для математического моделирования таких объектов, компоненты которых характеризуются многими состояниями. Между тем двузначная логика наряду с предельной простотой характеризуется и достаточной общностью, так как к ней можно свести и задачи моделирования многозначных структур.
Многозначная логика располагает собственным аппаратом и используется для математического моделирования таких объектов, компоненты которых характеризуются многими состояниями. Между тем двузначная логика наряду с предельной простотой характеризуется и достаточной общностью, так как к ней можно свести и задачи моделирования многозначных структур.
Количество всевозможных двоичных функций выражается числом  а область определения таких функций представляет собой всевозможные наборы из
а область определения таких функций представляет собой всевозможные наборы из  двоичных цифр и их общее количество равно
двоичных цифр и их общее количество равно  . При увеличении
. При увеличении  количество двоичных функций быстро возрастает (при
количество двоичных функций быстро возрастает (при  оно равно 256, а при
оно равно 256, а при  уже превышает 4 млрд.). Но функции одной и двух переменных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (4 при
уже превышает 4 млрд.). Но функции одной и двух переменных еще можно перечислить и подробно исследовать, так как их количество сравнительно невелико (4 при  и 16 при
и 16 при  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
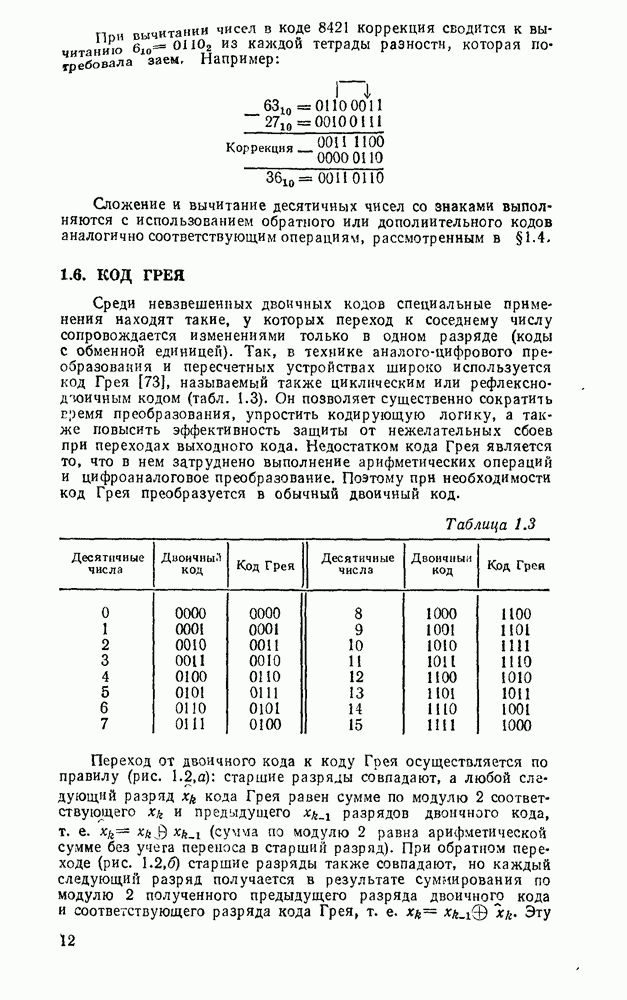
- 1.6. КОД ГРЕЯ
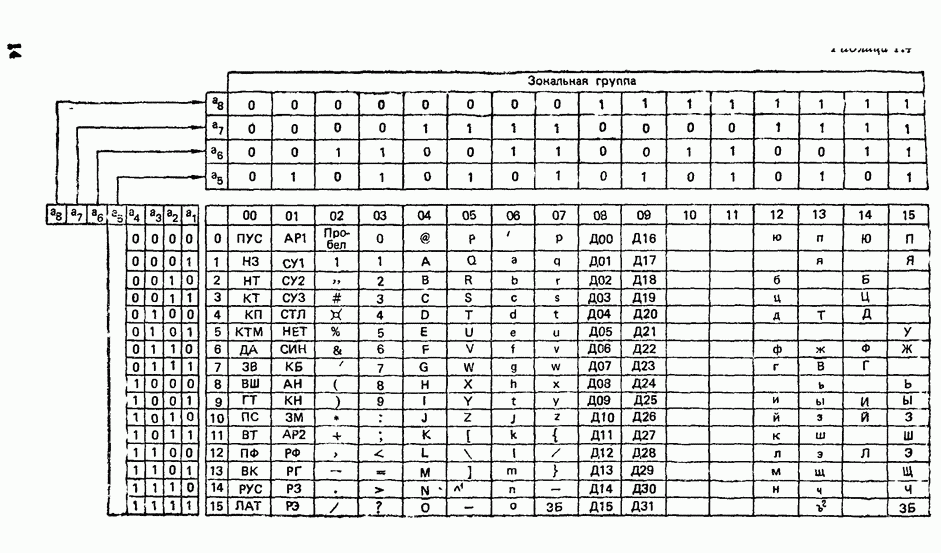
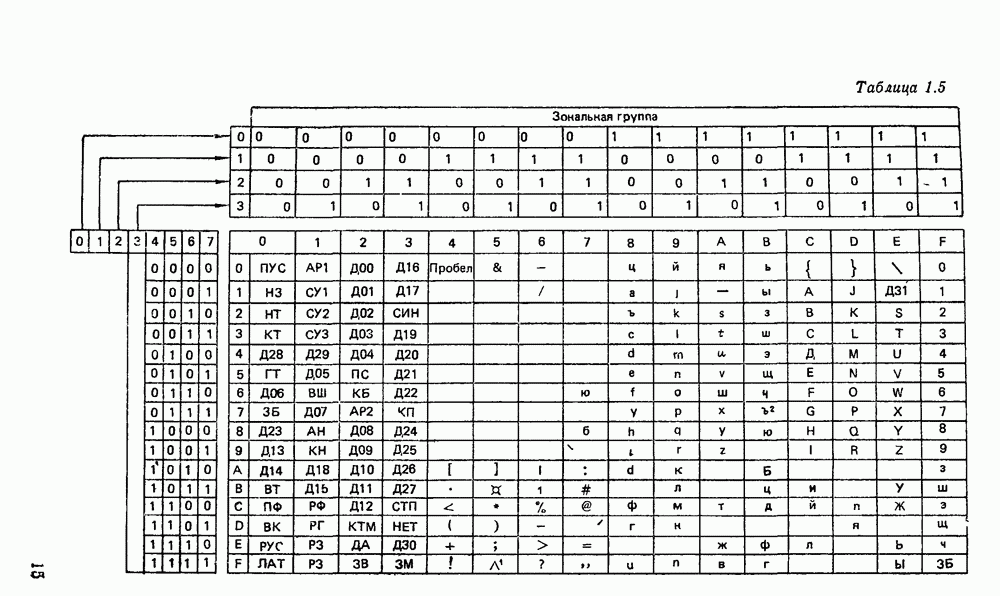
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
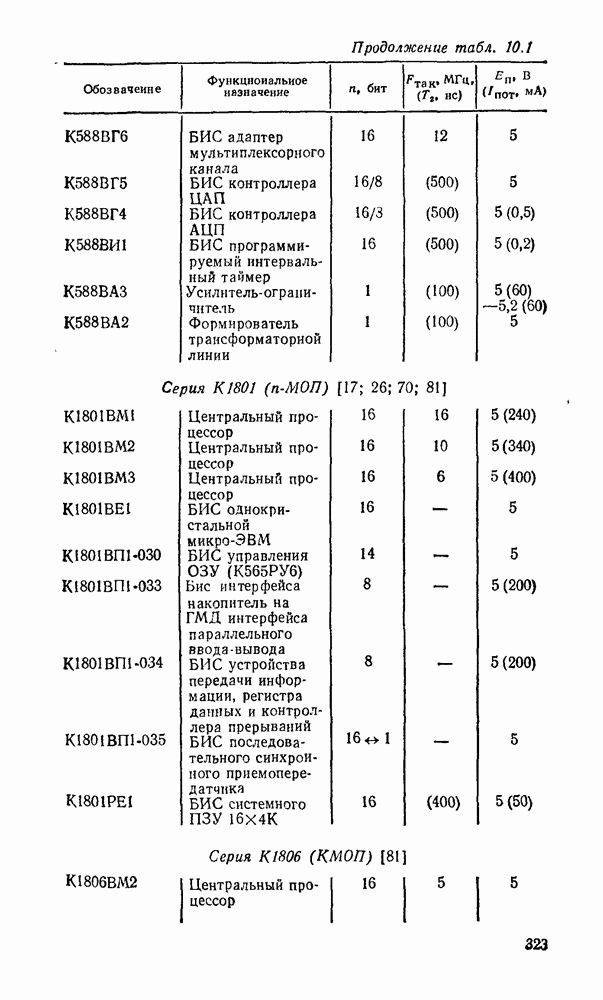
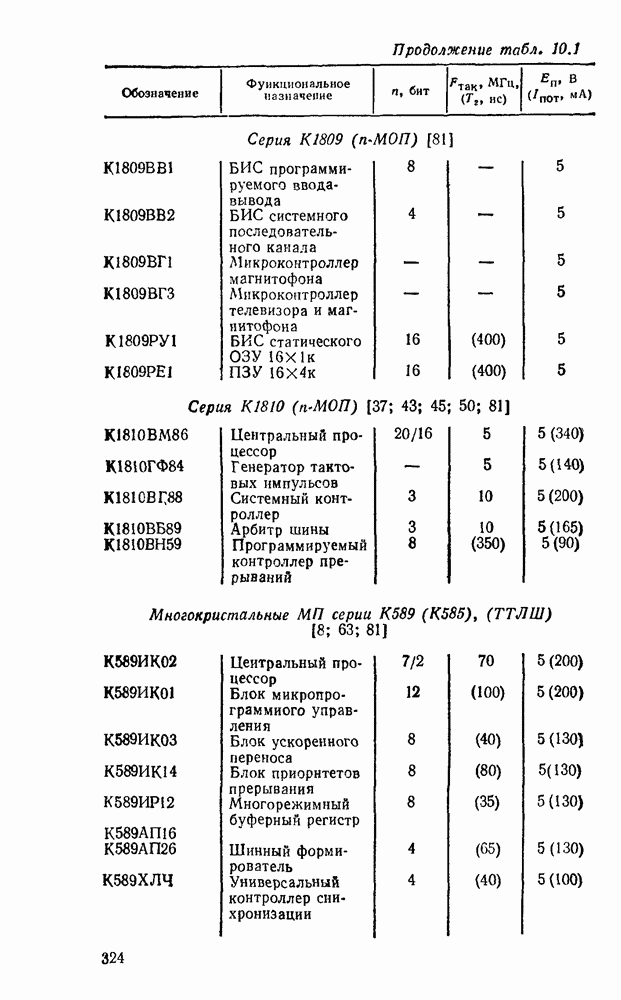
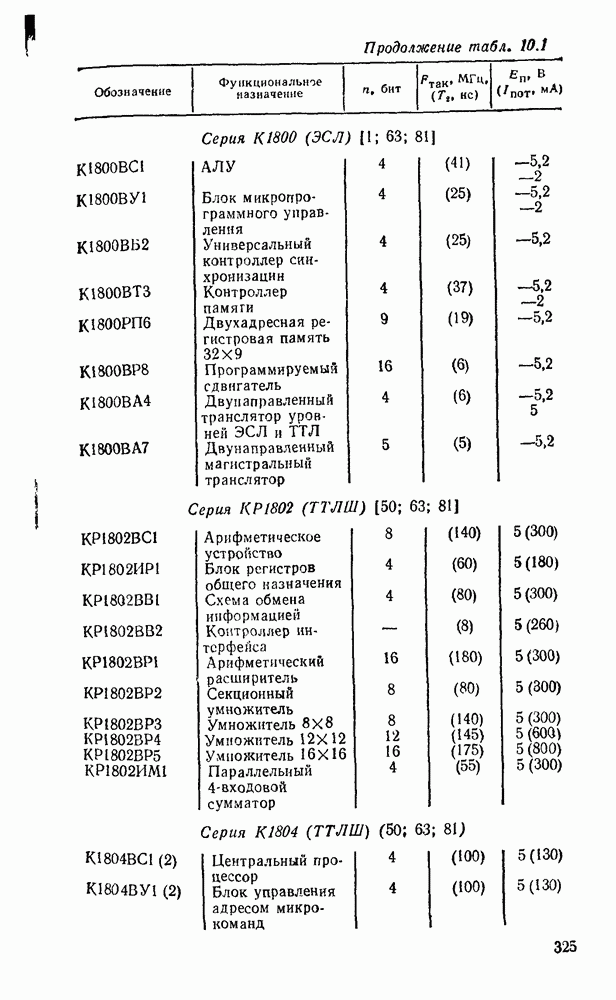
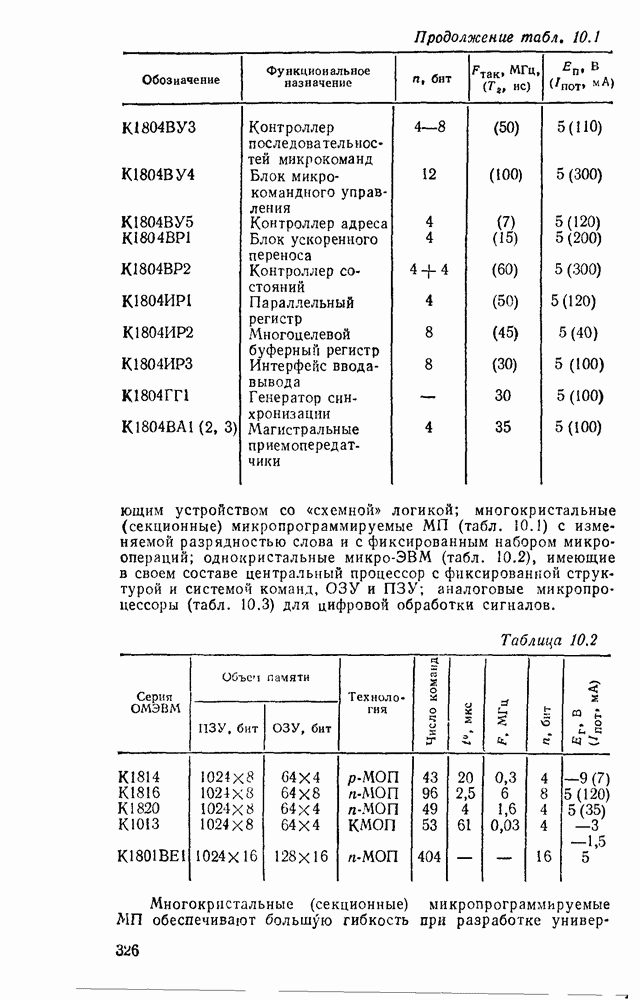
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
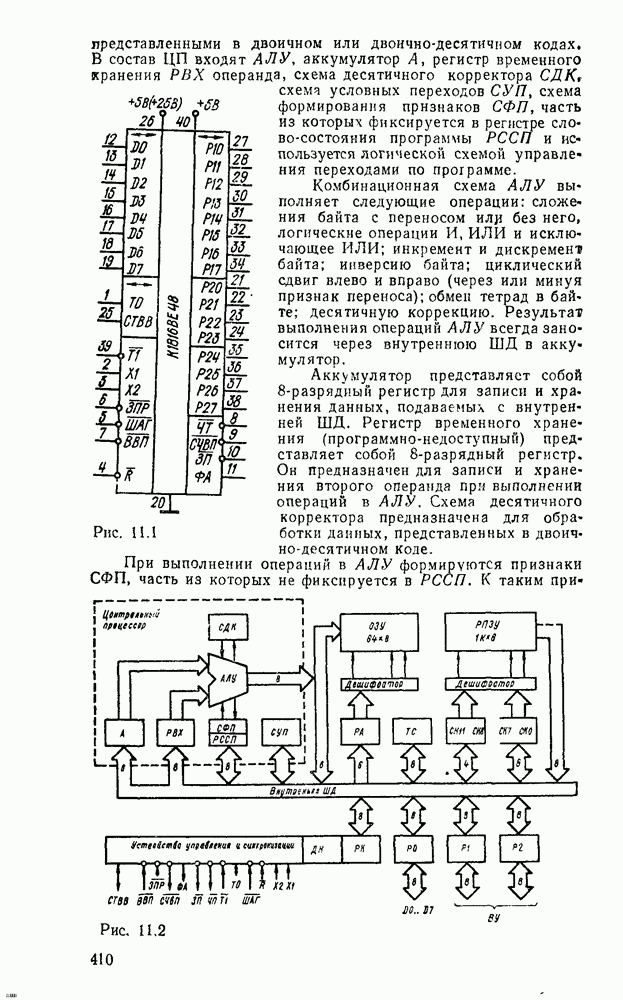
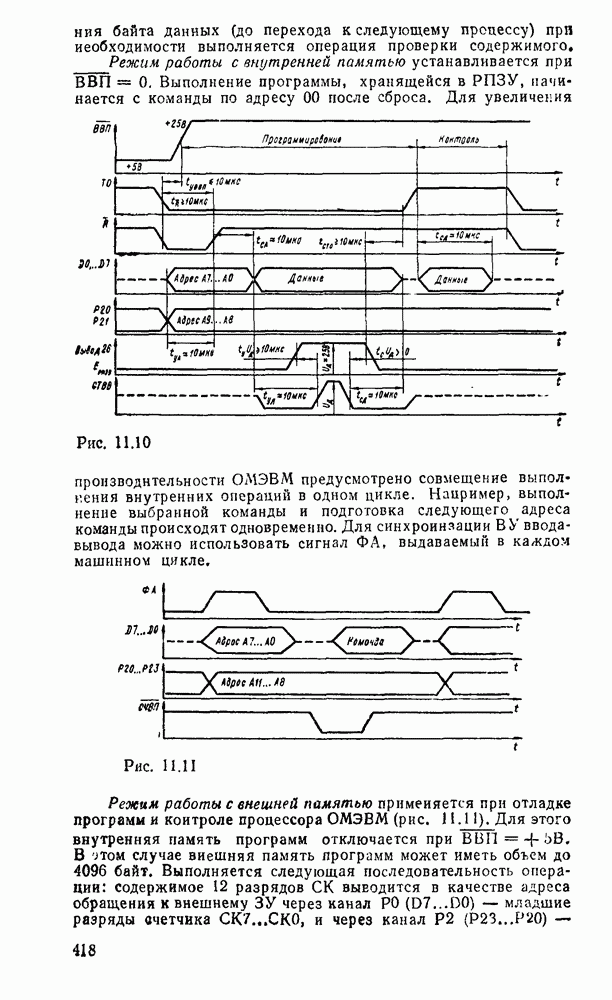
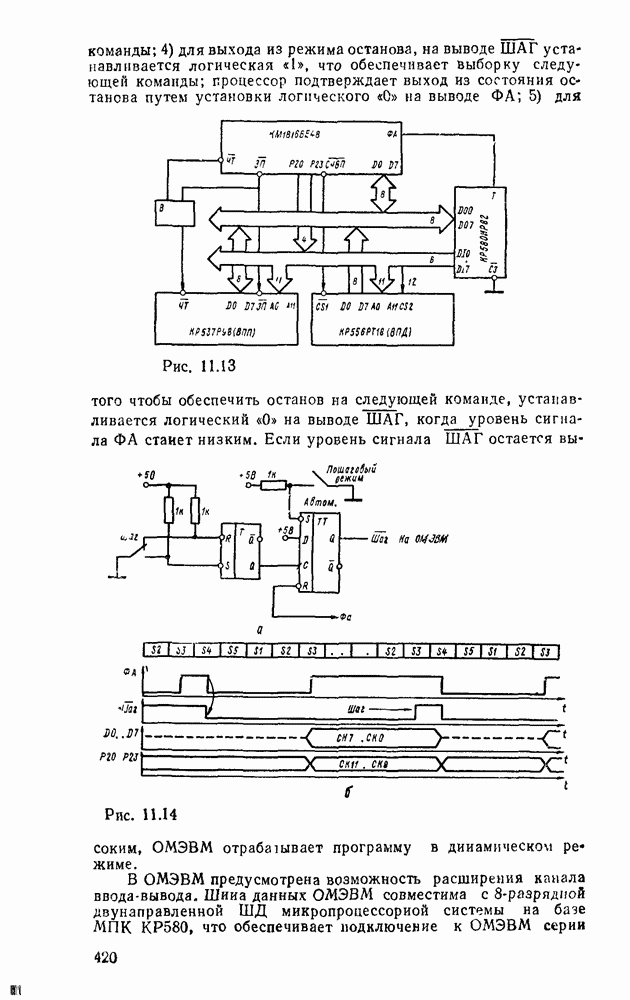
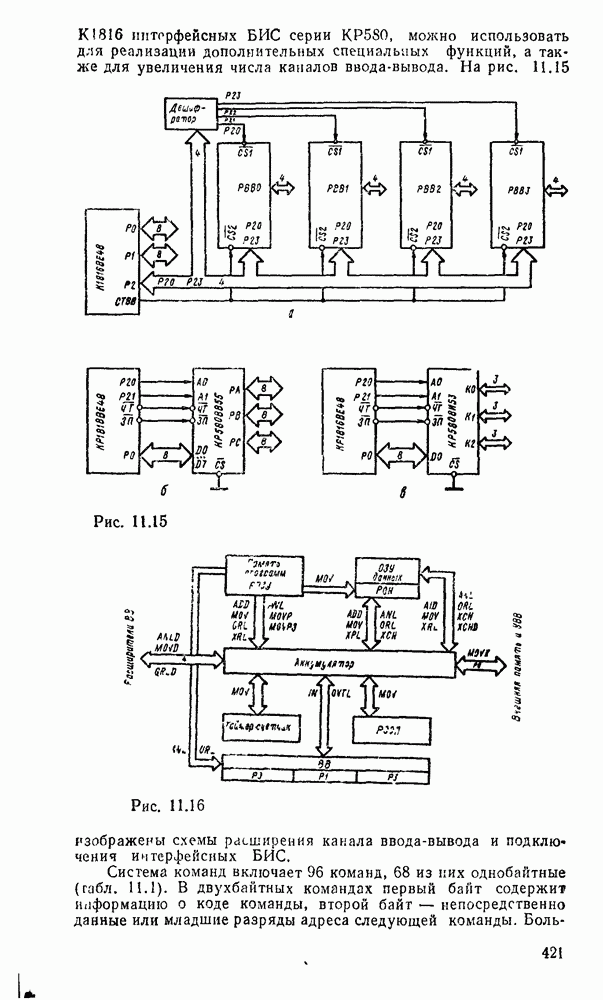
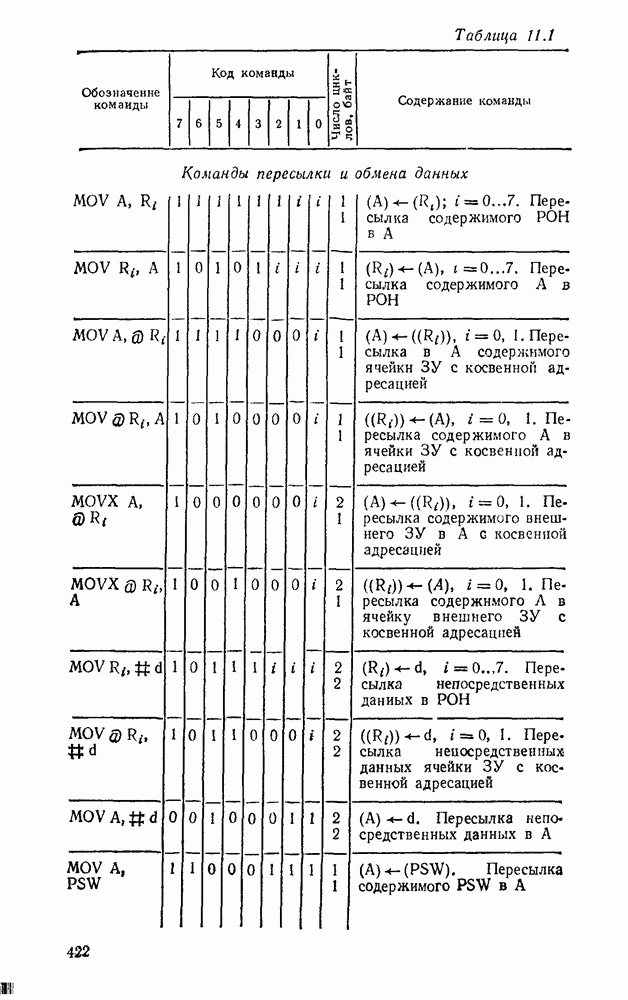
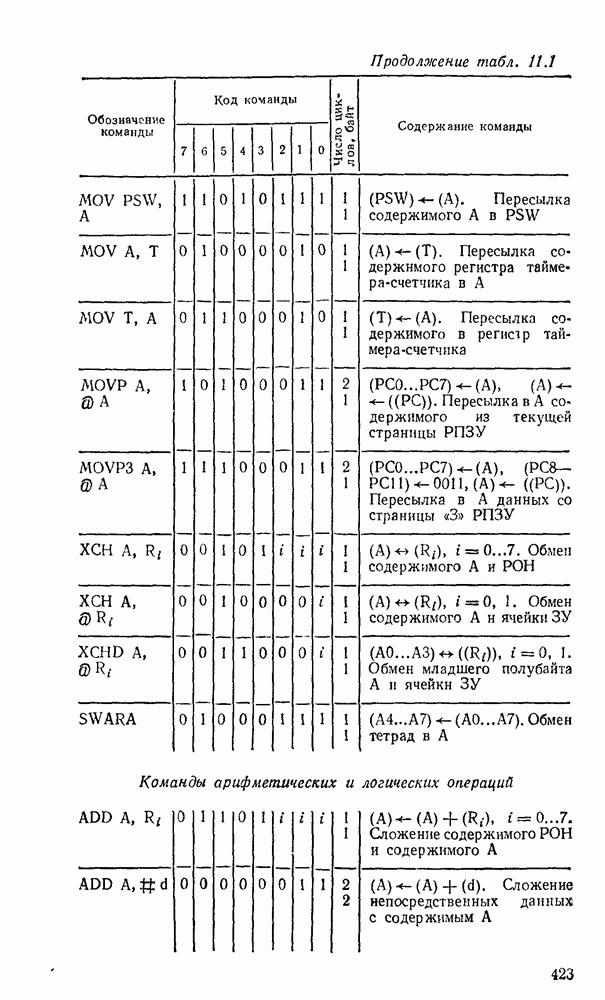
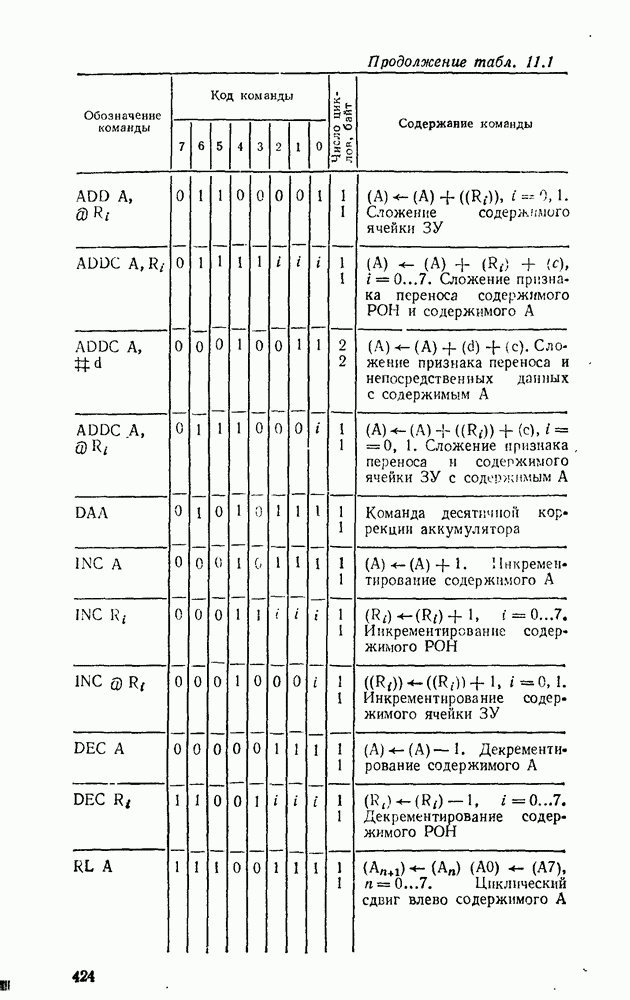
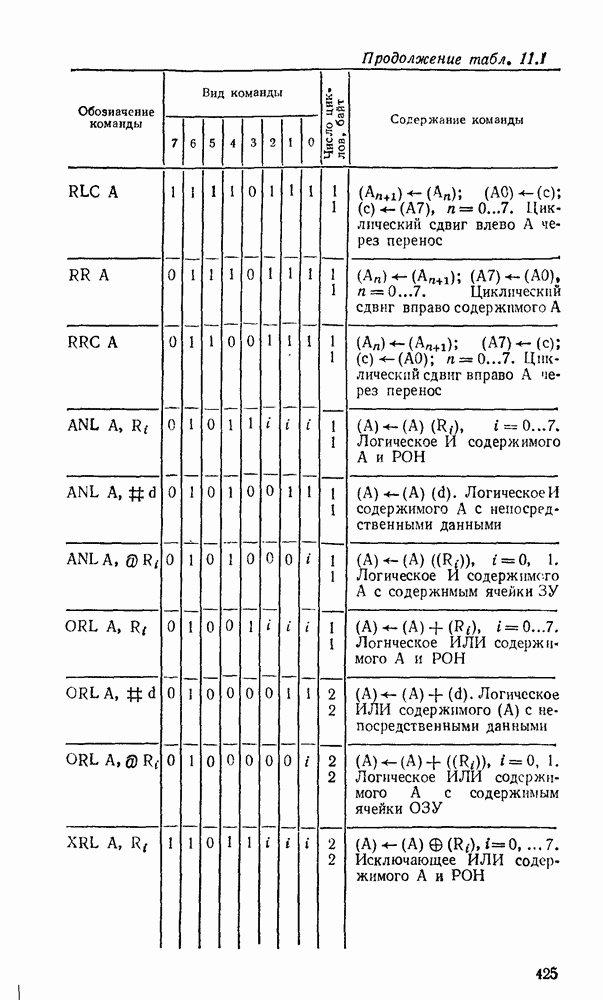
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ