| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
Дискретизацией сигнала называется измерительное преобразование непрерывного сигнала  в последовательность мгновенных значений этого сигнала
в последовательность мгновенных значений этого сигнала  , соответствующих определенным моментам времени
, соответствующих определенным моментам времени 

где  — шаг дискретизации;
— шаг дискретизации;  — значение снгнала в момент
— значение снгнала в момент  — функция Дирака.
— функция Дирака.

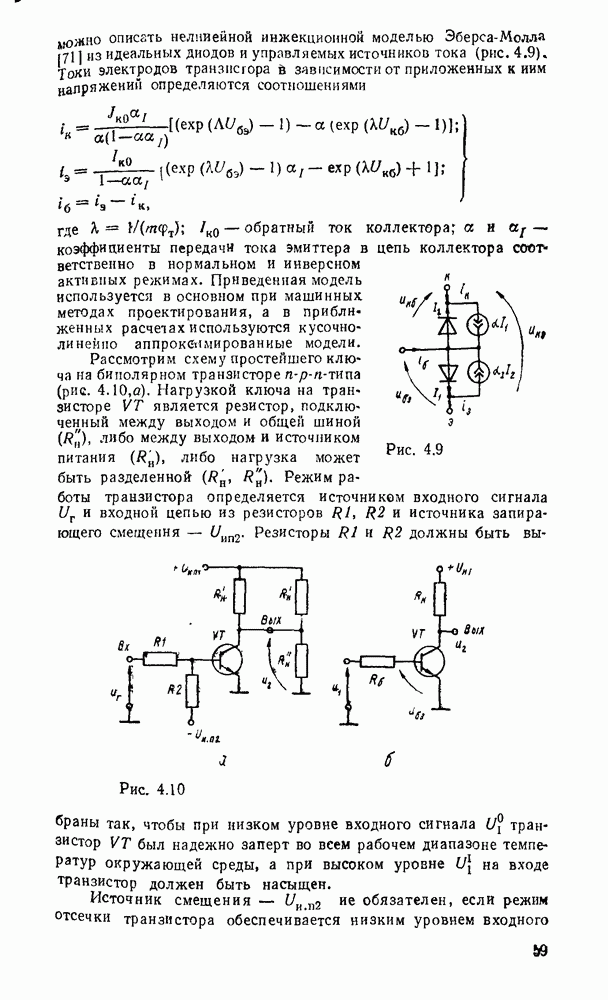
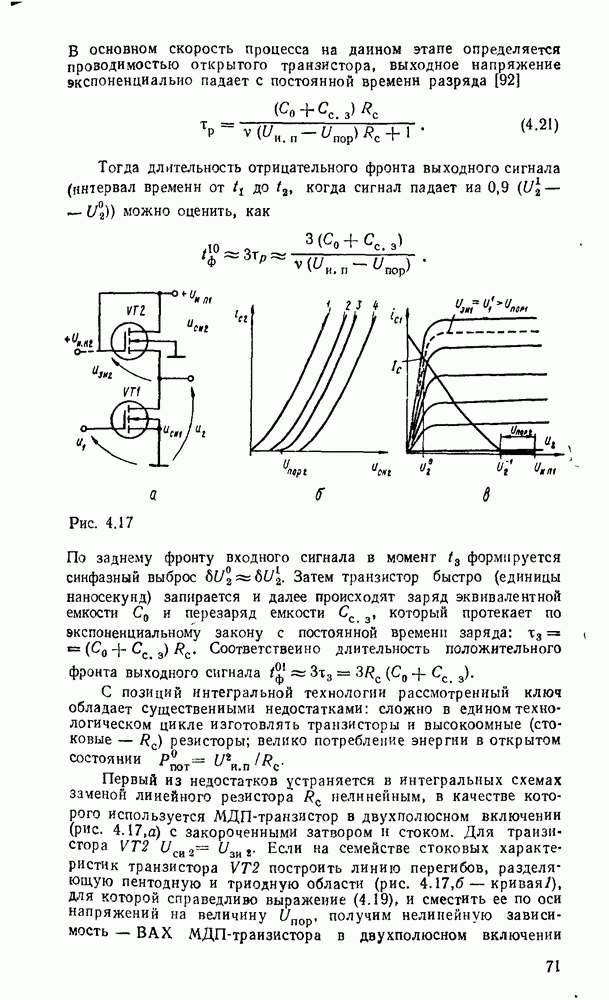
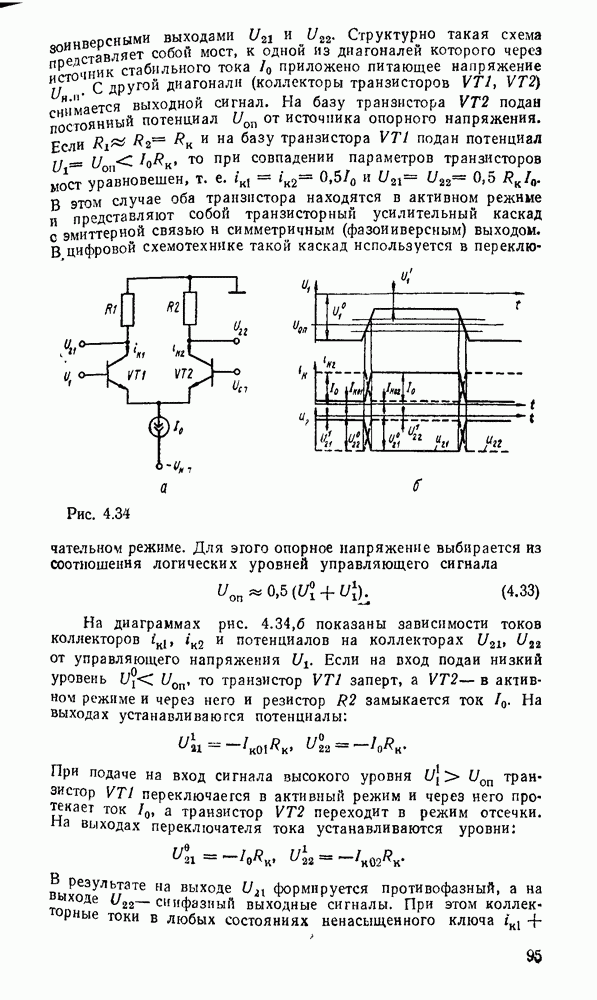
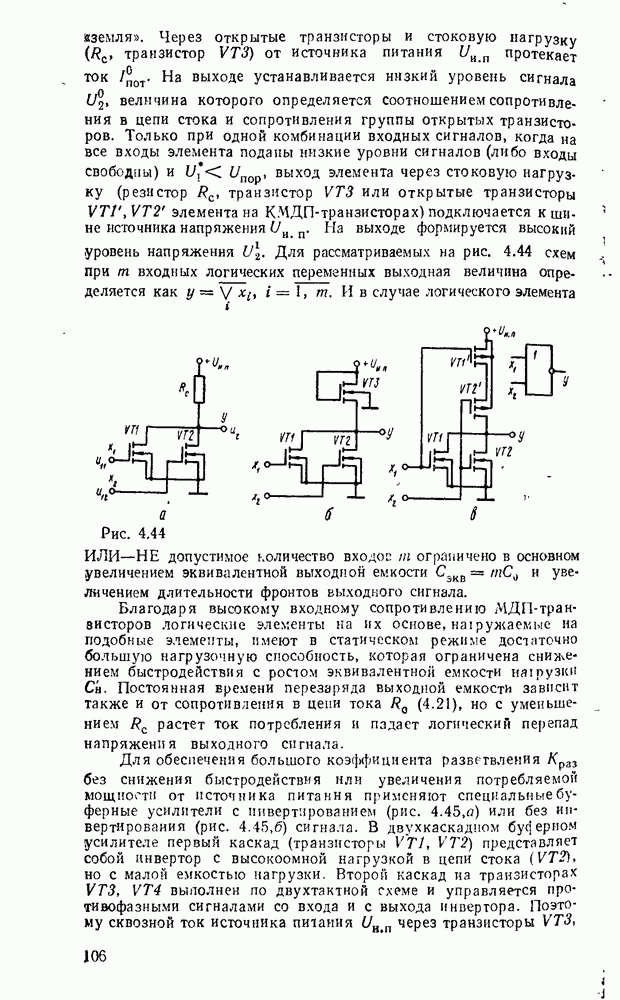
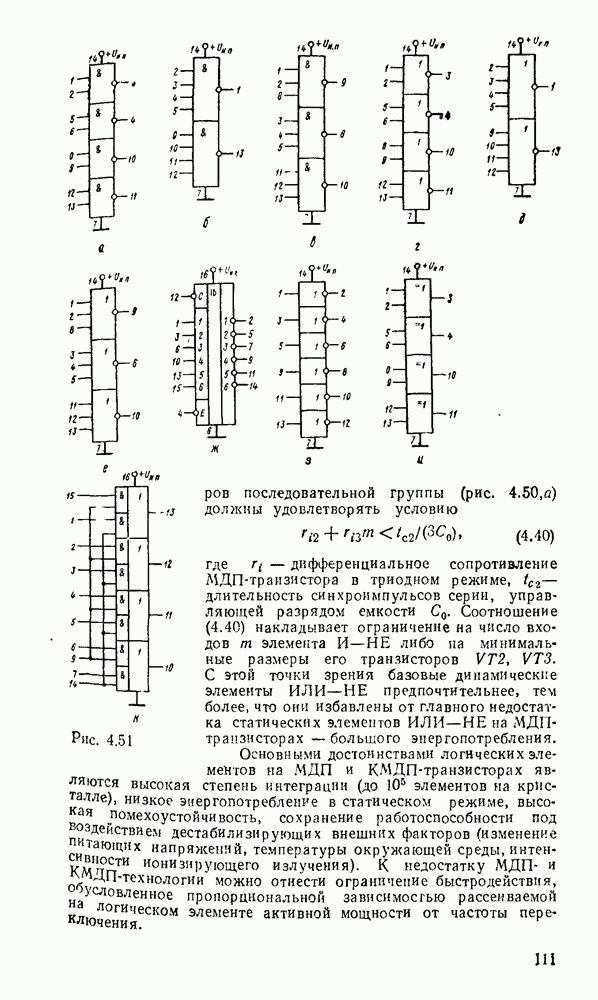
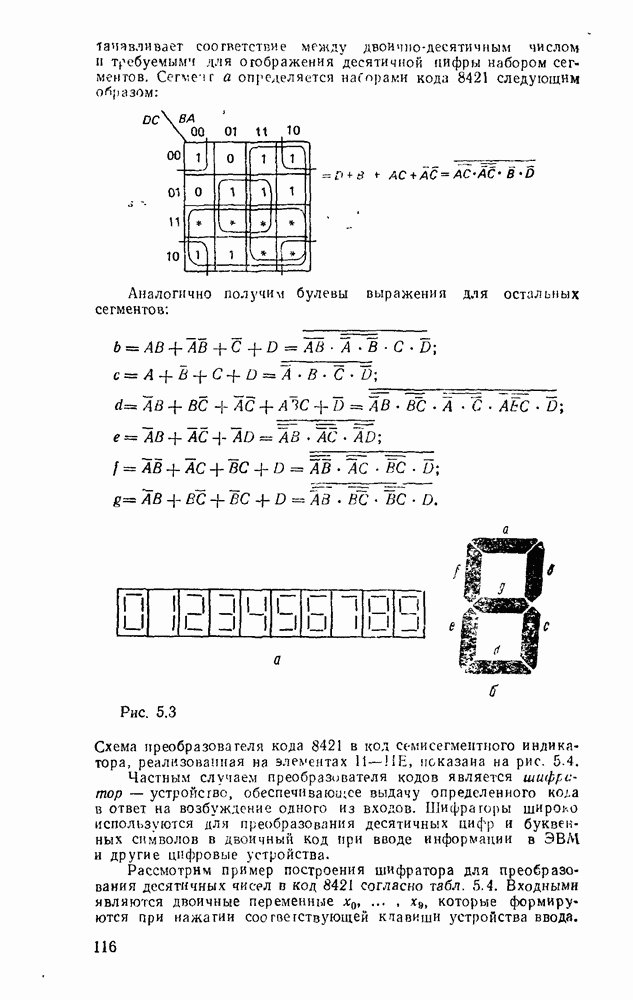
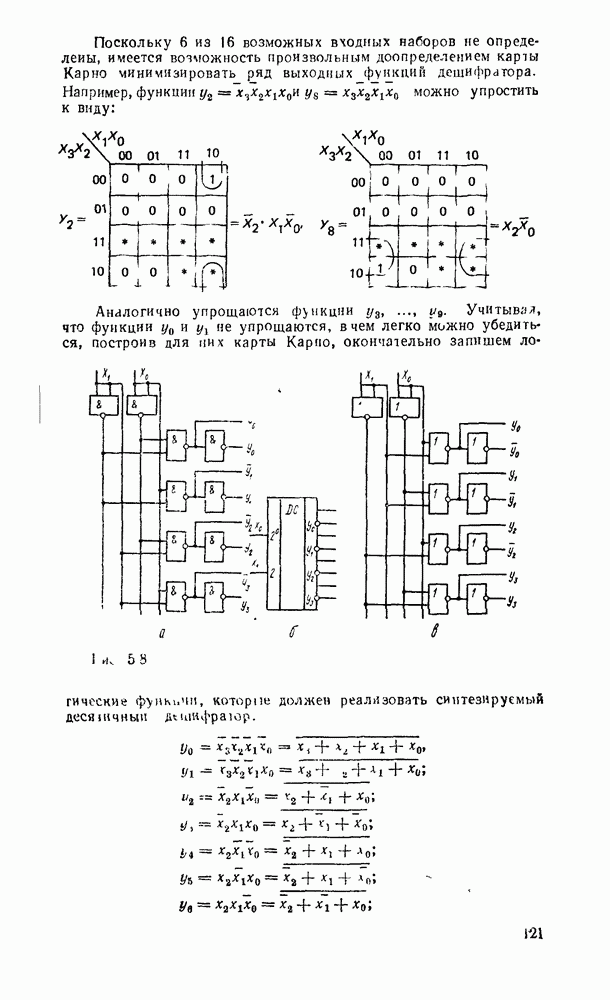
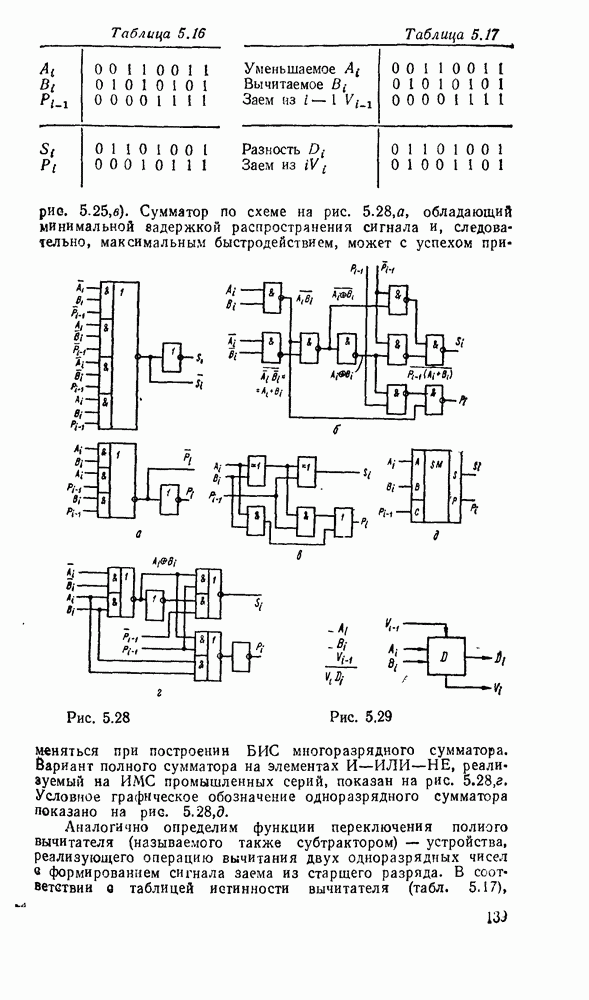
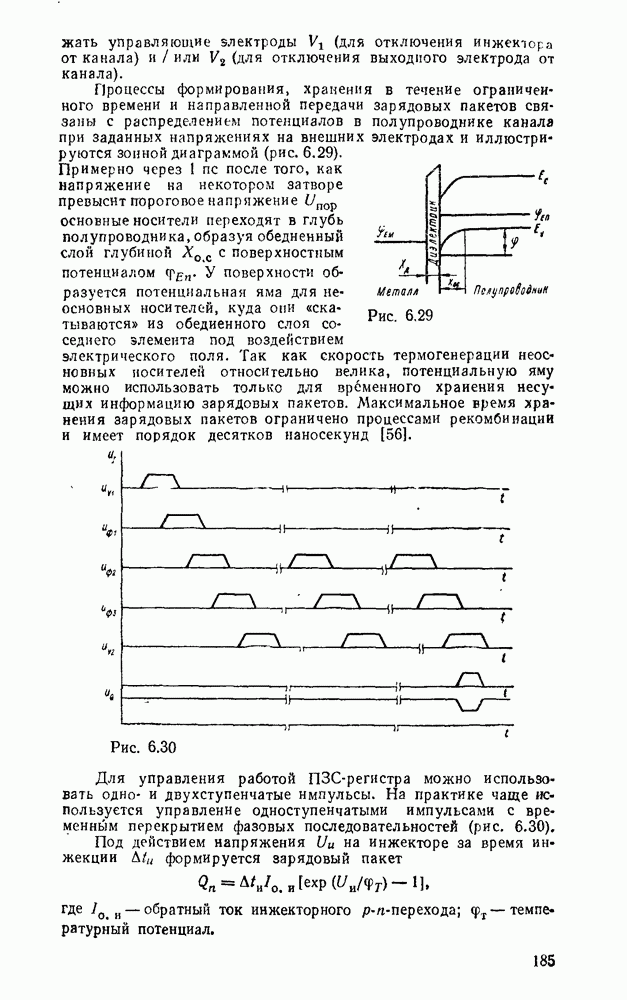
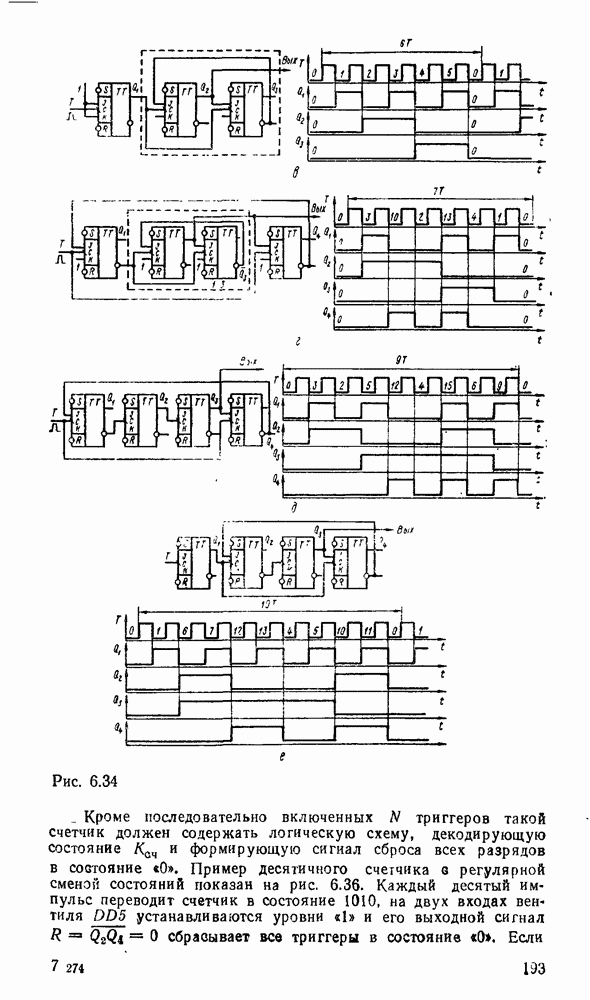
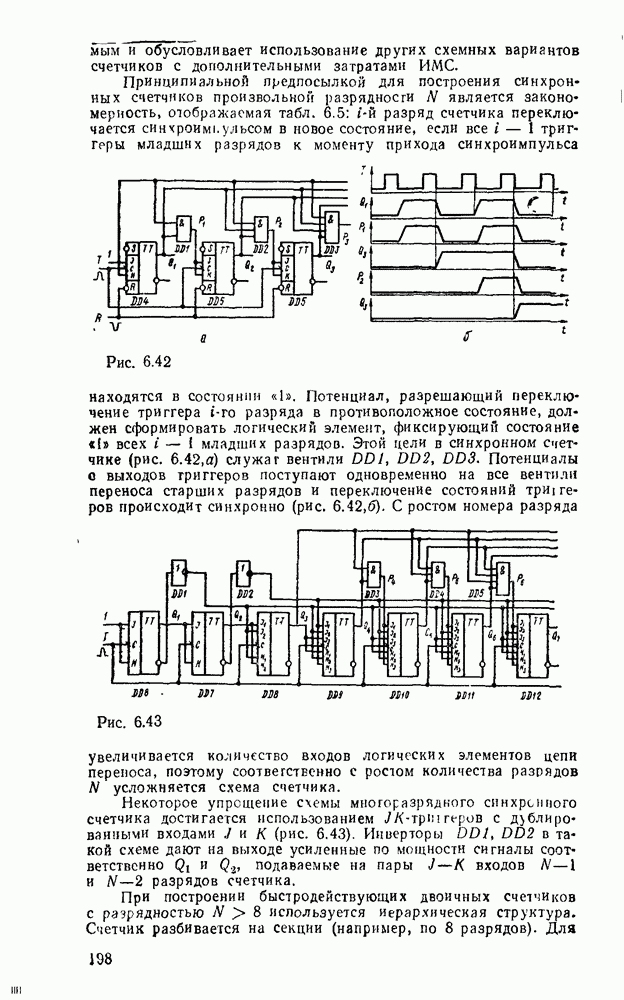
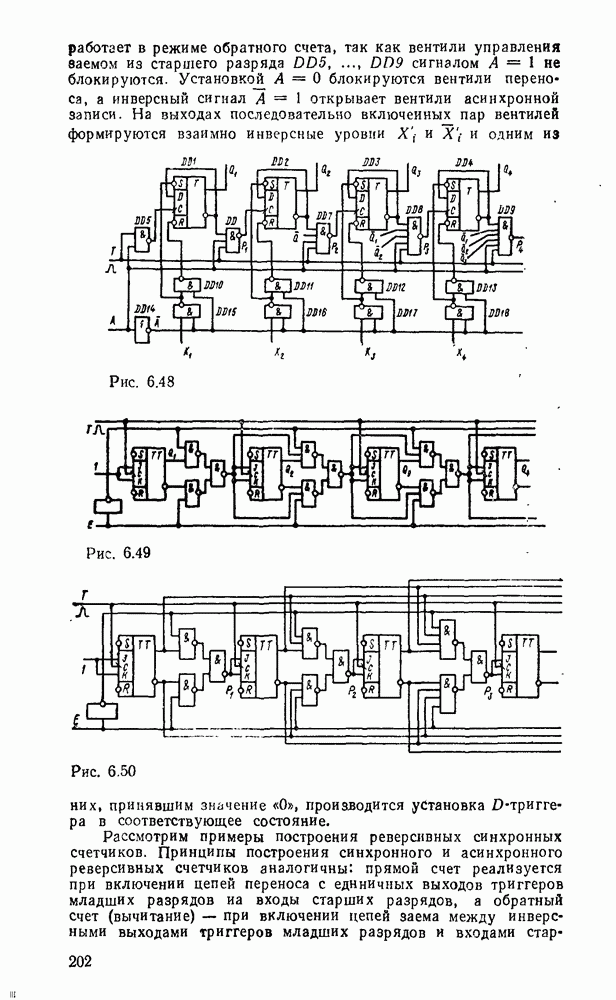
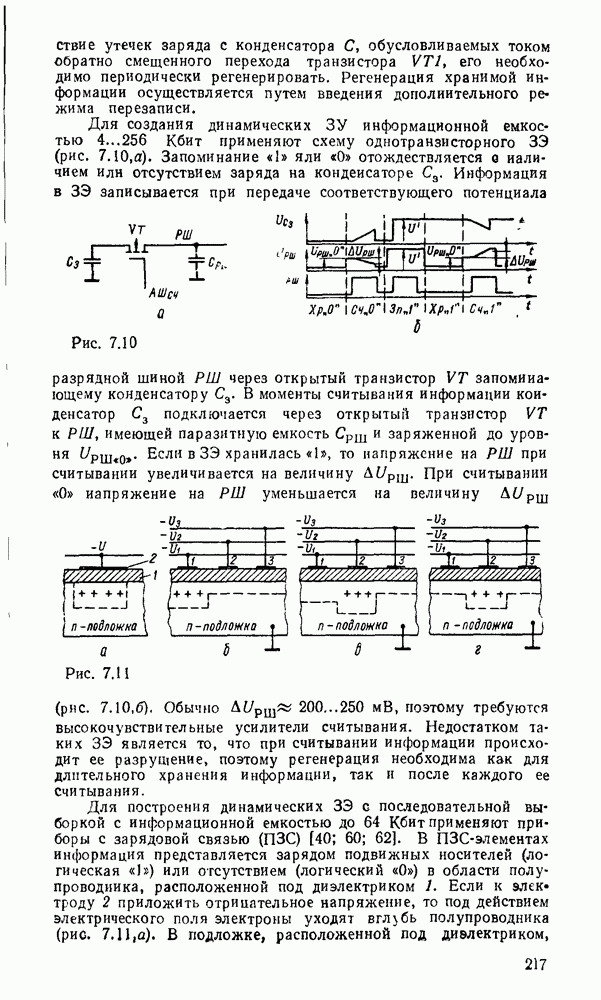
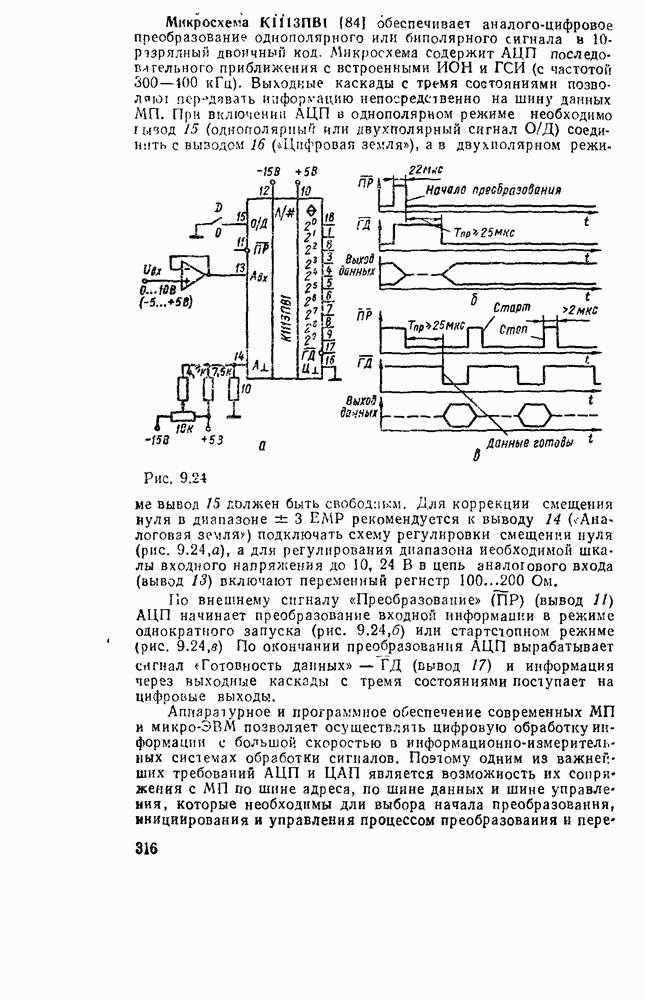
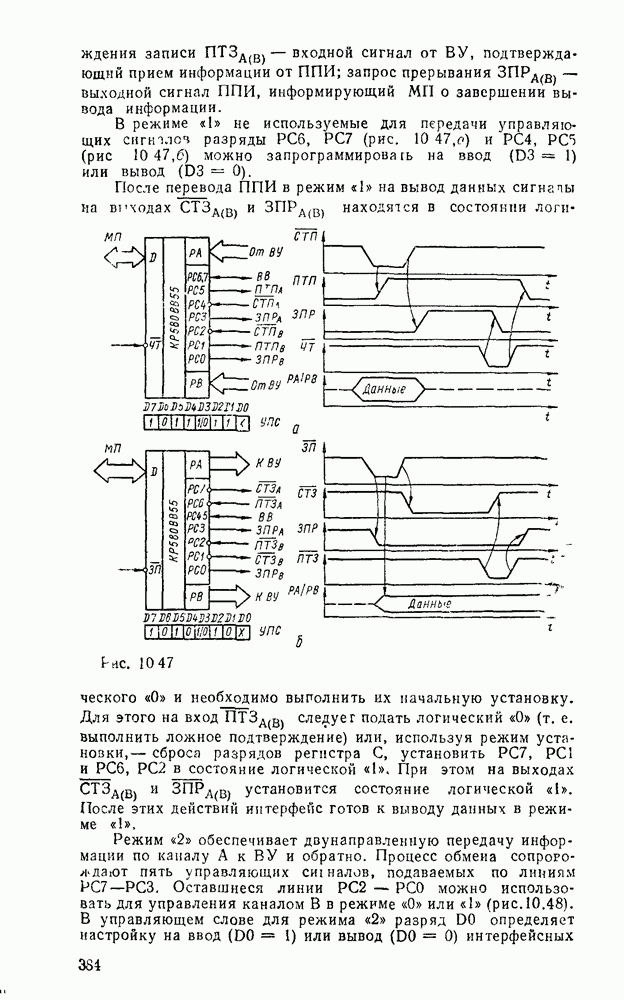
Рис. 9.1.
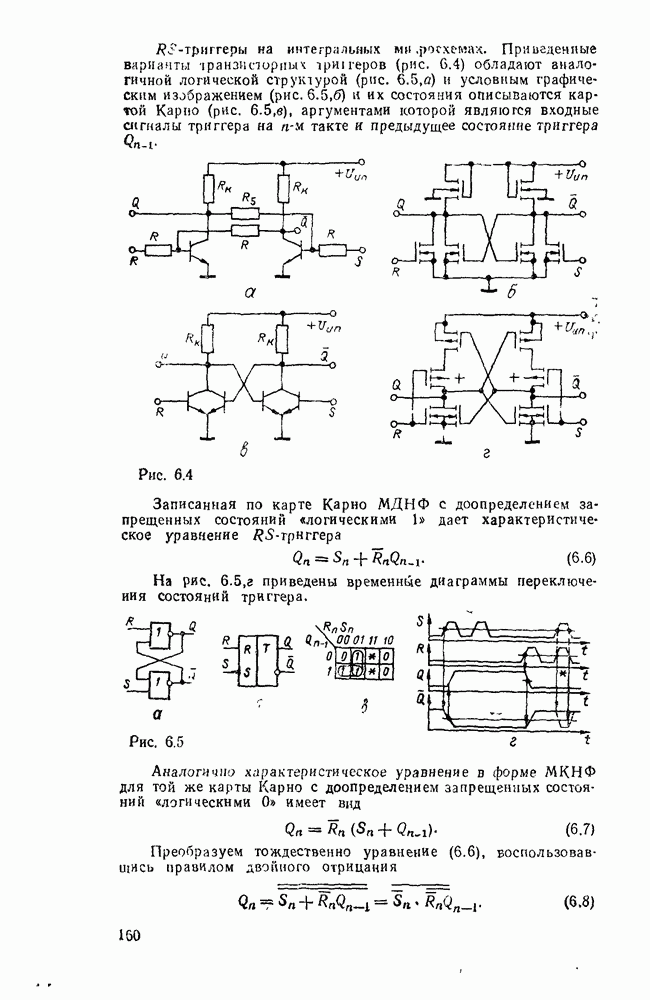
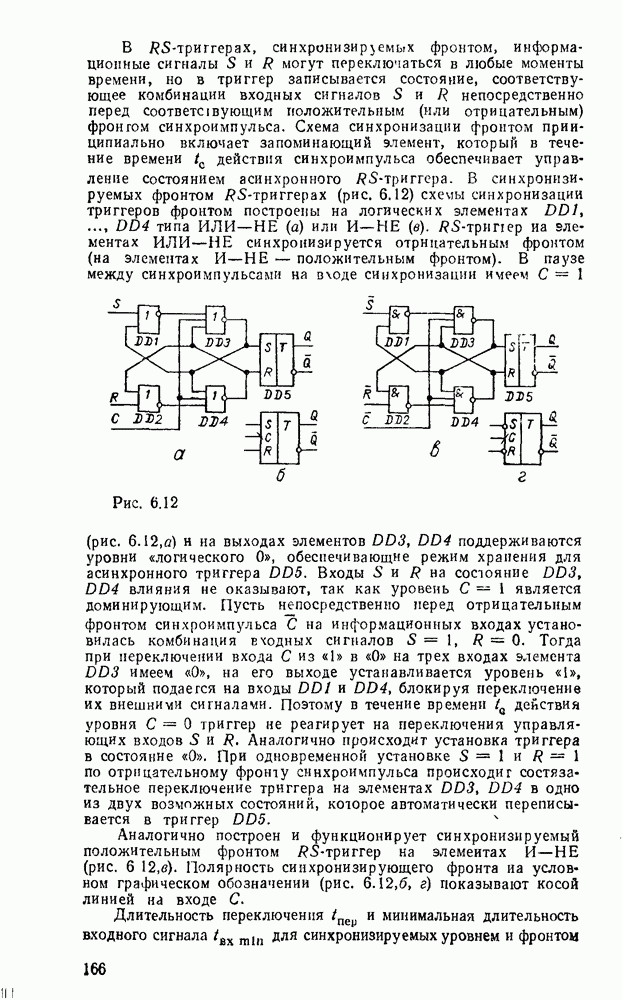
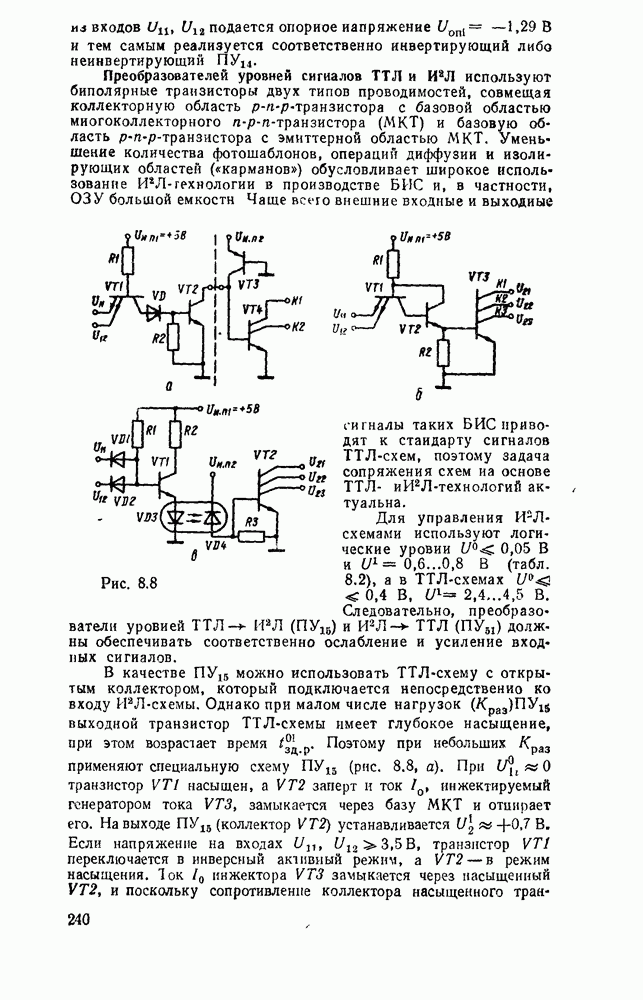
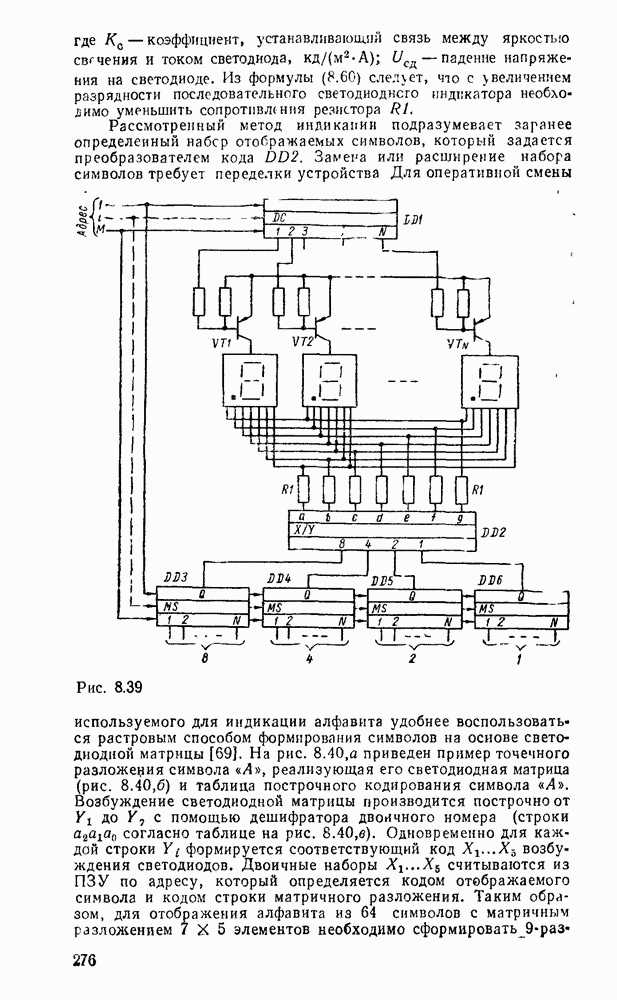
Дискретизацию сигнала по времени можно выполнить равномерно с посюянпым шагем  (рис. 9.1, а) и неравномерно с переменным шагом
(рис. 9.1, а) и неравномерно с переменным шагом  . Однако в дискретизированном сигнале отсутствуют промежуточные значения между моментами дискретизации
. Однако в дискретизированном сигнале отсутствуют промежуточные значения между моментами дискретизации  , поэтому во многих случаях необходимо восстановить в сигнале все промежуточные значения. При этом сигнал на интервале
, поэтому во многих случаях необходимо восстановить в сигнале все промежуточные значения. При этом сигнал на интервале  восстанавливается с заданной погрешностью.
восстанавливается с заданной погрешностью.
В качестве восстанавливающего сигнала используют сумму базисных функций

где  — коэффициенты ряда;
— коэффициенты ряда;  — система ортогональных базисных функций.
— система ортогональных базисных функций.
Коэффициенты ряда  и базисные функции СДО выбирают на основе критерия минимума средней квадратической погрешности восстановления или критерия совпадения восстанавливаемого сигнала с мгновенными значениями дискретизированного сигнала. Если коэффициенты ряда и базисные функции выбирают по критерию минимума средней квадратической погрешности восстановления
и базисные функции СДО выбирают на основе критерия минимума средней квадратической погрешности восстановления или критерия совпадения восстанавливаемого сигнала с мгновенными значениями дискретизированного сигнала. Если коэффициенты ряда и базисные функции выбирают по критерию минимума средней квадратической погрешности восстановления

то система базисных функций выбирается ортогональной, а коэффициенты ряда определяют как

При этом для периодических сигналов в качестве базисных функций можно использовать систему тригонометрических функций кратных аргументов  , ортогональную на интервале [0, Т).
, ортогональную на интервале [0, Т).
Если коэффициенты ряда и базисные функции выбирают по критерию совпадения в моменты дискретизации мгновенных Значений восстанавливаемого сигнала и мгновенных значений дискретизированного сигнала, то их параметры определяют путем решения системы уравнений

В случае, если сигнал  , обладающий спектром с граничной частотой
, обладающий спектром с граничной частотой  , дискретизирован циклически с периодом
, дискретизирован циклически с периодом  , то его можно восстановить с помощью ряда Котельникова
, то его можно восстановить с помощью ряда Котельникова

где  — функция отсчета, обладающая следующими свойствами: в моменты
— функция отсчета, обладающая следующими свойствами: в моменты  достигает максимума, равного 1; в моменты времени
достигает максимума, равного 1; в моменты времени  при
при  , равного любому целому числу, равна
, равного любому целому числу, равна  .
.
Однако реальные сигналы  всегда ограничены во времени и имеют бесконечный частотный спектр. Поэтому из-за ограничения верхней части спектра сигнала возникает погрешность восстановления. При этом относительное значение средней квадратической погрешности при восстановлении, возникающей в результате ограничения спектра сигнала частотой
всегда ограничены во времени и имеют бесконечный частотный спектр. Поэтому из-за ограничения верхней части спектра сигнала возникает погрешность восстановления. При этом относительное значение средней квадратической погрешности при восстановлении, возникающей в результате ограничения спектра сигнала частотой  , можно определить из следующего неравенства [58]:
, можно определить из следующего неравенства [58]:

где  — энергия погрешности сигнала, возникающая из-за ограничения спектра;
— энергия погрешности сигнала, возникающая из-за ограничения спектра;  — полная энергия сигнала;
— полная энергия сигнала;  — частотней спектр сигнала.
— частотней спектр сигнала.
В качестве базисных функций при восстановлении сигнала часто используют степенной полином  , где
, где  — полином
— полином  степени от
степени от  .
.
При восстановлении (аппроксимации) сигнала  на каждом участке между моментами дискретизации
на каждом участке между моментами дискретизации  базисная функция
базисная функция  изменяется по определенному закону (например, горизонтальной прямой при использовании степенного полинома нулевого порядка, отрезком наклонной прямой — первого порядка и участком параболы — второго порядка). Погрешность восстановления (аппроксимации)
изменяется по определенному закону (например, горизонтальной прямой при использовании степенного полинома нулевого порядка, отрезком наклонной прямой — первого порядка и участком параболы — второго порядка). Погрешность восстановления (аппроксимации)  зависит от зпкона изменения
зависит от зпкона изменения  , способа аппроксимации и шага дискретизации. Шаг дискретизации Т а следовательно, частоту дискретизации
, способа аппроксимации и шага дискретизации. Шаг дискретизации Т а следовательно, частоту дискретизации  определяют по заданной погрешности восстановления (аппроксимации).
определяют по заданной погрешности восстановления (аппроксимации).
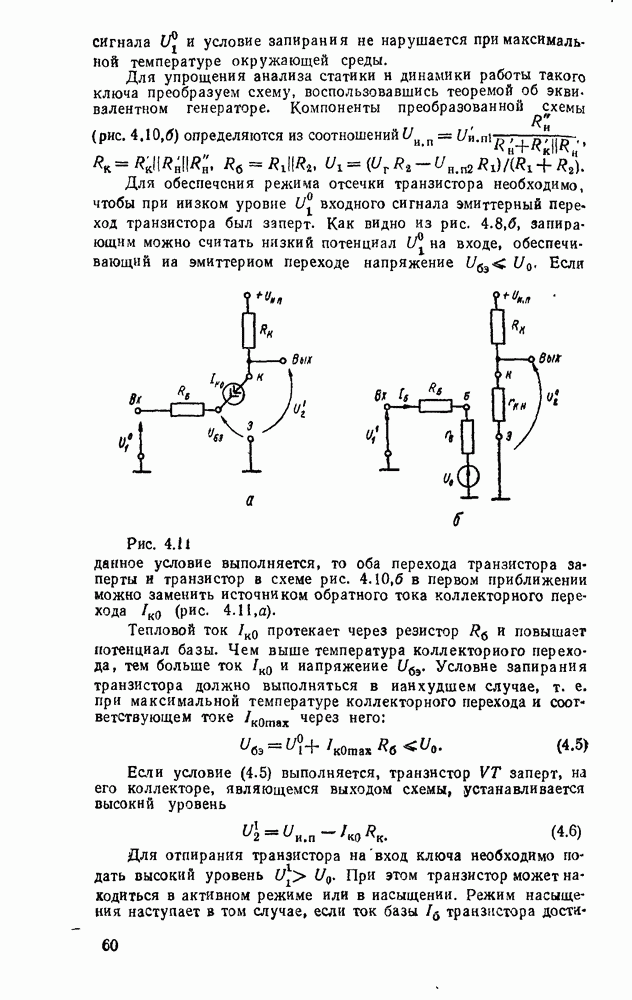
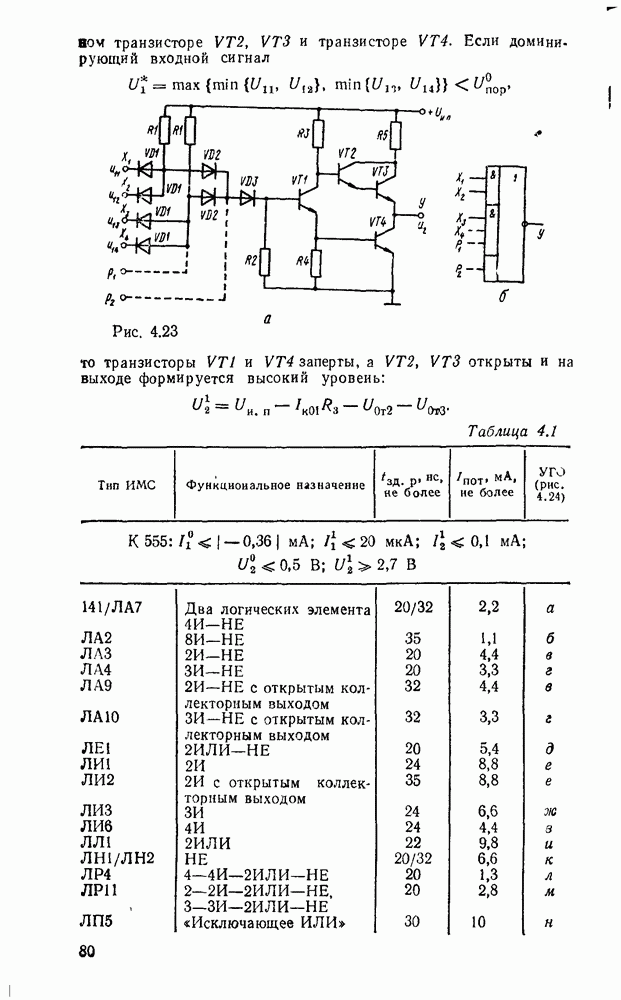
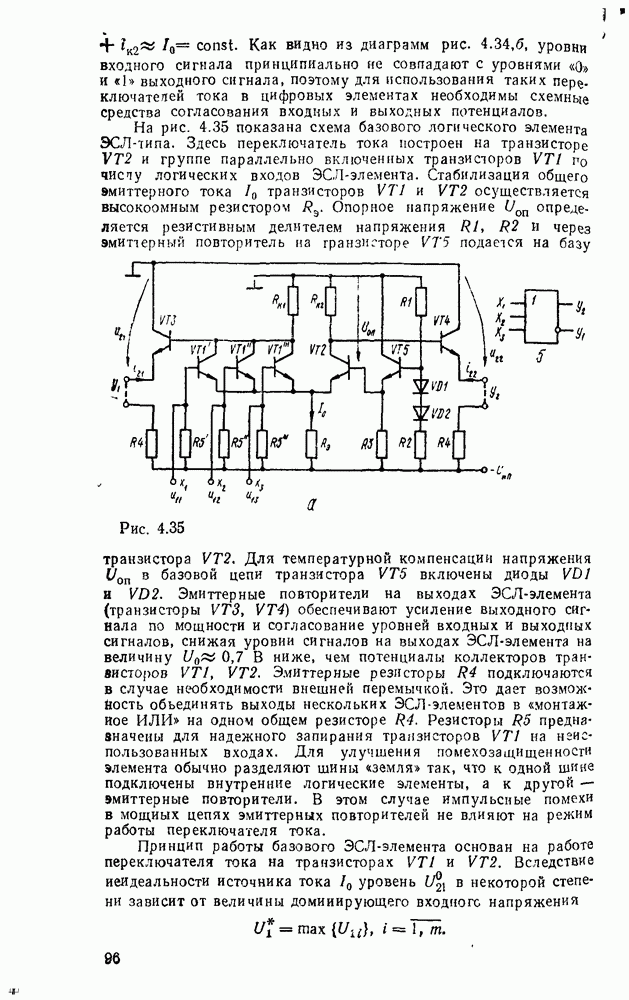
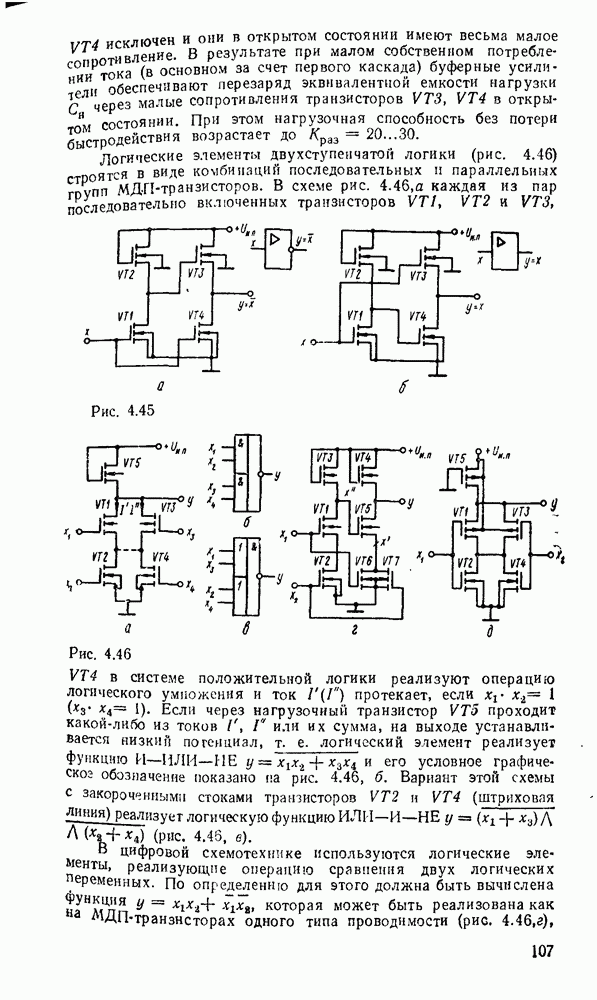
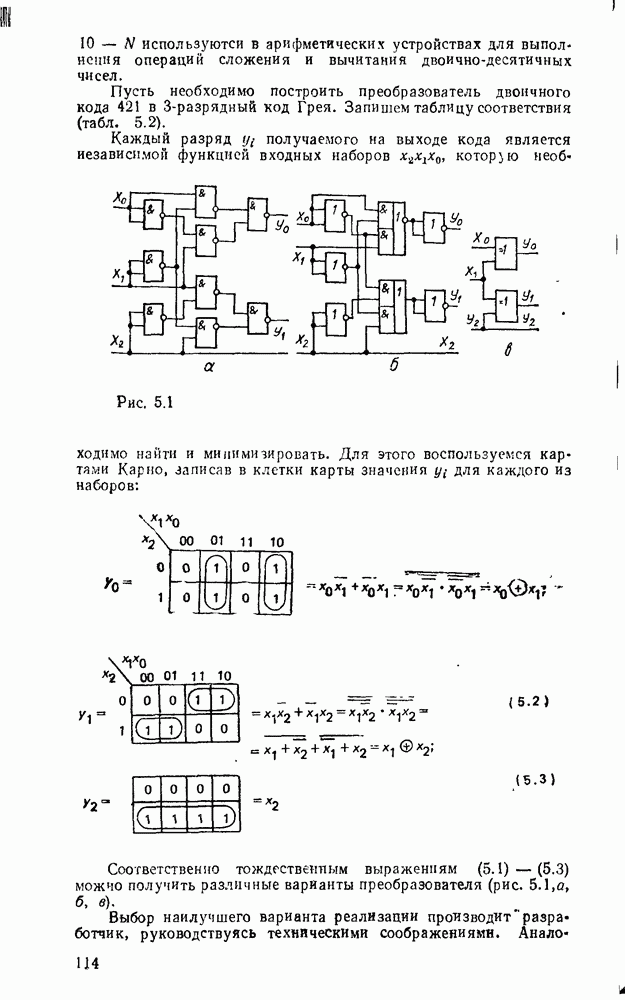
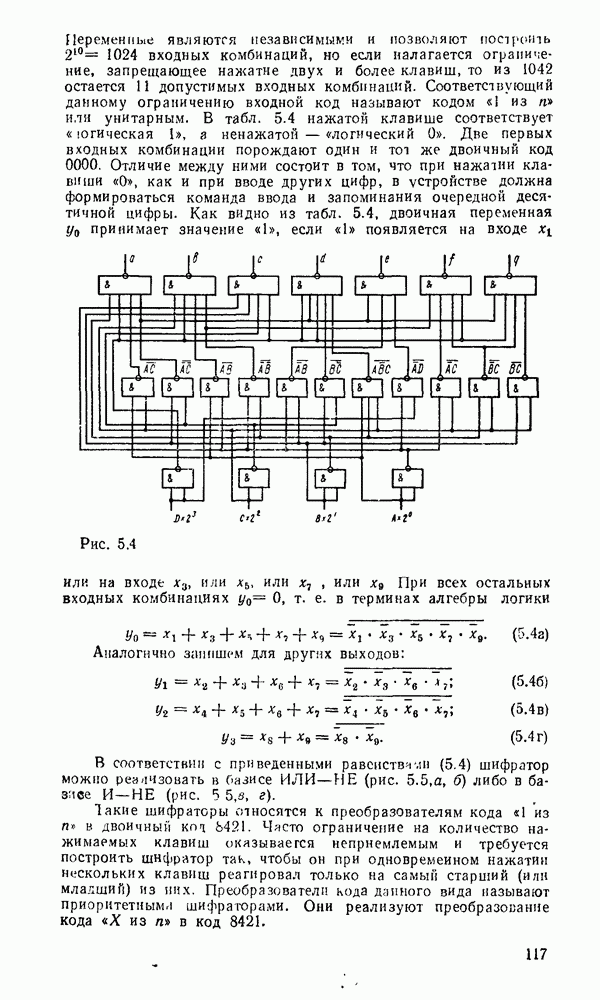
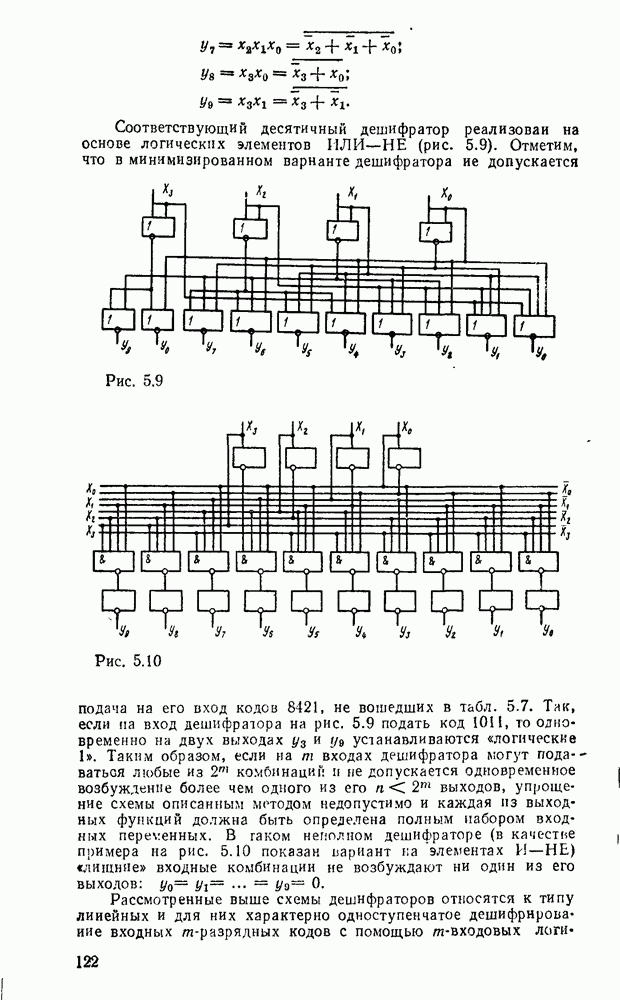
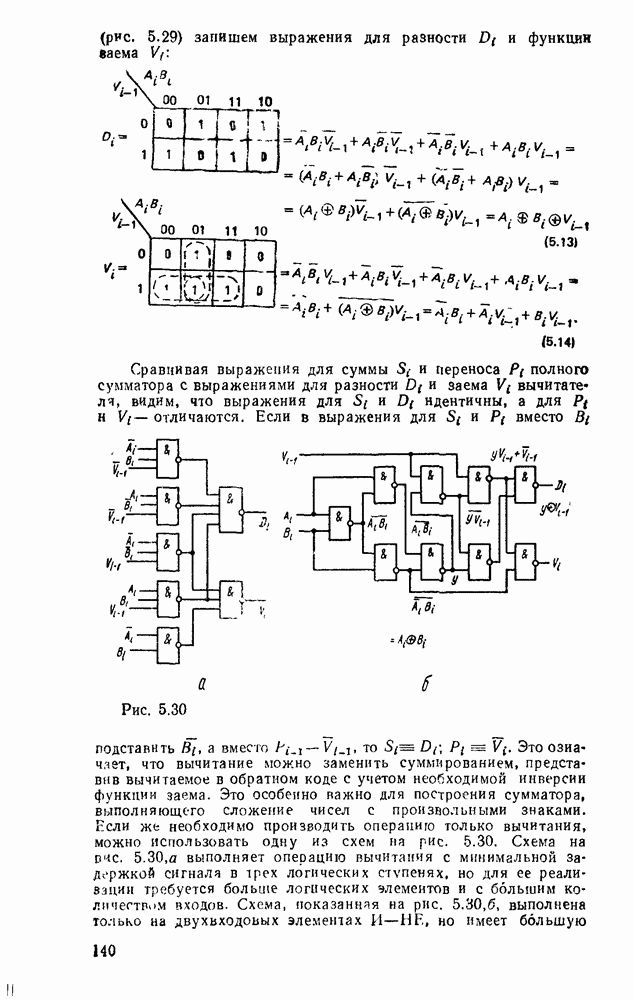
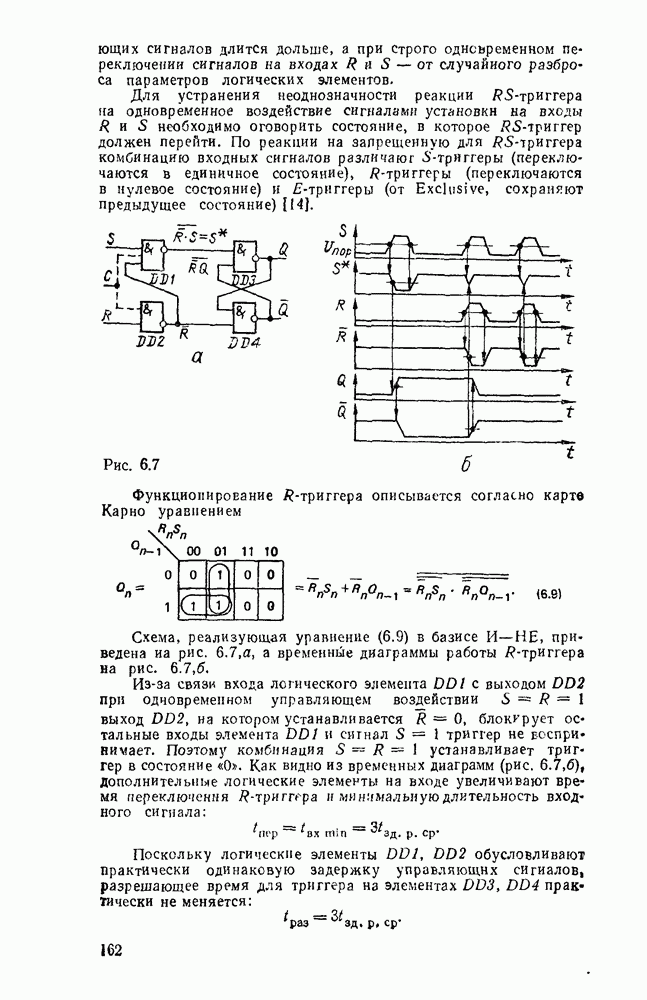
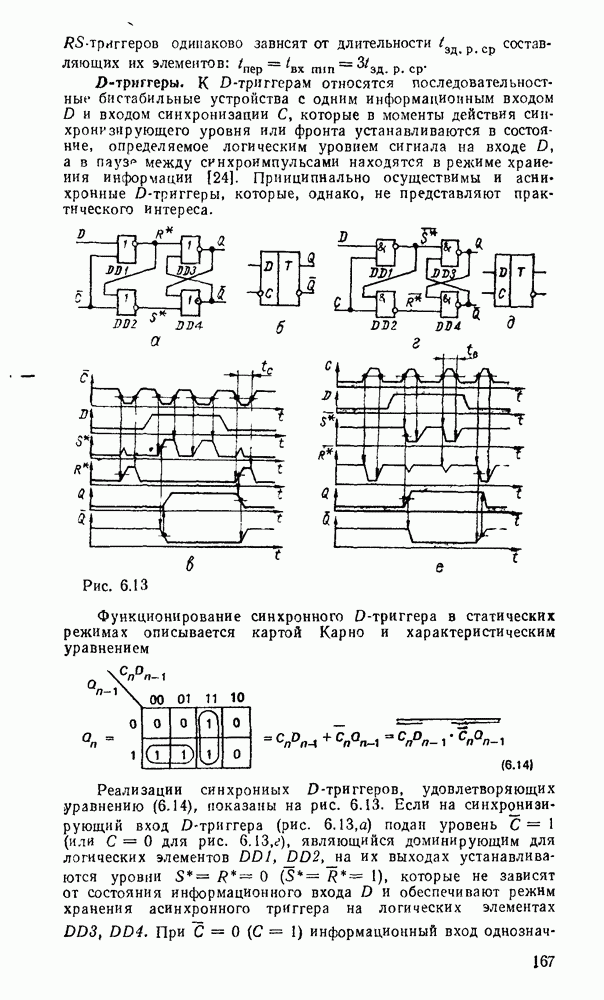
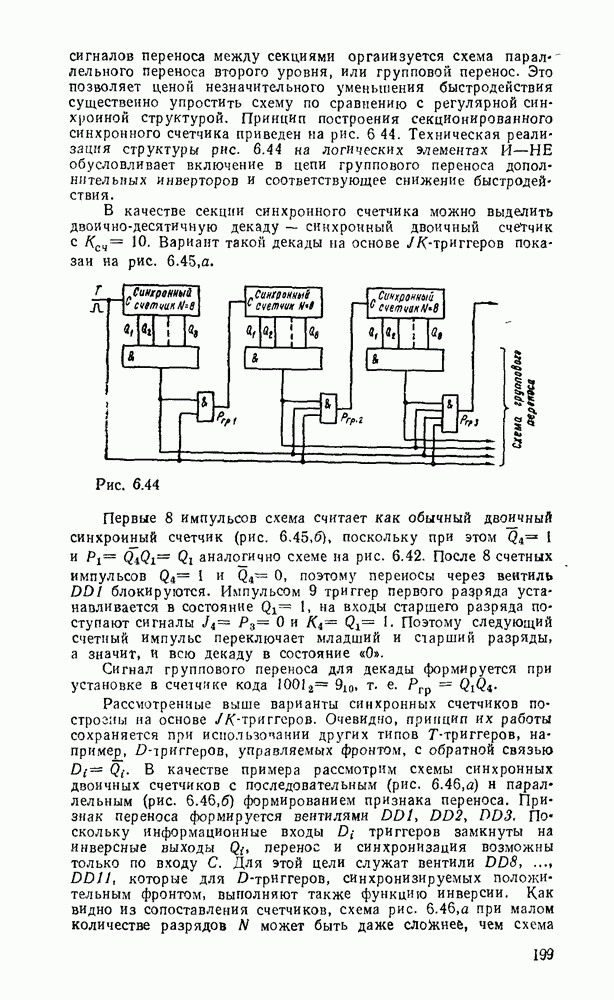
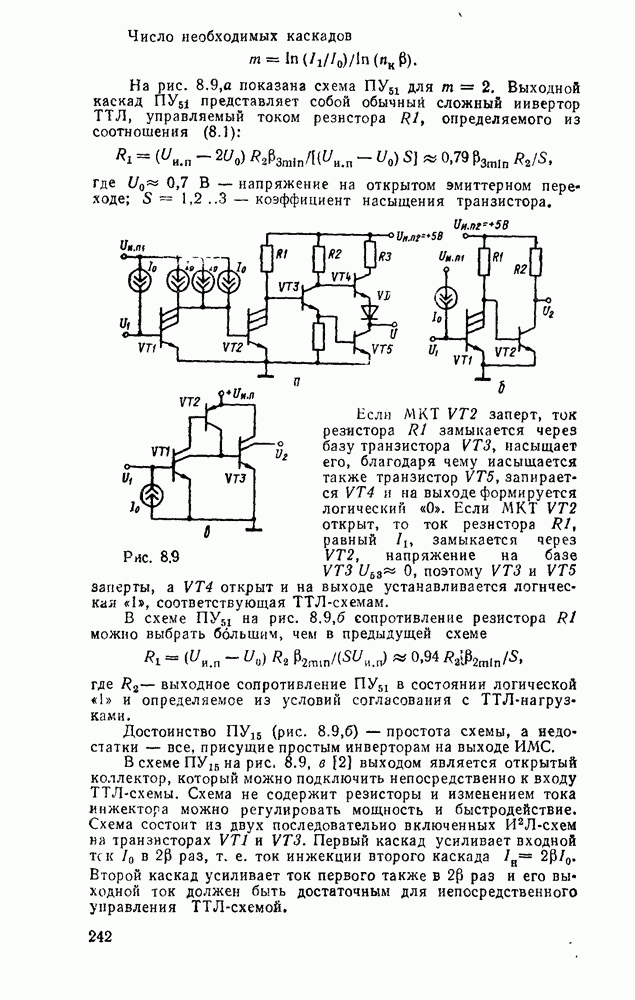
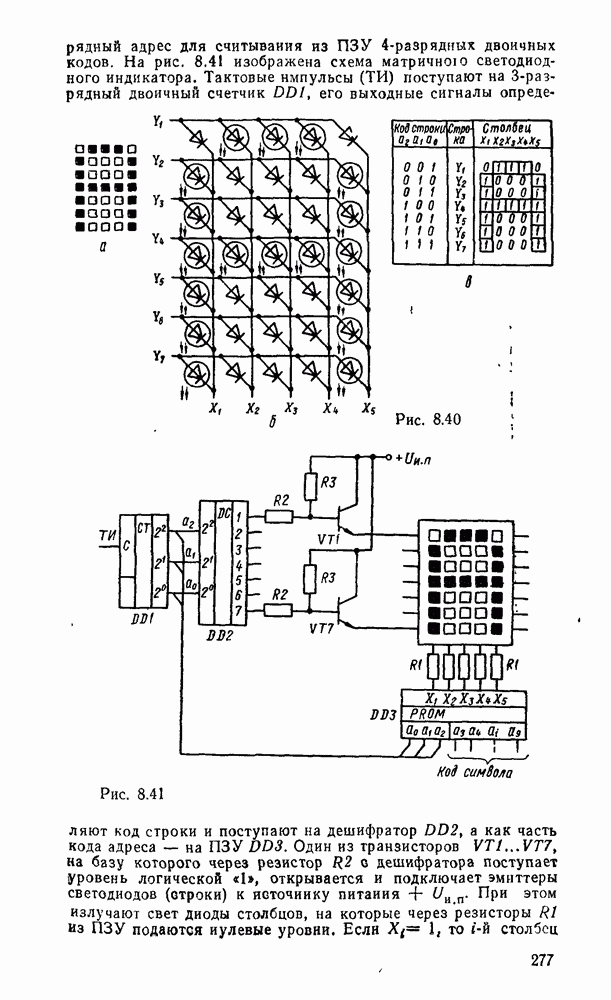
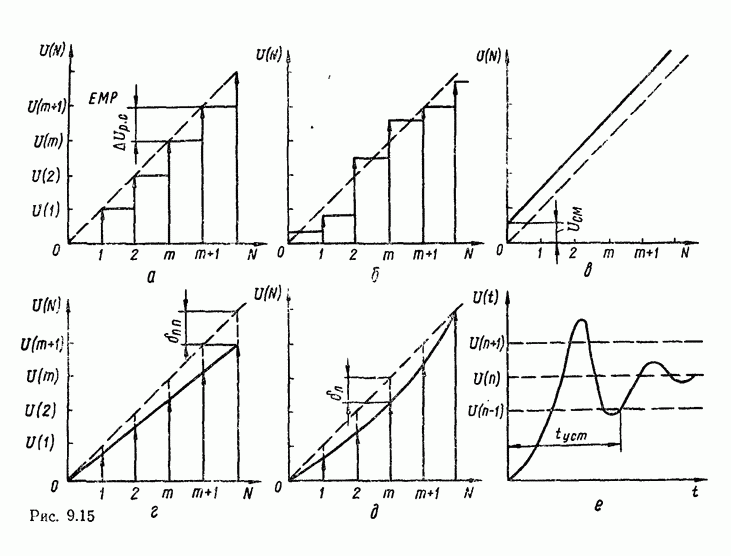
В случае использования степенных полиномов нулевого порядка  (ступенчатая аппроксимация, рис.
(ступенчатая аппроксимация, рис.  )
)  , тогда восстанавливаемый сигнал
, тогда восстанавливаемый сигнал

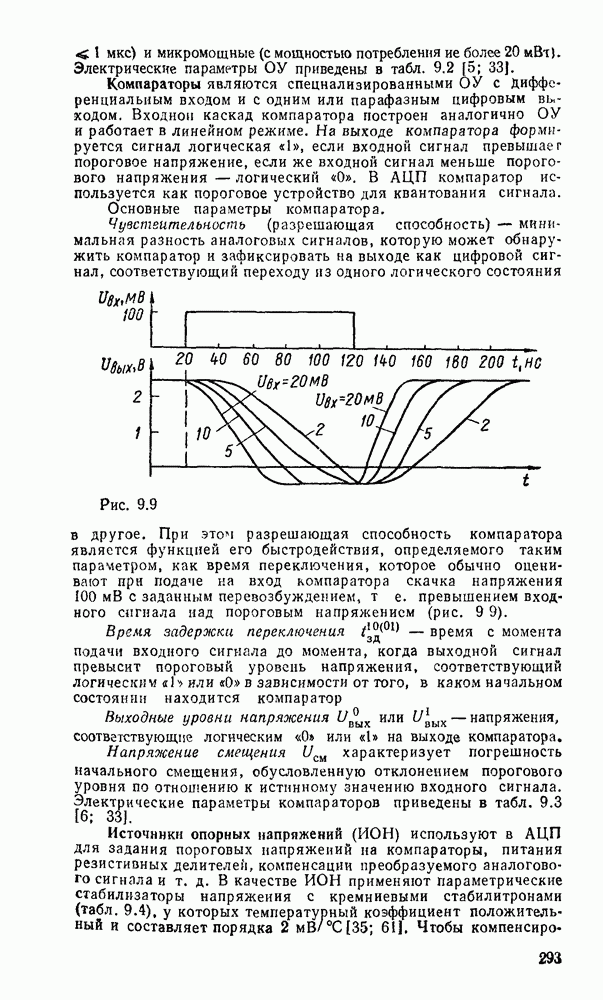
Максимальная погрешность аппроксимации в этом случае будет на участке сигнала, где первая производная  достигнет наибольшего значения
достигнет наибольшего значения


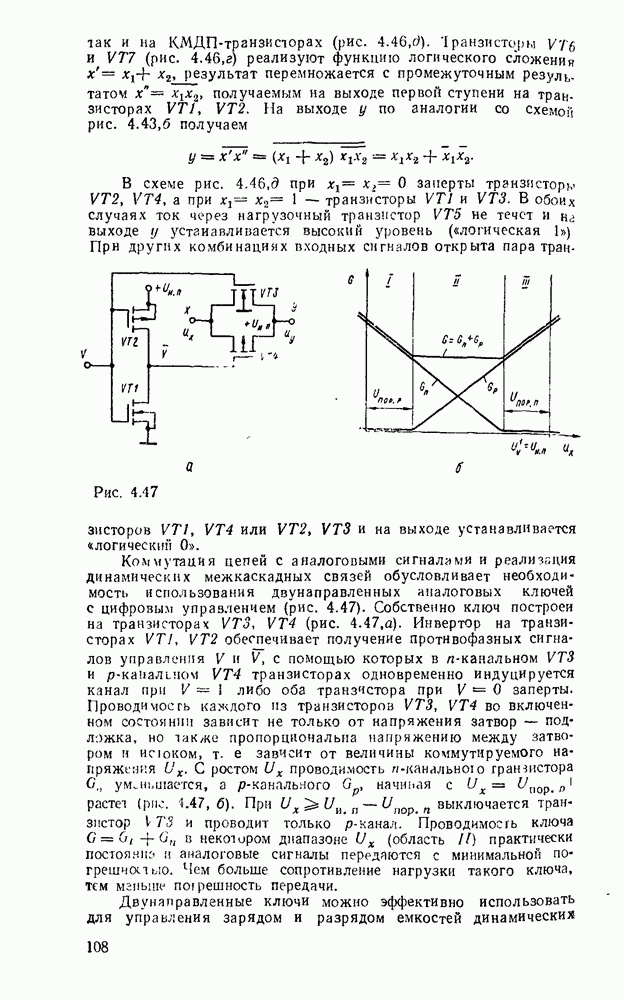
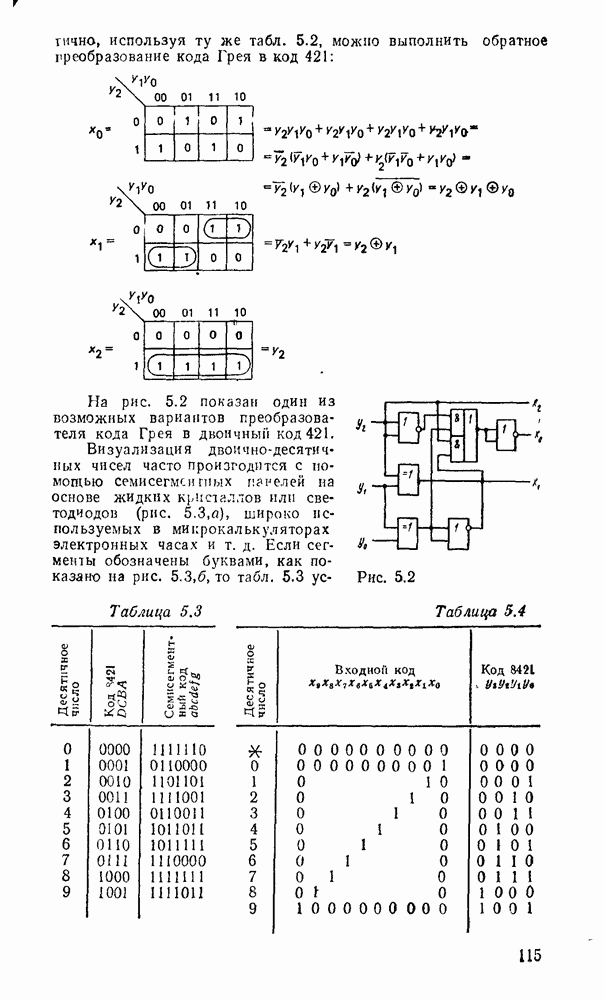
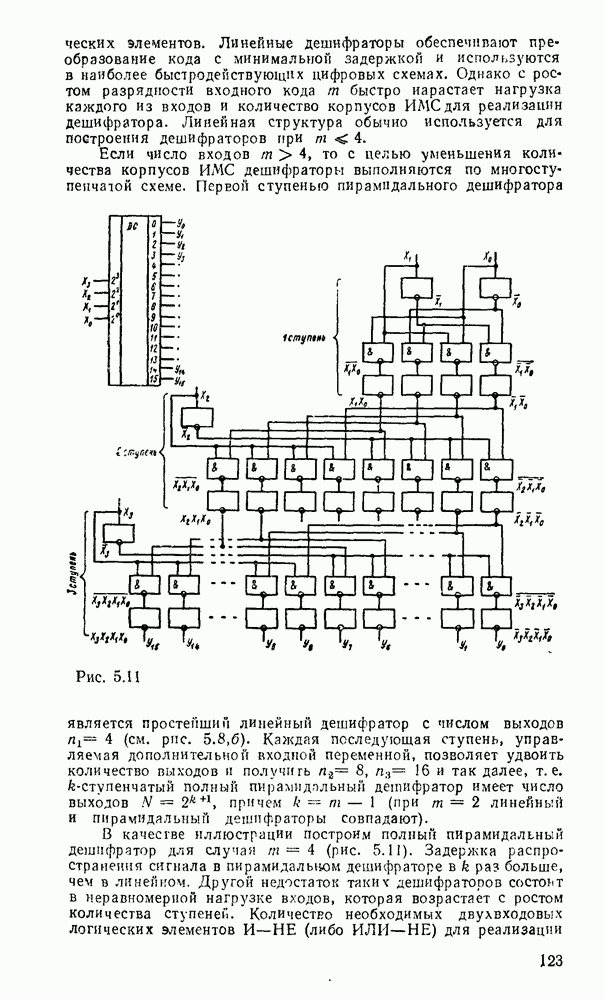
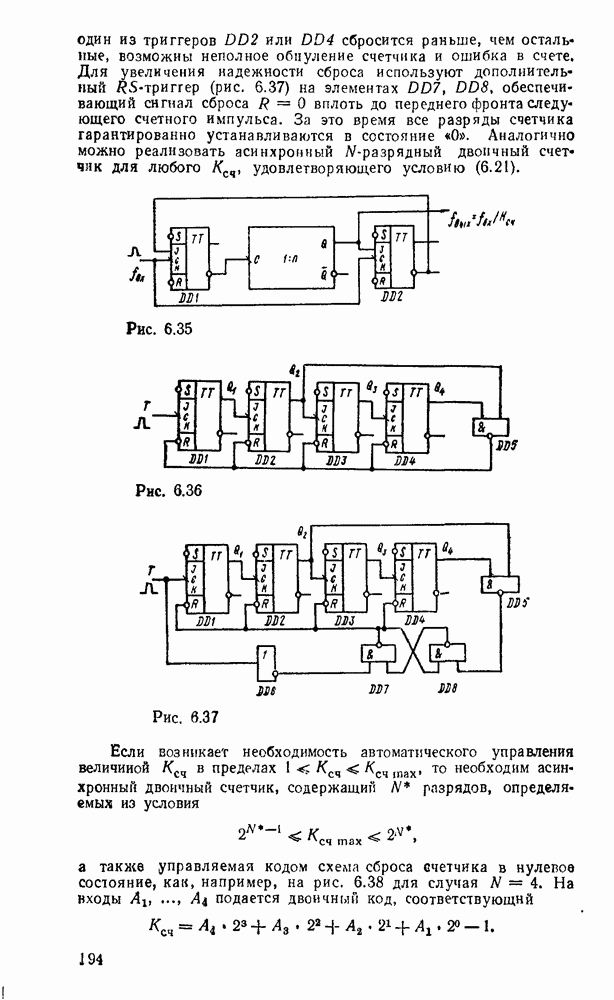
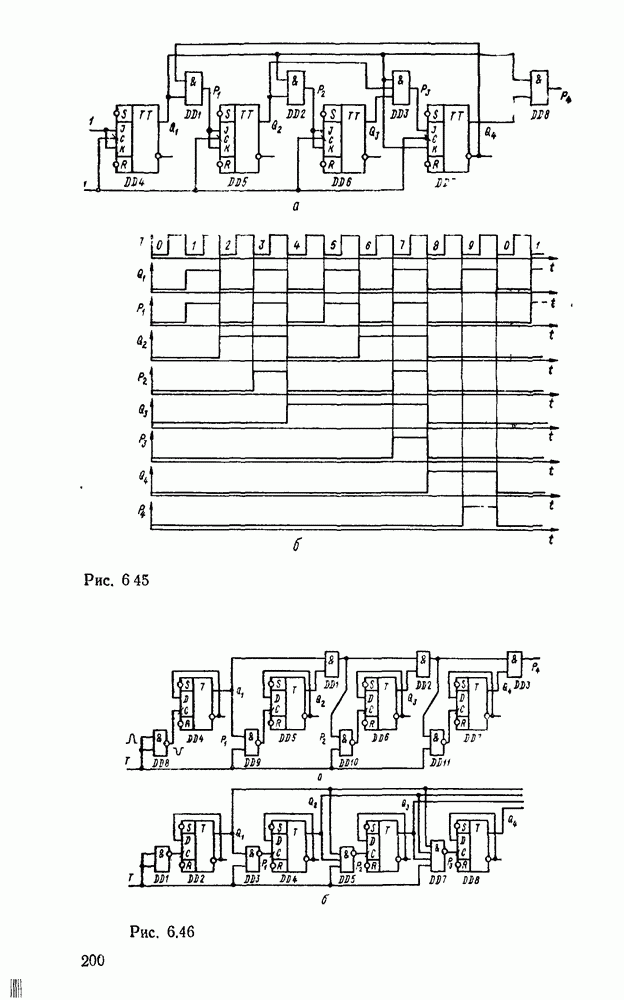
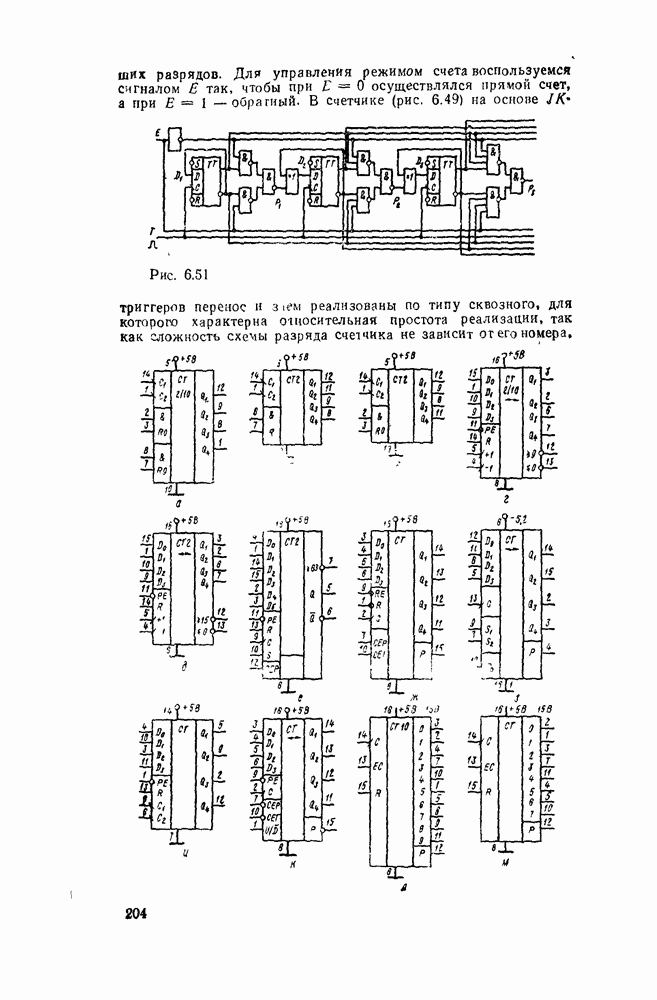
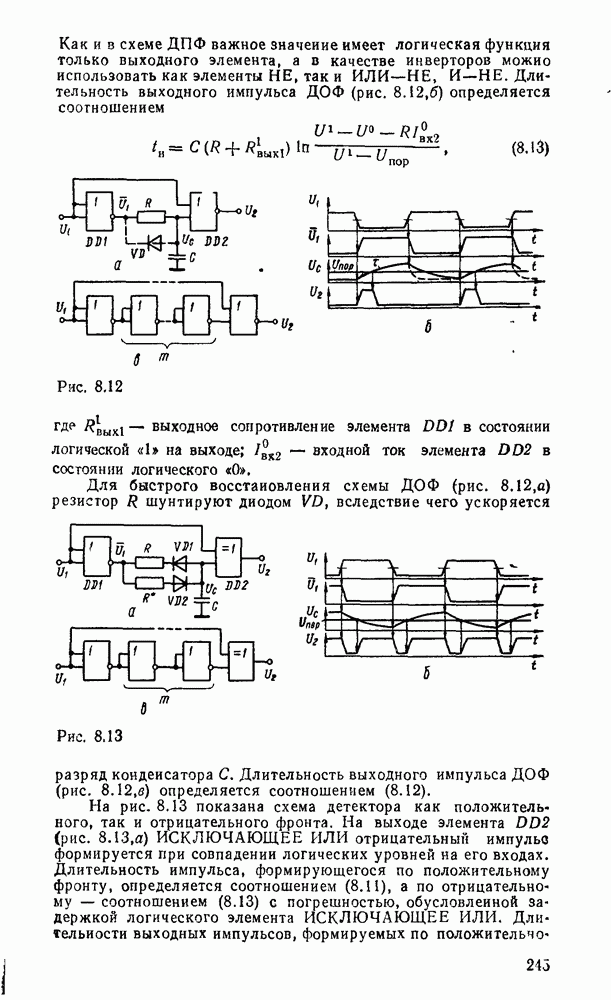
Рис. 9.2.
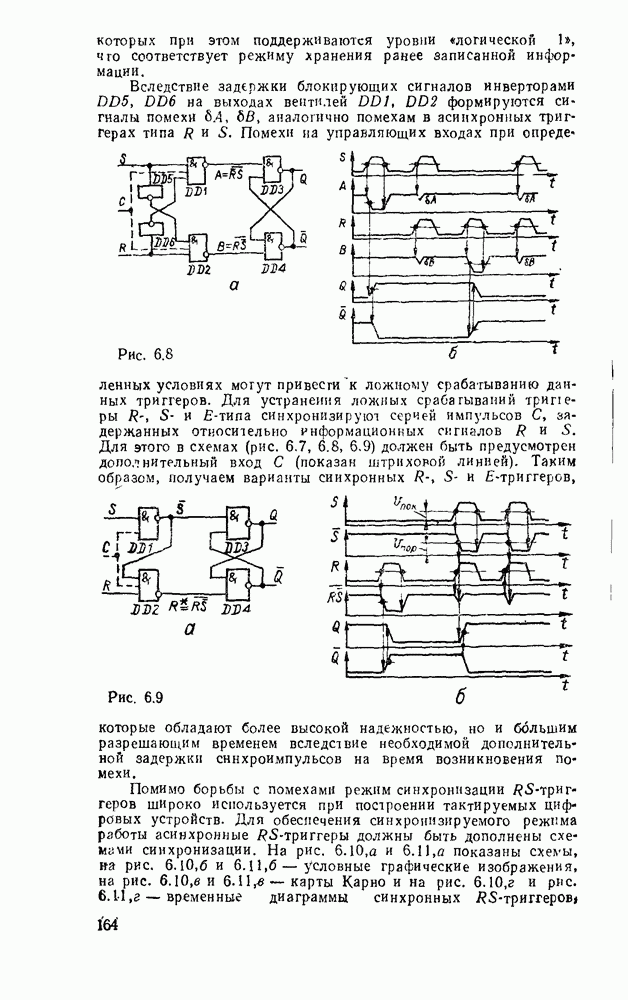
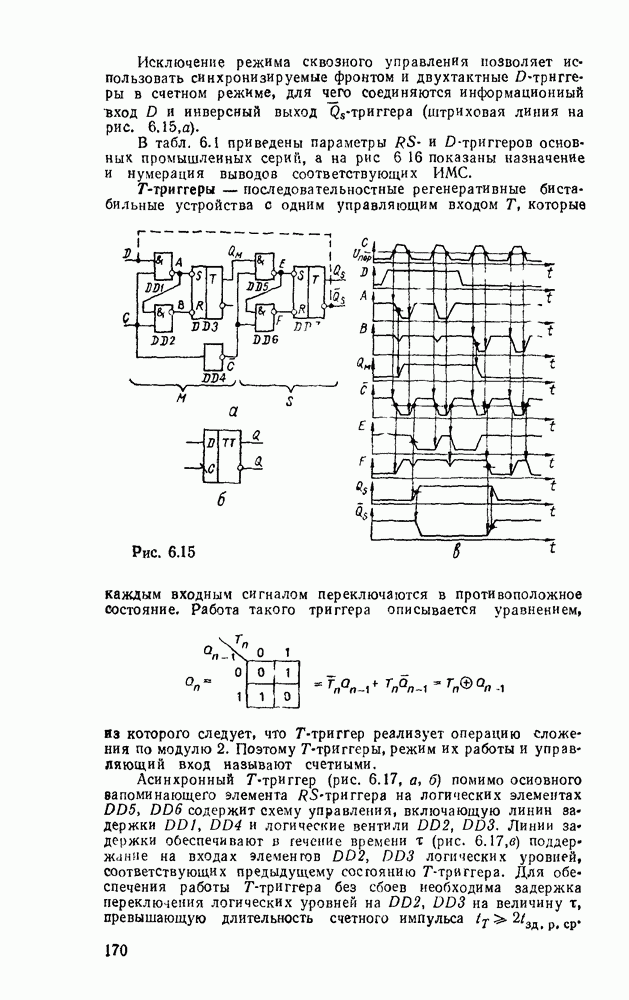
При использовании степенных полиномов первого порядка  (кусочно-линейиая аппроксимация, рис.
(кусочно-линейиая аппроксимация, рис.  ) восстанавливаемый сигнал имеет вид
) восстанавливаемый сигнал имеет вид

Погрешность аппроксимации при этом будет наибольшей на тех участках изменения сигнала, где вторая производная  достигает наибольшего значения
достигает наибольшего значения

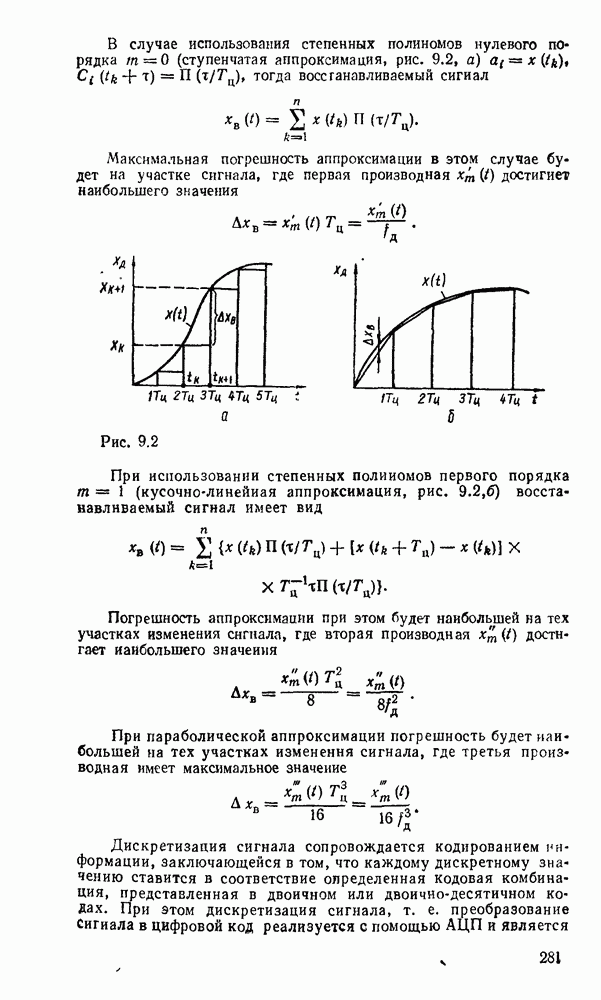
При параболической аппроксимации погрешность будет наибольшей на тех участках изменения сигнала, где третья производная имеет максимальное значение

Дискретизация сигнала сопровождается кодированием информации, заключающейся в том, что каждому дискретному значению ставится в соответствие определенная кодовая комбинация, представленная в двоичном или двоично-десятичном кодах. При этом дискретизация сигнала, т. е. преобразование Сигнала в цифровой код реализуется с помощью АЦП и является измерительным процессом, состоящим из ряда операций сравнения измеряемой величины с набором эталонных дискретных величин.
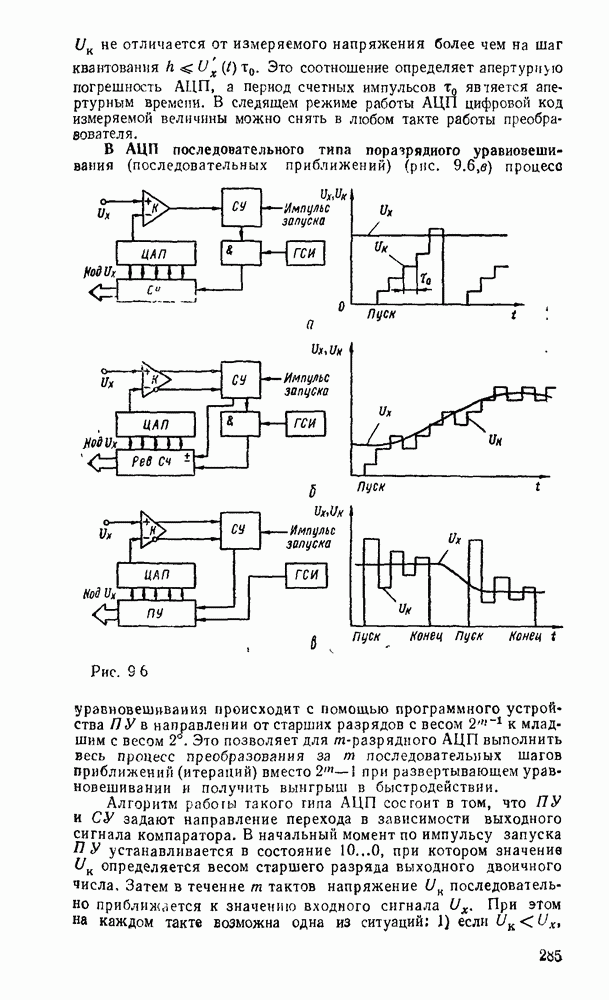
В АЦП аналоговая величина поступает на вход сравнивающего устройства, на второй вход которого в определенной последовательности подаются величины одинаковой природы с измеряемой величиной, вырабатываемые блоком эталонных величин (преобразование вида код — аналог, осуществляемое с помощью ЦАП). Сравнивающее устройство вырабатывает последовательность кодовых комбинаций, являющихся результатом сравнения измеряемой величины с эталонной и используемых для управления цифровым автоматом. При этом состояние цифрового автомата в конце преобразования определяет цифровой код измерительной величины.
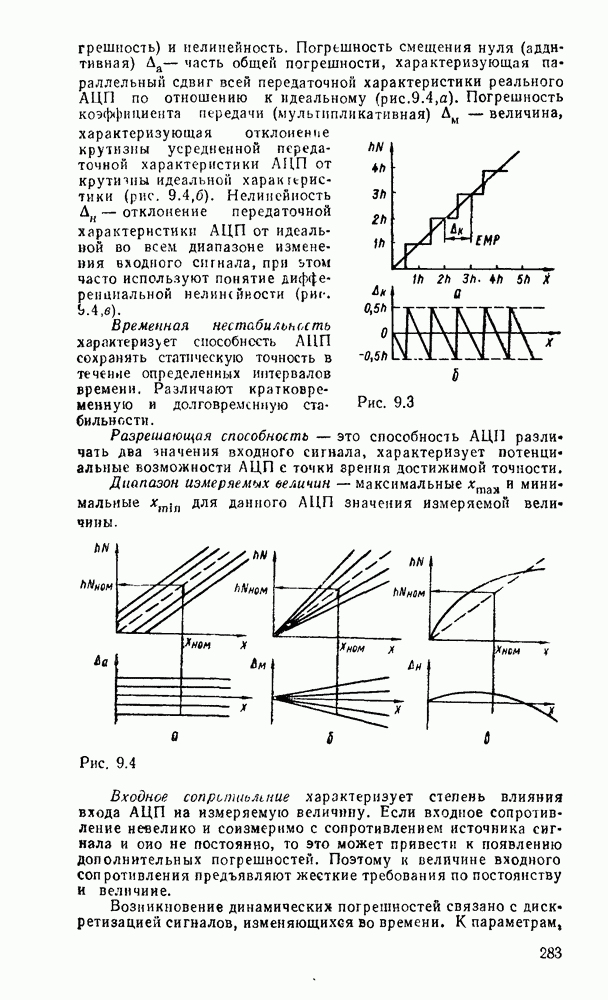
Основной особенностью дискретизации сигнала является то, что за счет конечного времени одного преобразования и неопределенности момента его окончания не удается получить однозначное соответствие между значениями отсчетов и Моментами времени, к которым их следует отнести. Таким образом, при дискретизации изменяющихся во времени сигналов возникают динамические погрешности, для оценки которых вводят понятие неопределенности [7]. При равномерной дискретизации возникают амплитудные погрешности, которые называются апертурными, численно равные приращению сигнала в течение апертурного времени, равного шагу дискретизации  . Для оценки апертурных погрешностей используют синусоидальный измерительный сигнал
. Для оценки апертурных погрешностей используют синусоидальный измерительный сигнал  , для которого максимальная - относительная апертурная погрешность
, для которого максимальная - относительная апертурная погрешность  . Если принять, что для
. Если принять, что для  -разрядного АЦП в разрешением
-разрядного АЦП в разрешением  апертурная погрешность не должна превышать шага квантования по уровню
апертурная погрешность не должна превышать шага квантования по уровню  , то между частотой синусоидального сигнала
, то между частотой синусоидального сигнала  , апертурным временем (шагом дискретизации
, апертурным временем (шагом дискретизации  ) и относительной апертурной погрешностью существует соотношение [7]
) и относительной апертурной погрешностью существует соотношение [7]

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
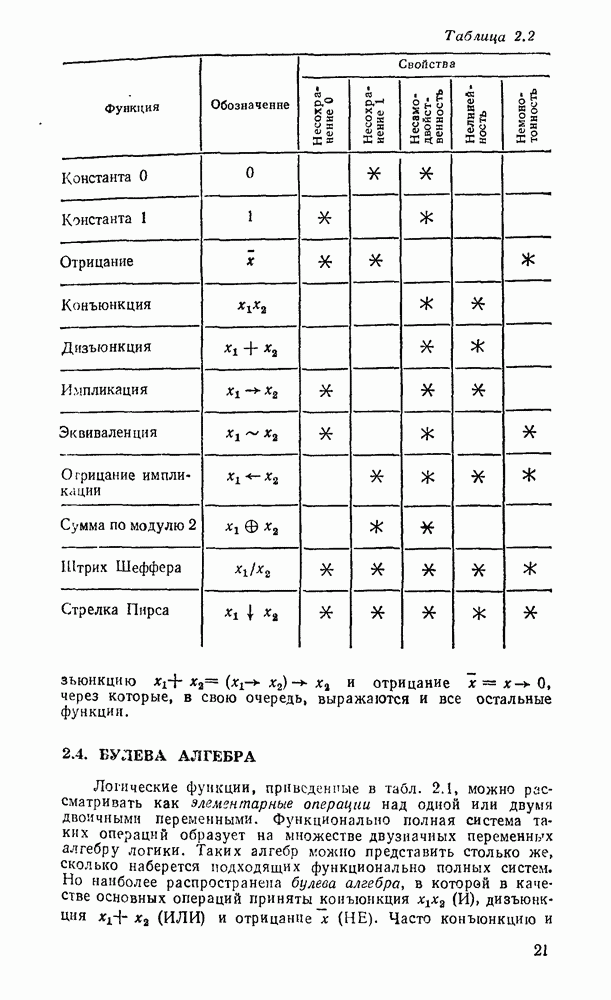
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
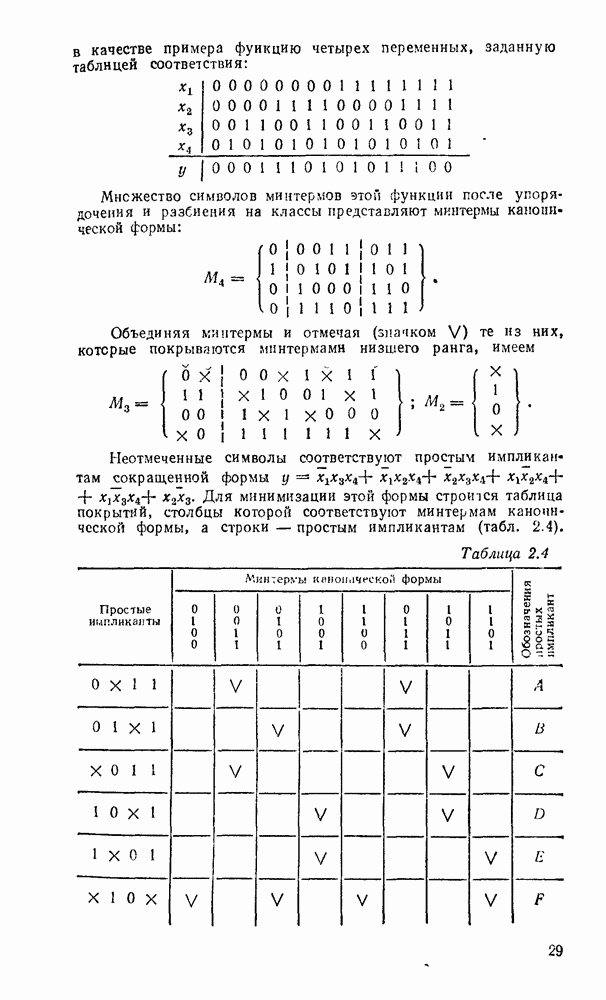
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
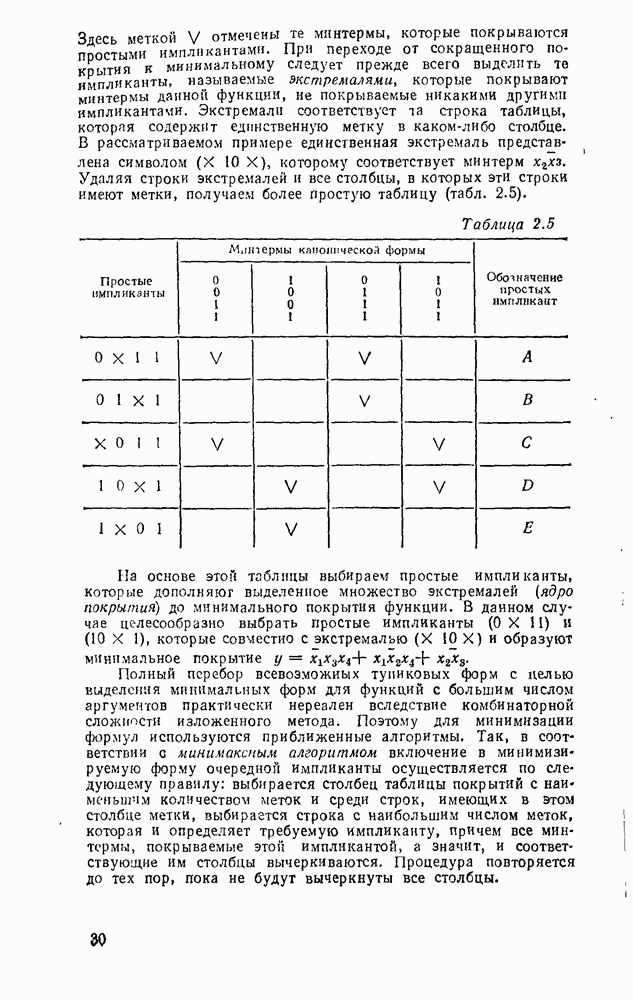
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
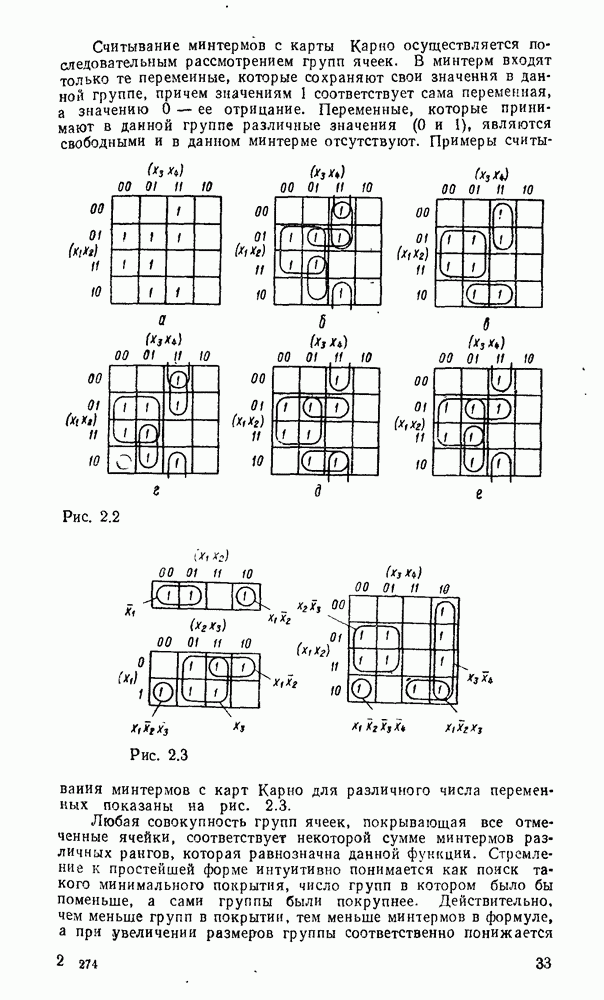
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
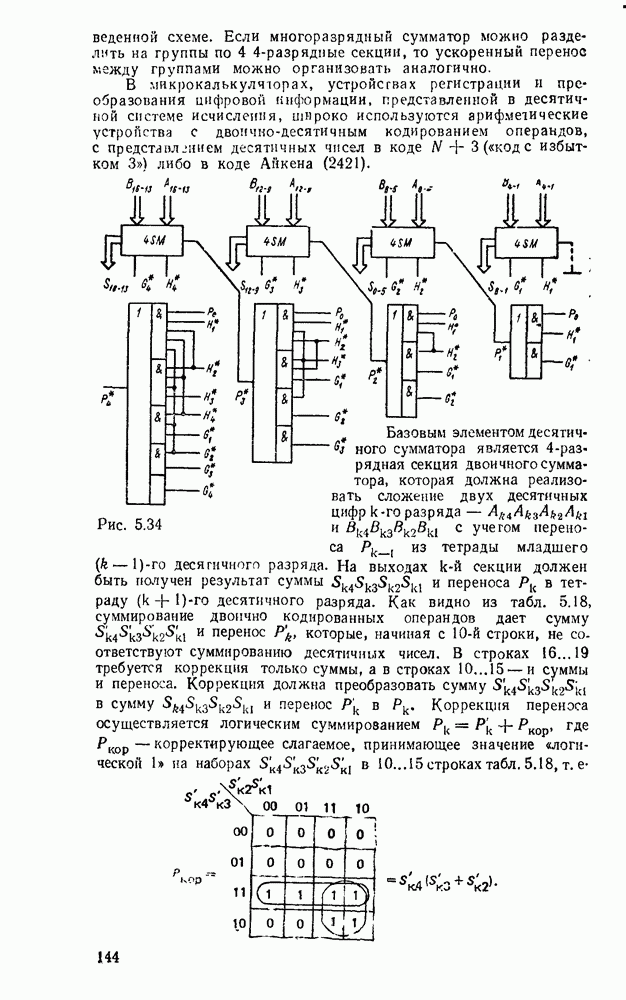
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
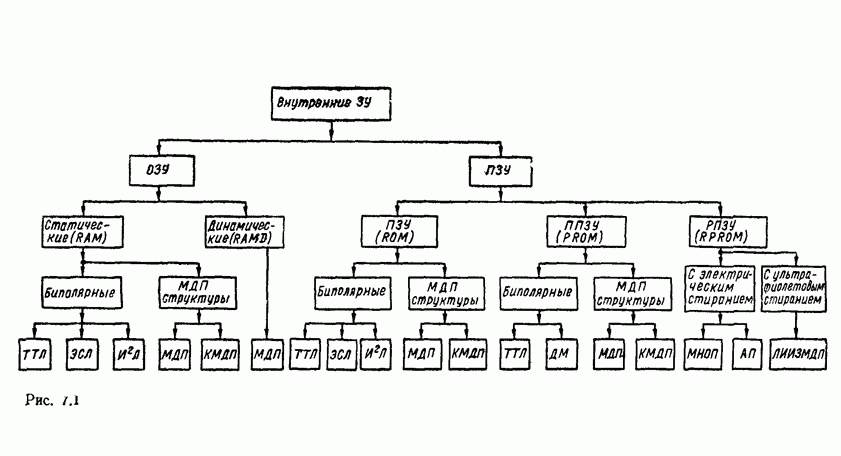
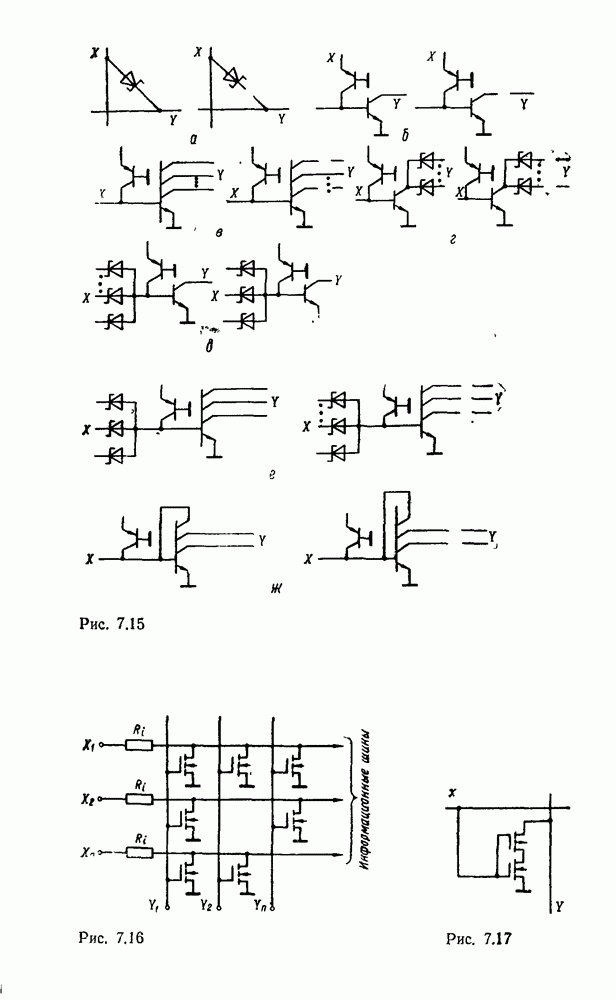
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
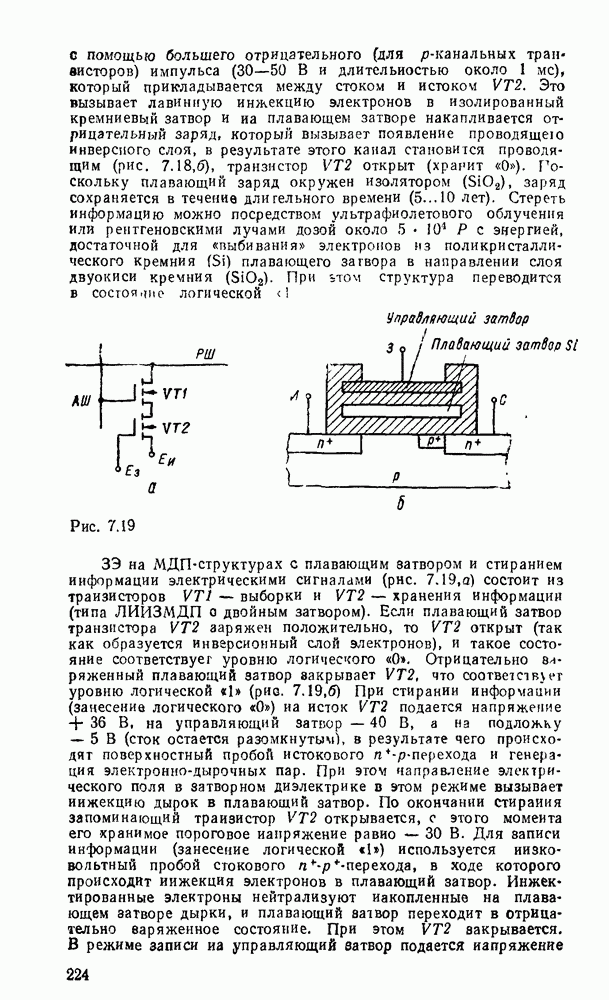
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
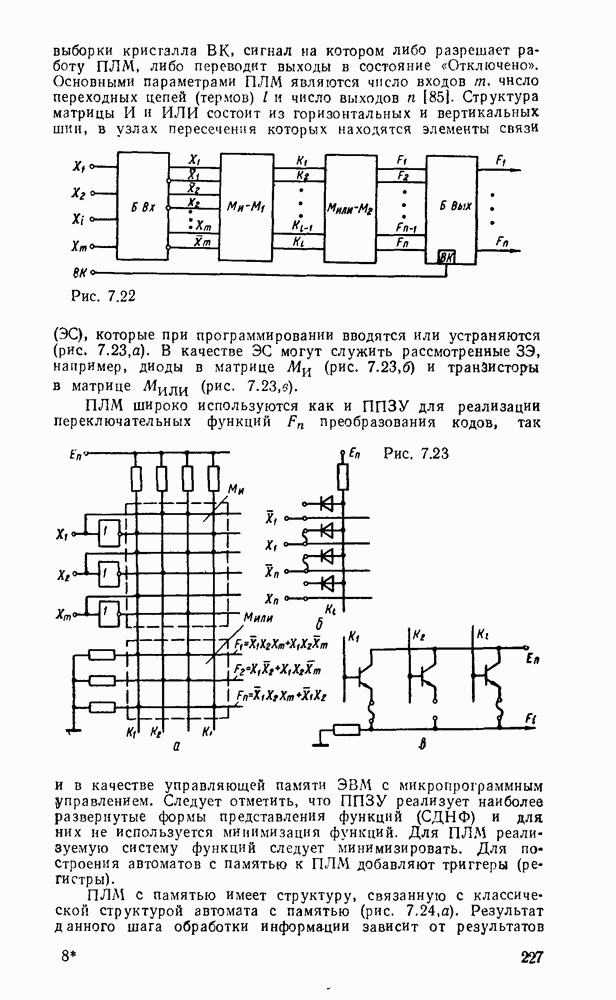
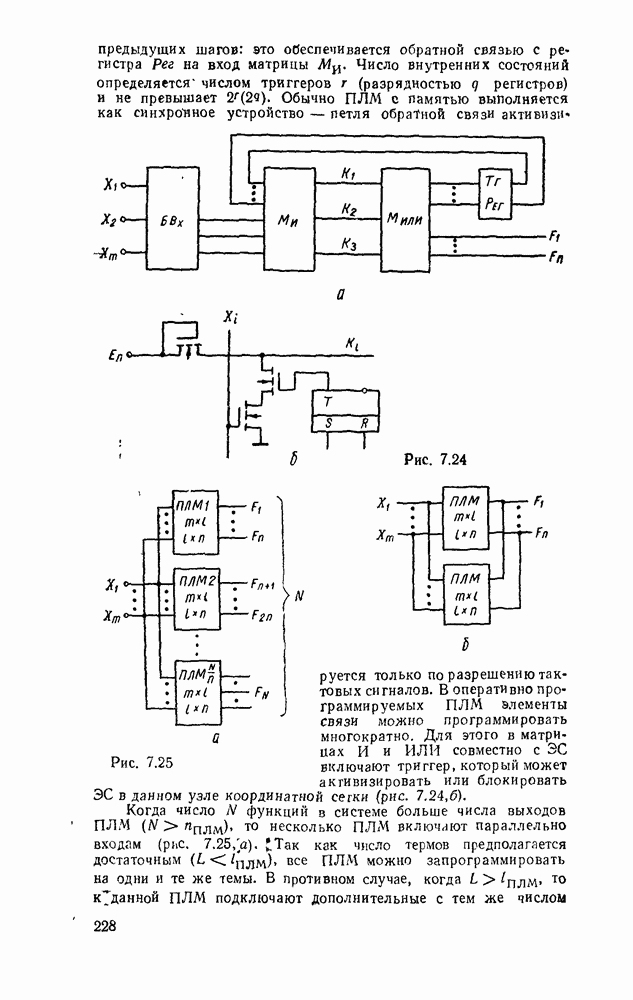
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
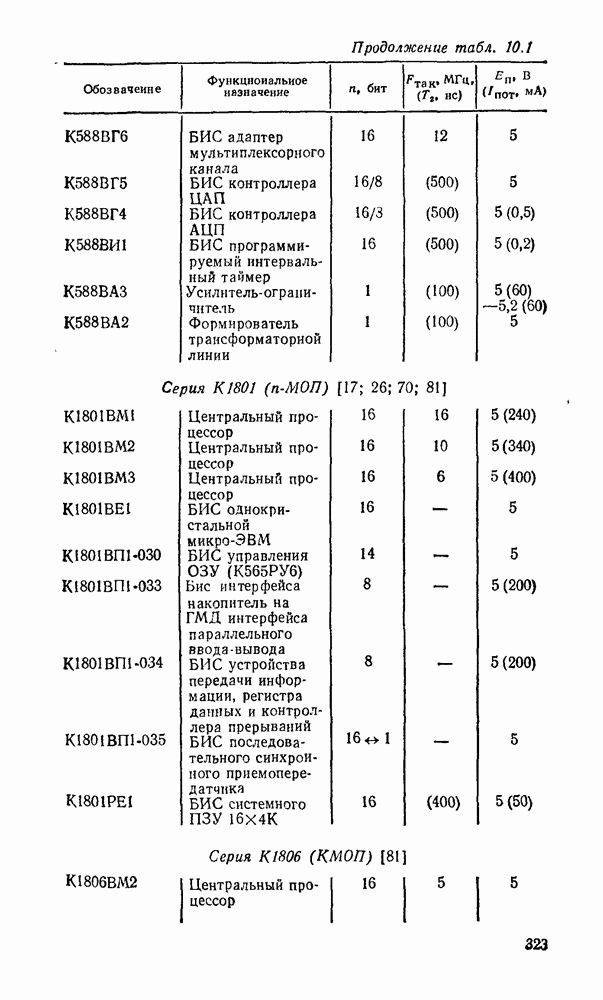
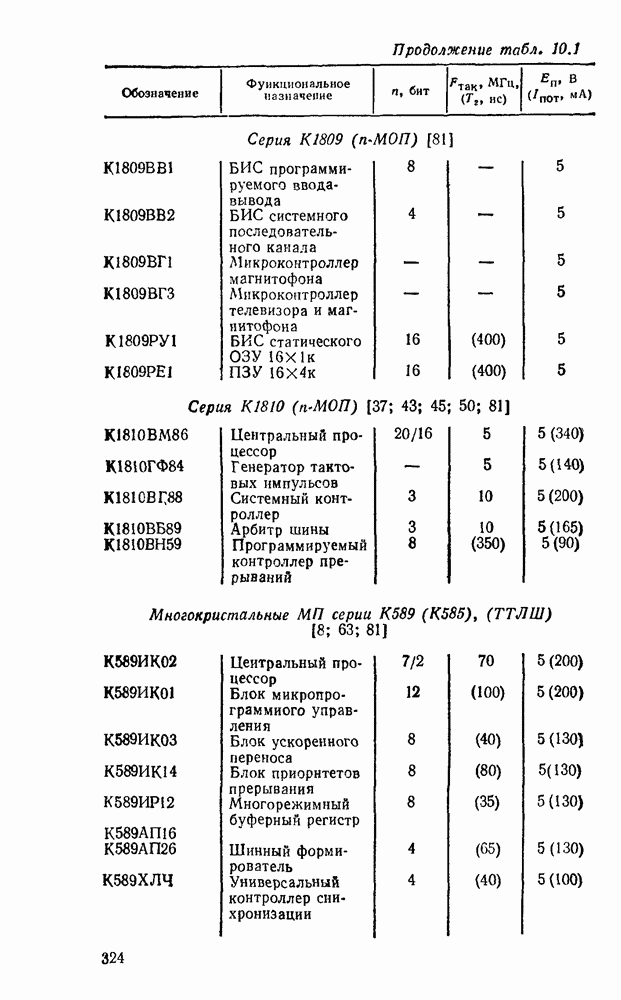
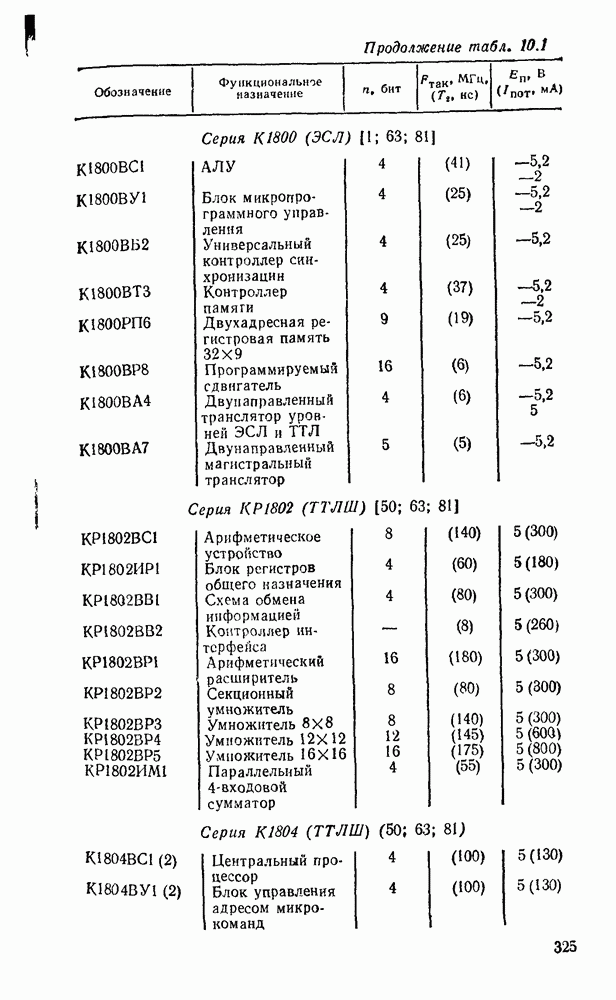
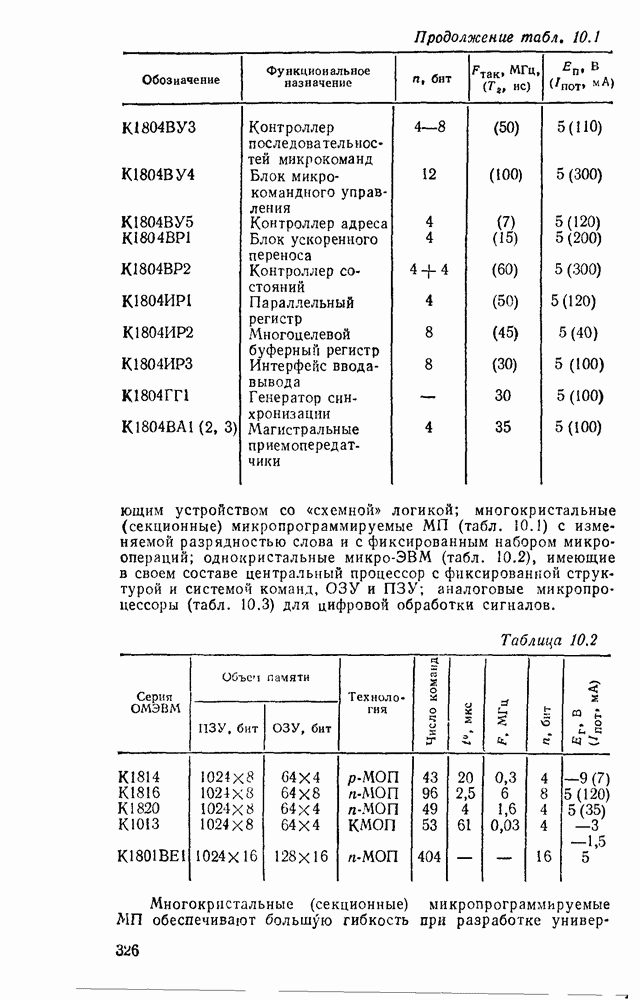
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
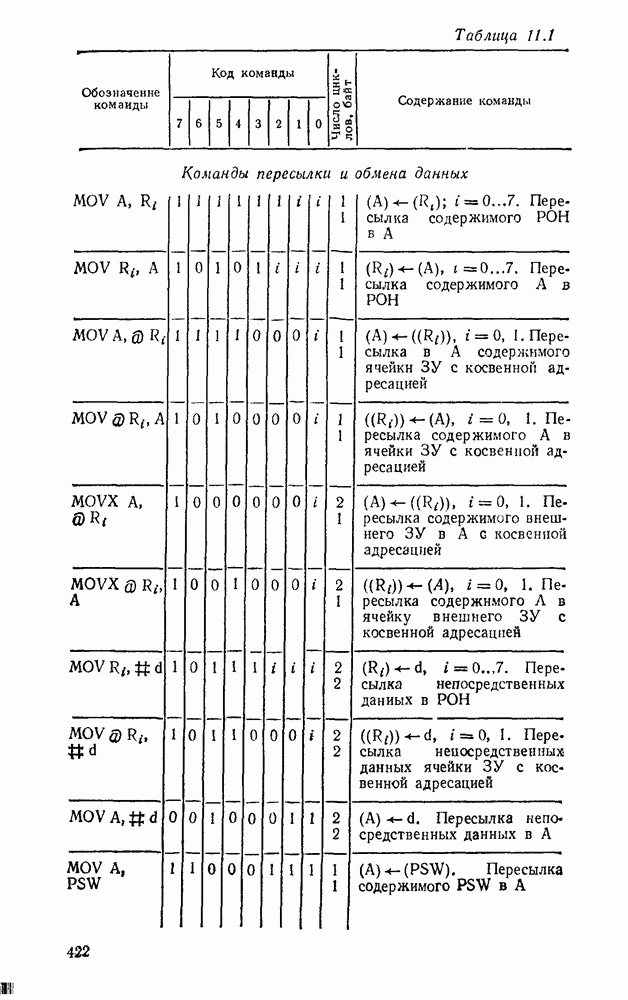
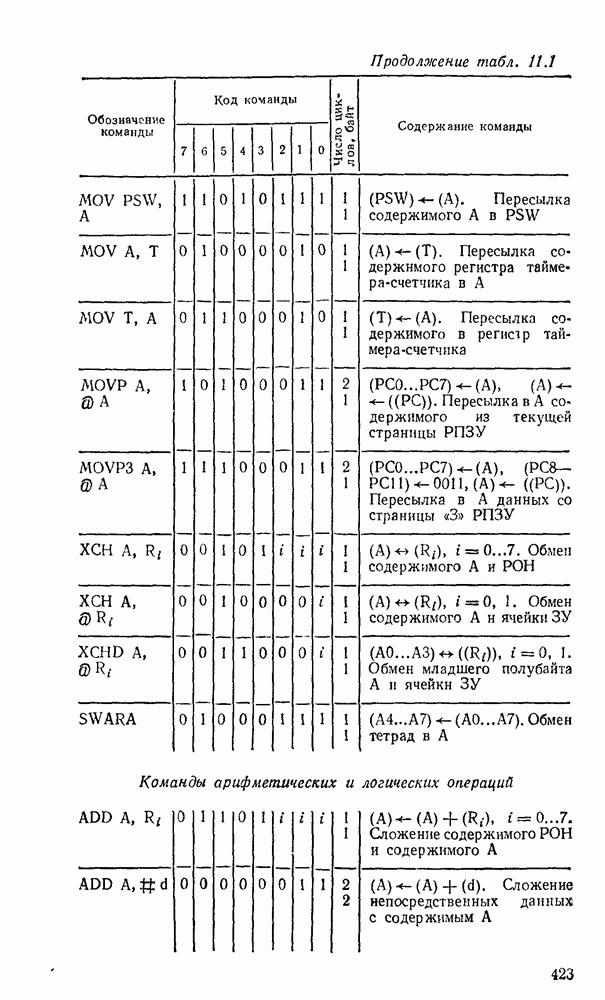
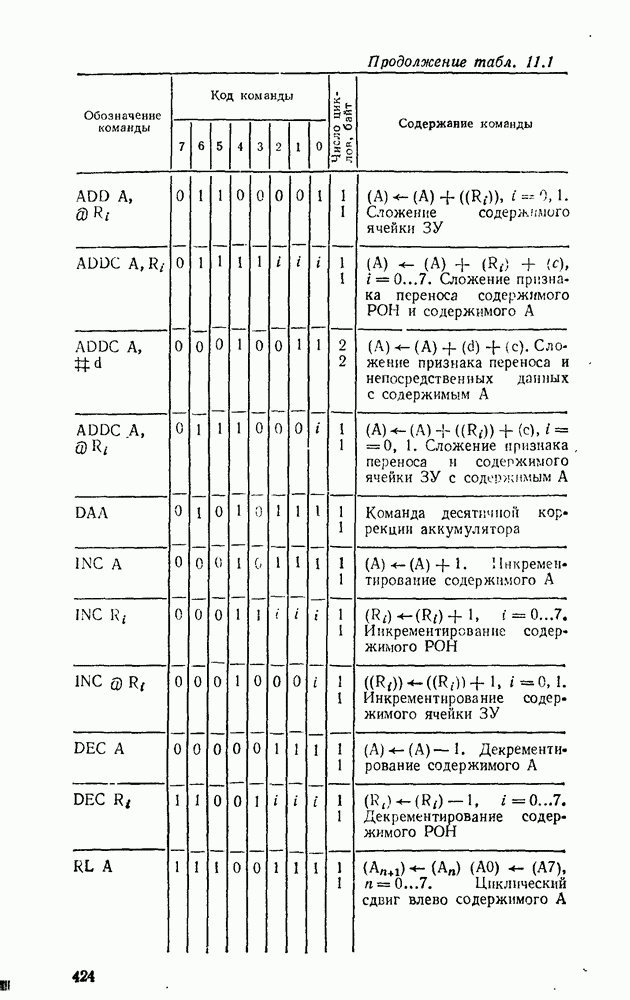
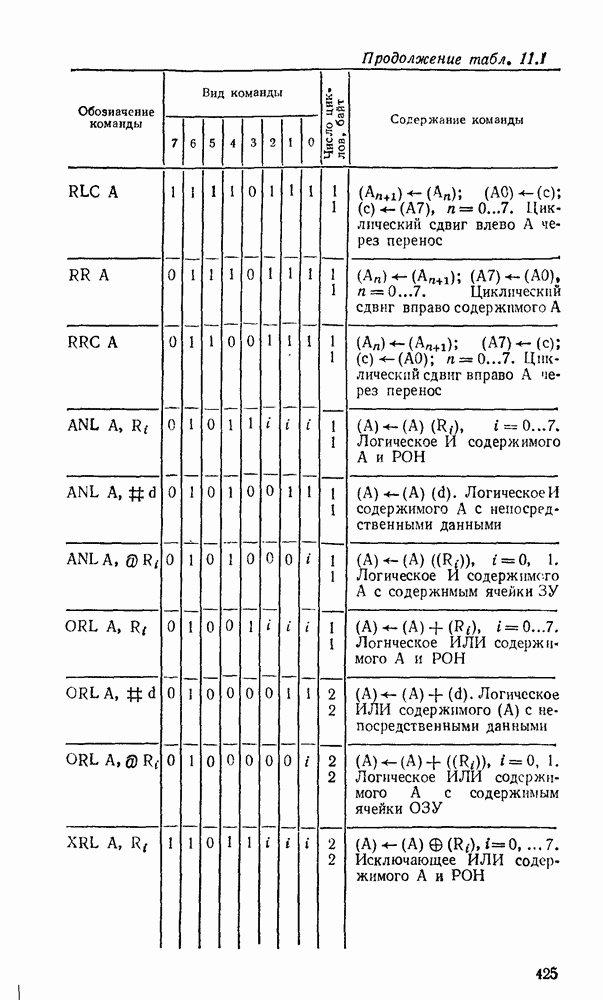
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ