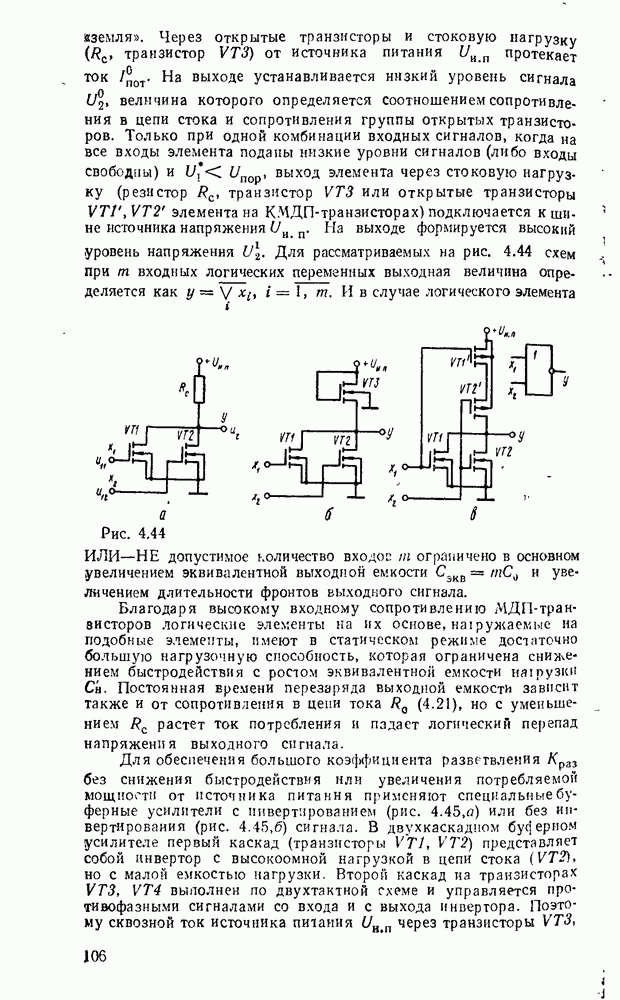
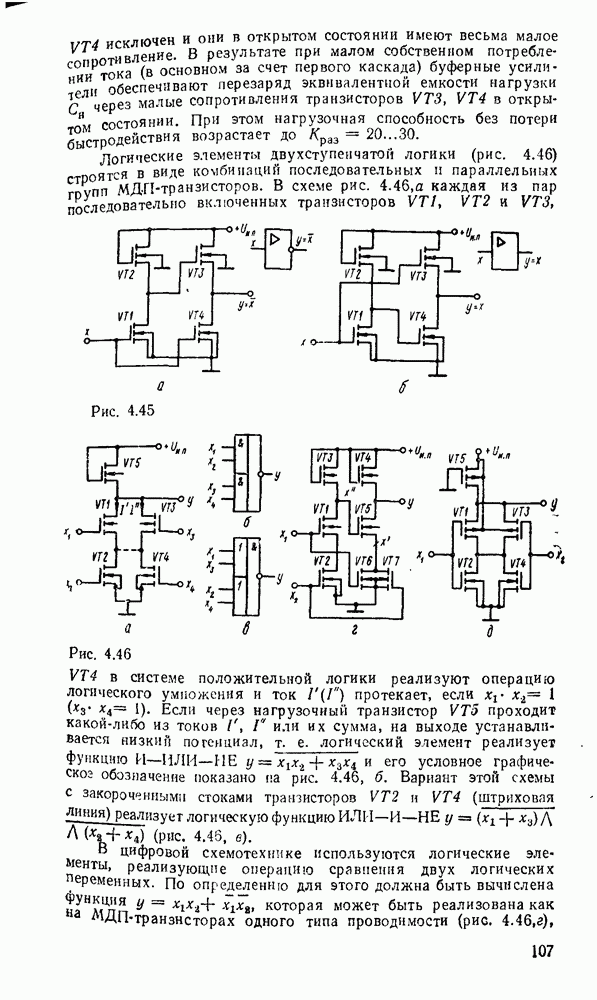
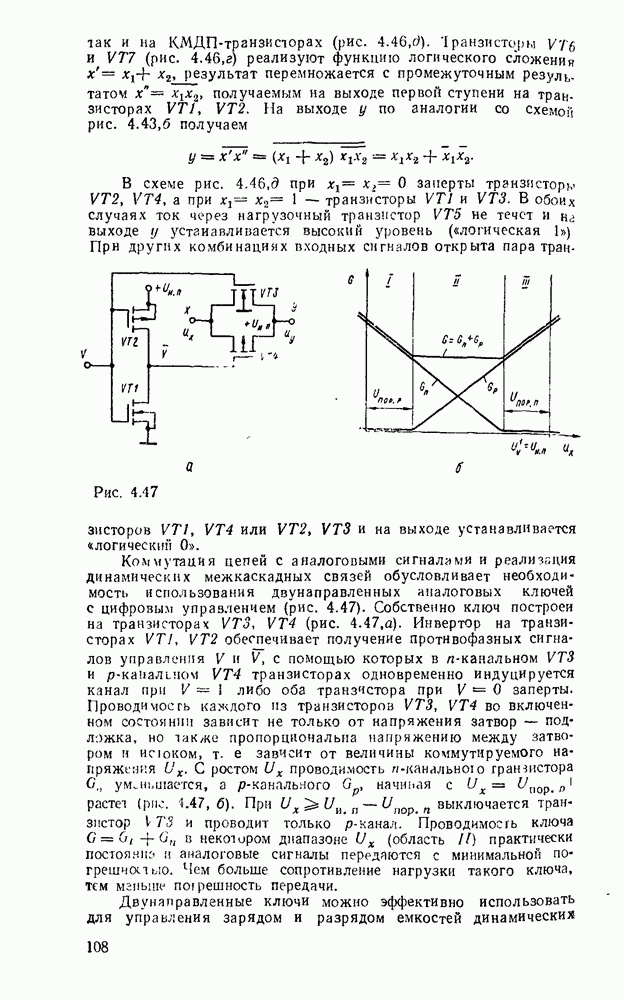
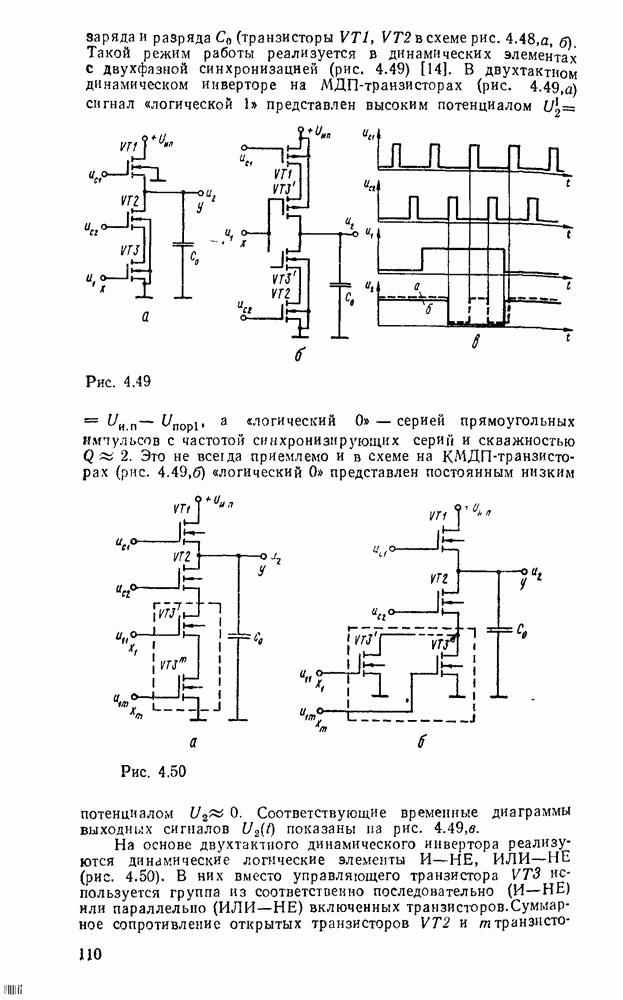
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
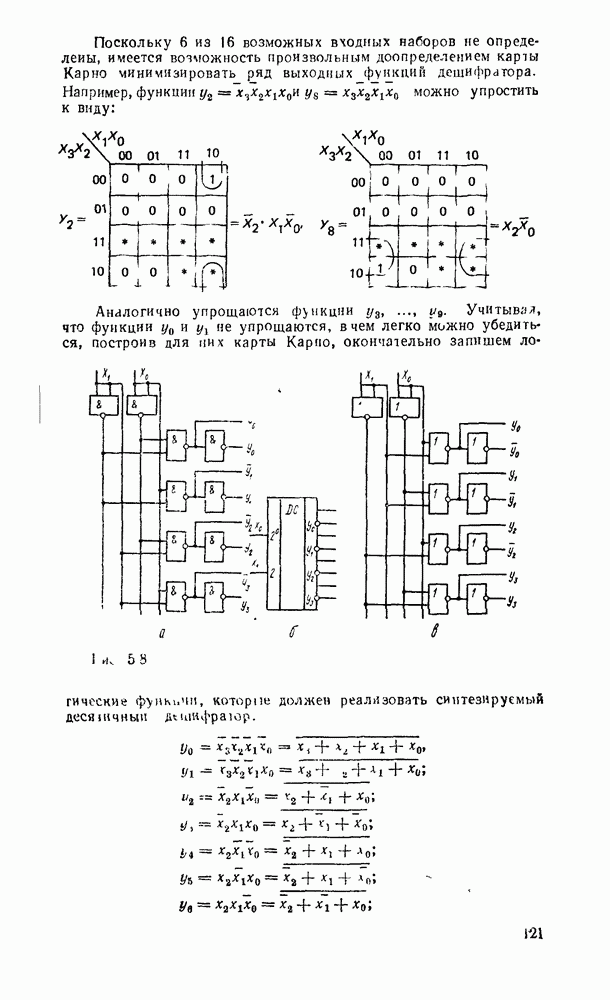
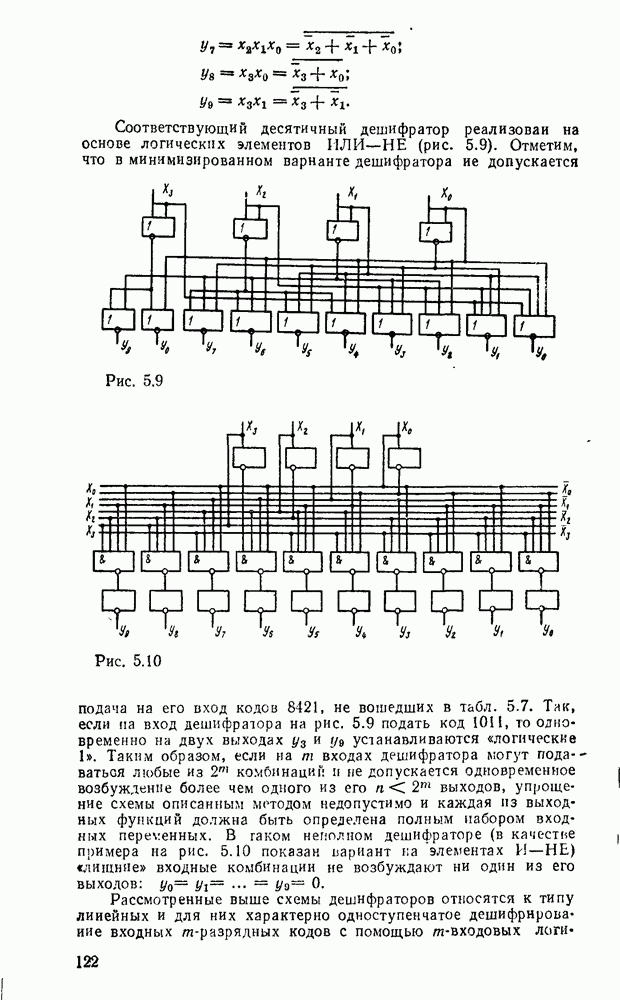
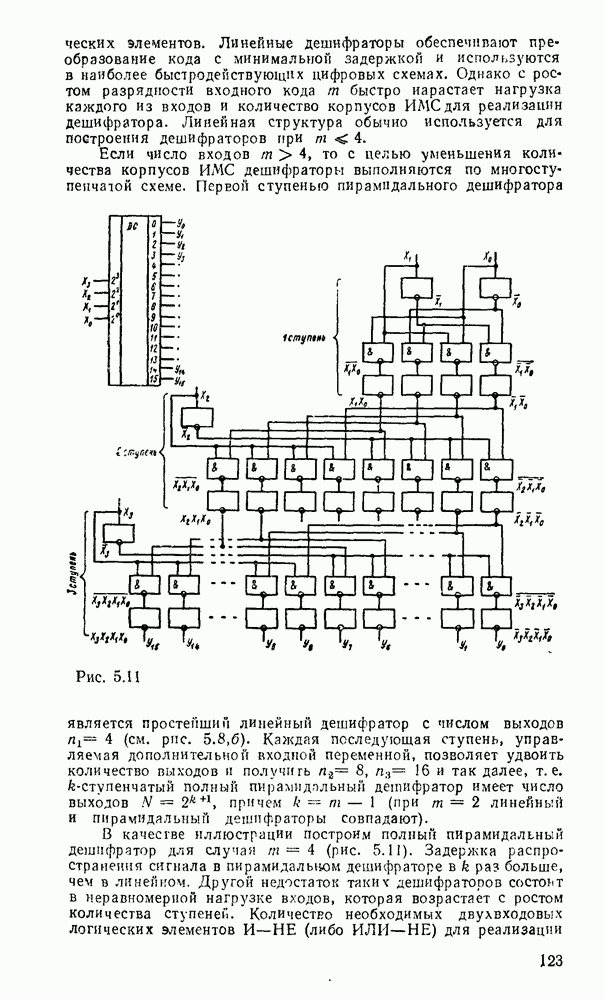
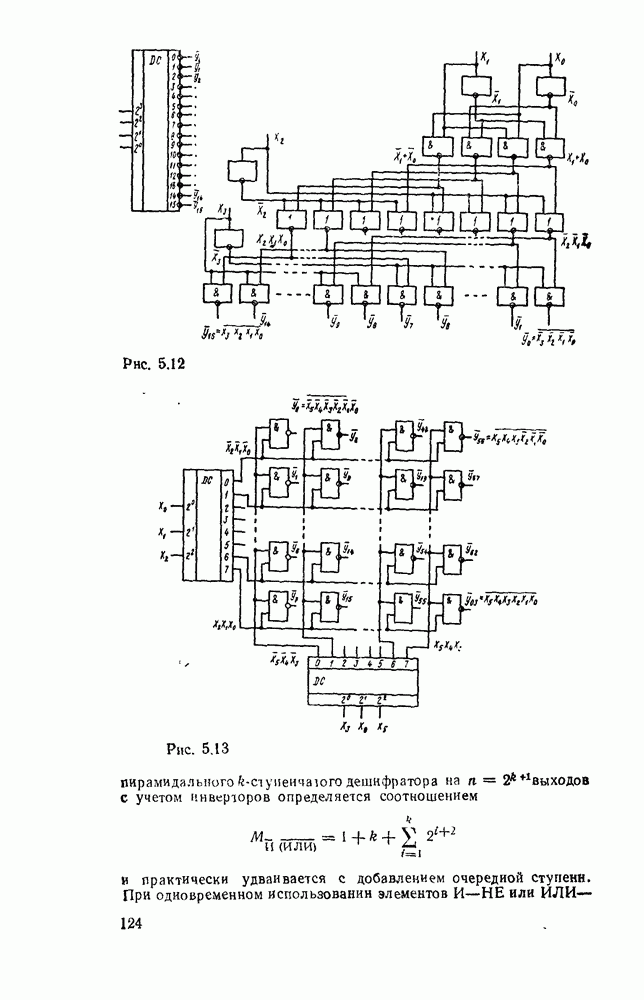
6.3. СЧЕТЧИКИ
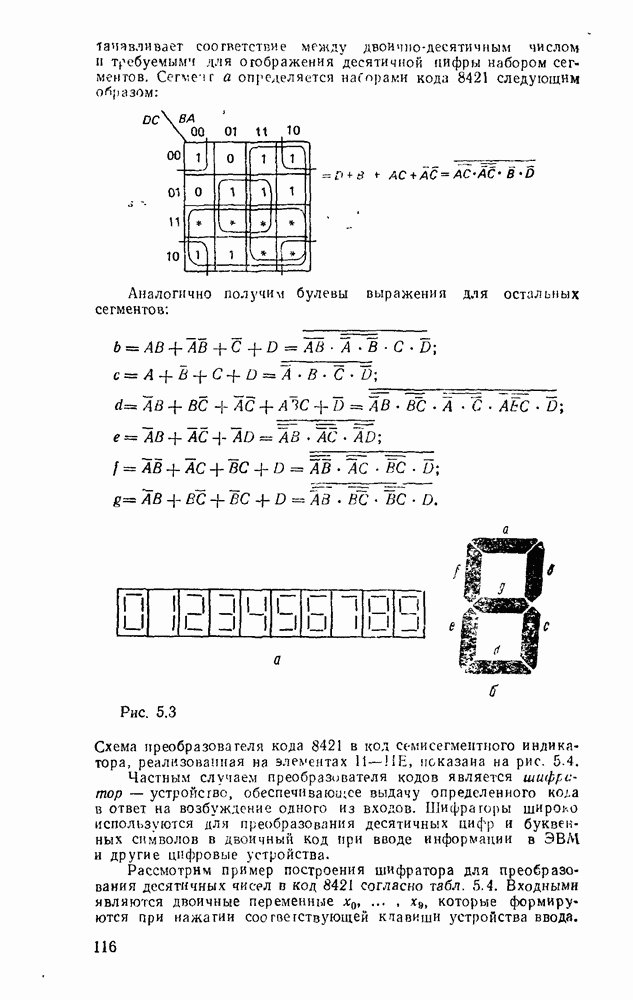
Счетчиками называют последовательностные цифровые устройства, предназначенные для подсчета и запоминания числа импульсов, поданных в определенном временном интервале на его счетный вход. Помимо счетного счетчики могут еще иметь входы асинхронный или синхронной установки начальных состояний. По характеру изменения состояний счетчика счетными импульсами различают суммирующие, вычитающие и реверсивные счетчики [61; 83]. По способу организации переносов между разрядами их можно разделить на счетчики с последовательным, сквозным, параллельным и комбинированным переносом. Счетчики с последовательным и сквозным переносом называют асинхронными, а с параллельным переносом — синхронными. Обычно счетчик содержит один или несколько идентичных разрядов, построенных на основе двоичных триггеров. Количество различимых состояний разряда счетчика является его классификационным признаком, согласно которому счетчики называют двоичными, двоично-десятичными и т. д.
Основными техническими параметрами счетчиков являются коэффициент пересчета  и быстродействие. Коэффициент
и быстродействие. Коэффициент  представляет собой число различимых устойчивых состояний счетчика и если каждый счетный импульс переводит счетчик в иовое состояние, то
представляет собой число различимых устойчивых состояний счетчика и если каждый счетный импульс переводит счетчик в иовое состояние, то  равно максимальному числу импульсов, которое счетчик может просчитать и запомнить без повторения состояний. Быстродействие счетчика определяется максимальной частотой следования счетных импульсов
равно максимальному числу импульсов, которое счетчик может просчитать и запомнить без повторения состояний. Быстродействие счетчика определяется максимальной частотой следования счетных импульсов  , регистрируемых счетчиком без сбоев, максимальной частотой переключения состояний счетчика
, регистрируемых счетчиком без сбоев, максимальной частотой переключения состояний счетчика  -тах и временем установки
-тах и временем установки  состояний счетчика, определяемое как максимальный временной интервал от момента поступления счетного импульса до момента перехода всех разрядов счетчика в новое устойчивое состояние.
состояний счетчика, определяемое как максимальный временной интервал от момента поступления счетного импульса до момента перехода всех разрядов счетчика в новое устойчивое состояние.
Асинхронные счетчики.
В асинхронных счетчиках отсутствует общая для всех разрядов синхронизация и переход разрядов в новые состояния происходит последовательно разряд за разрядом, начиная от входного, на который поступают счетные импульсы. Если рассмотреть последовательность состояний,  . папример,
. папример,  -разрядного суммирующего двоичного счетчика (табл. 6.6), то из нее видно, что признаком смены состояний любого из разрядов счетчика является переключение предыдущего разряда (или входного сигнала) из состояния «1» в
-разрядного суммирующего двоичного счетчика (табл. 6.6), то из нее видно, что признаком смены состояний любого из разрядов счетчика является переключение предыдущего разряда (или входного сигнала) из состояния «1» в  . Именно так себя ведут двухтактные Т и
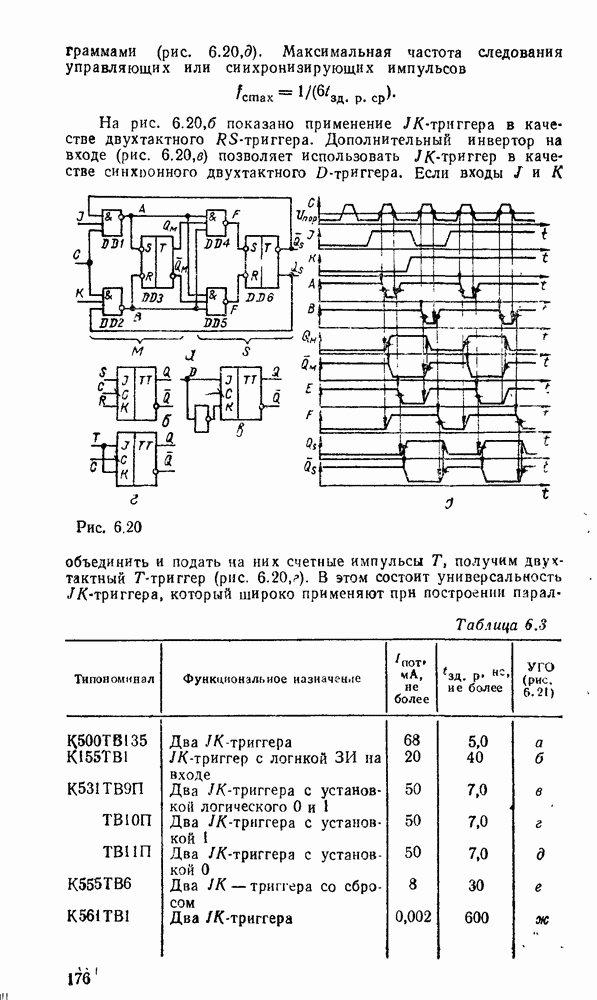
. Именно так себя ведут двухтактные Т и  -триггеры, рассмотренные в разделе 6.1. Таким образом, последовательный счетчик, работающий согласно табл. 6.6, можно выполнить в виде цепочки Г-триггеров, для каждого из которых счетный импульс формируется триггером соседнего младшего разряда (рис.
-триггеры, рассмотренные в разделе 6.1. Таким образом, последовательный счетчик, работающий согласно табл. 6.6, можно выполнить в виде цепочки Г-триггеров, для каждого из которых счетный импульс формируется триггером соседнего младшего разряда (рис.  ). Как было показано в разделе 6.1, счетный режим
). Как было показано в разделе 6.1, счетный режим  -триггера имеет место в случае
-триггера имеет место в случае  . На рис. 6.32,а входы
. На рис. 6.32,а входы  и К триггеров свободны, что обычно эквивалентно подаче на входы
и К триггеров свободны, что обычно эквивалентно подаче на входы  и К уровней «1».
и К уровней «1».
Таблица 6.6

Из временной диаграммы (рис. 6.32,б) видно, что время установления счетчика  . зависит от количества последовательно переключающихся разрядов и для
. зависит от количества последовательно переключающихся разрядов и для  -разрядного счетчика оно изменяется в пределах
-разрядного счетчика оно изменяется в пределах

где  - среднее время установления триггера. Максимальная частота следования счетных импульсов
- среднее время установления триггера. Максимальная частота следования счетных импульсов  определяется независимо от структуры счетчика предельной частотой переключения первого триггера. Если же требуется различать (дешифрировать) каждое состояние счетчика, то до подачи очередного счетного импульса все разряды должны установиться в новое состояние на время
определяется независимо от структуры счетчика предельной частотой переключения первого триггера. Если же требуется различать (дешифрировать) каждое состояние счетчика, то до подачи очередного счетного импульса все разряды должны установиться в новое состояние на время  .
.

Рис. 6.32.
В этом случае максимально допустимая частота смены состояний  определяется по наихудшему времени установления
определяется по наихудшему времени установления

Основное достоинство последовательного счетчика — минимальные затраты микросхем и минимум электрических связей, что упрощает разводку линий связи и повышает помехозащищенность схемы. Главный недостаток — низкое быстродействие, которое тем ниже, чем больше коэффициент счета  и чем, следовательно, больше в счетчике разрядов
и чем, следовательно, больше в счетчике разрядов  .
.
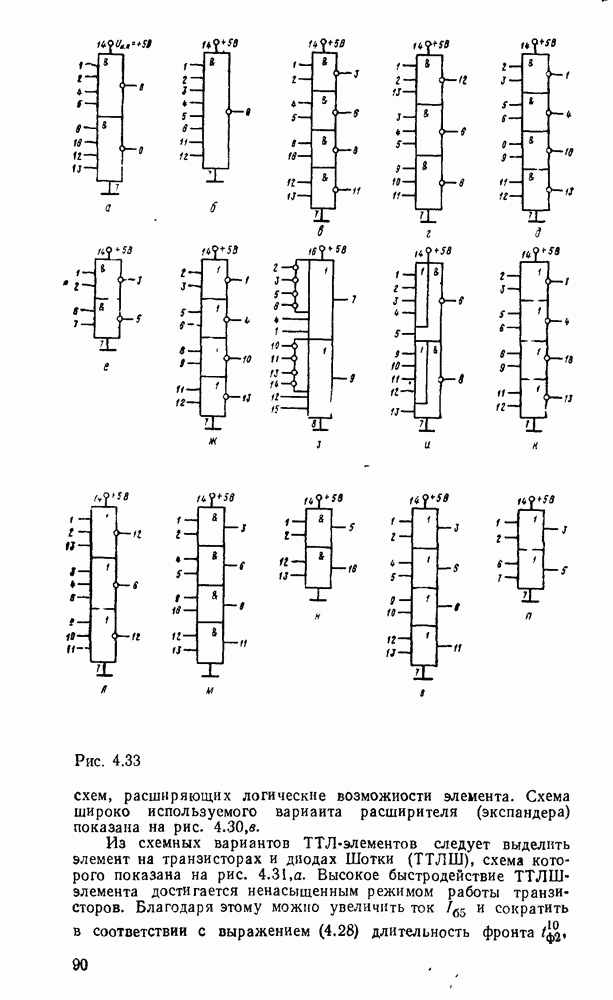
Один из способов увеличения быстродействия асинхронных счетчиков состоит в организации переносов между разрядами через дополнительные логические элементы (рис. 6.33). Если первый триггер ечетчика (рис. 6.33,а, в) находится в состоянии «1», то следующий счетный импульс Т сбрасывает его в состояние  отрицательным фронтом.
отрицательным фронтом.
Как видно из временных диаграмм (рис.  ), еще до переключения выхода триггера
), еще до переключения выхода триггера  счетный импульс Т через вентиль
счетный импульс Т через вентиль  поступает в виде импульса переноса
поступает в виде импульса переноса  на вход второго разряда и вентиль
на вход второго разряда и вентиль  , и если
, и если  то счетный импульс проходит дальше через вентиль
то счетный импульс проходит дальше через вентиль  и т. д. Счетный импульс Т проходит до вентиля, на второй вход которого поступает
и т. д. Счетный импульс Т проходит до вентиля, на второй вход которого поступает  . При этом триггеры с первого до
. При этом триггеры с первого до  устанавливаются в «0», а
устанавливаются в «0», а  триггер — в состояние «1» (рис. 6.33,б). В
триггер — в состояние «1» (рис. 6.33,б). В  -разрядном счетчике со сквозным переносом время установления определяется задержкой счетного импульса Т в цепях переноса и временем установления
-разрядном счетчике со сквозным переносом время установления определяется задержкой счетного импульса Т в цепях переноса и временем установления  последнего из переключающихся триггеров
последнего из переключающихся триггеров


Рис. 6.33.
Тогда максимальная частота счета

оказывается выше, чем частота последовательного счетчика, определяемая формулой (6.18), поскольку  вентиль И переключаются значительно быстрее, чем
вентиль И переключаются значительно быстрее, чем  триггер.
триггер.
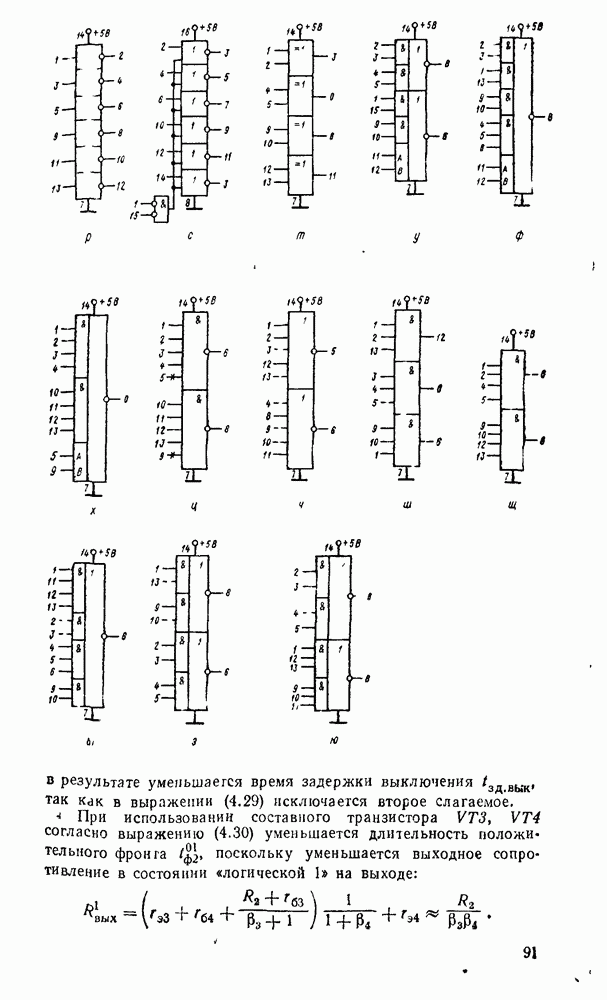
С точки зрения структуры, функционирования и технических параметров варианты асинхронных счетчиков (рис.  эквивалентны. В зависимости от количества разрядов N они реализуют коэффициент счета
эквивалентны. В зависимости от количества разрядов N они реализуют коэффициент счета  и их можио использовать в качестве делителей частоты
и их можио использовать в качестве делителей частоты

Часто при проектировании цифровых устройств возникает необходимость в делителях частоты, для которых  в выражении (6.19) — любое целое число. Если в арсенале схемотехника имеются простейшие делители частоты с коэффициентами счета
в выражении (6.19) — любое целое число. Если в арсенале схемотехника имеются простейшие делители частоты с коэффициентами счета  = 2, 3, 4, 5, 6, 7, 8, 9, 10, то большое количество делителей частоты с
= 2, 3, 4, 5, 6, 7, 8, 9, 10, то большое количество делителей частоты с  , разлагающимся на простейшие множители, строятся на их основе. Требуемые
, разлагающимся на простейшие множители, строятся на их основе. Требуемые  получают введением в счетчики обратных связей. На рис.
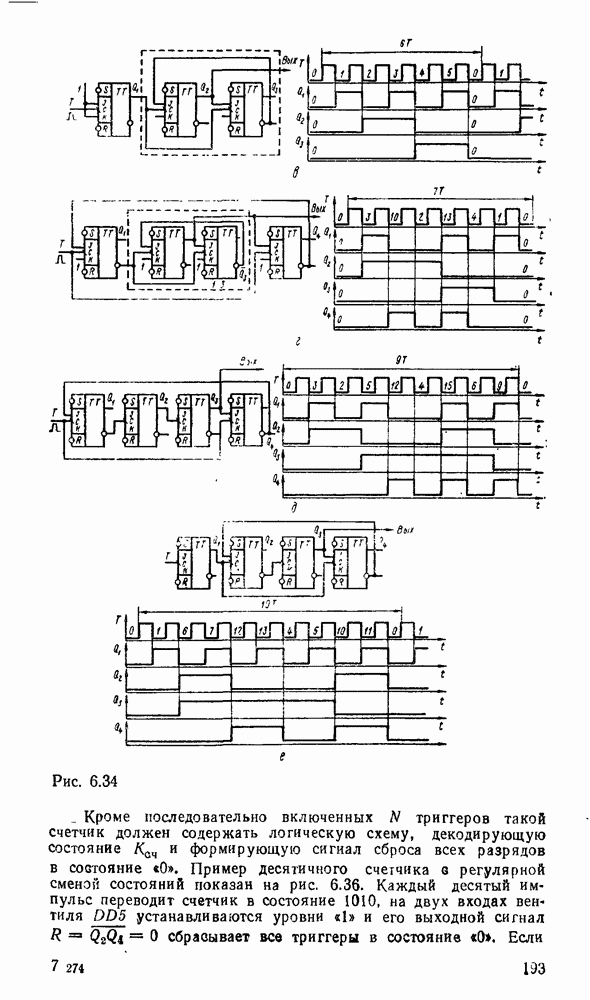
получают введением в счетчики обратных связей. На рис.  показаны последовательные счетчики для
показаны последовательные счетчики для  , заданных одноразрядным десятичным числом.
, заданных одноразрядным десятичным числом.
На  не показаны счетчики для
не показаны счетчики для  = 2, 4, 8, которые реализуются без введения обратных связей включением последовательно соответственно 1, 2 и 3 Т-триггеров.
= 2, 4, 8, которые реализуются без введения обратных связей включением последовательно соответственно 1, 2 и 3 Т-триггеров.
Общий принцип построения показанных на рис. 6.34 счетчиков с нечетным  показан на рис. 6.35. Если между входным и выходным триггерами включен делитель частоты на любое натуральное число
показан на рис. 6.35. Если между входным и выходным триггерами включен делитель частоты на любое натуральное число  , то такая схема обеспечивает деление частоты на
, то такая схема обеспечивает деление частоты на

Например, счетчик делитель частоты на 3 (рис. 6.34,а) реализован при  , что соответствует прямой связи между входным
, что соответствует прямой связи между входным  и выходным
и выходным  триггерами. Для
триггерами. Для  согласно выражению (6.20) необходимо
согласно выражению (6.20) необходимо  поэтому между входным и выходным триггерами должен быть включен один дополнительный триггер - делитель частоты на 2 (рис.
поэтому между входным и выходным триггерами должен быть включен один дополнительный триггер - делитель частоты на 2 (рис.  ). Делитель частоты
). Делитель частоты  (рис. 6.34,в) получен последовательным соединением делителей частоты на 2 и на 3 (рис.
(рис. 6.34,в) получен последовательным соединением делителей частоты на 2 и на 3 (рис.  ). Для реализации
). Для реализации  (рис. 6.34,г) и
(рис. 6.34,г) и  (рис.
(рис.  ) использована структура (рис. 6.35) соответственно при
) использована структура (рис. 6.35) соответственно при  полученном с помощью схемы (рис.
полученном с помощью схемы (рис.  ), и при
), и при  . Делитель частоты
. Делитель частоты  представлен (рис. 6.34,е) последовательным соединением делителя частоты на 5 и дополнительного триггера.
представлен (рис. 6.34,е) последовательным соединением делителя частоты на 5 и дополнительного триггера.
Приведенные на рис. 6.34 схемы последовательных счетчиков предназначены в основном для использования в режиме деления частоты без дешифрации их состояний, смена которых при использовании структуры на рис. 6.35 не соответствует естественному счету. Их достоинство — максимальное быстродействие, ограниченное предельной частотой переключения входного триггера, при минимальных затратах оборудования.
При построении счетчиков с дешифрацией состояний необходимо обеспечить регулярность смены состояний согласно двоичио-десятичному счету. Для их реализации необходимо определить требуемое количество триггеров N согласно соотношению



Рис. 6.34.
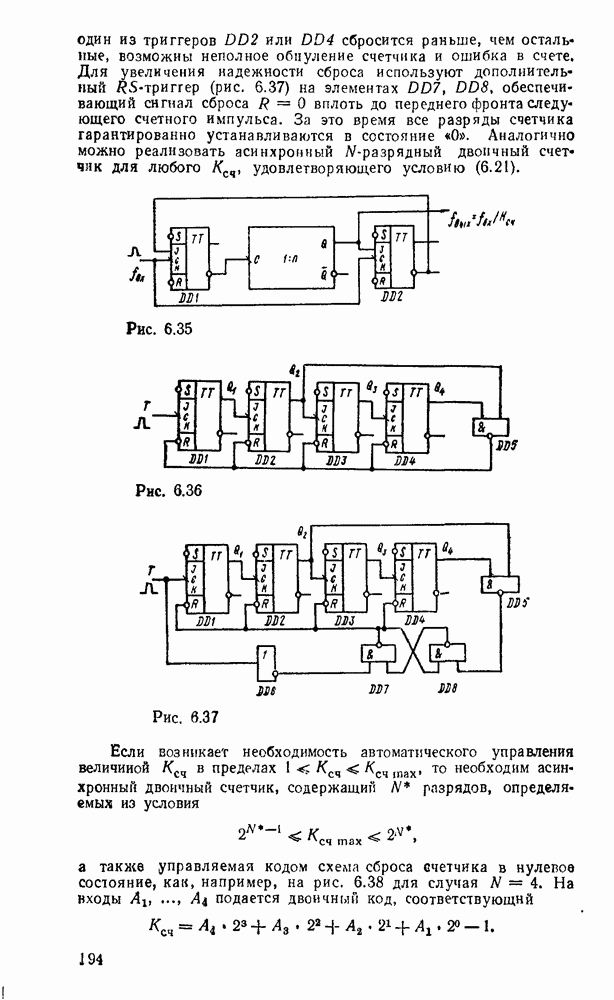
Кроме последовательно включенных N триггеров такой счетчик должен содержать логическую схему, декодирующую состояние  и формирующую сигнал сброса всех разрядов в состояние
и формирующую сигнал сброса всех разрядов в состояние  . Пример десятичного счетчика g регулярной сменой состояний показан на рис. 6.36. Каждый десятый импульс переводит счетчик в состояние 1010, на двух входах вентиля
. Пример десятичного счетчика g регулярной сменой состояний показан на рис. 6.36. Каждый десятый импульс переводит счетчик в состояние 1010, на двух входах вентиля  устанавливаются уровни «1» и его выходной сигнал
устанавливаются уровни «1» и его выходной сигнал  сбрасывает все триггеры в состояние «0».
сбрасывает все триггеры в состояние «0».
Если один из триггеров  или
или  сбросится раньше, чем остальные, возможны неполное обнуление счетчика и ошибка в счете. Для увеличения надежности сброса используют дополнительный
сбросится раньше, чем остальные, возможны неполное обнуление счетчика и ошибка в счете. Для увеличения надежности сброса используют дополнительный  -триггер (рис. 6.37) на элементах
-триггер (рис. 6.37) на элементах  , обеспечивающий сигнал сброса
, обеспечивающий сигнал сброса  вплоть до переднего фронта следующего счетного импульса. За это время все разряды счетчика гарантированно устанавливаются в состояние
вплоть до переднего фронта следующего счетного импульса. За это время все разряды счетчика гарантированно устанавливаются в состояние  . Аналогично можно реализовать асинхронный
. Аналогично можно реализовать асинхронный  -разрядный двоичный счетчик для любого
-разрядный двоичный счетчик для любого  , удовлетворяющего условию (6.21).
, удовлетворяющего условию (6.21).

Рис. 6.35.

Рис. 6.36.

Рис. 6.37.
Если возникает необходимость автоматического управления величиной  в пределах
в пределах  , то необходим асинхронный двоичный счетчик, содержащий
, то необходим асинхронный двоичный счетчик, содержащий  разрядов, определяемых из условия
разрядов, определяемых из условия

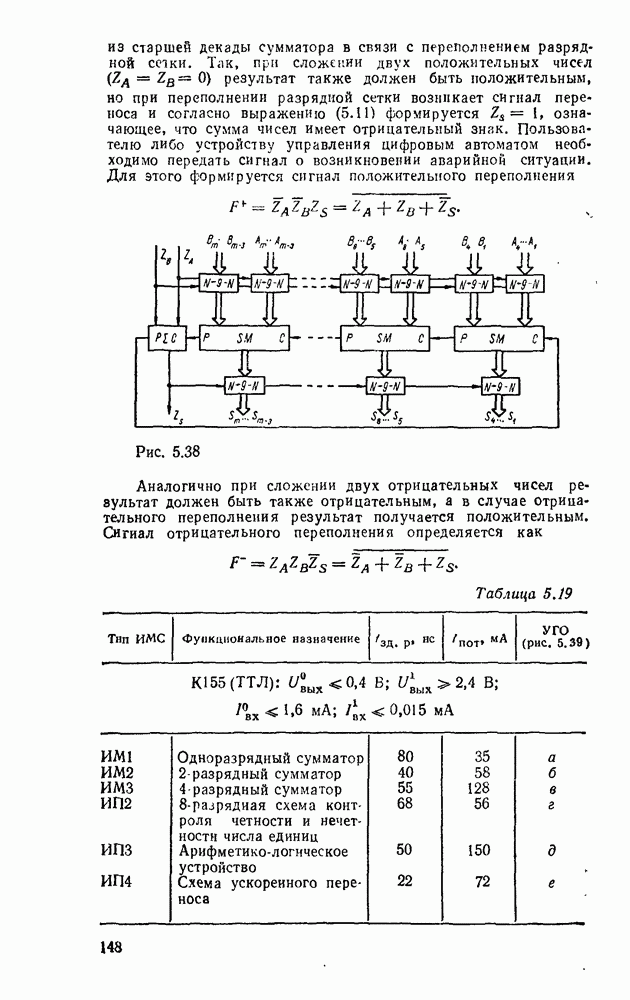
а также управляемая кодом схема сброса счетчика в нулевое состояние, как, например, на рис. 6.38 для случая  . На входы
. На входы  подается двоичный код, соответствующий
подается двоичный код, соответствующий

После  импульсов на выходах
импульсов на выходах  логических элементов
логических элементов  устанавливаются логические уровни
устанавливаются логические уровни

которые подаются на входы схемы совпадения  . Следующий счетный импульс
. Следующий счетный импульс  через вентиль
через вентиль  устанавливает
устанавливает  -триггер
-триггер  в единичное состояние и инверсный выход триггера
в единичное состояние и инверсный выход триггера  обусловливает установку разрядов счетчика в состояние
обусловливает установку разрядов счетчика в состояние  . Таким образом, через
. Таким образом, через  импульсов счетчик возвращается в исходное состояние. Например, для
импульсов счетчик возвращается в исходное состояние. Например, для  счета по модулю 10 на входы
счета по модулю 10 на входы  необходимо подать код 1001.
необходимо подать код 1001.

Рис. 6.38.
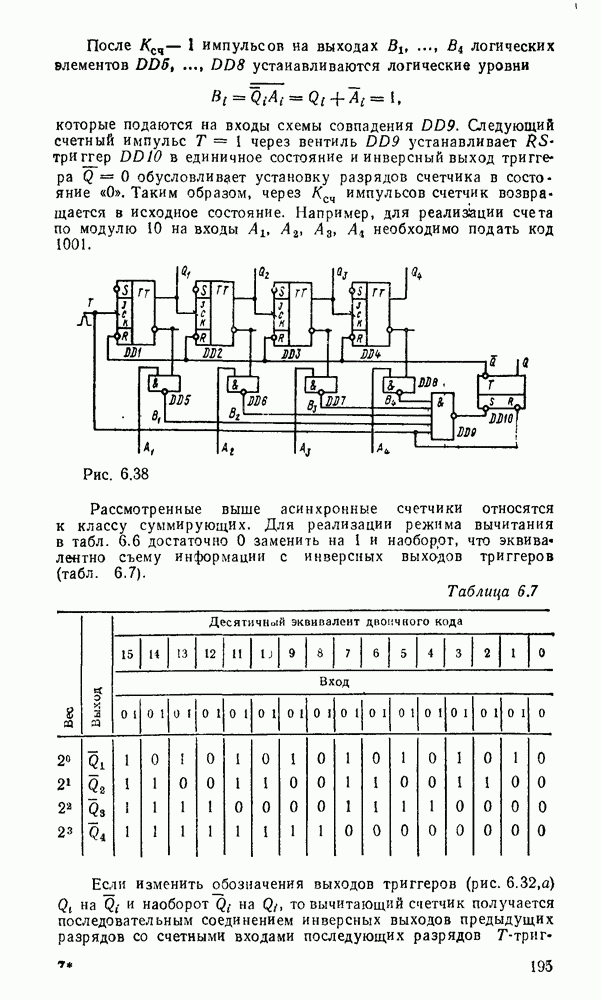
Рассмотренные выше асинхронные счетчики относятся к классу суммирующих. Для реализации режима вычитания в табл. 6.6 достаточно 0 заменить на 1 и наоборот, что эквивалентно съему информации с инверсных выходов триггеров (табл. 6.7).
Таблица 6.7

Если изменить обозначения выходов триггеров (рис. 6.32,а)  на
на  и наоборот
и наоборот  на
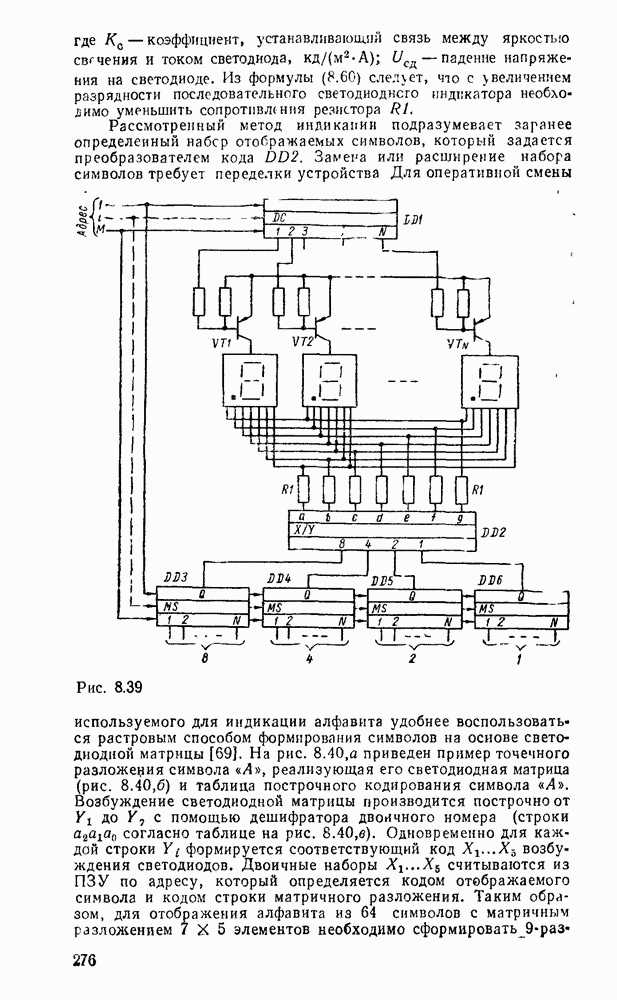
на  , то вычитающий счетчик получается последовательным соединением инверсных выходов предыдущих разрядов со счетными входами последующих разрядов Т-триггеров (рис. 6.39).
, то вычитающий счетчик получается последовательным соединением инверсных выходов предыдущих разрядов со счетными входами последующих разрядов Т-триггеров (рис. 6.39).
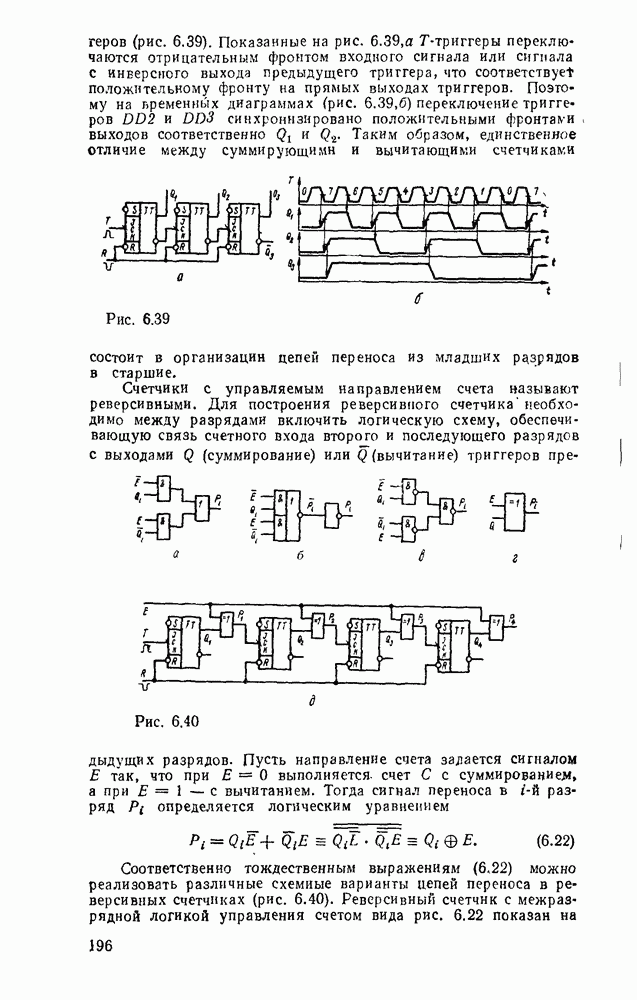
Показанные на рис. 6.39,а Т-триггеры переключаются отрицательным фронтом входного сигнала или сигнала с инверсного выхода предыдущего триггера, что соответствует положительному фронту на прямых выходах триггеров. Поэтому на временных диаграммах (рис.  ) переключение триггеров
) переключение триггеров  еинхроннзнровано положительными фронтами
еинхроннзнровано положительными фронтами  , выходов соответственно и
, выходов соответственно и  . Таким образом, единственное отличие между суммирующими и вычитающими счетчиками
. Таким образом, единственное отличие между суммирующими и вычитающими счетчиками

Рис. 6.39.
состоит в организации цепей переноса из младших рдзрядов в старшие.
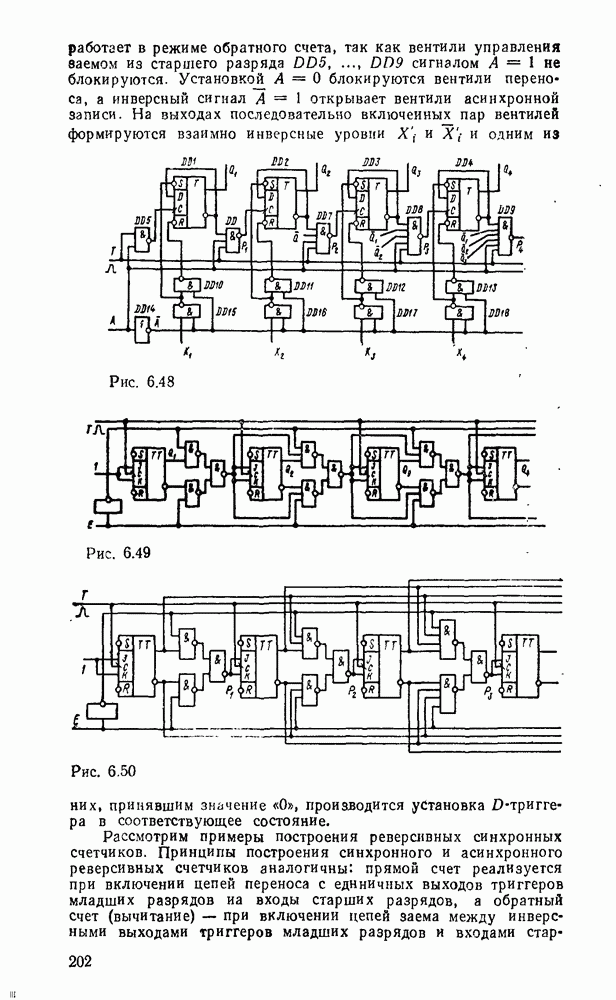
Счетчики с управляемым направлением счета называют реверсивными. Для построения реверсивного счетчика необходимо между разрядами включить логическую схему, обеспечивающую связь счетного входа второго и последующего разрядов с выходами Q (суммирование) или Q (вычитание) триггеров предыдущих разрядов.

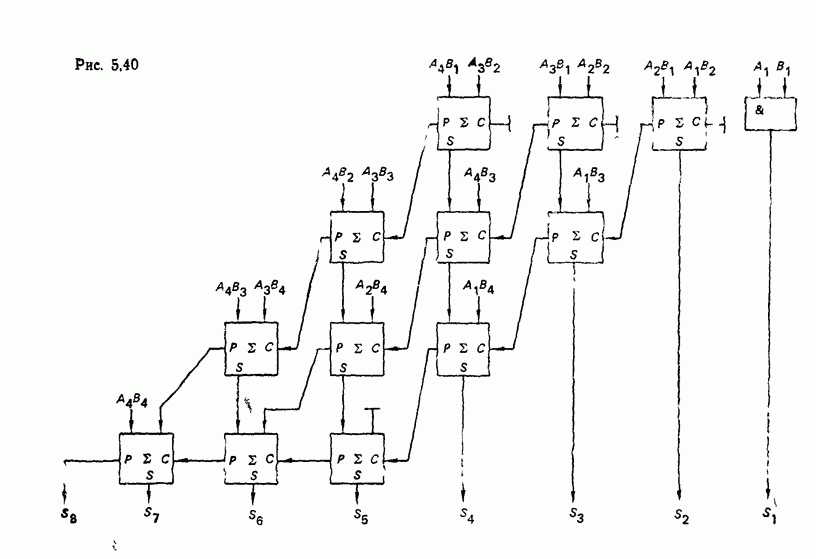
Рис. 6.40.
Пусть направление счета задается сигналом Е так, что при  выполняется, счет С с
выполняется, счет С с  , а при
, а при  — с вычитанием. Тогда сигнал переноса в
— с вычитанием. Тогда сигнал переноса в  разряд
разряд  определяется логическим уравнением
определяется логическим уравнением

Соответственно тождественным выражениям (6.22) можно реализовать различные схемные варианты цепей переноса в реверсивных счетчиках (рис. 6.40). Реверсивный счетчнк с межразрядной логикой управления счетом вида рис. 6.22 показан на рис. 6.40, д.
Включение дополнительных логических элементов между разрядами увеличивает время установления счетчика  и снижает максимальную частоту смены регистрируемых состояний. Не должна вводить в заблуждение кажущаяся проекта цепей переноса в виде рис. 6.40,г, так как время задержки одного логического элемента исключающее ИЛИ может и превышать время задержки сигнала в схемах на рис. 6,40,а, б, в.
и снижает максимальную частоту смены регистрируемых состояний. Не должна вводить в заблуждение кажущаяся проекта цепей переноса в виде рис. 6.40,г, так как время задержки одного логического элемента исключающее ИЛИ может и превышать время задержки сигнала в схемах на рис. 6,40,а, б, в.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
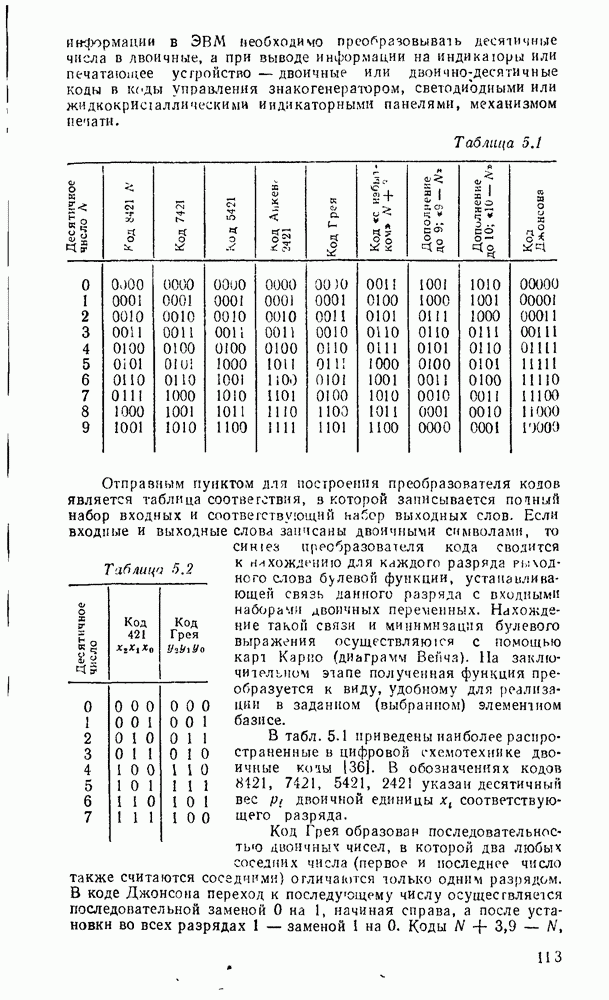
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
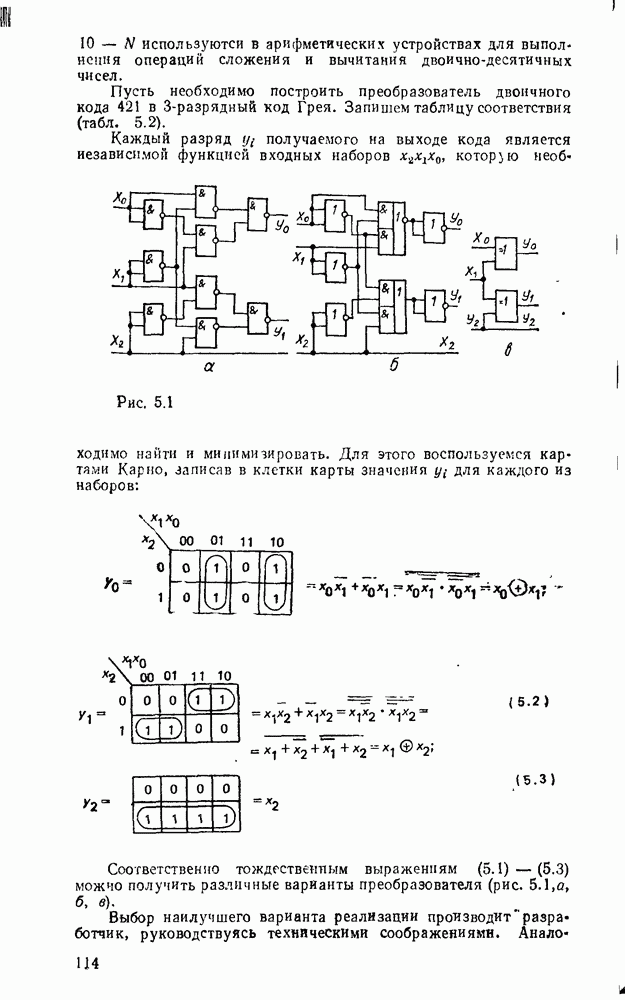
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
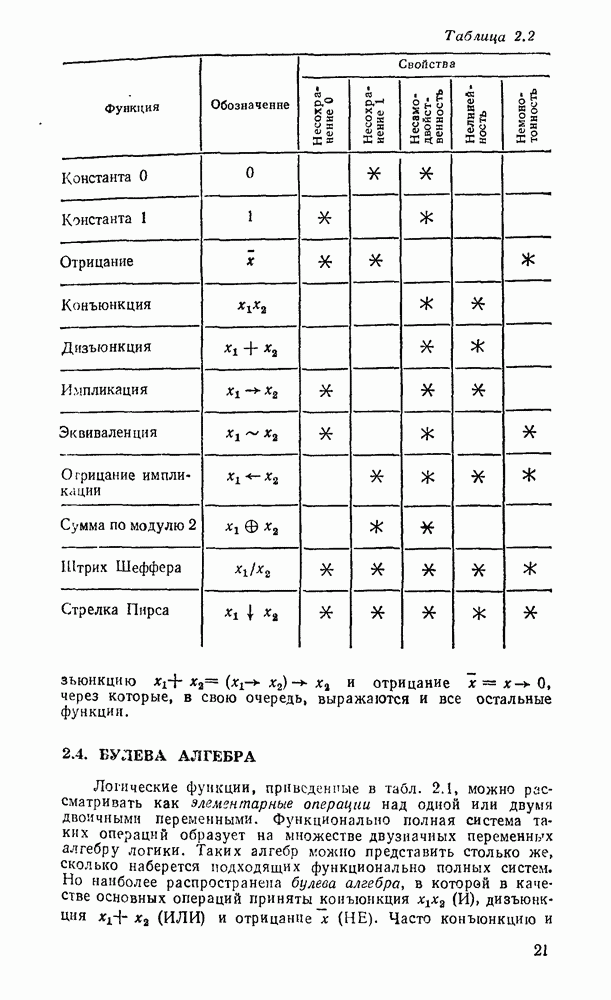
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
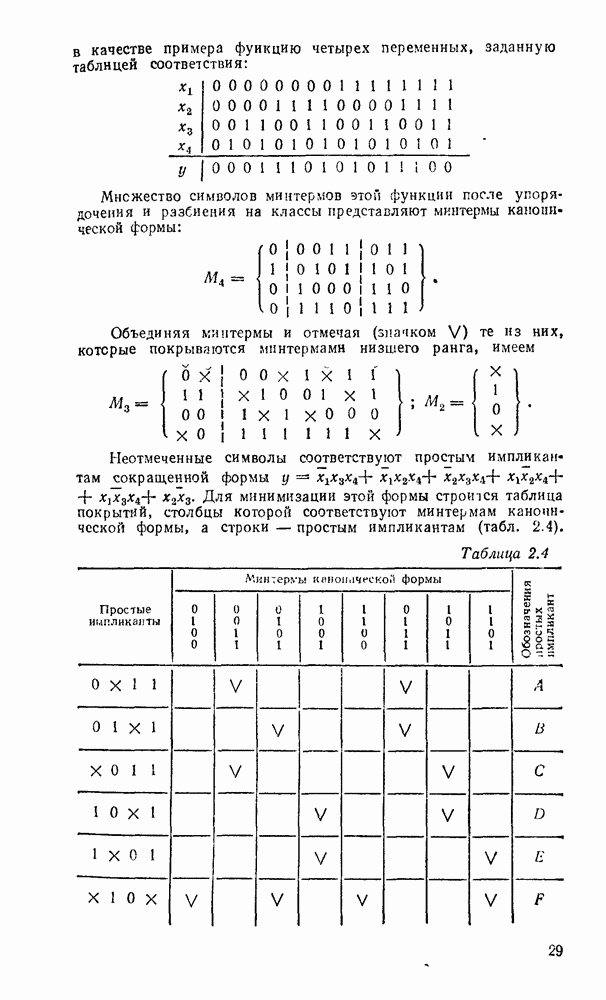
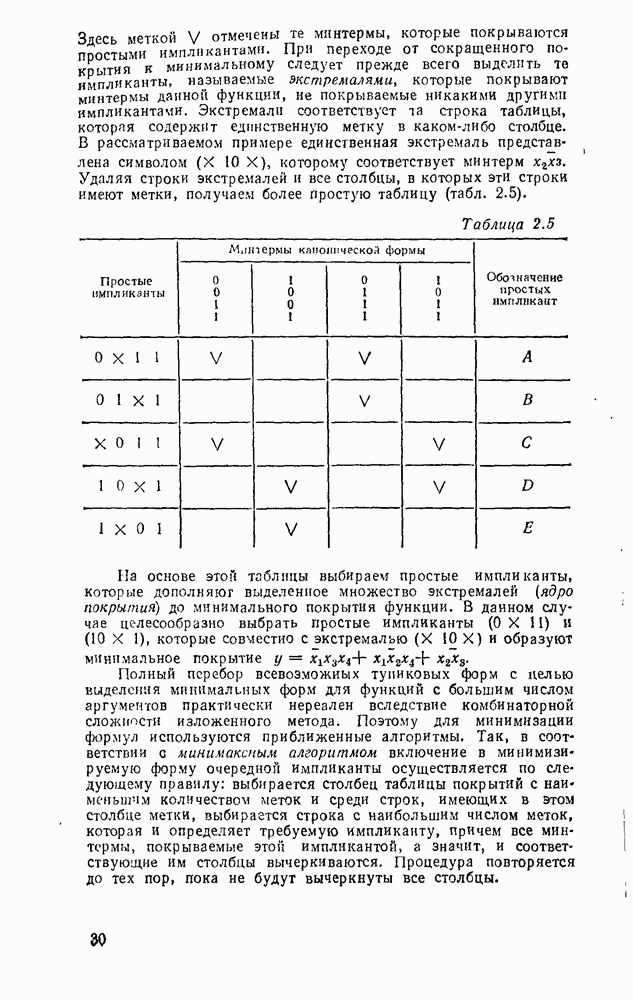
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
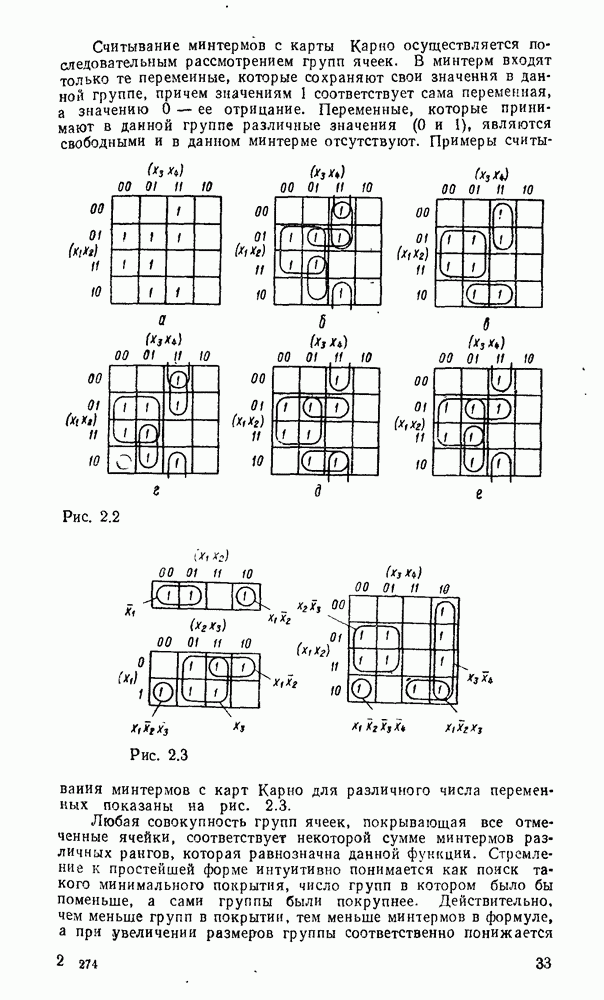
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
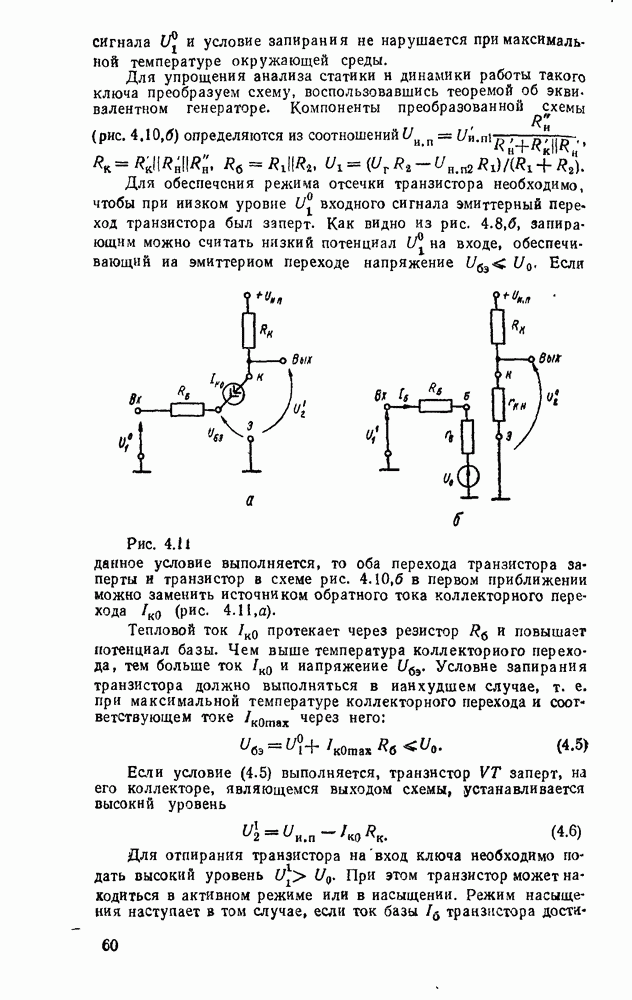
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
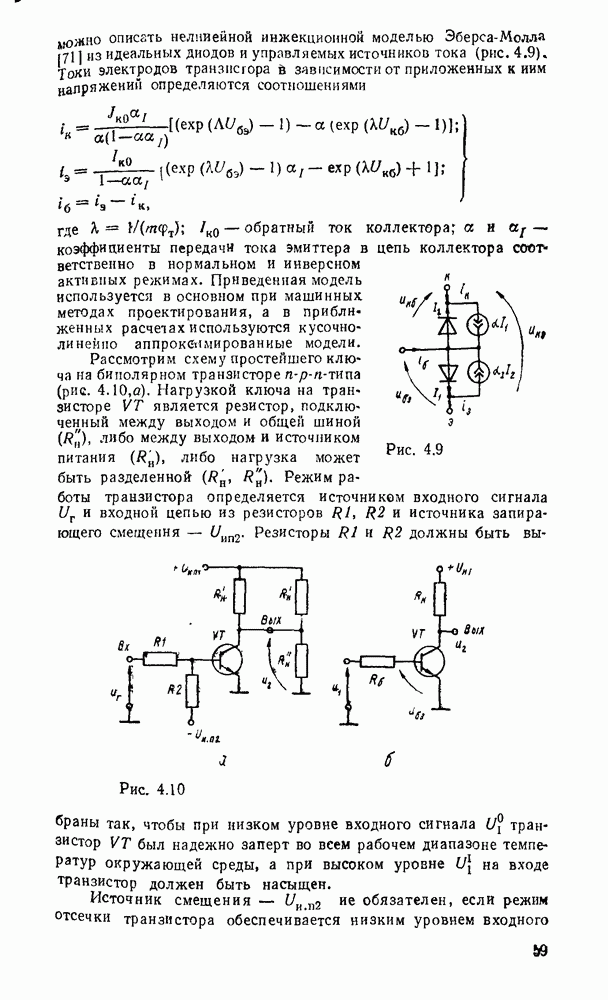
- Электронные ключи на биполярных транзисторах.
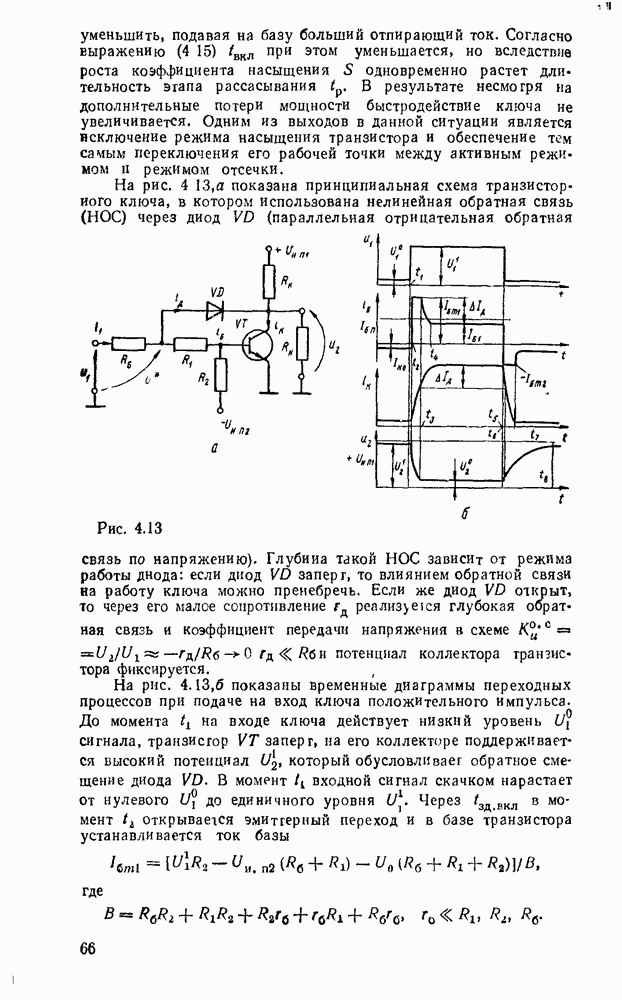
- Ключ на биполярном транзисторе с нелинейной обратной связью.
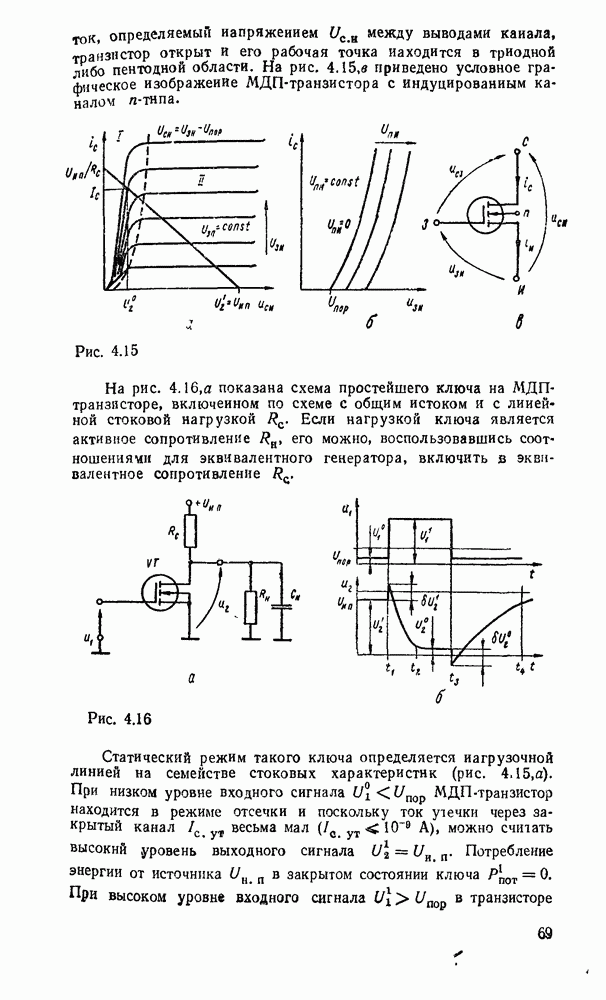
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
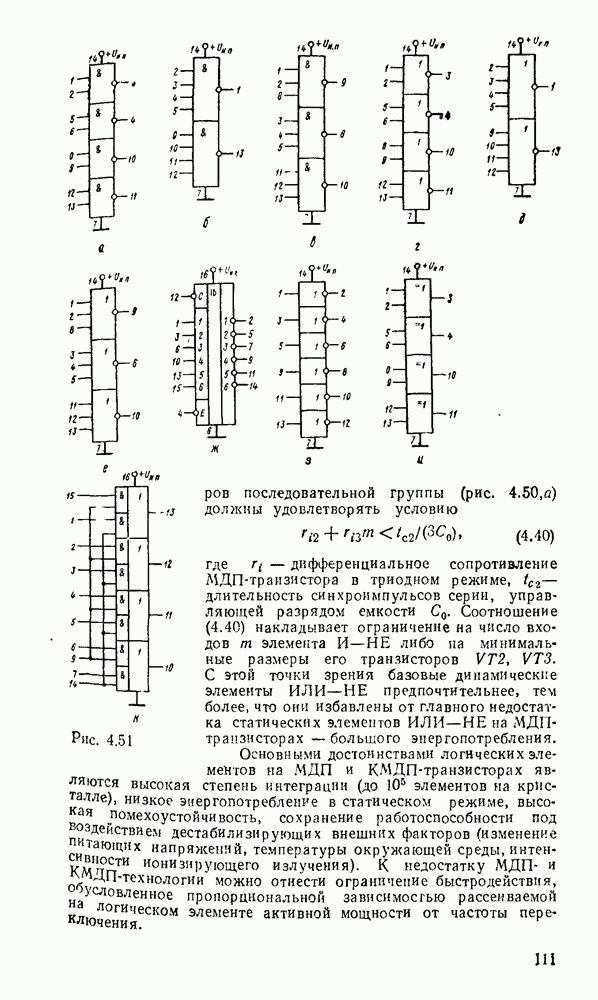
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
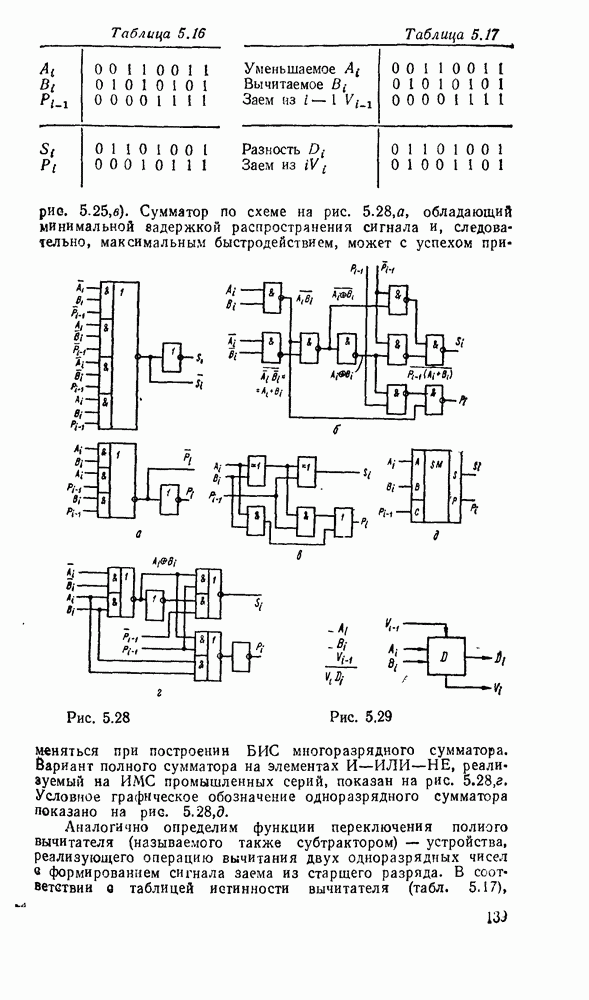
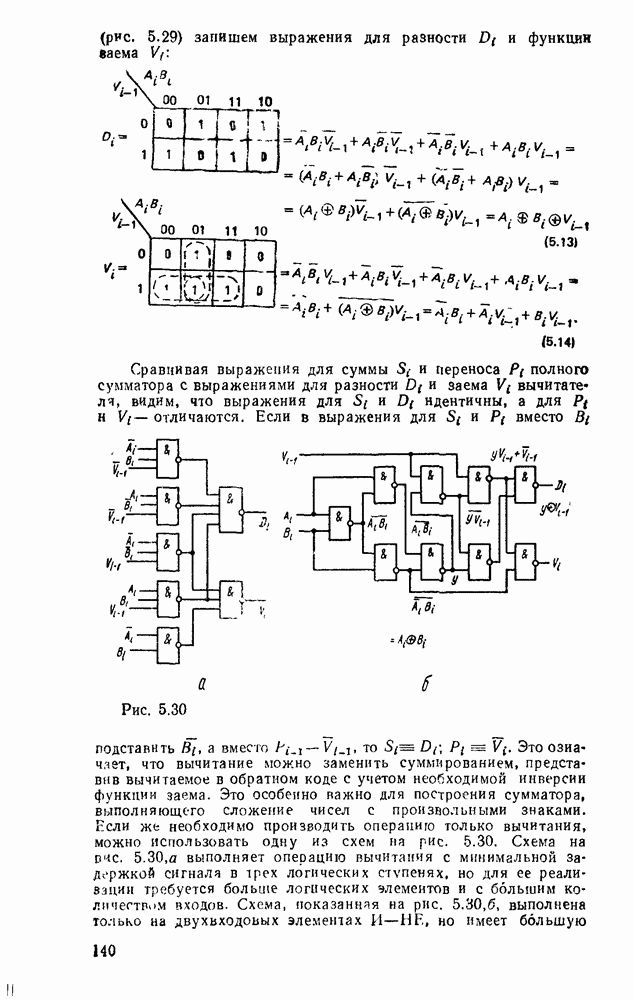
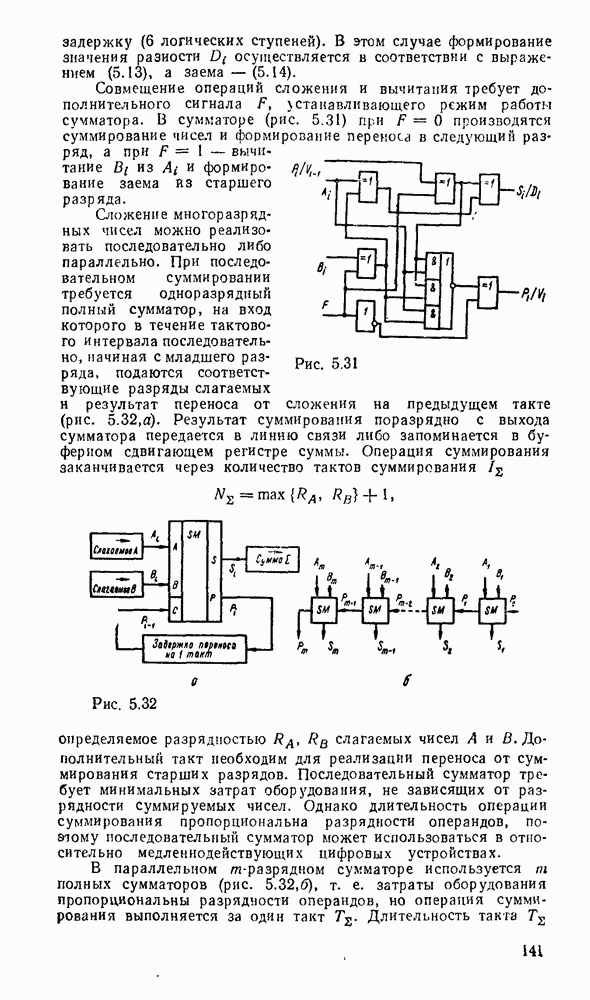
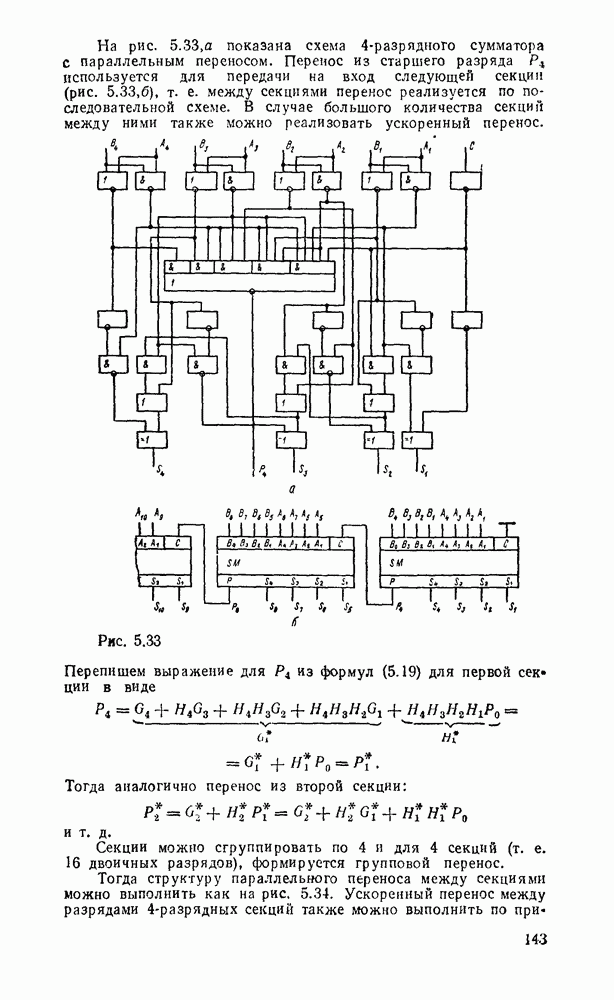
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
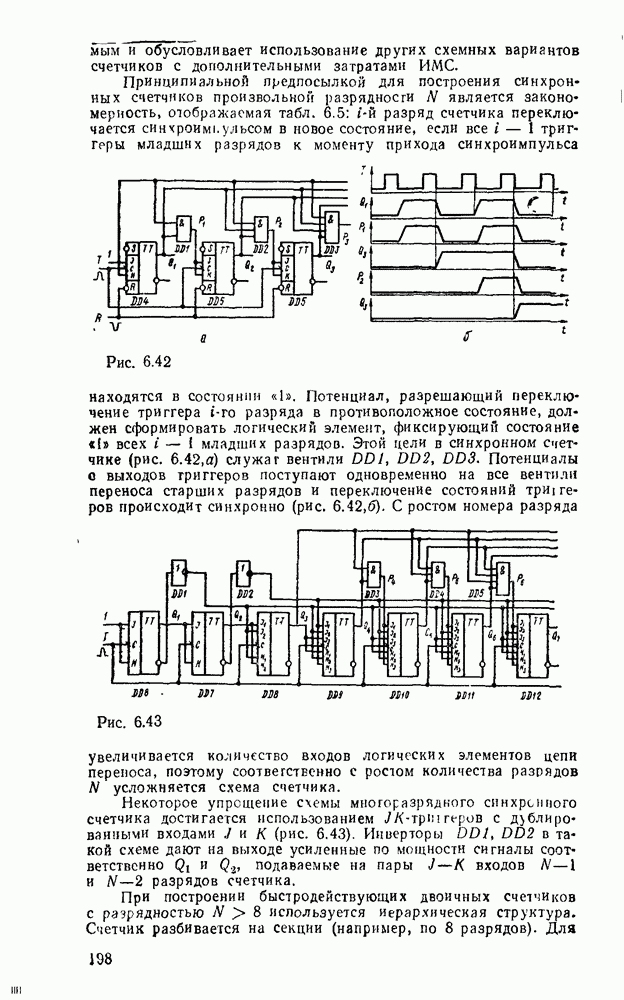
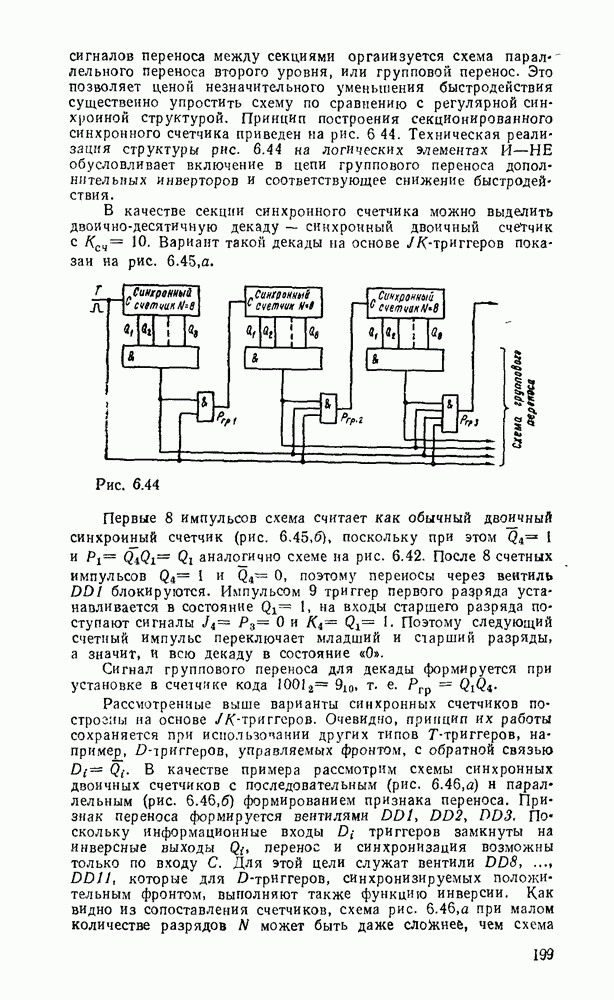
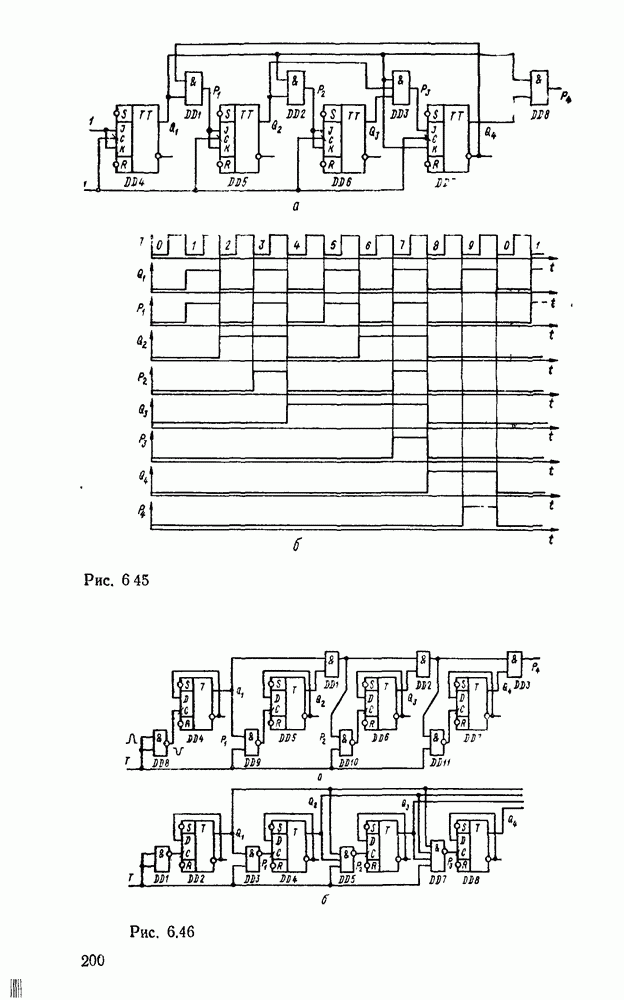
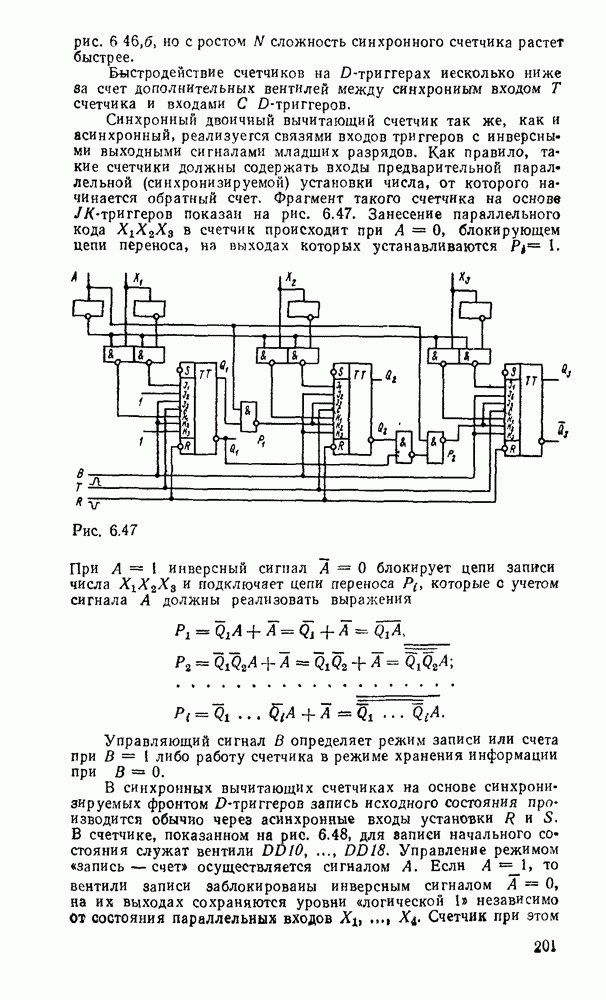
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
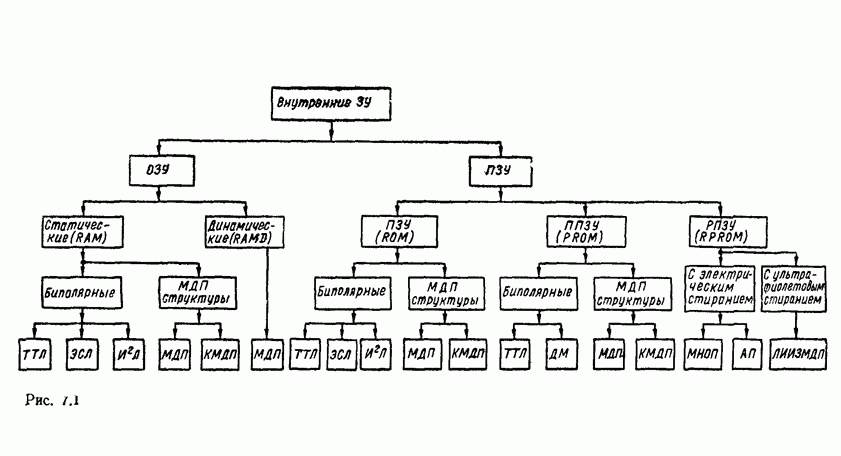
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
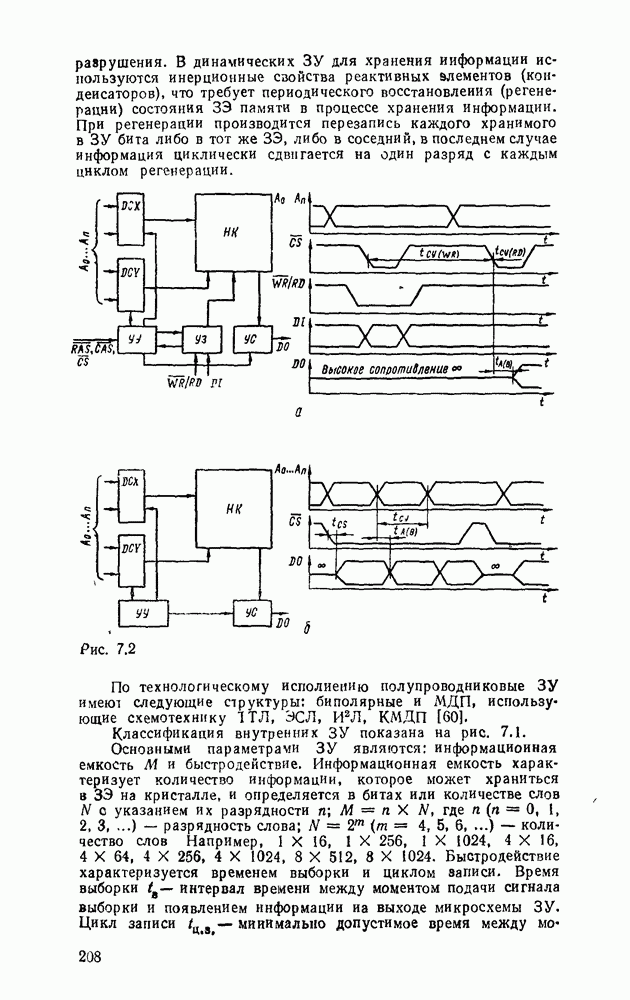
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
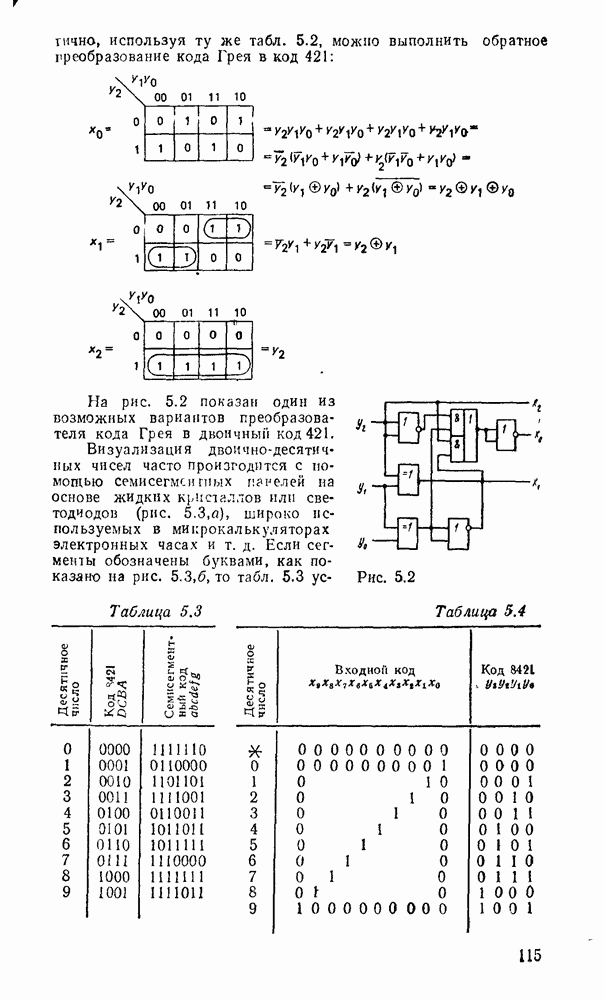
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
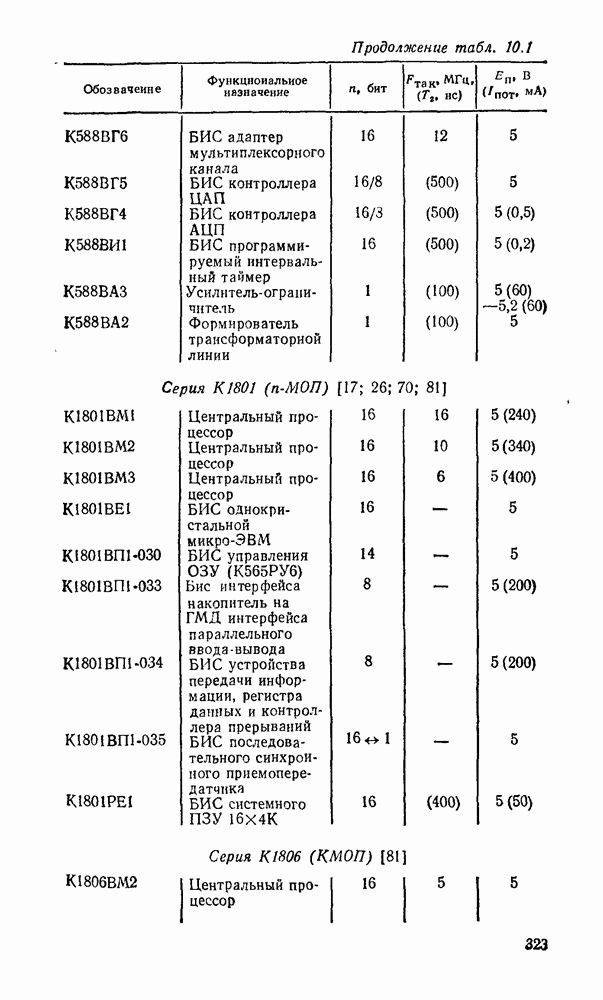
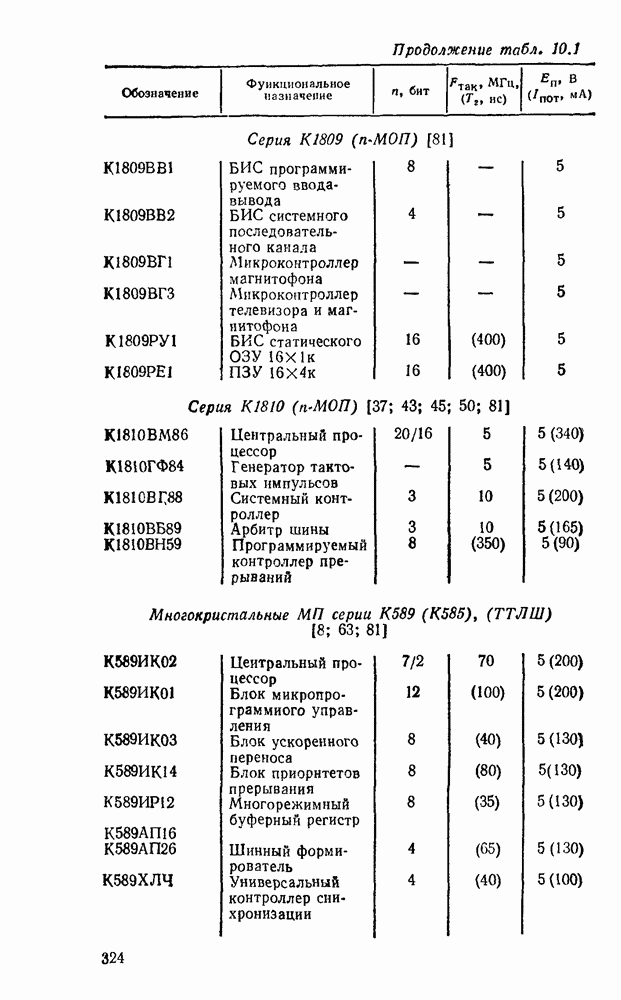
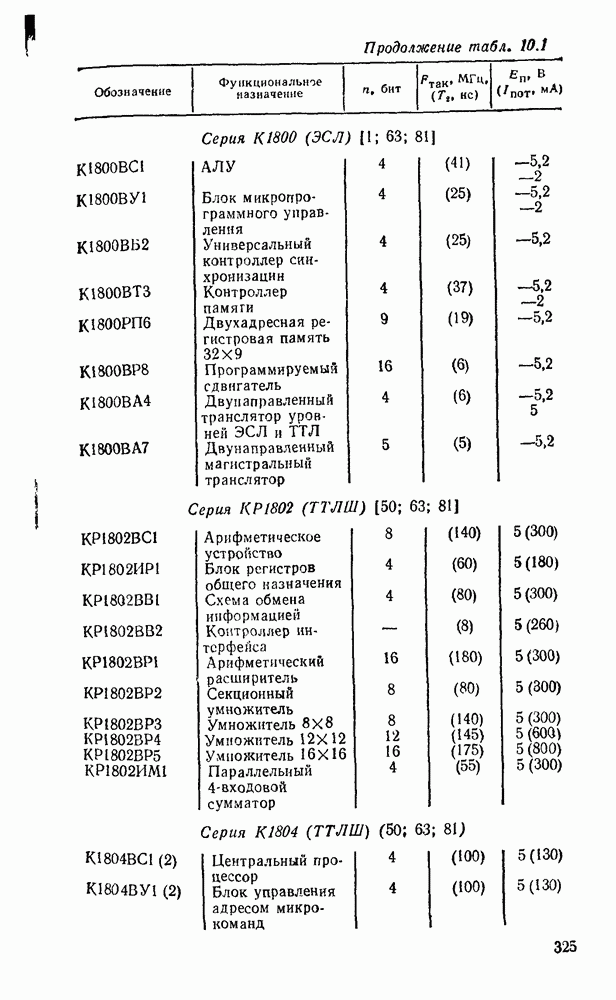
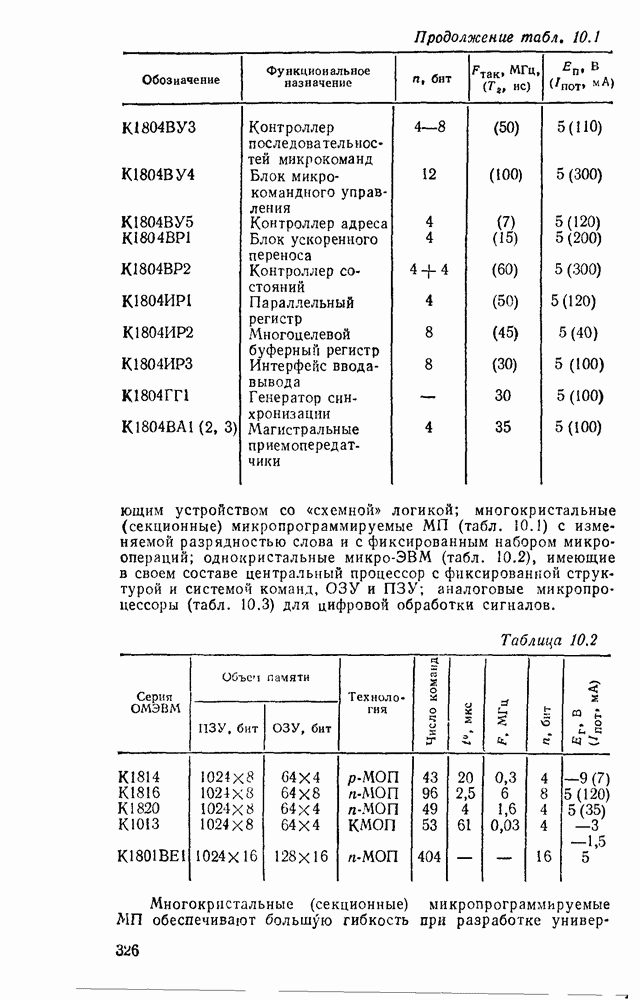
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
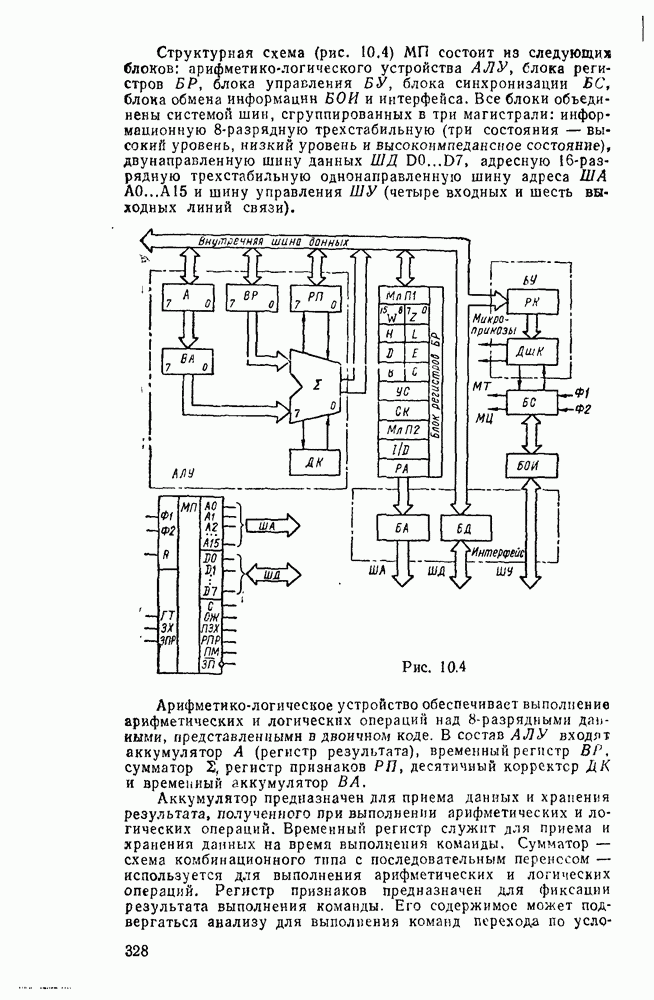
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
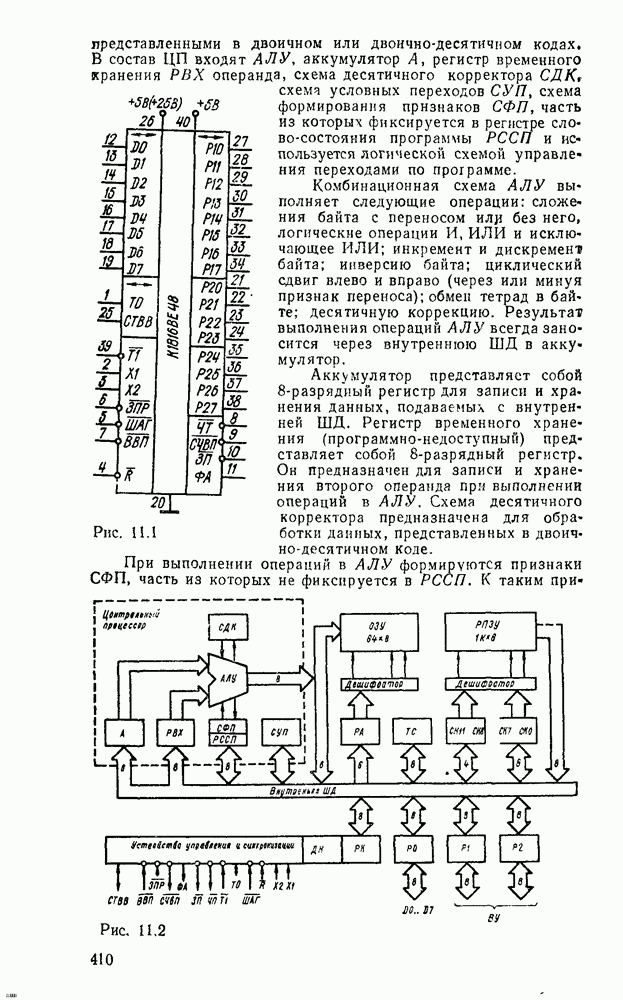
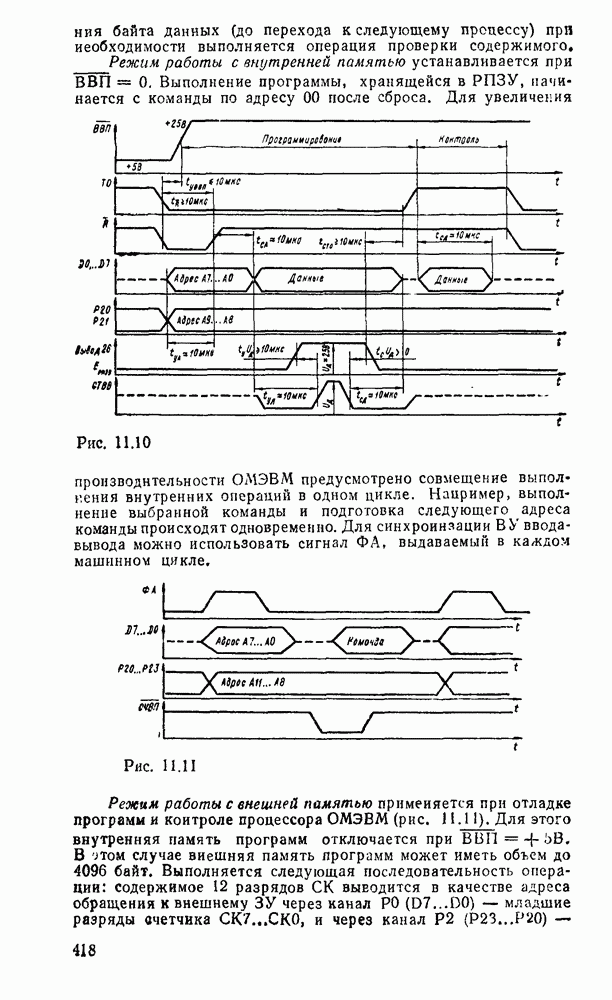
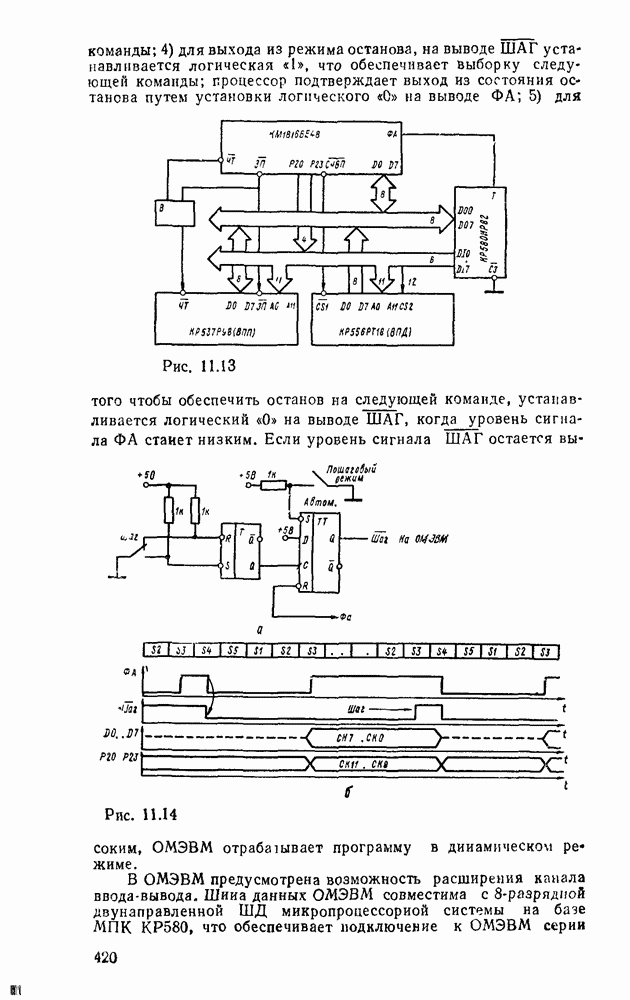
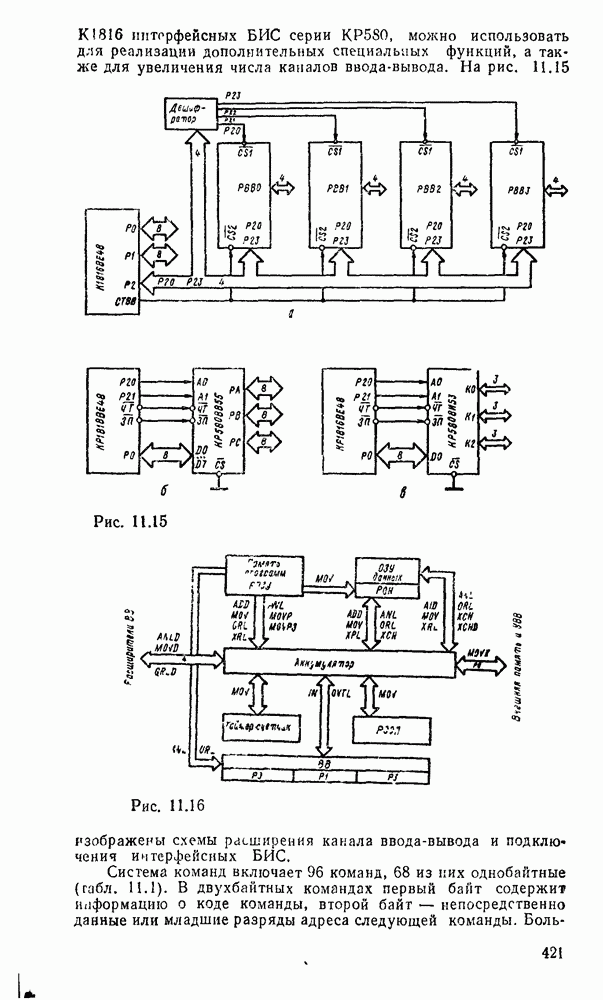
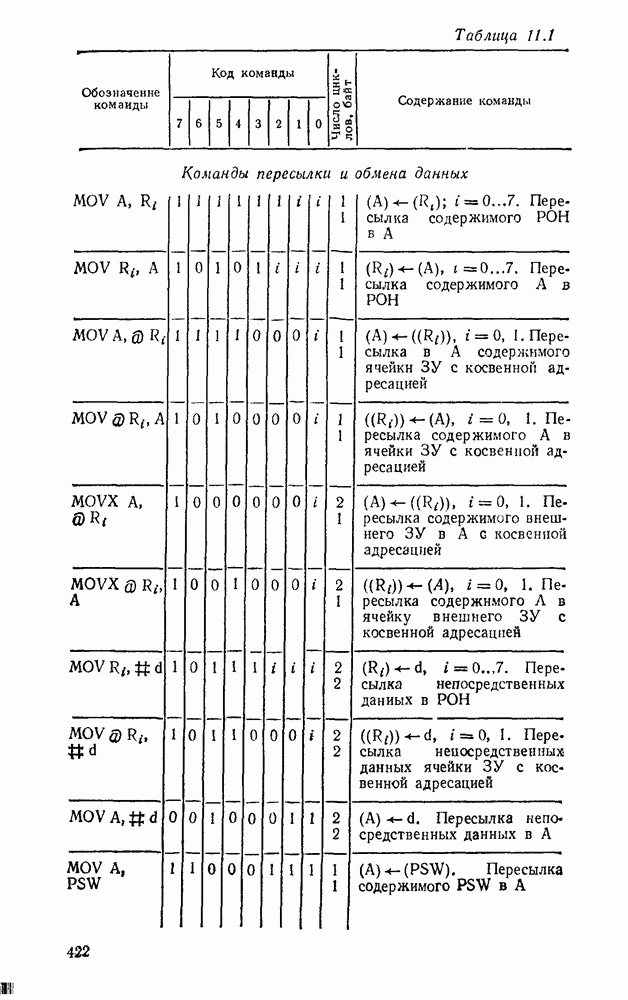
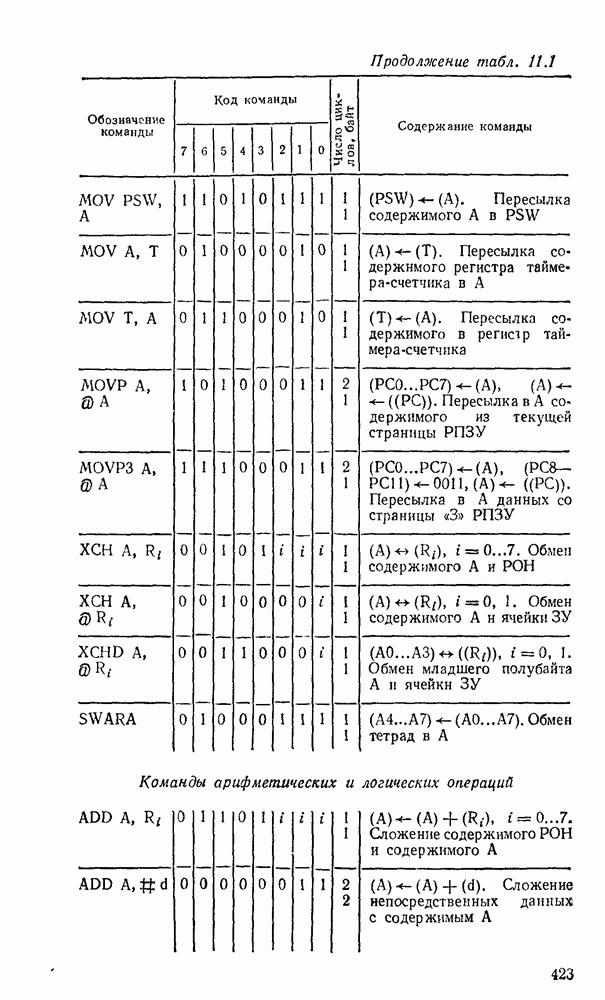
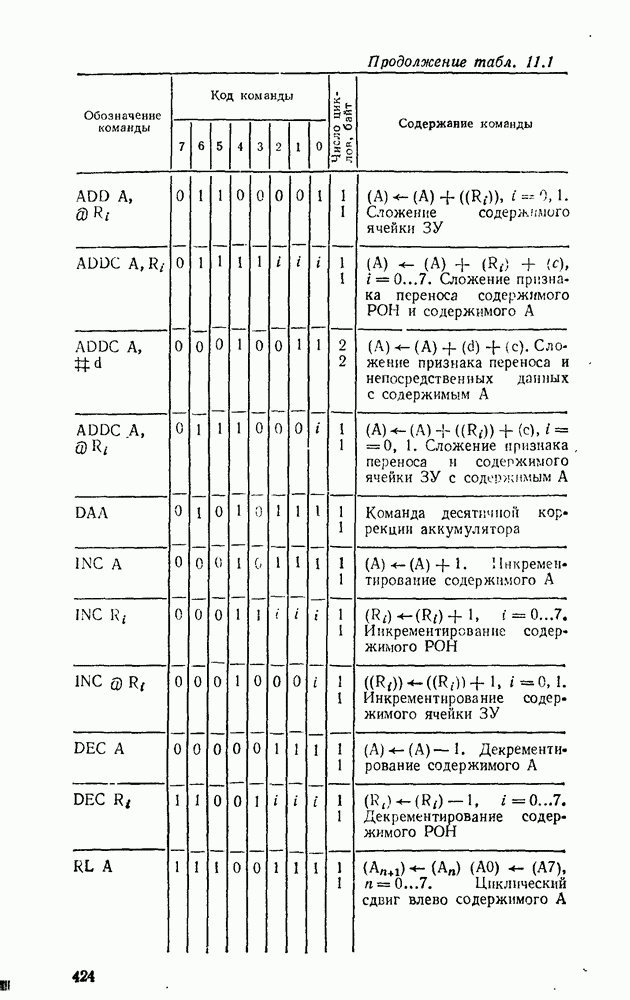
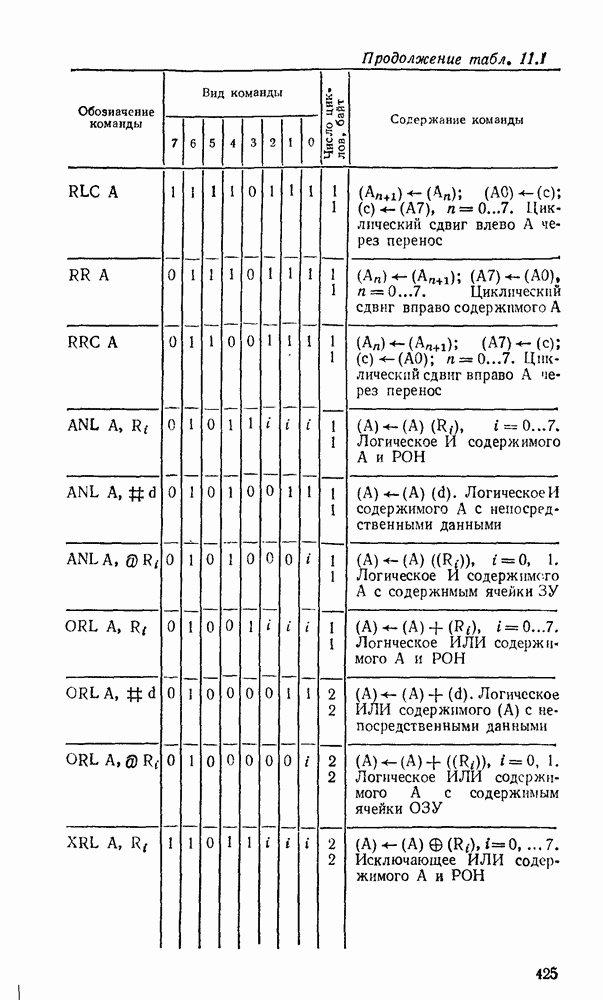
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
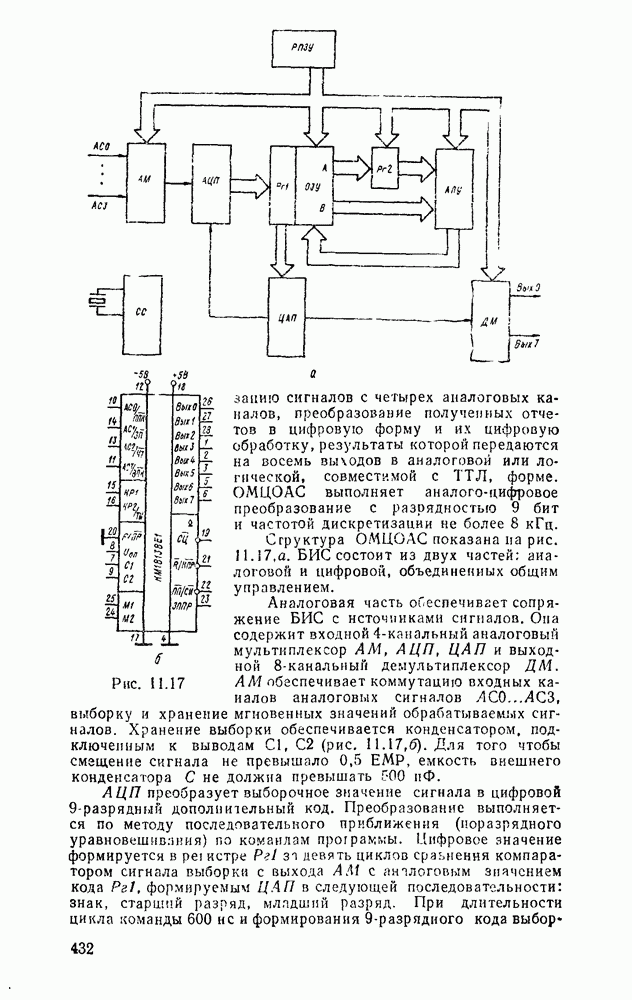
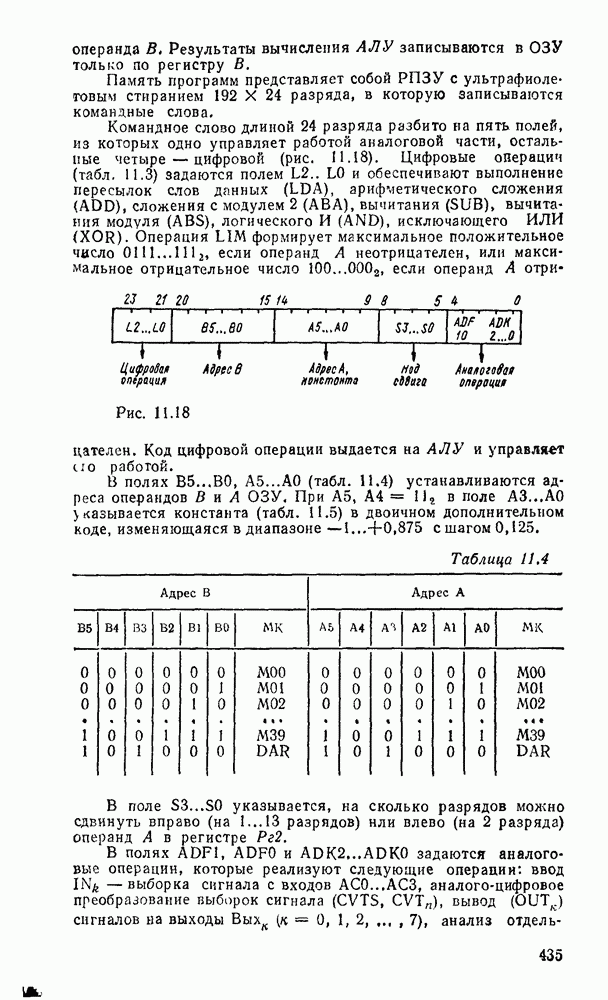
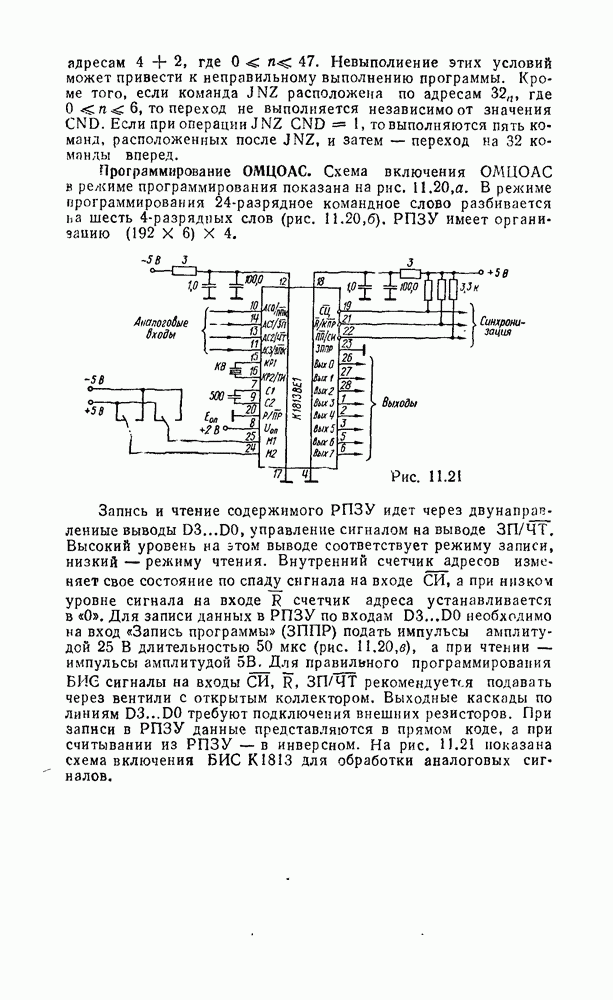
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ