| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
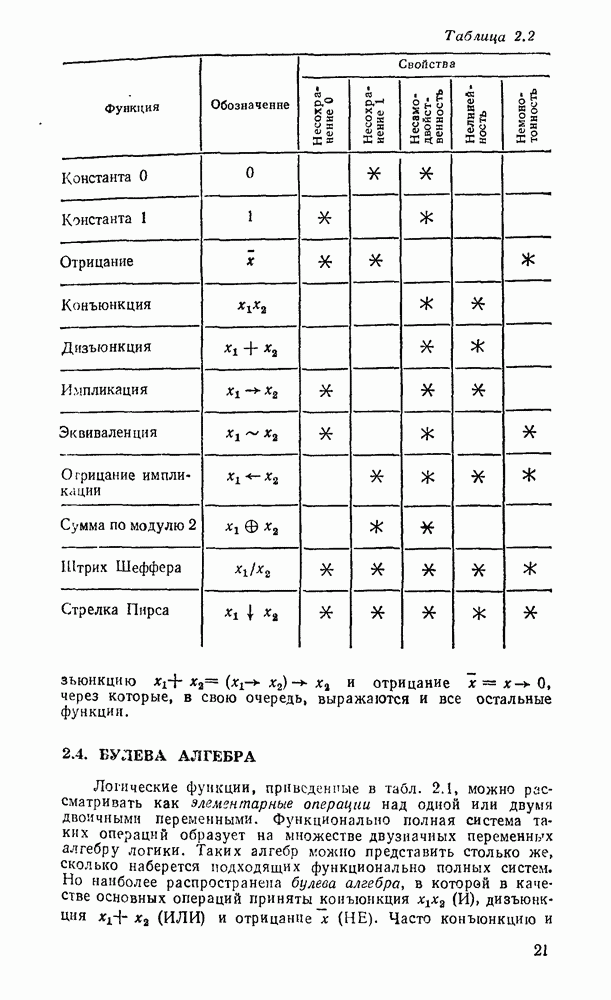
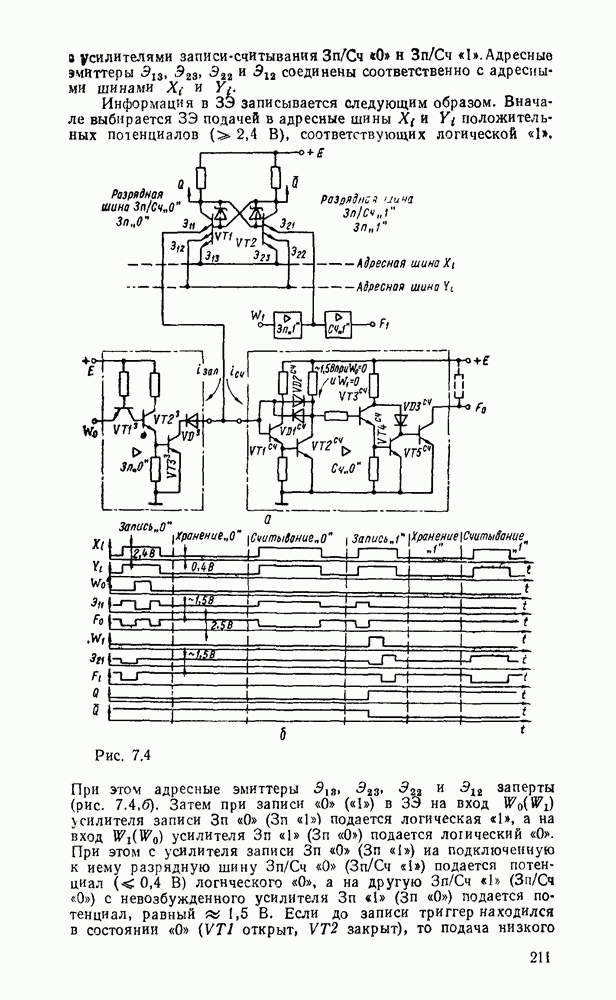
3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
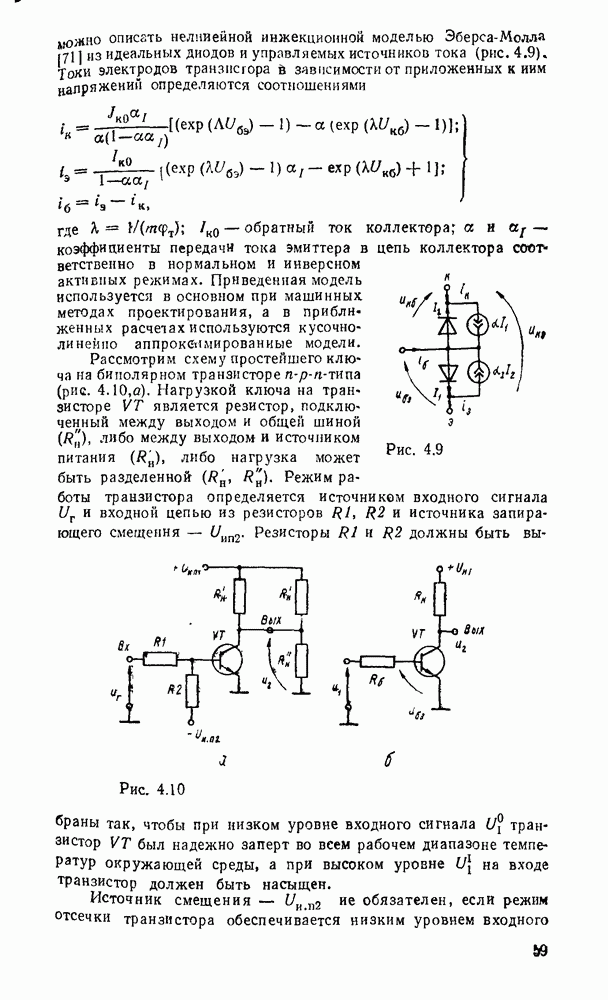
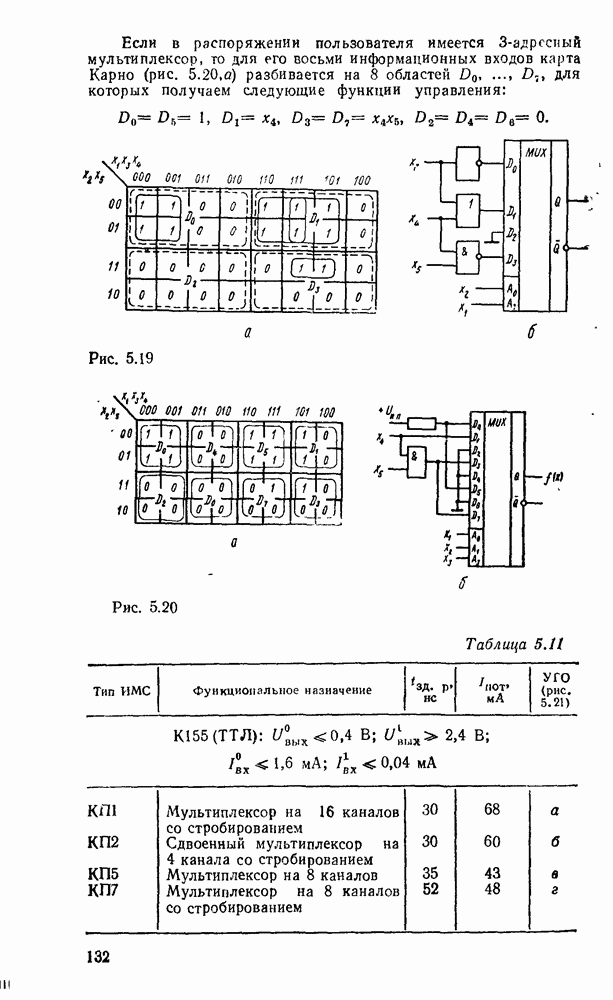
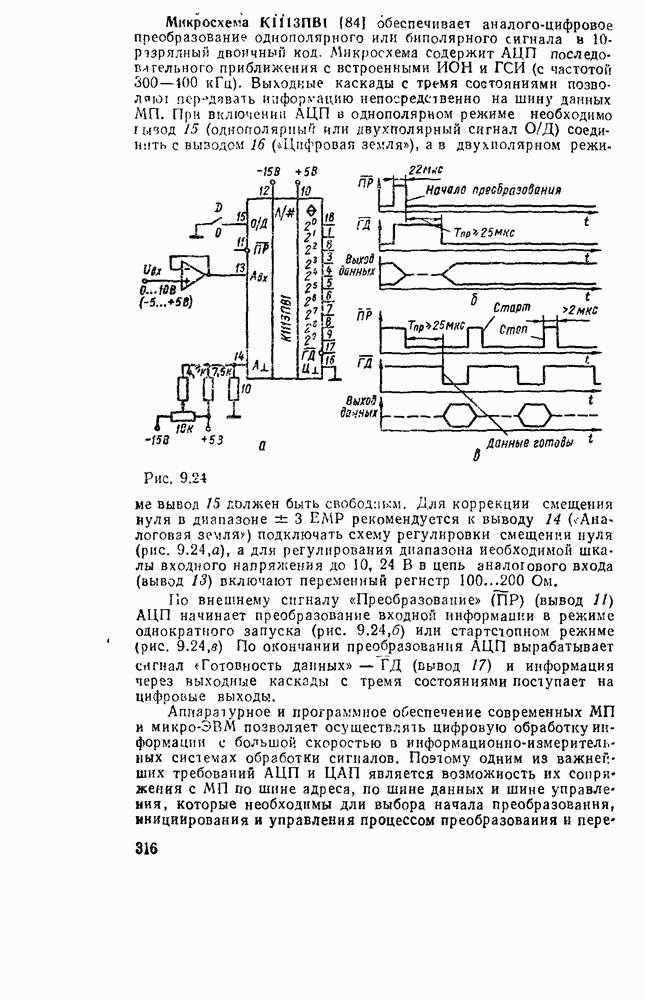
Реализацию нескольких функций одних и тех же переменных можно представить как простое объединение схем, реализующих каждую функцию отдельно. Но такой путь обычно не является наиболее экономичным. Часто бывает целесообразно преобразовать совокупность данных функций к такому виду, чтобы реализующие их схемы содержали  части, а схема с многими выходами представляла собой единое целое. Задача сводится к выбору для каждой функции такого покрытия, которое включало бы возможно больше импликант, содержащихся в покрытиях других функций.
части, а схема с многими выходами представляла собой единое целое. Задача сводится к выбору для каждой функции такого покрытия, которое включало бы возможно больше импликант, содержащихся в покрытиях других функций.
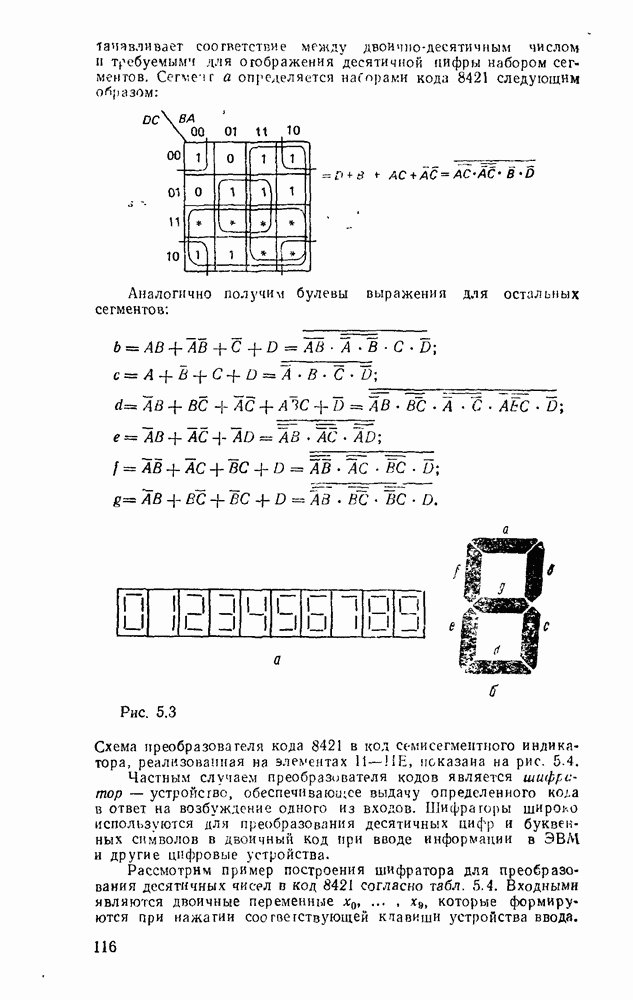
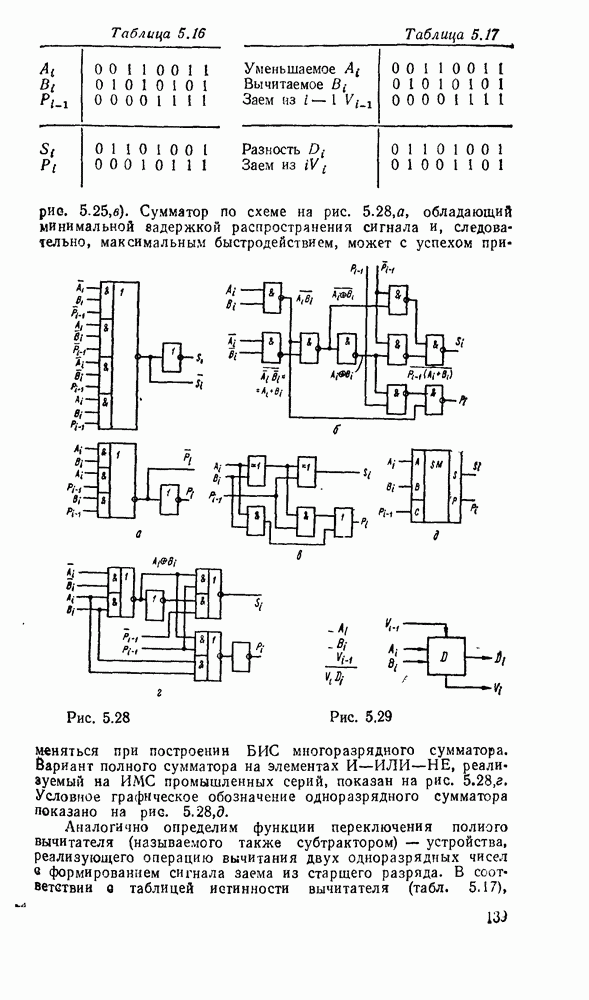
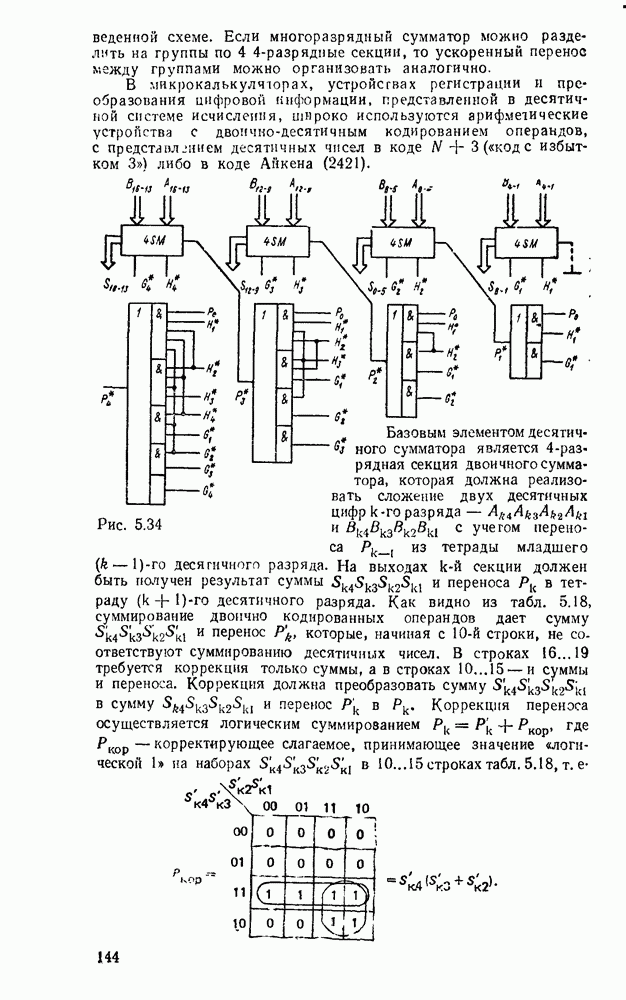
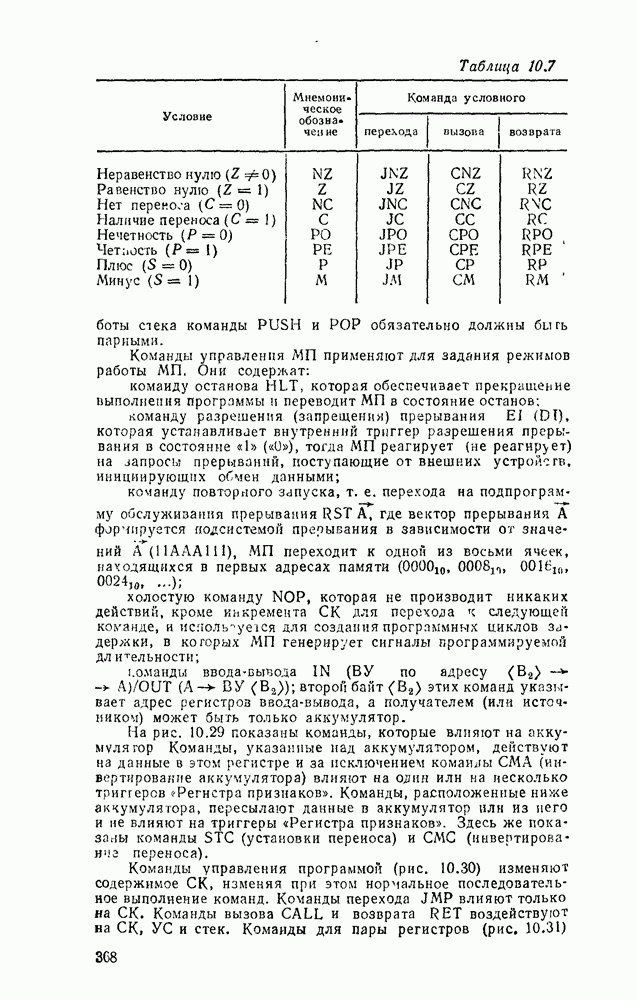
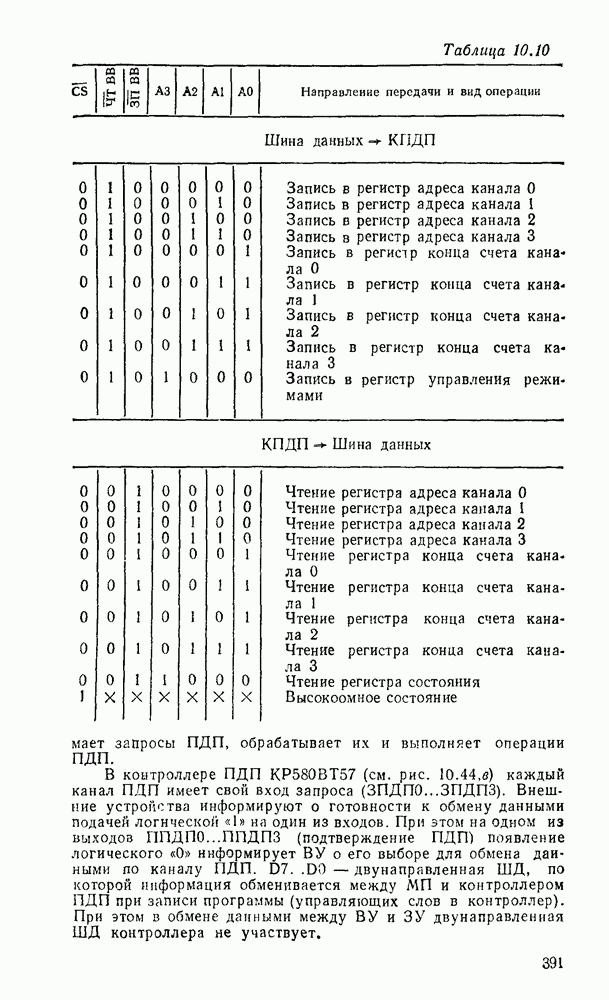
Примером такого подхода к синтезу схем с многими выходами может служить реализация преобразователя кода прямого замещения в двоично-десятичный код 2421, таблица соответствия которого имеет вид (табл. 3.2).
Таблица 3.2

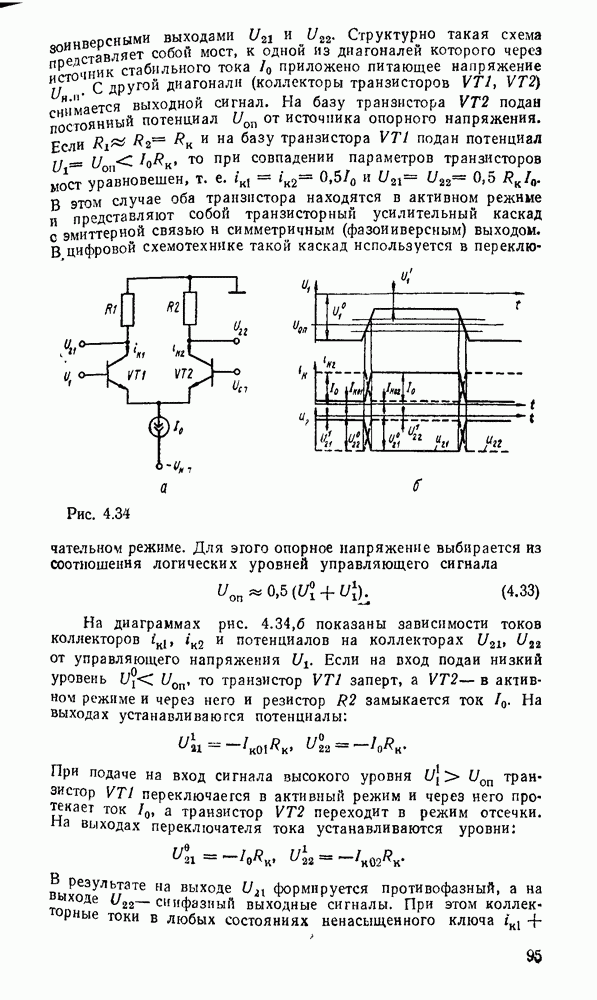
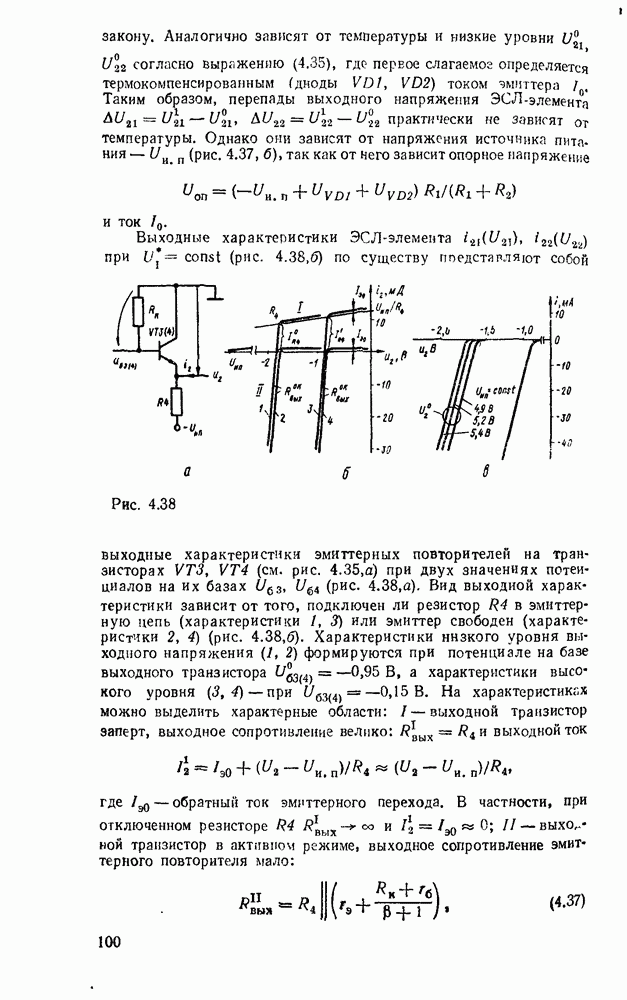
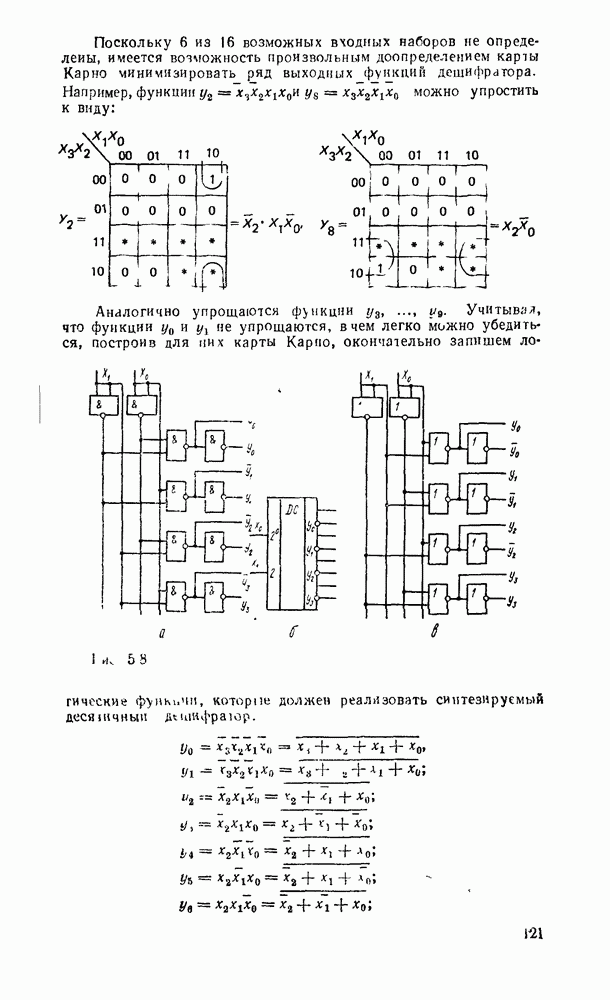
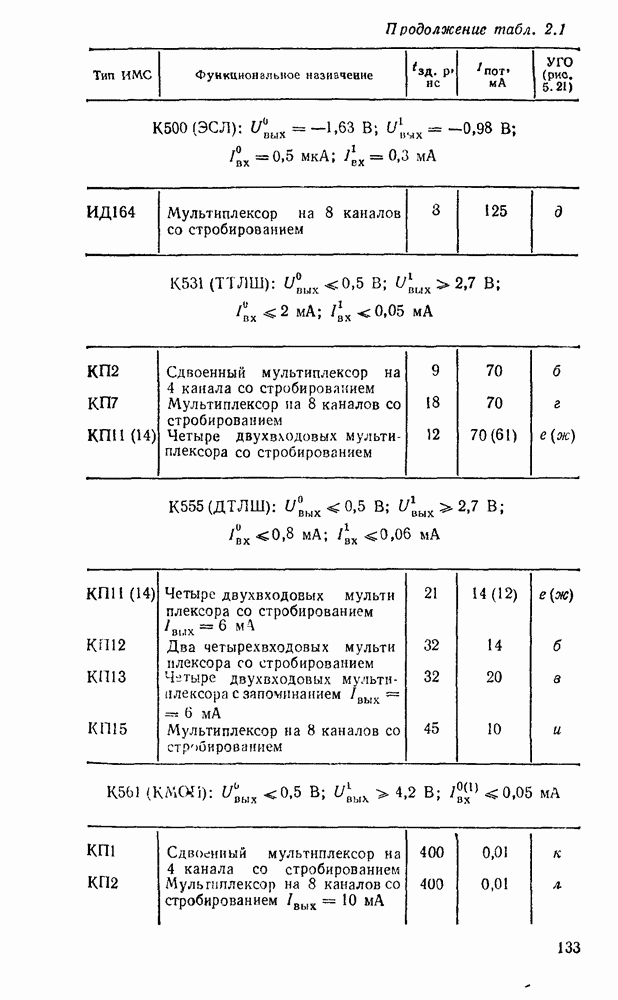
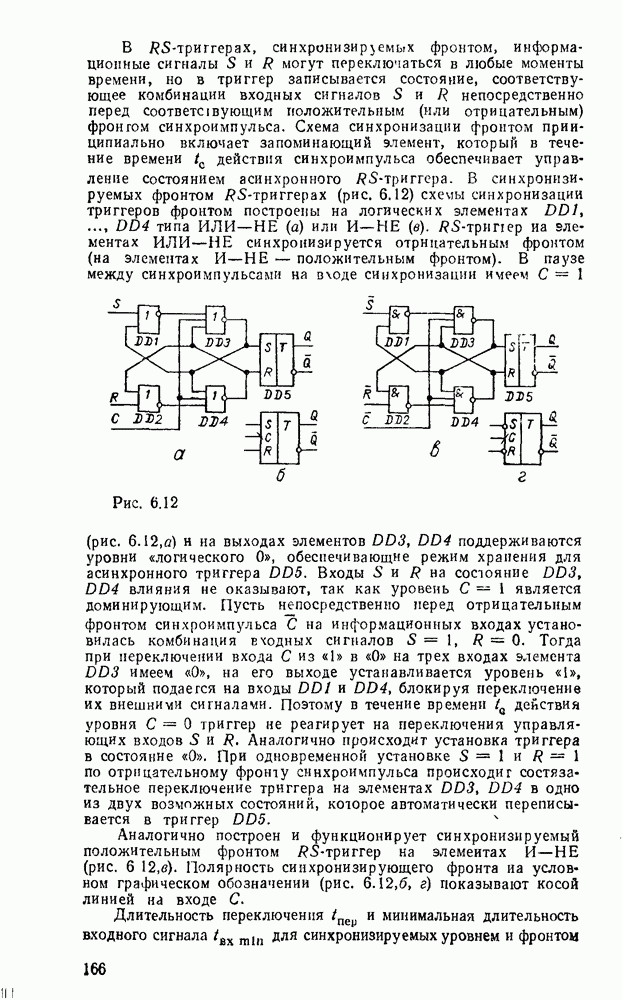
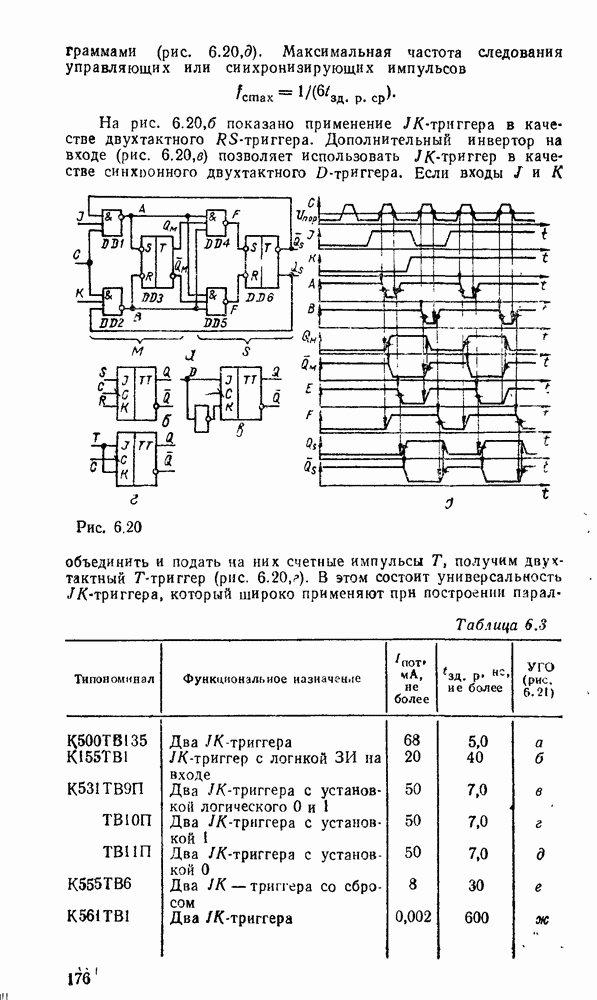
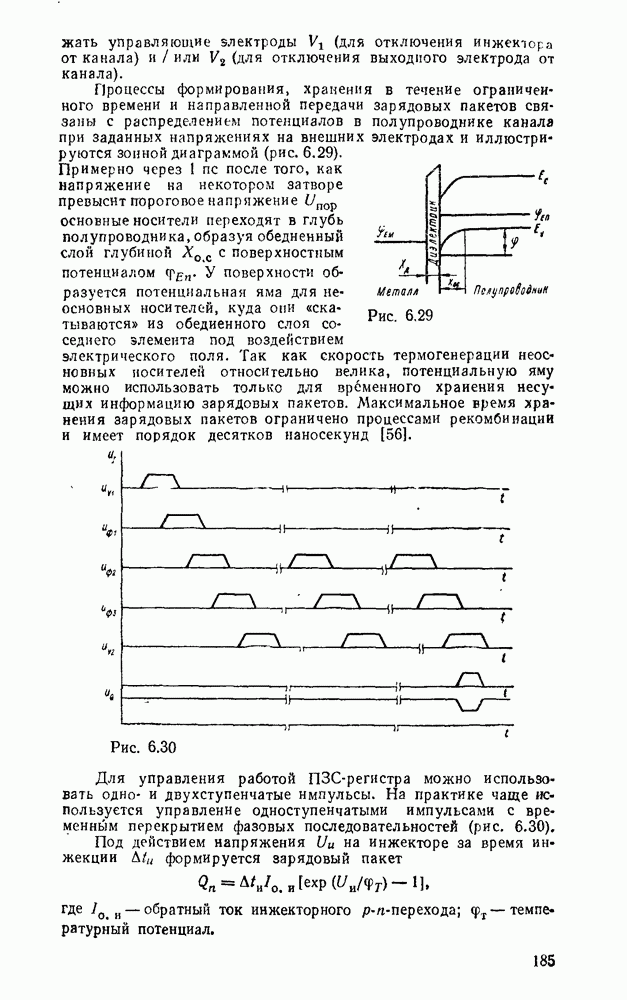
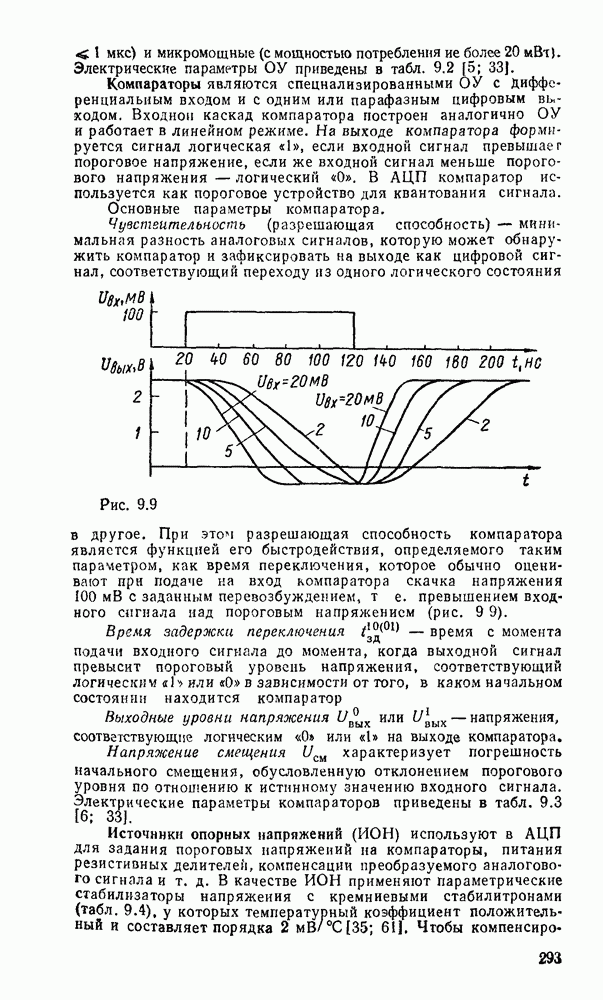
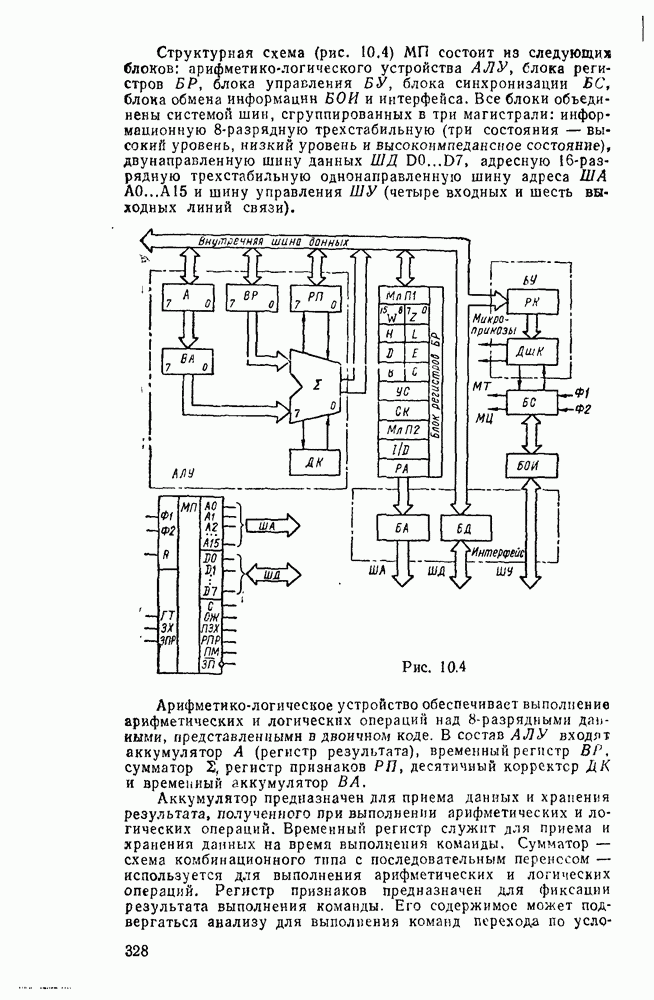
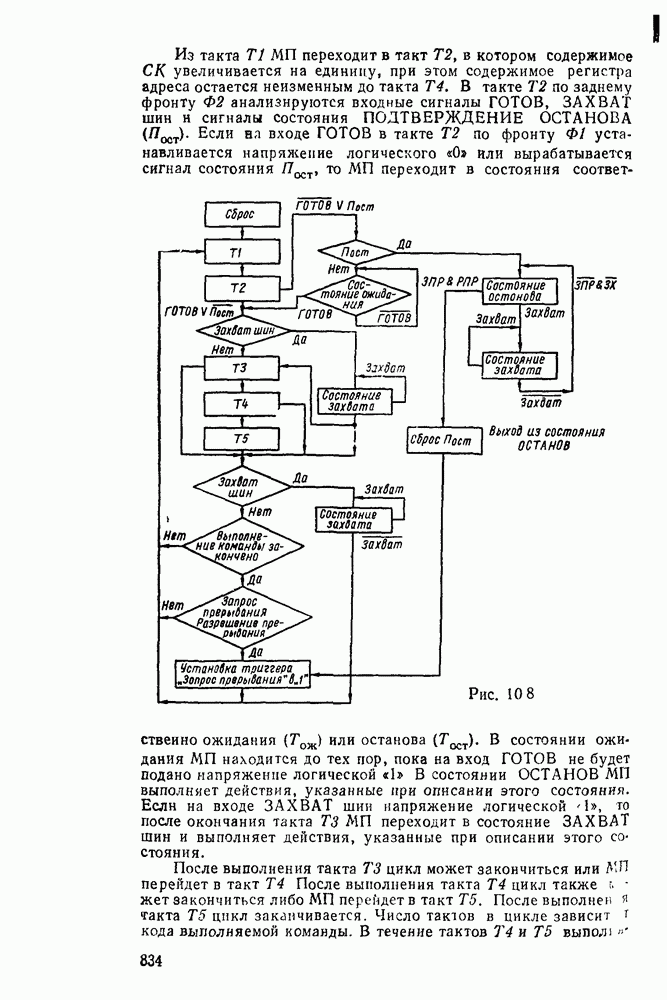
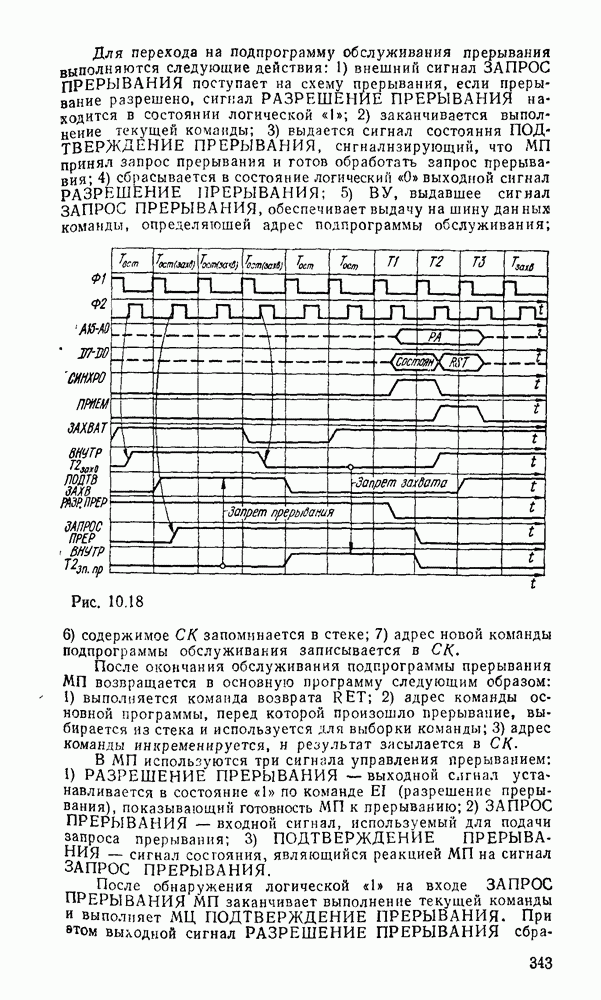
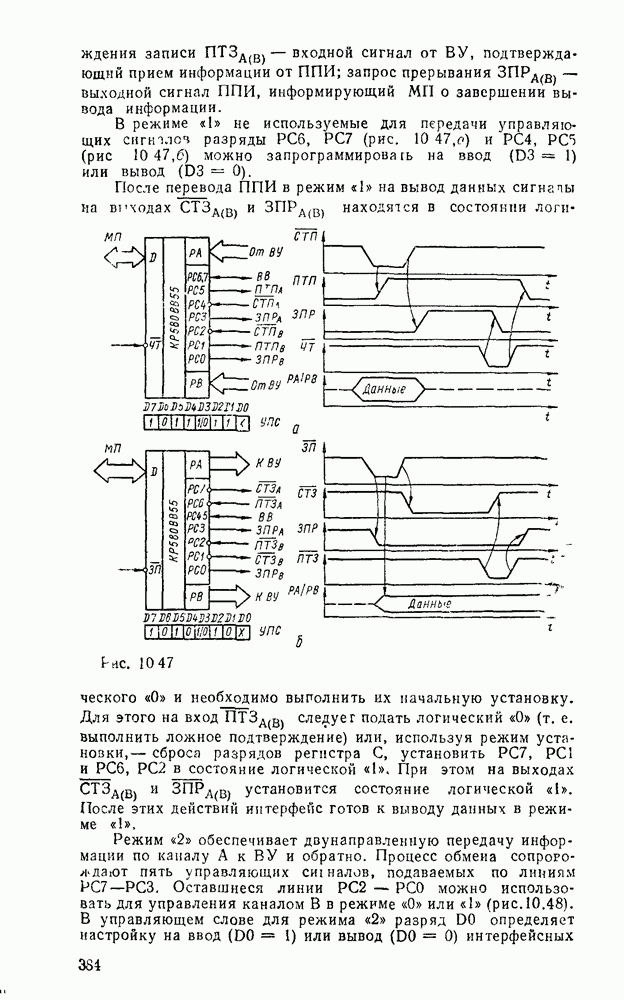
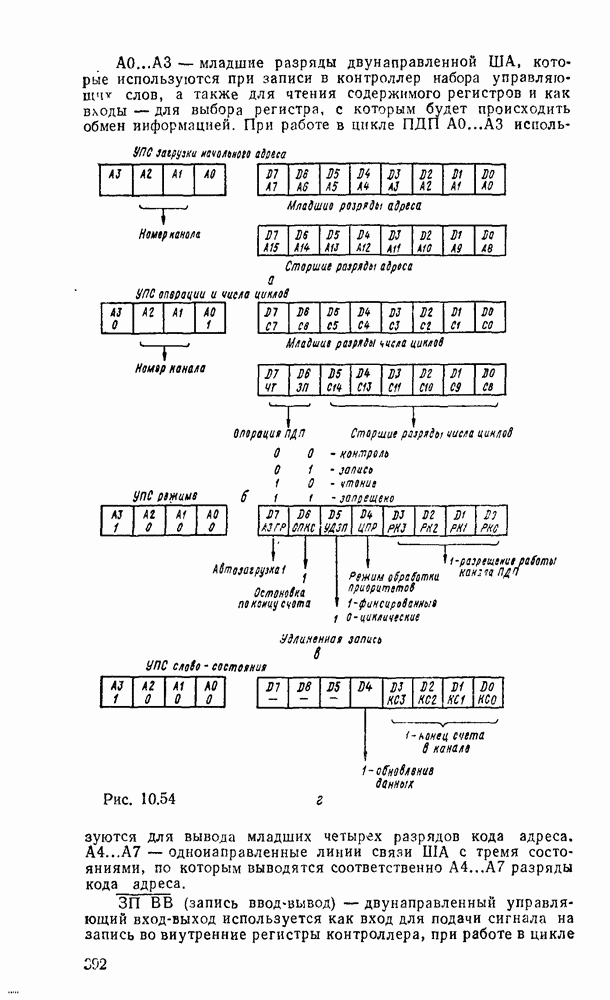
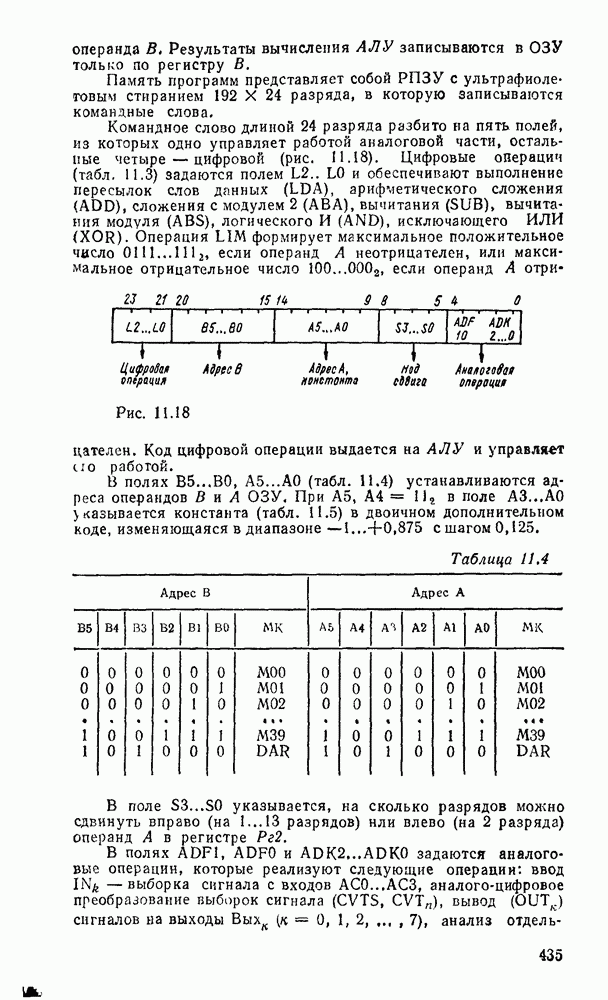
Преобразователь кодов представляет собой схему с четырьмя входами  и четырьмя выходами
и четырьмя выходами  причем шесть наборов входных переменных не используются, и поэтому безразлично, какие значения принимают функции на этих наборах — 0 или 1. Такие функции называют частично определенными. При реализации можно доопределить их на избыточных наборах таким образом, чтобы получить наиболее экономичную схему.
причем шесть наборов входных переменных не используются, и поэтому безразлично, какие значения принимают функции на этих наборах — 0 или 1. Такие функции называют частично определенными. При реализации можно доопределить их на избыточных наборах таким образом, чтобы получить наиболее экономичную схему.
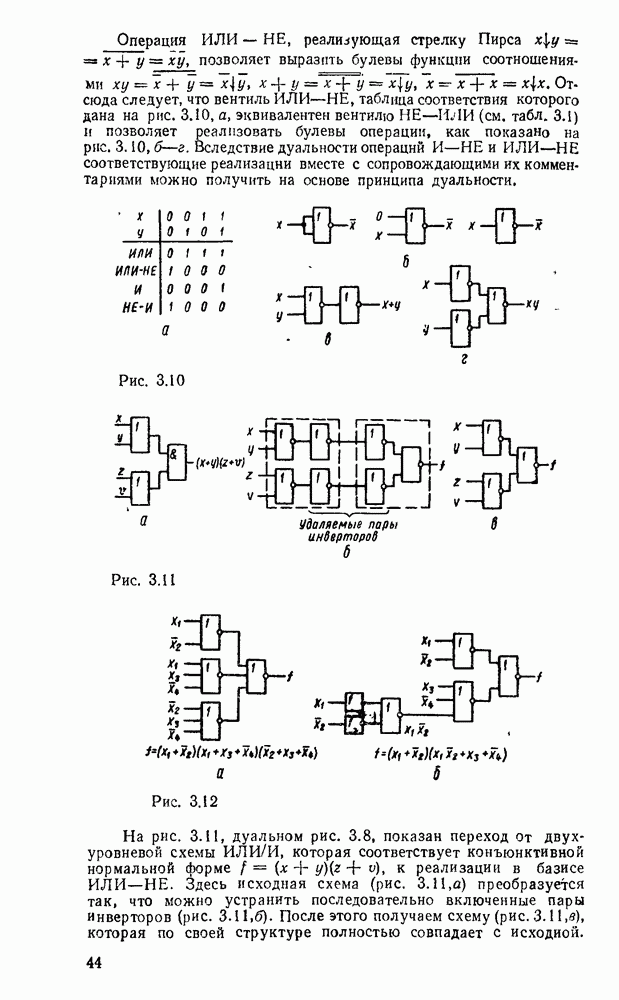
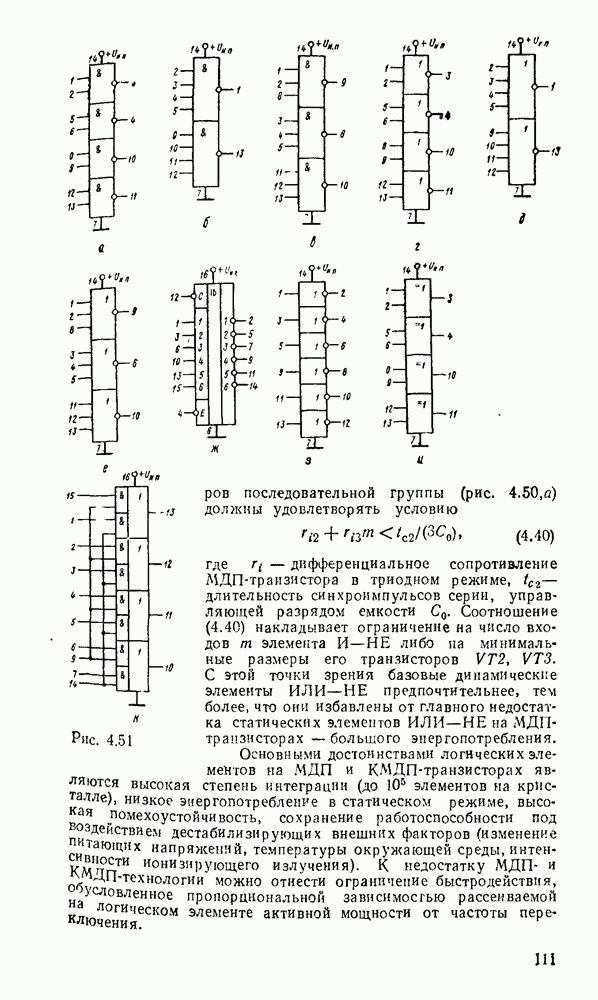
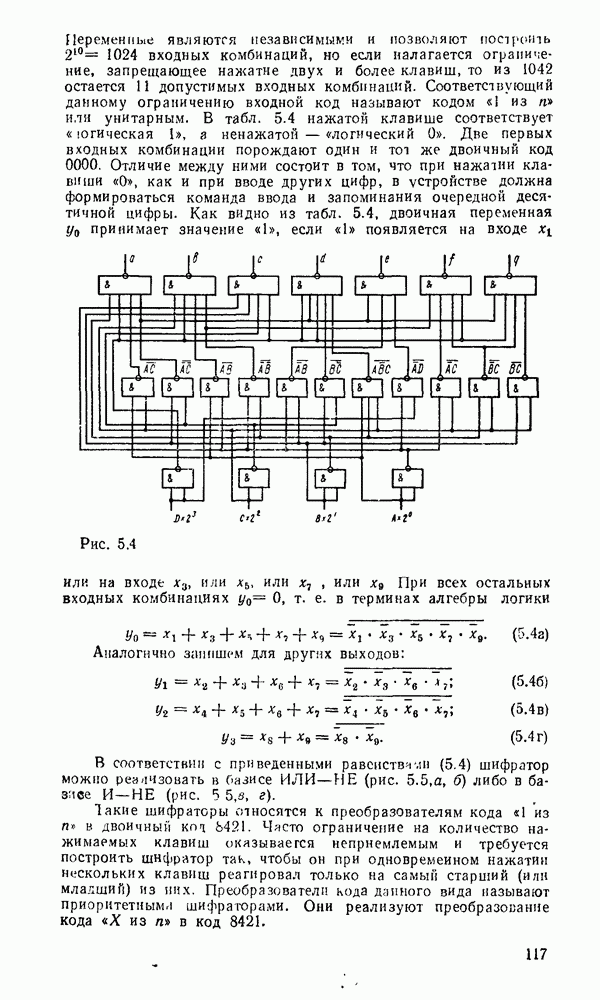
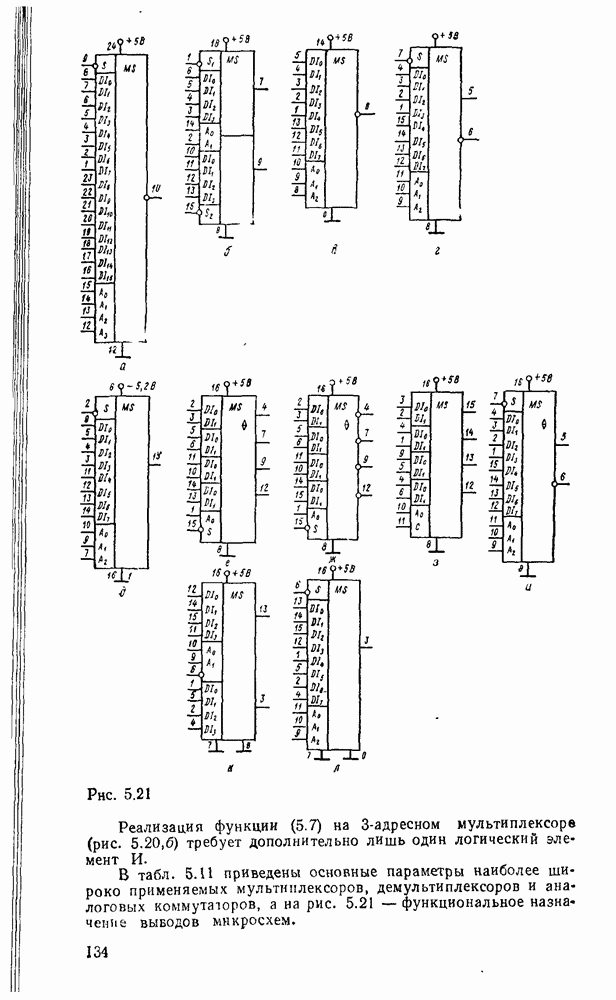
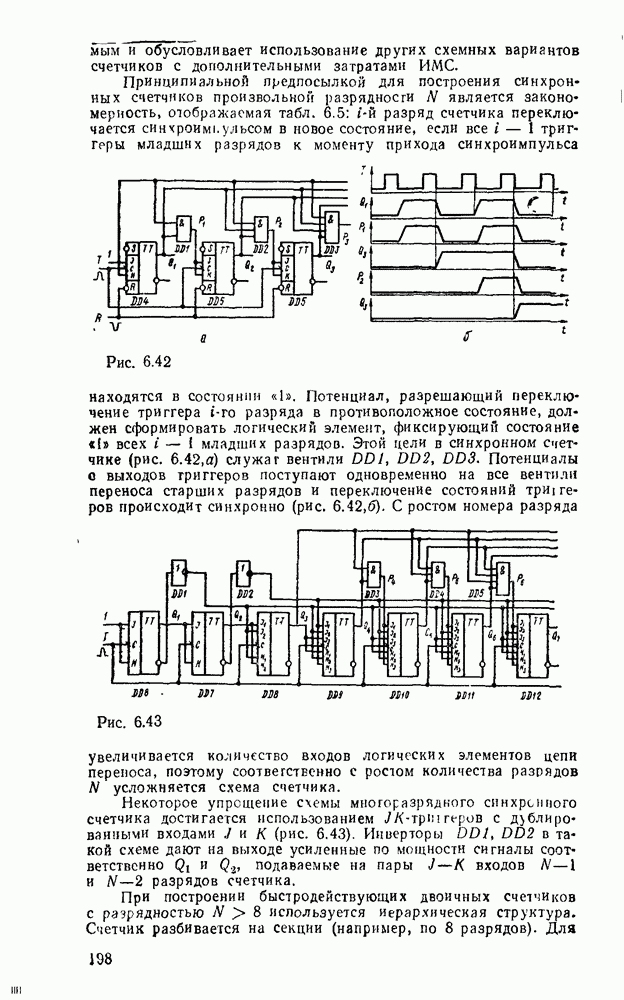
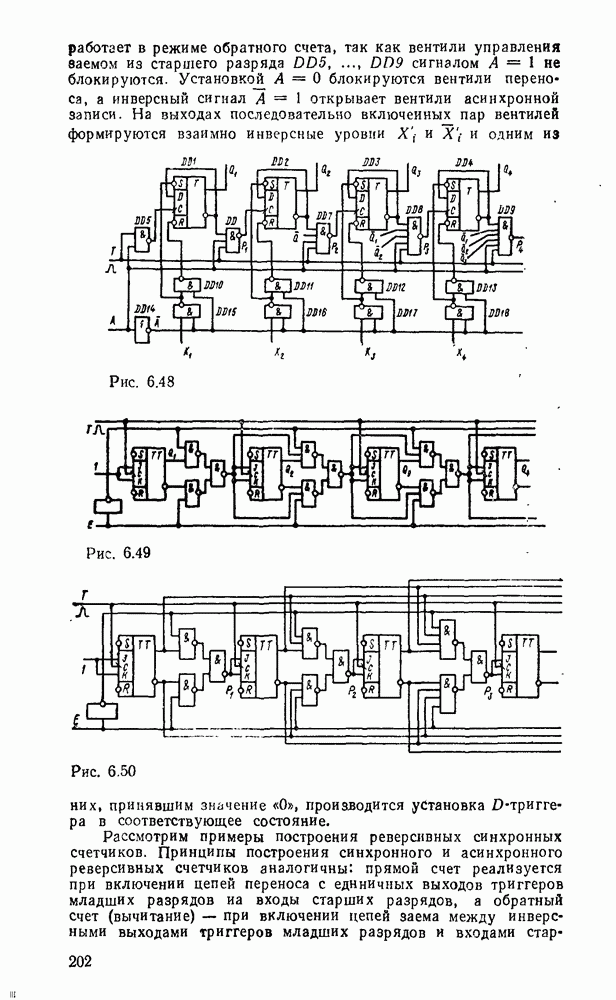
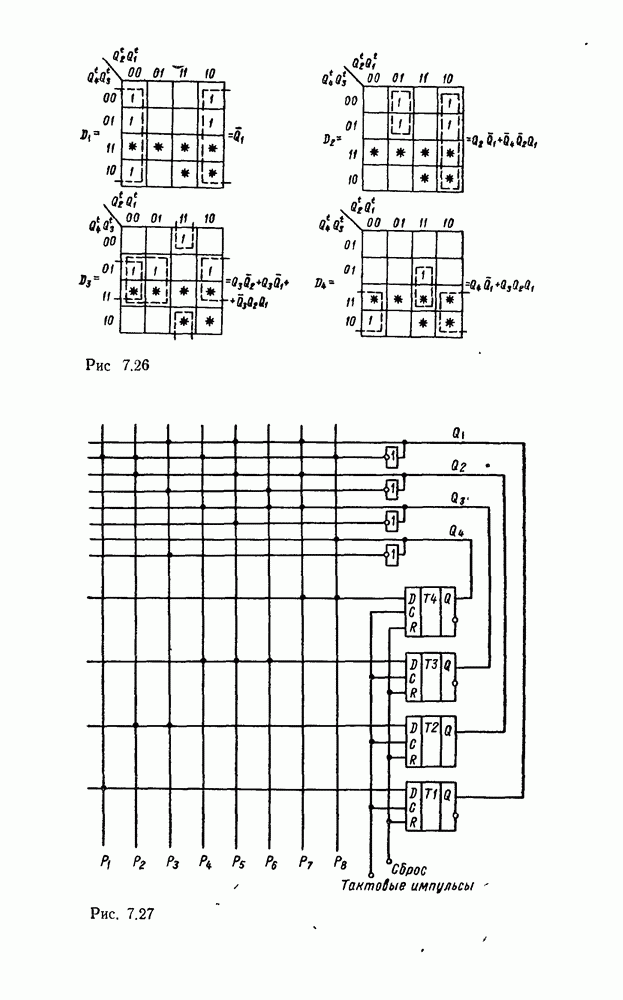
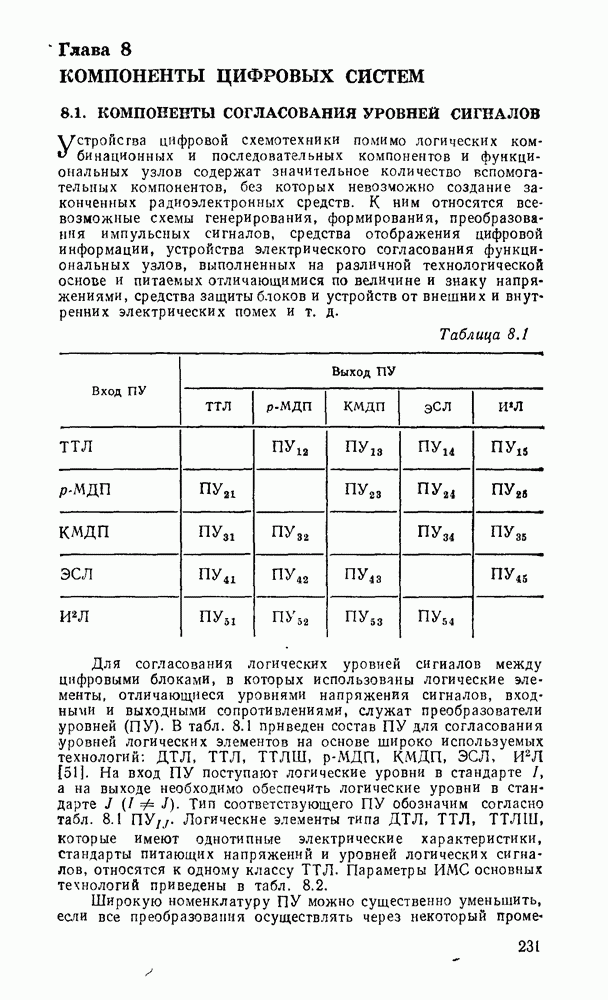
На рис. 3.13,а показано, как используется возможность доопределения функций на избыточных наборах для получения экономичных покрытий на картах Карно (избыточные наборы отмечены звездочками), которые включали бы возможно больше однотипных импликант. Соответствующая логическая схема показана на рис.  .
.
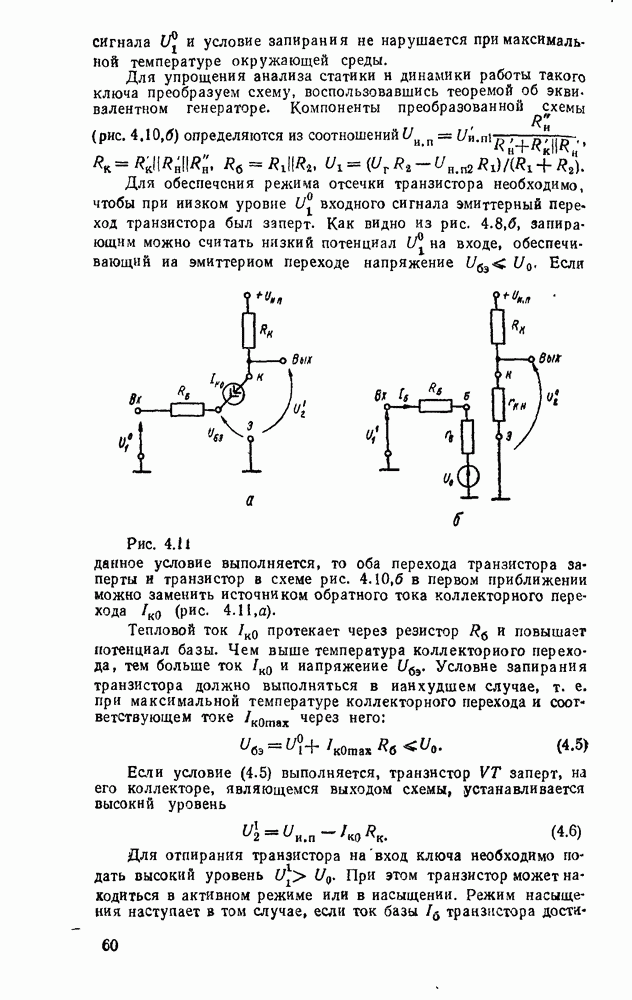
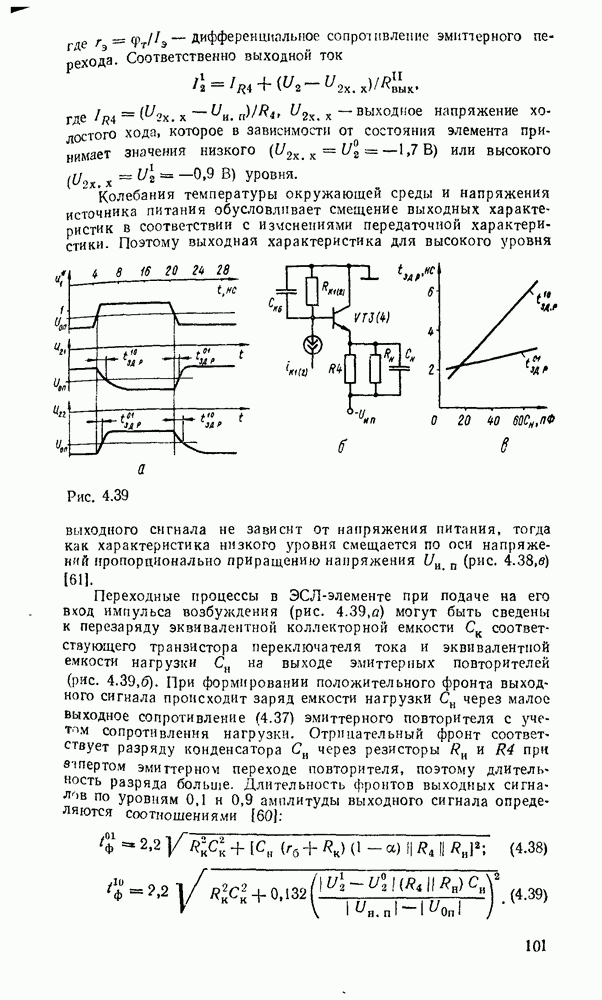
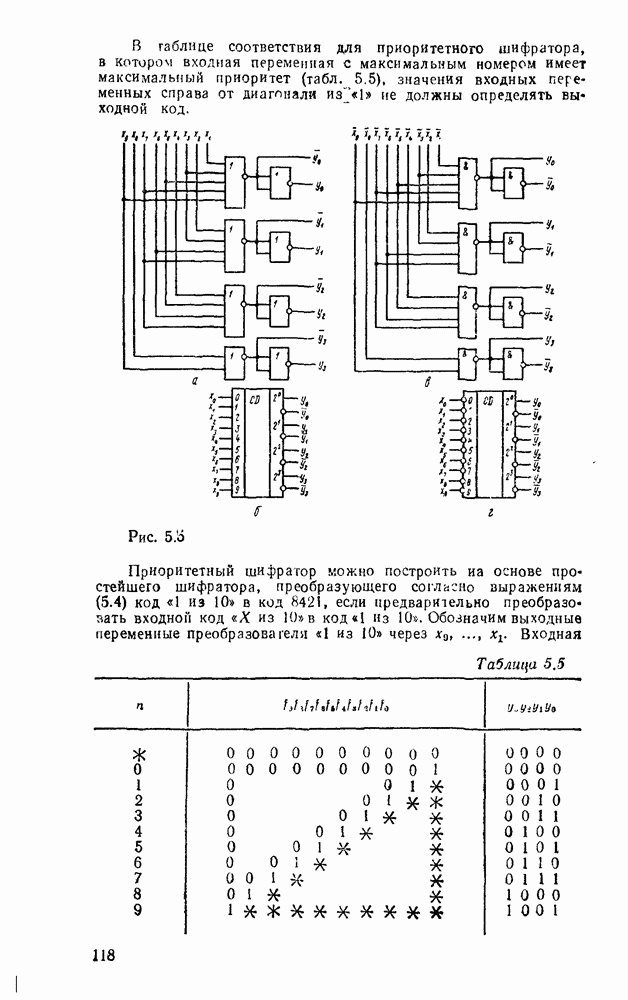
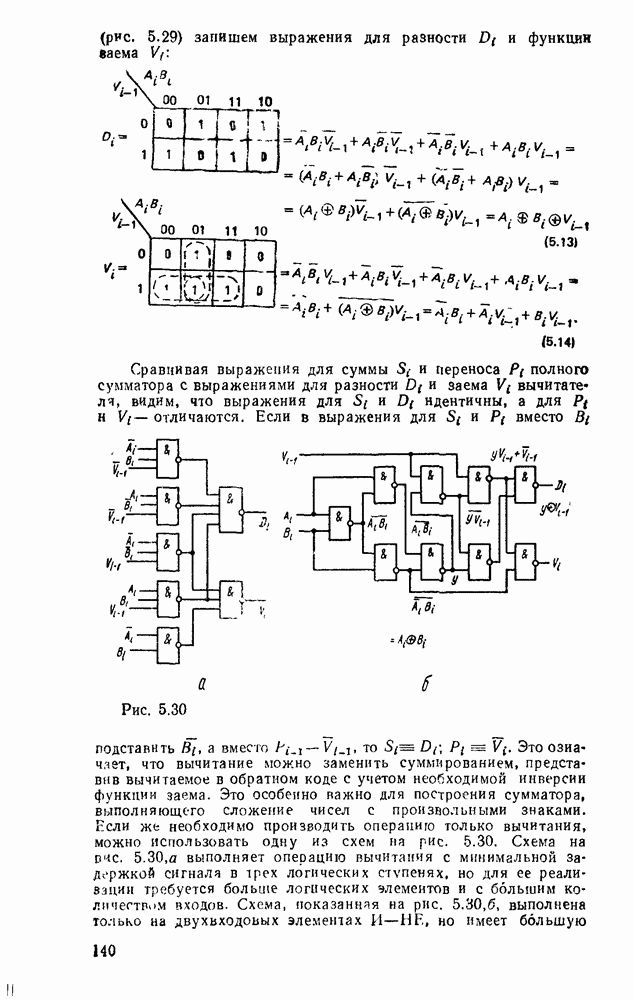
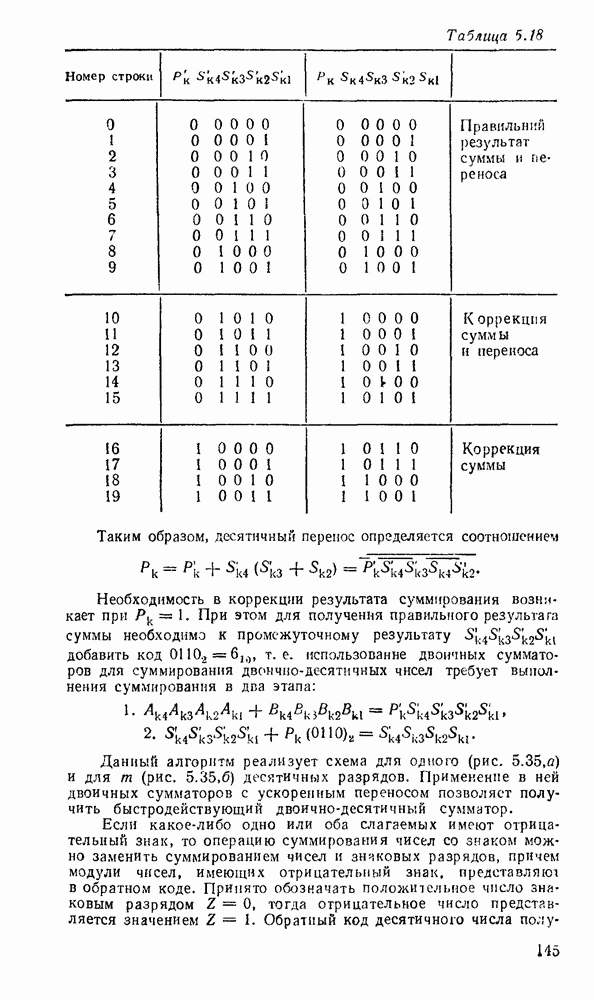
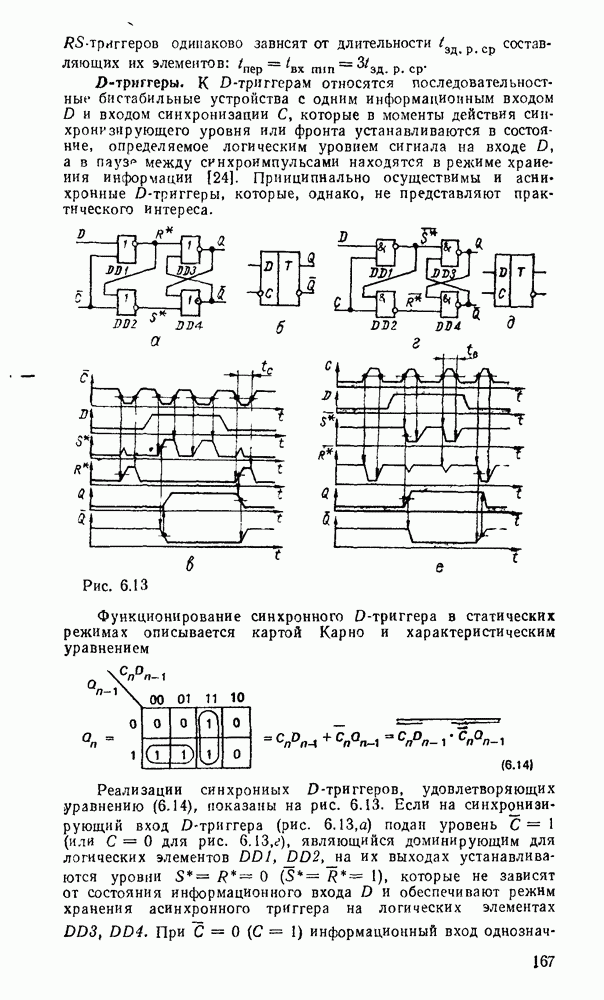
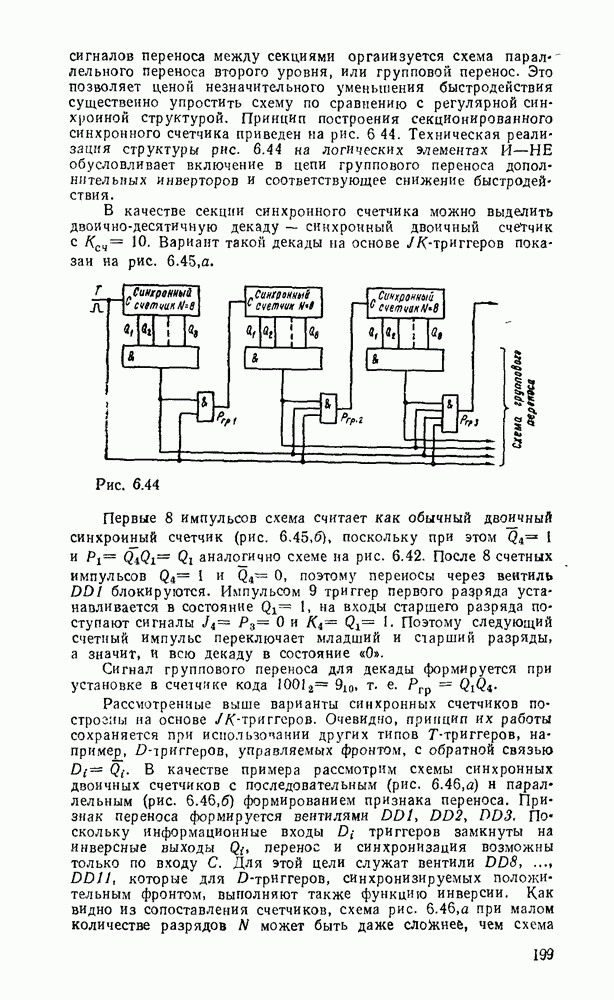
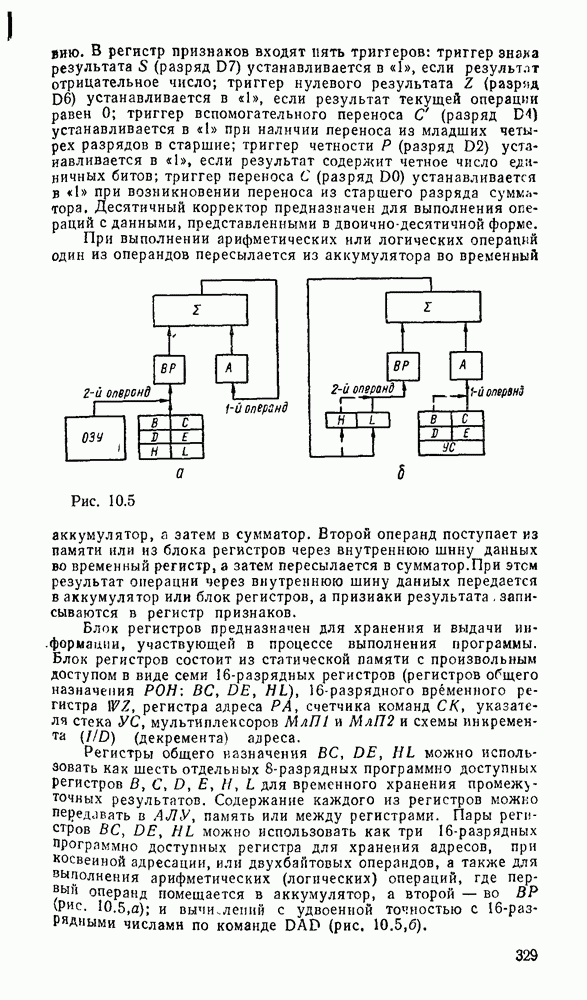
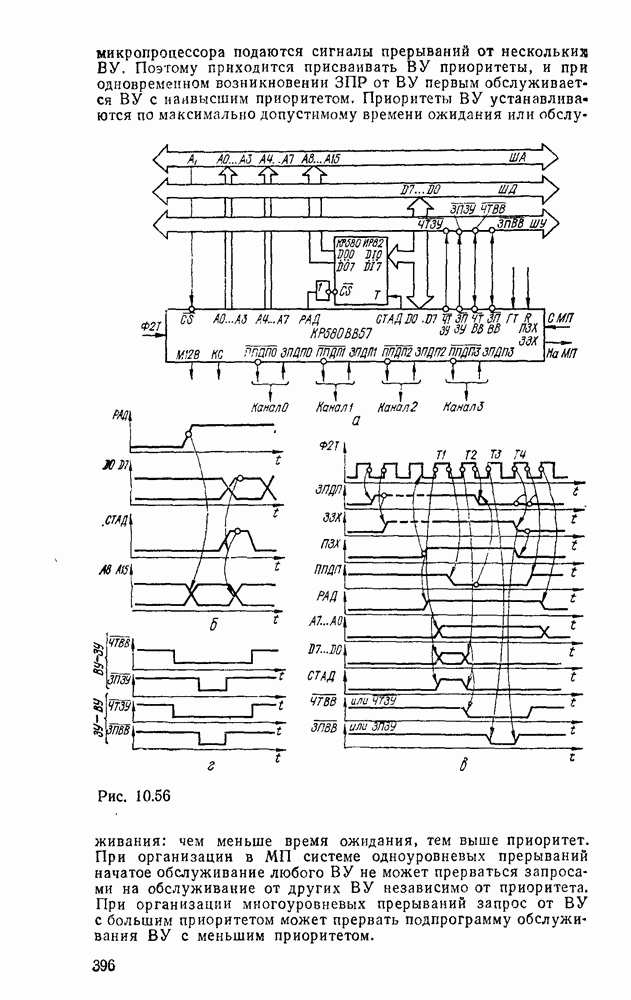
Другим примером, в котором используются частично определенные функции, является синтез одноразрядного сумматора, выполняющего арифметическое сложение двоичных чисел  разряда и переноса из младшего разряда
разряда и переноса из младшего разряда  .
.
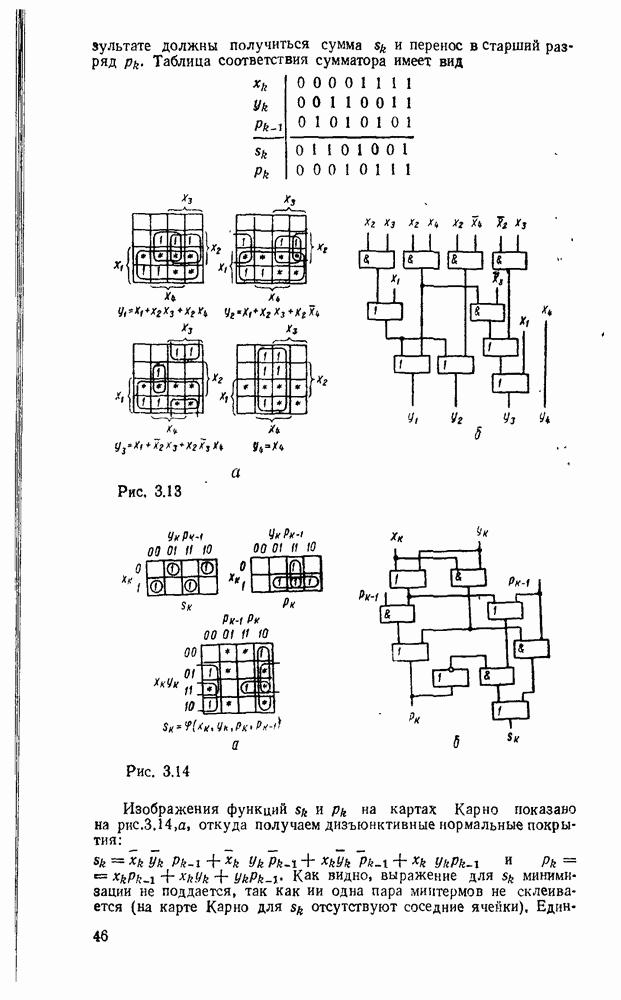
В результате должны получиться сумма  и перенос в старший разряд
и перенос в старший разряд  . Таблица соответствия сумматора имеет вид
. Таблица соответствия сумматора имеет вид


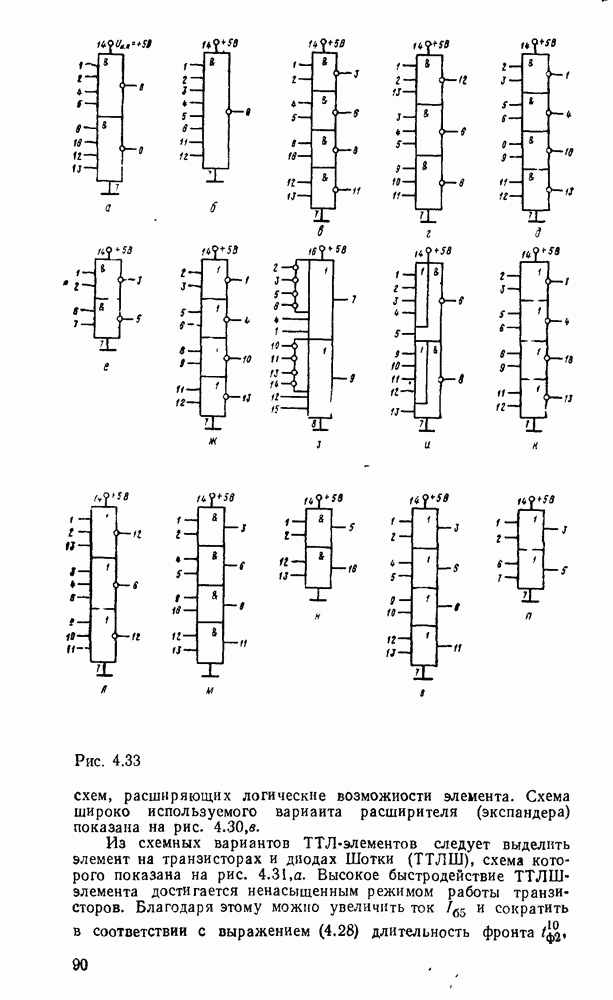
Рис. 3.13.

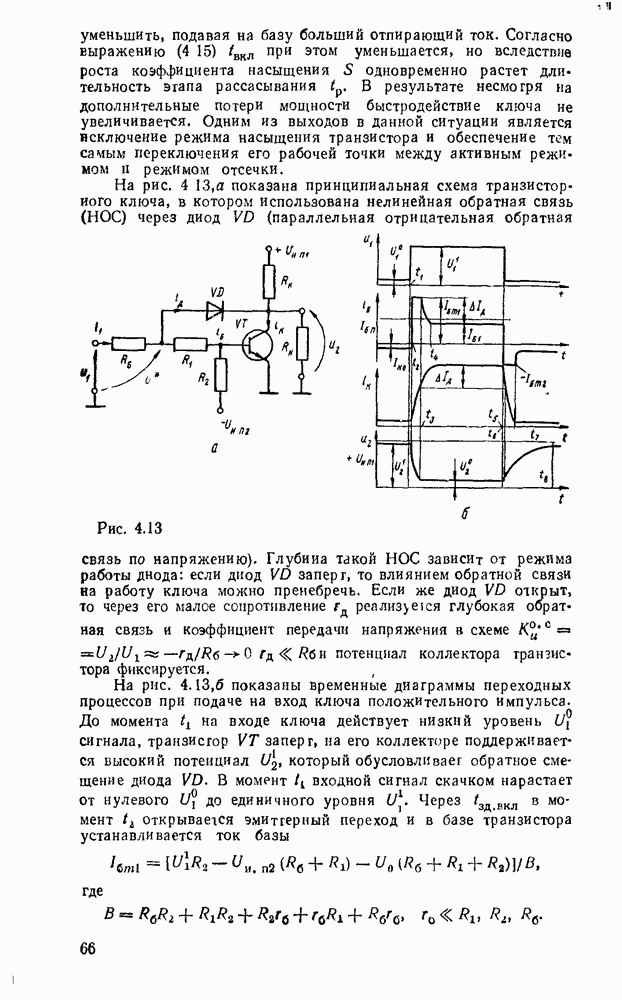
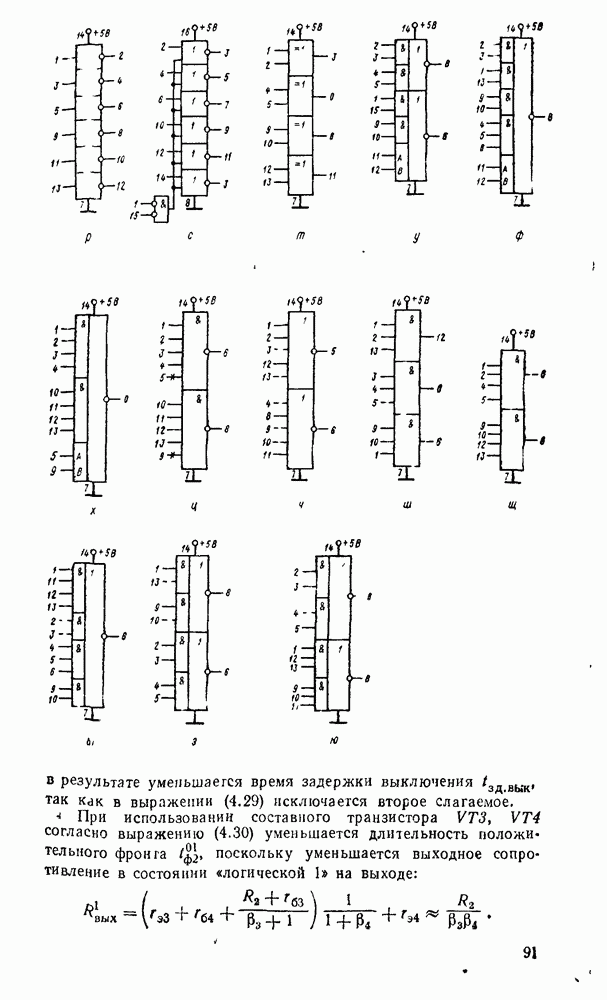
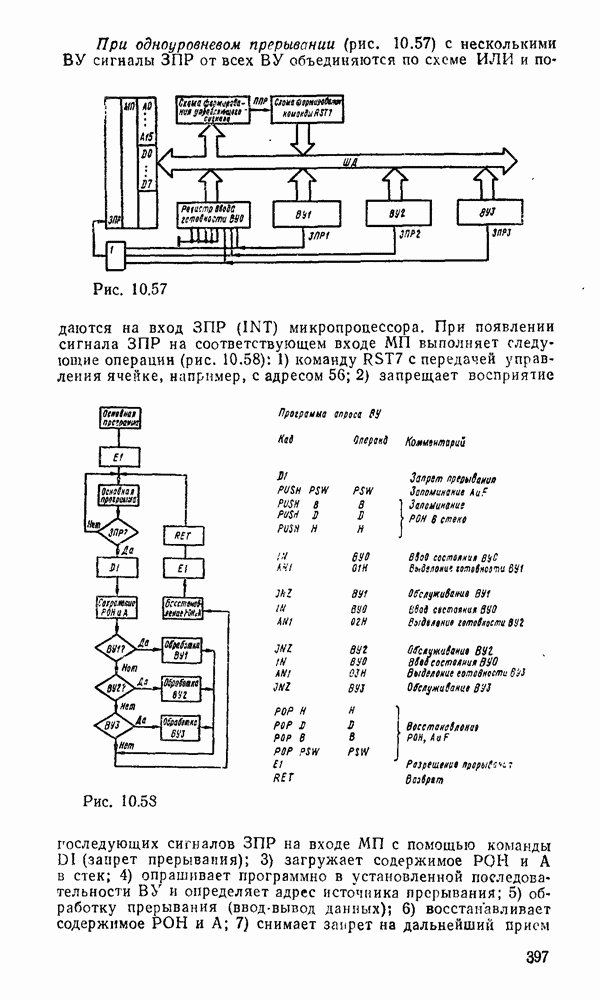
Рис. 3.14.
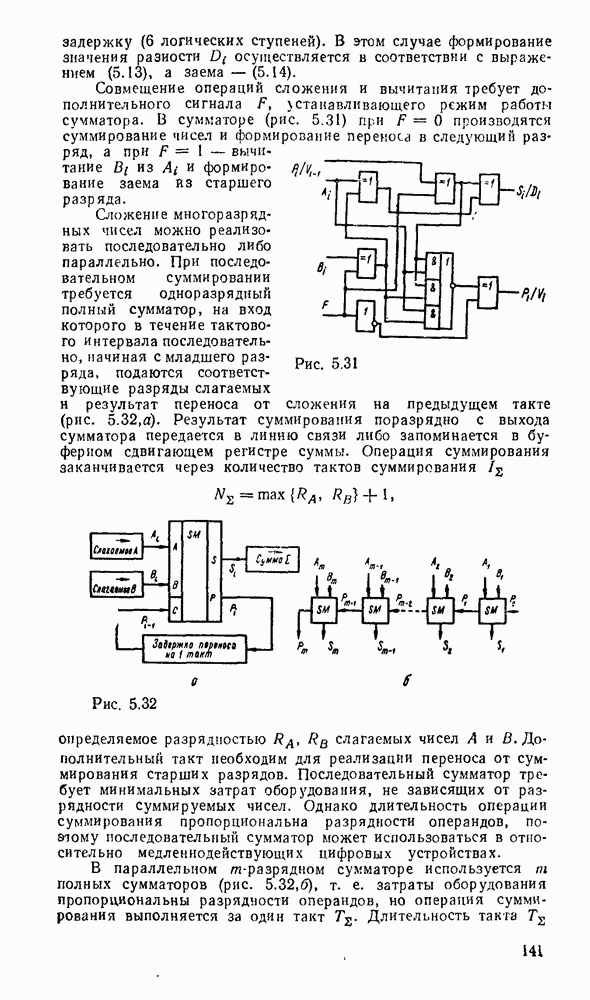
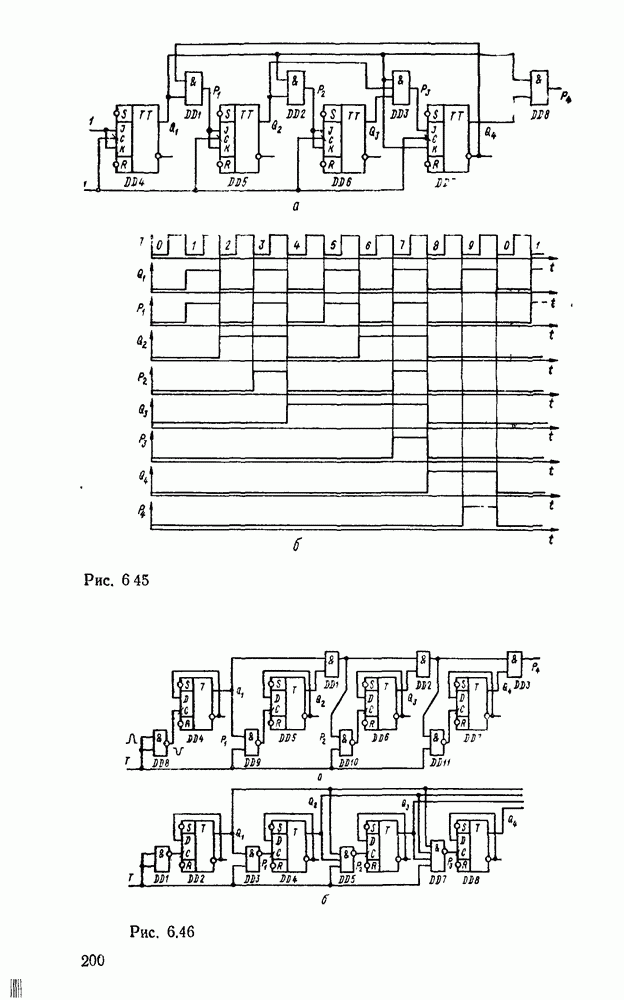
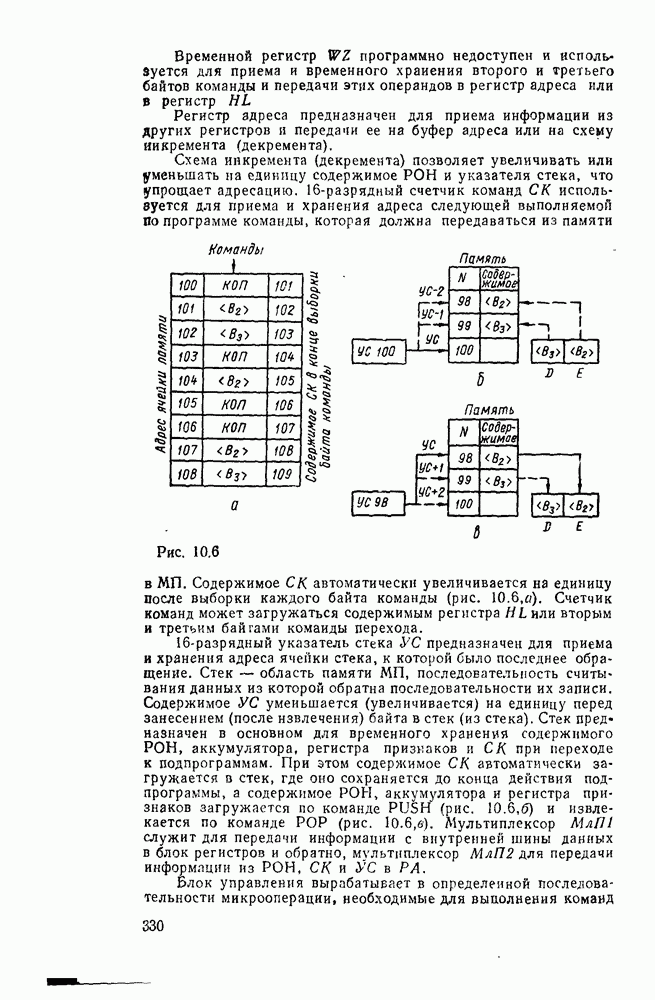
Изображения функций  и
и  на картах Карно показано на
на картах Карно показано на  , откуда получаем дизъюнктивные нормальные покрытия:
, откуда получаем дизъюнктивные нормальные покрытия:
 Как видно, выражение для
Как видно, выражение для  минимизации не поддается, так как
минимизации не поддается, так как  одна пара минтермов не склеивается (на карте Карно для
одна пара минтермов не склеивается (на карте Карно для  отсутствуют соседние ячейки).
отсутствуют соседние ячейки).
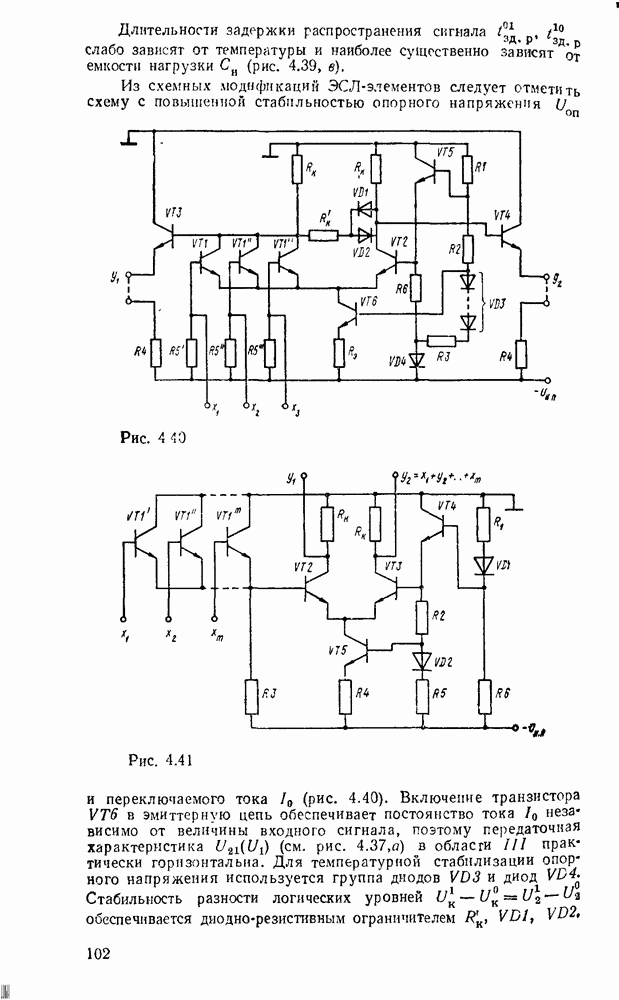
Единственная возможность его упростить — это использовать вынесение за скобки 
В подобных случаях для минимизации применяется прием, основанный на использовании более простой функции  в качестве составной части другой функции
в качестве составной части другой функции  . При этом
. При этом  рассматривается как переменная, т. е.
рассматривается как переменная, т. е.  таблица соответствия для
таблица соответствия для  теперь содержит избыточные наборы переменных, которые отмечены звездочками
теперь содержит избыточные наборы переменных, которые отмечены звездочками

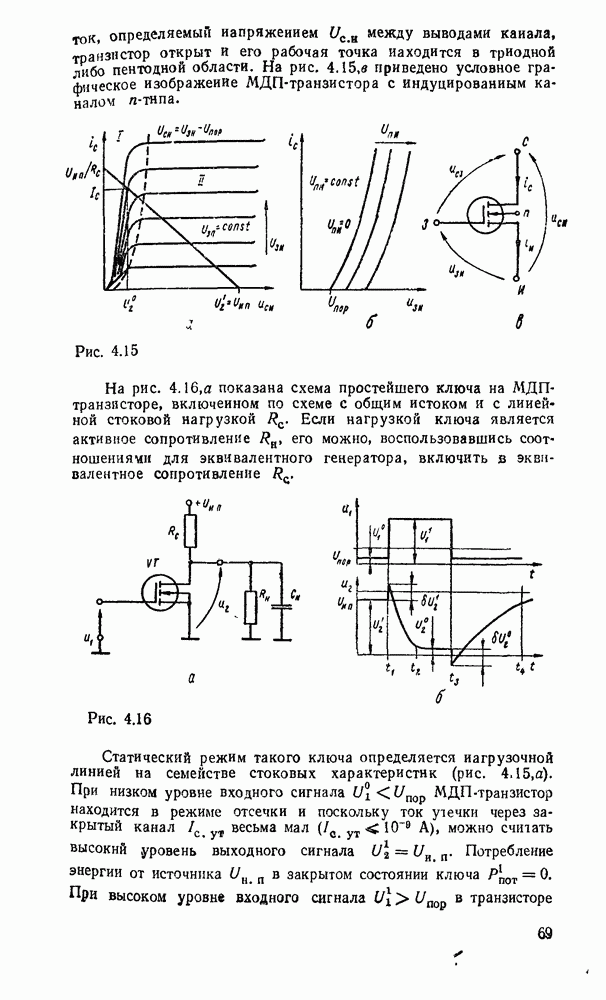
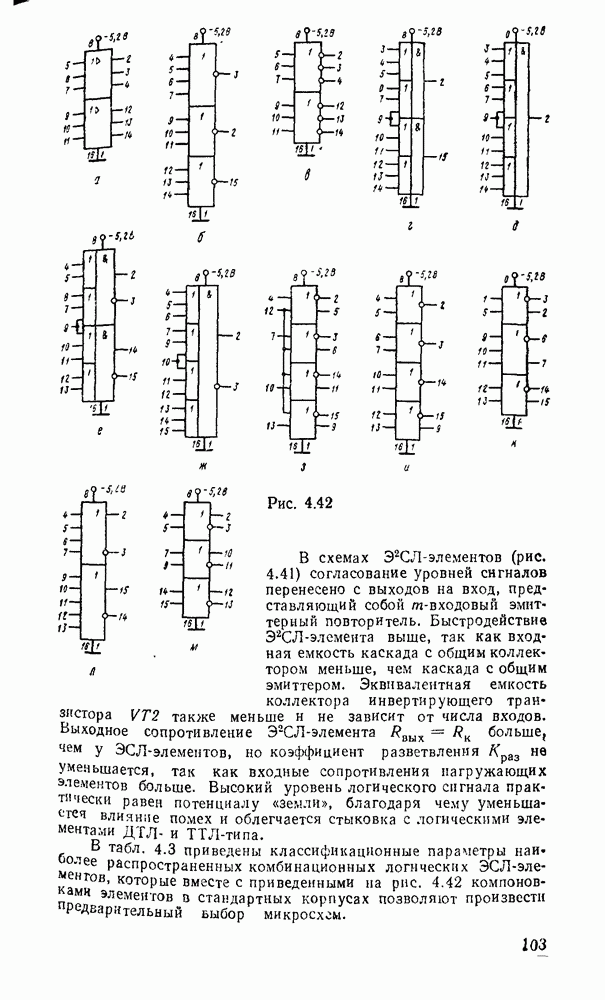
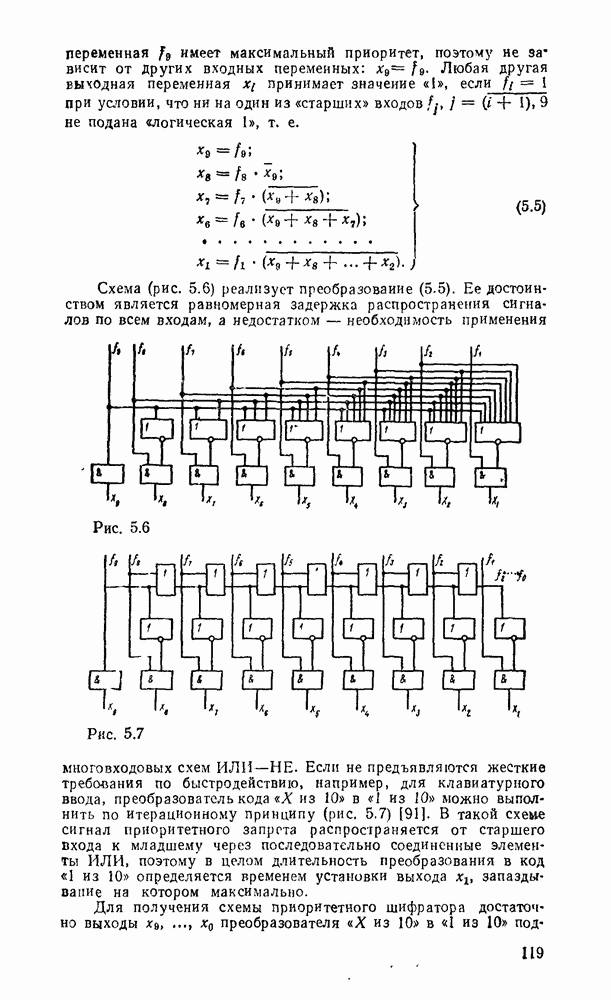
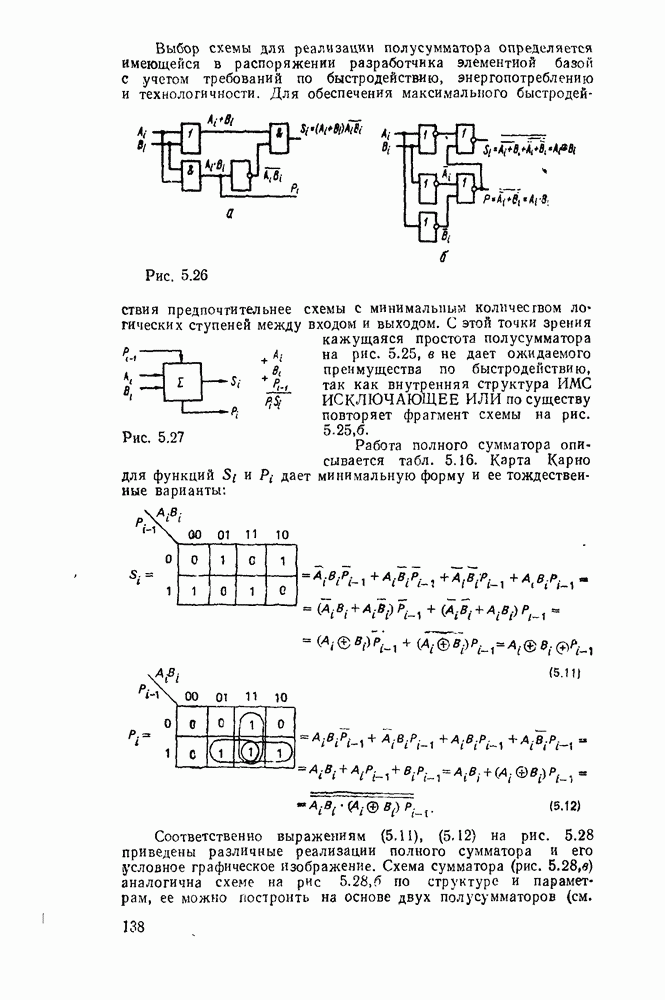
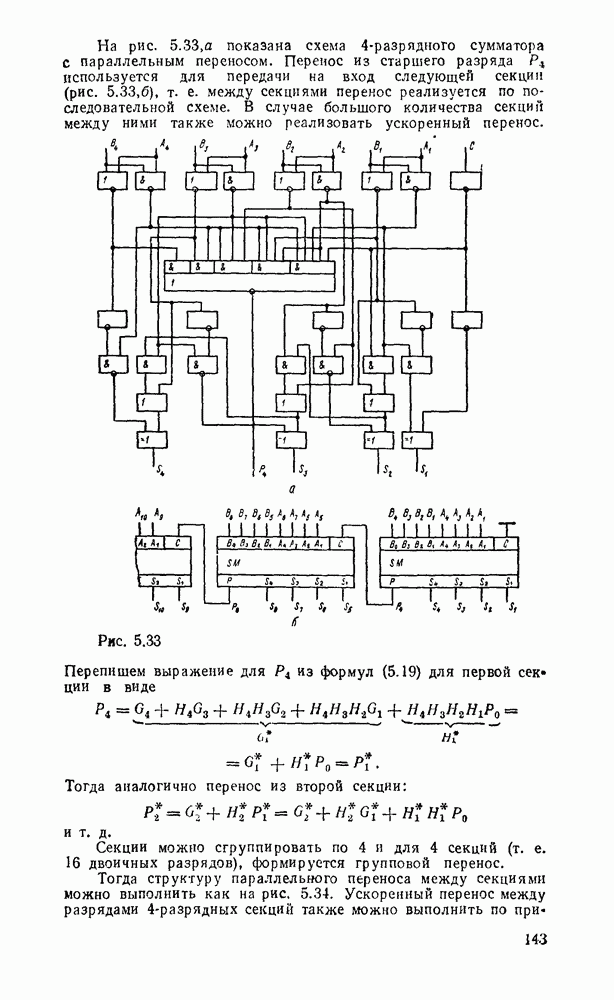
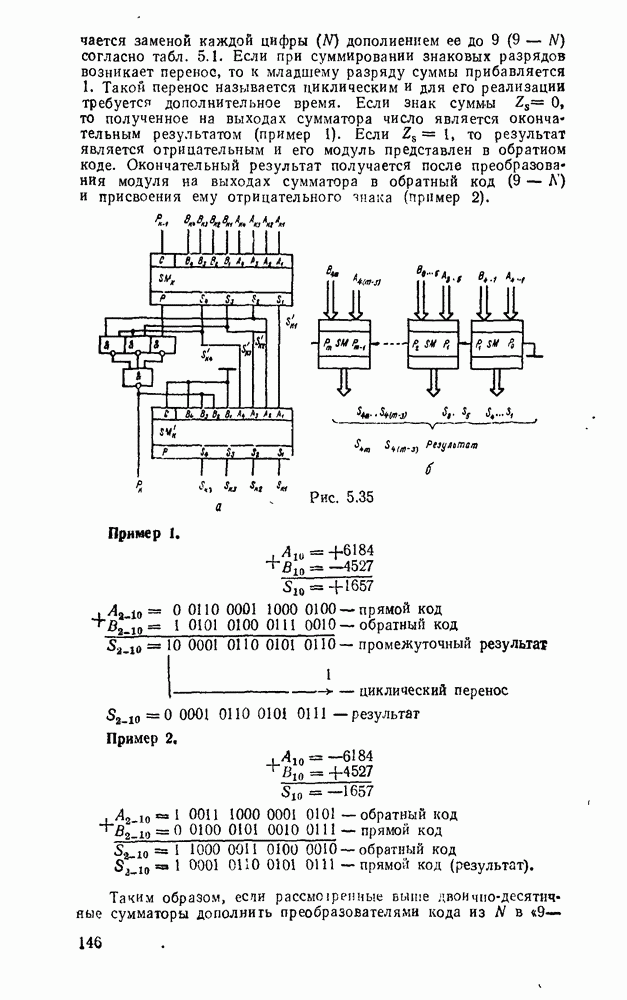
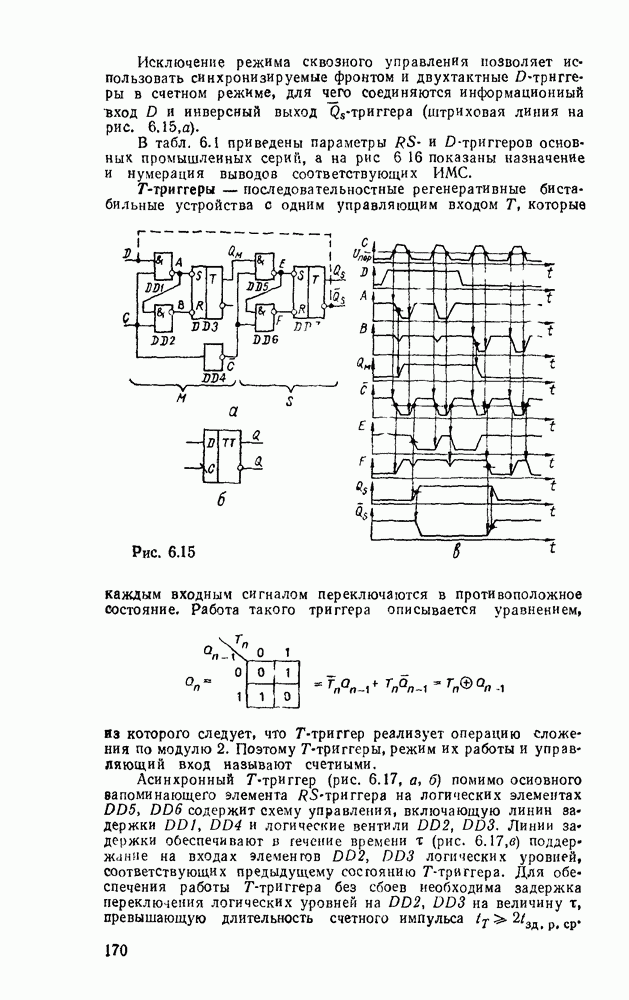
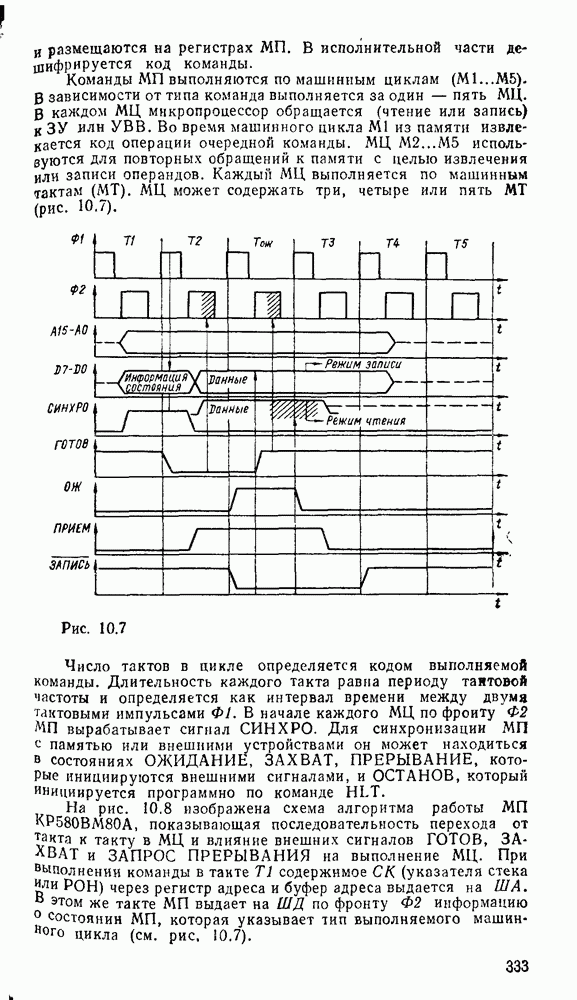
Минимальному покрытю на карте Карно соответствует выражений  . После вынесения за скобки получаем подготовленные для реализации выражения:
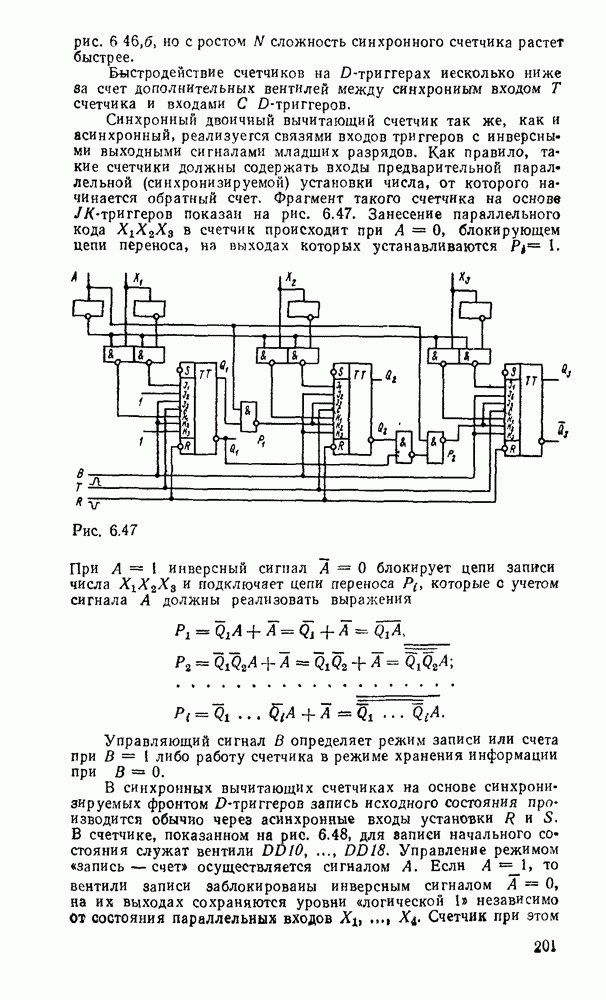
. После вынесения за скобки получаем подготовленные для реализации выражения:  . Соответствующая схема с двумя выходами показана на рис.
. Соответствующая схема с двумя выходами показана на рис.  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
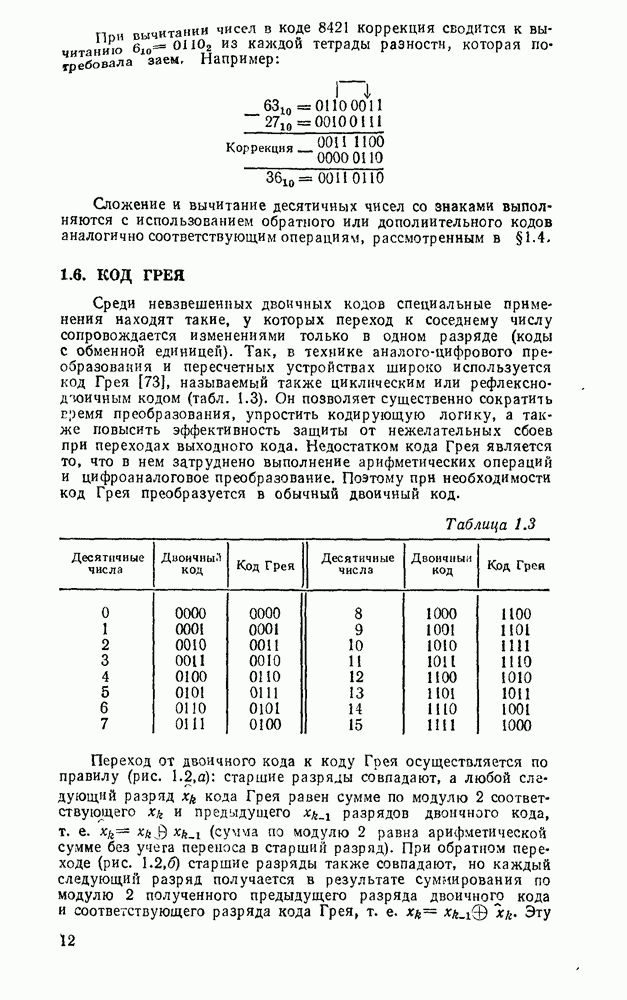
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
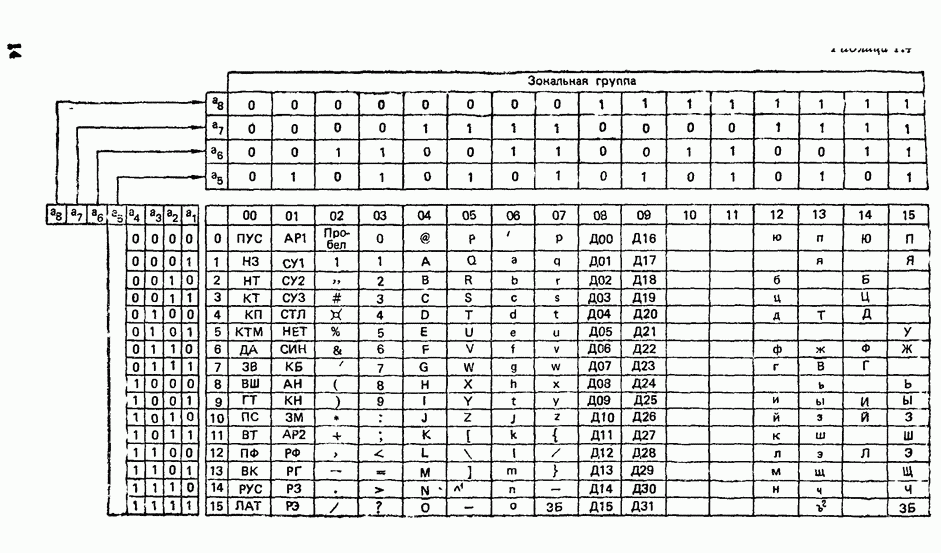
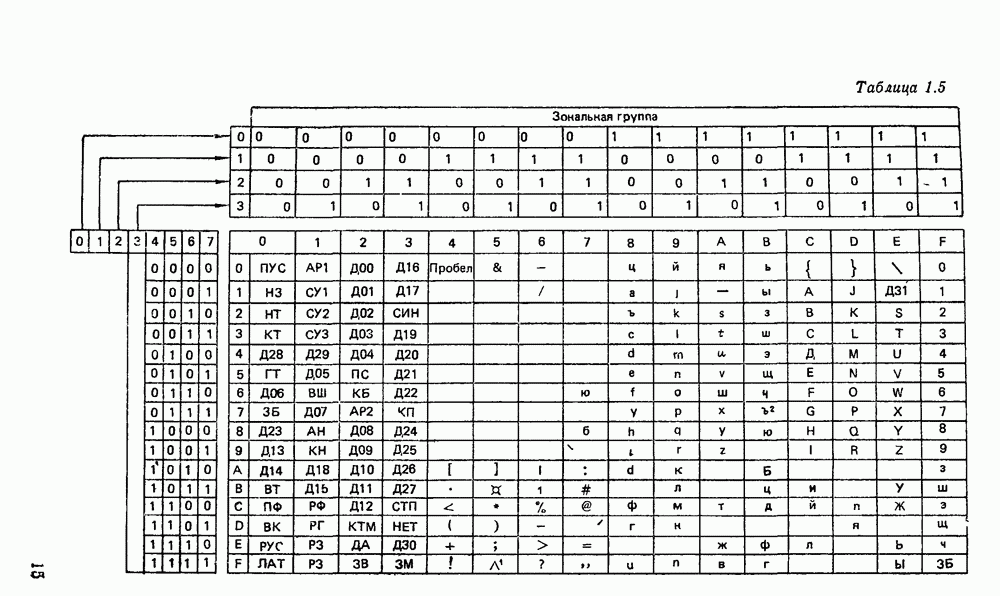
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
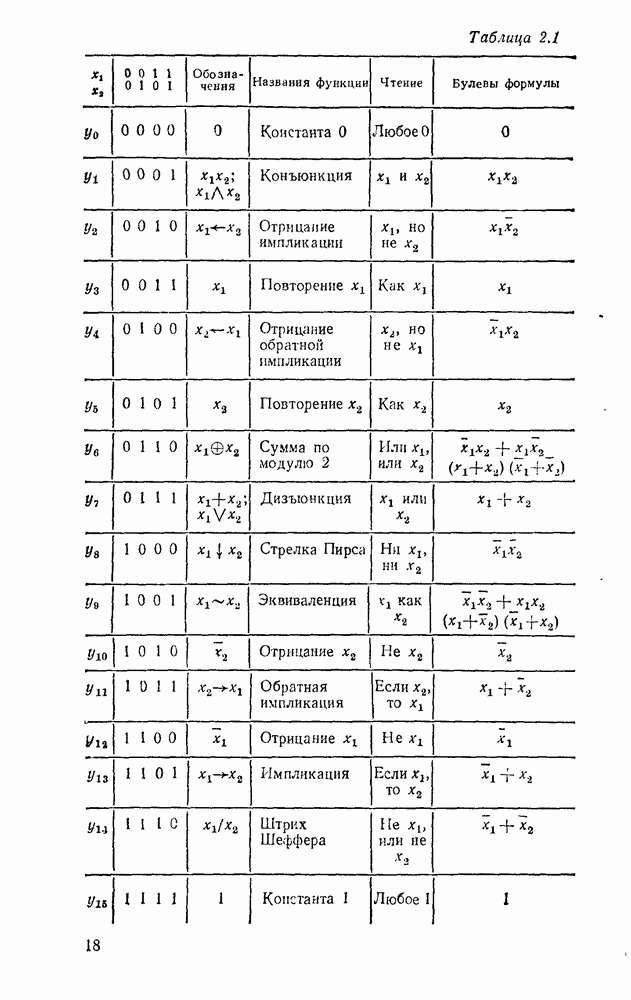
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
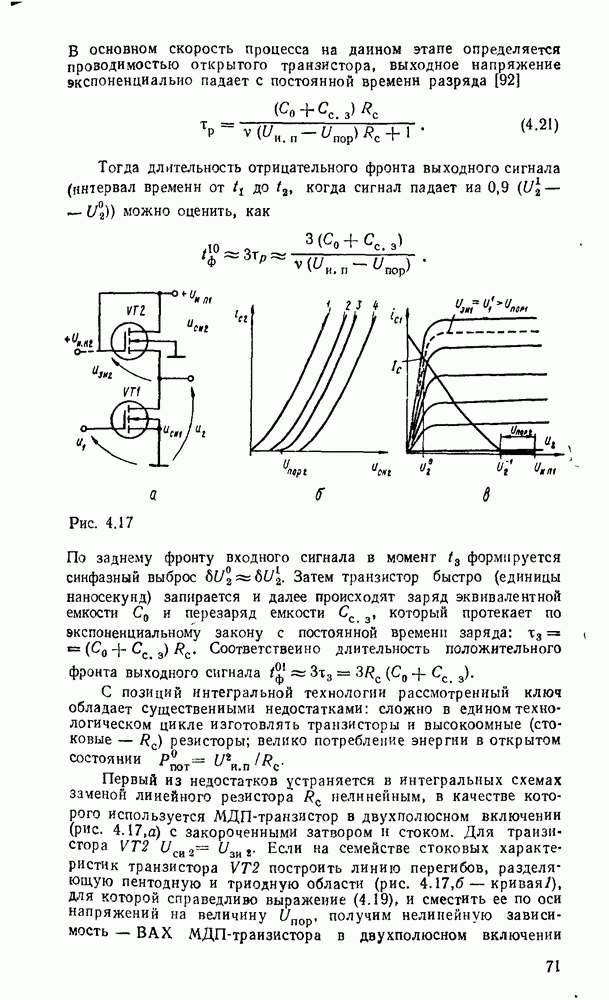
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
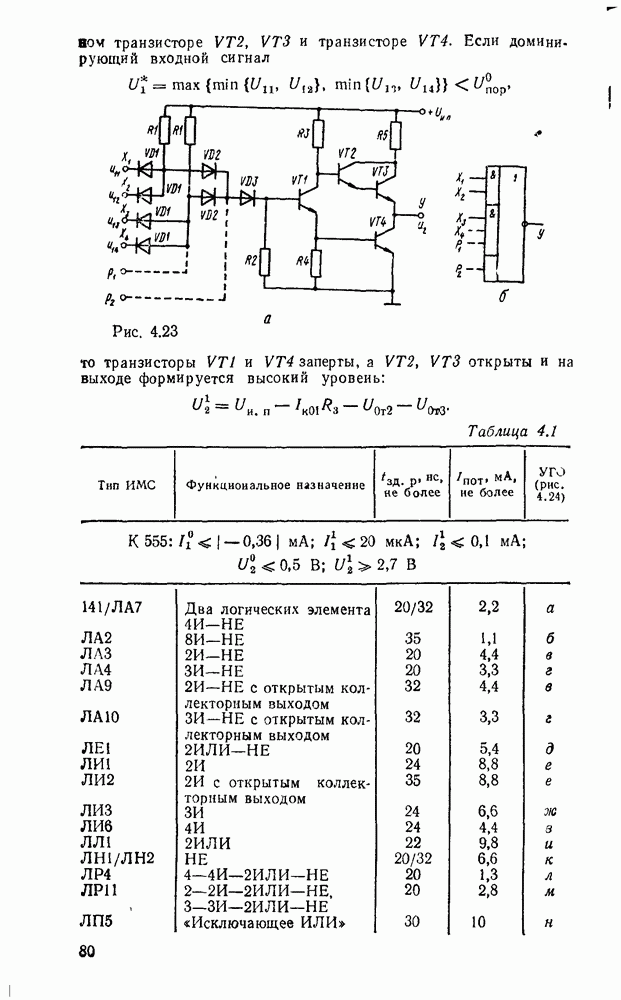
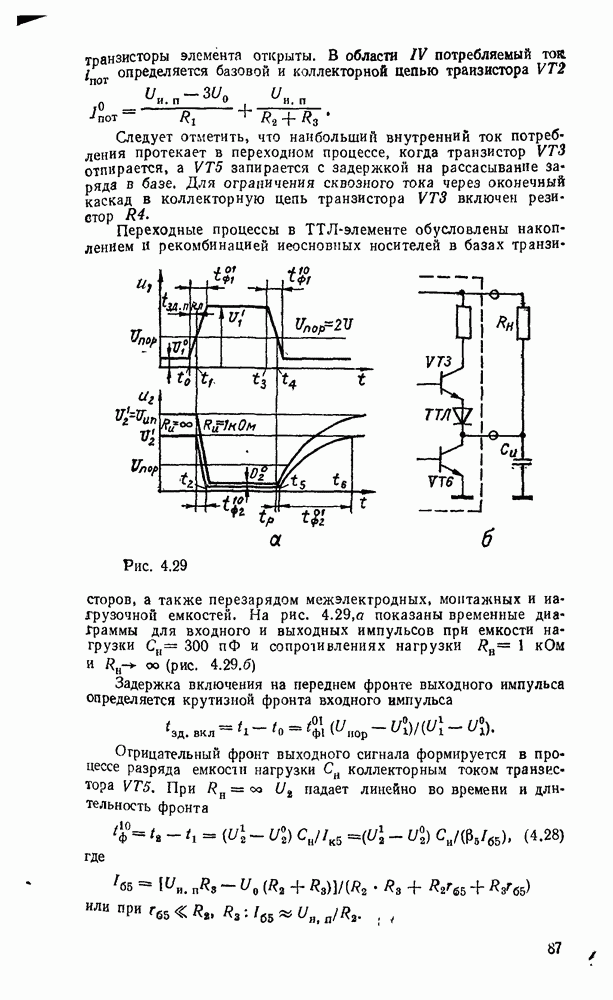
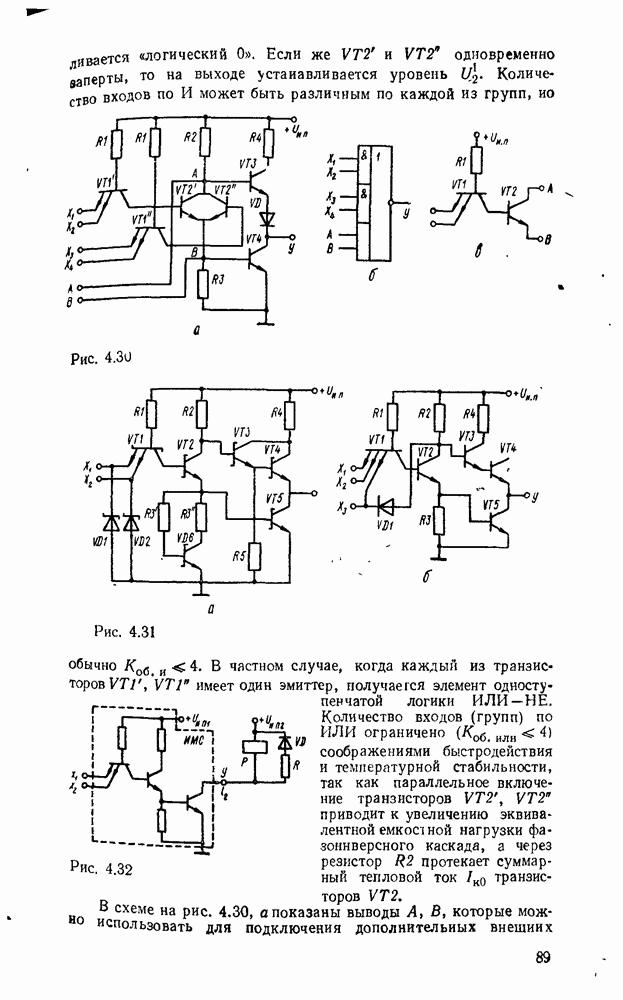
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
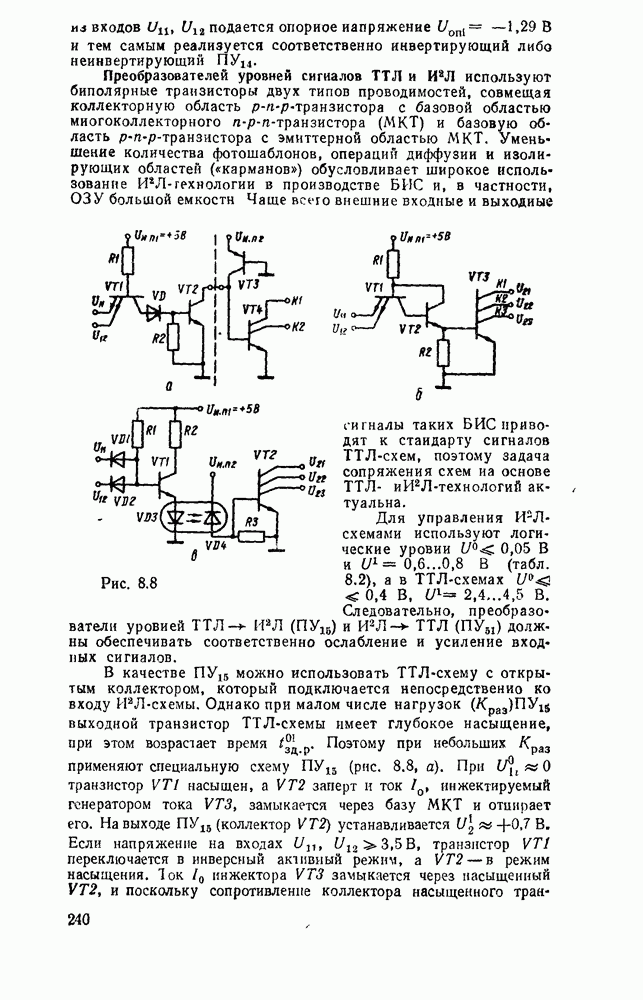
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
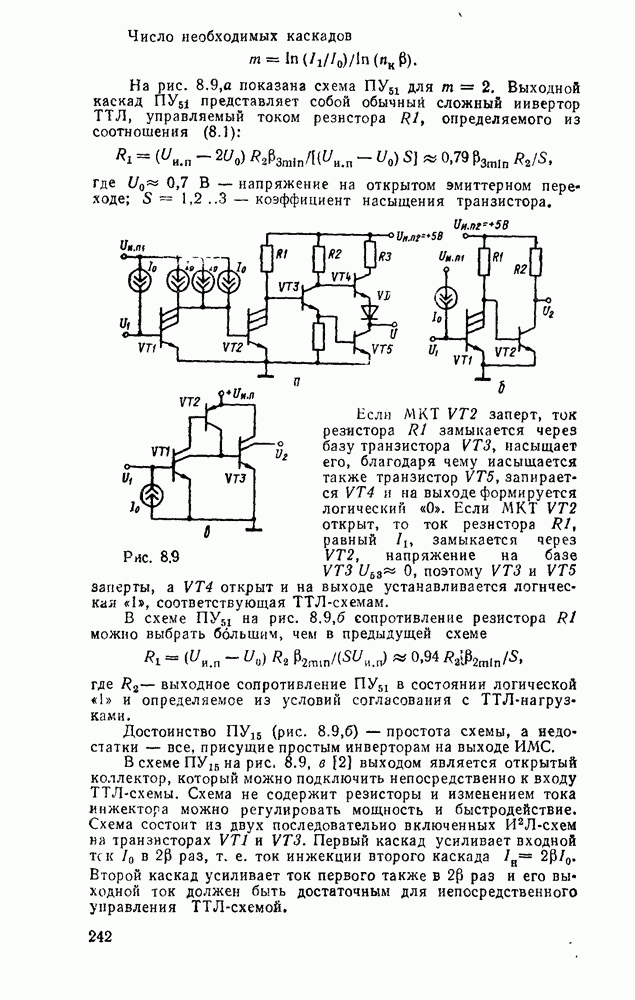
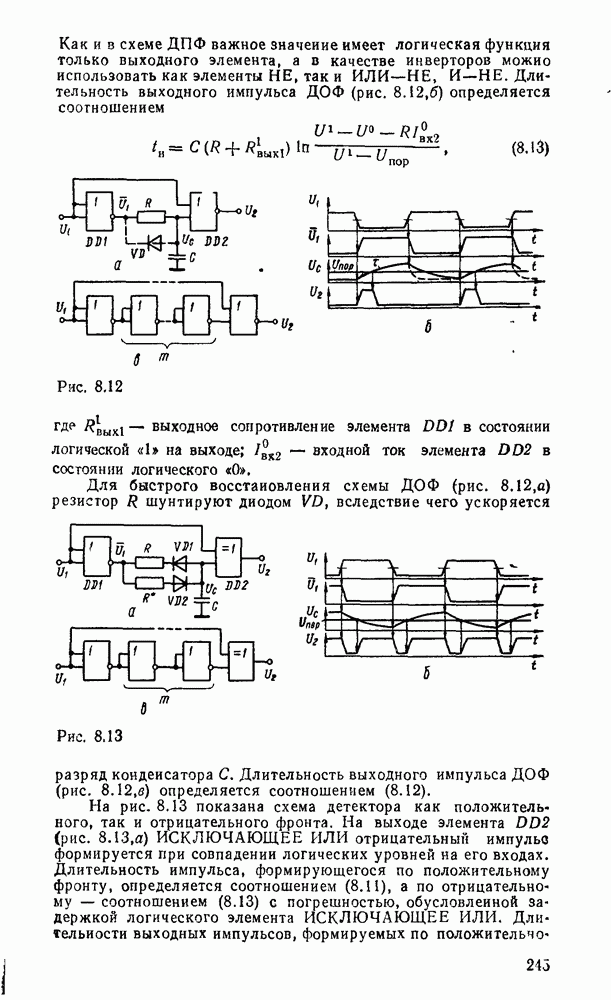
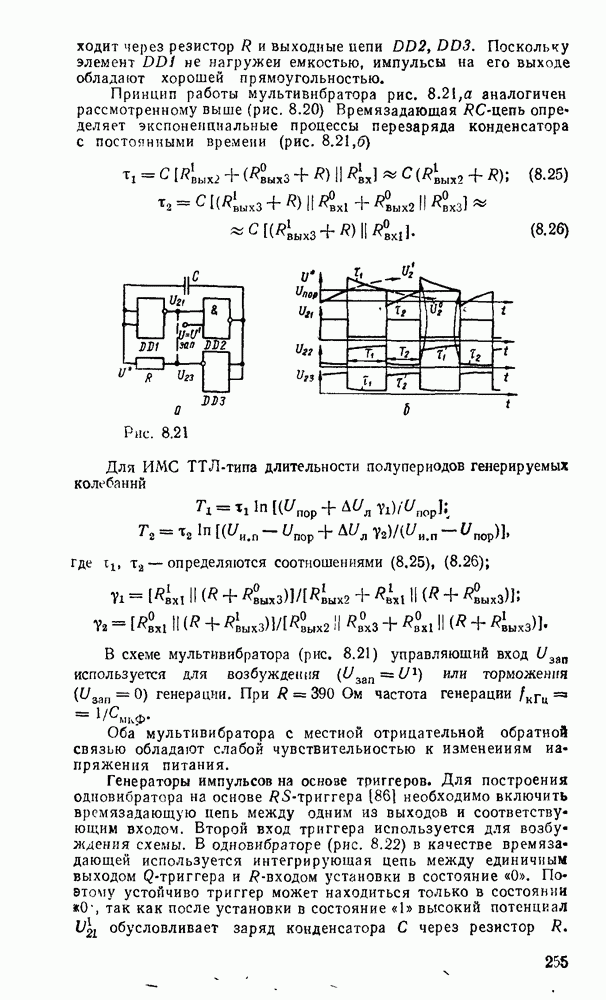
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
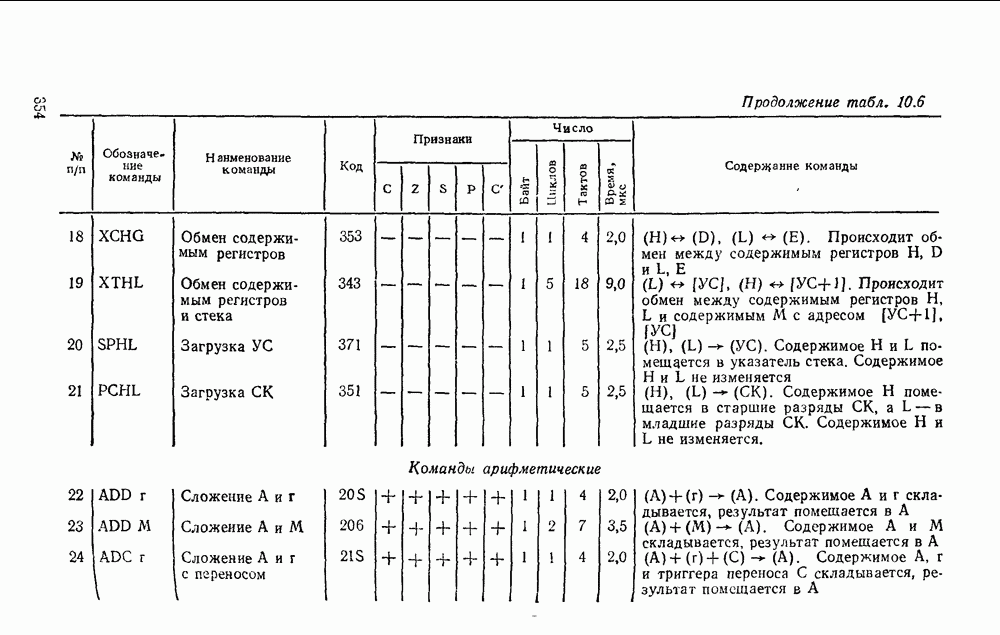
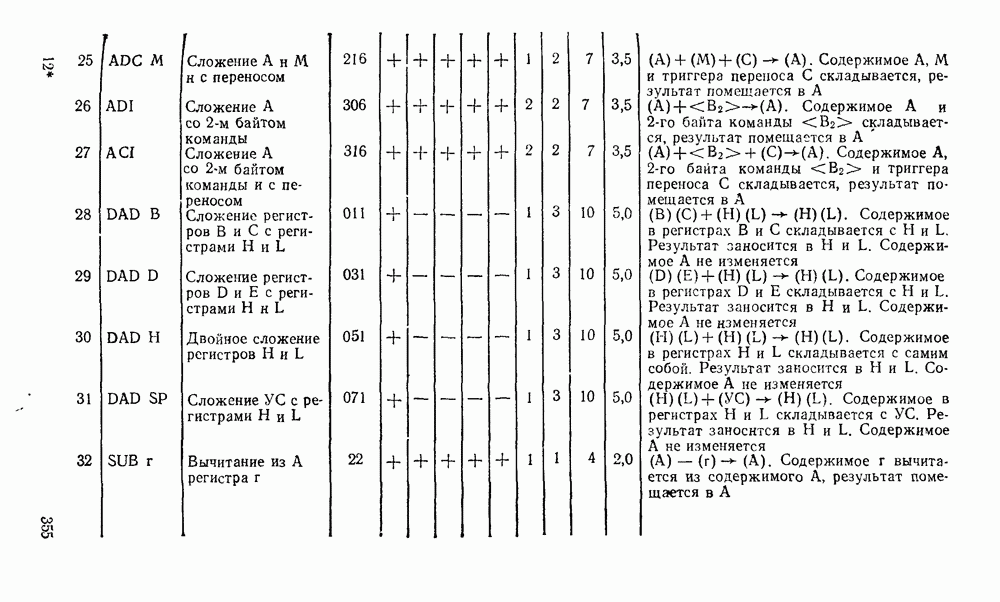
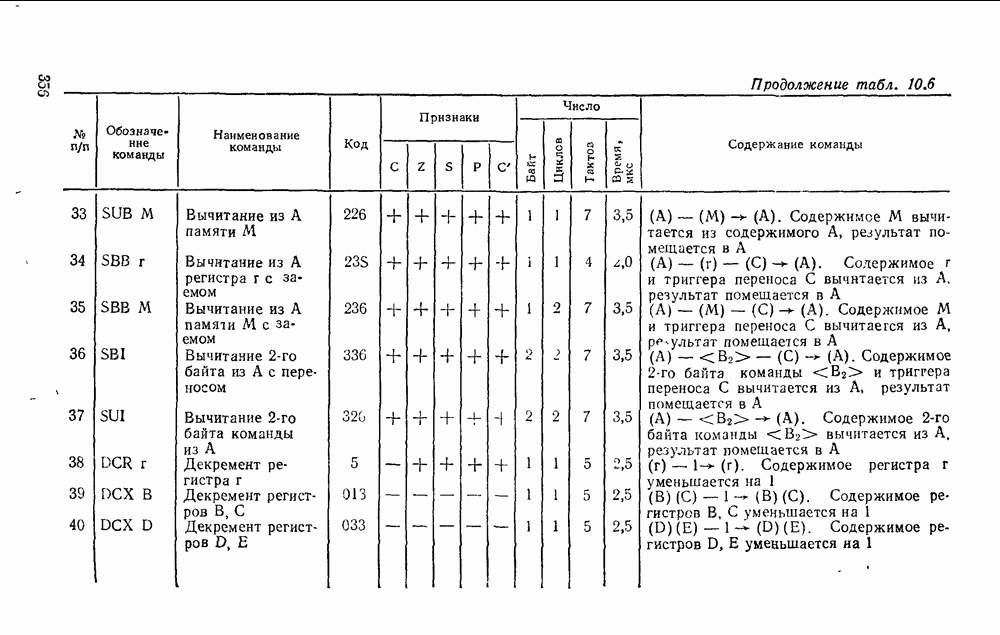
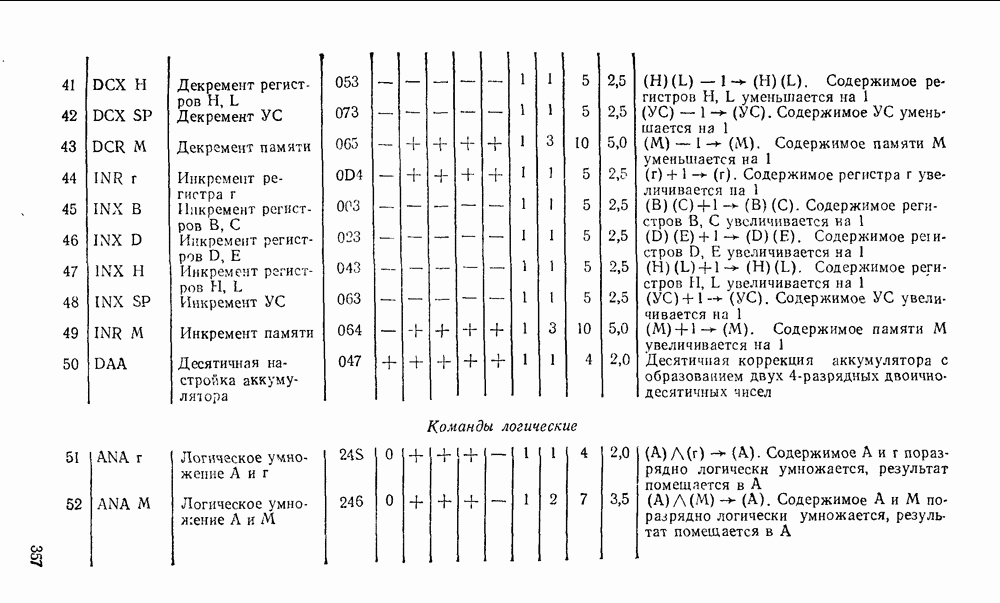
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
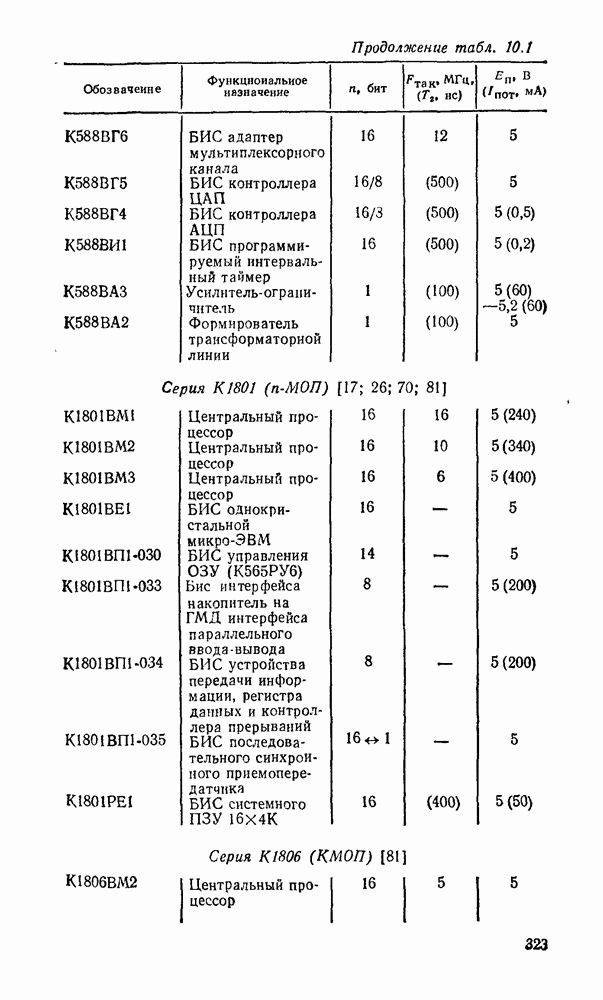
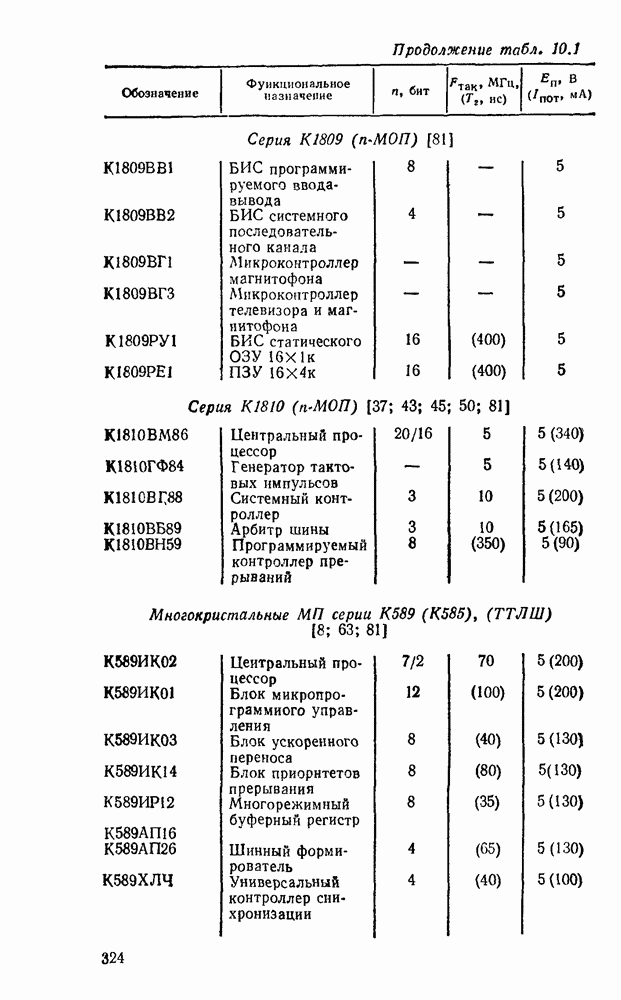
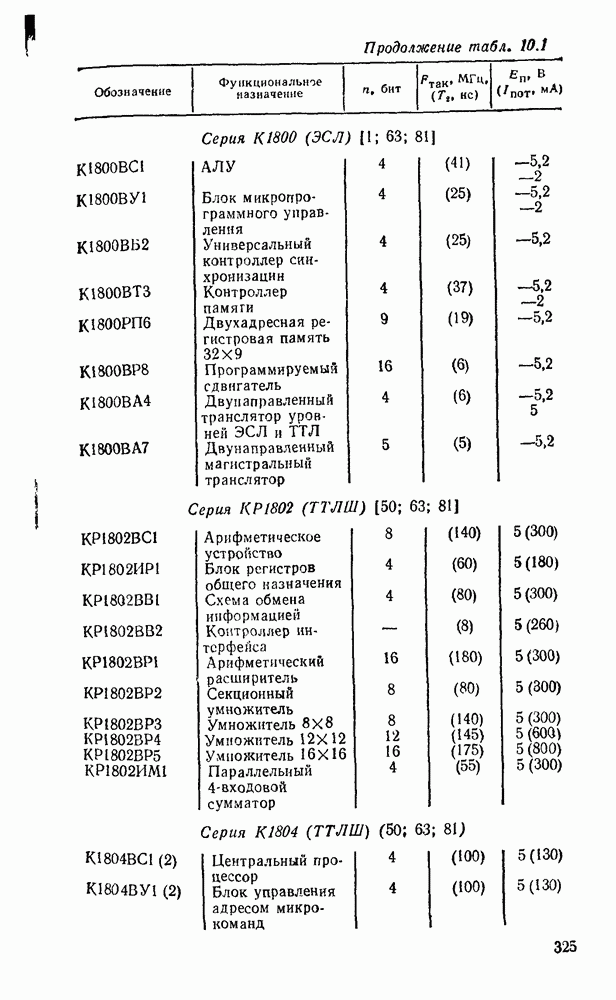
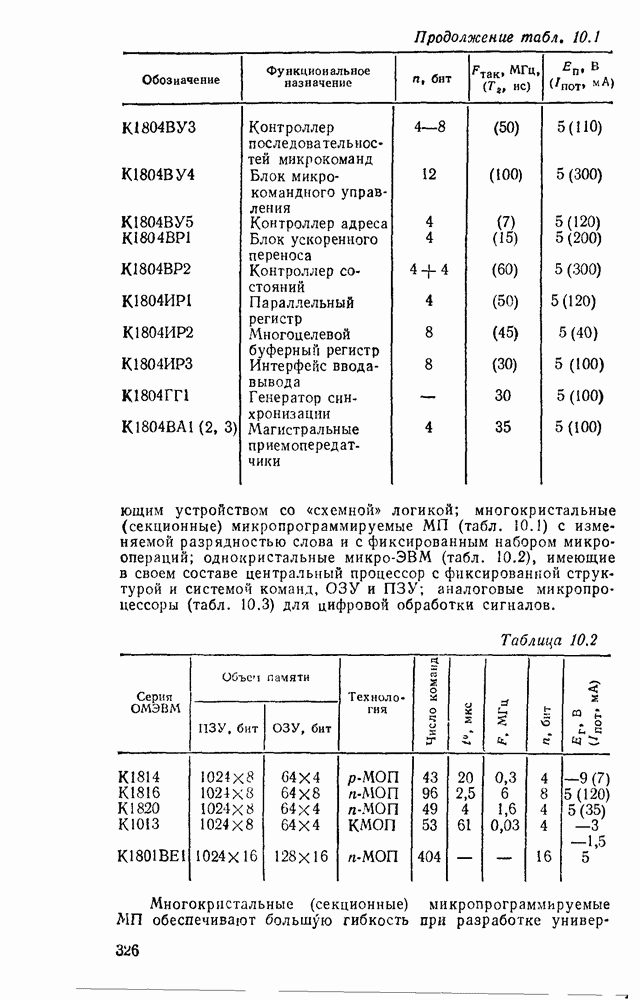
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
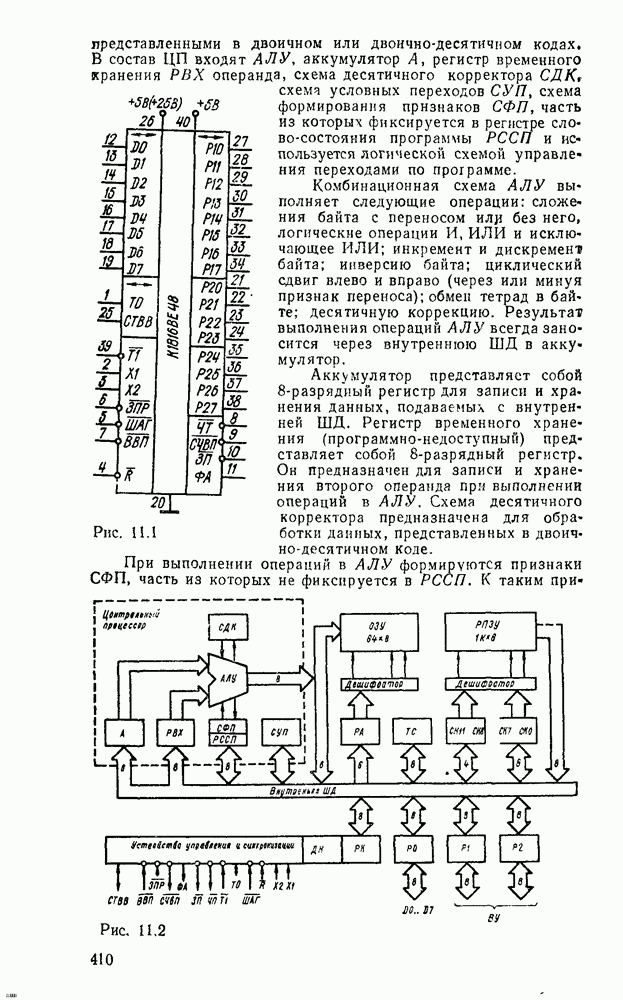
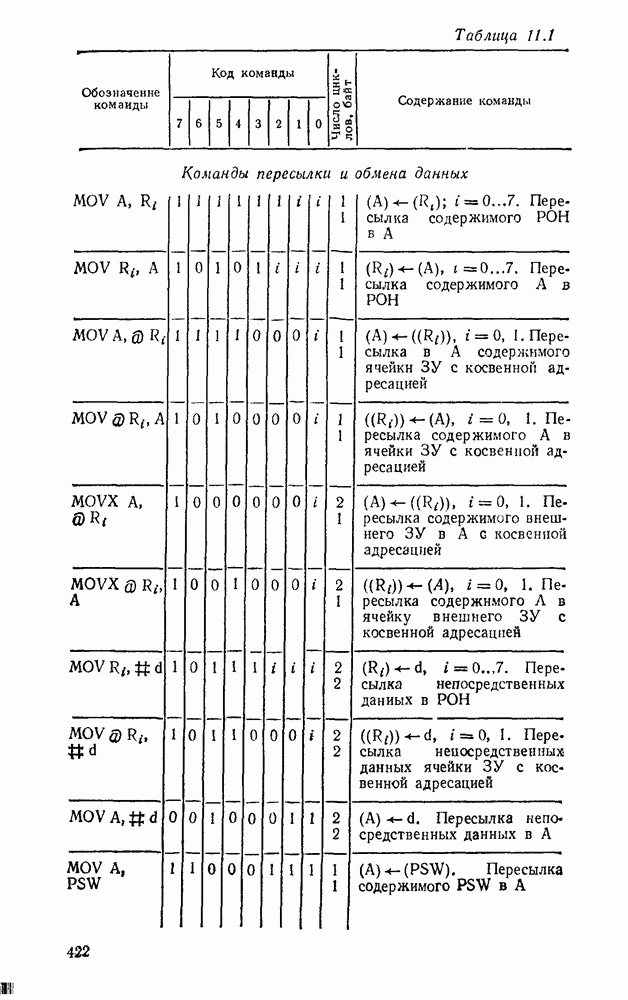
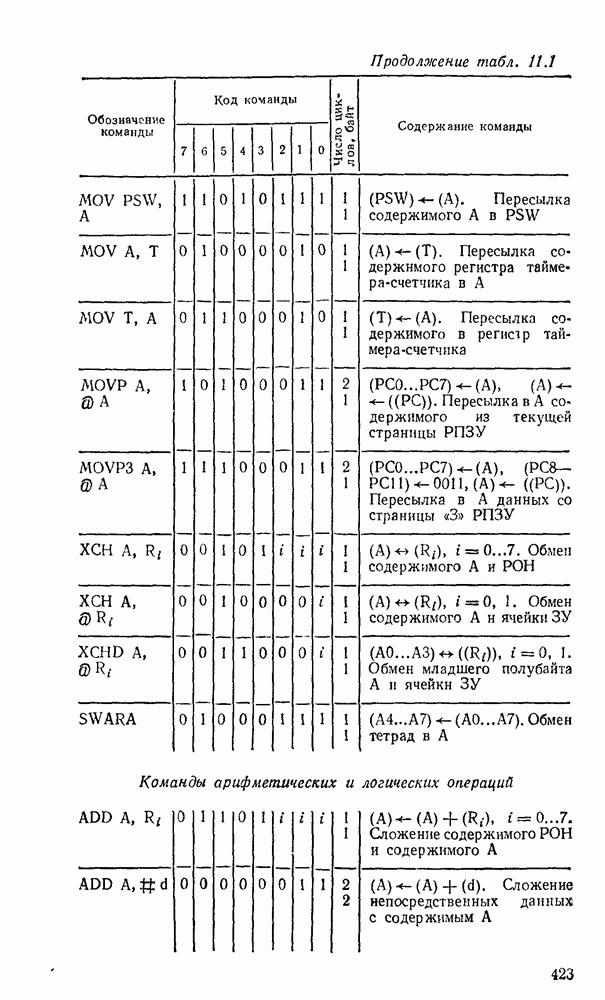
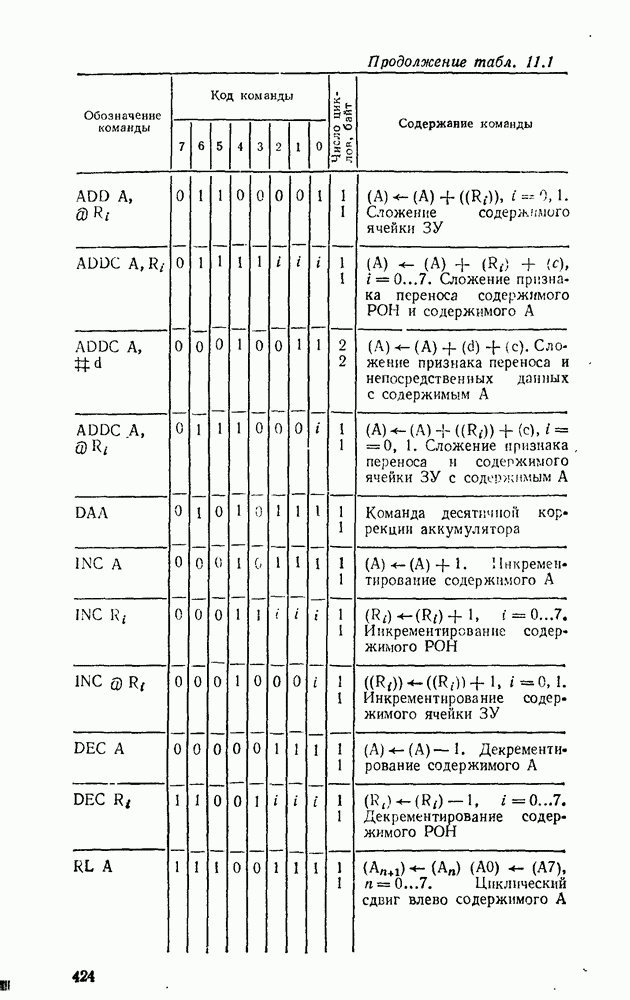
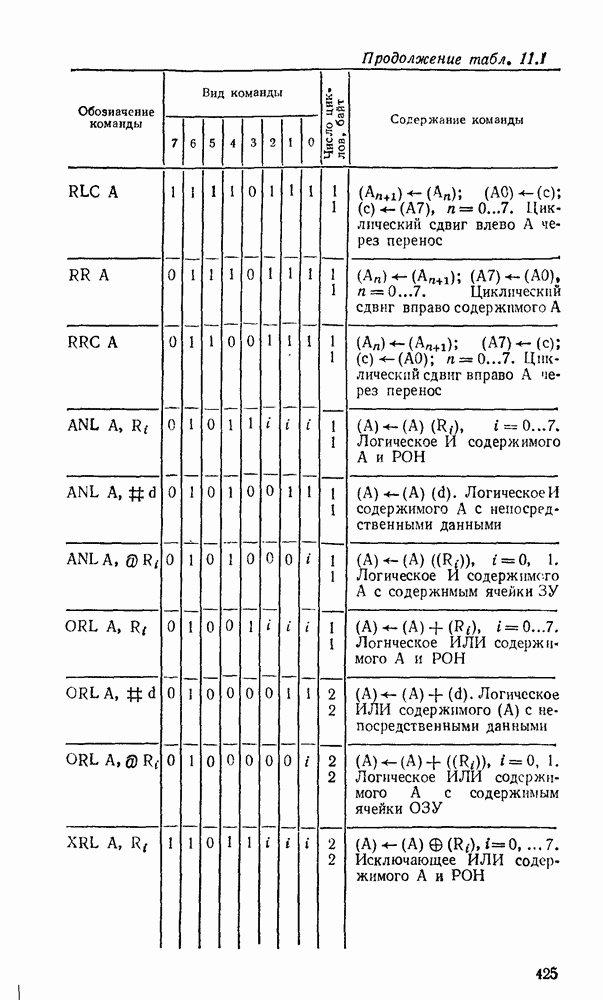
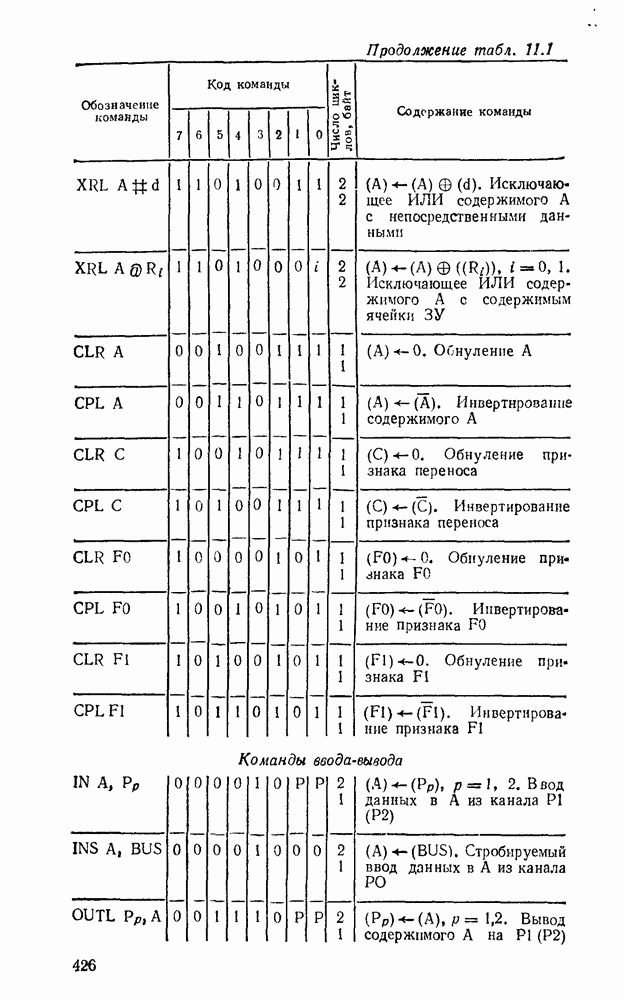
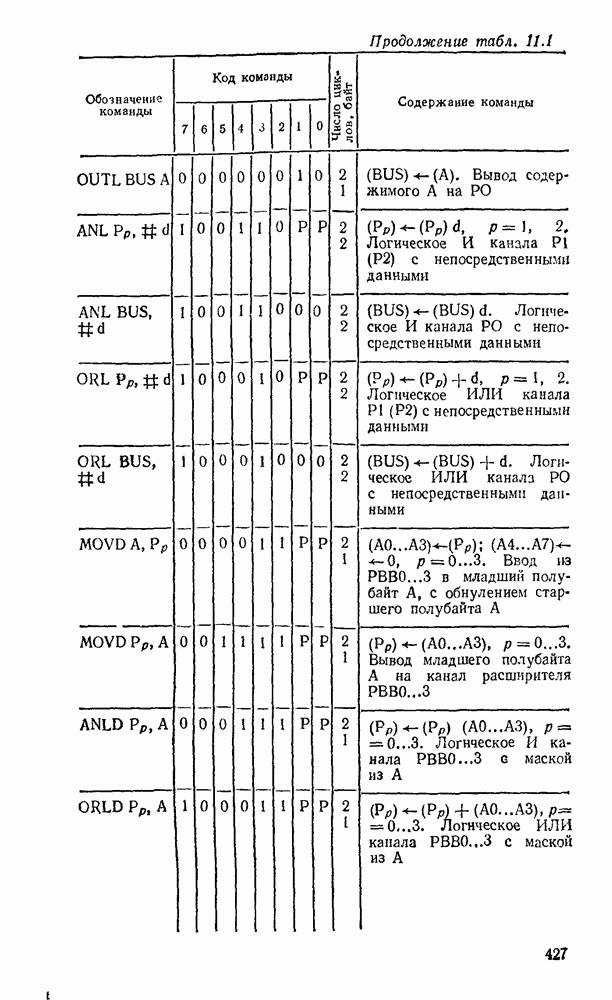
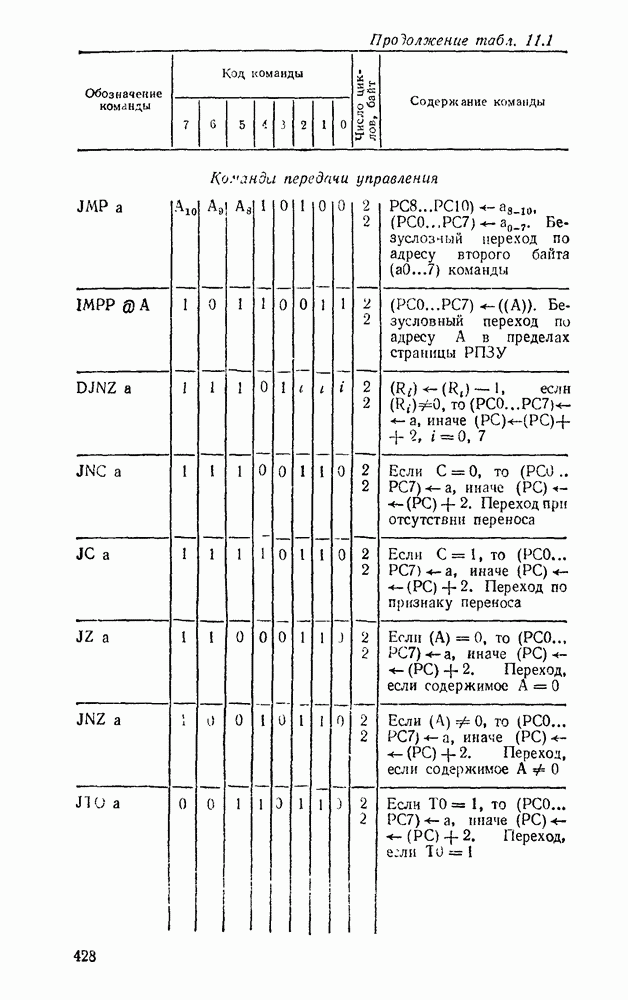
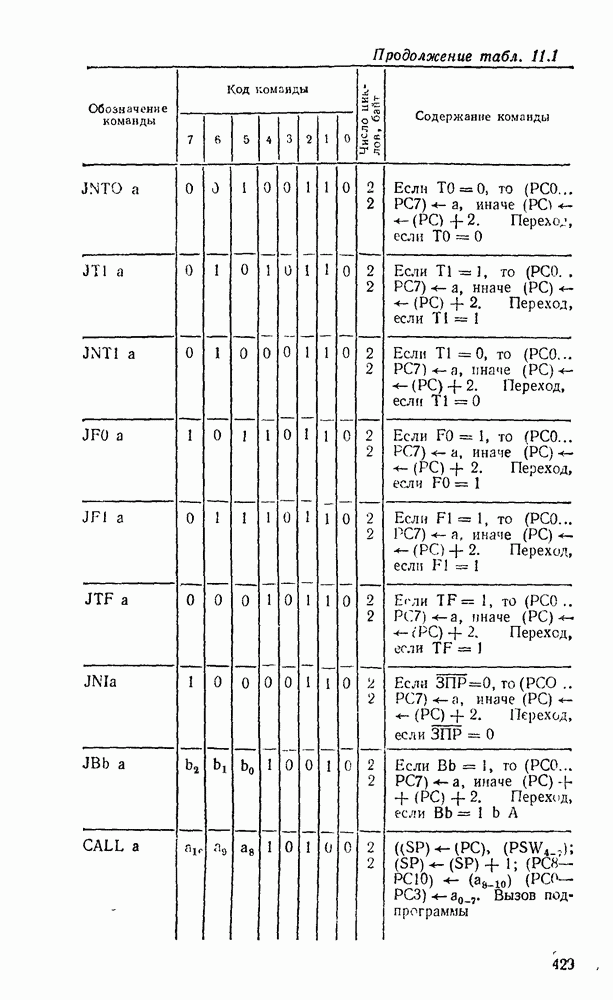
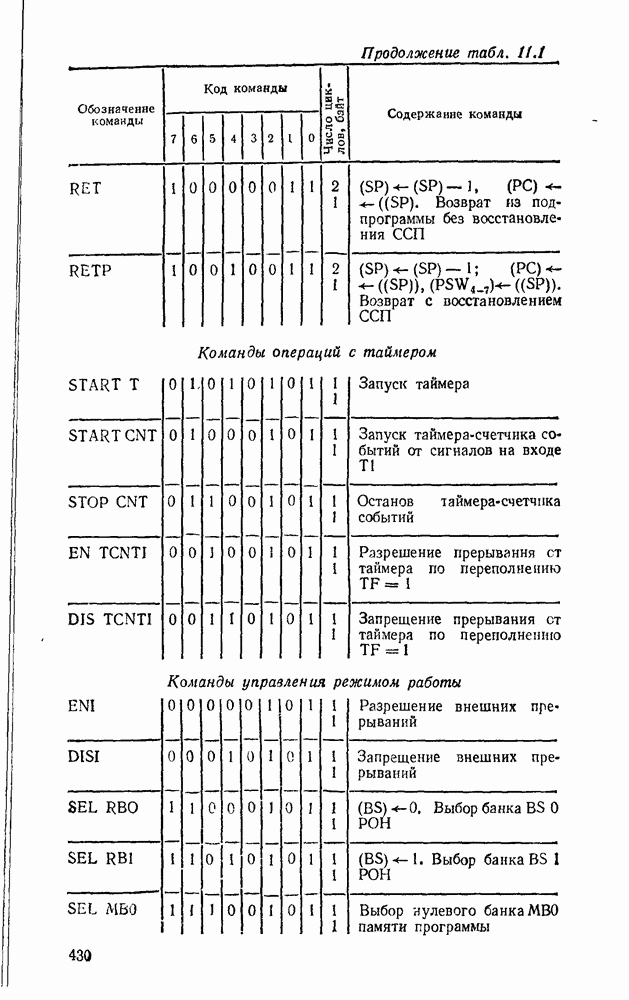
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
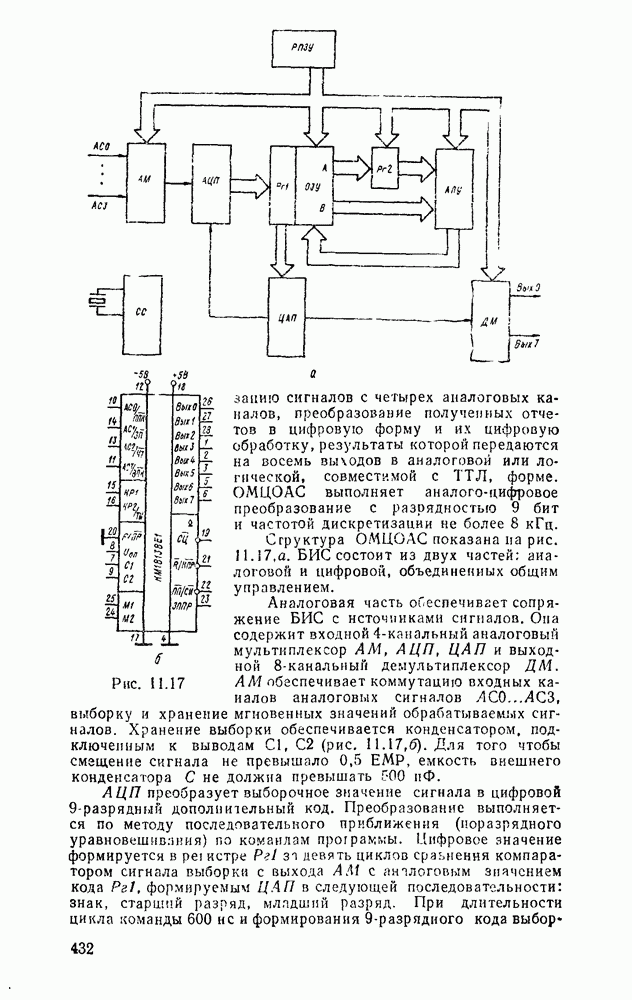
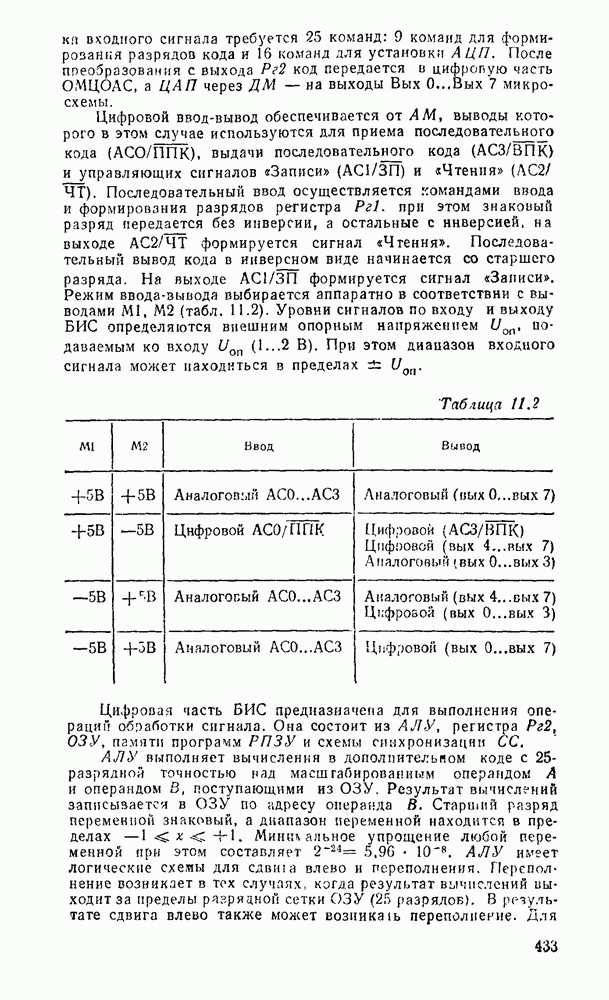
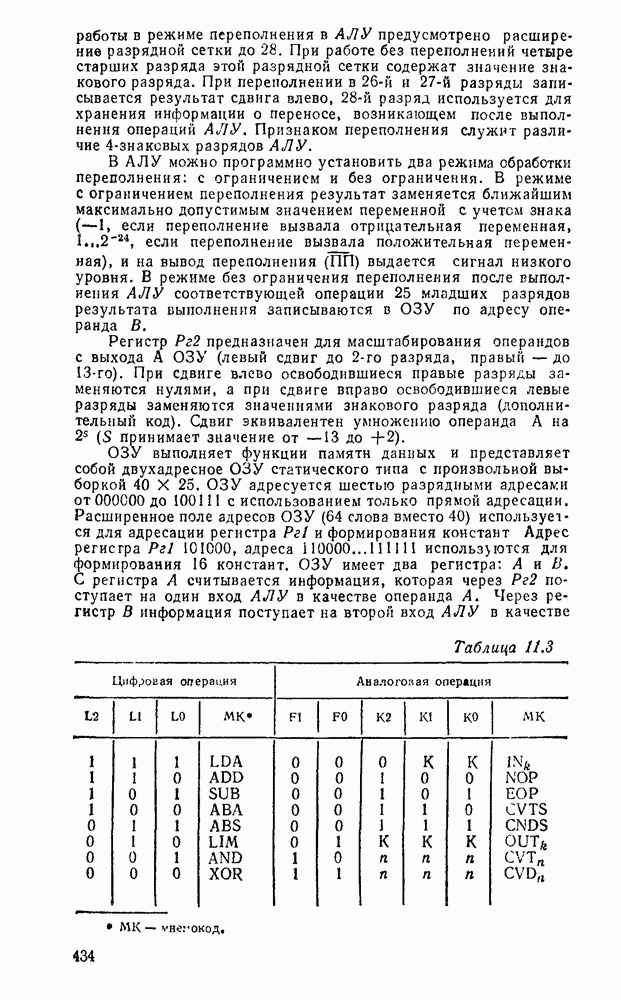
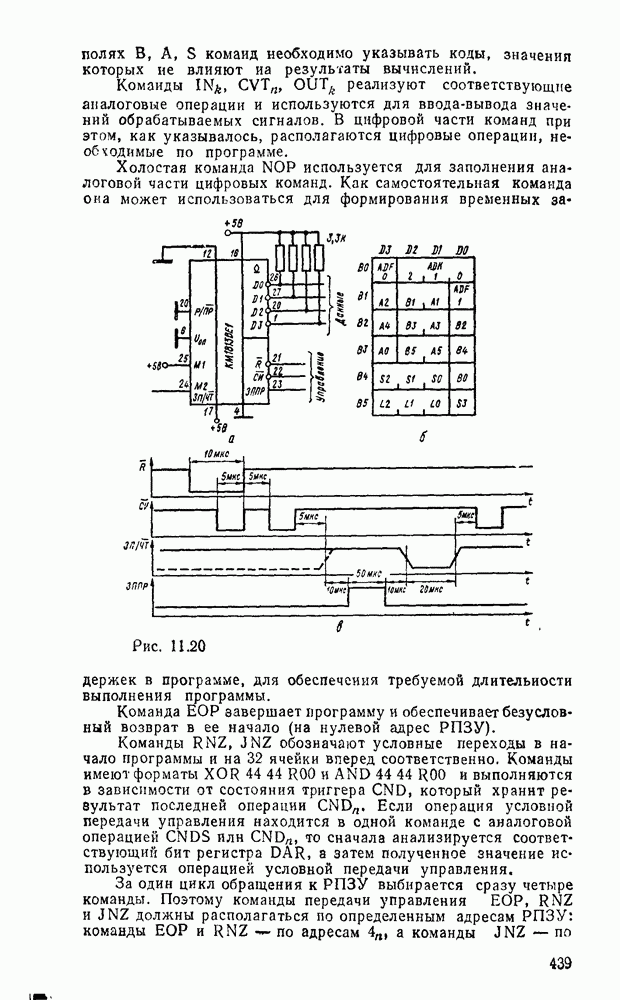
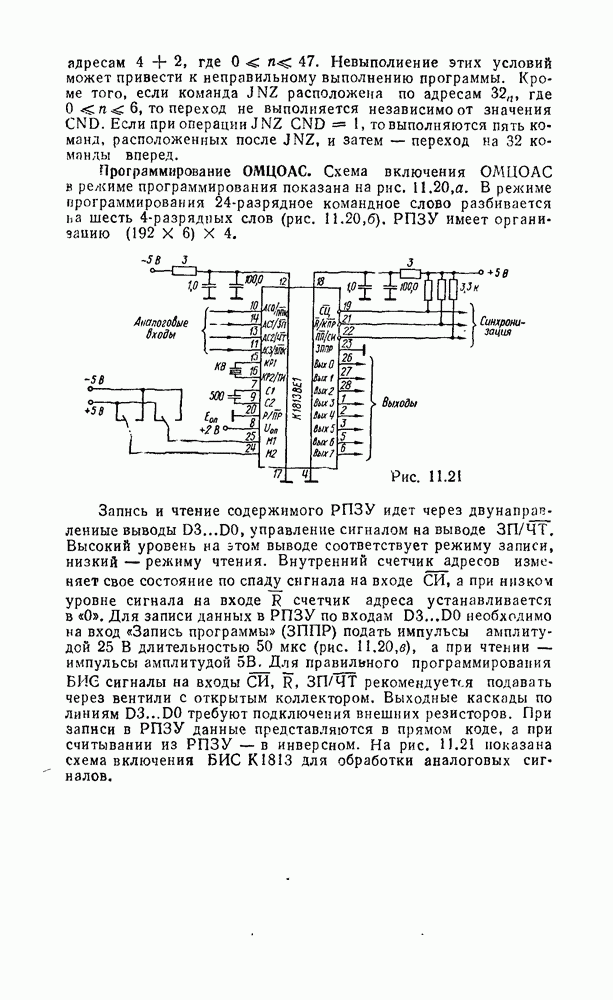
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ