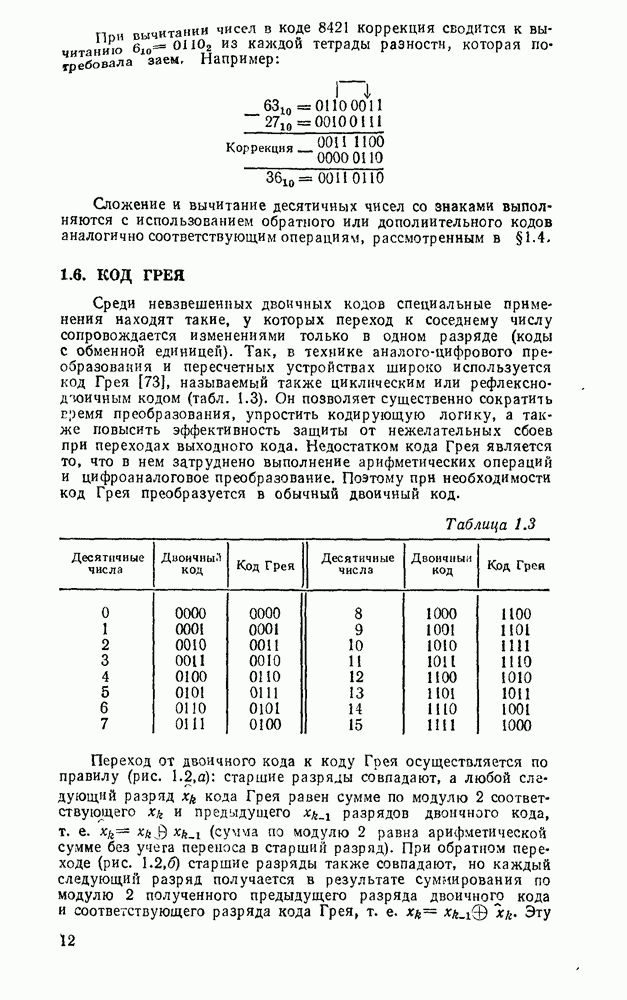
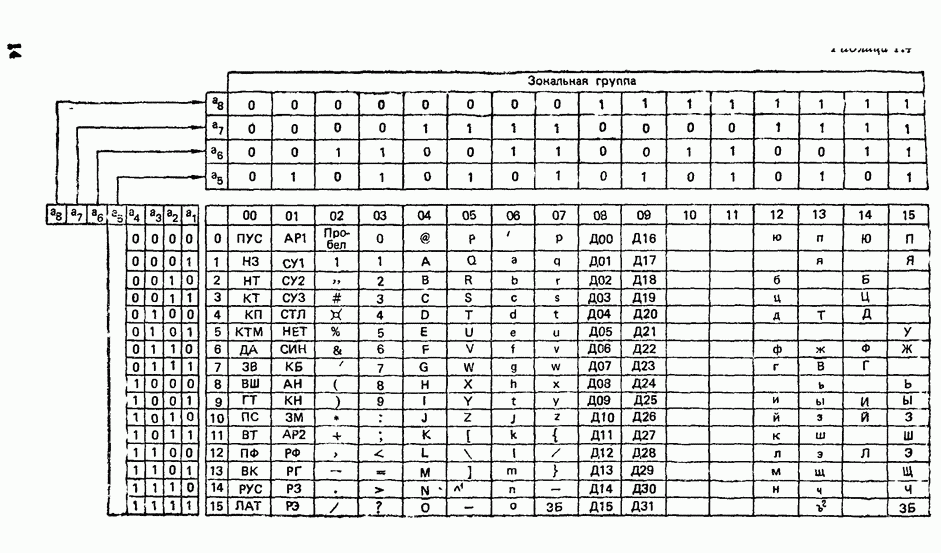
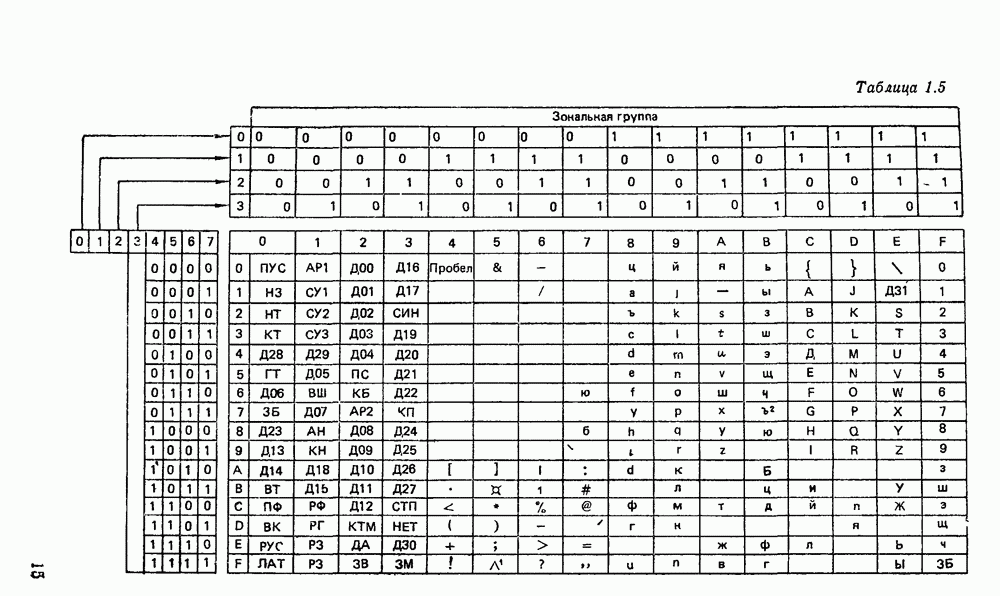
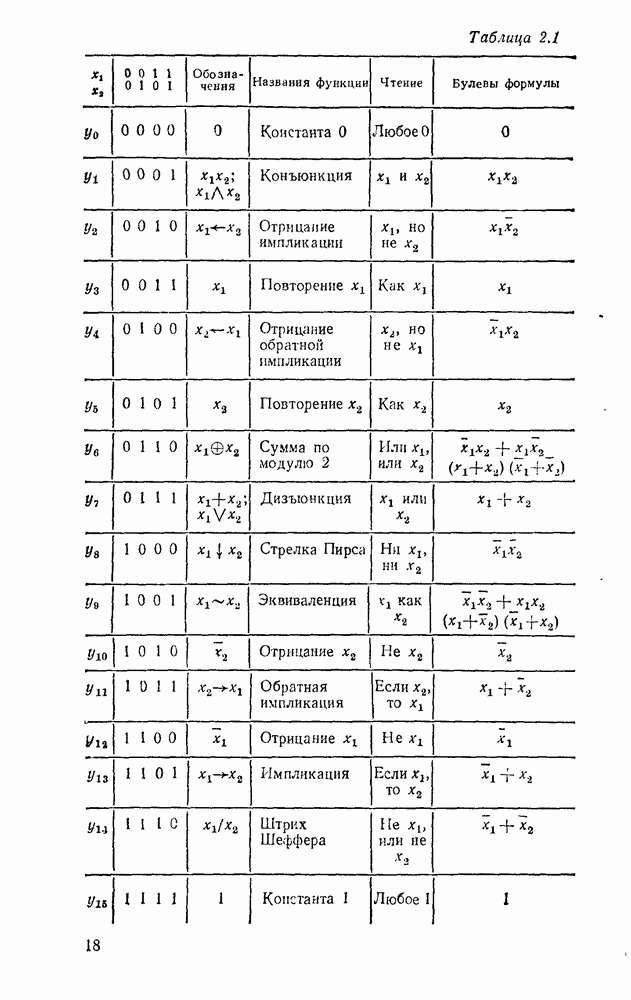
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
3.1. ЛОГИЧЕСКИЕ СХЕМЫ
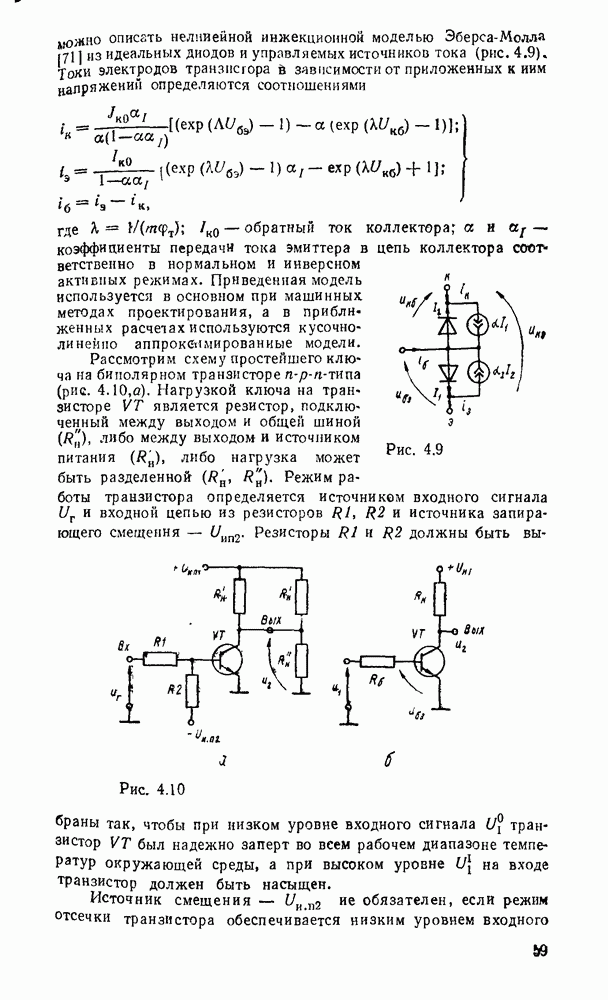
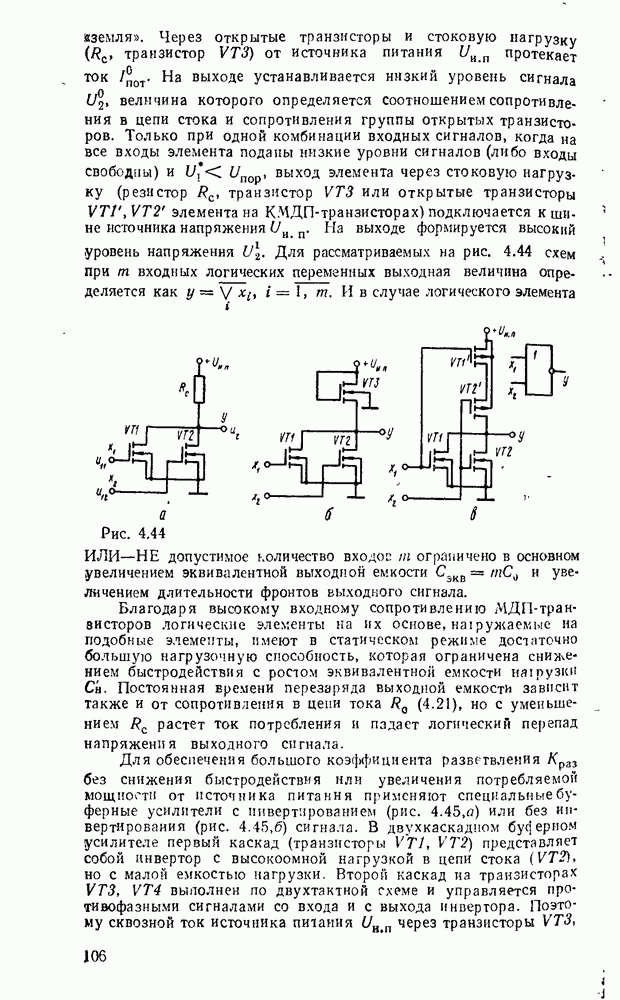
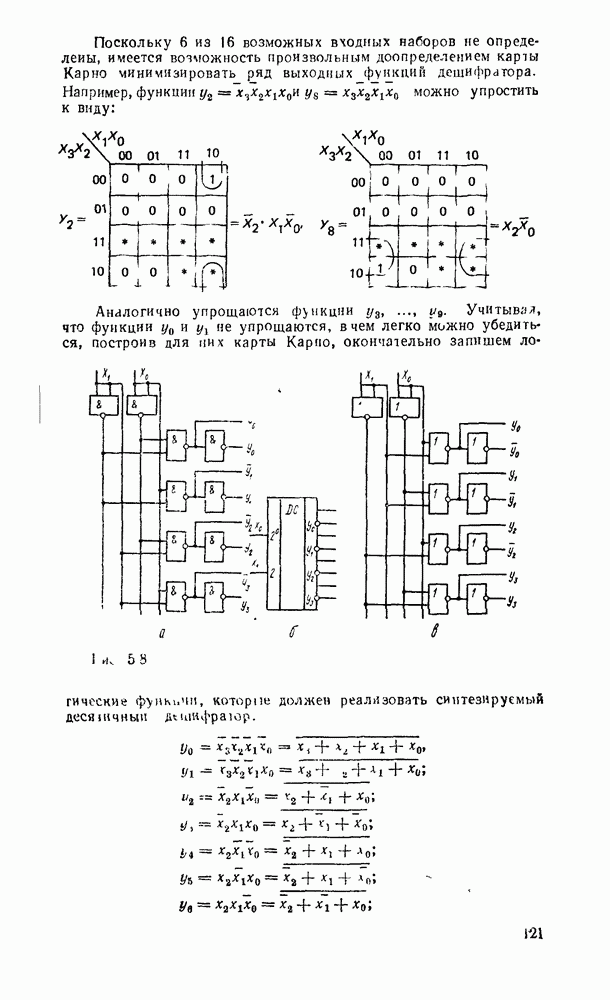
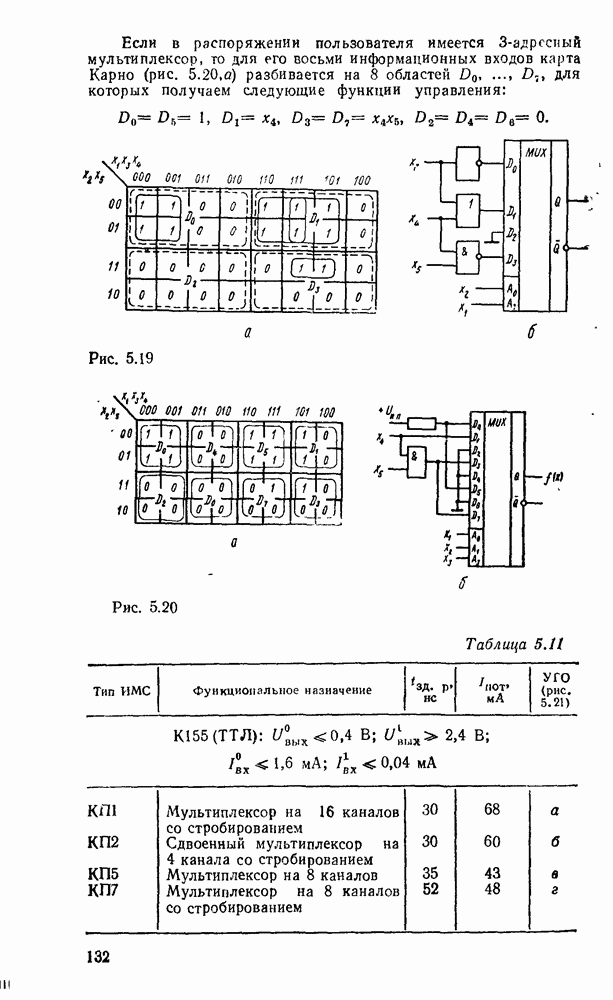
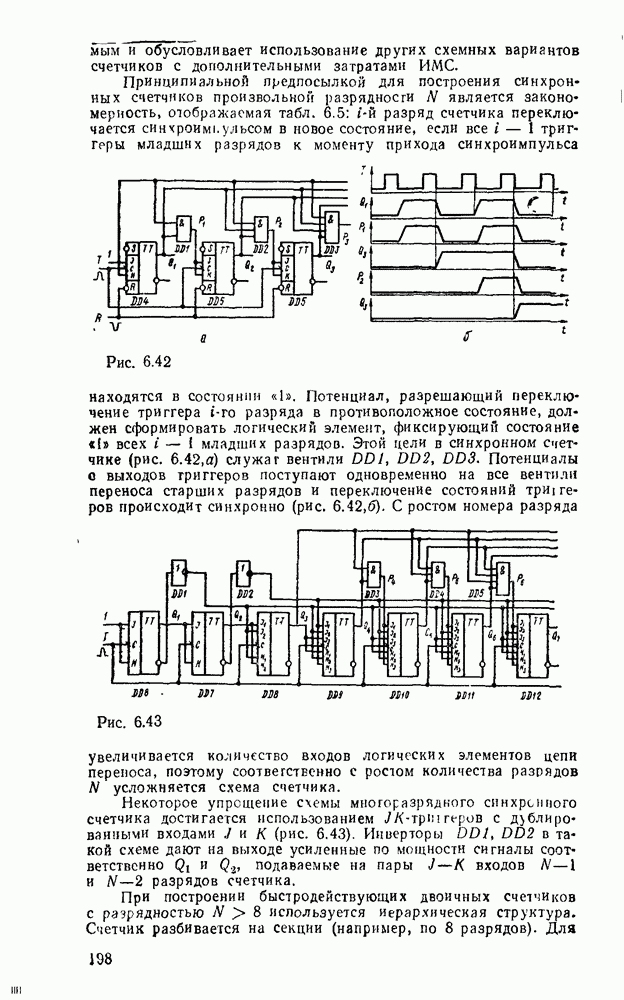
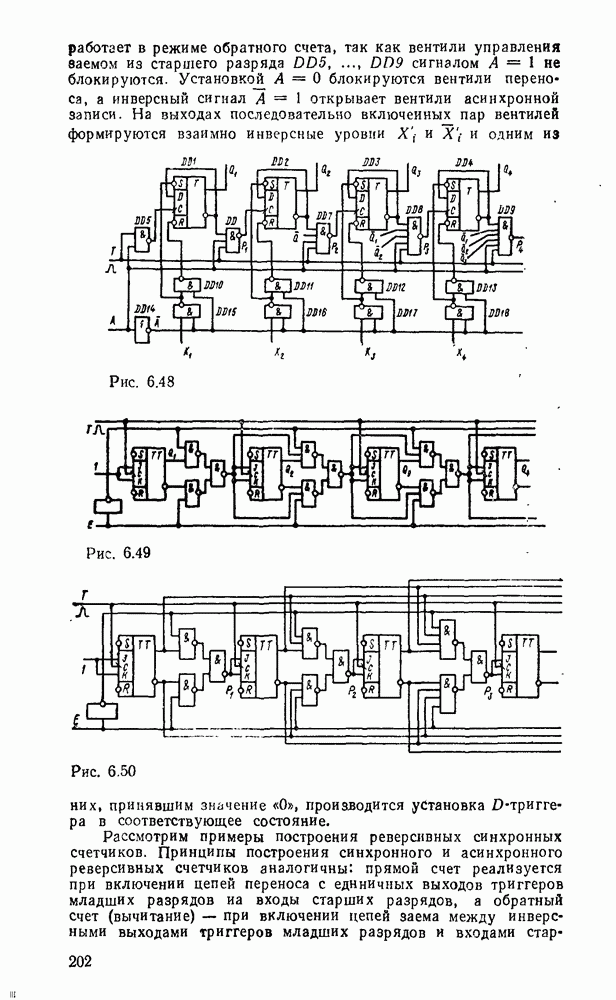
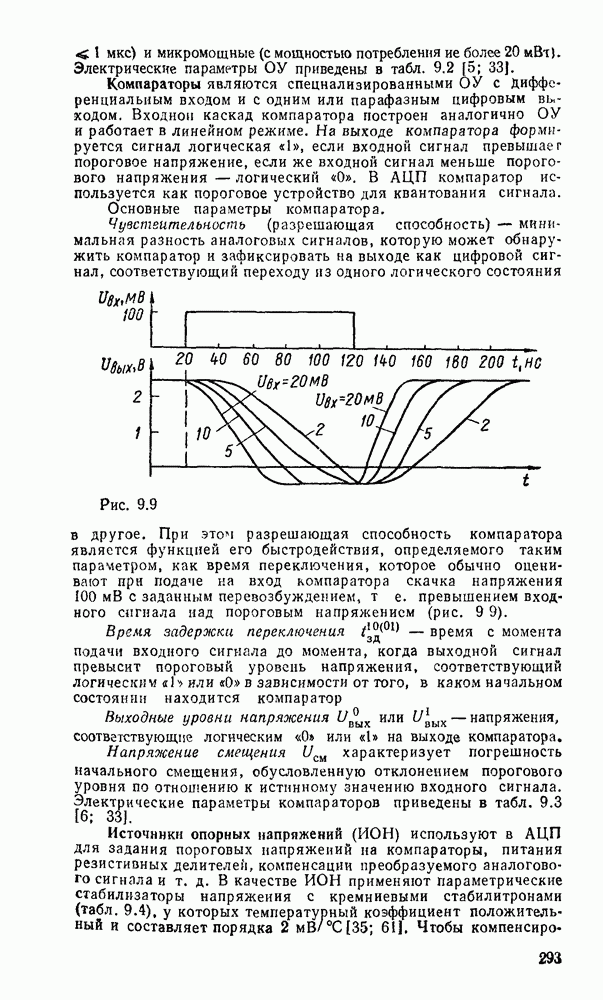
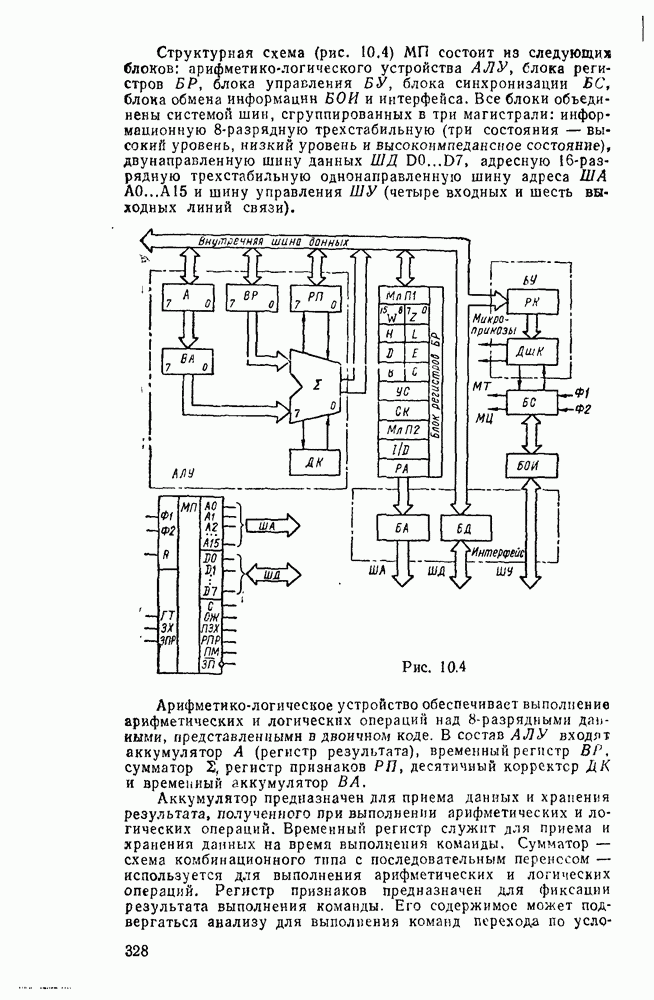
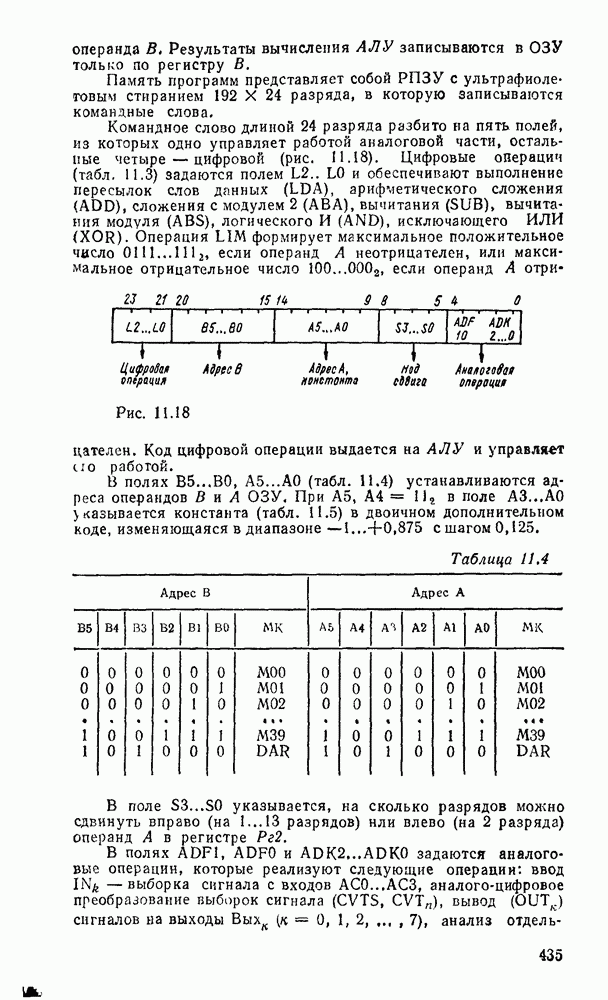
Логические схемы являются структурными моделями цифровых устройств, реализующих логические функции. Они отображают преобразование входных переменных  в выходные
в выходные  (рис. 3.1,а).
(рис. 3.1,а).

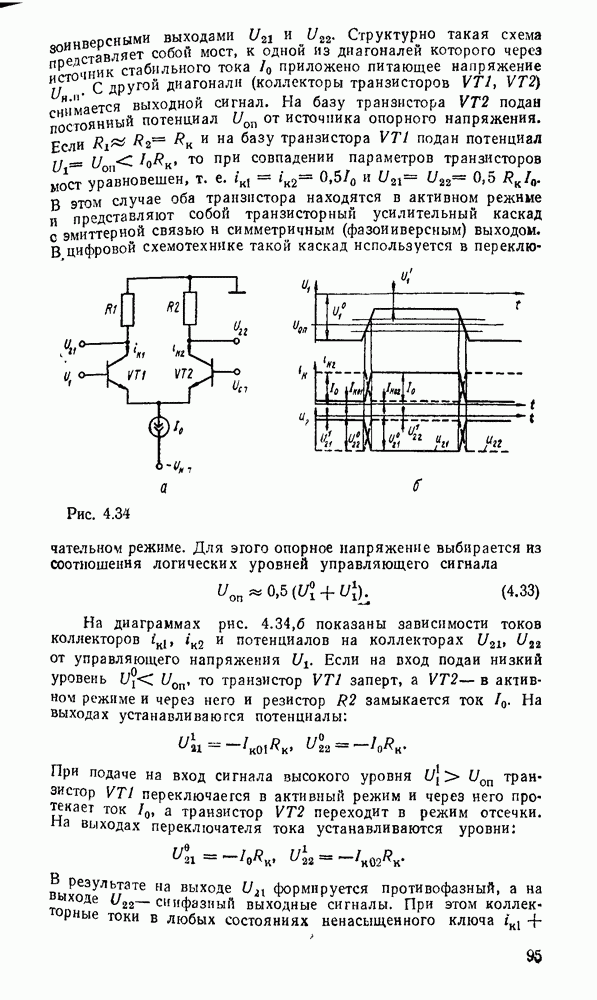
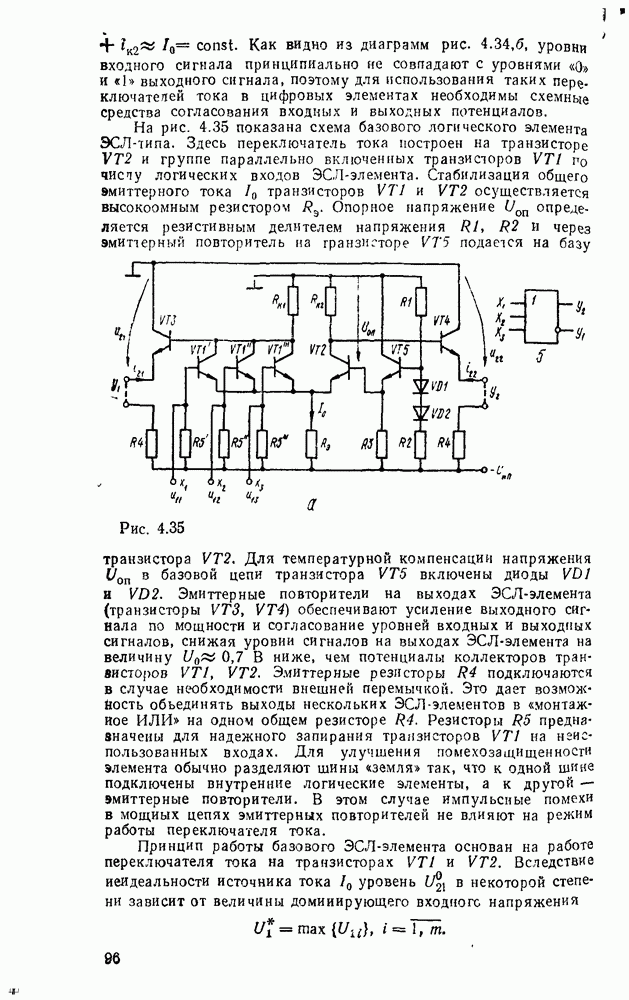
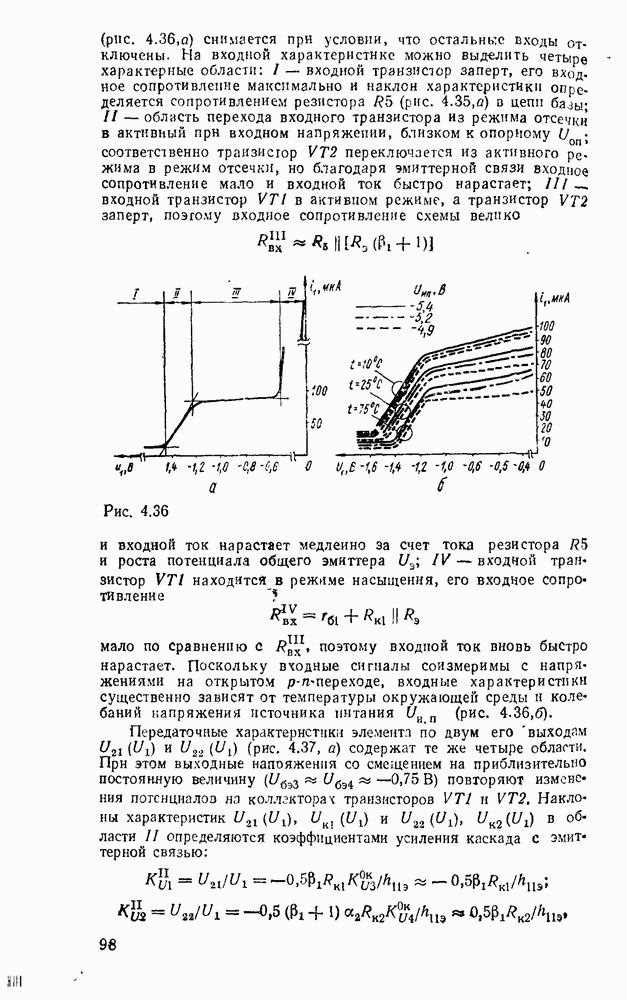
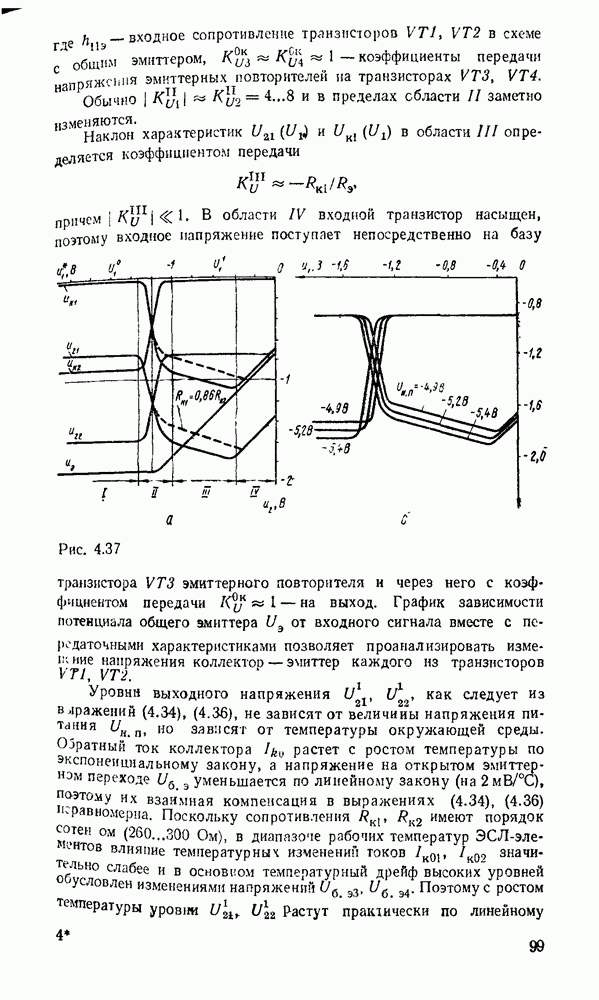
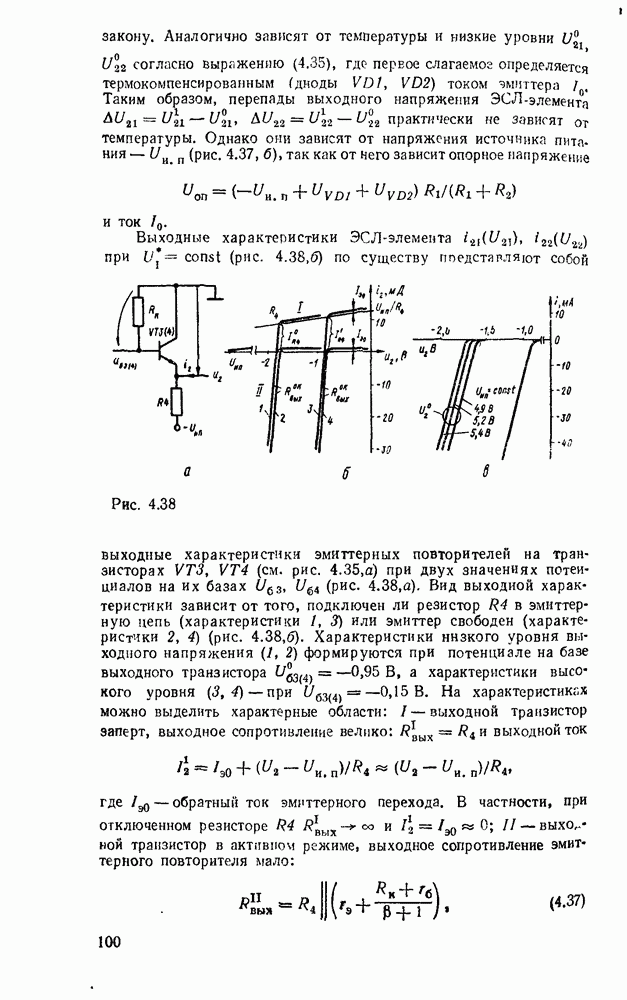
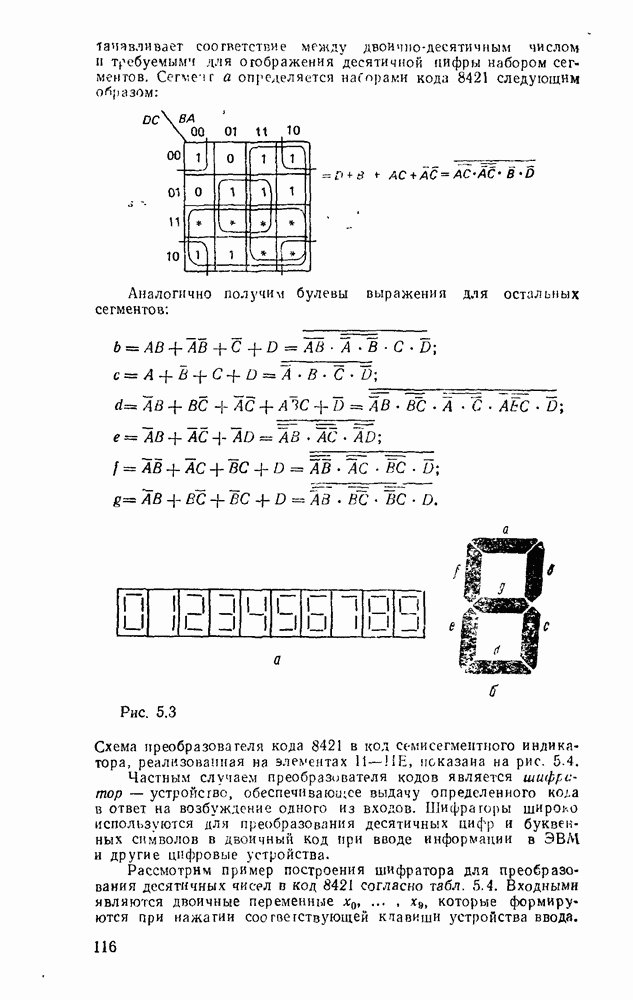
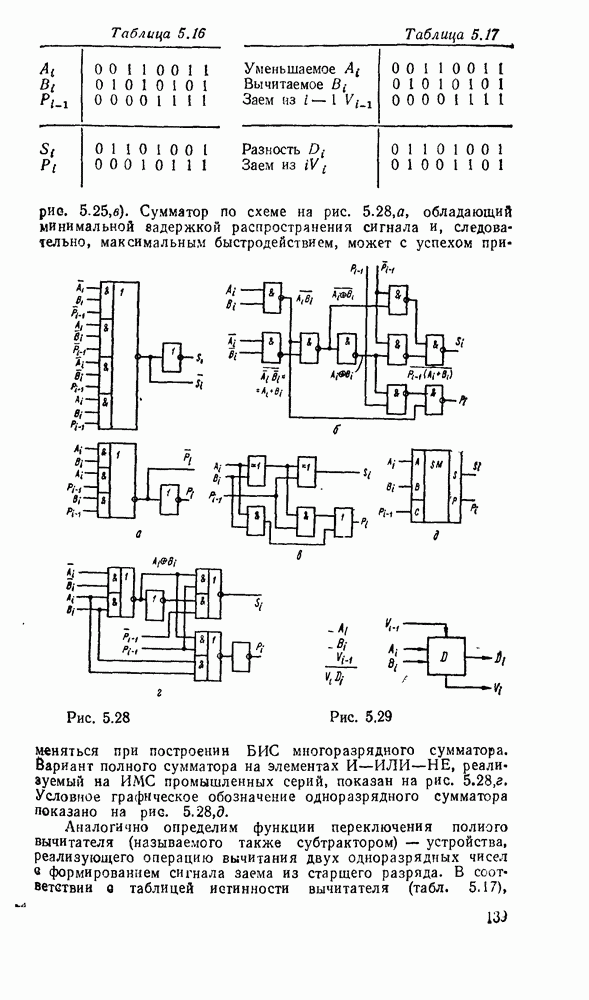
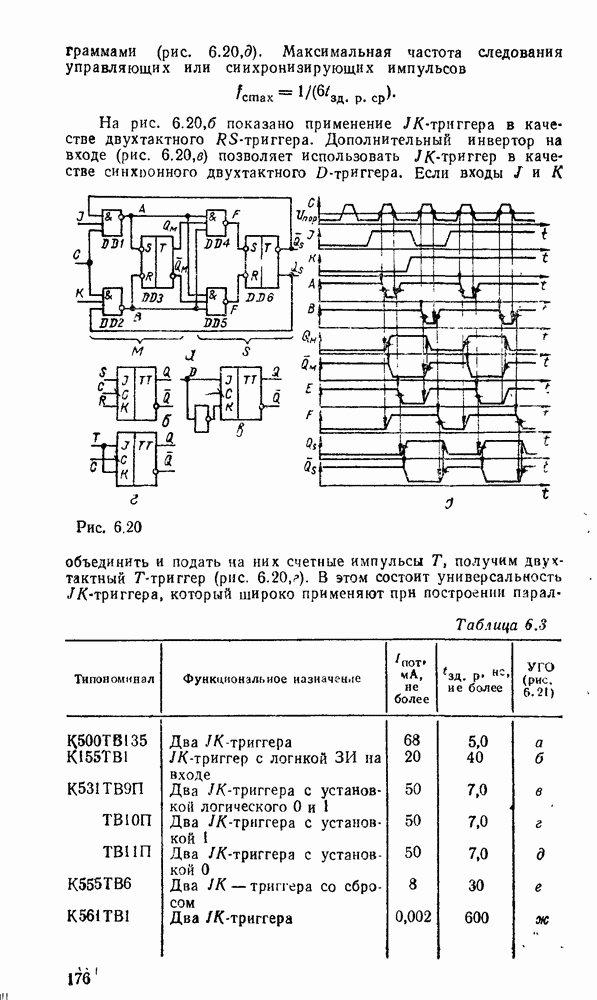
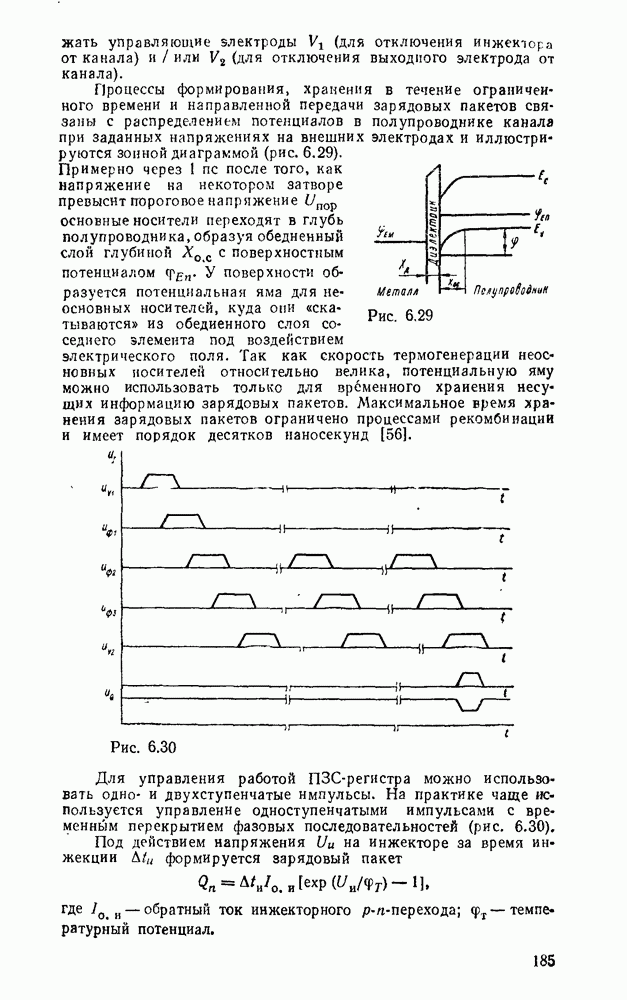
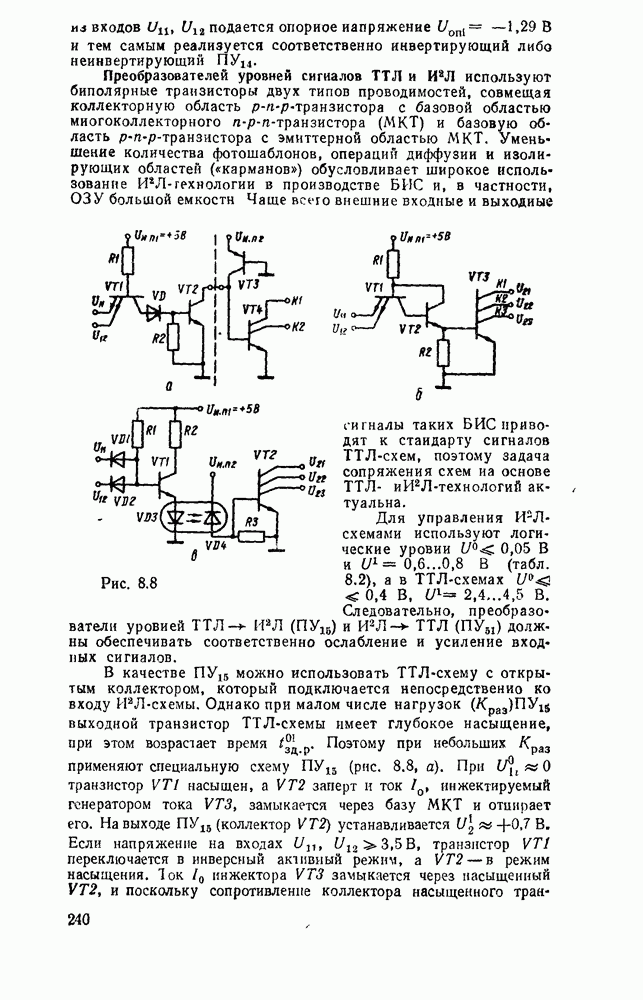
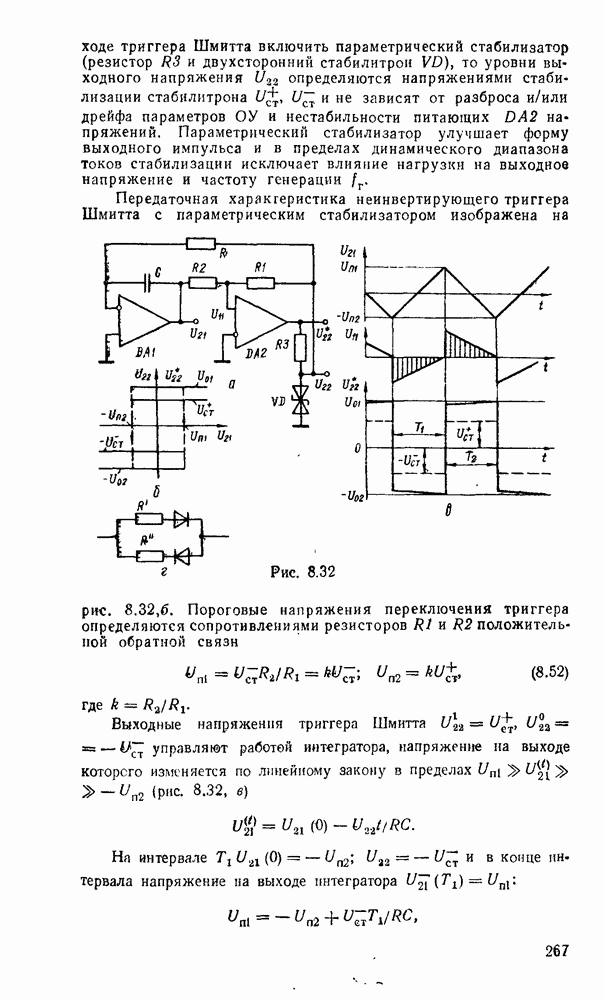
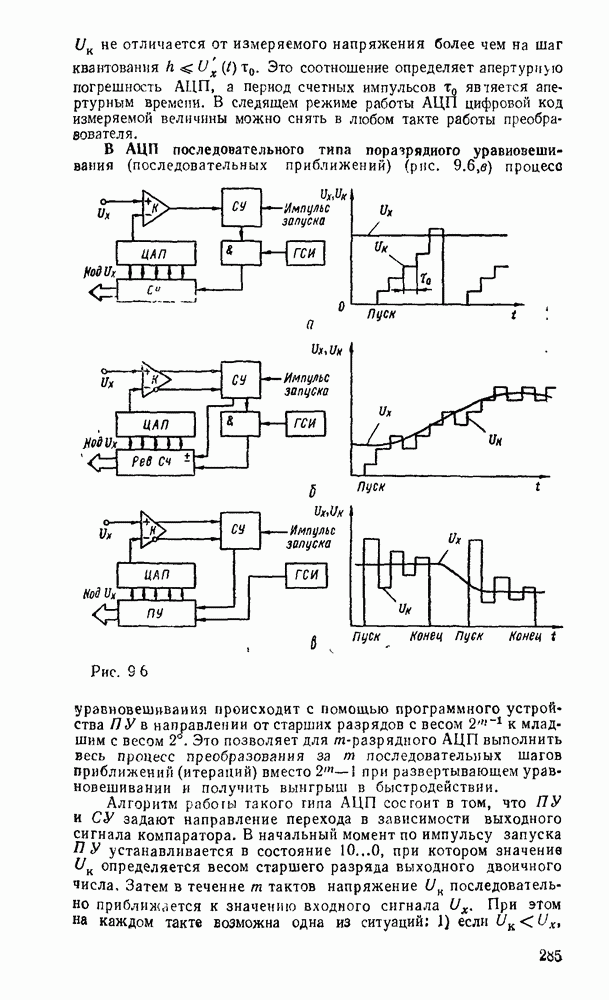
Рис. 3.1.
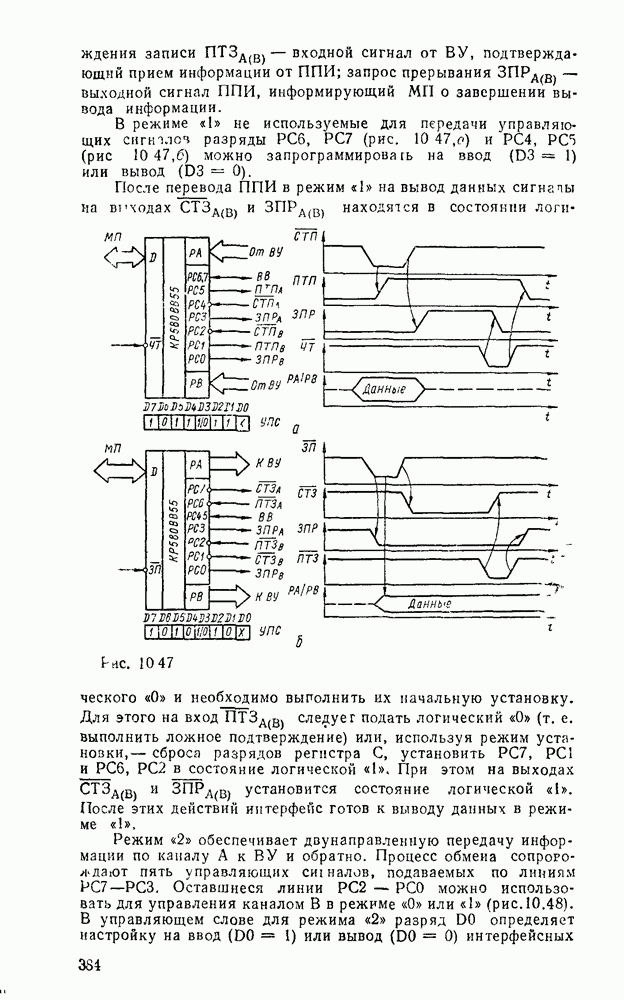
Если значения выходных переменных определяются комбинацией значений переменных на входах только в данный момент, то такие схемы называют комбинационными. Если же выход  зависит не только от входа
зависит не только от входа  в данный тактовый момент V, но и от состояния
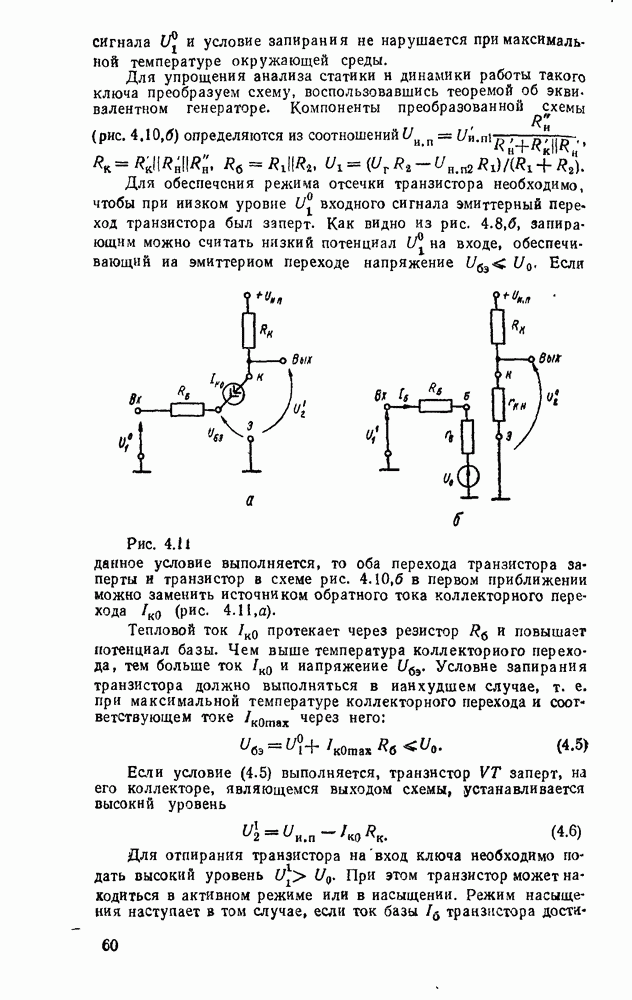
в данный тактовый момент V, но и от состояния  в предыдущий момент, то такие схемы называют последовательностными. Они содержат наряду с комбинационными схемами элементы памяти, которые сохраняют предыдущее состояние до следующего такта (рис.
в предыдущий момент, то такие схемы называют последовательностными. Они содержат наряду с комбинационными схемами элементы памяти, которые сохраняют предыдущее состояние до следующего такта (рис.  ). Оба тина схем объединяются иод названием конечные автоматы в предположении, что все переменные принимают значения из конечных алфавитов. Особое значение имеют конечные автоматы с двузначным структурным алфавитом, зависимости между входами и выходами которых выражаются булевыми функциями. Последовательностные схемы называются также конечными автоматами с памятью.
). Оба тина схем объединяются иод названием конечные автоматы в предположении, что все переменные принимают значения из конечных алфавитов. Особое значение имеют конечные автоматы с двузначным структурным алфавитом, зависимости между входами и выходами которых выражаются булевыми функциями. Последовательностные схемы называются также конечными автоматами с памятью.
Простейшими компонентами комбинационной схемы являются вентили, реализующие элементарные операции.
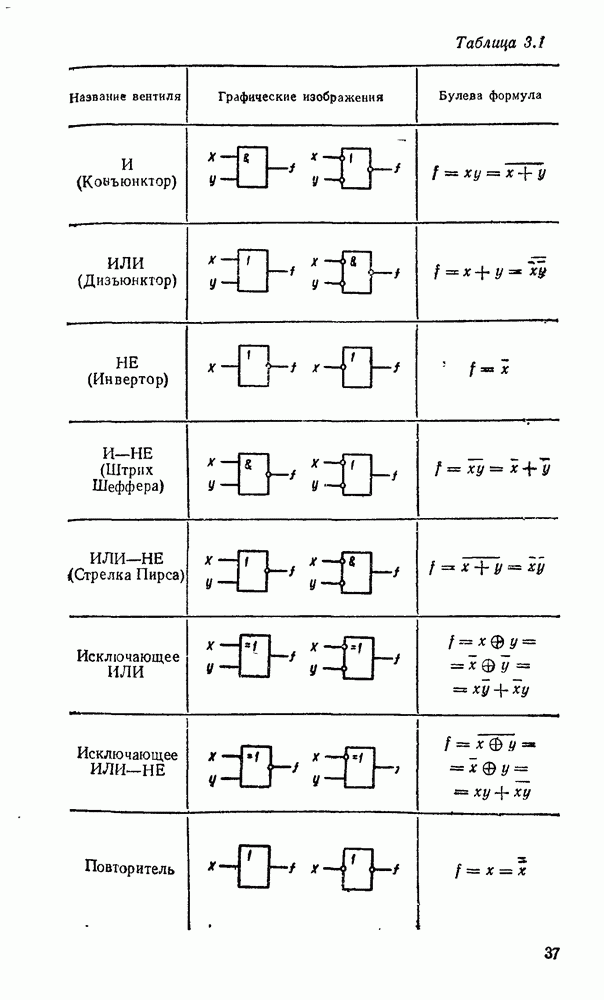
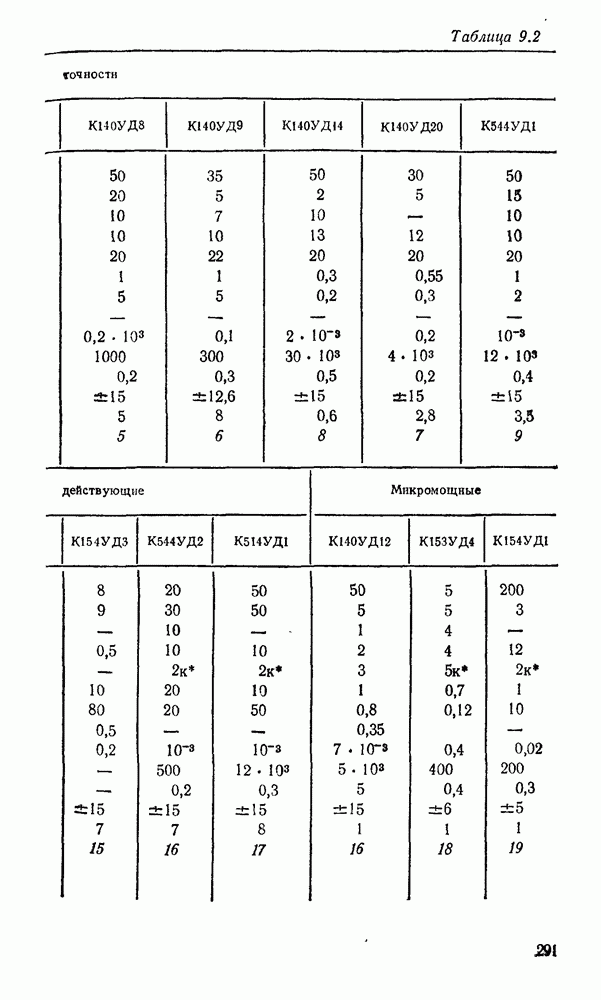
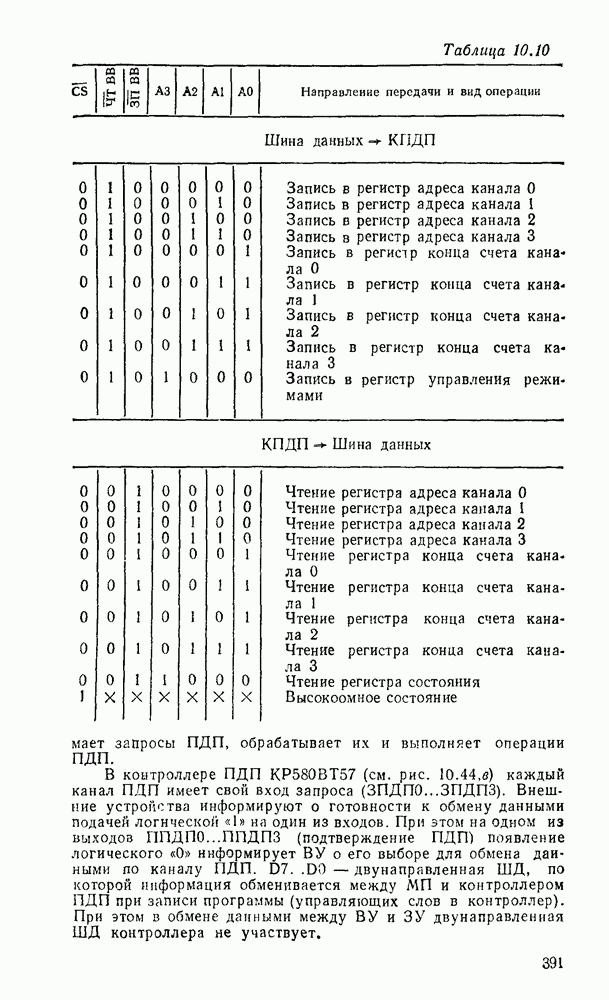
Таблица 3.1
(см. оригинал)
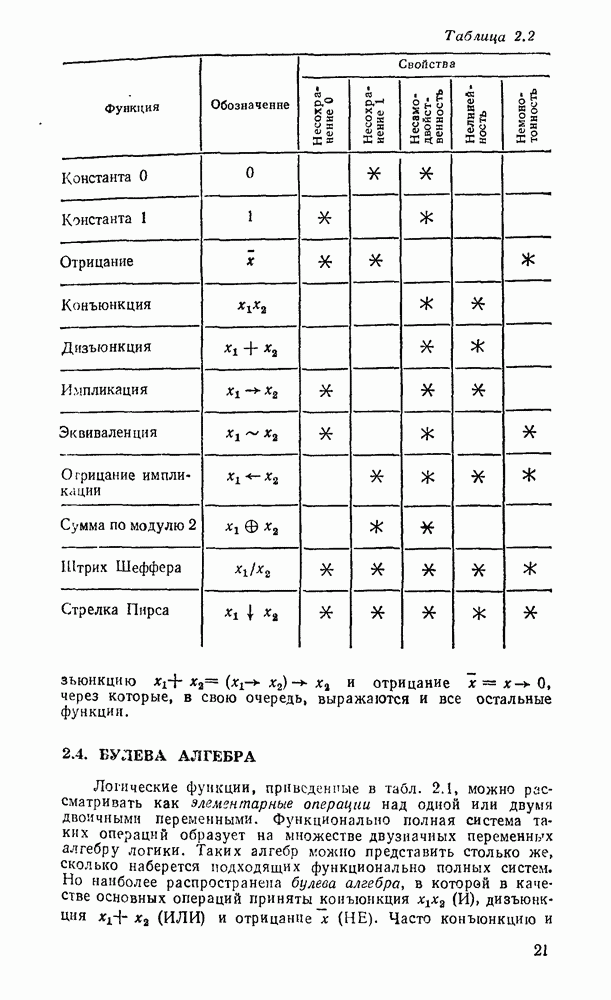
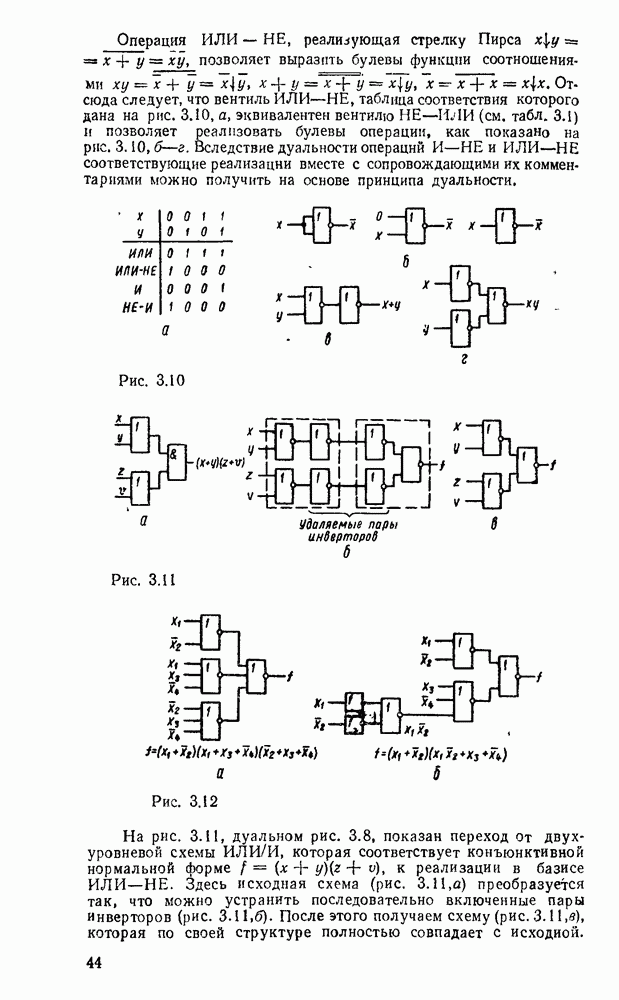
Графические изображения наиболее употребительных вентилей даны в табл. 3.1 (инверсные входы и выходы обозначаются маленькими кружочками). В качестве компонентов могут рассматриваться и некоторые соединения вентилей, образующих подсхемы. Соответственно говорят о логическом моделировании на различных уровнях — вентильном, регистровом и т. д. При моделировании на вентильном уровне логические формулы выражаются в булевом базисе И, ИЛИ, НЕ, поэтому и логические схемы обычно строятся с помощью аналогичного набора вентилей. Между тем могут оказаться удобными и другие вентили, преобразование к коюрым обеспечивается надлежащей методикой. В частности, широко используются логические схемы на основе вентиля  , реализующего штрих Шеффера, а также ИЛИ—НЕ, реализующего стрелку Пирса, что допустимо благодаря функциональной полноте каждой из этих операций (см. табл. 2.2). Логические схемы непосредственно не связаны с физической природой и конструкцией вентилей.
, реализующего штрих Шеффера, а также ИЛИ—НЕ, реализующего стрелку Пирса, что допустимо благодаря функциональной полноте каждой из этих операций (см. табл. 2.2). Логические схемы непосредственно не связаны с физической природой и конструкцией вентилей.

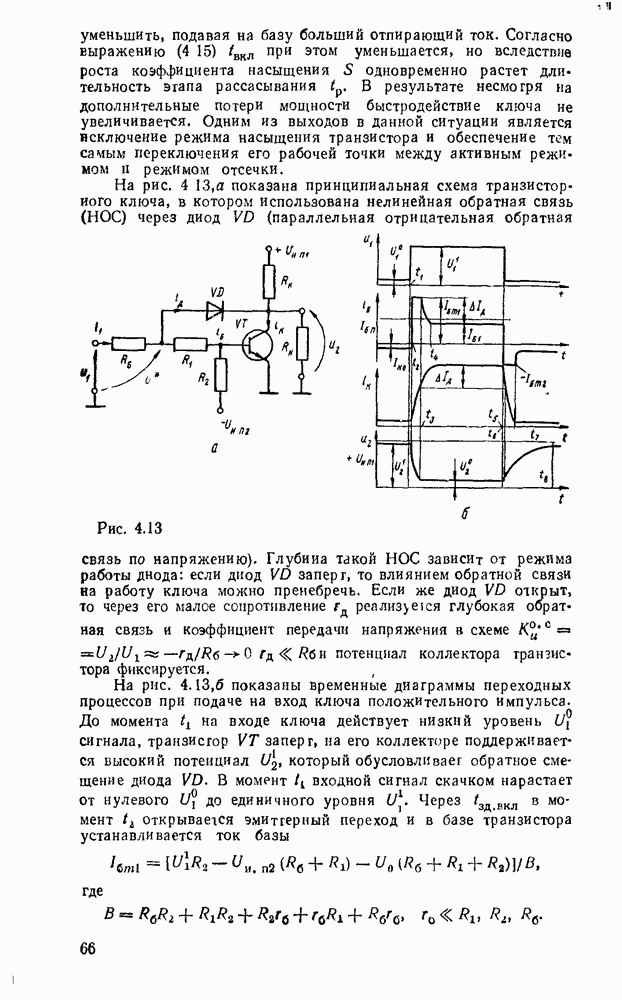
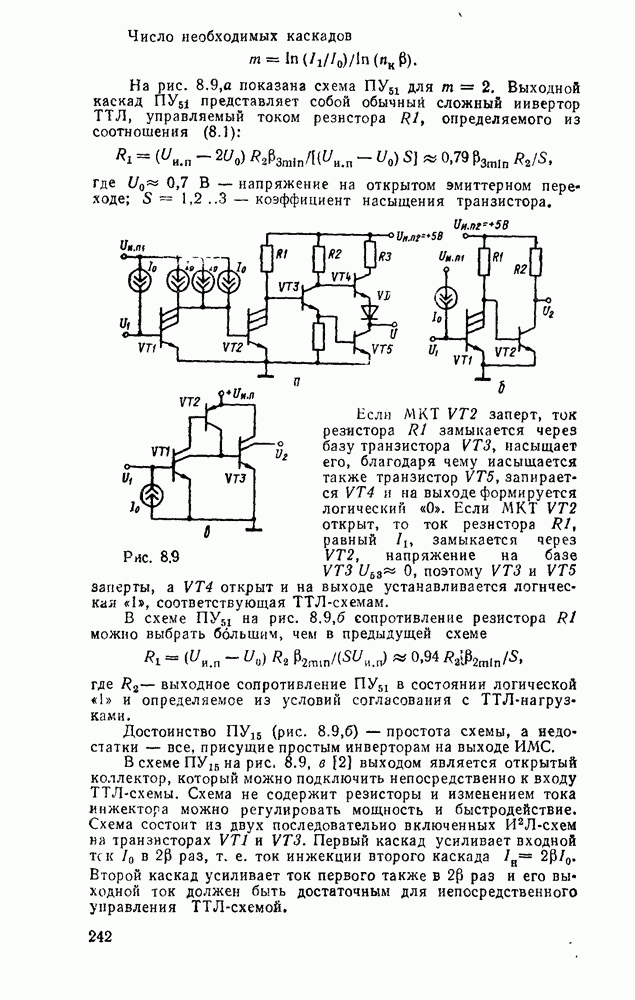
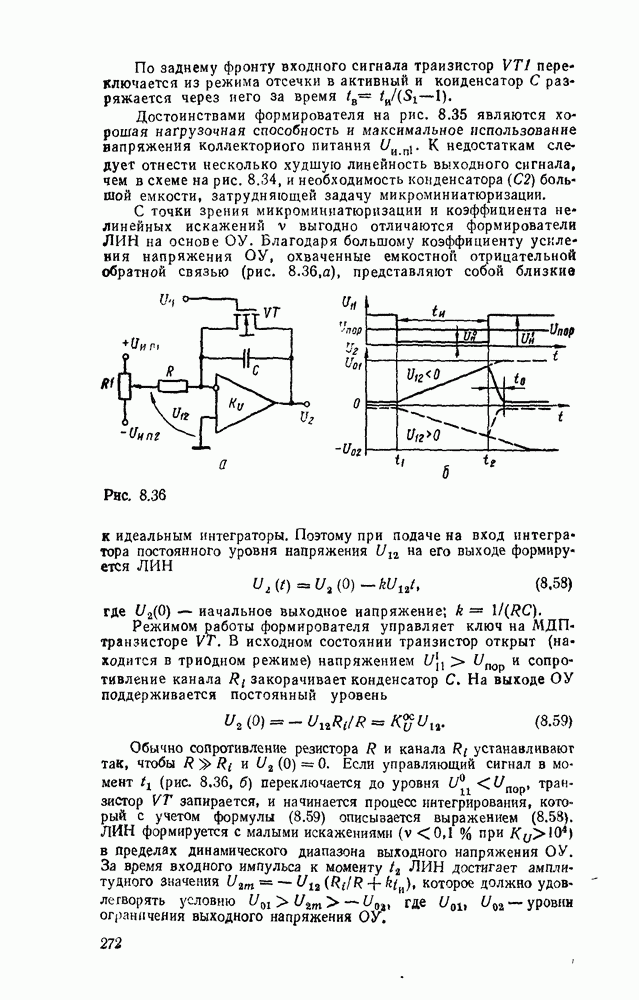
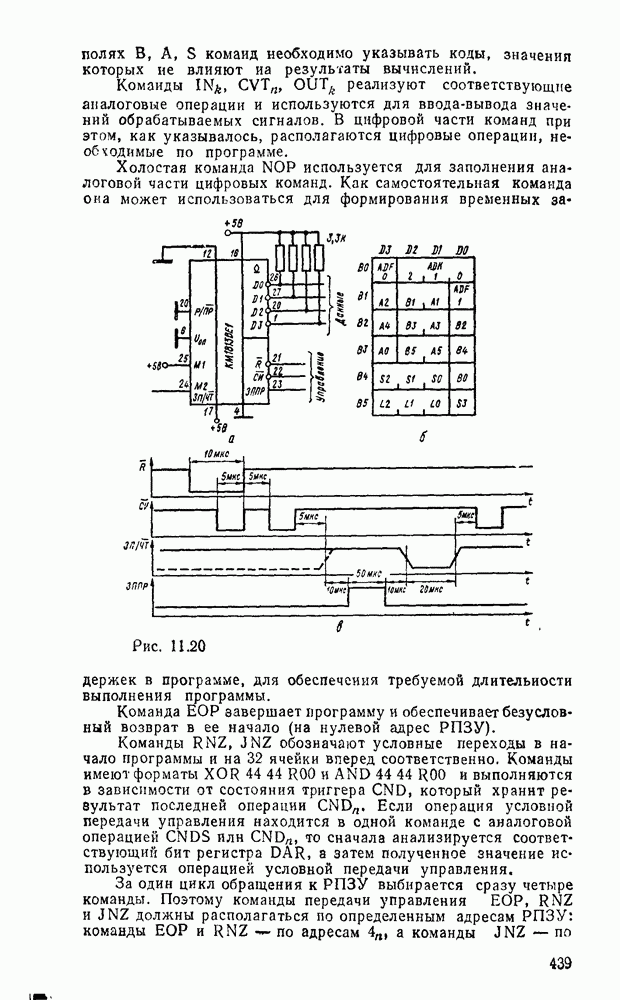
Рис. 3.2.
Тем не менее при выборе функционального базиса для реализации логических функций учитываются технико-экономические характеристики реальных компонентов цифровых устройств с тем, чтобы с наибольшей эффективностью обеспечить техническую реализацию логических схем.
Переход от булевой функции к логической схеме в булевом базисе очевиден: достаточно в соответствии с формулой обозначить входы вентилей и соединить их между собой надлежащим образом. Так, на рис. 3.2 показаны логические схемы, реализующие минимальные формы, полученные в примерах §§ 2.7 и 2.9.
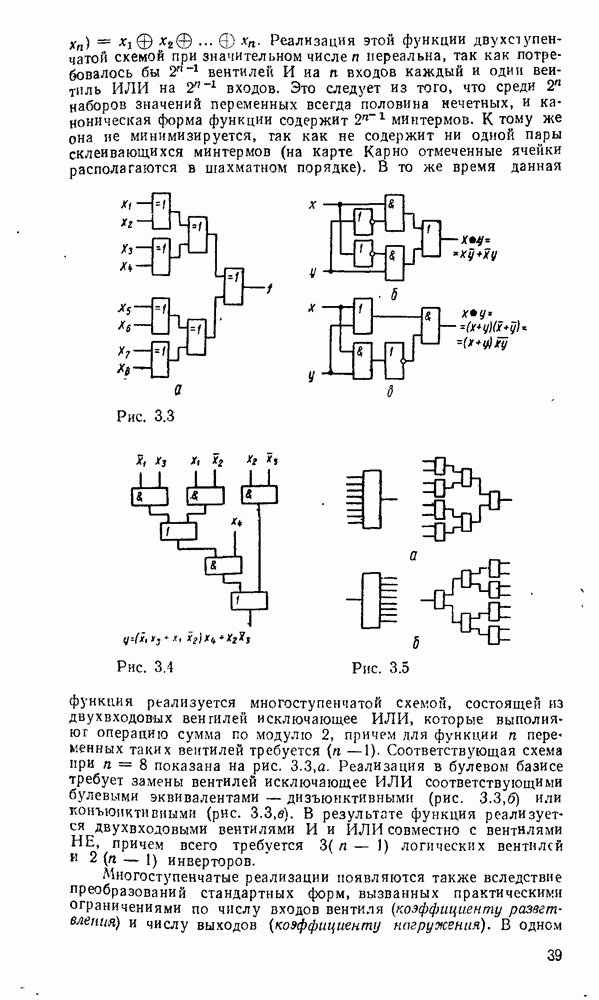
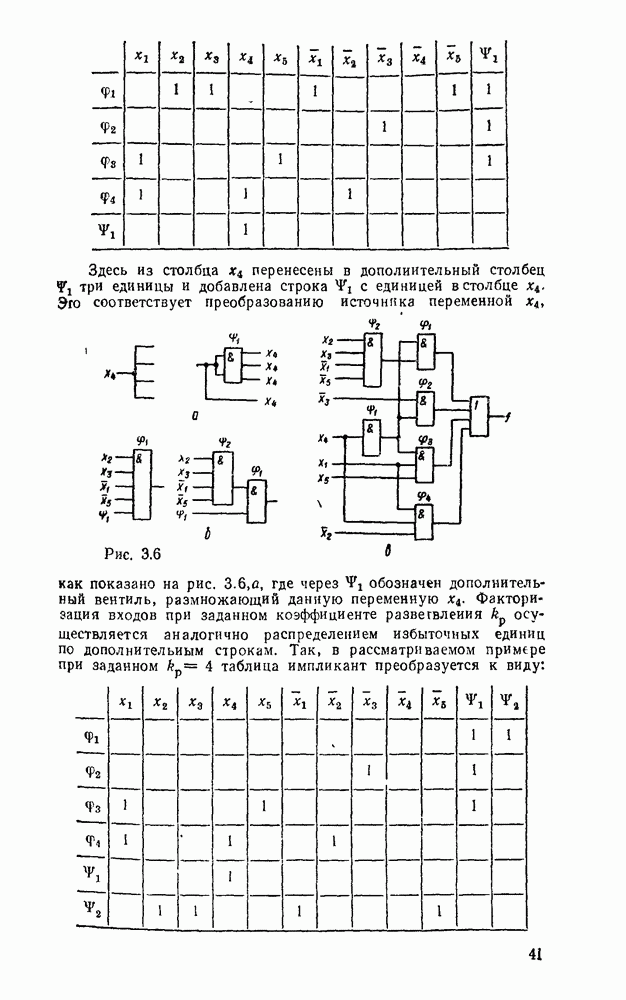
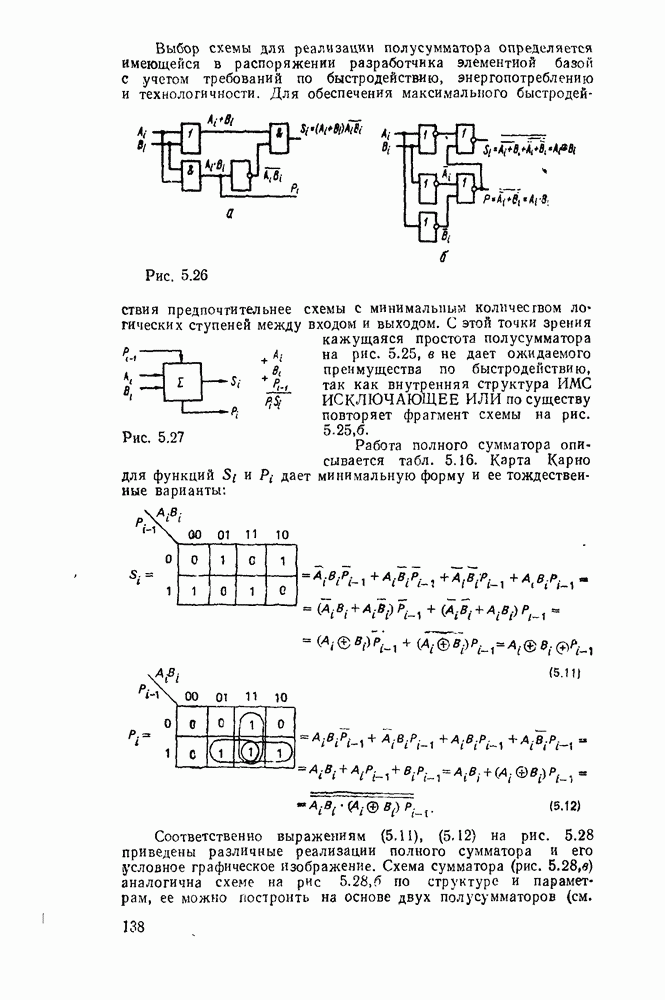
Функции, заданные в нормальной диъзюнктивной или конъюнктивной форме, реализуются двухступенчатыми схемами. Первая ступень реализует произведения или суммы переменных, а вторая — соответственно суммы минтермов или произведения  . Двухступенчатые схемы предпочтительны по быстродействию, которое вследствие инерционности логических вентилей пропорционально числу ступеней. Однако в инженерной практике приходится по различным причинам обращаться к многоступенчатым схемам.
. Двухступенчатые схемы предпочтительны по быстродействию, которое вследствие инерционности логических вентилей пропорционально числу ступеней. Однако в инженерной практике приходится по различным причинам обращаться к многоступенчатым схемам.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
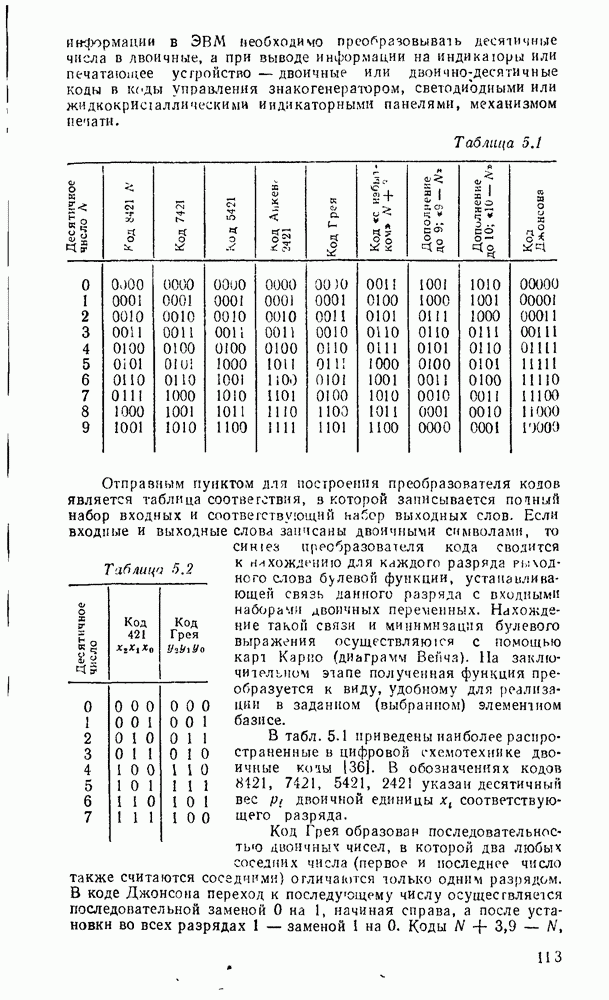
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
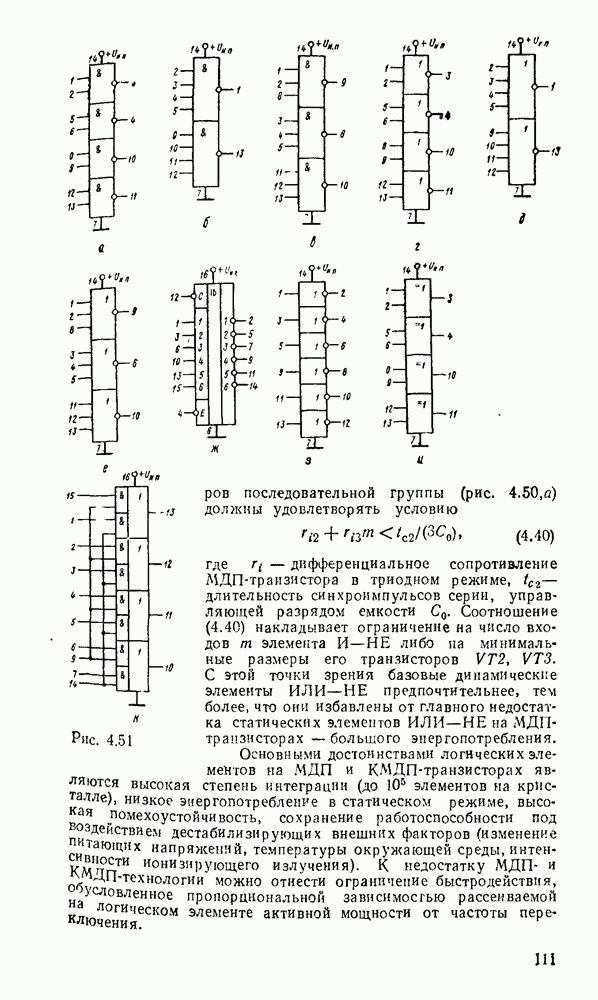
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
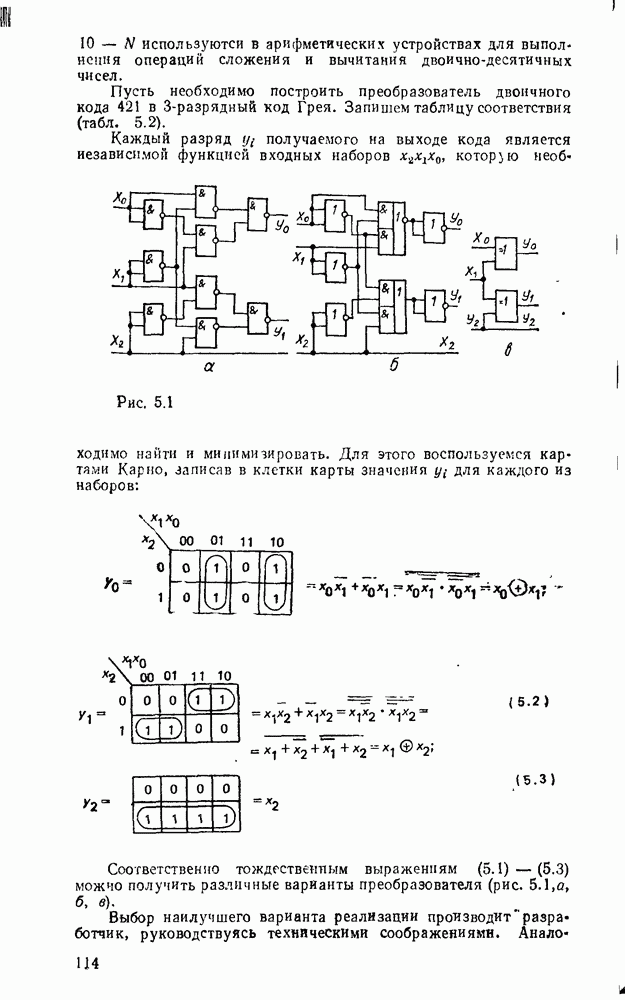
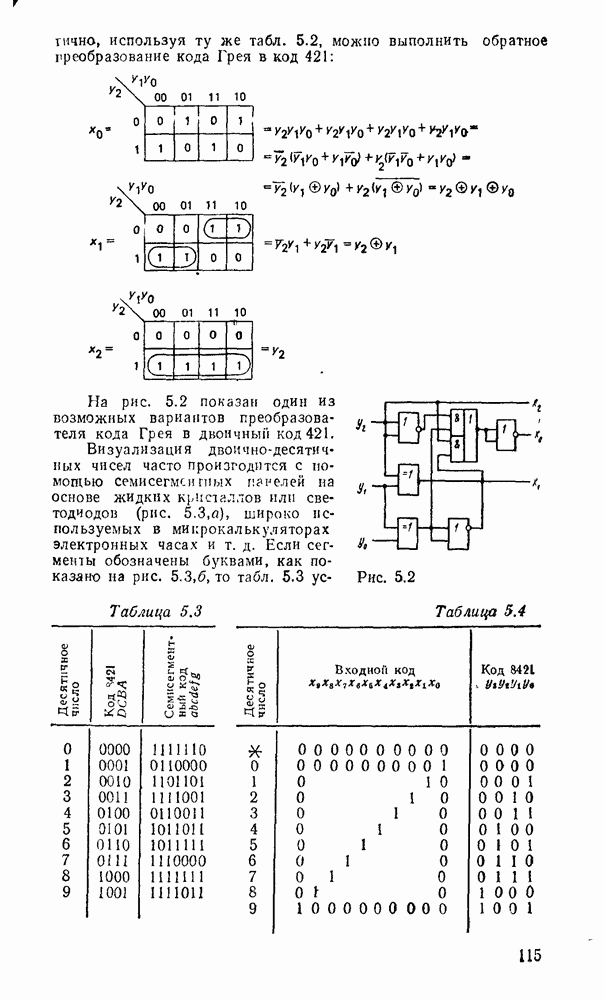
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
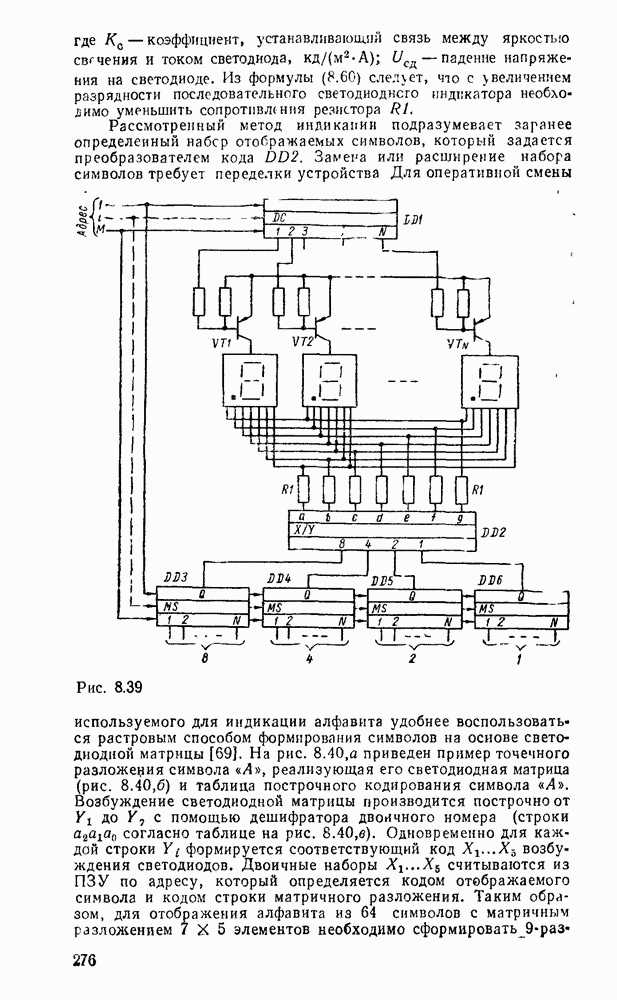
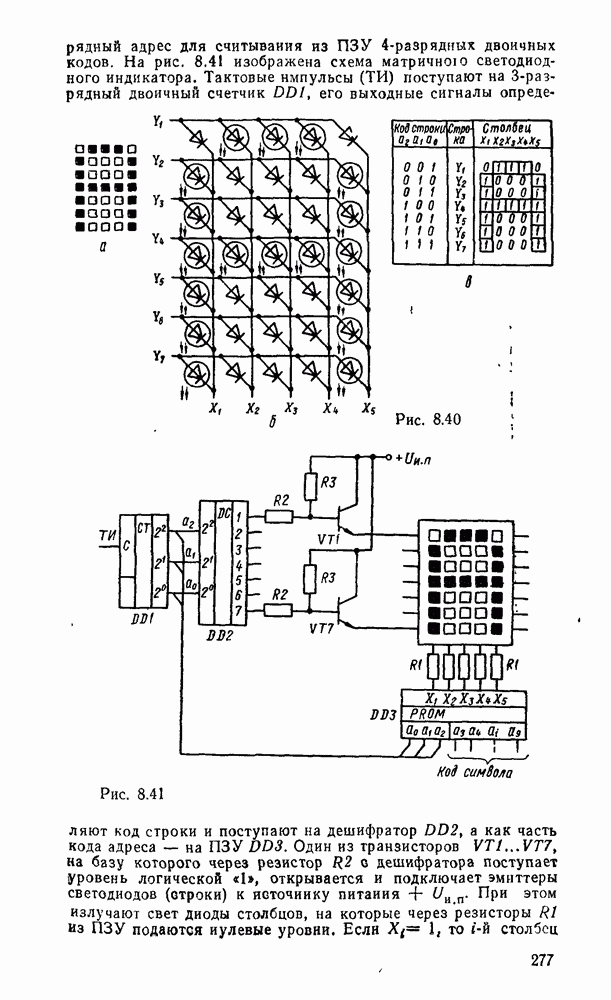
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
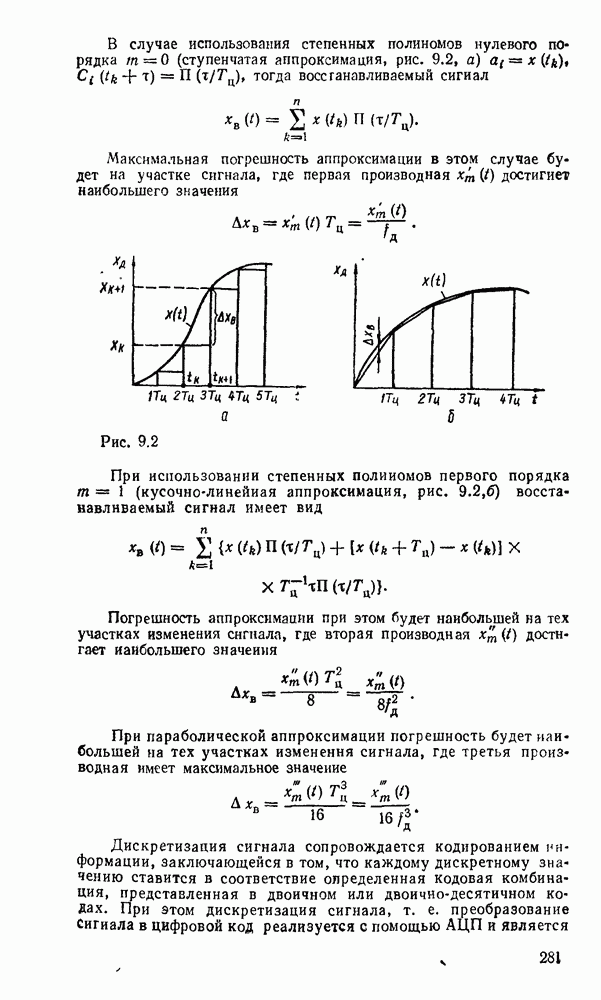
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
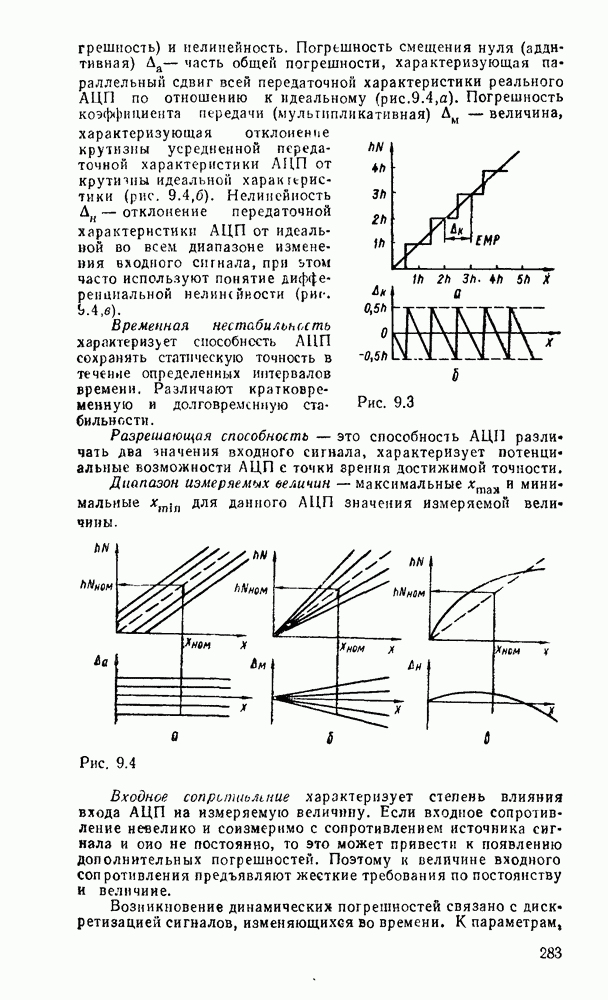
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
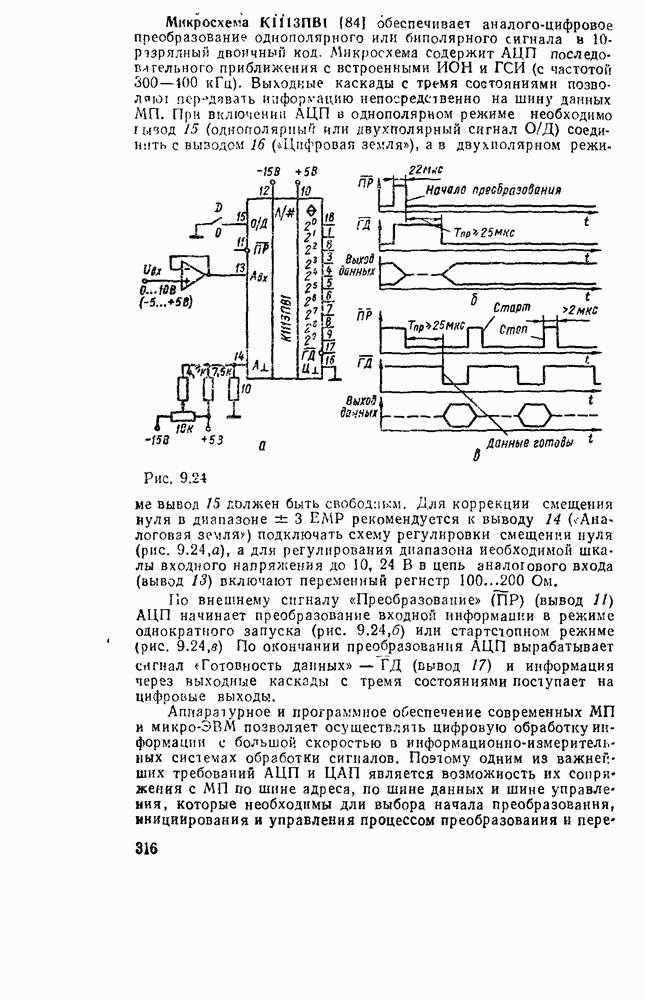
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
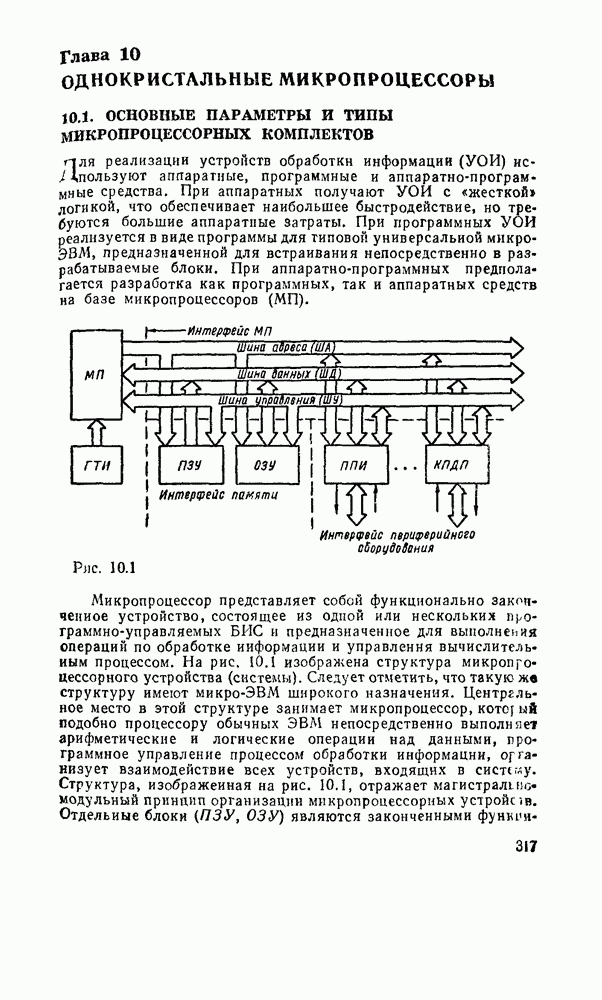
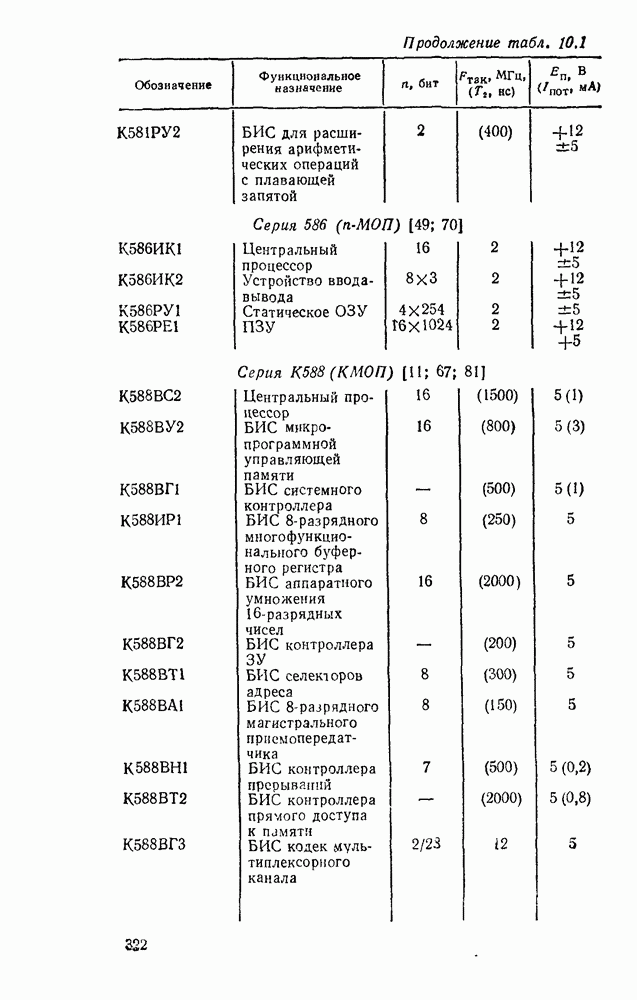
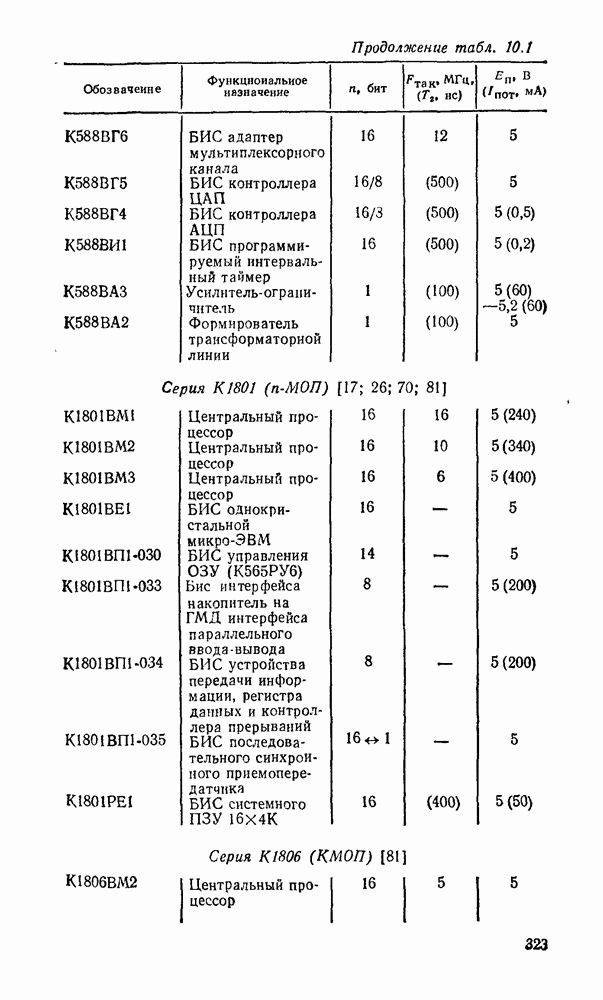
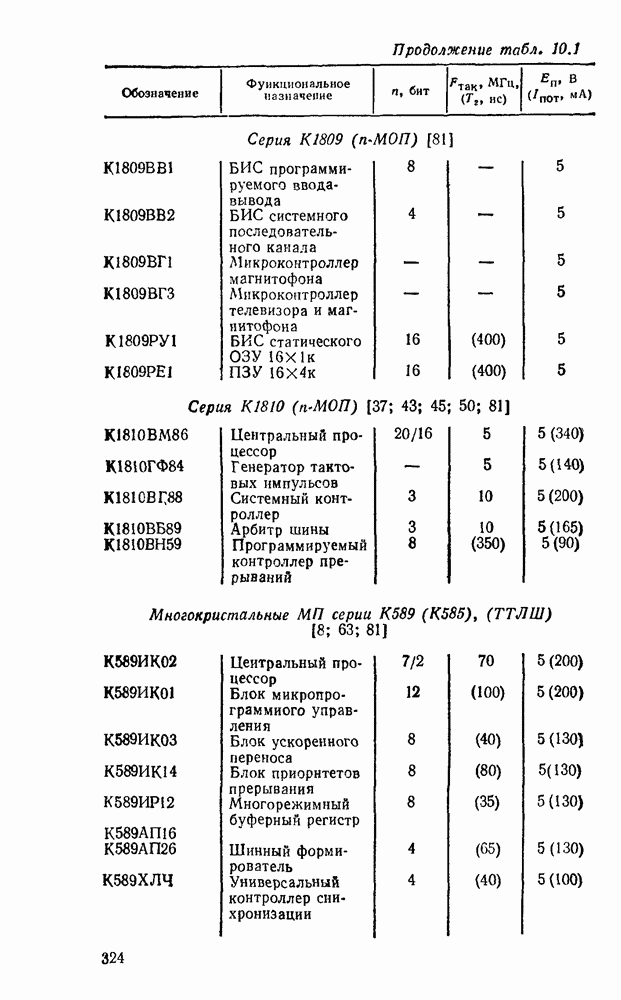
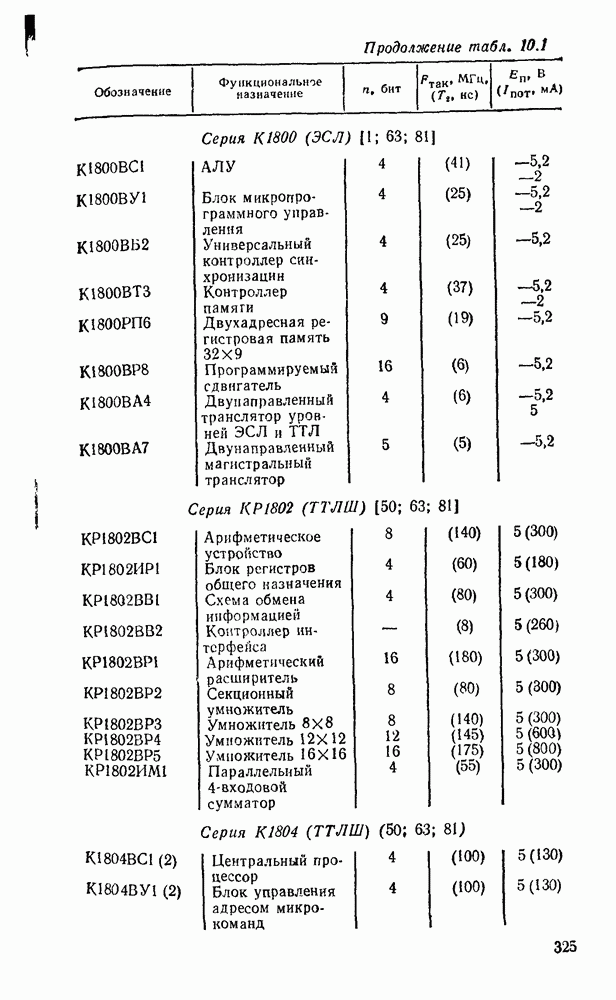
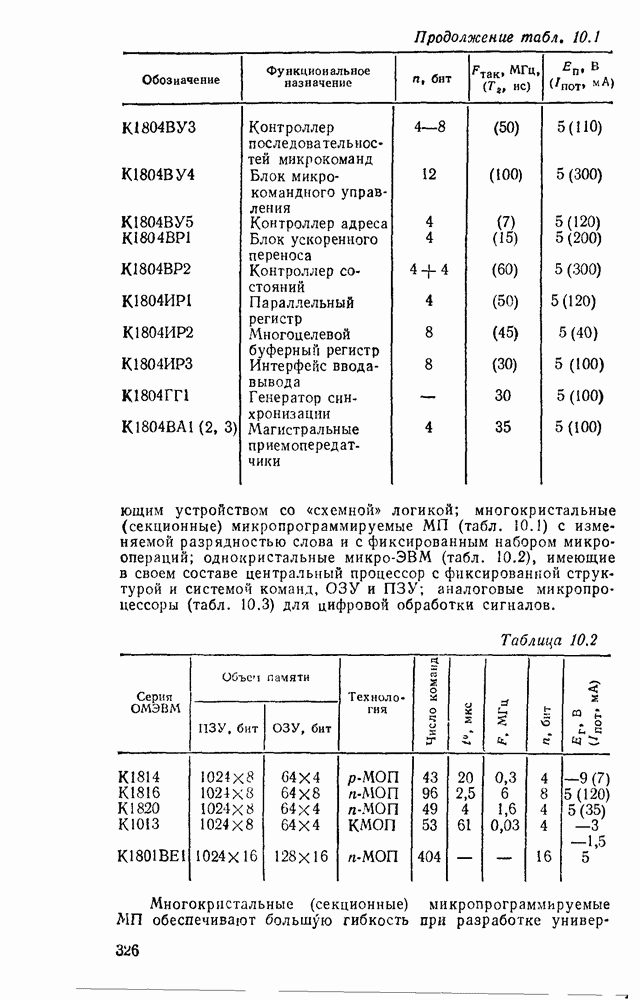
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
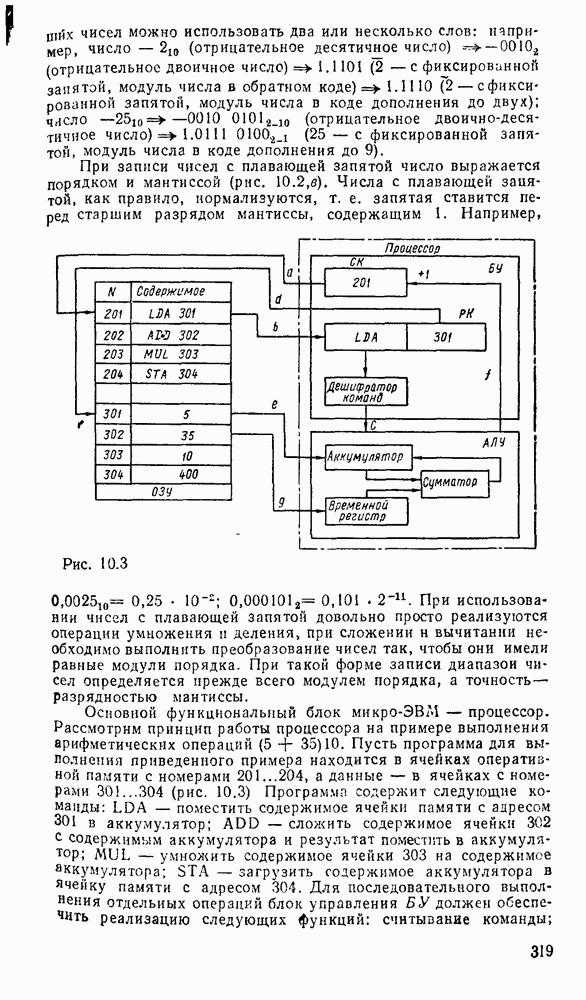
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
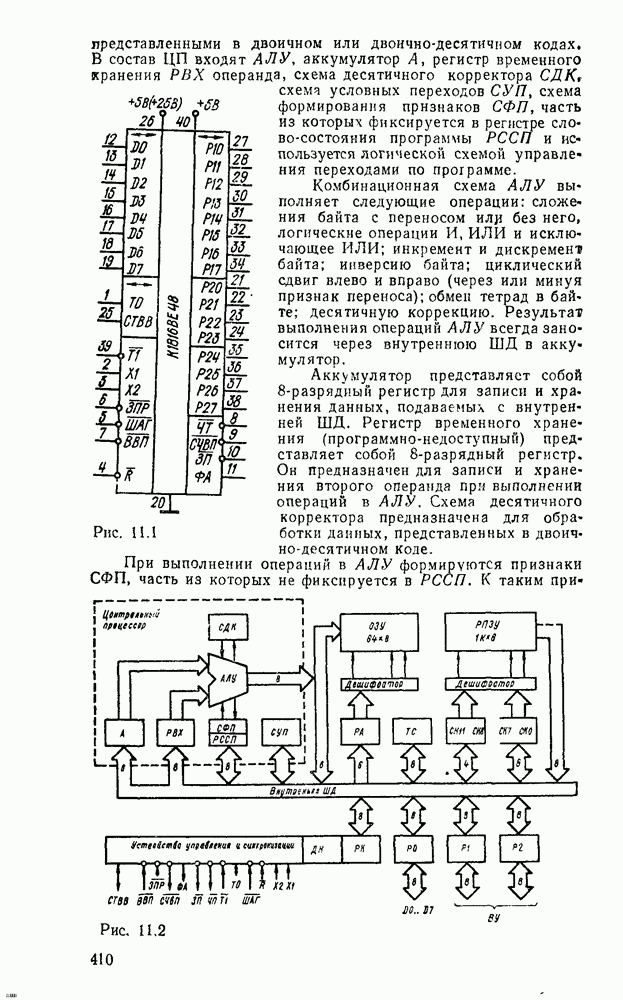
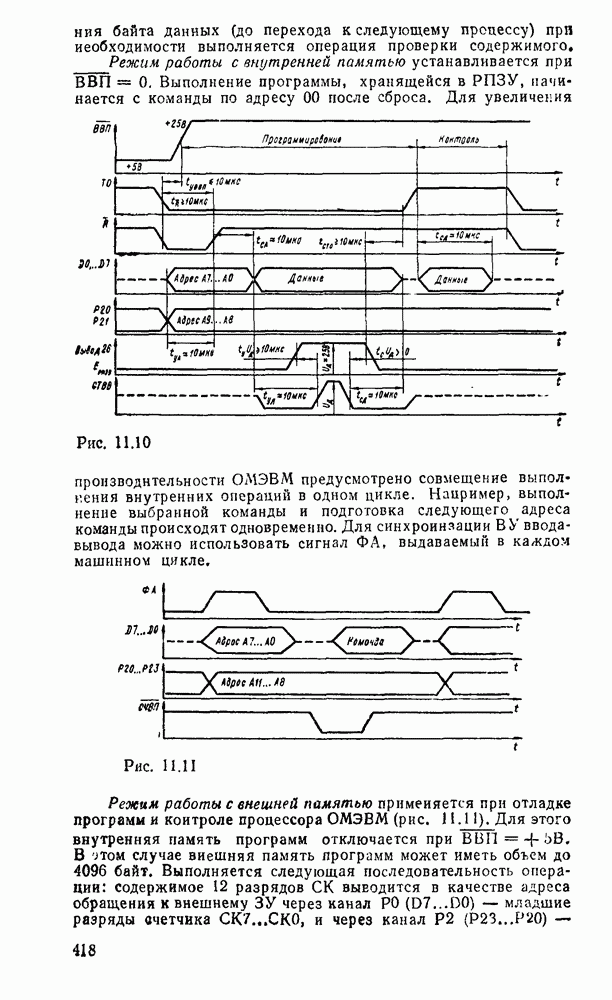
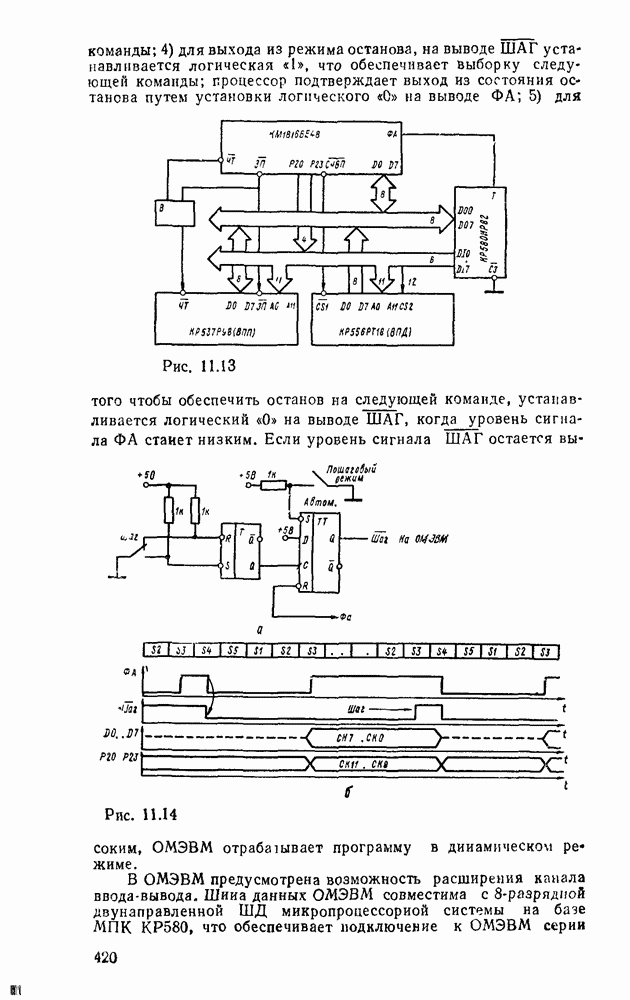
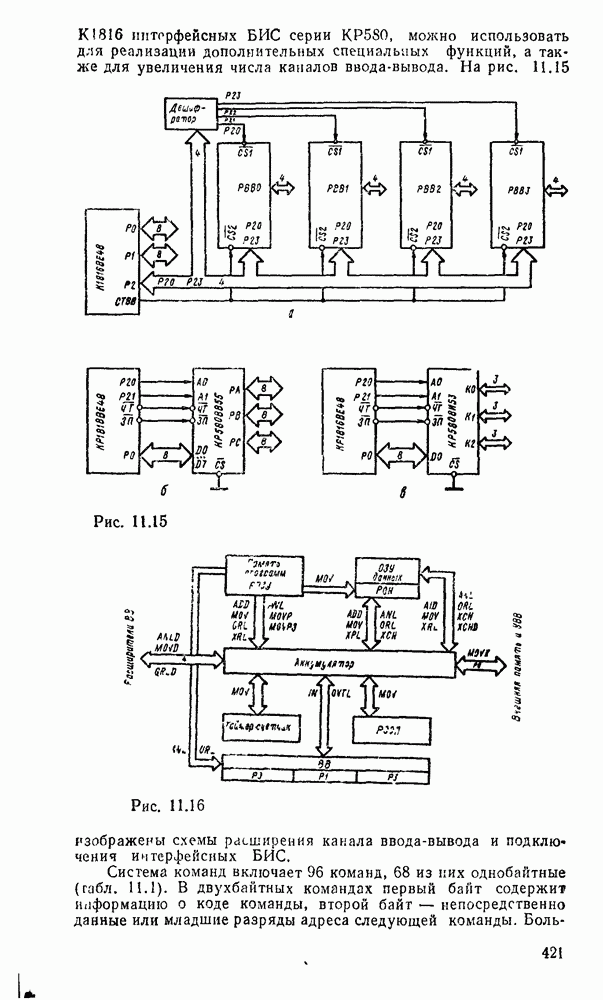
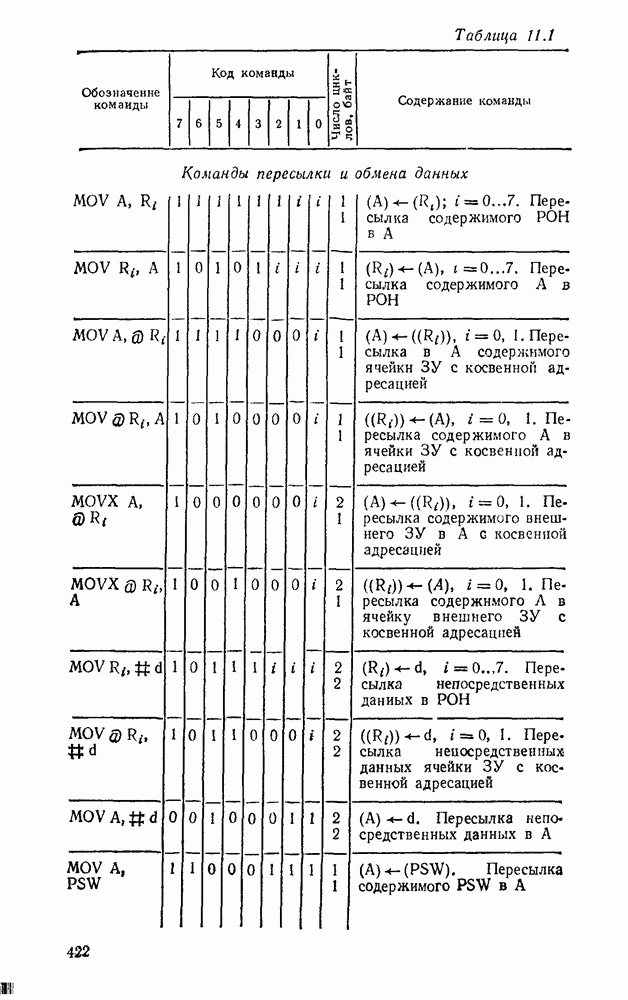
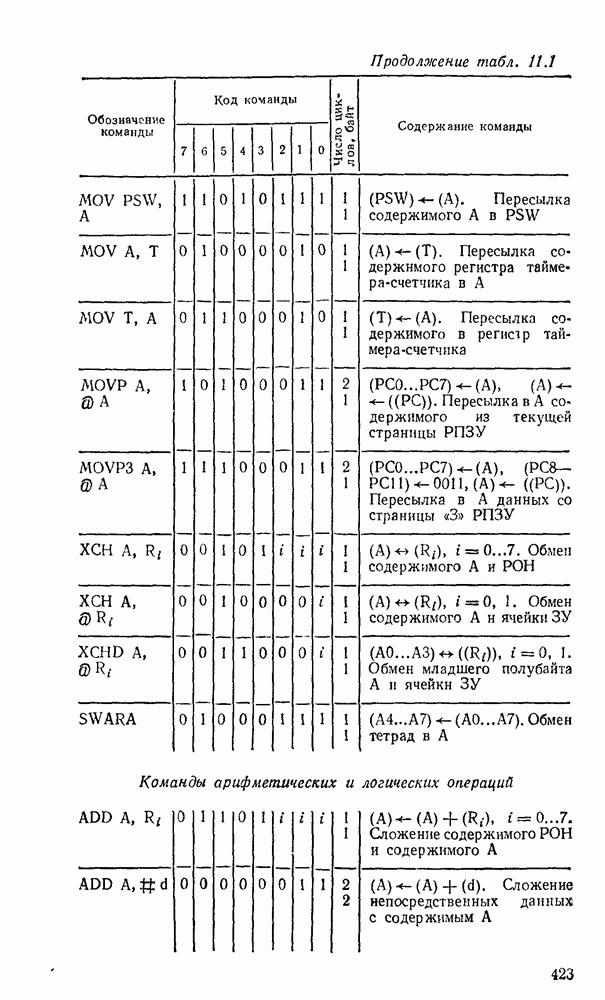
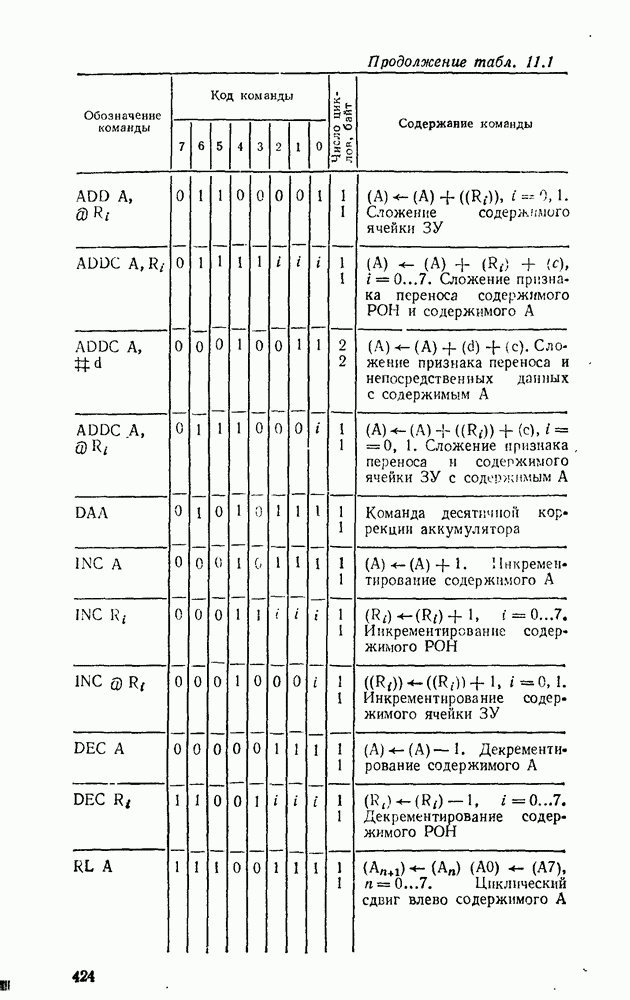
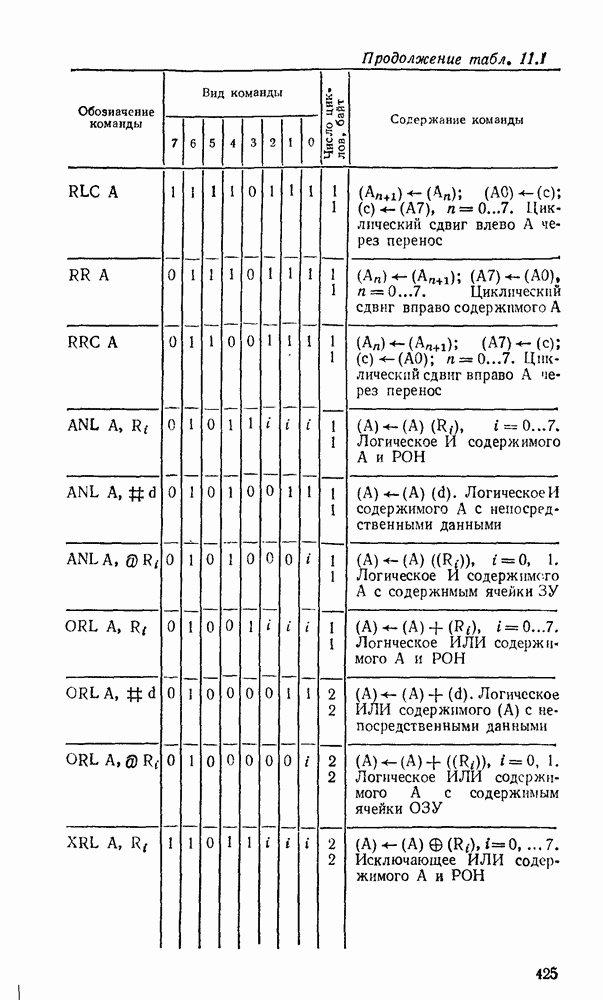
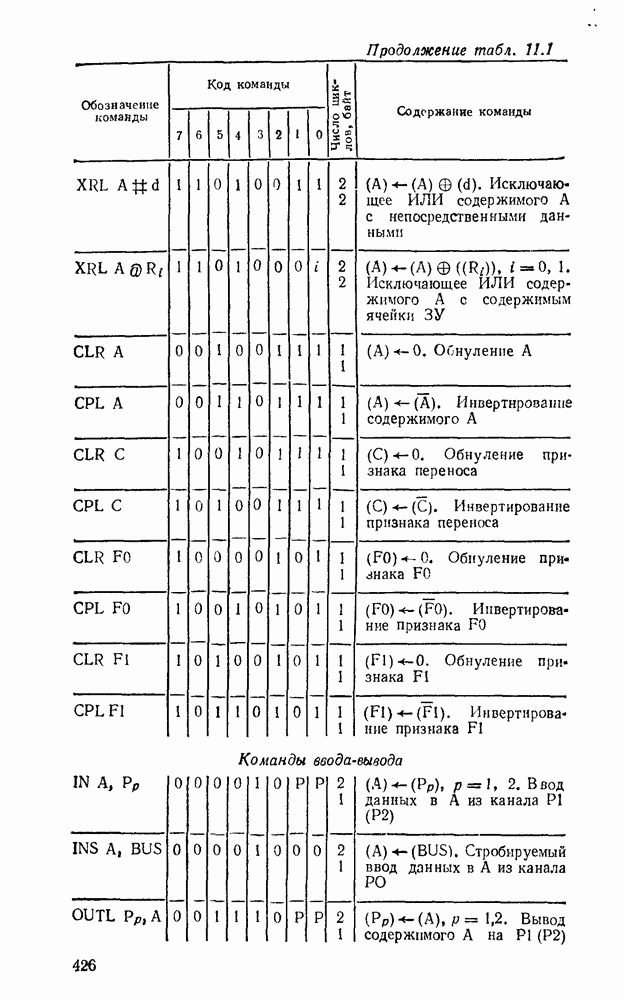
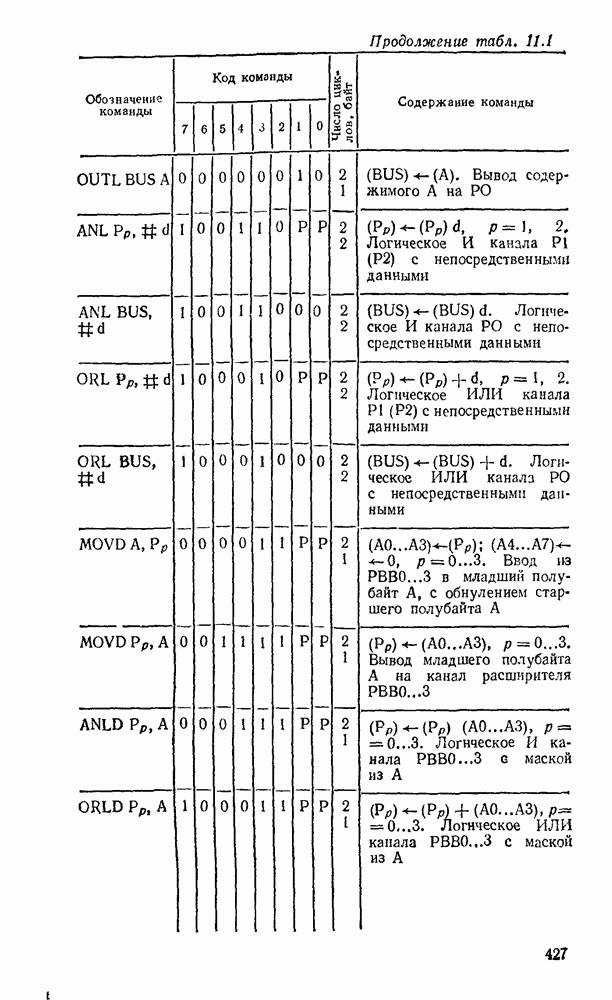
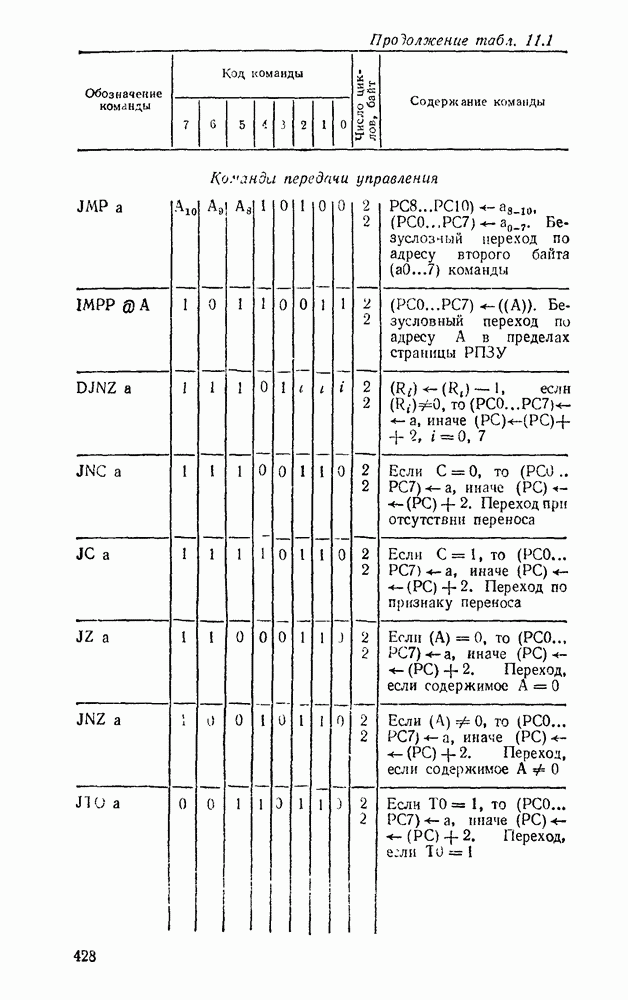
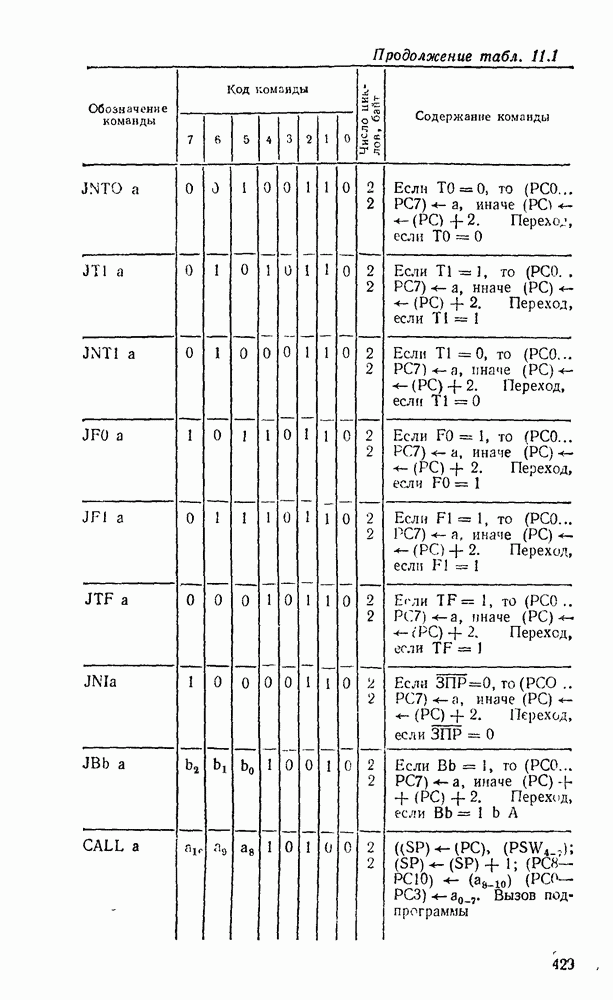
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
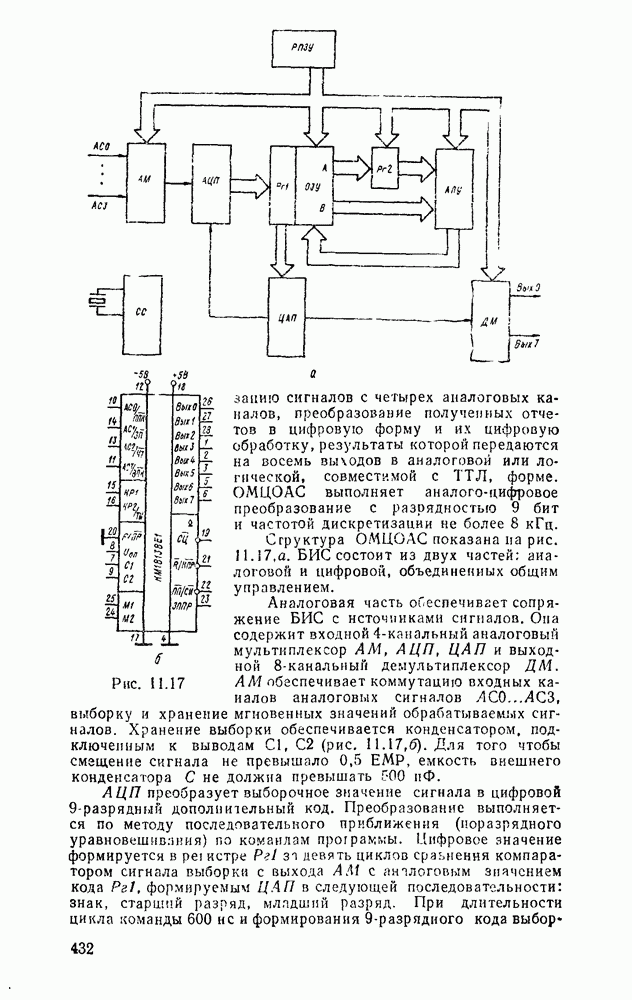
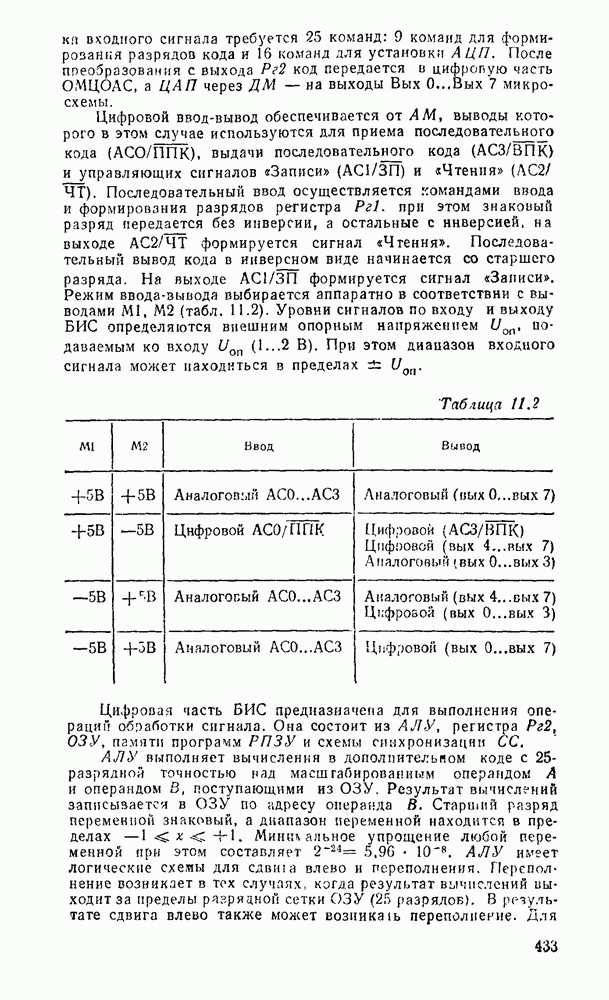
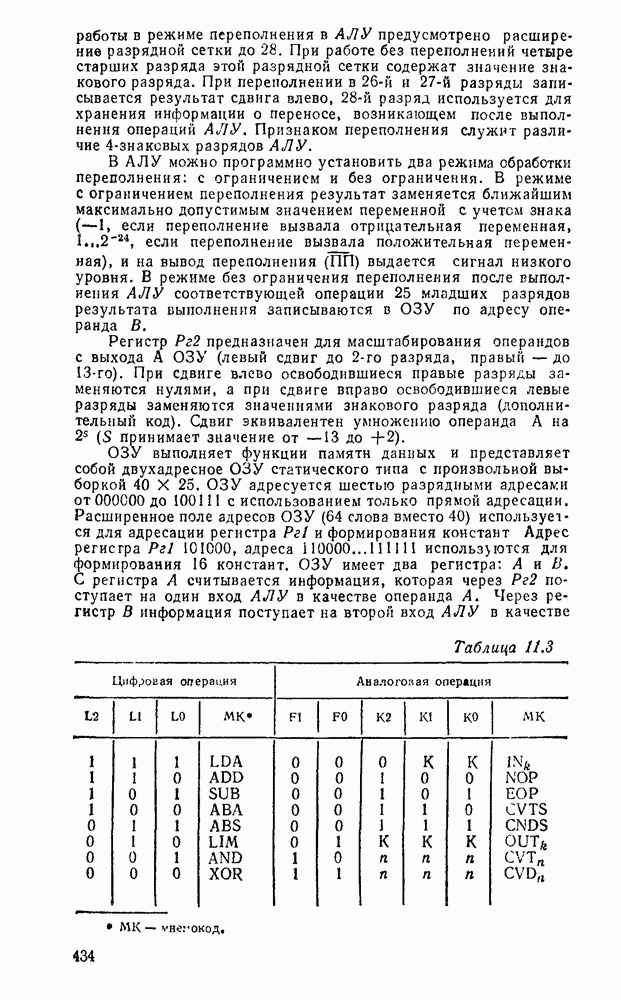
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ