| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
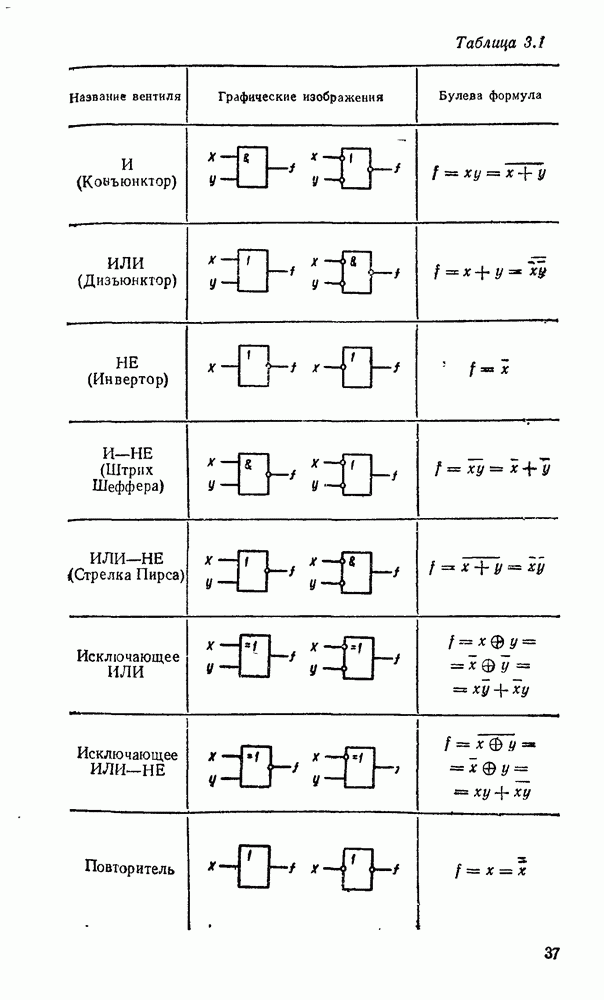
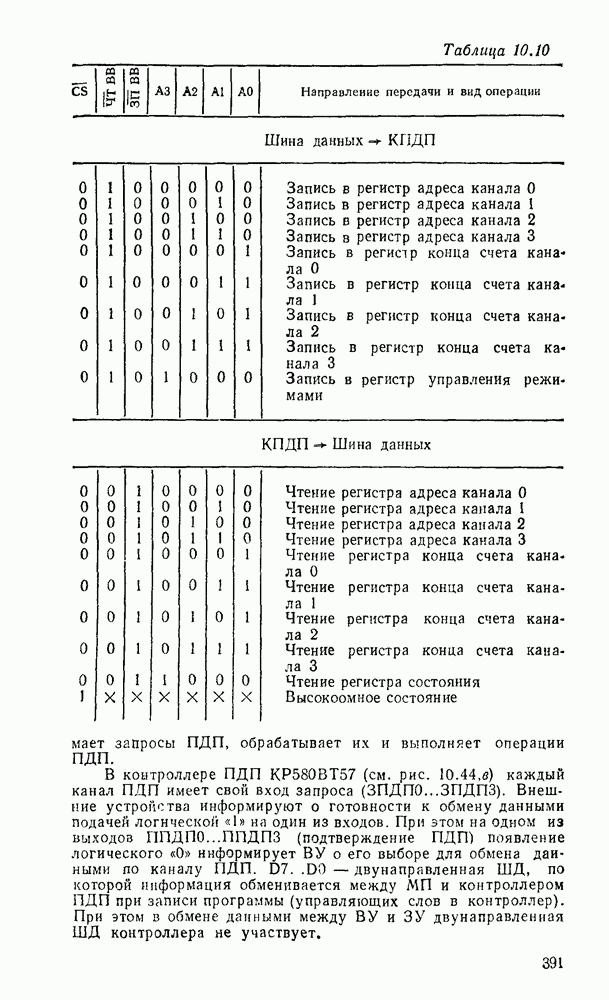
3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
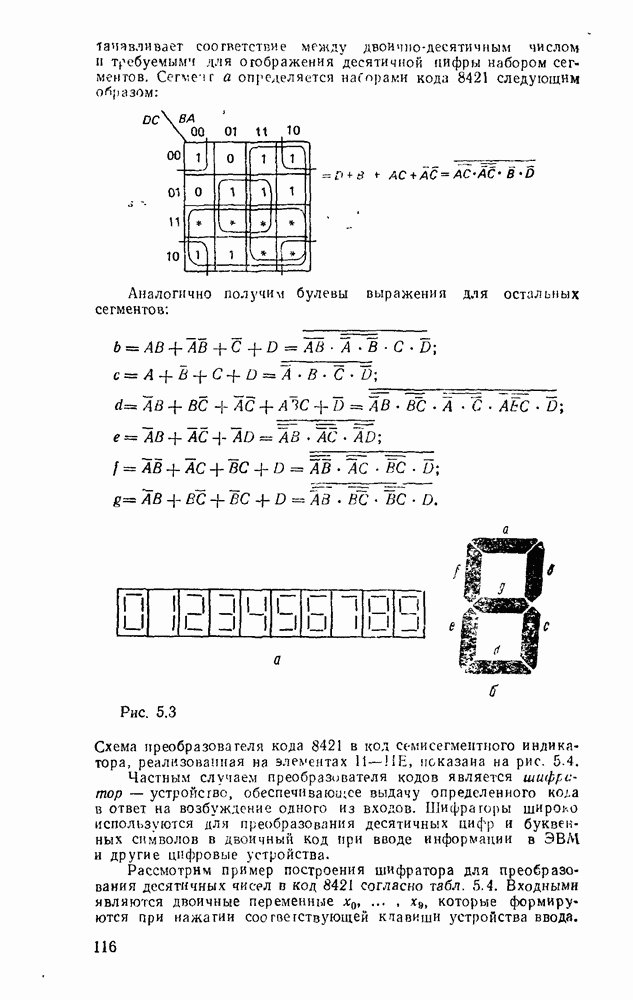
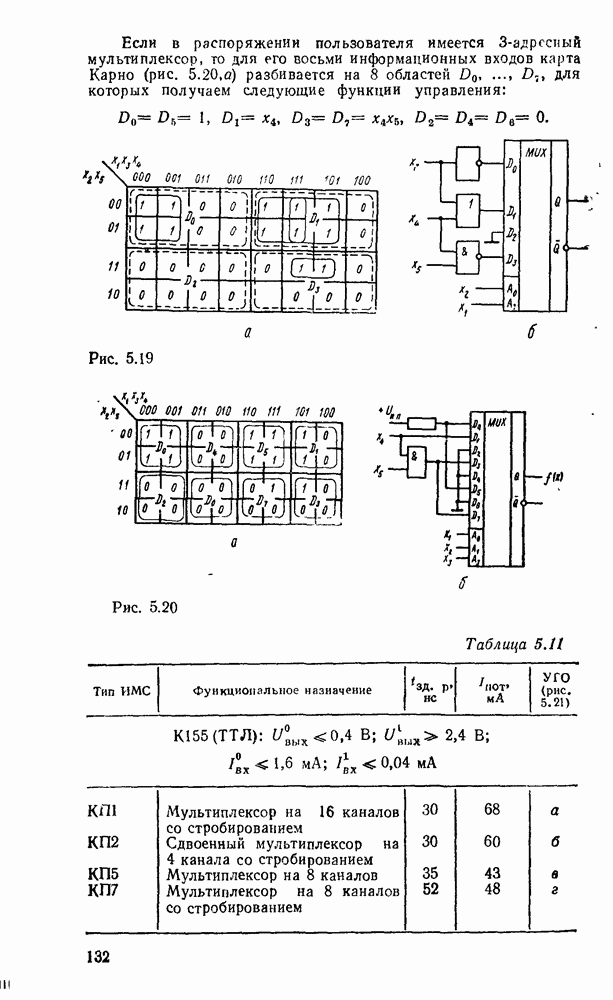
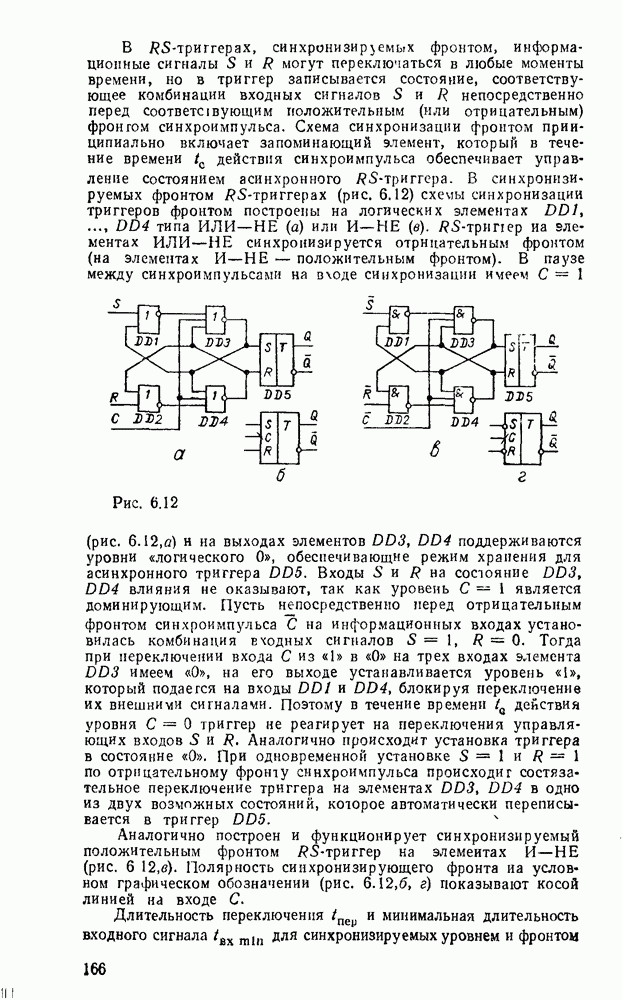
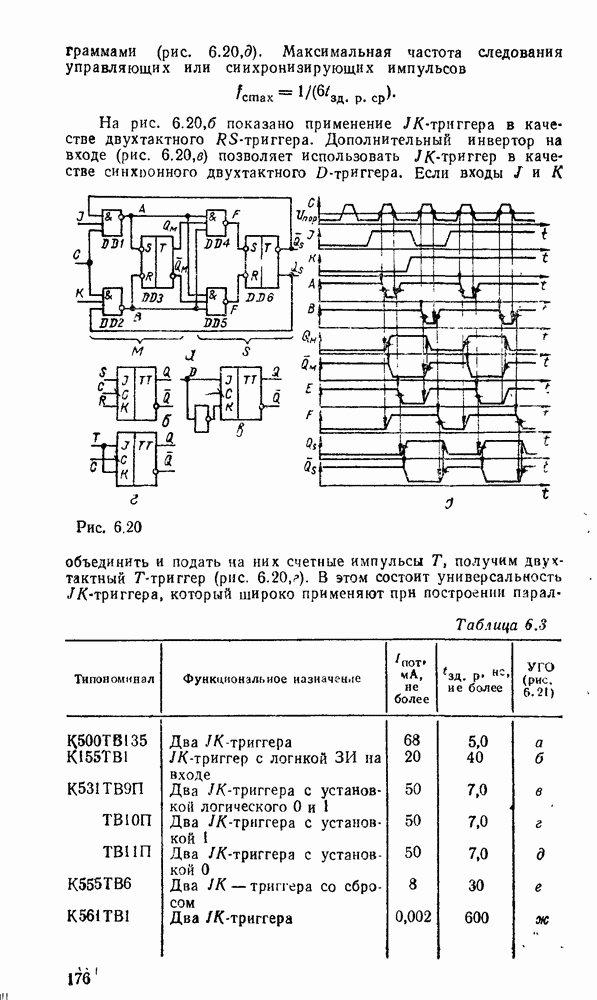
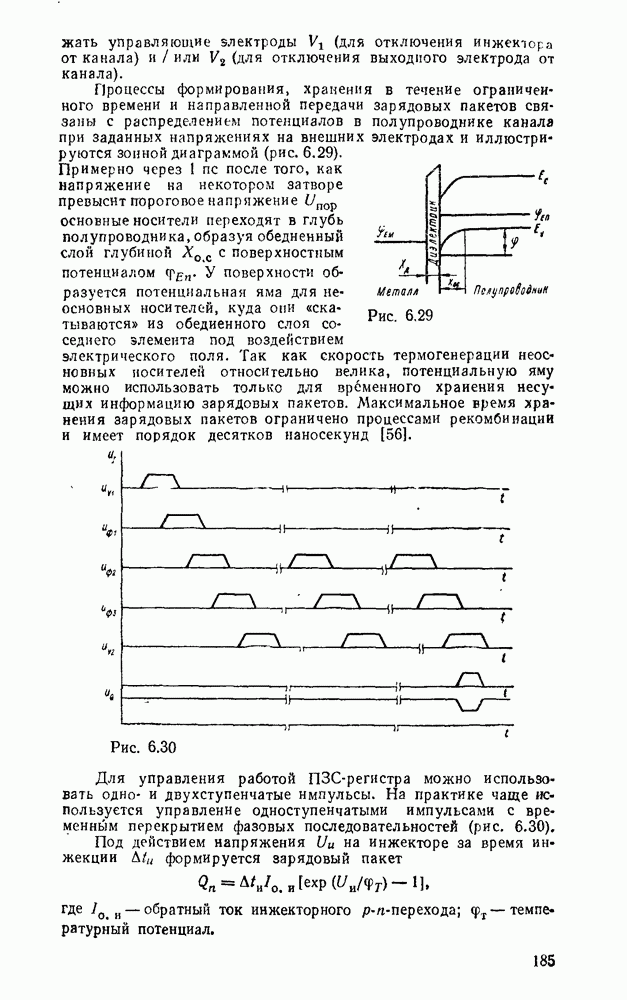
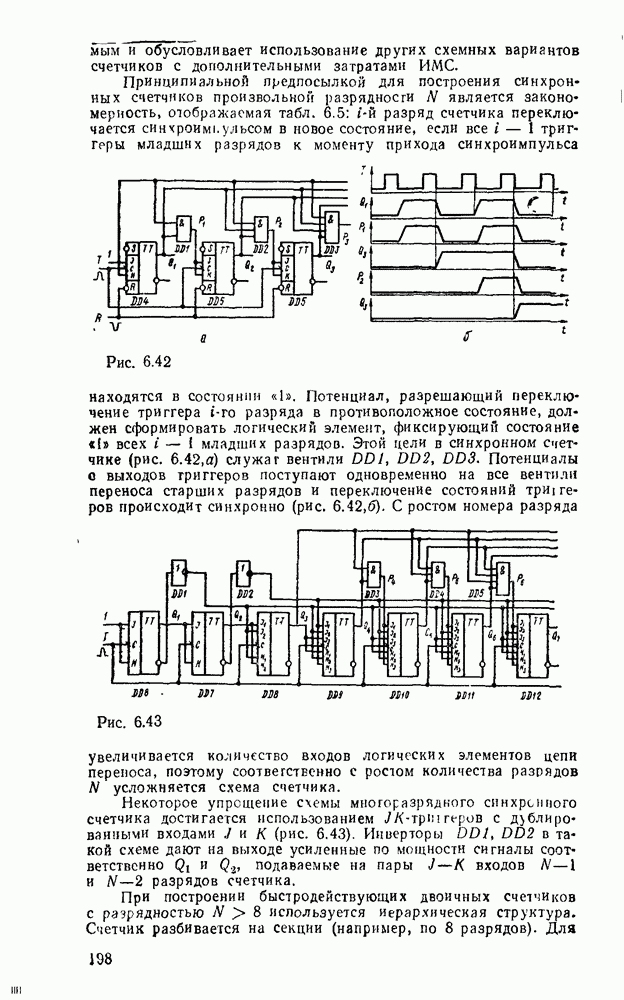
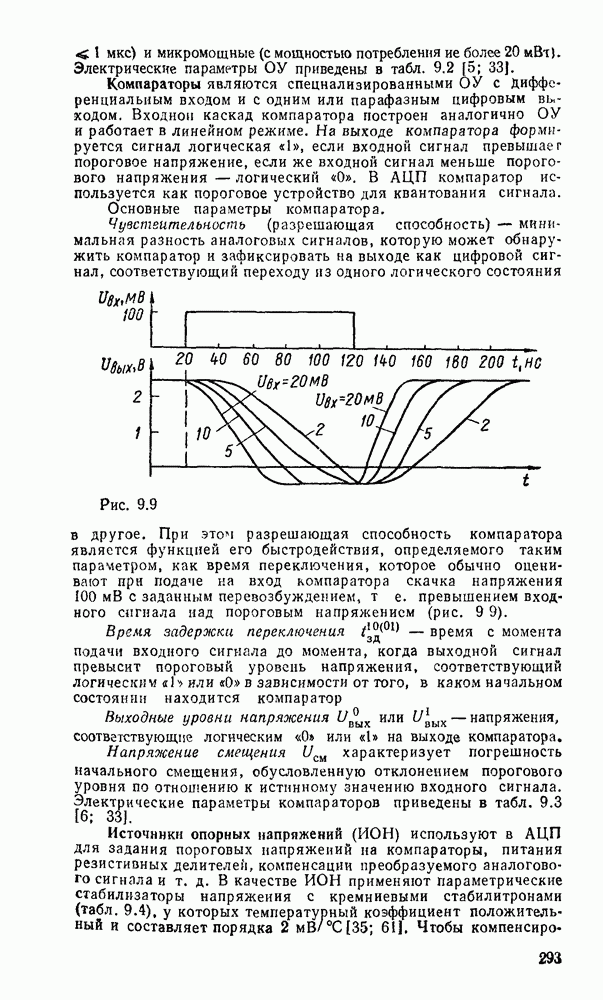
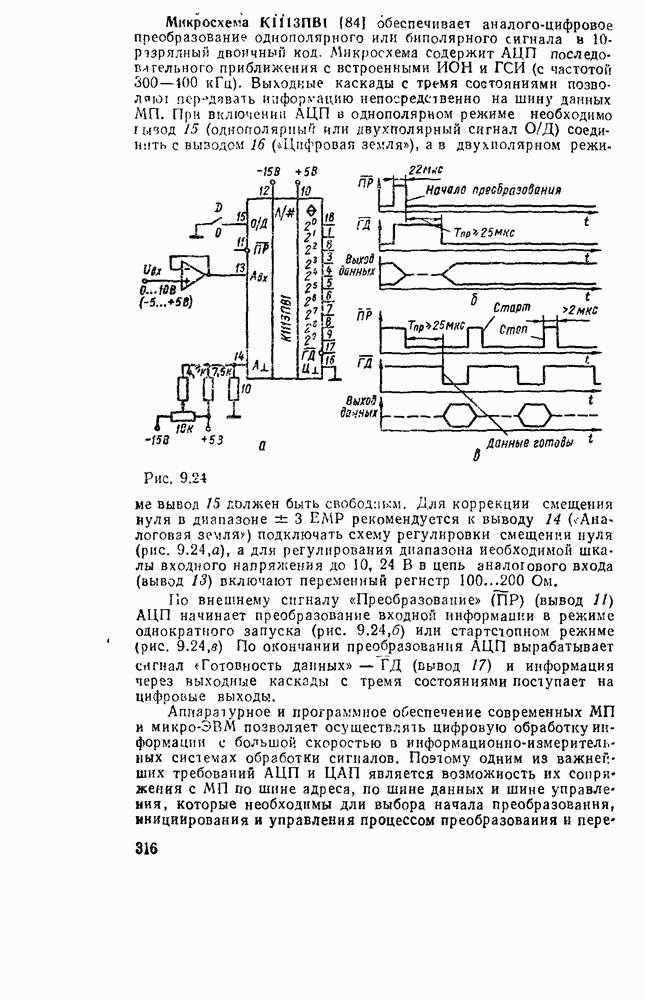
Характерным примером многоступенчатых схем может служить реализация функции, обеспечивающей проверку на четность набора из переменных. Она равна единице тогда и только тогда, когда число единичных значений входных переменных нечетное и выражается как сумма по модулю  .
.
Реализация этой функции двухступенчатой схемой при значительном числе  нереальна, так как потребовалось бы
нереальна, так как потребовалось бы  вентилей И на
вентилей И на  . входов каждый и один вентиль ИЛИ на
. входов каждый и один вентиль ИЛИ на  входов. Это следует из того, что среди
входов. Это следует из того, что среди  наборов значений переменных всегда половина нечетных, и каноническая форма функции содержит
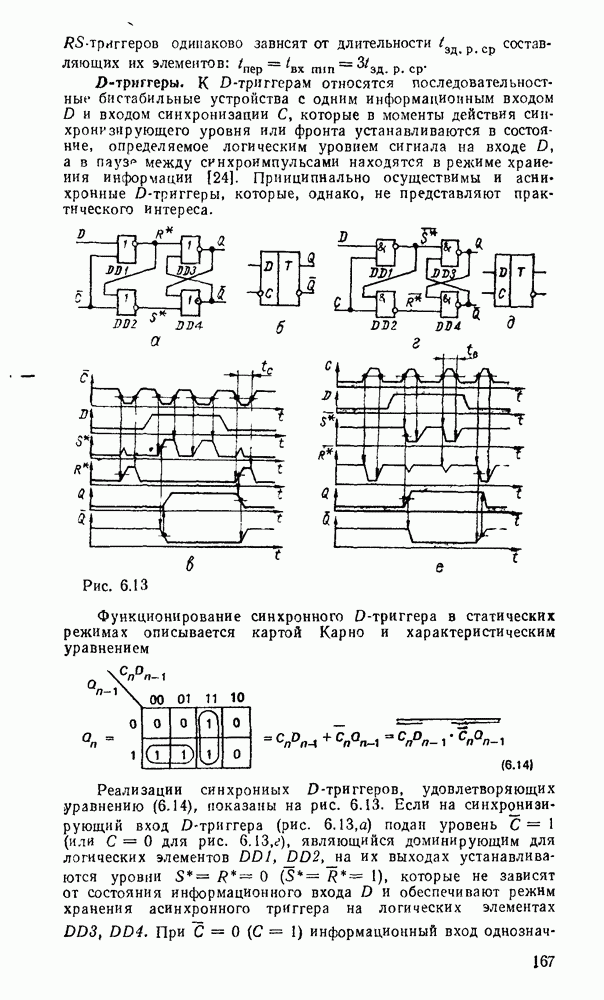
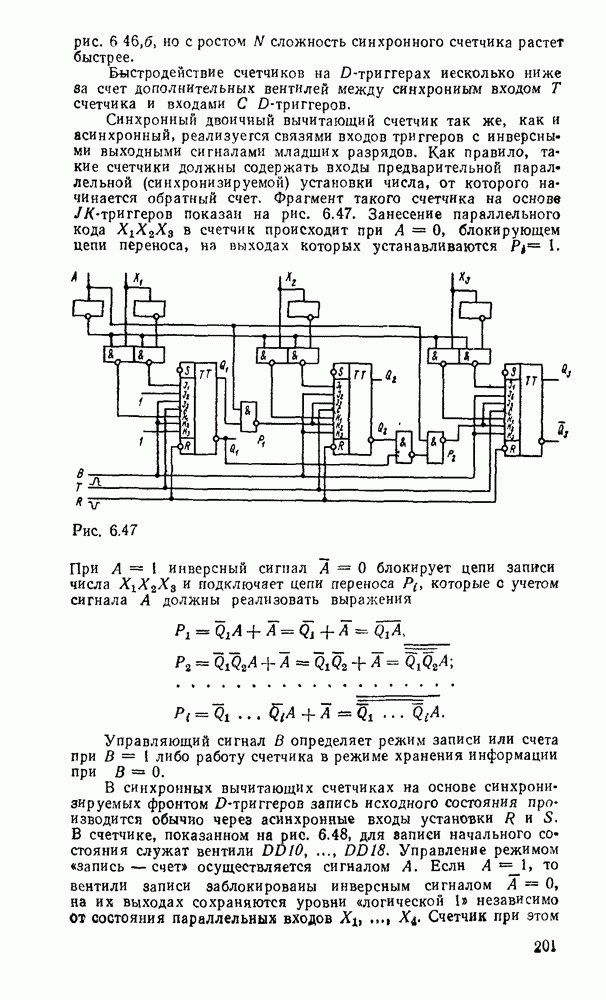
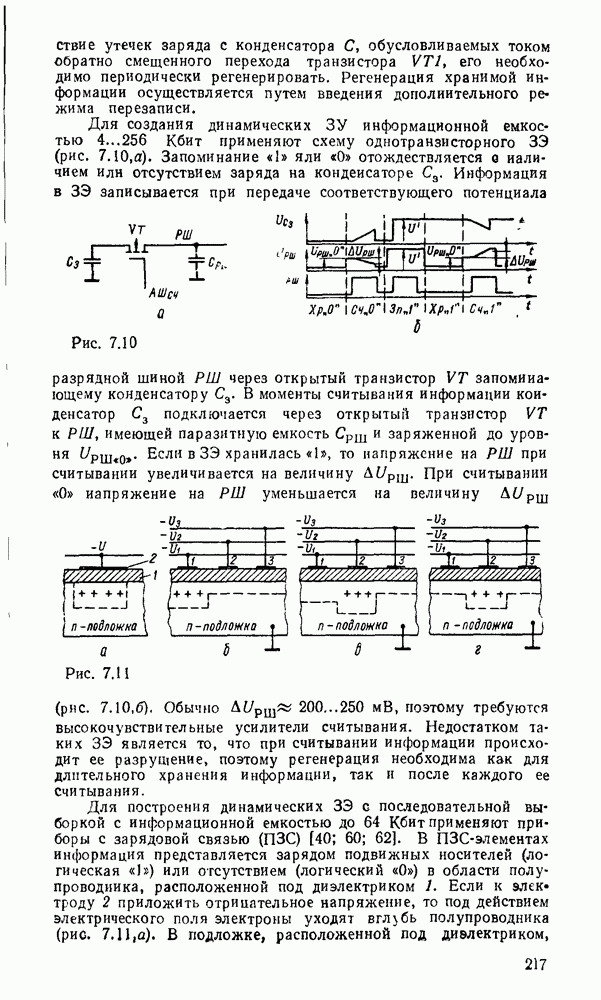
наборов значений переменных всегда половина нечетных, и каноническая форма функции содержит  минтермов. К тому же она не минимизируется, так как не содержит ни одной пары склеивающихся минтермов (на карте Карно отмеченные ячейки располагаются в шахматном порядке). В то же время данная функция реализуется многоступенчатой схемой, состоящей из двухвходовых вентилей исключающее ИЛИ, которые выполняют операцию сумма по модулю 2, причем для функции
минтермов. К тому же она не минимизируется, так как не содержит ни одной пары склеивающихся минтермов (на карте Карно отмеченные ячейки располагаются в шахматном порядке). В то же время данная функция реализуется многоступенчатой схемой, состоящей из двухвходовых вентилей исключающее ИЛИ, которые выполняют операцию сумма по модулю 2, причем для функции  переменных таких вентилей требуется
переменных таких вентилей требуется  . Соответствующая схема при
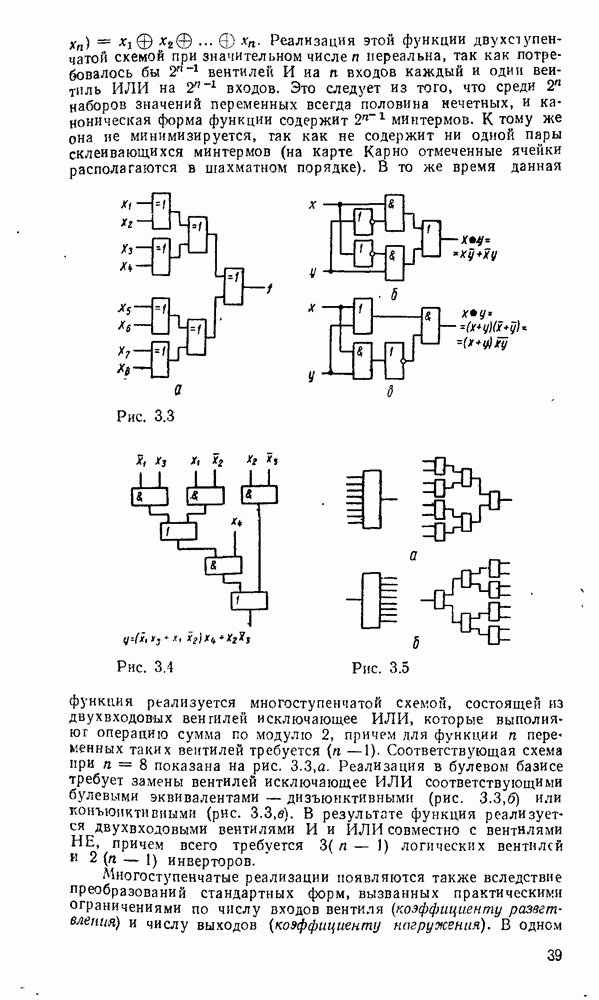
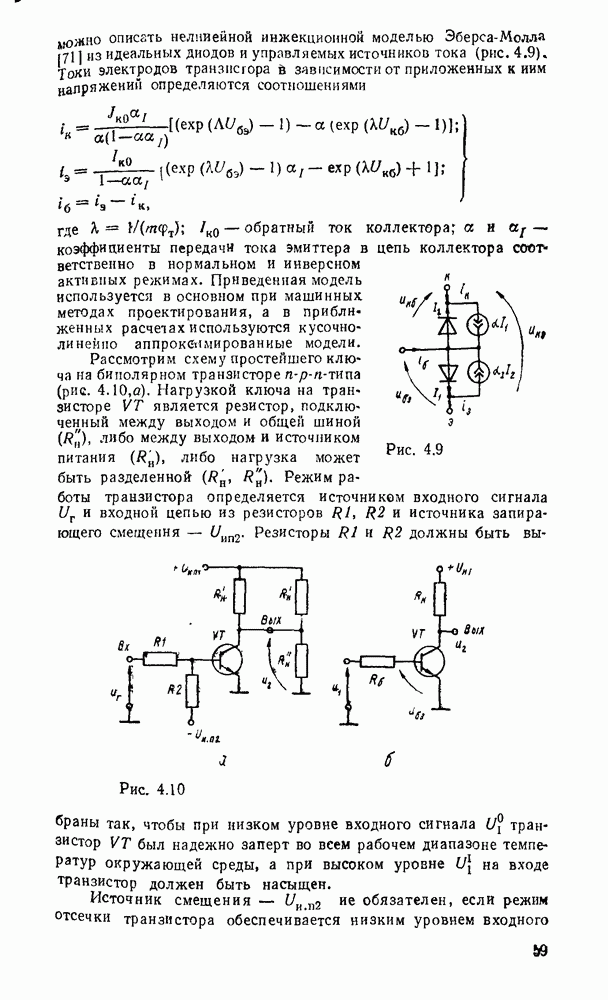
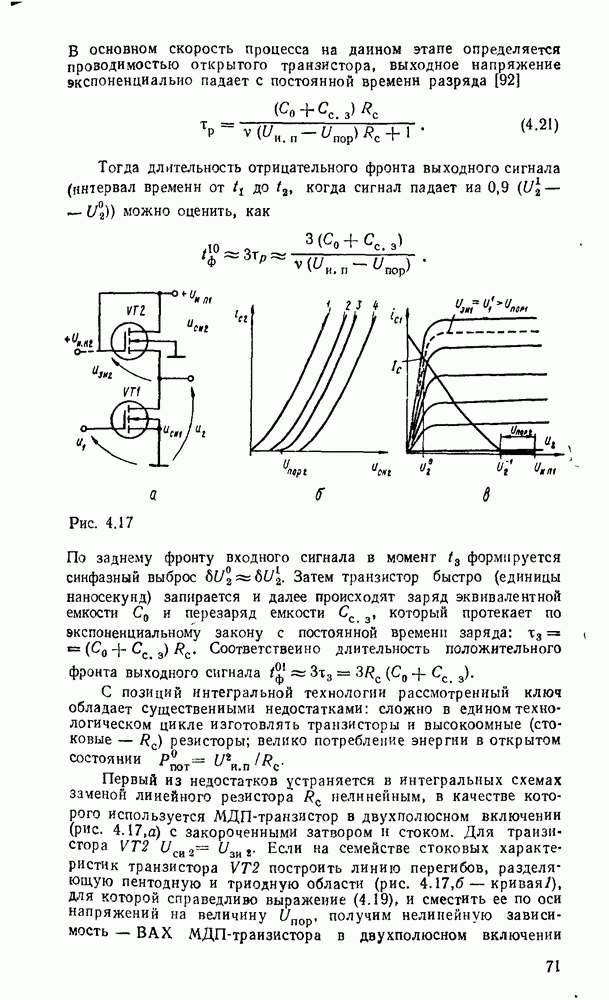
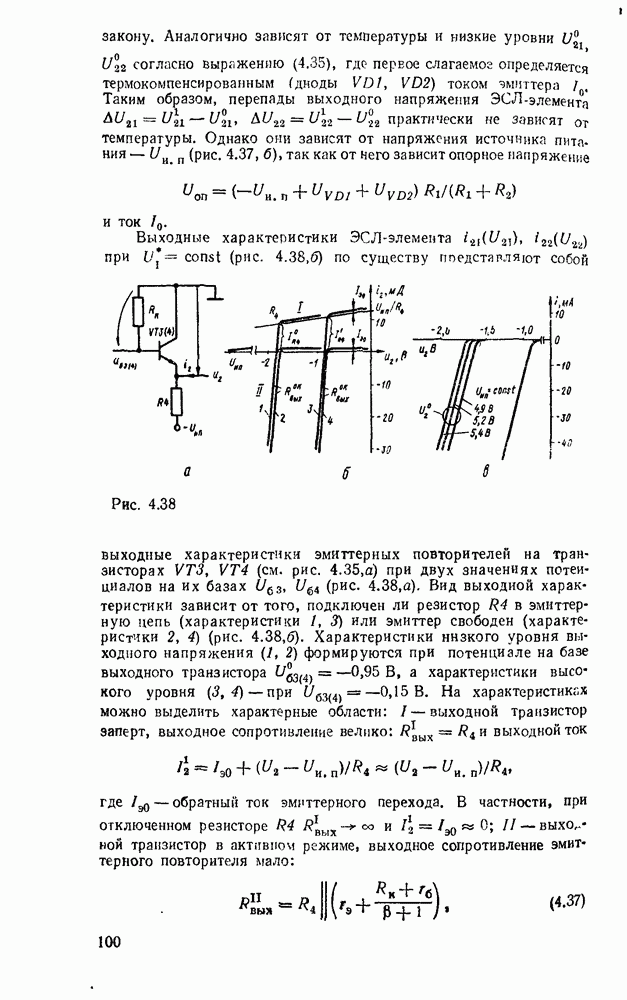
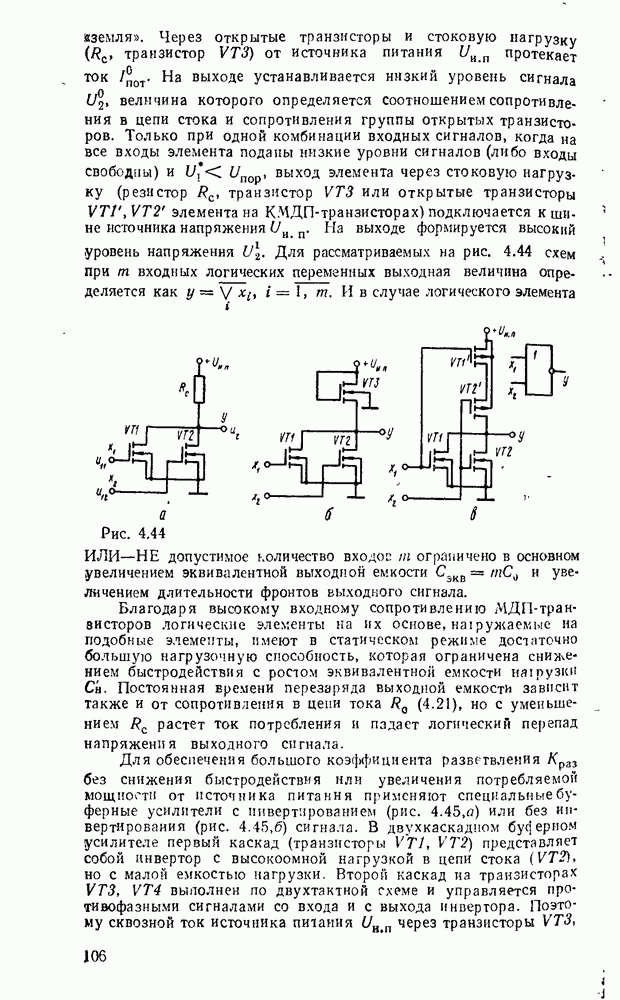
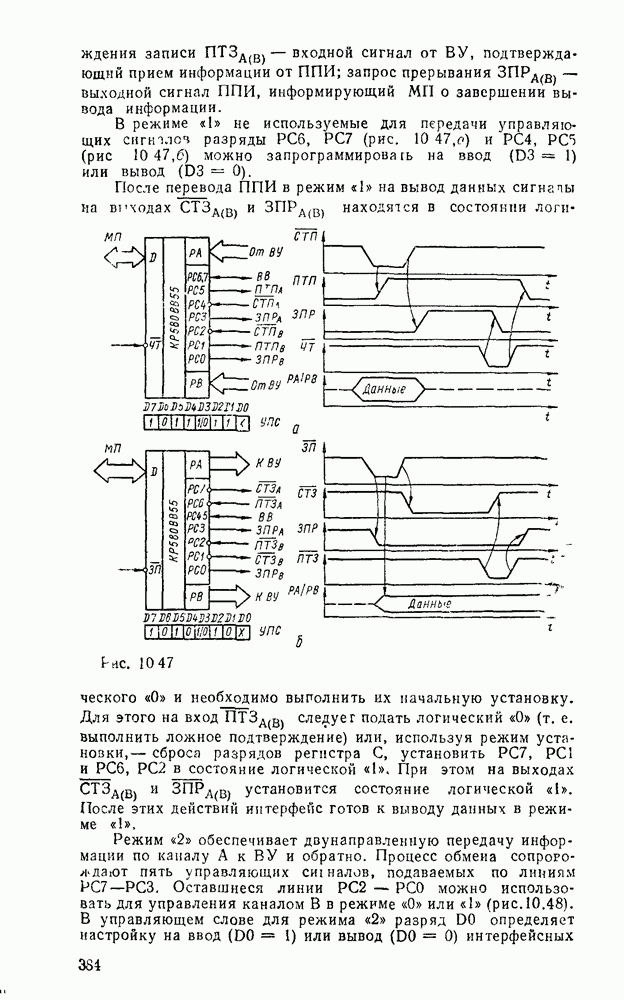
. Соответствующая схема при  показана на рис. 3.3,а. Реализация в булевом базисе требует замены вентилей исключающее ИЛИ соответствующими булевыми эквивалентами — дизъюнктивными (рис.
показана на рис. 3.3,а. Реализация в булевом базисе требует замены вентилей исключающее ИЛИ соответствующими булевыми эквивалентами — дизъюнктивными (рис.  ) или конъюнктивными (рис. 3.3,в). В результате функция реализуется двухвходовыми вентилями И и ИЛИ совместно с вентилями НЕ, причем всего требуется
) или конъюнктивными (рис. 3.3,в). В результате функция реализуется двухвходовыми вентилями И и ИЛИ совместно с вентилями НЕ, причем всего требуется  логических вентилей и
логических вентилей и  инверторов.
инверторов.

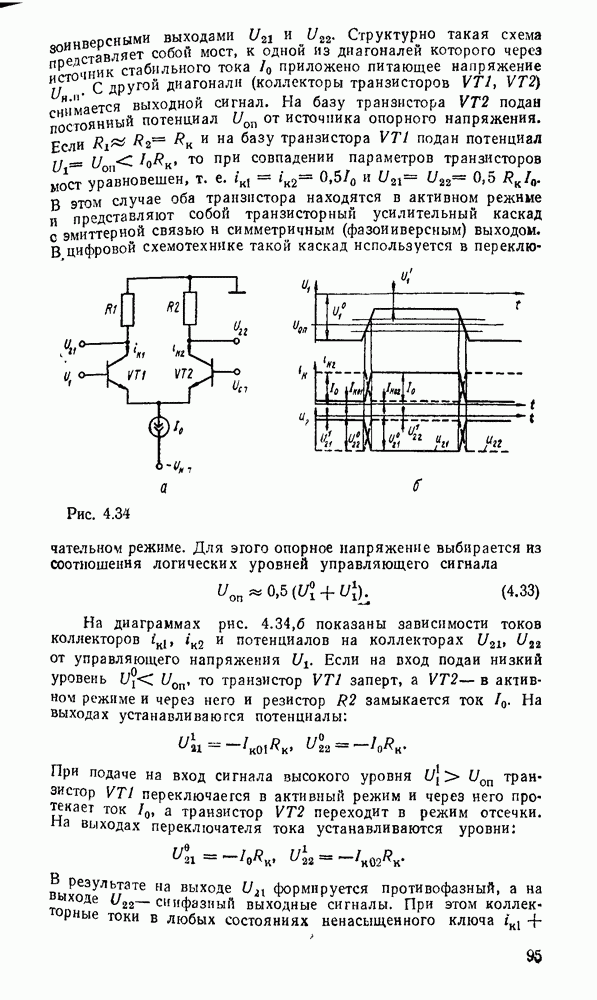
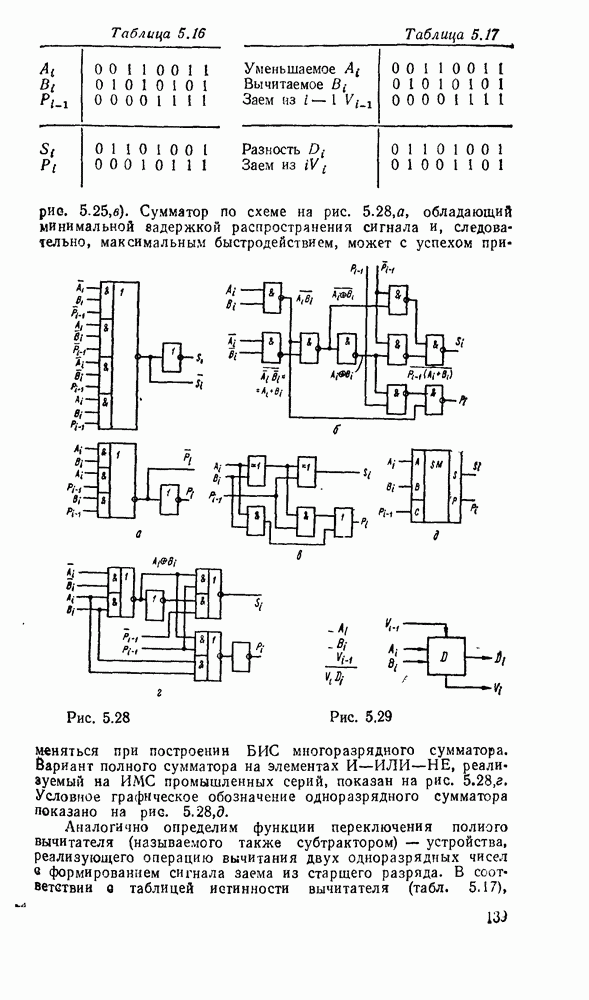
Рис. 3.3.

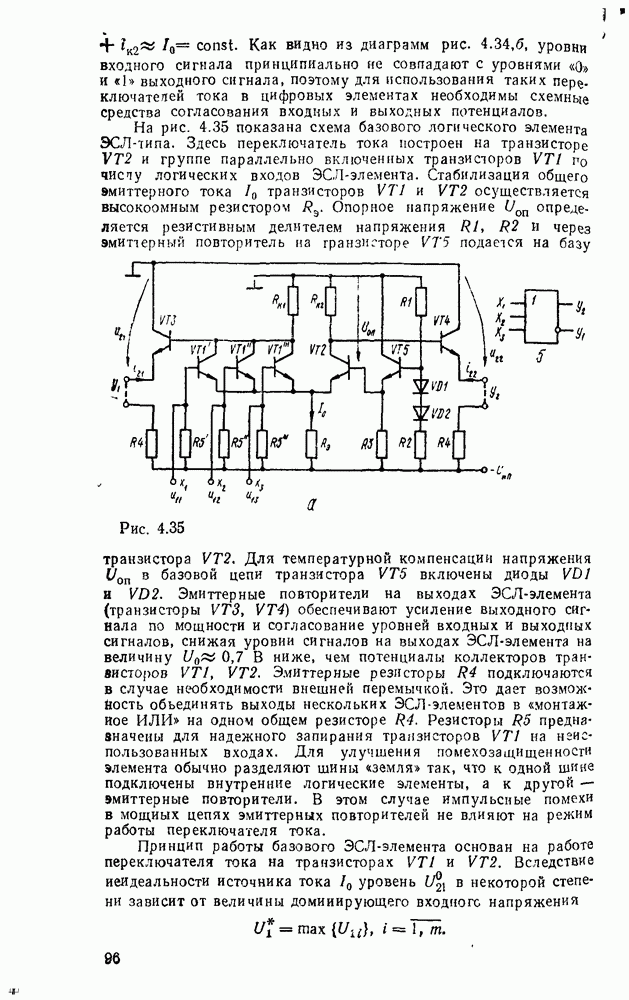
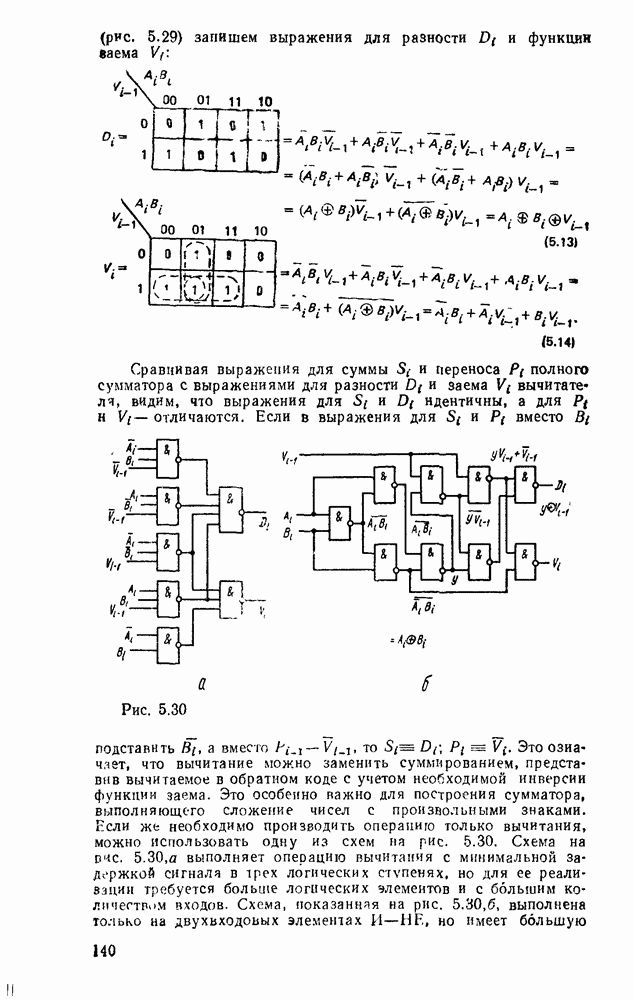
Рис. 3.4.

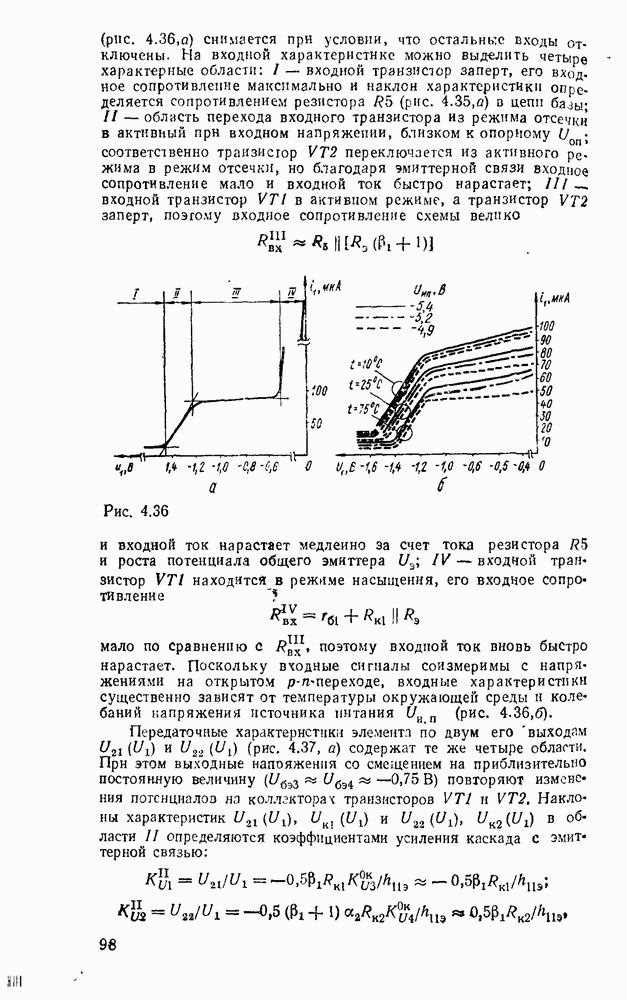
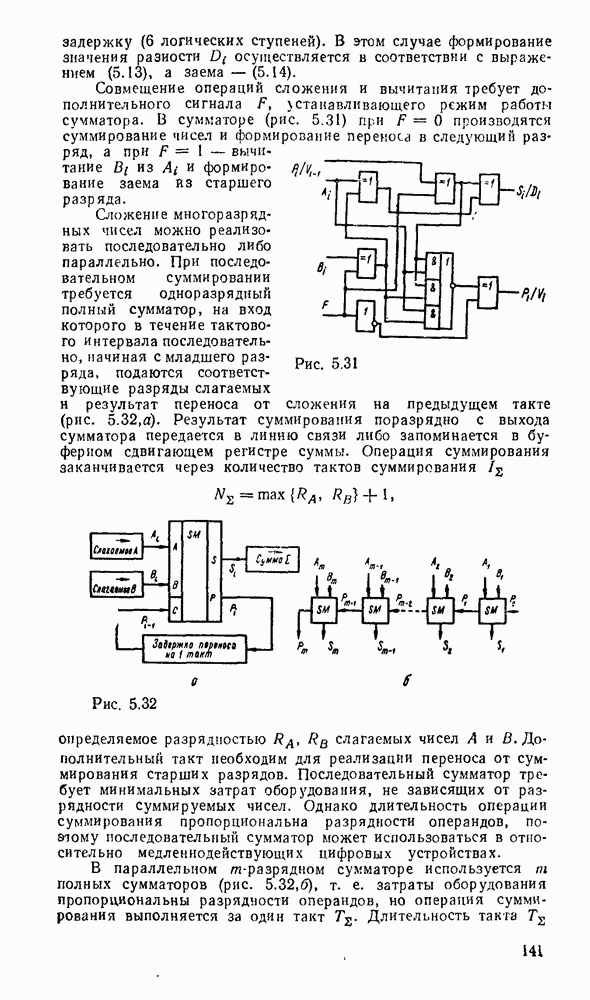
Рис. 3.5.
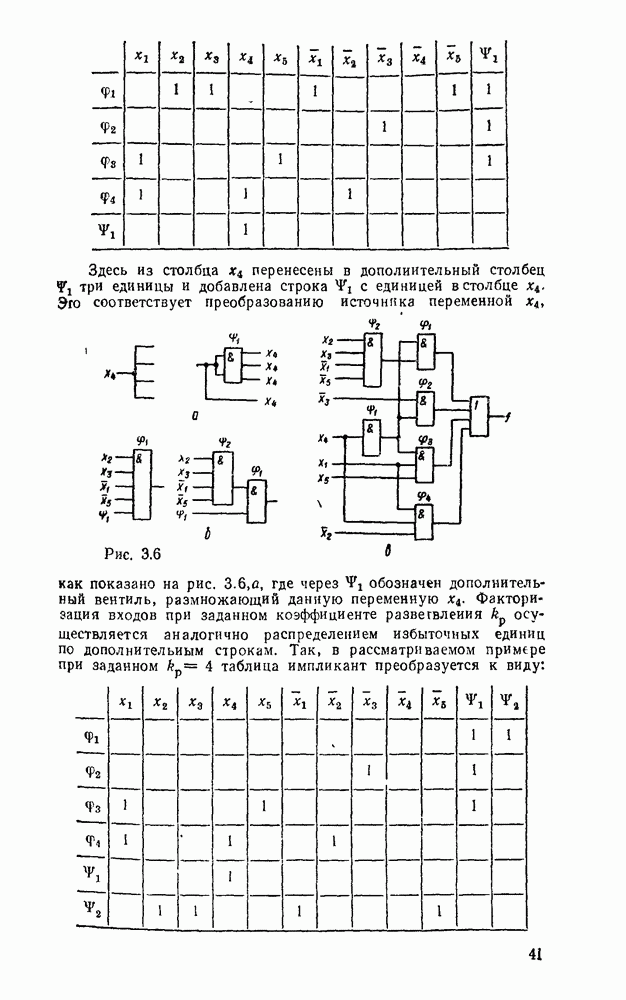
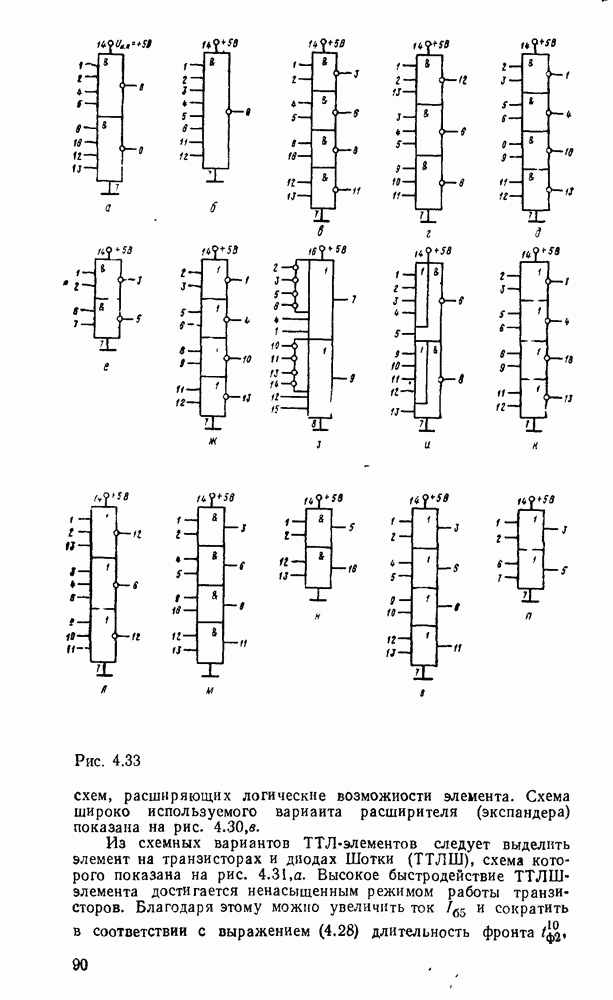
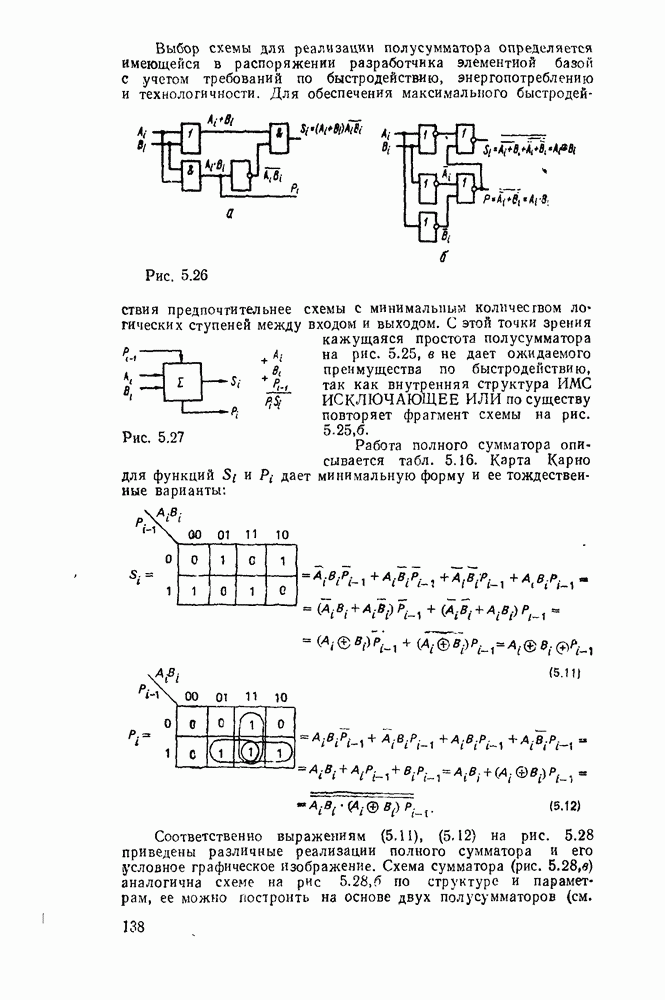
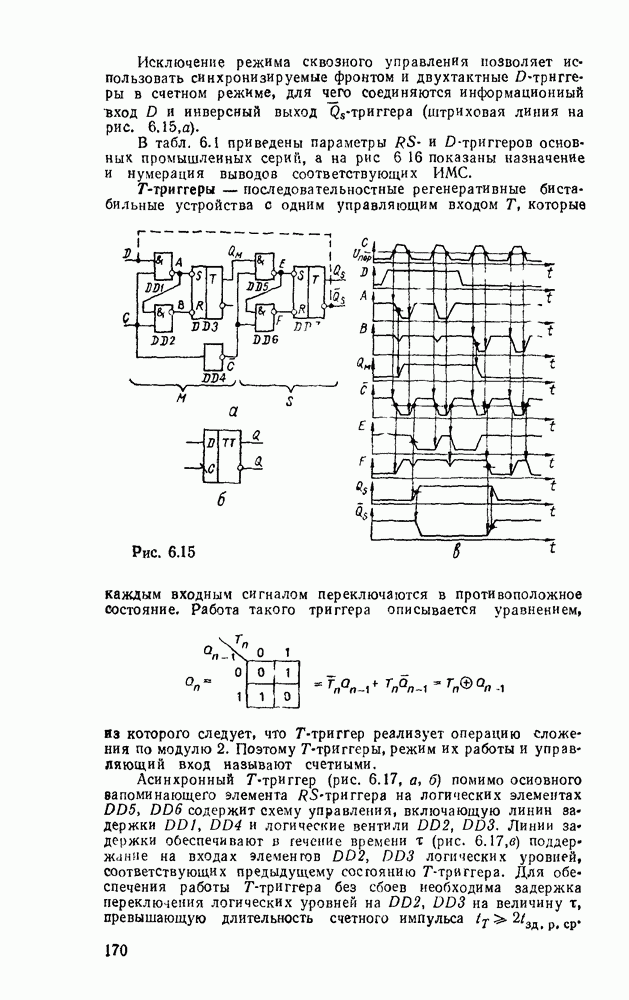
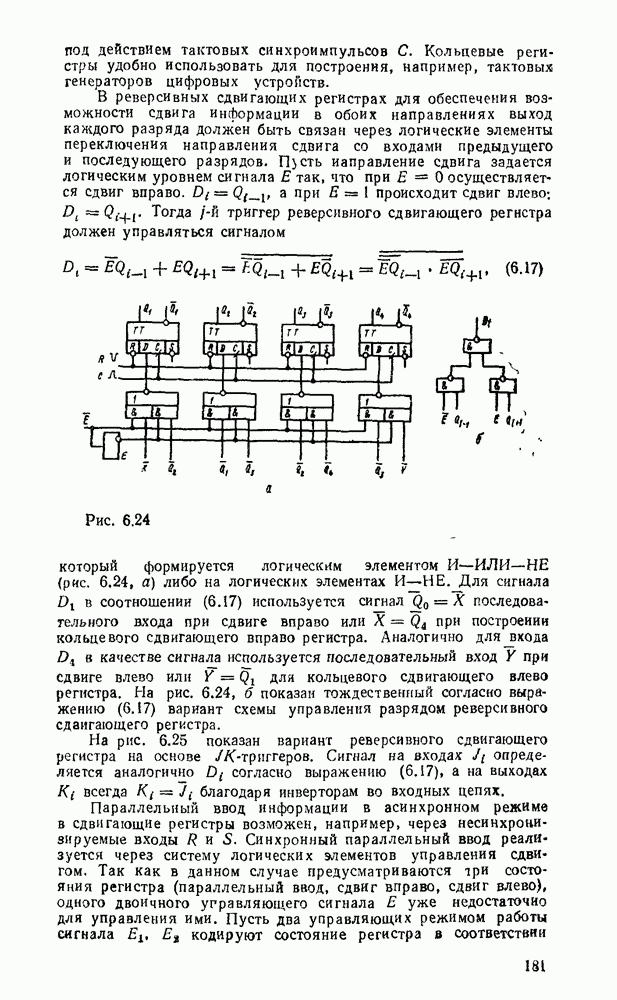
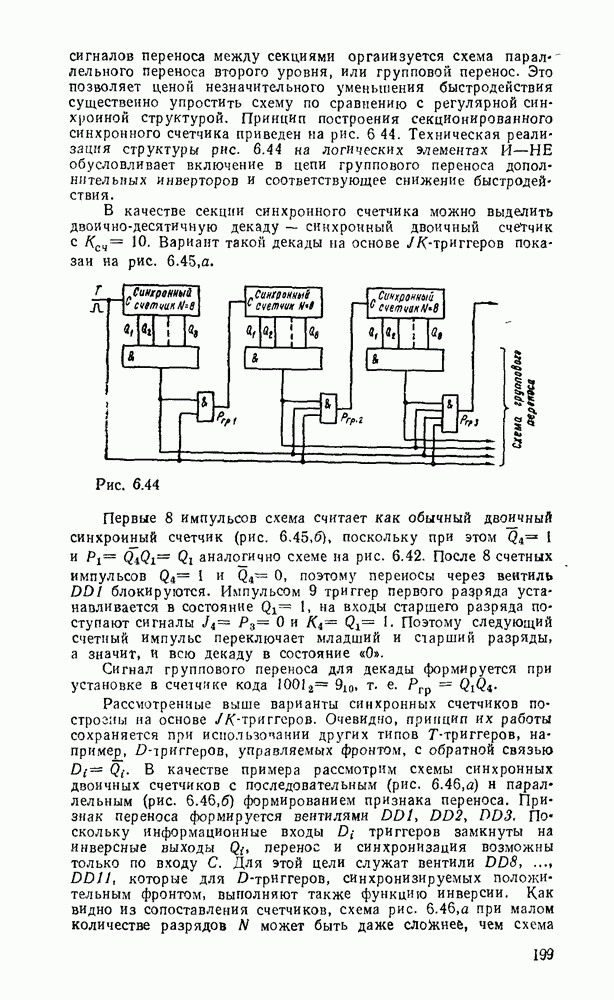
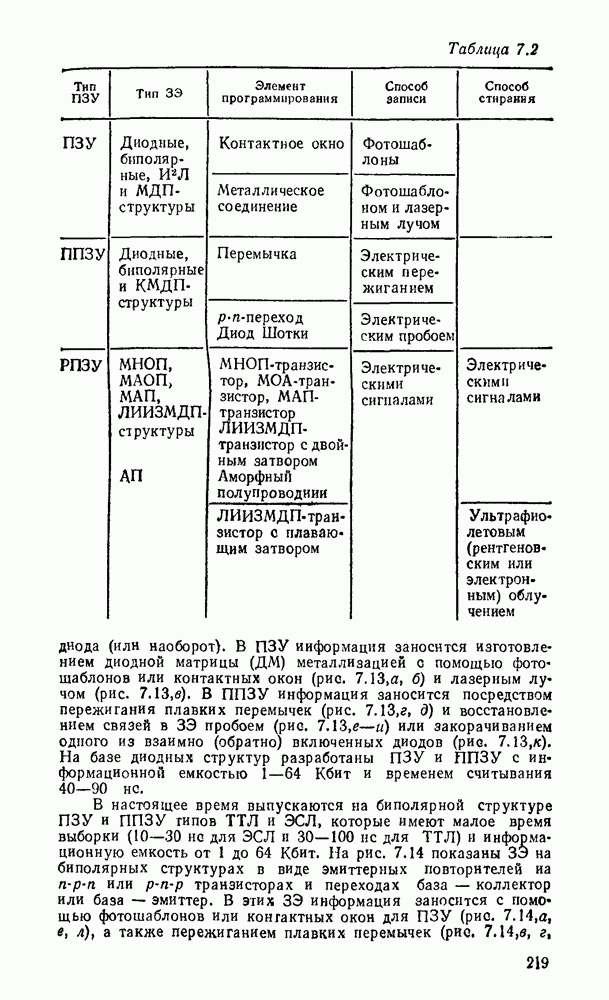
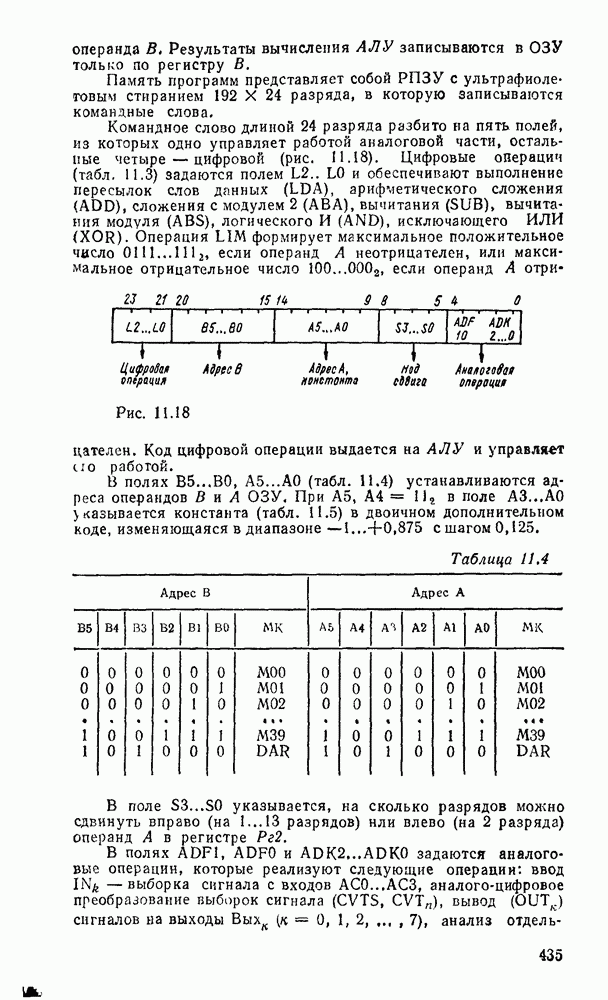
Многоступенчатые реализации появляются также вследствие преобразований стандартных форм, вызванных практическими ограничениями по числу входов вентиля (коэффициенту разветвления) и числу выходов (коэффициенту нагружения).
В одном из способов уменьшение числа входов достигается разложением булевой формулы на  . Например, функция
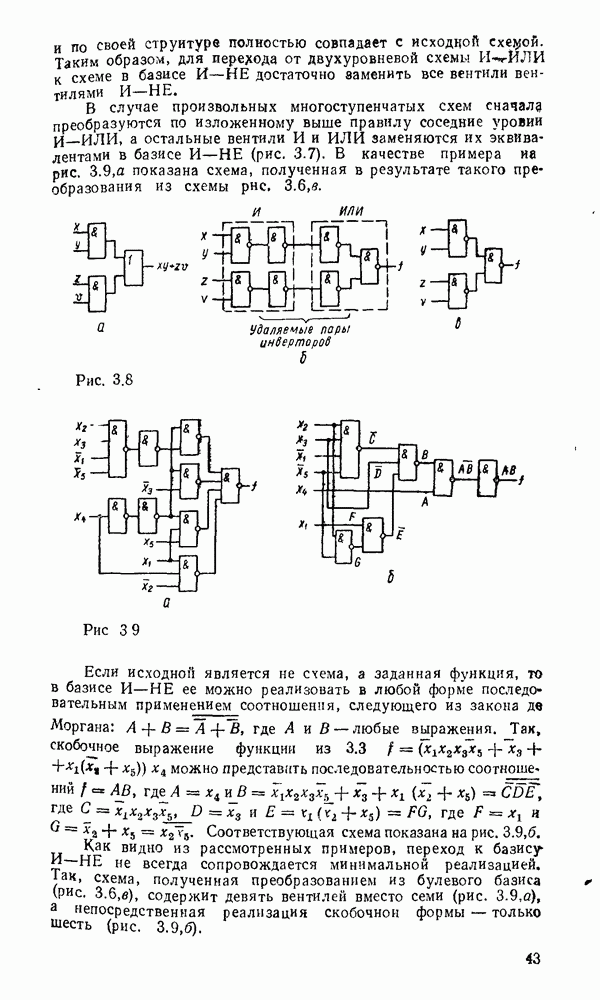
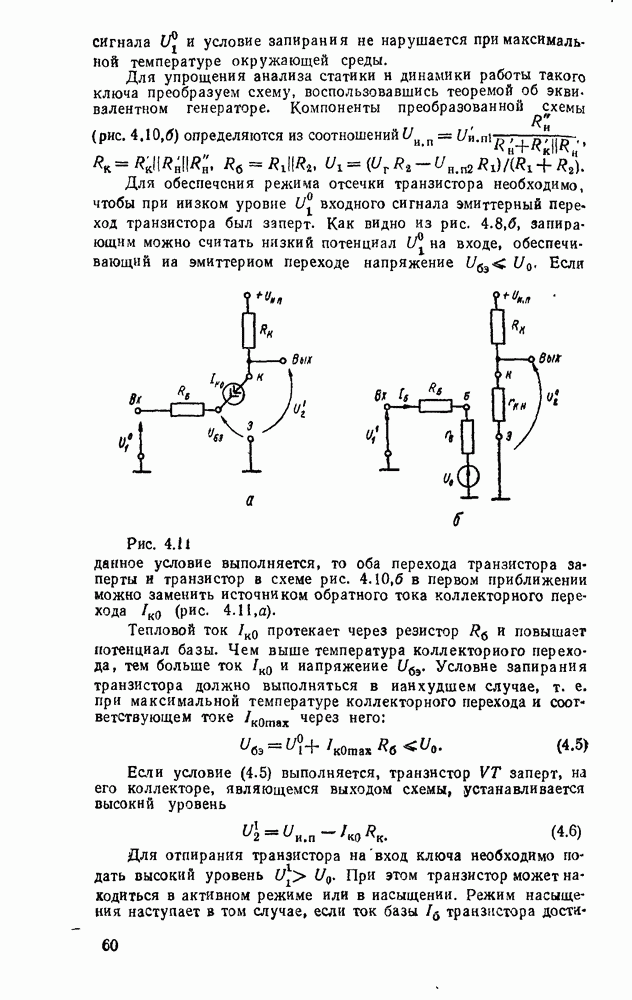
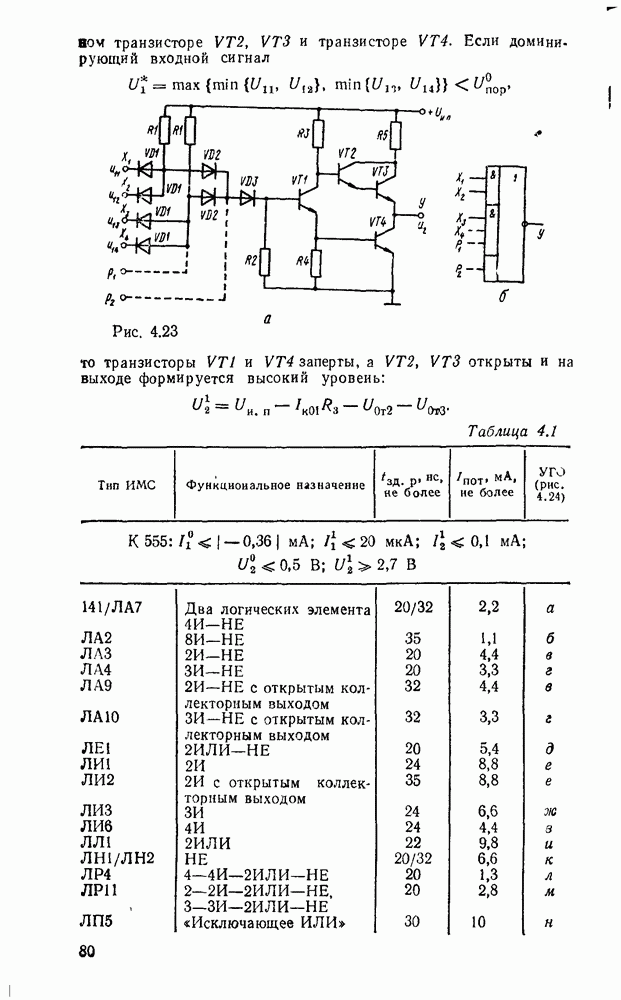
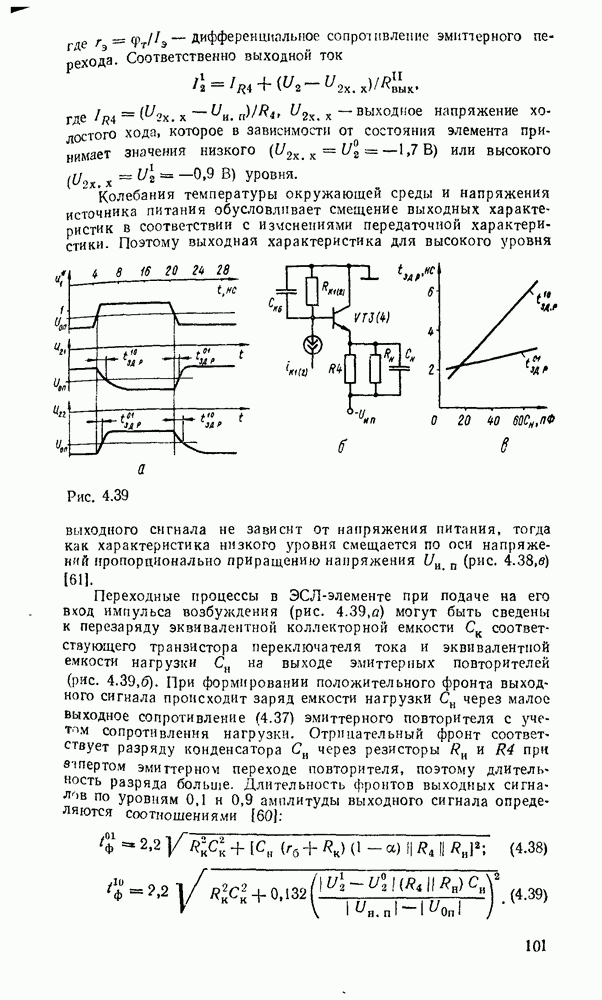
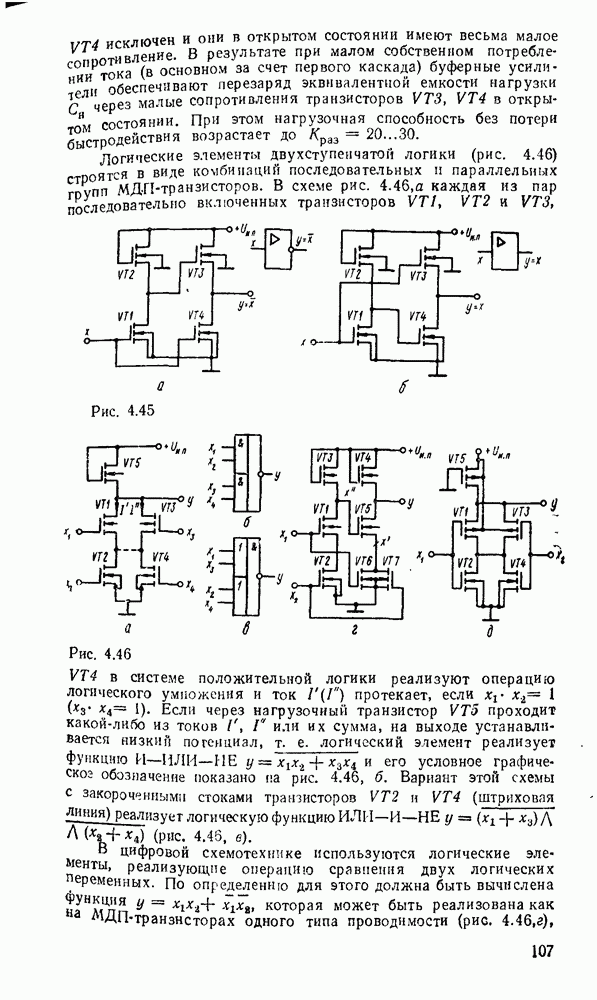
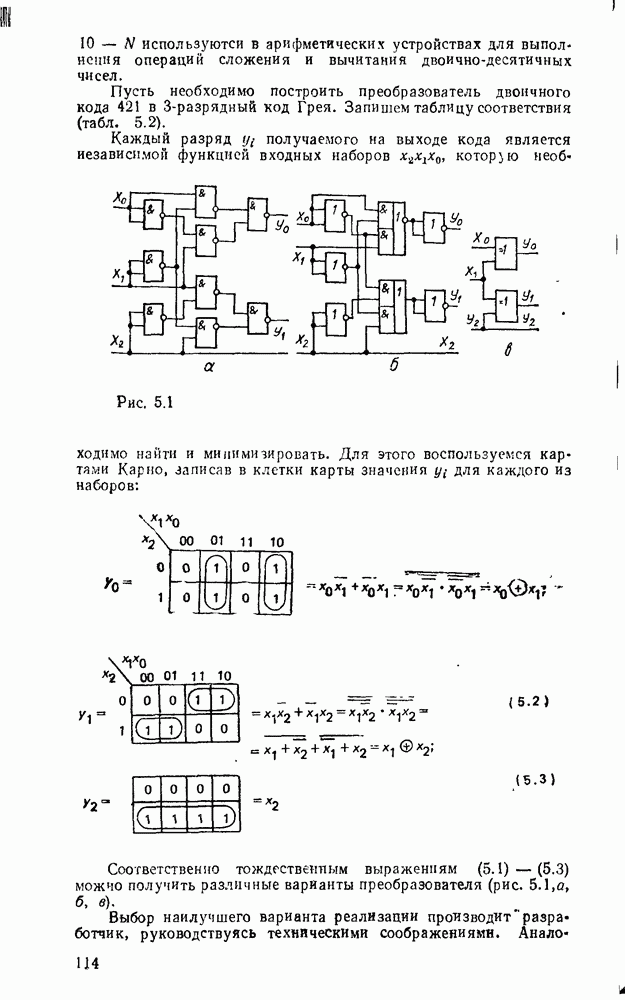
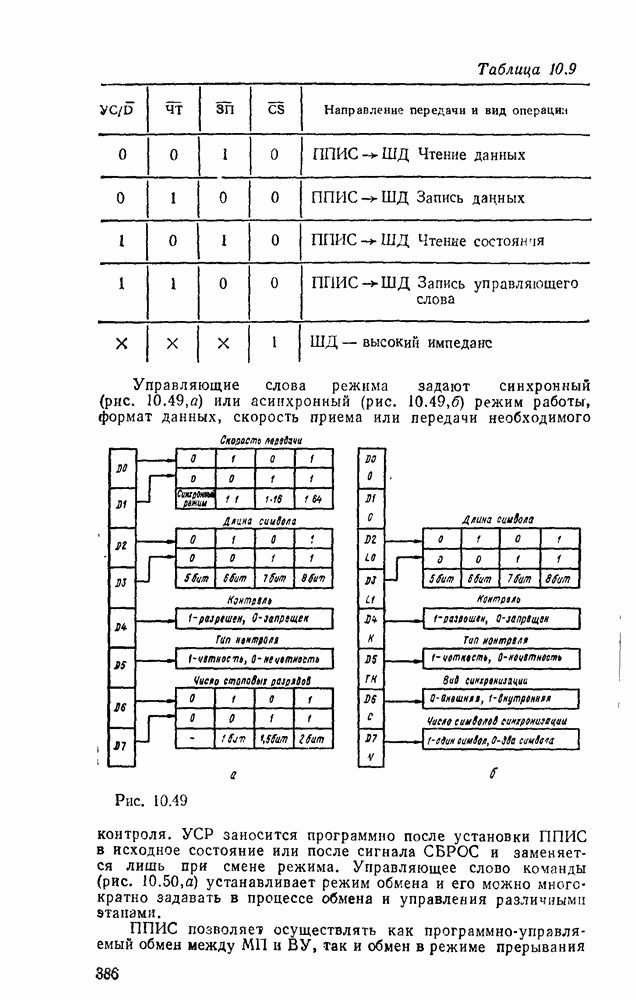
. Например, функция  , двухступенчатая реализация которой показана на рис. 3.2, преобразуется к виду:
, двухступенчатая реализация которой показана на рис. 3.2, преобразуется к виду:  . Соответствующая многоступенчатая реализация, в которой используются только двухвходовые вентили, показана на рис. 3.4.
. Соответствующая многоступенчатая реализация, в которой используются только двухвходовые вентили, показана на рис. 3.4.
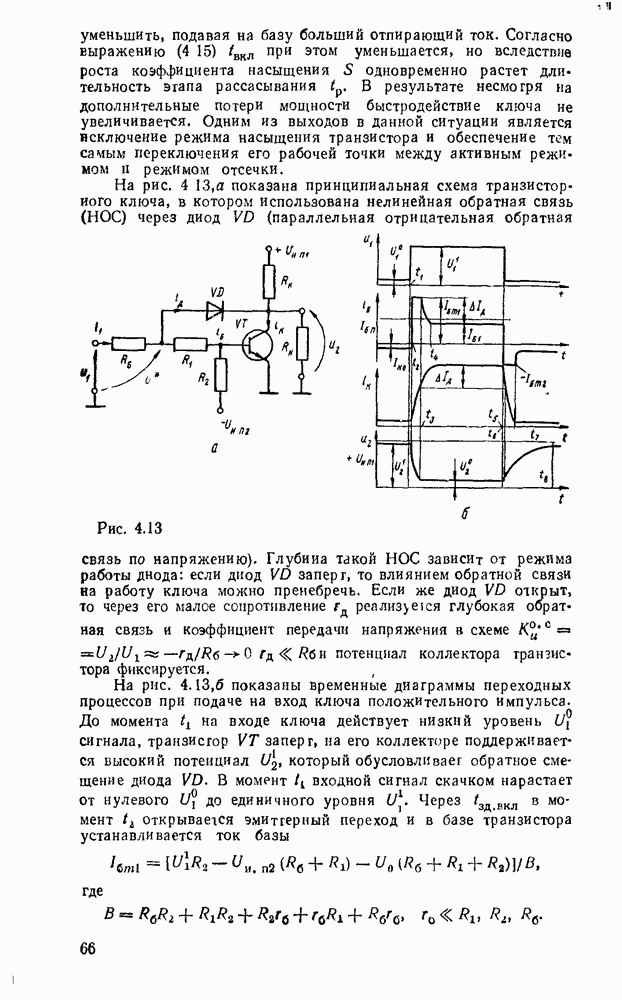
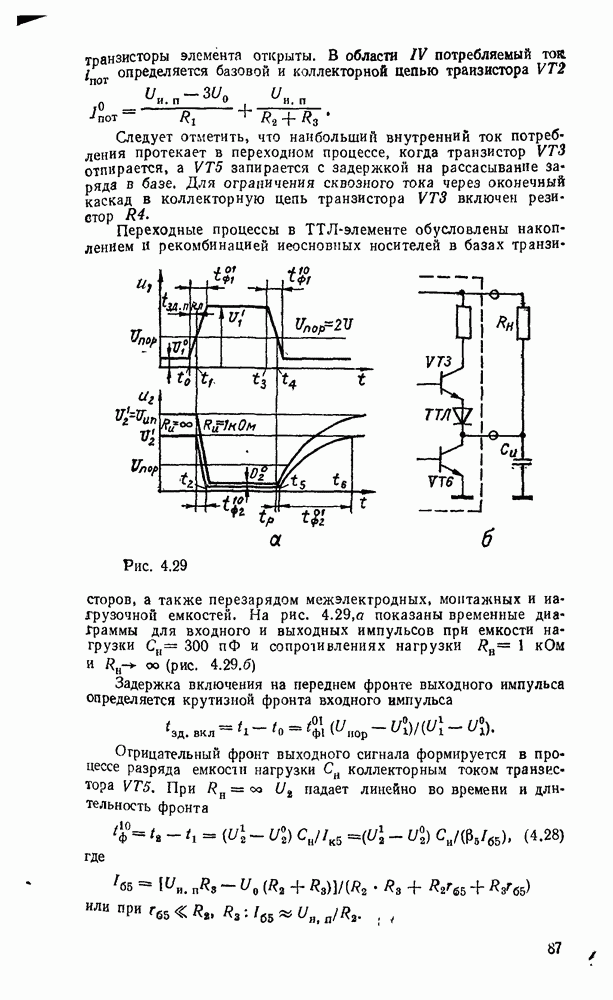
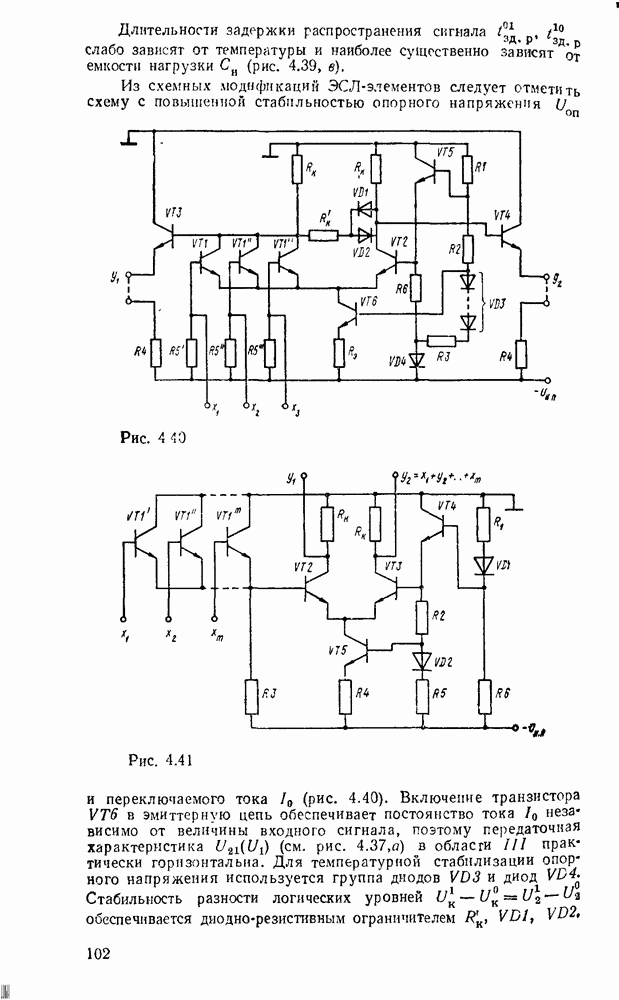
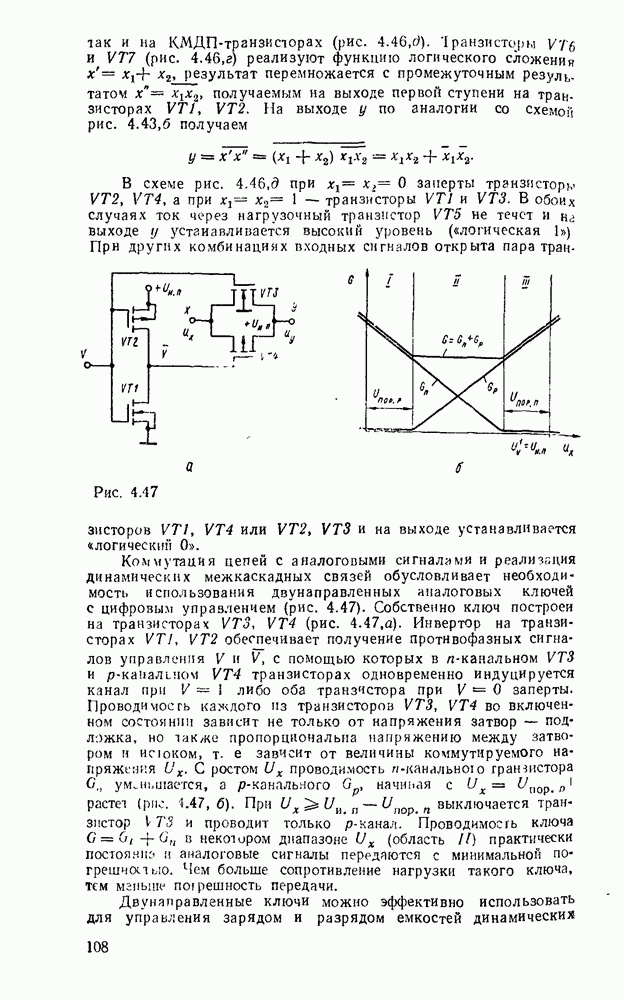
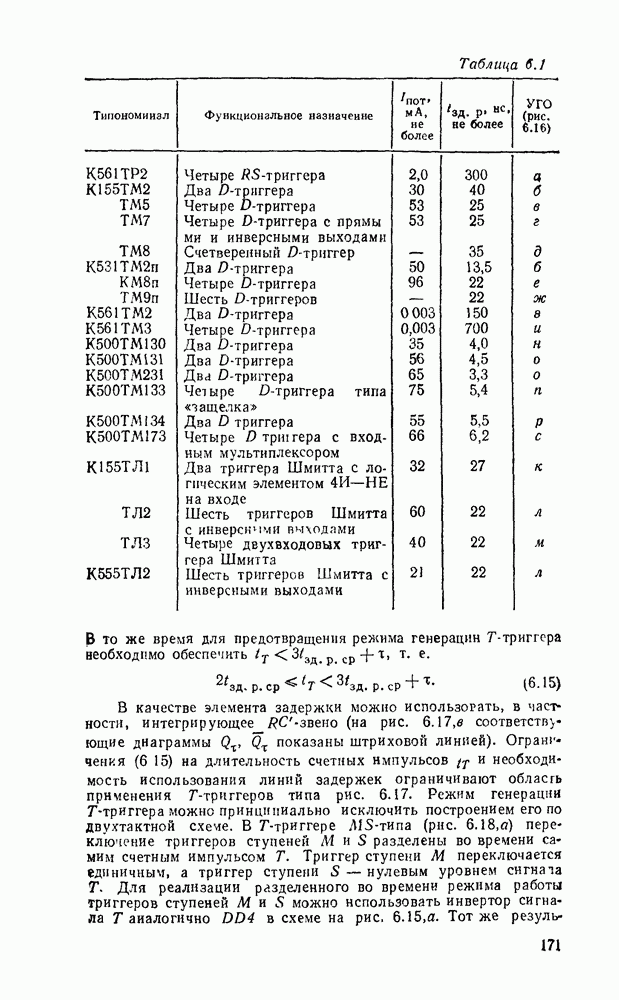
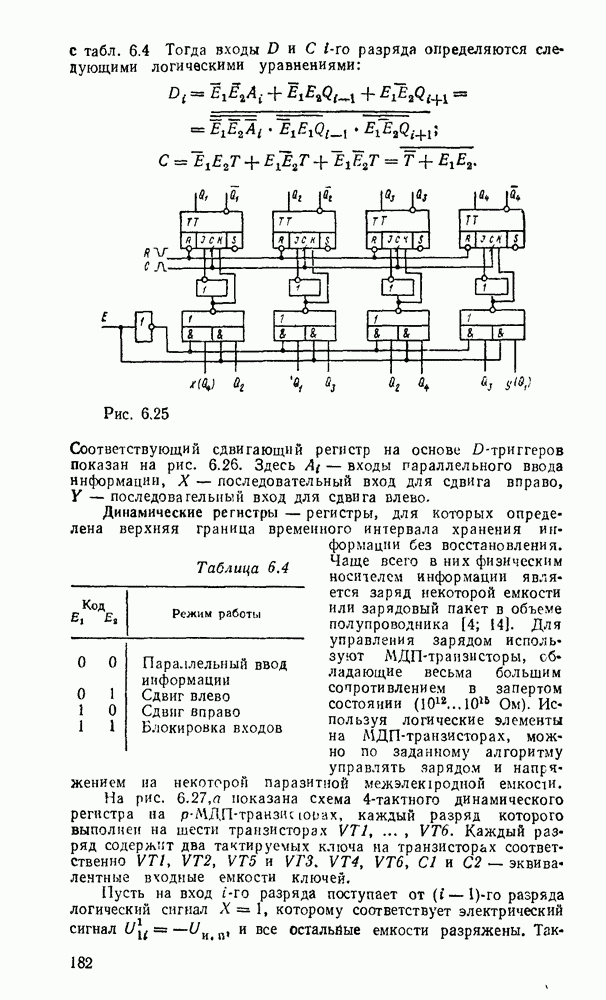
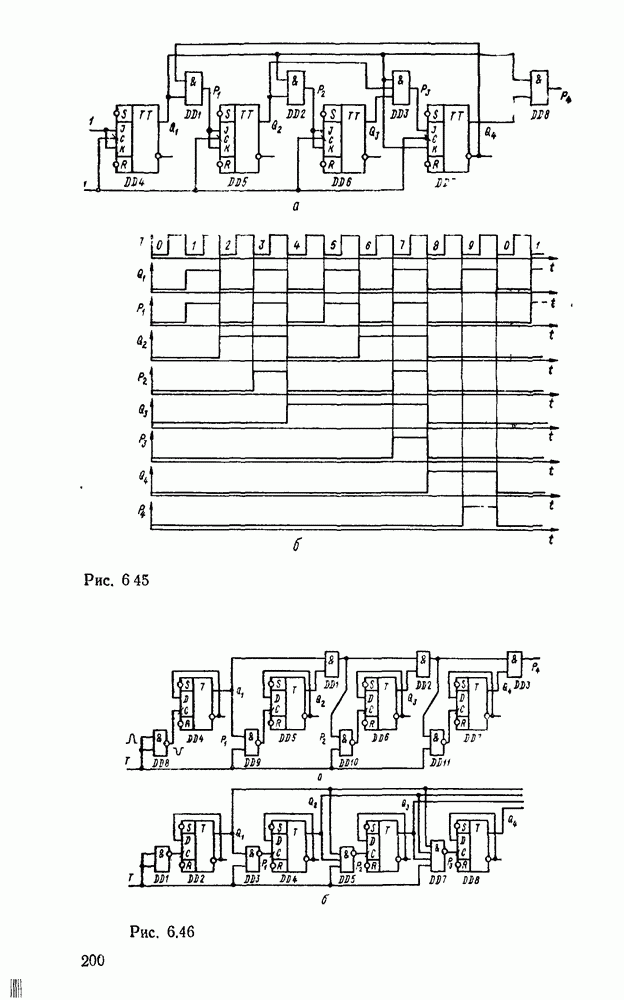
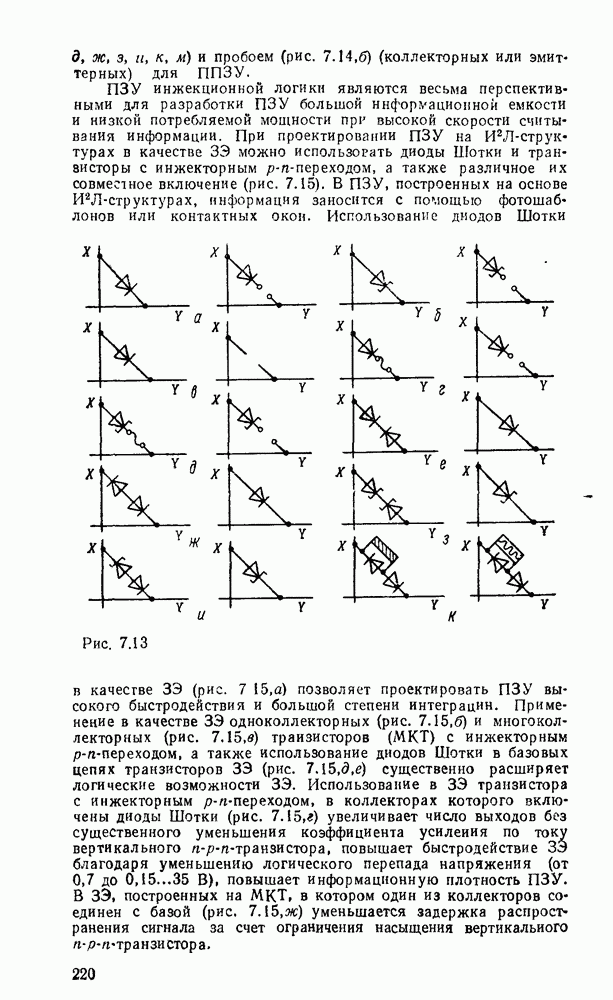
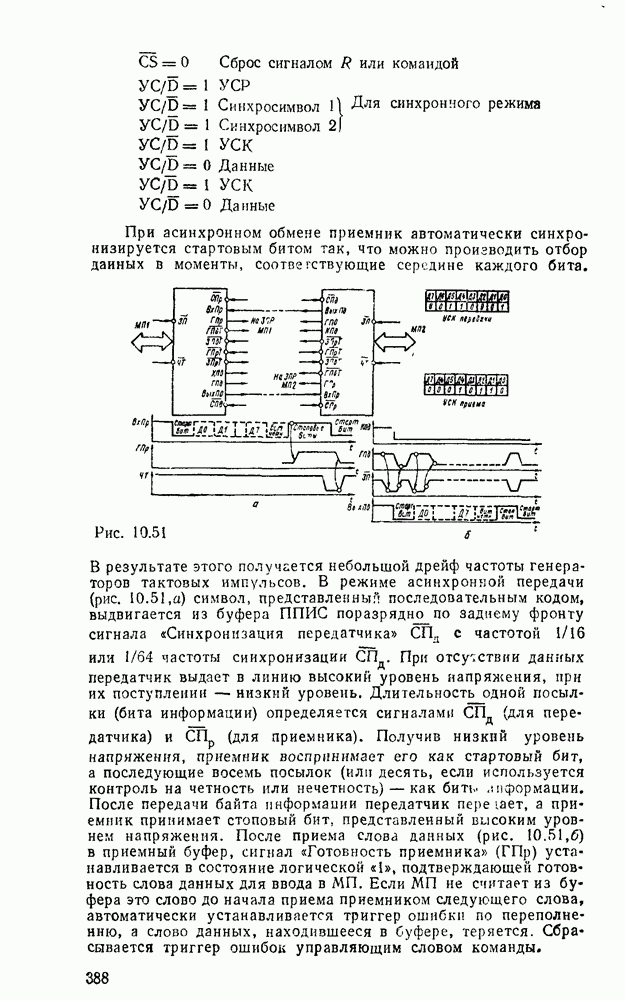
Любые ограничения на коэффициенты разветвления и нагружения можно удовлетворить заменой вентилей снедопустимо большим числом входов и выходов так называемыми древовидными схемами (рис. 3.5). Одна из таких схем уже использовалась выше для реализации функции проверки на четность. Вентиль на  входов реализуется древовидной схемой, состоящей из (
входов реализуется древовидной схемой, состоящей из ( ) двухвходовых вентилей, причем число ступеней равно
) двухвходовых вентилей, причем число ступеней равно  , т. е. наименьшему целому числу, большему или равному
, т. е. наименьшему целому числу, большему или равному  (рис.
(рис.  ). Аналогично вентиль с
). Аналогично вентиль с  выходами реализуется древовидной схемой, которая содержит также
выходами реализуется древовидной схемой, которая содержит также  ступеней, а каждый вентиль имеет один вход и два выхода (рис.
ступеней, а каждый вентиль имеет один вход и два выхода (рис.  ).
).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
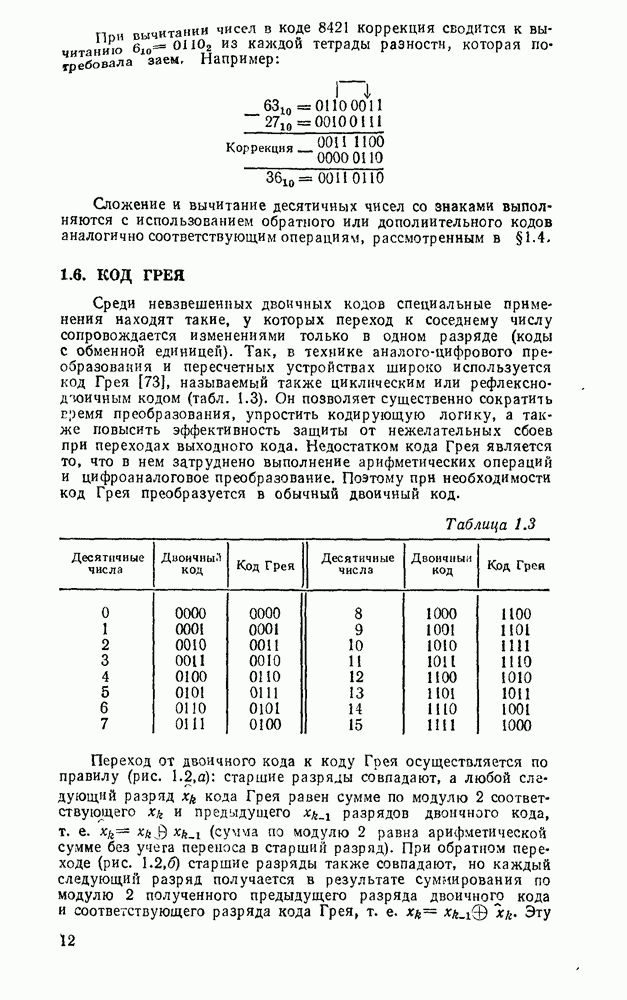
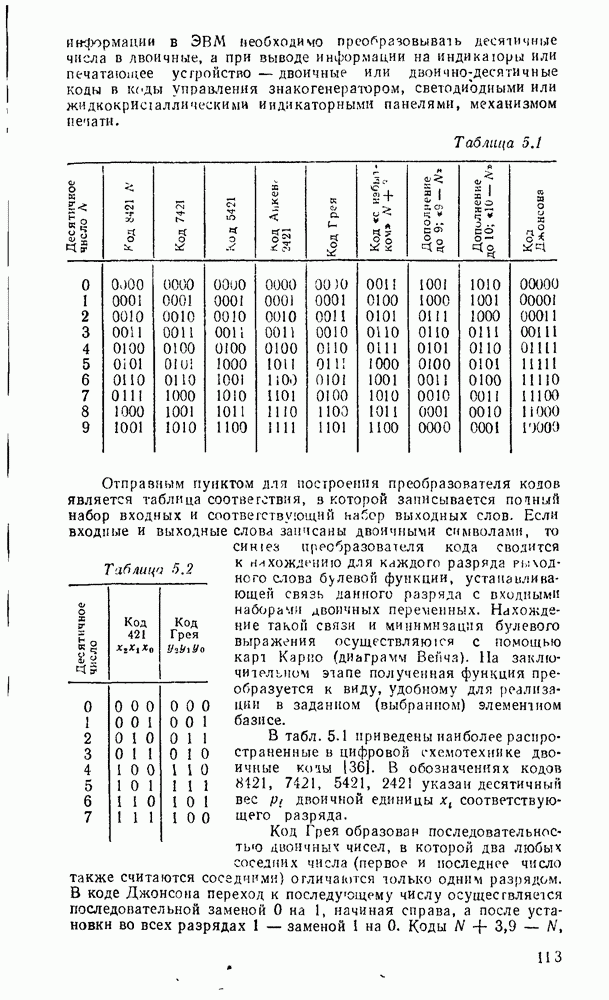
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
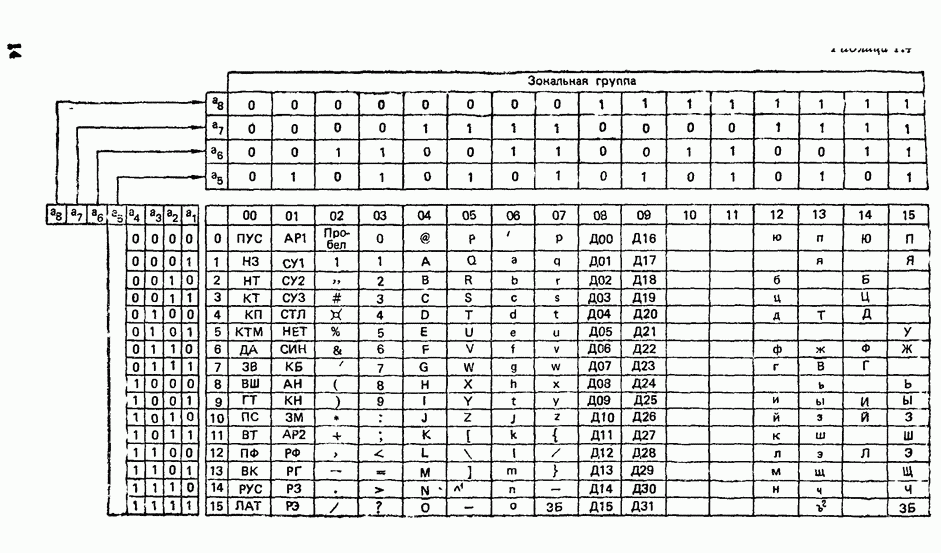
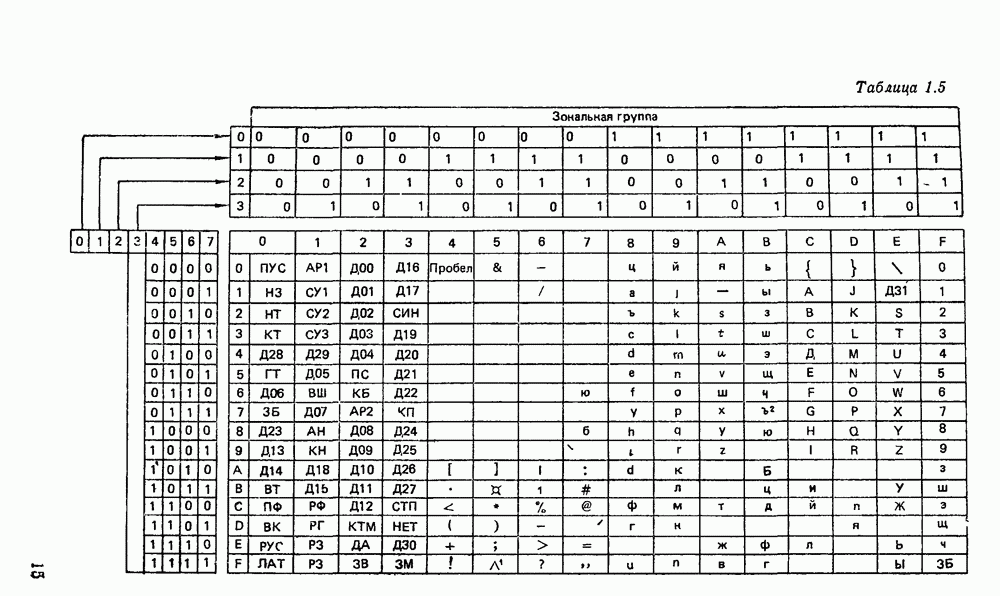
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
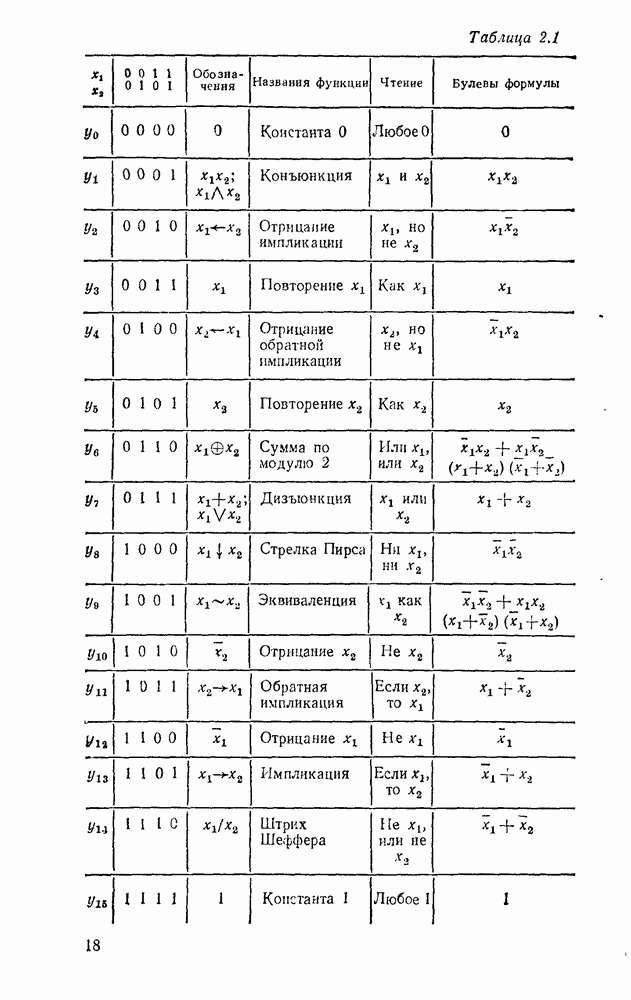
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
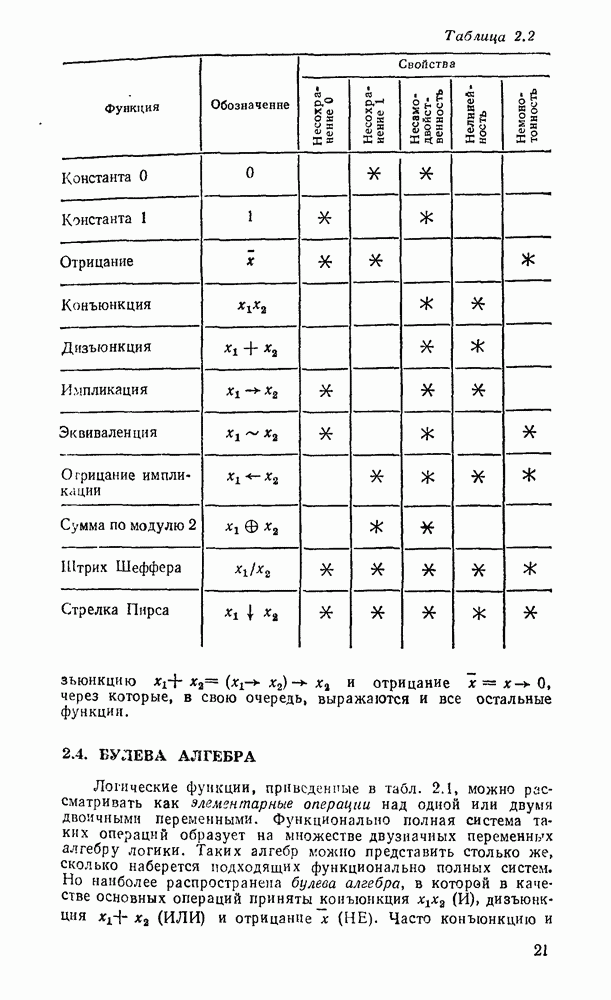
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
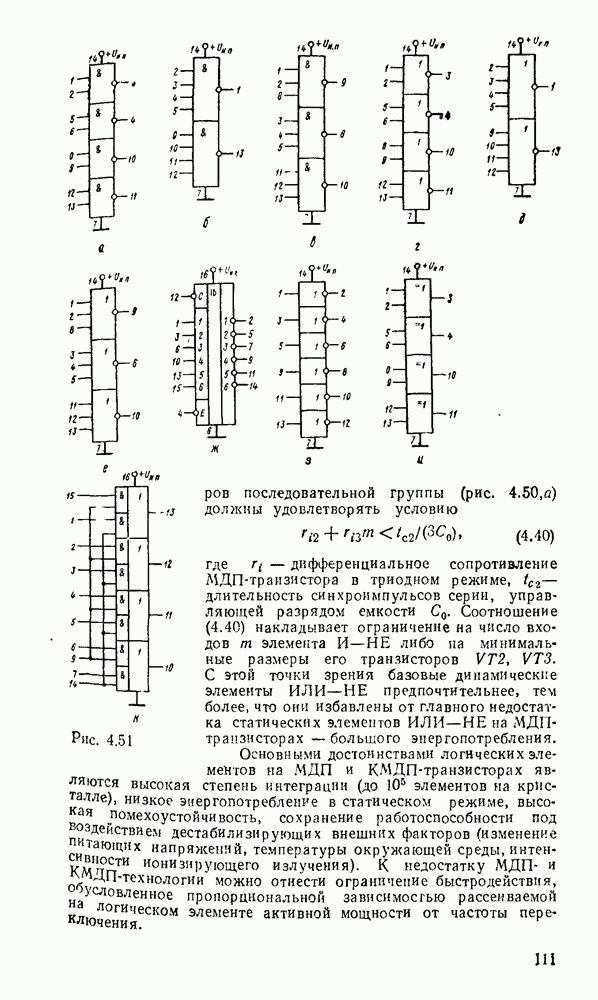
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
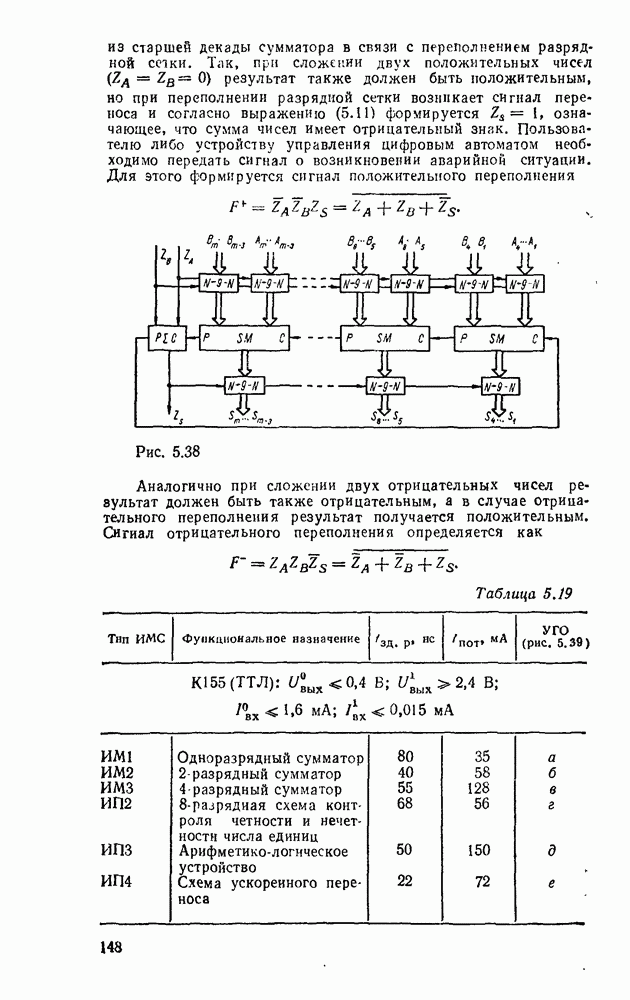
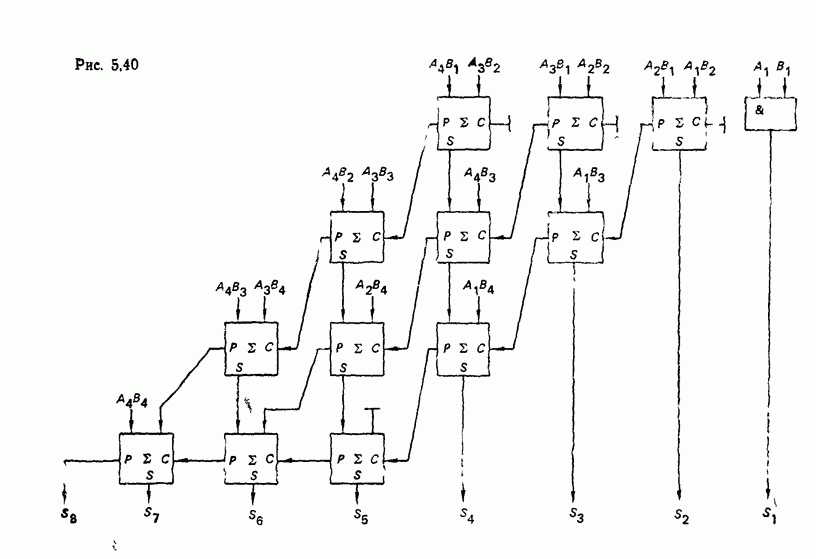
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
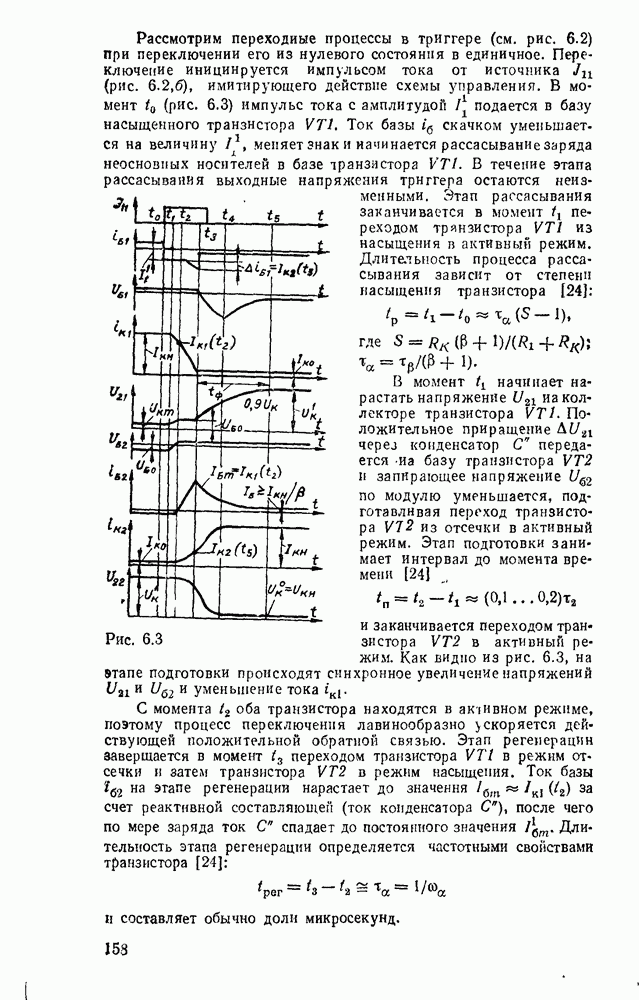
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
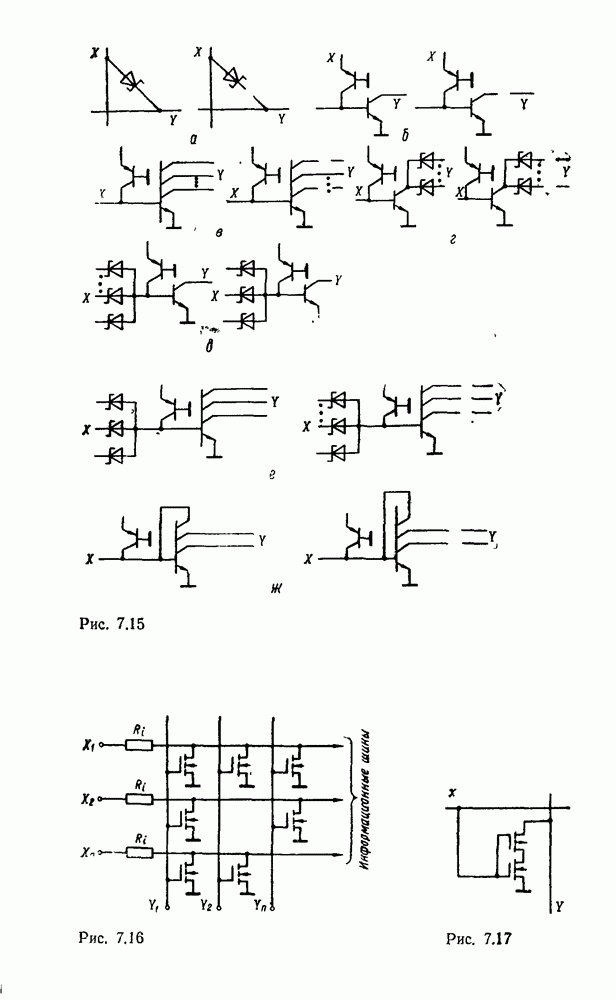
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
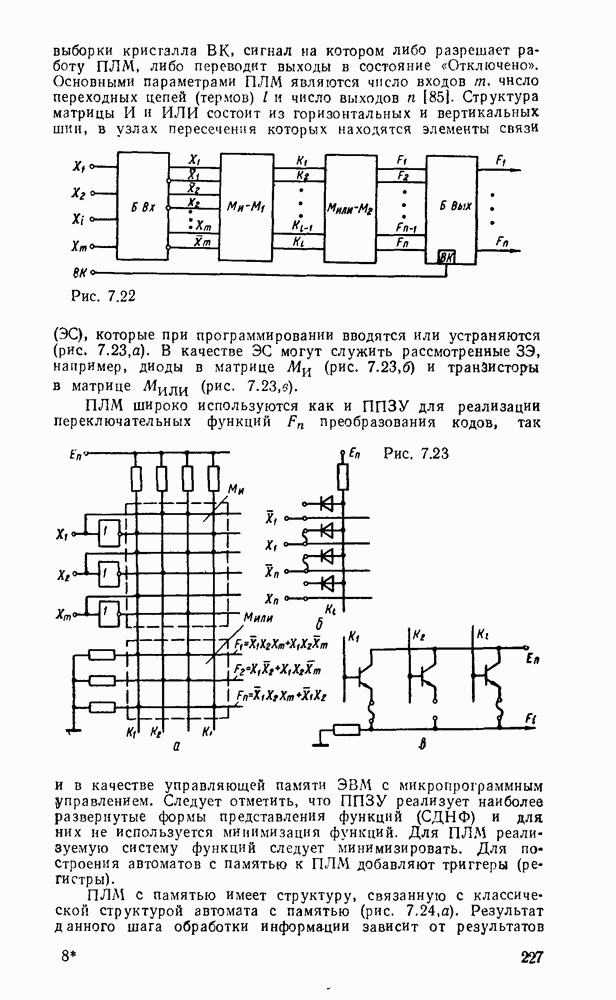
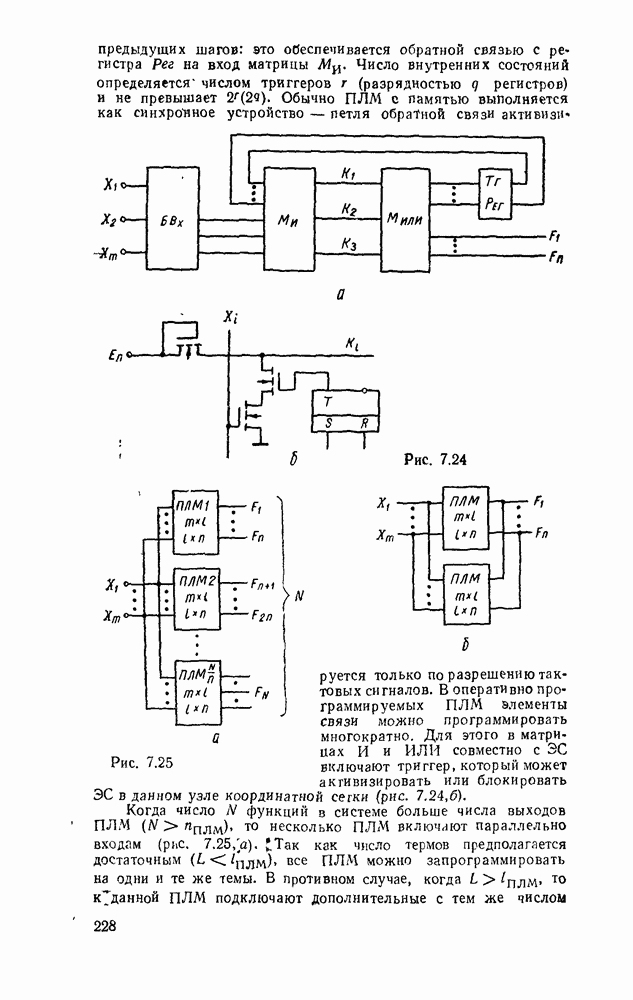
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
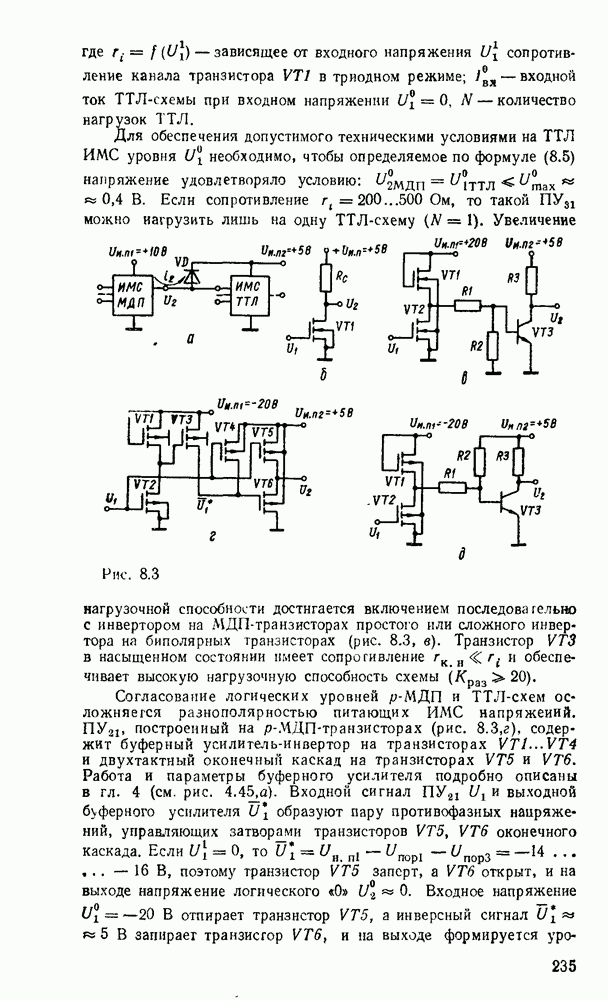
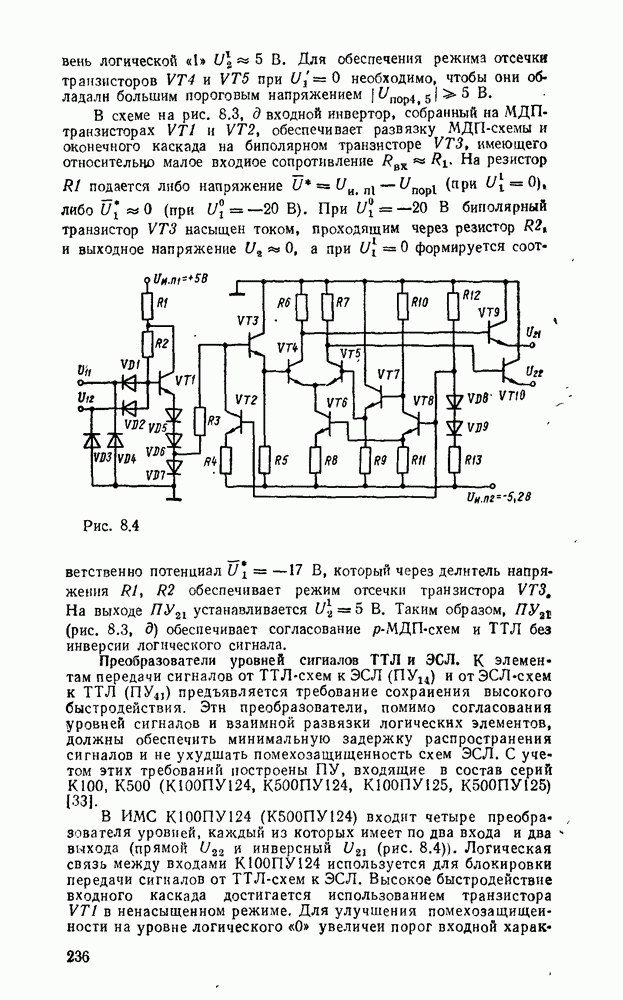
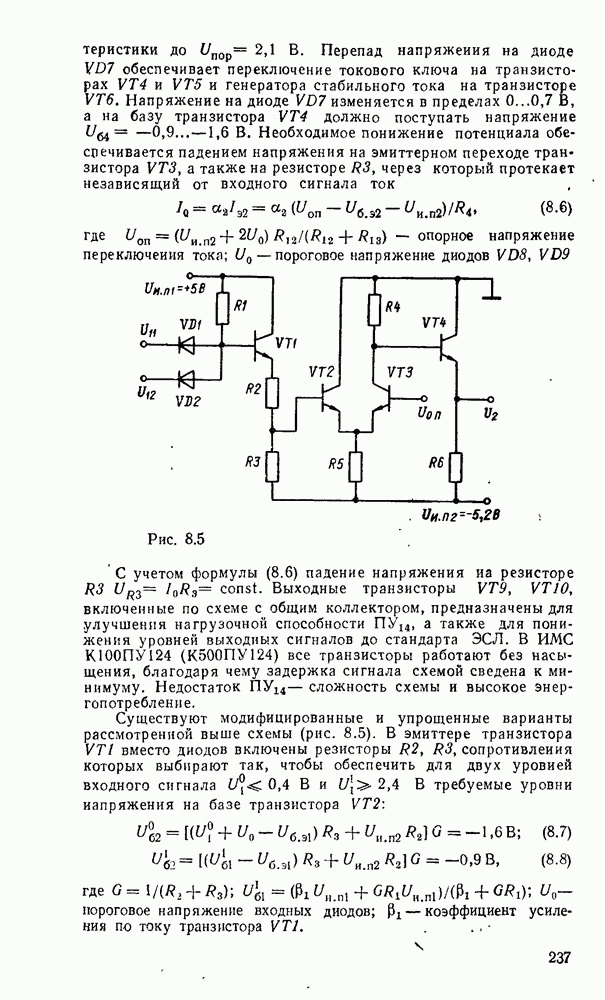
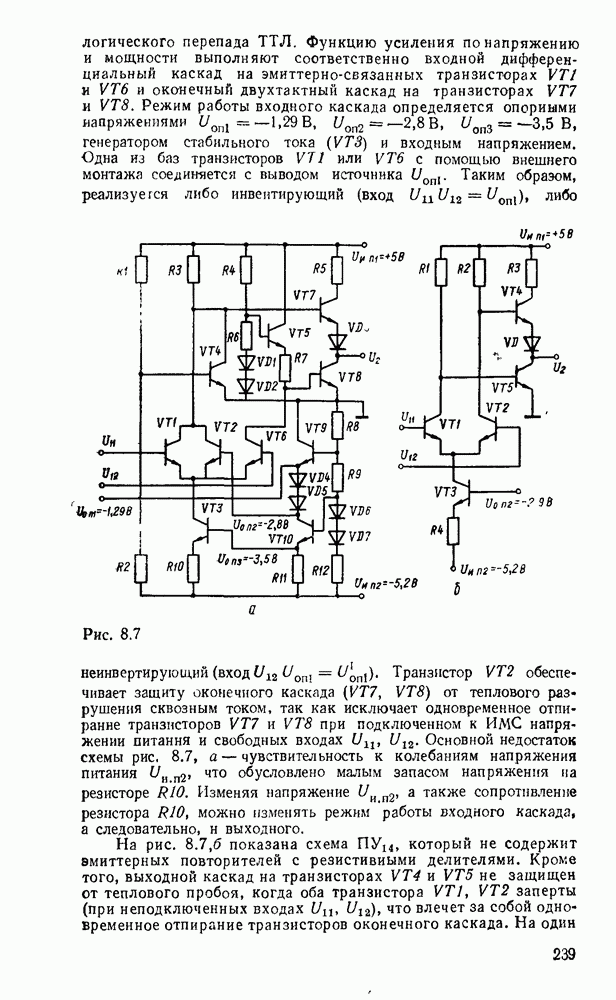
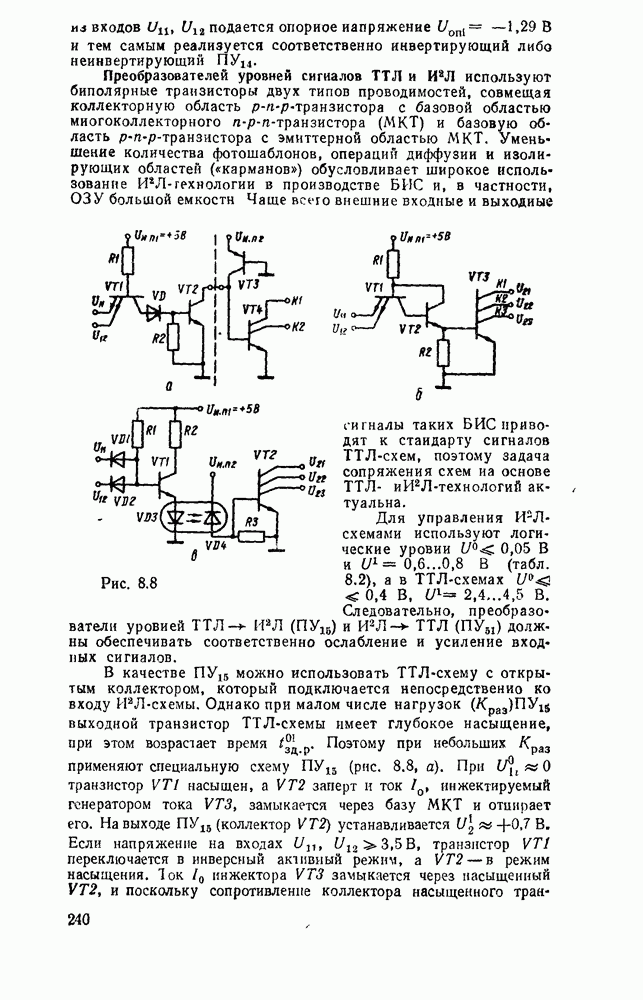
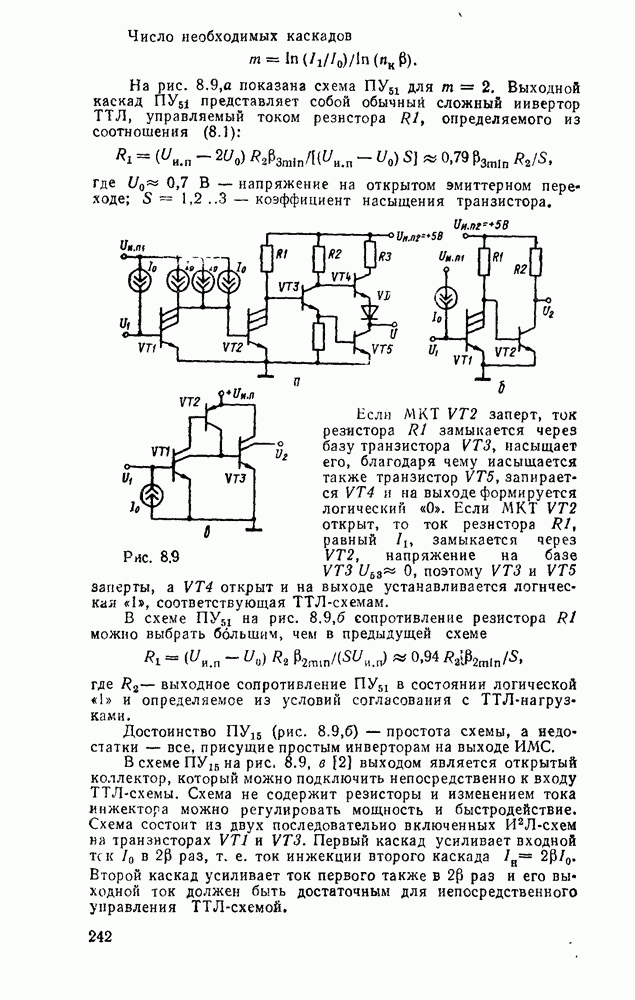
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
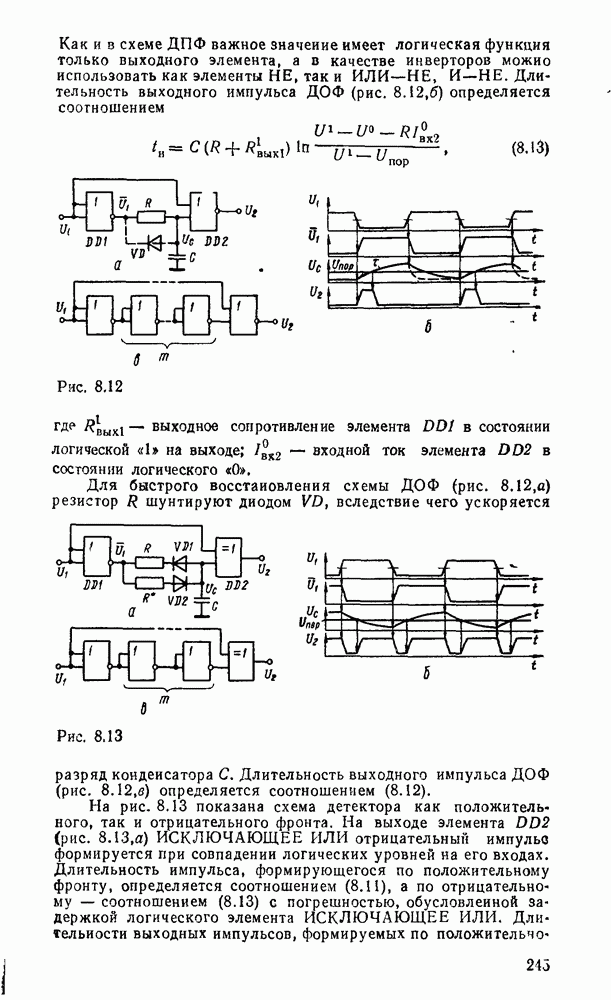
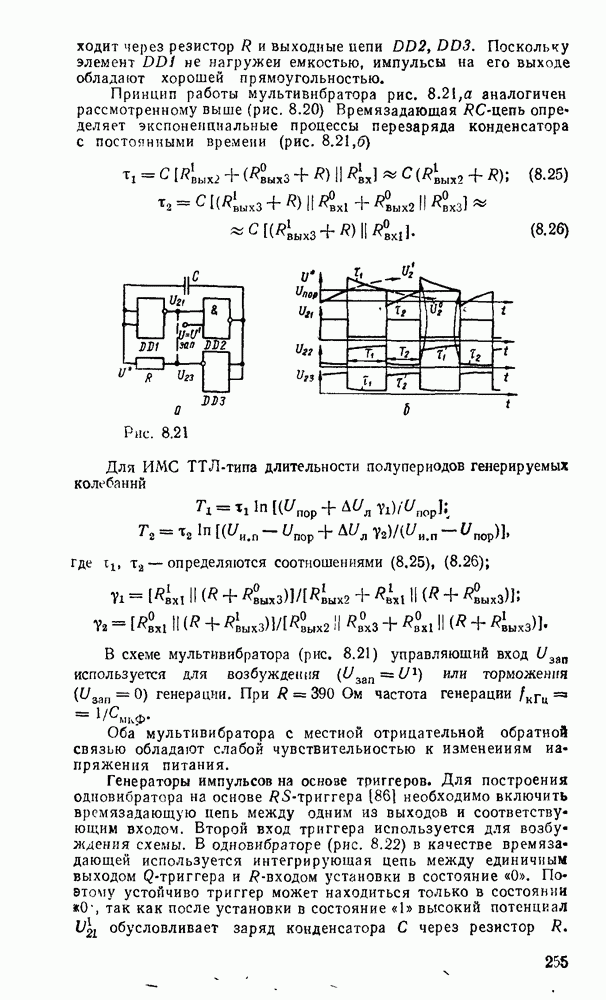
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
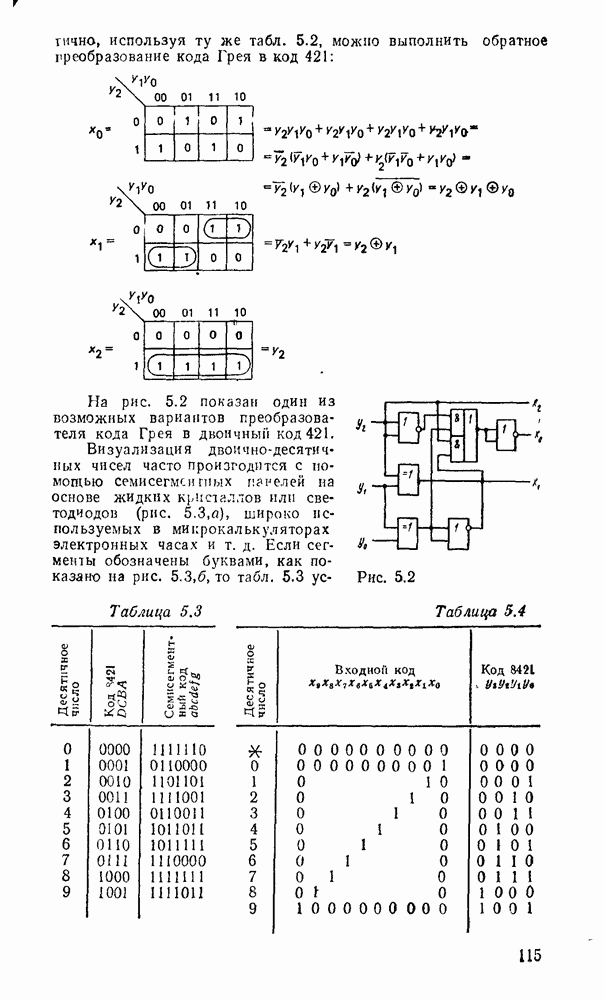
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
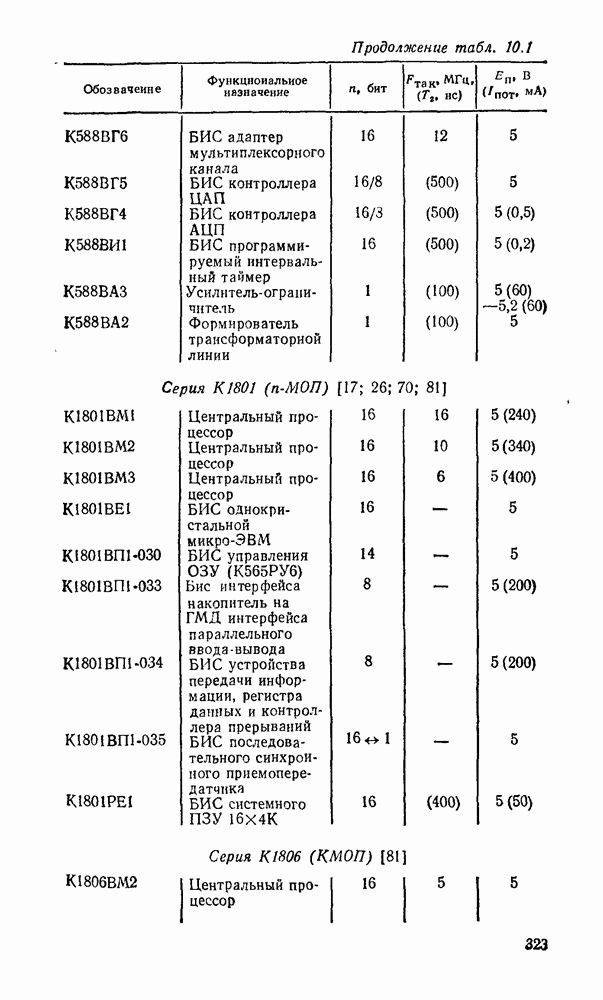
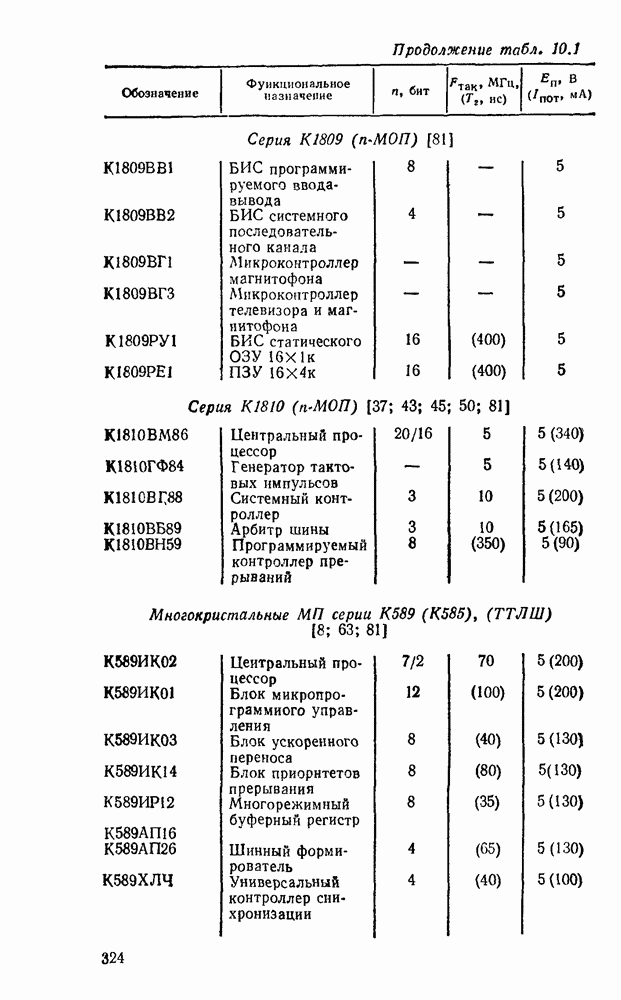
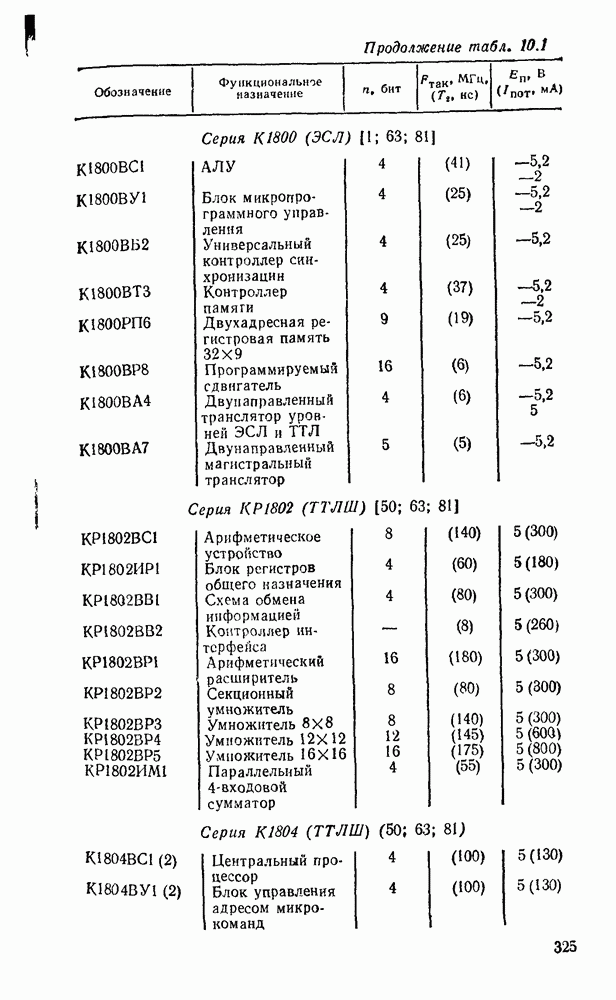
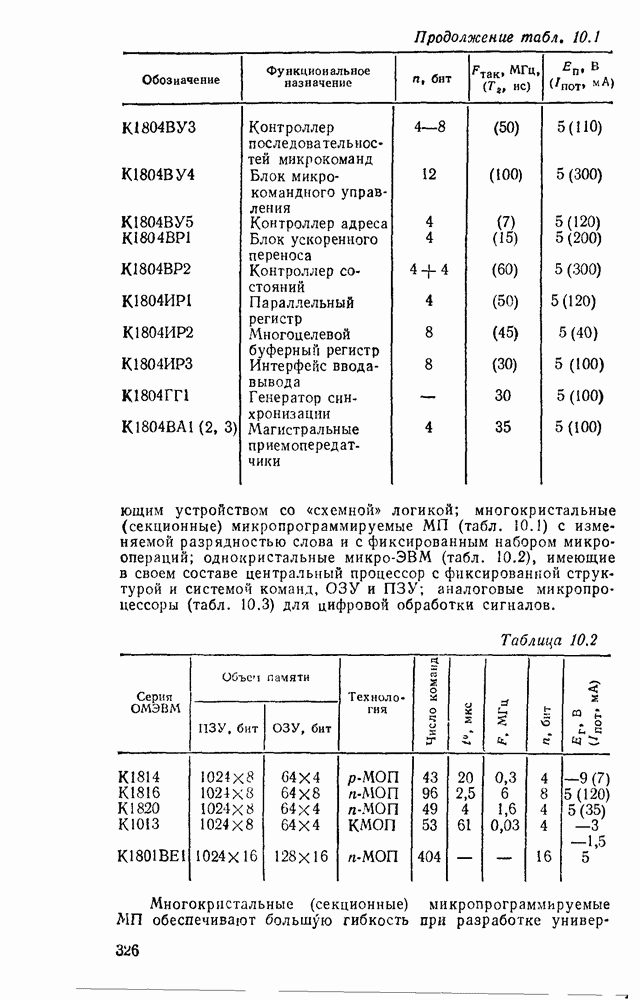
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
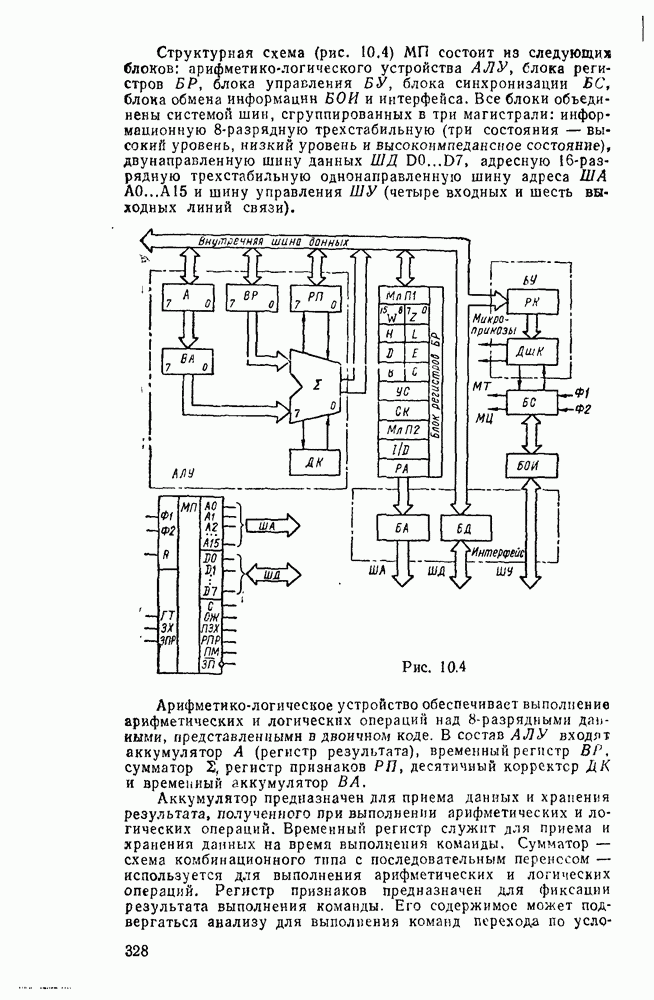
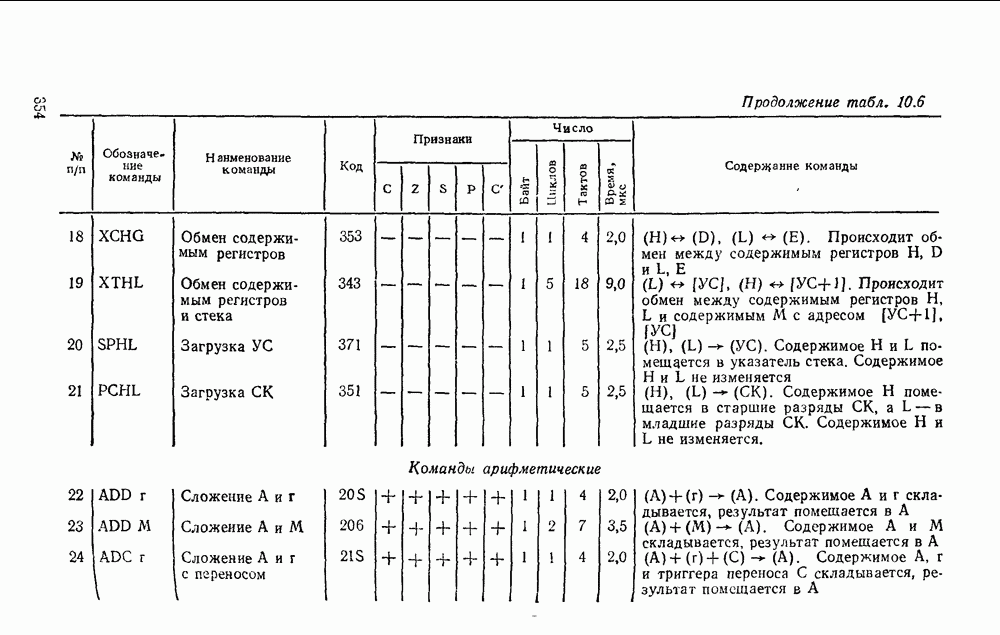
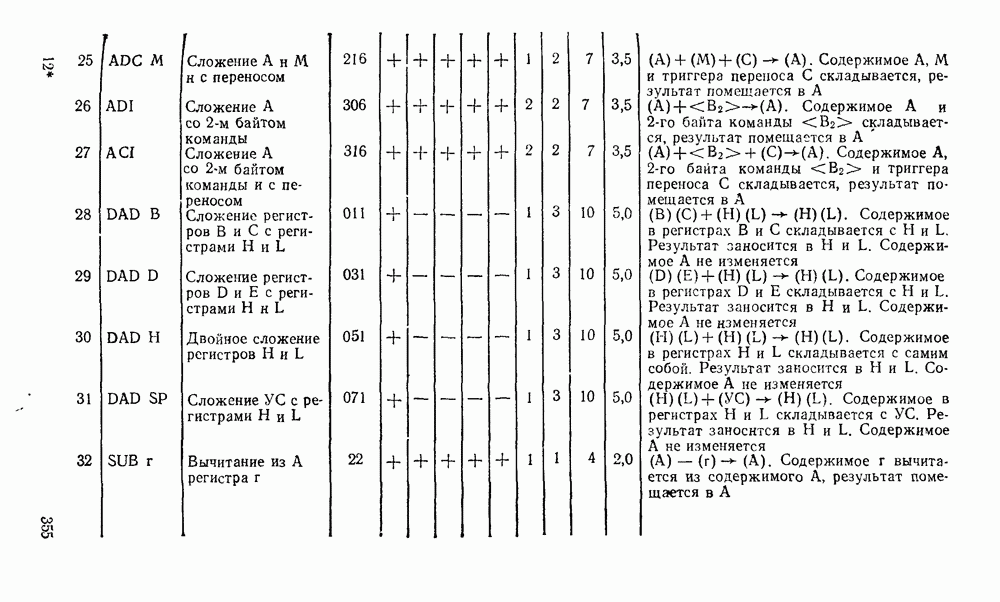
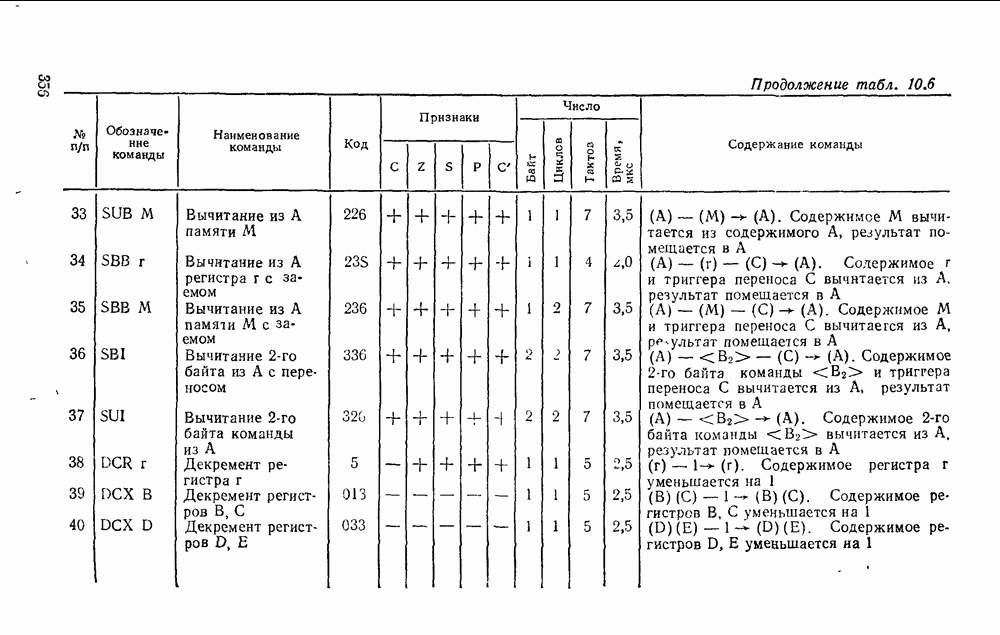
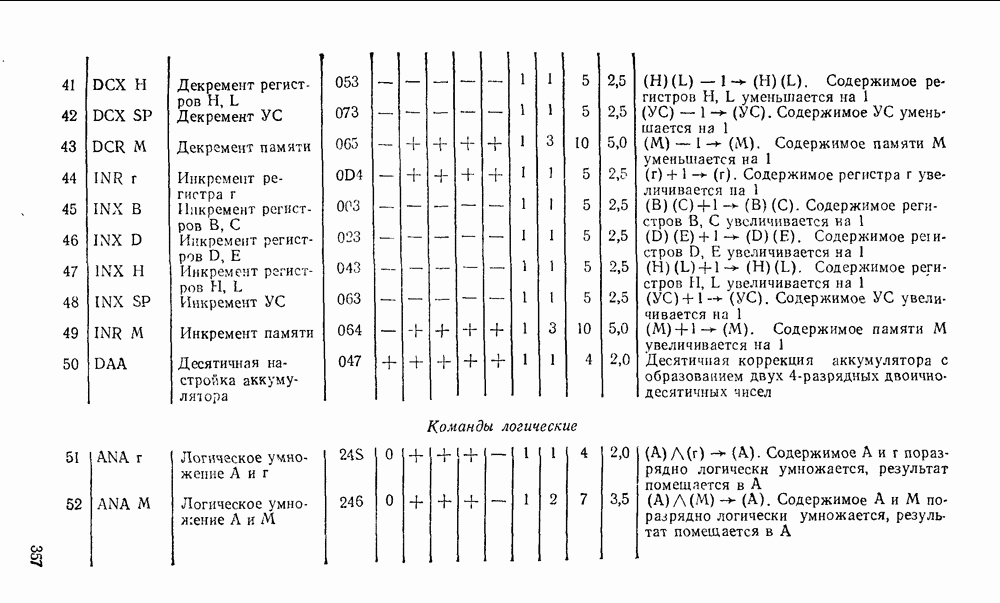
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
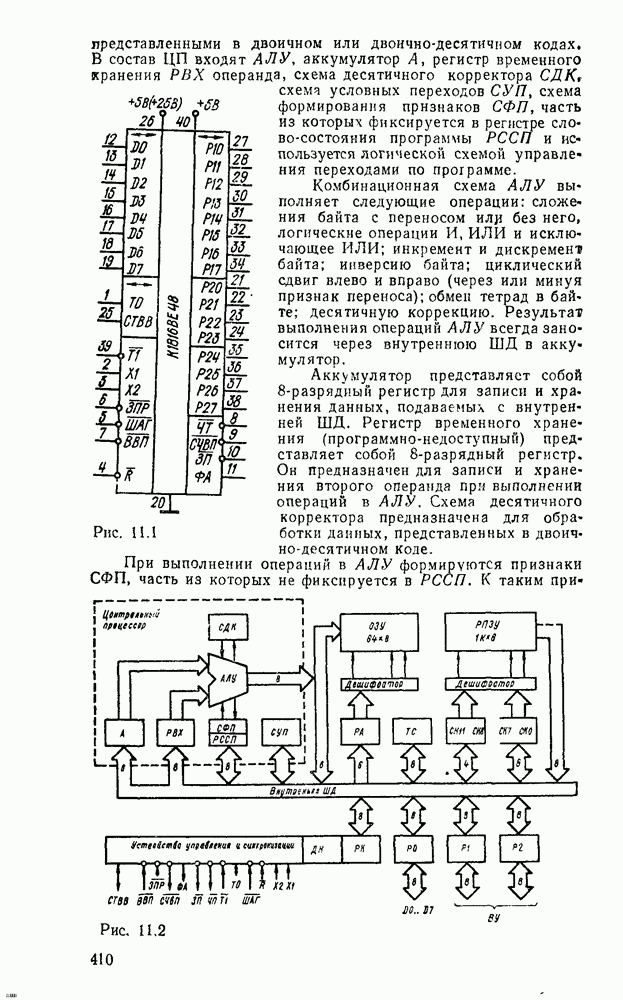
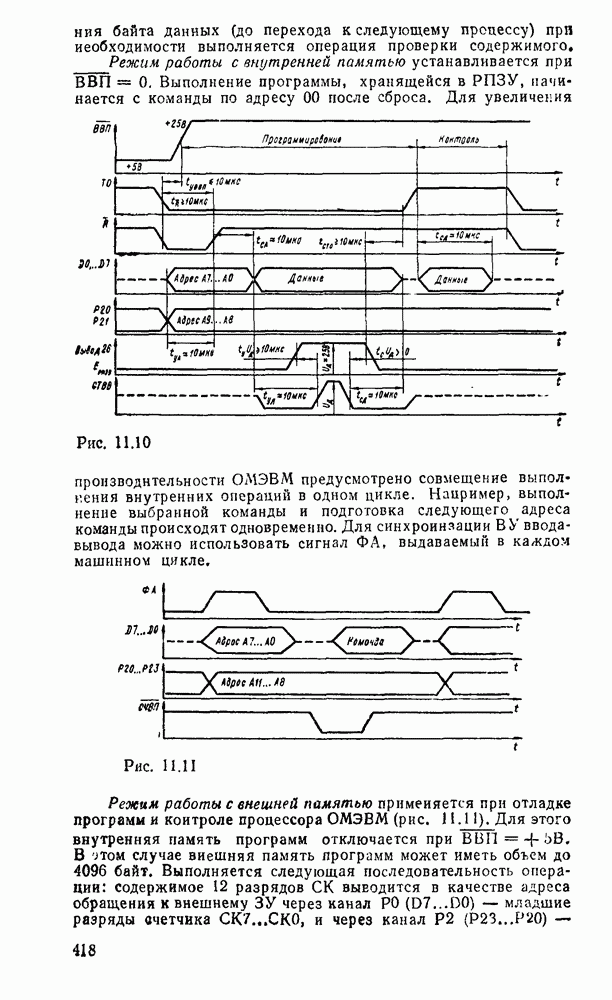
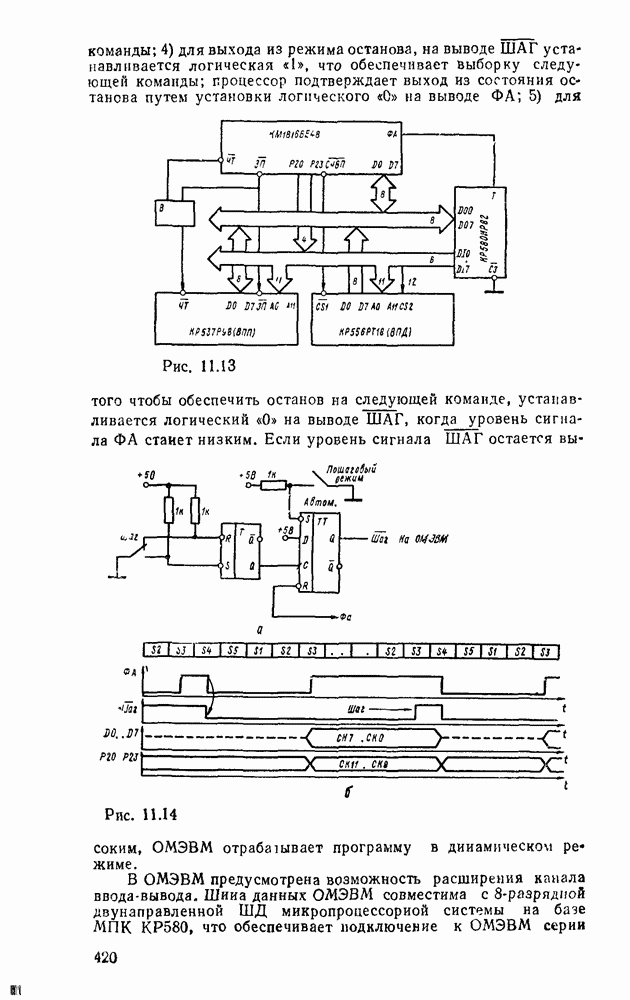
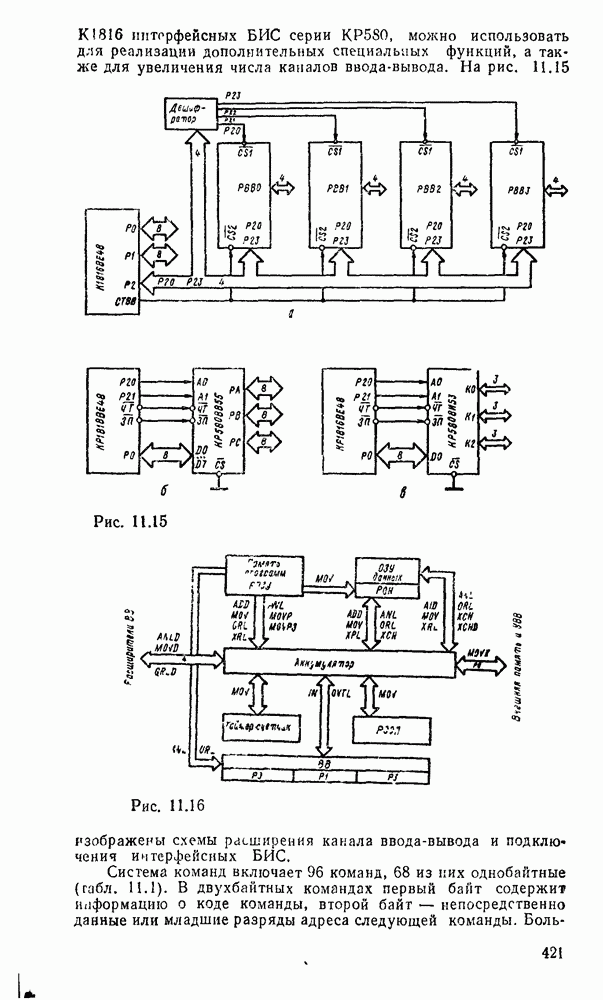
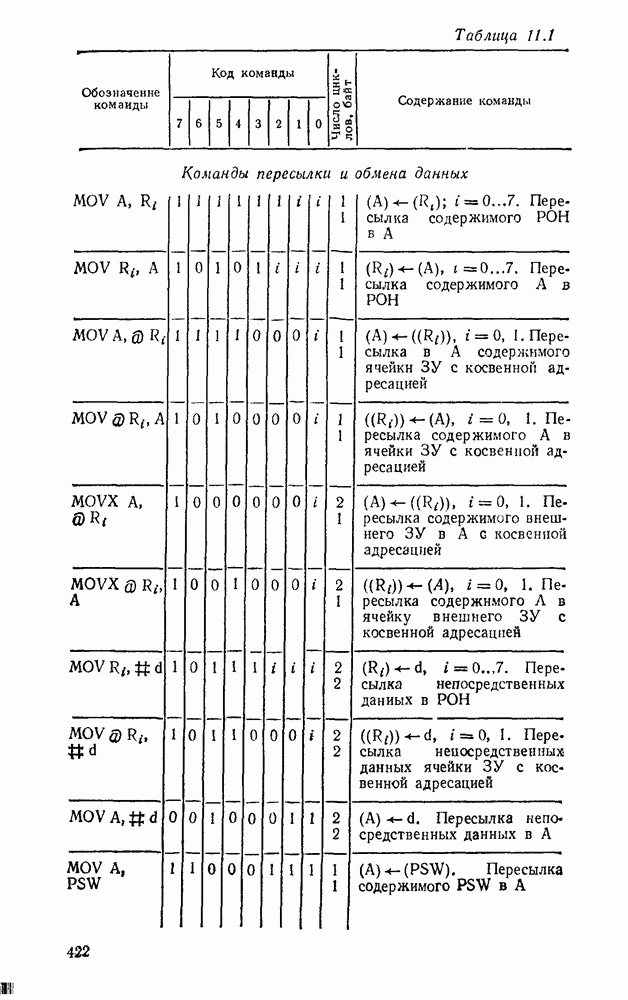
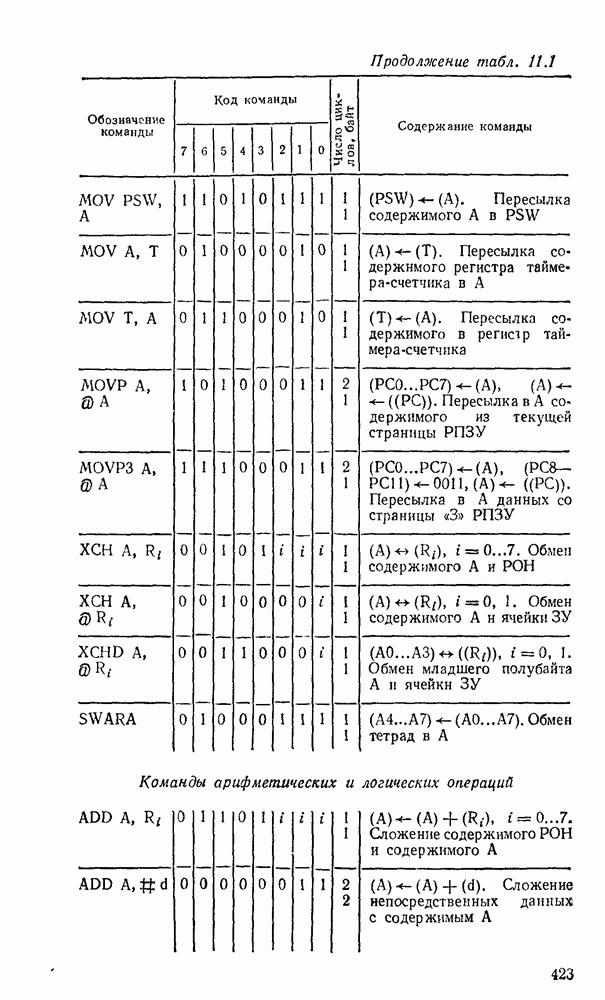
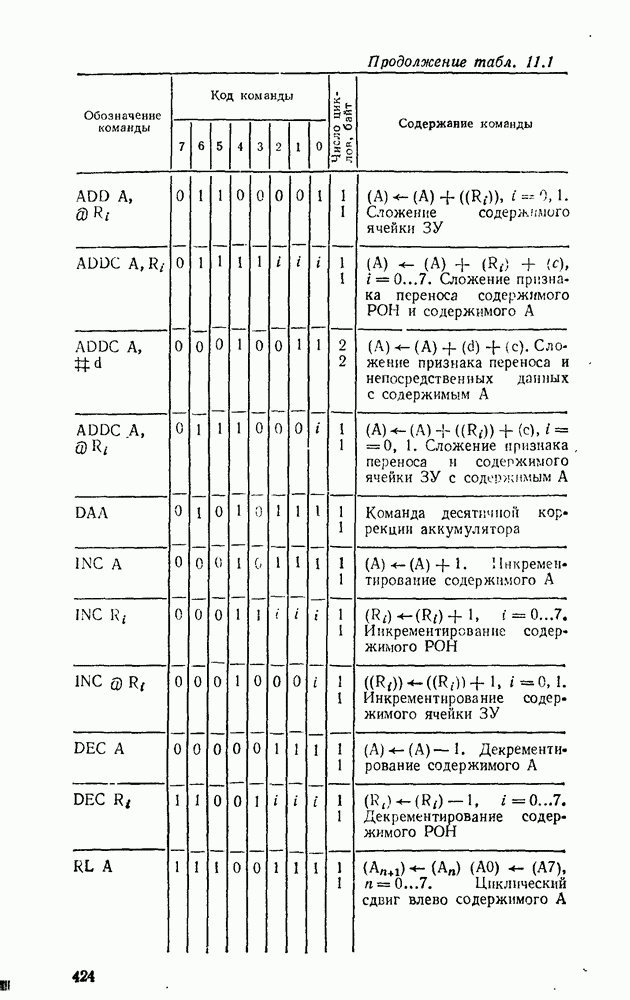
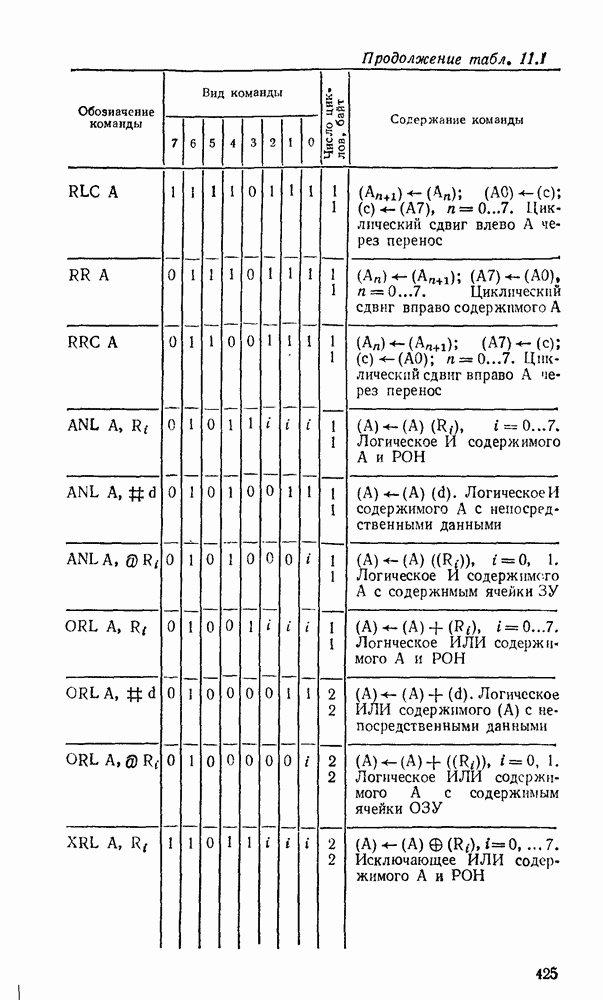
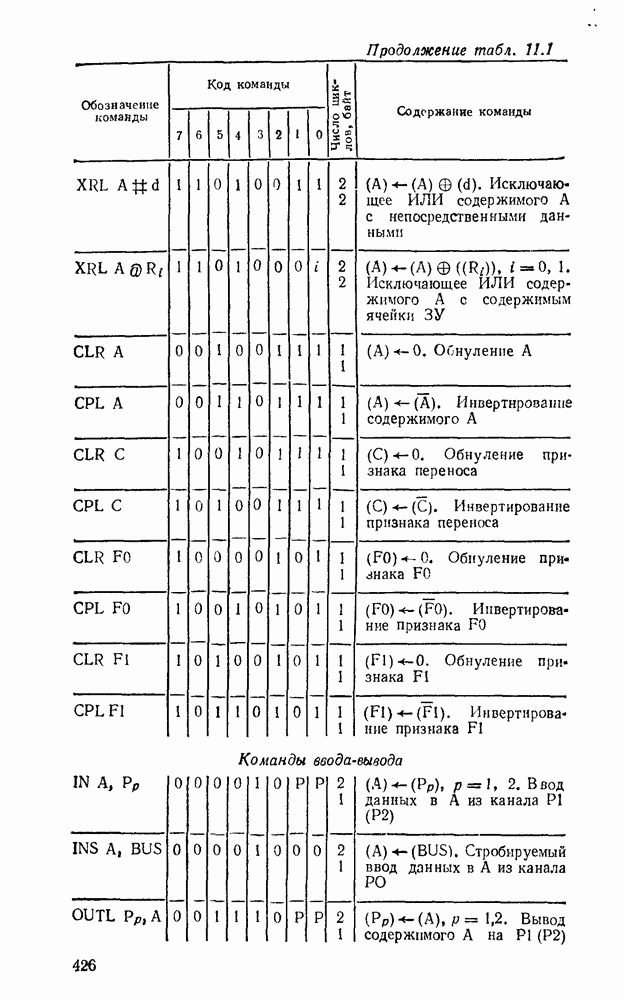
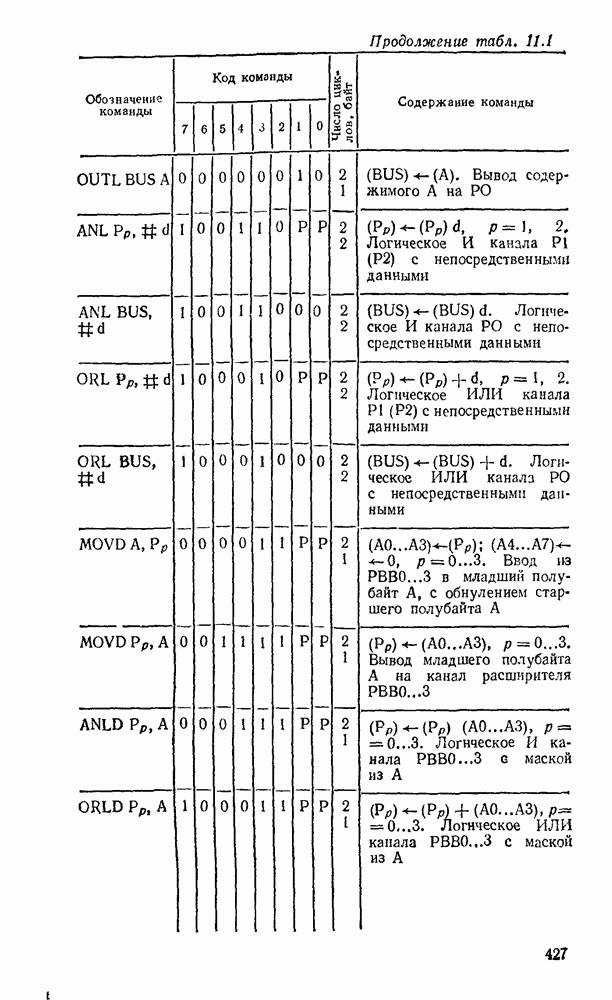
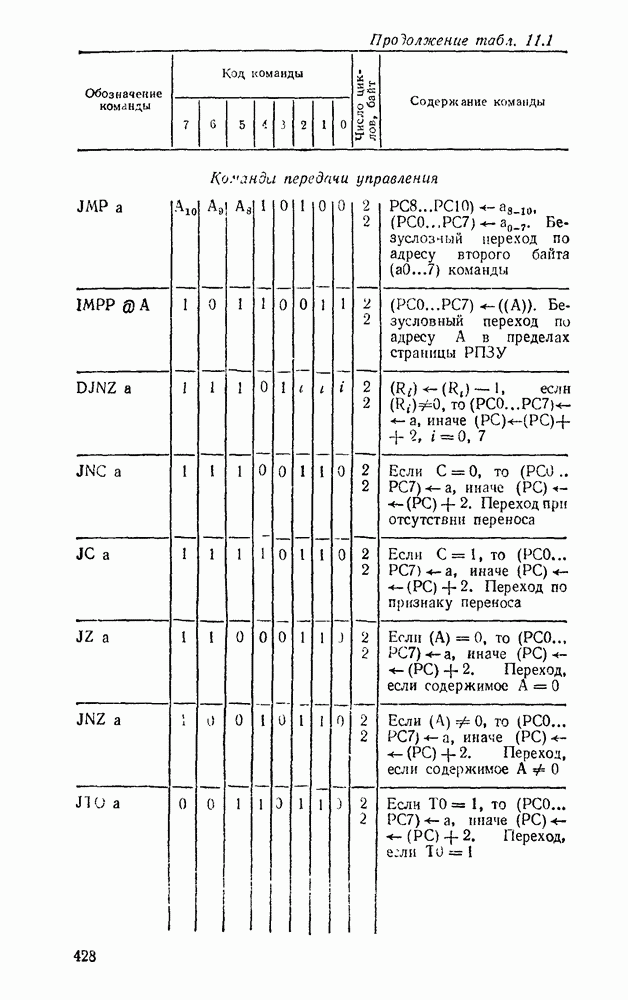
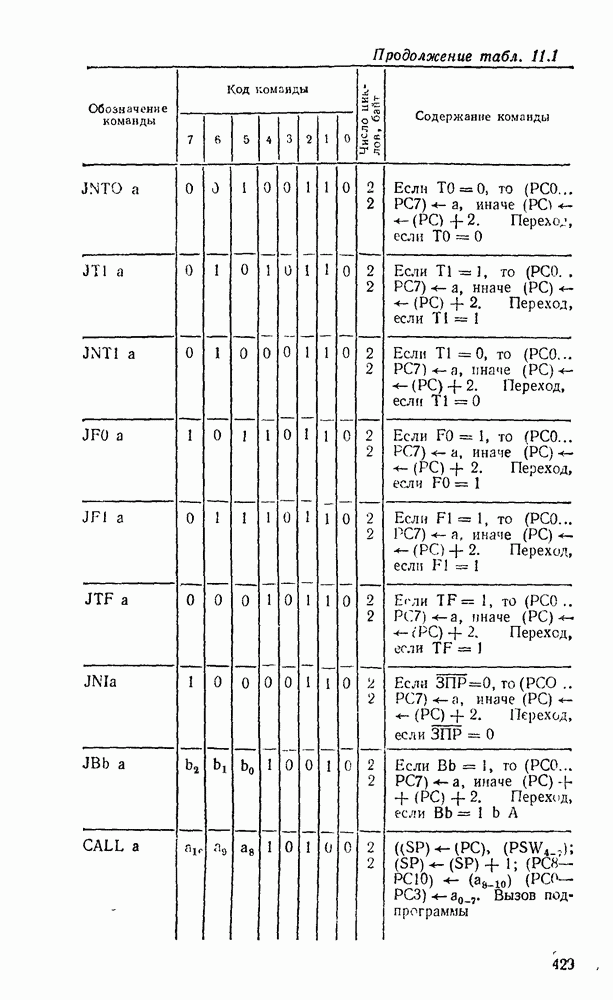
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
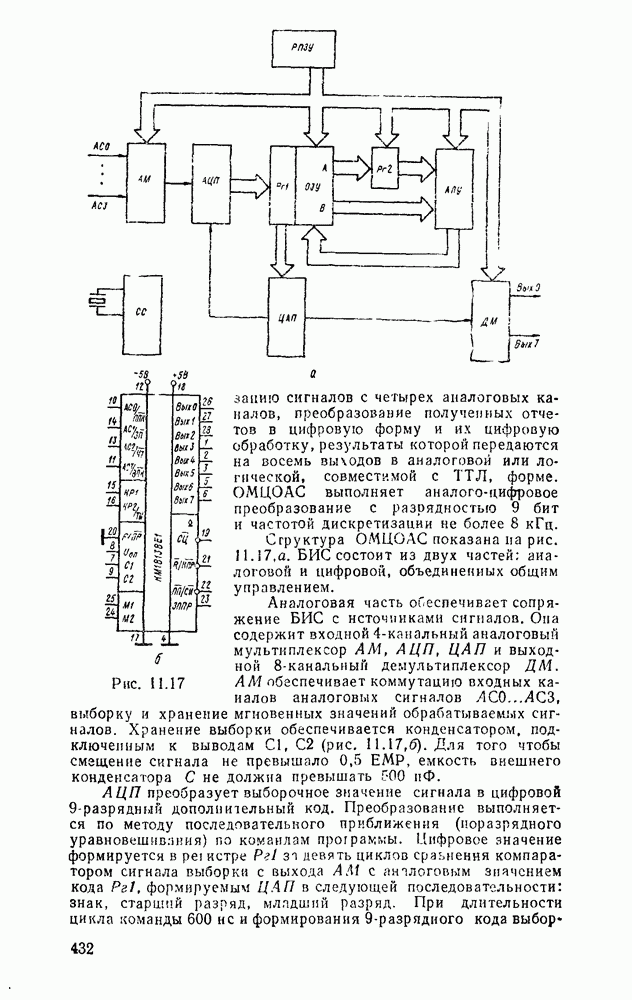
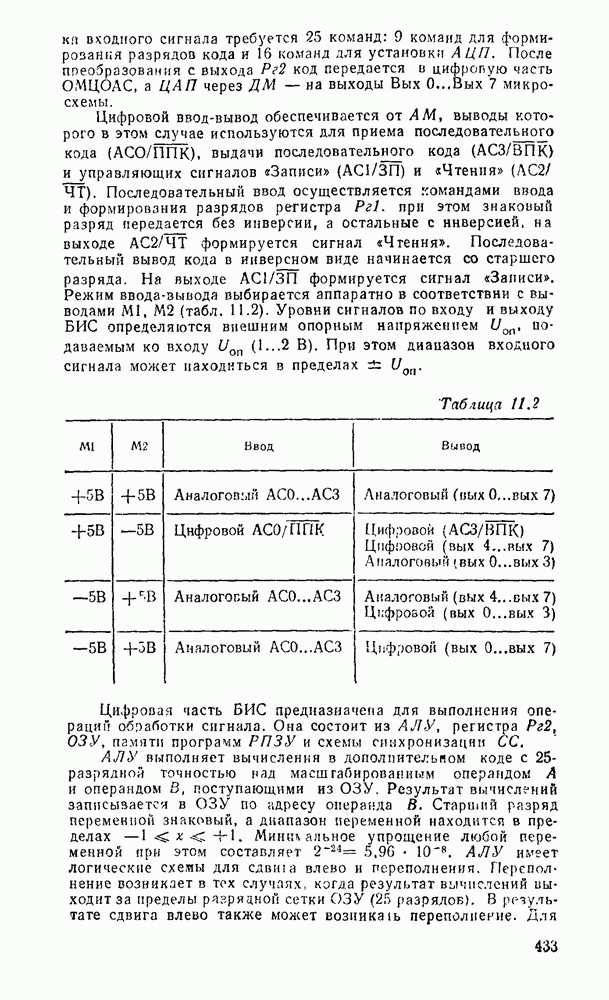
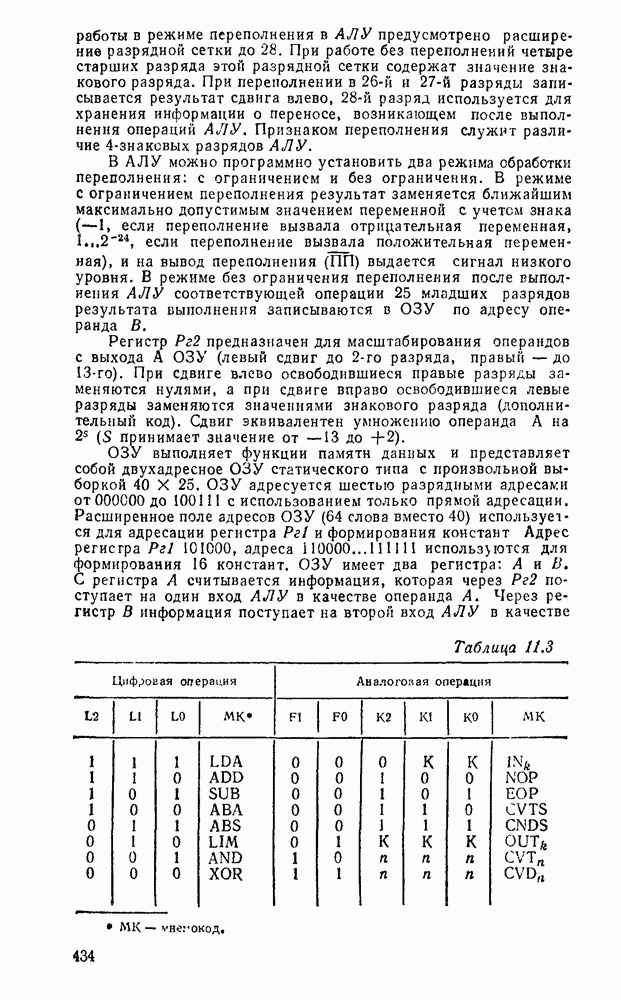
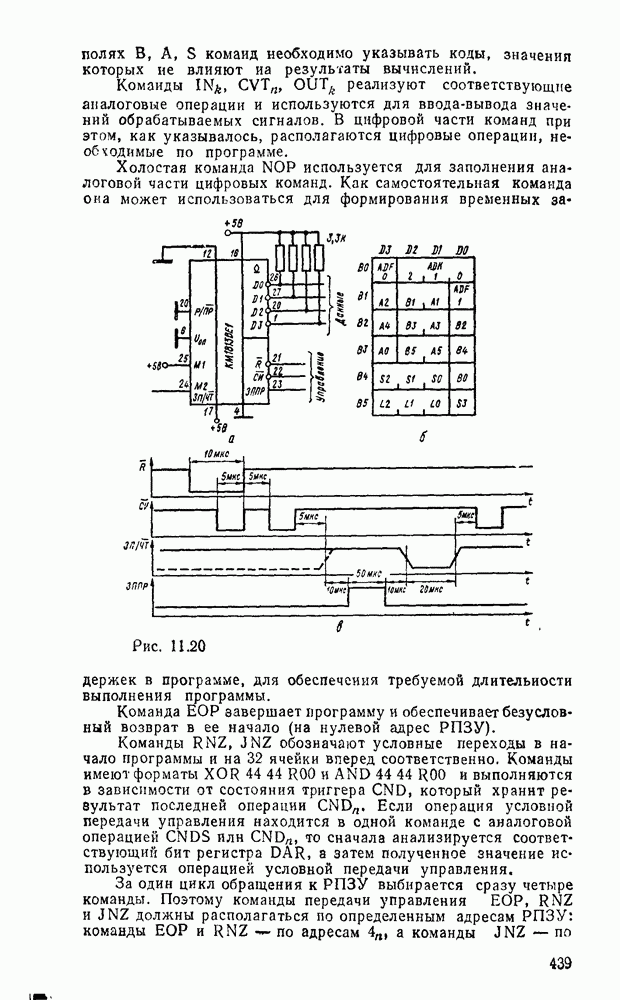
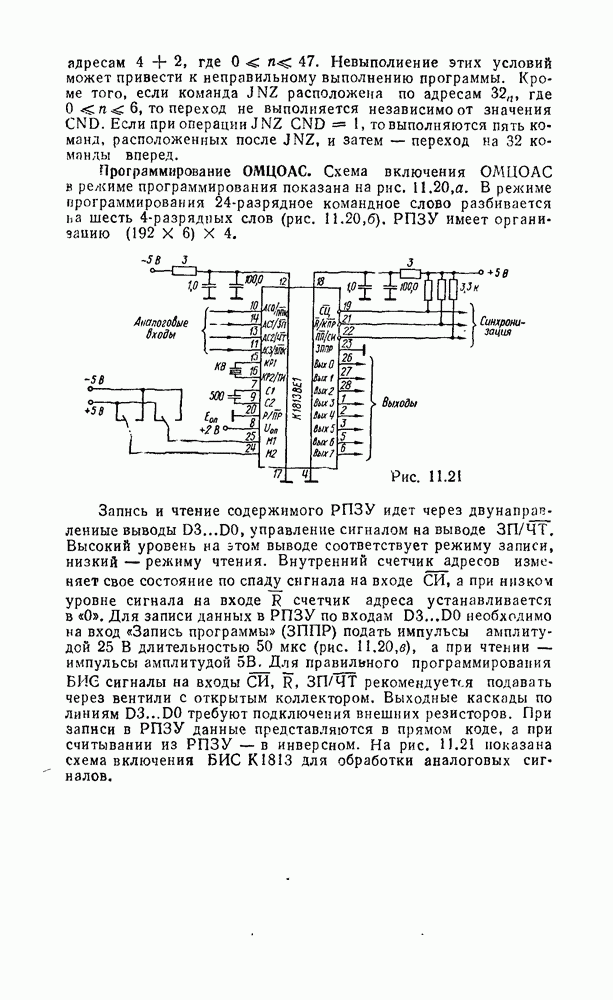
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ