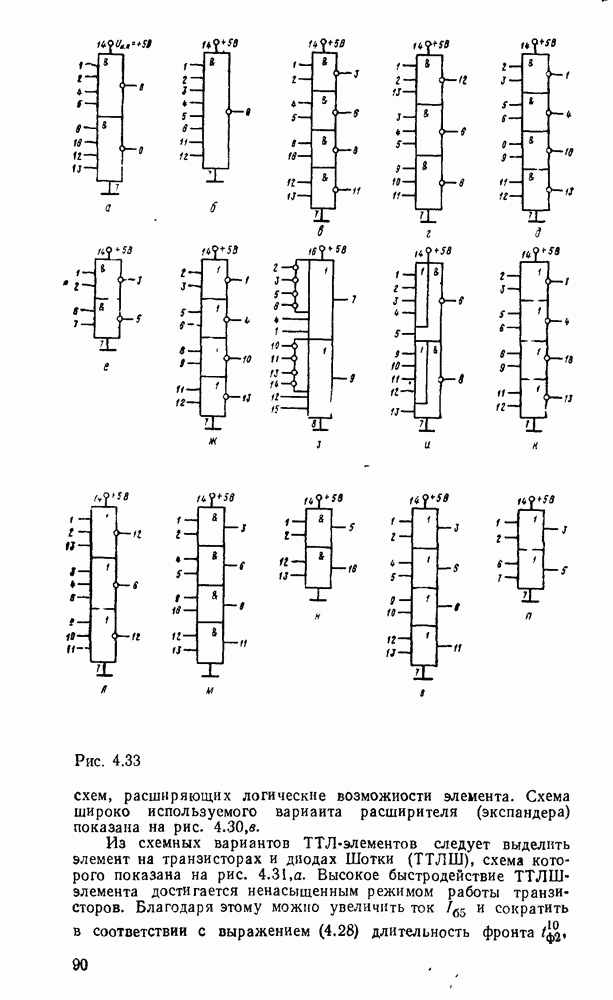
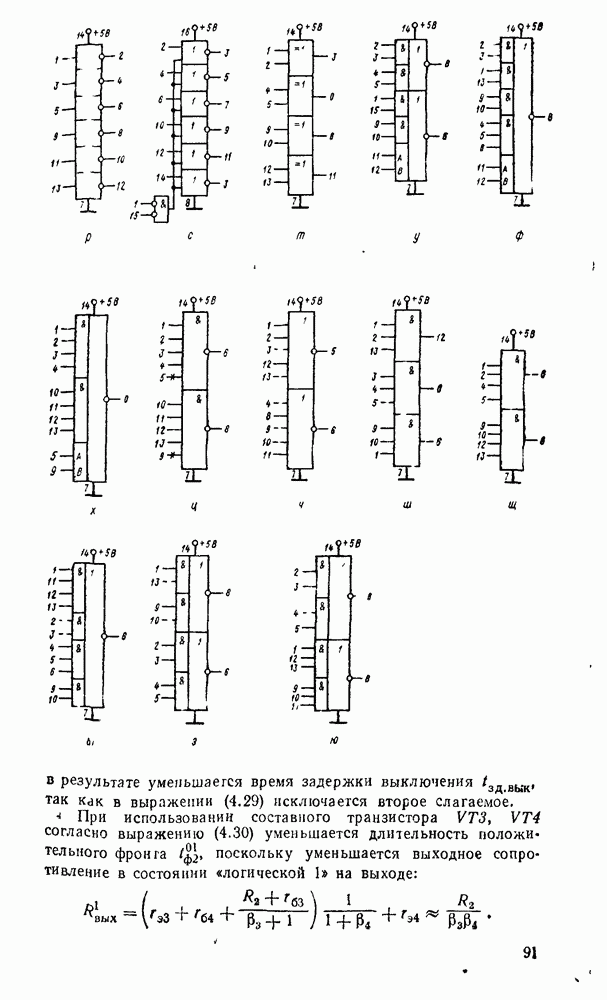
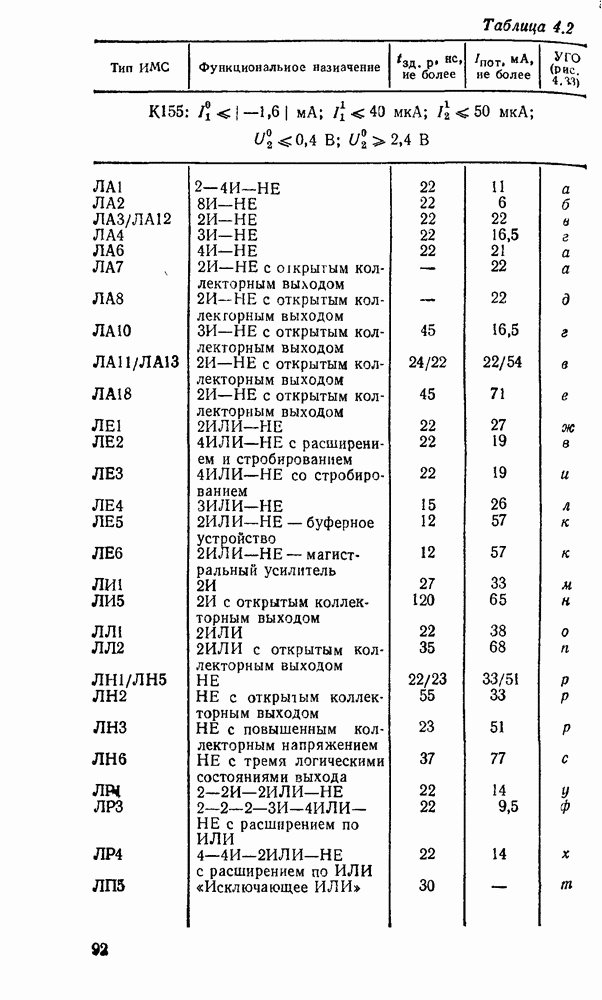
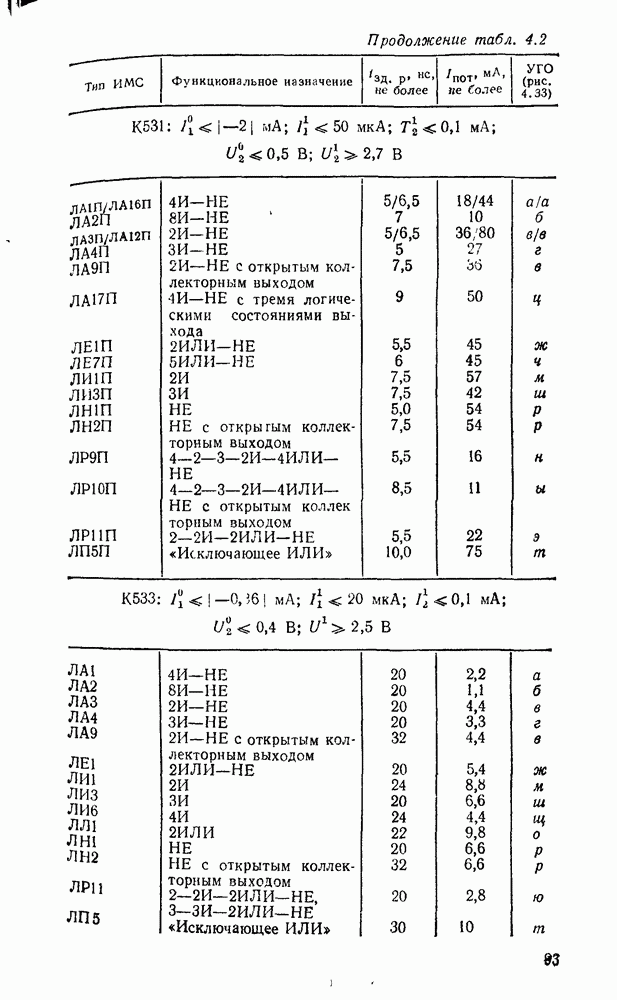
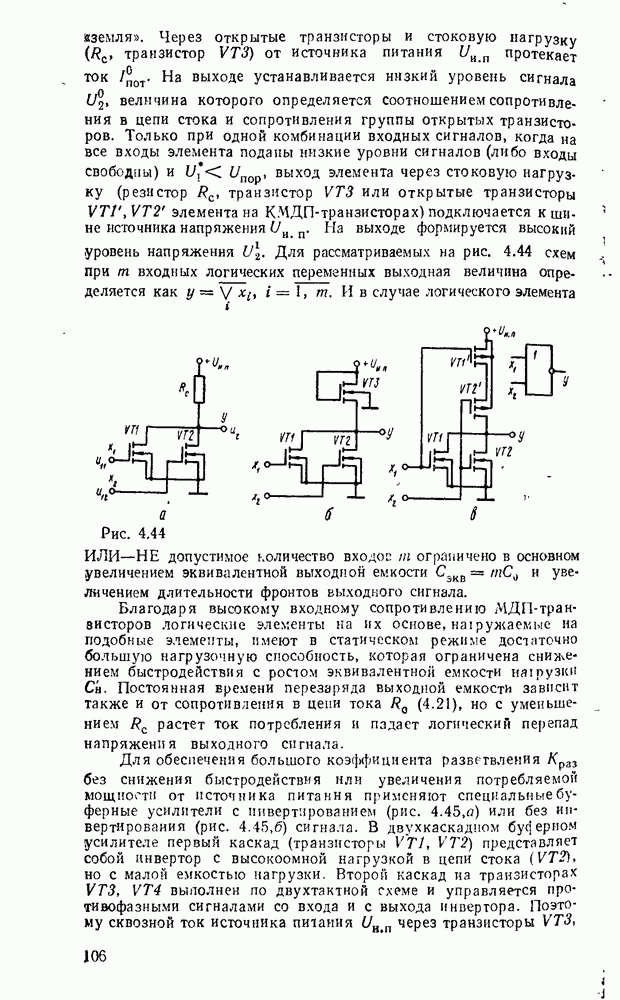
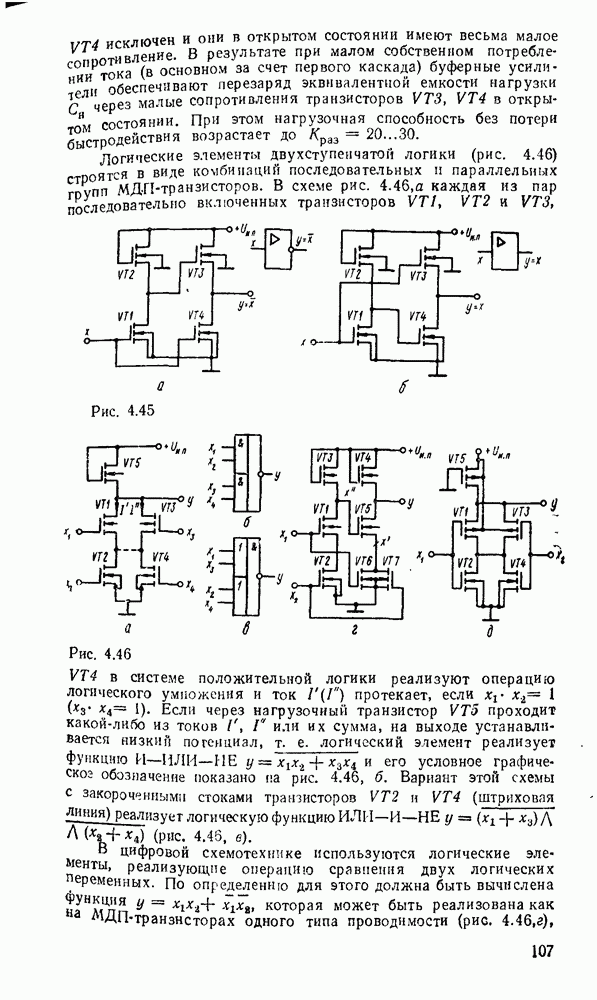
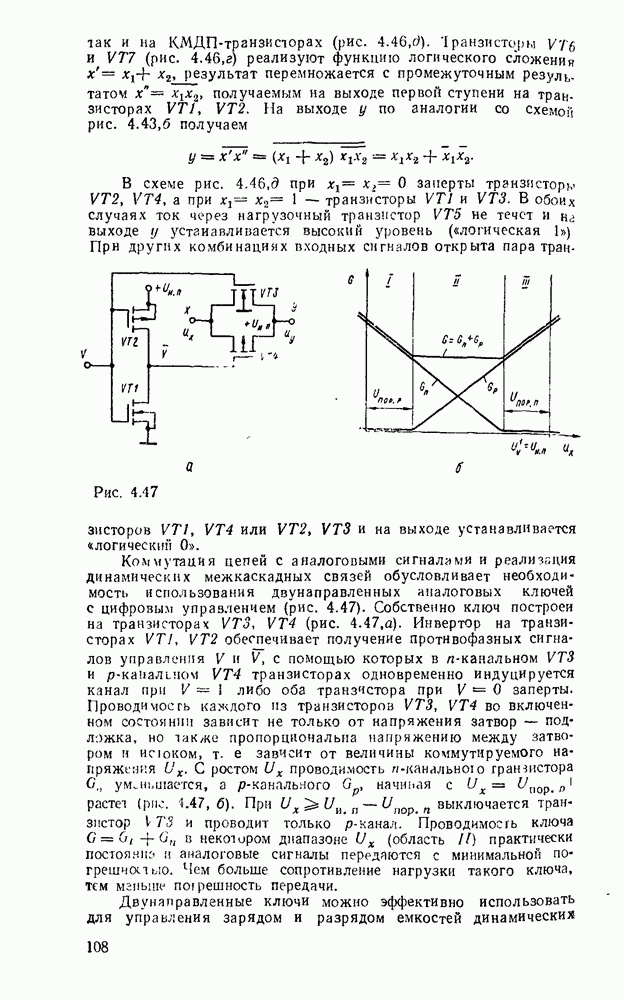
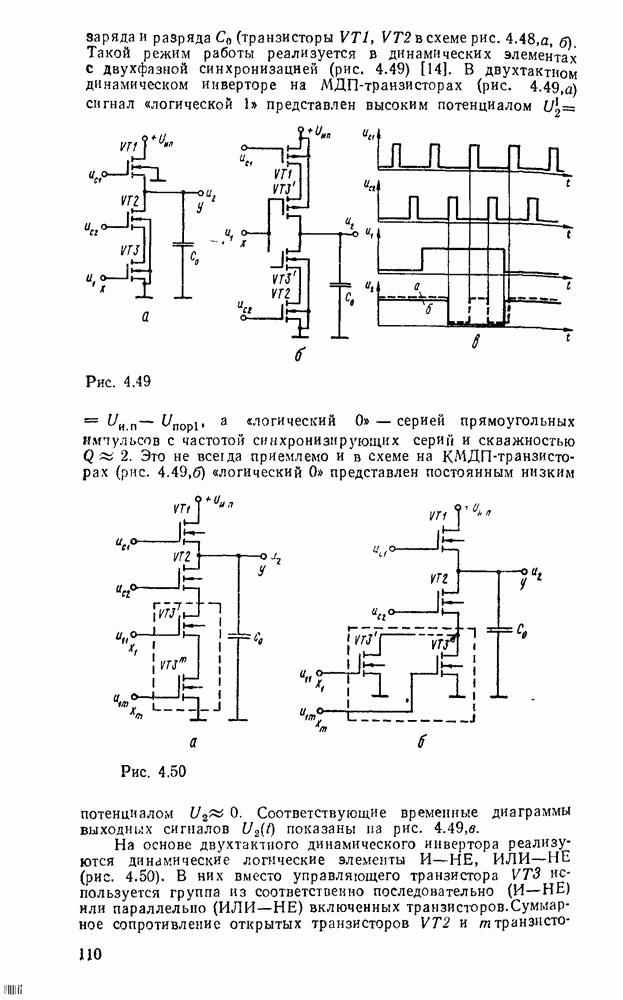
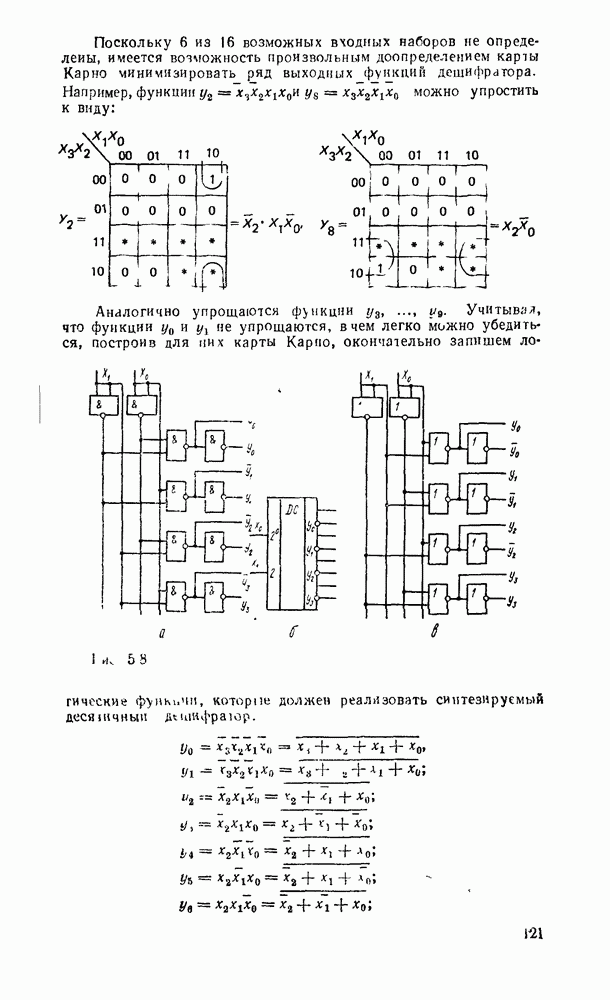
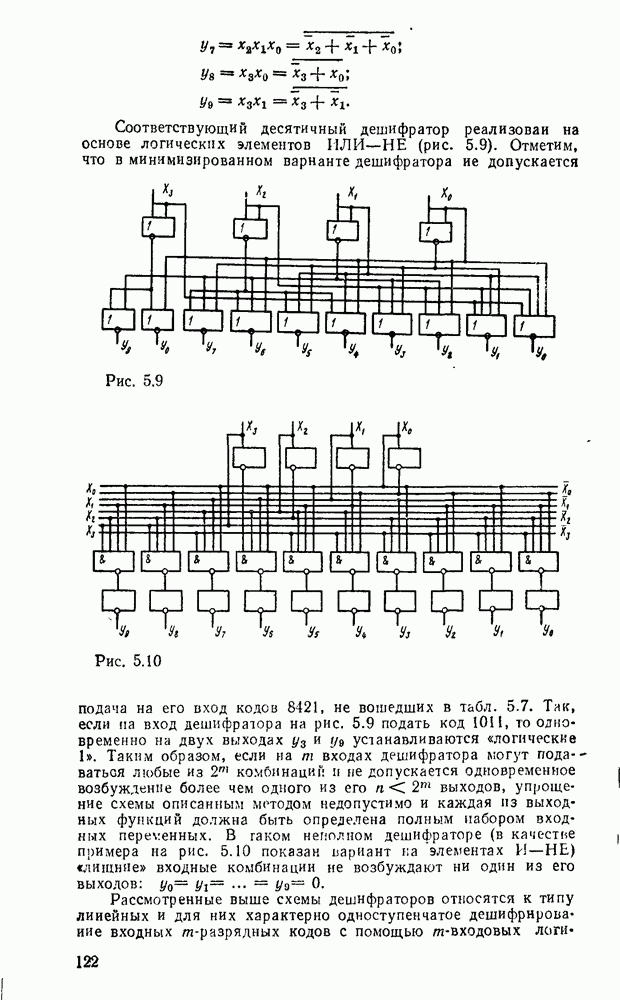
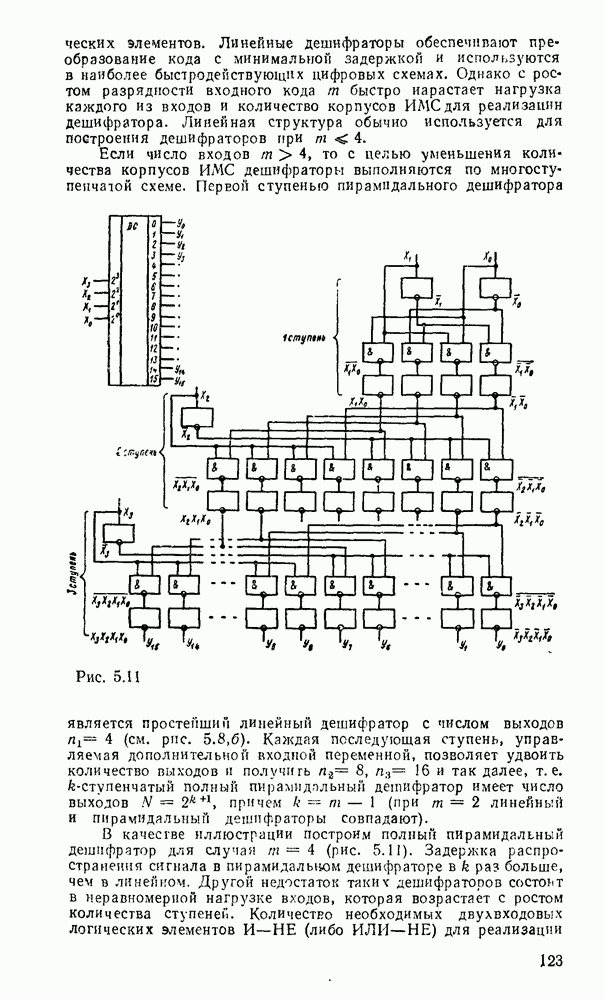
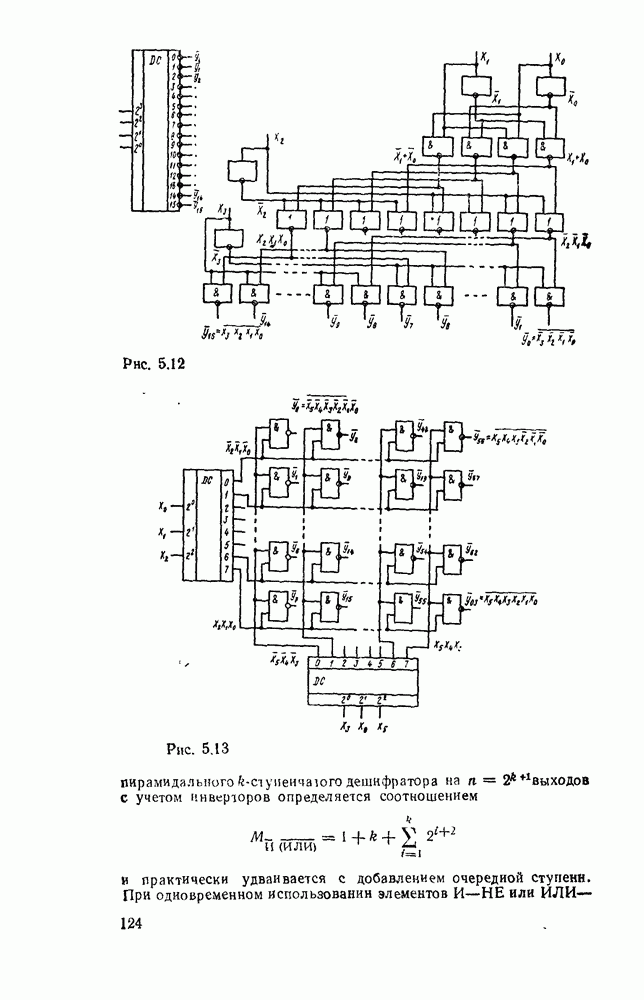
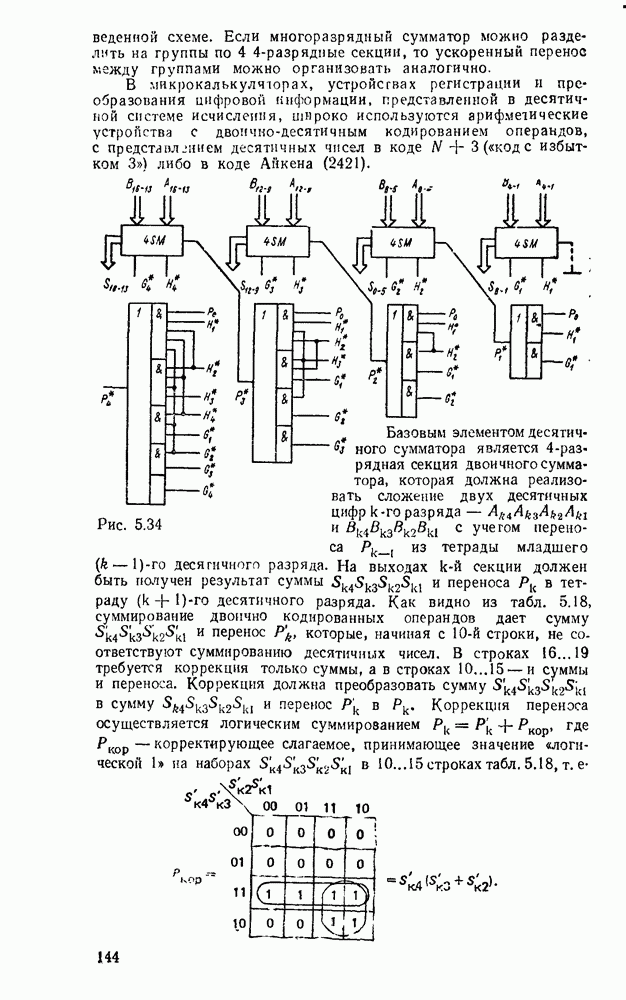
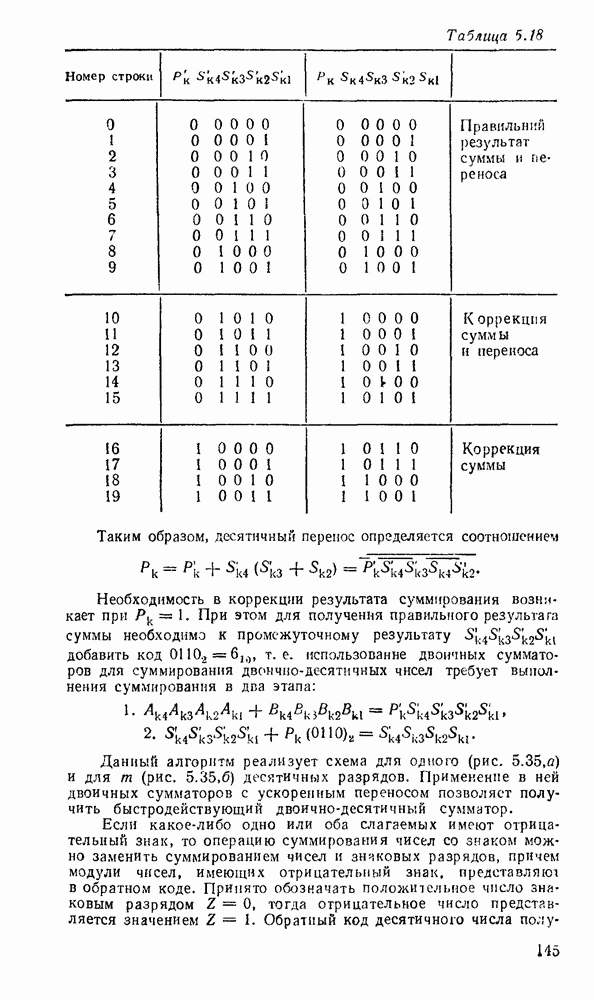
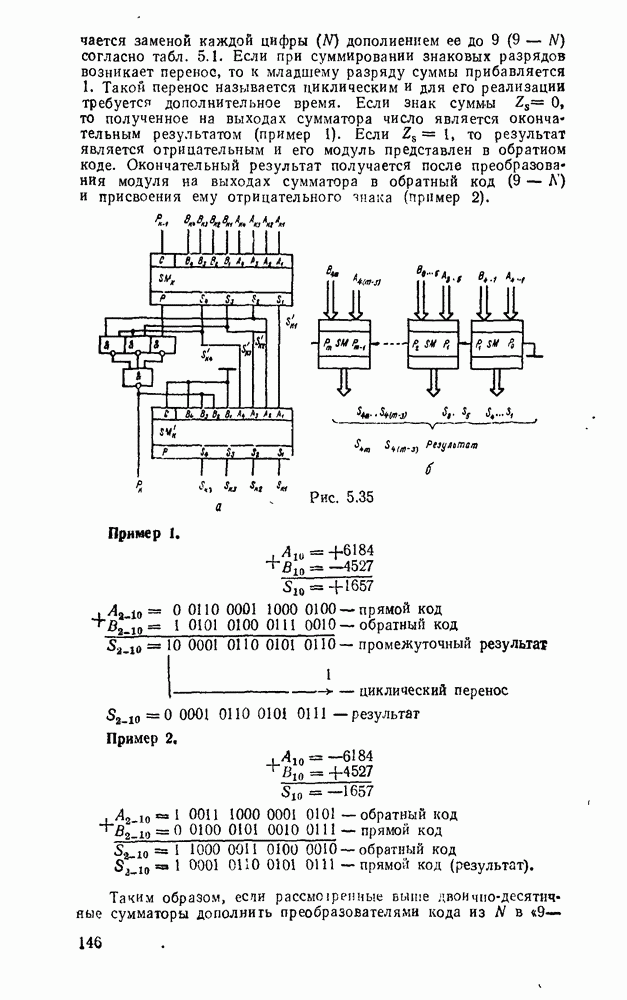
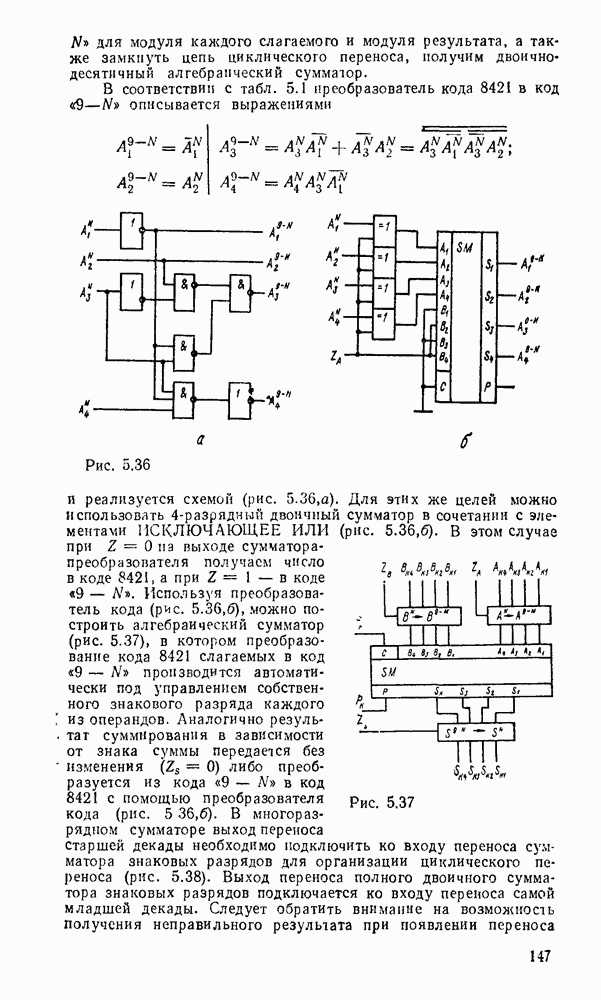
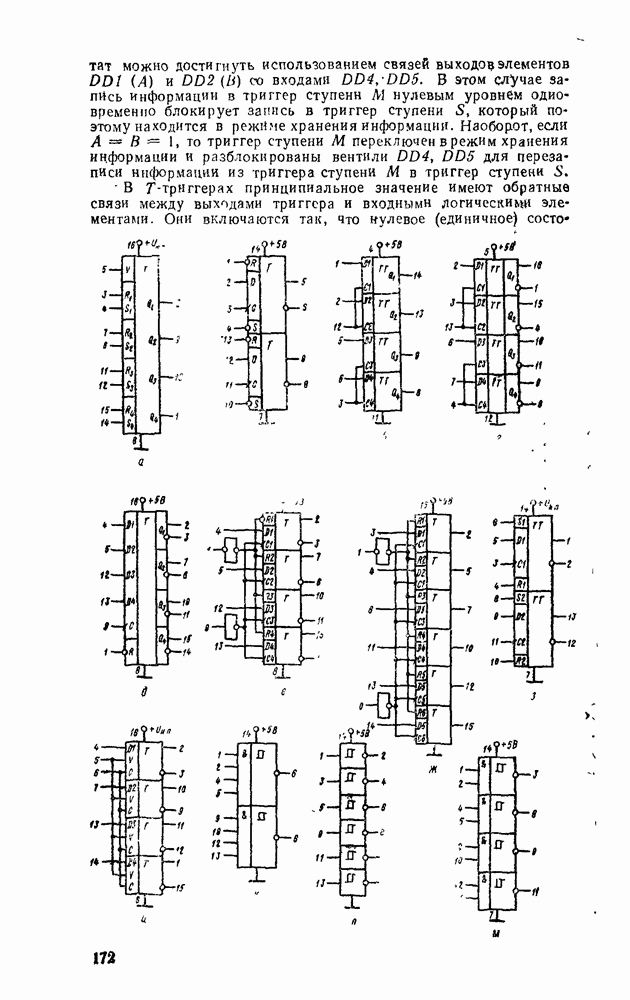
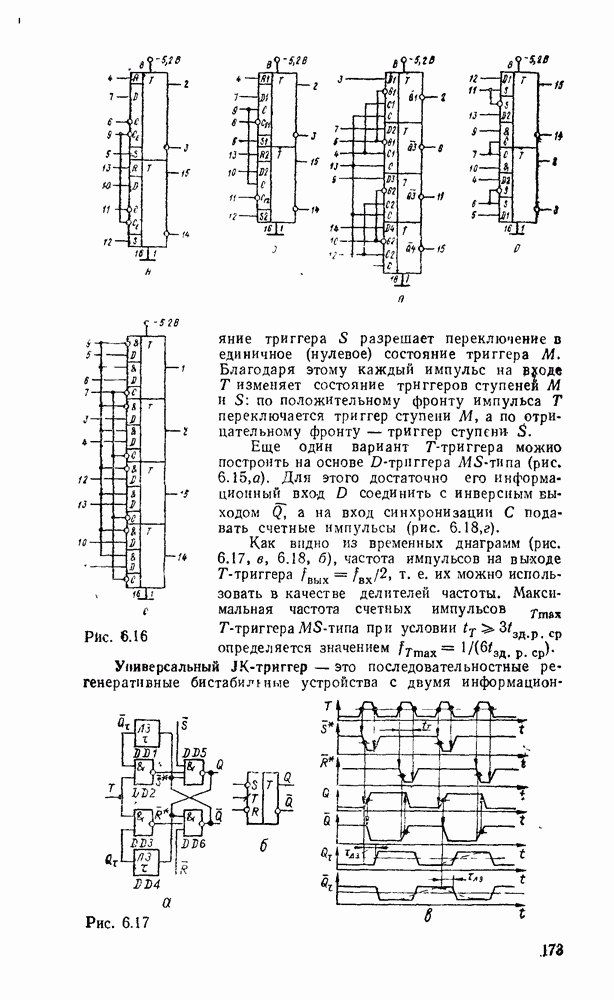
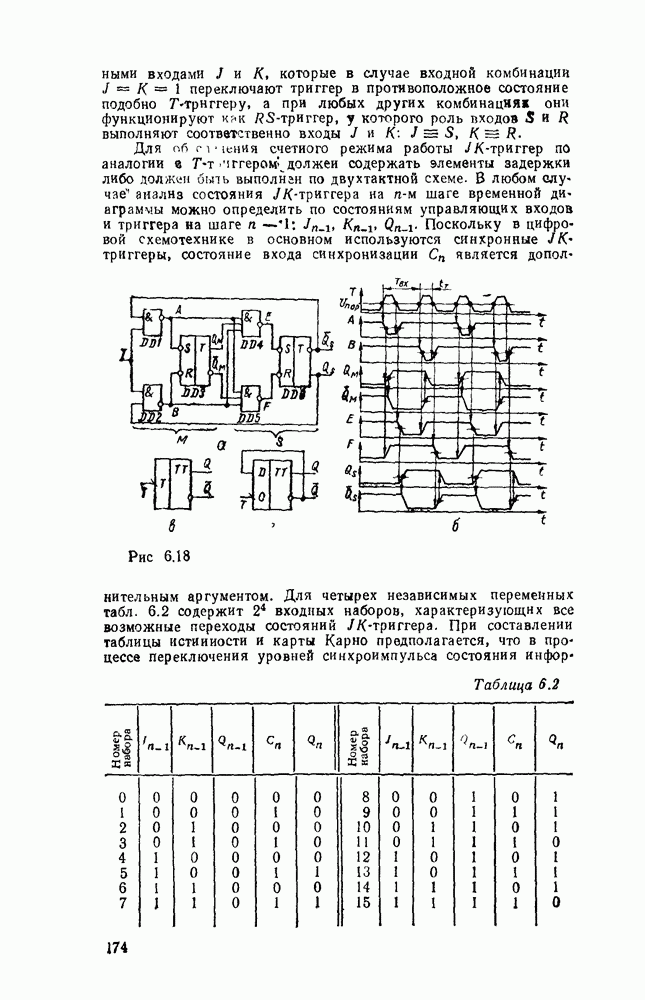
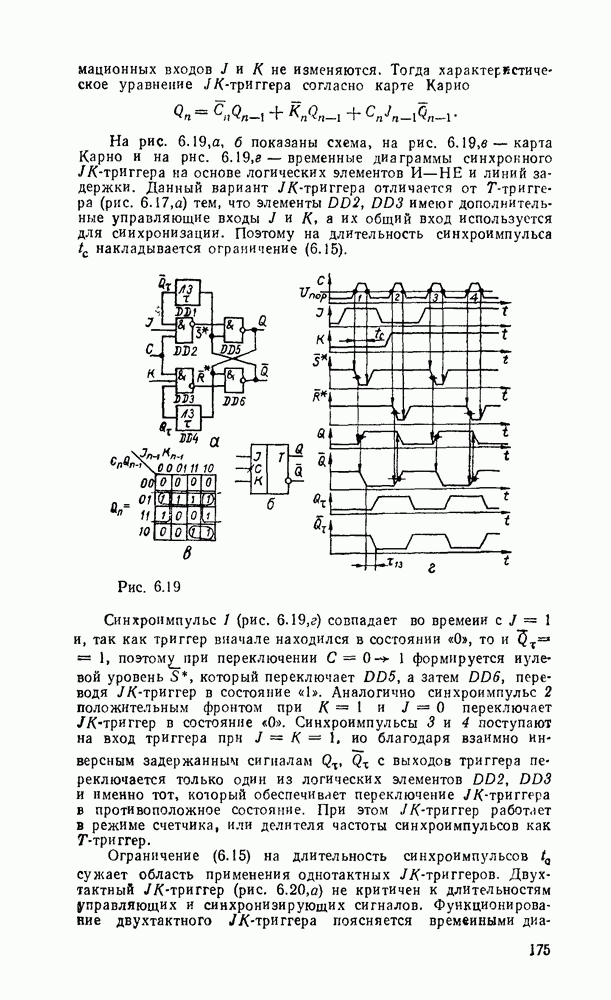
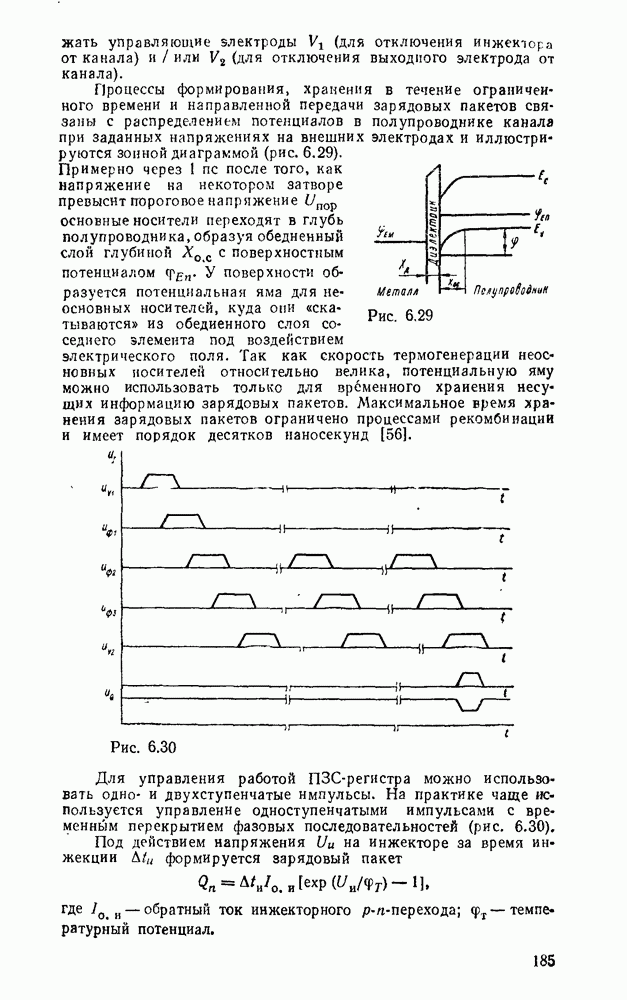
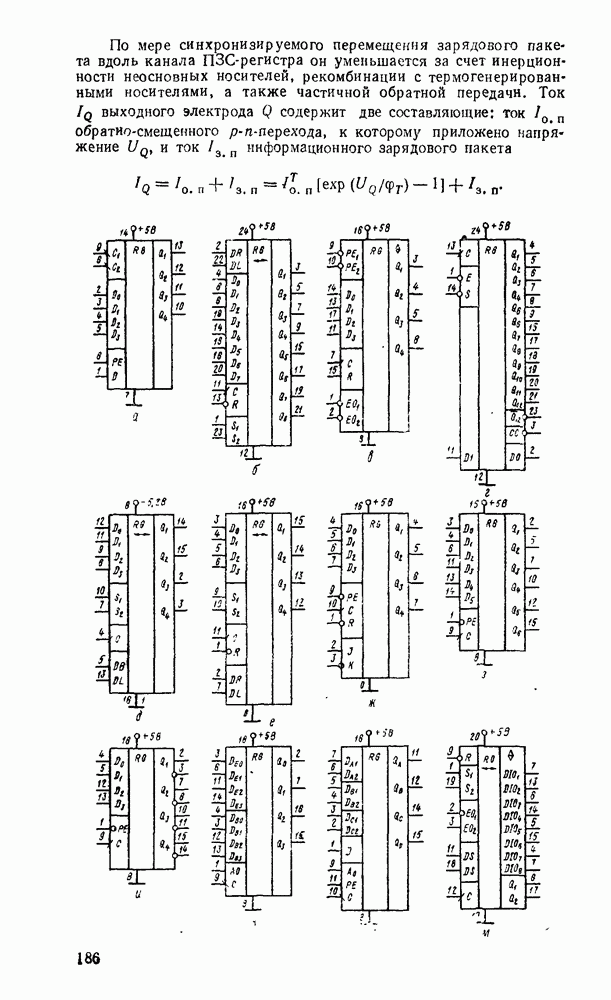
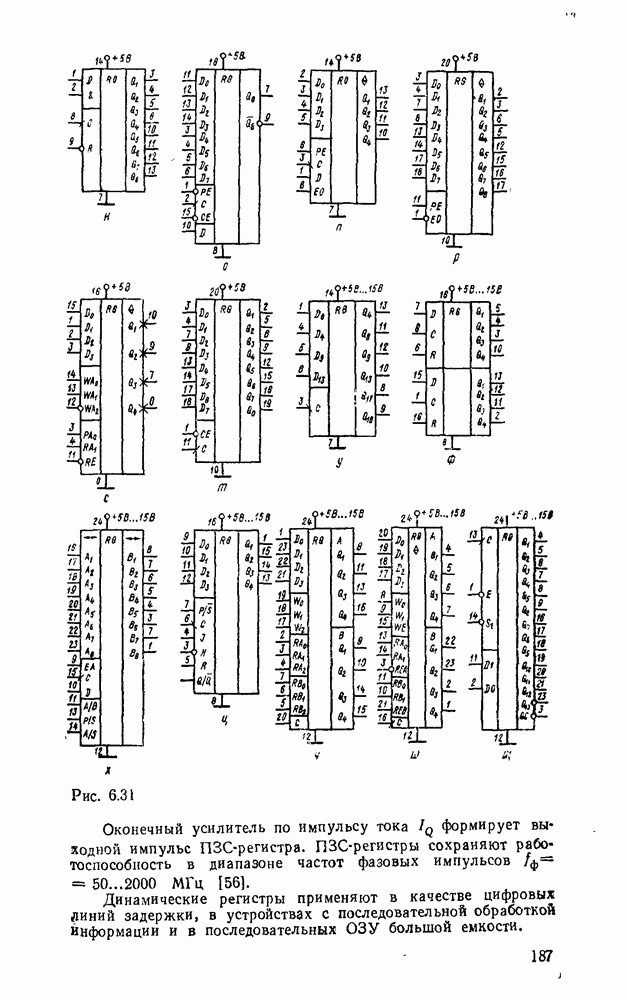
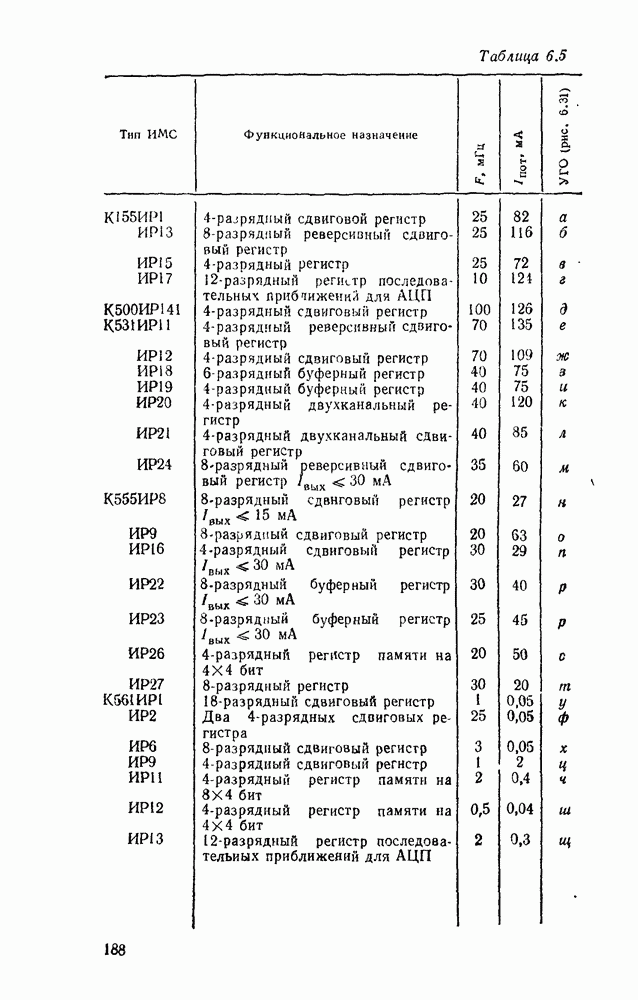
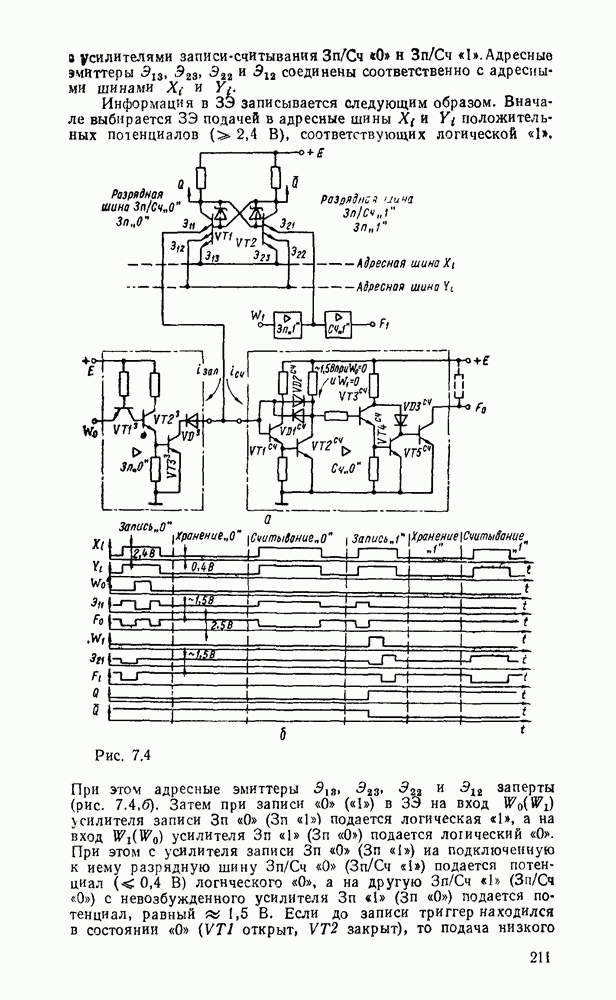
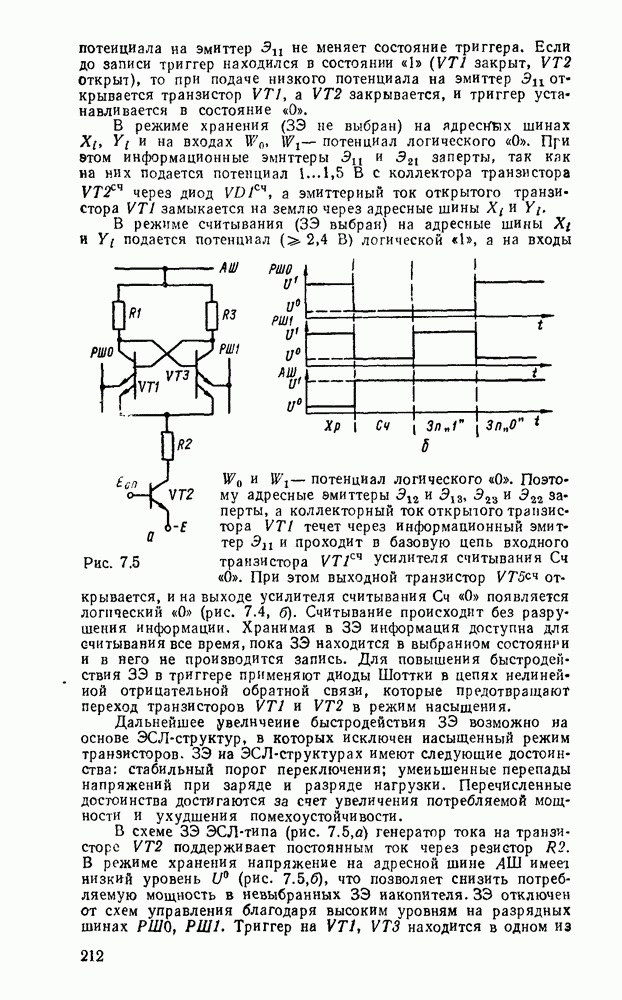
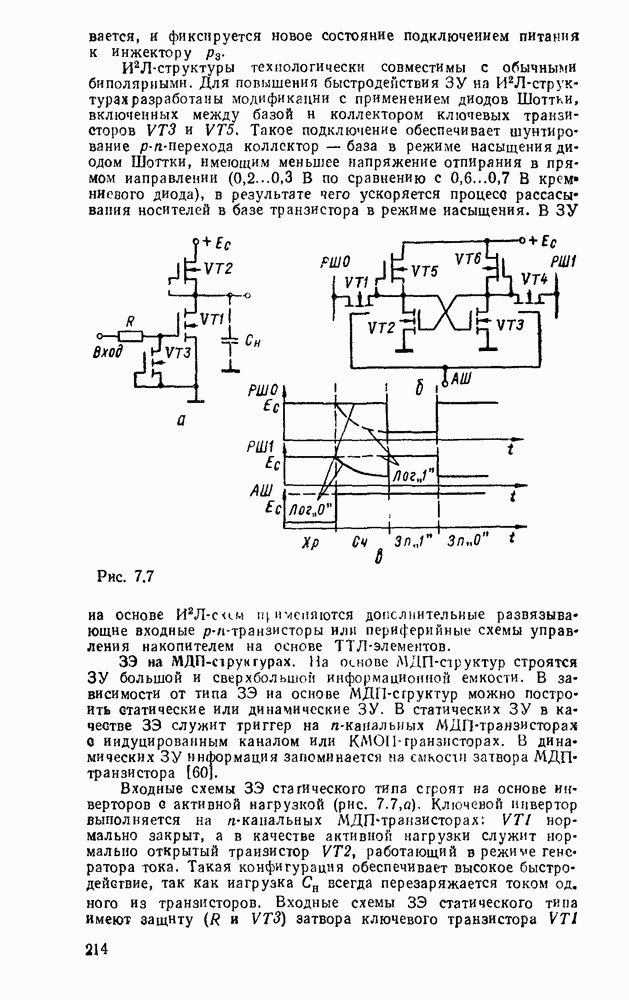
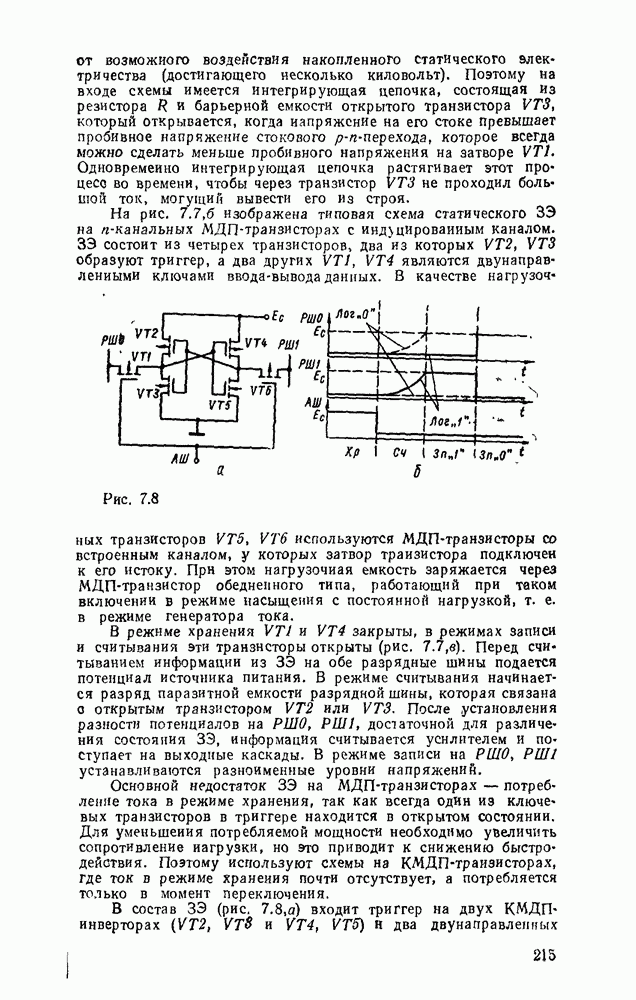
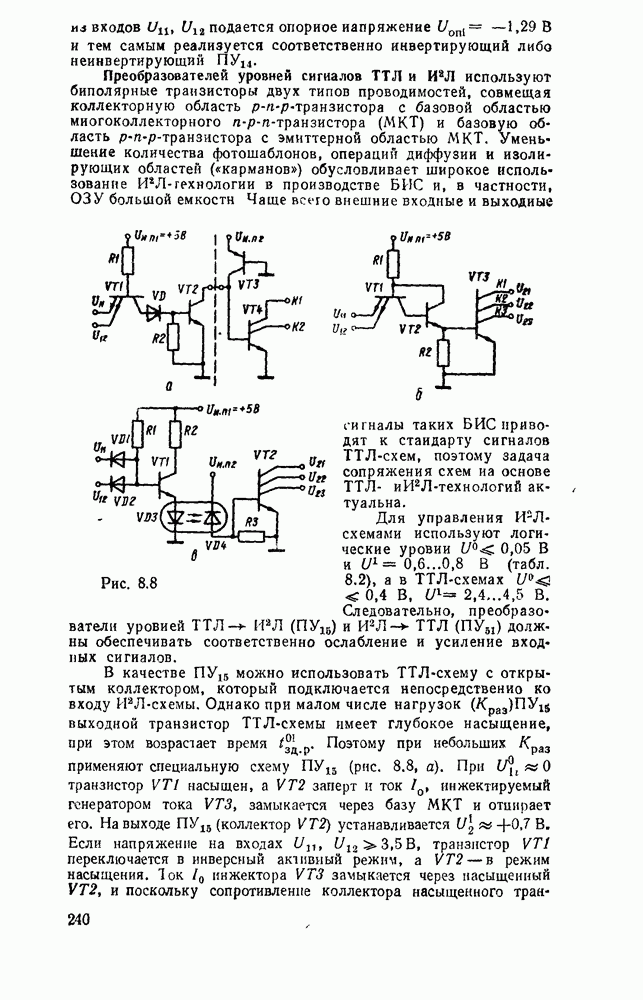
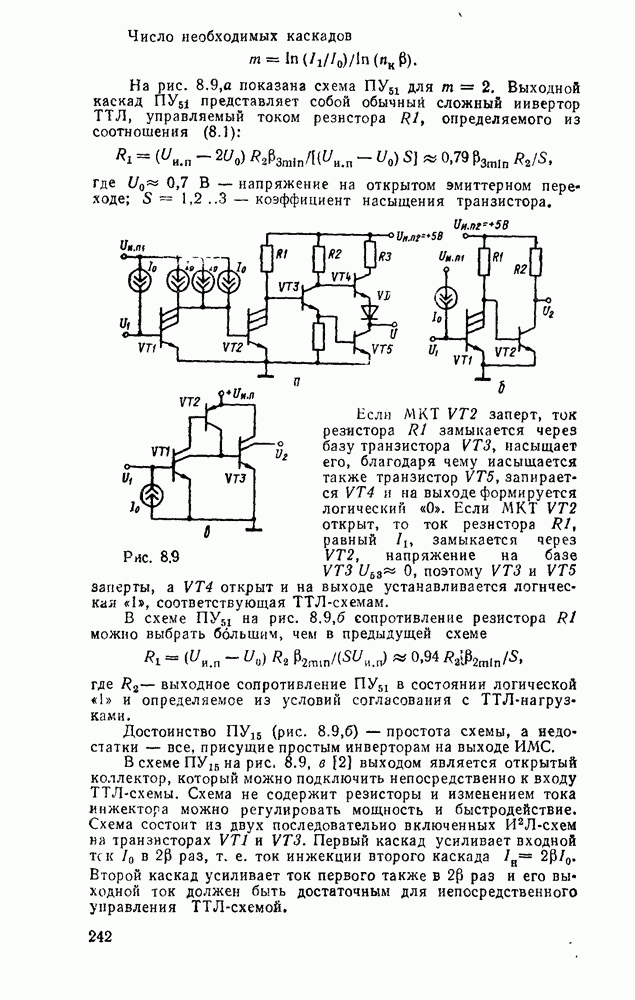
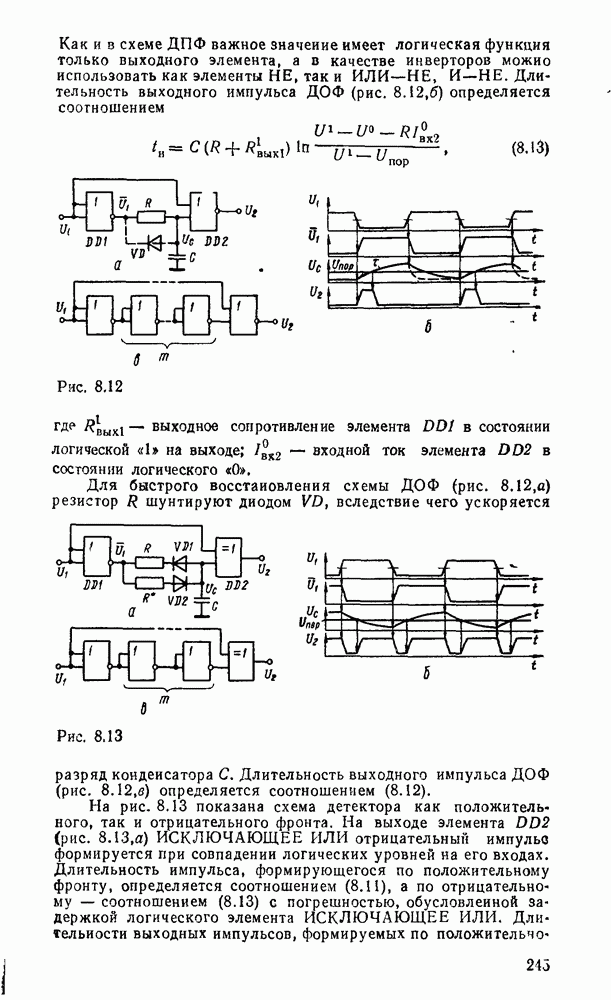
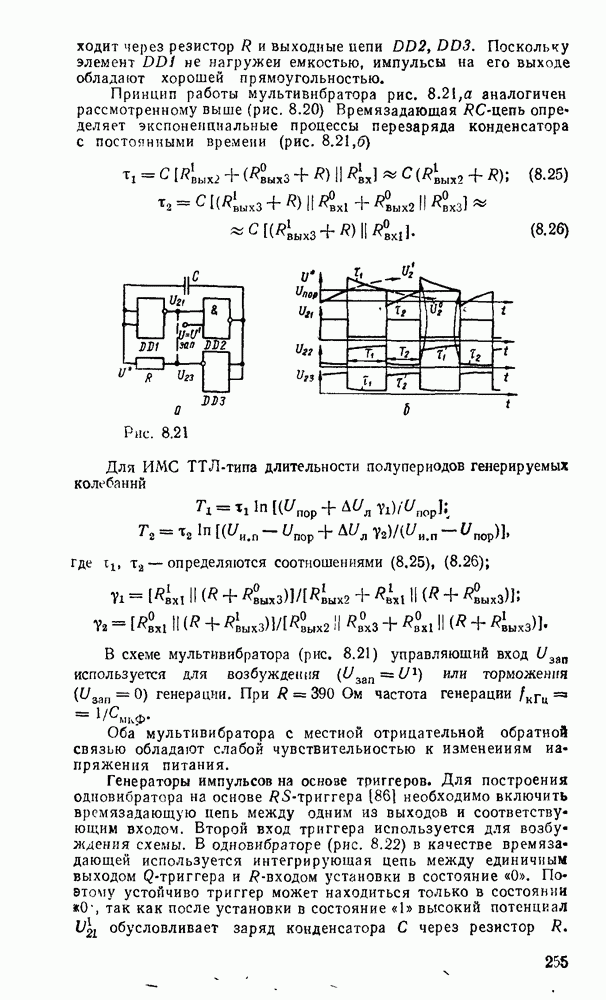
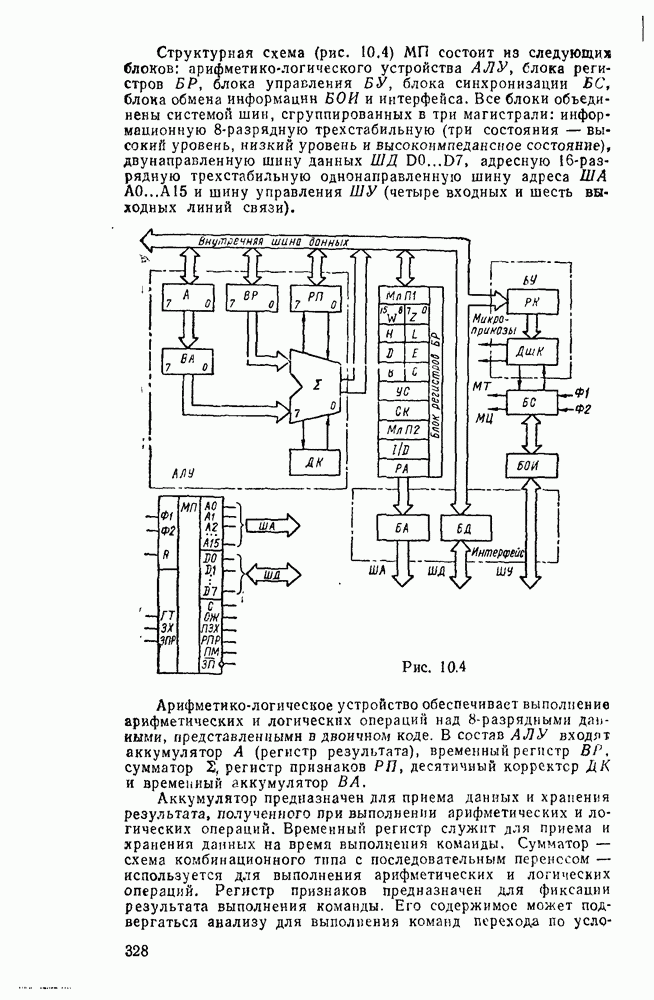
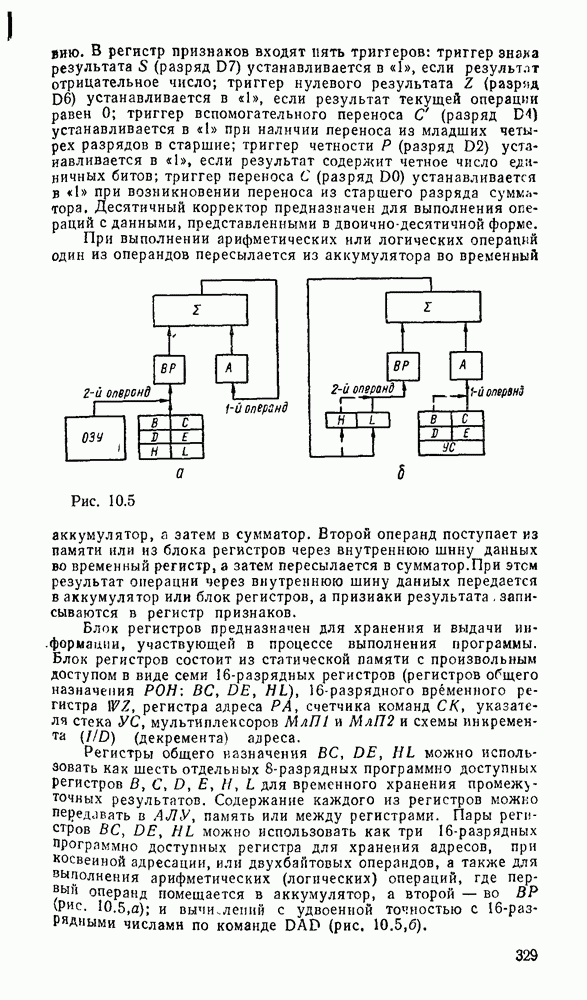
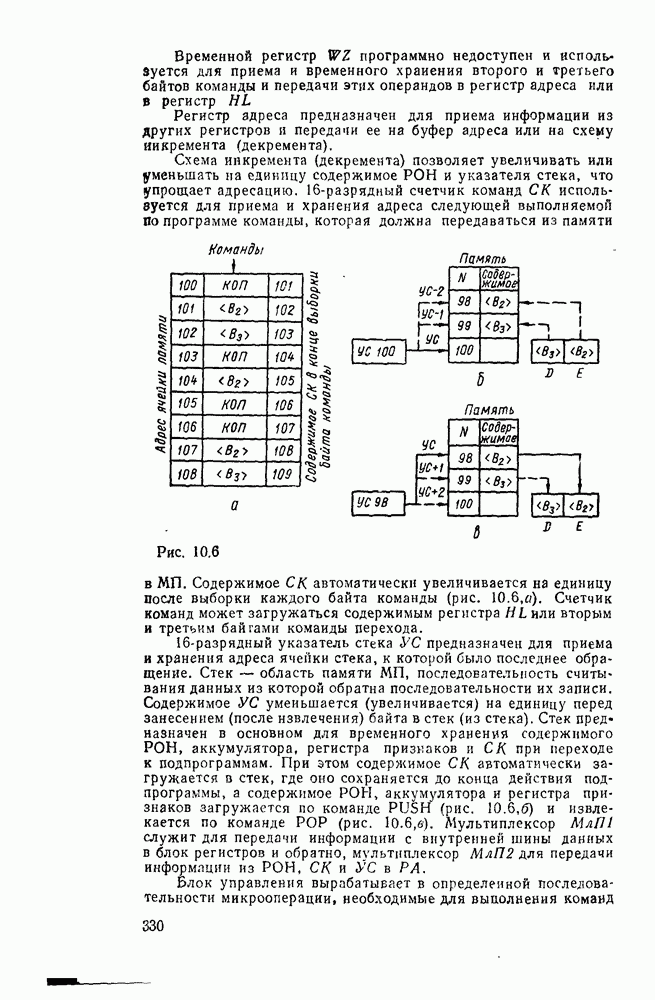
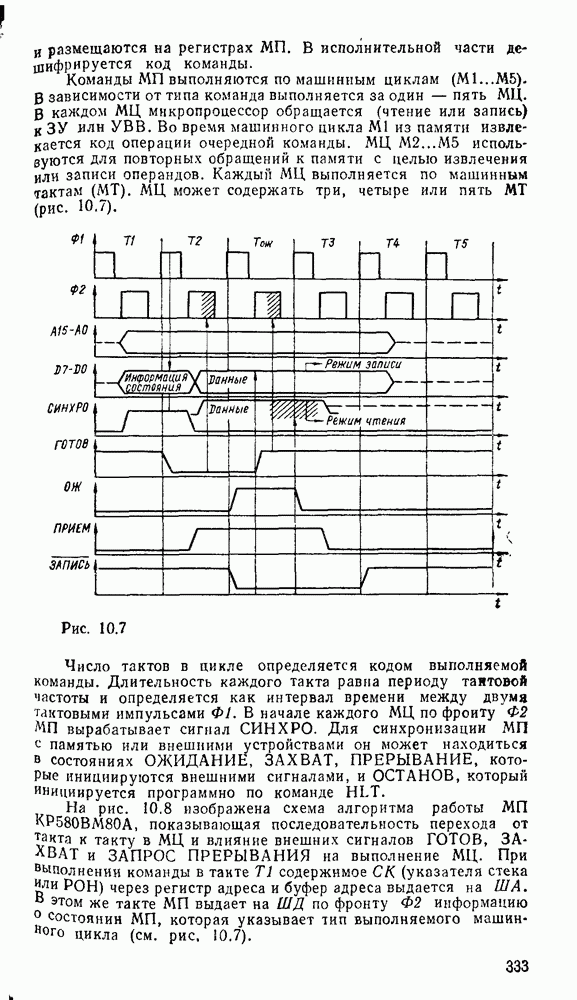
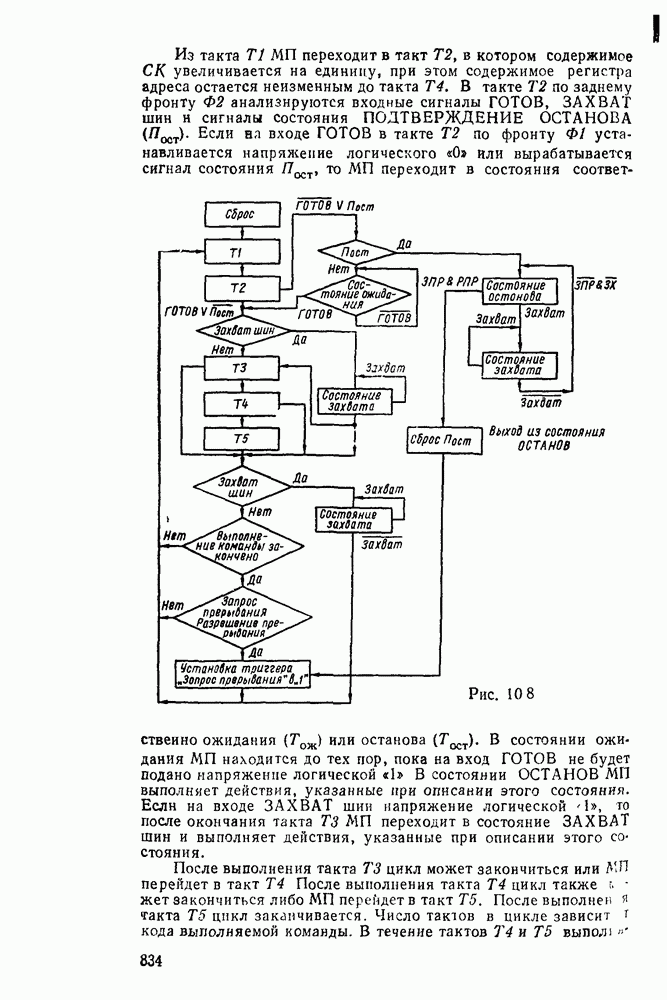
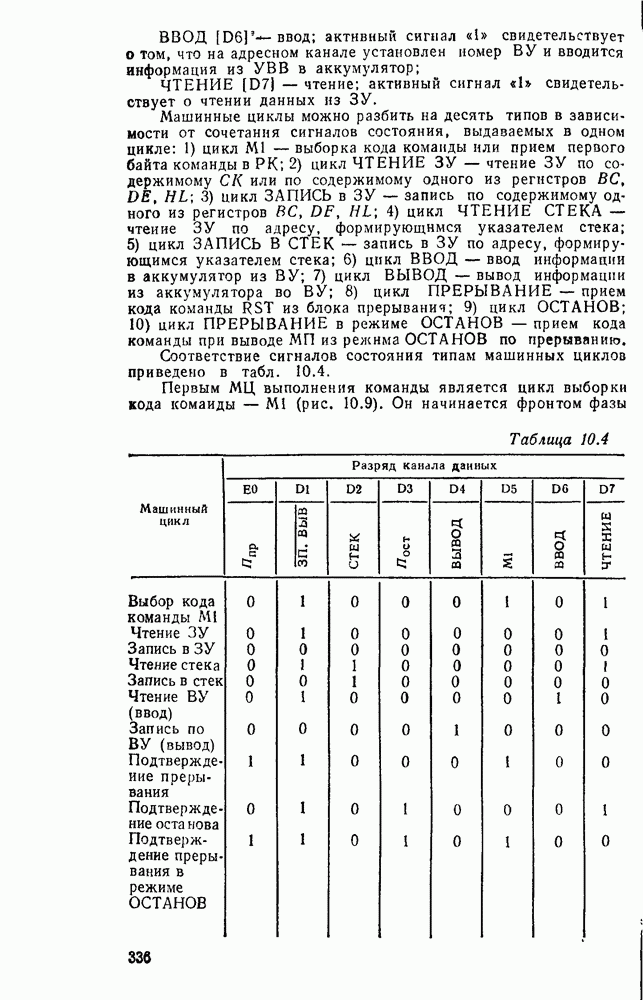
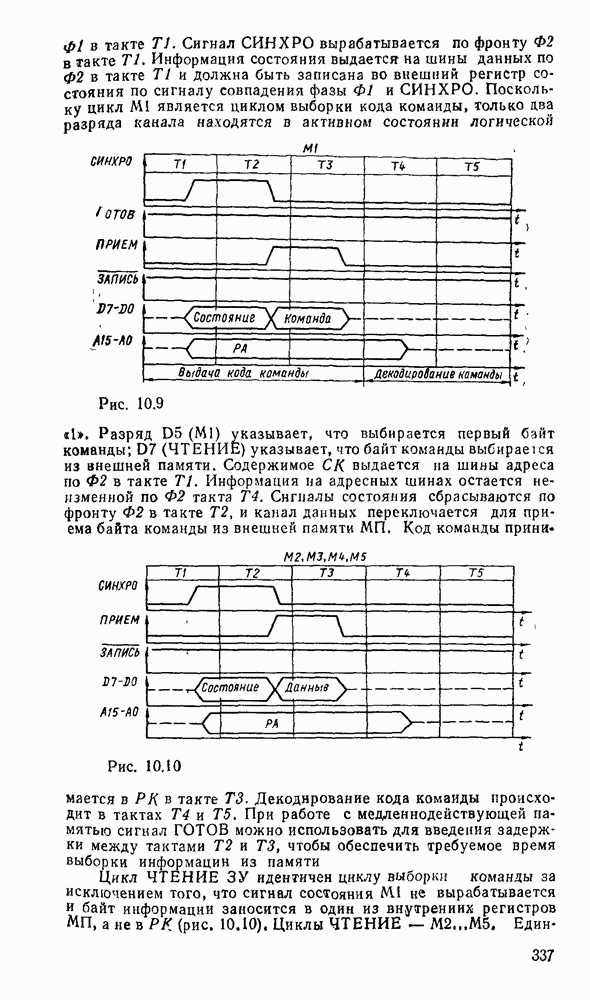
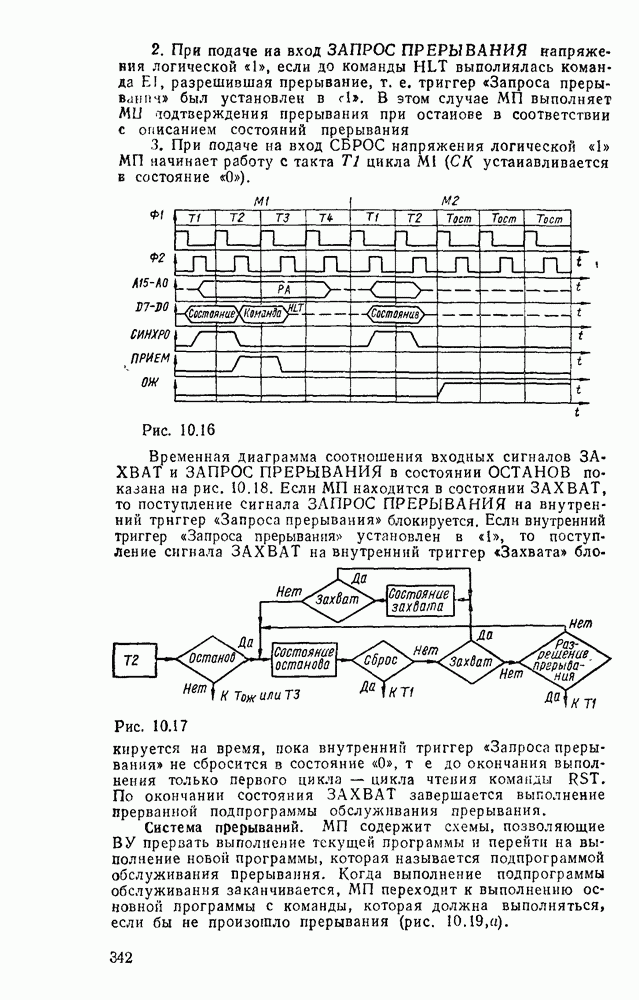
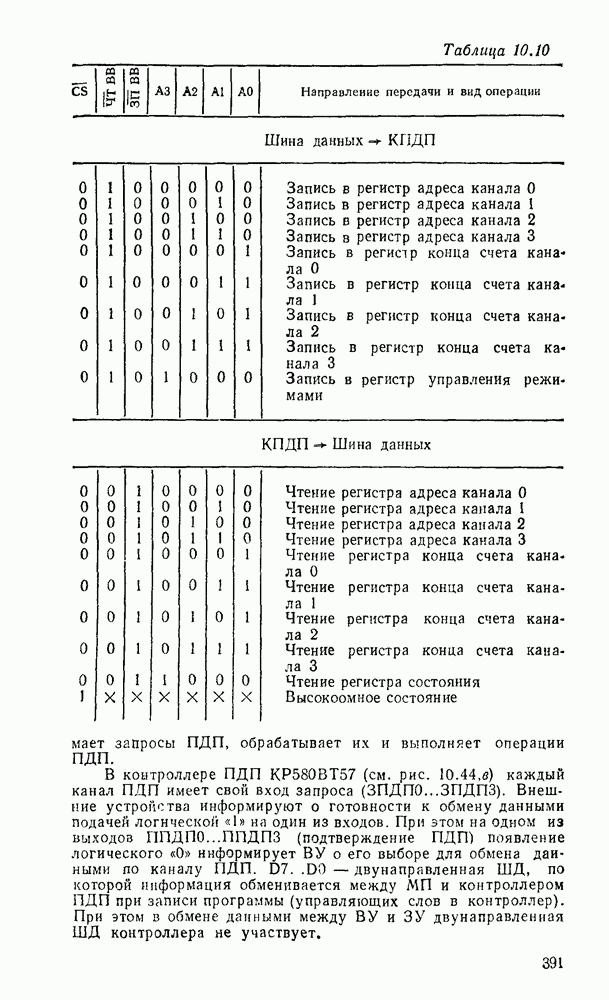
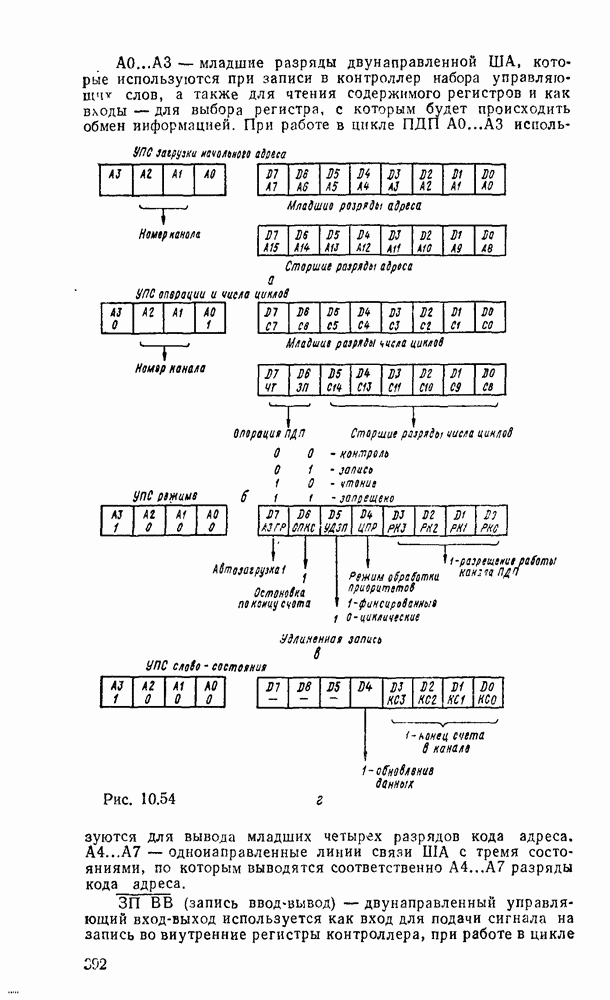
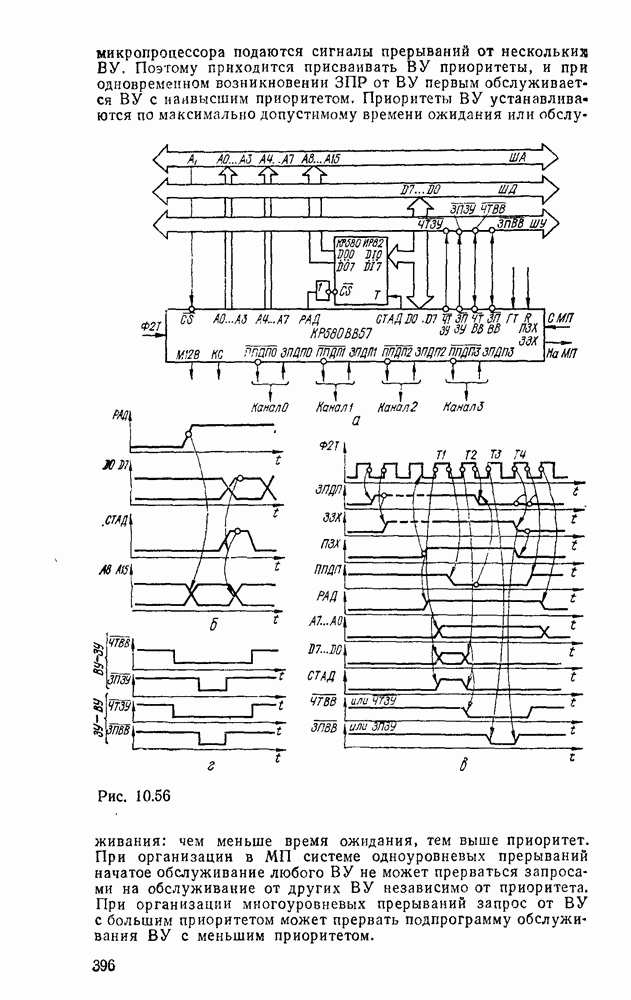
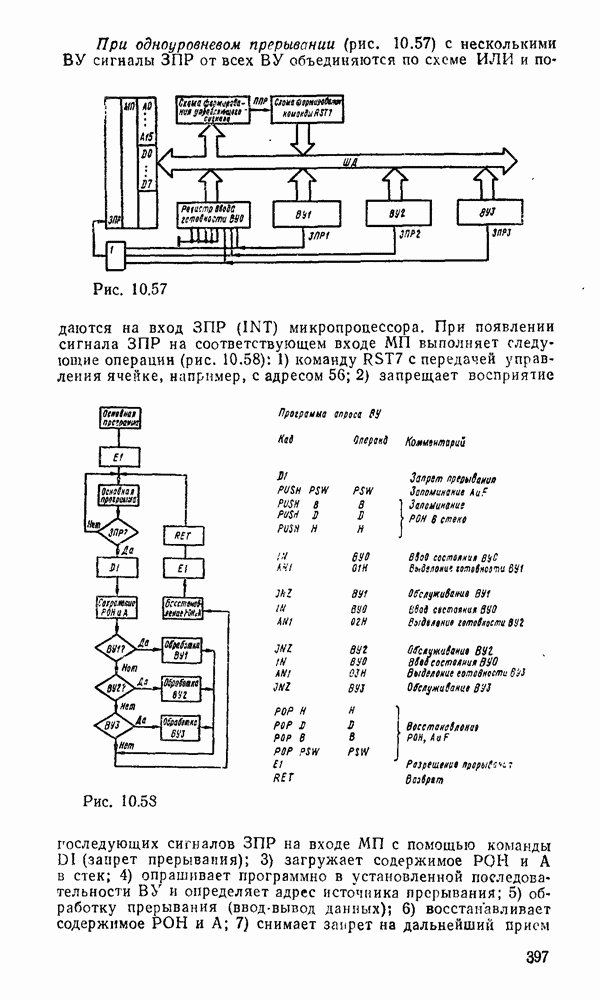
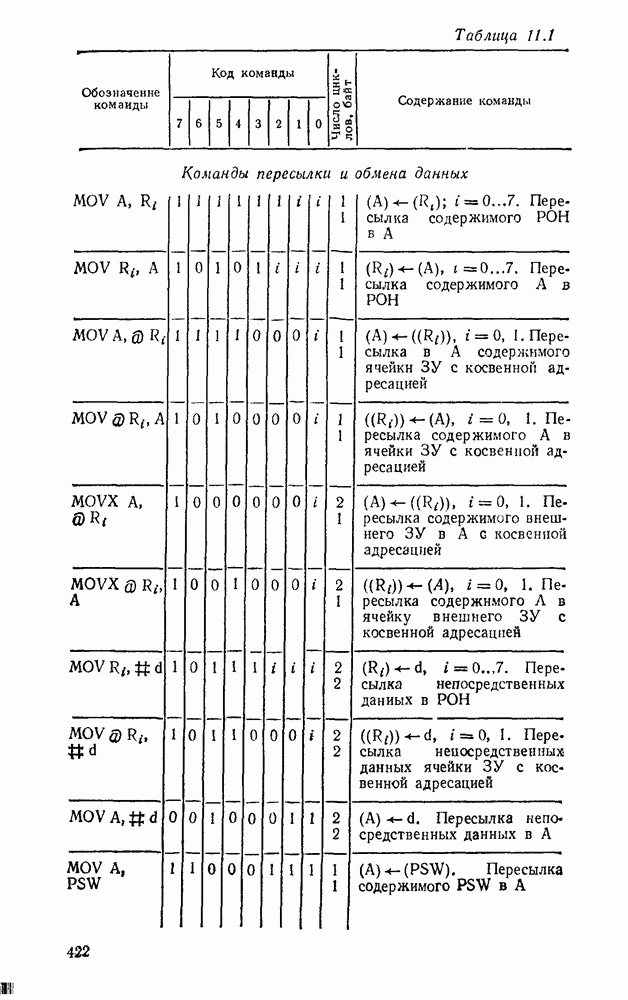
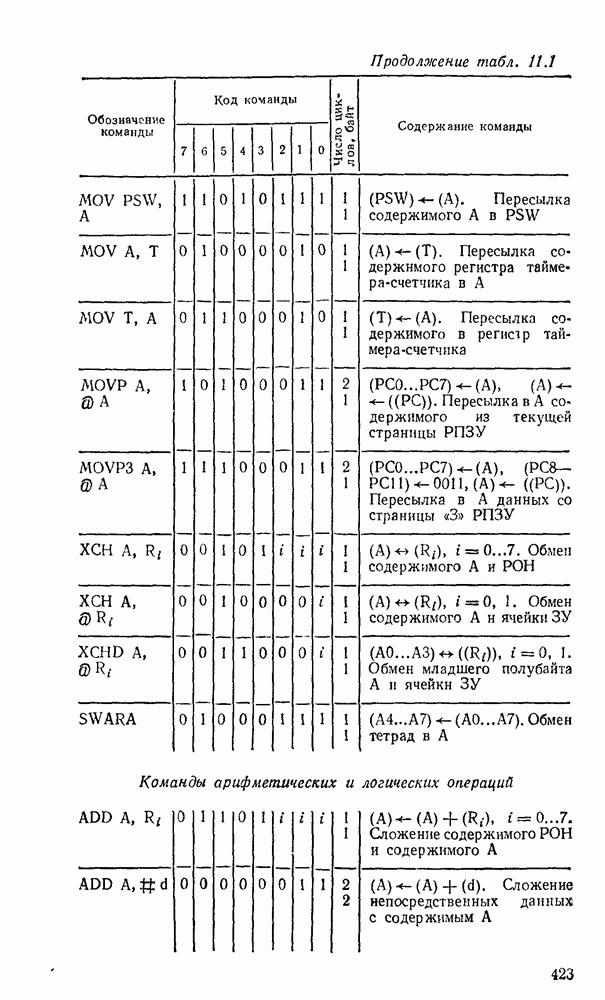
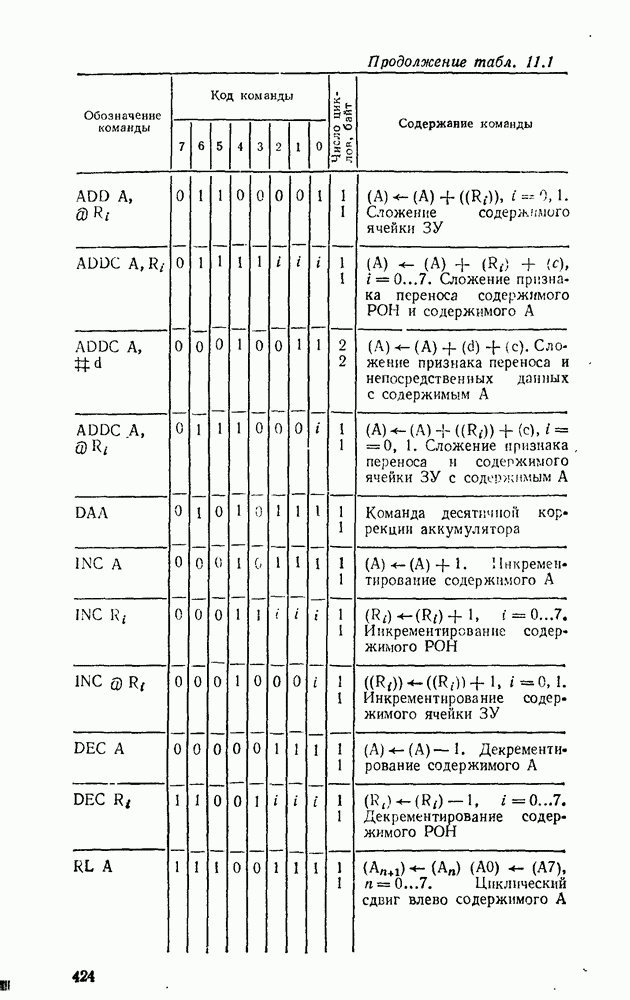
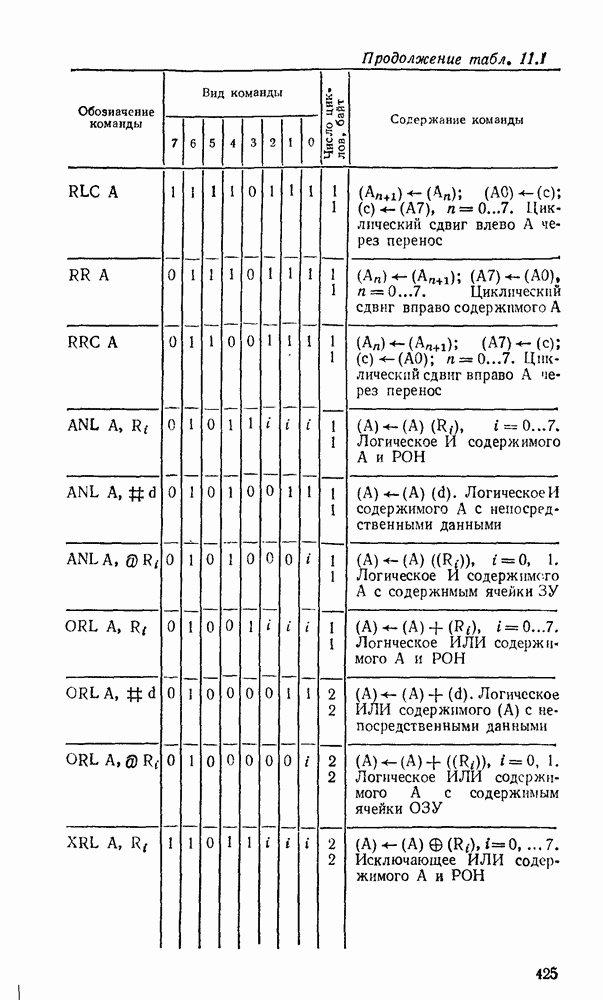
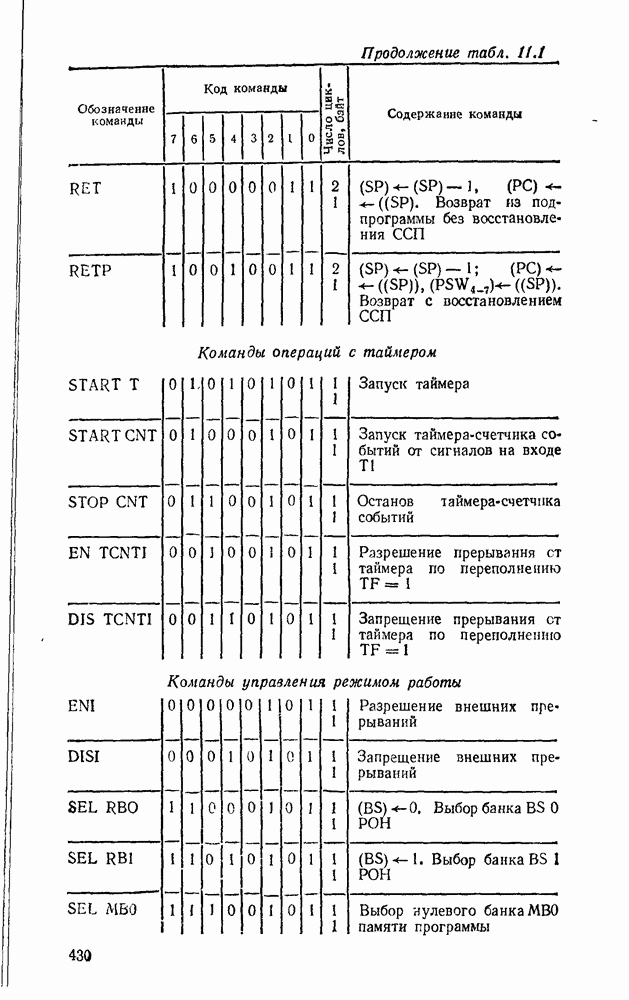
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
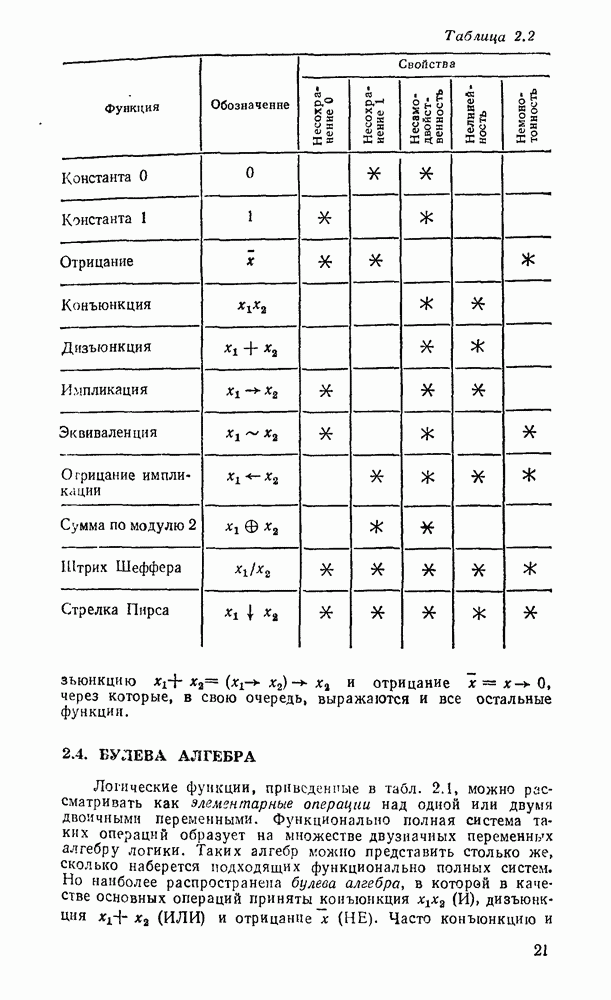
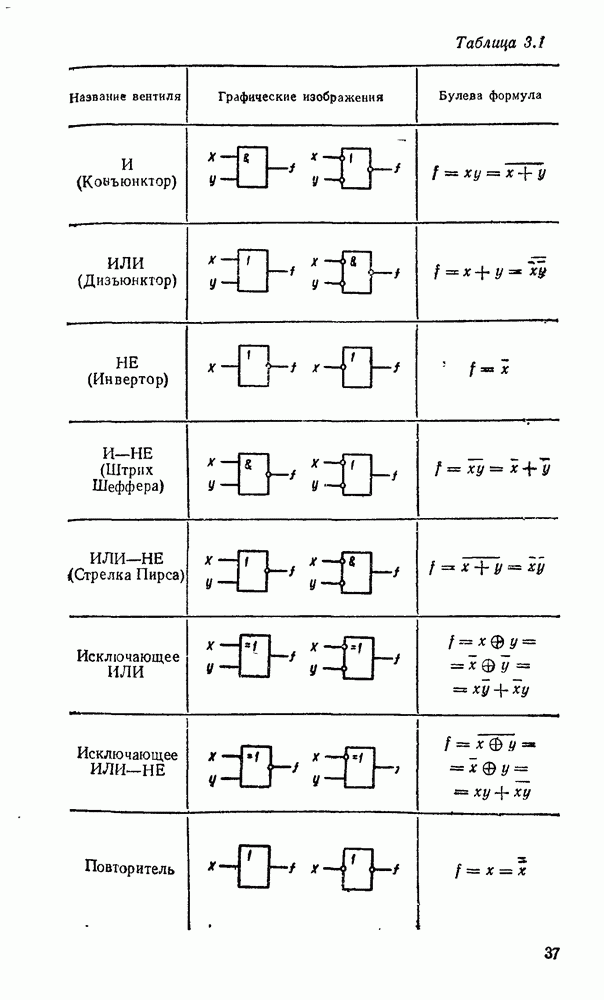
3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
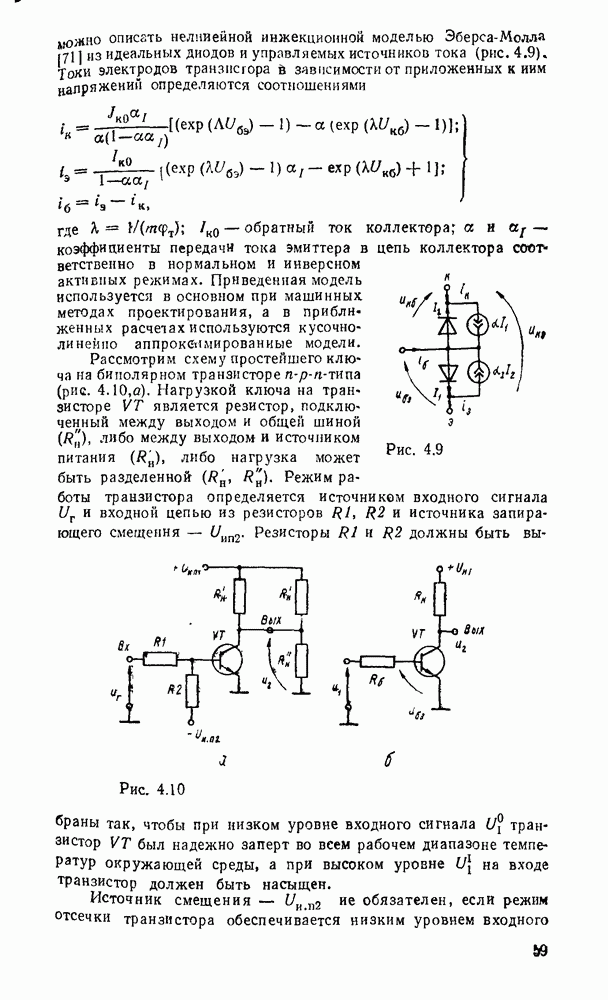
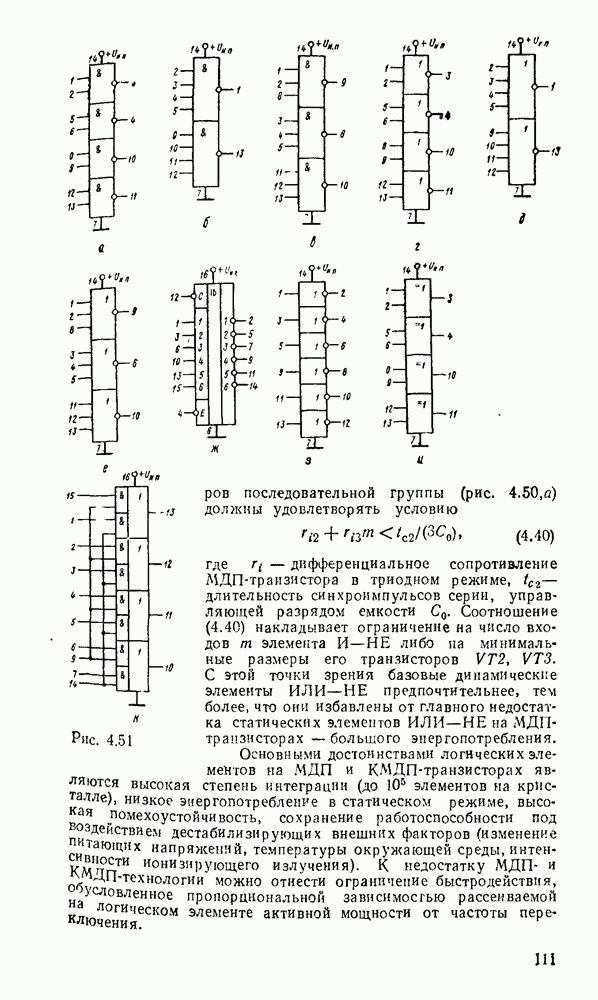
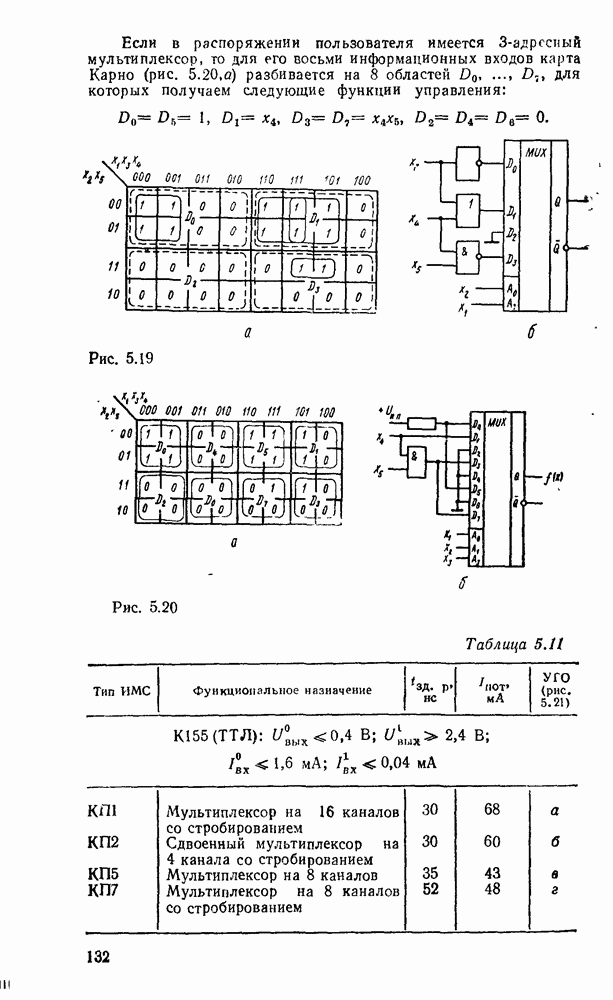
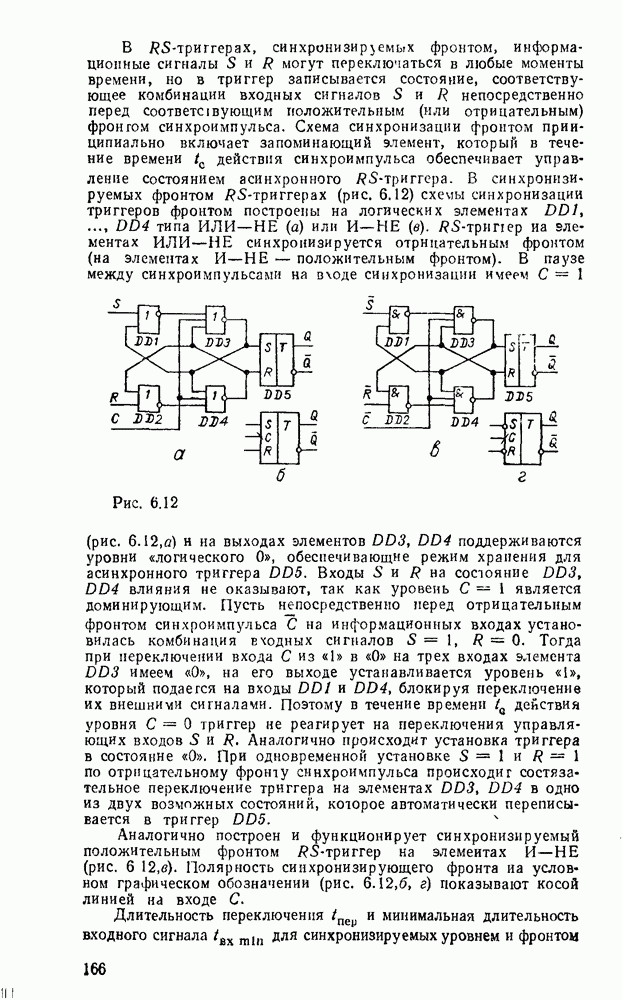
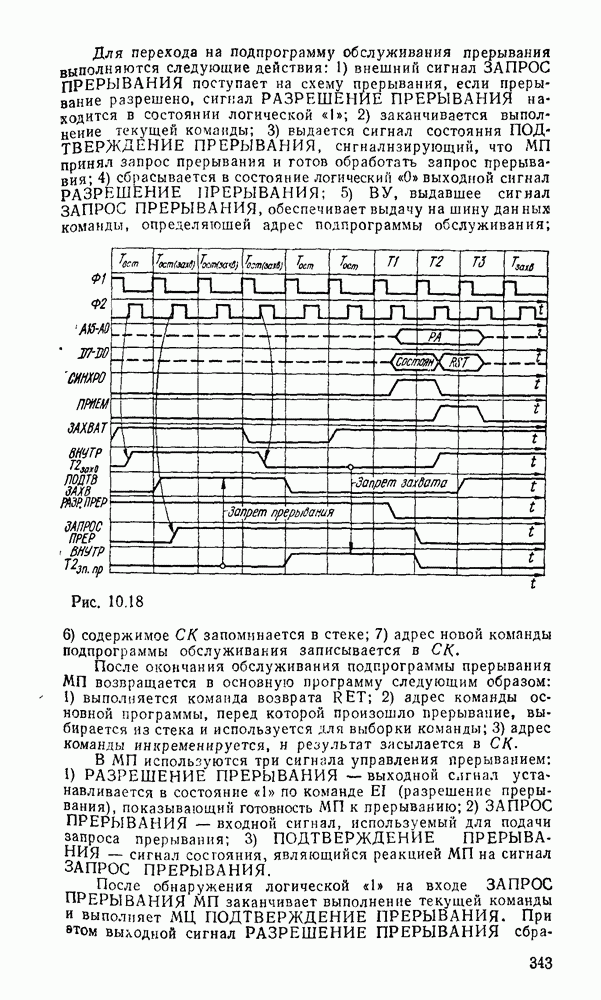
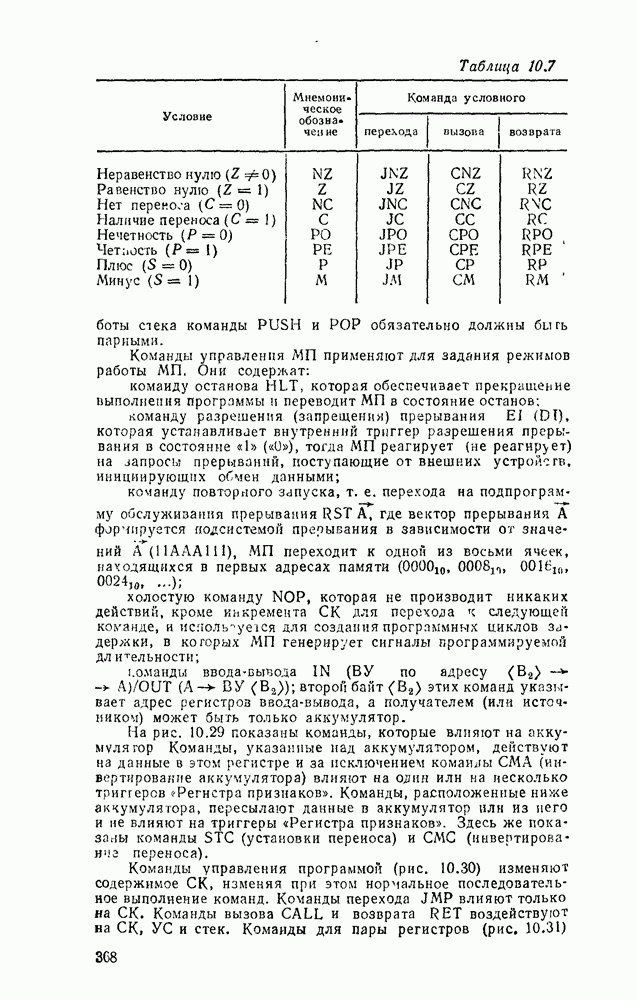
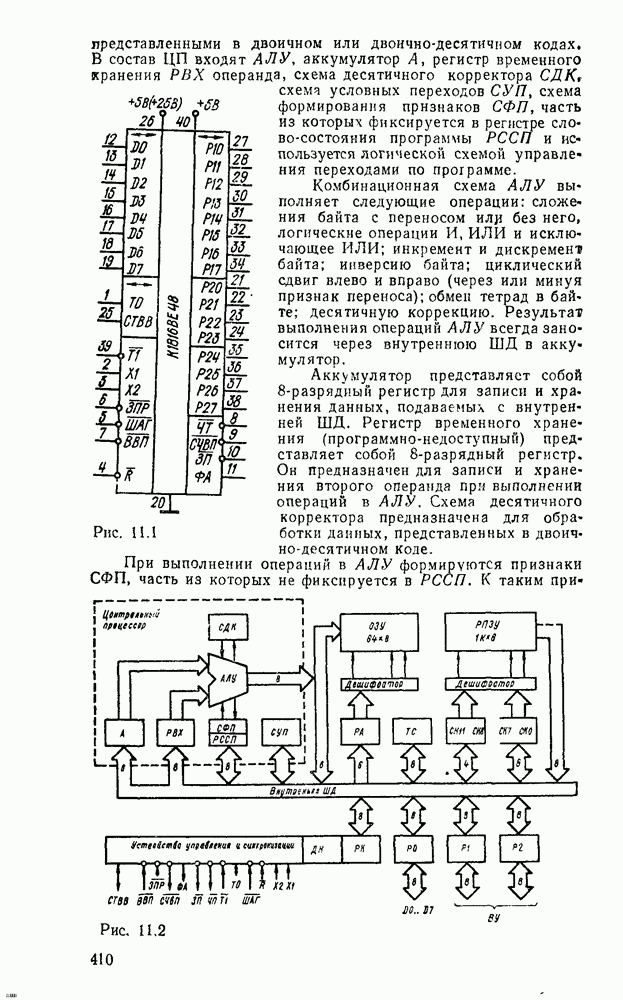
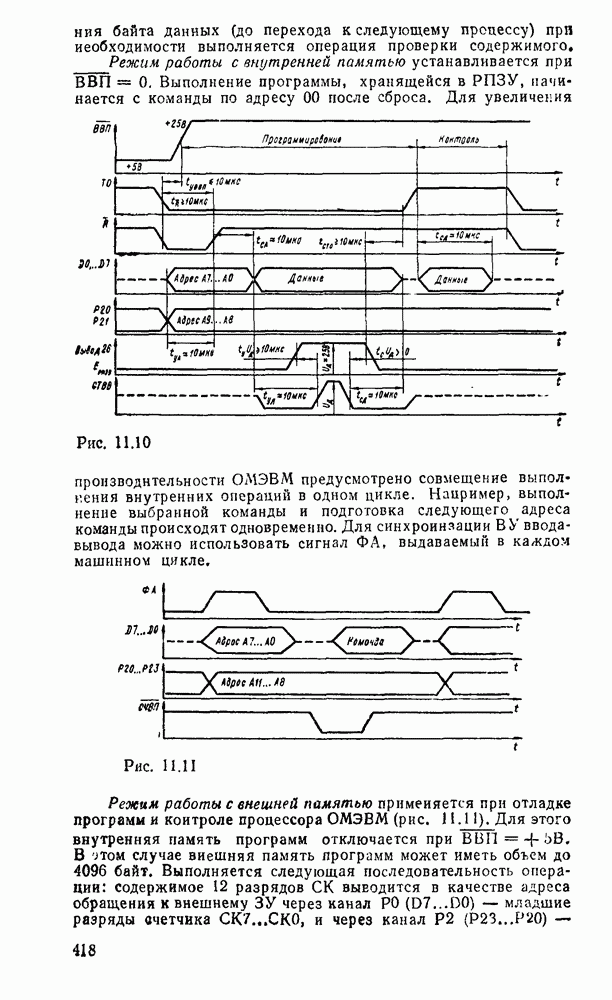
Вследствие функциональной полноты функций Шеффера и стрелки Пирса (см табл 2 2) реализующие их вентили  или ИЛИ—НЕ могут представлять любую булеву операцию И, ИЛИ, НЕ и таким образом самостоятельно образовать базис, в котором реализуется
или ИЛИ—НЕ могут представлять любую булеву операцию И, ИЛИ, НЕ и таким образом самостоятельно образовать базис, в котором реализуется  логическая функция. Это целесообразно с двух точек зрения. Во-первых, при проектировании логических схем можно обойтись одним единственным типом вентиля, что позволяет предельно унифицировать эгот процесс. Во-вторых, для большинства серий ТТЛ- и КМОП-логик вентиль
логическая функция. Это целесообразно с двух точек зрения. Во-первых, при проектировании логических схем можно обойтись одним единственным типом вентиля, что позволяет предельно унифицировать эгот процесс. Во-вторых, для большинства серий ТТЛ- и КМОП-логик вентиль  , как и ИЛИ—НЕ, является базисным и предпочтителен во многих отношениях. Вследствие этого реализация логических схем в базисах
, как и ИЛИ—НЕ, является базисным и предпочтителен во многих отношениях. Вследствие этого реализация логических схем в базисах  и ИЛИ—НЕ получила широкое распространение в практике.
и ИЛИ—НЕ получила широкое распространение в практике.
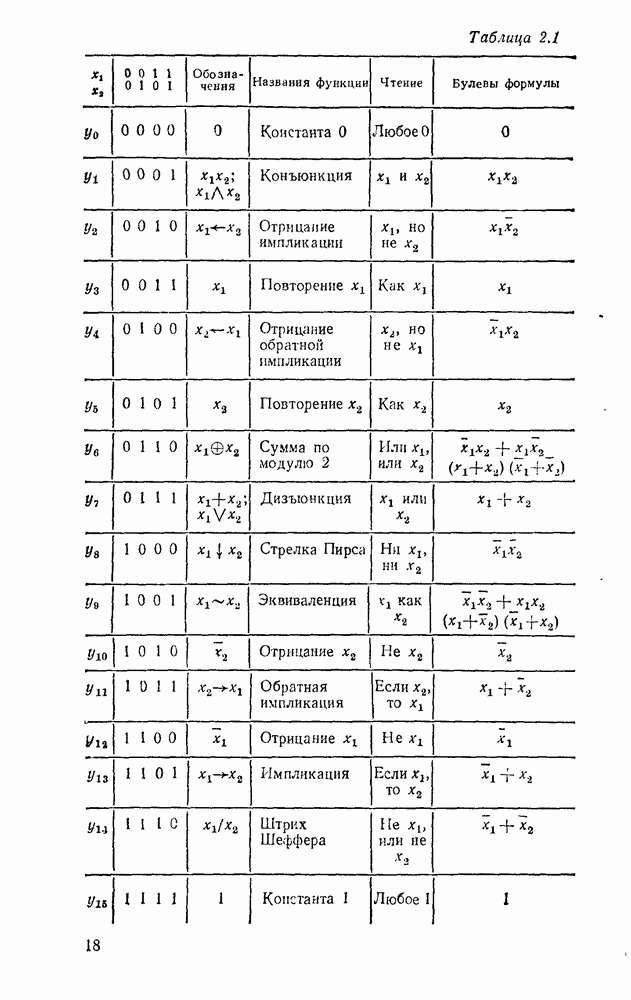
Булевы операции И, ИЛИ, НЕ  штрих Шеффера
штрих Шеффера  соотношениями
соотношениями  .
.

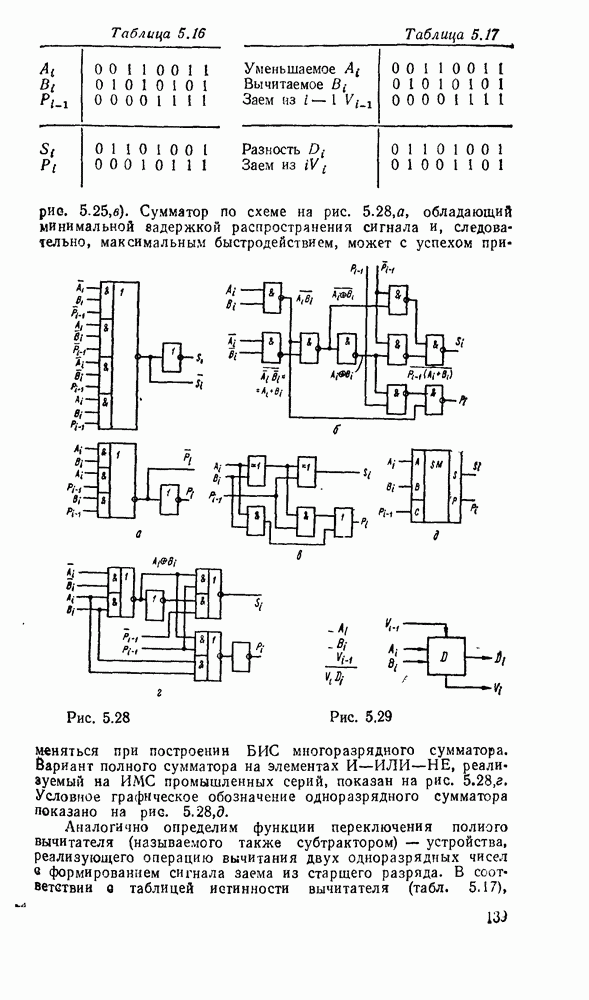
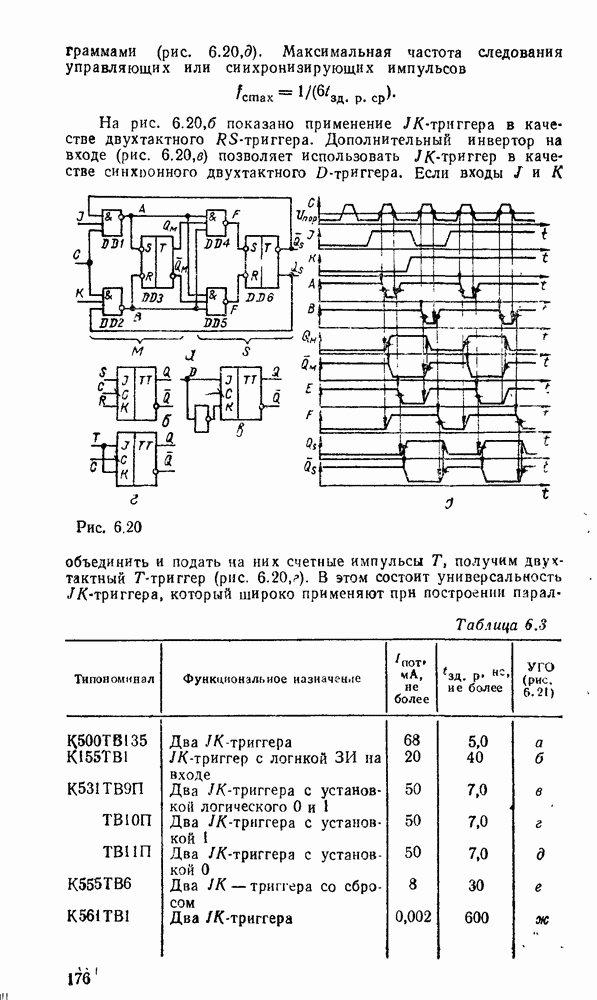
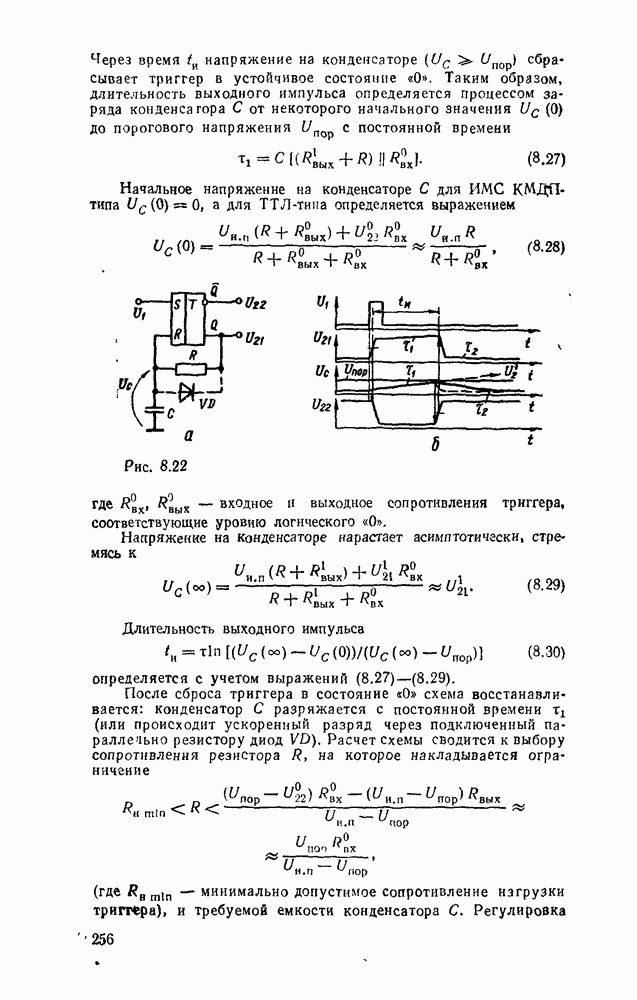
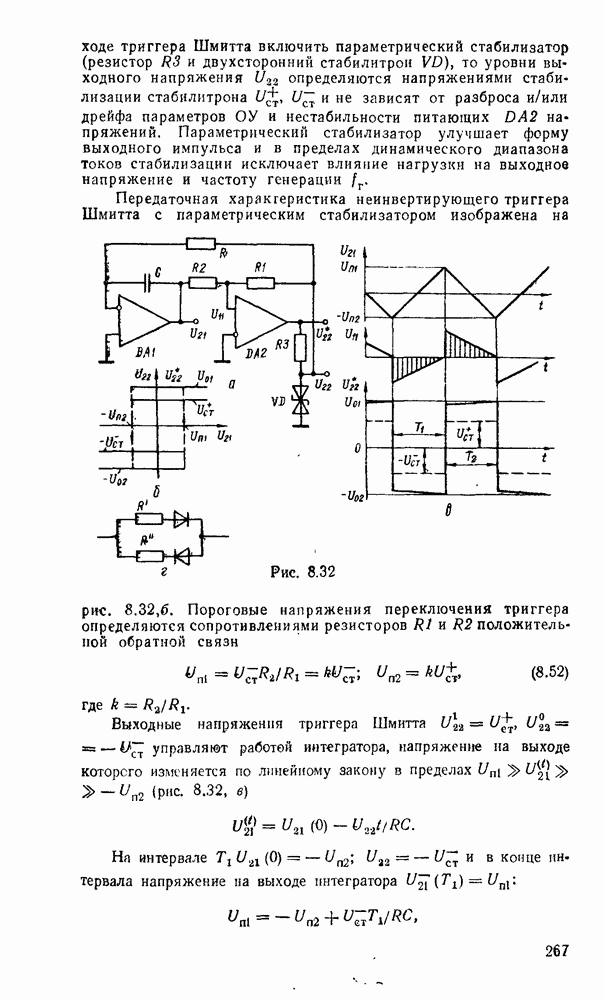
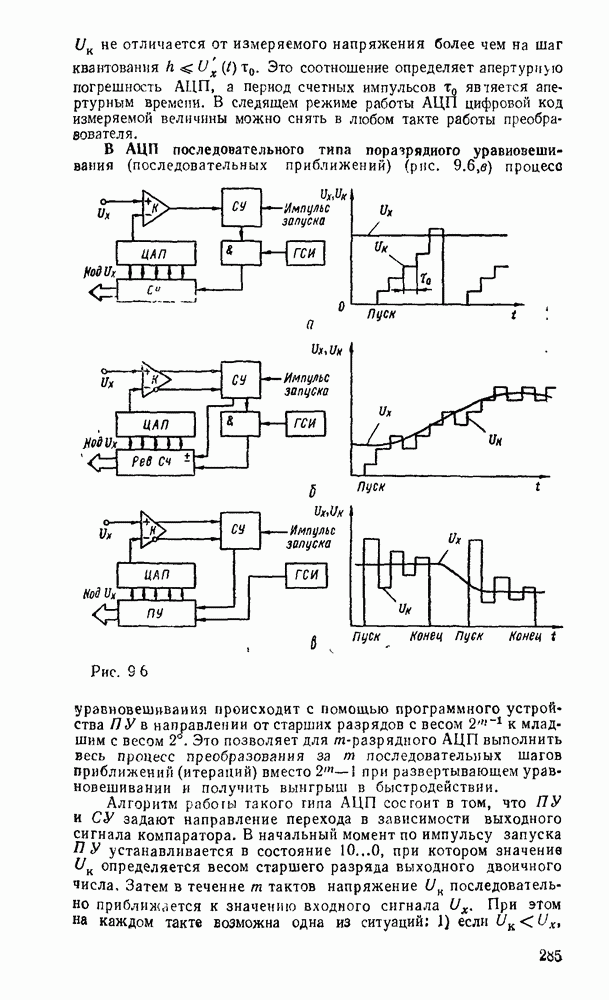
Рис. 3.7.
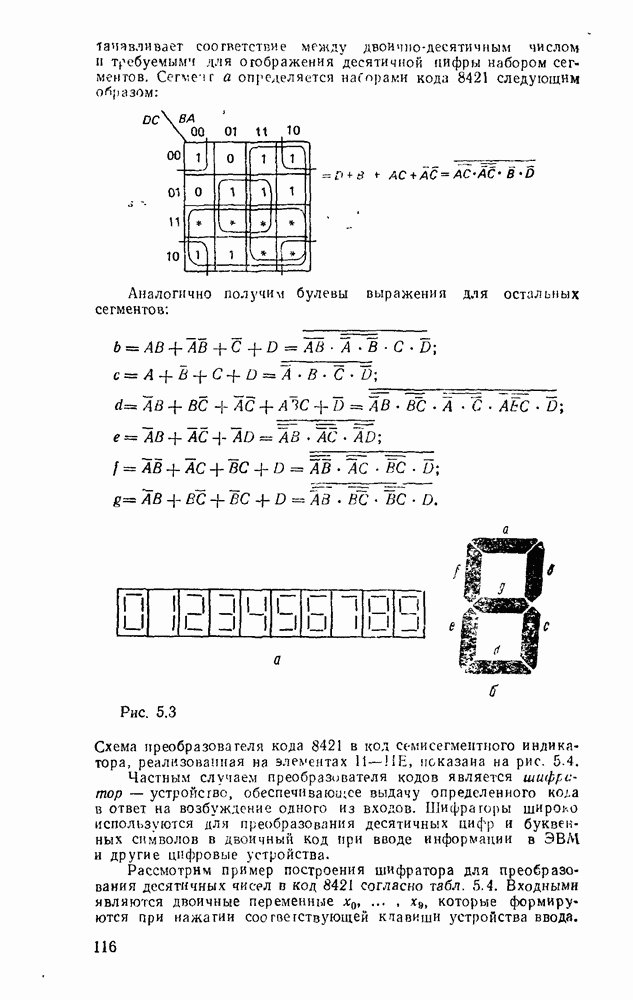
Отсюда следует, что вентиль  , таблица соответствия которого дана на рис. 3.7,а, эквивалентен вентилю НЕ—ИЛИ (см. табл. 3.1) и позволяет - реализовать булевы операции, как показано на рис.
, таблица соответствия которого дана на рис. 3.7,а, эквивалентен вентилю НЕ—ИЛИ (см. табл. 3.1) и позволяет - реализовать булевы операции, как показано на рис.  . Для реализации инверсии имеются два варианта: либо на все входы вентиля
. Для реализации инверсии имеются два варианта: либо на все входы вентиля  подается переменная
подается переменная  . либо на все входы, кроме входа
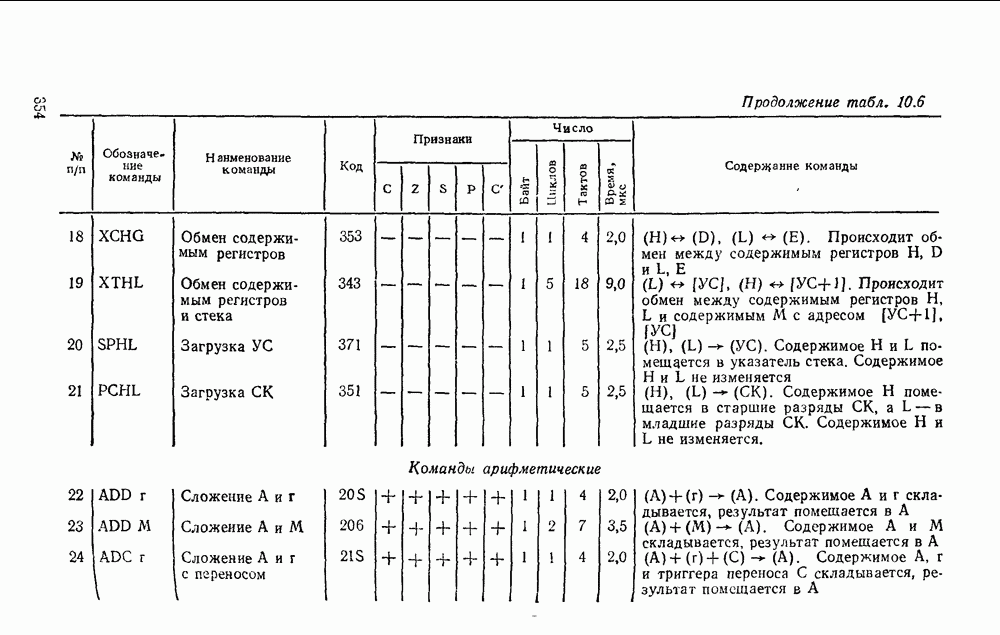
. либо на все входы, кроме входа  , подается единица. Обычно эти особенности на схемах отсутствуют и используется упрощенное представление с одним входом (рис.
, подается единица. Обычно эти особенности на схемах отсутствуют и используется упрощенное представление с одним входом (рис.  ).
).
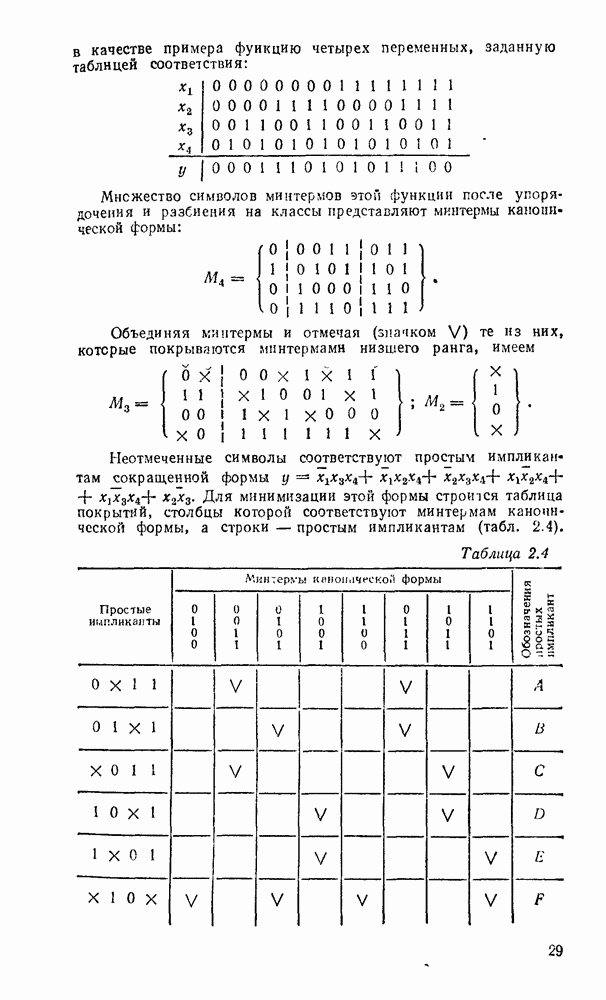
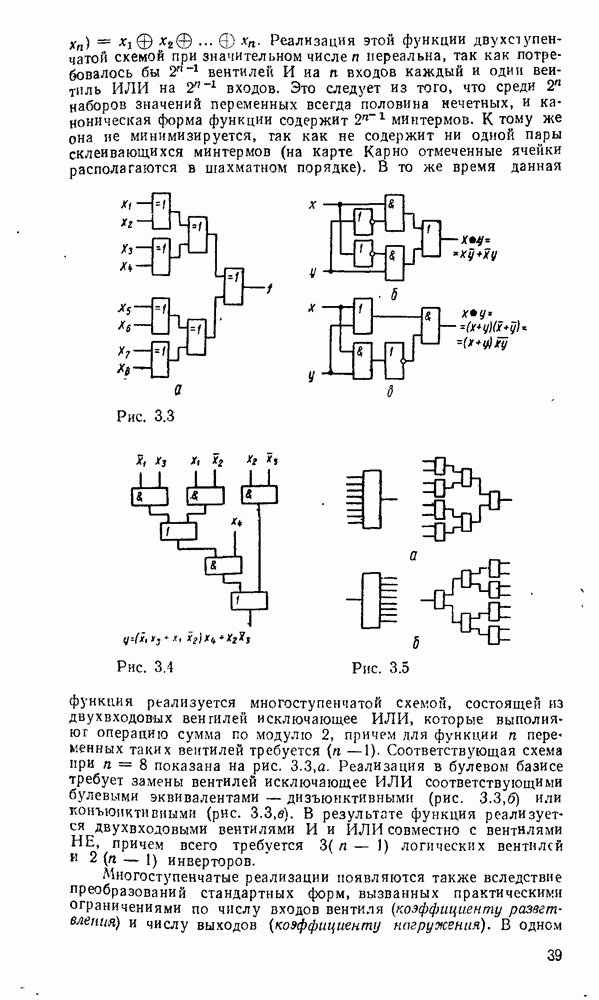
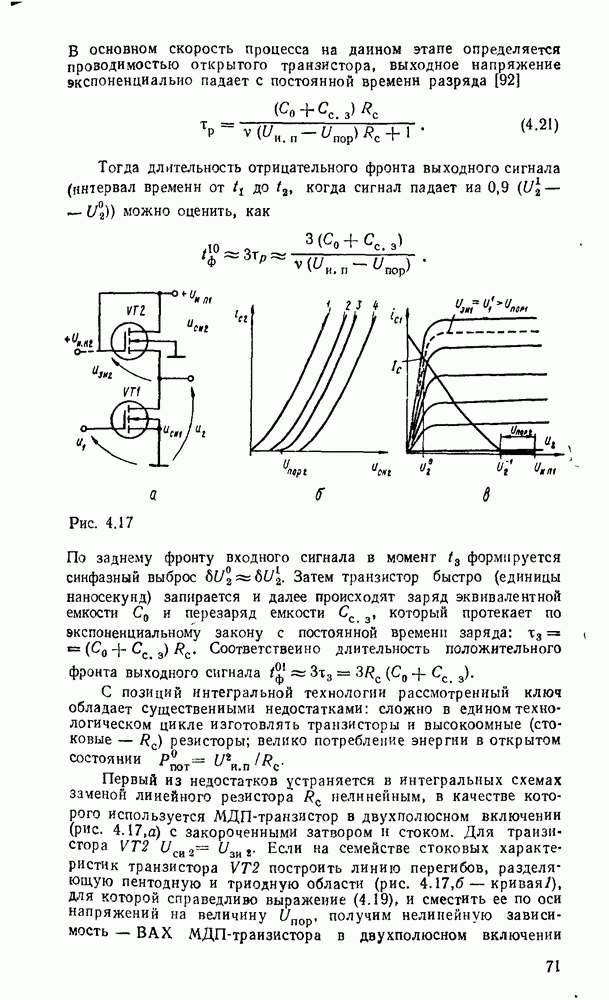
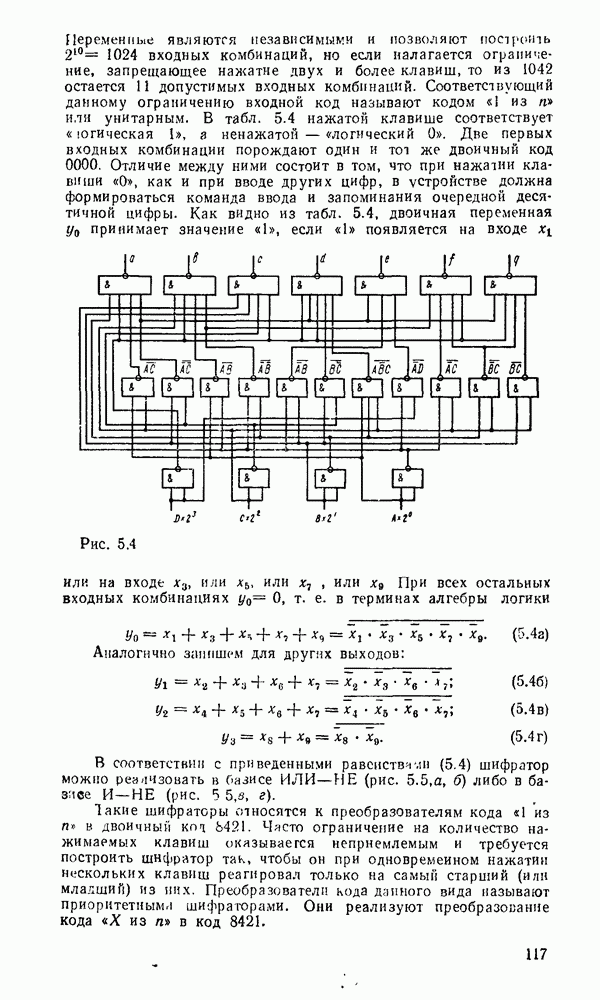
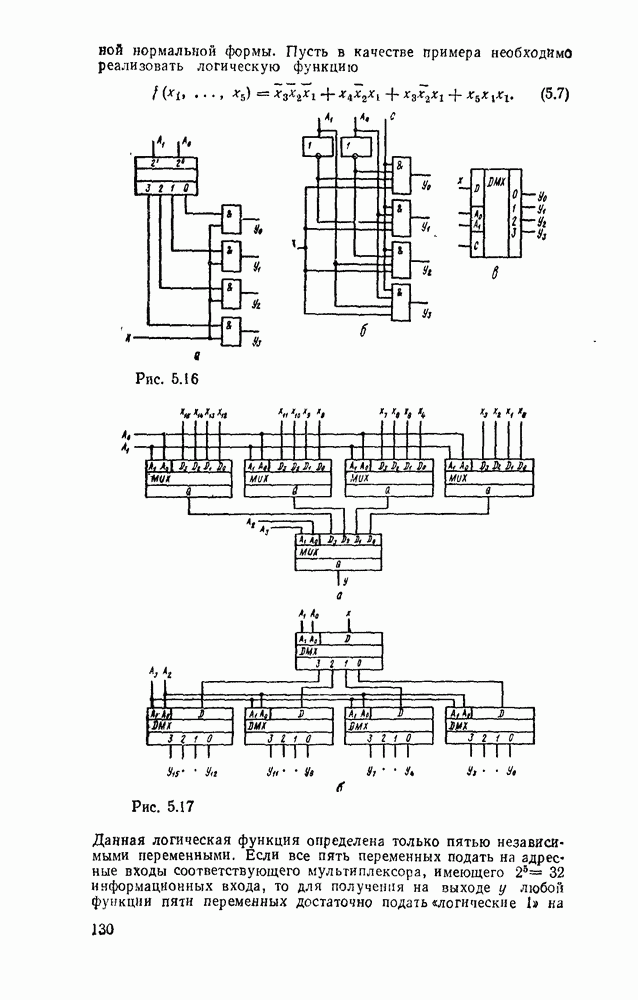
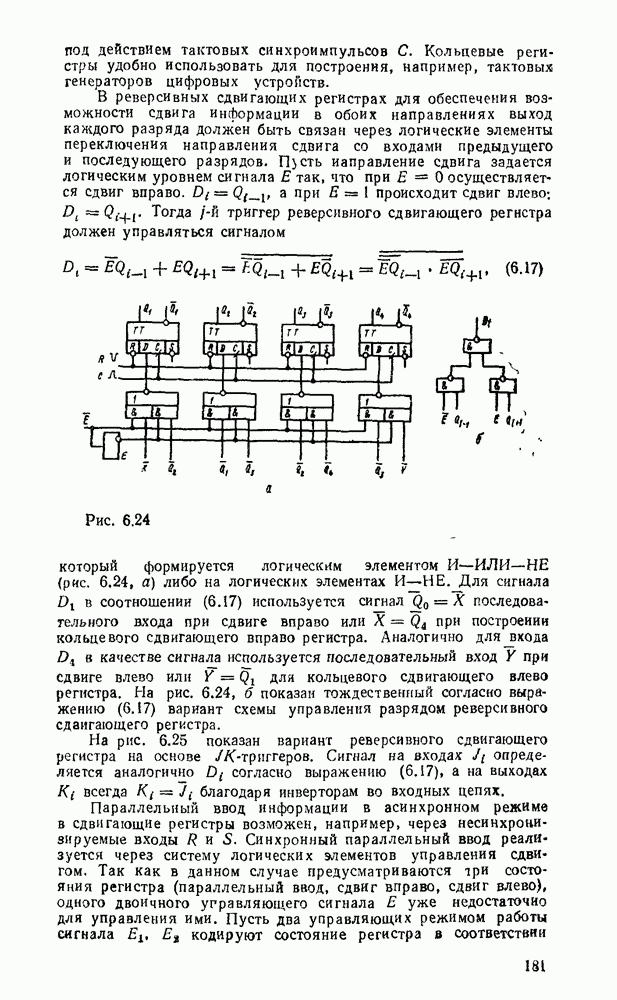
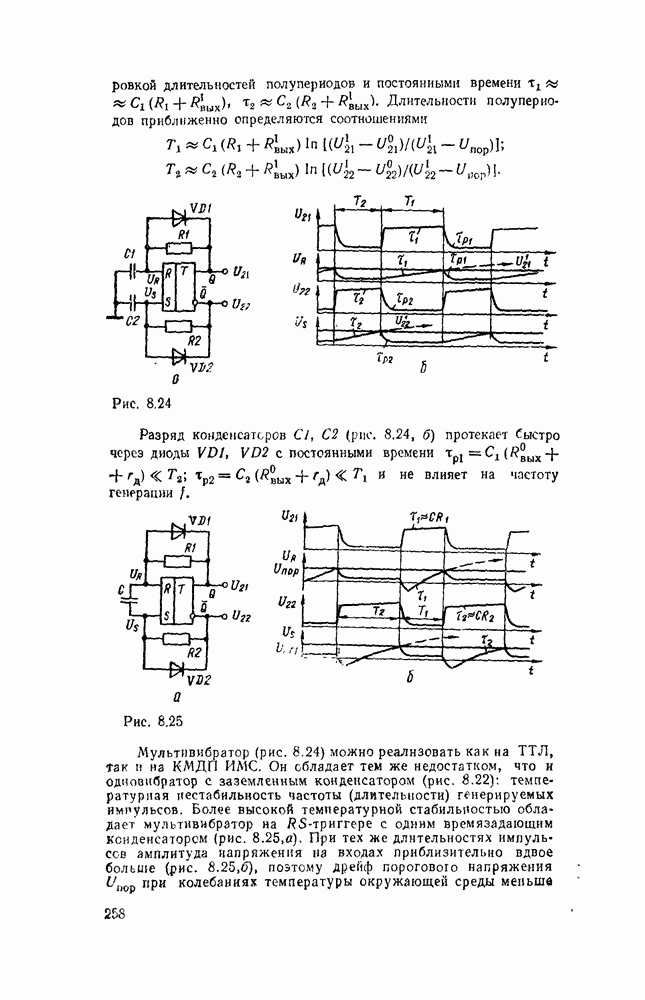
Переход к базису  осуществляется проще всего для двухуровневых схем И/ИЛИ или при задании функции в
осуществляется проще всего для двухуровневых схем И/ИЛИ или при задании функции в  форме суммы минтермов, что видно на простом примере
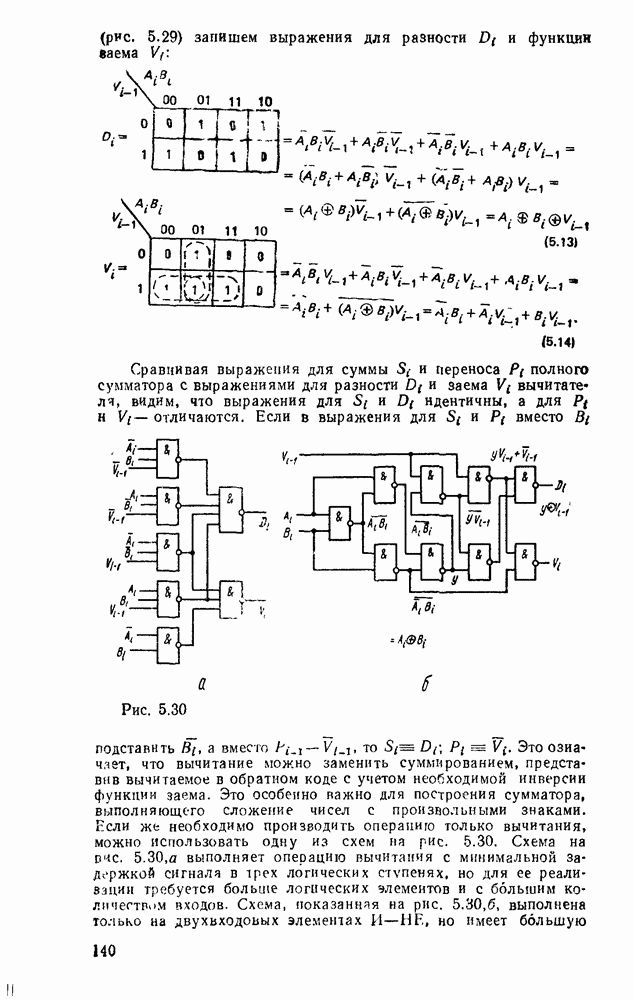
форме суммы минтермов, что видно на простом примере  (рис. 3.8). Исходная схема в булевом базисе (рис. 3.8,а) преобразуется к такому виду (рис.
(рис. 3.8). Исходная схема в булевом базисе (рис. 3.8,а) преобразуется к такому виду (рис.  ), что пары инверторов оказываются соединенными последовательно и выполняют двойную инверсию сигналов. После их удаления схема в вентилями
), что пары инверторов оказываются соединенными последовательно и выполняют двойную инверсию сигналов. После их удаления схема в вентилями  существенно упрощается (рис. 3.8,в) и по своей струитуре полностью совпадает с исходной схемой.
существенно упрощается (рис. 3.8,в) и по своей струитуре полностью совпадает с исходной схемой.
Таким образом, для перевода от двухуровневой схемы И-ИЛИ к схеме в базисе  достаточно заменить все вентили вентилями
достаточно заменить все вентили вентилями  .
.
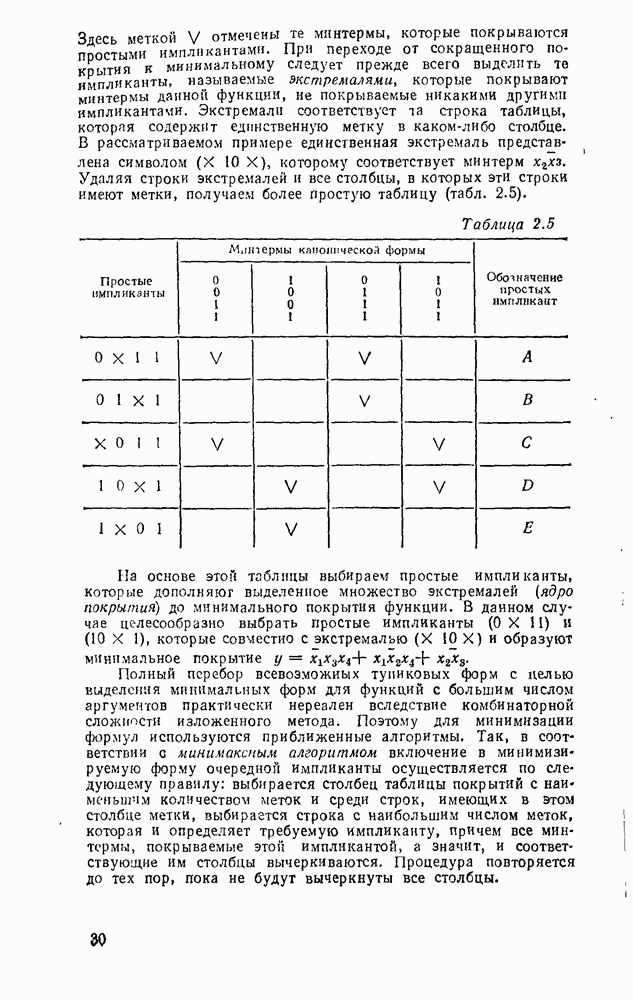
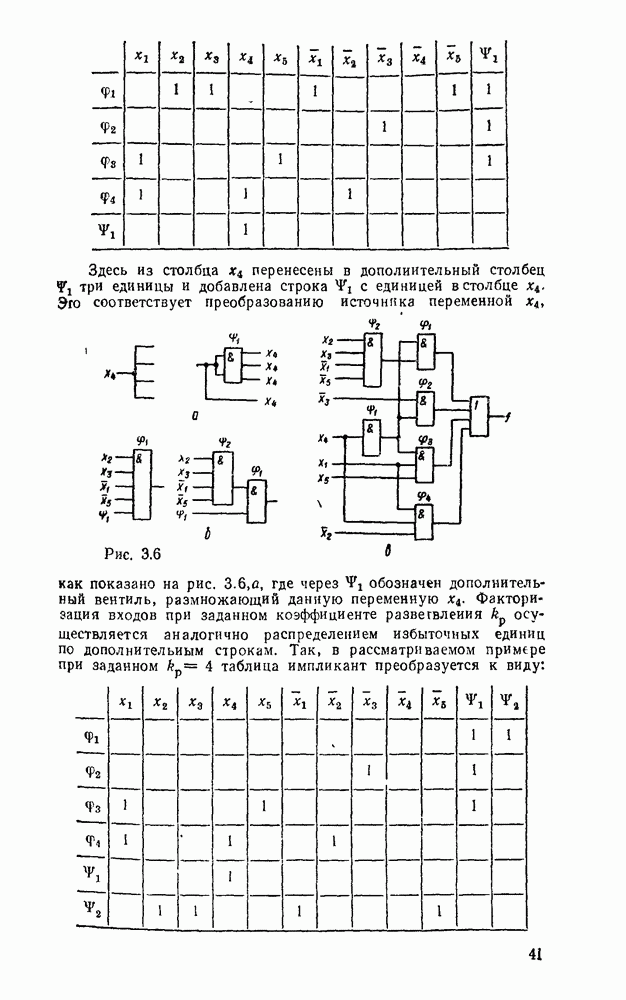
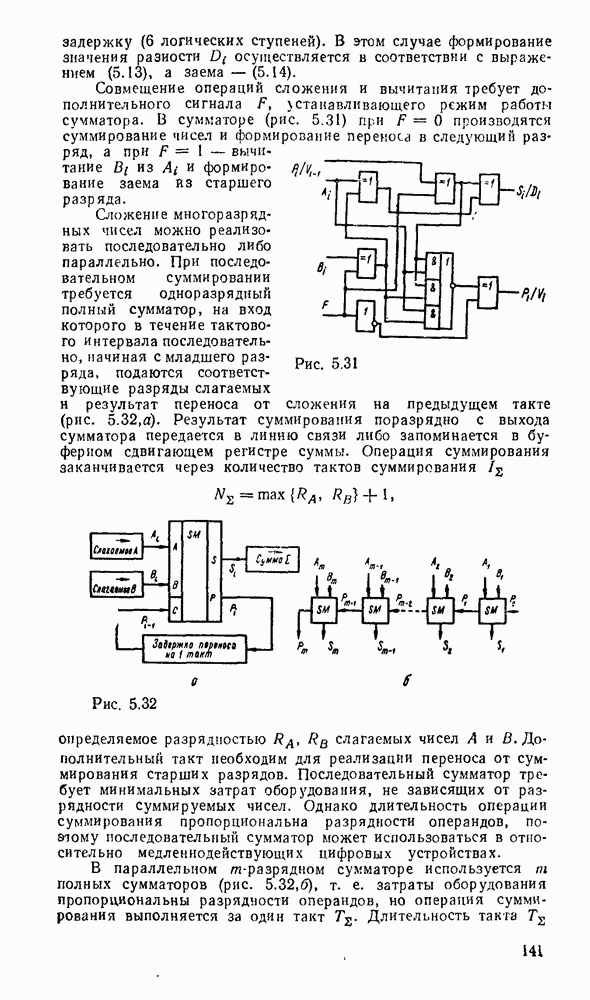
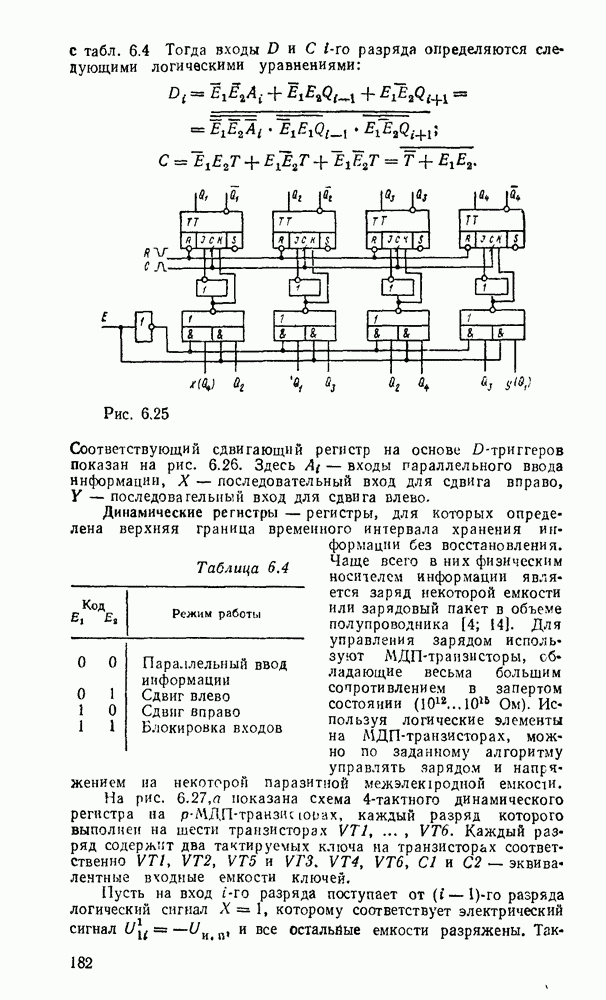
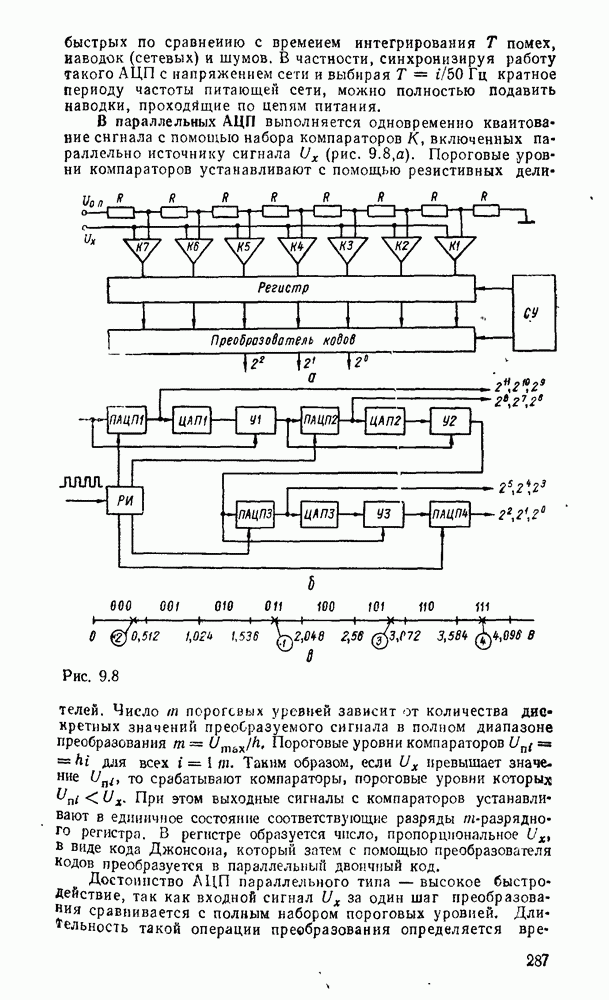
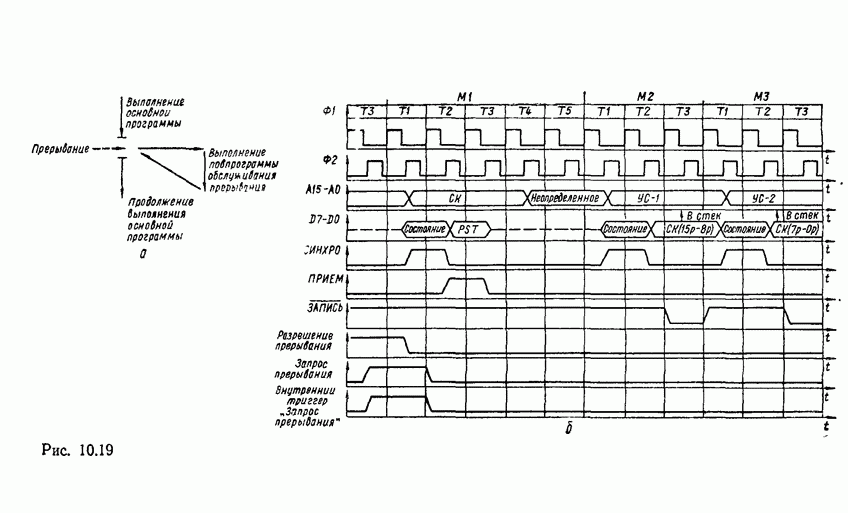
В случае произвольных многоступенчатых схем сначала преобразуются по изложенному выше правилу соседние уровни И—ИЛИ, а остальные вентили И и ИЛИ заменяются их эквивалентами в базисе  (рис. 3.7). В качестве примера на рис. 3.9,а показана схема, полученная в результате такого преобразования из схемы рис. 3.6,в.
(рис. 3.7). В качестве примера на рис. 3.9,а показана схема, полученная в результате такого преобразования из схемы рис. 3.6,в.

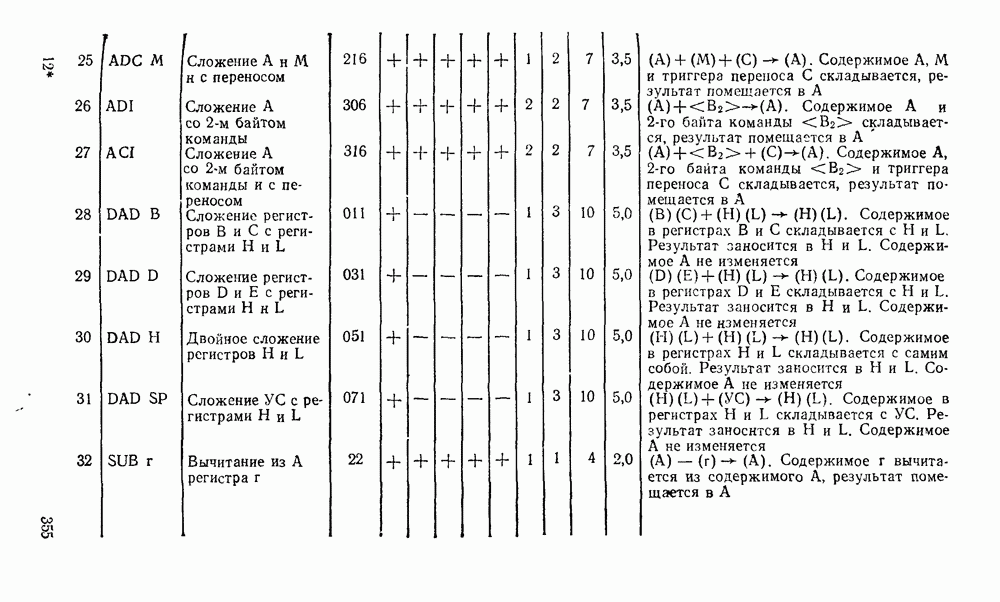
Рис. 3.8.

Рис. 3.9.
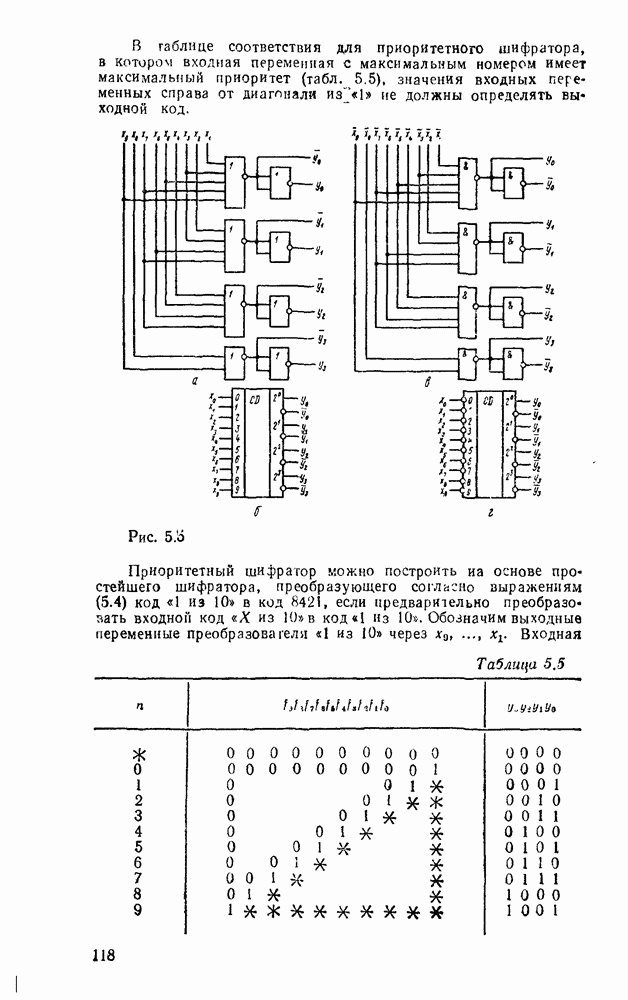
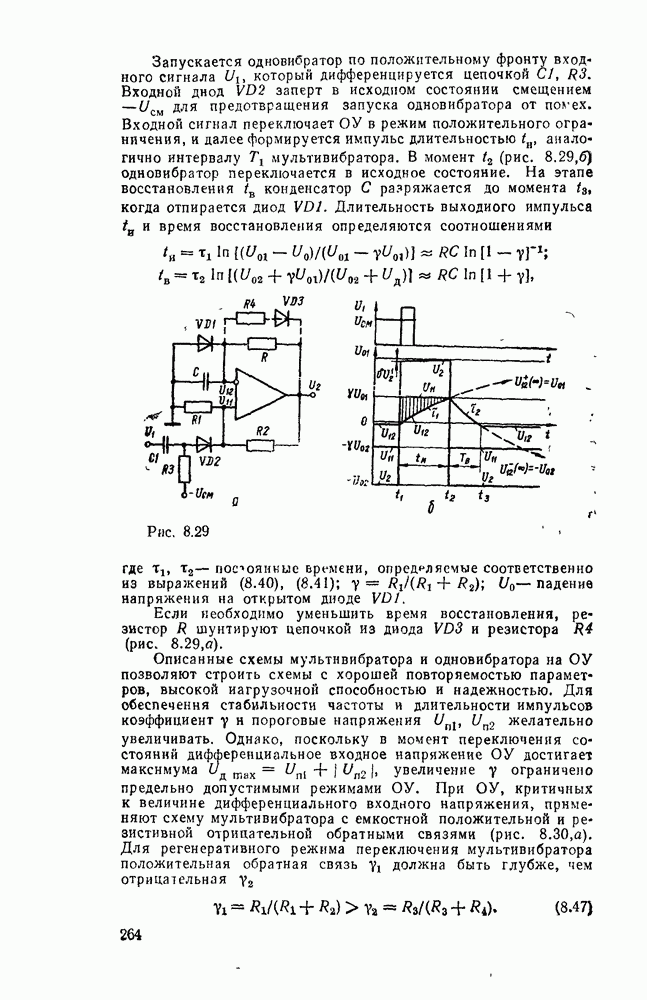
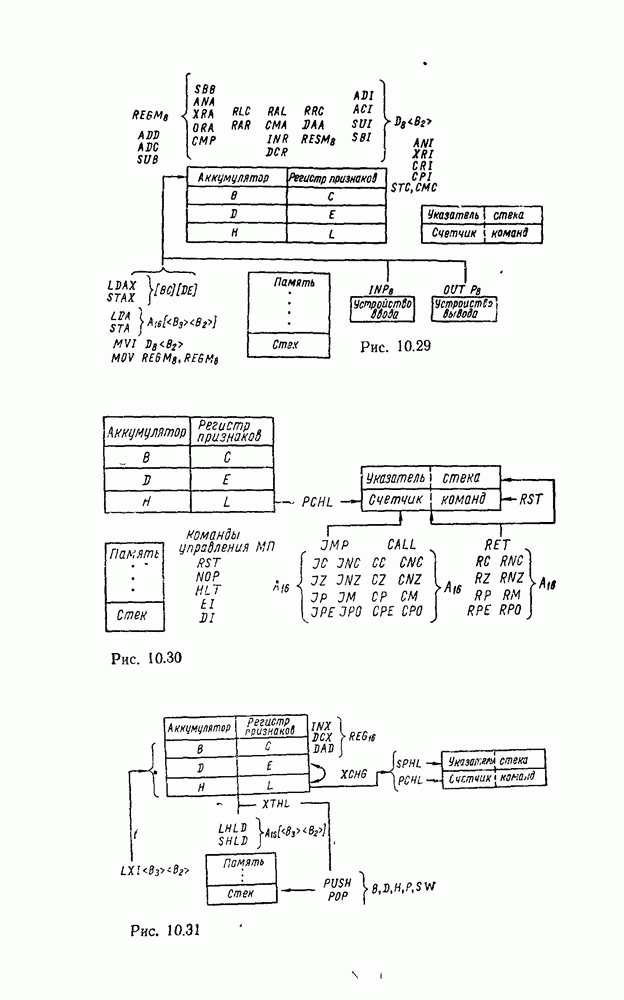
Если исходной является не схема, а заданная функция, то в базисе  ее можно реализовать в любой форме последовательным применением соотношения, следующего из закона де Моргана:
ее можно реализовать в любой форме последовательным применением соотношения, следующего из закона де Моргана:  , где А и В — любые выражения. Так, скобочное выражение функции из
, где А и В — любые выражения. Так, скобочное выражение функции из  можно представить последовательностью соотношений
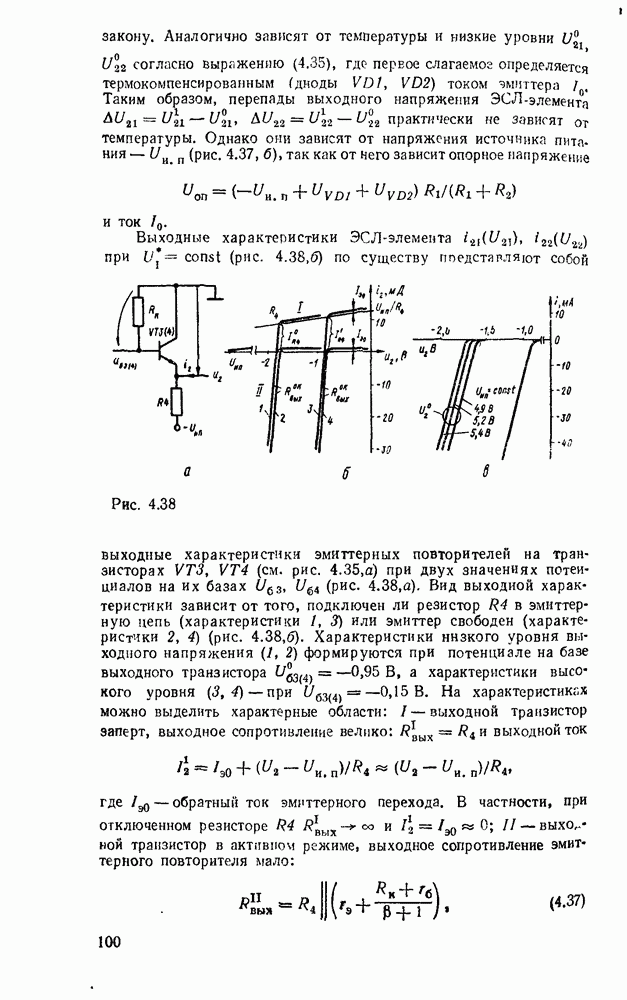
можно представить последовательностью соотношений  , где
, где  , где
, где  , где
, где  . Соответствующая схема показана на рис.
. Соответствующая схема показана на рис.  .
.
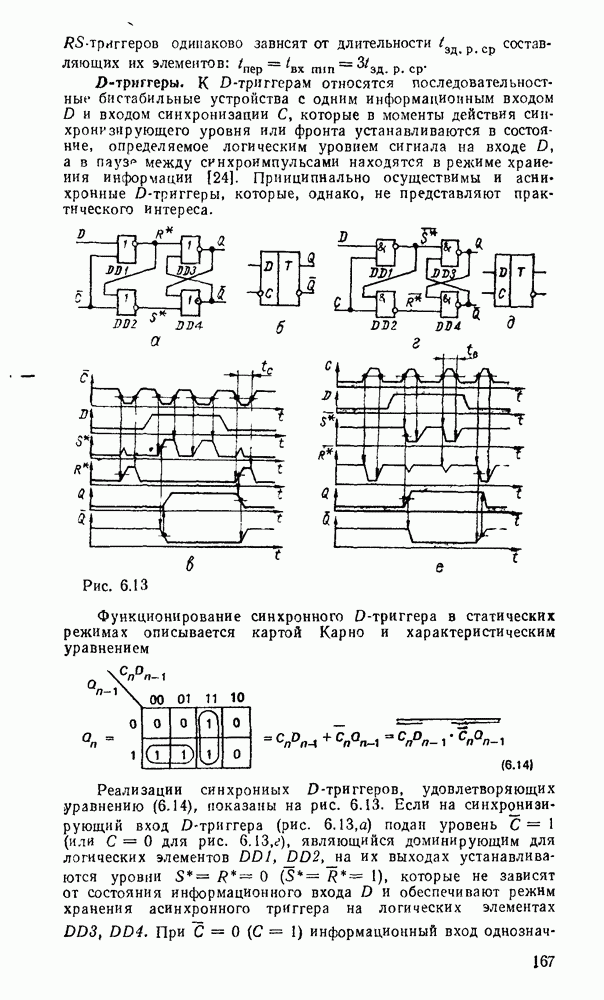
Как видно из рассмотренных примеров, переход к базису
НЕ не всегда сопровождается минимальной реализацией.  , схема, полученная преобразованием из булевого базиса (рис. 3.6,в), содержит девять вентилей вместо семи (рис.
, схема, полученная преобразованием из булевого базиса (рис. 3.6,в), содержит девять вентилей вместо семи (рис.  ), а непосредственная реализация скобочной формы — только шесть (рис. 3.9,б).
), а непосредственная реализация скобочной формы — только шесть (рис. 3.9,б).
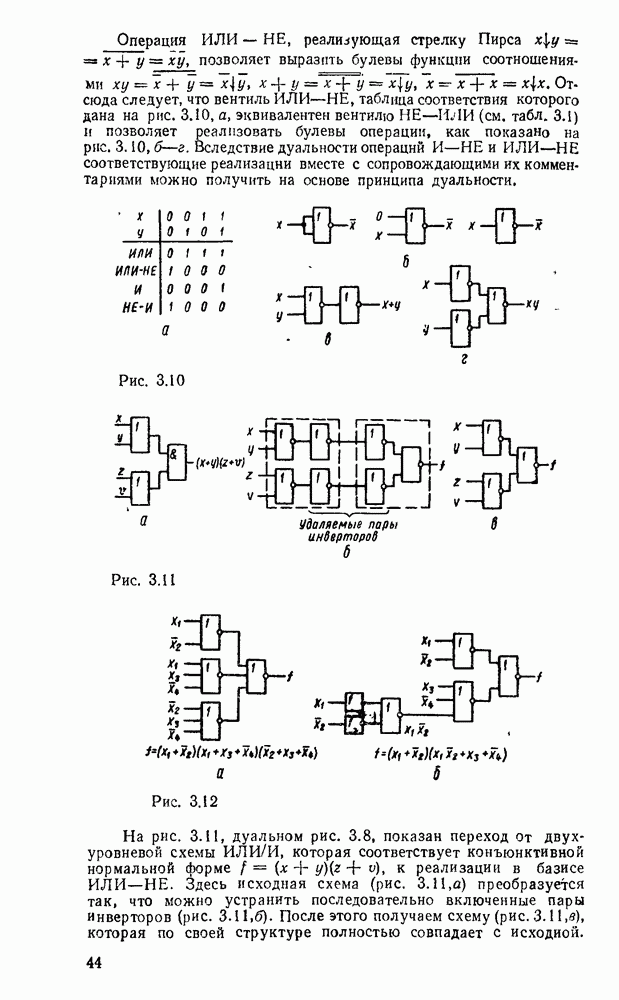
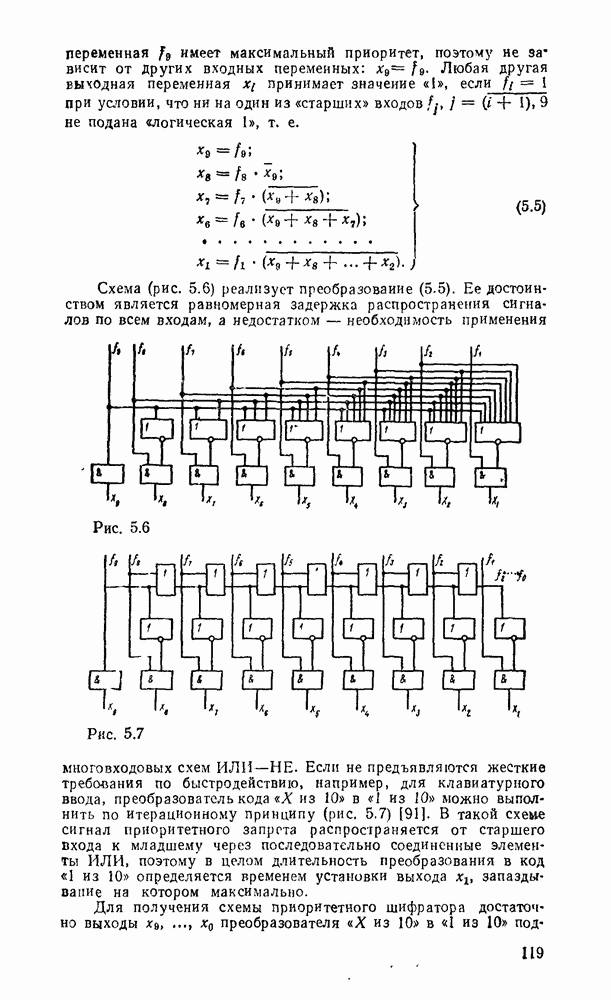
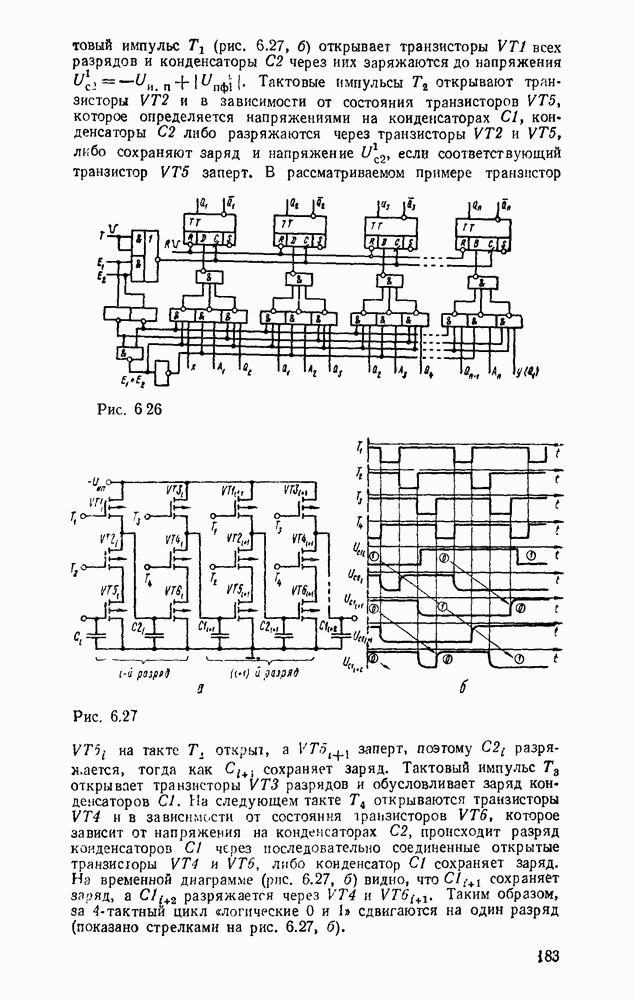
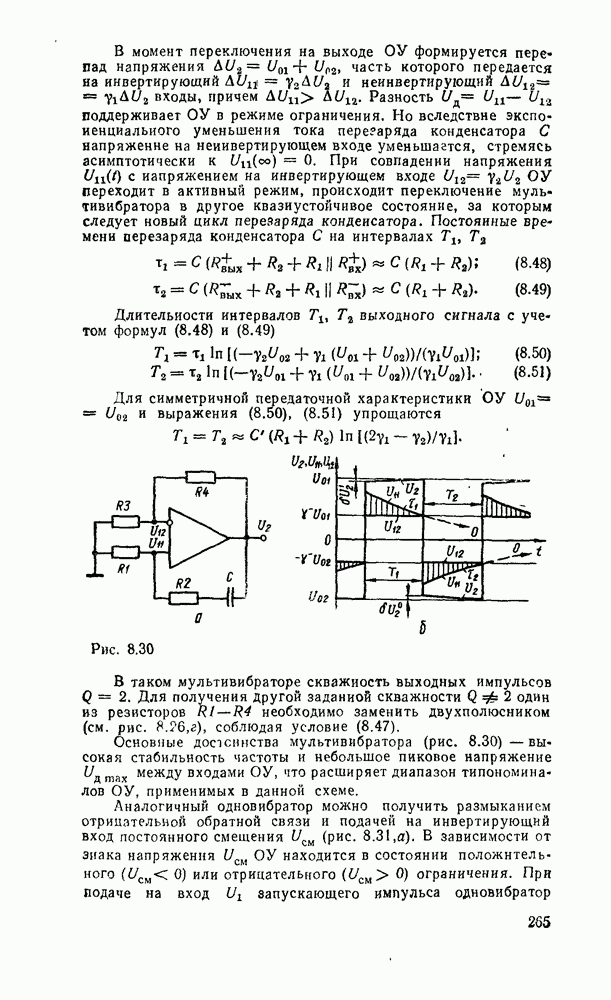
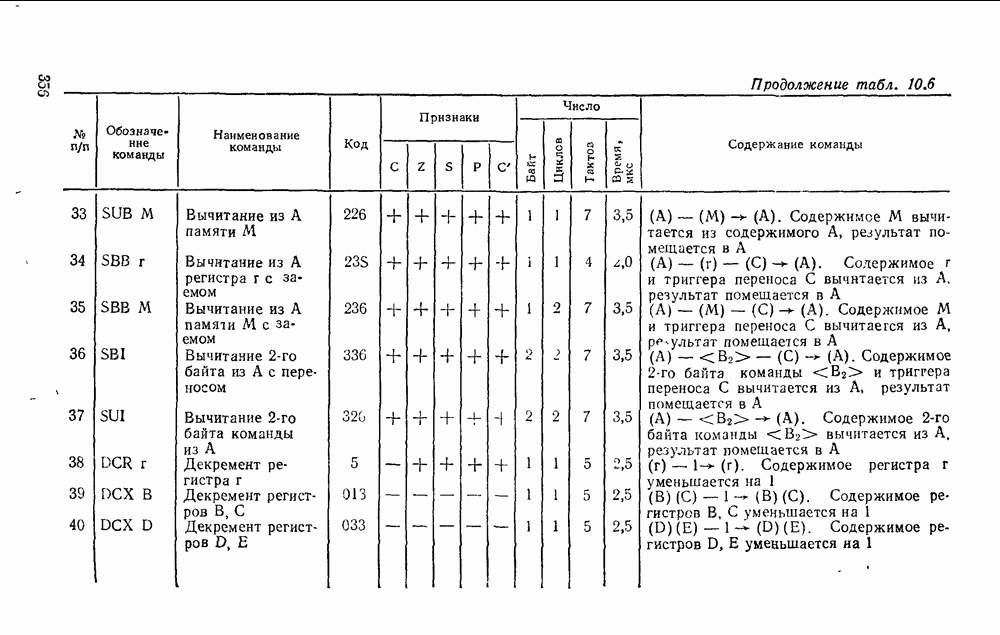
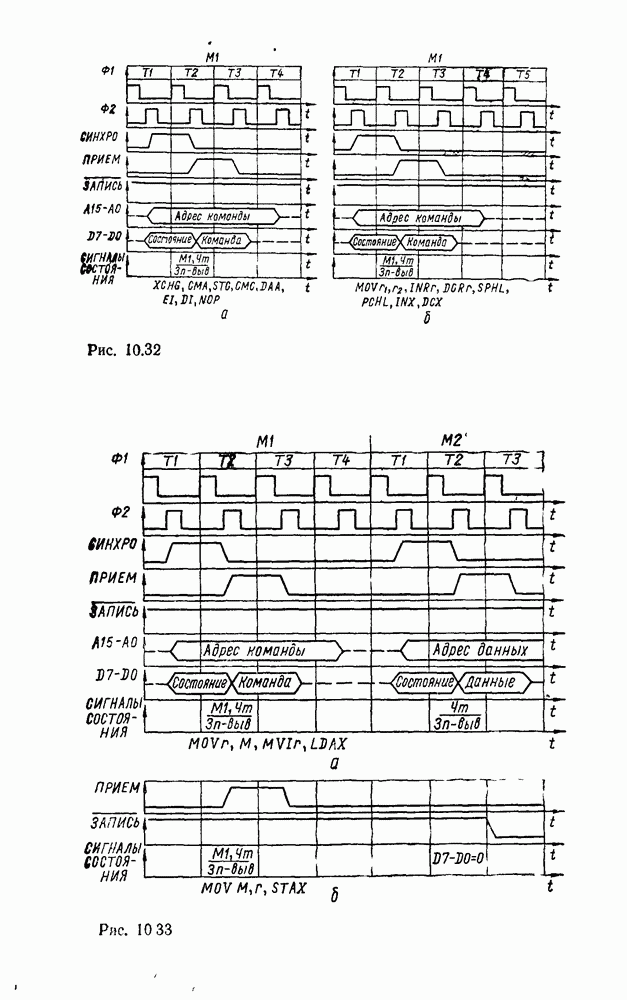
Операция ИЛИ — НЕ, реализующая стрелку Пирса  , позволяет выразить булевы функции соотношениями
, позволяет выразить булевы функции соотношениями  . Отсюда следует, что вентиль ИЛИ—НЕ, таблица соответствия которого дана на рис. 3.10, а, эквивалентен вентилю НЕ—ИЛИ (см. табл. 3.1) и позволяет реализовать булевы операции, как показано на рис.
. Отсюда следует, что вентиль ИЛИ—НЕ, таблица соответствия которого дана на рис. 3.10, а, эквивалентен вентилю НЕ—ИЛИ (см. табл. 3.1) и позволяет реализовать булевы операции, как показано на рис.  . Вследствие дуальности операций
. Вследствие дуальности операций  и ИЛИ—НЕ соответствующие реализации вместе с сопровождающими их комментариями можно получить на основе принципа дуальности.
и ИЛИ—НЕ соответствующие реализации вместе с сопровождающими их комментариями можно получить на основе принципа дуальности.

Рис. 3.10.

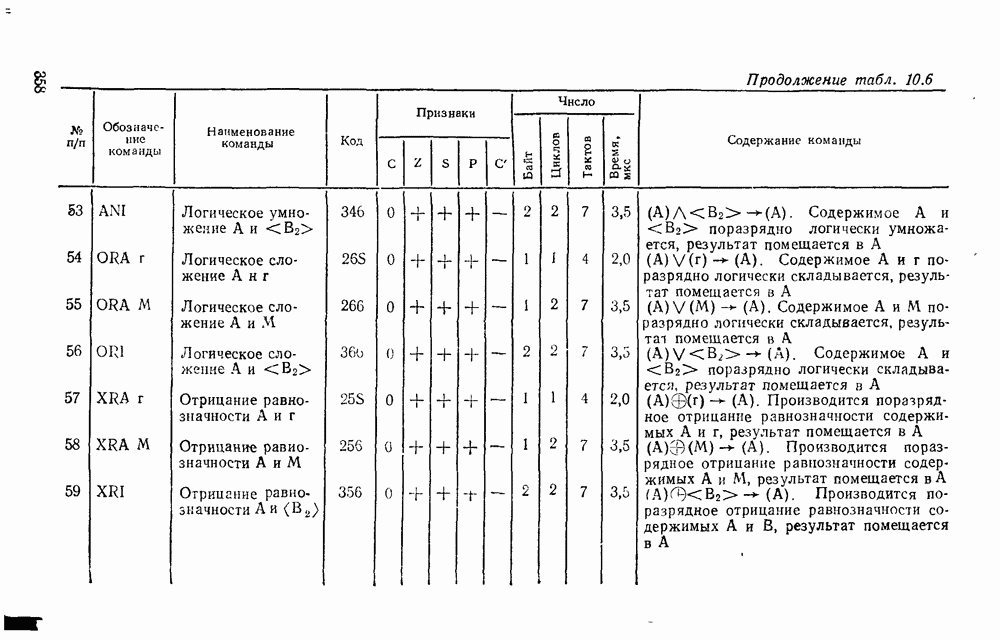
Рис. 3.11.

Рис. 3.12.
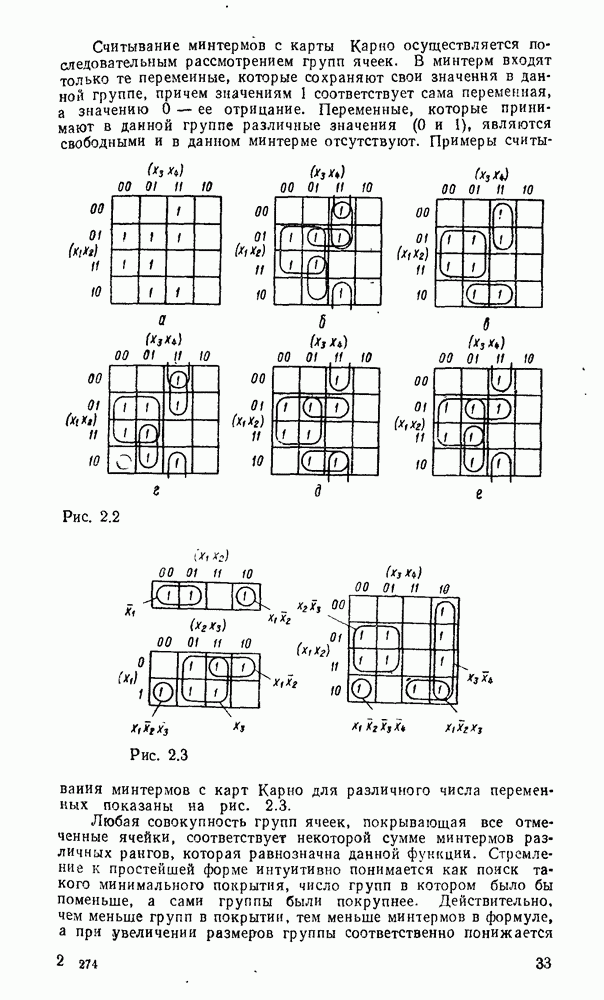
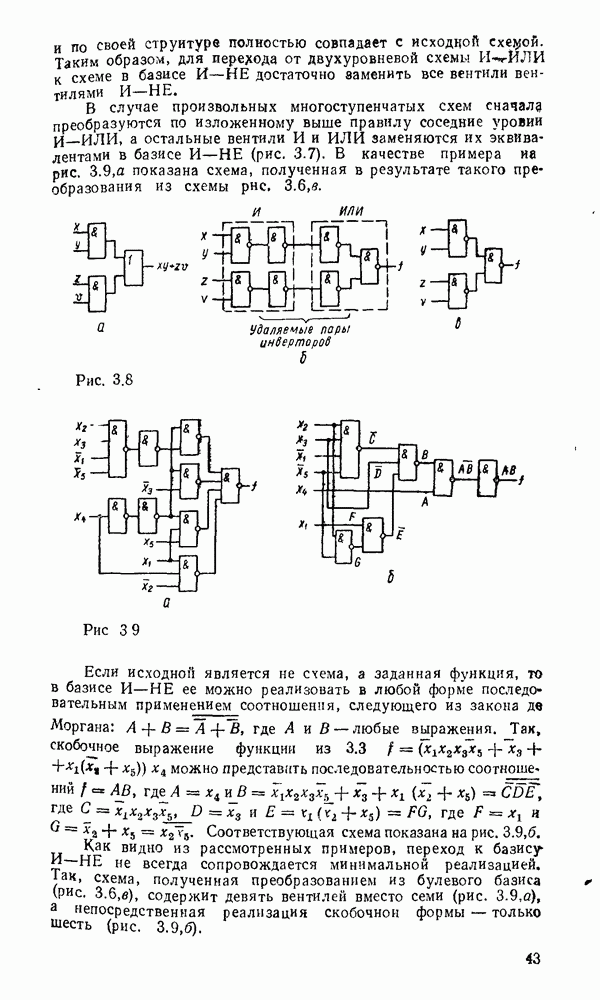
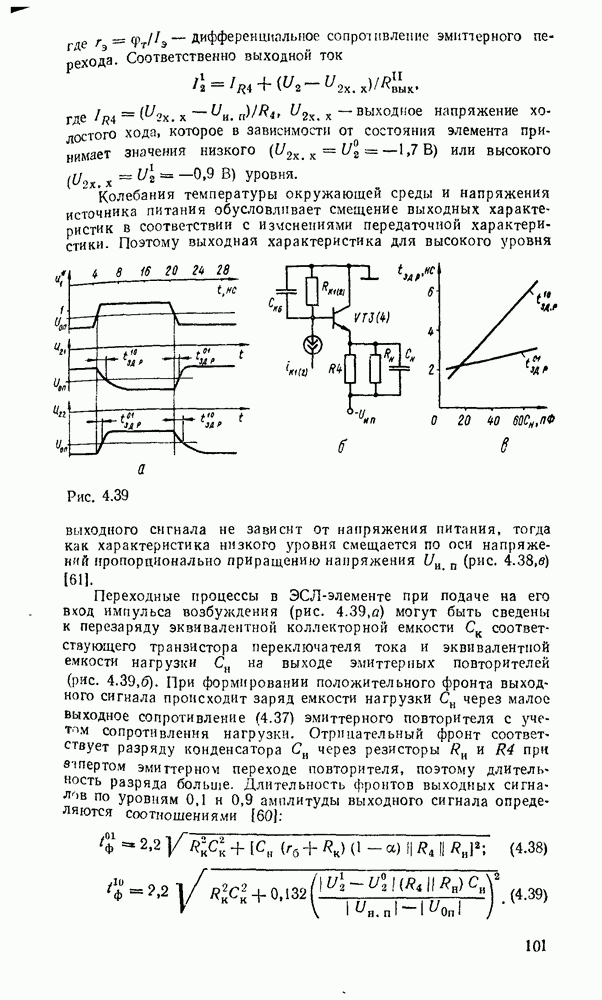
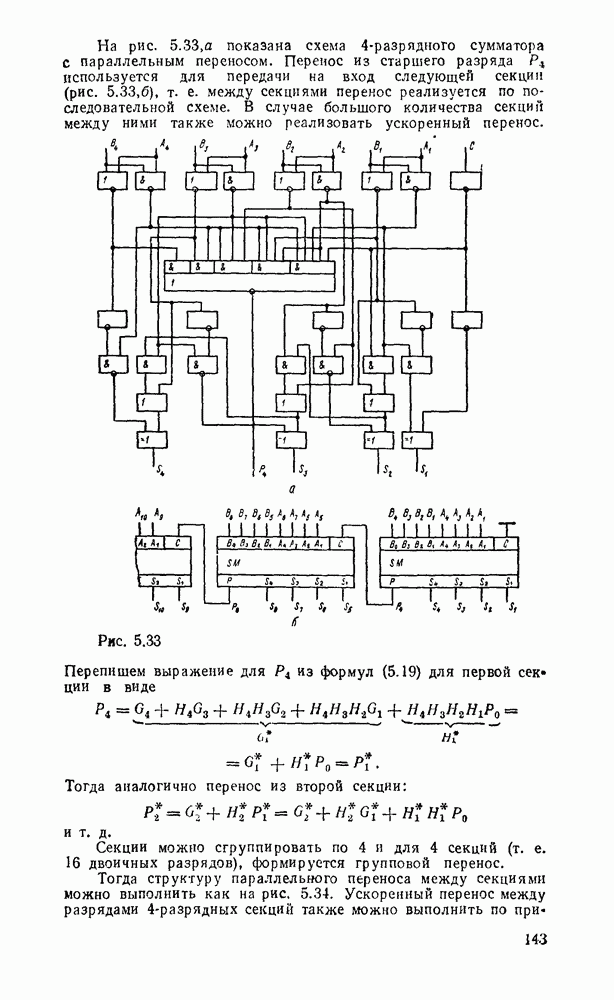
На рис. 3.11, дуальном рис. 3.8, показан переход от двухуровневой схемы ИЛИ/И, которая соответствует конъюнктивной нормальной форме  , к реализации в базисе ИЛИ—НЕ. Здесь исходная схема (рис. 3.11,а) преобразуется так, что можно устранить последовательно включенные пары инверторов (рис.
, к реализации в базисе ИЛИ—НЕ. Здесь исходная схема (рис. 3.11,а) преобразуется так, что можно устранить последовательно включенные пары инверторов (рис.  ). После этого получаем схему (рис. 3.11,в), которая по своей структуре полностью совпадает с исходной.
). После этого получаем схему (рис. 3.11,в), которая по своей структуре полностью совпадает с исходной.
На рис.  , б показаны две эквивалентные реализации в базисе ИЛИ—НЕ функции, заданной в нормальной и преобразованной формах.
, б показаны две эквивалентные реализации в базисе ИЛИ—НЕ функции, заданной в нормальной и преобразованной формах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
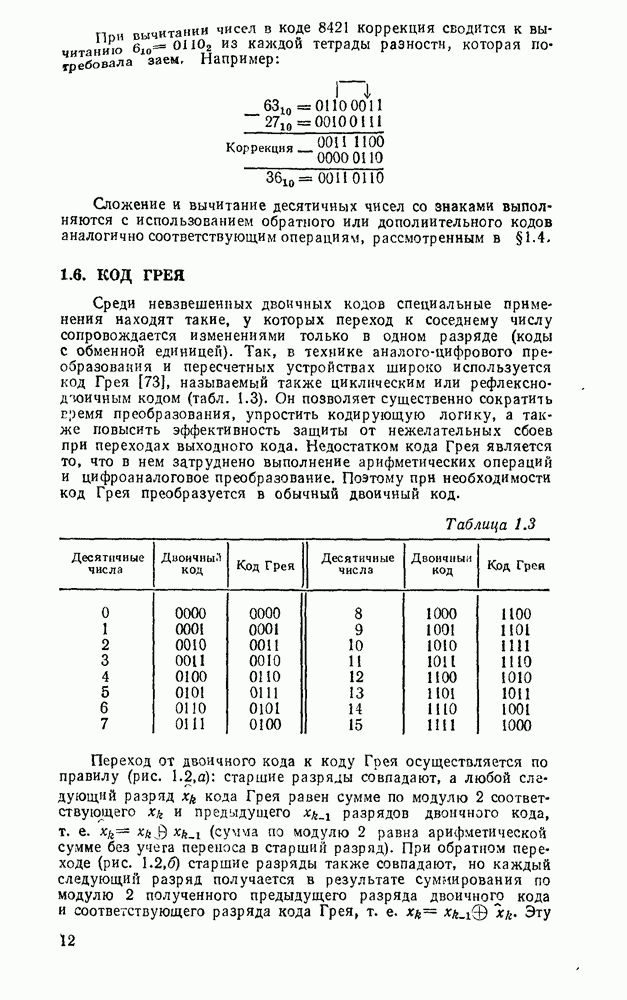
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
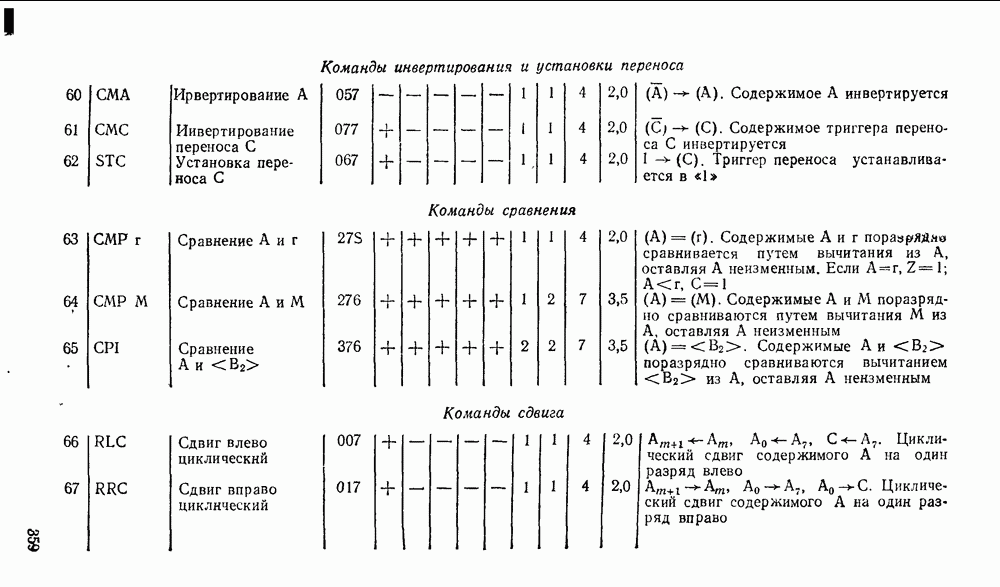
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
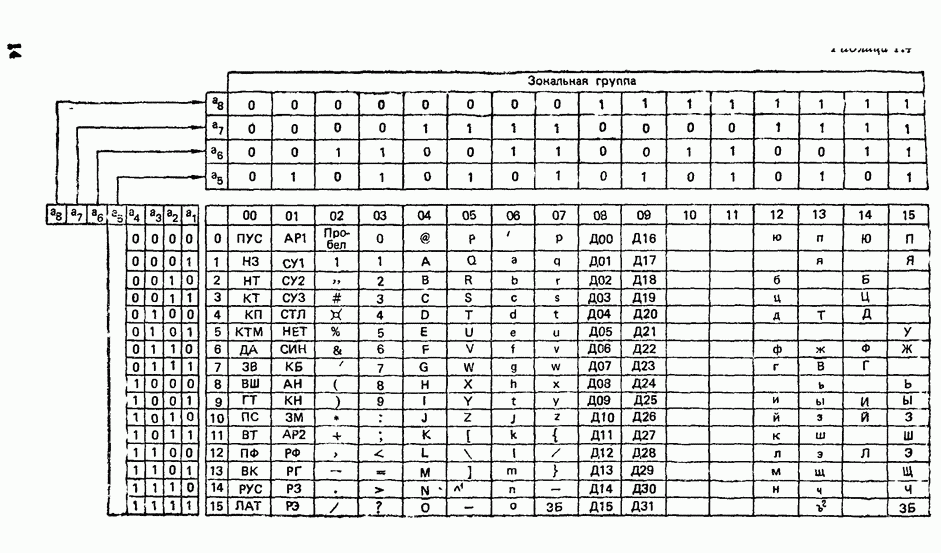
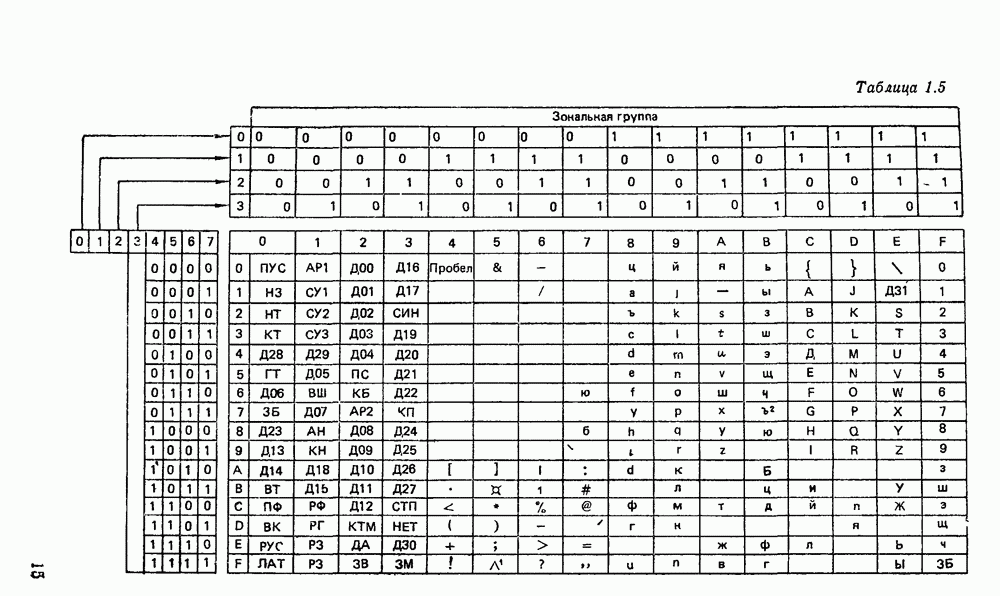
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
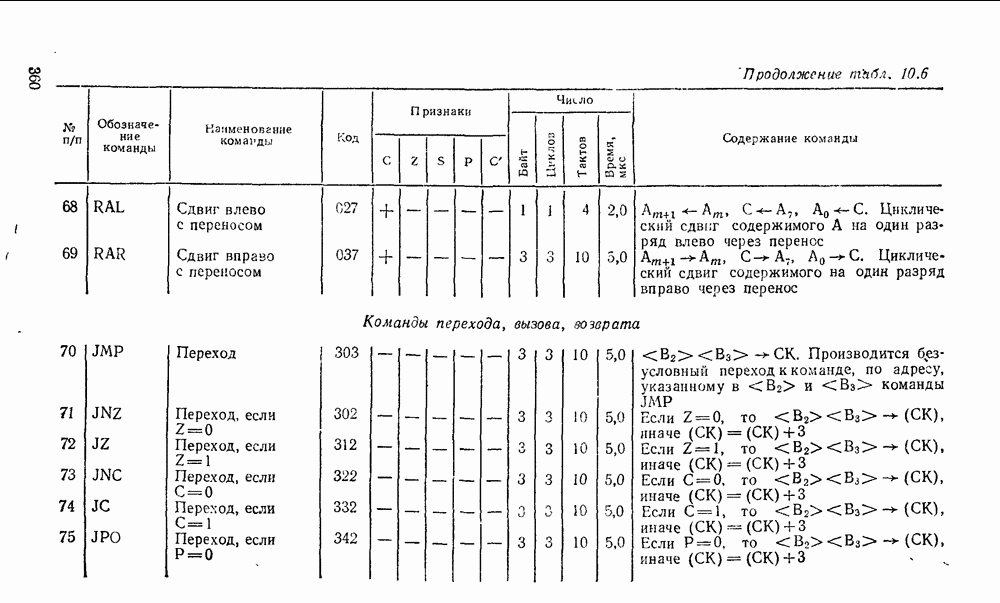
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
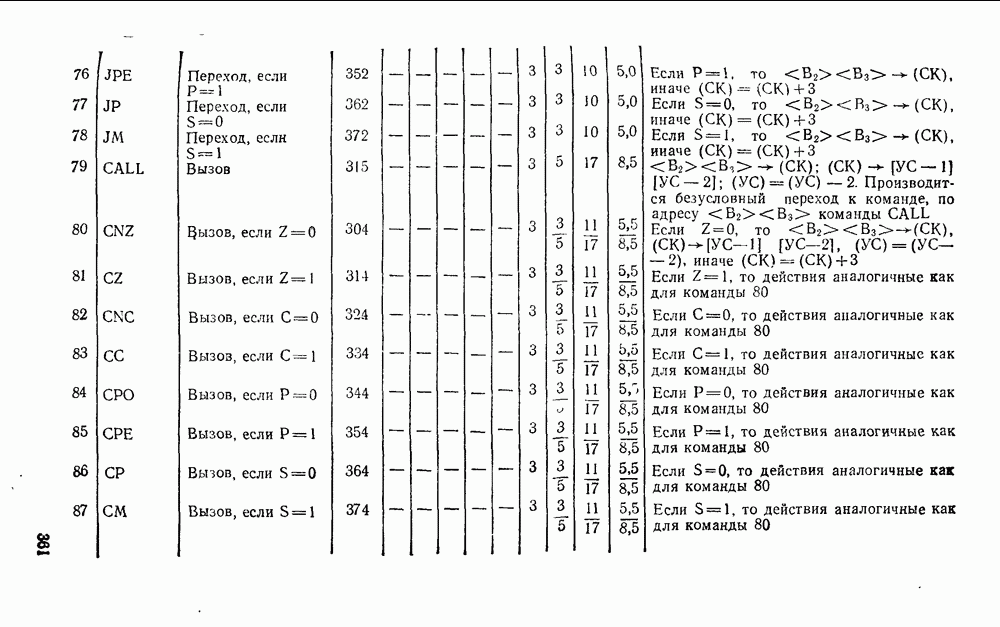
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
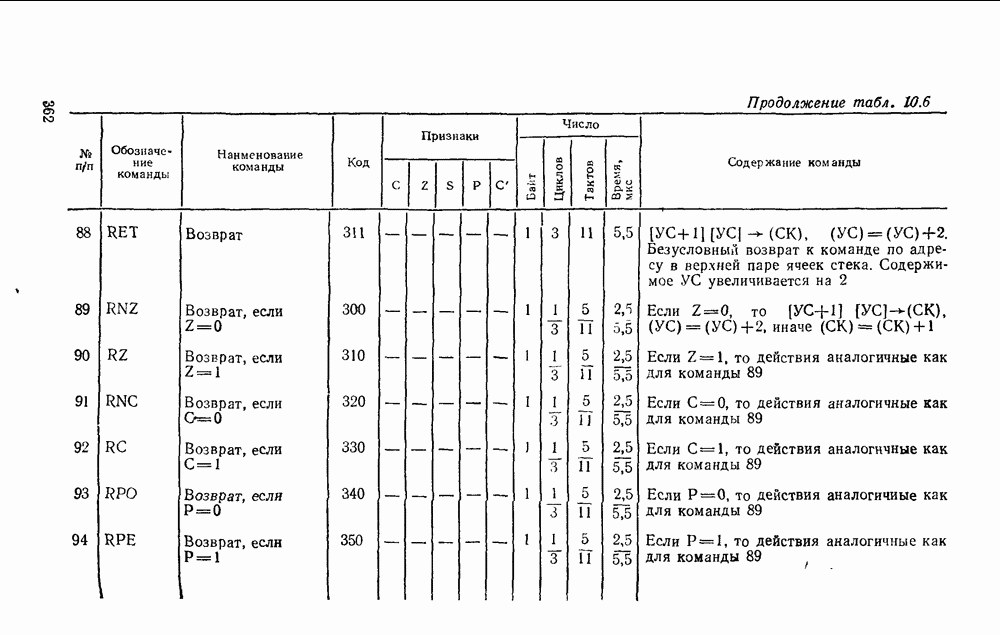
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
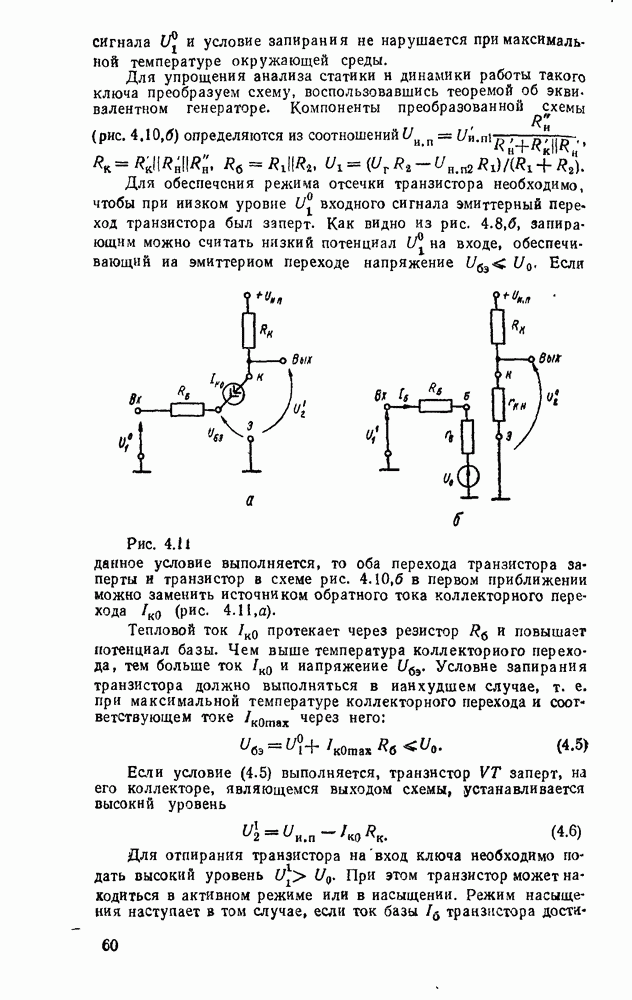
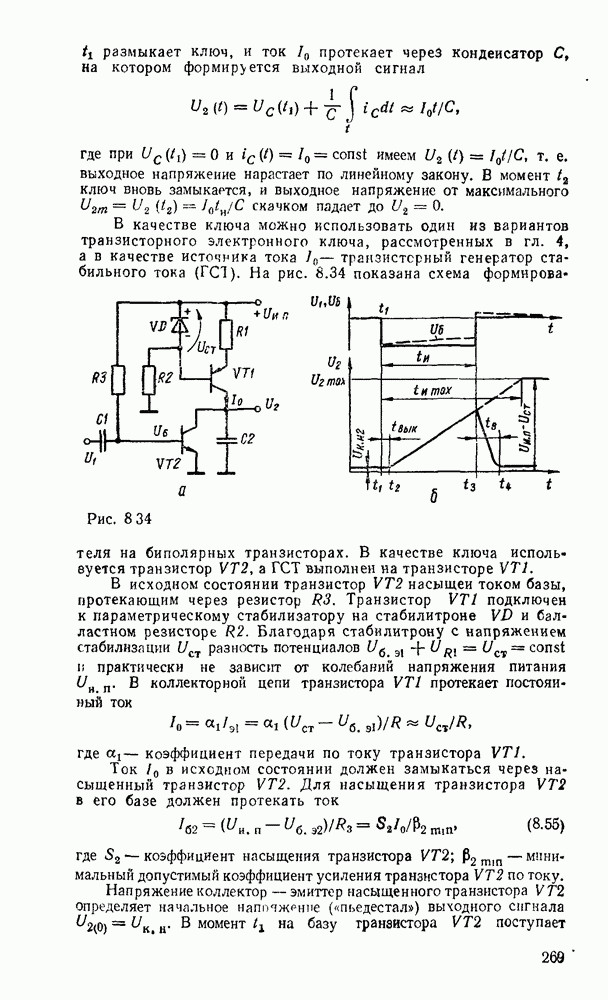
- Электронные ключи на биполярных транзисторах.
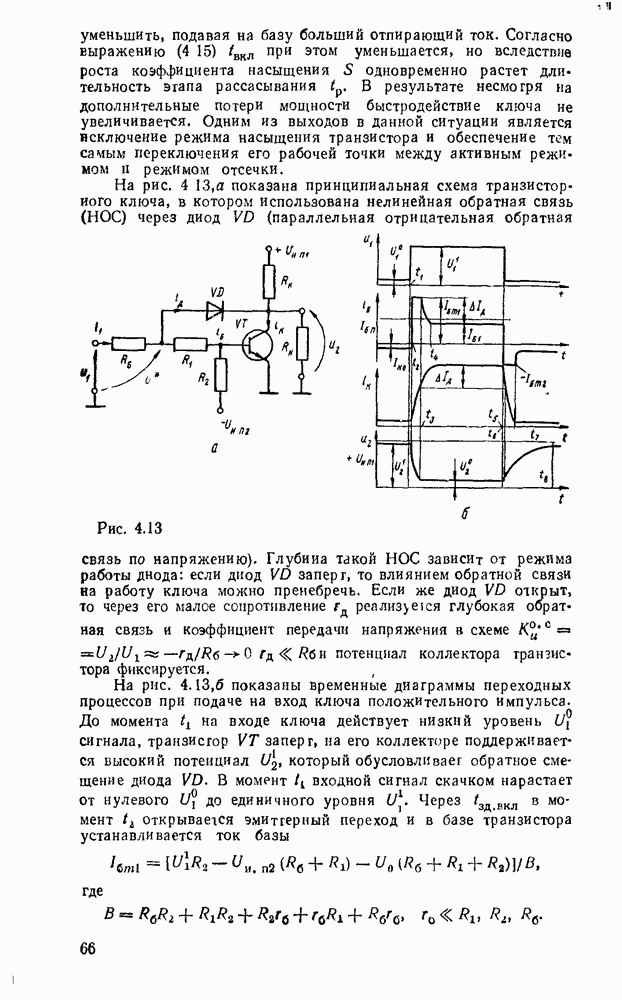
- Ключ на биполярном транзисторе с нелинейной обратной связью.
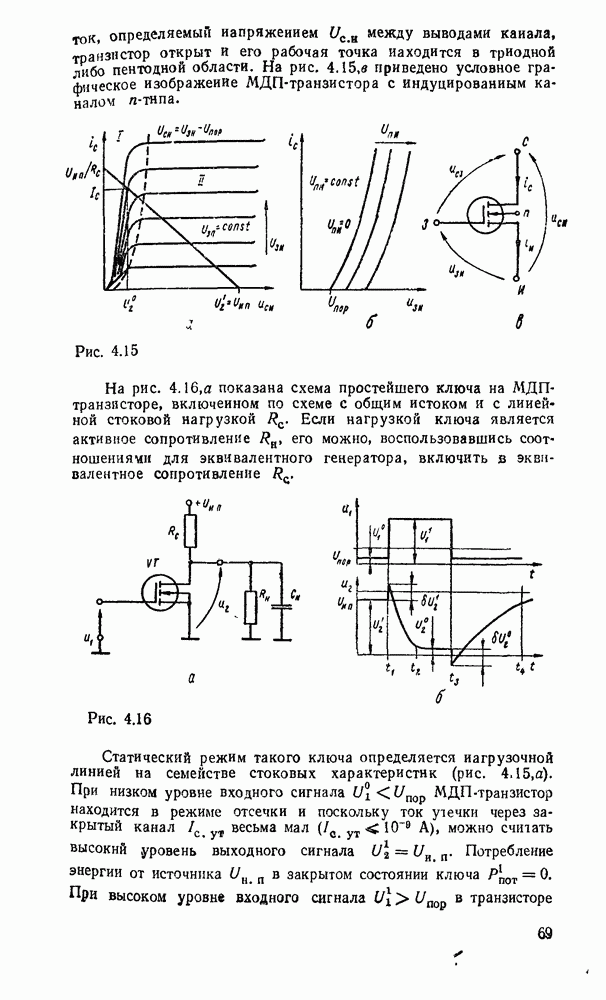
- Электронные ключи на полезых транзисторах.
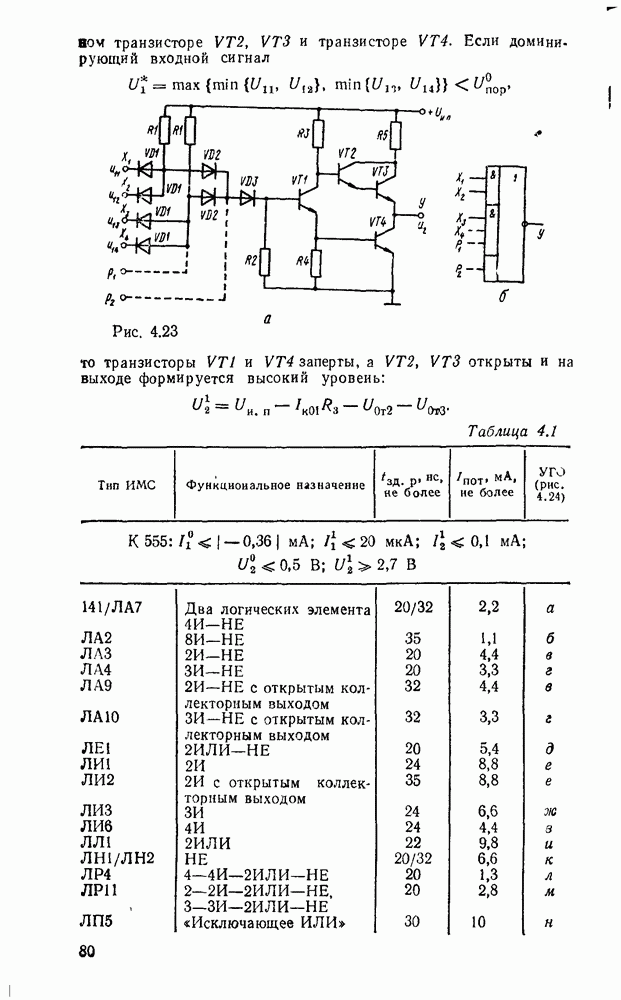
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
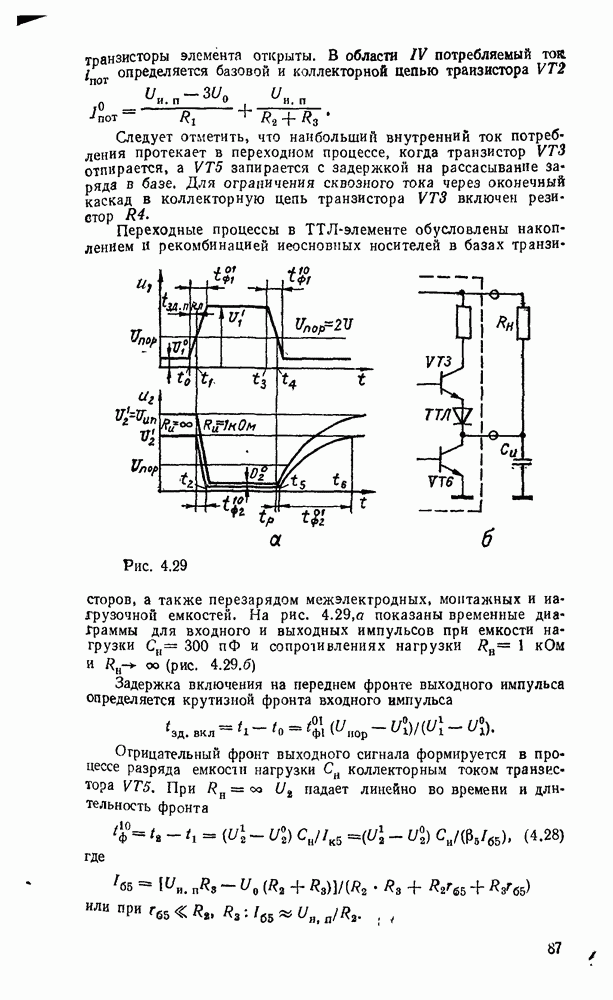
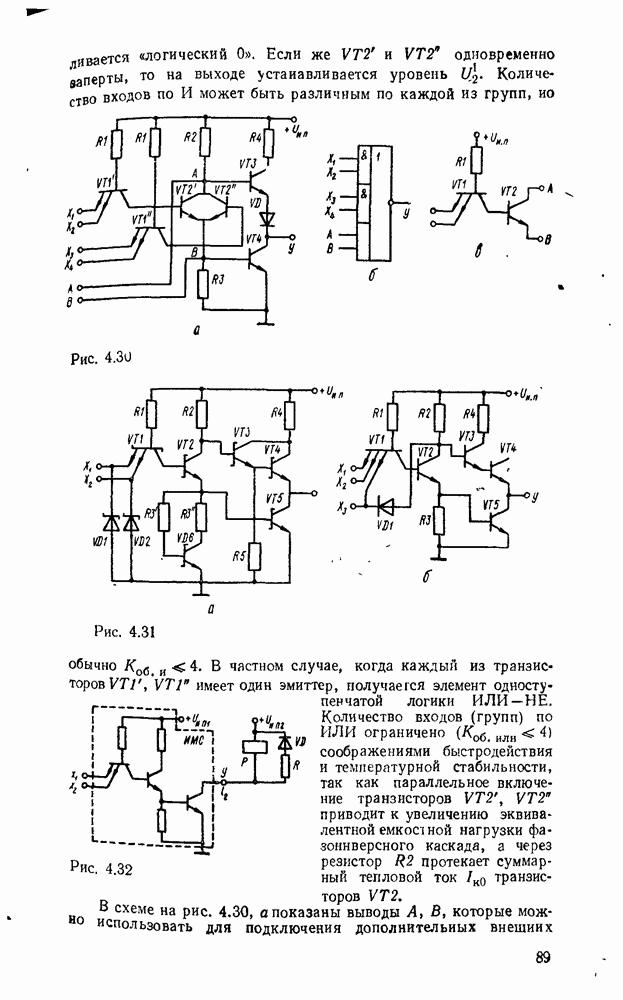
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
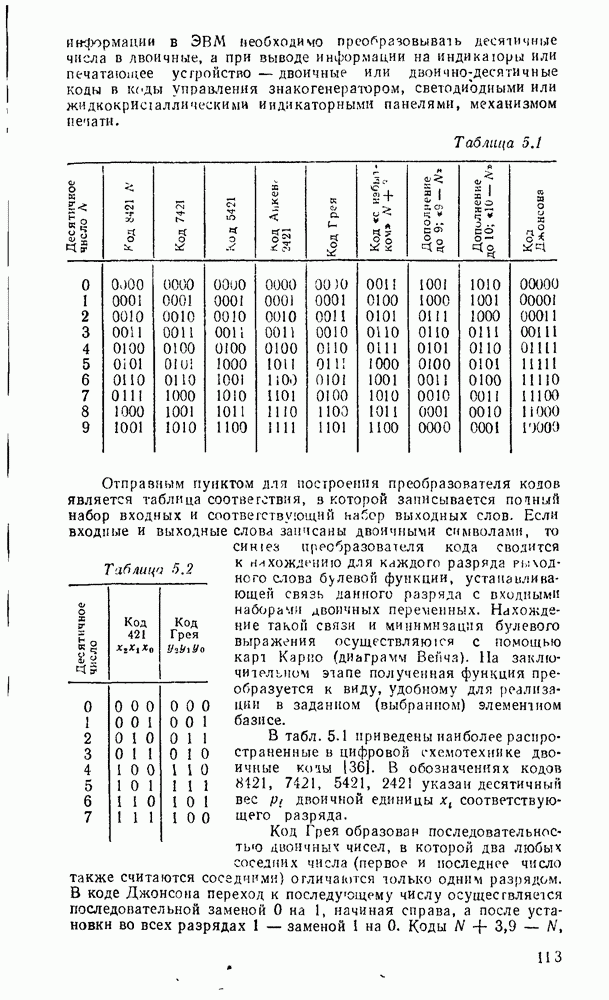
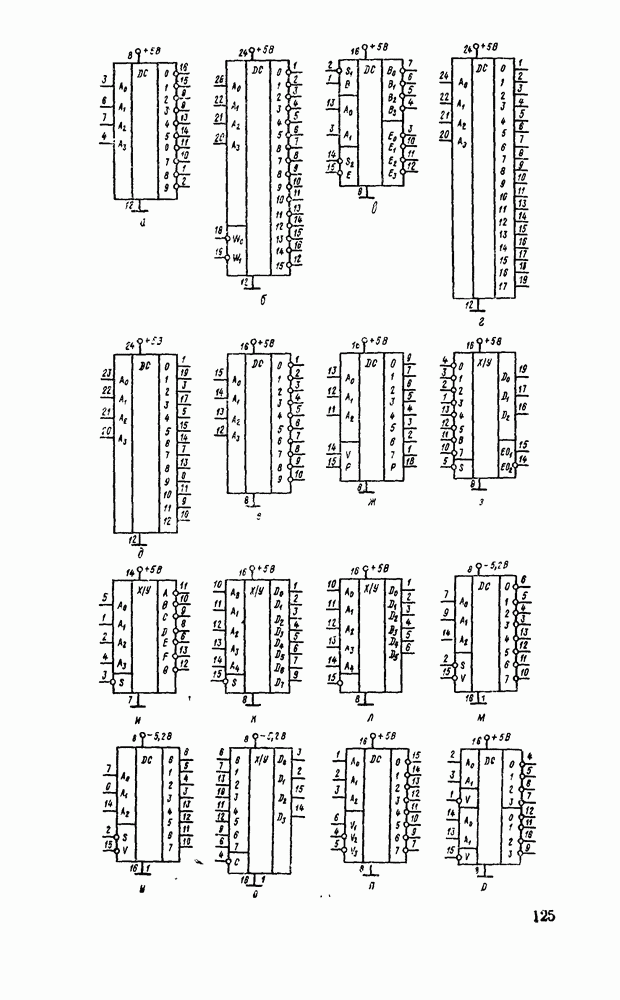
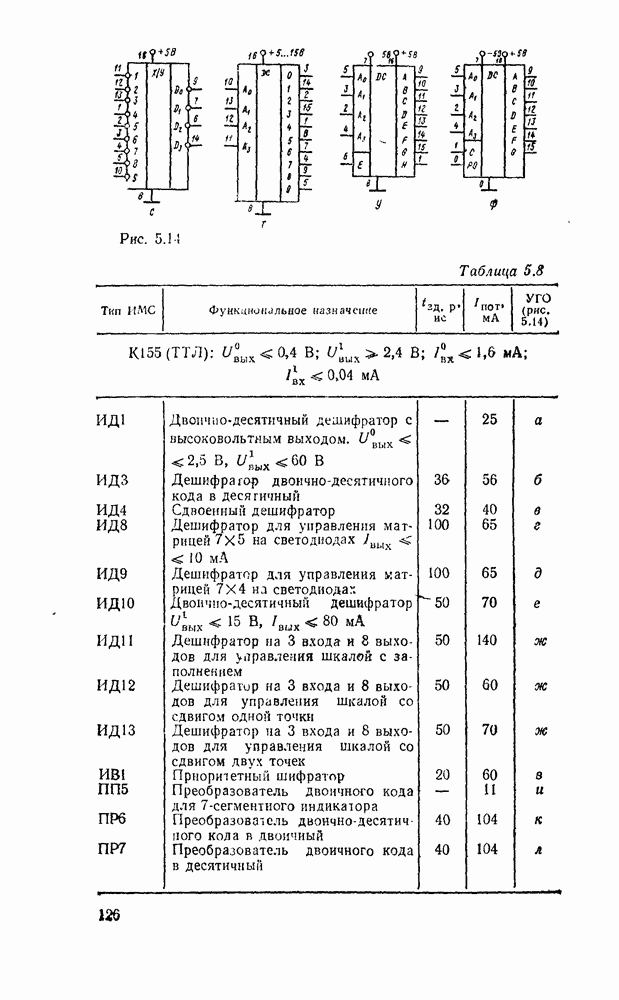
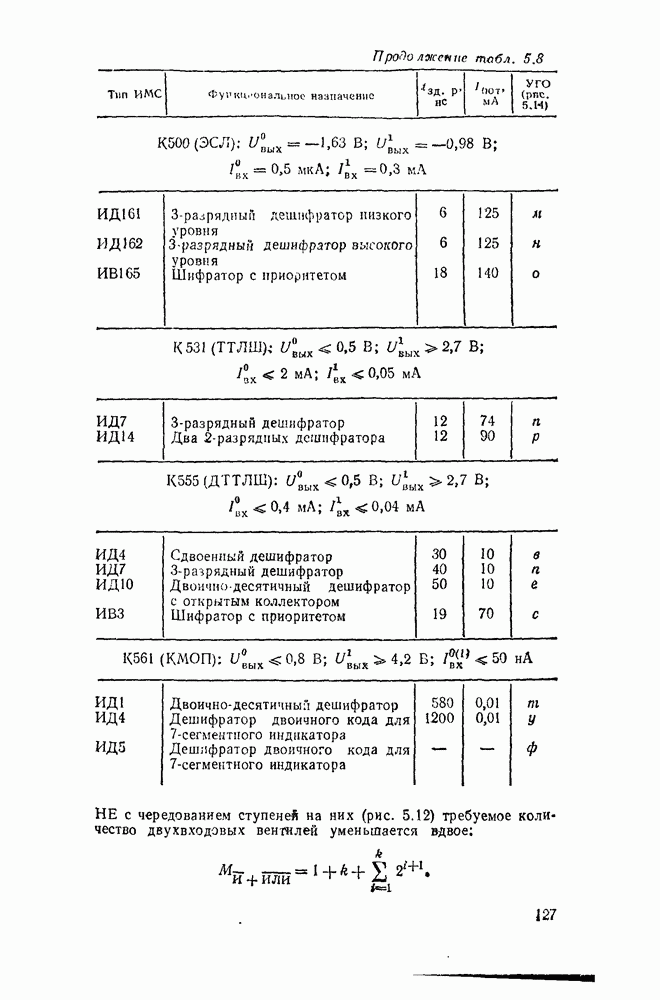
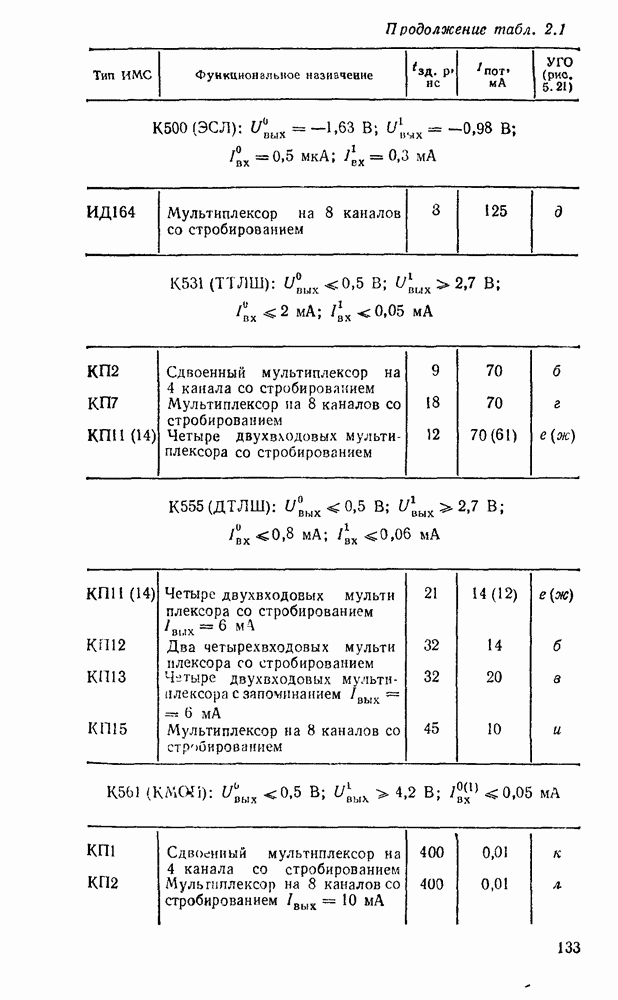
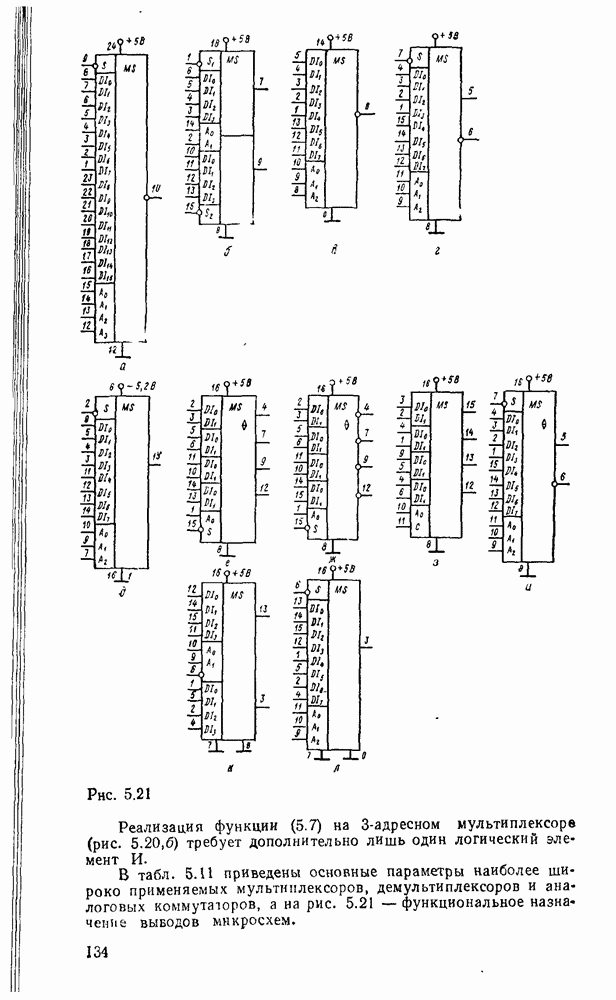
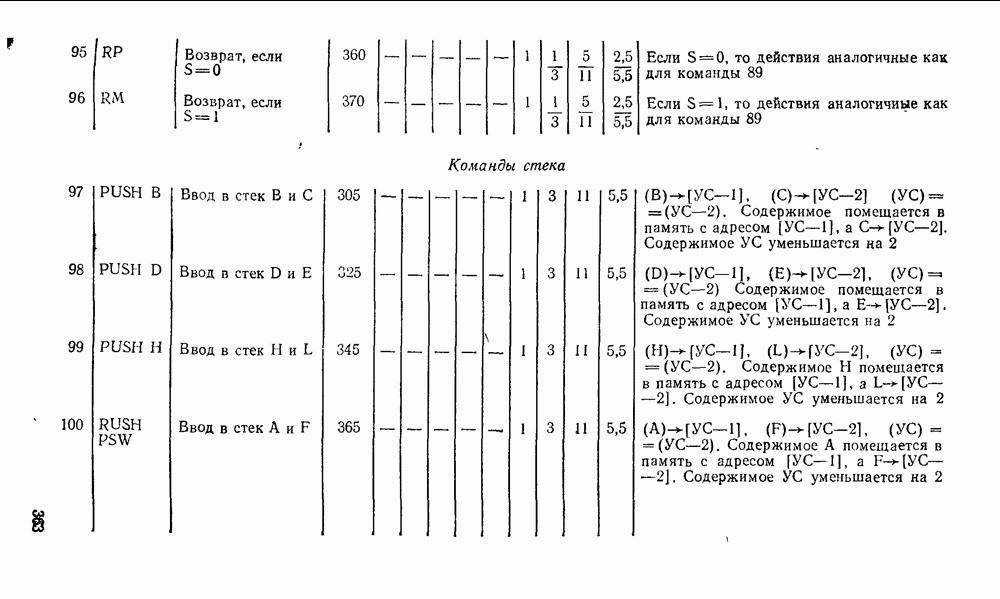
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
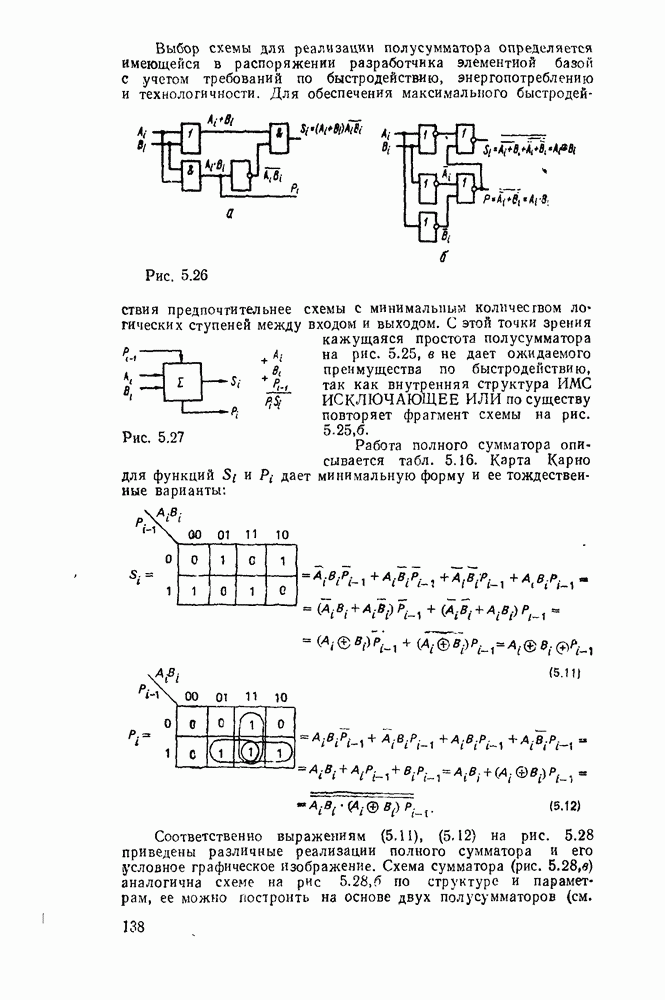
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
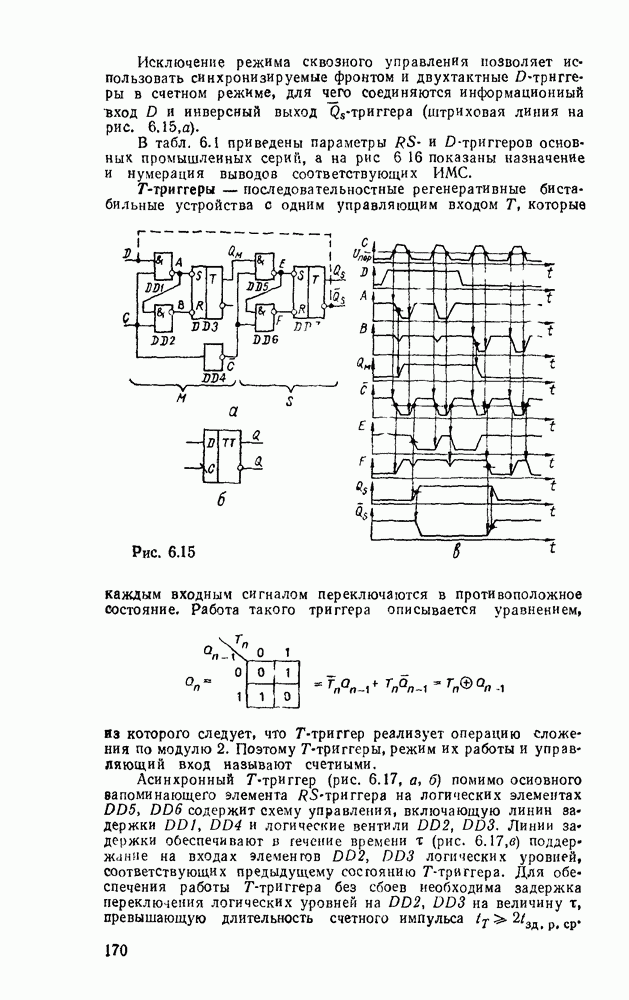
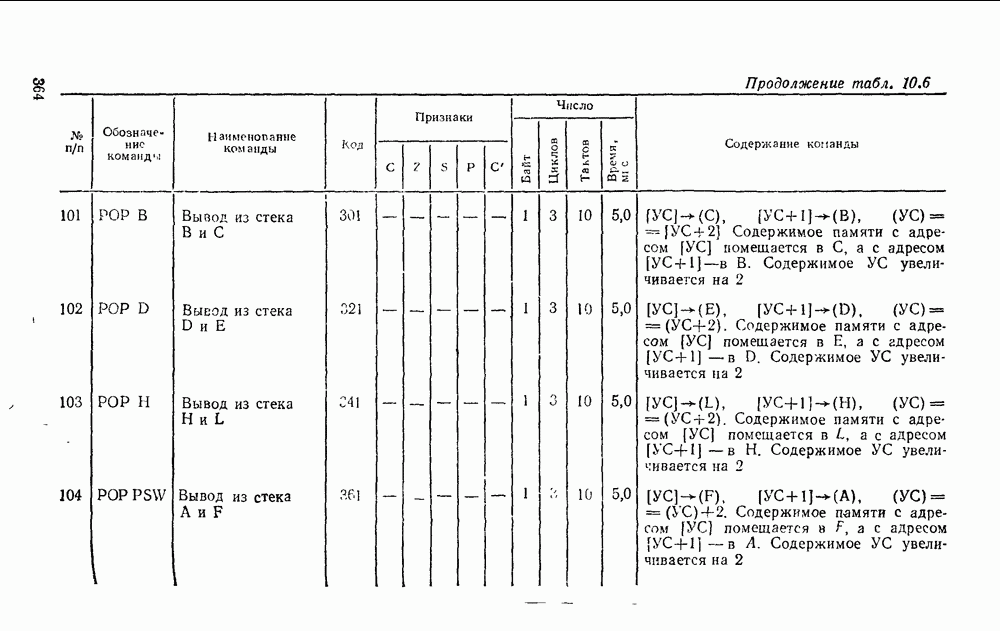
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
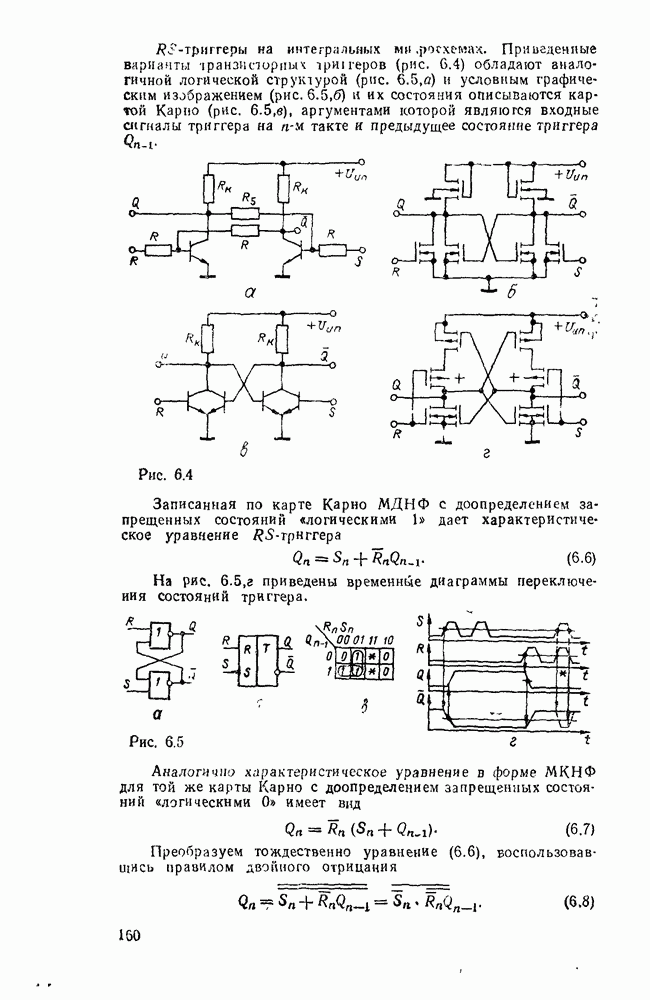
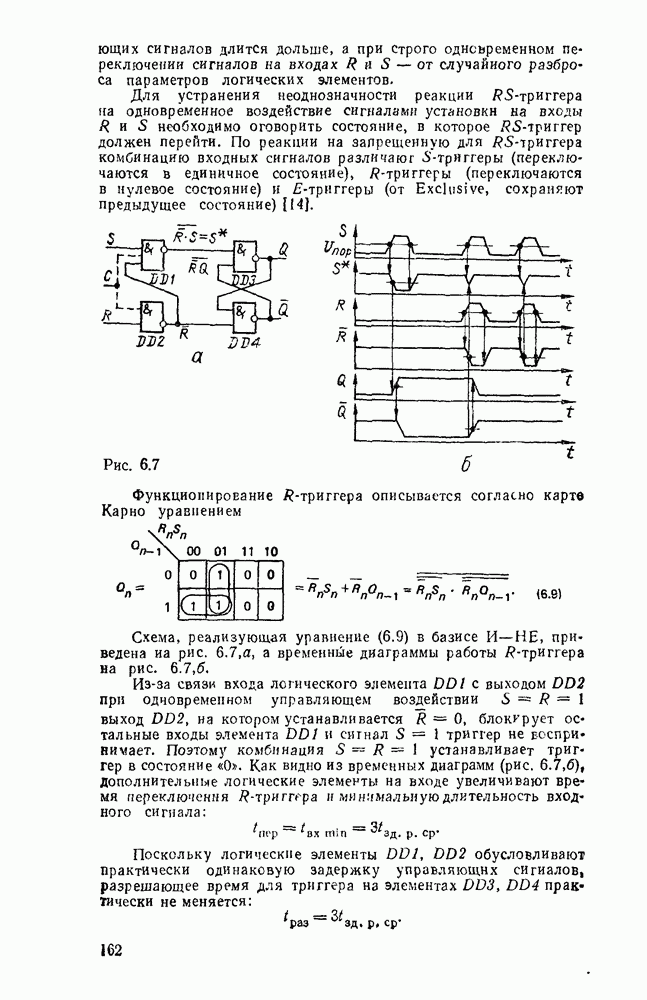
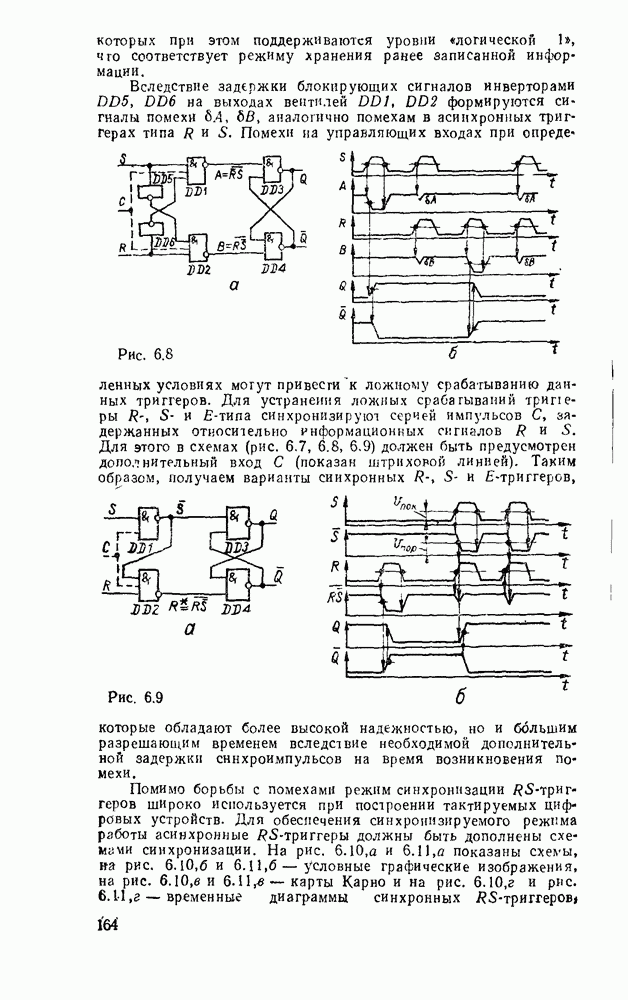
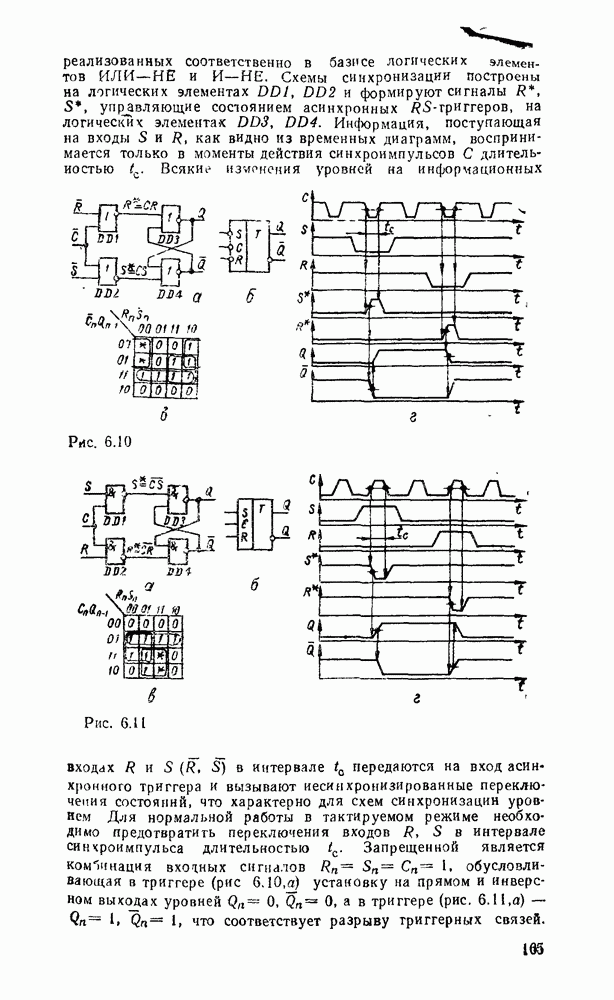
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
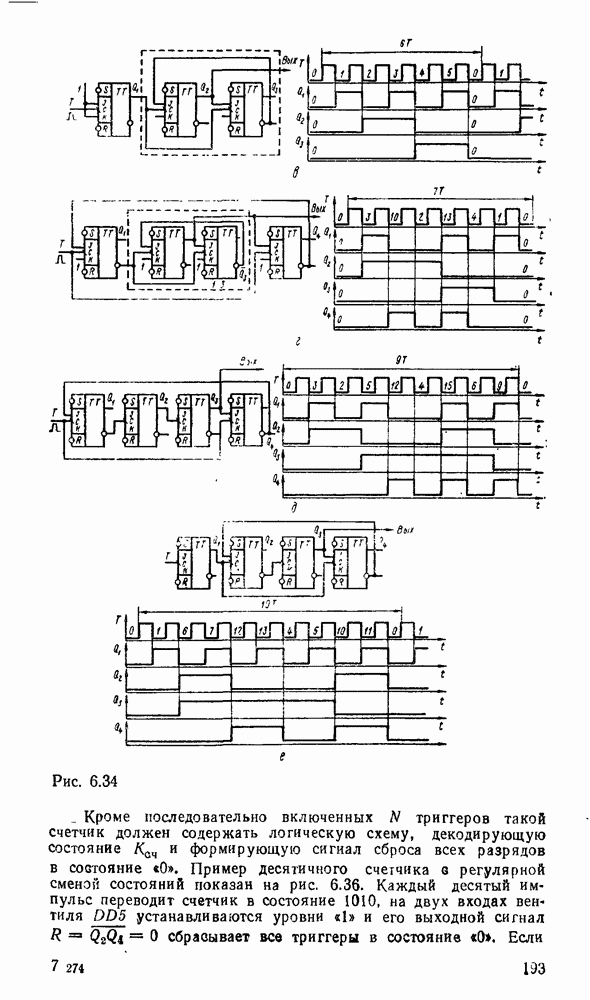
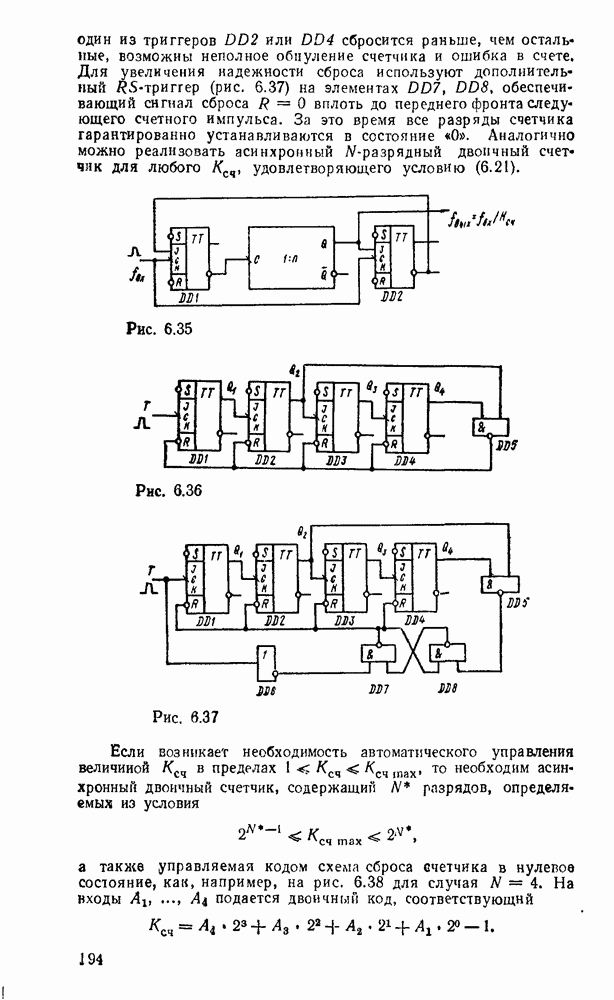
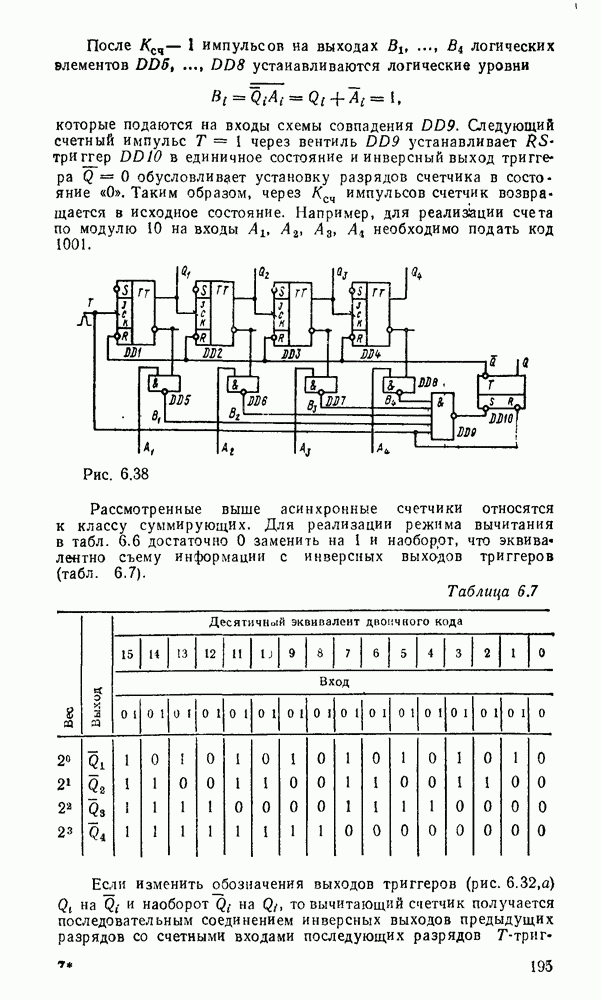
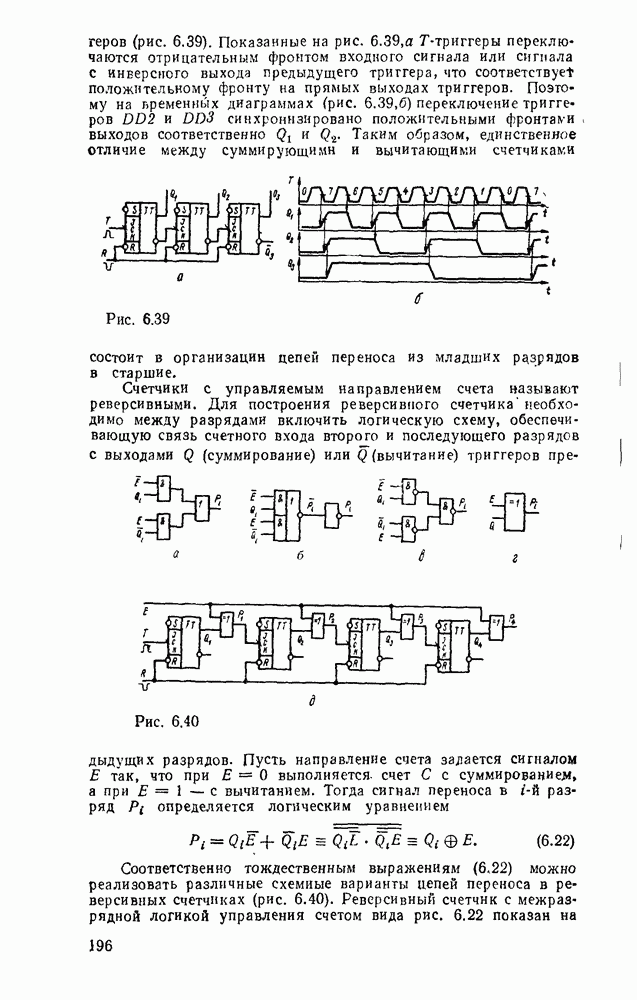
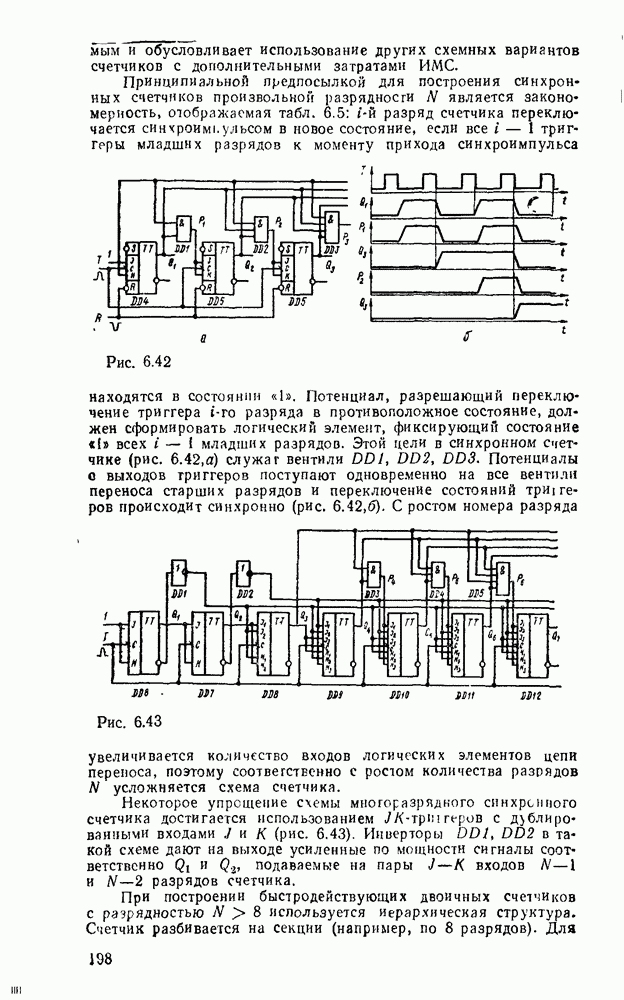
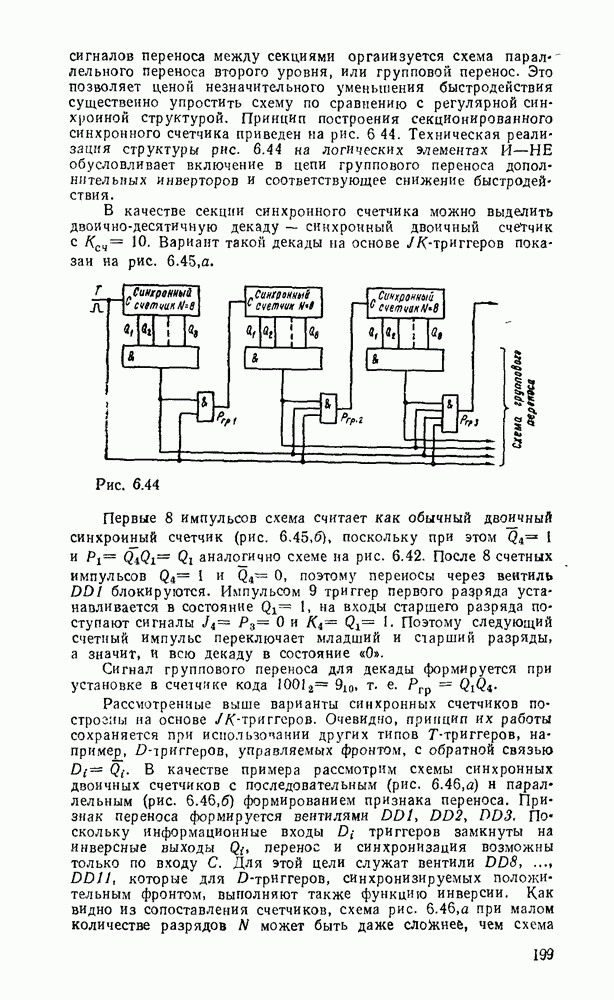
- 6.3. СЧЕТЧИКИ
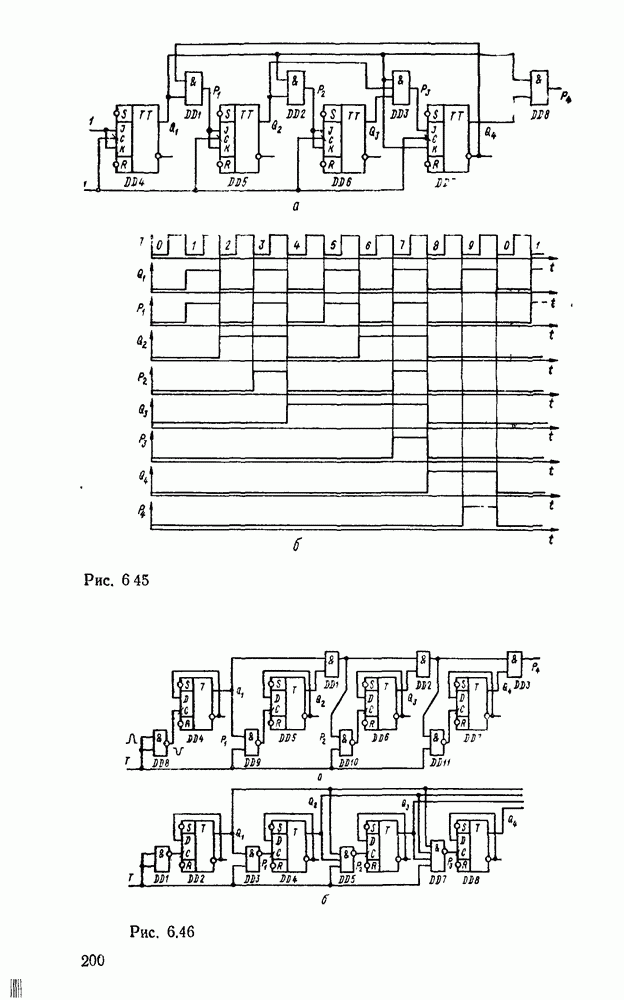
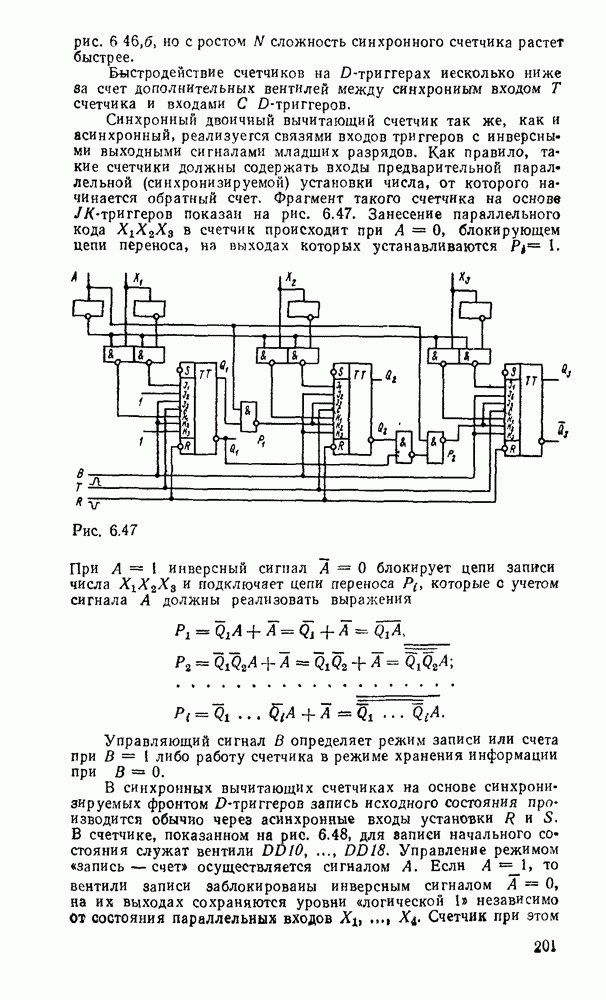
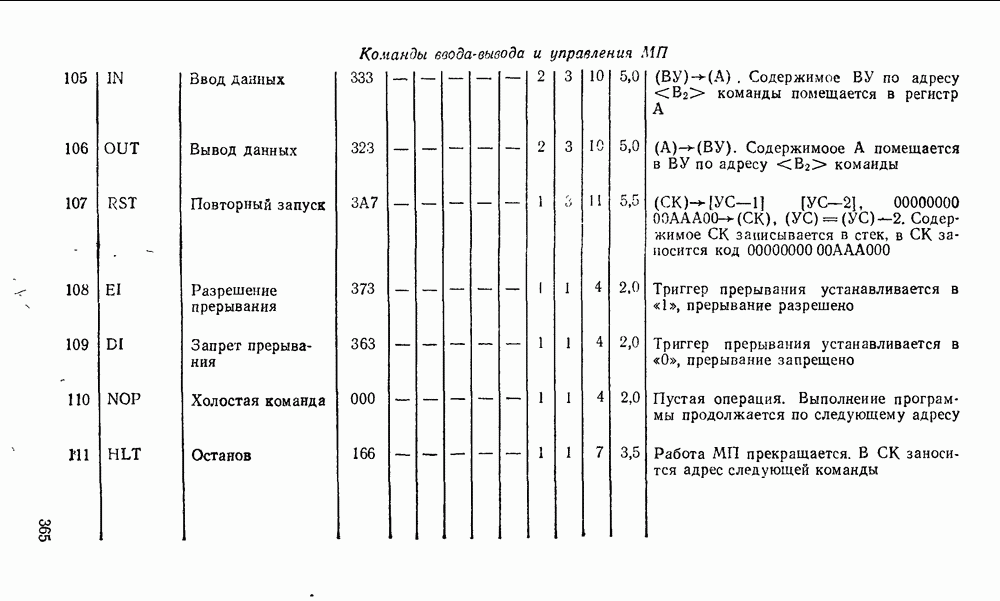
- Синхронные счетчики.
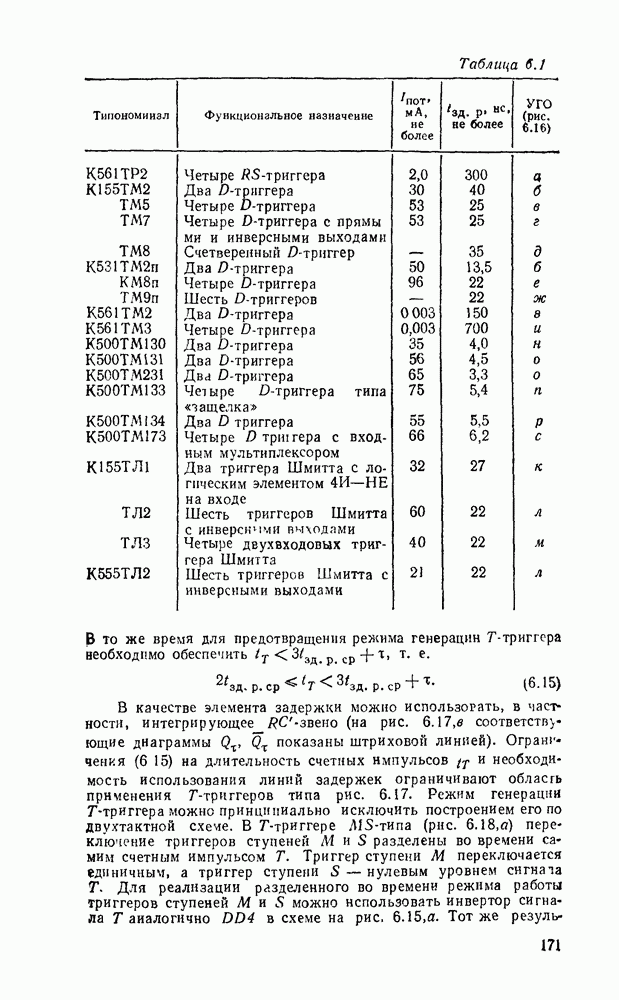
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
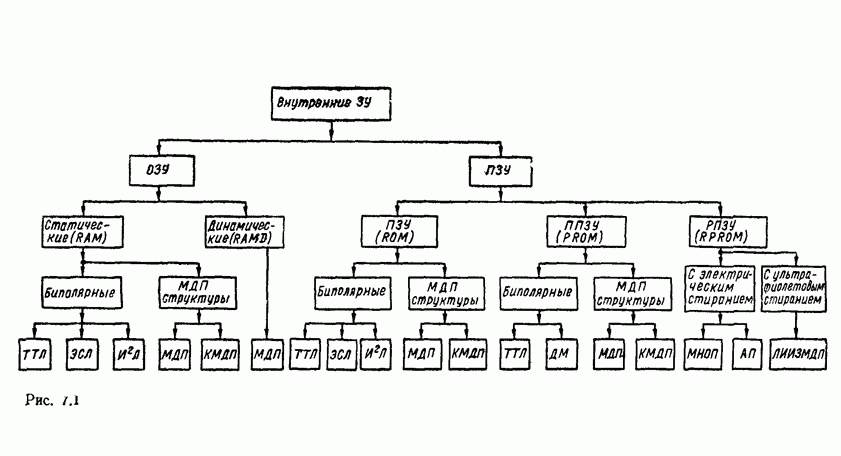
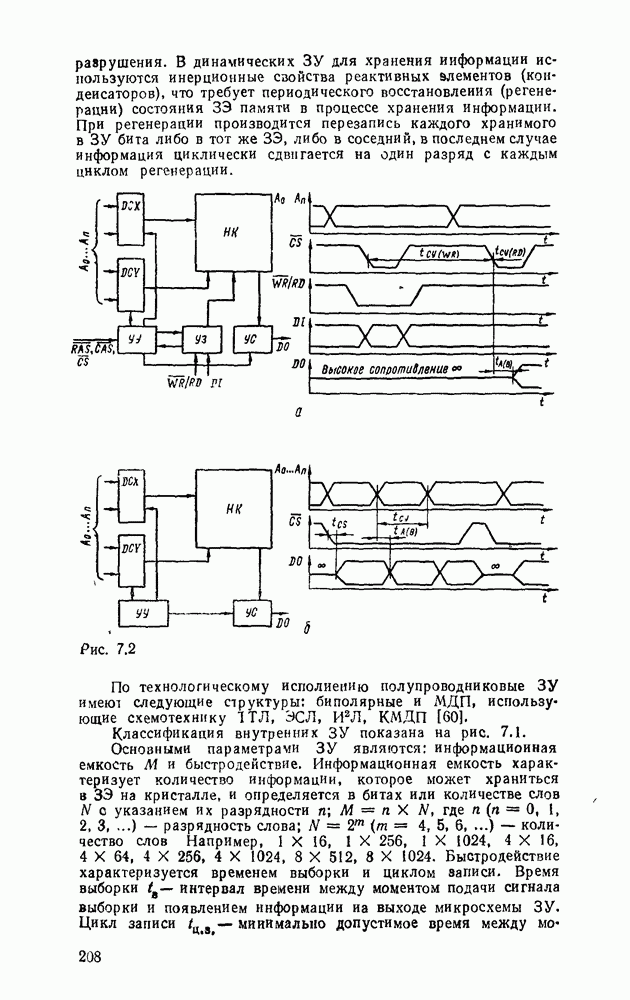
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
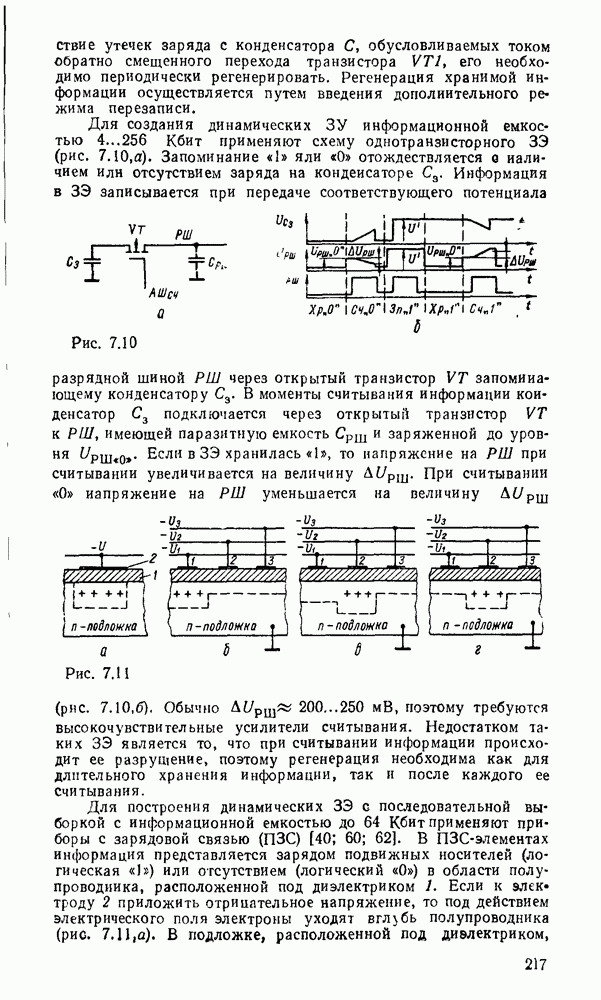
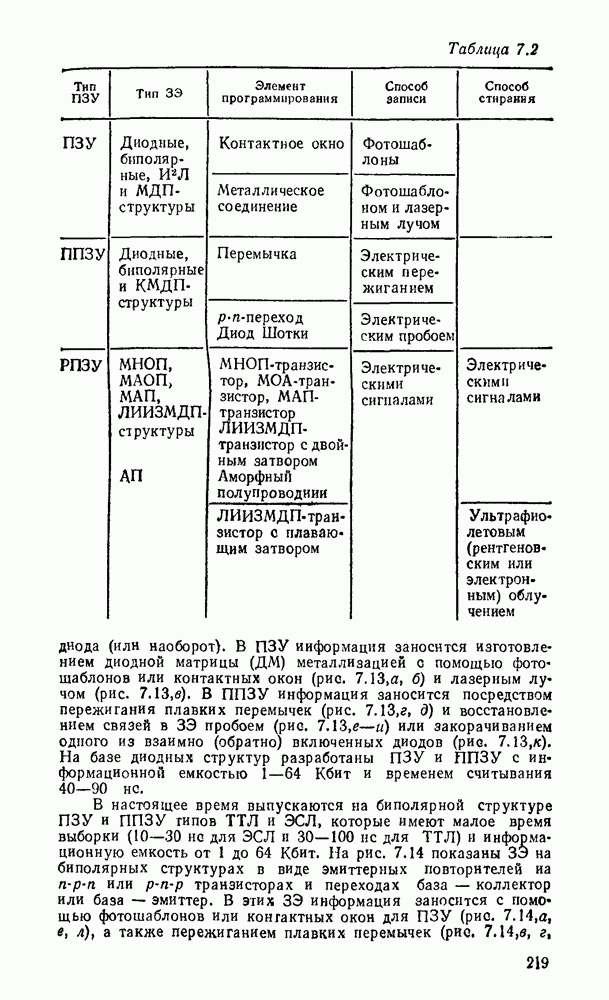
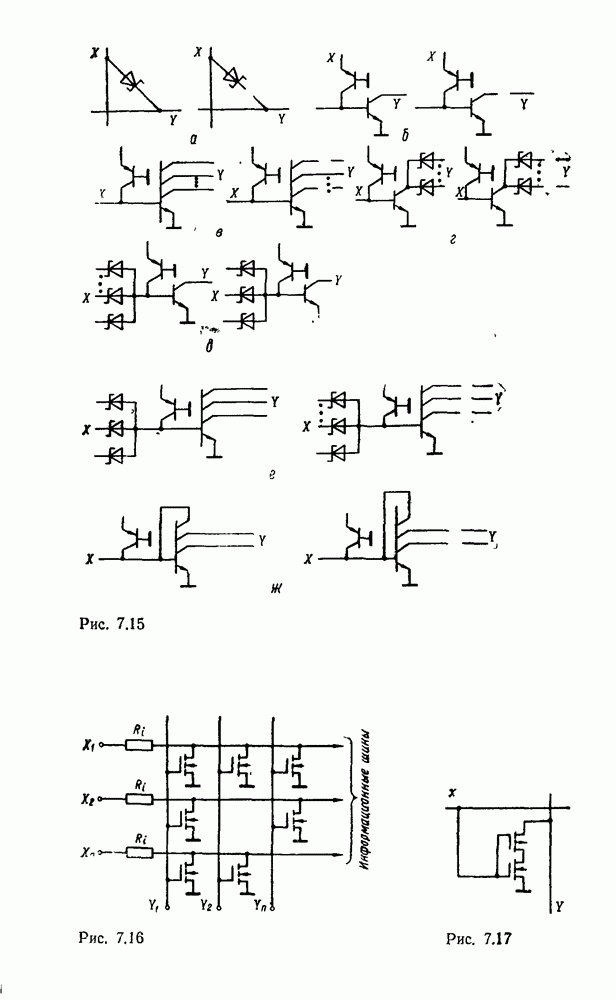
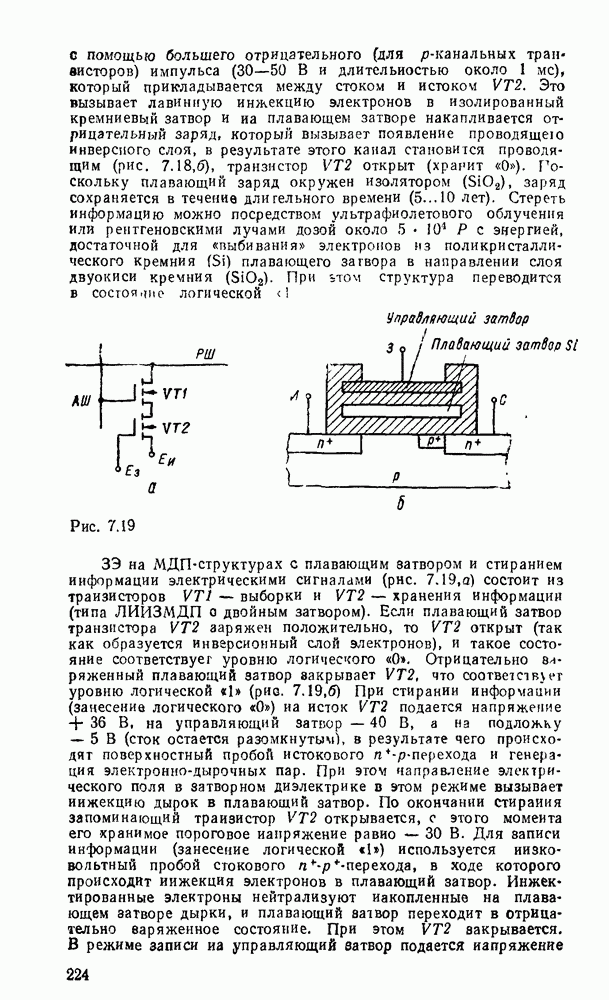
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
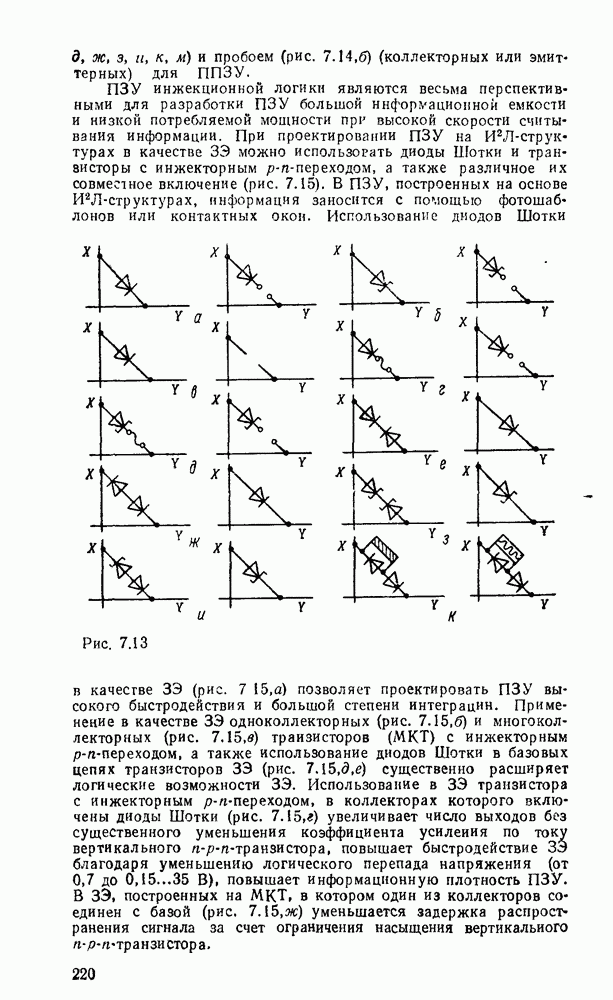
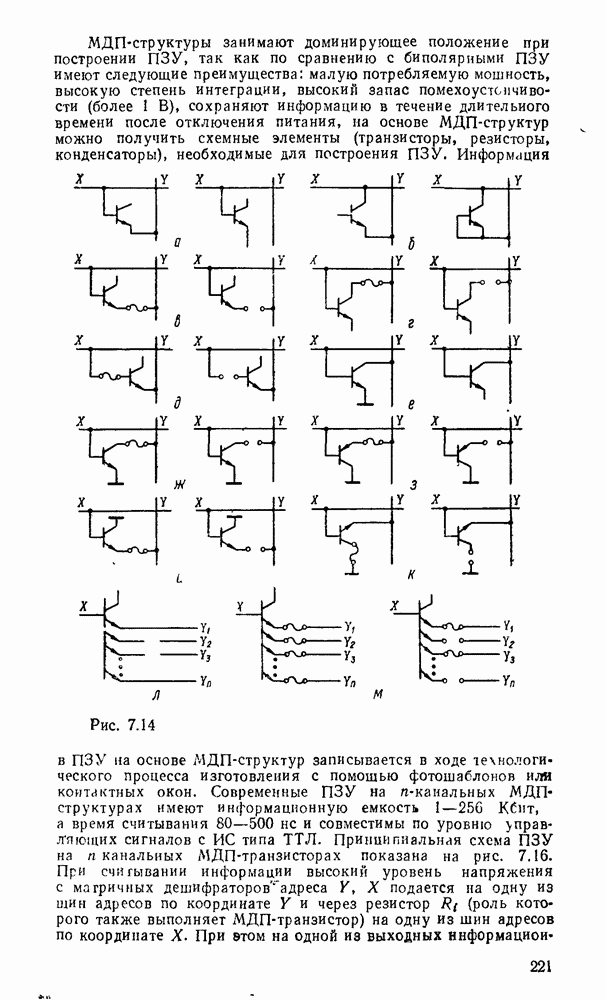
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
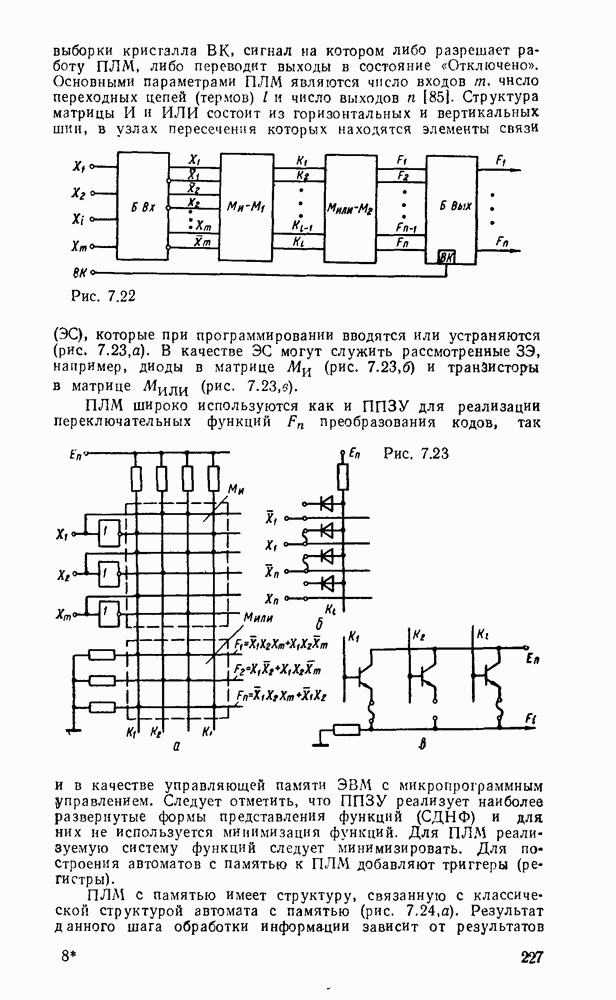
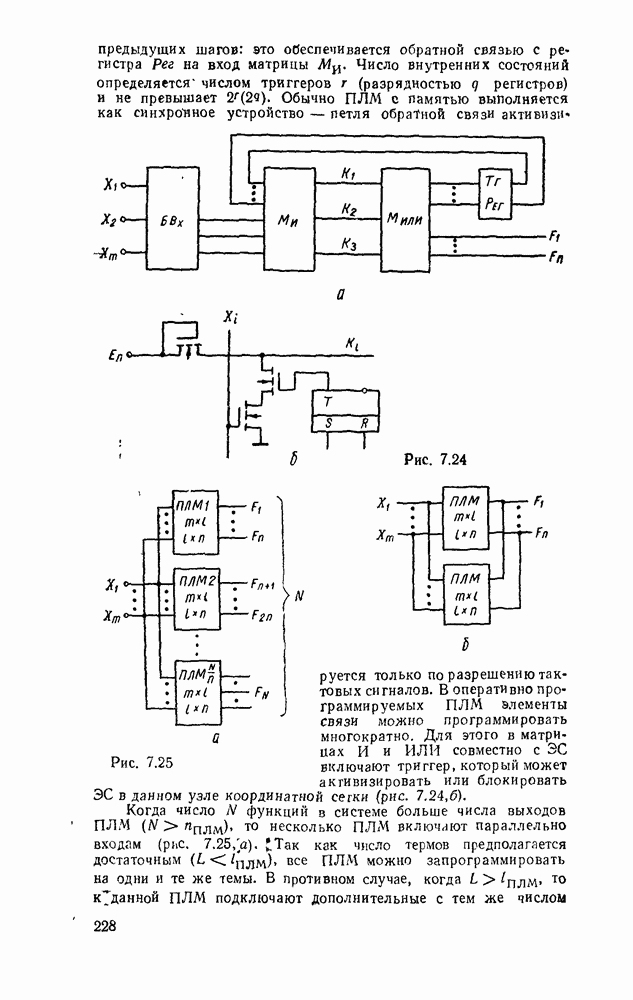
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
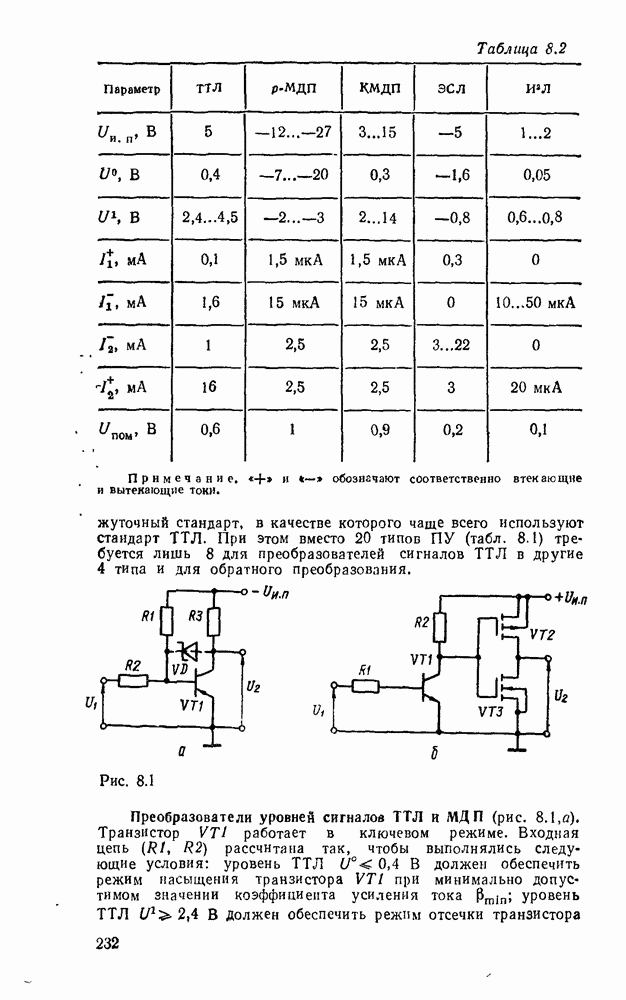
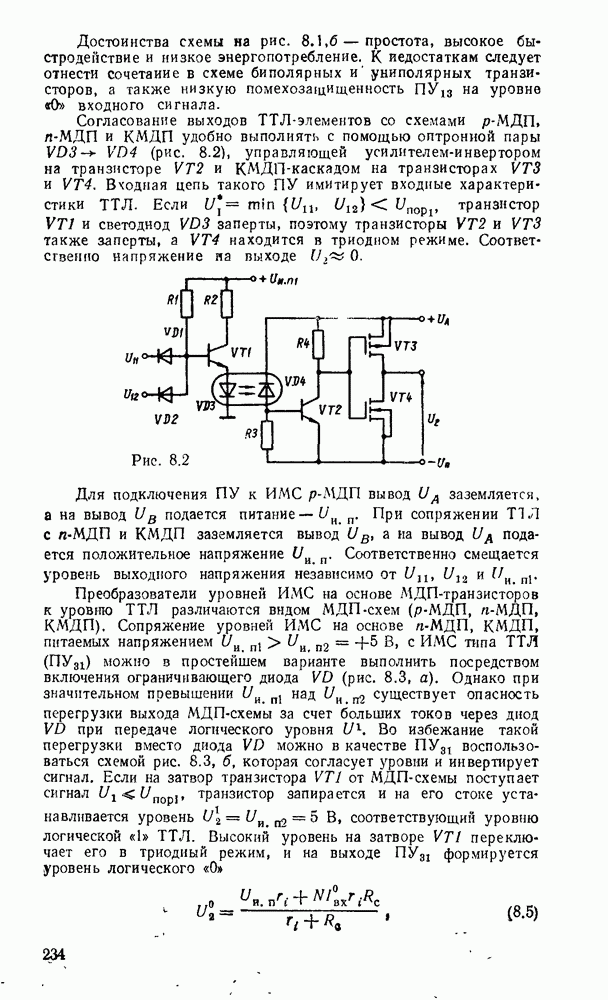
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
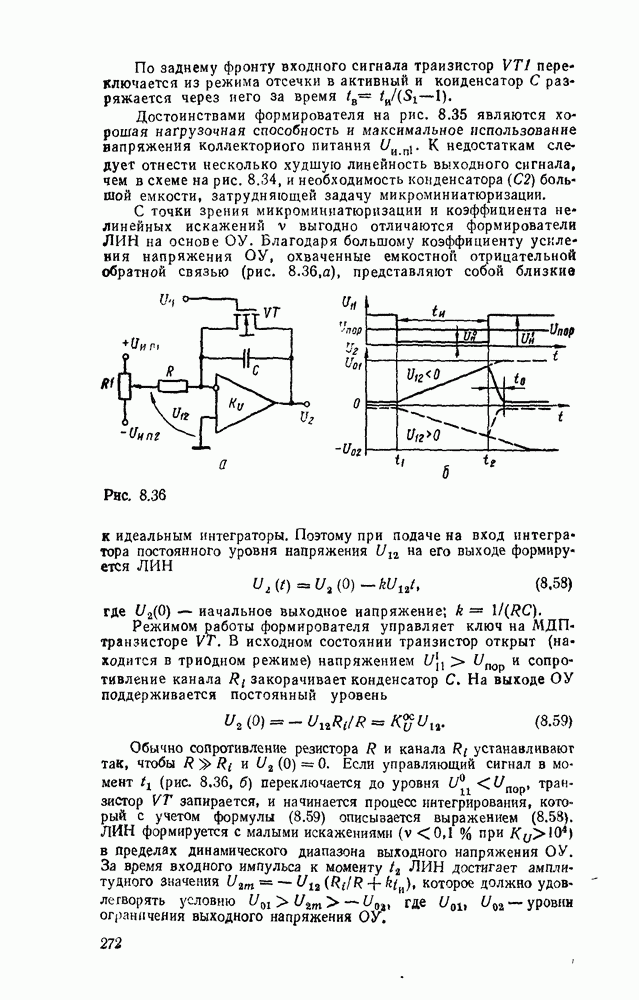
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
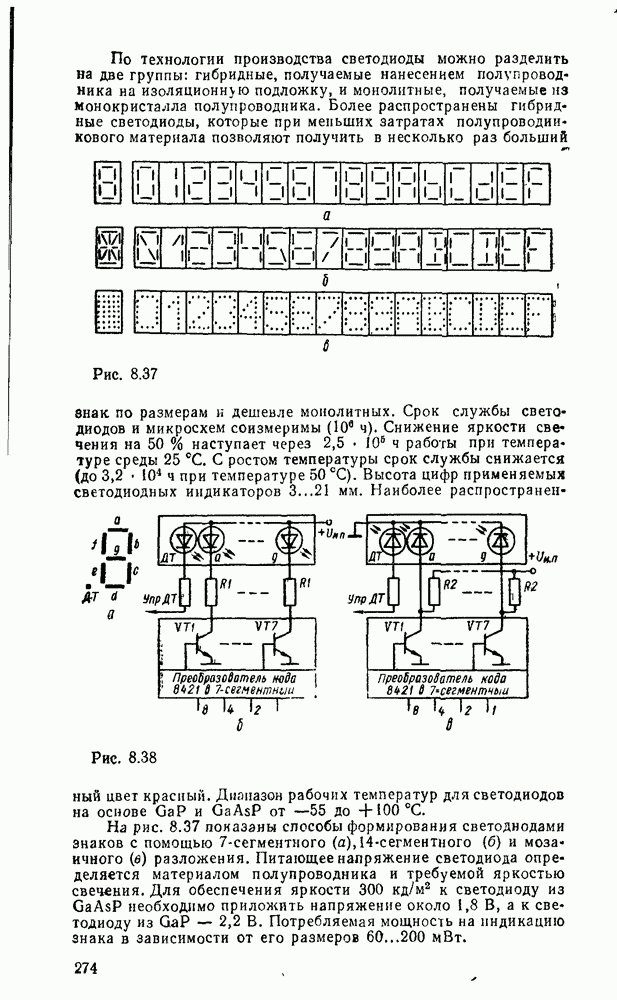
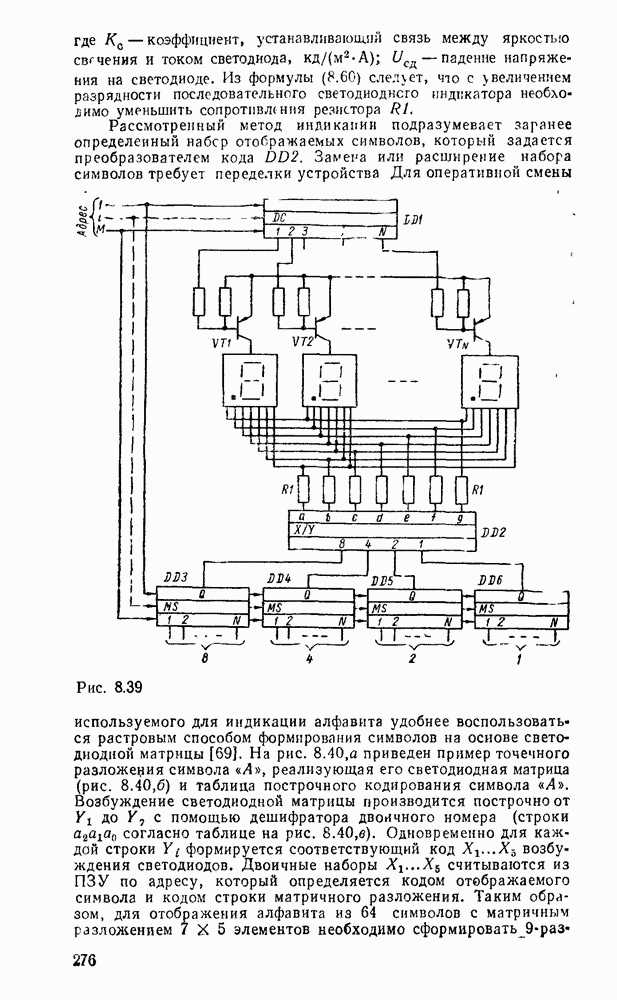
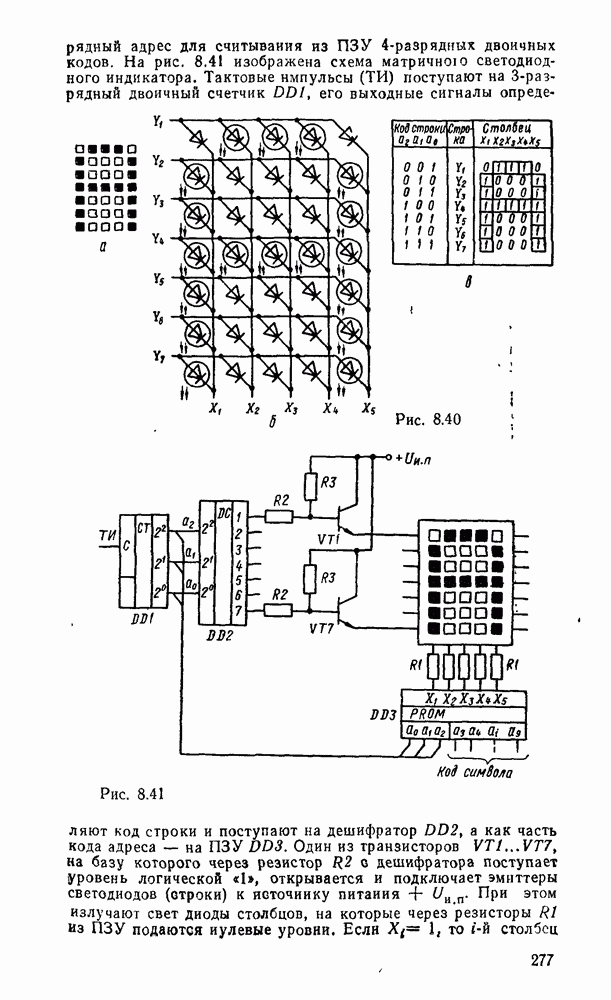
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
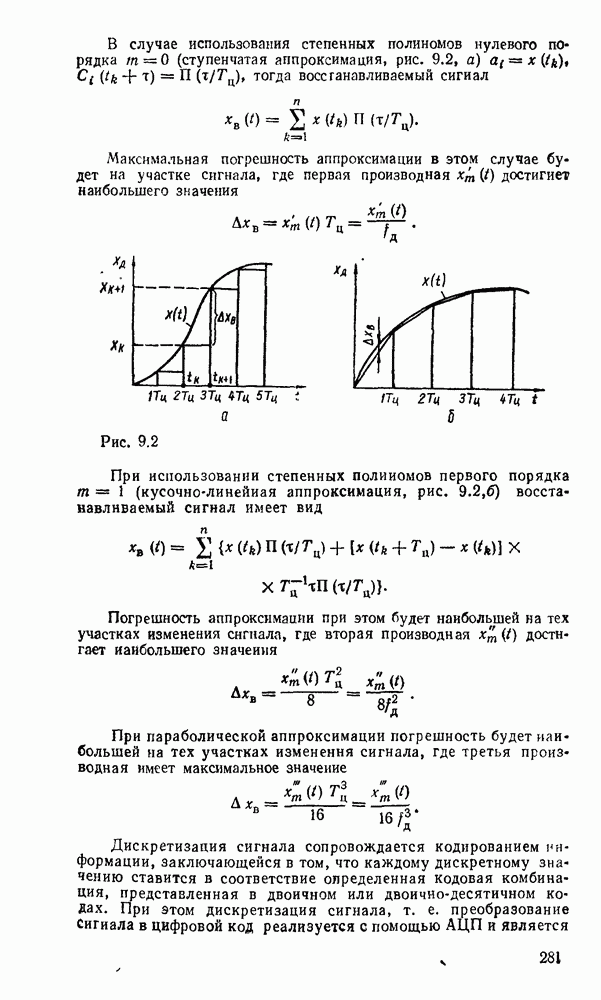
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
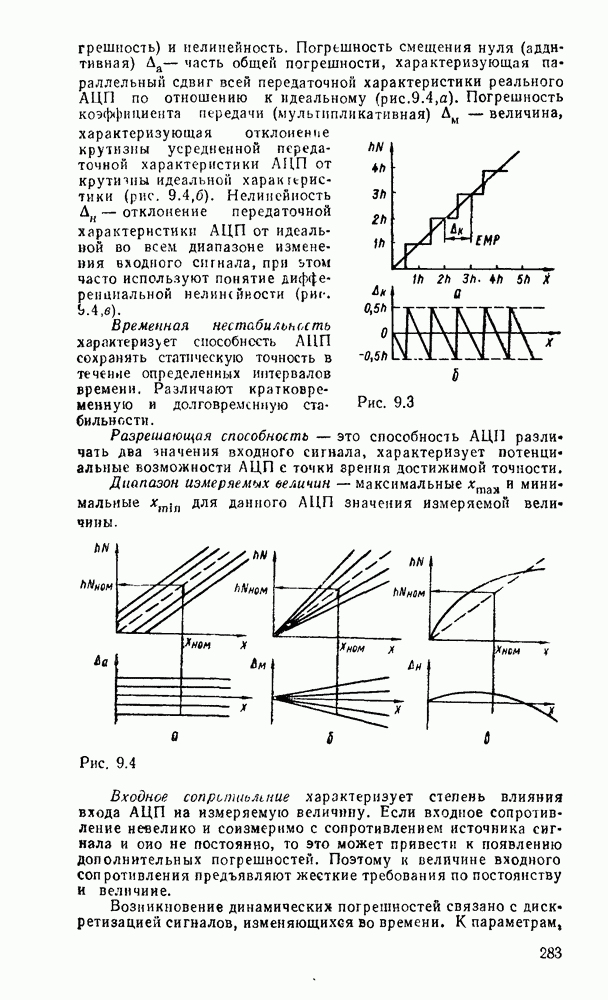
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
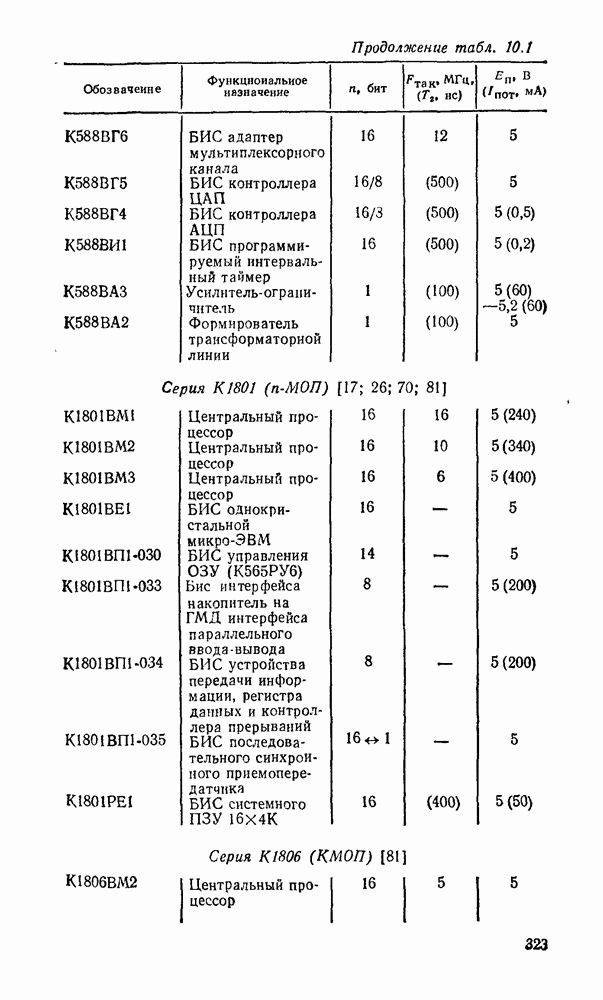
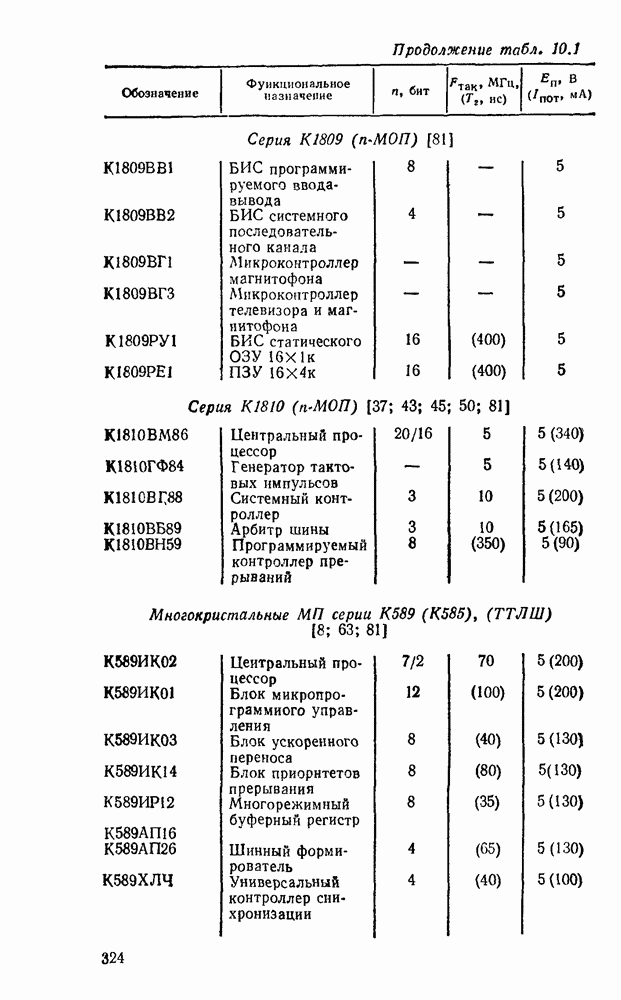
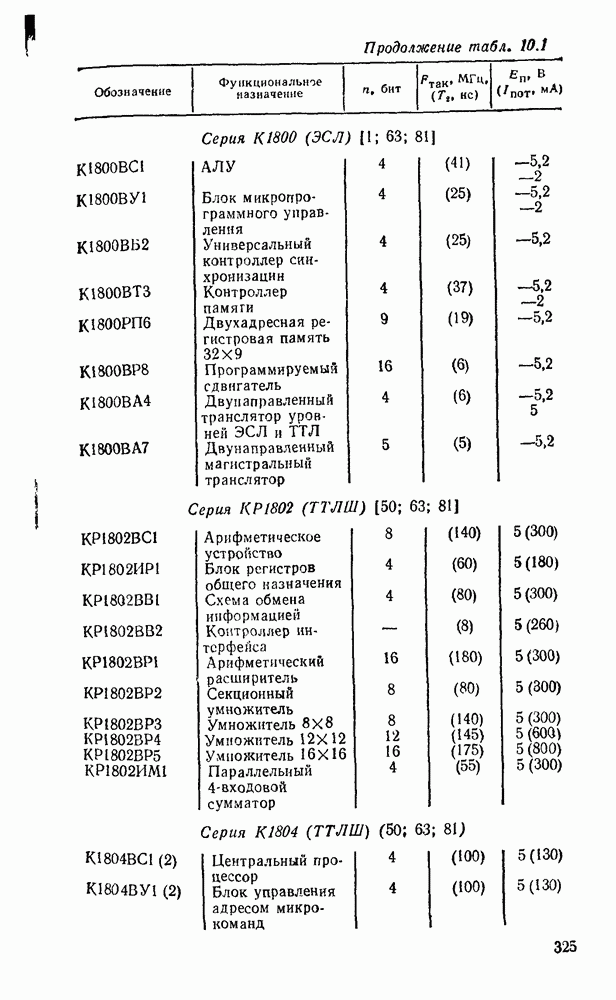
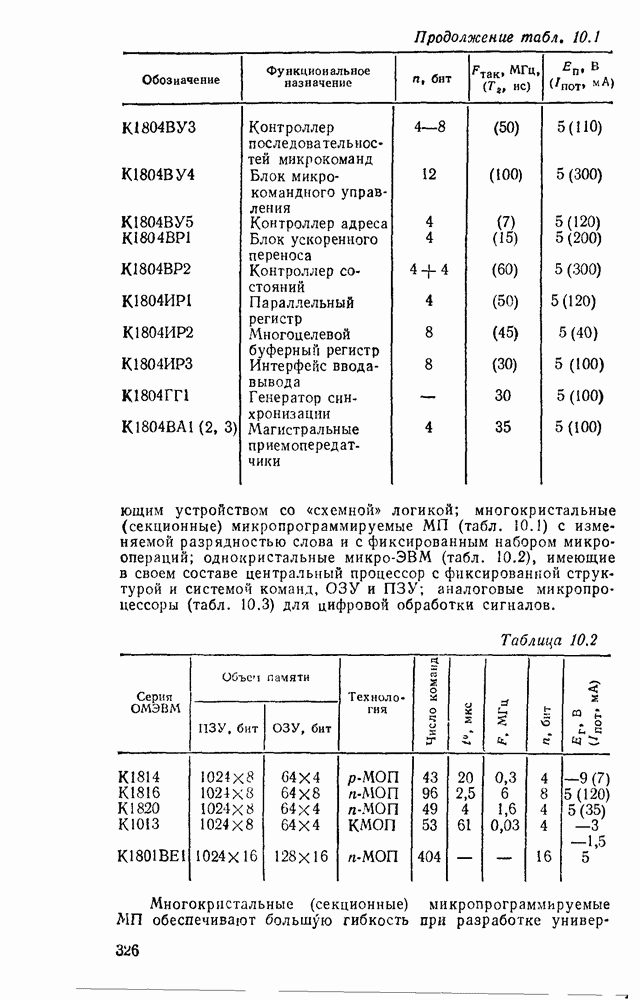
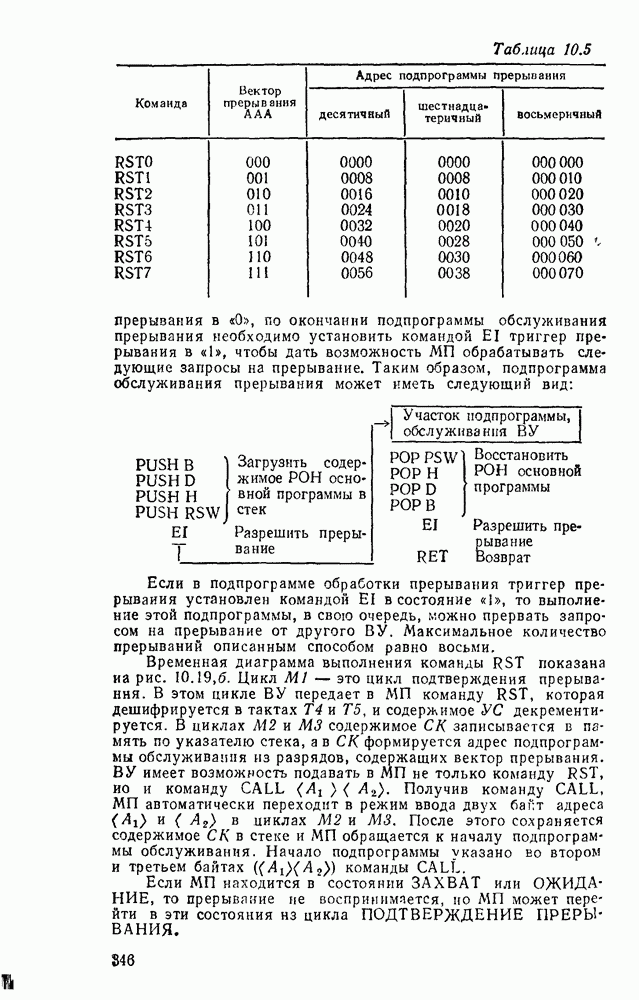
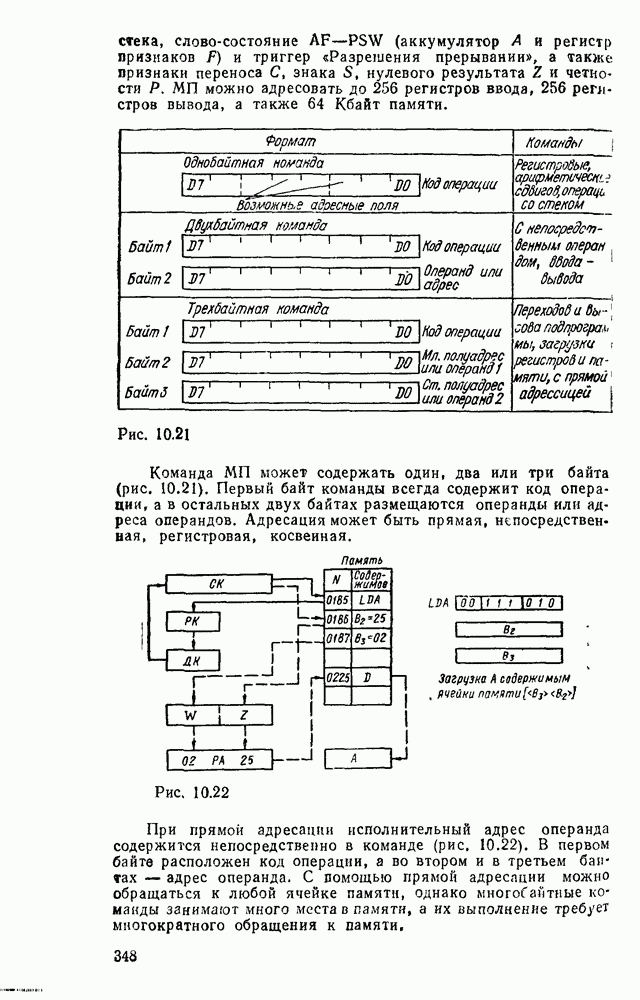
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ