| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.9. КАРТЫ КАРНО
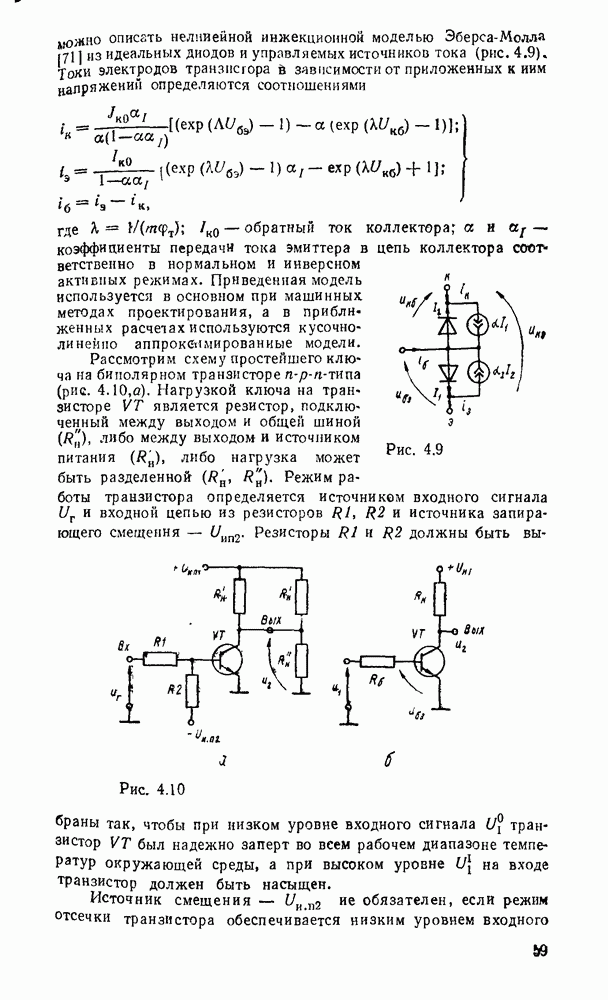
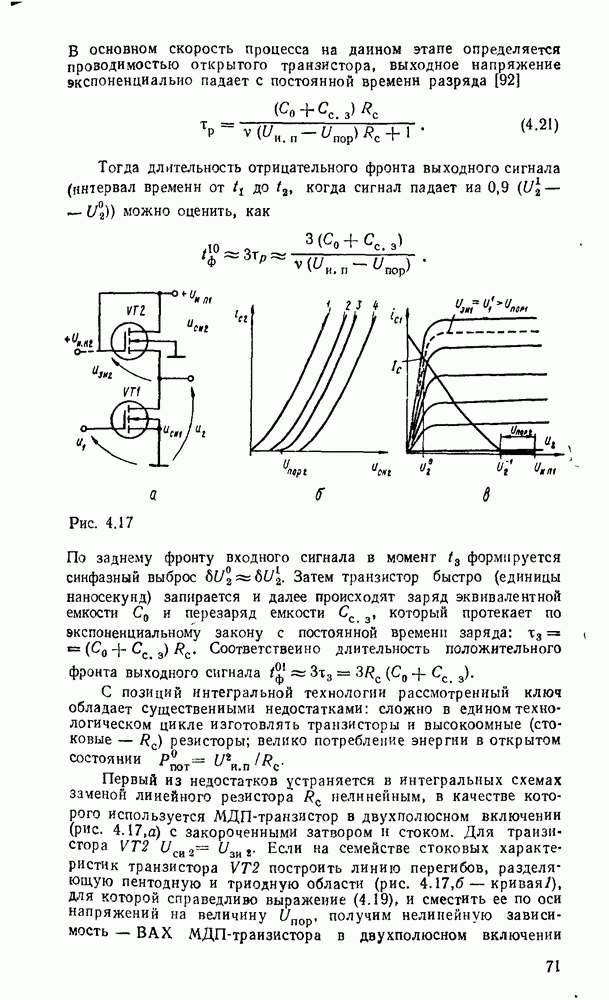
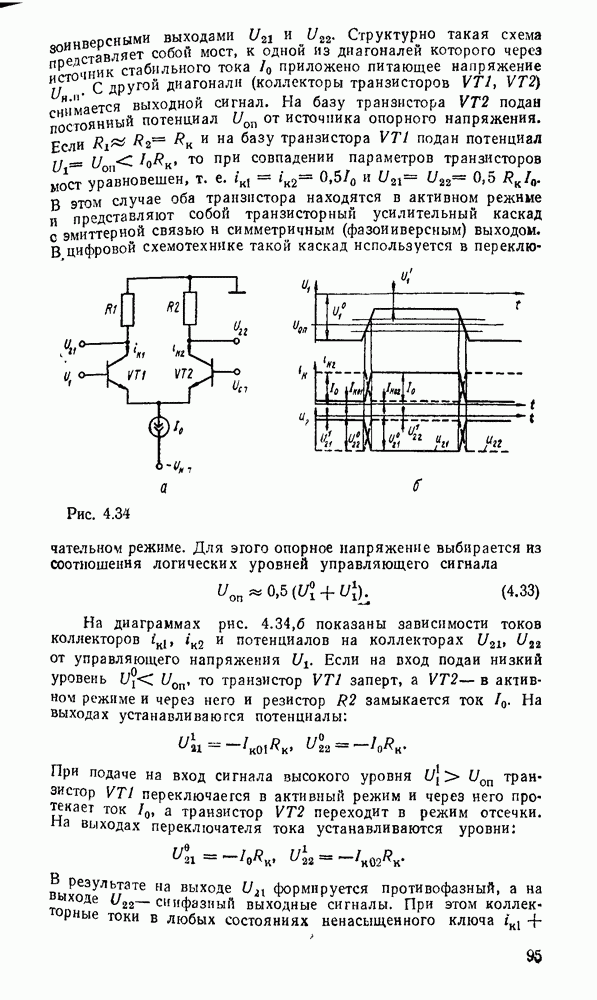
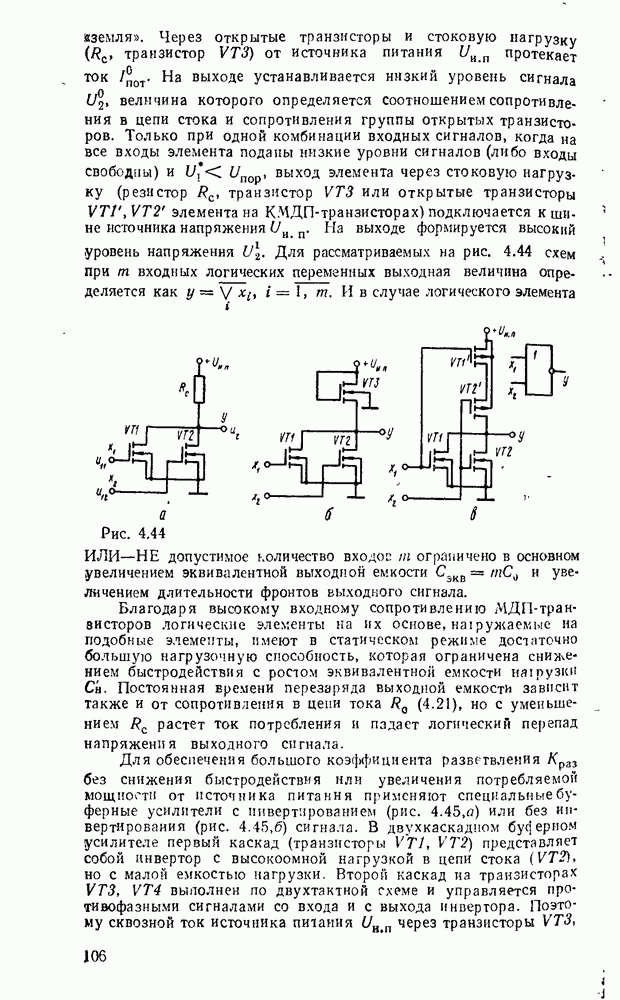
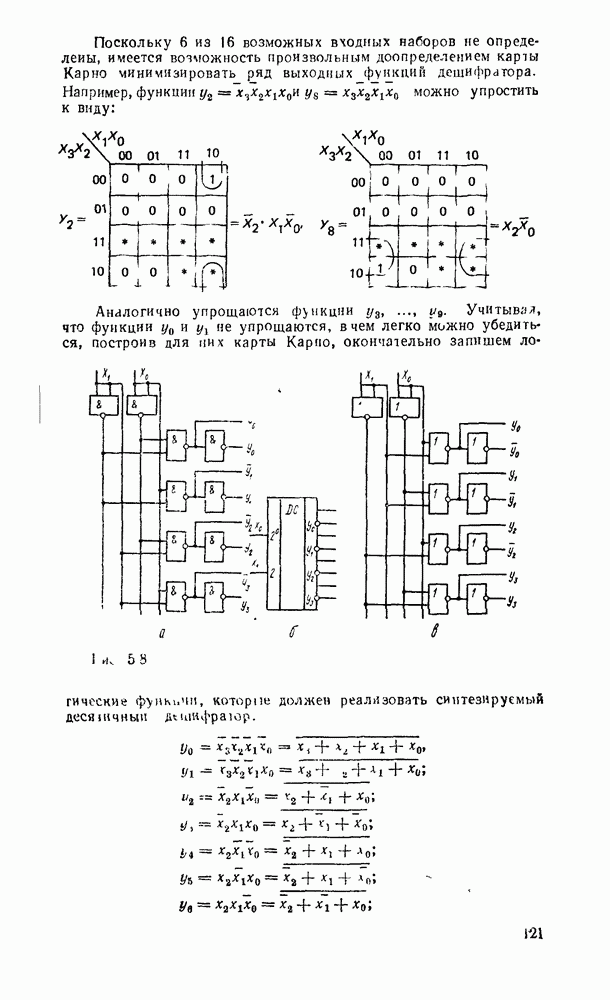
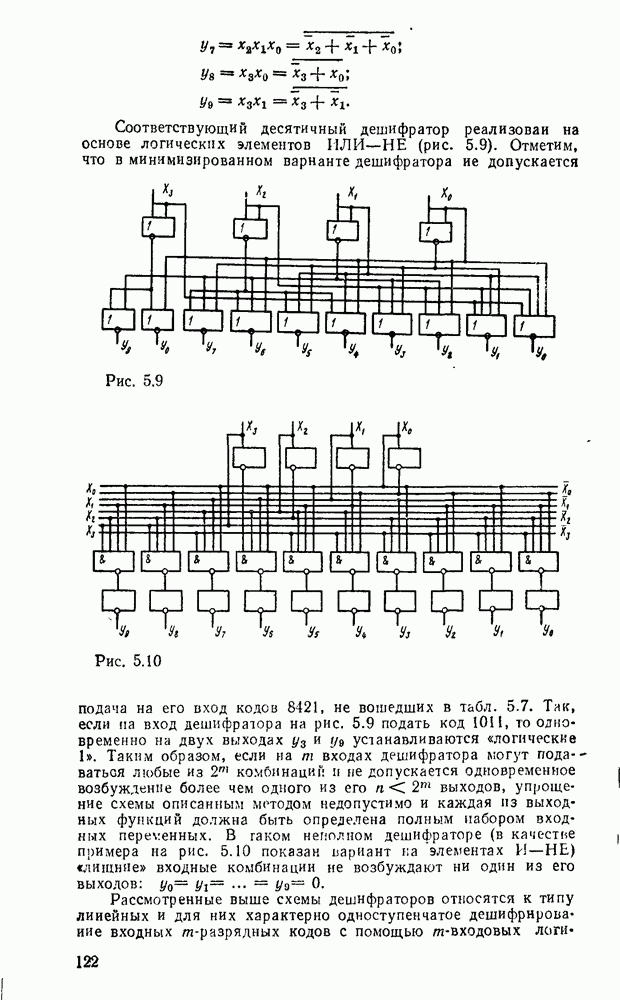
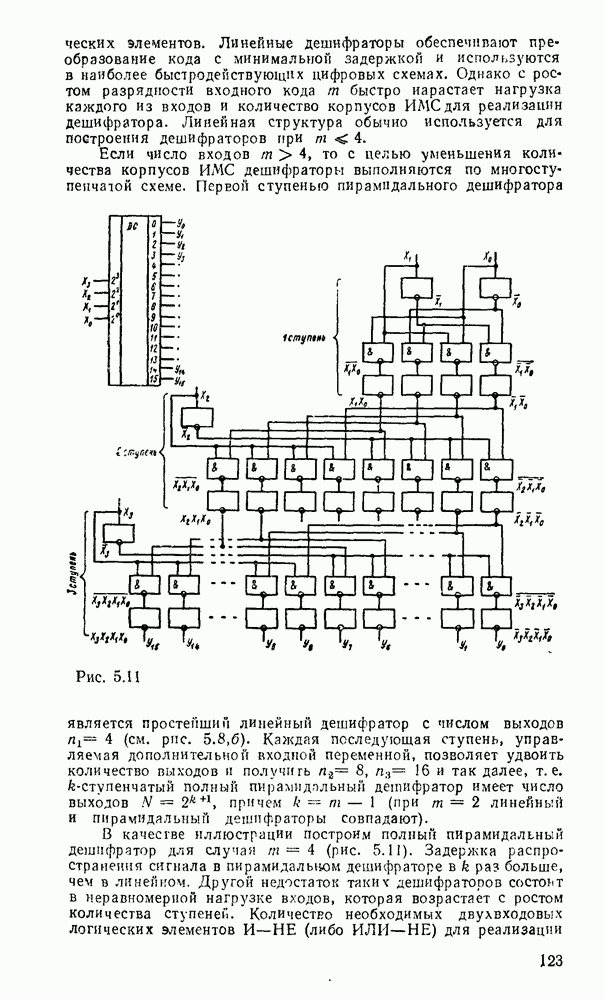
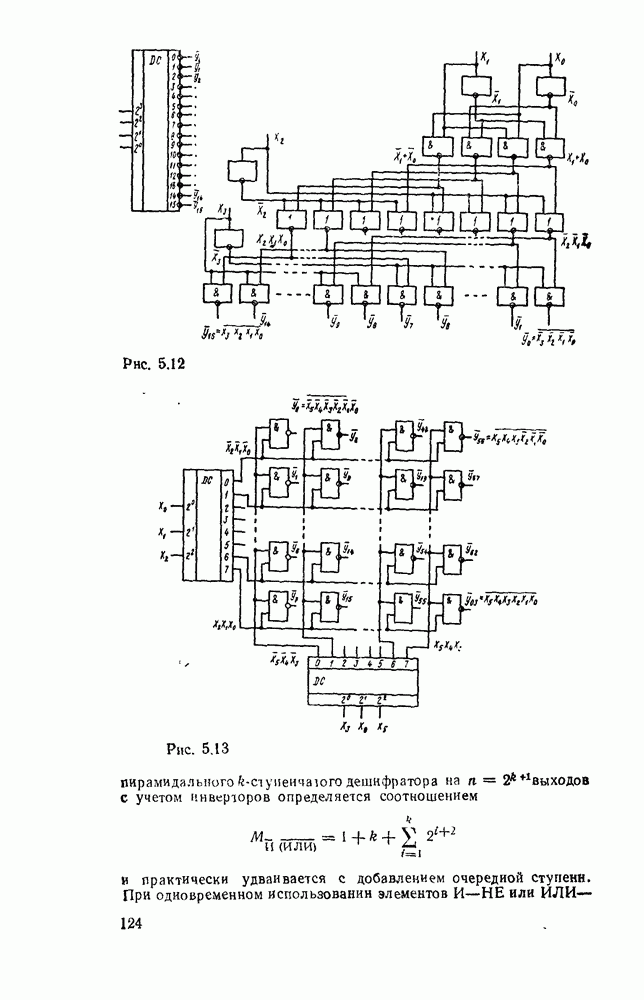
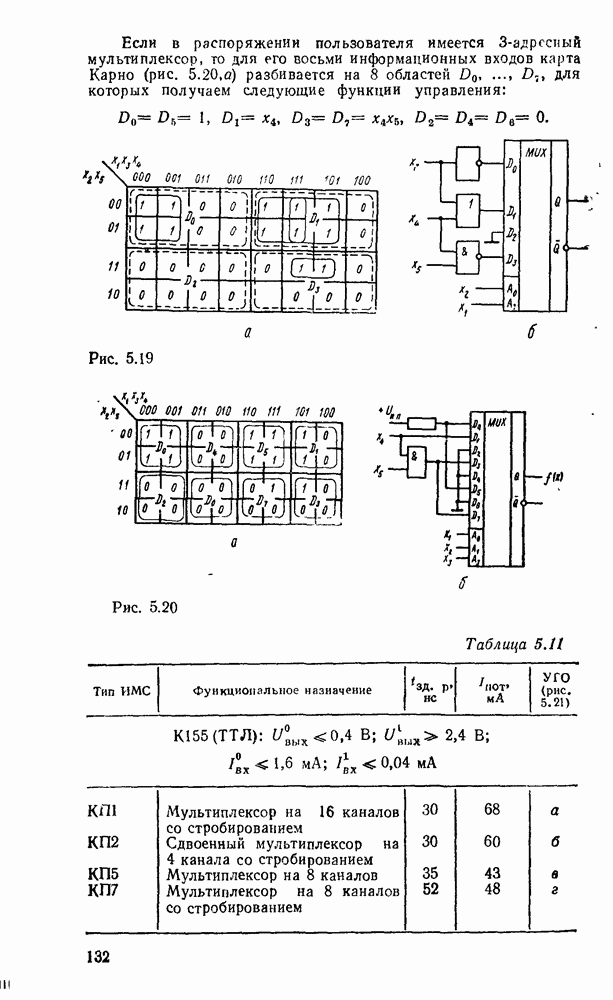
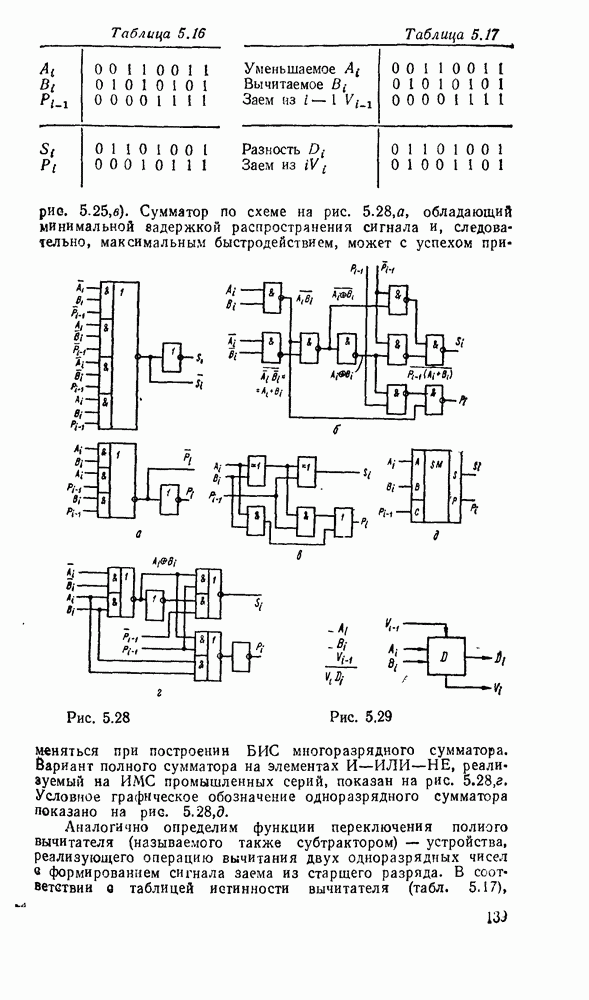
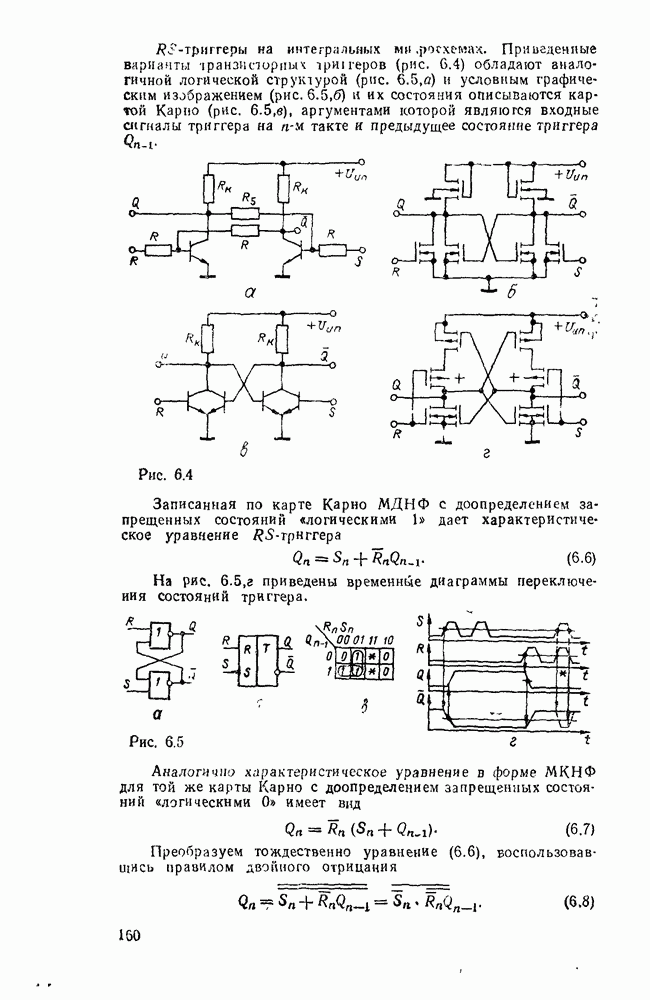
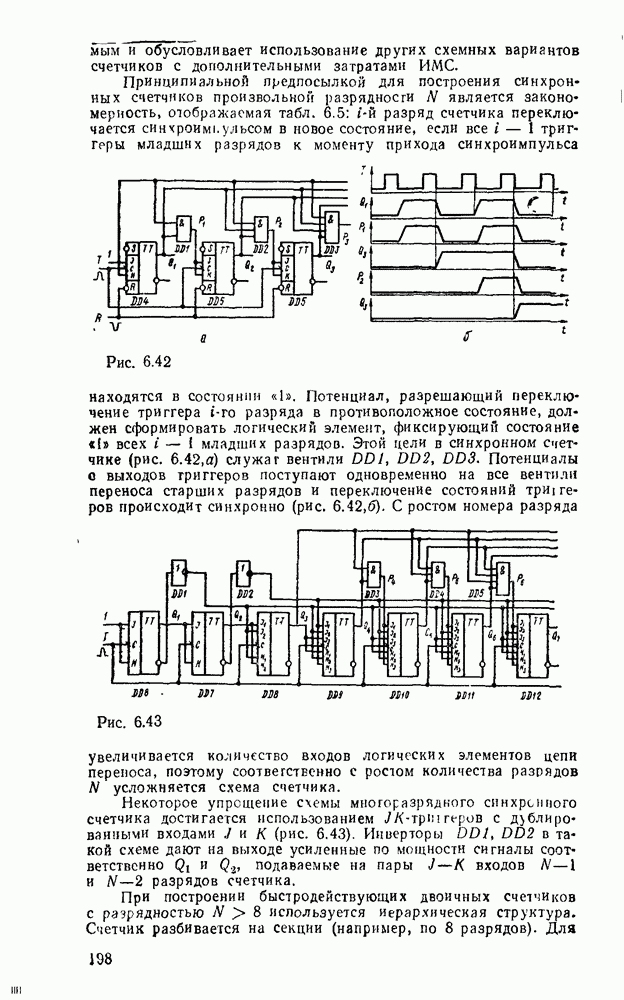
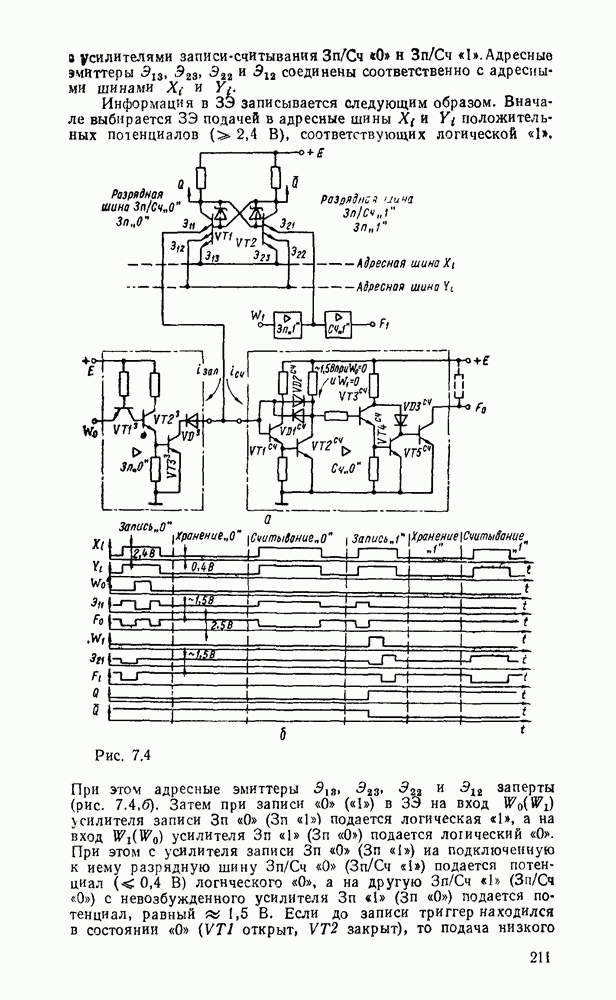
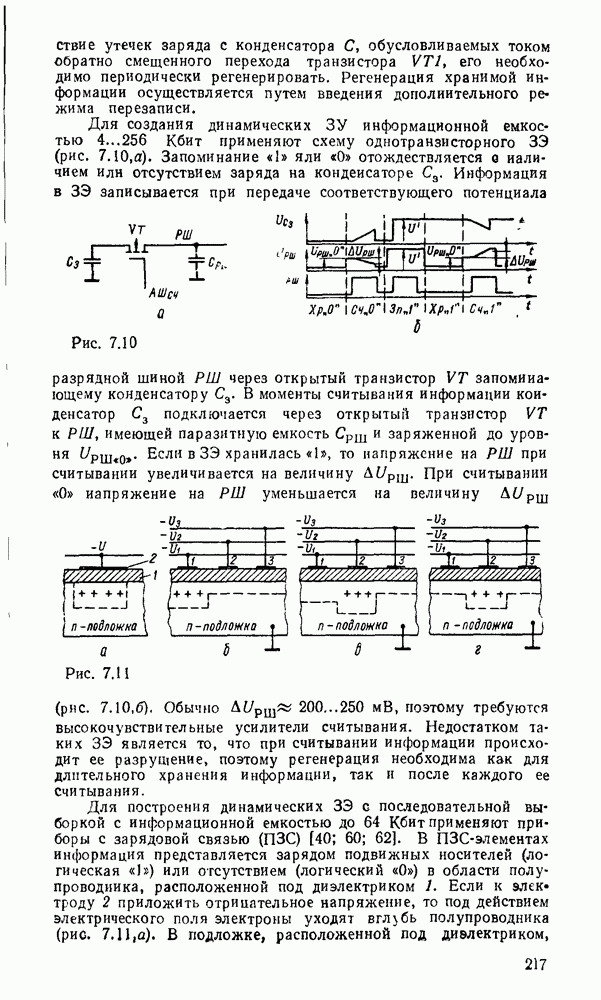
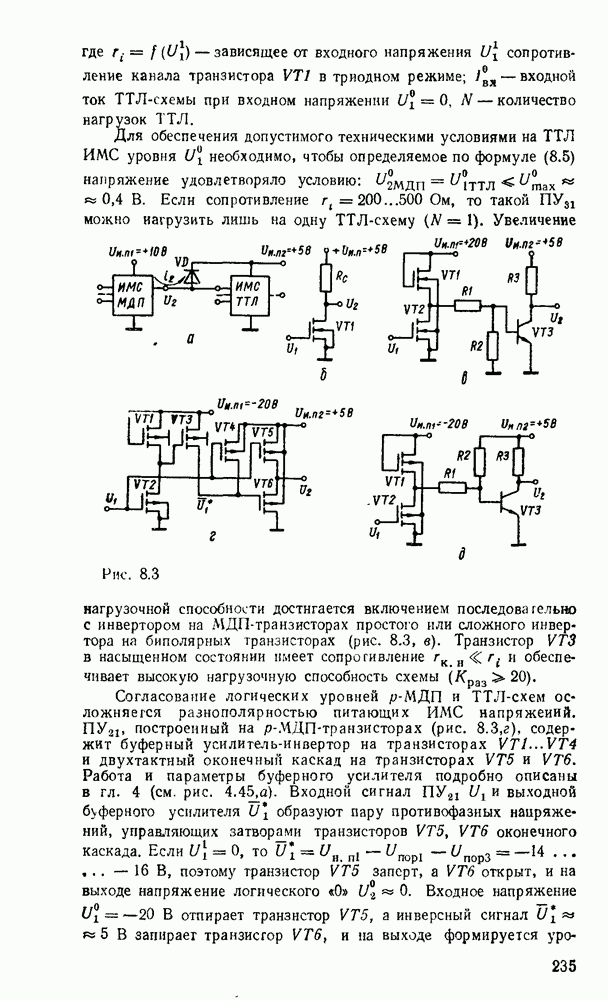
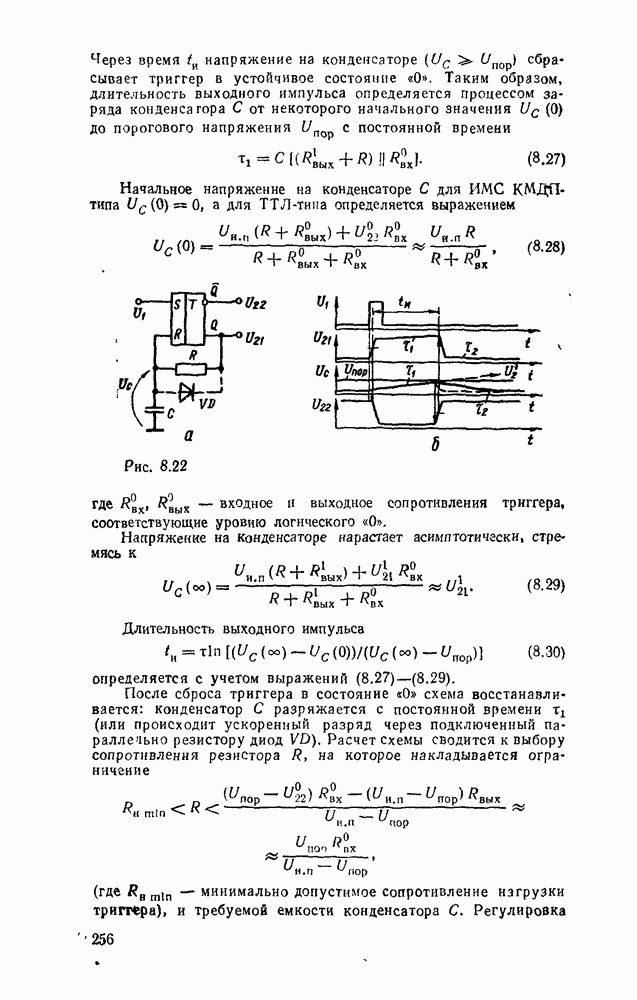
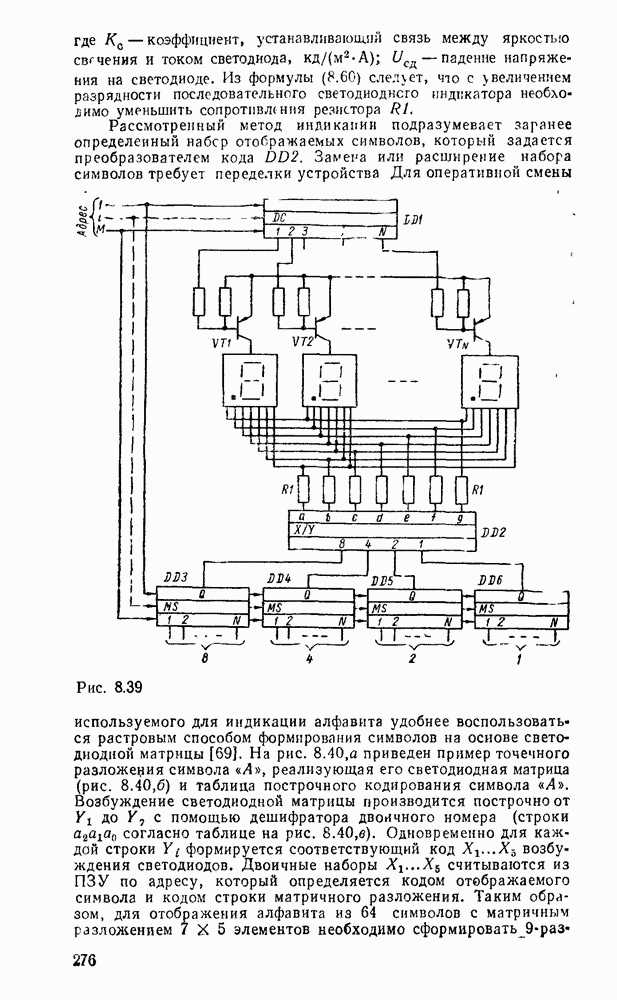
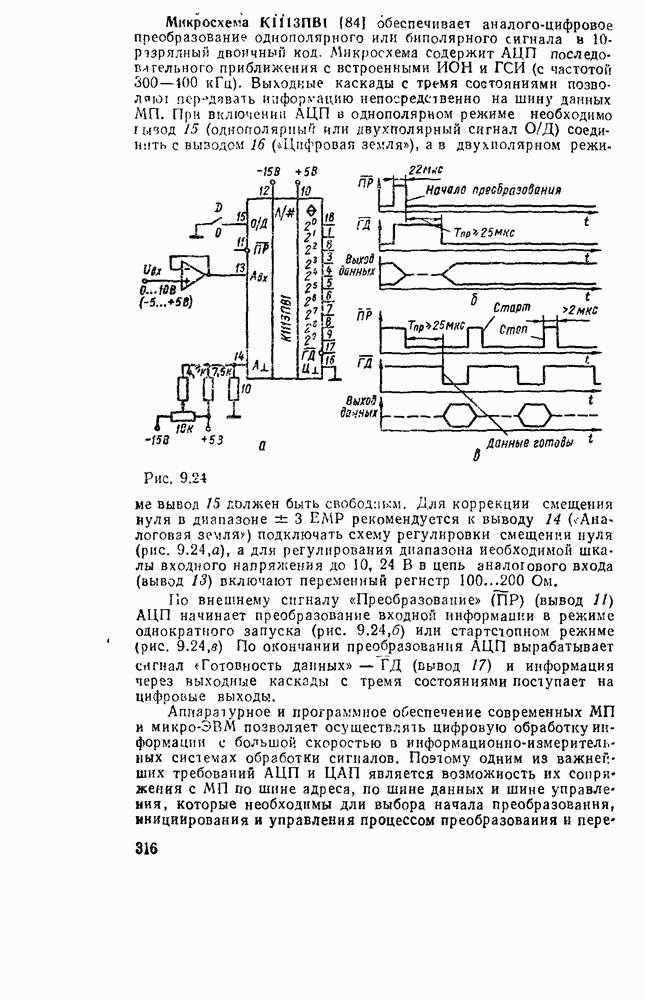
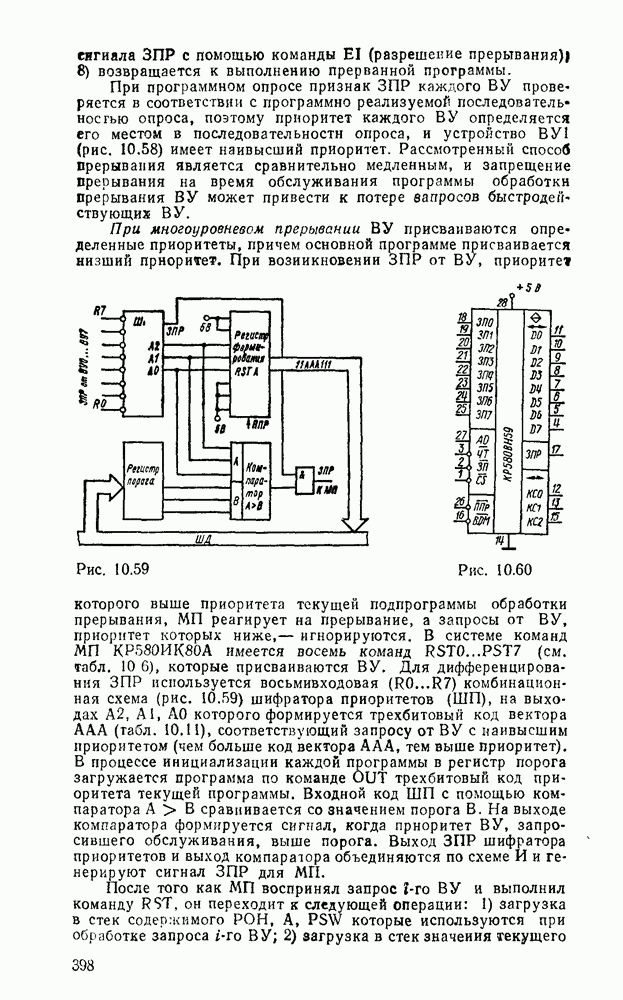
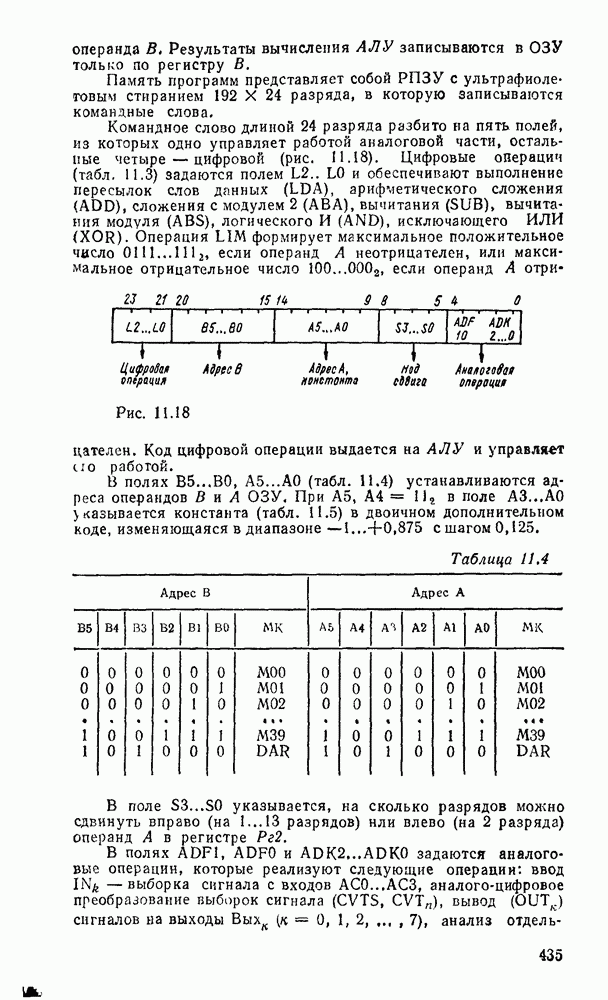
Карты Карио представляют собой специально организованные таблицы соответствия, на которых удобно осуществляются операции склеивания при упрощении функции на пути к минимальным формам. Столбчы и строки таблицы соответствуют всевозможным наборам значений переменных, причем эти наборы расположены в таком порядке, что каждый последующий отличается от предыдущего только одной из переменных. Благодаря этому соседнне ячейки по горизонтали и вертикали отличаются значением только одной переменной. Ячейки, расположенные по краям таблицы, также считаются соседними и обладают этим свойством. На рис. 2.1 показаны карты Карно для двух, трех и четырех переменных.

Рис. 2.1.
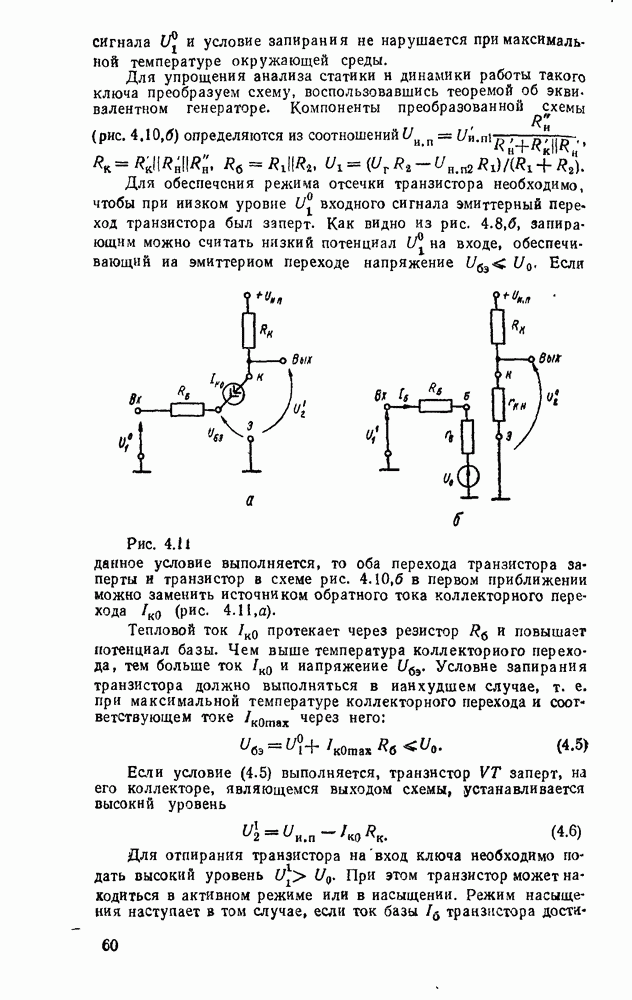
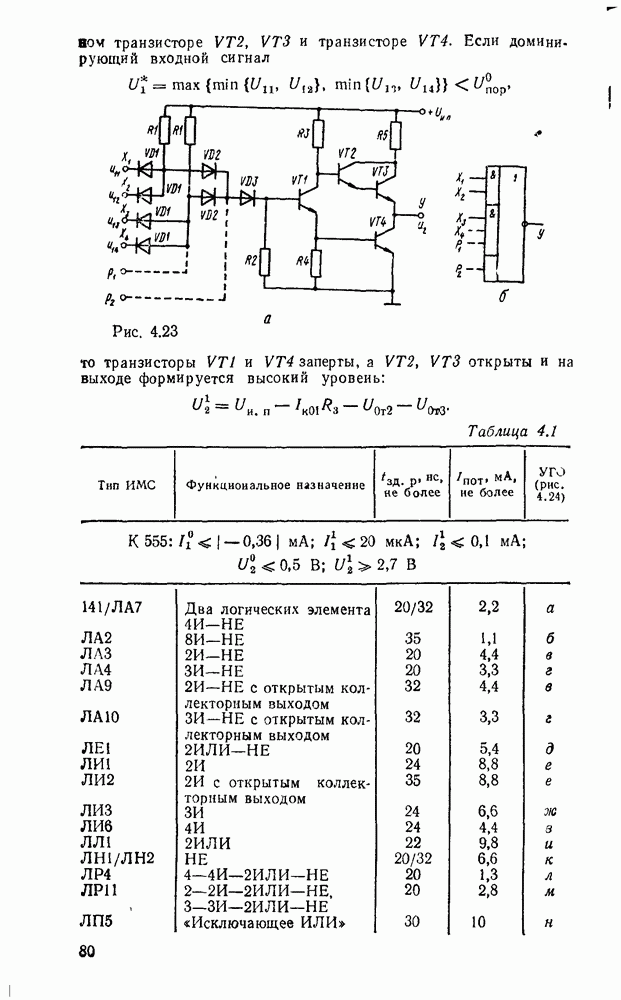
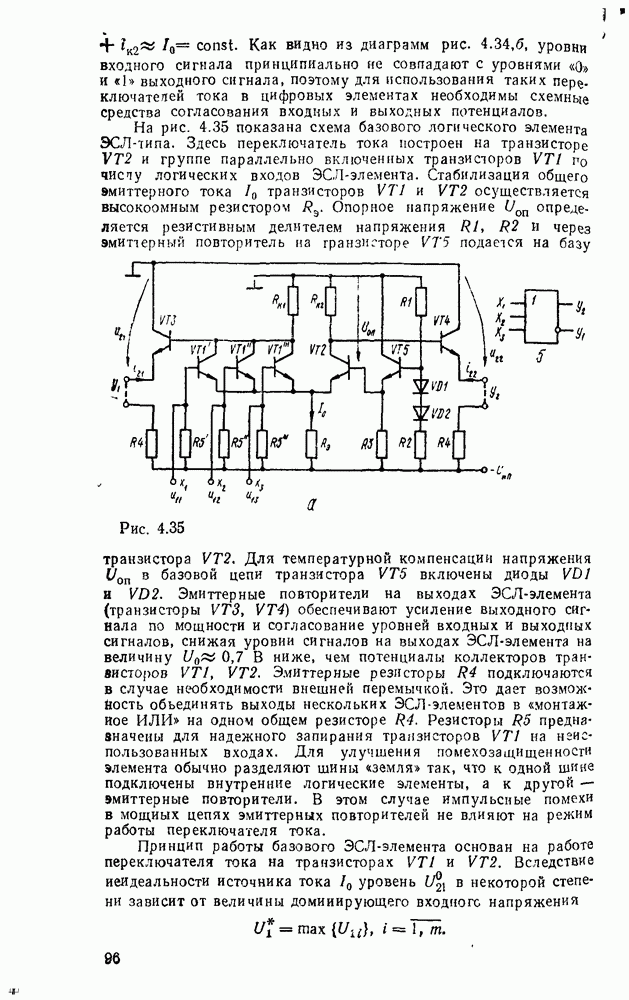
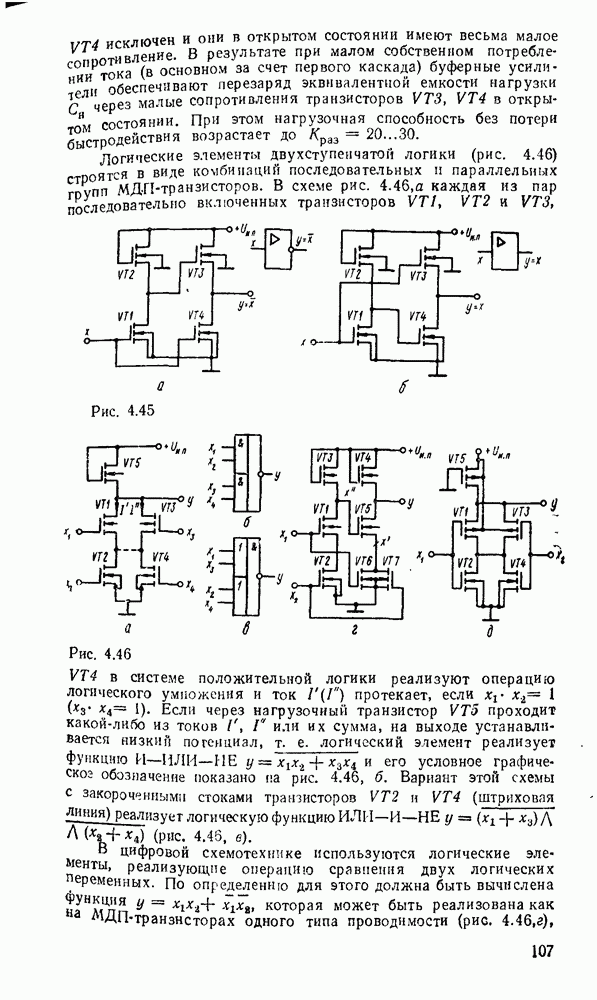
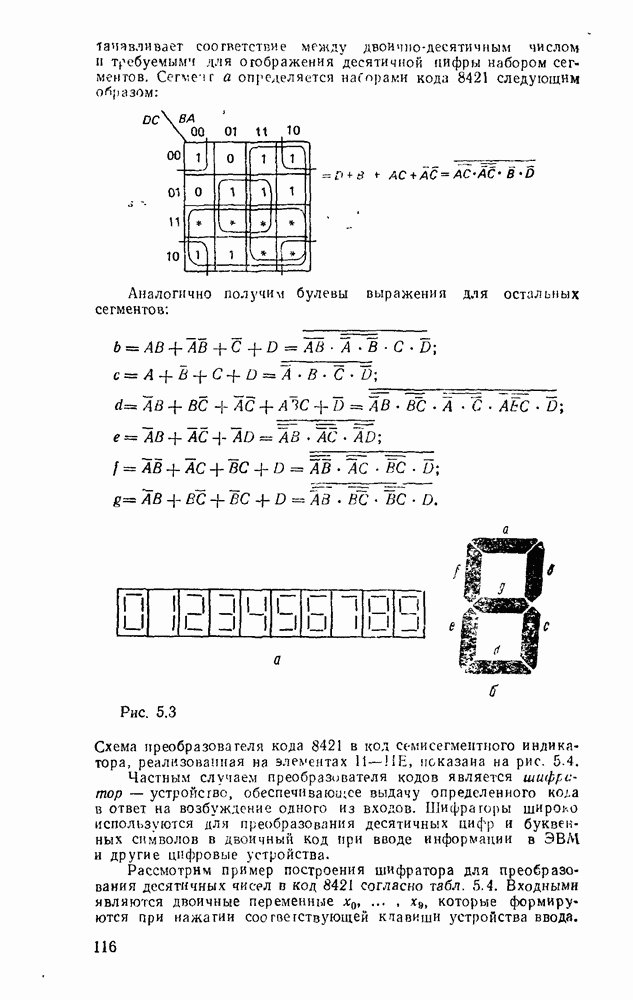
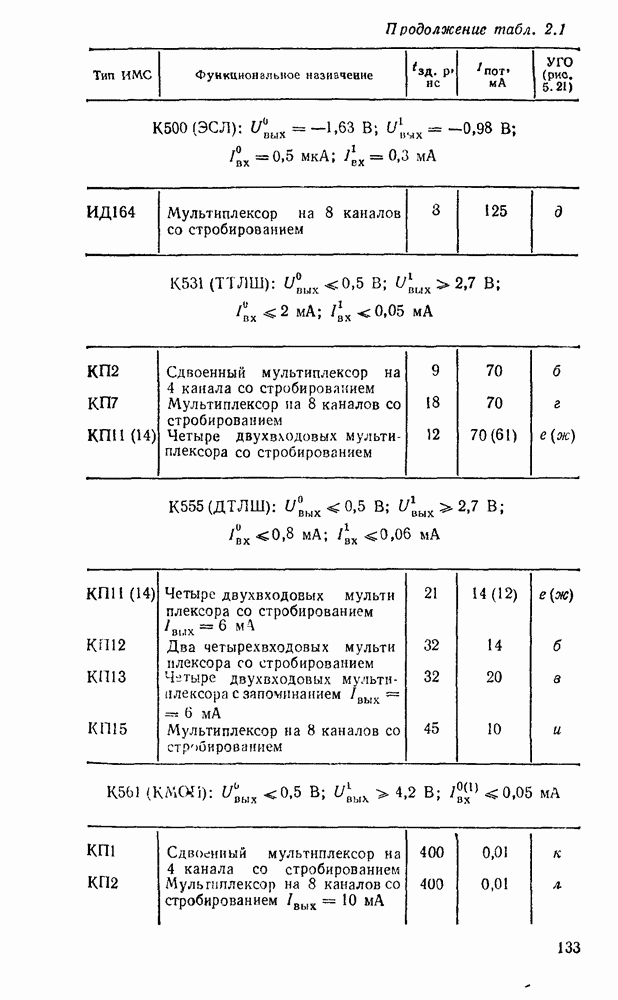
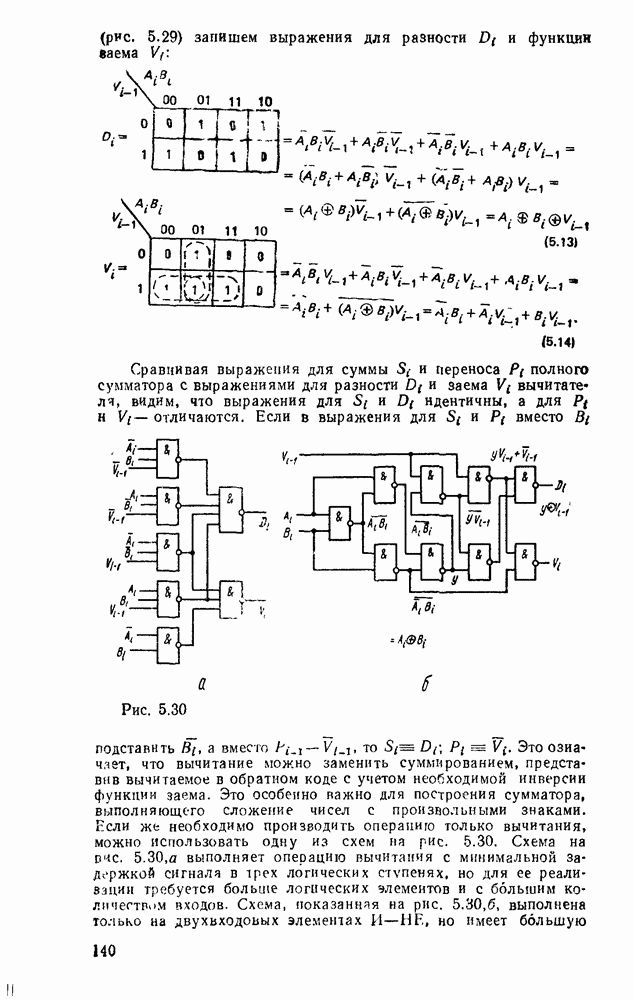
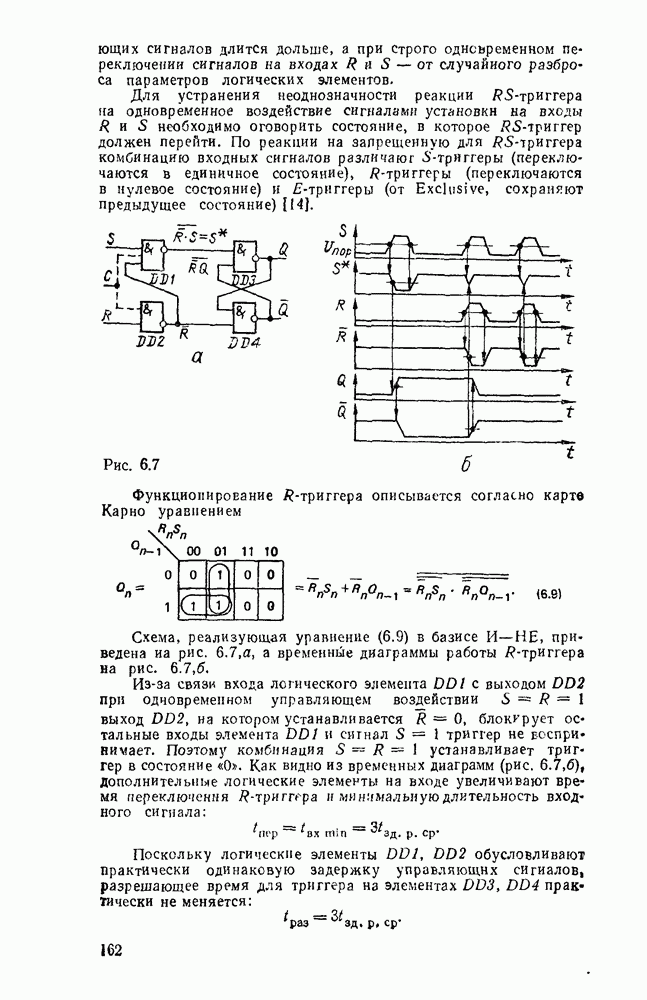
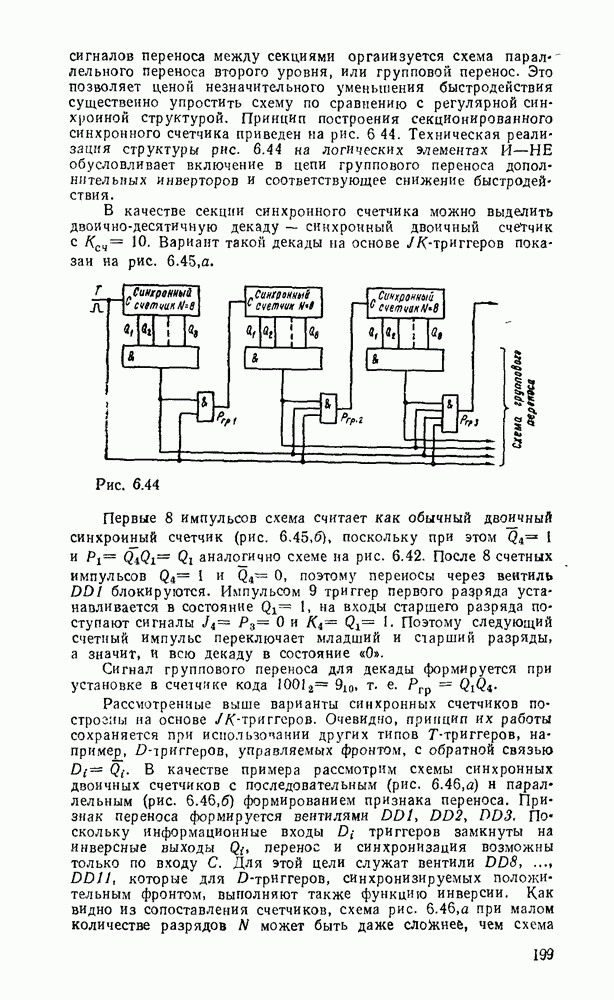
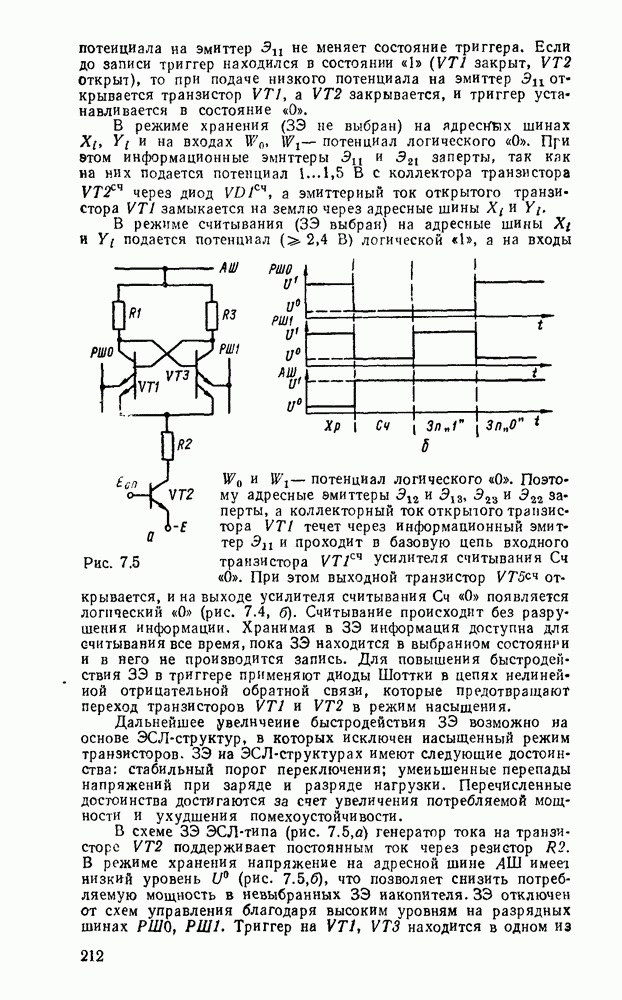
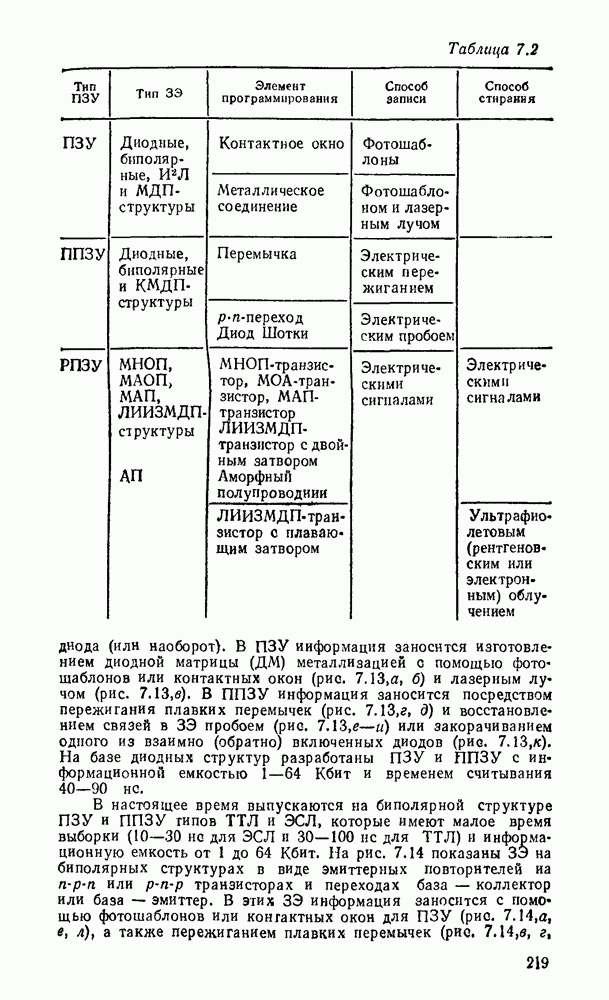
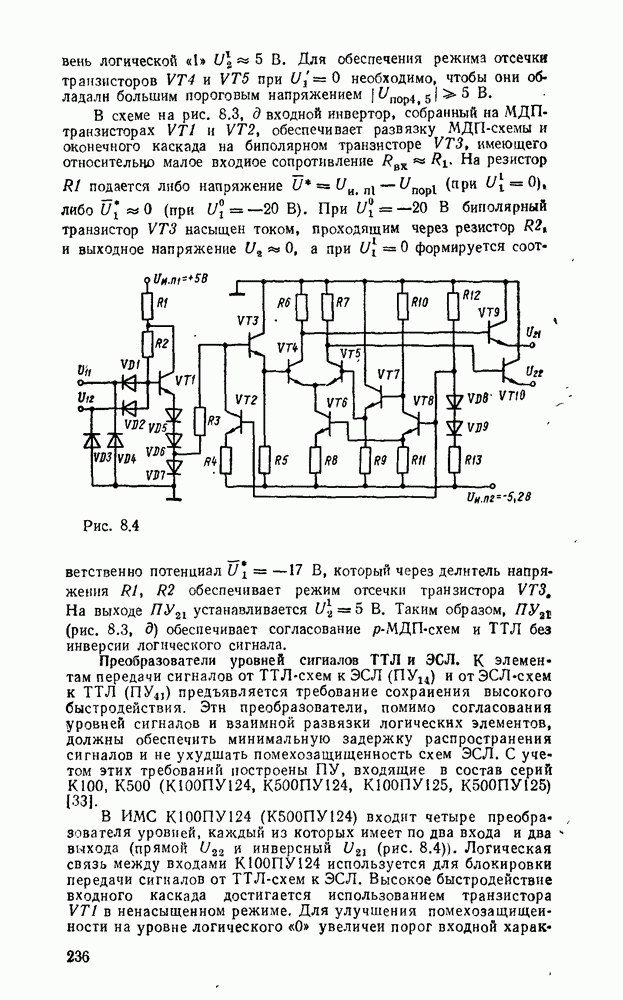
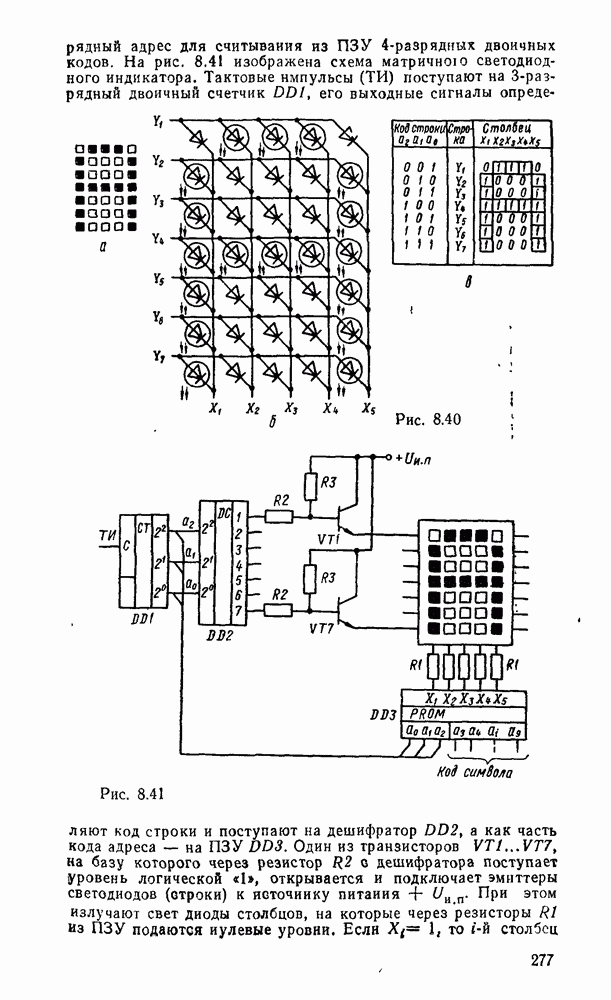
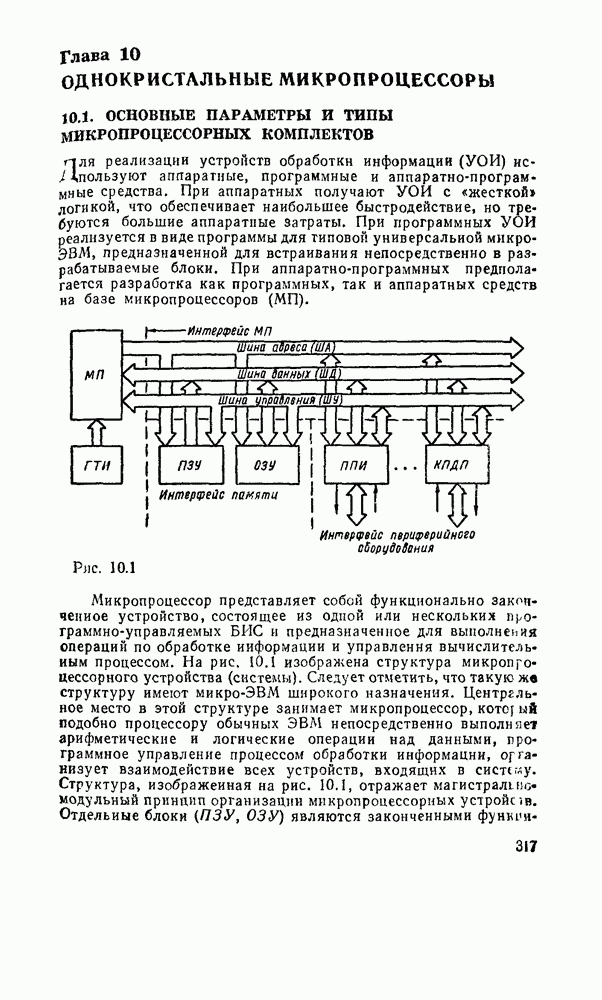
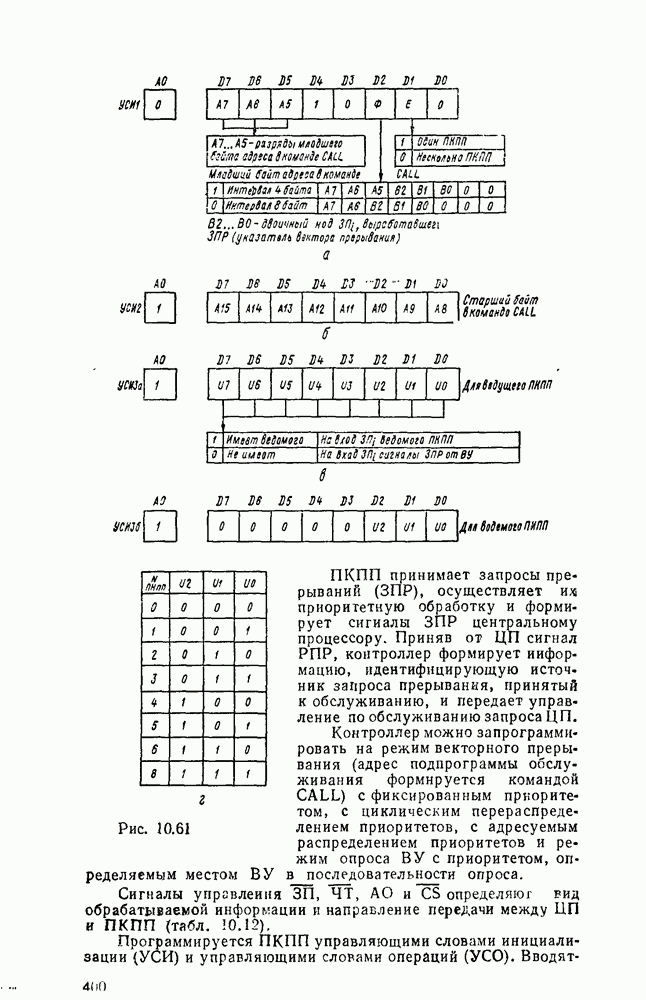
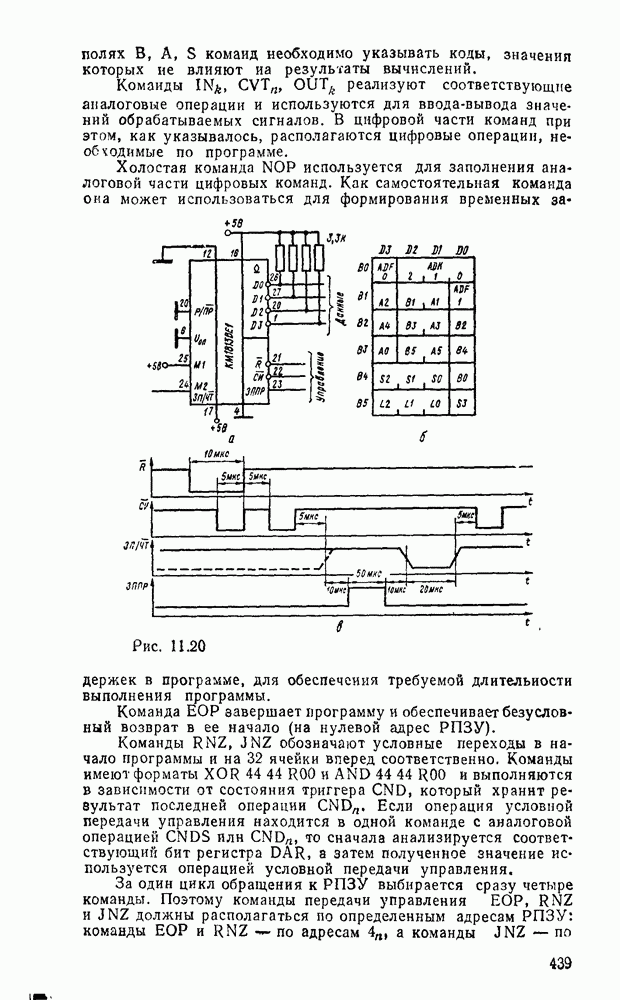
Каждому набору значений переменных по строкам и столбцам соответствует своя ячейка, расположенная на их пересечении. Она заполняется единицей, если на соответствующем наборе функция принимает единичное значение, или нулем при нулевом значении функции (нули обычно не вписываются, а оставляются пустые клетки). Таким образом, отмеченные ячейки соответствуют ыицтермам, а неотмеченные — макстермам канонических форм. Например, на рис. 2.2,а показана карта Карно для функцин, заданной таблицей соответствия из рассмотренного в § 2.7 примере.
Операции склеивания двух минтермов  ранга исходной формулы соответствует на карте Карно объединение двух соседних ячеек, отмеченных единицами, и эта объединенная пара ячеек представляет собой результирующий минтерм
ранга исходной формулы соответствует на карте Карно объединение двух соседних ячеек, отмеченных единицами, и эта объединенная пара ячеек представляет собой результирующий минтерм  ранга. Аналогично склеивание двух минтермов
ранга. Аналогично склеивание двух минтермов  ранга в минтерм
ранга в минтерм  ранга представляется объединением соответствующих пар ячеек в прямоугольную группу из четырех соседних ячеек и т. д. Полное число ичеек в любой группе всегда выражается целой степенью двойки
ранга представляется объединением соответствующих пар ячеек в прямоугольную группу из четырех соседних ячеек и т. д. Полное число ичеек в любой группе всегда выражается целой степенью двойки  , где а и b — соответственно целые числа пар ячеек по горизонтали и вертикали, причем каждая такая группа отображает минтерм
, где а и b — соответственно целые числа пар ячеек по горизонтали и вертикали, причем каждая такая группа отображает минтерм  ранга и покрывает
ранга и покрывает  минтермов
минтермов  ранга исходной канонической формы. Так, на рис.
ранга исходной канонической формы. Так, на рис.  показано сокращенное покрытие, импликанты которого образованы в результате склеивания минтермов функции, изображенной на рис. 2.2,а. На рис.
показано сокращенное покрытие, импликанты которого образованы в результате склеивания минтермов функции, изображенной на рис. 2.2,а. На рис.  показаны тупиковые покрытия рассматриваемой функции, причем покрытие на рис. 2.2,в является минимальным.
показаны тупиковые покрытия рассматриваемой функции, причем покрытие на рис. 2.2,в является минимальным.
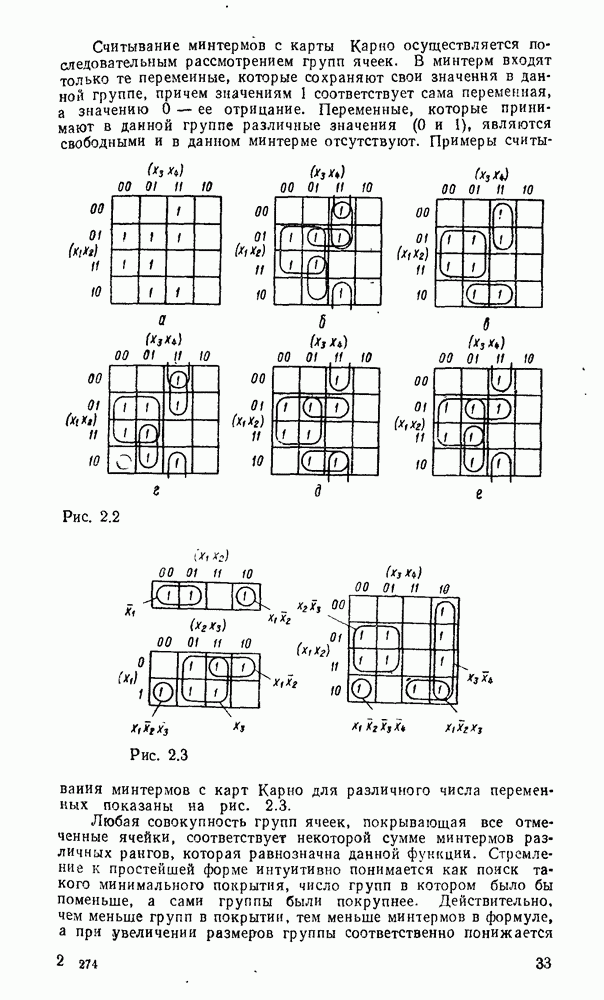
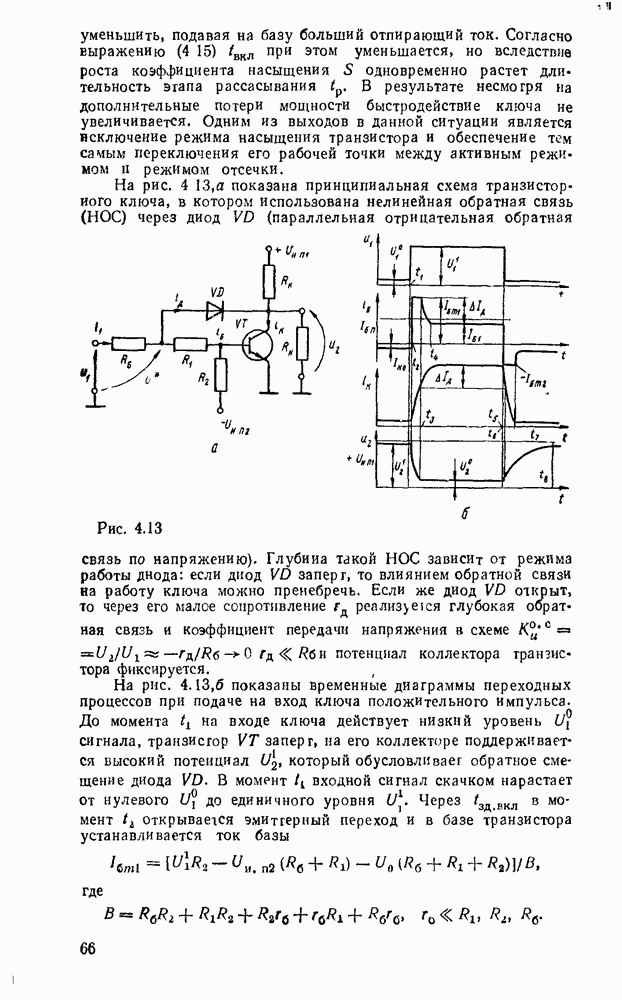
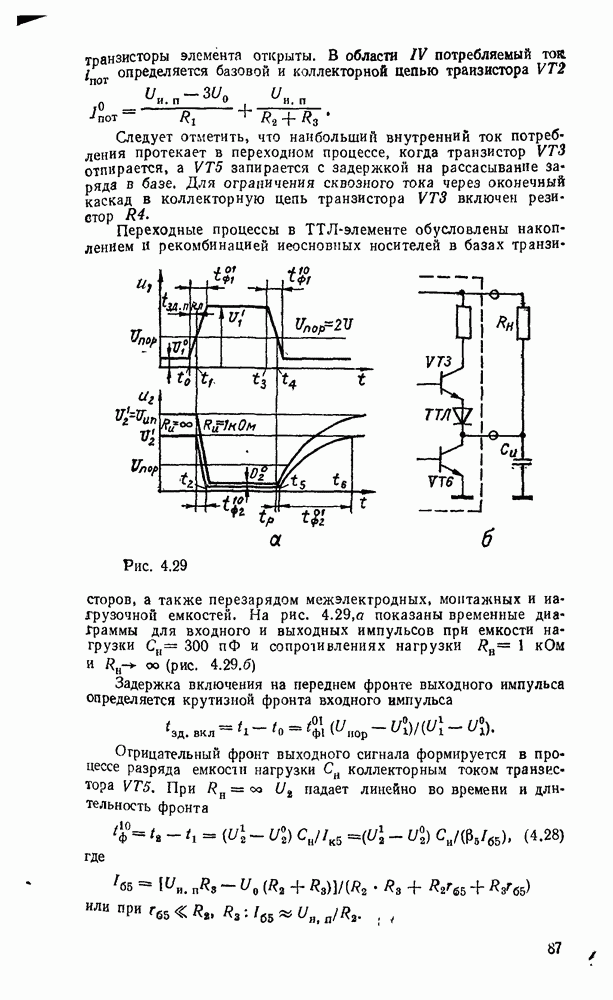
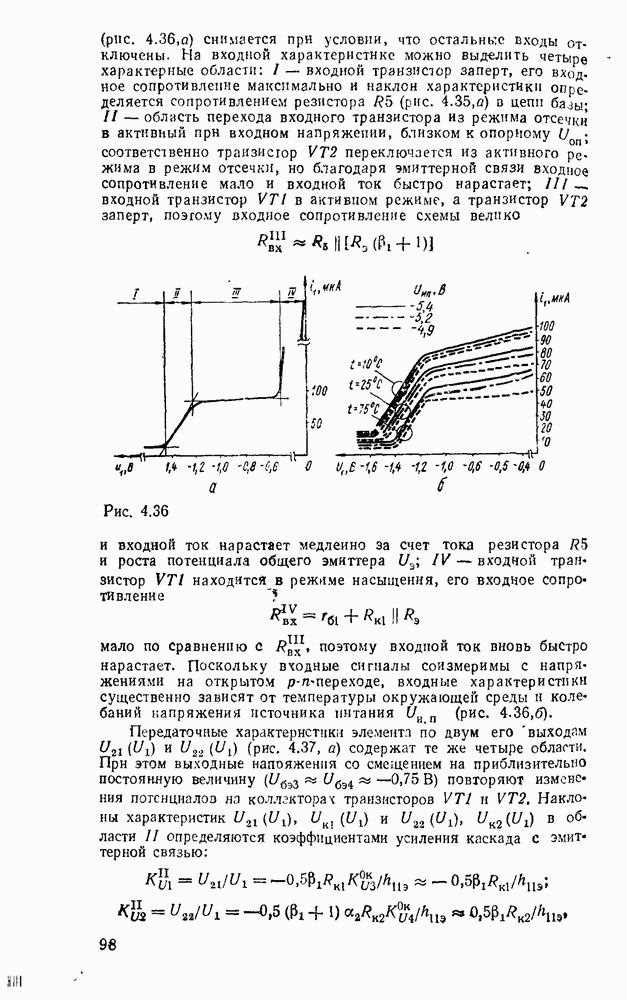
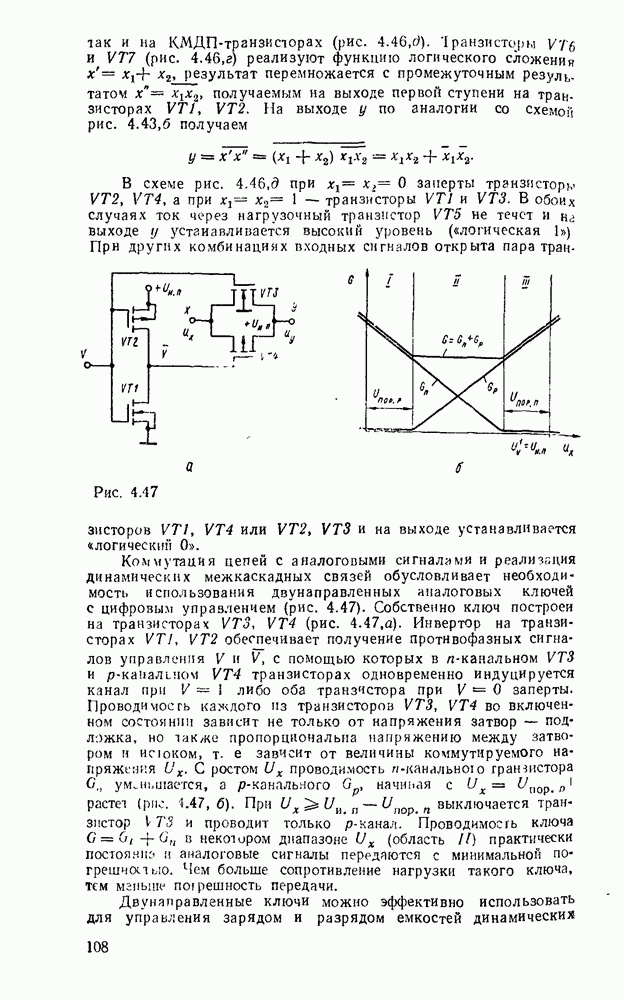
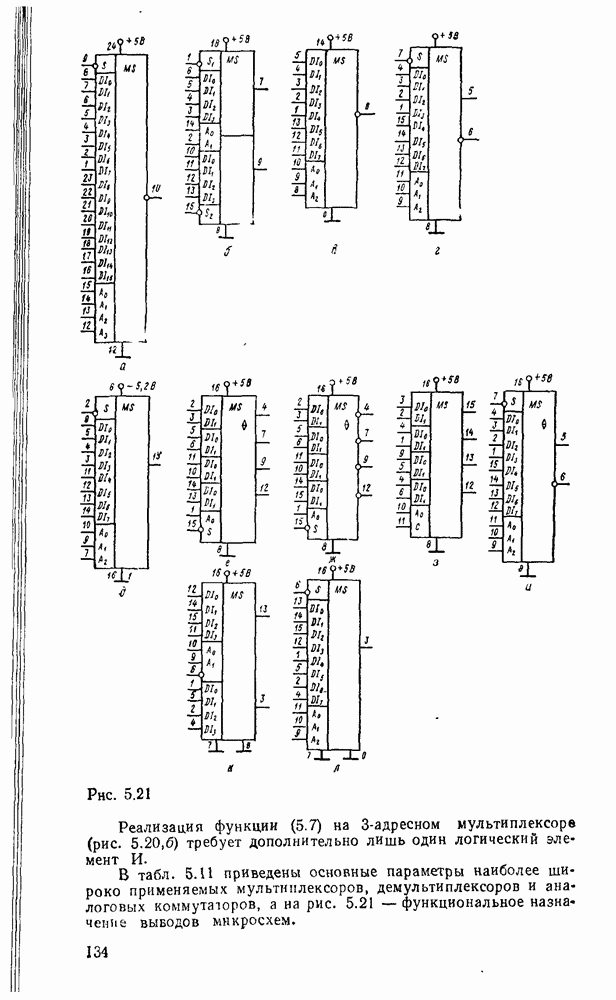
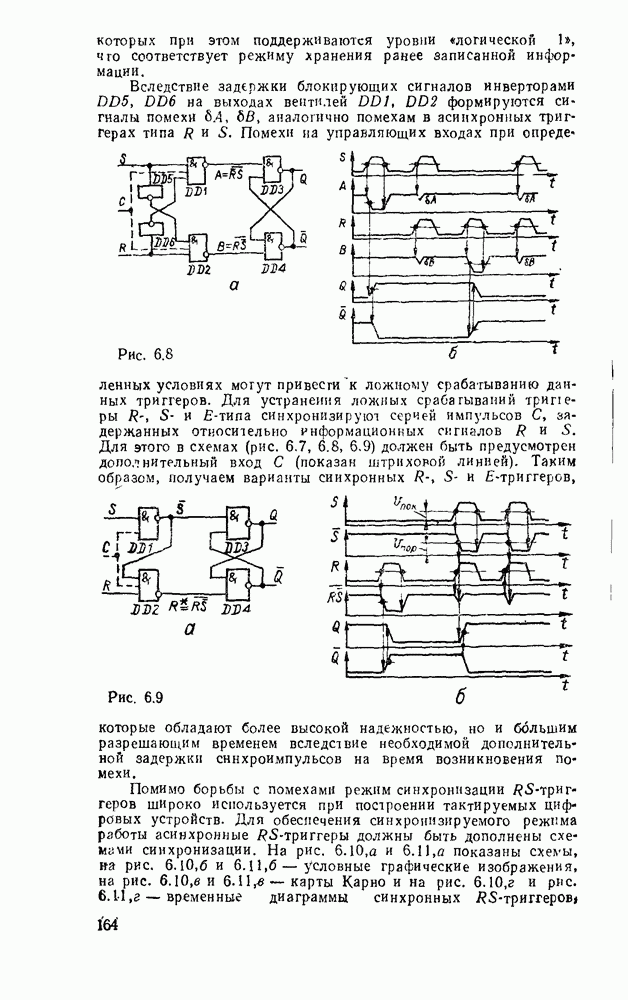
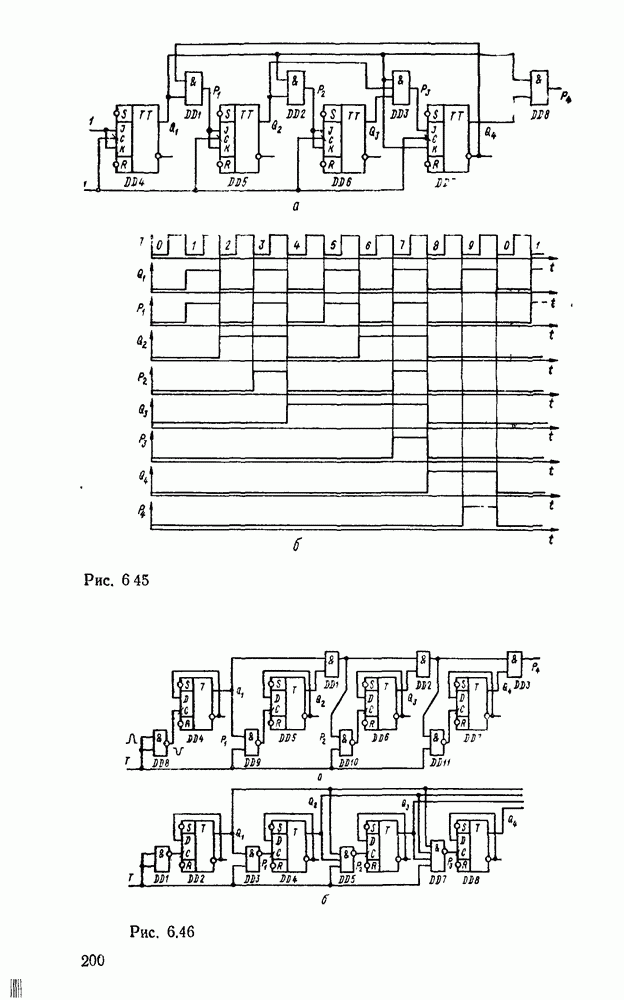
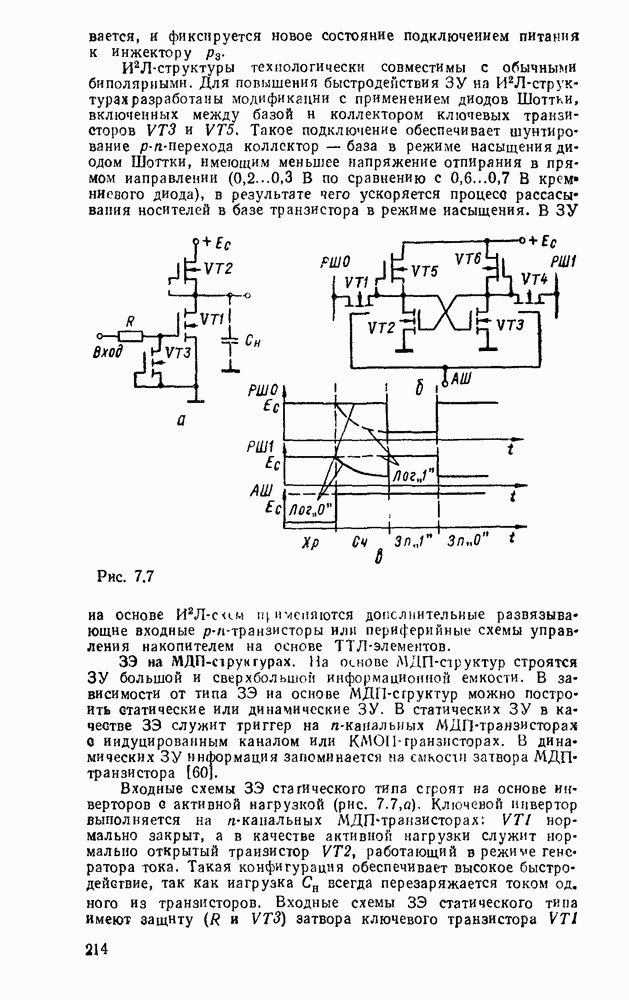
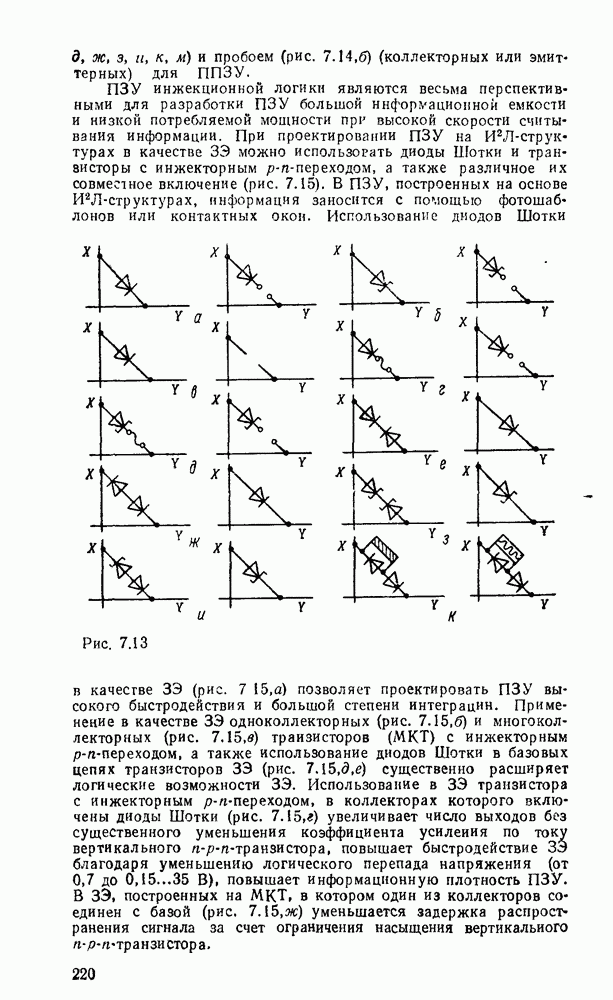
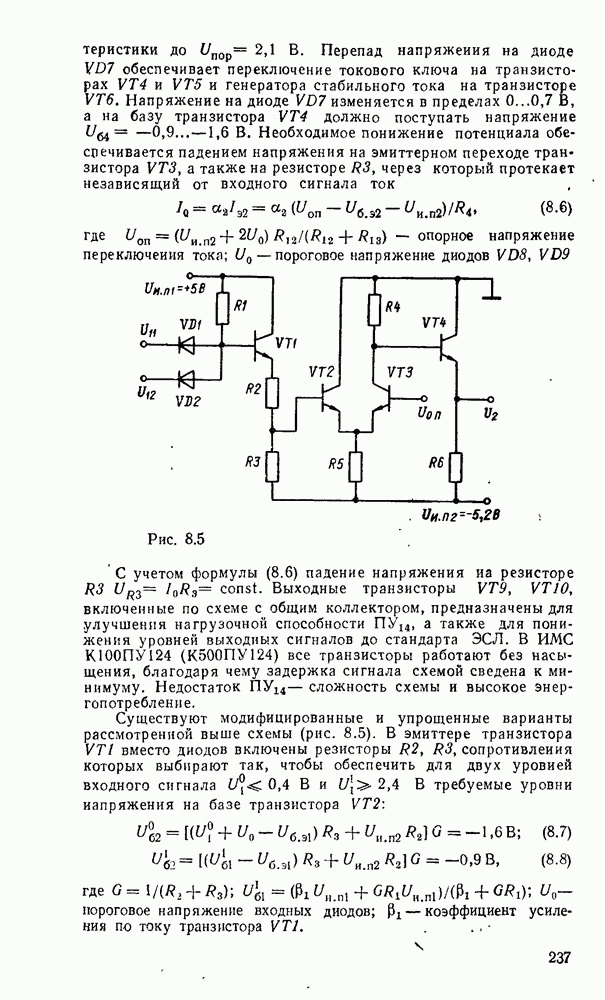
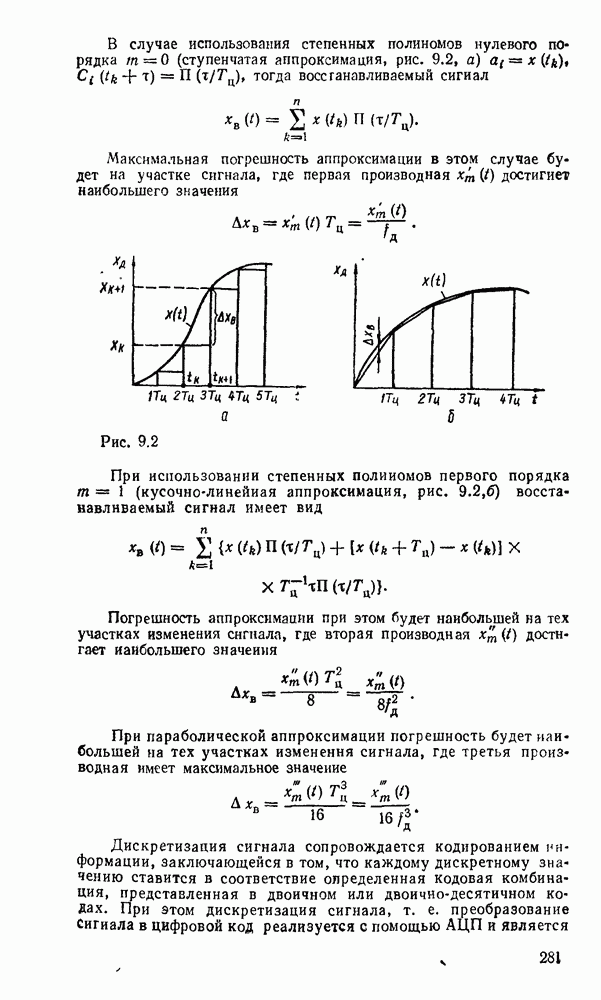
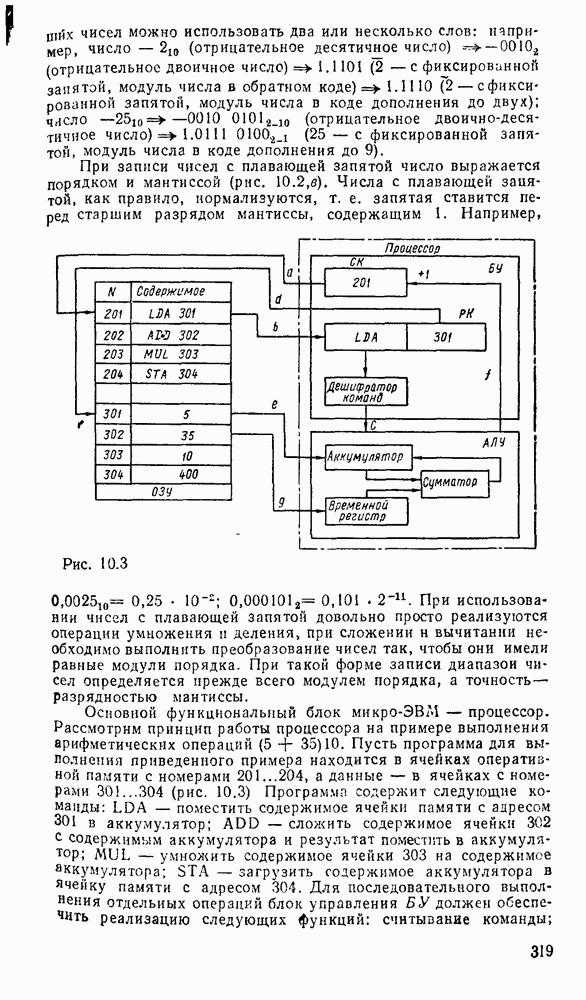
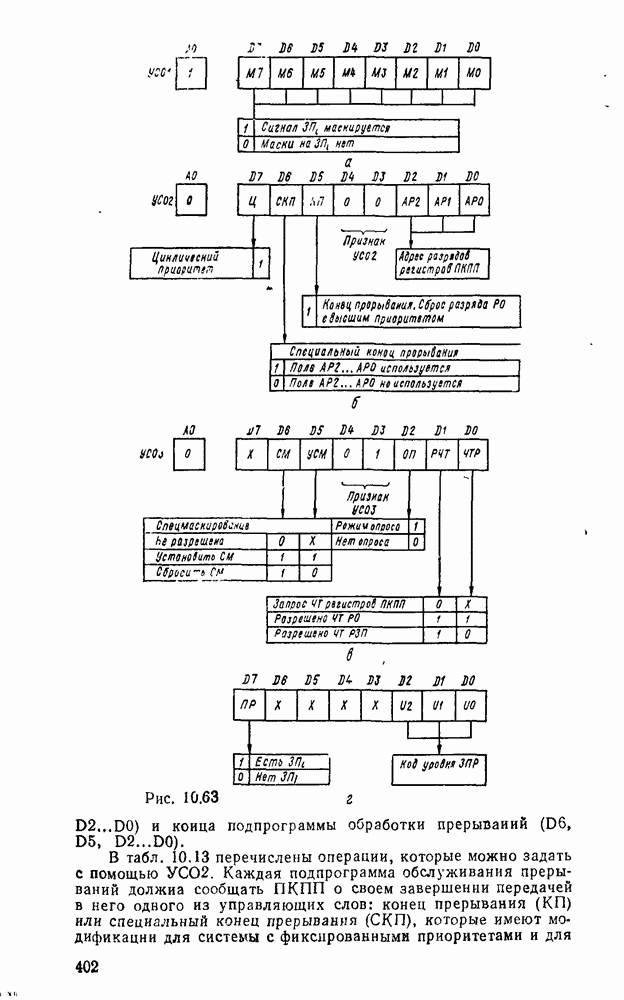
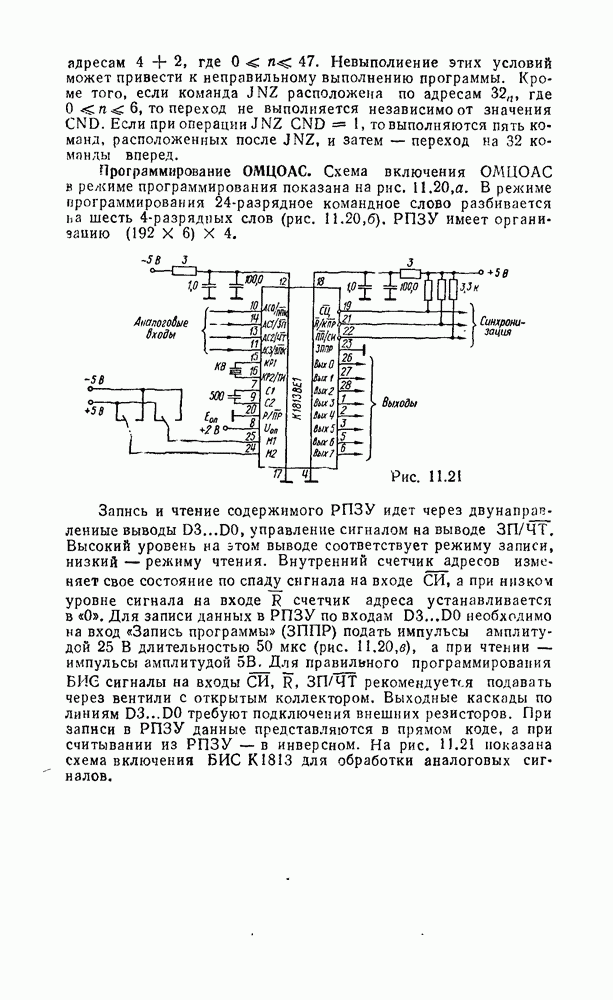
Считывание минтермов с карты Карно осуществляется последовательным рассмотрением групп ячеек. В минтерм входят только те переменные, которые сохраняют свои значения в данной группе, причем значениям 1 соответствует сама переменная, а значению 0 — ее отрицание. Переменные, которые принимают в данной группе различные значения (0 и 1), являются свободными и в данном минтерме отсутствуют. Примеры считывания минтермов с карт Карно для различного числа переменных показаны на рис. 2.3.

Рис. 2.2.

Рис. 2.3.
Любая совокупность групп ячеек, покрывающая все отмеченные ячейки, соответствует некоторой сумме минтермов различных рангов, которая равнозначна данной функции. Стремление к простейшей форме интуитивно понимается как поиск такого минимального покрытия, число групп в котором было бы поменьше, а сами группы были покрупнее. Действительно, чем меньше групп в покрытии, тем меньше минтермов в формуле, а при увеличении размеров группы соответственно понижается ранг минтерма, а значит, уменьшается количество содержащихся в нем переменных.
Практически для отыскания минимальною покрытия на карте Карно прежде всего выбирается отмеченная ячейка, входящая в такую наибольшую группу, которая покрывает любые другие возможные группы с этой ячейкой. После формирования этой наибольшей группы по тому же признаку выбираетси другая  не покрытая ячейка и формируется ее наибольшая группа. Эгот процесс продолжается до тех пор, пока все отмеченные ячейки окажутся в тех или иных группах либо останутся только такие непокрытые ячейки, которые можно сгруппировать различными способами. Из возможных вариантов выбираются те, которые приводят к минимальным покрытиям.
не покрытая ячейка и формируется ее наибольшая группа. Эгот процесс продолжается до тех пор, пока все отмеченные ячейки окажутся в тех или иных группах либо останутся только такие непокрытые ячейки, которые можно сгруппировать различными способами. Из возможных вариантов выбираются те, которые приводят к минимальным покрытиям.

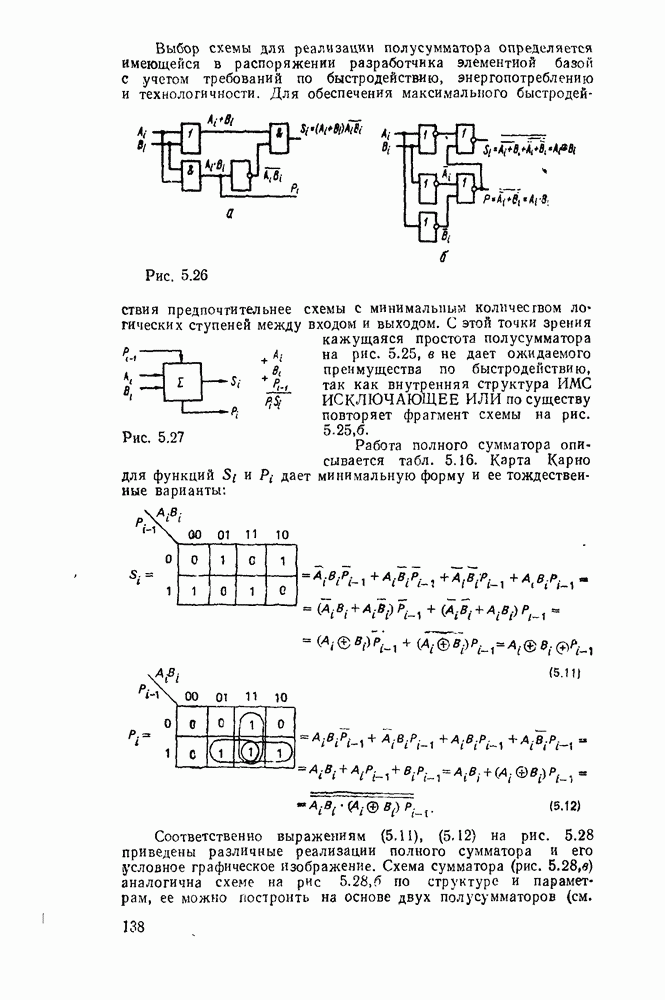
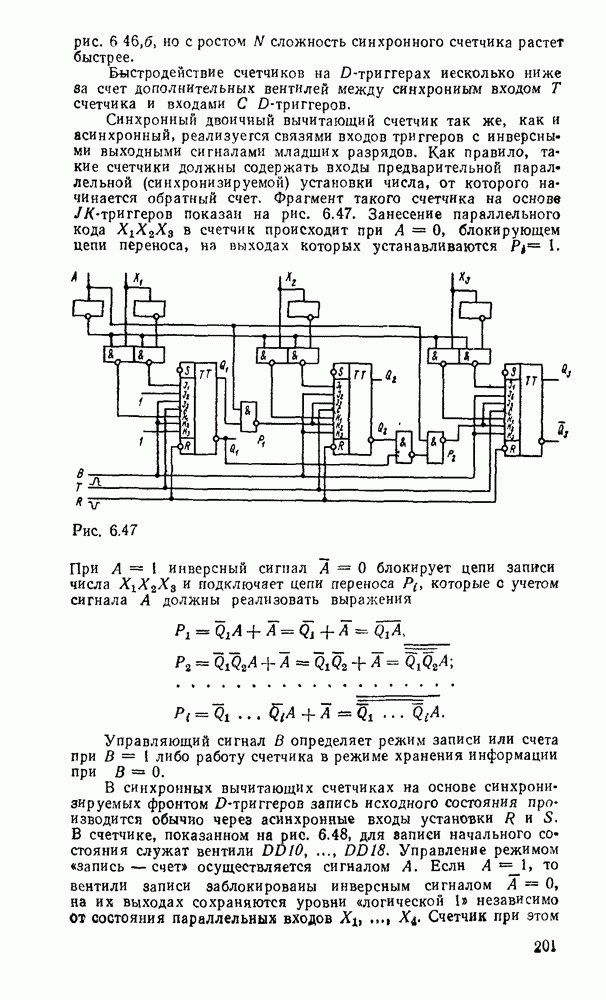
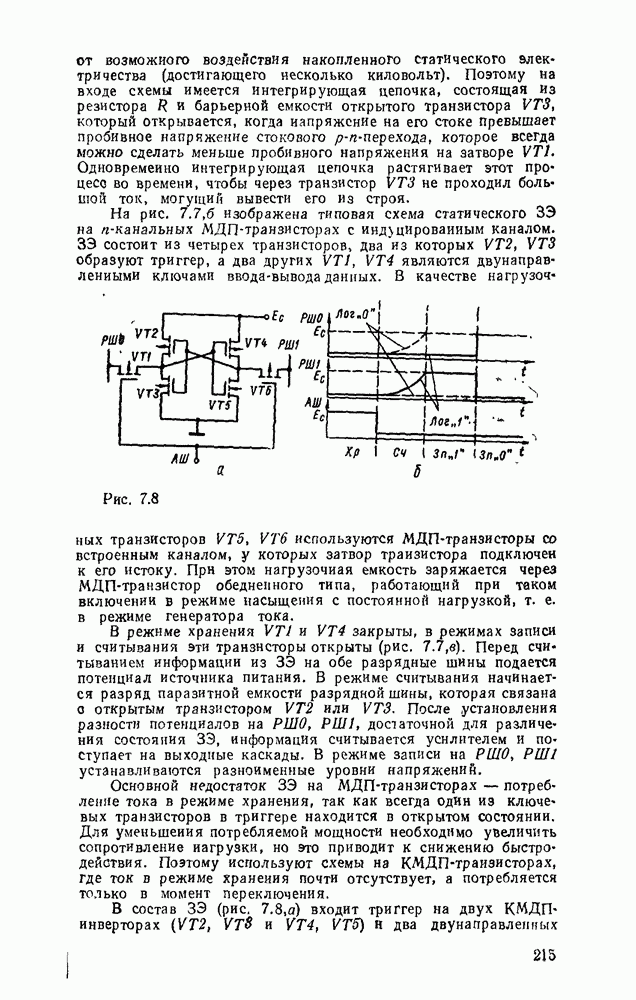
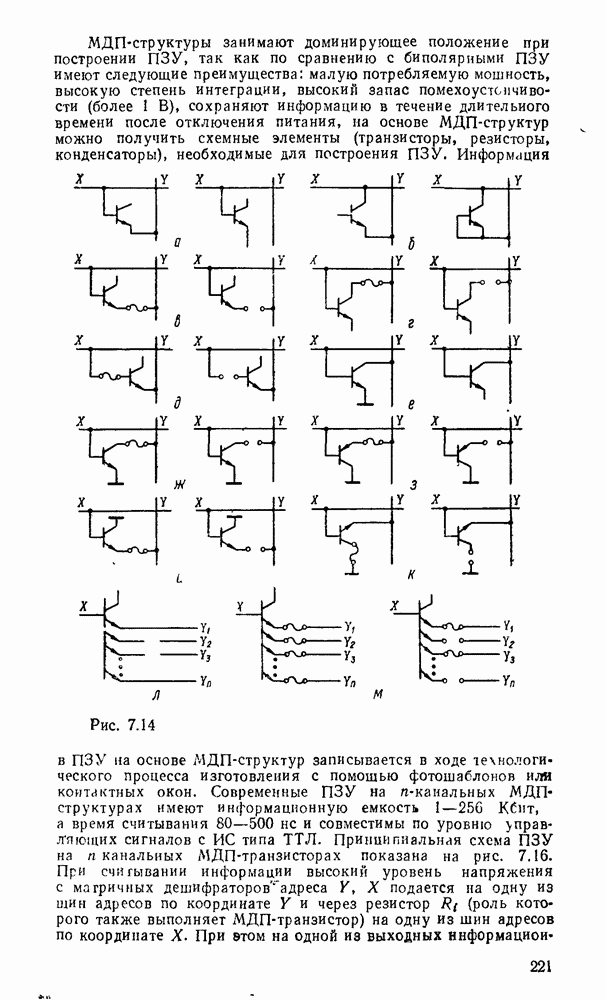
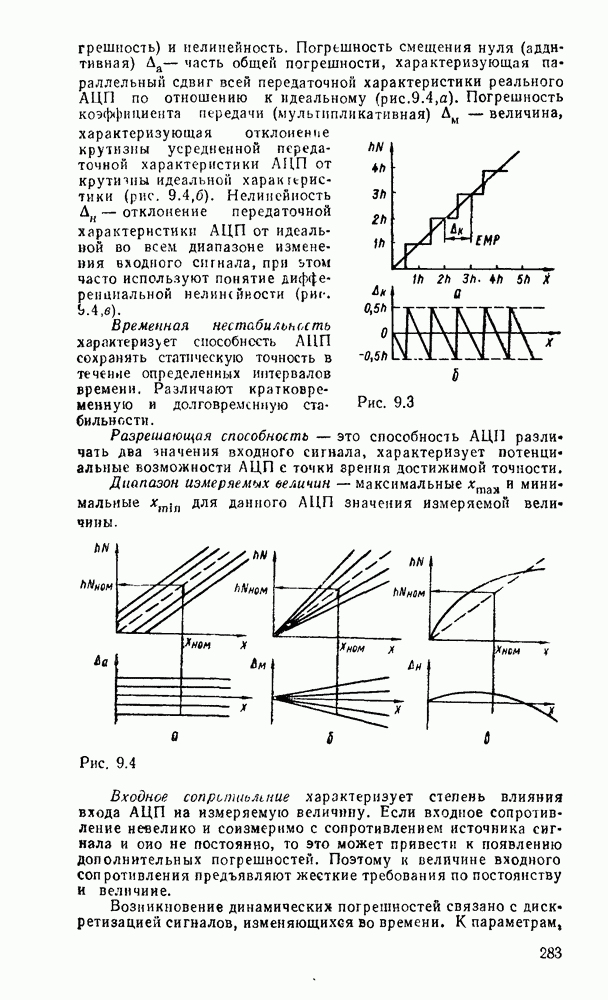
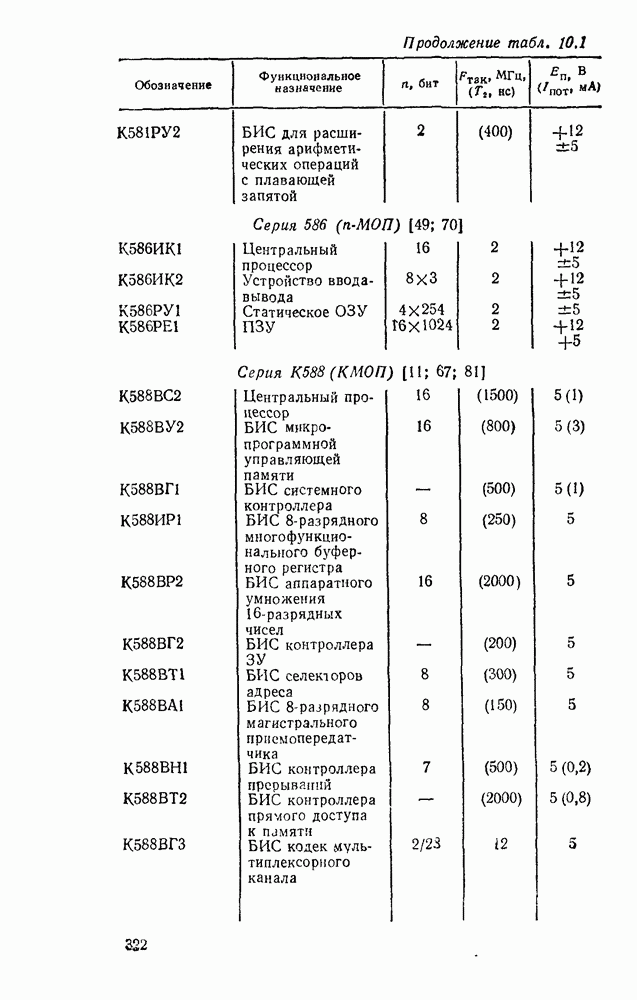
Рис. 2.4.
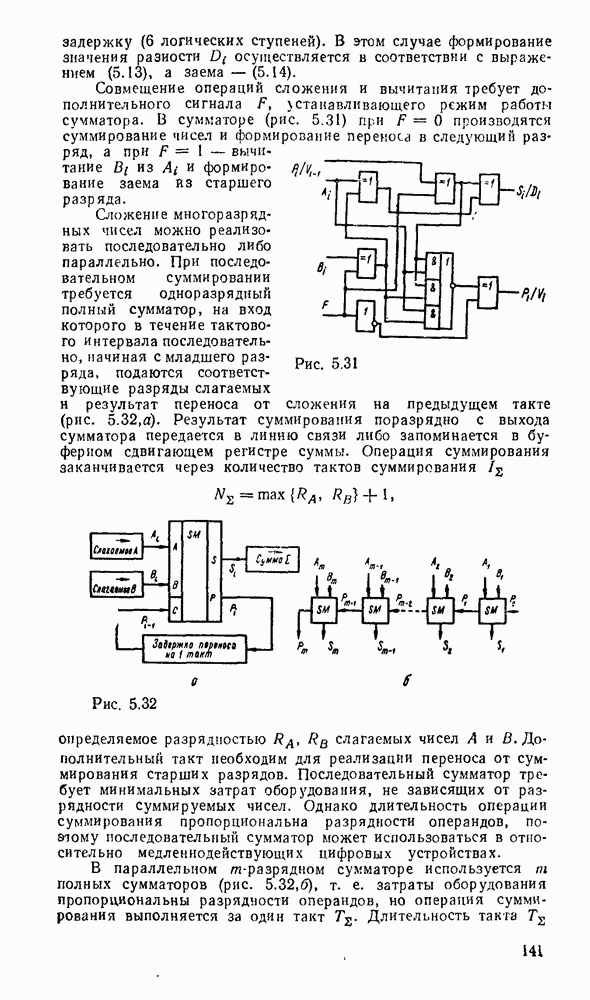
Наглядность карт Карно позволяет решать задачи минимизации, не прибегая к промежуточным покрытиям — сокращенным и тупиковым формам,  существенно упрощает этот процесс. К сожалению, возможности этого метода ограничиваются по существу функциями четырех переменных. При большем числе переменных приходится прибегать к различным ухищрениям и основное преимущество — наглядность теряется. Тем не менее этот метод еще используется в инженерной практике для пяти, шести, а иногда и большего числа переменных, что требует увеличения количества карт Карно. Так, при пяти переменных используются две карты, одна
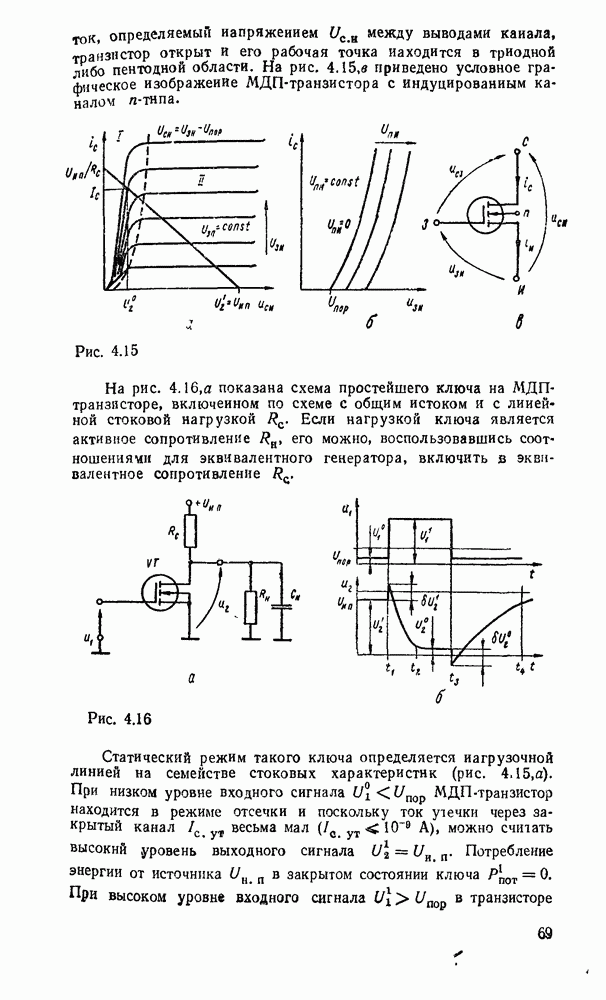
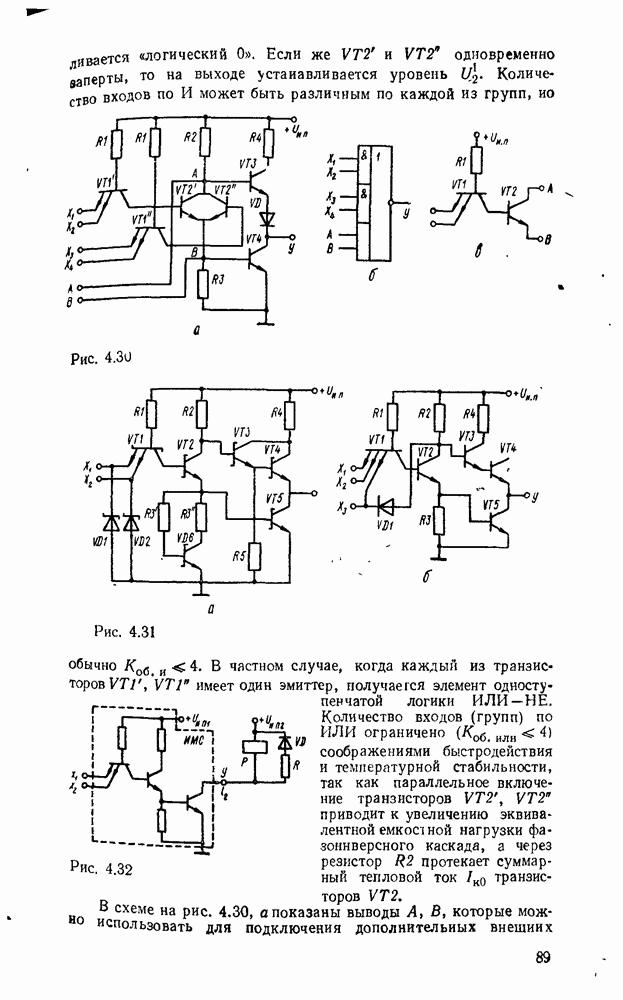
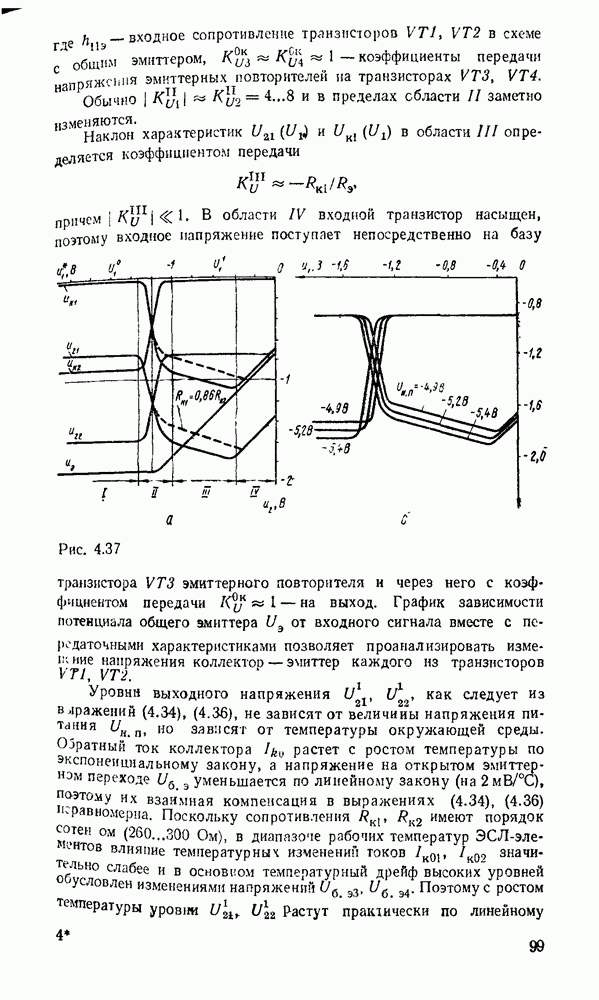
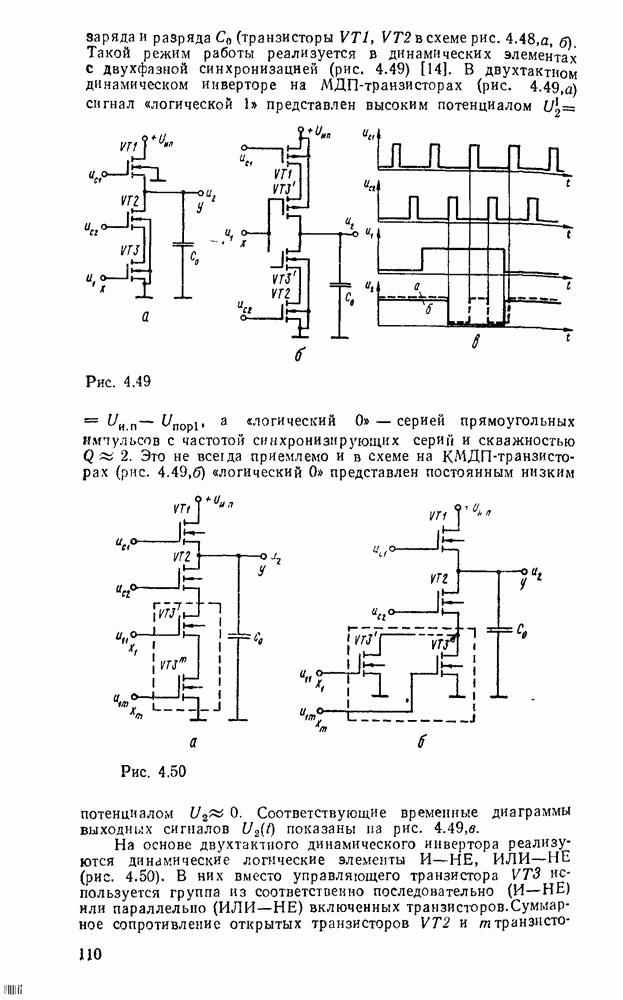
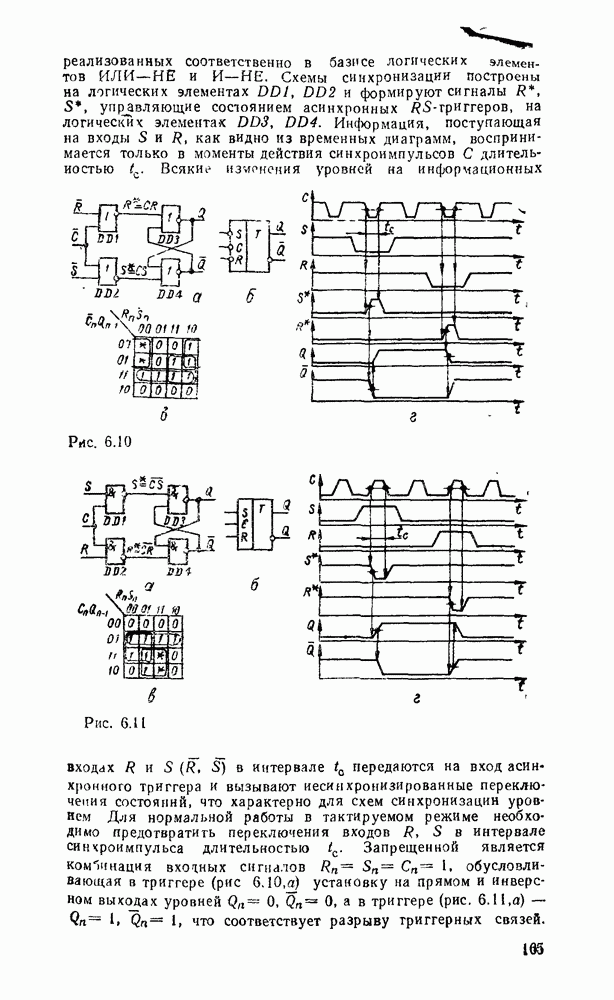
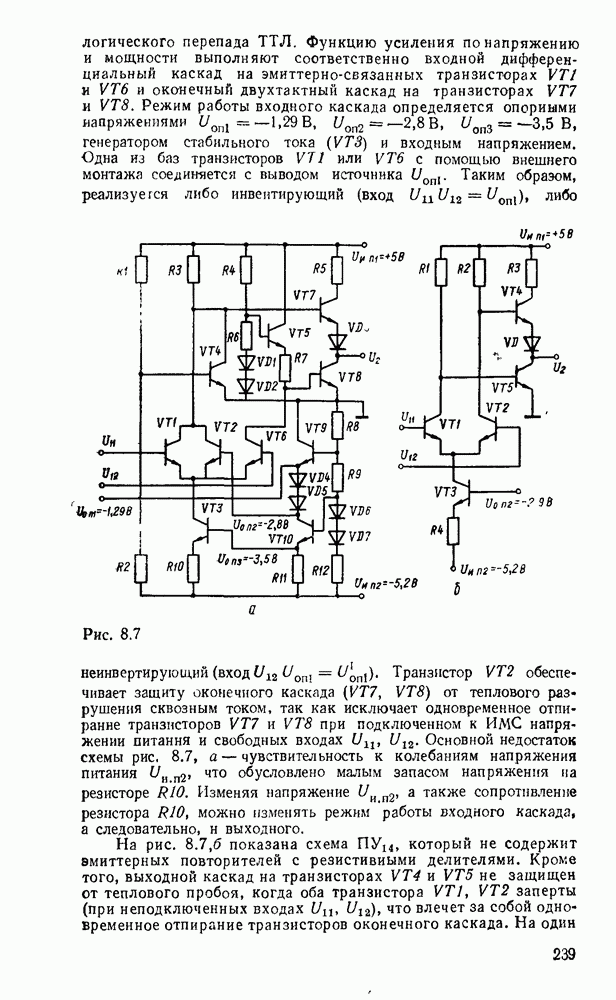
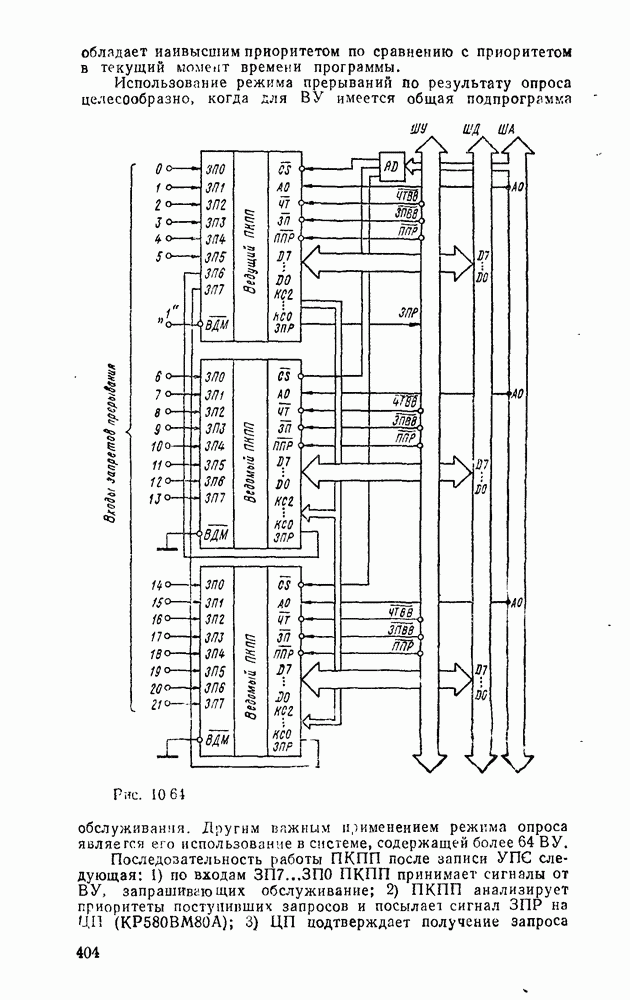
существенно упрощает этот процесс. К сожалению, возможности этого метода ограничиваются по существу функциями четырех переменных. При большем числе переменных приходится прибегать к различным ухищрениям и основное преимущество — наглядность теряется. Тем не менее этот метод еще используется в инженерной практике для пяти, шести, а иногда и большего числа переменных, что требует увеличения количества карт Карно. Так, при пяти переменных используются две карты, одна  которых соответствует инверсии пятой - переменной, а другая — этой же переменной без инверсии, причем они размечаются либо одинаково и сравниваются наложением (рис. 2.4,а), либо симметрично и сравниваются ошосительно оси симметрии (рис.
которых соответствует инверсии пятой - переменной, а другая — этой же переменной без инверсии, причем они размечаются либо одинаково и сравниваются наложением (рис. 2.4,а), либо симметрично и сравниваются ошосительно оси симметрии (рис.  ). Для упрощения разметки строки и столбцы, соответствующие значениям 1 для иекоюрой переменной, выделяются фигурной скобкой. Теперь смежными считаются и такие ячейки, которые занимают на картах одинаковые или симметричные области (в зависимости от способа разметки).
). Для упрощения разметки строки и столбцы, соответствующие значениям 1 для иекоюрой переменной, выделяются фигурной скобкой. Теперь смежными считаются и такие ячейки, которые занимают на картах одинаковые или симметричные области (в зависимости от способа разметки).
В качестве примера на рис. 2.4 показана функция, заданная таблицей соответствия:

Сначала строятся простейшие покрытия на каждой карте раздельно, с которых списываются две функции: для левой карты  и для правой карты
и для правой карты  .
.

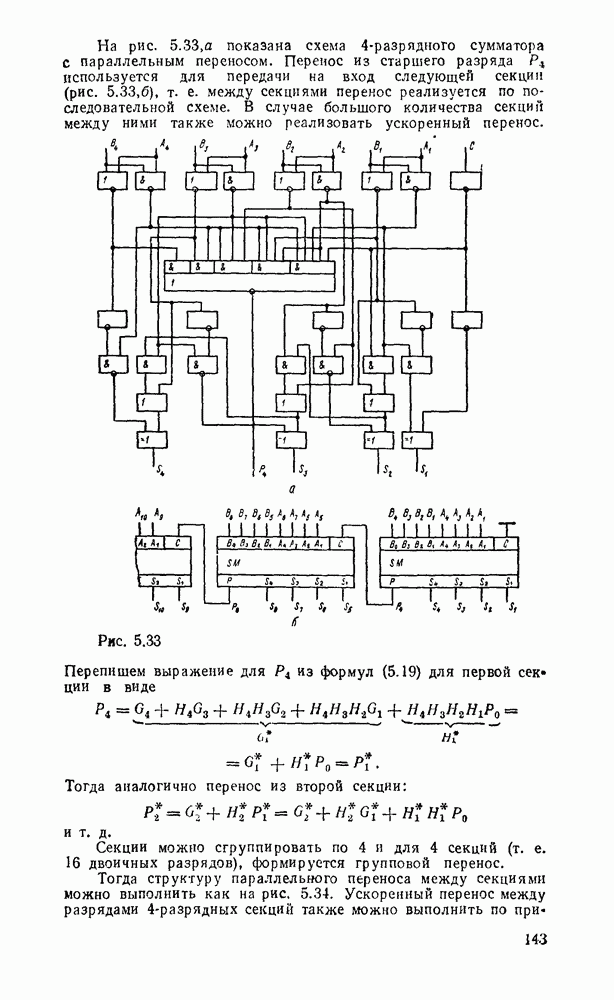
Рис. 2.5.
Затем ищутся такие импликанты в этих функциях, которые различаются только вхождением  и их можно объгдннить. В данном случае это
и их можно объгдннить. В данном случае это  (соответствующие им группы ячеек, обведенные жирной линией на рис. 2.4, а, совпадают при наложении, а на рис. 2.4, б они расположены симметрично), в результате объединения которых получается иыпликанта
(соответствующие им группы ячеек, обведенные жирной линией на рис. 2.4, а, совпадают при наложении, а на рис. 2.4, б они расположены симметрично), в результате объединения которых получается иыпликанта  . Наконец, можно также дополнять одну из карт несущественными нмпликантами, которые можно считать соседними имплшеантам другой карты и, объединяя их между собой, упрощать результирующее выражение. Так, в левую карту можно добавить импликанту
. Наконец, можно также дополнять одну из карт несущественными нмпликантами, которые можно считать соседними имплшеантам другой карты и, объединяя их между собой, упрощать результирующее выражение. Так, в левую карту можно добавить импликанту  (на рис. 2.4 она показана пунктиром), которая, объединяясь с имплнкантой правой карты
(на рис. 2.4 она показана пунктиром), которая, объединяясь с имплнкантой правой карты  , дает
, дает  . Окончательное выражение получаем как сумму
. Окончательное выражение получаем как сумму  с учетом выполненных преобразований:
с учетом выполненных преобразований:

Для функций шести переменных потребовалось бы четыре карты Карно, а с каждой новой переменной количество требуемых карт увеличивается вдвое и, например, для восьми переменных уже равно 16. В практике используются и другие графические структуры, например, карты Вейча, которые отличаются только способом разметки переменных. Ясно, что графические методы пригодны для минимизации вручную сравнительно простых функций.
В то же время машинные методы анализа и проектирования логических схем основаны на формальном алгоритме Квайиа-Мак-Класки и его разновидностях.
Для получения минимальной формы инверсии функции необходимо найти на карте Карно минимальное покрытие совокупности нулевых ячеек и описать соответствующую формулу по указанному выше правилу. Так, для функции на рис.  имеются два таких покрытия (рис. 2.5), отличающихся только одной импликантой. Если требуется найти минимальную форму как произведения макстермов, то в соответствии с изложенным в § 2.4 правилом достаточно в выражении для инверсной функции заменить все логические операции на дуальные, а вхождения переменных — на инверсные:
имеются два таких покрытия (рис. 2.5), отличающихся только одной импликантой. Если требуется найти минимальную форму как произведения макстермов, то в соответствии с изложенным в § 2.4 правилом достаточно в выражении для инверсной функции заменить все логические операции на дуальные, а вхождения переменных — на инверсные:  . Эти же формы можно записать на основе принципа дуальности непосредственно по минимальным покрытиям нулевых ячеек карты Карно. Для этого достаточно каждую группу ячеек идентифицировать как сумму переменных при инверсной разметке карты Карно, т. е. считая отмеченные значения переменных нулевыми.
. Эти же формы можно записать на основе принципа дуальности непосредственно по минимальным покрытиям нулевых ячеек карты Карно. Для этого достаточно каждую группу ячеек идентифицировать как сумму переменных при инверсной разметке карты Карно, т. е. считая отмеченные значения переменных нулевыми.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛА И КОДЫ
- 1.1. СИСТЕМЫ СЧИСЛЕНИЯ
- 1.3. МАШИННОЕ СЛОВО
- 1.4. ОБРАТНЫЙ И ДОПОЛНИТЕЛЬНЫЙ КОДЫ
- 1.5. ДВОИЧНО-ДЕСЯТИЧНЫЕ КОДЫ
- 1.6. КОД ГРЕЯ
- 1.7. АЛФАВИТНО-ЦИФРОВЫЕ КОДЫ
- Глава 2. АЛГЕБРА ЛОГИКИ
- 2.1. ЛОГИЧЕСКИЕ ФУНКЦИИ
- 2.2. ТАБЛИЦЫ СООТВЕТСТВИЯ
- 2.3. ФУНКЦИОНАЛЬНАЯ ПОЛНОТА
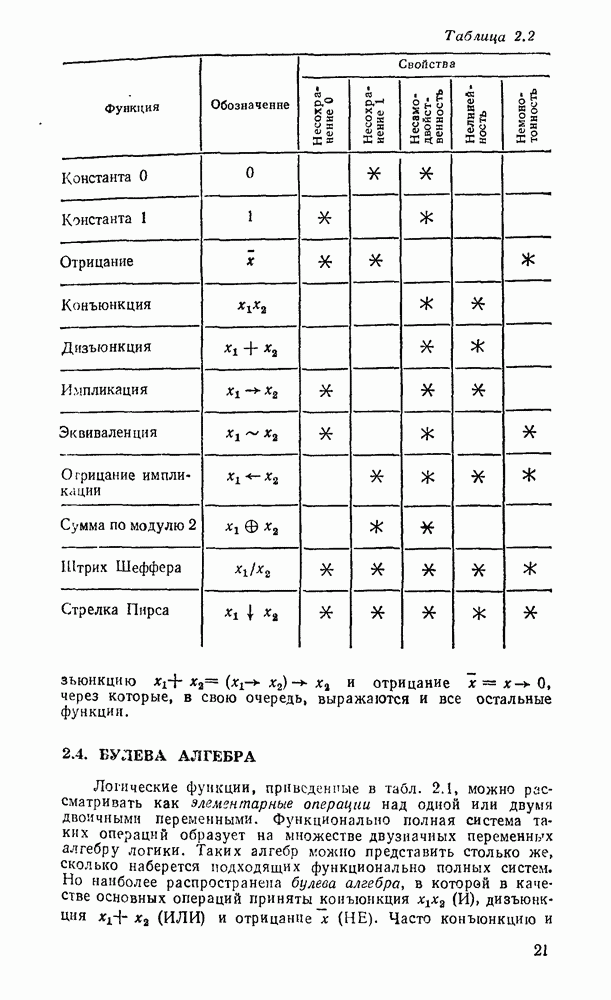
- 2.4. БУЛЕВА АЛГЕБРА
- 2.5. СТАНДАРТНЫЕ ФОРМЫ
- 2.6. ПРЕОБРАЗОВАНИЕ И УПРОЩЕНИЕ ФОРМУЛ
- 2.7. АЛГОРИТМ КВАЙНА — МАК-КЛАСКИ
- 2.8. АЛГЕБРАИЧЕСКИЙ МЕТОД ОБРАЗОВАНИЯ ТУПИКОВЫХ ФОРМ
- 2.9. КАРТЫ КАРНО
- Глава 3. РЕАЛИЗАЦИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ
- 3.1. ЛОГИЧЕСКИЕ СХЕМЫ
- 3.2. МНОГОСТУПЕНЧАТЫЕ РЕАЛИЗАЦИИ
- 3.3. ФАКТОРИЗАЦИЯ
- 3.4. БАЗИСЫ И — НЕ И ИЛИ — НЕ
- 3.5. СХЕМЫ С МНОГИМИ ВЫХОДАМИ
- Глава 4. ЭЛЕМЕНТЫ ЦИФРОВОЙ СХЕМОТЕХНИКИ
- 4.1. КЛАССИФИКАЦИЯ, ПАРАМЕТРЫ, ХАРАКТЕРИСТИКИ
- 4.2. ХАРАКТЕРИСТИКИ ЦИФРОВЫХ СХЕМ
- 4.3. ЭЛЕКТРОННЫЕ КЛЮЧИ
- Электронные ключи на биполярных транзисторах.
- Ключ на биполярном транзисторе с нелинейной обратной связью.
- Электронные ключи на полезых транзисторах.
- 4.4. ДИОДНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.5. ТРАНЗИСТОРНО-ТРАНЗИСТОРНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
- 4.6. ЭЛЕМЕНТЫ ЭМИТТЕРНО-СВЯЗАННОЙ ЛОГИКИ
- 4.7. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ НА МДП-ТРАНЗИСТОРАХ
- Глава 5. КОМБИНАЦИОННЫЕ ФУНКЦИОНАЛЬНЫЕ УЗЛЫ
- 5 1. ПРЕОБРАЗОВАТЕЛИ КОДОВ, ШИФРАТОРЫ, ДЕШИФРАТОРЫ
- 5.2. МУЛЬТИПЛЕКСОРЫ И ДЕМУЛЬТИПЛЕКСОРЫ
- 5.3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА СДВИГА
- 5.4. КОМБИНАЦИОННЫЕ СУММАТОРЫ
- Глава 6. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ СХЕМЫ
- 6 1. ТРИГГЕРЫ
- 6.2. РЕГИСТРЫ
- 6.3. СЧЕТЧИКИ
- Синхронные счетчики.
- Глава 7. ПОЛУПРОВОДНИКОВЫЕ ЗАПОМИНАЮЩИЕ УСТРОЙСТВА
- 7.1. КЛАССИФИКАЦИЯ И ОСНОВНЫЕ ПАРАМЕТРЫ ЗУ
- 7.2. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ОЗУ
- 7.3. ЗАПОМИНАЮЩИЕ ЭЛЕМЕНТЫ ПЗУ
- 7.4. ПРОГРАММИРУЕМЫЕ ЛОГИЧЕСКИЕ МАТРИЦЫ
- Глава 8. КОМПОНЕНТЫ ЦИФРОВЫХ СИСТЕМ
- 8.1. КОМПОНЕНТЫ СОГЛАСОВАНИЯ УРОВНЕЙ СИГНАЛОВ
- 8.2. ФОРМИРОВАТЕЛИ И ГЕНЕРАТОРЫ ИМПУЛЬСОВ
- Генераторы импульсов на полевых транзисторах.
- Генераторы импульсов на логических ИМС
- Генераторы импульсов на основе триггеров.
- Генераторы импульсов на основе операционных усилителей.
- Формирователи и генераторы линейно изменяющегося напряжения (ЛИН).
- 8.3. КОМПОНЕНТЫ ОТОБРАЖЕНИЯ ЦИФРОВОЙ ИНФОРМАЦИИ
- Глава 9. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.1. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
- 9.2. ПАРАМЕТРЫ И МЕТОДЫ ПОСТРОЕНИЯ АЦП
- 9.3. ЭЛЕМЕНТЫ АЦП
- 9.4. ЦИФРОАНАЛОГОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- 9.5. АНАЛОГО-ЦИФРОВЫЕ ПРЕОБРАЗОВАТЕЛИ
- Глава 10. ОДНОКРИСТАЛЬНЫЕ МИКРОПРОЦЕССОРЫ
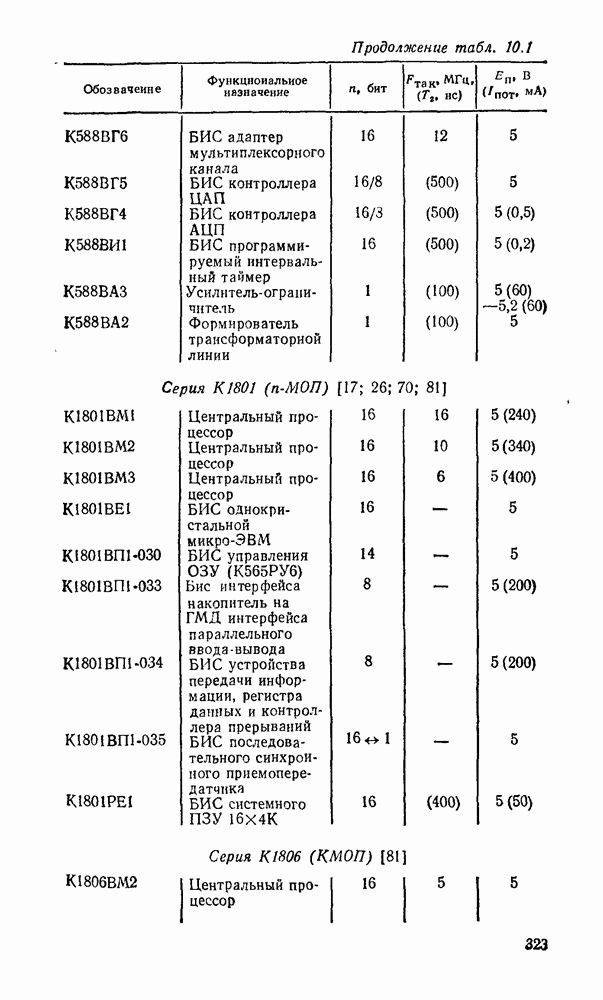
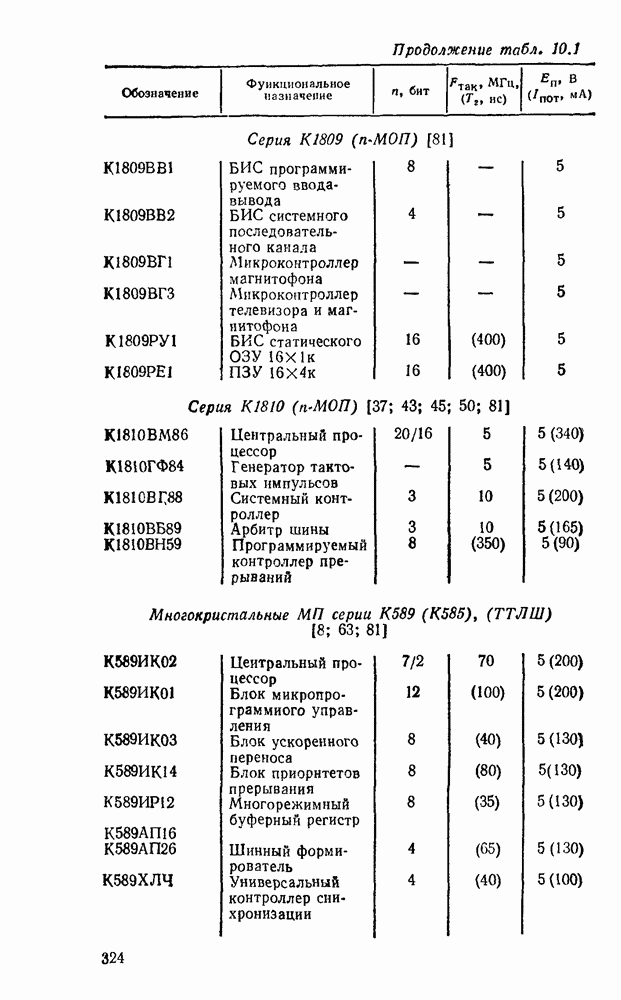
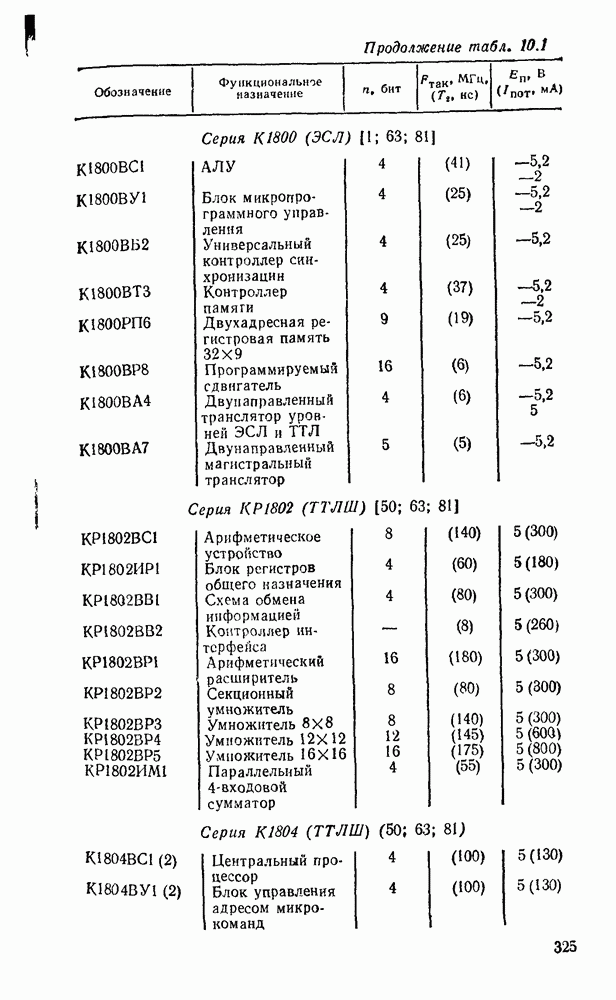
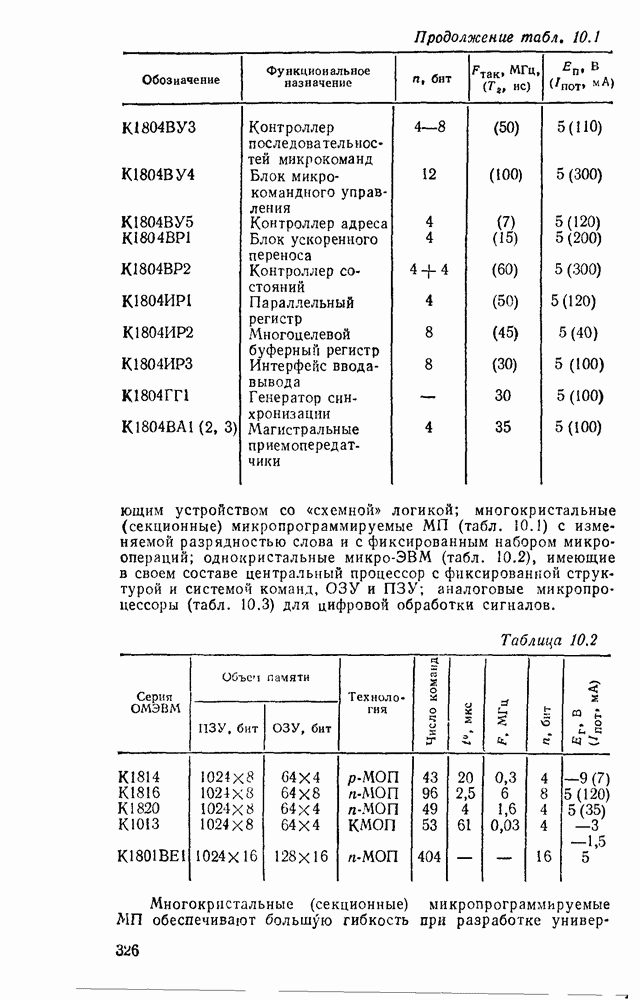
- 10.1. ОСНОВНЫЕ ПАРАМЕТРЫ И ТИПЫ МИКРОПРОЦЕССОРНЫХ КОМПЛЕКТОВ
- 10.2. МИКРОПРОЦЕССОР СЕРИИ КР580
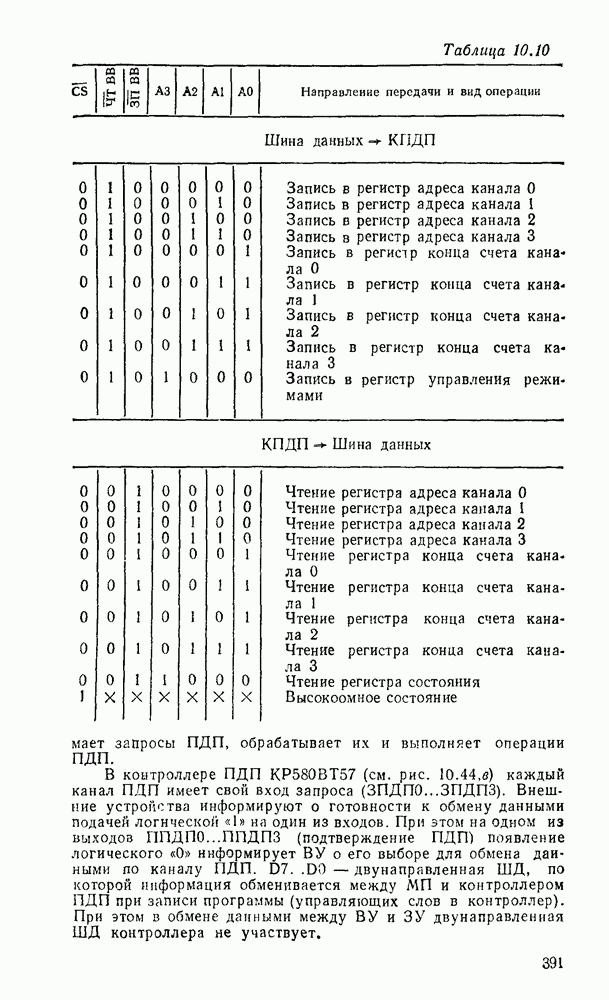
- 10.3. УНИВЕРСАЛЬНЫЕ ИНТЕРФЕЙСНЫЕ БИС СЕРИИ КР580
- Глава 11. ОДНОКРИСТАЛЬНЫЕ МИКРО-ЭВМ
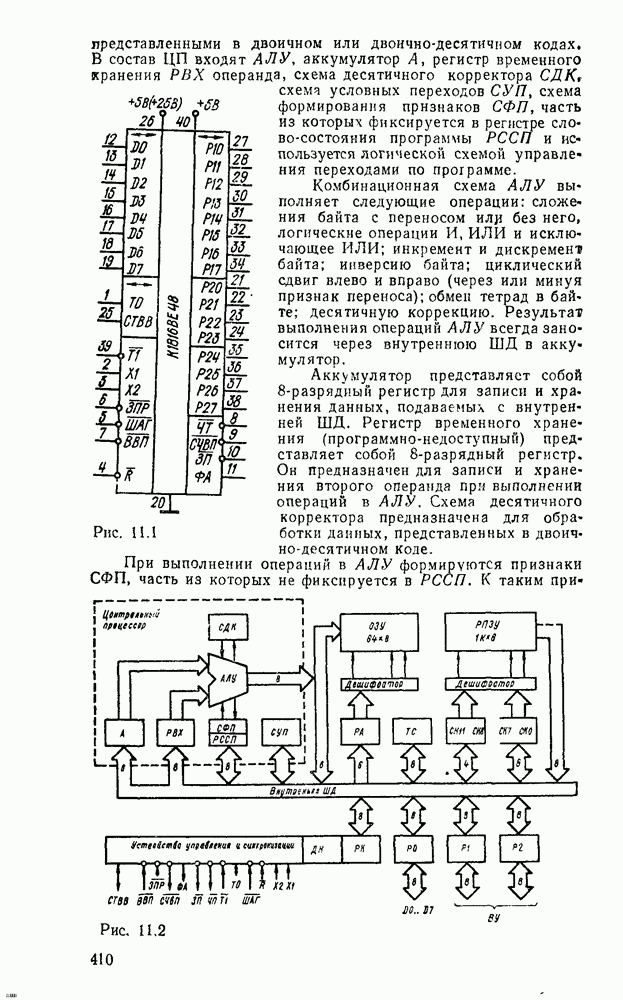
- 11.1. ОДНОКРИСТАЛЬНЫЕ 8-РАЗРЯДНЫЕ МИКРОЭВМ СЕРИИ К1816
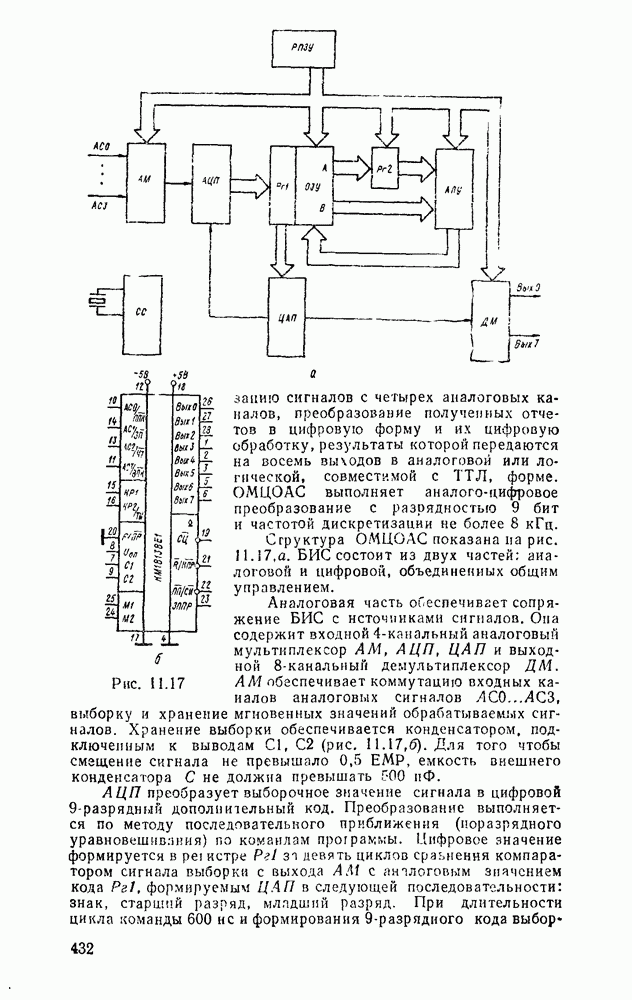
- 11.2. ОДНОКРИСТАЛЬНЫЕ МИКРОЭВМ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ СЕРИИ К1813
- СПИСОК ЛИТЕРАТУРЫ