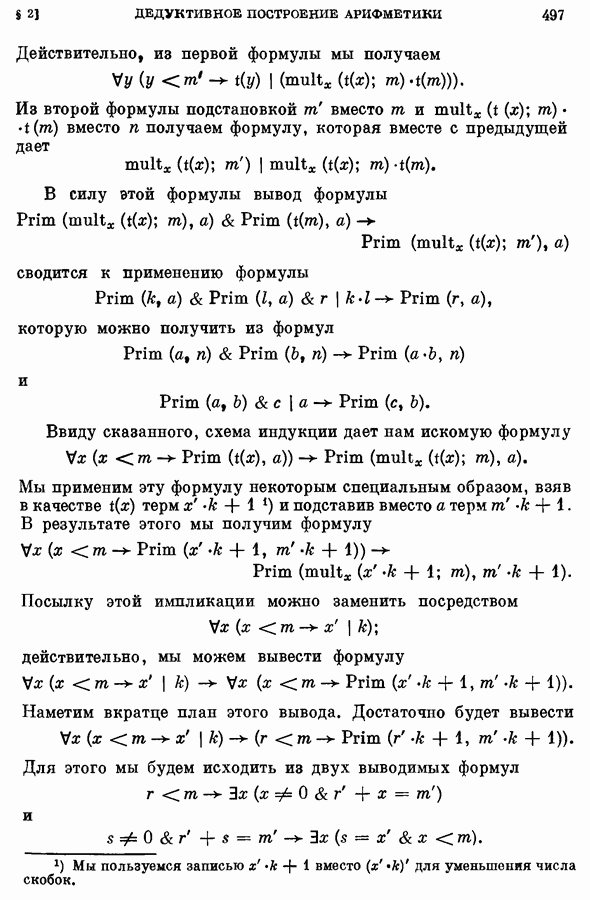| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА I. ПРОБЛЕМА НЕПРОТИВОРЕЧИВОСТИ В АКСИОМАТИЧЕСКИХ ИССЛЕДОВАНИЯХ КАК ЛОГИЧЕСКАЯ ПРОБЛЕМА РАЗРЕШИМОСТИ
§ 1. Формальная аксиоматика
1. Отношение формальной аксиоматики к содержательной; вопрос о непротиворечивости; арифметизация.
Уровень научных исследований в области оснований математики, из которого исходит наше изложение, характеризуется результатами, полученными в ходе работы, проводившейся по следующим трем направлениям:
1) совершенствование аксиоматического метода — прежде всего, на базе оснований геометрии;
2) построение анализа по принятой ныне строгой методике, путем сведения теории величин к теории, объектом рассмотрения которой являются числа и числовые множества;
3) исследования, направленные на обоснование понятий числа  множества.
множества.
Точка зрения, сформировавшаяся в результате этих исследований, в сочетании с повышенными требованиями методического характера ведет к определенной программе дальнейшей работы — программе, в рамках которой речь идет о новой трактовке проблемы бесконечного. Знакомство с этой программой мы хотели бы начать с рассмотрения аксиоматического метода.
Термин «аксиоматический» употребляется иногда в более широком, а иногда и в более узком смысле слова. При самом широком понимании этого термина построение какой-либо теории мы называем аксиоматическим, если основные понятия и основные гипотезы этой теории ставятся как таковые во главу угла, а дальнейшее ее содержание логически выводится из них с помощью определений и доказательств. Аксиоматически именно в этом смысле слова были построены геометрия Евклида, механика Ньютона, термодинамика Клаузиуса.
Усиление, которое аксиоматическая точка зрения получила в «Основаниях геометрии» Гильберта, заключается в том, что из всего материала реальных представлений, используемого для формирования основных понятий данной теории. при
аксиоматпческом ее построении мы принимаем в расчет лишь то, что в виде некоторого экстракта формулируется в ее аксиомах, а от всего остального содержания абстрагируемся. Когда аксиоматика начинает пониматься в таком наиболее узком смысле этого слова, в качестве очередного обстоятельства добавляется еще экзистенциалъностъ ее вида. Этим аксиоматический способ построения какой-либо теории и отличается от конструктивного, или генетического способа. В то время как при конструктивном способе построения объекты рассматриваемой теории вводятся только как вещи определенного вида, в аксиоматической теории нам приходится иметь дело с некоторой фиксированной системой вещей (или даже с несколькими такими системами), вводимой в качестве области субъектов для всех тех предикатов, из которых строятся высказывания этой теории.
В предположении, что эта «индивидная область» представляет собой некую единую совокупность, заключается — если отвлечься от рассмотрения тех тривиальных случаев, когда теория имеет дело лишь с конечной, четко выделенной совокупностью вещей — определенная идеализация. Эта идеализация присоединяется к допущениям данной теории, которые формулируются в ее аксиомах.
Аксиоматику в такой усиленной форме, возникающую в результате отвлечения от конкретного предметного содержания и сформулированную в экзистенциальном виде, мы кратко будем называть формальной аксиоматикой. Характерной особенностью формальной аксиоматики — в отличие от содержательной — является необходимость установления ее непротиворечивости. Между тем содержательная аксиоматика вводит свои основные понятия со ссылкой на имеющийся у нас опыт, а свои основные положения либо считает очевидными фактами, в которых можно непосредственно убедиться, либо формулирует их как итог определенного опыта и тем самым выражает нашу уверенность в том, что нам удалось напасть на след законов природы, а заодно и наше намерение подкрепить эту уверенность успехом развиваемой теории.
Формальная аксиоматика, разумеется, также нуждается в признании очевидности за вещами определенного рода — это необходимо как для осуществления дедукции, так и для установления непротиворечивости самой аксиоматики — однако с тем существенным различием, что этот род очевидности не основывается на каком-либо особом гносеологическом отношении к рассматриваемой конкретной области науки, а остается одним и тем же
в случае любой аксиоматики: мы имеем здесь в виду столь элементарный способ познания, что он вообще является предварительным условием любого точного теоретического исследования. Этот род очевидности мы еще должны будем подвергнуть более пристальному рассмотрению.
Чтобы правильно оценить соотношение между познавательным значением содержательной и формальной аксиоматик, необходимо в первую очередь принять во внимание следующие соображения.
Формальная аксиоматика по необходимости нуждается в содержательной как в своем дополнении, поскольку именно эта последняя поначалу руководит нами в процессе выбора соответствующих формализмов, а затем, когда формальная теория уже имеется в нашем распоряжении, она подсказывает нам, как эта теория должна быть применена к рассматриваемой области действительности.
С другой стороны, мы не можем ограничиться содержательной аксиоматикой по той простой причине, что в науке — если не всегда, то все же по преимуществу — мы имеем дело с такими теориями, которые отнюдь не полностью воспроизводят действительное положение вещей, а являются лишь упрощающей идеализацией этого положения, в чем и состоит их значение. Такого рода теория, конечно, не может быть обоснована путем ссылки на очевидность ее аксиом или на опыт. Более того, ее обоснование и может быть осуществлено только в том смысле, что будет установлена непротиворечивость произведенной в ней идеализации, т. е. той экстраполяции, в результате которой введенные в этой теории понятия и ее основные положения переступают границы наглядно очевидного или данных опыта. Придти к выводу о непротиворечивости этой теории нам не поможет и ссылка на приблизительную значимость ее основных положений. В самом деле, противоречие может наступать как раз в результате того, что мы считаем вполне определенным какое-нибудь отношение, которое имеет место только в некотором ограниченном смысле.
Таким образом, мы оказываемся вынужденными исследовать непротиворечивость теоретических систем в отрыве от рассмотрения фактических обстоятельств и уже тем самым мы становимся на точку зрения формальной аксиоматики.
Рассмотрение этой проблемы как в рамках геометрии, так и в рамках различных физических дисциплин до сих пор производилось с помощью метода арифметизации. Этот метод заключается в том, что основные объекты теории мы изображаем посредством чисел и числовых систем, а основные отношения между ними — посредством равенств и неравенств, причем таким образом, что в силу рассматриваемого перевода аксиомы теории переходят либо в числовые тождества и доказуемые предложения,
как это имеет место в в случае геометрии, либо, как в случае физики, - в систему условий, совместная выполнимость которых может быть установлена на основе тех или иных теорем существования области анализ. При этом способе решения рассматриваемой проблемы мы должны предполагать, что анализ, т. е. теория действительных чисел, является в определенном смысле пригодным и таким образом мы упираемся в вопрос о том, каков характер этой пригодности
Однако, прежде чем заняться этим вопросом, давайте посмотрим не существует ли какого-нибудь прямого способа атаковать проблему непротиворечивости. Кроме того, нам вообще хотелось бы поотчетливее рассмотреть структуру этой проблемы. Заодно, пользуясь представившейся возможностью, мы немного познакомимся с логической символикой, которая оказывается весьма полезной для наших Целей и которую в дальнейшем нам еще придется рассмотреть более подробно.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ПРОБЛЕМА НЕПРОТИВОРЕЧИВОСТИ В АКСИОМАТИЧЕСКИХ ИССЛЕДОВАНИЯХ КАК ЛОГИЧЕСКАЯ ПРОБЛЕМА РАЗРЕШИМОСТИ
- 2. Пример: аксиомы геометрии.
- 3. Чисто логический подход к аксиоматике.
- § 2. Проблема разрешимости
- 1. Общезначимость и выполнимость.
- 2. Распознавание в случае конечных индивидных областей.
- 3. Метод построения модели.
- § 3. Вопрос о непротиворечивости в случае бесконечной индивидной области
- 2. Проблематика бесконечного.
- 3. Установление непротиворечивости как доказательство невозможности; метод арифметизации.
- ГЛАВА II. ЭЛЕМЕНТАРНАЯ АРИФМЕТИКА. ФИНИТНЫЙ СПОСОБ РАССУЖДЕНИЙ И ЕГО ГРАНИЦЫ
- § 1. Рассуждения на интуитивном уровне и их применение в элементарной арифметике
- 2. Законы арифметических действий; полная индукция; умножение; делимость; простые числа.
- 3. Рекурсивные определения.
- 4. Одно доказательство невозможности.
- § 2. Дальнейшие применения интуитивных рассуждений
- 1. Отношение арифметики к учению о количестве.
- 2. Формальная точка зрения в алгебре.
- § 3. Финитная точка зрения; выход за ее пределы в области арифметики
- 2. «Tertium non datur» для целых чисел; принцип наименьшего числа.
- § 4. Нефинитные методы в анализе
- 2. Верхняя грань числовой последовательности; верхняя грань множества чисел.
- 3. Принцип выбора.
- § 5. Исследования, направленные на непосредственное финитное построение анализа; возврат к прежней постановке проблемы; теория доказательств
- ГЛАВА III. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ЛОГИЧЕСКОГО ВЫВОДА I: ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 1. Истинностные функции и их таблицы.
- 2. Заменимость; правила замены.
- 3. Примеры заменимости.
- 4. Двойственность; конъюнктивная и дизъюнктивная нормальные формы; тождественно истинные выражения; распознающая процедура.
- 5. Совершенная нормальная форма; распознавание заменимости; примеры.
- § 2. Применение теории истинностных функций к логическому выводу; формализация умозаключений в логике высказываний с помощью тождественно истинных выражений, правила подстановки и схемы заключения
- § 3. Дедуктивная логика высказываний
- 2. Одна система исходных формул для дедуктивной логики высказываний; полнота этой системы.
- 3. Позитивная логика; регулярные импликативные формулы; позитивно тождественные импликативные формулы; возможные упрощения.
- § 4. Доказательства независимости, проводимые методом оценок
- 2. Доказательетво независимости рассматриваемой системы исходных формул; еще одно доказательство независимости.
- 3. Применение метода оценок к вопросу о замене формул схемами.
- § 5. Возврат к рассмотренному в § 2 способу формализации вывода; сокращенные правила; замечание, касающееся противоречивости системы
- ГЛАВА IV. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ВЫВОДА II: ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- § 1. Введение индивидных переменных; понятие формулы; правило подстановки; пример; параллель с содержательными рассуждениями
- § 2. Связанные переменные и правила для кванторов всеобщности и существования
- 2. Введение связанных переменных; кванторы всеобщности и существования; правило переименования переменных; предотвращение неоднозначностей; обобщение понятия формулы и правила подстановки.
- 3. Эвристическое введение правил для кванторов всеобщности и существования; содержательный смысл формул и схем.
- 4. Окончательная формулировка правил исчисления предикатов; изображение форм категорических суждений; случай пустой индивидной области.
- § 3. Выводимость
- 2. Вывод некоторых формул. Теперь перейдем к выводу некоторых формул исчисления предикатов.
- § 4. Вопросы систематики
- 1. Понятия t-тождественной формулы и формулы, тождественной в конечном; дедуктивная замкнутость совокупности t-тождественных формул; непротиворечивость исчисления предикатов; вопросы полноты.
- 2. Экскурс в теоретике-множественную логику предикатов; предварительные замечания к вопросу о полноте; проблема разрешимости и ее уточнение с дедуктивной точки зрения.
- § 5. Изучение формализма исчисления предпкатов
- 2. Приведение формул к предваренному виду; примеры; описание разрешимых случаев проблемы разрешимости с помощью предваренной нормальной формы.
- 3. Разложение формул одноместного исчисления предикатов в примерные формулы; пример.
- § 6. Дедуктивное равенство и дедукционная теорема
- 1. Понятие дедуктивного равенства; два существенных случая дедуктивного равенства; переводимость и дедуктивное равенство.
- 2. Дедукционная теорема.
- 3. Применения дедукционной теоремы: сведение вопросов, связанных с аксиоматикой, к вопросам выводимости формул в исчислении предикатов; рассмотрение одного распространенного способа умозаключения.
- 4. Дедуктивное равенство произвольной формулы подходящей сколемовской нормальной форме, а также нормальной дизъюнкции; упрощение этого перехода.
- ГЛАВА V. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ С РАВЕНСТВОМ. ПОЛНОТА ОДНОМЕСТНОГО ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
- 1. Знак равенства; изображение высказываний о количестве; аксиомы равенства и формальные свойства равенства.
- 2. Применение аксиом равенства к различным преобразованиям, в частности к преобразованиям для оценок числа элементов в индивидной области; количественные формулы.
- 3. Разложение в примарные формулы для формул расширенного одноместного исчисления предикатов.
- 4. Обобщение понятия t-тождественной формулы; дедуктивная замкнутость совокупности t-тождественных формул; однозначность равенства.
- 5. Добавление функциональных знаков; понятие терма; выводимые формулы.
- § 2. Решение проблемы разрешимости; теоремы о полноте
- 1. Распознавание выводимости таких предваренных формул исчисления предикатов, у которых все кванторы всеобщности предшествуют всем кванторам существования; разрешимость в конечном.
- 2. Выводимость всякой тождественной в конечном формулы одноместного исчисления предикатов; доказательство с помощью прежней распознающей процедуры; теоретико-множественное доказательство и его финитное уточнение.
- 3. Нормальная форма формулы расширенного одноместного исчисления предикатов на основе дедуктивного равенства.
- 4. Теоремы о полноте для расширенного одноместного исчисления предикатов.
- ГЛАВА I. НЕПРОТИВОРЕЧИВОСТЬ СУЩЕСТВОВАНИЯ БЕСКОНЕЧНЫХ ИНДИВИДНЫХ ОБЛАСТЕЙ. НАЧАЛА АРИФМЕТИКИ
- 1. Замена формульных переменных предикатными символами; одна зависимость между рассматриваемыми формулами.
- 2. Привлечение аксиом равенства; дедекиндово определение бесконечности; введение штрих-символа.
- 3. Переход к аксиомам без связанных переменных с усилением экзистенциальных аксиом; символ 0; цифры в новом смысле; аксиомы, Пеано; получившаяся система аксиом.
- § 2. Общелогическая часть доказательства непротиворечивости
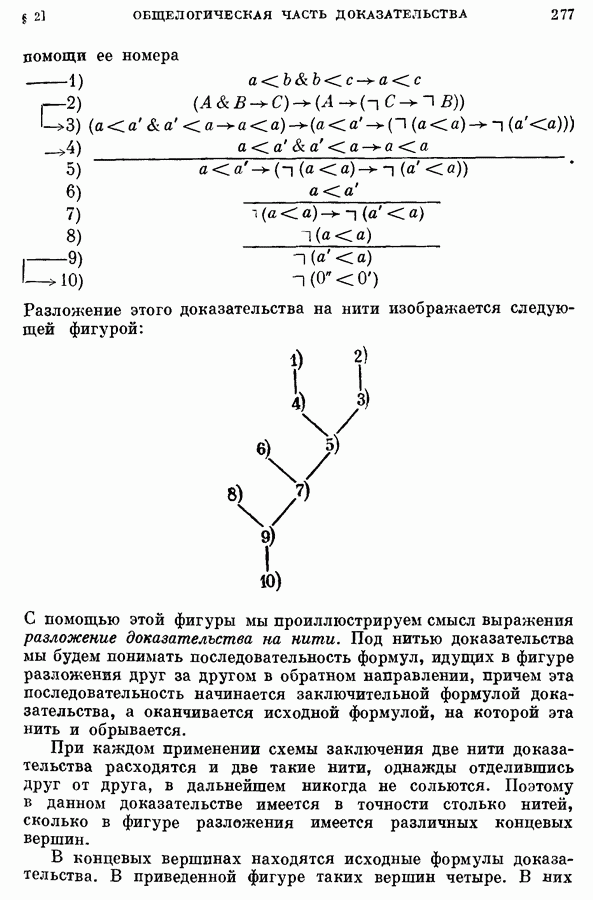
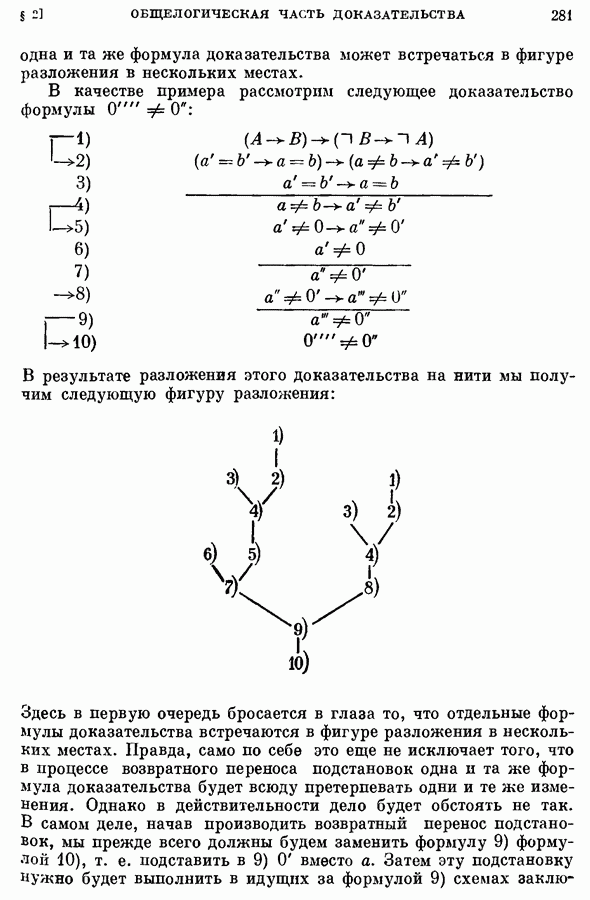
- 1. Выбор заключительной формулы; исключение связанных переменных; разложение доказательства на нити.
- 2. Возвратный перенос подстановок; исключение свободных переменных; нумерические формулы; определение истинности и ложности; истинность всякой формулы, выводимой без использования связанных переменных.
- 3. Включение связанных переменных; мероприятия по сохранению схем при возвратном переносе подстановок; недостаточность прежних методов.
- § 3. Доказательство непротиворечивости с помощью процедуры редукции
- 1. Исключение квантора всеобщности; этапы редуцирования; понятие редукции формулы.
- 2. Верифицируемые формулы; теорема об однозначности; леммы.
- 3. Вернфицируемость выводимых формул, не содержащих формульных переменных; заменимость аксиом схемами аксиом.
- § 4. Переход к одной (в области формул, не содержащих формульных переменных) дедуктивно завершенной системе аксиом
- 1. Выводимость ряда верифицируемых формул в рассматриваемой системе аксиом; доказательство с помощью «цифр второго рода».
- 2. Подход к пополнению этой системы аксиом; выводимость ряда эквивалентностей как достаточное условие.
- 3. Дедуктивное сведение этих эквивалентностей к пяти добавляемым к этой системе аксиом формулам; система (А).
- 4. Полнота системы (А).
- § 5. Включение полной индукции
- 2. Упрощение рассматриваемой системы аксиом в результате добавления аксиомы индукции; система (В).
- § 6. Доказательства независимости
- 1. Невыводимость аксиомы индукции из формул системы (А).
- 2. Доказательства независимости с помощью метода подстановок.
- 3. Установление ряда других независимостей с помощью модификации процедуры редукции.
- § 7. Изображение принципа наименьшего числа при помощи выражающей его формулы; равносильность этой формулы аксиоме индукции на основе прочих аксиом системы (В)
- ГЛАВА VII. РЕКУРСИВНЫЕ ОПРЕДЕЛЕНИЯ
- 1. Простейшая схема рекурсии; формализация интуитивной процедуры вычисления; сопоставление явных определений с рекурсивными.
- 2. Доказательство непротиворечивости добавления рекурсивных определений в рамках элементарного исчисления со свободными переменными; привлечение схемы индукции.
- 3. Невозможность вывода непротиворечивости рекурсивных определений в качестве следствия непротиворечивости систем предыдущих аксиом
- § 2. Рекурсивная арифметика
- 2. Изображение высказываний равенствами вида t=0; суммы и произведения с переменным числом членов; изображение высказываний с ограниченными кванторами; изображение максимума и минимума.
- 3. Делимость; деление с остатком; наименьший отличный от 1 делитель; последовательность простых чисел; разложение числа на простые множители; нумерация конечных последовательностей чисел; нумерация числовых пар; наибольший общий делитель; наименьшее общее кратное.
- § 3. Некоторые обобщения схем рекурсии и индукции
- 1. Рекурсии, допускающие сведение к простейшей схеме рекурсии (примитивная рекурсия); рекурсии пробега, одновременные рекурсии.
- 2. Перекрестные рекурсии; несводимость перекрестных рекурсий определенного типа к примитивным рекурсиям.
- 3. Обобщенная схема индукции; устранимость этой схемы.
- § 4. Представимость рекурсивных функций; переход к удовлетворительной системе аксиом для арифметики
- 1. Возврат к полному формализму; система (С); понятие существенного расширения формализма; примеры несущественных расширений; представимость функции.
- 2. Доказательство того, что сумма и разность не представимы в формализме системы (В); рекурсивные равенства для сложения как аксиомы; система (D).
- 3. Доказательство непротиворечивости и полноты системы (D) с помощью метода редукции; непредставимость умножения в формализме системы (D).
- 4. Изменение ситуации в случае добавления рекурсивных равенств для умножения; система (Z).
- § 5. Дополнительное рассмотрение аксиом равенства
- 1. Замена второй аксиомы равенства аксиомами более специального характера.
- 2. Применение к системам (А), (В) и (Z).
- 3. Применение к проблеме разрешимости; устранимость аксиом равенства из выводов формул исчисления предикатов.
- ГЛАВА VIII. ПОНЯТИЕ «ТОТ, КОТОРЫЙ» И ЕГО УСТРАНИМОСТЬ
- 1. Разъяснения неформального характера; введение i-правила; предотвращение коллизий; изображение функций посредством i-термов.
- 2. Вложение и подчинение; символы для сокращений.
- 3. Функция w(A); формализация понятия наименьшего числа с помощью функции mxA(x); формулы однозначности.
- § 2. Дедуктивное построение арифметики на основе системы аксиом (Z) с добавлением формализованного понятия наименьшего числа
- 2. Наименьшее общее кратное двух чисел и конечной последовательности чисел; максимум конечной последовательности чисел.
- § 3. Сведение примитивных рекурсий к явным определениям посредством функции mxA(x) на основе аксиом системы (Z)
- 2. Формальная реализация; возможность обобщения этого метода.
- § 4. Устранимость характеристик (i-символов)
- 2. Россеровский подход и его упрощение, произведенное Хазенъегером; подстановка i-термов; аксиома (i); свойства рассматриваемых формальных систем.
- 3. Определение редукции формулы и сведение требующегося доказательства к доказательству выводимости без i-символов для формул, построенных по определенным схемам.
- 4. Доказательство.
- 5. Формулировка теоремы об устранимости; переводимость всякой формулы в ее редукцию; сравнение различных методов устранения.
- § 5. Следствия, вытекающие из устранимости характеристик
- 2. Общий способ исключения функциональных знаков путем введения предикатных символов; исключение индивидных символов.
- 3. Применение этой процедуры к системе (Z); перспективы дальнейших исследований.
- § 6. Добавление: распространение теоремы о возможности замены аксиомы равенства (J2) в случае добавления i-правила