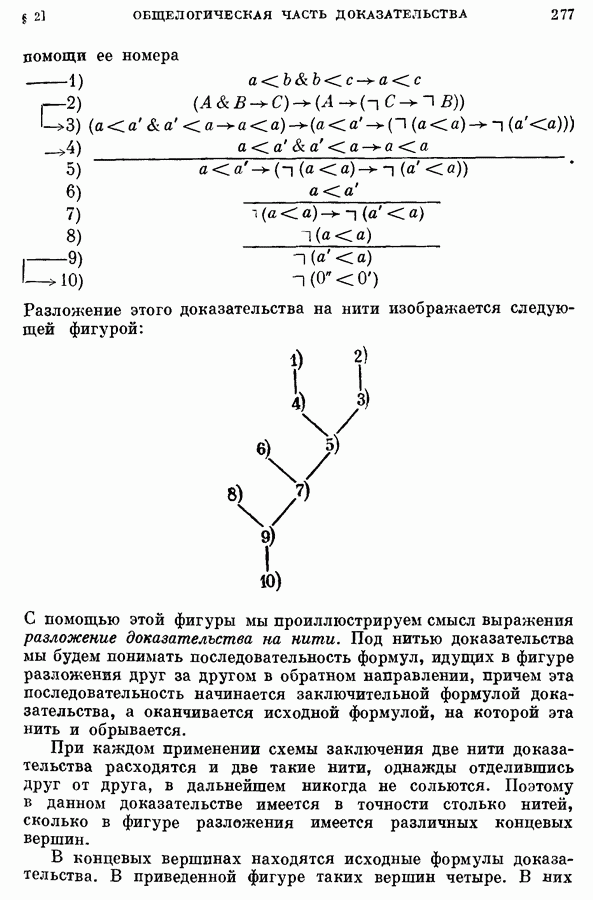
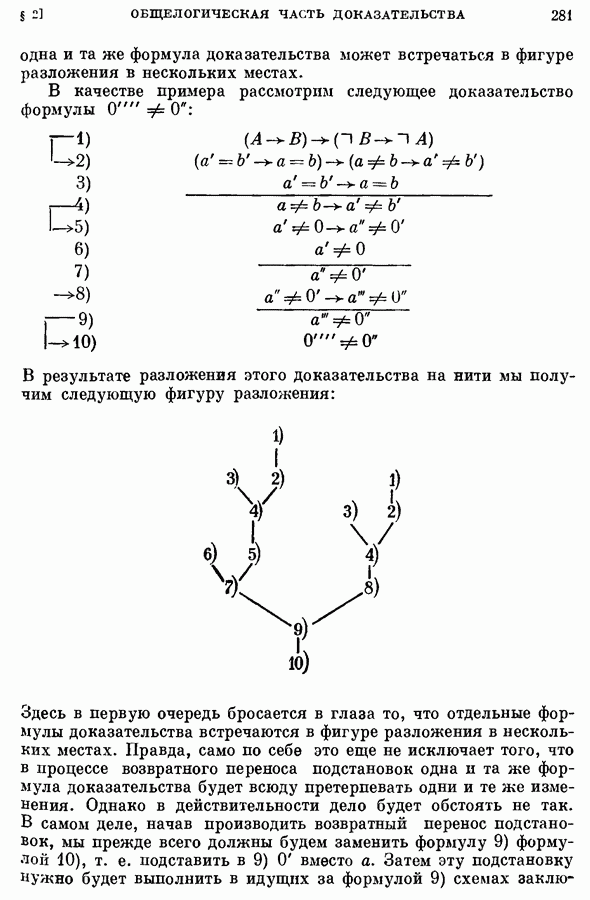
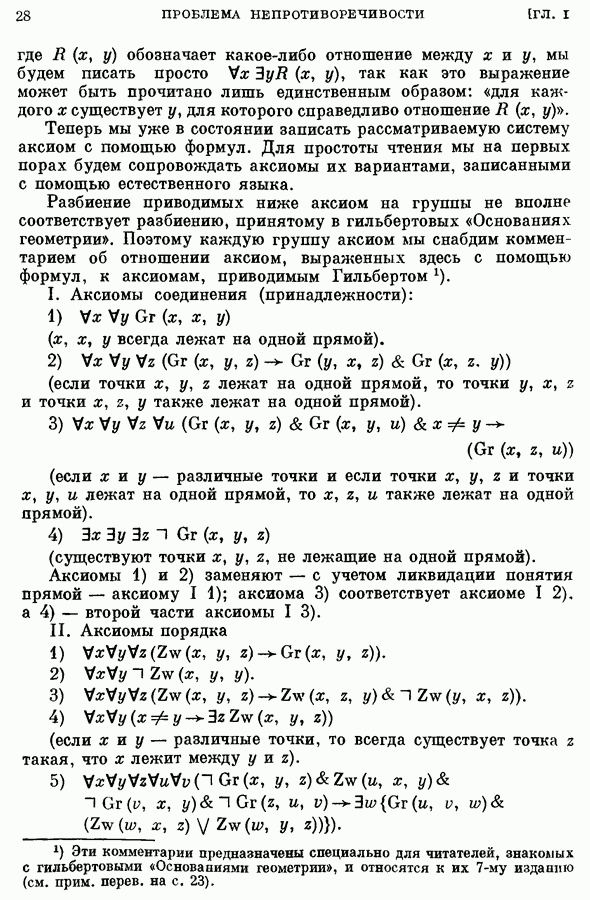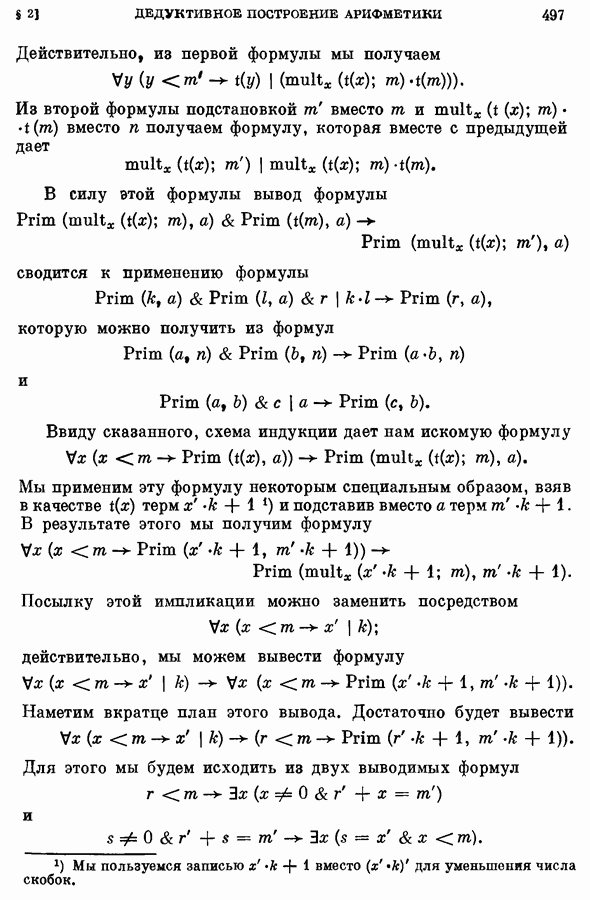| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Некоторые обобщения схем рекурсии и индукции
1. Рекурсии, допускающие сведение к простейшей схеме рекурсии (примитивная рекурсия); рекурсии пробега, одновременные рекурсии.
Отличительной чертой рекурсивной арифметики по сравнению с интуитивной теорией являются ограничения,
которые накладываются на ее формальный аппарат; она имеет единственный, не считая явных определений, способ образования новых понятий — схему рекурсии; применяемые в ней способы дедукции также подвергнуты сильным ограничениям.
Правда, не меняя ничего, что было бы характерным для методов рекурсивной арифметики, мы можем произвести определенные обобщения схемы рекурсии, а также схемы индукции. Об этих обобщениях мы и хотели бы немного поговорить.
Прежде всего, что касается рекурсий, то мы должны делать различие между такими модификациями схемы рекурсии, которые сводятся к последовательному применению рекурсий ранее рассматривавшегося вида, и такими, допущение которых представляет собой действительное расширение формализма рекурсивной арифметики. Рассмотрим сначала несколько таких видов рекурсии, которые хотя и отклоняются от обычной схемы рекурсии

но все-таки могут быть сведены к рекурсиям, проводимым по этой схеме, — в дальнейшем эти последние мы будем кратко называть примитивными рекурсиями.
Пример такого рода рекурсии вообще, сводимой к примитивным рекурсиям, представляет собой схема

в которой вместо  должен быть взят функциональный знак с одним аргументом, а
должен быть взят функциональный знак с одним аргументом, а

обозначают уже введенные термы, для которых выводимы формулы

Сведение этой схемы к примитивным рекурсиям производится таким образом, что сначала вместо  в качестве рекурсивно определяемой функции берется функция
в качестве рекурсивно определяемой функции берется функция

Эта функция  определяется при помощи следующей примитивной рекурсии:
определяется при помощи следующей примитивной рекурсии:

Затем  получается из
получается из  с помощью явного определения
с помощью явного определения

Рассмотренная схема рекурсии представляет собой рекурсию типа «рекурсии пробега», т. е. такой рекурсии, при которой значение  зависит не только от
зависит не только от  но и от всего пробега значений функции
но и от всего пробега значений функции  до аргумента
до аргумента  Эту схему, не нарушая ее сводимости к примитивным рекурсиям, мы можем обобщить путем введения параметров, так что получится следующая схема:
Эту схему, не нарушая ее сводимости к примитивным рекурсиям, мы можем обобщить путем введения параметров, так что получится следующая схема:

где снова  означают термы, для которых выводимы формулы
означают термы, для которых выводимы формулы

В эту схему  могут быть, в частности, включены рекурсии следующего вида:
могут быть, в частности, включены рекурсии следующего вида:

где  Действительно,
Действительно,  равенства этой схемы могут быть сведены в следующие два равенства:
равенства этой схемы могут быть сведены в следующие два равенства:

а эти равенства уже укладываются в схему так как выводимы формулы

Пример рекурсивных равенств вида  дает нам алгоритм Евклида для нахождения наибольшего общего делителя чисел
дает нам алгоритм Евклида для нахождения наибольшего общего делителя чисел  Возникающая в процессе применения этого алгоритма последовательность равенств
Возникающая в процессе применения этого алгоритма последовательность равенств

представляет собой не что иное, как рекурсивное определение некоторой функции

которое производится с помощью функции

следующими равенствами:

К схеме  может быть сведен другой тип обобщенной рекурсии — одновременная рекурсия для двух или большего числа функций. Схема одновременной рекурсии в простейшем случае, когда речь идет о двух одновременно определяемых функциях одного аргумента
может быть сведен другой тип обобщенной рекурсии — одновременная рекурсия для двух или большего числа функций. Схема одновременной рекурсии в простейшем случае, когда речь идет о двух одновременно определяемых функциях одного аргумента  выглядит следующим образом:
выглядит следующим образом:

В качестве примера такой одновременной рекурсии мы дадим второе определение для функций  обращающих функцию а
обращающих функцию а  т. е. для тех двух функций, которые в определенной последовательности сопоставляют числам числовые пары. Это определение по сравнению с предыдущим будет иметь то преимущество, что оно получится непосредственно из процедуры нумерации без вспомогательных арифметических рассмотрений; оно выглядит следующим образом:
т. е. для тех двух функций, которые в определенной последовательности сопоставляют числам числовые пары. Это определение по сравнению с предыдущим будет иметь то преимущество, что оно получится непосредственно из процедуры нумерации без вспомогательных арифметических рассмотрений; оно выглядит следующим образом:

Сведение указанной схемы одновременной рекурсии для  к схеме осуществляется путем написания рекурсивных равенств для функции
к схеме осуществляется путем написания рекурсивных равенств для функции  значения которой определяются равенствами
значения которой определяются равенствами

Для этой цели мы используем функцию  которая для четного аргумента принимает значение 0, а для нечетного — значение 1, и функцию
которая для четного аргумента принимает значение 0, а для нечетного — значение 1, и функцию  которая для четного
которая для четного  удовлетворяет равенству
удовлетворяет равенству  а для нечетного
а для нечетного  равенству
равенству  Рекурсивные равенства для
Рекурсивные равенства для  выглядят следующим образом:
выглядят следующим образом:

После того как мы таким образом ввели функцию  функции
функции  можно будет получить с помощью явных определений:
можно будет получить с помощью явных определений:

Совершенно аналогичным образом к обобщенной схеме рекурсии для одной функции сводится и одновременная рекурсия для нескольких функций; эта рекурсия может также содержать параметры:

Для этого сведения устраивается рекурсия для некоторой функции

значения которой связаны со значениями функций

равенствами

при этом нужно воспользоваться функциями  и
и 
Из сводимости одновременной рекурсии к рекурсии вида вытекает также сводимость ее к примитивным рекурсиям.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ПРОБЛЕМА НЕПРОТИВОРЕЧИВОСТИ В АКСИОМАТИЧЕСКИХ ИССЛЕДОВАНИЯХ КАК ЛОГИЧЕСКАЯ ПРОБЛЕМА РАЗРЕШИМОСТИ
- 2. Пример: аксиомы геометрии.
- 3. Чисто логический подход к аксиоматике.
- § 2. Проблема разрешимости
- 1. Общезначимость и выполнимость.
- 2. Распознавание в случае конечных индивидных областей.
- 3. Метод построения модели.
- § 3. Вопрос о непротиворечивости в случае бесконечной индивидной области
- 2. Проблематика бесконечного.
- 3. Установление непротиворечивости как доказательство невозможности; метод арифметизации.
- ГЛАВА II. ЭЛЕМЕНТАРНАЯ АРИФМЕТИКА. ФИНИТНЫЙ СПОСОБ РАССУЖДЕНИЙ И ЕГО ГРАНИЦЫ
- § 1. Рассуждения на интуитивном уровне и их применение в элементарной арифметике
- 2. Законы арифметических действий; полная индукция; умножение; делимость; простые числа.
- 3. Рекурсивные определения.
- 4. Одно доказательство невозможности.
- § 2. Дальнейшие применения интуитивных рассуждений
- 1. Отношение арифметики к учению о количестве.
- 2. Формальная точка зрения в алгебре.
- § 3. Финитная точка зрения; выход за ее пределы в области арифметики
- 2. «Tertium non datur» для целых чисел; принцип наименьшего числа.
- § 4. Нефинитные методы в анализе
- 2. Верхняя грань числовой последовательности; верхняя грань множества чисел.
- 3. Принцип выбора.
- § 5. Исследования, направленные на непосредственное финитное построение анализа; возврат к прежней постановке проблемы; теория доказательств
- ГЛАВА III. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ЛОГИЧЕСКОГО ВЫВОДА I: ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 1. Истинностные функции и их таблицы.
- 2. Заменимость; правила замены.
- 3. Примеры заменимости.
- 4. Двойственность; конъюнктивная и дизъюнктивная нормальные формы; тождественно истинные выражения; распознающая процедура.
- 5. Совершенная нормальная форма; распознавание заменимости; примеры.
- § 2. Применение теории истинностных функций к логическому выводу; формализация умозаключений в логике высказываний с помощью тождественно истинных выражений, правила подстановки и схемы заключения
- § 3. Дедуктивная логика высказываний
- 2. Одна система исходных формул для дедуктивной логики высказываний; полнота этой системы.
- 3. Позитивная логика; регулярные импликативные формулы; позитивно тождественные импликативные формулы; возможные упрощения.
- § 4. Доказательства независимости, проводимые методом оценок
- 2. Доказательетво независимости рассматриваемой системы исходных формул; еще одно доказательство независимости.
- 3. Применение метода оценок к вопросу о замене формул схемами.
- § 5. Возврат к рассмотренному в § 2 способу формализации вывода; сокращенные правила; замечание, касающееся противоречивости системы
- ГЛАВА IV. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ВЫВОДА II: ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- § 1. Введение индивидных переменных; понятие формулы; правило подстановки; пример; параллель с содержательными рассуждениями
- § 2. Связанные переменные и правила для кванторов всеобщности и существования
- 2. Введение связанных переменных; кванторы всеобщности и существования; правило переименования переменных; предотвращение неоднозначностей; обобщение понятия формулы и правила подстановки.
- 3. Эвристическое введение правил для кванторов всеобщности и существования; содержательный смысл формул и схем.
- 4. Окончательная формулировка правил исчисления предикатов; изображение форм категорических суждений; случай пустой индивидной области.
- § 3. Выводимость
- 2. Вывод некоторых формул. Теперь перейдем к выводу некоторых формул исчисления предикатов.
- § 4. Вопросы систематики
- 1. Понятия t-тождественной формулы и формулы, тождественной в конечном; дедуктивная замкнутость совокупности t-тождественных формул; непротиворечивость исчисления предикатов; вопросы полноты.
- 2. Экскурс в теоретике-множественную логику предикатов; предварительные замечания к вопросу о полноте; проблема разрешимости и ее уточнение с дедуктивной точки зрения.
- § 5. Изучение формализма исчисления предпкатов
- 2. Приведение формул к предваренному виду; примеры; описание разрешимых случаев проблемы разрешимости с помощью предваренной нормальной формы.
- 3. Разложение формул одноместного исчисления предикатов в примерные формулы; пример.
- § 6. Дедуктивное равенство и дедукционная теорема
- 1. Понятие дедуктивного равенства; два существенных случая дедуктивного равенства; переводимость и дедуктивное равенство.
- 2. Дедукционная теорема.
- 3. Применения дедукционной теоремы: сведение вопросов, связанных с аксиоматикой, к вопросам выводимости формул в исчислении предикатов; рассмотрение одного распространенного способа умозаключения.
- 4. Дедуктивное равенство произвольной формулы подходящей сколемовской нормальной форме, а также нормальной дизъюнкции; упрощение этого перехода.
- ГЛАВА V. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ С РАВЕНСТВОМ. ПОЛНОТА ОДНОМЕСТНОГО ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
- 1. Знак равенства; изображение высказываний о количестве; аксиомы равенства и формальные свойства равенства.
- 2. Применение аксиом равенства к различным преобразованиям, в частности к преобразованиям для оценок числа элементов в индивидной области; количественные формулы.
- 3. Разложение в примарные формулы для формул расширенного одноместного исчисления предикатов.
- 4. Обобщение понятия t-тождественной формулы; дедуктивная замкнутость совокупности t-тождественных формул; однозначность равенства.
- 5. Добавление функциональных знаков; понятие терма; выводимые формулы.
- § 2. Решение проблемы разрешимости; теоремы о полноте
- 1. Распознавание выводимости таких предваренных формул исчисления предикатов, у которых все кванторы всеобщности предшествуют всем кванторам существования; разрешимость в конечном.
- 2. Выводимость всякой тождественной в конечном формулы одноместного исчисления предикатов; доказательство с помощью прежней распознающей процедуры; теоретико-множественное доказательство и его финитное уточнение.
- 3. Нормальная форма формулы расширенного одноместного исчисления предикатов на основе дедуктивного равенства.
- 4. Теоремы о полноте для расширенного одноместного исчисления предикатов.
- ГЛАВА I. НЕПРОТИВОРЕЧИВОСТЬ СУЩЕСТВОВАНИЯ БЕСКОНЕЧНЫХ ИНДИВИДНЫХ ОБЛАСТЕЙ. НАЧАЛА АРИФМЕТИКИ
- 1. Замена формульных переменных предикатными символами; одна зависимость между рассматриваемыми формулами.
- 2. Привлечение аксиом равенства; дедекиндово определение бесконечности; введение штрих-символа.
- 3. Переход к аксиомам без связанных переменных с усилением экзистенциальных аксиом; символ 0; цифры в новом смысле; аксиомы, Пеано; получившаяся система аксиом.
- § 2. Общелогическая часть доказательства непротиворечивости
- 1. Выбор заключительной формулы; исключение связанных переменных; разложение доказательства на нити.
- 2. Возвратный перенос подстановок; исключение свободных переменных; нумерические формулы; определение истинности и ложности; истинность всякой формулы, выводимой без использования связанных переменных.
- 3. Включение связанных переменных; мероприятия по сохранению схем при возвратном переносе подстановок; недостаточность прежних методов.
- § 3. Доказательство непротиворечивости с помощью процедуры редукции
- 1. Исключение квантора всеобщности; этапы редуцирования; понятие редукции формулы.
- 2. Верифицируемые формулы; теорема об однозначности; леммы.
- 3. Вернфицируемость выводимых формул, не содержащих формульных переменных; заменимость аксиом схемами аксиом.
- § 4. Переход к одной (в области формул, не содержащих формульных переменных) дедуктивно завершенной системе аксиом
- 1. Выводимость ряда верифицируемых формул в рассматриваемой системе аксиом; доказательство с помощью «цифр второго рода».
- 2. Подход к пополнению этой системы аксиом; выводимость ряда эквивалентностей как достаточное условие.
- 3. Дедуктивное сведение этих эквивалентностей к пяти добавляемым к этой системе аксиом формулам; система (А).
- 4. Полнота системы (А).
- § 5. Включение полной индукции
- 2. Упрощение рассматриваемой системы аксиом в результате добавления аксиомы индукции; система (В).
- § 6. Доказательства независимости
- 1. Невыводимость аксиомы индукции из формул системы (А).
- 2. Доказательства независимости с помощью метода подстановок.
- 3. Установление ряда других независимостей с помощью модификации процедуры редукции.
- § 7. Изображение принципа наименьшего числа при помощи выражающей его формулы; равносильность этой формулы аксиоме индукции на основе прочих аксиом системы (В)
- ГЛАВА VII. РЕКУРСИВНЫЕ ОПРЕДЕЛЕНИЯ
- 1. Простейшая схема рекурсии; формализация интуитивной процедуры вычисления; сопоставление явных определений с рекурсивными.
- 2. Доказательство непротиворечивости добавления рекурсивных определений в рамках элементарного исчисления со свободными переменными; привлечение схемы индукции.
- 3. Невозможность вывода непротиворечивости рекурсивных определений в качестве следствия непротиворечивости систем предыдущих аксиом
- § 2. Рекурсивная арифметика
- 2. Изображение высказываний равенствами вида t=0; суммы и произведения с переменным числом членов; изображение высказываний с ограниченными кванторами; изображение максимума и минимума.
- 3. Делимость; деление с остатком; наименьший отличный от 1 делитель; последовательность простых чисел; разложение числа на простые множители; нумерация конечных последовательностей чисел; нумерация числовых пар; наибольший общий делитель; наименьшее общее кратное.
- § 3. Некоторые обобщения схем рекурсии и индукции
- 1. Рекурсии, допускающие сведение к простейшей схеме рекурсии (примитивная рекурсия); рекурсии пробега, одновременные рекурсии.
- 2. Перекрестные рекурсии; несводимость перекрестных рекурсий определенного типа к примитивным рекурсиям.
- 3. Обобщенная схема индукции; устранимость этой схемы.
- § 4. Представимость рекурсивных функций; переход к удовлетворительной системе аксиом для арифметики
- 1. Возврат к полному формализму; система (С); понятие существенного расширения формализма; примеры несущественных расширений; представимость функции.
- 2. Доказательство того, что сумма и разность не представимы в формализме системы (В); рекурсивные равенства для сложения как аксиомы; система (D).
- 3. Доказательство непротиворечивости и полноты системы (D) с помощью метода редукции; непредставимость умножения в формализме системы (D).
- 4. Изменение ситуации в случае добавления рекурсивных равенств для умножения; система (Z).
- § 5. Дополнительное рассмотрение аксиом равенства
- 1. Замена второй аксиомы равенства аксиомами более специального характера.
- 2. Применение к системам (А), (В) и (Z).
- 3. Применение к проблеме разрешимости; устранимость аксиом равенства из выводов формул исчисления предикатов.
- ГЛАВА VIII. ПОНЯТИЕ «ТОТ, КОТОРЫЙ» И ЕГО УСТРАНИМОСТЬ
- 1. Разъяснения неформального характера; введение i-правила; предотвращение коллизий; изображение функций посредством i-термов.
- 2. Вложение и подчинение; символы для сокращений.
- 3. Функция w(A); формализация понятия наименьшего числа с помощью функции mxA(x); формулы однозначности.
- § 2. Дедуктивное построение арифметики на основе системы аксиом (Z) с добавлением формализованного понятия наименьшего числа
- 2. Наименьшее общее кратное двух чисел и конечной последовательности чисел; максимум конечной последовательности чисел.
- § 3. Сведение примитивных рекурсий к явным определениям посредством функции mxA(x) на основе аксиом системы (Z)
- 2. Формальная реализация; возможность обобщения этого метода.
- § 4. Устранимость характеристик (i-символов)
- 2. Россеровский подход и его упрощение, произведенное Хазенъегером; подстановка i-термов; аксиома (i); свойства рассматриваемых формальных систем.
- 3. Определение редукции формулы и сведение требующегося доказательства к доказательству выводимости без i-символов для формул, построенных по определенным схемам.
- 4. Доказательство.
- 5. Формулировка теоремы об устранимости; переводимость всякой формулы в ее редукцию; сравнение различных методов устранения.
- § 5. Следствия, вытекающие из устранимости характеристик
- 2. Общий способ исключения функциональных знаков путем введения предикатных символов; исключение индивидных символов.
- 3. Применение этой процедуры к системе (Z); перспективы дальнейших исследований.
- § 6. Добавление: распространение теоремы о возможности замены аксиомы равенства (J2) в случае добавления i-правила