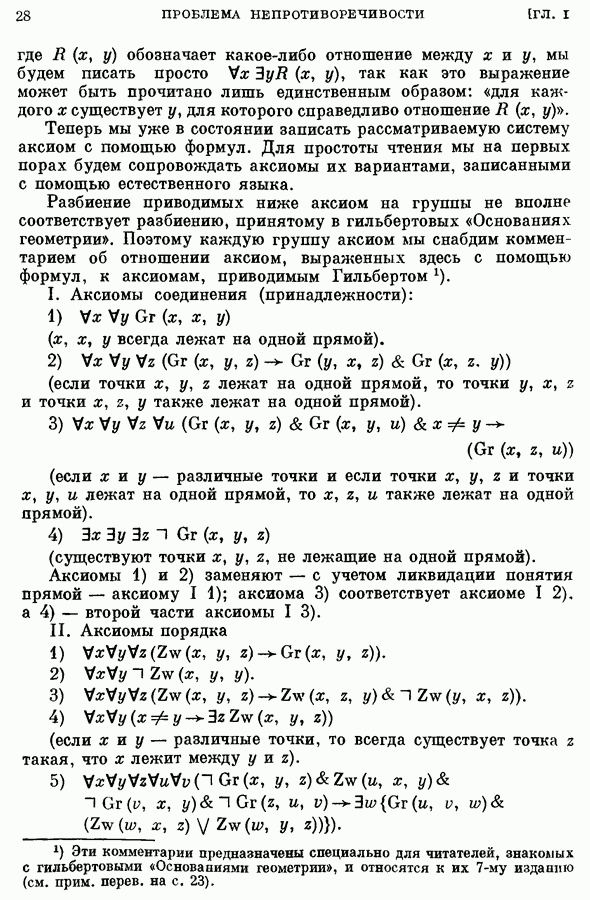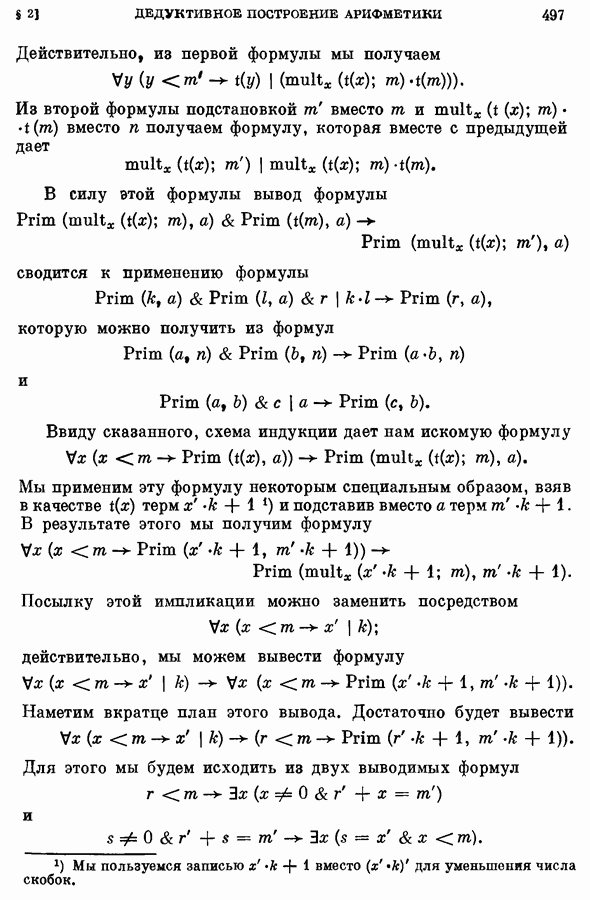| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
ГЛАВА V. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ С РАВЕНСТВОМ. ПОЛНОТА ОДНОМЕСТНОГО ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
§ 1. Расширенный формализм
1. Знак равенства; изображение высказываний о количестве; аксиомы равенства и формальные свойства равенства.
Равенство, которое мы в речевом обиходе выражаем фразами типа «a представляет собой тот же самый объект, что и b», при внешнем рассмотрении имеет вид предиката с двумя субъектами.
Но по содержанию оно соответствует чему-то такому, что в известном смысле предшествует определению какого бы то ни было предиката, а именно — возможности различения элементов индивидной области. Во всяком случае, так это выглядит с той точки зрения, которой мы придерживаемся в аксиоматических теориях, а также в теоретико-множественной логике предикатов.
В любой аксиоматической теории основные грамматические конструкции связываются с одной или несколькими системами объектов, внутри которых различение индивидов предполагается имеющимся с самого начала. Такому воззрению соответствует и тот факт, что в этих теориях равенство, как и его антипод — различие, обычно не фигурирует среди основных отношений, подлежащих неявной характеризации при помощи аксиом (речь идет о таких, например, отношениях, как отношения принадлежности, порядка и конгруэнтности в геометрии), а используется как некоторое понятие содержательной логики.
Теперь, чтобы учесть, с одной стороны, лингвистическую форму высказываний о равенстве, а с другой стороны, их особый содержательный характер, мы рассмотрим равенство как некоторый выделенный по отношению к логике основной предикат.
Определенная формализация равенства в нашем распоряжении имеется уже благодаря возможности идентификации переменных. Так, например, формула

выражает тот факт, что отношение  имеет места между объектом
имеет места между объектом  и им же самим. Однако этого нам не хватит уже, например, в том случае, если мы захотим воспроизвести предложение «если а не меньше
и им же самим. Однако этого нам не хватит уже, например, в том случае, если мы захотим воспроизвести предложение «если а не меньше  не меньше
не меньше  , то а представляет собой тот же самый объект, что и
, то а представляет собой тот же самый объект, что и 
Мы введем для равенства специальный предикатный символ. В качестве этого символа мы возьмем — поскольку у нас нет причин отличать данное равенство от «равенства» арифметического — обычный знак равенства

Прежде всего, к этому символу будет применимо правило подстановки, т. е. выражение

мы сможем подставлять вместо любой формульной переменной с аргументами  . В прочих отношениях роль знака равенства в нашем формализме будет определяться следующими двумя аксиомами равенства
. В прочих отношениях роль знака равенства в нашем формализме будет определяться следующими двумя аксиомами равенства

которые в процессе вывода можно будет использовать в качестве исходных формул.
Отрицание равенства есть различие. В дальнейшем мы будем пользоваться обычным знаком различия, применяя его, однако, лишь как сокращение для отрицания равенства. Таким образом, мы соглашаемся, что вместо

всегда можно будет писать

и наоборот.
В тесной связи с понятиями равенства и различия находятся укладывающиеся в элементарные рамки представления о количестве, и в результате введения знака равенства мы получаем средства для формального изображения этих представлений. В частности, с помощью знака равенства мы сможем формулировать условия, выражающие количество элементов в той индивидной области, к которой относятся связанные индивидные переменные. Так, формула

выражает высказывание о том, что в индивидной области имеется только один элемент. Точно так же формула

выражает (при содержательном ее понимании) тот факт, что в индивидной области имеется самое большее два элемента, а формула

говорит о том, что их имеется по меньшей мере два.
Аналогичным же образом посредством специальной формулы, не содержащей формульных переменных и имеющей в качестве единственного предикатного символа знак равенства, может быть выражена любая наперед заданная конечная верхняя и нижняя оценка числа элементов в рассматриваемой индивидной области.
Эти формулы являются более простыми и элементарными, чем те, которые были использованы Фреге и Расселом для логического определения конкретных конечных чисел, т. е. чем формулы, выражающие 1-численность, 2-численность и т. д. одноместных предикатов.
1-численность одноместного предиката  выражается посредством формулы
выражается посредством формулы

(«существует элемент х такой, что  выполняется для у тогда и только тогда, когда х представляет собой тот же самый элемент, что и у»),
выполняется для у тогда и только тогда, когда х представляет собой тот же самый элемент, что и у»),
2-численность предиката  изображается формулой
изображается формулой

В тесной связи с понятием 1-численности находятся понятия однозначности и взаимной однозначности. Их тоже можно формализовать с помощью знака равенства. Так, формула

выражает свойство отношения  (предиката с двумя субъектами), заключающееся в том, что для всякого элемента а существует один и только один элемент
(предиката с двумя субъектами), заключающееся в том, что для всякого элемента а существует один и только один элемент  для которого имеет место
для которого имеет место  . А формула
. А формула

выражает то обстоятельство, что посредством отношения  индивидная область взаимно однозначно отображается на себя.
индивидная область взаимно однозначно отображается на себя.
Приведенные примеры иллюстрируют разнообразие изобразительных возможностей, открывающихся перед нами в результате введения знака равенства. Рассмотрим теперь аксиомы равенства и способы их использования в процессе дедукции.
Относительно этих аксиом в первую очередь необходимо заметить, что от формул  можно легко перейти к соответствующим им формулам со связанными переменными. В самом деле, формулы
можно легко перейти к соответствующим им формулам со связанными переменными. В самом деле, формулы  дедуктивно равны формулам
дедуктивно равны формулам

и

что является непосредственным следствием одной из первых наших теорем о дедуктивном равенстве.
С точки зрения содержания формула  может рассматриваться как формализация «закона тождества», а формула
может рассматриваться как формализация «закона тождества», а формула  соответствует принципу замены равного равным.
соответствует принципу замены равного равным.
Теперь мы перейдем к выводу из аксиом равенства ряда специальных формул. При этом мы начнем с тех из них, которые выражают общеизвестные формальные свойства равенства. Эти формулы мы получим следующим образом. Прежде всего, мы подставим в формулу  равенство
равенство  вместо
вместо  Тогда у нас получится формула
Тогда у нас получится формула

В полученную формулу подставим а вместо с, а затем поменяем местами посылки. Тогда получится

а эта формула вместе с (3) по схеме заключения дает

Формулу эту можно получить и без применения  Действительно, подставим в
Действительно, подставим в  вместо
вместо  формулу
формулу  . Тогда получится
. Тогда получится

Здесь опять можно поменять местами посылки, и так как  получается подстановкой из тождественной формулы С
получается подстановкой из тождественной формулы С  то по схеме заключения мы получаем
то по схеме заключения мы получаем

а отсюда — средствами исчисления высказываний — формулу 2)). Из этой формулы с помощью контрапозиции и подстановки можно, кроме того, получить

Далее, из 1)) при помощи подстановок мы получаем

а эта формула совместно с 2)) по правилу силлогизма дает

Формула 2)) выражает свойство симметрии равенства, а формула 3)) - свойство транзитивности;  выражает свойство рефлексивности.
выражает свойство рефлексивности.
Вообще, о предикате  мы говорим, что он рефлексивен, если имеет место
мы говорим, что он рефлексивен, если имеет место

что он симметричен, если имеет место

и что он, транзитивен, если имеет место

Эти три свойства — рефлексивность, симметрия и транзитивность — часто вместе называются характеристическими свойствами отношения равенства. Но при этом речь обычно идет не о равенстве в смысле тождественности, а скорее только о некотором роде совпадения
В самом деле, любое отношение между двумя объектами, имеющее характер какого-либо совпадения, — такое, как подобие фигур, параллельность прямых, равенство длин отрезков или топологическое равенство многообразий, — обладает указанными тремя свойствами.
Среди всех такого рода отношений равенство выделяется тем, что оно означает не какое-нибудь одностороннее совпадение, а совпадение вообще — по меньшей мере постольку, поскольку в расчет принимаются признаки, могущие быть выраженными посредством основных предикатов рассматриваемой теории. Эта полнота совпадения и находит свое выражение во второй аксиоме равенства.
Приведенные выше выводы формул  из формул
из формул  показывают, что для установления указанных трех свойств у какого-либо отношения
показывают, что для установления указанных трех свойств у какого-либо отношения  всегда будет достаточно вывести две формулы:
всегда будет достаточно вывести две формулы:

и

Обратно, вторая из этих формул может быть получена из формул для симметрии и транзитивности с помощью правила силлогизма, так что система из трех формул для рефлексивности, симметрии и транзитивности равнозначна системе, состоящей из двух последних формул.
Из формул 2)) и 3)) мы можем также вывести формулу

соответствующую утверждению о том, что два объекта, порознь равные третьему, равны между собой.
Из формулы 4)) по правилу контрапозиции мы получаем

а отсюда, переставляя посылки и применяя правило замены для импликации, получаем формулу

Из формулы  подстановкой вместо формульной переменной
подстановкой вместо формульной переменной  получаем
получаем

а отсюда, применяя контрапозицию,

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
- ГЛАВА I. ПРОБЛЕМА НЕПРОТИВОРЕЧИВОСТИ В АКСИОМАТИЧЕСКИХ ИССЛЕДОВАНИЯХ КАК ЛОГИЧЕСКАЯ ПРОБЛЕМА РАЗРЕШИМОСТИ
- 2. Пример: аксиомы геометрии.
- 3. Чисто логический подход к аксиоматике.
- § 2. Проблема разрешимости
- 1. Общезначимость и выполнимость.
- 2. Распознавание в случае конечных индивидных областей.
- 3. Метод построения модели.
- § 3. Вопрос о непротиворечивости в случае бесконечной индивидной области
- 2. Проблематика бесконечного.
- 3. Установление непротиворечивости как доказательство невозможности; метод арифметизации.
- ГЛАВА II. ЭЛЕМЕНТАРНАЯ АРИФМЕТИКА. ФИНИТНЫЙ СПОСОБ РАССУЖДЕНИЙ И ЕГО ГРАНИЦЫ
- § 1. Рассуждения на интуитивном уровне и их применение в элементарной арифметике
- 2. Законы арифметических действий; полная индукция; умножение; делимость; простые числа.
- 3. Рекурсивные определения.
- 4. Одно доказательство невозможности.
- § 2. Дальнейшие применения интуитивных рассуждений
- 1. Отношение арифметики к учению о количестве.
- 2. Формальная точка зрения в алгебре.
- § 3. Финитная точка зрения; выход за ее пределы в области арифметики
- 2. «Tertium non datur» для целых чисел; принцип наименьшего числа.
- § 4. Нефинитные методы в анализе
- 2. Верхняя грань числовой последовательности; верхняя грань множества чисел.
- 3. Принцип выбора.
- § 5. Исследования, направленные на непосредственное финитное построение анализа; возврат к прежней постановке проблемы; теория доказательств
- ГЛАВА III. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ЛОГИЧЕСКОГО ВЫВОДА I: ИСЧИСЛЕНИЕ ВЫСКАЗЫВАНИЙ
- 1. Истинностные функции и их таблицы.
- 2. Заменимость; правила замены.
- 3. Примеры заменимости.
- 4. Двойственность; конъюнктивная и дизъюнктивная нормальные формы; тождественно истинные выражения; распознающая процедура.
- 5. Совершенная нормальная форма; распознавание заменимости; примеры.
- § 2. Применение теории истинностных функций к логическому выводу; формализация умозаключений в логике высказываний с помощью тождественно истинных выражений, правила подстановки и схемы заключения
- § 3. Дедуктивная логика высказываний
- 2. Одна система исходных формул для дедуктивной логики высказываний; полнота этой системы.
- 3. Позитивная логика; регулярные импликативные формулы; позитивно тождественные импликативные формулы; возможные упрощения.
- § 4. Доказательства независимости, проводимые методом оценок
- 2. Доказательетво независимости рассматриваемой системы исходных формул; еще одно доказательство независимости.
- 3. Применение метода оценок к вопросу о замене формул схемами.
- § 5. Возврат к рассмотренному в § 2 способу формализации вывода; сокращенные правила; замечание, касающееся противоречивости системы
- ГЛАВА IV. ФОРМАЛИЗАЦИЯ ПРОЦЕССА ВЫВОДА II: ИСЧИСЛЕНИЕ ПРЕДИКАТОВ
- § 1. Введение индивидных переменных; понятие формулы; правило подстановки; пример; параллель с содержательными рассуждениями
- § 2. Связанные переменные и правила для кванторов всеобщности и существования
- 2. Введение связанных переменных; кванторы всеобщности и существования; правило переименования переменных; предотвращение неоднозначностей; обобщение понятия формулы и правила подстановки.
- 3. Эвристическое введение правил для кванторов всеобщности и существования; содержательный смысл формул и схем.
- 4. Окончательная формулировка правил исчисления предикатов; изображение форм категорических суждений; случай пустой индивидной области.
- § 3. Выводимость
- 2. Вывод некоторых формул. Теперь перейдем к выводу некоторых формул исчисления предикатов.
- § 4. Вопросы систематики
- 1. Понятия t-тождественной формулы и формулы, тождественной в конечном; дедуктивная замкнутость совокупности t-тождественных формул; непротиворечивость исчисления предикатов; вопросы полноты.
- 2. Экскурс в теоретике-множественную логику предикатов; предварительные замечания к вопросу о полноте; проблема разрешимости и ее уточнение с дедуктивной точки зрения.
- § 5. Изучение формализма исчисления предпкатов
- 2. Приведение формул к предваренному виду; примеры; описание разрешимых случаев проблемы разрешимости с помощью предваренной нормальной формы.
- 3. Разложение формул одноместного исчисления предикатов в примерные формулы; пример.
- § 6. Дедуктивное равенство и дедукционная теорема
- 1. Понятие дедуктивного равенства; два существенных случая дедуктивного равенства; переводимость и дедуктивное равенство.
- 2. Дедукционная теорема.
- 3. Применения дедукционной теоремы: сведение вопросов, связанных с аксиоматикой, к вопросам выводимости формул в исчислении предикатов; рассмотрение одного распространенного способа умозаключения.
- 4. Дедуктивное равенство произвольной формулы подходящей сколемовской нормальной форме, а также нормальной дизъюнкции; упрощение этого перехода.
- ГЛАВА V. ИСЧИСЛЕНИЕ ПРЕДИКАТОВ С РАВЕНСТВОМ. ПОЛНОТА ОДНОМЕСТНОГО ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
- 1. Знак равенства; изображение высказываний о количестве; аксиомы равенства и формальные свойства равенства.
- 2. Применение аксиом равенства к различным преобразованиям, в частности к преобразованиям для оценок числа элементов в индивидной области; количественные формулы.
- 3. Разложение в примарные формулы для формул расширенного одноместного исчисления предикатов.
- 4. Обобщение понятия t-тождественной формулы; дедуктивная замкнутость совокупности t-тождественных формул; однозначность равенства.
- 5. Добавление функциональных знаков; понятие терма; выводимые формулы.
- § 2. Решение проблемы разрешимости; теоремы о полноте
- 1. Распознавание выводимости таких предваренных формул исчисления предикатов, у которых все кванторы всеобщности предшествуют всем кванторам существования; разрешимость в конечном.
- 2. Выводимость всякой тождественной в конечном формулы одноместного исчисления предикатов; доказательство с помощью прежней распознающей процедуры; теоретико-множественное доказательство и его финитное уточнение.
- 3. Нормальная форма формулы расширенного одноместного исчисления предикатов на основе дедуктивного равенства.
- 4. Теоремы о полноте для расширенного одноместного исчисления предикатов.
- ГЛАВА I. НЕПРОТИВОРЕЧИВОСТЬ СУЩЕСТВОВАНИЯ БЕСКОНЕЧНЫХ ИНДИВИДНЫХ ОБЛАСТЕЙ. НАЧАЛА АРИФМЕТИКИ
- 1. Замена формульных переменных предикатными символами; одна зависимость между рассматриваемыми формулами.
- 2. Привлечение аксиом равенства; дедекиндово определение бесконечности; введение штрих-символа.
- 3. Переход к аксиомам без связанных переменных с усилением экзистенциальных аксиом; символ 0; цифры в новом смысле; аксиомы, Пеано; получившаяся система аксиом.
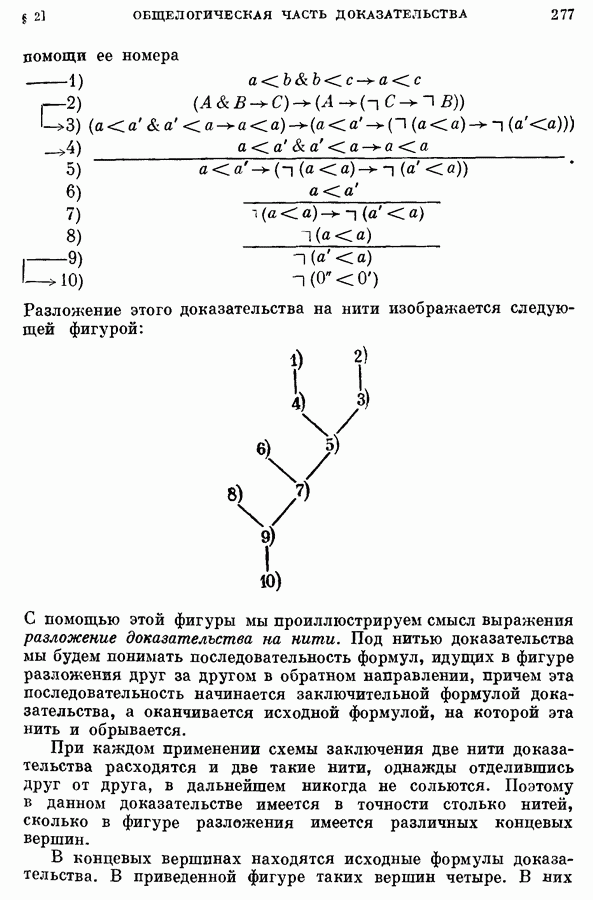
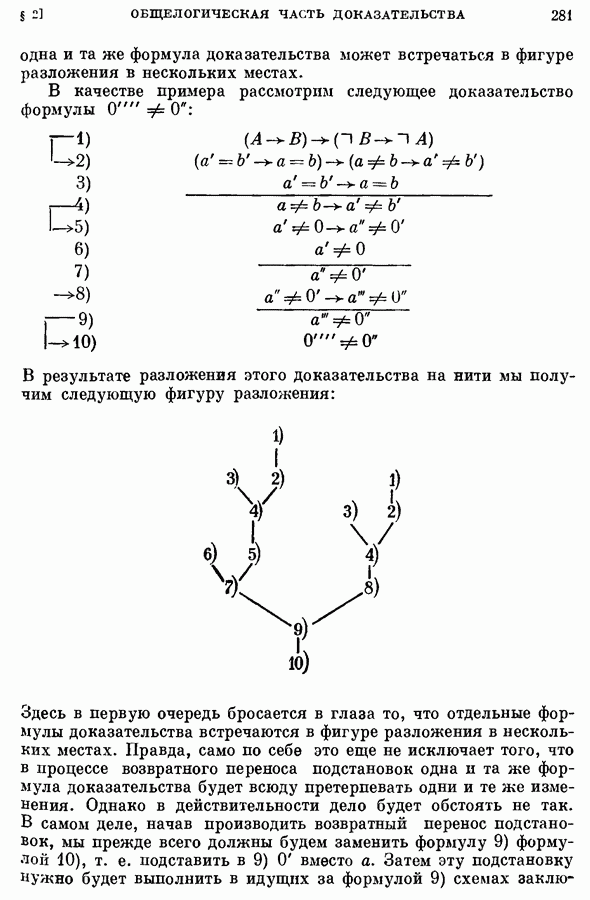
- § 2. Общелогическая часть доказательства непротиворечивости
- 1. Выбор заключительной формулы; исключение связанных переменных; разложение доказательства на нити.
- 2. Возвратный перенос подстановок; исключение свободных переменных; нумерические формулы; определение истинности и ложности; истинность всякой формулы, выводимой без использования связанных переменных.
- 3. Включение связанных переменных; мероприятия по сохранению схем при возвратном переносе подстановок; недостаточность прежних методов.
- § 3. Доказательство непротиворечивости с помощью процедуры редукции
- 1. Исключение квантора всеобщности; этапы редуцирования; понятие редукции формулы.
- 2. Верифицируемые формулы; теорема об однозначности; леммы.
- 3. Вернфицируемость выводимых формул, не содержащих формульных переменных; заменимость аксиом схемами аксиом.
- § 4. Переход к одной (в области формул, не содержащих формульных переменных) дедуктивно завершенной системе аксиом
- 1. Выводимость ряда верифицируемых формул в рассматриваемой системе аксиом; доказательство с помощью «цифр второго рода».
- 2. Подход к пополнению этой системы аксиом; выводимость ряда эквивалентностей как достаточное условие.
- 3. Дедуктивное сведение этих эквивалентностей к пяти добавляемым к этой системе аксиом формулам; система (А).
- 4. Полнота системы (А).
- § 5. Включение полной индукции
- 2. Упрощение рассматриваемой системы аксиом в результате добавления аксиомы индукции; система (В).
- § 6. Доказательства независимости
- 1. Невыводимость аксиомы индукции из формул системы (А).
- 2. Доказательства независимости с помощью метода подстановок.
- 3. Установление ряда других независимостей с помощью модификации процедуры редукции.
- § 7. Изображение принципа наименьшего числа при помощи выражающей его формулы; равносильность этой формулы аксиоме индукции на основе прочих аксиом системы (В)
- ГЛАВА VII. РЕКУРСИВНЫЕ ОПРЕДЕЛЕНИЯ
- 1. Простейшая схема рекурсии; формализация интуитивной процедуры вычисления; сопоставление явных определений с рекурсивными.
- 2. Доказательство непротиворечивости добавления рекурсивных определений в рамках элементарного исчисления со свободными переменными; привлечение схемы индукции.
- 3. Невозможность вывода непротиворечивости рекурсивных определений в качестве следствия непротиворечивости систем предыдущих аксиом
- § 2. Рекурсивная арифметика
- 2. Изображение высказываний равенствами вида t=0; суммы и произведения с переменным числом членов; изображение высказываний с ограниченными кванторами; изображение максимума и минимума.
- 3. Делимость; деление с остатком; наименьший отличный от 1 делитель; последовательность простых чисел; разложение числа на простые множители; нумерация конечных последовательностей чисел; нумерация числовых пар; наибольший общий делитель; наименьшее общее кратное.
- § 3. Некоторые обобщения схем рекурсии и индукции
- 1. Рекурсии, допускающие сведение к простейшей схеме рекурсии (примитивная рекурсия); рекурсии пробега, одновременные рекурсии.
- 2. Перекрестные рекурсии; несводимость перекрестных рекурсий определенного типа к примитивным рекурсиям.
- 3. Обобщенная схема индукции; устранимость этой схемы.
- § 4. Представимость рекурсивных функций; переход к удовлетворительной системе аксиом для арифметики
- 1. Возврат к полному формализму; система (С); понятие существенного расширения формализма; примеры несущественных расширений; представимость функции.
- 2. Доказательство того, что сумма и разность не представимы в формализме системы (В); рекурсивные равенства для сложения как аксиомы; система (D).
- 3. Доказательство непротиворечивости и полноты системы (D) с помощью метода редукции; непредставимость умножения в формализме системы (D).
- 4. Изменение ситуации в случае добавления рекурсивных равенств для умножения; система (Z).
- § 5. Дополнительное рассмотрение аксиом равенства
- 1. Замена второй аксиомы равенства аксиомами более специального характера.
- 2. Применение к системам (А), (В) и (Z).
- 3. Применение к проблеме разрешимости; устранимость аксиом равенства из выводов формул исчисления предикатов.
- ГЛАВА VIII. ПОНЯТИЕ «ТОТ, КОТОРЫЙ» И ЕГО УСТРАНИМОСТЬ
- 1. Разъяснения неформального характера; введение i-правила; предотвращение коллизий; изображение функций посредством i-термов.
- 2. Вложение и подчинение; символы для сокращений.
- 3. Функция w(A); формализация понятия наименьшего числа с помощью функции mxA(x); формулы однозначности.
- § 2. Дедуктивное построение арифметики на основе системы аксиом (Z) с добавлением формализованного понятия наименьшего числа
- 2. Наименьшее общее кратное двух чисел и конечной последовательности чисел; максимум конечной последовательности чисел.
- § 3. Сведение примитивных рекурсий к явным определениям посредством функции mxA(x) на основе аксиом системы (Z)
- 2. Формальная реализация; возможность обобщения этого метода.
- § 4. Устранимость характеристик (i-символов)
- 2. Россеровский подход и его упрощение, произведенное Хазенъегером; подстановка i-термов; аксиома (i); свойства рассматриваемых формальных систем.
- 3. Определение редукции формулы и сведение требующегося доказательства к доказательству выводимости без i-символов для формул, построенных по определенным схемам.
- 4. Доказательство.
- 5. Формулировка теоремы об устранимости; переводимость всякой формулы в ее редукцию; сравнение различных методов устранения.
- § 5. Следствия, вытекающие из устранимости характеристик
- 2. Общий способ исключения функциональных знаков путем введения предикатных символов; исключение индивидных символов.
- 3. Применение этой процедуры к системе (Z); перспективы дальнейших исследований.
- § 6. Добавление: распространение теоремы о возможности замены аксиомы равенства (J2) в случае добавления i-правила