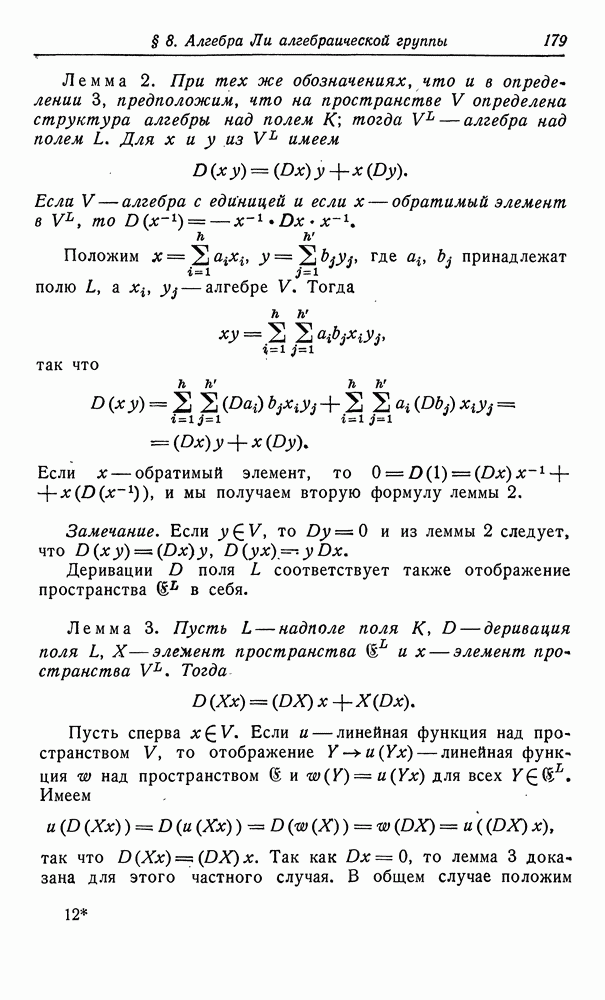§ 7. Параметрические представления

На протяжении всего параграфа мы будем предполагать, что в пространстве 6 раз навсегда выбрана система координатных функций

Определение 1. Пусть неприводимая алгебраическая группа автоморфизмов пространства надполе поля К, такое, что группа содержит общую точку группы Предположим, что поле можно получить присоединением к полю К конечного числа элементов и что заданы рациональных дробей от переменных с коэффициентами из поля К, определенных для значений своих аргументов и таких, что

В этом случае мы будем говорить, что формулой (1) за дается параметрическое представление группы и называть параметрами этого параметрического представления. Если поле совпадает с полем то параметрическое представление называется собственным. Если алгебраически независимы над К, то параметрическое представление называется рациональным. Пусть элементы некоторого надполя поля К, удовлетворяющие следующим условиям: а) существует гомоморфизм кольца в поле , отображающий, элементы поля К в себя, а элементы рациональные дроби определены для значений своих аргументов; в) определитель матрицы не равен 0. В этом случае мы будем говорить, что элементы образуют систему допустимых значений параметров.

Предположим, что элементы образуют систему допустимых значений параметров, и пусть гомоморфизм, кольца в поле оставляющий на месте элементы поля К и переводящий элементы в элементы Элементы поля представимые в виде где х и у — элементы из такие, что образуют подкольцо поля и гомоморфизм может быть продолжен (одним единственным способом) в некоторый гомоморфизм кольца в поле (гл. I, § 7, лемма 1). Кольцо будет называться подкольцом поля соответствующим

системе значений параметров, гомоморфизмом соответствующим этой системе. Так как, образуют допустимую систему значений параметров, то элементы принадлежат Таким образом, индуцирует гомоморфизм кольца в поле Этот гомоморфизм переводит элементы и Пусть тарй элемент пространства что

Тогда ясно, что обратимый элемент, который принадлежит группе (так как является специализацией точки 5 по отношению к полю

Определение 2. При таких же обозначениях, как в определении 1, предположим, элементы образуют допустимую систему значений параметров.

У — точка группы такая,

то мы будем говорить, точка накрывается параметрическим представлением и что она получается для значений параметров.

Замечание. Если, например, мы будем говорить, что точка 5 группы накрывается параметрическим представлением, то под этим мы будем подразумевать, что она получается при системе значений параметров, лежащей в самом поле

Предложение 1. При обозначениях, введенных в определении 1, предположим, что выполнено одно из следующих двух условий: а) заданное параметрическое представление — собственное; б) алгебраически замкнуто. Пусть полином от переменных с коэффициентами из поля К, для которого Множество точек группы накрываемых рассматриваемым параметрическим представлением и получающихся при значениях параметров, для которых алгебраически плотно. Каждый элемент группы может быть представлен в виде произведения двух элементов множества

Запишем рациональные дроби о которых говорится в определении 1, в виде частного двух взаимно простых

полиномов, и пусть произведение знаменателей всех этих выражений. Тогда

В случае а) из леммы 2 § 7 гл. I следует существование полиномиальной функции на 6, для которой такой, что всякий гомоморфизм кольца в поле К, не переводящий в нуль, может быть продолжен в гомоморфизм кольца в поле К, не отображающий в элемент Функция такого рода существует также и в случае б). Действительно, элемент принадлежит тогда полю и может быть представлен в виде где полиномиальные функции на Положим . Лемма 1 из § 7 гл. I показывает, что функция обладает требуемыми свойствами. Множество точек группы для которых алгебраически плотно в Пусть точка из Ограничение на гомоморфизма специализации продолжается в гомоморфизм кольца в поле такой, что

Положим Так как то функции определены для значений своих аргументов. Имеем

и условие в) определения 1 удовлетворяется, так как Поэтому чем и доказывается алгебраическая плотность множества Последнее утверждение предложения 1 вытекает из леммы

Предложение 2. Пусть К — алгебраически замкнутое поле. Пусть. далее; неприводимая алгебраическая группа автоморфизмов пространства V, и пусть всюду определенное рациональное отображение группы в пространство эндоморфизмов конечномерного векторного пространства над полем К. Предположим, что переводит группу в множество автоморфизмов пространства в частности, единицу группы в тождественный автоморфизм пространства Группа порождаемая элементами множества является неприводимой алгебраической группой. При этом существует целое число

такое, что каждый элемент группы представим в виде произведения элементов множества

Пусть наименьшая алгебраическая группа автоморфизмов пространства содержащая множество Как известно, группа неприводима и существуют такие обобщенные точки группы что

является общей точкой группы Я (предложение 7 из § 6) Для элементов пространства обозначим через произведение определителей элементов Функция индуцирует полиномиальную функцию на произведении из экземпляров группы Согласно предложению 2 § 7 гл. I, существует полиномиальная функция на пространстве эндоморфизмов пространства обладающая следующими свойствами: если — точка группы такая, что то существует специализация, точки такая, что ( специализация точки и

Ясно, что точки являются специализациями точек и что определители точек не равны нулю, так что Отображение

произведения в пространство рациональное, всюду определенное отображение. Его значение в точке тождественный автоморфизм. Из предложения 2 § 5 следует, что

Множество точек и группы для которых алгебраически плотно, и, как мы видели, какдый элемент из является произведением элементов множества Из леммы 4 § 4 вытекает, что каждый элемент из группы представим в виде произведения элементов множества Это показывает, что и предложение 2 доказано.

Следствие 1. Пусть алгебраическая группа автоморфизмов пространства рациональное представление группы автоморфизмами некоторого конечномерного

векторного пространства над полем К. Если поле К алгебраически замкнуто, то алгебраическая группа.

Пусть алгебраическая компонента единицы группы Предложение 2 показывает, что алгебраическая группа. С другой стороны, индекс группы в группе конечен, и, следовательно, алгебраическая группа (предложение 3 из § 3).

Следствие 2. Пусть неприводимая алгебраическая группа автоморфизмов пространства Если основное поле К алгебраически замкнуто, то коммутант группы О является алгебраической неприводимой группой. При этом существует такое целое число что каждый элемент группы представим в виде произведения коммутаторов от пар элементов группы

Для доказательства этого утверждения достаточно применить предложение 2 к группе и рациональному отображению этой группы в пространство 6.

Следствие 3. Пусть неприводимые алгебраические группы автоморфизмов пространства Если основное поле К алгебраически замкнуто, то группа порождаемая группами неприводимая алгебраическая группа и существует такое целое число что всякий элемент группы И записывается в виде произведения элементов, каждый из которых принадлежит одной из групп

Для доказательства достаточно применить предложение 2 к группе и к рациональному отображению этой группы в пространство

Замечание. Следствие 3 перестает быть справедливым, если опустить условие неприводимости групп Действительно, если V — векторное пространство размерности 2 и основное поле К — поле комплексных чисел, то нетрудно указать два автоморфизма порядка 2 пространства V, порождающее незамкнутую и поэтому не алгебраическую группу.

Пусть теперь К — некоторое бесконечное поле характеристики и пусть В — невырожденная билинейная форма над произведением V XV. Пусть множество

эндоморфизмов 5 пространства V, оставляющих неизменной форму таких, что

Если то из условия следует В(х, у)~ О для всех V, так что таким образом, элементы множества обратимы. Кроме того, легко видеть, что множество есть группа. Для данных элементов х и у пространства V отображение очевидно, является полиномиальной функцией над пространством 6, так что алгебраическая группа. Выберем базис пространства V и уовимся обозначать одной и той же буквой эндоморфизм пространства V и матрицу, соответствующую этому эндоморфизму в выбранном базисе. Кроме того, условимся обозначать буквой В также и матрицу При этих обозначениях эндоморфизм 5 принадлежит группе в том и только в том случае, если (где А обозначает матрицу, которая получается из А транспонированием).

Построим некоторое параметрическое представление группы алгебраической компоненты единицы группы Обозначим через подпространство пространства 6, состоящее из тех элементов для которых и пусть базис пространства Пусть надполе поля К, получающееся присоединением к полю элементов алгебраически независимых над Положим

Обозначим через определитель матрицы А и через единичную матрицу. Элемент принадлежит кольцу и отличен от 0, так как он принимает значение 1, если вместо всех подставить Положим

Тогда

так как, очевидно, Определители матриц не равны нулю, так что Это показывает, что -обобщенная точка группы Мы

можем даже утверждать, что обобщенная точка группы Действительно, пусть -полиномиальная функция над пространством 6, равная нулю на Тогда существует полиномиальная функция на 6, такая, что обращается в нуль на группе Имеем, следовательно, Легко видеть, что - специализация точки как коэффициенты матрицы являются рациональными функциями от определенными при значениях своих аргументов и принимающими при этих значениях аргументов значения, равные коэффициентам матрицы Поэтому так что что и доказывает наше утверждение.

Имеют место равенства

отсюда Это показывает, что

Пусть — элемент группы для которого

Как легко видеть, если положить

то Отсюда вытекает, что — специализация точки Пусть полиномиальная функция над пространством 6, такая, что тогда функция обращается в нуль на группе следовательно., на группе Но функция на группе 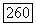не обращается в нуль (так как 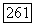Так как группа 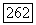неприводима, то мы можем заключить, что функция 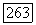равна нулю на группе 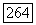Это показывает, что 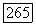общая точка группы 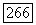Если представить координаты точки 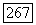в виде рациональных дробей от переменных 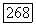то получается собственное рациональное параметрическое представление, называемое параметрическим представлением Кэли.

Рассмотрим теперь случай, когда билинейная форма В симметрична или кососимметрична. Предположим сначала, что форма В симметрична, так что 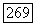Условие 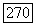записывается тогда в виде 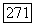Последнее равенство означает, что матрица 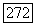кососимметрична. Так как, по предположению, форма В не вырождена, то 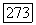и размерность 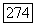пространства 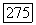равна размерности пространства кососимметрических матриц порядка 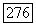размерность пространства V), так что 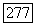Но число 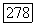равно также размерности группы 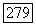[так как 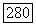]. Таким

образом, в случае симметричной формы В размерность группы 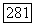равна 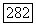Из условия 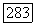вытекает, что так что 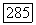Функция

равна нулю на 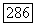но функция 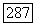не равна нулю на Следовательно, определитель каждого элемента из 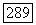равен 1. Обратно, все элементы из 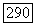с определителем, равным 1, принадлежат группе Действительно, всякий элемент 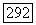группы 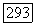может быть представлен в виде произведения конечного числа симметрий (ср. Dieudonn6, Sur les groupes classiques, Hermann, Paris, 1948, предложение 8, стр. 20). 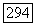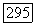Определитель симметрий равен — 1; если то является произведением четного числа симметрий. Достаточно показать, что произведение двух симметрий всегда принадлежит группе 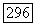Пусть и 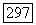симметрии по отношению к двум неизотропным гиперплоскостям 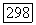и пусть 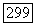Покажем, что если 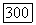то гиперплоскости ортогональны. Пусть элемент из V, для которого Точка принадлежит гиперплоскости с другой стороны, эта точка совпадает с точкой и тем самым ортогональна гиперплоскости Наше утверждение доказано для случая Если то х ортогональна к и принадлежит так как

поскольку мы вновь можем заключить, что гиперплоскости ортогональны. Но всегда можно найти неизотропную гиперплоскость не ортогональную ни к ни к Пусть симметрия относительно тогда

Но тогда специализации точки и принадлежат, следовательно, группе так что

Пусть теперь форма В кососимметрична. Условие равносильно тогда тому, что матрица симметрична. Как и выше, мы можем заключить, что размерность группы равна тогда размерности пространства симметрических матриц порядка , т. е. В рассматриваемом случае группа совпадает с группой Действительно, так как поле К бесконечно, то всякий нормальный делитель группы отличный от самой группы содержится в центре

группы который является конечной группой порядка 2 (Dieudonne, там же, теорема 1, стр. 12). Наше утверждение вытекает теперь из того факта, что для группа не может быть конечной.