| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.16. ПРОВОДИМОСТЬ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
В курсе общей физики для расчета электрических цепей используют, в основном, законы Ома и Кирхгофа, в которые входят напряжения, токи и сопротивления. Однако для расчета сложных электрических цепей, и в особенности цепей переменного тока, целесообразно вместо сопротивления использовать проводимость.
Проводимость в цепи постоянного тока g — величина, обратная сопротивлению 

Единицей измерения проводимости в СИ является сименс (в честь немецкого электротехника XIX в. Э. В. Сименса).
1 Сим — это проводимость проводника сопротивлением 1 Ом.
В цепях переменного тока, как известно, существует три типа сопротивлений: активное R, реактивное  и полное г. По аналогии с этим введено и три типа проводимостей: активная g, реактивная b и полная у. Однако только полная проводимость у является величиной, обратной полному сопротивлению
и полное г. По аналогии с этим введено и три типа проводимостей: активная g, реактивная b и полная у. Однако только полная проводимость у является величиной, обратной полному сопротивлению  :
:

Для введения активной g и реактивной b проводимостей рассмотрим цепь переменного тока из последовательно соединенных активного R и индуктивного  сопротивлений (рис. 1-25, а). Построим для нее векторную диаграмму (рис. 1-25, б). Ток в цепи
сопротивлений (рис. 1-25, а). Построим для нее векторную диаграмму (рис. 1-25, б). Ток в цепи  разложим на активную
разложим на активную  и реактивную
и реактивную  составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлений (рис. 1-25, в). Из последнего имеем:
составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлений (рис. 1-25, в). Из последнего имеем:


Рис. 1-25
Из векторной диаграммы (см. рис. 1-25, б) с учетом формулы (1.30) имеем:

где  активная проводимость,
активная проводимость,

где  реактивная проводимость.
реактивная проводимость.
Теперь установим взаимосвязь между проводимостями. Для рассматриваемой цепи имеем:

Подставив значения  соответственно из соотношений (1.31) и (1.32), получим:
соответственно из соотношений (1.31) и (1.32), получим:

где  полная проводимость цепи.
полная проводимость цепи.
По аналогии с треугольником сопротивлений (рис. 1-25, в) строим треугольник проводимостей (рис. 1-25, г). По аналогии с индуктивным  и емкостным
и емкостным  сопротивлениями различают индуктивную
сопротивлениями различают индуктивную  и емкостную
и емкостную  проводимости.
проводимости.

Рис. 1-26
В случае разветвленной цепи (рис. 1-26, а) схему легко преобразовать в так называемую эквивалентную схему (рис. 1-26, б), в которой две ветви заменены одной с соответствующими эквивалентными активным  и
и
реактивным  сопротивлениями. Расчет последних сопротивлении, как и других параметров схемы, проще с использованием проводимостей. Установим основные закономерности для проводимостей в разветвленной цепи.
сопротивлениями. Расчет последних сопротивлении, как и других параметров схемы, проще с использованием проводимостей. Установим основные закономерности для проводимостей в разветвленной цепи.
Выразим общий ток через его составляющие или эквивалентные проводимости:

В свою очередь, активная составляющая общего тока равна сумме активных составляющих токов ветвей:

откуда

т. е. эквивалентная активная проводимость разветвления равна арифметической сумме активных проводимостей ветвей.
Так как реактивные составляющие ветвей рассматриваемой цепи находятся в противофазе, то для реактивной составляющей общего тока имеем:

откуда

т. е. эквивалентная реактивная проводимость разветвления равна алгебраической сумме реактивных проводимостей параллельных ветвей, при этом  берется со знаком «плюс», а
берется со знаком «плюс», а  — со знаком «минус».
— со знаком «минус».
Тогда по соотношению (1.33) полная эквивалентная проводимость разветвления равна

Кратко рассмотрим порядок расчета цепи при смешанном соединении потребителей (рис. 1-27, а).
Сначала параллельные ветви заменяем эквивалентной схемой из  (рис. 1-27, б), для чего по найденным активным
(рис. 1-27, б), для чего по найденным активным  реактивным
реактивным  и полным и
и полным и  проводимостям находим эквивалентные проводимости
проводимостям находим эквивалентные проводимости  а затем и эквивалентные сопротивления
а затем и эквивалентные сопротивления 
После преобразования схемы в общую последовательную цепь легко находим общие сопротивления:

и схема еще раз преобразуется в наиболее простую (рис. 1-27, в),

Рис. 1-27
содержащую два элемента  . По этой схеме находят ее основные параметры:
. По этой схеме находят ее основные параметры:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1. ОДНОФАЗНЫЕ ЦЕПИ
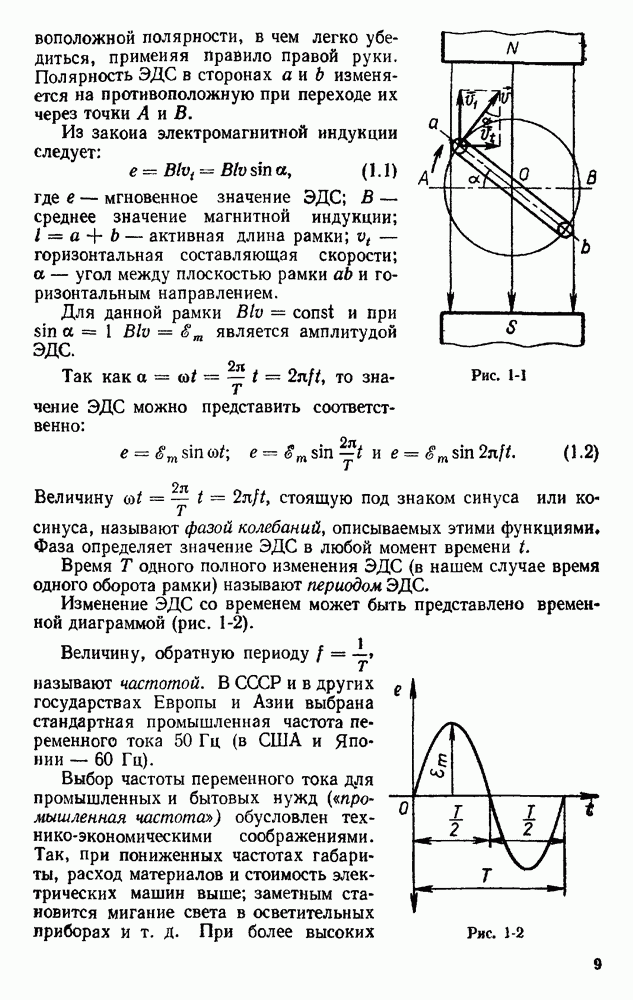
- § 1.2. ПРИНЦИП ПОЛУЧЕНИЯ ПЕРЕМЕННОЙ СИНУСОИДАЛЬНОЙ ЭДС
- § 1.3. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ ТОКА И НАПРЯЖЕНИЯ
- § 1.4. СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- § 1.5. МЕТОД ВЕКТОРНЫХ ДИАГРАММ
- § 1.6. СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
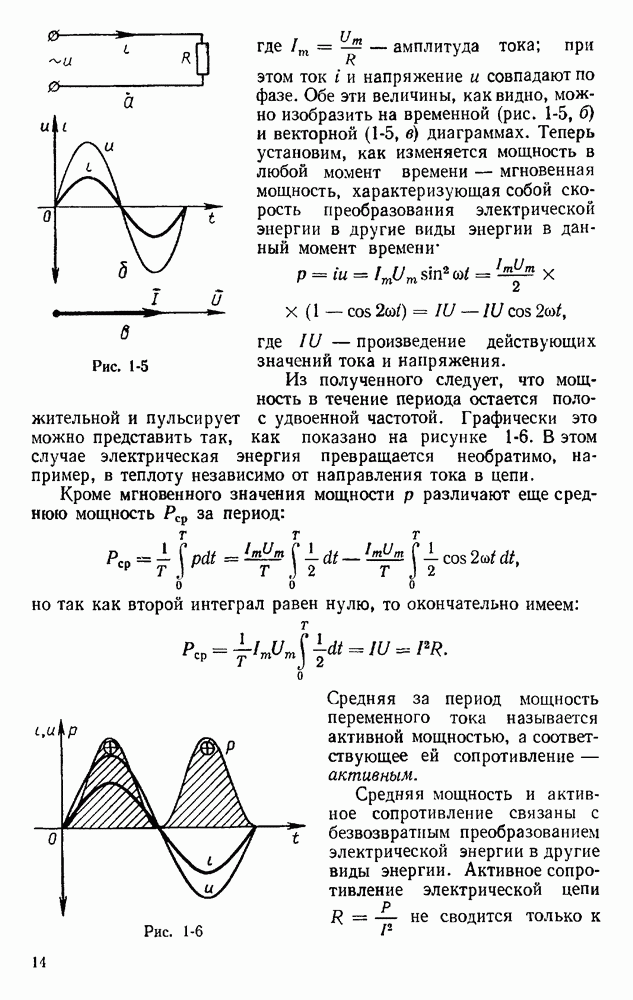
- § 1.7. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ
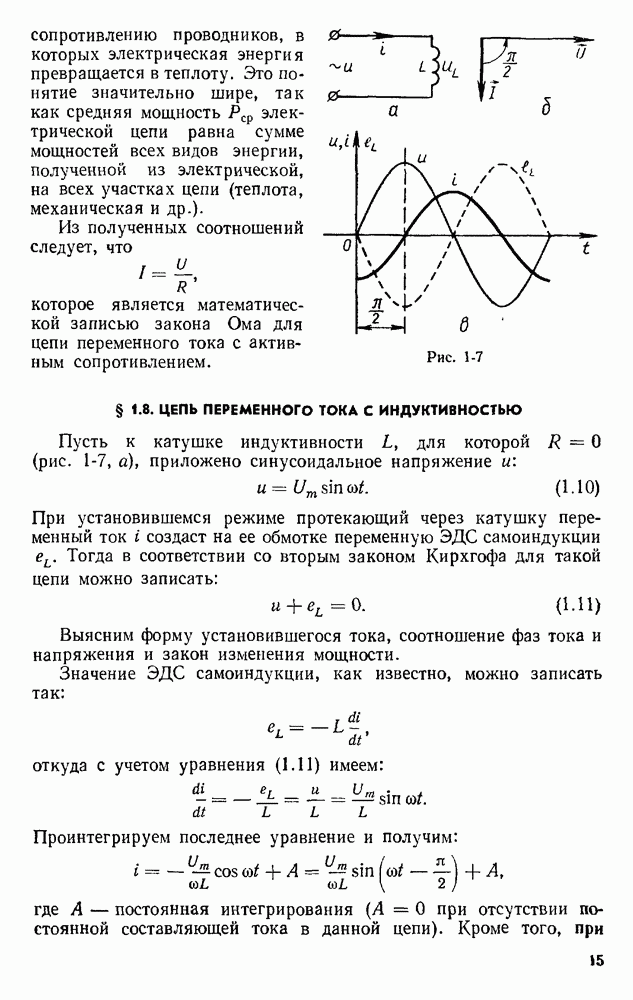
- § 1.8. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ИНДУКТИВНОСТЬЮ
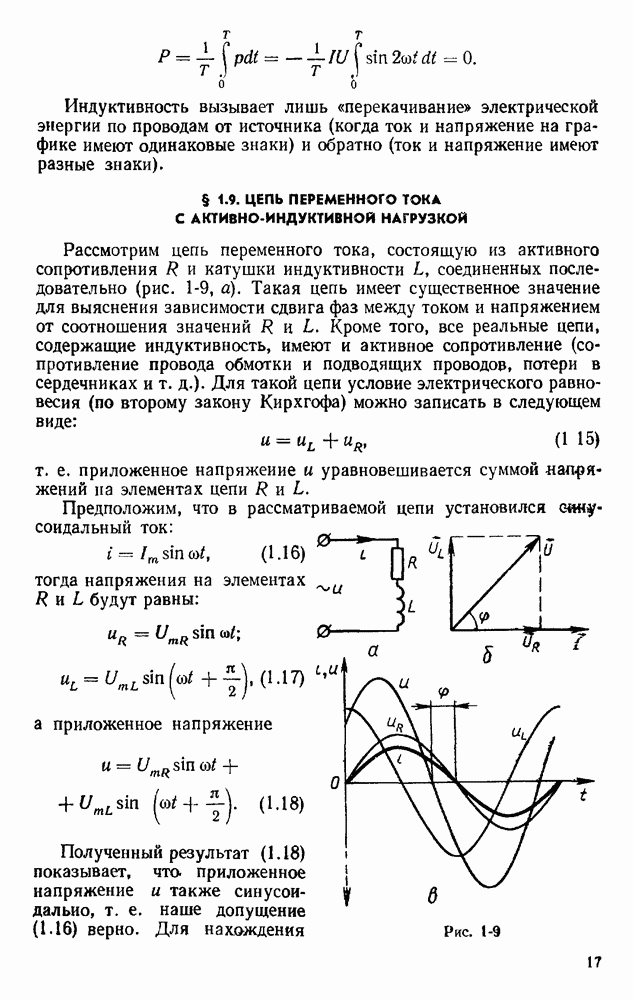
- § 1.9. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
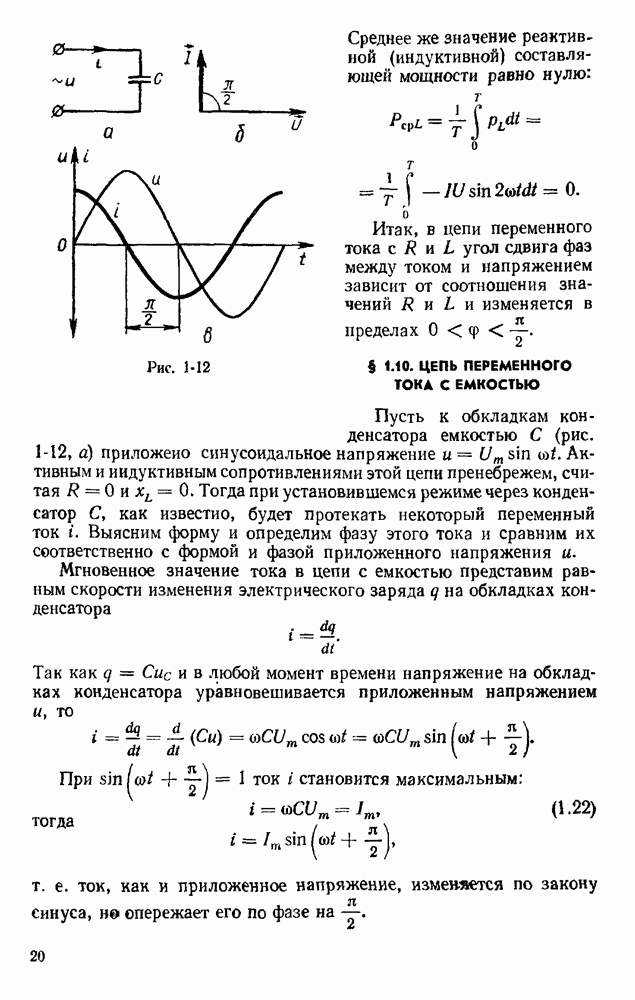
- § 1.10. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ЕМКОСТЬЮ
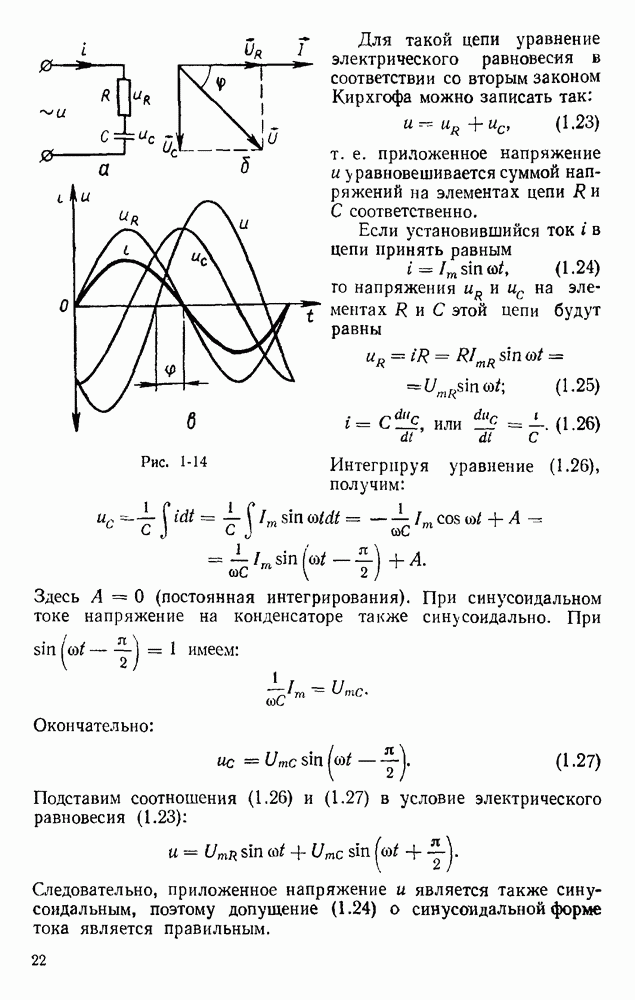
- § 1.11. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ЕМКОСТНОЙ НАГРУЗКОЙ
- § 1.12. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L И С. КОЭФФИЦИЕНТ МОЩНОСТИ
- § 1.13. РЕЗОНАНС НАПРЯЖЕНИЙ
- § 1.14. РЕЗОНАНС ТОКОВ
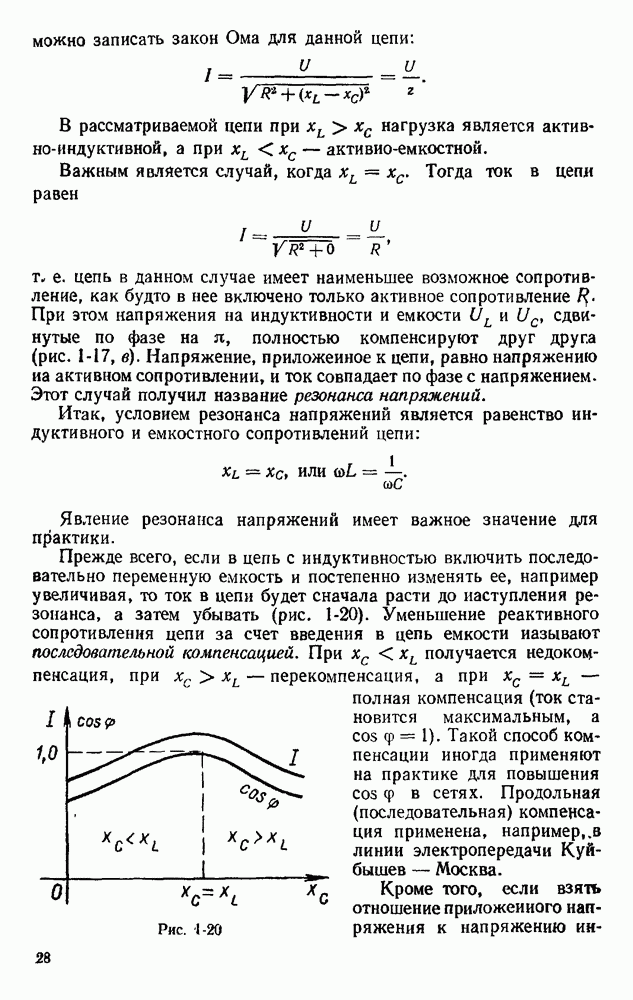
- § 1.15. СПОСОБЫ ПОВЫШЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 1.16. ПРОВОДИМОСТЬ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- § 1.17. СИМВОЛИЧЕСКИЙ МЕТОД
- 2. ТРЕХФАЗНЫЕ ЦЕПИ
- § 1.19. ПРИНЦИП ПОСТРОЕНИЯ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 1.20. СОЕДИНЕНИЕ ЗВЕЗДОЙ
- § 1.21. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- § 1.22. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ
- ГЛАВА II. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ И ПРИБОРЫ
- § 2.3. ПОГРЕШНОСТИ ЭЛЕКТРИЧЕСКИХ ИЗМЕРЕНИЙ
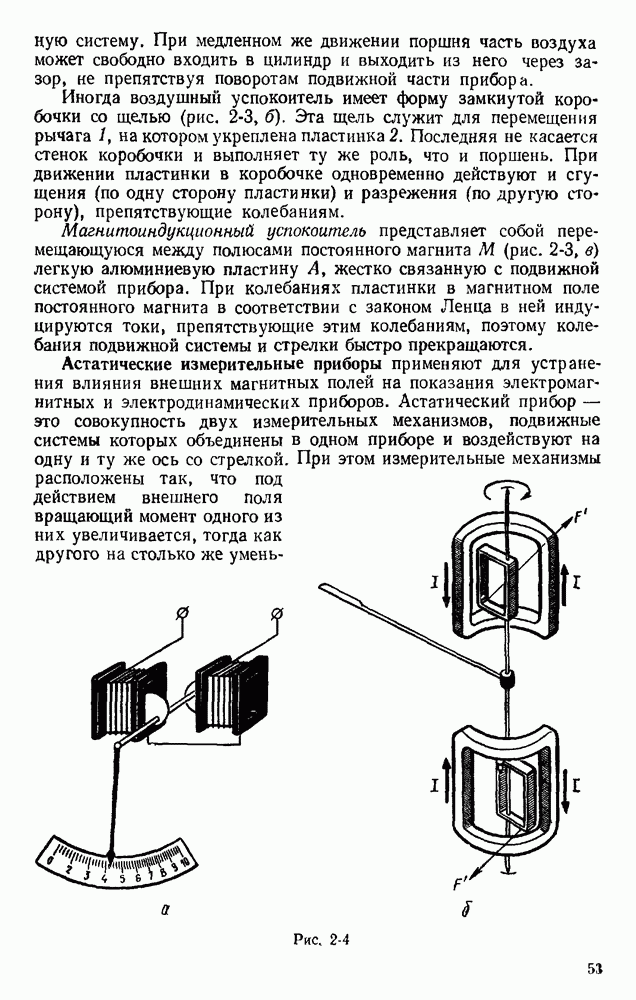
- § 2.4. ОСНОВНЫЕ ДЕТАЛИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- § 2.5. МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.6. ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- § 2.7. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.8. ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.9. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВАТТМЕТРЫ
- § 2.10. ОДНОФАЗНЫЙ ФАЗОМЕТР
- § 2.11. ОДНОФАЗНЫЙ ИНДУКЦИОННЫЙ СЧЕТЧИК ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
- § 2.12. ОММЕТРЫ
- § 2.13. ЛОГОМЕТРЫ
- § 2.14. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.15. ДЕТЕКТОРНЫЕ ПРИБОРЫ
- § 2.16. ШКОЛЬНЫЕ ДЕМОНСТРАЦИОННЫЕ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- § 2.17. ПОНЯТИЕ О ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРАХ
- § 2.18. ИЗМЕРЕНИЕ МОЩНОСТИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.19. ИЗМЕРЕНИЕ ЭНЕРГИИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.20. СПОСОБЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 2.21. ПОНЯТИЕ ОБ ИЗМЕРЕНИЯХ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН ЭЛЕКТРИЧЕСКИМИ МЕТОДАМИ
- ГЛАВА III. ТРАНСФОРМАТОРЫ
- § 3.2. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ТРАНСФОРМАТОРА
- § 3.3. ХОЛОСТОЙ РЕЖИМ РАБОТЫ ТРАНСФОРМАТОРА
- § 3.4. РАБОЧИЙ РЕЖИМ ТРАНСФОРМАТОРА
- § 3.5. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- § 3.6. ТРЕХФАЗНЫЕ ТРАНСФОРМАТОРЫ
- § 3.7. КОНСТРУКЦИИ ТРАНСФОРМАТОРОВ
- § 3.8. АВТОТРАНСФОРМАТОР
- § 3.9. ИЗМЕРИТЕЛЬНЫЕ ТРАНСФОРМАТОРЫ
- Глава IV. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ВЫПРЯМИТЕЛИ
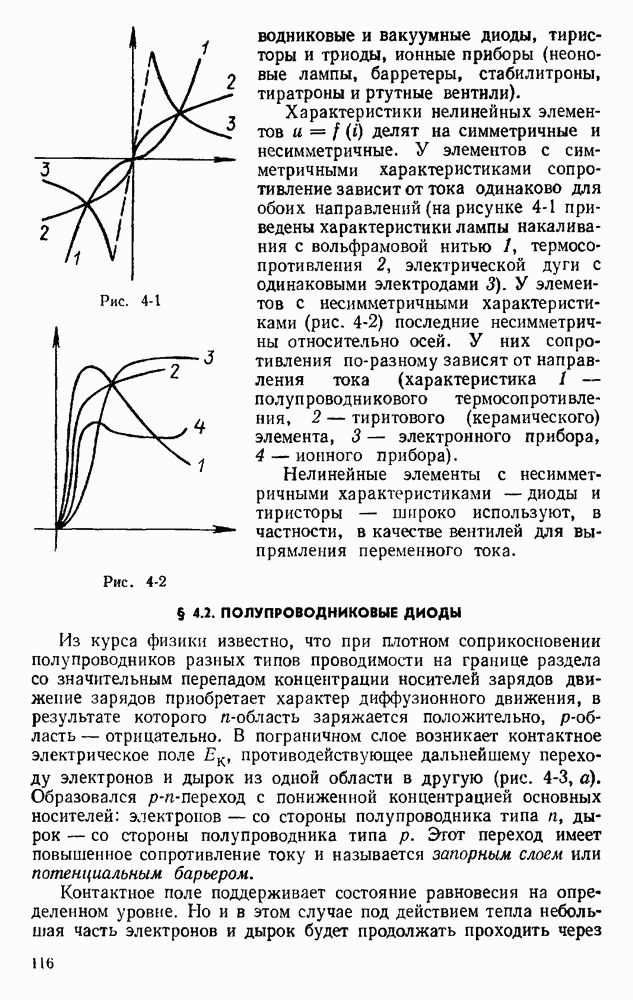
- 4.1. ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И ЭЛЕМЕНТОВ
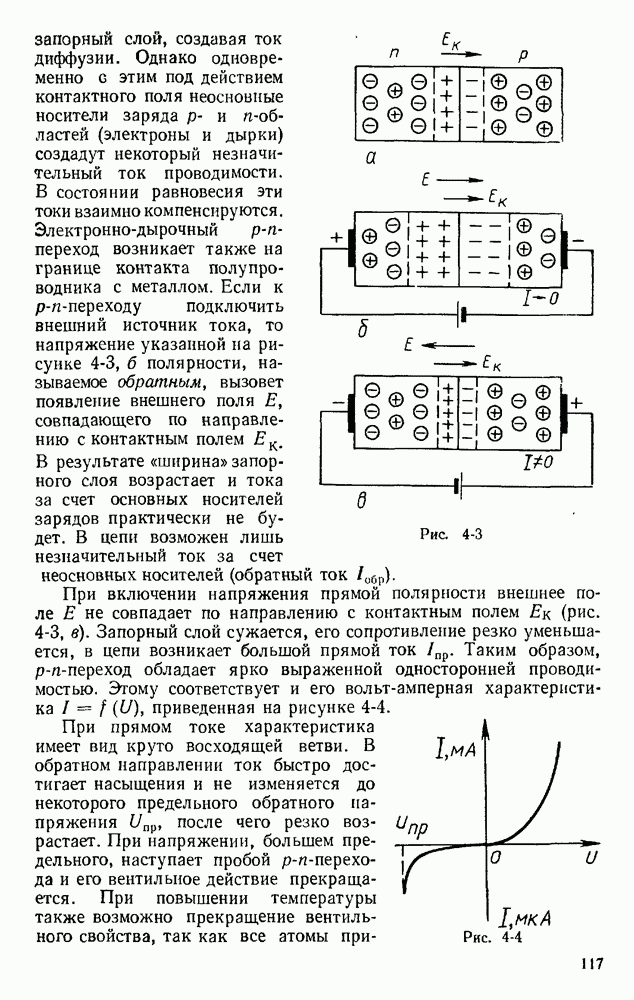
- § 4.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- § 4.3. ТИРИСТОРЫ
- § 4.4. ОСНОВНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ ПЕРЕМЕННОГО ТОКА
- § 4.5. ПРИМЕНЕНИЕ ТИРИСТОРОВ ДЛЯ ВЫПРЯМЛЕНИЯ И РЕГУЛИРОВАНИЯ ТОКА
- § 4.6. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ
- § 4.7. ПОНЯТИЕ ОБ ИНВЕРТОРАХ
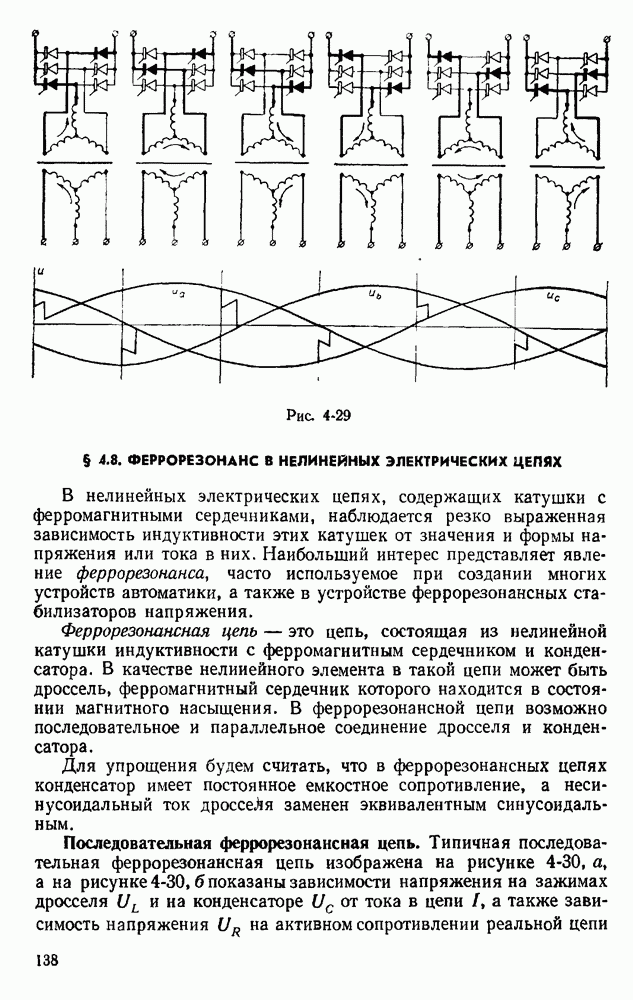
- § 4.8. ФЕРРОРЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 4.9. ФЕРРОРЕЗОНАНСНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- § 4.10. ШКОЛЬНЫЕ ВЫПРЯМИТЕЛИ
- ГЛАВА V. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- § 5.1. КЛАССИФИКАЦИЯ МАШИН ПЕРЕМЕННОГО ТОКА
- § 5.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.3. СОЗДАНИЕ ВРАЩАЮЩЕГОСЯ МАГНИТНОГО ПОЛЯ ТРЕХФАЗНОЙ СИСТЕМОЙ
- § 5.4. СКОРОСТЬ ВРАЩЕНИЯ МАГНИТНОГО ПОЛЯ. ТИПЫ ОБМОТОК СТАТОРА
- § 5.5. СКОЛЬЖЕНИЕ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 1.6. МАГНИТНЫЙ ПОТОК ЭДС И ТОКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.7. ВЕКТОРНАЯ ДИАГРАММА АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.8. АСИНХРОННЫЙ ДВИГАТЕЛЬ С КОНТАКТНЫМИ КОЛЬЦАМИ
- § 5.9. РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.10. ПУСК В ХОД АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.11. РЕВЕРСИРОВАНИЕ И РЕГУЛИРОВАНИЕ СКОРОСТИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.12. ОДНОФАЗНЫЕ АСИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.13. ПРИМЕНЕНИЕ ТРЕХФАЗНЫХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.14. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.15. ЭДС СИНХРОННОГО ГЕНЕРАТОРА
- § 5.16. РЕАКЦИЯ ЯКОРЯ
- § 5.17. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.18. УПРОЩЕННАЯ ВЕКТОРНАЯ ДИАГРАММА СИНХРОННОГО ГЕНЕРАТОРА
- § 5.19. РАБОТА СИНХРОННОГО ГЕНЕРАТОРА ПАРАЛЛЕЛЬНО С СЕТЬЮ
- § 5.20. ОБРАТИМОСТЬ СИНХРОННЫХ МАШИН. ПРИНЦИП РАБОТЫ СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.21. ПУСК И ОСТАНОВКА СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.22. ВЛИЯНИЕ ТОКА ВОЗБУЖДЕНИЯ НА РАБОТУ СИНХРОННОГО ДВИГАТЕЛЯ. СИНХРОННЫЙ КОМПЕНСАТОР
- § 5.23. РЕАКТИВНЫЕ СИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.24. ПРИМЕНЕНИЕ СИНХРОННЫХ ДВИГАТЕЛЕЙ
- ГЛАВА VI. МАШИНЫ ПОСТОЯННОГО ТОКА
- § 6.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА. ТИПЫ ОБМОТОК ЯКОРЯ
- § 6.3. ЭДС И ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА
- § 6.4. РЕАКЦИЯ ЯКОРЯ
- § 6.5. КОММУТАЦИЯ
- § 6.6. СПОСОБЫ ВОЗБУЖДЕНИЯ ГЕНЕРАТОРОВ ПОСТОЯННОГО ТОКА
- § 6.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. ДВИГАТЕЛИ
- § 6.8. ДВИГАТЕЛЬ ПАРАЛЛЕЛЬНОГО И НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ
- § 6.9. ДВИГАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ
- § 6.10. ДВИГАТЕЛЬ СМЕШАННОГО ВОЗБУЖДЕНИЯ
- § 6.11. КОЛЛЕКТОРНЫЕ ДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА VII. ЭЛЕМЕНТЫ АВТОМАТИКИ
- § 7.2. РЕЛЕ
- § 7.3. ДАТЧИКИ
- § 7.4. АВТОМАТИЧЕСКИЙ КОНТРОЛЬ
- § 7.5. АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ
- § 7.6. АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ
- § 7.7. ТЕЛЕМЕХАНИКА
- § 7.8. КОМПЛЕКСНАЯ АВТОМАТИЗАЦИЯ
- ГЛАВА VIII. ПРОИЗВОДСТВО, ПЕРЕДАЧА И ИСПОЛЬЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ В НАРОДНОМ ХОЗЯЙСТВЕ
- § 8.1. ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ
- § 8.2. ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ
- § 8.3. ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПОСТОЯННЫМ ТОКОМ
- § 8.4. АВТОМАТИЗАЦИЯ ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ И ПОДСТАНЦИЙ
- ГЛАВА IX. СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РАЗВИТИЯ ЭЛЕКТРОЭНЕРГЕТИКИ
- ГЛАВА X. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ
- § 10.1. ОПАСНОСТЬ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ ДЛЯ ОРГАНИЗМА ЧЕЛОВЕКА
- § 10.2. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ ТЕЛА ЧЕЛОВЕКА
- § 10.3. ОСНОВНЫЕ ПРИЧИНЫ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ
- § 10.4. ЗАЩИТНОЕ ЗАЗЕМЛЕНИЕ И ЗАЗЕМЛЕНИЕ НА НЕЙТРАЛЬ (ЗАНУЛЕНИЕ)
- § 10.5. ЗАЩИТНЫЕ СРЕДСТВА И КОНТРОЛЬ СОСТОЯНИЯ ИЗОЛЯЦИИ ЭЛЕКТРОУСТАНОВОК
- § 10.6. ОКАЗАНИЕ ПЕРВОЙ ПОМОЩИ ПОРАЖЕННОМУ ЭЛЕКТРИЧЕСКИМ ТОКОМ
- § 10.7. ОСНОВНЫЕ ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ В УЧЕБНЫХ ЛАБОРАТОРИЯХ
- ЛИТЕРАТУРА