| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6.3. ЭДС И ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА
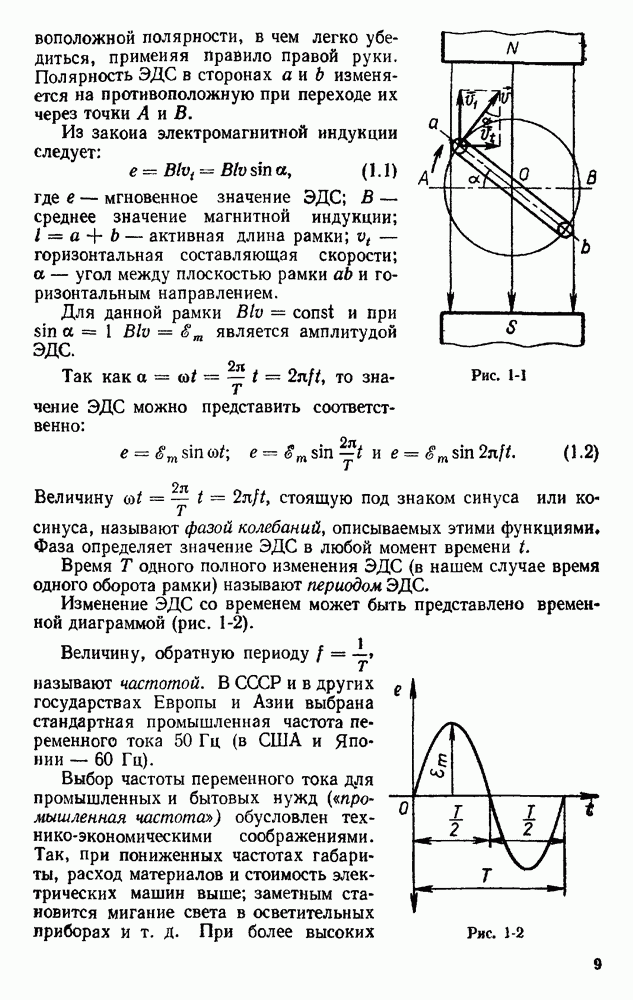
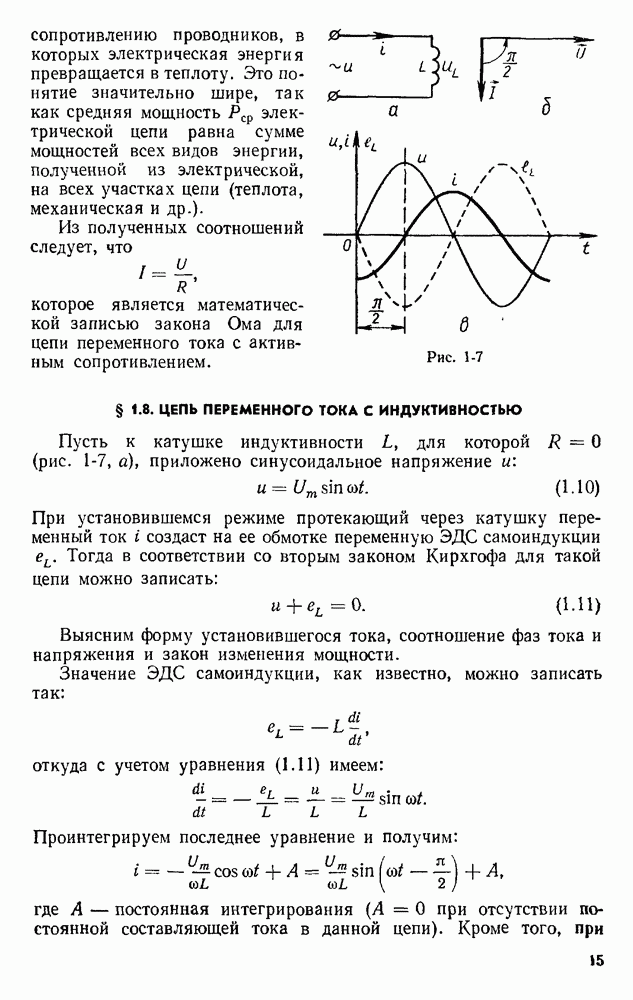
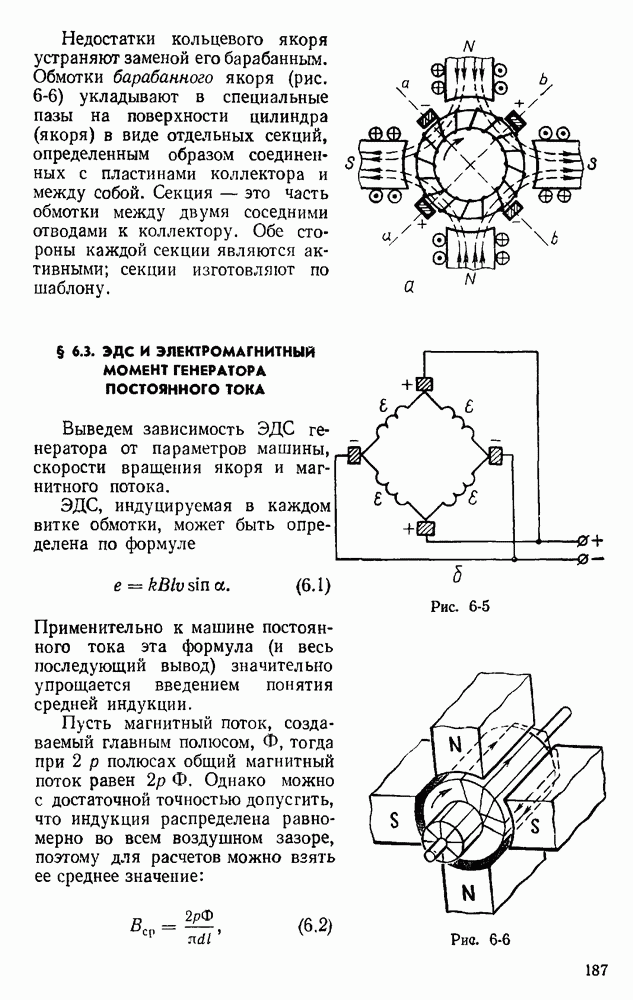
Выведем зависимость ЭДС генератора от параметров машины, скорости вращения якоря и магнитного потока.
ЭДС, индуцируемая в каждом витке обмотки, может быть определена по формуле

Применительно к машине постоянного тока эта формула (и весь последующий вывод) значительно упрощается введением понятия средней индукции.
Пусть магнитный поток, создаваемый главным полюсом, Ф, тогда при  полюсах общий магнитный поток равен
полюсах общий магнитный поток равен  . Однако можно с достаточной точностью допустить, что индукция распределена равномерно во всем воздушном зазоре, поэтому для расчетов можно взять ее среднее значение:
. Однако можно с достаточной точностью допустить, что индукция распределена равномерно во всем воздушном зазоре, поэтому для расчетов можно взять ее среднее значение:

где d — диаметр сердечника якоря, I — образующая цилиндра якоря (длина якоря). Тогда средняя ЭДС одного проводника обмотки при  равна
равна

где l — длина активной части проводника (равна образующей цилиндра якоря); v — линейная (окружная) скорость движения проводника.
Подставим в формулу (6.3) значение средней индукции  и линейной скорости
и линейной скорости  после преобразования получим:
после преобразования получим:

где  — скорость вращения якоря.
— скорость вращения якоря.
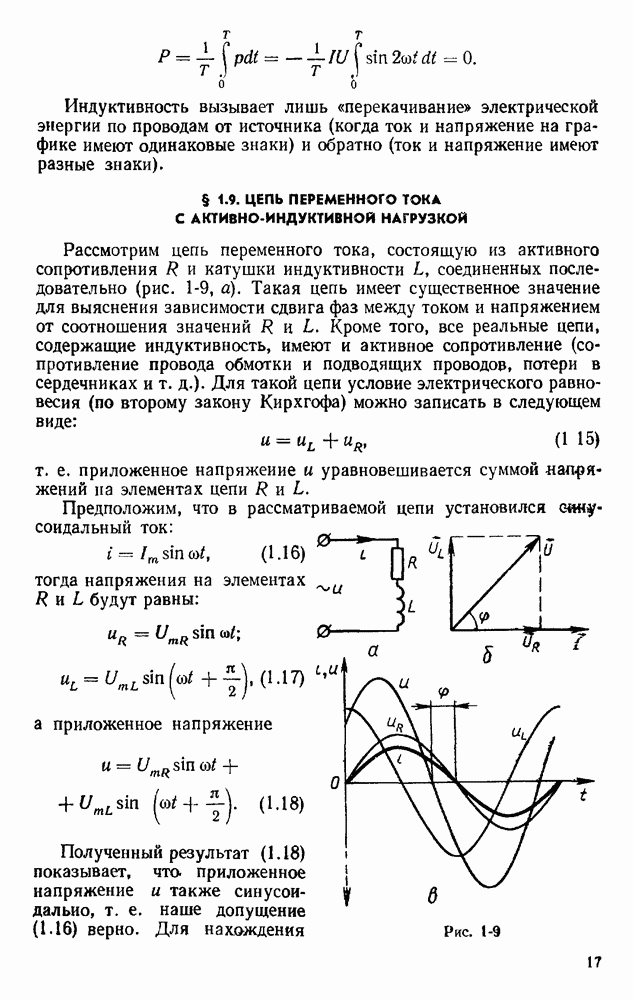
Пусть обмотка содержит 2а параллельных ветвей, тогда в каждой параллельной ветви будет — активных проводников. Так как ЭДС генератора равна ЭДС параллельной ветви, то можно записать:

где  — ЭДС генератора,
— ЭДС генератора,
Подставим выражение (6.4) в уравнение (6.3), после сокращения получим:

В полученной формуле выделенная дробь содержит параметры, зависящие от конструкции машины. Для данной конструкции машины эта величина постоянная. Обозначим эту дробь через с, тогда для ЭДС генератора окончательно имеем:

Таким образом, ЭДС генератора постоянного тока пропорциональна значению магнитного потока Ф и скорости вращения якоря п. Следовательно, для поддержания постоянного напряжения на зажимах генератора можно изменять ЭДС либо значением магнитного потока, либо скоростью вращения ротора (либо тем и другим). На практике ротор генератора приводят во вращение двигателем, работающим нормально при определенной скорости вращения вала, а магнитный поток изменяют путем изменения тока в обмотке возбуждения.
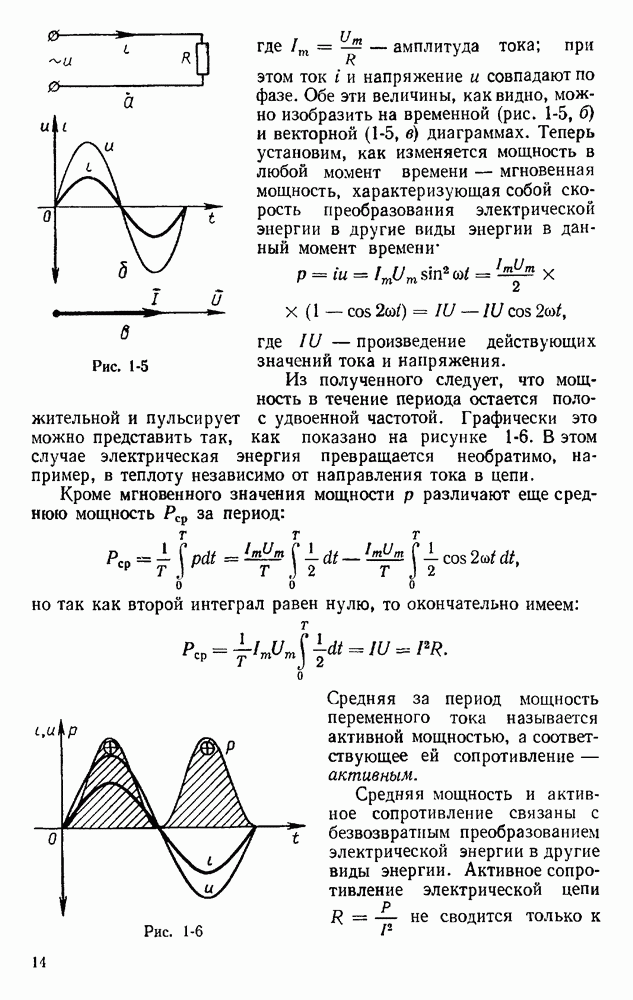
Мощность генератора постоянного тока можно представить формулой механической мощности  причем под работой А следует понимать работу, затрачиваемую на преодоление
причем под работой А следует понимать работу, затрачиваемую на преодоление
тормозного момента, развиваемого якорем, за один оборот при вращении якоря со скоростью  (без потерь). Тогда эту формулу можно записать так:
(без потерь). Тогда эту формулу можно записать так:

где F — сила, действующая на якорь.
При таком взаимодействии на каждый проводник обмотки якоря с током I действует сила  , а на N проводников обмотки
, а на N проводников обмотки

Учитывая соотношение (6.2), последнее уравнение можно записать следующим образом:

Подставив уравнение (6.10) в уравнение (6.8), получим выражение для мощности:

Так как  то окончательно имеем:
то окончательно имеем:

Для общего момента машины М можно записать:

где  — постоянный для данной машины коэффициент, зависящий от особенностей ее конструкции.
— постоянный для данной машины коэффициент, зависящий от особенностей ее конструкции.
Таким образом, электромагнитный момент машины выражается формулой

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1. ОДНОФАЗНЫЕ ЦЕПИ
- § 1.2. ПРИНЦИП ПОЛУЧЕНИЯ ПЕРЕМЕННОЙ СИНУСОИДАЛЬНОЙ ЭДС
- § 1.3. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ ТОКА И НАПРЯЖЕНИЯ
- § 1.4. СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- § 1.5. МЕТОД ВЕКТОРНЫХ ДИАГРАММ
- § 1.6. СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
- § 1.7. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ
- § 1.8. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ИНДУКТИВНОСТЬЮ
- § 1.9. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
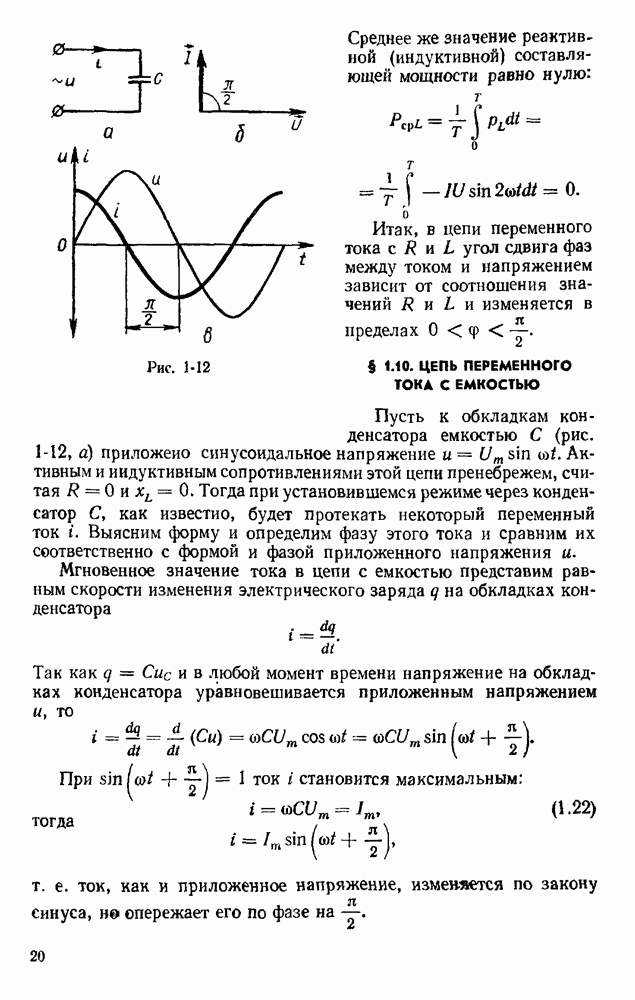
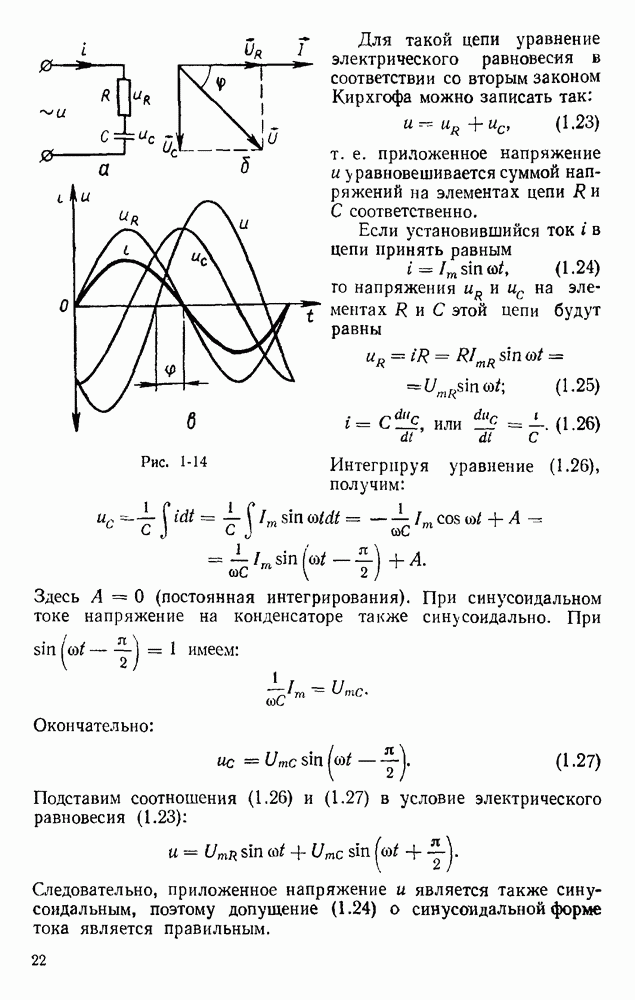
- § 1.10. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ЕМКОСТЬЮ
- § 1.11. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ЕМКОСТНОЙ НАГРУЗКОЙ
- § 1.12. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L И С. КОЭФФИЦИЕНТ МОЩНОСТИ
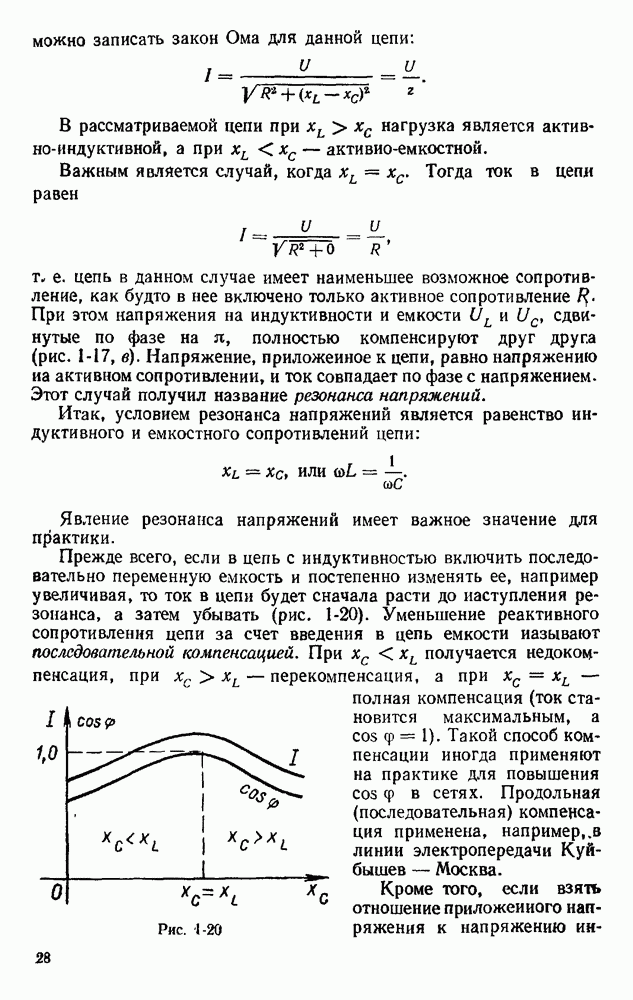
- § 1.13. РЕЗОНАНС НАПРЯЖЕНИЙ
- § 1.14. РЕЗОНАНС ТОКОВ
- § 1.15. СПОСОБЫ ПОВЫШЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 1.16. ПРОВОДИМОСТЬ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- § 1.17. СИМВОЛИЧЕСКИЙ МЕТОД
- 2. ТРЕХФАЗНЫЕ ЦЕПИ
- § 1.19. ПРИНЦИП ПОСТРОЕНИЯ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 1.20. СОЕДИНЕНИЕ ЗВЕЗДОЙ
- § 1.21. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- § 1.22. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ
- ГЛАВА II. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ И ПРИБОРЫ
- § 2.3. ПОГРЕШНОСТИ ЭЛЕКТРИЧЕСКИХ ИЗМЕРЕНИЙ
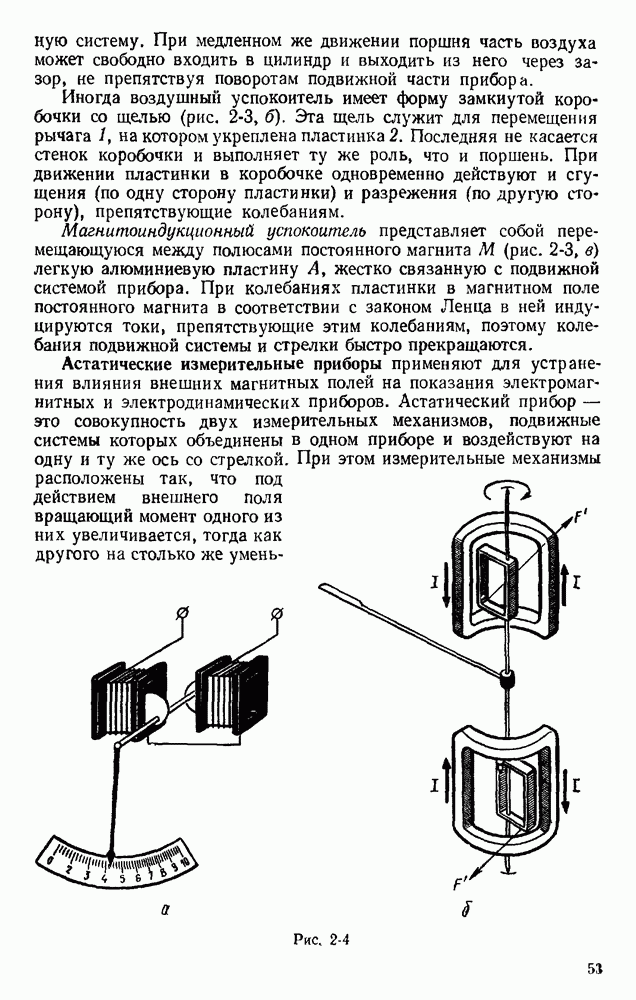
- § 2.4. ОСНОВНЫЕ ДЕТАЛИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- § 2.5. МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.6. ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- § 2.7. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.8. ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.9. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВАТТМЕТРЫ
- § 2.10. ОДНОФАЗНЫЙ ФАЗОМЕТР
- § 2.11. ОДНОФАЗНЫЙ ИНДУКЦИОННЫЙ СЧЕТЧИК ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
- § 2.12. ОММЕТРЫ
- § 2.13. ЛОГОМЕТРЫ
- § 2.14. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.15. ДЕТЕКТОРНЫЕ ПРИБОРЫ
- § 2.16. ШКОЛЬНЫЕ ДЕМОНСТРАЦИОННЫЕ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- § 2.17. ПОНЯТИЕ О ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРАХ
- § 2.18. ИЗМЕРЕНИЕ МОЩНОСТИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.19. ИЗМЕРЕНИЕ ЭНЕРГИИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.20. СПОСОБЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 2.21. ПОНЯТИЕ ОБ ИЗМЕРЕНИЯХ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН ЭЛЕКТРИЧЕСКИМИ МЕТОДАМИ
- ГЛАВА III. ТРАНСФОРМАТОРЫ
- § 3.2. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ТРАНСФОРМАТОРА
- § 3.3. ХОЛОСТОЙ РЕЖИМ РАБОТЫ ТРАНСФОРМАТОРА
- § 3.4. РАБОЧИЙ РЕЖИМ ТРАНСФОРМАТОРА
- § 3.5. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- § 3.6. ТРЕХФАЗНЫЕ ТРАНСФОРМАТОРЫ
- § 3.7. КОНСТРУКЦИИ ТРАНСФОРМАТОРОВ
- § 3.8. АВТОТРАНСФОРМАТОР
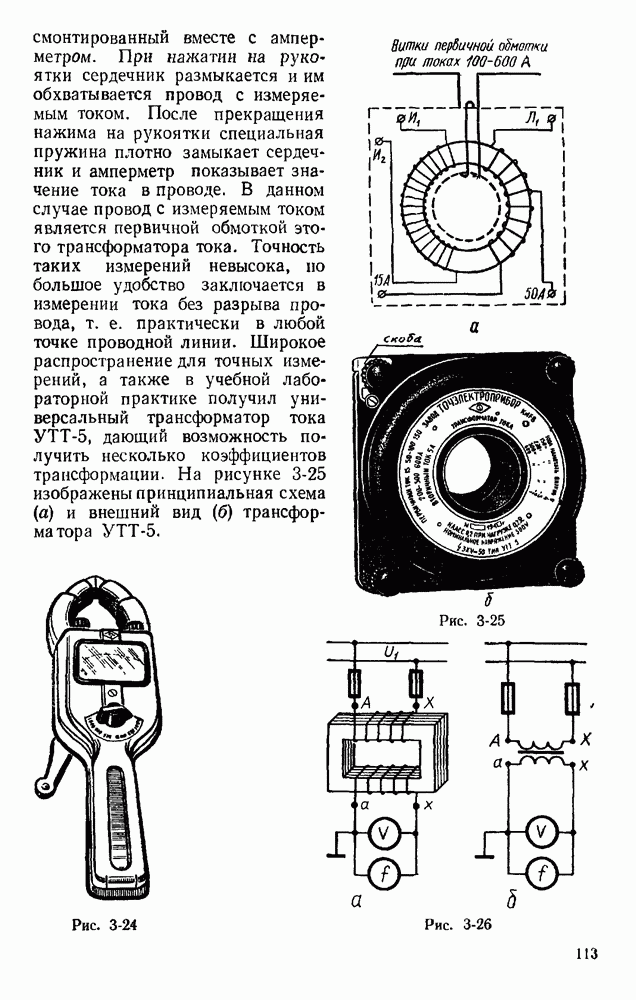
- § 3.9. ИЗМЕРИТЕЛЬНЫЕ ТРАНСФОРМАТОРЫ
- Глава IV. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ВЫПРЯМИТЕЛИ
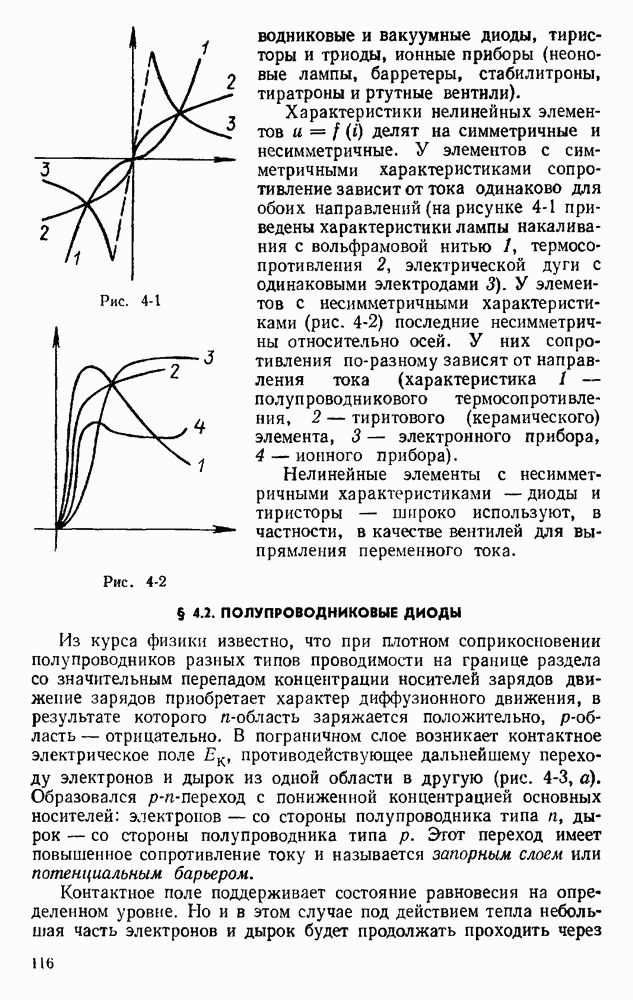
- 4.1. ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И ЭЛЕМЕНТОВ
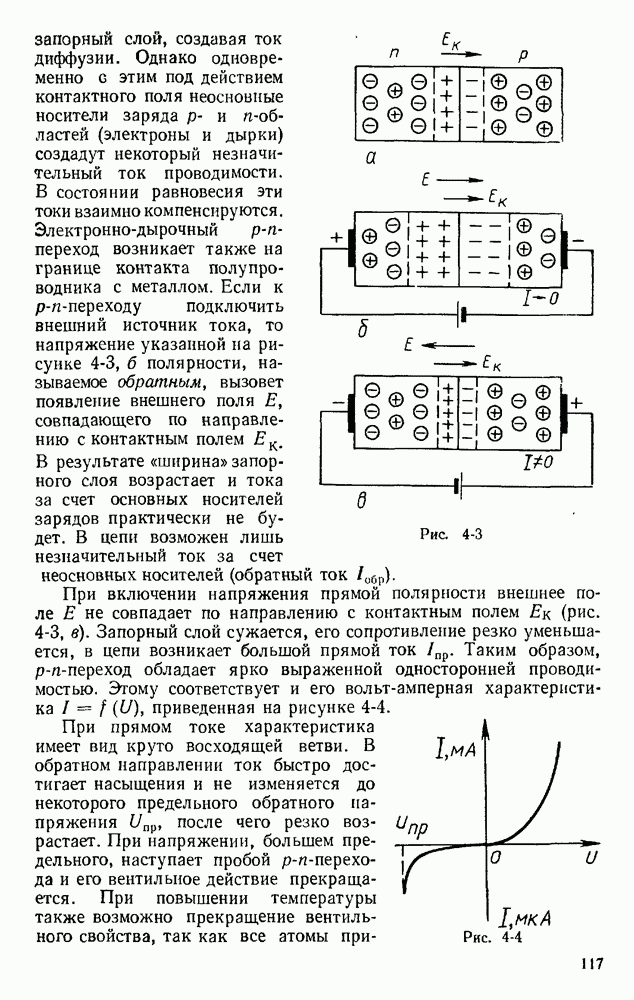
- § 4.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- § 4.3. ТИРИСТОРЫ
- § 4.4. ОСНОВНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ ПЕРЕМЕННОГО ТОКА
- § 4.5. ПРИМЕНЕНИЕ ТИРИСТОРОВ ДЛЯ ВЫПРЯМЛЕНИЯ И РЕГУЛИРОВАНИЯ ТОКА
- § 4.6. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ
- § 4.7. ПОНЯТИЕ ОБ ИНВЕРТОРАХ
- § 4.8. ФЕРРОРЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 4.9. ФЕРРОРЕЗОНАНСНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- § 4.10. ШКОЛЬНЫЕ ВЫПРЯМИТЕЛИ
- ГЛАВА V. МАШИНЫ ПЕРЕМЕННОГО ТОКА
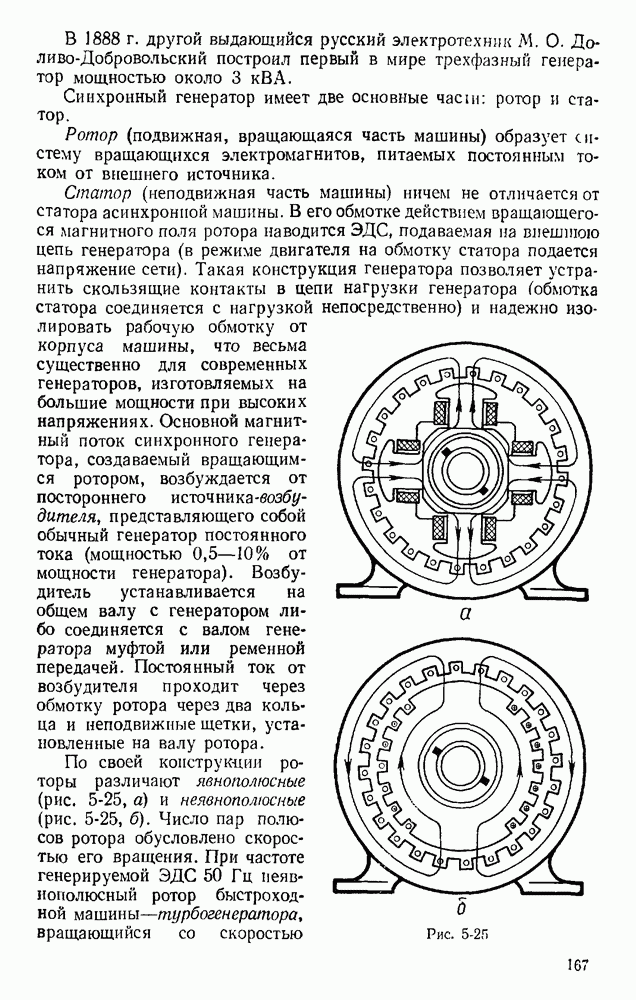
- § 5.1. КЛАССИФИКАЦИЯ МАШИН ПЕРЕМЕННОГО ТОКА
- § 5.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.3. СОЗДАНИЕ ВРАЩАЮЩЕГОСЯ МАГНИТНОГО ПОЛЯ ТРЕХФАЗНОЙ СИСТЕМОЙ
- § 5.4. СКОРОСТЬ ВРАЩЕНИЯ МАГНИТНОГО ПОЛЯ. ТИПЫ ОБМОТОК СТАТОРА
- § 5.5. СКОЛЬЖЕНИЕ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 1.6. МАГНИТНЫЙ ПОТОК ЭДС И ТОКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.7. ВЕКТОРНАЯ ДИАГРАММА АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.8. АСИНХРОННЫЙ ДВИГАТЕЛЬ С КОНТАКТНЫМИ КОЛЬЦАМИ
- § 5.9. РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.10. ПУСК В ХОД АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.11. РЕВЕРСИРОВАНИЕ И РЕГУЛИРОВАНИЕ СКОРОСТИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.12. ОДНОФАЗНЫЕ АСИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.13. ПРИМЕНЕНИЕ ТРЕХФАЗНЫХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.14. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.15. ЭДС СИНХРОННОГО ГЕНЕРАТОРА
- § 5.16. РЕАКЦИЯ ЯКОРЯ
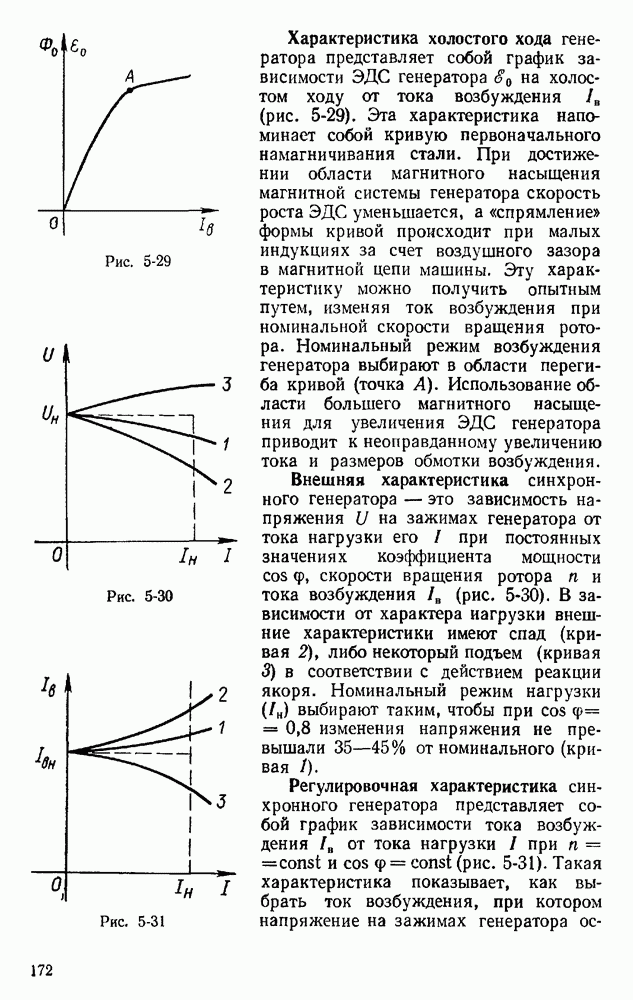
- § 5.17. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.18. УПРОЩЕННАЯ ВЕКТОРНАЯ ДИАГРАММА СИНХРОННОГО ГЕНЕРАТОРА
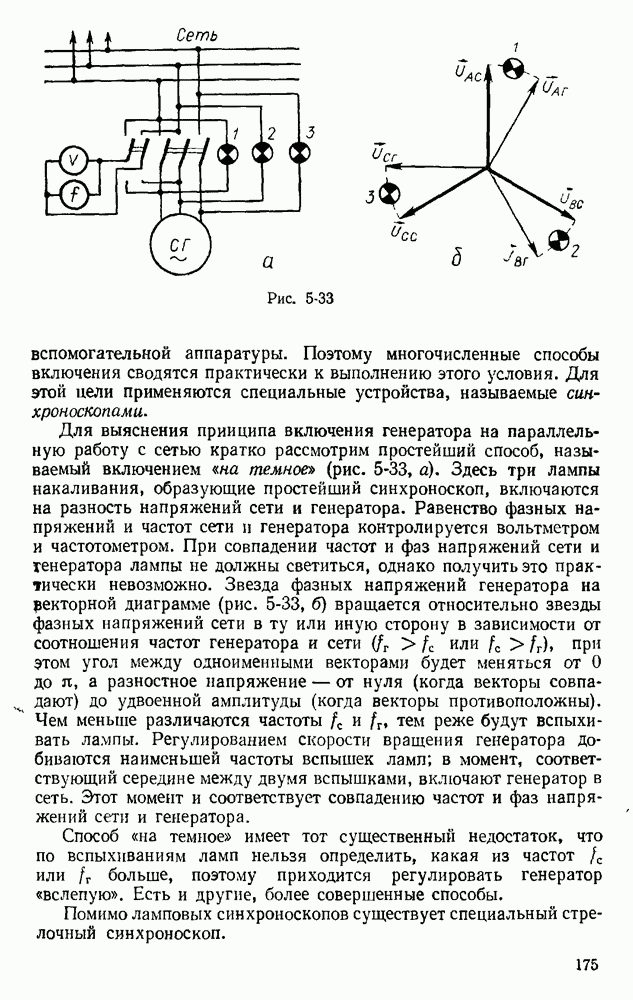
- § 5.19. РАБОТА СИНХРОННОГО ГЕНЕРАТОРА ПАРАЛЛЕЛЬНО С СЕТЬЮ
- § 5.20. ОБРАТИМОСТЬ СИНХРОННЫХ МАШИН. ПРИНЦИП РАБОТЫ СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.21. ПУСК И ОСТАНОВКА СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.22. ВЛИЯНИЕ ТОКА ВОЗБУЖДЕНИЯ НА РАБОТУ СИНХРОННОГО ДВИГАТЕЛЯ. СИНХРОННЫЙ КОМПЕНСАТОР
- § 5.23. РЕАКТИВНЫЕ СИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.24. ПРИМЕНЕНИЕ СИНХРОННЫХ ДВИГАТЕЛЕЙ
- ГЛАВА VI. МАШИНЫ ПОСТОЯННОГО ТОКА
- § 6.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА. ТИПЫ ОБМОТОК ЯКОРЯ
- § 6.3. ЭДС И ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА
- § 6.4. РЕАКЦИЯ ЯКОРЯ
- § 6.5. КОММУТАЦИЯ
- § 6.6. СПОСОБЫ ВОЗБУЖДЕНИЯ ГЕНЕРАТОРОВ ПОСТОЯННОГО ТОКА
- § 6.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. ДВИГАТЕЛИ
- § 6.8. ДВИГАТЕЛЬ ПАРАЛЛЕЛЬНОГО И НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ
- § 6.9. ДВИГАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ
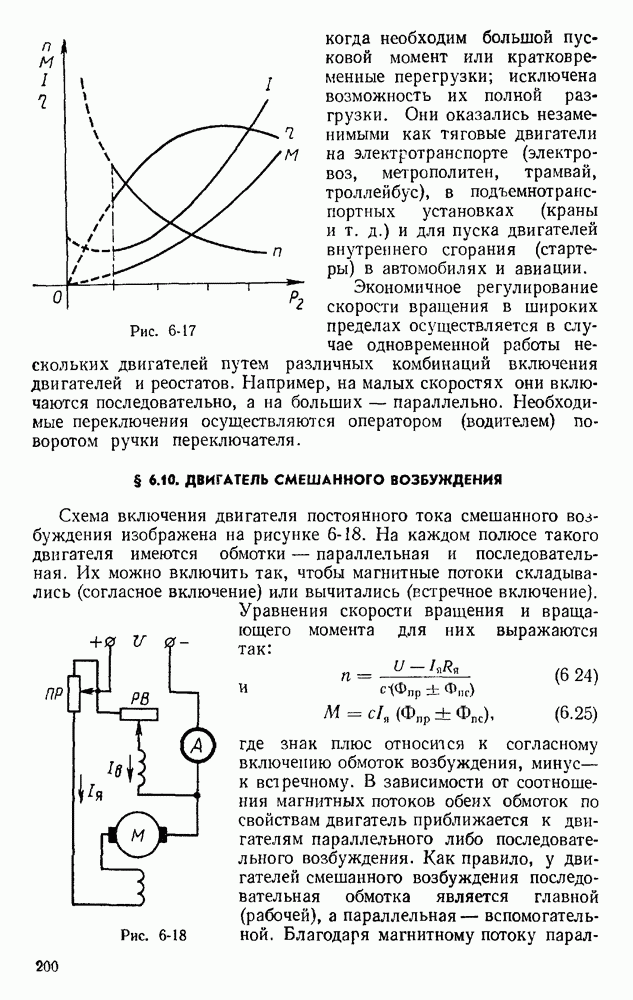
- § 6.10. ДВИГАТЕЛЬ СМЕШАННОГО ВОЗБУЖДЕНИЯ
- § 6.11. КОЛЛЕКТОРНЫЕ ДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА VII. ЭЛЕМЕНТЫ АВТОМАТИКИ
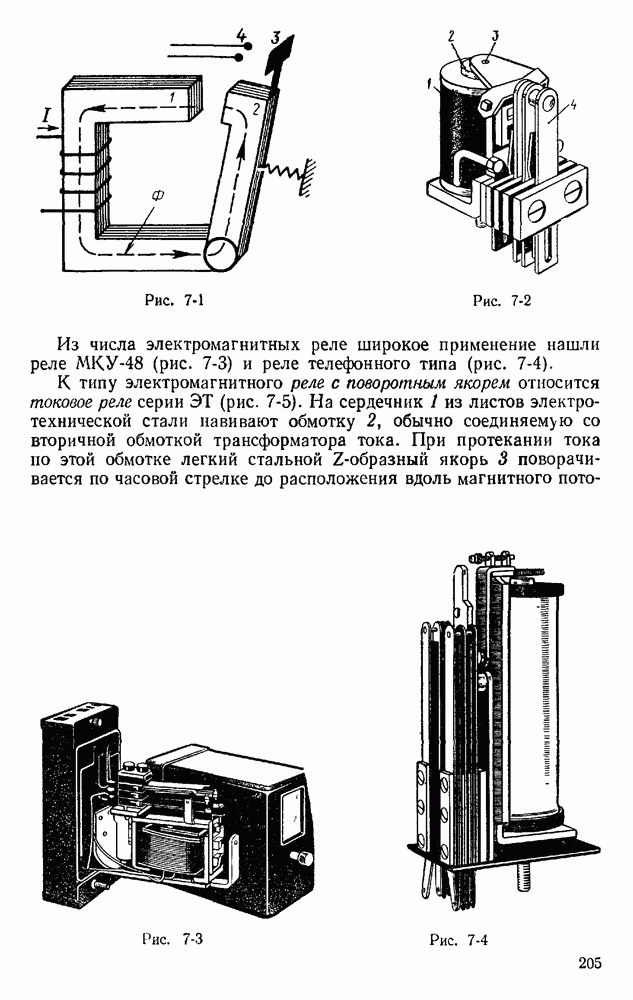
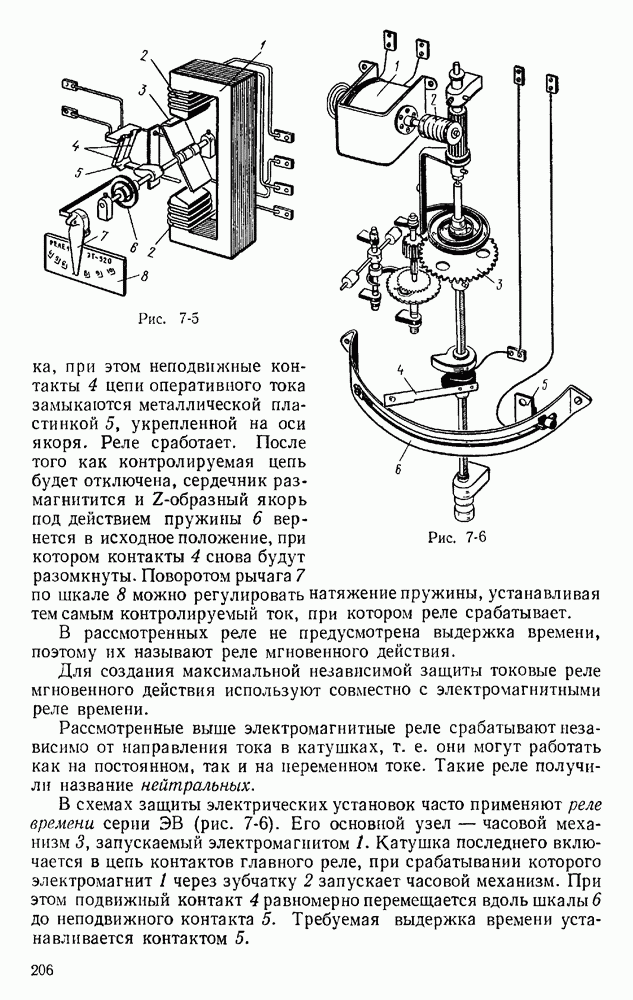
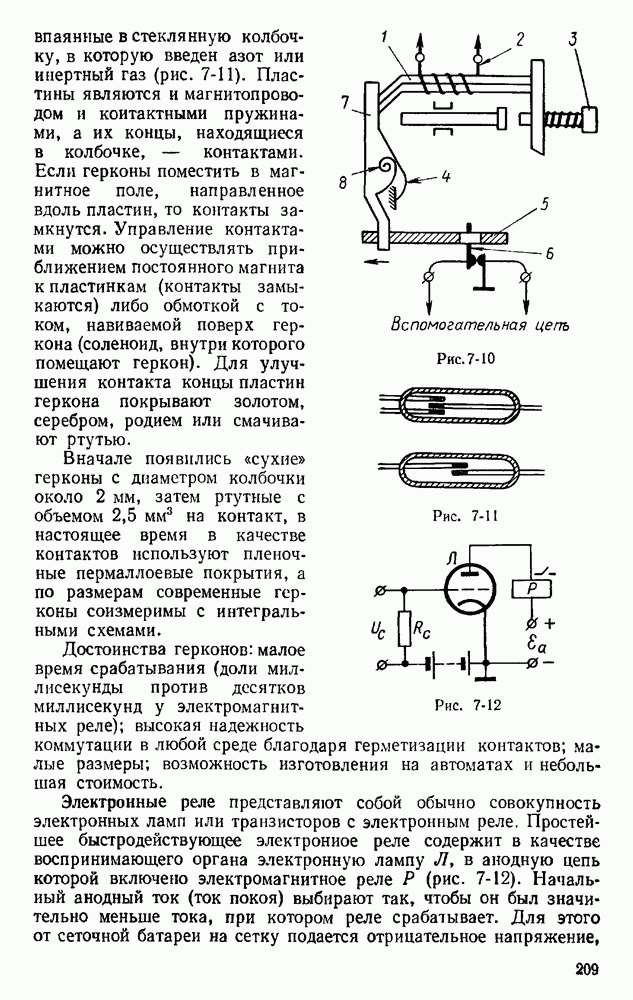
- § 7.2. РЕЛЕ
- § 7.3. ДАТЧИКИ
- § 7.4. АВТОМАТИЧЕСКИЙ КОНТРОЛЬ
- § 7.5. АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ
- § 7.6. АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ
- § 7.7. ТЕЛЕМЕХАНИКА
- § 7.8. КОМПЛЕКСНАЯ АВТОМАТИЗАЦИЯ
- ГЛАВА VIII. ПРОИЗВОДСТВО, ПЕРЕДАЧА И ИСПОЛЬЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ В НАРОДНОМ ХОЗЯЙСТВЕ
- § 8.1. ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ
- § 8.2. ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ
- § 8.3. ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПОСТОЯННЫМ ТОКОМ
- § 8.4. АВТОМАТИЗАЦИЯ ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ И ПОДСТАНЦИЙ
- ГЛАВА IX. СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РАЗВИТИЯ ЭЛЕКТРОЭНЕРГЕТИКИ
- ГЛАВА X. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ
- § 10.1. ОПАСНОСТЬ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ ДЛЯ ОРГАНИЗМА ЧЕЛОВЕКА
- § 10.2. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ ТЕЛА ЧЕЛОВЕКА
- § 10.3. ОСНОВНЫЕ ПРИЧИНЫ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ
- § 10.4. ЗАЩИТНОЕ ЗАЗЕМЛЕНИЕ И ЗАЗЕМЛЕНИЕ НА НЕЙТРАЛЬ (ЗАНУЛЕНИЕ)
- § 10.5. ЗАЩИТНЫЕ СРЕДСТВА И КОНТРОЛЬ СОСТОЯНИЯ ИЗОЛЯЦИИ ЭЛЕКТРОУСТАНОВОК
- § 10.6. ОКАЗАНИЕ ПЕРВОЙ ПОМОЩИ ПОРАЖЕННОМУ ЭЛЕКТРИЧЕСКИМ ТОКОМ
- § 10.7. ОСНОВНЫЕ ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ В УЧЕБНЫХ ЛАБОРАТОРИЯХ
- ЛИТЕРАТУРА