| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.17. СИМВОЛИЧЕСКИЙ МЕТОД
Для расчета цепей переменного тока, а также для аналнза процессов в электрических машинах широкое примененне получил так называемый символический метод, основанный на использовании комплексных чисел. Поэтому символический метод часто называют еще комплексным методом.
Как известно, комплексное число А (рис. 1-28) может быть записано в трех формах: алгебраической, тригонометрической и показательной:

где  — модуль комплексного числа;
— модуль комплексного числа;  — аргумент, показывающий ориентировку вектора на числовой плоскости, и
— аргумент, показывающий ориентировку вектора на числовой плоскости, и 
Если аргумент а изменяется со временем, например  то точка на числовой плоскости, соответствующая комплексному числу
то точка на числовой плоскости, соответствующая комплексному числу  описывает окружность радиуса А с центром в начале координат. Поэтому комплексное число
описывает окружность радиуса А с центром в начале координат. Поэтому комплексное число  может быть представлено вектором А, вращающимся против часовой стрелки с угловой скоростью
может быть представлено вектором А, вращающимся против часовой стрелки с угловой скоростью  . Эта особенность комплексных чисел и дает возможность применять их к гармонически изменяющимся величинам.
. Эта особенность комплексных чисел и дает возможность применять их к гармонически изменяющимся величинам.
Пусть в некоторой цепи напряжение и ток изменяются по закону синуса с разностью фаз  :
:


Рис. 1-28

Рис. 1-29
Так, в активно-индуктнвной цепи (рис. 1-29, а и б), где за основной вектор выбран  вектор тока
вектор тока  комплекс тока
комплекс тока  будет равен
будет равен  вектор
вектор  совпадает с вектором тока
совпадает с вектором тока  поэтому комплекс падения напряжения на активном сопротивлении равен
поэтому комплекс падения напряжения на активном сопротивлении равен

Вектор  (длина которого
(длина которого  опережает вектор тока
опережает вектор тока  на
на  поэтому комплекс этого вектора
поэтому комплекс этого вектора  равен
равен

так как поворот вектора против часовой стрелки на — соответствует его умножению на 
По второму закону Кирхгофа приложенное напряжение U равно

или в комплексной форме

где  — комплекс полного сопротивления (не вектор!) для активно-индуктивной цепи;
— комплекс полного сопротивления (не вектор!) для активно-индуктивной цепи;  фаз.
фаз.
Тогда закон Ома для цепи переменного тока в комплексной форме имеет вид

а для активно-индуктивной цепи можно получить 

Комплекс полного сопротивления  может быть выражен и в показательной форме:
может быть выражен и в показательной форме:

где  модуль полного сопротивления.
модуль полного сопротивления.

Рис. 1-30
В активно-емкостной цепи (рис. 1-30, а и б)  вектор
вектор  модуль которого
модуль которого  отстает от вектора тока
отстает от вектора тока  на
на  поэтому
поэтому

так как поворот вектора по часовой стрелке на — соответствует его умножению на 
Для этой цепи напряжение в комплексной форме равно

где  комплекс полного сопротивления активно-емкостной цепи;
комплекс полного сопротивления активно-емкостной цепи;  фаз;
фаз;  — модуль полного сопротивления.
— модуль полного сопротивления.
Для активно-емкостной цепи можно получить:

 получения мощности в комплексной форме принято брать произведение комплекса напряжения U на сопряженный комплекс
получения мощности в комплексной форме принято брать произведение комплекса напряжения U на сопряженный комплекс 

Здесь вещественная часть  представляет собой активную мощность, а мнимая
представляет собой активную мощность, а мнимая  множителя
множителя  ) — реактивную. Модуль комплекса мощности дает полную (кажущуюся) мощность:
) — реактивную. Модуль комплекса мощности дает полную (кажущуюся) мощность:

В заключение в качестве примера рассмотрим порядок расчета сложной цепи (рис. 1-31) переменного тока на основе символического метода.
Пусть известно приложенное напряжение и все сопротивления, включенные в цепь. Необходимо найти токи.

Рис. 1-31
Сначала записываем комплексы полных сопротивлений участков цепи:

Затем находим комплекс полного сопротивления  всей цепи:
всей цепи:

и комплекс общего тока 

Так как  , то
, то

По комплексам токов можно найти их модули (действующие значения).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- ГЛАВА I. ЛИНЕЙНЫЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
- 1. ОДНОФАЗНЫЕ ЦЕПИ
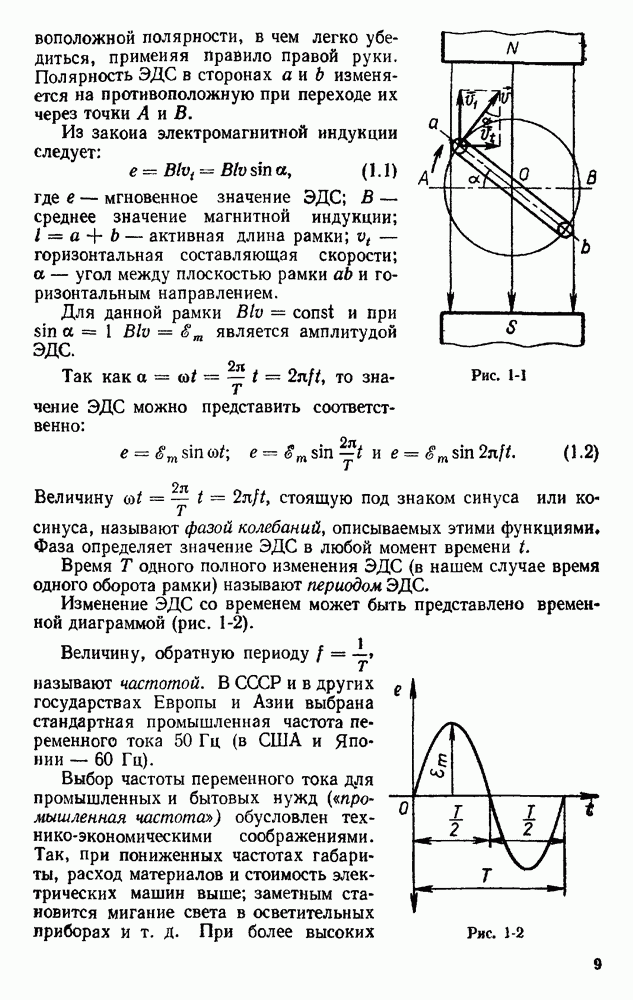
- § 1.2. ПРИНЦИП ПОЛУЧЕНИЯ ПЕРЕМЕННОЙ СИНУСОИДАЛЬНОЙ ЭДС
- § 1.3. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ ТОКА И НАПРЯЖЕНИЯ
- § 1.4. СРЕДНЕЕ ЗНАЧЕНИЕ ПЕРЕМЕННОГО ТОКА
- § 1.5. МЕТОД ВЕКТОРНЫХ ДИАГРАММ
- § 1.6. СОПРОТИВЛЕНИЯ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА
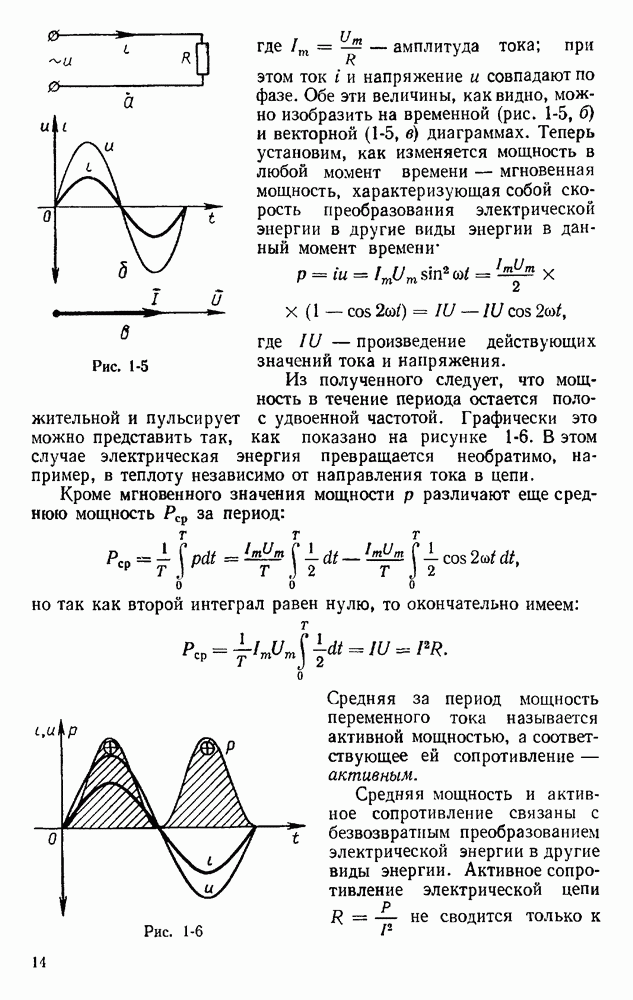
- § 1.7. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ СОПРОТИВЛЕНИЕМ
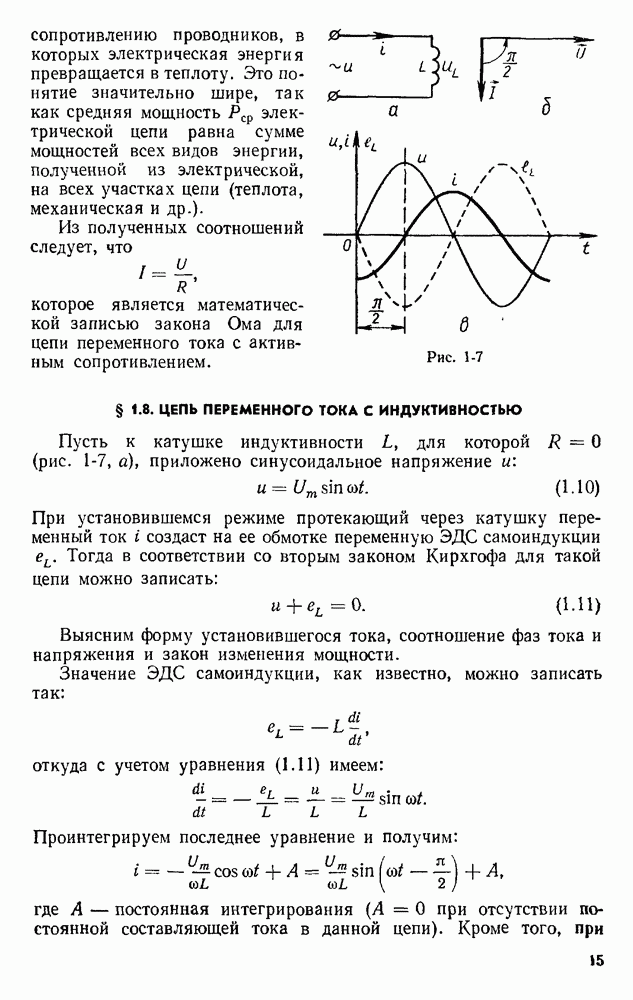
- § 1.8. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ИНДУКТИВНОСТЬЮ
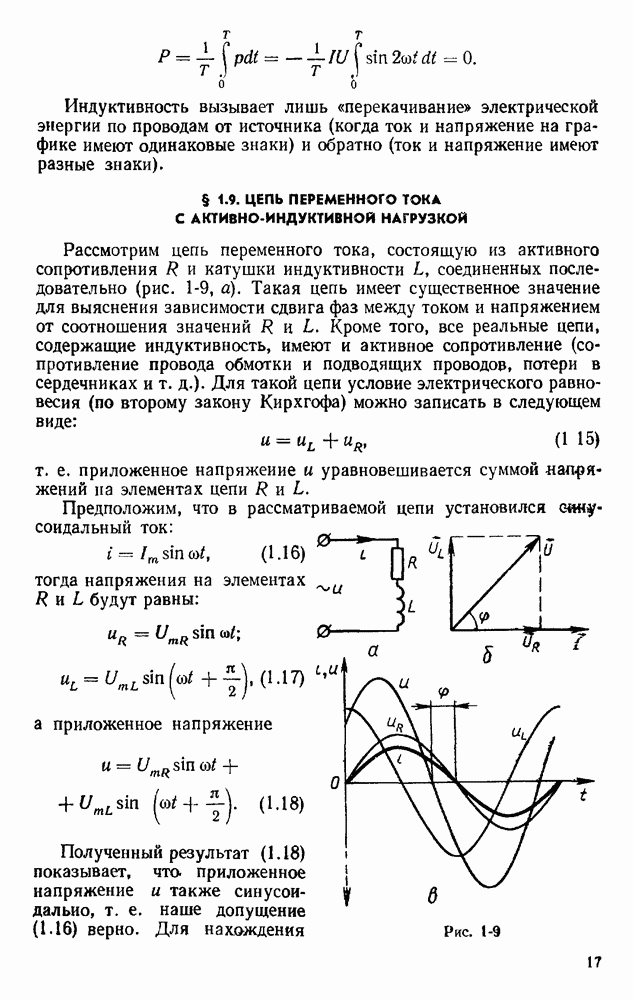
- § 1.9. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ИНДУКТИВНОЙ НАГРУЗКОЙ
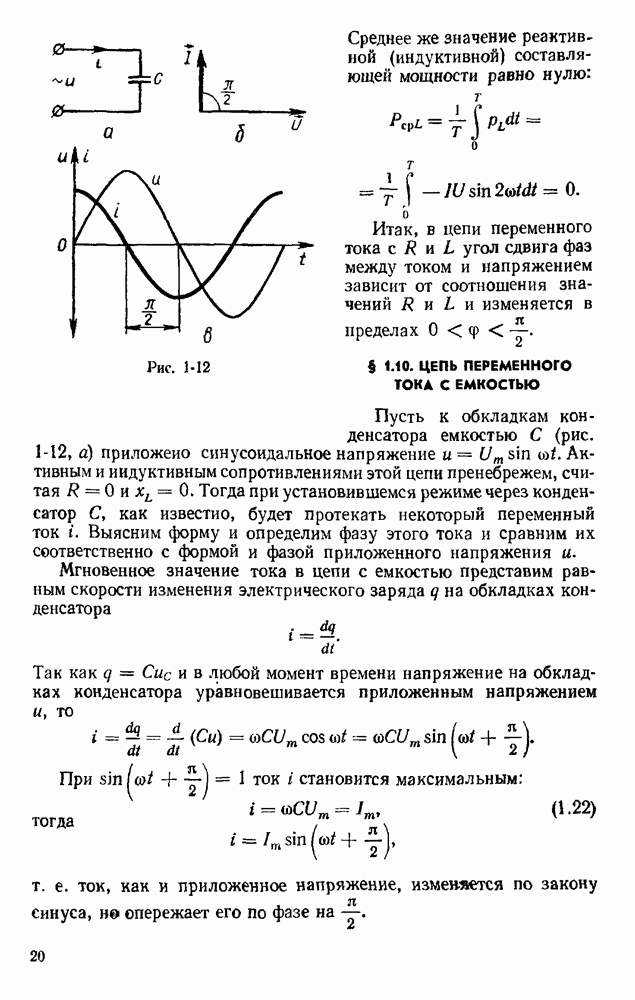
- § 1.10. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ЕМКОСТЬЮ
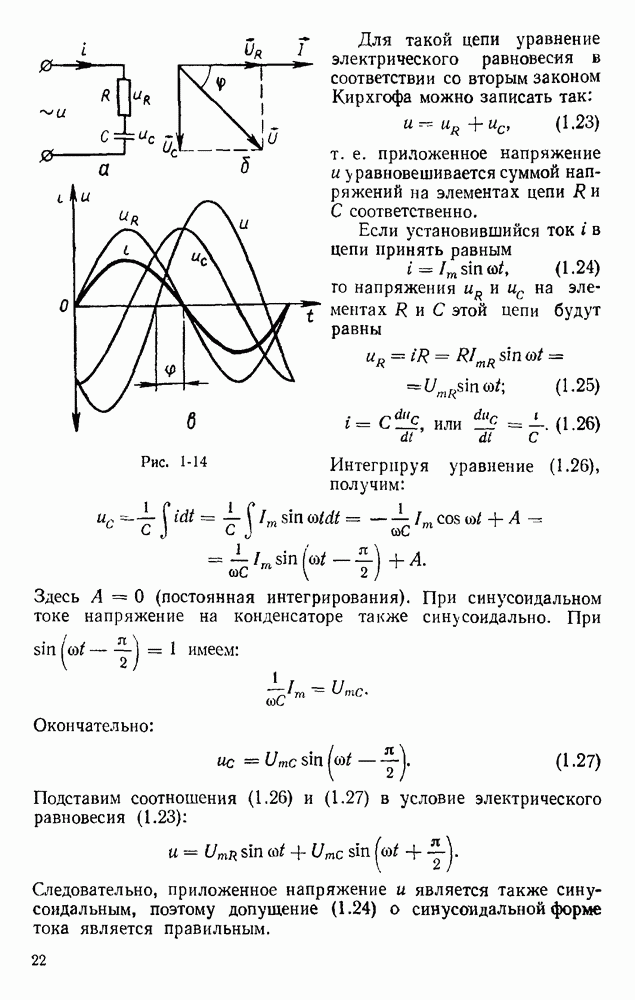
- § 1.11. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНО-ЕМКОСТНОЙ НАГРУЗКОЙ
- § 1.12. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L И С. КОЭФФИЦИЕНТ МОЩНОСТИ
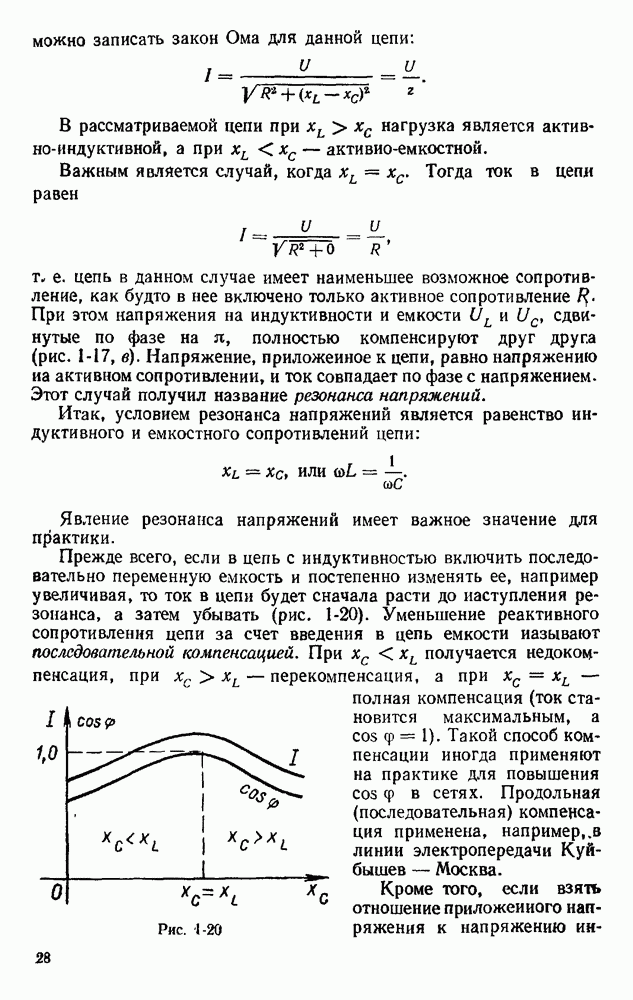
- § 1.13. РЕЗОНАНС НАПРЯЖЕНИЙ
- § 1.14. РЕЗОНАНС ТОКОВ
- § 1.15. СПОСОБЫ ПОВЫШЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 1.16. ПРОВОДИМОСТЬ И РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
- § 1.17. СИМВОЛИЧЕСКИЙ МЕТОД
- 2. ТРЕХФАЗНЫЕ ЦЕПИ
- § 1.19. ПРИНЦИП ПОСТРОЕНИЯ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 1.20. СОЕДИНЕНИЕ ЗВЕЗДОЙ
- § 1.21. СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ
- § 1.22. МОЩНОСТЬ ТРЕХФАЗНОЙ СИСТЕМЫ
- ГЛАВА II. ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ И ПРИБОРЫ
- § 2.3. ПОГРЕШНОСТИ ЭЛЕКТРИЧЕСКИХ ИЗМЕРЕНИЙ
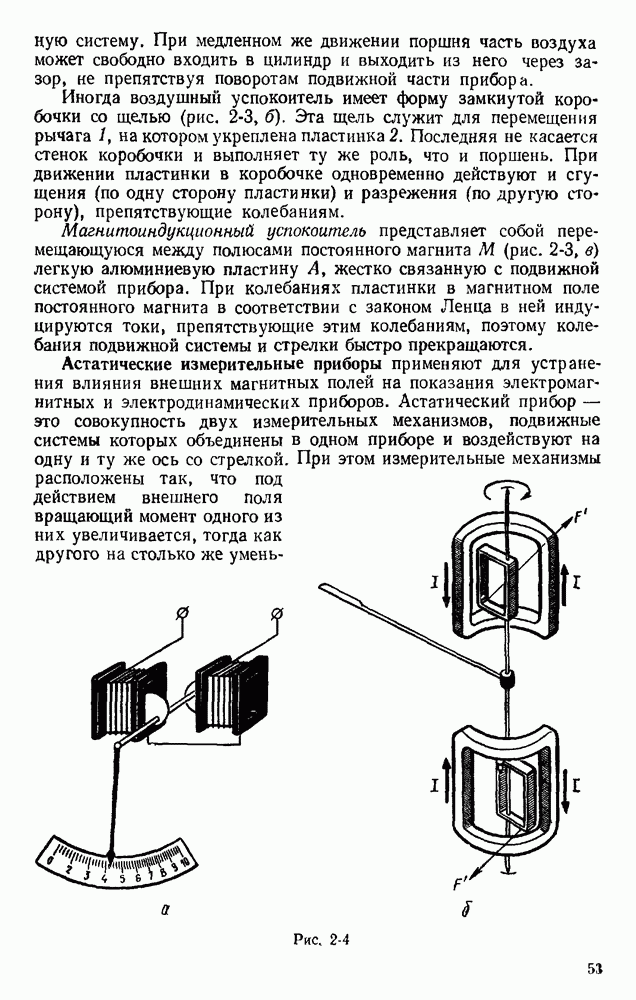
- § 2.4. ОСНОВНЫЕ ДЕТАЛИ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- § 2.5. МАГНИТОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.6. ЭЛЕКТРОМАГНИТНЫЕ ПРИБОРЫ
- § 2.7. ЭЛЕКТРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.8. ФЕРРОДИНАМИЧЕСКИЕ ПРИБОРЫ
- § 2.9. ЭЛЕКТРОДИНАМИЧЕСКИЕ ВАТТМЕТРЫ
- § 2.10. ОДНОФАЗНЫЙ ФАЗОМЕТР
- § 2.11. ОДНОФАЗНЫЙ ИНДУКЦИОННЫЙ СЧЕТЧИК ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ
- § 2.12. ОММЕТРЫ
- § 2.13. ЛОГОМЕТРЫ
- § 2.14. ТЕРМОЭЛЕКТРИЧЕСКИЕ ПРИБОРЫ
- § 2.15. ДЕТЕКТОРНЫЕ ПРИБОРЫ
- § 2.16. ШКОЛЬНЫЕ ДЕМОНСТРАЦИОННЫЕ ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ
- § 2.17. ПОНЯТИЕ О ЦИФРОВЫХ ИЗМЕРИТЕЛЬНЫХ ПРИБОРАХ
- § 2.18. ИЗМЕРЕНИЕ МОЩНОСТИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.19. ИЗМЕРЕНИЕ ЭНЕРГИИ ТРЕХФАЗНОЙ СИСТЕМЫ
- § 2.20. СПОСОБЫ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МОЩНОСТИ
- § 2.21. ПОНЯТИЕ ОБ ИЗМЕРЕНИЯХ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН ЭЛЕКТРИЧЕСКИМИ МЕТОДАМИ
- ГЛАВА III. ТРАНСФОРМАТОРЫ
- § 3.2. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ ТРАНСФОРМАТОРА
- § 3.3. ХОЛОСТОЙ РЕЖИМ РАБОТЫ ТРАНСФОРМАТОРА
- § 3.4. РАБОЧИЙ РЕЖИМ ТРАНСФОРМАТОРА
- § 3.5. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ТРАНСФОРМАТОРА
- § 3.6. ТРЕХФАЗНЫЕ ТРАНСФОРМАТОРЫ
- § 3.7. КОНСТРУКЦИИ ТРАНСФОРМАТОРОВ
- § 3.8. АВТОТРАНСФОРМАТОР
- § 3.9. ИЗМЕРИТЕЛЬНЫЕ ТРАНСФОРМАТОРЫ
- Глава IV. НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ВЫПРЯМИТЕЛИ
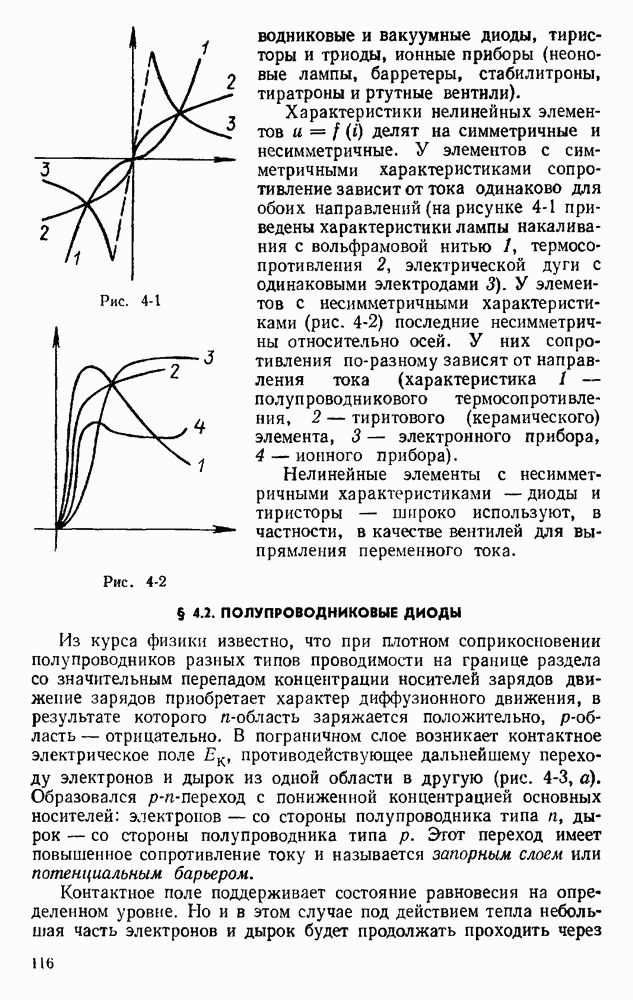
- 4.1. ХАРАКТЕРИСТИКИ НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ И ЭЛЕМЕНТОВ
- § 4.2. ПОЛУПРОВОДНИКОВЫЕ ДИОДЫ
- § 4.3. ТИРИСТОРЫ
- § 4.4. ОСНОВНЫЕ СХЕМЫ ВЫПРЯМЛЕНИЯ ПЕРЕМЕННОГО ТОКА
- § 4.5. ПРИМЕНЕНИЕ ТИРИСТОРОВ ДЛЯ ВЫПРЯМЛЕНИЯ И РЕГУЛИРОВАНИЯ ТОКА
- § 4.6. СГЛАЖИВАЮЩИЕ ФИЛЬТРЫ
- § 4.7. ПОНЯТИЕ ОБ ИНВЕРТОРАХ
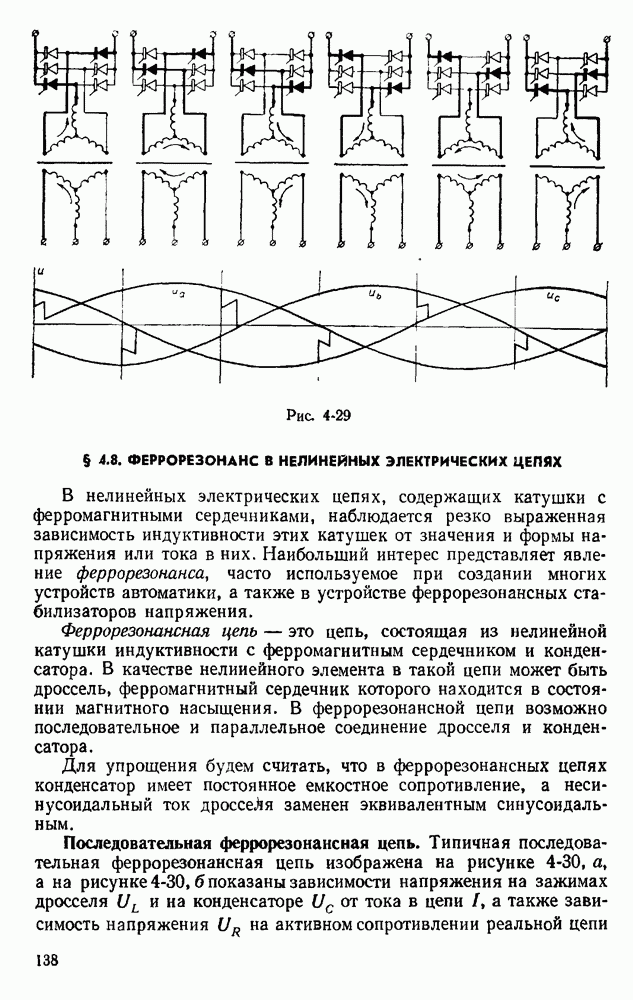
- § 4.8. ФЕРРОРЕЗОНАНС В НЕЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
- § 4.9. ФЕРРОРЕЗОНАНСНЫЙ СТАБИЛИЗАТОР НАПРЯЖЕНИЯ
- § 4.10. ШКОЛЬНЫЕ ВЫПРЯМИТЕЛИ
- ГЛАВА V. МАШИНЫ ПЕРЕМЕННОГО ТОКА
- § 5.1. КЛАССИФИКАЦИЯ МАШИН ПЕРЕМЕННОГО ТОКА
- § 5.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.3. СОЗДАНИЕ ВРАЩАЮЩЕГОСЯ МАГНИТНОГО ПОЛЯ ТРЕХФАЗНОЙ СИСТЕМОЙ
- § 5.4. СКОРОСТЬ ВРАЩЕНИЯ МАГНИТНОГО ПОЛЯ. ТИПЫ ОБМОТОК СТАТОРА
- § 5.5. СКОЛЬЖЕНИЕ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 1.6. МАГНИТНЫЙ ПОТОК ЭДС И ТОКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.7. ВЕКТОРНАЯ ДИАГРАММА АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.8. АСИНХРОННЫЙ ДВИГАТЕЛЬ С КОНТАКТНЫМИ КОЛЬЦАМИ
- § 5.9. РАБОЧИЕ ХАРАКТЕРИСТИКИ АСИНХРОННОГО ДВИГАТЕЛЯ
- § 5.10. ПУСК В ХОД АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.11. РЕВЕРСИРОВАНИЕ И РЕГУЛИРОВАНИЕ СКОРОСТИ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.12. ОДНОФАЗНЫЕ АСИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.13. ПРИМЕНЕНИЕ ТРЕХФАЗНЫХ АСИНХРОННЫХ ДВИГАТЕЛЕЙ
- § 5.14. УСТРОЙСТВО И ПРИНЦИП РАБОТЫ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.15. ЭДС СИНХРОННОГО ГЕНЕРАТОРА
- § 5.16. РЕАКЦИЯ ЯКОРЯ
- § 5.17. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СИНХРОННОГО ГЕНЕРАТОРА
- § 5.18. УПРОЩЕННАЯ ВЕКТОРНАЯ ДИАГРАММА СИНХРОННОГО ГЕНЕРАТОРА
- § 5.19. РАБОТА СИНХРОННОГО ГЕНЕРАТОРА ПАРАЛЛЕЛЬНО С СЕТЬЮ
- § 5.20. ОБРАТИМОСТЬ СИНХРОННЫХ МАШИН. ПРИНЦИП РАБОТЫ СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.21. ПУСК И ОСТАНОВКА СИНХРОННОГО ДВИГАТЕЛЯ
- § 5.22. ВЛИЯНИЕ ТОКА ВОЗБУЖДЕНИЯ НА РАБОТУ СИНХРОННОГО ДВИГАТЕЛЯ. СИНХРОННЫЙ КОМПЕНСАТОР
- § 5.23. РЕАКТИВНЫЕ СИНХРОННЫЕ ДВИГАТЕЛИ
- § 5.24. ПРИМЕНЕНИЕ СИНХРОННЫХ ДВИГАТЕЛЕЙ
- ГЛАВА VI. МАШИНЫ ПОСТОЯННОГО ТОКА
- § 6.2. ПРИНЦИП РАБОТЫ И УСТРОЙСТВО ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА. ТИПЫ ОБМОТОК ЯКОРЯ
- § 6.3. ЭДС И ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ ГЕНЕРАТОРА ПОСТОЯННОГО ТОКА
- § 6.4. РЕАКЦИЯ ЯКОРЯ
- § 6.5. КОММУТАЦИЯ
- § 6.6. СПОСОБЫ ВОЗБУЖДЕНИЯ ГЕНЕРАТОРОВ ПОСТОЯННОГО ТОКА
- § 6.7. ОБРАТИМОСТЬ МАШИН ПОСТОЯННОГО ТОКА. ДВИГАТЕЛИ
- § 6.8. ДВИГАТЕЛЬ ПАРАЛЛЕЛЬНОГО И НЕЗАВИСИМОГО ВОЗБУЖДЕНИЯ
- § 6.9. ДВИГАТЕЛЬ ПОСЛЕДОВАТЕЛЬНОГО ВОЗБУЖДЕНИЯ
- § 6.10. ДВИГАТЕЛЬ СМЕШАННОГО ВОЗБУЖДЕНИЯ
- § 6.11. КОЛЛЕКТОРНЫЕ ДВИГАТЕЛИ ПЕРЕМЕННОГО ТОКА
- ГЛАВА VII. ЭЛЕМЕНТЫ АВТОМАТИКИ
- § 7.2. РЕЛЕ
- § 7.3. ДАТЧИКИ
- § 7.4. АВТОМАТИЧЕСКИЙ КОНТРОЛЬ
- § 7.5. АВТОМАТИЧЕСКОЕ УПРАВЛЕНИЕ
- § 7.6. АВТОМАТИЧЕСКОЕ РЕГУЛИРОВАНИЕ
- § 7.7. ТЕЛЕМЕХАНИКА
- § 7.8. КОМПЛЕКСНАЯ АВТОМАТИЗАЦИЯ
- ГЛАВА VIII. ПРОИЗВОДСТВО, ПЕРЕДАЧА И ИСПОЛЬЗОВАНИЕ ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ В НАРОДНОМ ХОЗЯЙСТВЕ
- § 8.1. ЭЛЕКТРИЧЕСКИЕ СТАНЦИИ
- § 8.2. ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ
- § 8.3. ПЕРЕДАЧА ЭЛЕКТРИЧЕСКОЙ ЭНЕРГИИ ПОСТОЯННЫМ ТОКОМ
- § 8.4. АВТОМАТИЗАЦИЯ ЭЛЕКТРИЧЕСКИХ СТАНЦИЙ И ПОДСТАНЦИЙ
- ГЛАВА IX. СОВРЕМЕННЫЕ ТЕНДЕНЦИИ РАЗВИТИЯ ЭЛЕКТРОЭНЕРГЕТИКИ
- ГЛАВА X. ЭЛЕМЕНТЫ ТЕХНИКИ БЕЗОПАСНОСТИ
- § 10.1. ОПАСНОСТЬ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ ДЛЯ ОРГАНИЗМА ЧЕЛОВЕКА
- § 10.2. ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ ТЕЛА ЧЕЛОВЕКА
- § 10.3. ОСНОВНЫЕ ПРИЧИНЫ ПОРАЖЕНИЯ ЭЛЕКТРИЧЕСКИМ ТОКОМ
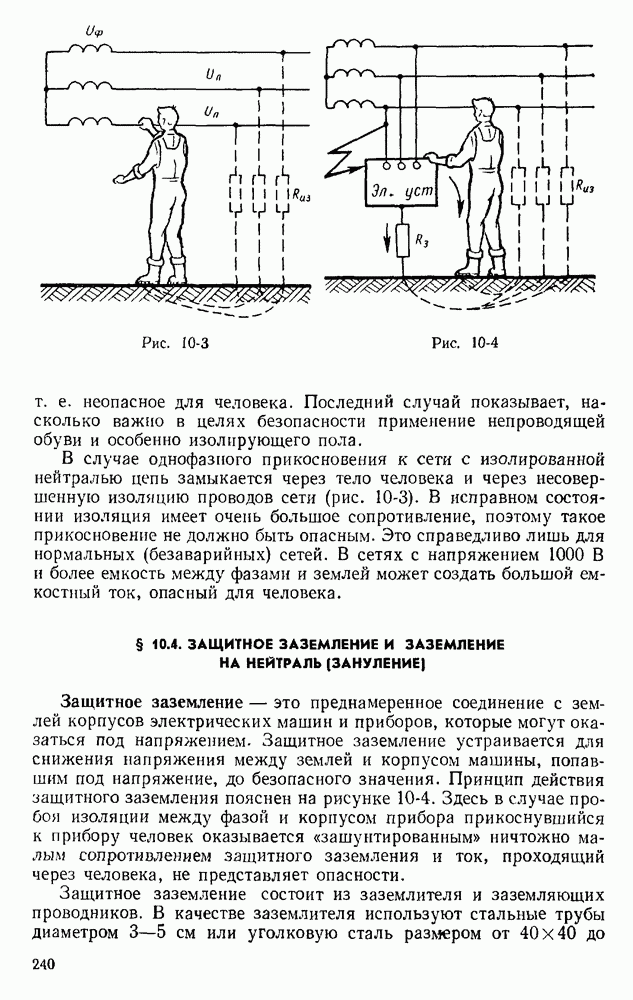
- § 10.4. ЗАЩИТНОЕ ЗАЗЕМЛЕНИЕ И ЗАЗЕМЛЕНИЕ НА НЕЙТРАЛЬ (ЗАНУЛЕНИЕ)
- § 10.5. ЗАЩИТНЫЕ СРЕДСТВА И КОНТРОЛЬ СОСТОЯНИЯ ИЗОЛЯЦИИ ЭЛЕКТРОУСТАНОВОК
- § 10.6. ОКАЗАНИЕ ПЕРВОЙ ПОМОЩИ ПОРАЖЕННОМУ ЭЛЕКТРИЧЕСКИМ ТОКОМ
- § 10.7. ОСНОВНЫЕ ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ В УЧЕБНЫХ ЛАБОРАТОРИЯХ
- ЛИТЕРАТУРА