| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
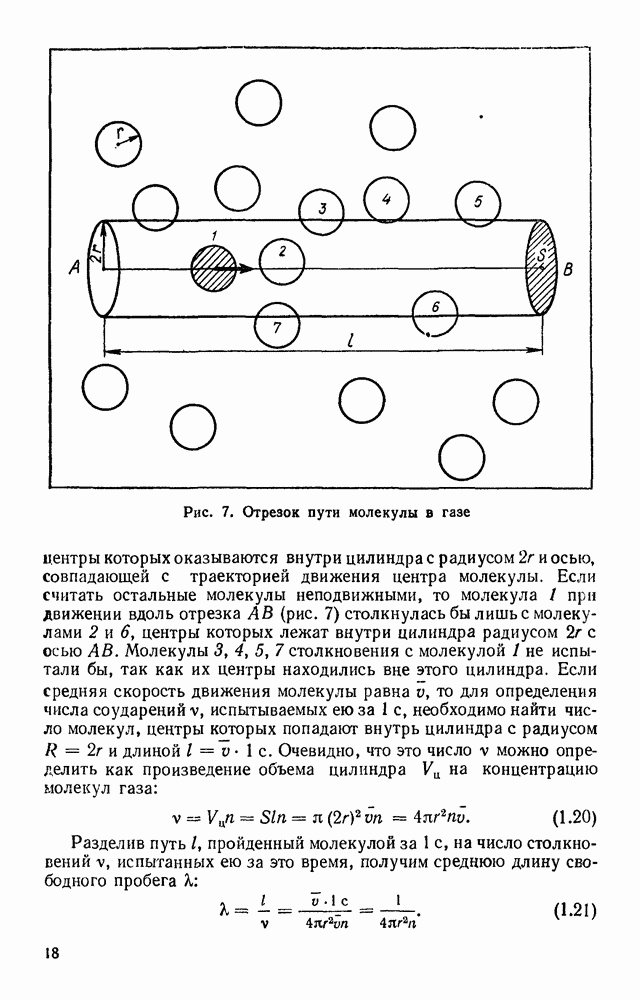
Диффузия в газах. Покажем теперь, что если молекула газа при каждом столкновении изменяет направление движения совершенно случайным образом, то среднее расстояние  на которое удалится молекула от первоначального своего местонахождения за время
на которое удалится молекула от первоначального своего местонахождения за время  можно определить, если известны средняя длина ее свободного пробега К и средняя частота столкновений
можно определить, если известны средняя длина ее свободного пробега К и средняя частота столкновений 
Кажется правдоподобным предположение, что результатом хаотического блуждания каждой молекулы должно быть «топтание» ее вблизи одного и того же места, сколько бы времени ни прошло.
Однако простые наблюдения за процессами диффузии заставляют отказаться от этого предположения. В комнате, где только что выкрашены полы или стены, запах краски ощущается в любой точке пространства комнаты и даже за ее пределами, а не только вблизи окрашенных поверхностей. Значит, молекулы растворителя, испарившись с окрашенной поверхности, не «толкутся» вблизи места своего освобождения, а удаляются от него на большие расстояния.
Попытаемся найти математическое выражение зависимости от времени  среднего расстояния
среднего расстояния  на которое удаляется молекула от первоначального положения.
на которое удаляется молекула от первоначального положения.
Для упрощения вывода будем считать, что движение молекулы происходит в плоскости  Это предположение не изменяет ни способа, ни строгости вывода.
Это предположение не изменяет ни способа, ни строгости вывода.
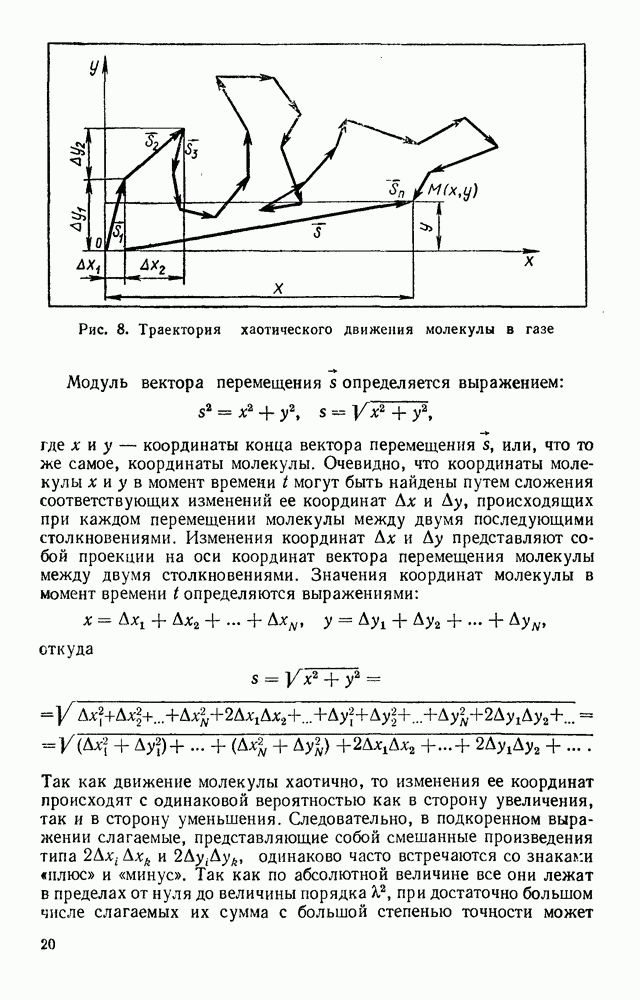
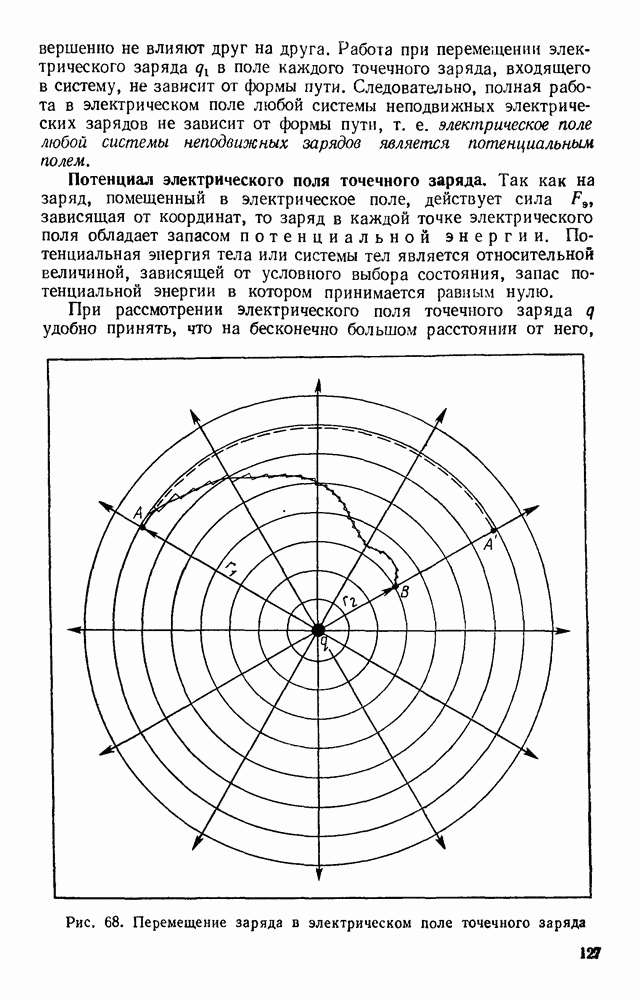
Пусть в начальный момент времени  молекула находилась в точке О, которую примем за начало координат. Через время
молекула находилась в точке О, которую примем за начало координат. Через время  достаточно большое по сравнению со средним временем между двумя последующими столкновениями, она окажется в некоторой точке М с координатами
достаточно большое по сравнению со средним временем между двумя последующими столкновениями, она окажется в некоторой точке М с координатами  (рис. 8). Вектор перемещения
(рис. 8). Вектор перемещения  является результатом сложения векторов
является результатом сложения векторов  каждый из которых представляет собой вектор перемещения молекулы между двумя последующими столкновениями.
каждый из которых представляет собой вектор перемещения молекулы между двумя последующими столкновениями.

Рис. 8. Траектория хаотического движения молекулы в газе
Модуль вектора перемещения  определяется выражением:
определяется выражением:

где х и у — координаты конца вектора перемещения  или, что то же самое, координаты молекулы. Очевидно, что координаты молекулы х и у в момент времени
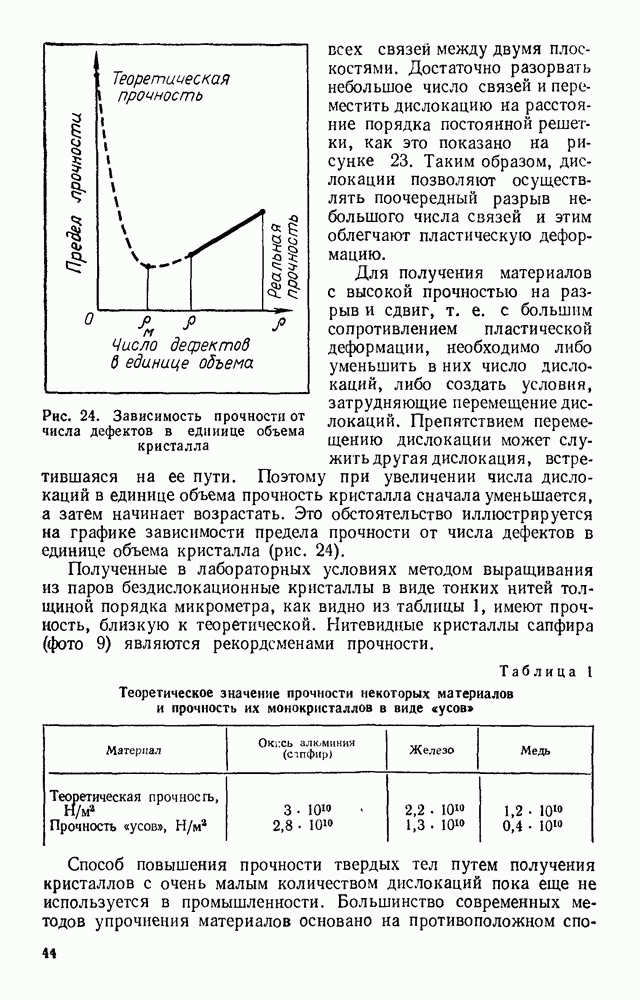
или, что то же самое, координаты молекулы. Очевидно, что координаты молекулы х и у в момент времени  могут быть найдены путем сложения соответствующих изменений ее координат
могут быть найдены путем сложения соответствующих изменений ее координат  происходящих при каждом перемещении молекулы между двумя последующими столкновениями. Изменения координат
происходящих при каждом перемещении молекулы между двумя последующими столкновениями. Изменения координат  представляют собой проекции на оси координат вектора перемещения молекулы между двумя столкновениями. Значения координат молекулы в момент времени
представляют собой проекции на оси координат вектора перемещения молекулы между двумя столкновениями. Значения координат молекулы в момент времени  определяются выражениями:
определяются выражениями:

откуда

Так как движение молекулы хаотично, то изменения ее координат происходят с одинаковой вероятностью как в сторону увеличения, так и в сторону уменьшения. Следовательно, в подкоренном выражении слагаемые, представляющие собой смешанные произведения типа  одинаково часто встречаются со знаками «плюс» и «минус». Так как по абсолютной величине все они лежат в пределах от нуля до величины порядка
одинаково часто встречаются со знаками «плюс» и «минус». Так как по абсолютной величине все они лежат в пределах от нуля до величины порядка  при достаточно большом числе слагаемых их сумма с большой степенью точности может
при достаточно большом числе слагаемых их сумма с большой степенью точности может
считаться равной нулю. Сумма остальных слагаемых может быть представлена как сумма N квадратов перемещений молекулы, которая равна по определению произведению числа N на квадрат средней длины свободного пробега  :
:

Таким образом, мы получили, что модуль перемещения молекулы  за время
за время  пропорционален корню квадратному из числа столкновений N, испытанных ею за это время, и средней длине свободного пробега X. Отсюда связь между модулем перемещения
пропорционален корню квадратному из числа столкновений N, испытанных ею за это время, и средней длине свободного пробега X. Отсюда связь между модулем перемещения  временем
временем  и средней скоростью молекул
и средней скоростью молекул  определяется выражением:
определяется выражением:

Полученное соотношение открывает возможность определения средней длины свободного пробега газовых молекул К по экспериментальным данным о среднем значении перемещения  молекул газа путем диффузии за известное время
молекул газа путем диффузии за известное время  и вычисленной средней скорости их движения и.
и вычисленной средней скорости их движения и.
Скорость диффузии. Интересно сравнить скорость диффузионного распространения молекул газа со средней скоростью их теплового движения.
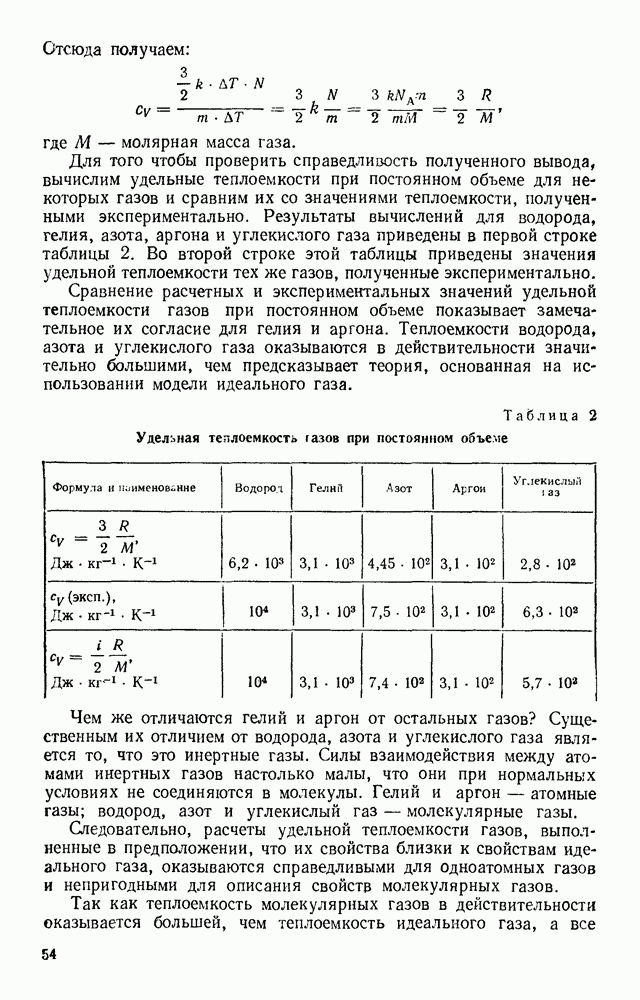
Выполним расчет для воздуха при нормальном атмосферном давлении и температуре 20 °С. Средняя скорость теплового движения молекул газов воздуха при этих условиях составляет примерно 500 м/с, средний свободный пробег их около  тогда среднее значение модуля перемещения
тогда среднее значение модуля перемещения  молекулы за одну секунду равно:
молекулы за одну секунду равно:

При нормальных условиях молекула газа пробегает за одну секунду путь около 0,5 км, но из-за хаотических изменений направления движения в результате большого числа столкновений с другими молекулами смещается от своего первоначального положения в среднем всего на 0,5 см!
Здесь следует обратить внимание на то, что процесс диффузии газовых молекул нельзя охарактеризовать понятием средней скорости диффузии, как это хотелось бы сделать. Объясняется это тем, что модуль среднего перемещения  молекулы пропорционален времени не в первой степени, а в степени
молекулы пропорционален времени не в первой степени, а в степени  . Следовательно, скорость диффузии является не постоянной величиной, а убывает с увеличением интервала времени.
. Следовательно, скорость диффузии является не постоянной величиной, а убывает с увеличением интервала времени.
Законы броуновского движения. Броуновское движение частиц обнаруживает большое сходство с диффузионным движением молекул и атомов.
Беспорядочное движение мелких твердых частиц, находящихся в жидкости или газе, впервые обнаружил в 1827 г. при наблюдении в микроскоп английский ботаник Б роун. Это явление смогла объяснить лишь молекулярно-кинетическая теория на основе использования представлений о существовании молекул. Молекулы жидкости или газа сталкиваются с тсердой частицей и изменяют направление и модуль скорости ее движения. Число молекул, ударяющих частицу с различных сторон, и направление передаваемого ими импульса непостоянны во времени. Чем меньше размеры и масса частицы, тем более заметными становятся изменения ее импульса во времени.
Сам факт обнаружения броуновского движения часто называют доказательством справедливости молекулярно-кинетической теории. Однако более точным будет утверждение, что факт существования броуновского движения свидетельствует о молекулярном строении вещества и движении молекул.
Действительно, решающими экспериментами были опыты французского физика Жана Перрена по изучению количественных закономерностей броуновского движения, выполненные в 1908— 1911 гг.
Эти опыты были поставлены после того, как А. Эйнштейн в 1905 г., используя молекулярно-кинетическую теорию, разработал теорию броуновского движения. А. Эйнштейн доказал, что хаотическое движение броуновской частицы должно подчиняться закону:

где  — средний квадрат смещения броуновской частицы за время
— средний квадрат смещения броуновской частицы за время  — температура,
— температура,  — число Авогадро,
— число Авогадро,  — постоянная, зависящая от формы и размеров броуновской частицы и свойств жидкости.
— постоянная, зависящая от формы и размеров броуновской частицы и свойств жидкости.
Опыты Перрена показали, что закономерности броуновского движения, предсказанные молекулярно-кинетической теорией, полностью подтверждаются экспериментом, т. е. средний квадрат смещения броуновской частицы прямо пропорционален абсолютной температуре газа или жидкости и первой степени интервала времени, за которое происходит смещение. Это совпадение результатов теории и эксперимента является одним из решающих доказательств справедливости основных положений молекулярно-кинетической теории.
| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
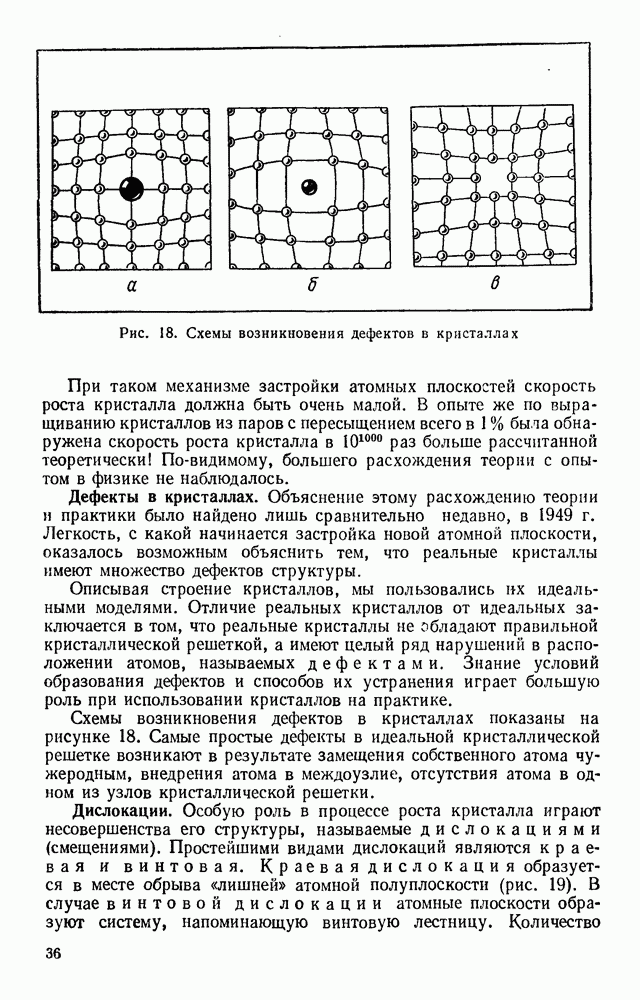
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
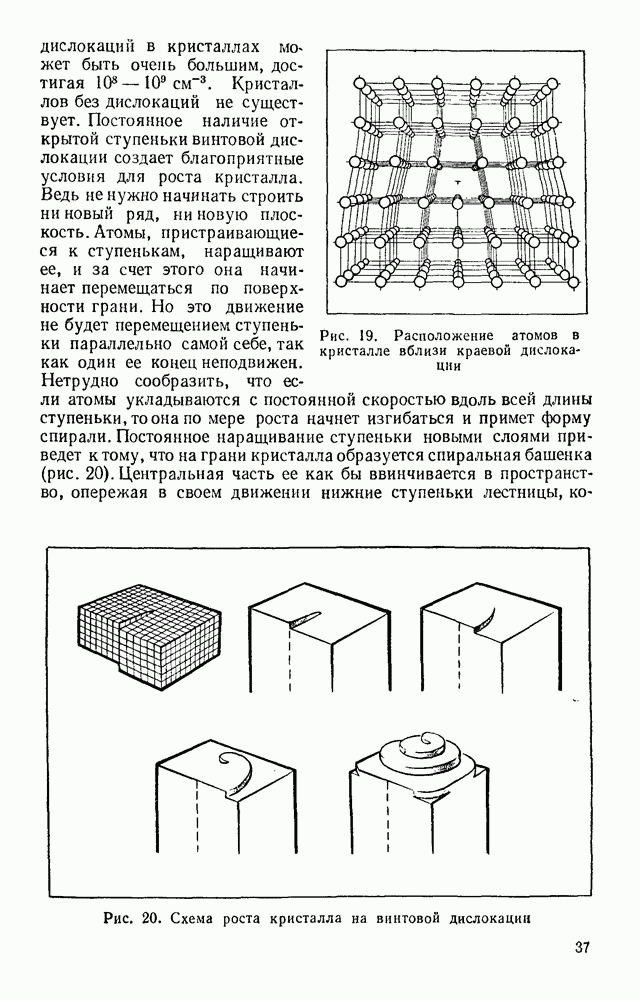
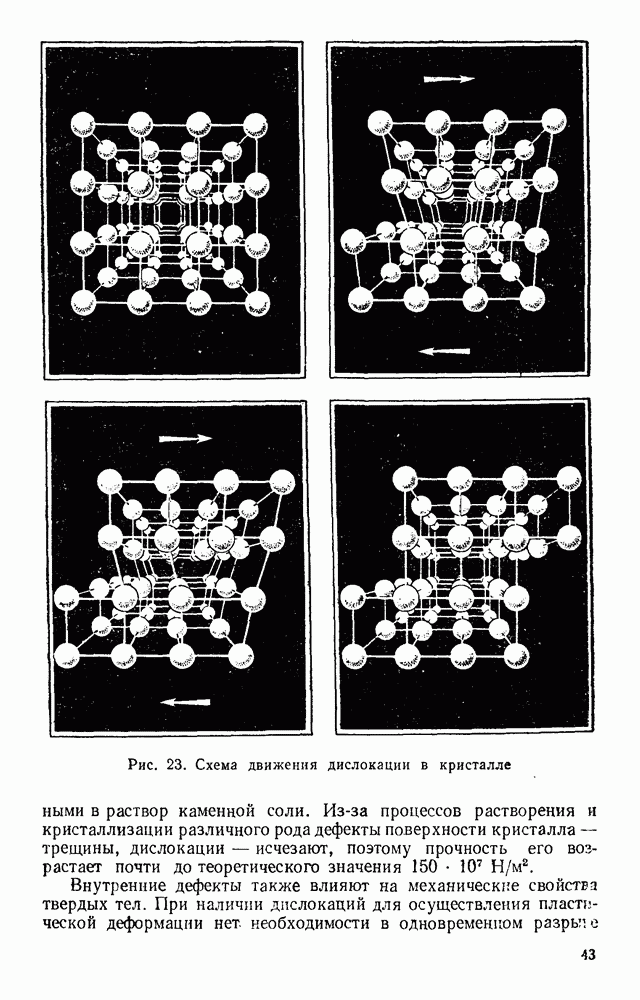
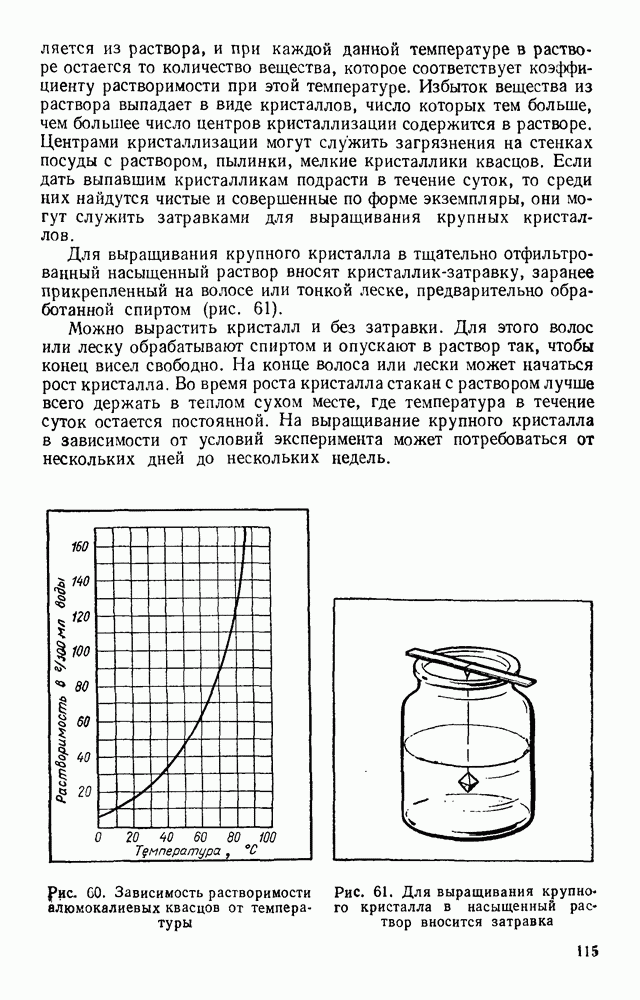
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
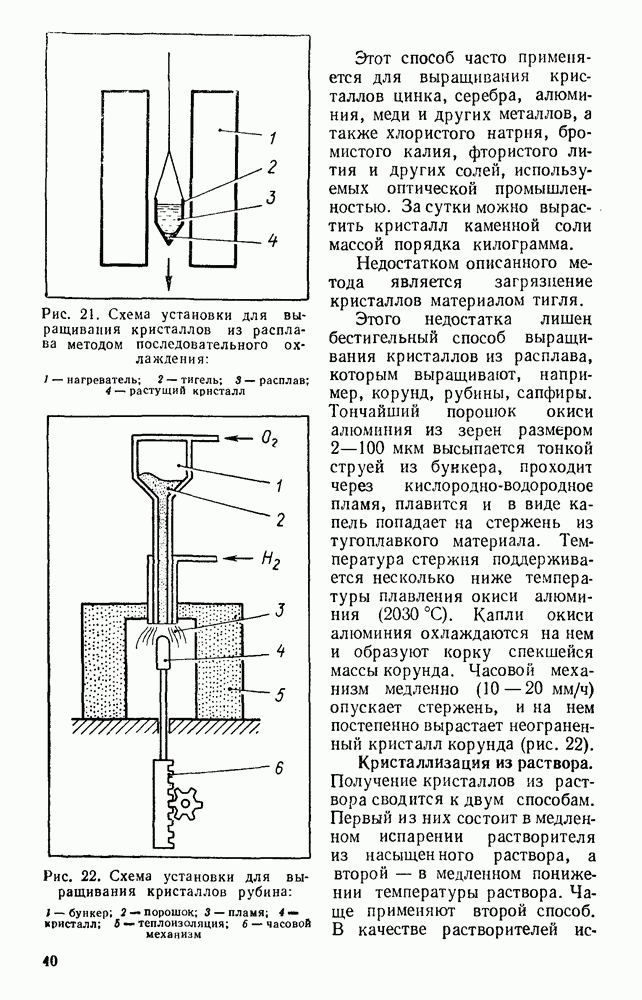
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
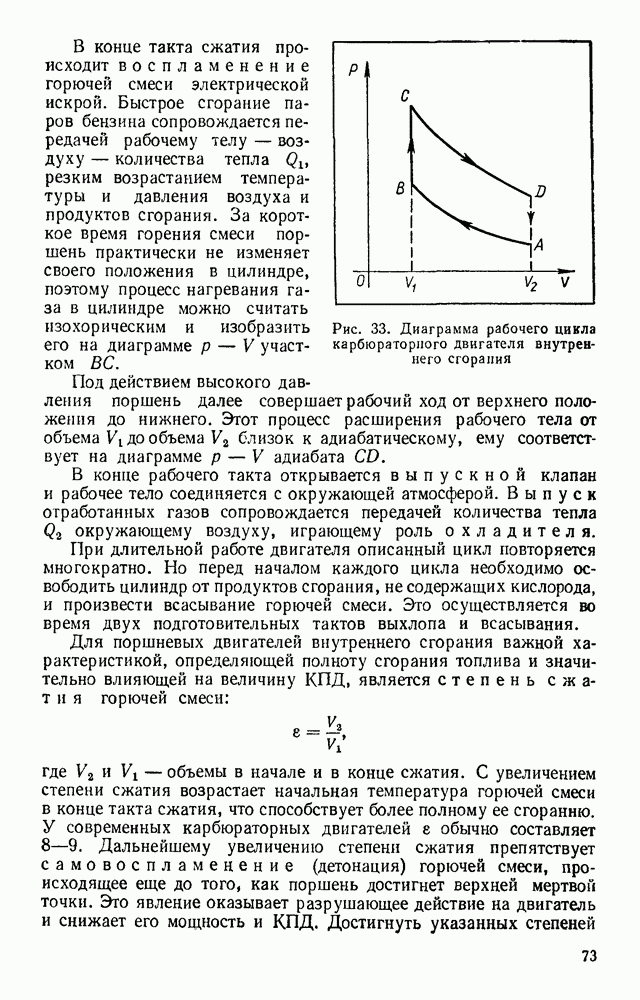
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
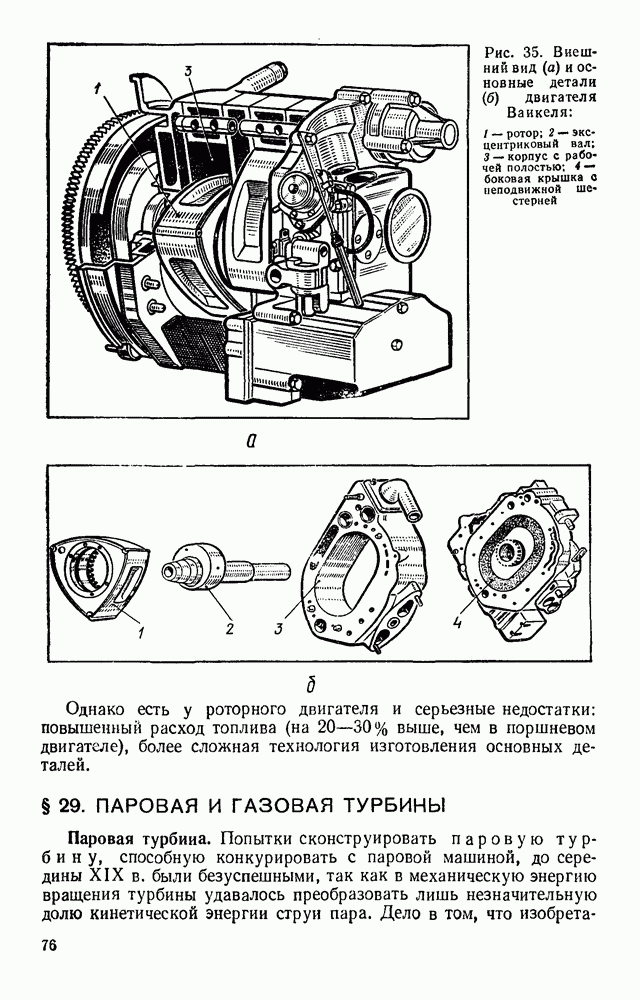
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
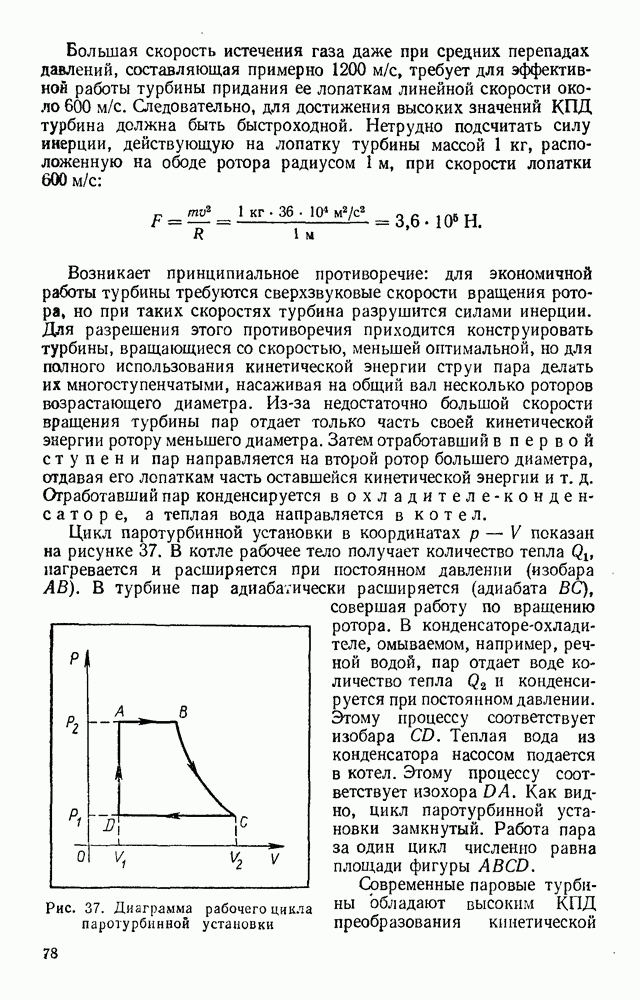
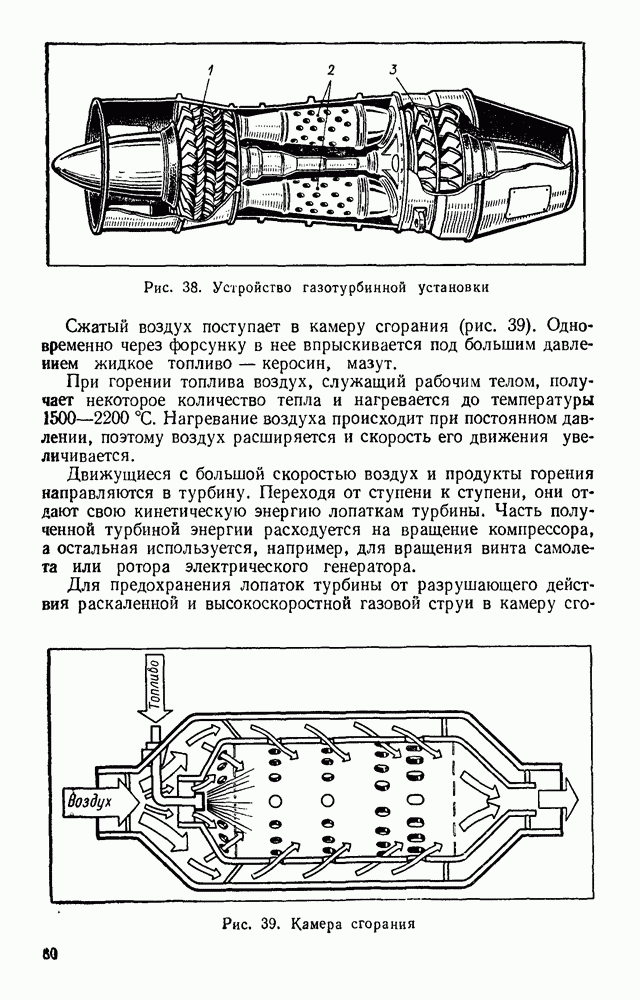
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
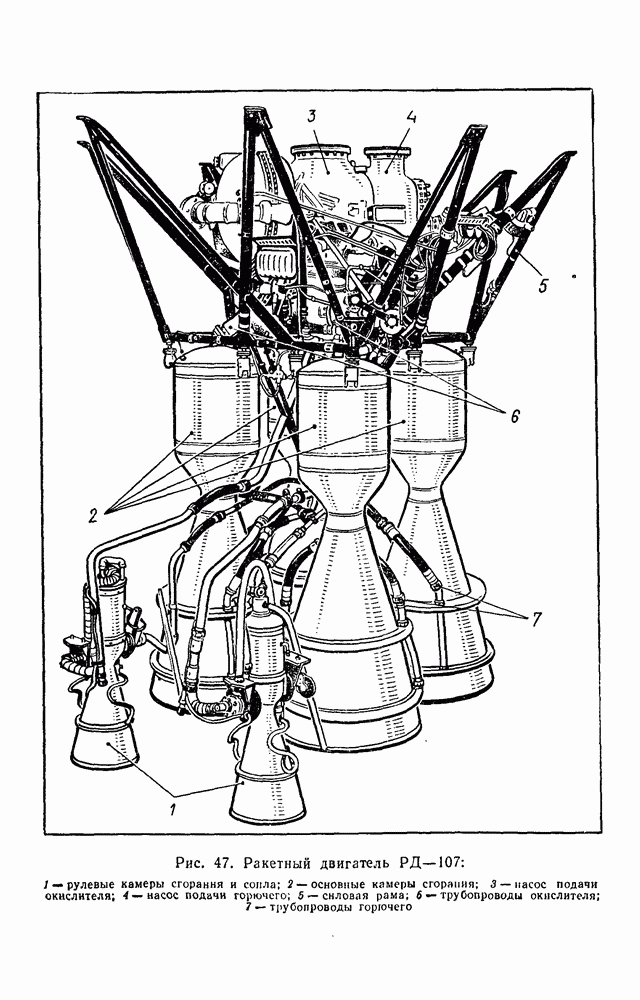
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
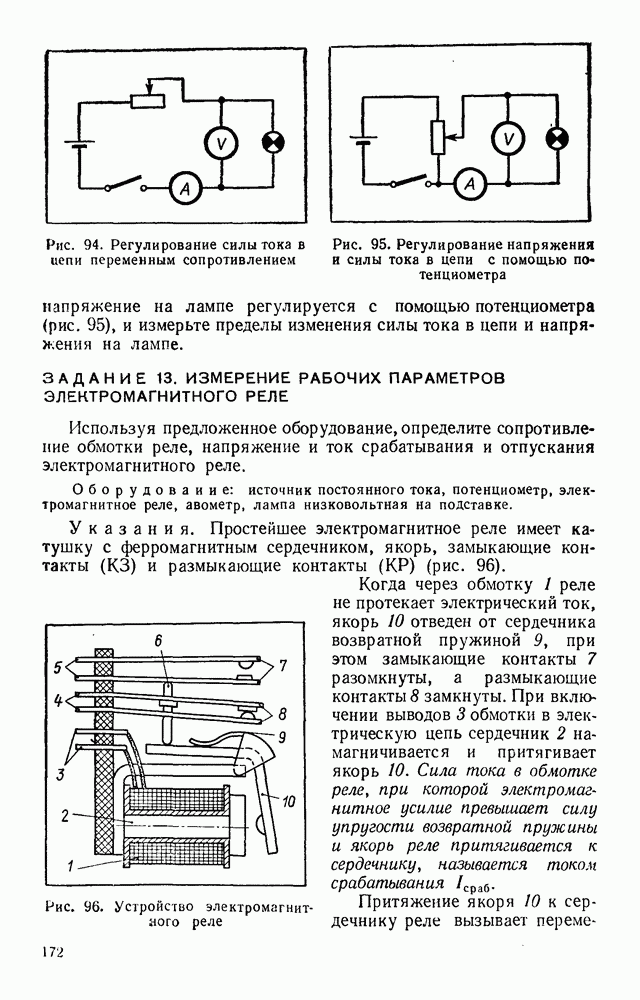
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
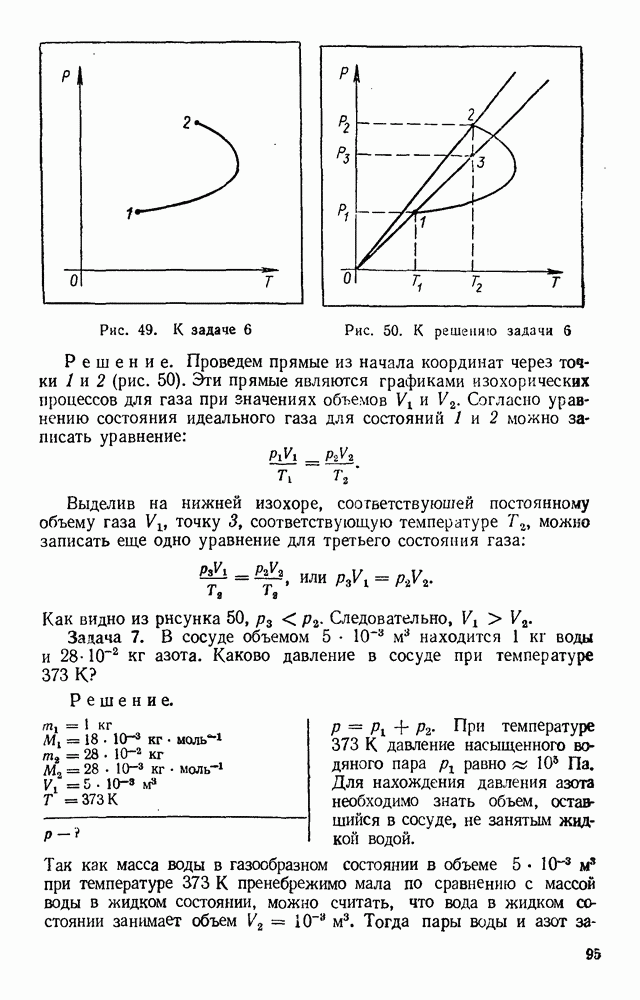
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
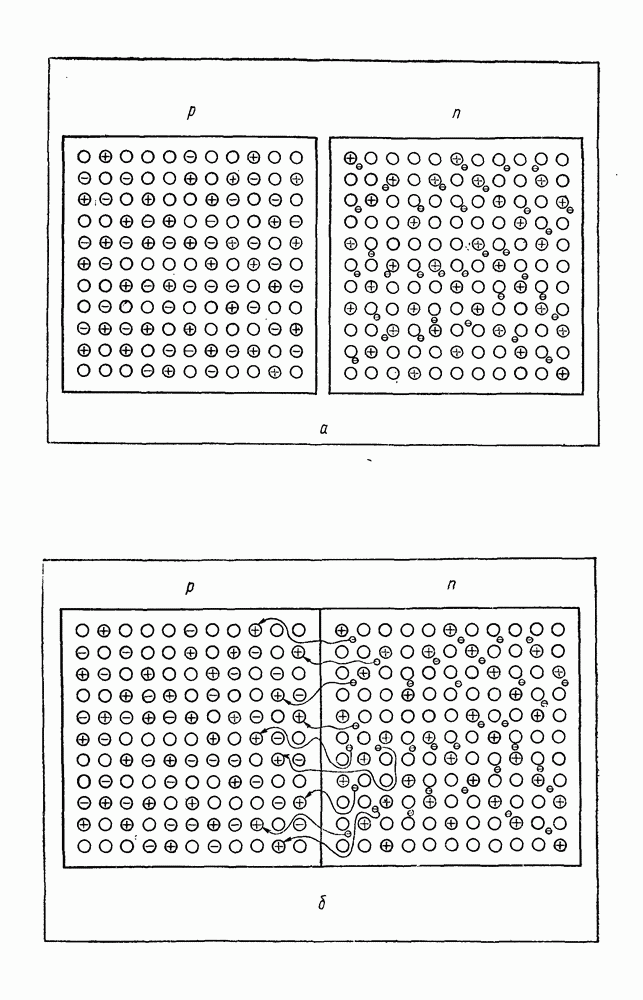
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
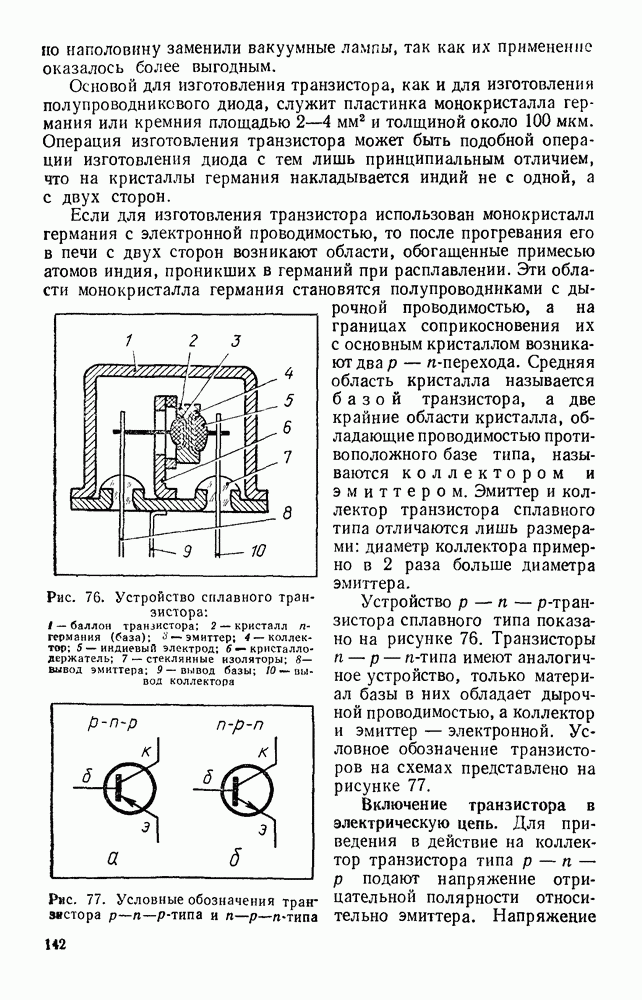
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
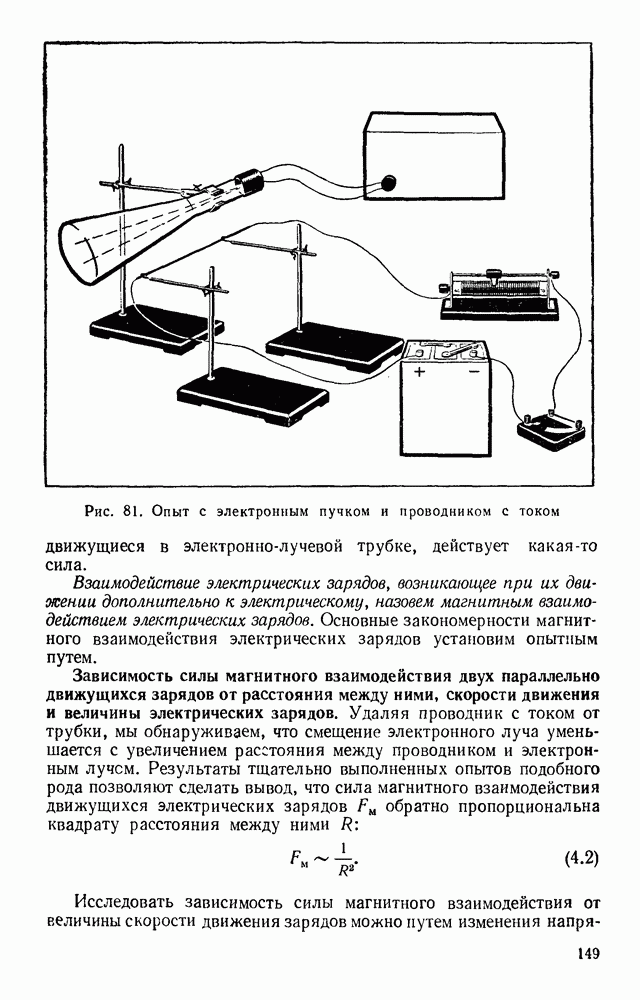
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
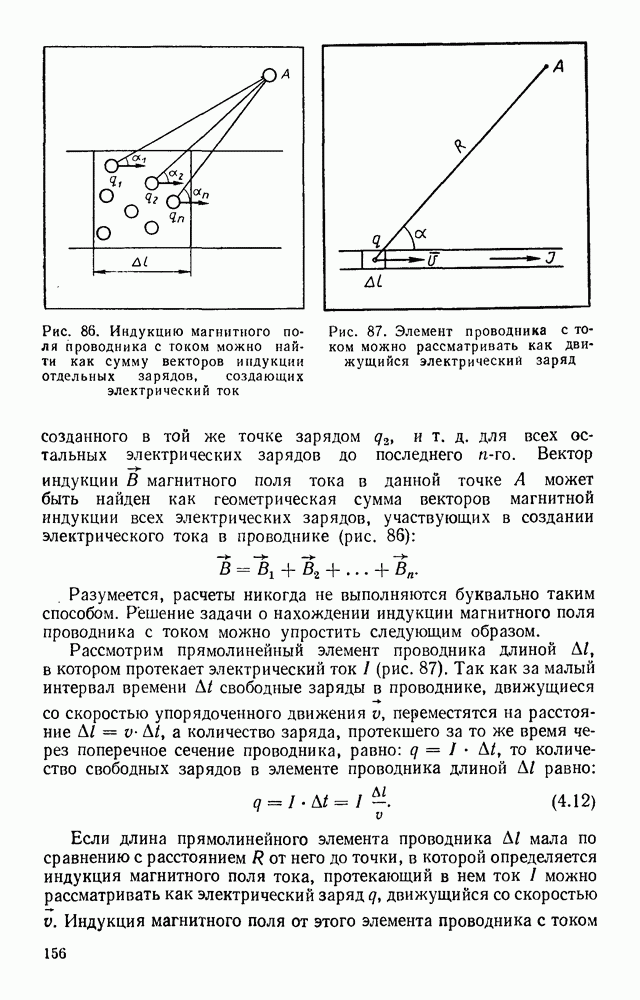
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
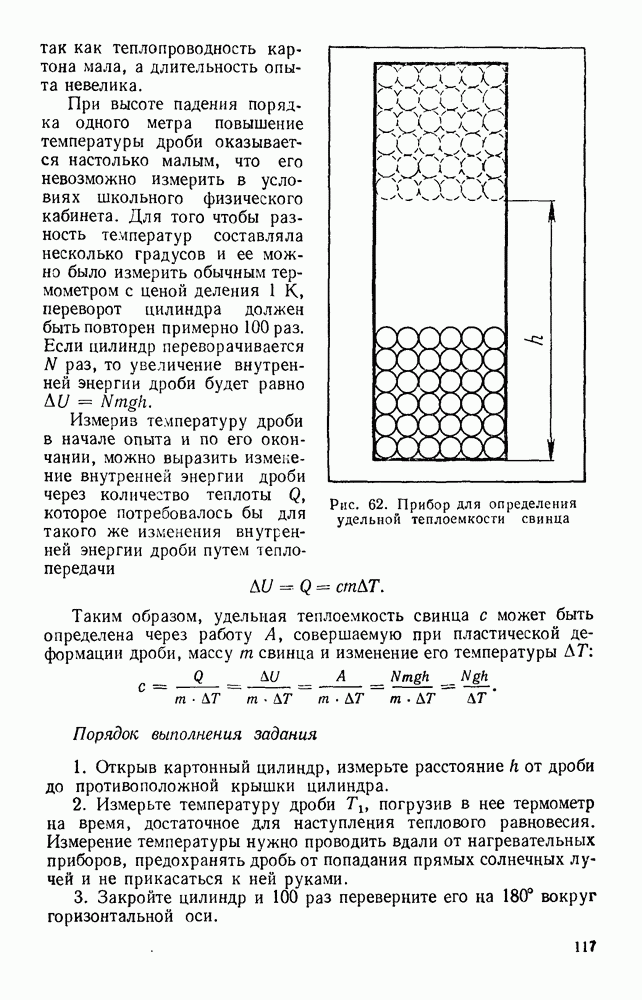
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
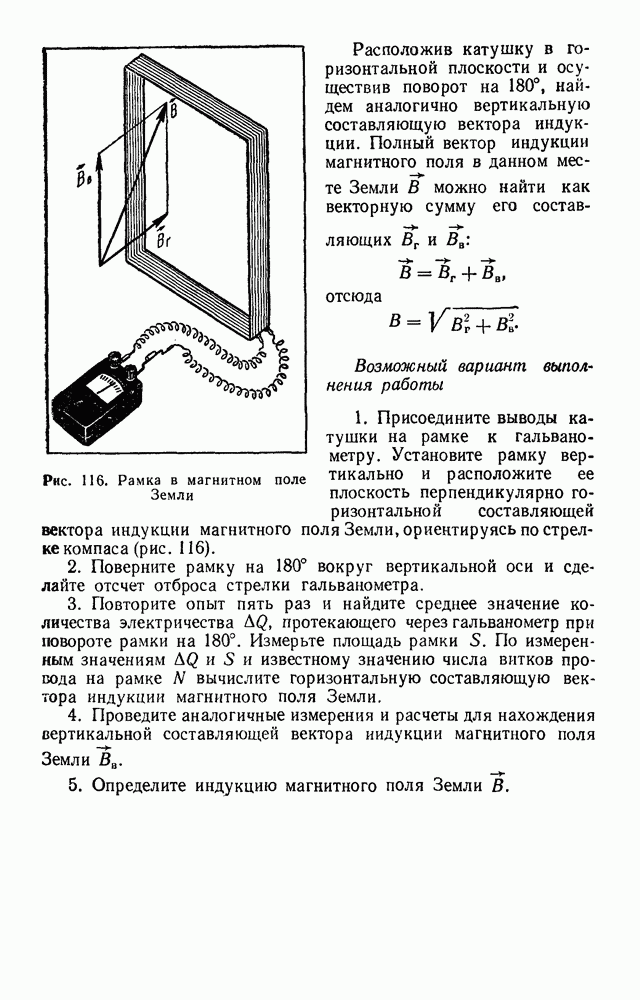
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ