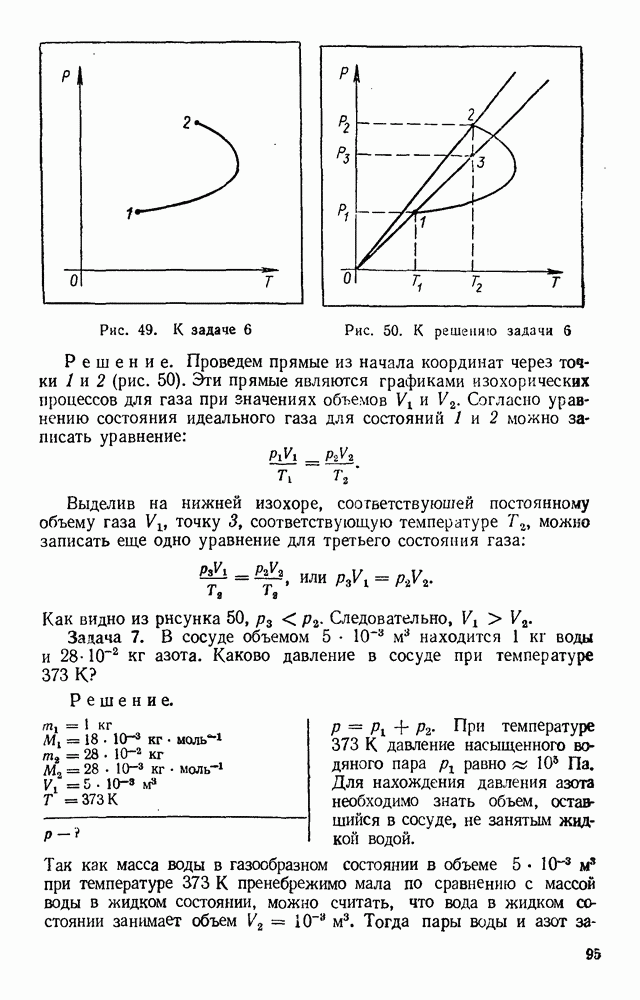
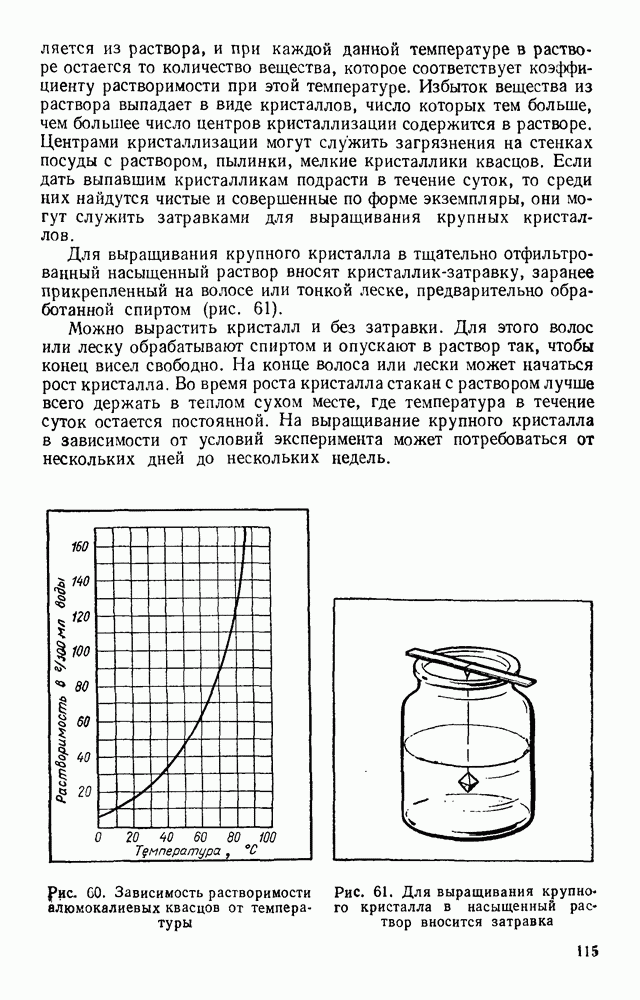
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
Одним из важнейших отличий реальных газов от воображаемого идеального газа являются конечные размеры молекул любого реального газа. Вследствие этого молекулы реального газа испытывают столкновения не только со стенками сосуда, но и друг с другом. Поэтому одним из основных параметров реального газа является средняя длина свободного пробега его молекул.
Длиной свободного пробега молекулы газа называется длина пути, пройденного ею между двумя последовательными столкновениями (рис. 6). Так как молекулы газа распределены в пространстве беспорядочно, движутся во всевозможных направлениях и с различными скоростями, то длина пути между каждыми двумя последовательными столкновениями молекулы оказывается величиной непостоянной. Однако можно найти среднее значение длины свободного пробега молекулы газа для большого числа столкновений и пользоваться этим параметром для характеристики газа.
Среднюю длину свободного пробега X можно вычислить теоретически, если известны радиус молекул  и концентрация их в единице объема
и концентрация их в единице объема  При расчетах будем считать, что молекулы газа при столкновении ведут себя как упругие шары, отталкивающиеся только при соприкосновении, когда расстояние между их центрами равно удвоенному радиусу
При расчетах будем считать, что молекулы газа при столкновении ведут себя как упругие шары, отталкивающиеся только при соприкосновении, когда расстояние между их центрами равно удвоенному радиусу  . Силы взаимного притяжения молекул во внимание принимать не будем.
. Силы взаимного притяжения молекул во внимание принимать не будем.
Для определения средней длины свободного пробега вычисли сначала число столкновений, которое испытывает молекула за 1 с. Мы предположили, что молекулы взаимодействуют друг с другом при сближении до расстояния  . Следовательно, при движении одной молекулы с ней испытывают соударения все молекулы
. Следовательно, при движении одной молекулы с ней испытывают соударения все молекулы

Рис. 6. Движение молекул газа характеризуется длиной свободного пробега

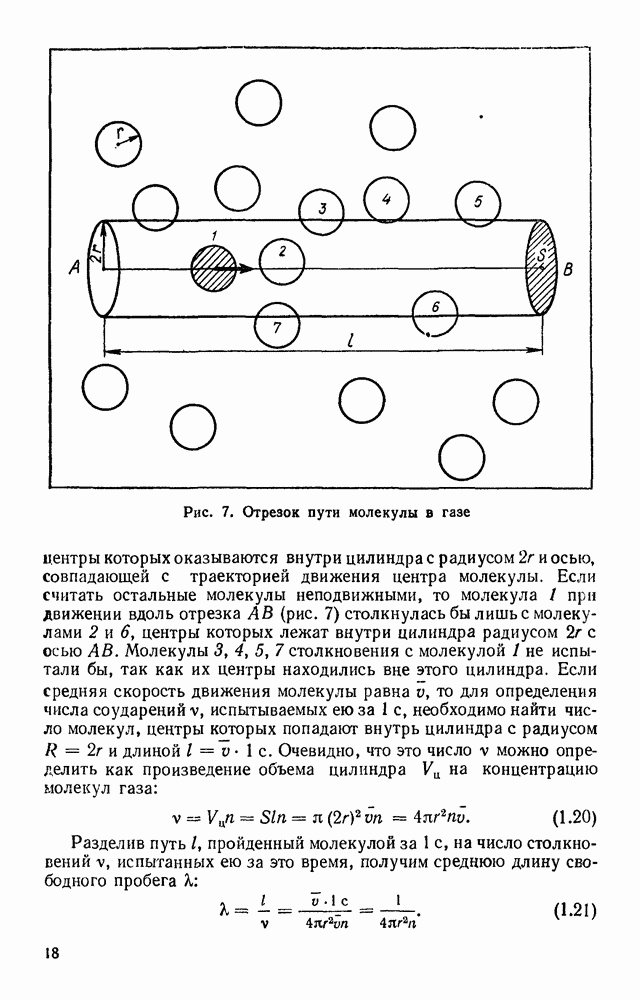
Рис. 7. Отрезок пути молекулы в газе
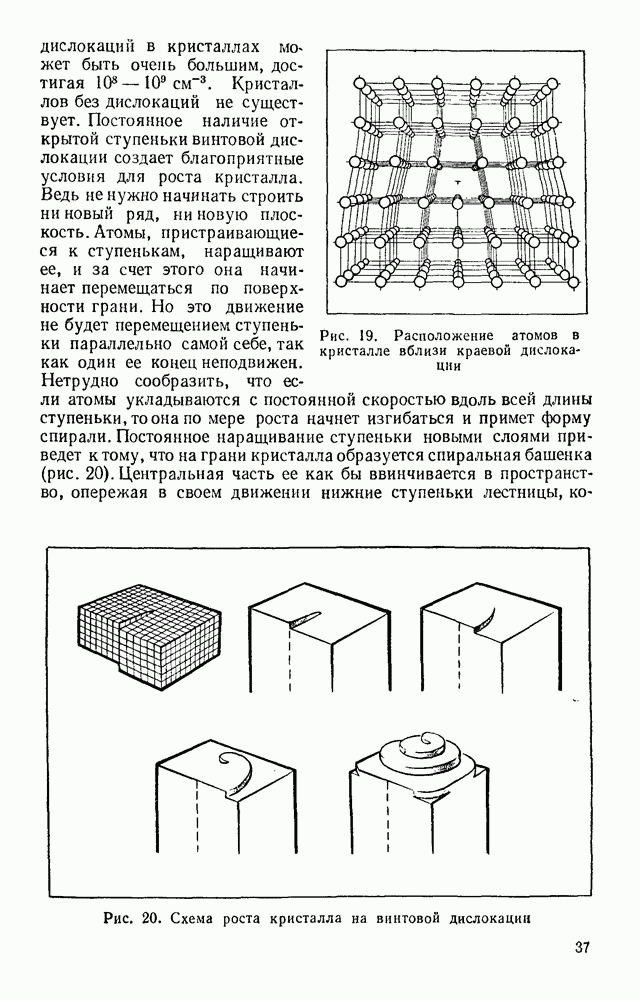
центры которых оказываются внутри цилиндра с радиусом  и осью, совпадающей с траекторией движения центра молекулы. Если считать остальные молекулы неподвижными, то молекула
и осью, совпадающей с траекторией движения центра молекулы. Если считать остальные молекулы неподвижными, то молекула  при движении вдоль отрезка АВ (рис. 7) столкнулась бы лишь с молекулами 2 и 6, центры которых лежат внутри цилиндра радиусом
при движении вдоль отрезка АВ (рис. 7) столкнулась бы лишь с молекулами 2 и 6, центры которых лежат внутри цилиндра радиусом  с осью АВ. Молекулы 3, 4, 5, 7 столкновения с молекулой 1 не испытали бы, так как их центры находились вне этого цилиндра. Если средняя скорость движения молекулы равна у, то для определения числа соударений
с осью АВ. Молекулы 3, 4, 5, 7 столкновения с молекулой 1 не испытали бы, так как их центры находились вне этого цилиндра. Если средняя скорость движения молекулы равна у, то для определения числа соударений  испытываемых ею за 1 с, необходимо найти число молекул, центры которых попадают внутрь цилиндра с радиусом
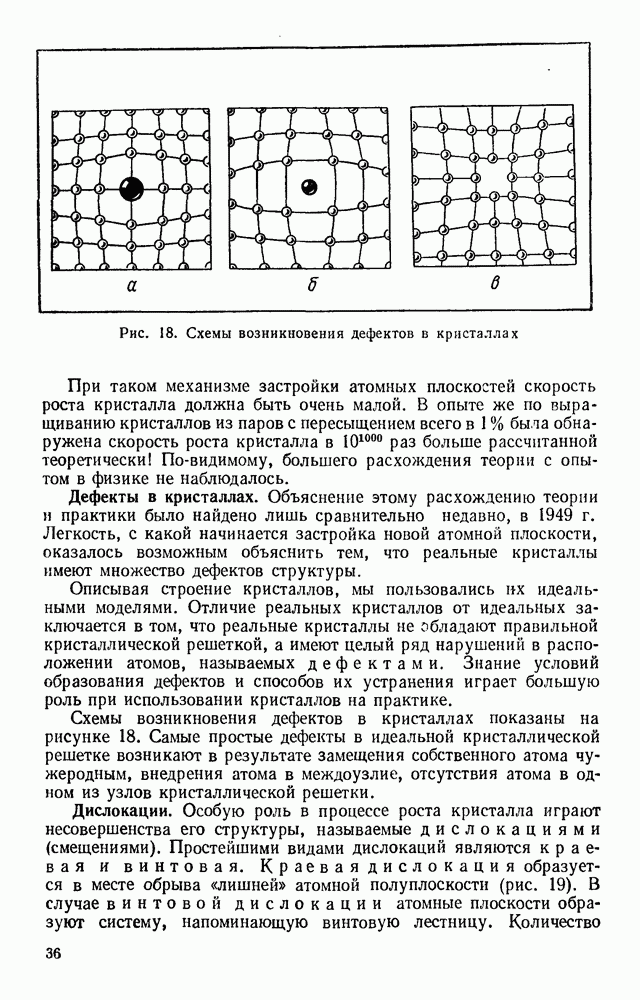
испытываемых ею за 1 с, необходимо найти число молекул, центры которых попадают внутрь цилиндра с радиусом  и длиной
и длиной  . Очевидно, что это число
. Очевидно, что это число  можно определить как произведение объема цилиндра
можно определить как произведение объема цилиндра  на концентрацию молекул газа:
на концентрацию молекул газа:

Разделив путь  пройденный молекулой за 1 с, на число столкновений
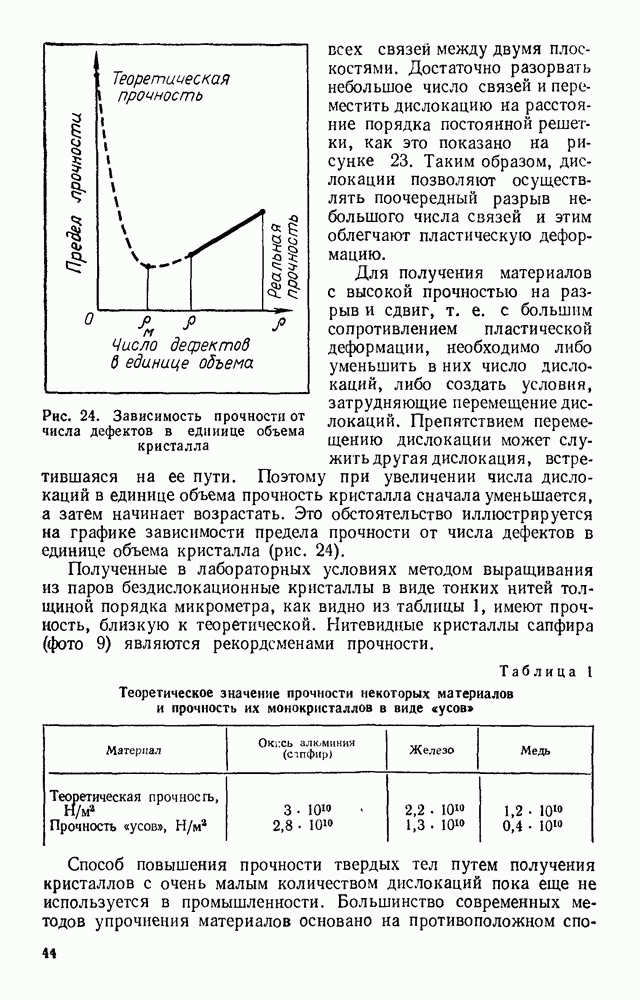
пройденный молекулой за 1 с, на число столкновений  испытанных ею за это время, получим среднюю длину свободного пробега К:
испытанных ею за это время, получим среднюю длину свободного пробега К:

После вывода формул для вычисления средней длины свободного пробега молекулы и частоты ее столкновений с другими молекулами можно произвести интересный анализ физического смысла полученных результатов.
Обратим сначала внимание на то, что произведение  определяет площадь поверхности всех молекул, заключенных в единице объема газа, если считать молекулы шариками радиусом
определяет площадь поверхности всех молекул, заключенных в единице объема газа, если считать молекулы шариками радиусом  . Тогда из выражения (1.21) следует, что средняя длина свободного пробега молекулы газа во столько раз меньше единицы длины, во сколько раз площадь поверхности всех молекул газа в единице объема больше единицы площади.
. Тогда из выражения (1.21) следует, что средняя длина свободного пробега молекулы газа во столько раз меньше единицы длины, во сколько раз площадь поверхности всех молекул газа в единице объема больше единицы площади.
| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
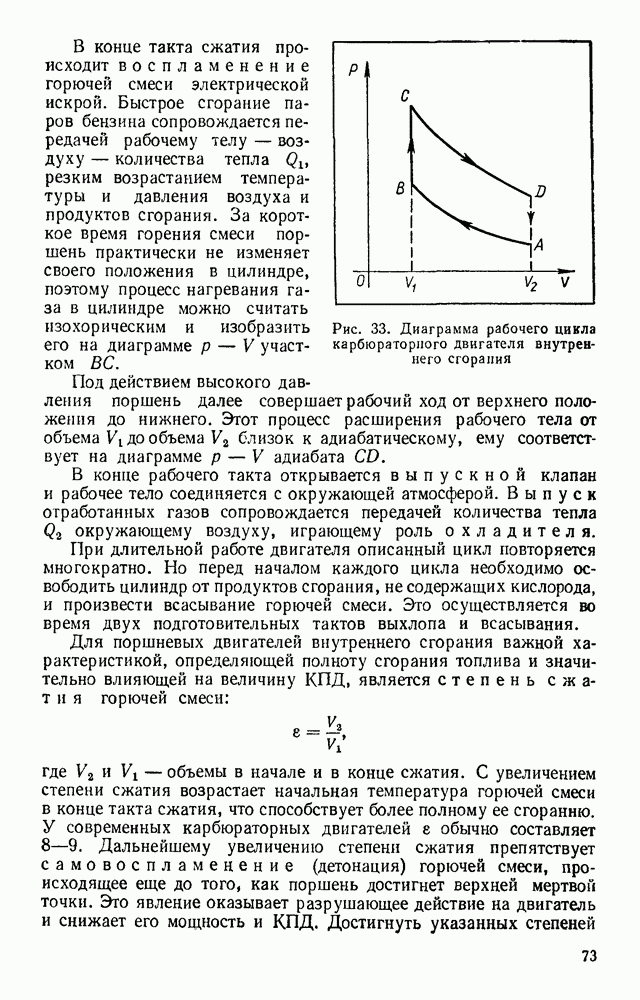
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
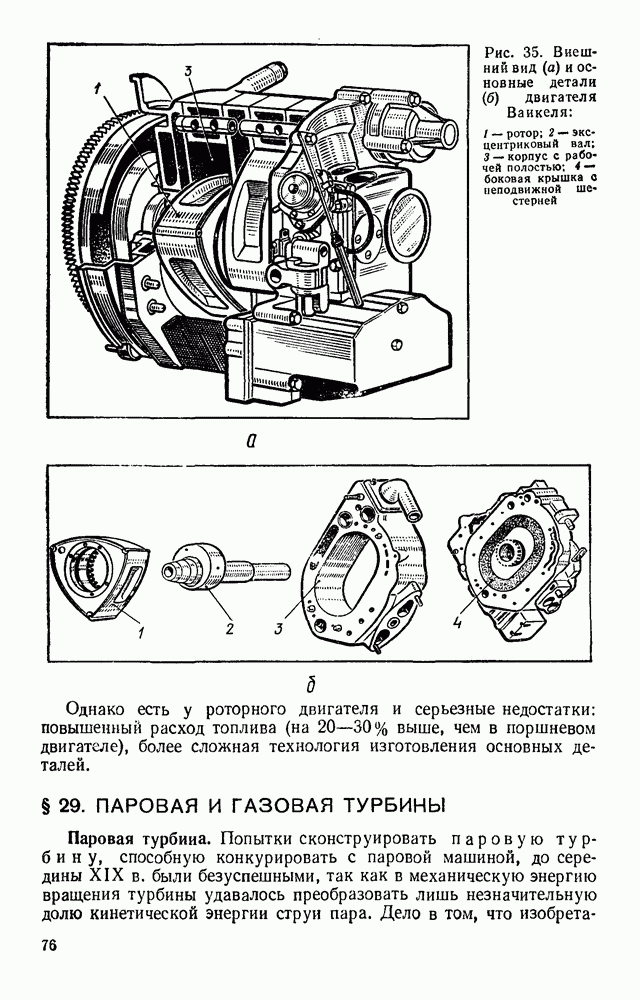
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
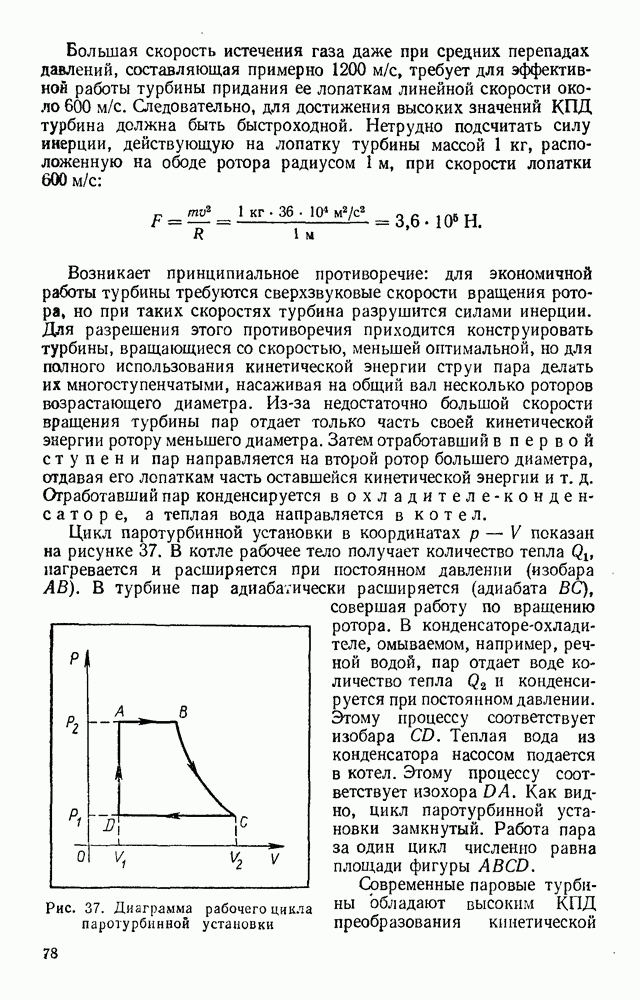
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
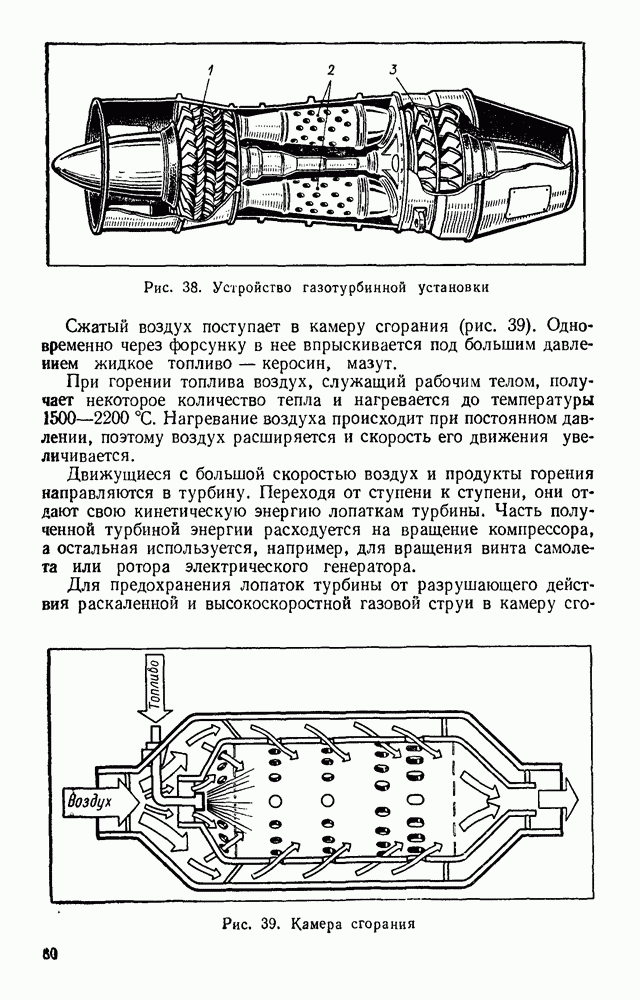
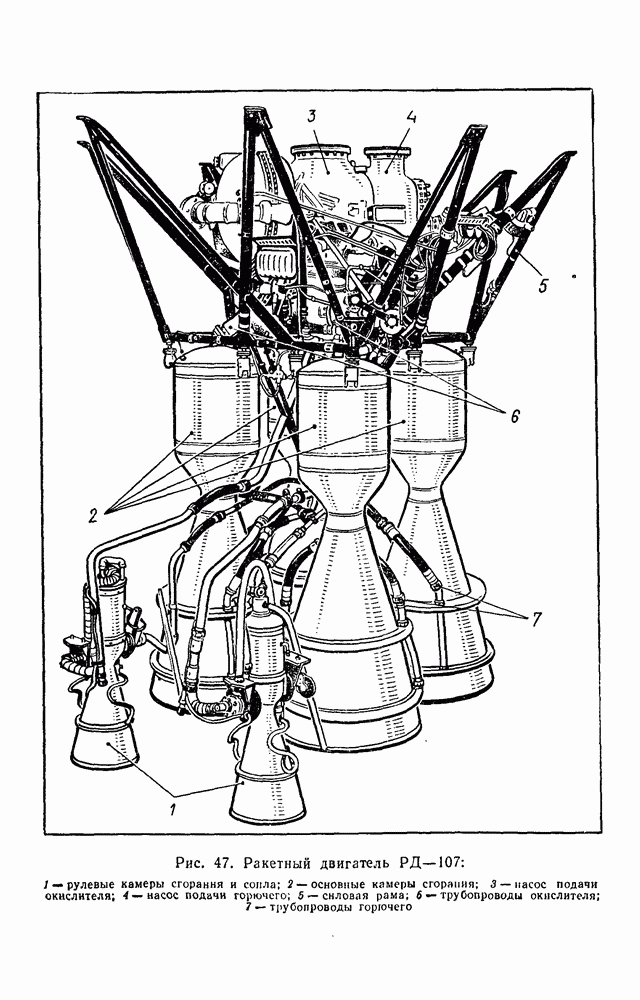
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
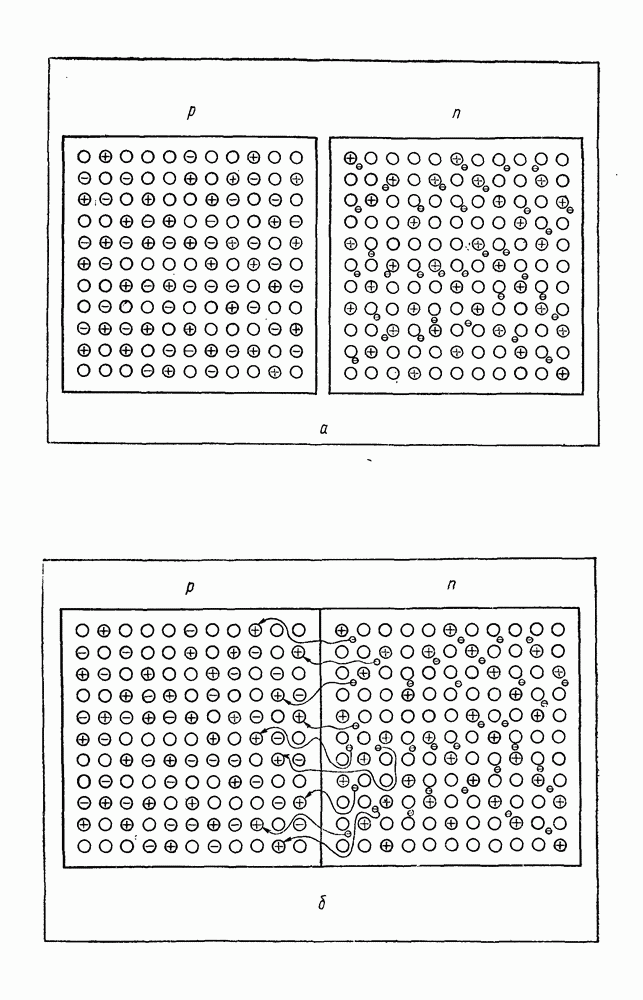
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
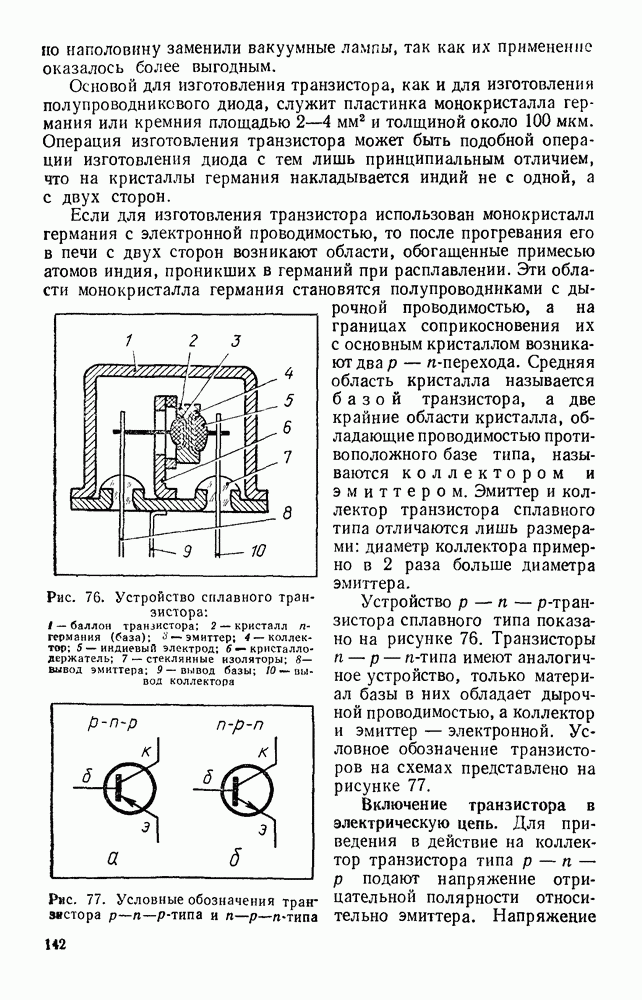
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
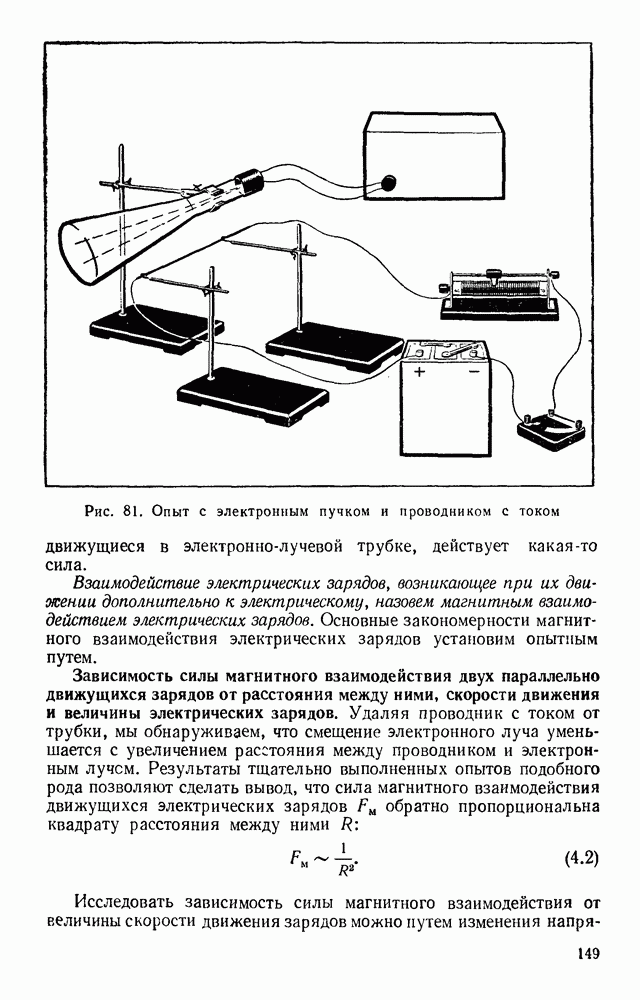
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
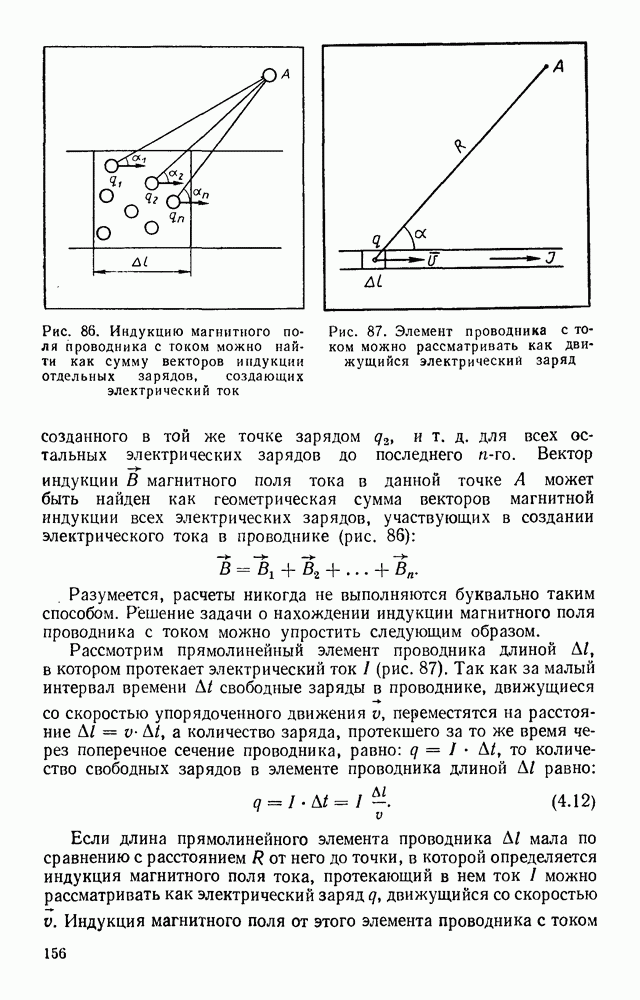
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ