| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
Количество теплоты  передаваемое телу при теплопередаче, не определяет однозначно температуру тела Т, так как внутренняя энергия тела может изменяться и за счет совершения над ним работы А. Поэтому в отличие от такой, например, неизменной характеристики вещества, как его молярная масса М, удельная теплоемкость зависит от условий, при которых происходит передача тепла.
передаваемое телу при теплопередаче, не определяет однозначно температуру тела Т, так как внутренняя энергия тела может изменяться и за счет совершения над ним работы А. Поэтому в отличие от такой, например, неизменной характеристики вещества, как его молярная масса М, удельная теплоемкость зависит от условий, при которых происходит передача тепла.
Теплоемкость идеального газа при постоянном объеме. Рассмотрим случай передачи тепла идеальному газу при условии неизменности занимаемого им объема.
Условие передачи тепла газу при постоянном объеме выбрано нами не случайно. Работа, совершаемая внешними силами над газом, при постоянном объеме равна нулю:  Из первого закона термодинамики
Из первого закона термодинамики  следует, что в этом случае количество переданного газу тепла равно изменению его внутренней энергии:
следует, что в этом случае количество переданного газу тепла равно изменению его внутренней энергии:  Поэтому удельную теплоемкость газа при постоянном объеме можно найти, вычислив изменение внутренней энергии единицы массы газа при изменении его температуры на 1 К:
Поэтому удельную теплоемкость газа при постоянном объеме можно найти, вычислив изменение внутренней энергии единицы массы газа при изменении его температуры на 1 К:

Внутренняя энергия идеального газа является кинетической энергией теплового движения молекул и может быть найдена как произведение средней кинетической энергии теплового движения молекулы Е на число молекул N:

Изменение внутренней энергии идеального газа при увеличении его температуры на величину  определится выражением:
определится выражением:

Отсюда получаем:

где  — молярная масса газа.
— молярная масса газа.
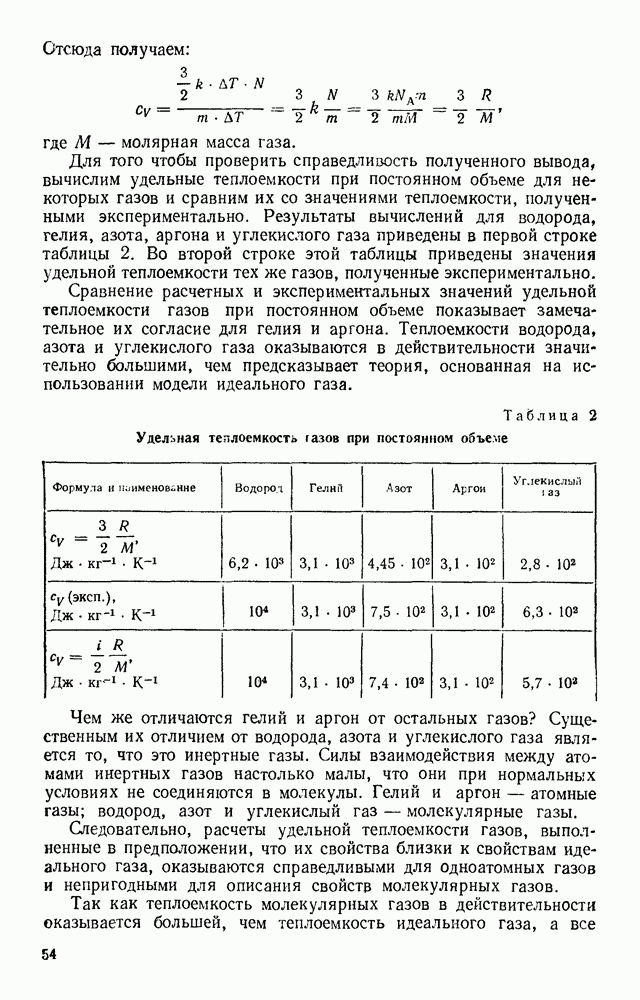
Для того чтобы проверить справедливость полученного вывода, вычислим удельные теплоемкости при постоянном объеме для некоторых газов и сравним их со значениями теплоемкости, полученными экспериментально. Результаты вычислений для водорода, гелия, азота, аргона и углекислого газа приведены в первой строке таблицы 2. Во второй строке этой таблицы приведены значения удельной теплоемкости тех же газов, полученные экспериментально.
Сравнение расчетных и экспериментальных значений удельной теплоемкости газов при постоянном объеме показывает замечательное их согласие для гелия и аргона. Теплоемкости водорода, азота и углекислого газа оказываются в действительности значительно большими, чем предсказывает теория, основанная на использовании модели идеального газа.
Таблица 2. Удельная теплоемкость газов при постоянном объеме

Чем же отличаются гелий и аргон от остальных газов? Существенным их отличием от водорода, азота и углекислого газа является то, что это инертные газы. Силы взаимодействия между атомами инертных газов настолько малы, что они при нормальных условиях не соединяются в молекулы. Гелий и аргон — атомные газы; водород, азот и углекислый газ — молекулярные газы.
Следовательно, расчеты удельной теплоемкости газов, выполненные в предположении, что их свойства близки к свойствам идеального газа, оказываются справедливыми для одноатомных газов и непригодными для описания свойств молекулярных газов.
Так как теплоемкость молекулярных газов в действительности оказывается большей, чем теплоемкость идеального газа, а все
тепло, передаваемое газу в условиях неизменности занимаемого им объема, идет на увеличение внутренней энергии, необходимо признать, что внутренняя энергия молекулярного газа не определяется точно выражением:

Распределение энергии по степеням свободы. Сделаем попытку уточнения теории. До сих пор при рассмотрении свойств атомов или молекул газа предполагалось, что их размеры очень малы. Поэтому в расчетах учитывалась лишь кинетическая энергия поступательного движения, а кинетическая энергия вращательного движения считалась пренебрежимо малой. Согласие расчетов с экспериментом при вычислении теплоемкости одноатомных газов показывает, что для них такое предположение оказывается справедливым. Поскольку теплоемкости многоатомных газов оказываются большими, чем следует из расчетов при учете только кинетической энергии поступательного движения молекул, можно предположить, что внутренняя энергия молекулярных газов складывается из кинетической энергии поступательного движения молекул и кинетической энергии их вращательного движения.
Такое предположение правдоподобно, но если только им и ограничиться, то уточнить результаты расчетов не удается, так как остается неизвестным, какова величина кинетической энергии вращения молекул.
Решение этой проблемы оказывается довольно простым. Пространство, в котором происходит поступательное движение молекул, имеет три измерения. В прямоугольной системе координат эти три измерения задаются тремя координатами положения молекулы и тремя проекциями вектора скорости  на эти координатные оси:
на эти координатные оси:  Если вероятность движения тела в любом из трех возможных направлений в пространстве одинакова, то говорят, что оно обладает тремя степенями свободы.
Если вероятность движения тела в любом из трех возможных направлений в пространстве одинакова, то говорят, что оно обладает тремя степенями свободы.
Так как движение молекул газа совершенно хаотично, квадраты проекций скорости на каждую из координатных осей в среднем оказываются одинаковыми:

Отсюда следует, что кинетическая энергия поступательного движения, приходящаяся на каждую из трех степеней свободы движения, в среднем одинакова. Так как средняя кинетическая энергия поступательного движения молекулы  равна:
равна:  кинетическая энергия, приходящаяся на одну степень свободы движения, равна
кинетическая энергия, приходящаяся на одну степень свободы движения, равна 
Теплоемкость многоатомных газов. Двухатомная молекула, кроме трех степеней свободы поступательного движения, обладает еще и двумя степенями свободы вращательного движения, так как

Рис. 27. Модели молекул: а — одноатомной; б — двухатомной; в — трех атомной
может совершать вращение вокруг двух взаимно перпендикулярных осей. Предполагая, что кинетическая энергия молекулы распределяется между всеми возможными видами ее движения поровну, мы получим, что кинетическая энергия молекулы равна:

Вращением двухатомной молекулы вокруг третьей оси, проходящей через центры атомов, можно пренебречь, так как предположение об отсутствии вращения атомов вокруг своих осей подтверждалось в случае вычисления теплоемкостей одноатомных газов.
Молекулы, состоящие более чем из двух атомов, обладают тремя степенями свободы вращательного движения и тремя степенями свободы поступательного движения (рис. 27).
Для газа, молекулы которого обладают числом степеней свободы  получаем следующее выражение для удельной теплоемкости при постоянном объеме:
получаем следующее выражение для удельной теплоемкости при постоянном объеме:

Используя это выражение, вычислим удельные теплоемкости двухатомных газов — водорода и азота и трехатомного углекислого газа. Результаты вычислений приведены в третьей строке таблицы 2.
Хорошее согласие теоретических и экспериментальных значений теплоемкости многоатомных газов доказывает справедливость сделанного при выполнении расчетов предположения о равном распределении энергии по степеням свободы движения. Такое распределение энергии по степеням свободы строго доказывается в молекулярно-кинетической теории и называется законом равнораспределения.
Теплоемкость газа при постоянном давлении. До сих пор мы искали способы определения теплоемкости газа при постоянном объеме. Интересным в практике является также случай передачи тепла газу, находящемуся при постоянном давлении. Используя первый закон термодинамики, количество тепла  переданного газу, можно выразить через изменение внутренней энергии
переданного газу, можно выразить через изменение внутренней энергии  газа и работу А, совершенную над газом при нагревании:
газа и работу А, совершенную над газом при нагревании:

Вместо работы А, произведенной внешними силами, можно пользоваться в расчетах равной по модулю и противоположной по знаку работой А, совершенной газом:

Тогда для удельной теплоемкости  газа при постоянном давлении получим выражение:
газа при постоянном давлении получим выражение:

Первое слагаемое в этом выражении — удельная теплоемкость газа при постоянном объеме  второе слагаемое имеет физический смысл работы, совершаемой единицей массы газа при нагревании на 1 К при постоянном давлении:
второе слагаемое имеет физический смысл работы, совершаемой единицей массы газа при нагревании на 1 К при постоянном давлении:

| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
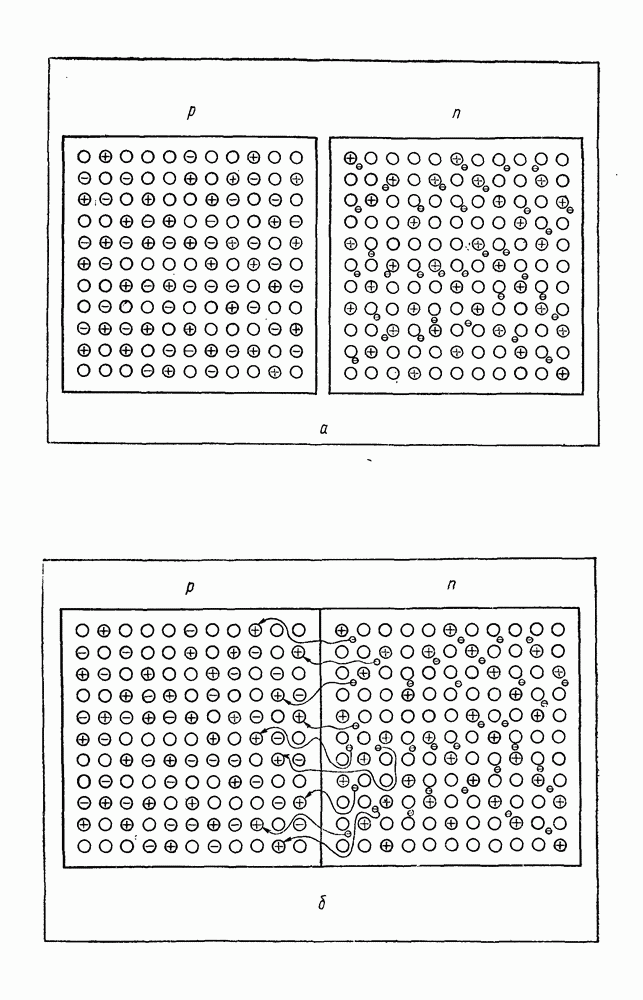
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
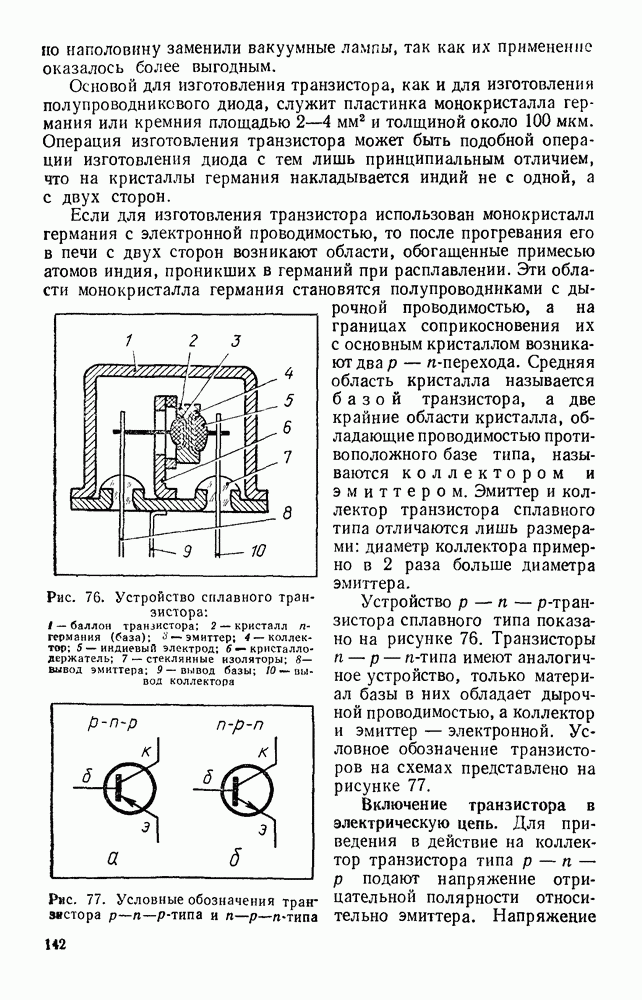
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
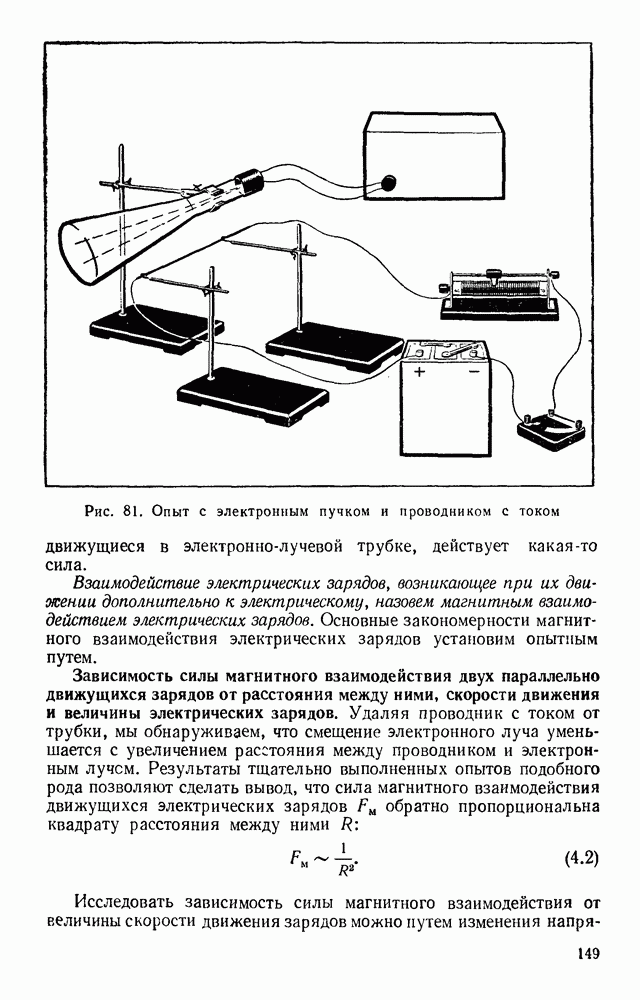
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
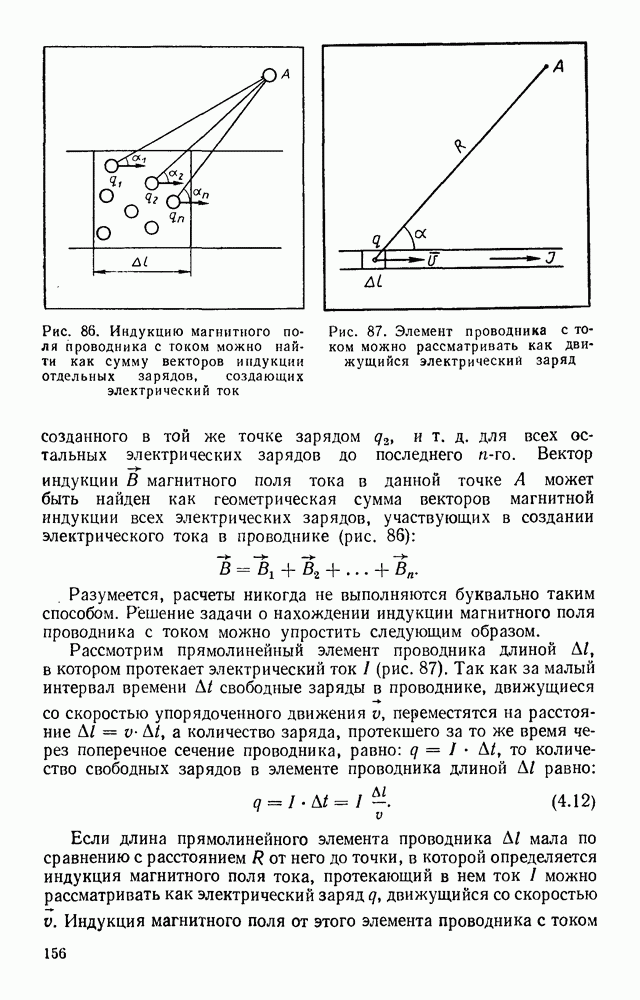
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ