| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
СТРОЕНИЕ И СВОЙСТВА ВЕЩЕСТВА
Задача 1. В опытах Резерфорда было получено, что в герметичном сосуде, в который помещен  радия, накапливается за год
радия, накапливается за год  газообразного гелия при нормальных условиях. Исходя из этих данных, определите число Авогадро, если известно, что
газообразного гелия при нормальных условиях. Исходя из этих данных, определите число Авогадро, если известно, что  радия испускает за 1 с
радия испускает за 1 с  -частиц, т. е. атомов гелия.
-частиц, т. е. атомов гелия.
Решение. Для определения числа атомов гелия  в объеме
в объеме  необходимо число
необходимо число  -частиц (атомов гелия), испускаемых 1 г ргдия за 1 с, умножить на число секунд в году:
-частиц (атомов гелия), испускаемых 1 г ргдия за 1 с, умножить на число секунд в году:

Из этих данных, используя закон Авогадро, можно получить значение числа Авогадро:

Задача 2. Определите радиус атома алюминия, приняв, что в алюминии, находящемся в твердом состоянии, атомы располагаются вплотную друг к другу.
Решение. Для решения задачи найдем сначала сбъем V, занимаемый одним атомом.
Объем V, занимаемый одним атомом алюминия, определится делением объема  занимаемого 1 молем алюминия, на число атомоз алюминия в одном моле
занимаемого 1 молем алюминия, на число атомоз алюминия в одном моле  :
:

Длина  ребра куба, занимаемого атомом, равна:
ребра куба, занимаемого атомом, равна:

Считая атом алюминия шаром, вписанным в этот куб; мы получим, что радиус атома алюминия равен половине ребра этого куба:

Задача 3. Для того чтобы проверить, насколько близки к истине ваши представления об атмосферном воздухе, попробуйте, не прибегая к вычислениям, оценить массу воздуха, находящегося в физическом кабинете.
Какой объем займет воздух, находящийся в физическом кабинете, если его перевести в жидкое состояние? Поместится ли он тогда в вашу сумку для книг?
После того как вы сделали свои оценки, проверьте их расчетами.
Решение. Определим сначала массу воздуха в кабинете. Для кабинета физики размером  получаем объем воздуха, равный
получаем объем воздуха, равный 
Принимая среднюю молярную массу воздуха равной  найдем массу воздуха в кабинете при температуре
найдем массу воздуха в кабинете при температуре 

Так как плотность воздуха в жидком состоянии равна  кг
кг  то в жидком состоянии объем воздуха физического кабинета равен:
то в жидком состоянии объем воздуха физического кабинета равен: 
Задача 4. Оцените, во сколько раз изменится расстояние между молекулами при переходе воды из жидкого в газообразное состояние.
Решение. Очевидно, на этот вопрос не может быть дан однозначный ответ, так как объем, занимаемый газом, определяется только размерами сосуда. Для примера сравним воду и водяной пар при нормальном атмосферном давлении. Вычислим, какой объем приходится на долю одной молекулы воды в жидком состоянии. Для этого разделим объем V, занимаемый одним молем воды, на число молекул в одном моле, т. е. на число Авогадро  :
:

Подчеркнем, что полученное число не есть объем молекулы воды, это объем условной кубической ячейки, занимаемой одной молекулой. Все такие кубические ячейки без зазоров примыкают одна к другой. Ребро куба  объемом
объемом  равно диаметру молекулы, если ее считать шаром, вписанным в эту кубическую ячейку, или расстоянию между центрами соседних молекул
равно диаметру молекулы, если ее считать шаром, вписанным в эту кубическую ячейку, или расстоянию между центрами соседних молекул  Это расстояние можно определить, найдя длину ребра куба
Это расстояние можно определить, найдя длину ребра куба  имеющего объем
имеющего объем  :
:

Рассмотрим теперь водяной пар при нормальном атмосферном давлении и температуре 100 °С. Объем, занимаемый молем водяного пара при этих условиях, можно определить, воспользовавшись уравнением Клапейрона — Менделеева:

Разделив молярный объем водяного пара при атмосферном давлении V на число Авогадро  получим объем
получим объем  приходящийся на долю одной молекулы водяного пара при этих условиях:
приходящийся на долю одной молекулы водяного пара при этих условиях:

Если представить себе, что на какое-то мгновение хаос в расположении молекул водяного пара сменился порядком и каждая из них находится в центре кубической ячейки, то расстояние между соседними молекулами  определилось бы выражением:
определилось бы выражением:

Для реального газа, состоящего из хаотически движущихся молекул, величина  имеет смысл среднего расстояния между молекулами.
имеет смысл среднего расстояния между молекулами.
Получив численные характеристики распределения в пространстве молекул вещества в жидком и газообразном состояниях, сравним их между собой:

Наши расчеты показывают, что при переходе воды из жидкого состояния в газообразное при условиях, близких к нормальным, объем, приходящийся на долю одной молекулы, увеличивается почти в 2000 раз. Однако среднее расстояние между молекулами при этих условиях изменяется не так значительно, примерно в 12 раз.
Задача 5. Основываясь на представлениях молекулярно-кинетической теории, оцените давление и температуру внутри Солнца. Масса Солнца  кг, радиус
кг, радиус  . В расчетах можно принять, что Солнце состоит в основном из атомарного водорода.
. В расчетах можно принять, что Солнце состоит в основном из атомарного водорода.
Решение. Согласно молекулярно-кинетической теории давление газа  связано с его температурой Т и концентрацией молекул
связано с его температурой Т и концентрацией молекул  соотношением
соотношением  отсюда
отсюда

Поскольку Солнце не расширяется и не сжимается, на любой глубине давление его внутренних слоев равно давлению вышележащих слоев, создаваемому действием силы тяжести 

Отсюда следует, что для определения температуры на какой-то глубине внутри Солнца необходимо определить концентрацию атомов  на этой глубине и давление вышележащих слоев
на этой глубине и давление вышележащих слоев 
Для упрощения зададимся целью определить температуру на расстоянии  от центра Солнца, где концентрацию атомов водорода можно считать приближенно равной среднему значению для Солнца:
от центра Солнца, где концентрацию атомов водорода можно считать приближенно равной среднему значению для Солнца:

Выделив вертикальный столб газа с площадью основания  давление верхних слоев на лежащие ниже можно оценить, пренебрегая зависимостью плотности
давление верхних слоев на лежащие ниже можно оценить, пренебрегая зависимостью плотности  газа от глубины. Примем расстояние до центра масс верхней половины столба газа равным
газа от глубины. Примем расстояние до центра масс верхней половины столба газа равным  и произведем расчет силы тяготения, пренебрегая отличием формы тяготеющих тел от точечных и шарообразных тел:
и произведем расчет силы тяготения, пренебрегая отличием формы тяготеющих тел от точечных и шарообразных тел:

Тогда давление будет равно:

а температура:

Получим численные значения давления и температуры:

Мы получили, что в недрах Солнца давление газа примерно в 20 млрд. раз превышает нормальное атмосферное давление, а температура составляет около 20 млн. К. При всей приблизительности расчетов результаты весьма близки к полученным более строгим путем.
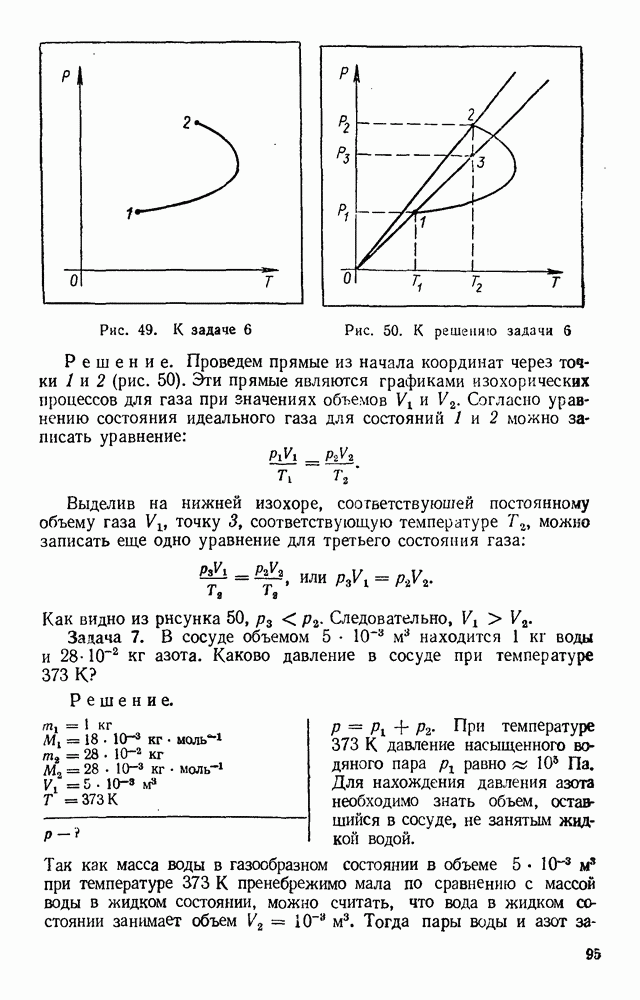
Задача 6. На рисунке 49 представлен график процесса изменения состояния идеального газа. Уменьшился или увеличился объем газа при переходе из состояния 1 в состояние 2? Масса газа постоянна.

Рис. 49. К задаче 6

Рис. 50. К решению задачи 5
Решение. Проведем прямые из начала координат через точки 1 и 2 (рис. 50). Эти прямые являются графиками изохорических процессов для газа при значениях объемов  и
и  . Согласно уравнению состояния идеального газа для состояний
. Согласно уравнению состояния идеального газа для состояний  можно записать уравнение:
можно записать уравнение:

Выделив на нижней изохоре, соответствующей постоянному объему газа точку 3, соответствующую температуре  можно записать еще одно уравнение для третьего состояния газа:
можно записать еще одно уравнение для третьего состояния газа:

Как видно из рисунка  Следовательно,
Следовательно, 
Задача 7. В сосуде объемом  находится 1 кг воды и
находится 1 кг воды и  кг азота. Каково давление в сосуде при температуре 373 К?
кг азота. Каково давление в сосуде при температуре 373 К?
Решение.

 При температуре 373 К давление насыщенного водяного пара
При температуре 373 К давление насыщенного водяного пара  равно
равно  Па. Для нахождения давления азота необходимо знать объем, оставшийся в сосуде, не занятым жидкой водой.
Па. Для нахождения давления азота необходимо знать объем, оставшийся в сосуде, не занятым жидкой водой.
Так как масса воды в газообразном состоянии в объеме  при температуре 373 К пренебрежимо мала по сравнению с массой воды в жидком состоянии, можно считать, что вода в жидком состоянии занимает объем
при температуре 373 К пренебрежимо мала по сравнению с массой воды в жидком состоянии, можно считать, что вода в жидком состоянии занимает объем  . Тогда пары воды и азот
. Тогда пары воды и азот
занимают объем  Следовательно,
Следовательно,

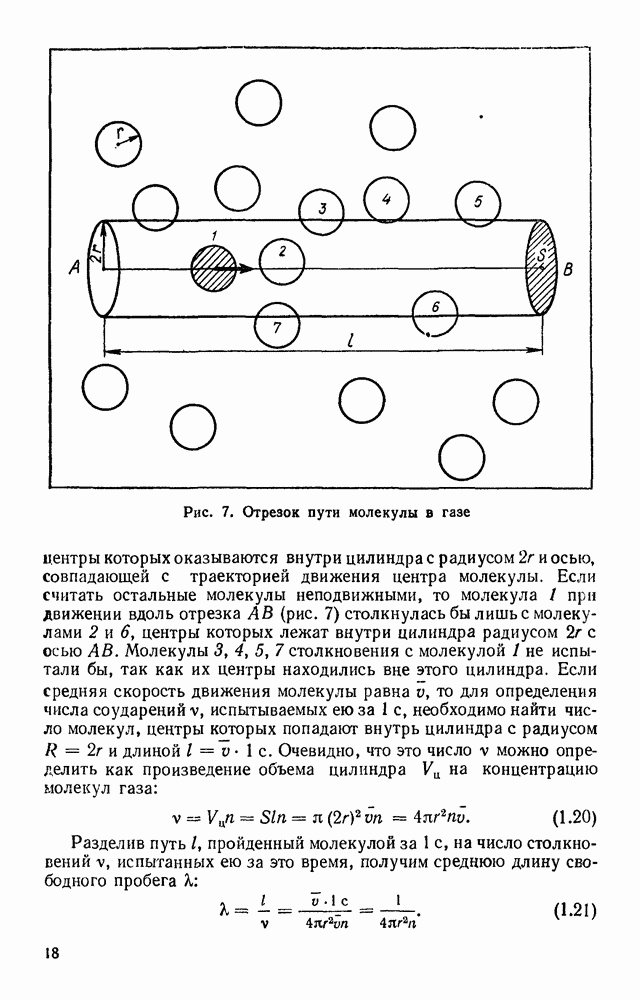
Задача 8. Вычислите площадь поверхности молекул, находящихся в  воздуха при температуре 20 °С, среднюю длину свободного пробега молекулы и число столкновений за 1 с. Решение.
воздуха при температуре 20 °С, среднюю длину свободного пробега молекулы и число столкновений за 1 с. Решение.

Мы получили, что площадь поверхности всех молекул, заключенных в  воздуха при нормальных условиях, составляет почти 10 млн.
воздуха при нормальных условиях, составляет почти 10 млн.  средняя длина свободного пробега молекулы равна примерно одной десятимиллионной доле метра, а число столкновений молекулы за одну секунду достигает примерно 3,5 миллиардов.
средняя длина свободного пробега молекулы равна примерно одной десятимиллионной доле метра, а число столкновений молекулы за одну секунду достигает примерно 3,5 миллиардов.
Задача 9. Определите число элементарных ячеек в  свинца. Кристаллическая решетка свинца гранецентрированная кубическая.
свинца. Кристаллическая решетка свинца гранецентрированная кубическая.
Решение. Как видно из рисунка 16, в, одной элементарной ячейке гранецентрированной кубической решетки принадлежит  атома.
атома.
Число элементарных ячеек  в
в  можно определить, разделив число атомов N свинца, содержащихся в этом объеме, на число атомов свинца
можно определить, разделив число атомов N свинца, содержащихся в этом объеме, на число атомов свинца  содержащихся в одной элементарной ячейке.
содержащихся в одной элементарной ячейке.

| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
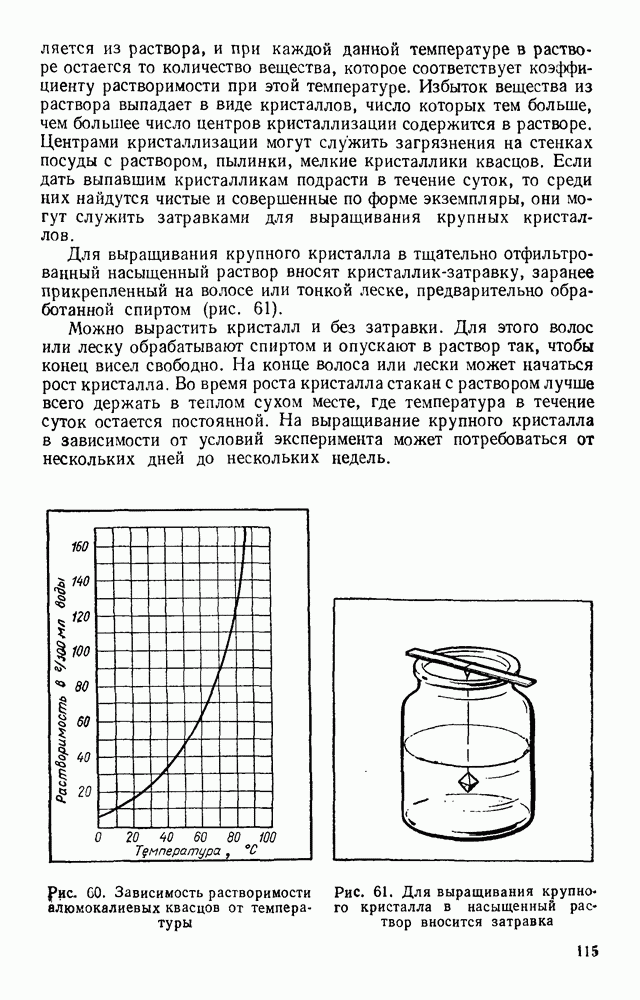
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
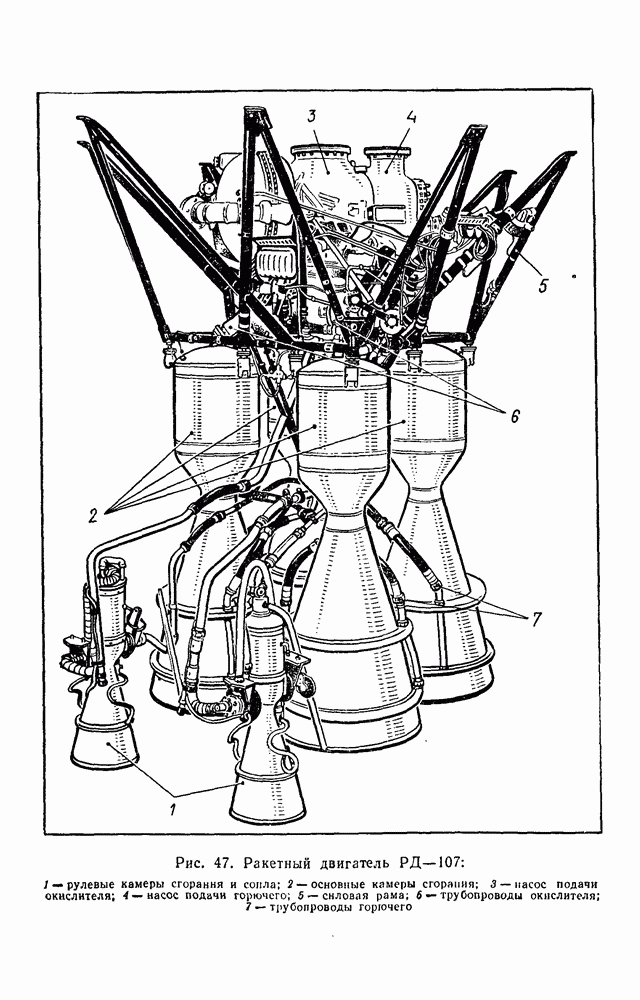
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
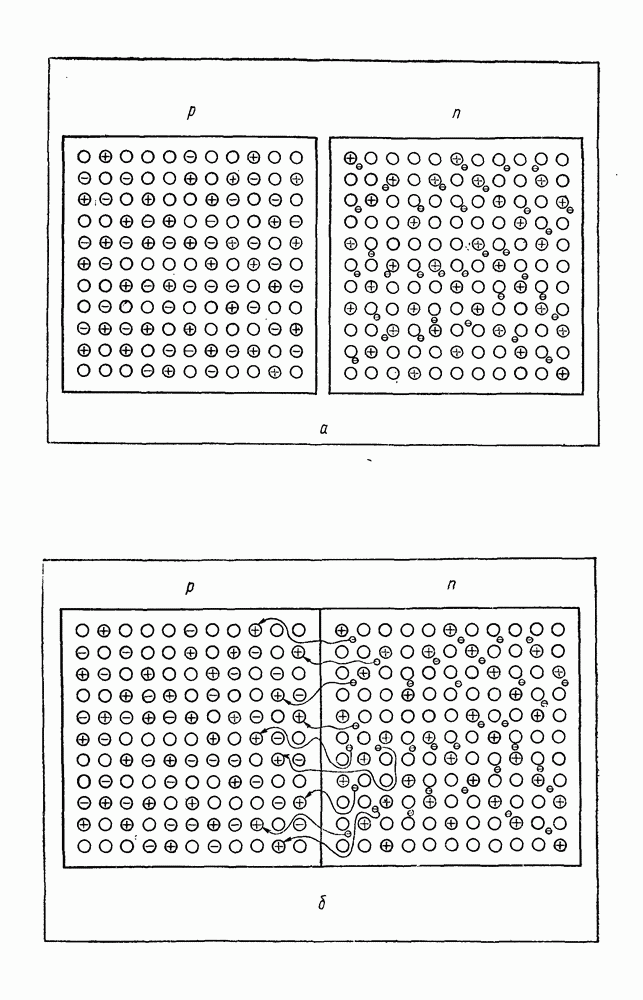
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
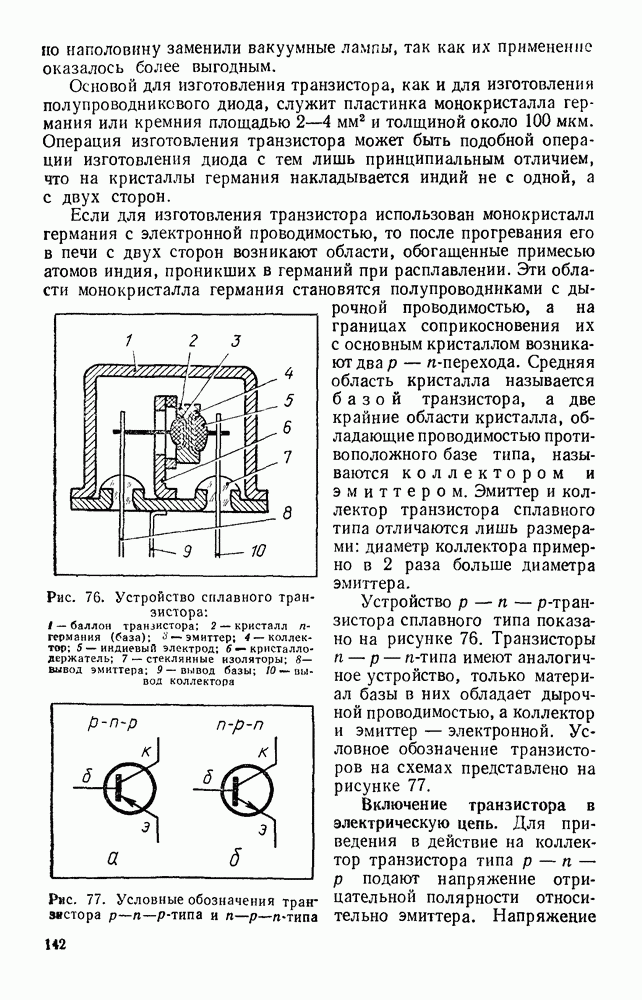
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
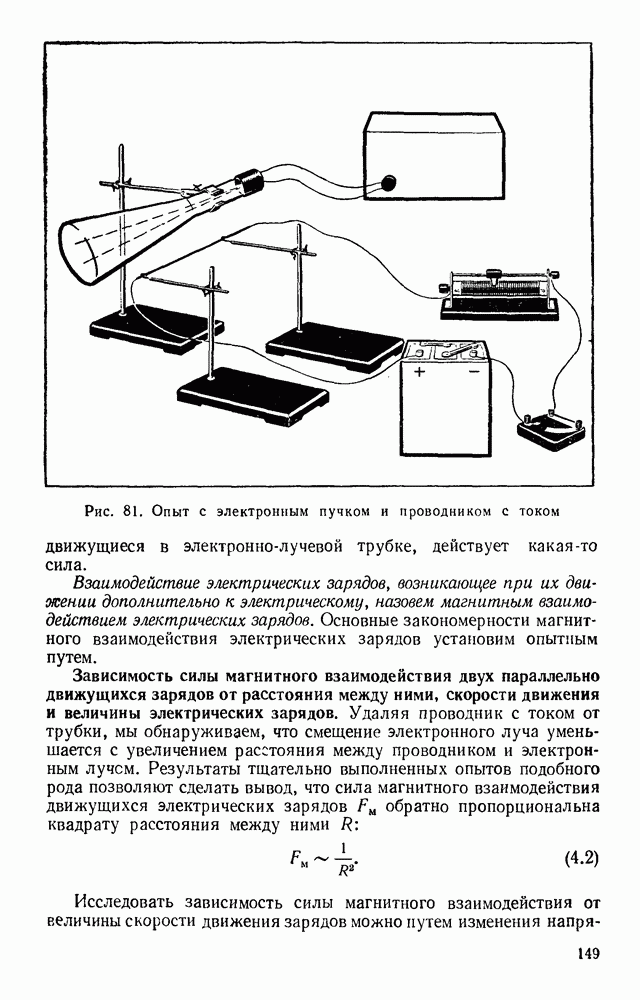
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
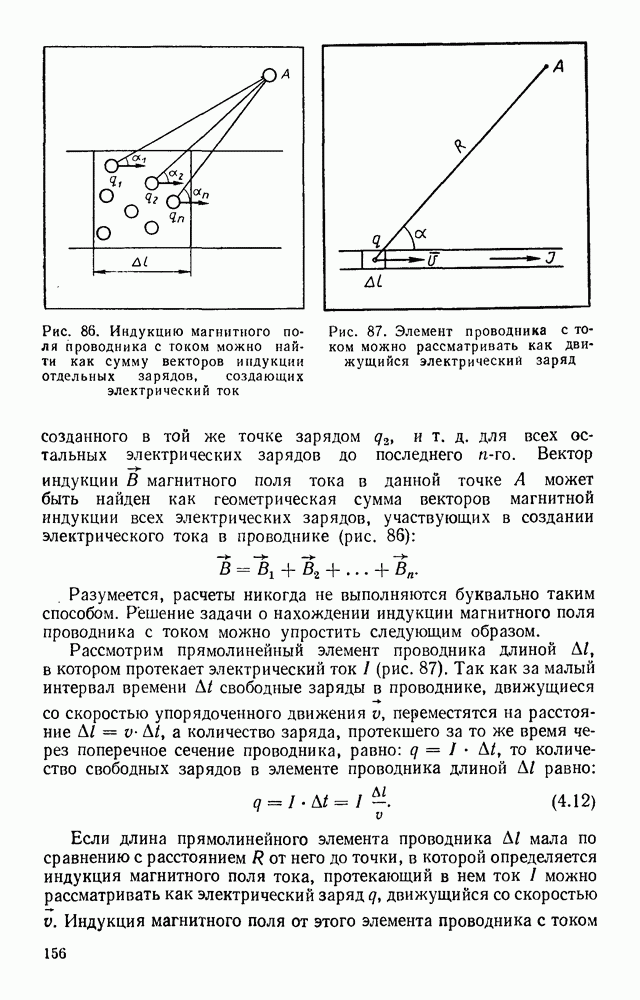
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ