ЭЛЕКТРОДИНАМИКА

Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК

§ 33. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Основные законы взаимодействия электрических зарядов. Все известные закономерности взаимодействия неподвижных электрических зарядов можно получить как следствия из трех основных законов, установленных экспериментально: закона сохранения электрического заряда, закона Кулона и принципа суперпозиции.

Закон сохранения электрического заряда утверждает, что электрический заряд изолированной системы остается постоянным при любых физических процессах, происходящих в системе. Так как электрические заряды бывают двух знаков, положительные и отрицательные, закон сохранения электрического заряда не утверждает, что невозможно возникновение или исчезновение электрических зарядов в замкнутой системе. Положительные и отрицательные заряды в замкнутой системе могут возникать или исчезать, но всегда так, чтобы их алгебраическая сумма оставалась постоянной.

Закон Кулона записывается в форме

и означает, что между двумя точечными электрическими зарядами действует сила прямо пропорциональная произведению зарядов и обратно пропорциональная квадрату расстояния между ними. Сила направлена вдоль прямой, соединяющей заряды.

Закон Кулона определяет силы взаимодействия двух точечных электрических зарядов. А по каким законам происходит взаимодействие трех, четырех и т. д. зарядов? Опыт показывает, что сила взаимодействия двух электрических зарядов совершенно не изме. няется при появлении вблизи них третьего, четвертого и т. д. электрических зарядов. Вместе с тем взаимодействие каждого из этих двух зарядов с третьим, четвертым и т. д. зарядами определяется в свою очередь законом Кулона. Результирующая сила

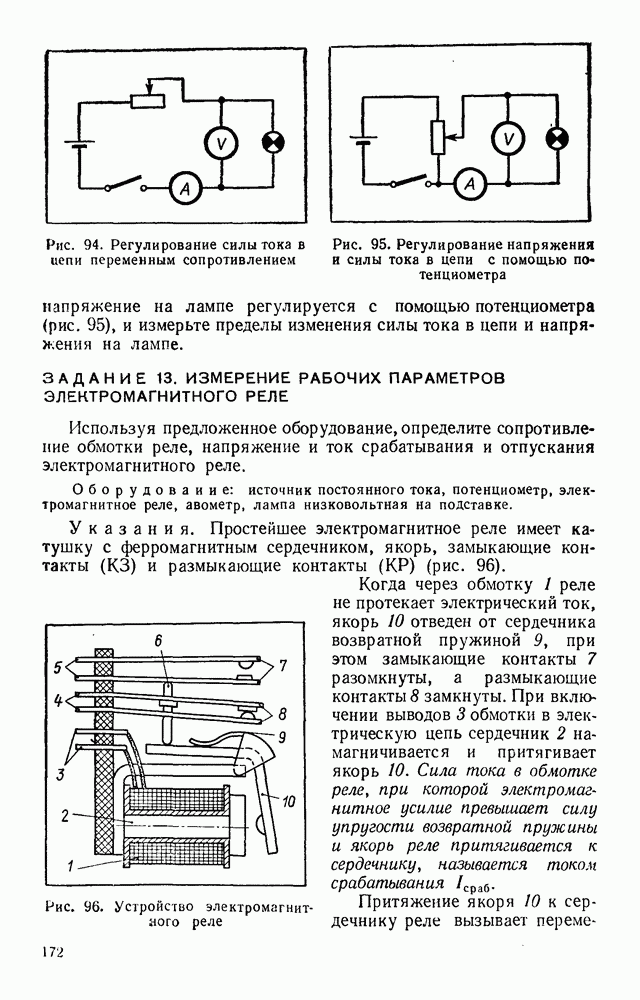
Рис. 63. Взаимодействие электрических зарядов

действия нескольких зарядов на один заряд является геометрической суммой сил, определяемых по закону Кулона для попарного взаимодействия с каждым из них (рис. 63),

Эта закономерность взаимодействия электрических зарядов называется принципом суперпозиции.

Электрическое поле. Итак, экспериментально установлено, что на расстоянии от одного электрического заряда в пространстве, которое кажется нам совершенно пустым, на другой электрический заряд действует сила Этот факт позволяет высказать предположение, что вокруг каждого электрического заряда существует нечто материальное, неразрывно связанное с этим зарядом. Это «нечто» назовем электрическим полем.

Если существует электрическое поле, то взаимодействие точечных электрических зарядов есть результат действия поля заряда на заряд и поля заряда на заряд

Напряженность электрического поля. Для количественного описания действия электрического поля на заряд, помещенный в данную точку поля, введем силовую характеристику электрического поля — напряженность Е.

Напряженность электрического поля Е определяется как отношение силы действующей на электрический заряд помещенный в данную точку поля, к заряду

Определим напряженность электрического поля на расстоянии от точечного заряда

На расстоянии от электрического заряда на заряд по закону Кулона действует сила

С другой стороны, используя понятие напряженности Е электрического поля заряда для той же силы можно записать выражение:

Из этих двух выражений для одной и той же силы следует:

Мы получили, что напряженность электрического поля точечного электрического заряда прямо пропорциональна заряду и обратно пропорциональна квадрату расстояния от него до данной точки поля.

Направление вектора напряженности Е электрического поля совпадает с направлением вектора силы действующей со стороны поля на положительный заряд, помещенный в данную точку поля.

Экспериментально установленный факт независимости сил взаимодействия двух зарядов от наличия других зарядов является доказательством того, что электрические поля не взаимодействуют между собой. В одной и той же точке пространства одновременно существуют электрические поля сколько угодно большого числа различных электрических зарядов и не оказывают друг на друга никакого влияния, т. е. электрические поля подчиняются принципу суперпозиции. При одновременном действии на электрический заряд двух электрических полей с напряженностями равнодействующая сила является геометрической суммой сил

Производя опыты по обнаружению электрического поля в данной точке пространства, мы всегда можем измерить лишь равнодействующую силу но не можем узнать, является ли эта сила следствием существования одного электрического поля с напряженностью Е или в данной точке пространства происходит наложение нескольких электрических полей и геометрическая сумма их векторов напряженности равна Е:

Линии напряженности электрического поля и поток вектора напряженности. Наглядную картину для описания электрического поля можно получить, введя понятие линии напряженности электрического поля — линии, касательная к которой в каждой точке совпадает с вектором напряженности электрического поля в точке касания.

Направление линии напряженности принимается совпадающим с направлением вектора силы, действующей в данной точке поля на точечный положительный электрический заряд. В соответствии с этим линии напряженности считаются выходящими из положительных зарядов и входящими в отрицательные заряды (рис. 64).

Условимся проводить в пространстве вокруг электрического заряда столько линий напряженности электрического поля, чтобы

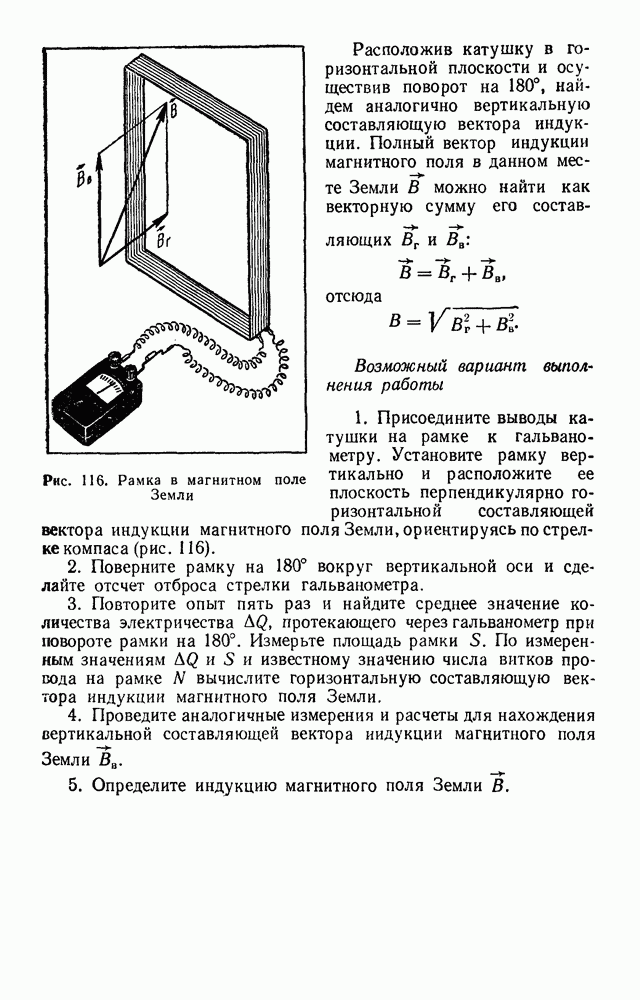
Рис. 64. Линии напряженности электрического поля

через единицу поверхности, к которой они в каждой точке перпендикулярны, проходило число линий, равное напряженности Е. Тогда отношение алгебраической суммы числа силовых линий Ф, пронизывающих такую поверхность, к площади поверхности равно напряженности Е электрического поля у данной поверхности. При счете число силовых линий, выходящих из поверхности, принимается положительным, а входящих — отрицательным. Алгебраическая сумма Ф числа входящих и выходящих силовых линий называется потоком вектора напряженности электрического поля.

Теорема Гаусса. Определим полный поток вектора напряженности электрического поля точечного электрического заряда Для этого представим себе, что заряд окружен сферической поверхностью радиусом центр которой совпадает с зарядом Так как на расстоянии от точечного заряда напряженность электрического поля равна:

и силовые линии в любой точке перпендикулярны поверхности шара, то полное число силовых линий Ф, пронизывающи поверхность шара, равно:

т. е. из положительного заряда выходит — силовых линий.

Так как электрические поля не влияют друг на друга, поток Ф вектора напряженности электрического поля любой системы электрических зарядов через любую замкнутую поверхность, окружающую эти заряды, равен алгебраической сумме электрических зарядов, деленной на электрическую постоянную вакуума

Это утверждение называется теоремой Гаусса.

Используя теорему Гаусса, можно вычислять напряженность электрического поля вокруг заряженных тел различной формы.

Напряженность поля заряженной плоскости. Применим теорему Гаусса для определения напряженности электрического поля заряженной плоскости. Если плоскость заряжена равномерно, т. е. поверхностная плотность заряда о одинакова в любом ее месте, то

Рис. 65. Электрическое поле заряженной плоскости

линии напряженности электрического поля в любой точке перпендикулярны заряженной плоскости. Такое же направление они сохраняют и на любом расстоянии от плоскости.

Так как линии напряженности электрического поля бесконечной равномерно заряженной плоскости параллельны друг другу, поток Еектора напряженности Ф электрического поля через участок поверхности площадью параллельной заряженной плоскости, остается одинаковым на любом расстоянии от плоскости. Следовательно, и напряженность Е электрического поля одинакова на любом расстоянии от плоскости.

Для нахождения напряженности электрического поля заряженной плоскости мысленно выделим в пространстве цилиндр, боковая поверхность которого перпендикулярна заряженной плоскости, а основания параллельны ей. Цилиндр вырезает из заряженной плоскости участок площадью такую же площадь имеют основания цилиндра, расположенные по разные стороны от плоскости (рис. 65).

Согласно теореме Гаусса поток Ф вектора напряженности электрического поля через поверхность цилиндра связан с электрическим зарядом внутри цилиндра выражением:

С другой стороны, так как линии напряженности пересекают лишь основания цилиндра, поток вектора напряженности можно

выразить через напряженность электрического поля у оснований цилиндра:

Из двух выражений для потока вектора напряженности получим:

Отсюда можно получить приближенное выражение для нахождения напряженности электрического поля между обкладками плоского конденсатора. Если размеры пластин плоского конденсатора значительно превосходят расстояние между ними, то электрическое поле каждой из пластин внутри конденсатора можно считать близким к полю бесконечной равномерно заряженной плоскости. Так как направление силовых линий напряженности электрического поля разноименно заряженных пластин внутри конденсатора совпадает, то напряженность поля внутри плоского конденсатора равна:

Так как , где заряд одной пластины конденсатора, S — ее площадь, то

Во внешнем пространстве силовые линии напряженности электрического поля разноименно заряженных пластин имеют противоположное направление, поэтому вне конденсатора результирующее значение напряженности электрического поля практически равно нулю (рис. 66).