| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
Используя модель идеального газа, вычислим давление газа на стенку сосуда. Пусть в сферическом сосуде радиусом  находится N молекул идеального газа массой
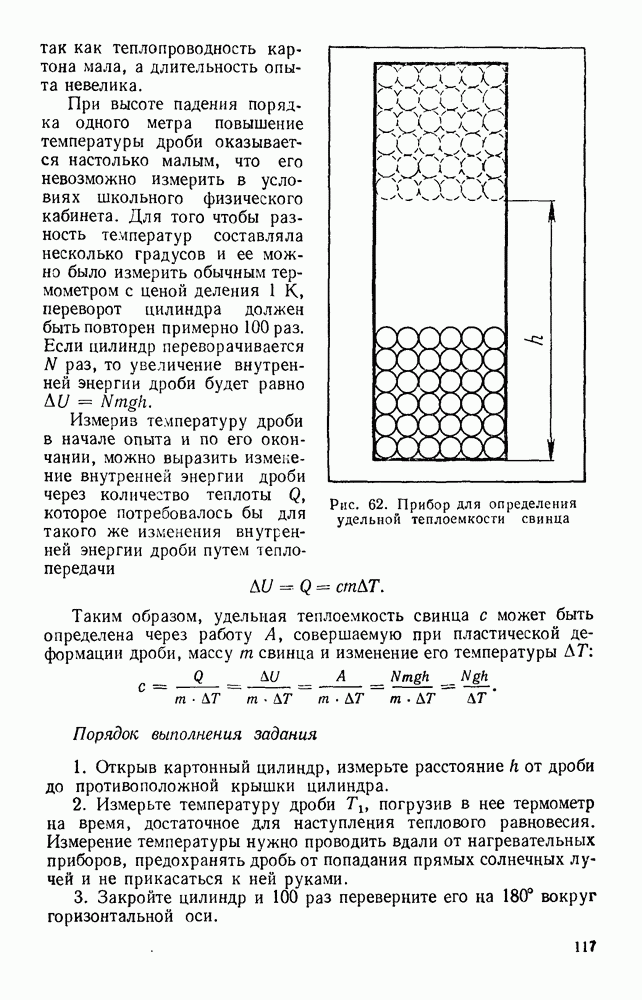
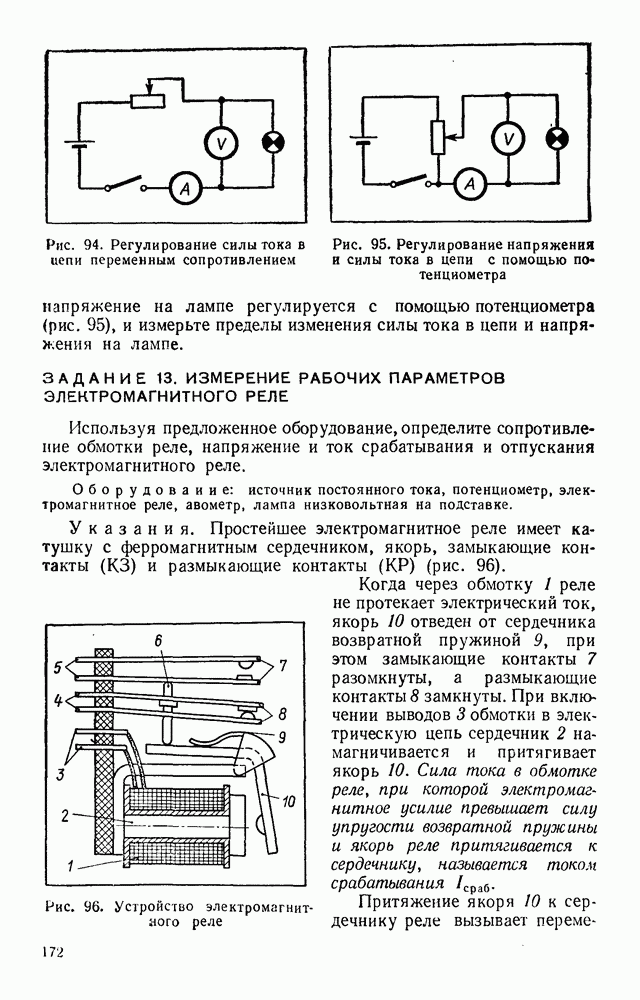
находится N молекул идеального газа массой  каждая. Согласно представлениям молекулярно-кинетической теории молекулы газа имеют различные скорости движения, движутся хаотически и испытывают упругие соударения между собой и со стенкой сосуда. Если не рассматривать взаимные соударения молекул, то, как следует из геометрических соображений, в результате упругих соударений со стенкой сферы траектория движения одной молекулы в таком сосуде должна быть ломаной линией ABCDE..., лежать в плоскости, проходящей через центр сферы, и состоять из отрезков равной длины (рис. 3).
каждая. Согласно представлениям молекулярно-кинетической теории молекулы газа имеют различные скорости движения, движутся хаотически и испытывают упругие соударения между собой и со стенкой сосуда. Если не рассматривать взаимные соударения молекул, то, как следует из геометрических соображений, в результате упругих соударений со стенкой сферы траектория движения одной молекулы в таком сосуде должна быть ломаной линией ABCDE..., лежать в плоскости, проходящей через центр сферы, и состоять из отрезков равной длины (рис. 3).
При каждом столкновении со стенкой нормальная (перпендикулярная стенке сосуда) составляющая импульса молекулы изменяется по направлению на 180°, оставаясь неизменной по модулю. Тангенциальная (касательная к поверхности сосуда) составляющая импульса остается неизменной, следовательно, изменение импульса молекулы, движущейся со скоростью  после одного столкновения со стенкой сосуда равно по модулю:
после одного столкновения со стенкой сосуда равно по модулю:

Подсчитаем сумму модулей изменения импульса одной молекулы при ударах о стенку сосуда за интервал времени  . Для этого умножим изменение импульса молекулы при одном столкновении на число ее столкновений
. Для этого умножим изменение импульса молекулы при одном столкновении на число ее столкновений  со стенкой сосуда за интервал времени Ы. Число столкновений молекулы со стенкой сосуда найдем, разделив путь, пройденный молекулой за время
со стенкой сосуда за интервал времени Ы. Число столкновений молекулы со стенкой сосуда найдем, разделив путь, пройденный молекулой за время  на длину пути между столкновениями d:
на длину пути между столкновениями d:

Отсюда сумма модулей изменений импульса молекулы или сумма модулей импульса, передаваемого молекулой стенке сосуда за время  равна:
равна:

Поскольку

то

Заменяя  получим:
получим:

где  — радиус сферы,
— радиус сферы,  — площадь ее поверхности. Используя далее
— площадь ее поверхности. Используя далее  получим:
получим:


Рис. 3. Траектория движения молекулы в сферическом сосуде
Удары о стенку сосуда  молекул, заключенных в нем и движущихся с различными скоростями
молекул, заключенных в нем и движущихся с различными скоростями  приводят к возникновению давления:
приводят к возникновению давления:

Введя обозначение для среднего значения квадрата скорости молекулы

и учитывая, что объем шара радиусом  равен:
равен:

получим:

Мы получили, что давление газа  пропорционально массе одной молекулы
пропорционально массе одной молекулы  концентрации молекул
концентрации молекул  и среднему квадрату скорости поступательного движения
и среднему квадрату скорости поступательного движения  при их хаотическом тепловом движении.
при их хаотическом тепловом движении.
Вывод получен для сосуда сферической формы и без учета столкновений молекул между собой. Более строгие вычисления дают точно такой же результат для сосуда произвольной формы и с учетом взаимных соударений молекул.
Используя выражение, определяющее кинетическую энергию Е поступательно движущегося со скоростью  тела массой
тела массой 

установим связь между средним значением кинетической энергии поступательного движения молекул Е и давлением газа на стенки сосуда  :
:

| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
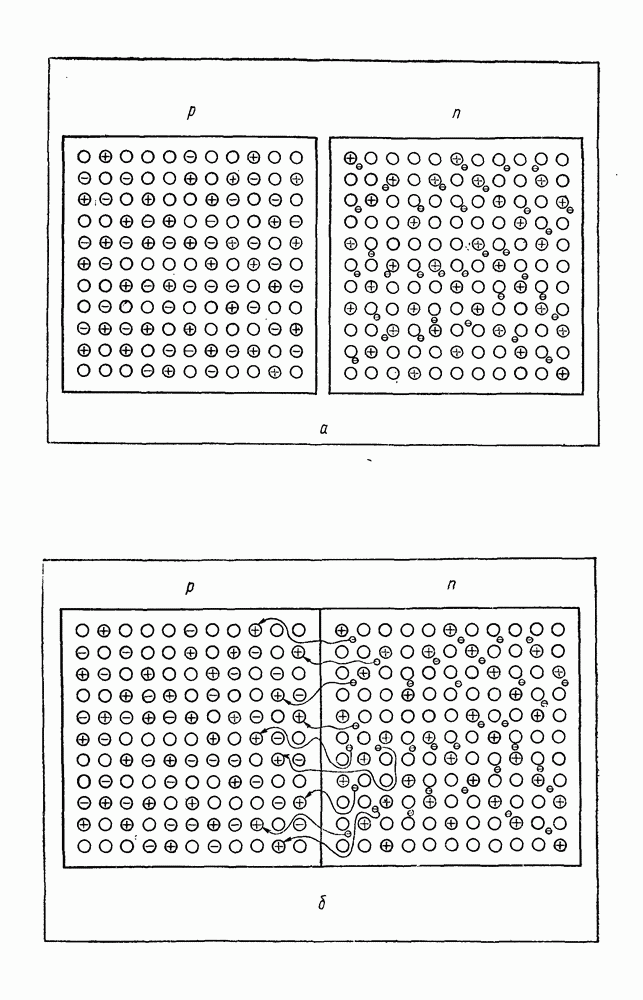
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
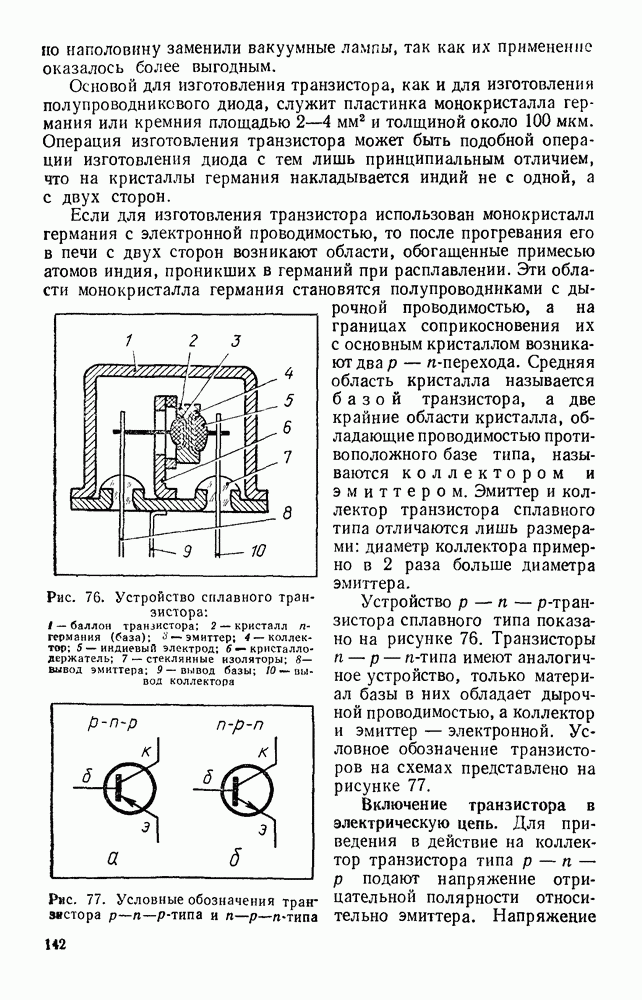
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
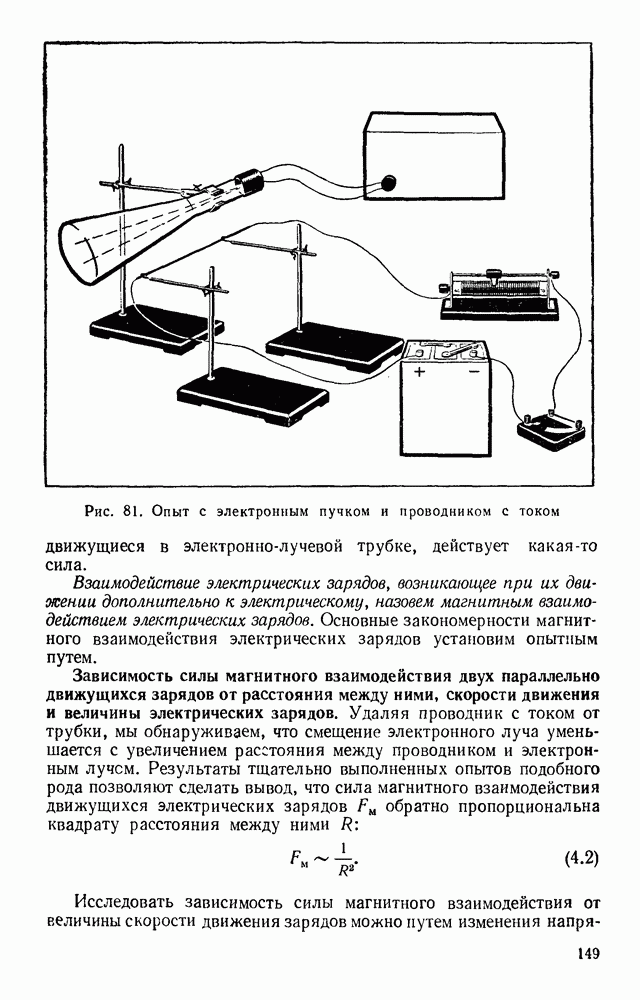
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
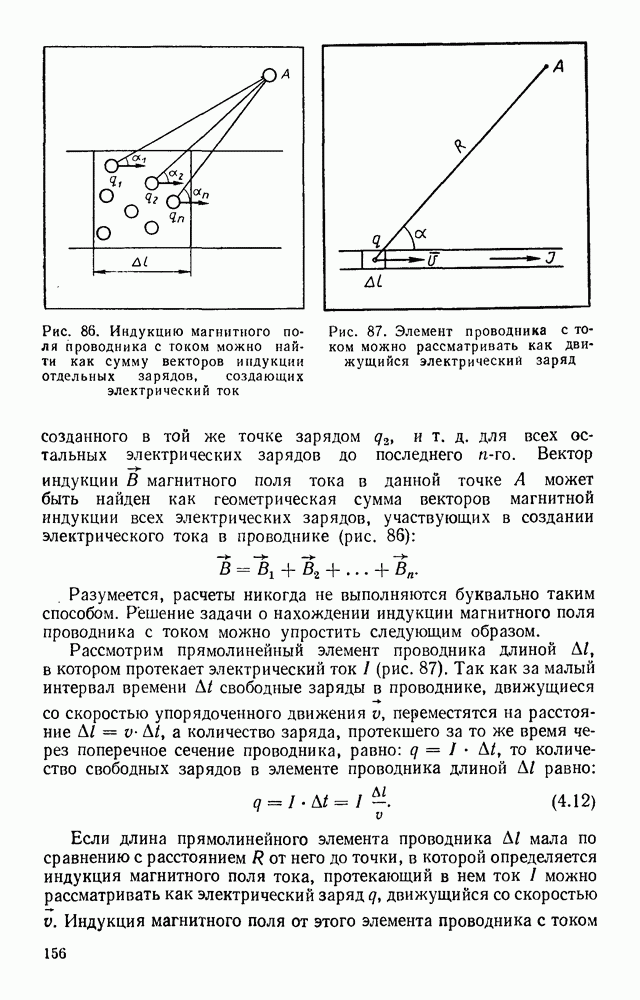
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
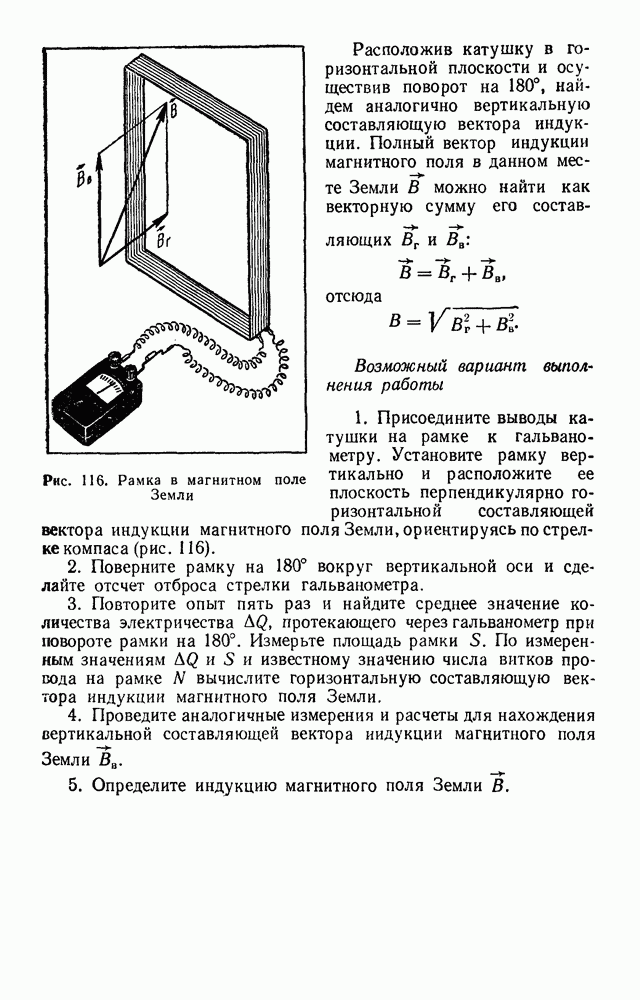
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ