| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ТЕРМОДИНАМИКА
Задача 23. Цилиндр длиной 11 см заполнен воздухом при нормальных условиях. Используя молекулярно-кинетическую теорию, оцените повышение температуры воздуха в цилиндре при сжатии воздуха, если поршень двигался со скоростью  и переместился на 10 см.
и переместился на 10 см.
Решение. При одном упругом столкновении с поршнем скорость молекулы газа увеличивается на  , где
, где  — скорость движения поршня. Оценим изменение температуры газа при условии, что все его молекулы испытали по одному столкновению с поршнем:
— скорость движения поршня. Оценим изменение температуры газа при условии, что все его молекулы испытали по одному столкновению с поршнем:

Так как  то второе слагаемое можно считать пренебрежимо малым, тогда
то второе слагаемое можно считать пренебрежимо малым, тогда

откуда

Для получения количественного результата используем исходные данные:

Для определения изменения температуры газа при перемещении поршня на 10 см нужно подсчитать число столкновений молекул с поршнем за время его движения. Приближенно это число можно определить, зная среднюю скорость движения поршня и длину пройденного им пути  Длительность интервала времени, в течение которого двигался поршень:
Длительность интервала времени, в течение которого двигался поршень:

Так как средняя скорость теплового движения молекулы в атмосферном воздухе при температуре 293 К равна примерно 500 м/с, за 0,1 с она проходит путь, равный

Если принять, что молекула движется в направлении, перпендикулярном поверхности поршня, и не испытывает столкновений с другими молекулами, то в начале интервала времени  от одного столкновения с поршнем до второго она проходила путь, равный
от одного столкновения с поршнем до второго она проходила путь, равный  а в конце интервала времени
а в конце интервала времени  этот путь сокращается до
этот путь сокращается до  Поэтому примем среднюю длину пути
Поэтому примем среднюю длину пути  молекулы между двумя столкновениями с поршнем равной
молекулы между двумя столкновениями с поршнем равной

Тогда число столкновений молекулы с поршнем  за время его движения
за время его движения  равно:
равно:

Увеличение температуры газа после 400 столкновений его молекул с поршнем должно быть равно:

Таким образом, мы получили качественное объяснение результатов опыта (см. с. 47) с помощью молекулярно-кинетической теории, так как увеличения температуры воздуха на 920 К вполне достаточно для зажигания ваты в «воздушном огниве».
Задача 24. Вычислите работу, совершаемую одним молем идеального газа при нагревании его на 1 К при постоянном давлении.
Решение

Мы получили, что при нагревании на 1 К при постоянном давлении 1 моль идеального газа совершает работу, численно равную молярной газовой постоянной 
Задача 25. Удельная теплоемкость кислорода при постоянном давлении равна  Определите удельную теплоемкость кислорода при постоянном объеме.
Определите удельную теплоемкость кислорода при постоянном объеме.

Задача 26. В квартире объемом  израсходовано количество теплоты
израсходовано количество теплоты  Дж на нагревание воздуха. Определите изменения внутренней энергии и температуры воздуха в квартире. Начальная температура воздуха в комнате 20 °С.
Дж на нагревание воздуха. Определите изменения внутренней энергии и температуры воздуха в квартире. Начальная температура воздуха в комнате 20 °С.
Решение. Согласно первому закону термодинамики изменение внутренней энергии  воздуха равно разности переданного ему количества теплоты
воздуха равно разности переданного ему количества теплоты  и работы А, совершенной воздухом:
и работы А, совершенной воздухом:

Так как квартира негерметична, нагревание воздуха в ней происходит при постоянном давлении. Для нахождения работы А совершенной воздухом при нагревании, воспользуемся уравнением состояния идеального газа и выражением, определяющим работу газа при изобарическом процессе:

Для нахождения изменения температуры  воздуха воспользуемся уравнением теплового баланса:
воздуха воспользуемся уравнением теплового баланса:  Тогда
Тогда

Используя данные задачи, получим:

Однако в действительности близким к истине при таком способе оказывается лишь расчет изменения температуры воздуха, а расчет изменения внутренней энергии в принципе неверен.
В задаче требуется определить увеличение внутренней энергии воздуха, находящегося в квартире. Часть воздуха при нагревании вышла из квартиры, и при расчете это изменение массы воздуха необходимо учитывать.
Произведем расчет другим способом. Считая воздух идеальным двухатомным газом, изменение внутренней энергии воздуха в квартире найдем как разность внутренней энергии  воздуха после нагревания и
воздуха после нагревания и  до нагревания:
до нагревания:

Число молекул воздуха до нагревания и  после нагревания найдем, используя уравнение состояния идеального газа:
после нагревания найдем, используя уравнение состояния идеального газа:

Аналогично можно получить:

Следовательно, при постоянном объеме и давлении внутренняя энергия идеального газа остается постоянной при любых
изменениях температуры газа. Этот парадоксальный результат является следствием того, что давление газа прямо пропорционально средней кинетической энергии молекул Е и их концентрации 

т. е. прямо пропорционально кинетической энергии молекул в единице объема газа.
Так как кинетическая энергия молекул в единице объема при постоянном давлении идеального газа остается постоянной, то и внутренняя энергия всего газа в сосуде постоянного объема при постоянном давлении остается одинаковой при любой температуре. Качественно этот результат можно объяснить тем, что при нагревании идеального газа при постоянном давлении увеличение его внутренней энергии за счет повышения температуры в сосуде постоянного объема в точности равно уменьшению внутренней энергии за счет выхода части молекул газа из сосуда.
Задача 27. Одним из способов получения высоких температур является адиабатическое сжатие газов. Для этого можно воспользоваться, например, толстостенным цилиндром, закрытым с обеих сторон, с перемещающимся в нем поршнем. По одну сторону от поршня помещается пороховой заряд, а по другую — газ. При взрыве пороха поршень «выстреливается» и производит адиабатическое сжатие газа в трубе.
Вычислите максимальное нагревание 2 г водорода при сжатии таким образом, если пороховой заряд сообщает поршню массой 10 кг начальную скорость 1 км/с.
Решение

Полученный результат представляет собой лишь оценку изменения температуры водорода, так как в расчетах не учитывались такие явления, как распад молекул и ионизация атомов водорода при высоких температурах.
Задача 28. Кабина космического корабля объемом  заполнена кислородом при температуре 20° С и давлении
заполнена кислородом при температуре 20° С и давлении  Па. Сколько времени может пребывать космонавт массой 70 кг в этой
Па. Сколько времени может пребывать космонавт массой 70 кг в этой
кабине, если перестанут работать системы, обеспечивающие постоянство состава искусственной атмосферы, ее температуры и давления? Кабину корабля можно считать теплоизолированной.
Приблизительные данные о жизнедеятельности человеческого организма:
суточное потребление кислорода — 1 кг,
суточное потребление снергии —  Дж.
Дж.
Решение. Оценим сначала массу кислорода в кабине космического корабля.

Расчет показывает, что запаса кислорода в кабине достаточно более чем на 5 сут. Оценим теперь время, в течение которого тепло, выделяемое в процессе жизнедеятельности человеческого организма, вызовет нагревание атмосферы в кабине от 20 до 37 °С. В расчете будем сначала полагать, что вся потребляемая человеческим организмом энергия расходуется на нагревание атмосферы корабля.

Далее теплопередачу атмосфере можно не учитывать, так как масса тела космонавта значительно больше массы атмосферы в корабле. Приняв за максимально допустимое значение температуры тела космонавта 42 °С, произведем расчет, учитывая лишь нагревание тела космонавта. Удельную теплоемкость тела человека примем равной удельной теплоемкости воды:

Такое изменение температуры тела лежит за пределами биологических возможностей человека. Полученный результат показывает, что система терморегулирования в космическом корабле играет очень важную роль, без нее длительное существование человека в замкнутом теплоизолированном пространстве малого объема невозможно.
Задача 29. В цилиндре тепловой машины заключен один моль одноатомного идеального газа. Определите КПД тепловой машины, если изменение состояния газа в цилиндре осуществляется по циклу, представленному на рисунке 54.

Из уравнения Клапейрона—Менделеева для состояний А и В получим:

Далее аналогично получим для состояний В и С;

Обозначив  подставим найденные значения
подставим найденные значения  в выражение для КПД:
в выражение для КПД:

Так как  получаем:
получаем:

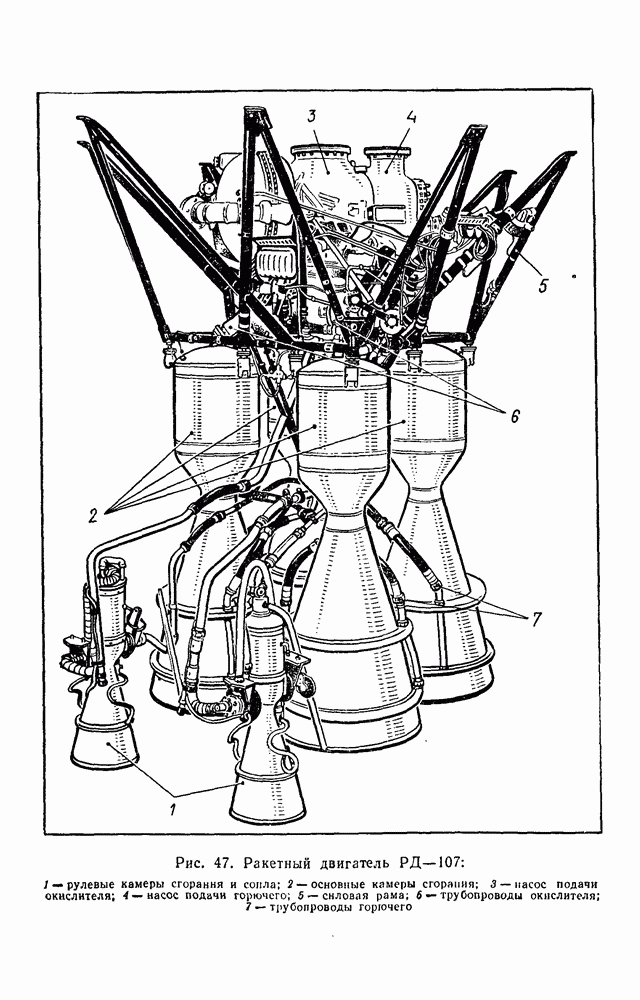
Задача 30. Первая ступень американской ракеты-носителя «Сатурн-5», которая использовалась для запуска космических кораблей «Аполлон» на Луну,

Рис. 54. К задаче 29
имеет пять жидкостных ракетных двигателей. Эти пять двигателей расходуют  кг горючего и окислителя в секунду, выбрасывая продукты сгорания со скоростью
кг горючего и окислителя в секунду, выбрасывая продукты сгорания со скоростью  Масса космической ракеты на старте равна
Масса космической ракеты на старте равна  кг, из них примерно
кг, из них примерно  кг приходится на горючее и окислитель.
кг приходится на горючее и окислитель.
Вычислите силу тяги двигателей первой ступени ракеты и КПД ракеты как тепловой машины. Рассматривая ракету как машину для разгона космического корабля, масса которого равна 4-104 кг, оцените ее КПД через 1 с после начала работы двигателей и в конце работы двигателей, когда космический корабль достигает скорости  .
.
Теплотворная способность на 1 кг горючего и окислителя для двигателей всех ступеней ракеты примерно одинакова и равна 

При оценке КПД ракеты как машины для разгона космического корабля полезная работа равна кинетической энергии космического корабля. Скорость космического корабля через 1 с после начала работы двигателей первой ступени можно найти, считая, что в течение 1 с масса ракеты остается практически неизменной. Тогда на основании закона сохранения импульса 

Отсюда КПД ракеты за 1 с после начала работы двигателей первой ступени равен:

По окончании работы двигателей всех ступеней КПД ракеты оказывается равным:

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
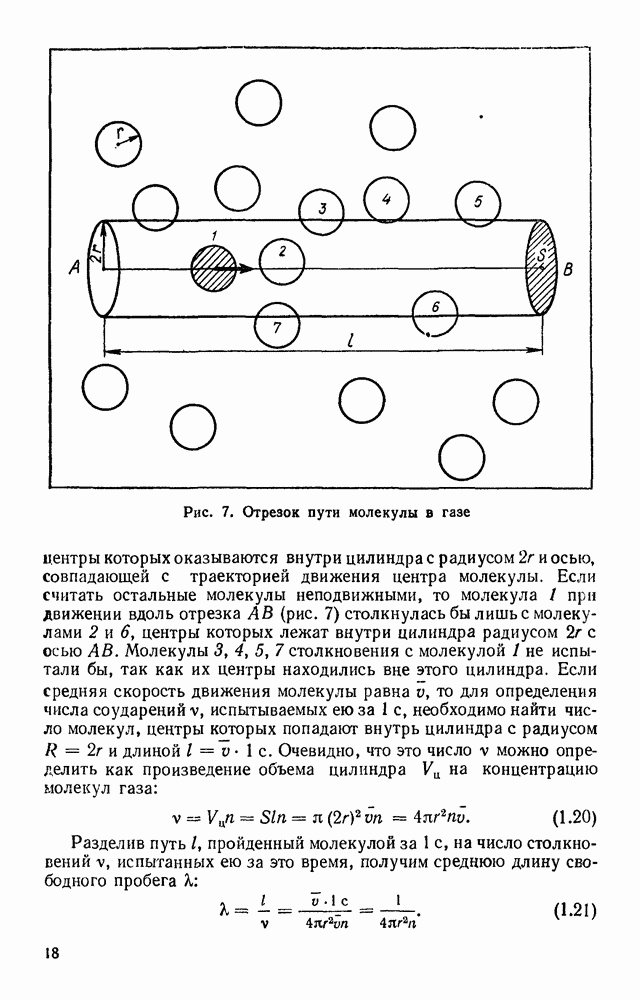
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
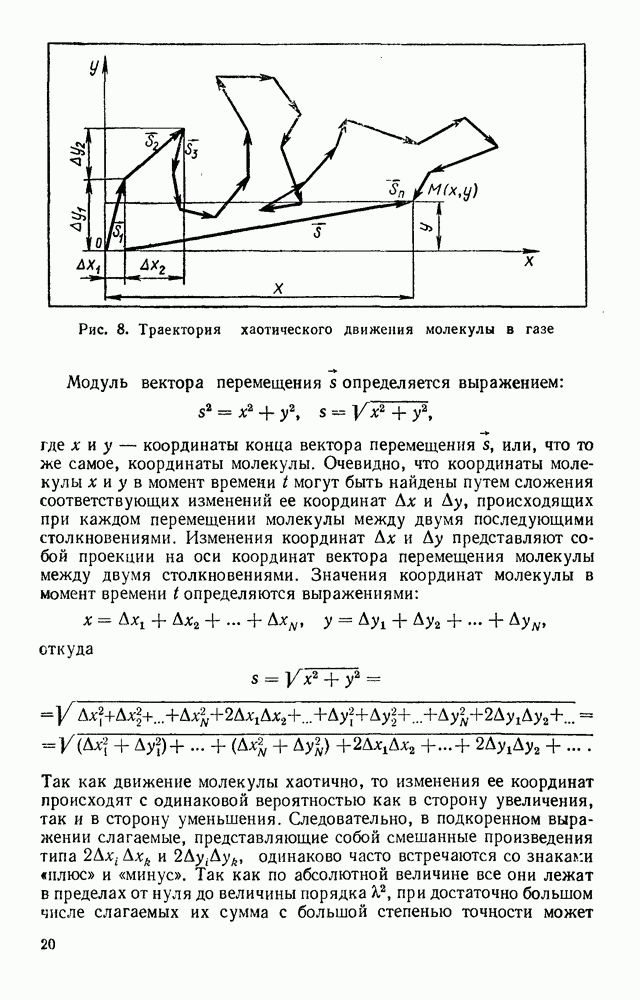
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
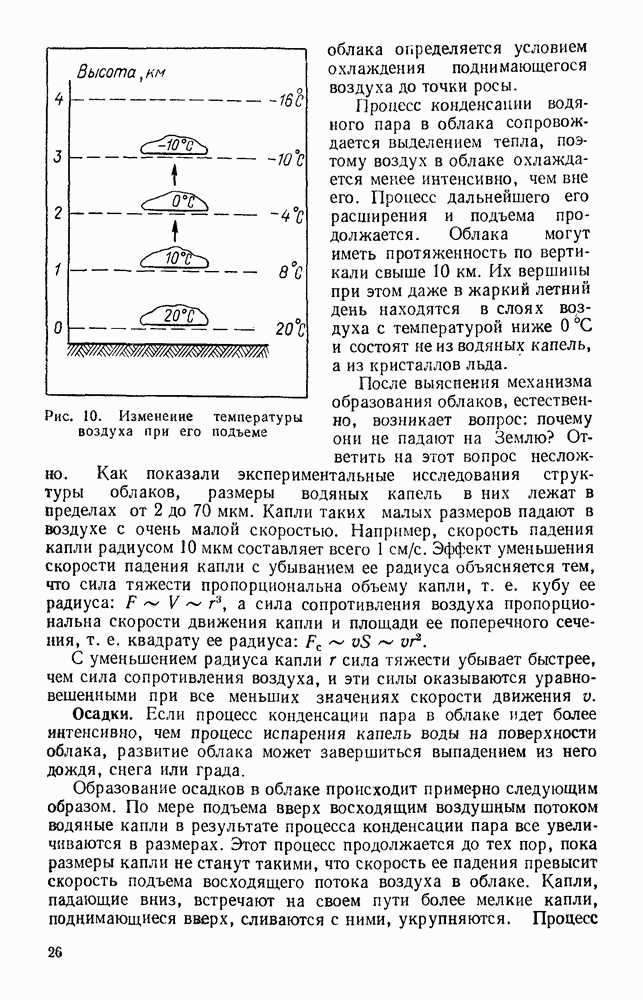
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
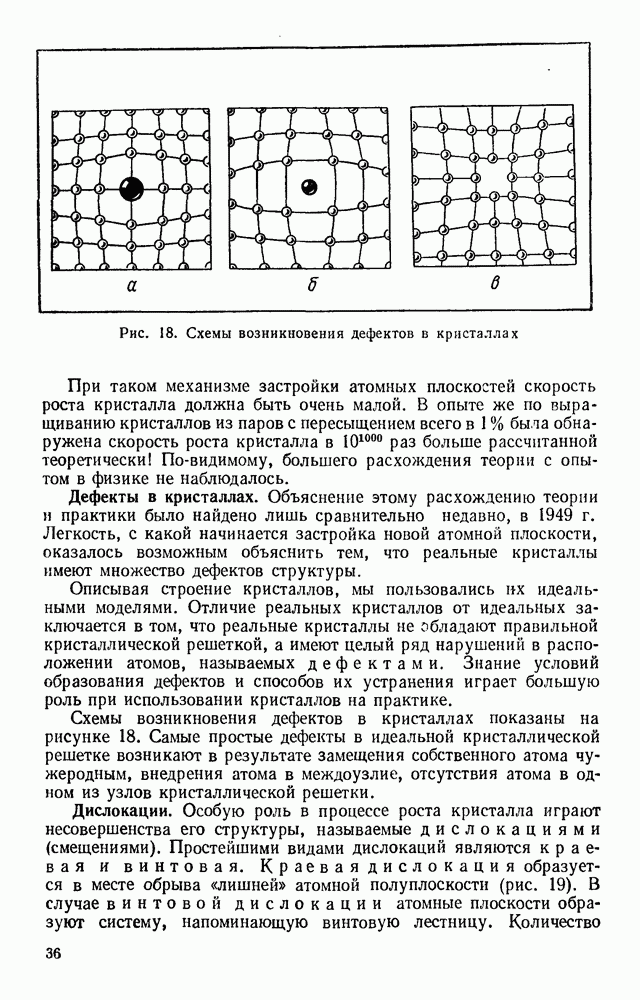
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
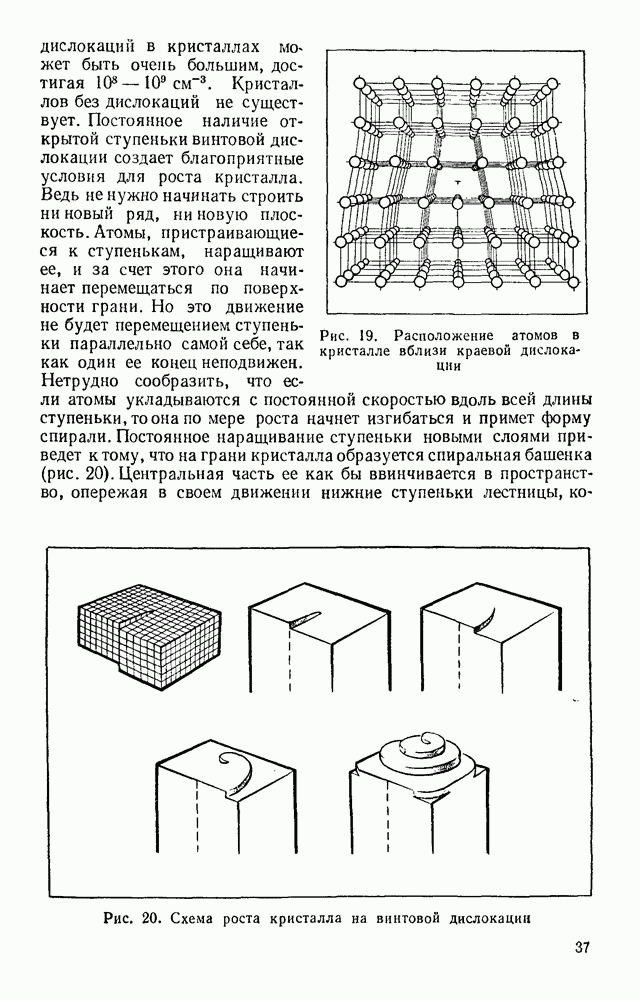
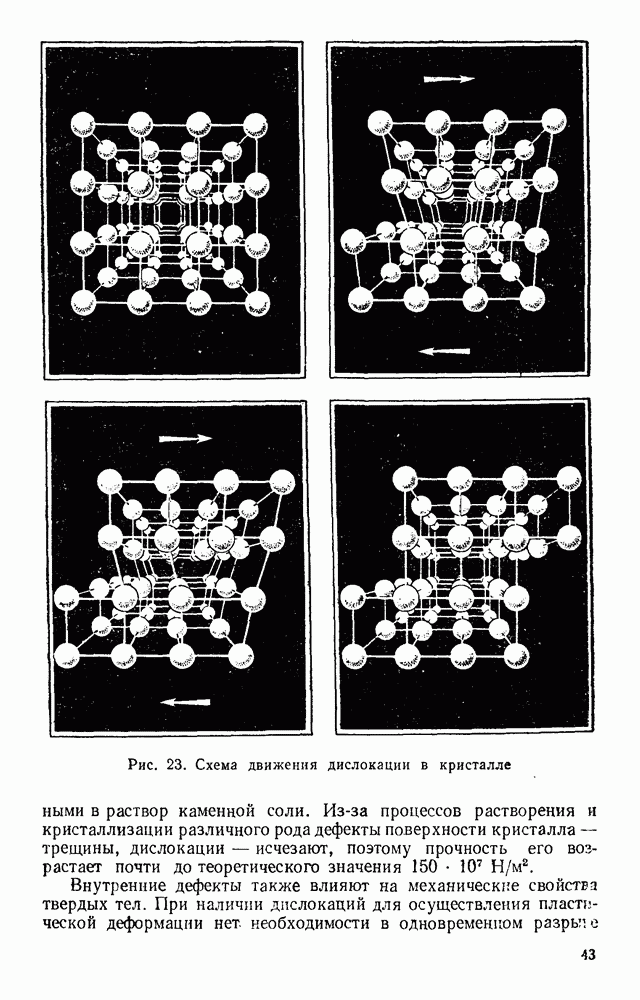
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
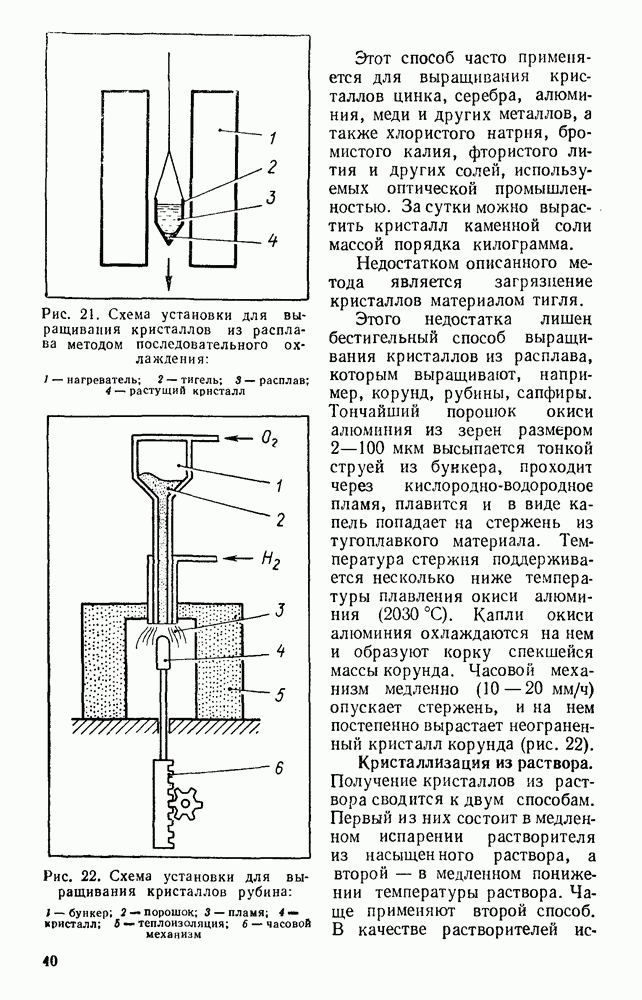
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
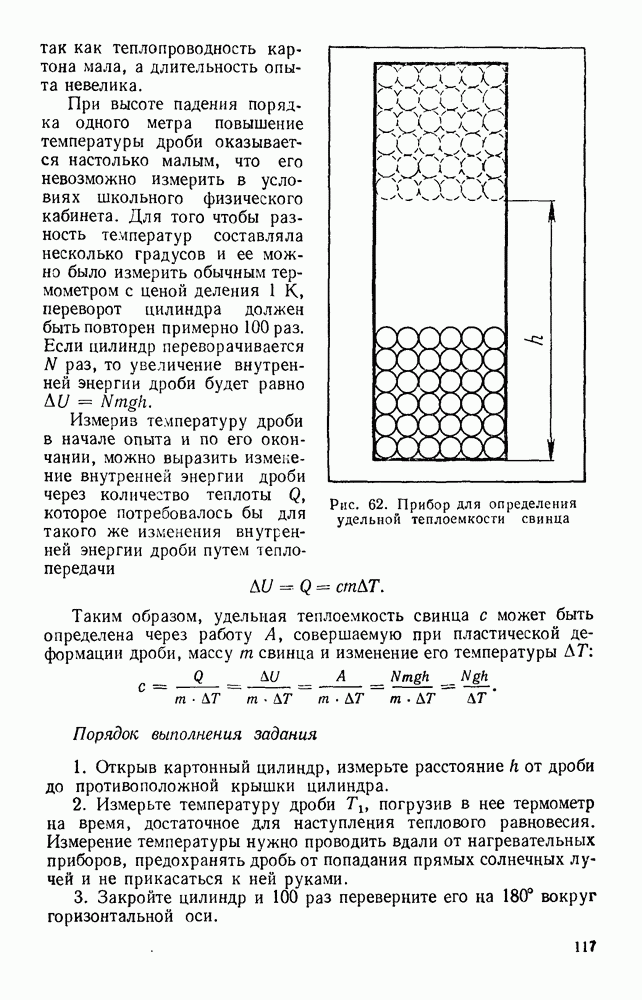
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
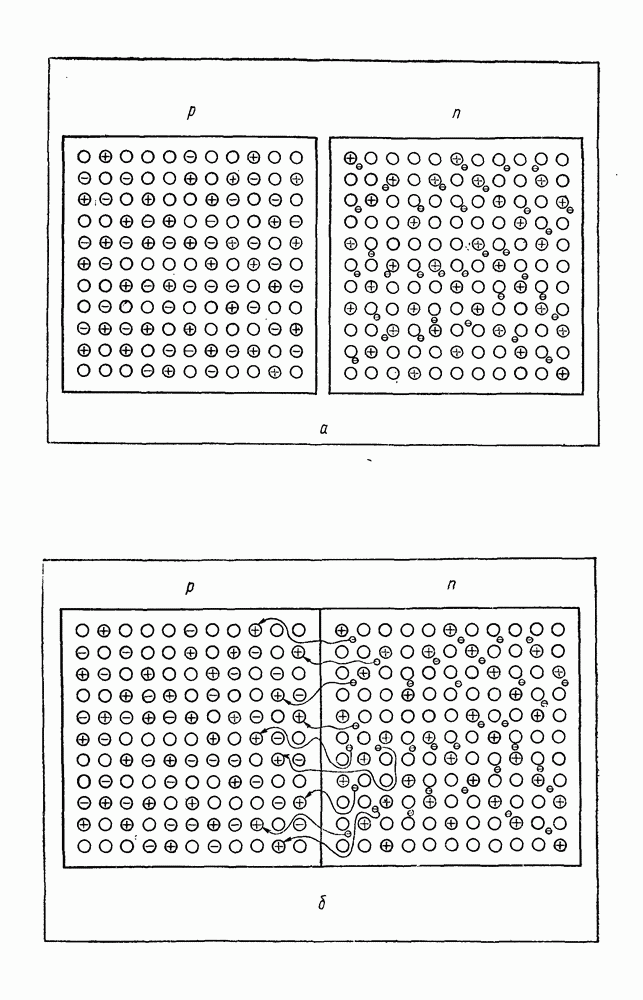
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
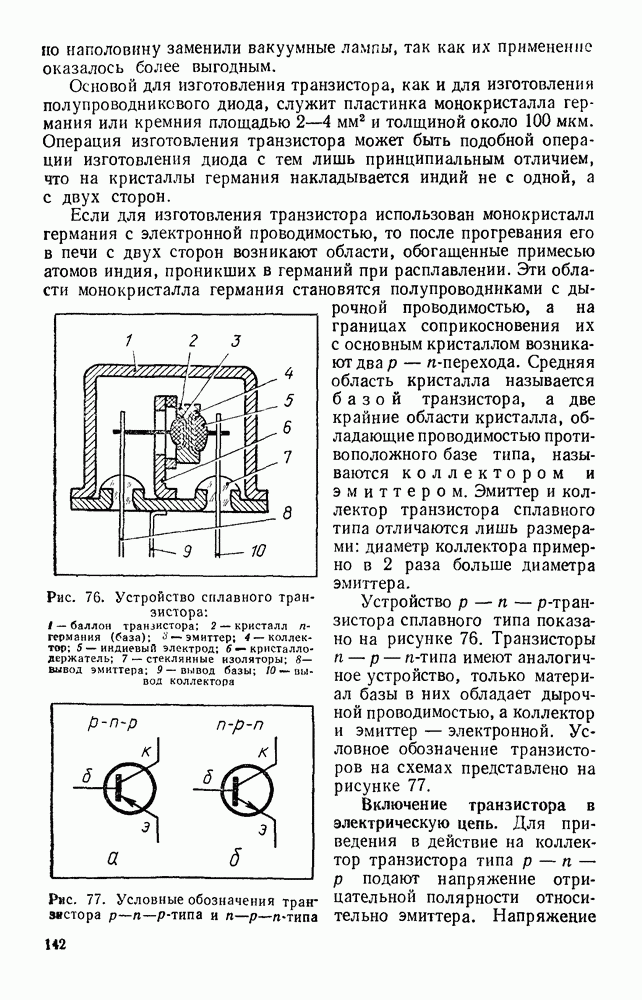
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
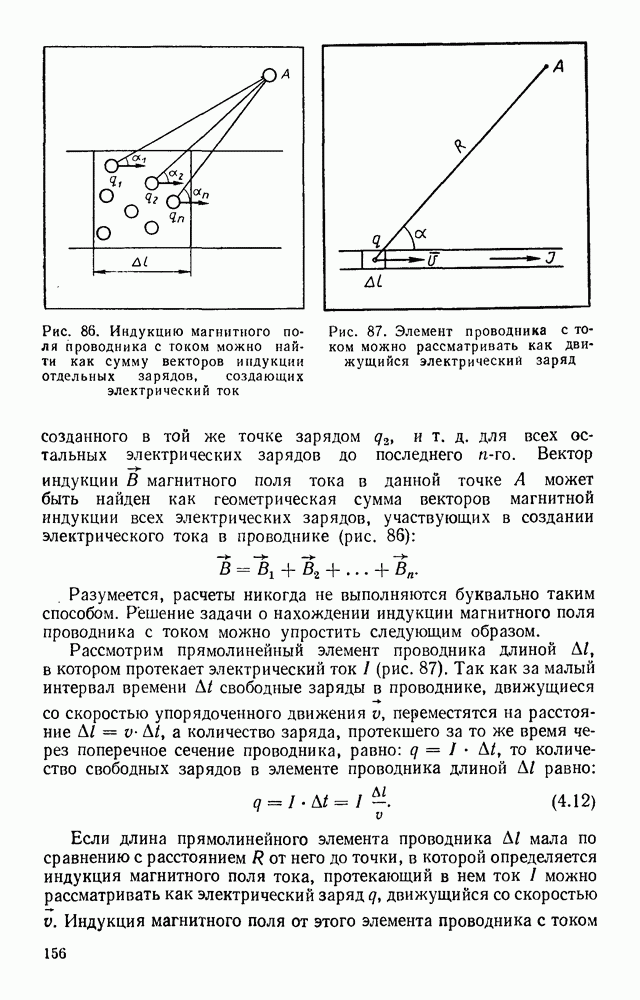
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ