| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 8. РЕАЛЬНЫЕ ГАЗЫ
Уравнение Клапейрона — Менделеева было получено на основе обобщения экспериментальных данных о свойствах реальных газов раньше, чем была создана молекулярно-кинетическая теория и получено уравнение состояния идеального газа. Совпадение уравнения Клапейрона—Менделеева с полученным теоретически уравнением состояния идеального газа свидетельствовало о больших возможностях применения молекулярно-кинетической теории в практике. Однако экспериментальные исследования свойств газов при высоких давлениях и низких температурах, выполненные еще в конце прошлого века, убедительно показали, что уравнение состояния идеального газа дает хорошее согласие с экспериментом для каждого исследуемого газа лишь при температурах выше некоторого значения, вполне определенного для каждого вещества, и при не очень высоких давлениях. Расхождение результатов теории и практики в области низких температур и высоких давлений газоз свидетельствует о непригодности при этих условиях упрощенной модели строения газов, в которой не учитываются размеры молекул и силы их взаимного притяжения.
Уравнение Ван-дер-Ваальса. В 1873 г. голландский физик Ван-дер-Ваальс показал, что согласие результатов теории и эксперимента оказывается значительно лучшим, если изменить представления о свойствах молекул и считать, что они не только отталкиваются при непосредственном соприкосновении, но еще и притягиваются сравнительно слабыми силами на расстояниях, сравнимых с размерами молекул. При движении молекулы вдали от стенок сосуда, в который заключен газ, на нее действуют силы притяжения соседних с ней газовых молекул, но равнодействующая всех этих сил в среднем равна нулю, так как молекула испытывает одинаковое притяжение по всем направлениям.
При приближении одной молекулы к стенке сосуда все остальные молекулы газа оказываются по одну сторону от нее и равнодействующая всех сил взаимодействия направлена от стенки сосуда. Молекулы газа своим притяжением как бы притормаживают каждую молекулу, движущуюся к стенке сосуда, и уменьшают величину импульса, передаваемого молекулой стенке сосуда. В результате давление газа на стенки сосуда оказывается меньшим, чем оно было бы в отсутствие сил притяжения между молекулами.
Уменьшение импульса, переданного одной молекулой при ударе о стенку, пропорционально силе притяжения, действующей на эту молекулу со стороны ее ближайших соседей, т. е. пропорционально концентрации молекул  Полный же импульс, передаваемый всеми молекулами газа стенкам сосуда, в свою очередь пропорционален их концентрации
Полный же импульс, передаваемый всеми молекулами газа стенкам сосуда, в свою очередь пропорционален их концентрации  . Таким образом, взаимное притяжение газовых молекул уменьшает давление газа на стенки сосуда на величину, пропорциональную
. Таким образом, взаимное притяжение газовых молекул уменьшает давление газа на стенки сосуда на величину, пропорциональную  , или для заданной массы газа
, или для заданной массы газа  обратно пропорциональную квадрату занимаемого газом объема V.
обратно пропорциональную квадрату занимаемого газом объема V.
Уравнение состояния для одного моля идеального газа  можно записать в виде
можно записать в виде

Для одного моля реального газа с учетом эффекта взаимного притяжения молекул уравнение состояния запишется в виде

или

Приведенные рассуждения могут показаться неправдоподобными, так как в них учитывается притяжение между молекулами газа, но не учитывается возможность существования сил притяжения между молекулами газа и молекулами стенки сосуда. И так как концентрация молекул в твердом веществе обычно значительно превосходит концентрацию их в газе, притяжение молекул стенок сосуда, казалось бы, должно значительно превосходить противоположно направленное притяжение молекул газа.
На молекулу газа, приближающуюся к стенке сосуда, конечно, действуют силы притяжения ее молекул, и величина их может быть большой. Но независимо от величины этих сил их влияние на процесс взаимодействия молекулы со стенкой сосуда в конечном счете оказывается нулевым и поэтому не учитывается.
Вторую поправку в уравнение, описывающее состояние реального газа, Ван-дер-Ваальс ввел, руководствуясь следующими соображениями. Молекулы реального газа занимают часть объема сосуда, и движение молекул газа происходит как бы не во всем объеме V сосуда, а в уменьшенном на некоторую величину  . С введением второй поправки уравнение состояния реального газа для одного моля приобретает вид:
. С введением второй поправки уравнение состояния реального газа для одного моля приобретает вид:

Это уравнение называется уравнением Ван-дер-Ваальса.
Хотя уравнение Ван-дер-Ваальса дает лучшее согласие теории с результатами эксперимента, точность расчетов, выполненных на его основе, обычно оказывается недостаточной для решения практических задач на уровне требований современной техники. Поэтому в практике приходится использовать уравнения состояния реального газа еще более сложного вида. Уравнение же Ван-дер-Ваальса интересно тем, что дает качественное объяснение основных отличий в поведении реального газа от идеального.
| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
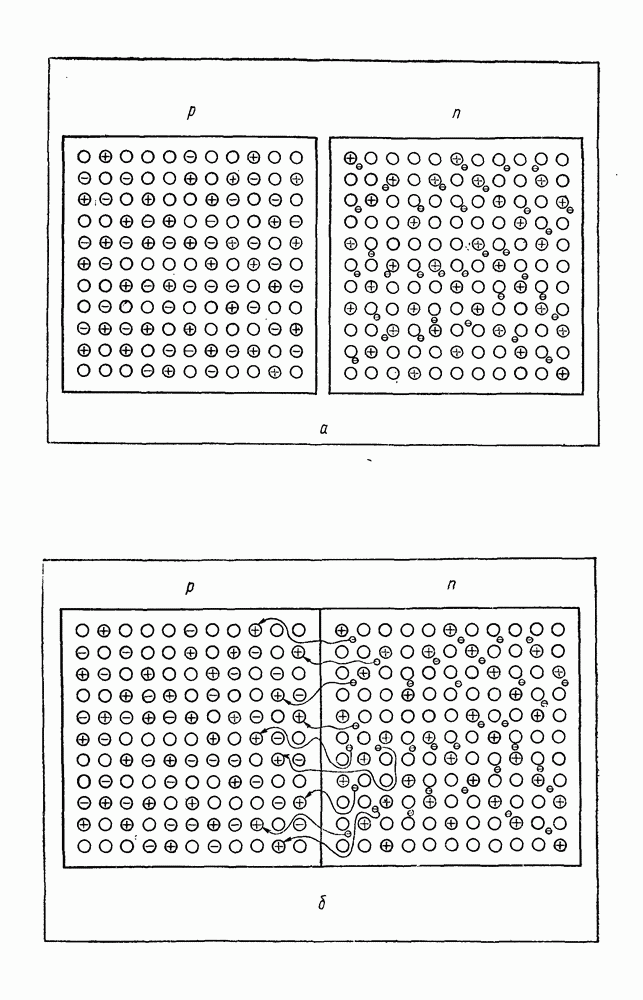
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
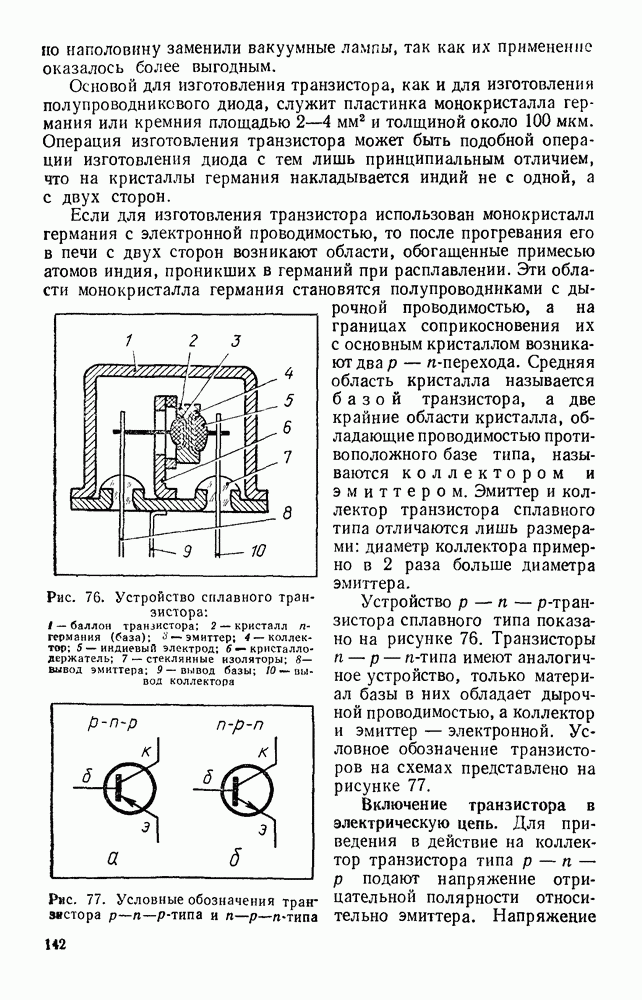
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
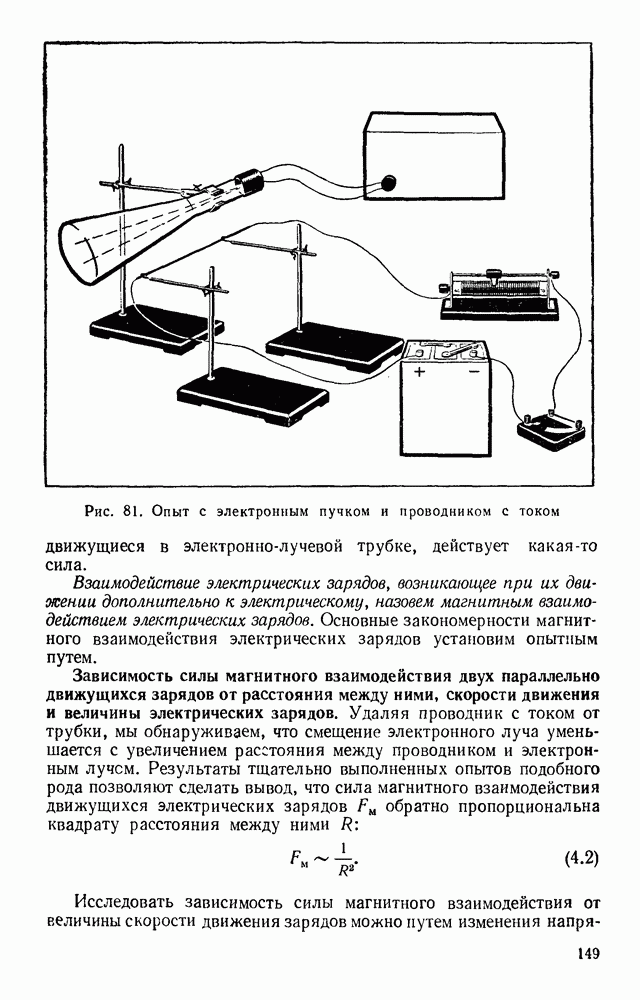
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
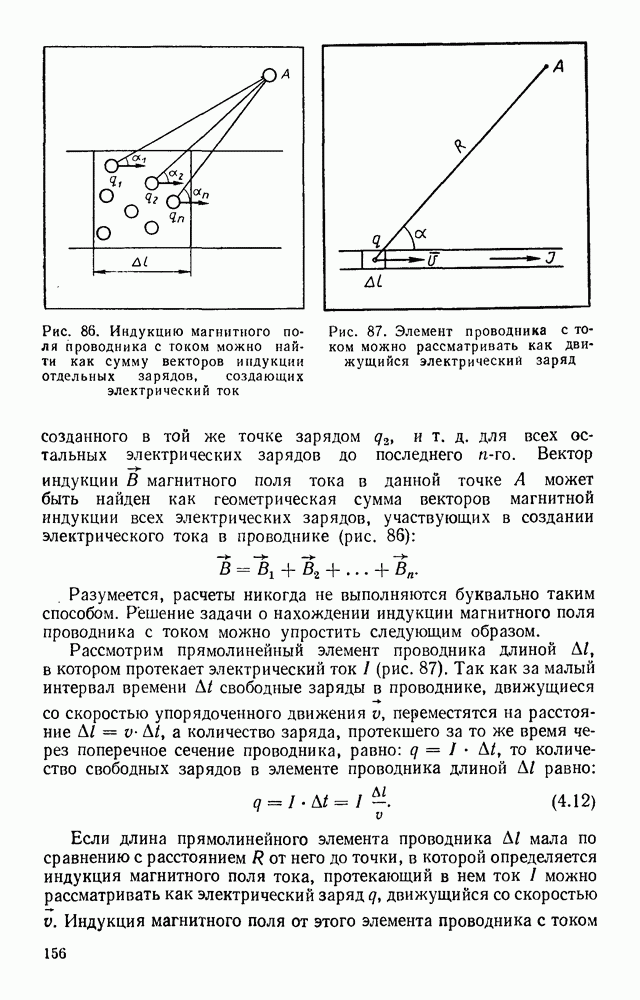
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ