| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
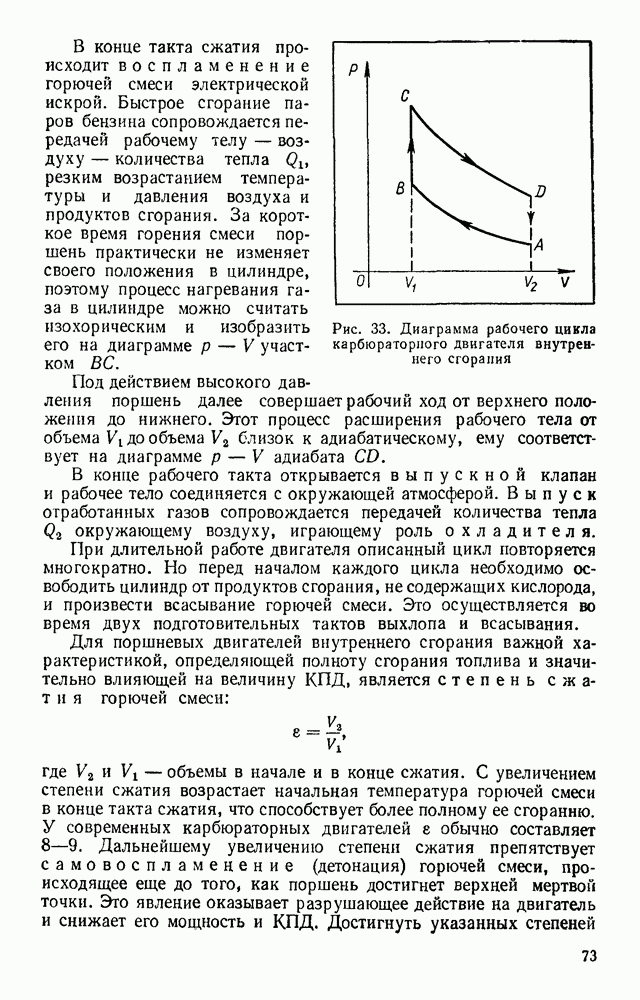
§ 34. ПОТЕНЦИАЛ
Работа при перемещении заряда в электрическом поле. При перемещении заряда в электрическом поле совершается работа. Выясним сначала, от чего зависит работа в поле точечного заряда. Два наиболее простых случая — это перемещение вдоль линий напряженности электрического поля и в направлении, перпендикулярном этим линиям. При перемещении заряда  в направлении действия силы
в направлении действия силы  вдоль линии напряженности
вдоль линии напряженности

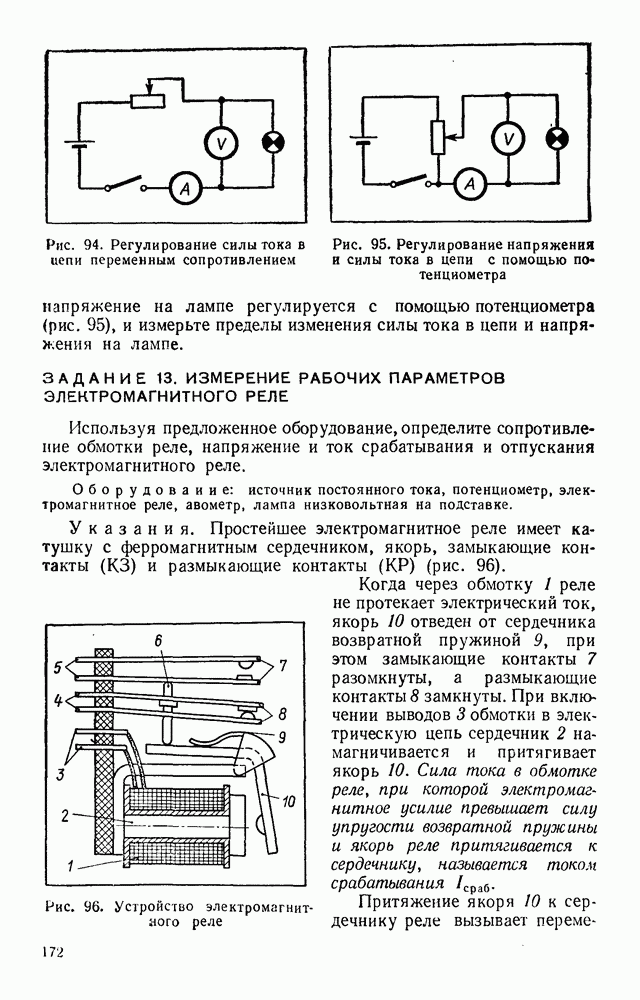
Рис. 66. Электрическое поле плоского конденсатора

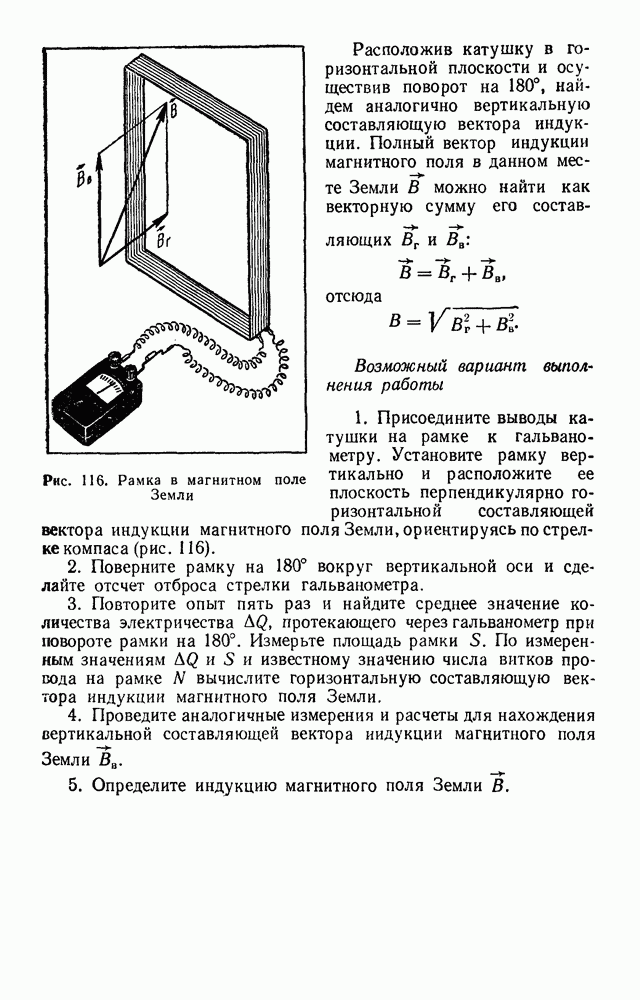
Рис. 67. Перемещение заряда вдоль ланий напряженности электрического поля
работа положительна, при движении в противоположном направлении — отрицательна.
В результате перенос заряда  например, из точки А сначала в точку С (рис. 67), а затем из точки С в точку А сопровождается совершением суммарной работы электрического поля, равной нулю, так как
например, из точки А сначала в точку С (рис. 67), а затем из точки С в точку А сопровождается совершением суммарной работы электрического поля, равной нулю, так как 
А. Поэтому перемещение заряда  в электрическом поле точечного заряда
в электрическом поле точечного заряда  из точки А в точку В по путям
из точки А в точку В по путям  или
или  сопровождается совершением одинаковой работы.
сопровождается совершением одинаковой работы.
Сила  взаимодействия заряда
взаимодействия заряда  с электрическим полем точечного заряда изменяется по одному и тому же закону в зависимости от расстояния до заряда
с электрическим полем точечного заряда изменяется по одному и тому же закону в зависимости от расстояния до заряда  вдоль любой из линий напряженности. Поэтому работа по перемещению электрического заряда
вдоль любой из линий напряженности. Поэтому работа по перемещению электрического заряда  вдоль различных линий напряженности при одинаковых расстояниях от заряда начальной и конечной точек пути оказывается одинаковой. При перемещении заряда
вдоль различных линий напряженности при одинаковых расстояниях от заряда начальной и конечной точек пути оказывается одинаковой. При перемещении заряда  по поверхности сферы, центр которой совпадает с зарядом
по поверхности сферы, центр которой совпадает с зарядом  электрическое поле заряда
электрическое поле заряда  не совершает работы, так как в любой точке пути направление вектора перемещения оказывается перпендикулярным направлению вектора силыэ.
не совершает работы, так как в любой точке пути направление вектора перемещения оказывается перпендикулярным направлению вектора силыэ.
Рассмотрим теперь перемещение заряда  из точки А в точку В при произвольном их расположении в поле точечного заряда
из точки А в точку В при произвольном их расположении в поле точечного заряда  Траекторию АВ движения заряда можно представить состоящей из чередующихся участков пути, совпадающих с линиями напряженности, и дуг окружностей, центр которых совпадает с зарядом
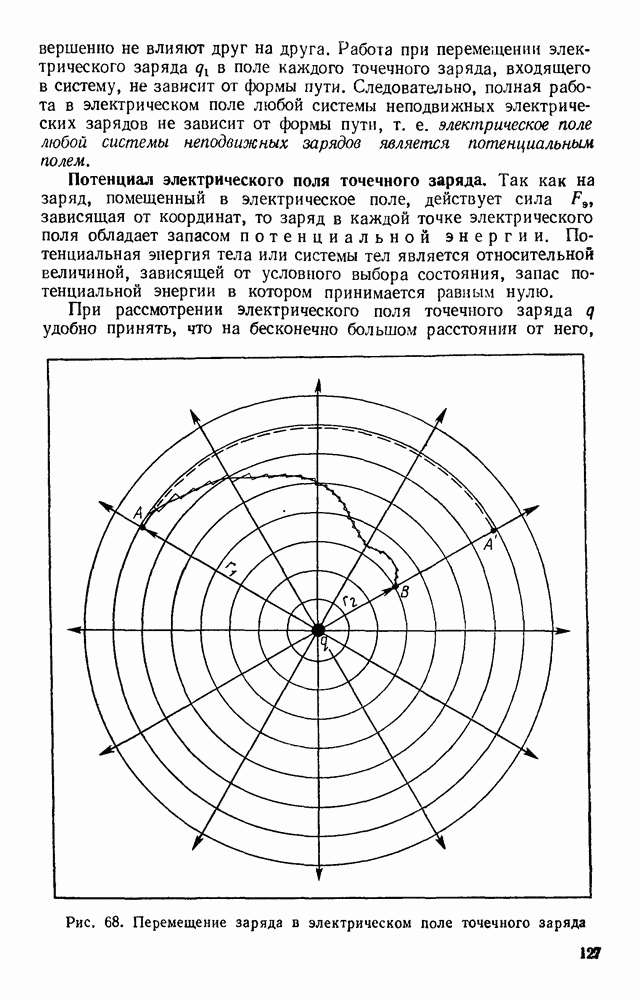
Траекторию АВ движения заряда можно представить состоящей из чередующихся участков пути, совпадающих с линиями напряженности, и дуг окружностей, центр которых совпадает с зарядом  (рис. 68). При перемещении заряда
(рис. 68). При перемещении заряда  по дугам окружностей работа электрического поля равна нулю, при перемещении вдоль любой линии напряженности работа на одинаковом расстоянии от заряда
по дугам окружностей работа электрического поля равна нулю, при перемещении вдоль любой линии напряженности работа на одинаковом расстоянии от заряда  одинакова. Поэтому работа при любом перемещении заряда
одинакова. Поэтому работа при любом перемещении заряда  в поле точечного заряда
в поле точечного заряда  из точки А на расстоянии
из точки А на расстоянии  от заряда
от заряда  до точки В на расстоянии
до точки В на расстоянии  от заряда
от заряда  равна работе по перемещению того же заряда
равна работе по перемещению того же заряда  вдоль одной силовой линии между точками, находящимися на расстояниях
вдоль одной силовой линии между точками, находящимися на расстояниях  от заряда
от заряда  . Следовательно, работа электрического поля точечного заряда при перемещении любого заряда из одной точки поля в другую не зависит от формы пути. Поля, обладающие таким свойством, называются потенциальными полями.
. Следовательно, работа электрического поля точечного заряда при перемещении любого заряда из одной точки поля в другую не зависит от формы пути. Поля, обладающие таким свойством, называются потенциальными полями.
В любой системе электрических зарядов электрические поля отдельных точечных зарядов согласно принципу суперпозиции
совершенно не влияют друг на друга. Работа при перемещении электрического заряда  в поле каждого точечного заряда, входящего в систему, не зависит от формы пути. Следовательно, полная работа в электрическом поле любой системы неподвижных электрических зарядов не зависит от формы пути, т. е. электрическое поле любой системы неподвижных зарядов является потенциальным полем.
в поле каждого точечного заряда, входящего в систему, не зависит от формы пути. Следовательно, полная работа в электрическом поле любой системы неподвижных электрических зарядов не зависит от формы пути, т. е. электрическое поле любой системы неподвижных зарядов является потенциальным полем.
Потенциал электрического поля точечного заряда. Так как на заряд, помещенный в электрическое поле, действует сила  зависящая от координат, то заряд в каждой точке электрического поля обладает запасом потенциальной энергии. Потенциальная энергия тела или системы тел является относительной величиной, зависящей от условного выбора состояния, запас потенциальной энергии в котором принимается равным нулю.
зависящая от координат, то заряд в каждой точке электрического поля обладает запасом потенциальной энергии. Потенциальная энергия тела или системы тел является относительной величиной, зависящей от условного выбора состояния, запас потенциальной энергии в котором принимается равным нулю.
При рассмотрении электрического поля точечного заряда  удобно принять, что на бесконечно большом расстоянии от него,
удобно принять, что на бесконечно большом расстоянии от него,
Рис. 68. (см. скан) Перемещение заряда в электрическом поле точечного заряда
где напряженность поля стремится к нулю, потенциальная энергия взаимодействия любого другого заряда  с зарядом
с зарядом  равна нулю. При таком условии потенциальную энергию
равна нулю. При таком условии потенциальную энергию  заряда
заряда  в точке, находящейся на расстоянии
в точке, находящейся на расстоянии  от заряда
от заряда  можно найти, вычислив работу, совершаемую полем при перемещении заряда
можно найти, вычислив работу, совершаемую полем при перемещении заряда  из этой точки на бесконечно большое расстояние от заряда
из этой точки на бесконечно большое расстояние от заряда 
При перемещении заряда работа электрического поля равна изменению потенциальной энергии заряда, взятому с обратным знаком:

Если  т. е. заряд
т. е. заряд  удаляется на бесконечно большое расстояние от заряда
удаляется на бесконечно большое расстояние от заряда  то
то

т. е. потенциальная энергия заряда  в электрическом поле равна работе электрического поля, совершаемой при удалении заряда на бесконечно большое расстояние от заряда
в электрическом поле равна работе электрического поля, совершаемой при удалении заряда на бесконечно большое расстояние от заряда 
Работа электрического поля пропорциональна силе  действующей на заряд
действующей на заряд  со стороны электрического поля:
со стороны электрического поля:

а сила  пропорциональна перемещаемому заряду
пропорциональна перемещаемому заряду  так как в любой точке поля равна:
так как в любой точке поля равна:

Следовательно, потенциальная энергия  заряда в электрическом поле пропорциональна заряду:
заряда в электрическом поле пропорциональна заряду:

Величина  определяемая как отношение потенциальной энергии
определяемая как отношение потенциальной энергии  заряда в данной точке электрического поля к заряду
заряда в данной точке электрического поля к заряду

является энергетической характеристикой поля в данной точке и называется потенциалом поля.
Связь между потенциалом электрического поля в данной точке и потенциальной энергией заряда позволяет выразить работу электрического поля при перемещении заряда из одной точки в другую через разность потенциалов поля в этих точках:

При перемещении заряда  в электрическом поле неподвижных варядов работа равна произведению заряда
в электрическом поле неподвижных варядов работа равна произведению заряда  на разность потенциалов начальной и конечной точек пути.
на разность потенциалов начальной и конечной точек пути.
Найдем потенциал электрического поля на расстоянии  от точечного заряда
от точечного заряда  Для этого сначала определим работу, совершаемую полем при некотором перемещении заряда
Для этого сначала определим работу, совершаемую полем при некотором перемещении заряда  вдоль линии напряженности поля заряда
вдоль линии напряженности поля заряда 
Трудность решения этой задачи заключается в том, что в каждой новой точке пути сила  действующая на заряд
действующая на заряд  со стороны электрического поля, принимает новое значение. С вычислением работы переменной силы мы встречались, например, при определении работы силы упругости. Так как сила упругости изменяется пропорционально деформации
со стороны электрического поля, принимает новое значение. С вычислением работы переменной силы мы встречались, например, при определении работы силы упругости. Так как сила упругости изменяется пропорционально деформации  работа переменной силы оказывается равной произведению среднего арифметического значения силы упругости на перемещение.
работа переменной силы оказывается равной произведению среднего арифметического значения силы упругости на перемещение.
Этот способ нахождения работы переменной силы оказывается непригодным для вычисления работы электрического поля точечного заряда, так как зависимость силы  от координат нелинейная. При обратно пропорциональной зависимости силы
от координат нелинейная. При обратно пропорциональной зависимости силы  от квадрата расстояния до заряда работа электрического поля при перемещении вдоль линии напряженности оказывается равной произведению среднего геометрического значения силы
от квадрата расстояния до заряда работа электрического поля при перемещении вдоль линии напряженности оказывается равной произведению среднего геометрического значения силы  на перемещение
на перемещение  :
:

Преобразуя это выражение, получим:

При удалении заряда на бесконечно далекое расстояние от заряда  работа электрического поля по определению равна потенциальной энергии заряда в данной точке
работа электрического поля по определению равна потенциальной энергии заряда в данной точке

С другой стороны, по определению потенциала  электрического поля
электрического поля

Следовательно, потенциал  электрического поля на расстоянии
электрического поля на расстоянии  от точечного заряда
от точечного заряда  определяется выражением:
определяется выражением:

| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
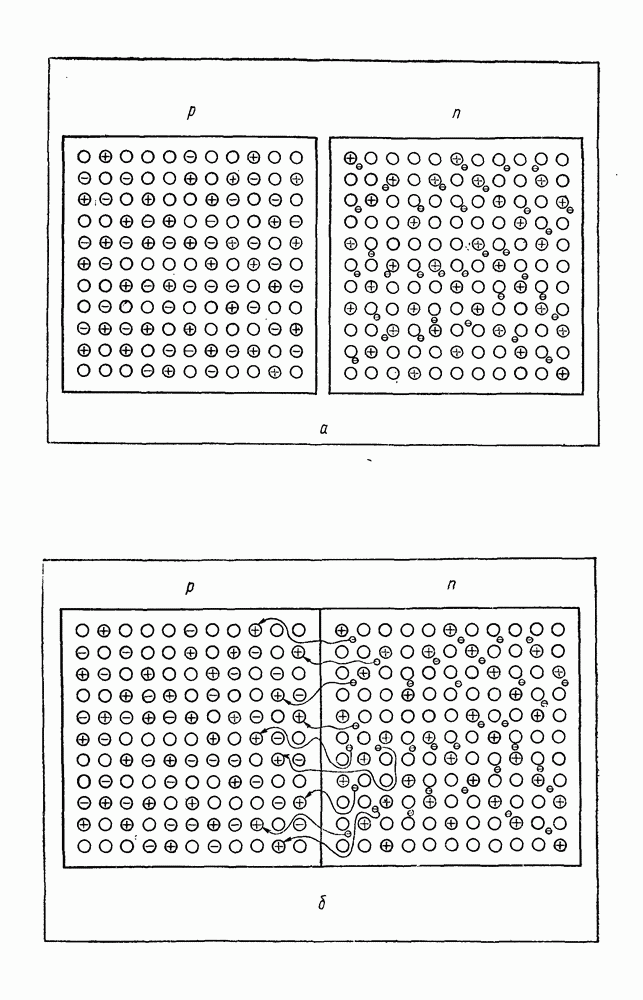
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
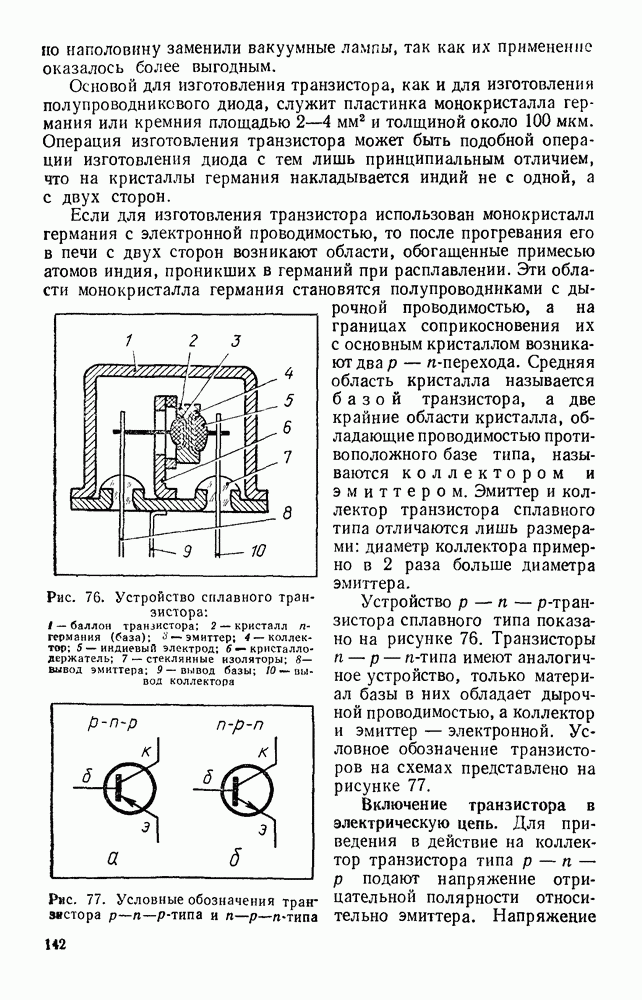
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
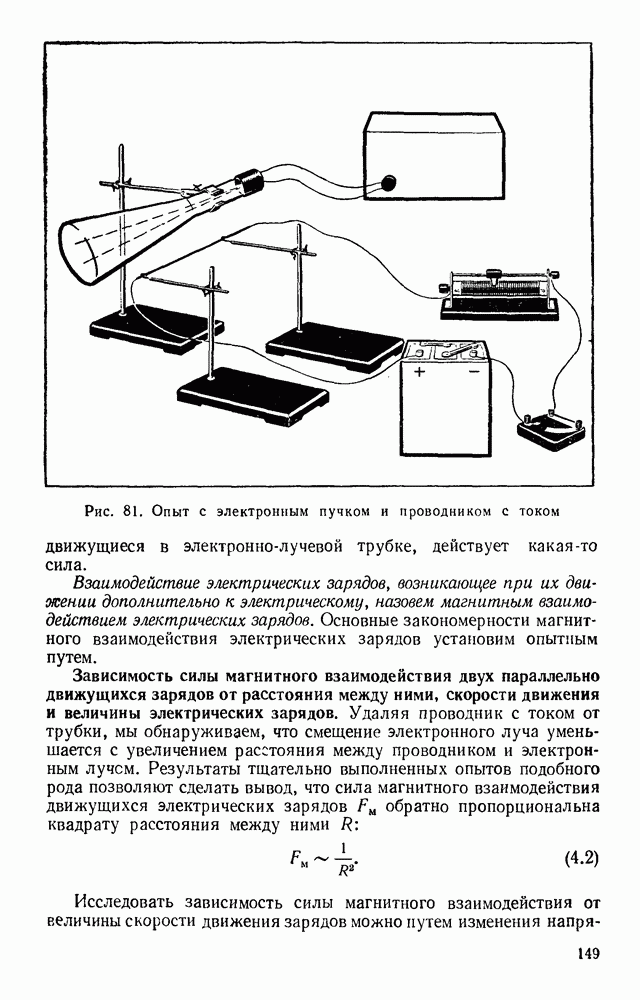
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
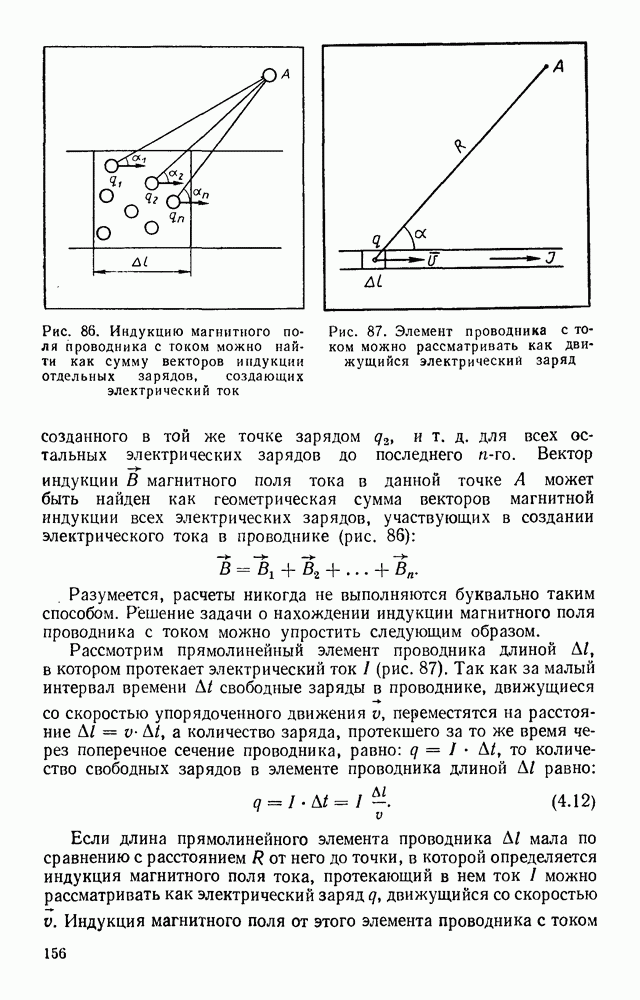
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ