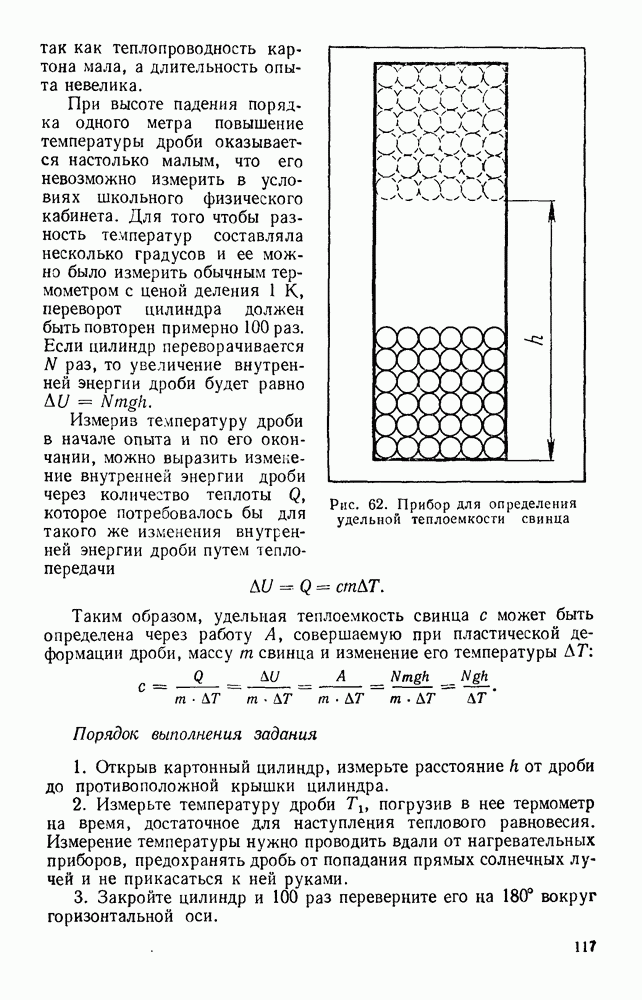
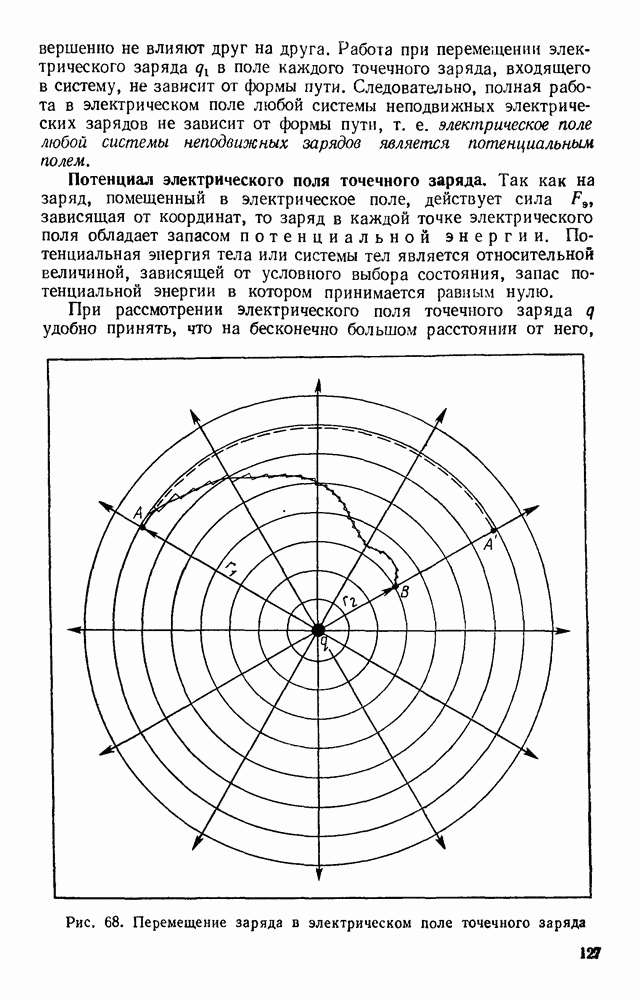
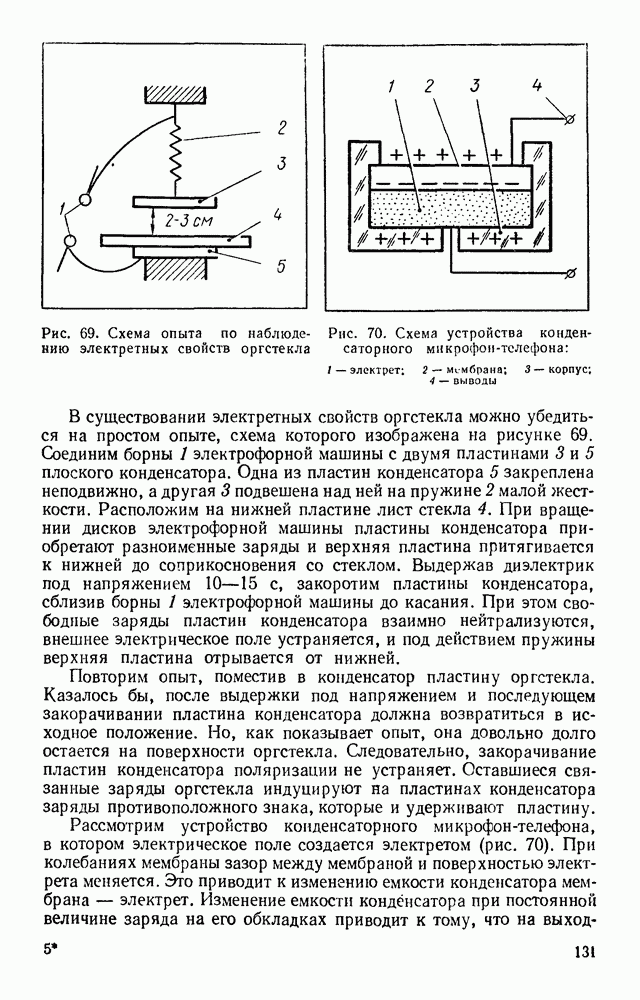
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 14. СТРОЕНИЕ КРИСТАЛЛОВ
Кристаллические тела. Кристаллическими называются твердые тела, физические свойства которых неодинаковы в различных направлениях, но совпадают в параллельных направлениях. Именко анизотропия физических свойств, а не геометрически правильная форма является важнейшим признаком кристаллического тела (см. передний форзац).
Простейший пример анизотропии кристаллов — неодинаковая их прочность по различным направлениям. Это свойство наглядно проявляется при дроблеиии многих кристаллических тел. Результаты опыта по раскалыванию двух тел, одно из которых было аморфным, а другое кристаллическим, представлены на фотографиях 2—5.
Стеклянная бусина с плоскими гранями раскололась на части различной формы, не имеющие плоских участков поверхности. Это свидетельствует об отсутствии анизотропии механической прочности в стекле.
Кусок каменной соли при раскалывании разделился на части, ограниченные плоскими поверхностями, пересекающимися под одинаковыми углами.
Очевидко, эти плоскости перпендикулярны особым направлениям в образце каменной соли, по которым его прочность минимальна. Существование направлений с особенными механическими свойствами, т. е. анизотропия образца каменной соли, доказывает его кристаллическую природу.
Замечательное свойство многих кристаллов давать при дроблении осколки, подобные друг другу по форме, позволило французскому ученому Рене Гаюи высказать в конце XVIII в. гипотезу, что все кристаллы состоят из плотно уложенных рядами маленьких, невидимых в микроскоп частиц, имеющих присущую данному веществу геометрическую форму.
Многообразие геометрических форм кристаллов Гаюи объяснял не только различной формой «кирпичиков», из которых они состоят, но и различными способами их укладки.
Плотная упаковка. Английский ученый Роберт Гуки голландский ученый Христиан Гюйгенс обратили внимание на возможность построения правильных многогранников из плотно укладываемых шаров. Они предположили, что кристаллы построены из шарообразных частиц — атомов или молекул. Внешние формы кристаллов согласно этой гипотезе являются следствием особенностей плотной упаковки атомов или молекул. Независимо от них к такому же выводу пришел в 1748 г. великий русский ученый Михаил Васильевич Ломоносов.
При плотнейшей укладке шаров в один плоский слой каждый шар оказывается окруженным шестью другими шарами, центры которых образуют правильный шестиугольник (рис. 13, а). Если укладку второго слоя вести по лункам между шарами первого слоя, то второй слой окажется таким же, как и первый, только смещенным относительно него в пространстве (рис, 13, б).
Укладка третьего слоя шаров может быть осуществлена двумя способами (рис. 13). В первом способе шары третьего слоя укладываются в лунки, находящиеся точно над шарами первого слоя, и третий слой оказывается точной копией первого. При последующем повторении укладки слоев этим способом получается структура, называемая гексагональной плотноупакованной

Рис. 13. Два способа плотнейшей упаковки равновеликих шаров: а — укладка одного слоя шаров; б — укладка двух слоев шаров; в — гексагональная упаковка трех слоев шаров; г — кубическая упаковка трех слоев шаров
структурой (рис. 13, в). Во втором способе шары третьего слоя укладываются в лунки, не находящиеся точно над шарами первого слоя. При этом способе упаковки получается структура, называемая кубической плотноупакованной структурой (рис. 13, г). Обе упаковки дают степень заполнения объема 74%. Никакой другой способ расположения шаров в пространстве при условии отсутствия их деформации большей степени заполнения объема не дает.
При укладке шаров ряд за рядом способом гексагональной плотной упаковки можно получить правильную шестигранную призму, второй способ упаковки ведет к возможности построения куба из шаров.
Если при построении кристаллов из атомов или молекул действует принцип плотной упаковки, то, казалось бы, в природе должны встречаться кристаллы только в виде кубов и шестигранных призм. Кристаллы такой формы действительно очень распространены. Гексагональной плотной упаковке атомов соответствует, например, форма кристаллов цинка, магния, кадмия. Кубической плотной упаковке соответствует форма кристаллов меди, алюминия, серебра, золота и ряда других металлов.
Но этими двумя формами многообразие мира кристаллов вовсе не ограничивается. Существование форм кристаллов, не соответствующих принципу плотной упаковки равновеликих шаров, может иметь разные причины.
Во-первых, кристалл может быть построен с соблюдением принципа плотной упаковки, но из атомов разных размеров (рис. 14). Во-вторых, отличие упаковки атомов или молекул от плотнейшей может быть вызвано различием сил связей между атомами или молекулами по разным направлениям.
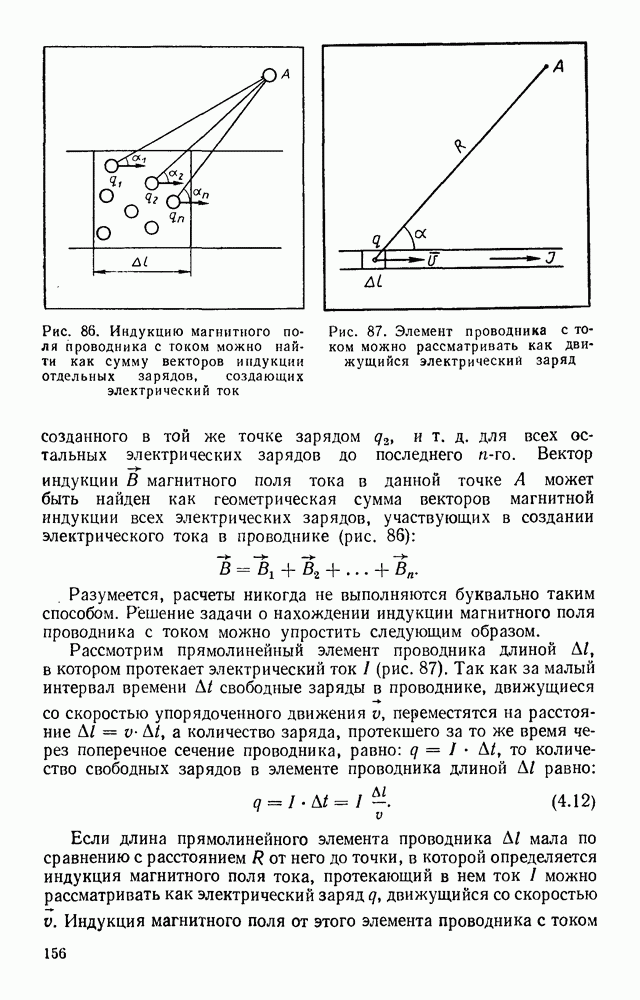
Пространственная решетка. Элементарная ячейка. Для наглядного представления внутренней структуры кристалла применяется способ его изображения с помощью пространственной кристаллической решетки — пространственной сетки, узлы которой совпадают с положением центров атомов или молекул в кристалле.
В основе кристаллической решетки лежит элементарная ячейка — фигура наименьшего размера, последовательным переносом которой можно построить весь кристалл. Как правило, атом принадлежит не одной элементарной ячейке, а входит одновременно в состав нескольких соседних элементарных ячеек. Рассмотрим, к примеру, элементарную ячейку

Рис. 14. Зависимость способа плотной упаковки от размеров шаров, укладываемых в один слой на плоскости

Рис. 15. Модель элементарной ячейки кристалла каменной соли
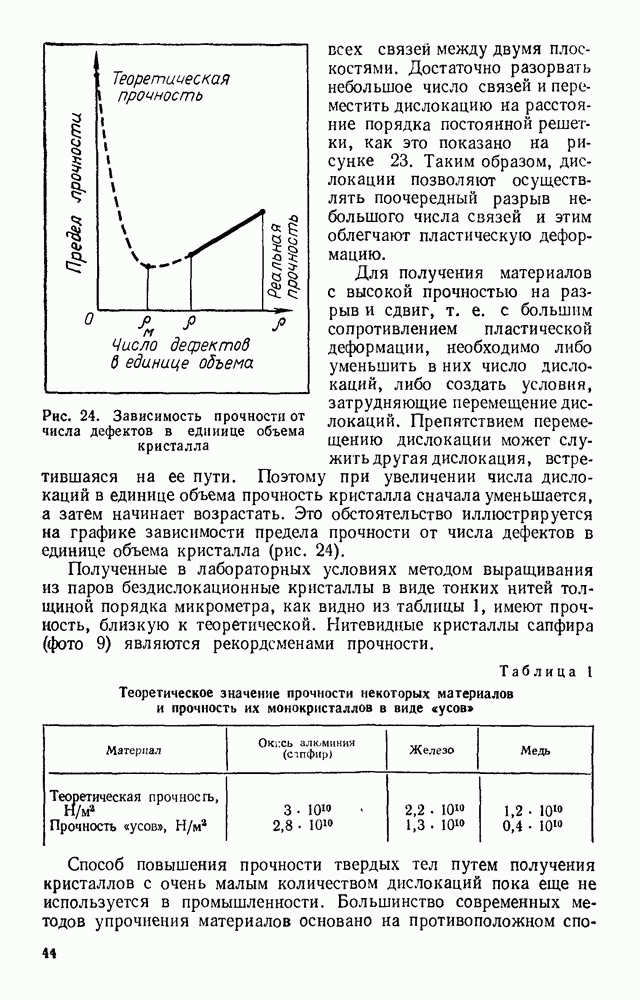
кристалла каменной соли, представленную на рисунке 15. От ионов, находящихся в вершинах ячейки, ей принадлежит лишь по одной восьмой иона: от ионов, лежащих на ребрах ячейки, ей принадлежит по одной четвертой каждого; от ионов, лежащих на гранях, на долю каждой из двух соседних элементарных ячеек приходится по половине иона.
Подсчитаем число ионов натрия и число ионов хлора, входящих в состав одной элементарной ячейки каменной соли. Ячейке целиком принадлежит один ион хлора, расположенный в центре ячейки, и по одной четверти каждого из 12 ионов, расположенных в ребрах ячейки. Всего ионов хлора в одной ячейке  Иснсв натрия в элементарной ячейке шесть половинок на гранях и восемь «восьмушек» в вершинах. Всего ионов хлора в одной ячейке
Иснсв натрия в элементарной ячейке шесть половинок на гранях и восемь «восьмушек» в вершинах. Всего ионов хлора в одной ячейке 
Сравнение элементарных ячеек кристаллических решеток различного типа может проводиться по разным параметрам, среди которых часто употребляются атомный радиус, плотность упаковки и количество атомов в элементарной ячейке. Атомный радиус определяют как половину расстояния между центрами ближайших соседних атомов в кристалле. Доля объема, занятая атомами в элементарной ячейке, называется плотностью упаковки.
На рисунке 16 представлены объемные изображения элементарных ячеек четырех типов.
Симметрия кристаллов. Классификация кристаллов и объяснение их физических свойств оказываются возможными только на основе изучения их симметрии. Учение о симметрии является основой всей кристаллографии.
Для количественной оценки степени симметричности служат элементы симметрии — оси, плоскости и центр симметрии.

Рис. 16. Кубические ячейки и их объемные изображения: а — простая кубическая; б — объемно-центрированная; в — гранецентрированная; г — решетка алмаза
Осью симметрии называют воображаемую прямую, при вращении вокруг которой на 360° кристалл (или его решетка) несколько раз совмещается сам с собой. Число этих совмещений называют порядком оси.
Плоскостью симметрии называют плоскость, рассекающую кристалл на две части, каждая из которых является зеркальным отображением одна другой. Плоскость симметрии как бы выполняет роль двустороннего зеркала. Число плоскостей симметрии может быть различным. Например, в кубе их девять, а в снежинках любой формы — шесть.
Центром симметрии называют точку внутри кристалла, в которой пересекаются все оси симметрии.
Каждый кристалл характеризуется определенным сочетанием элементов симметрии. Ввиду того что число элементов симметрии кевелико, задача отыскания всех возможных форм кристаллов не является безнадежной. Выдающийся русский кристаллограф Евграф Степанович Федоров установил, что в природе может существовать только 230 различных кристаллических решеток, обладающих осями симметрии второго, третьего, четвертого и шестого порядка. Иначе говоря, кристаллы могут иметь (орму различных призм и пирамид, в основании которых могут лежать только правильный треугольник, квадрат, параллелограмм и шестиугольник.
Представления о периодической структуре кристаллов и симметрии расположения атомов в них в настоящее время имеют
строгое экспериментальное подтверждение. Фотография I получена с помощью ионного микро проектора от кристалла вольфрама. Пунктир из светлых точек на фотографии отмечает край слоя атомов, а сами светлые точки — отдельные атомы. Вся картина хорошо передает периодичность и симметрию расположения атомов вольфрама в кристалле.
| << Предыдущий параграф | Следующий параграф >> |
- МОЛЕКУЛЯРНАЯ ФИЗИКА
- § 2. ЧИСЛО АВОГАДРО
- § 3. ИДЕАЛЬНЫЙ ГАЗ
- § 4. ДАВЛЕНИЕ ИДЕАЛЬНОГО ГАЗА
- § 5. ГАЗОВЫЙ ТЕРМОМЕТР
- § 6. ТЕМПЕРАТУРА КАК МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ
- § 7. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
- § 8. РЕАЛЬНЫЕ ГАЗЫ
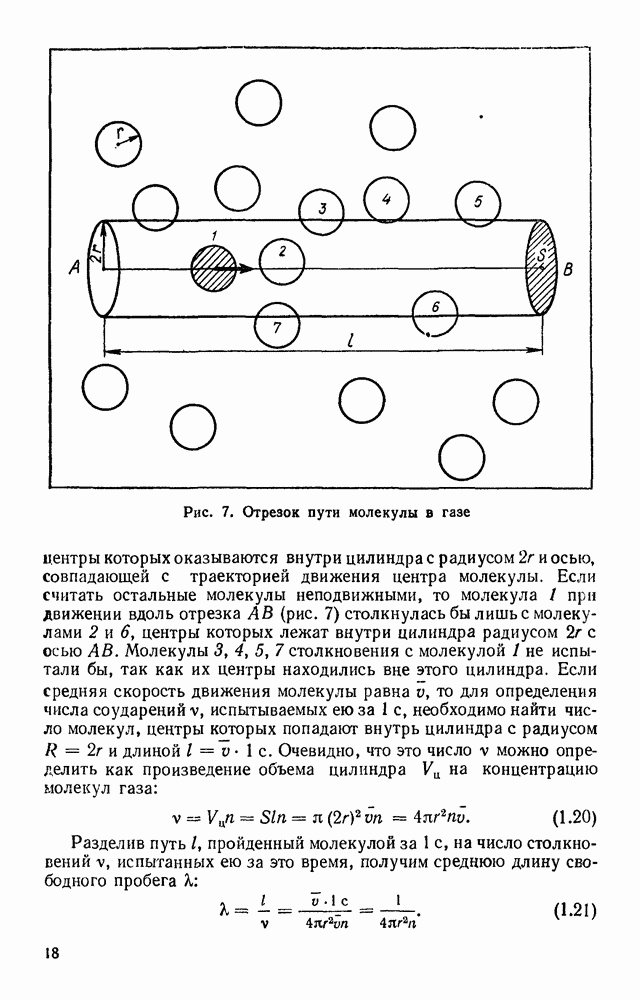
- § 9. СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА
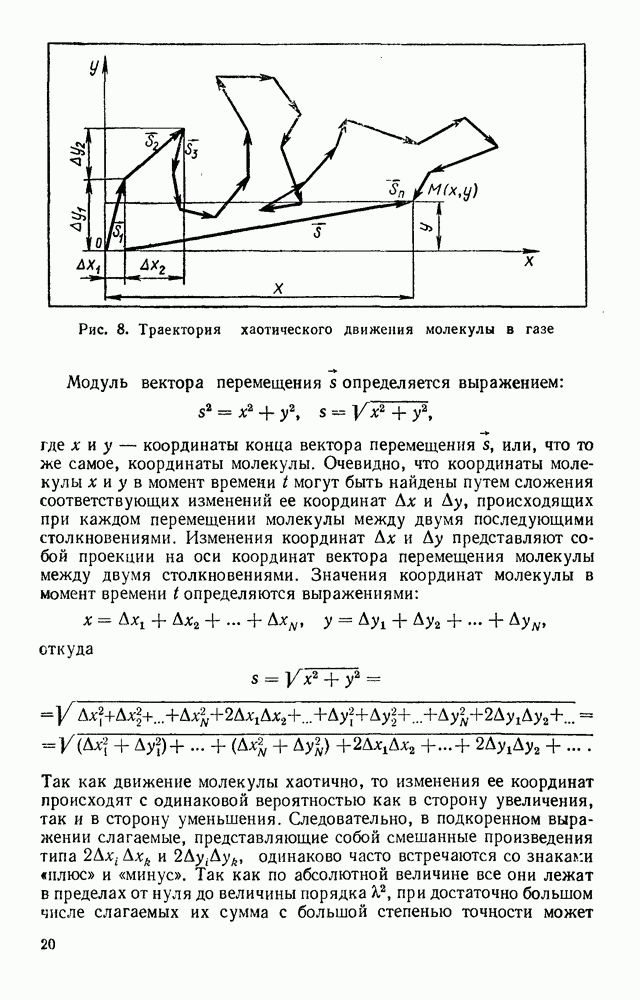
- § 10. ДИФФУЗИЯ И БРОУНОВСКОЕ ДВИЖЕНИЕ
- § 11. СЖИЖЕНИЕ ГАЗОВ
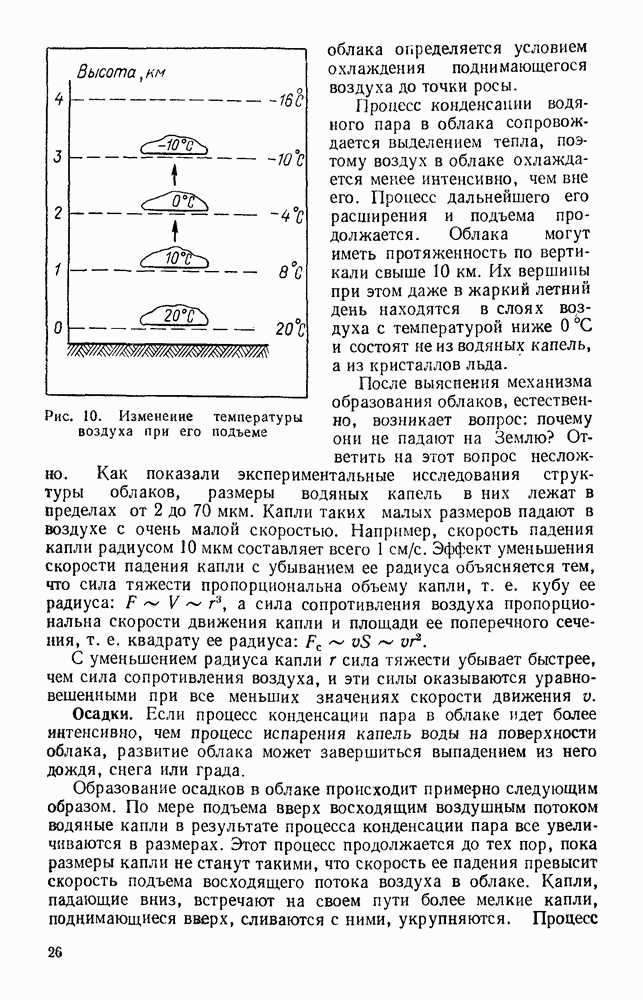
- § 12. ОБЛАКА И ОСАДКИ
- § 13. ЗАВИСИМОСТЬ АГРЕГАТНОГО СОСТОЯНИЯ ВЕЩЕСТВА ОТ ТЕМПЕРАТУРЫ И ДАВЛЕНИЯ
- § 14. СТРОЕНИЕ КРИСТАЛЛОВ
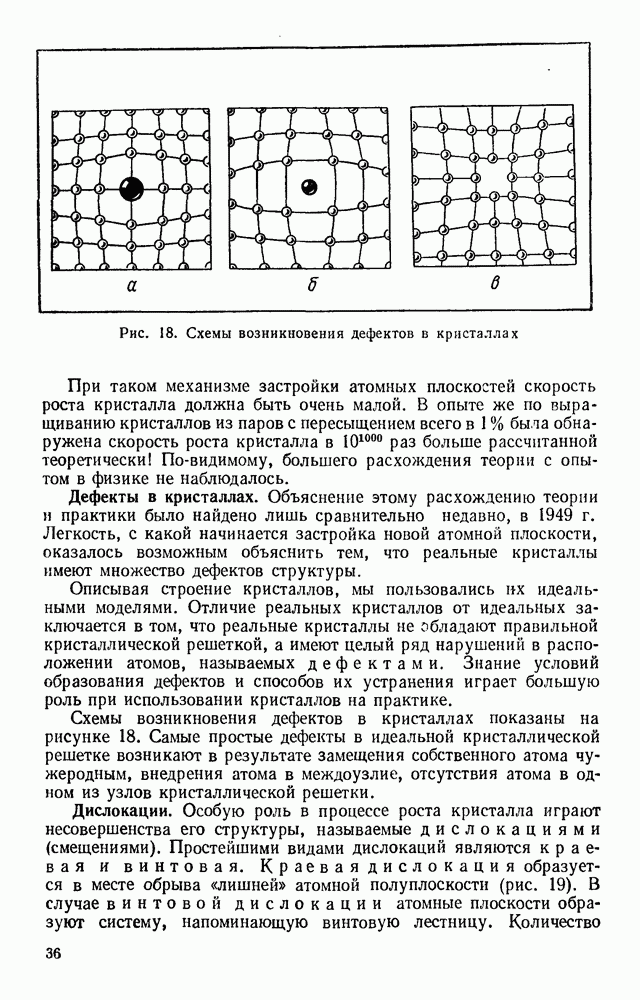
- § 15. ПРОЦЕССЫ РОСТА КРИСТАЛЛОВ
- § 16. ПОЛУЧЕНИЕ МОНОКРИСТАЛЛОВ
- § 17. ПРИМЕНЕНИЯ КРИСТАЛЛИЧЕСКИХ ТЕЛ
- § 18. КРИСТАЛЛЫ И ЖИЗНЬ
- Глава 2. ТЕРМОДИНАМИКА
- § 19. ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
- § 20. РАБОТА И КОЛИЧЕСТВО ТЕПЛОТЫ В ТЕРМОДИНАМИКЕ
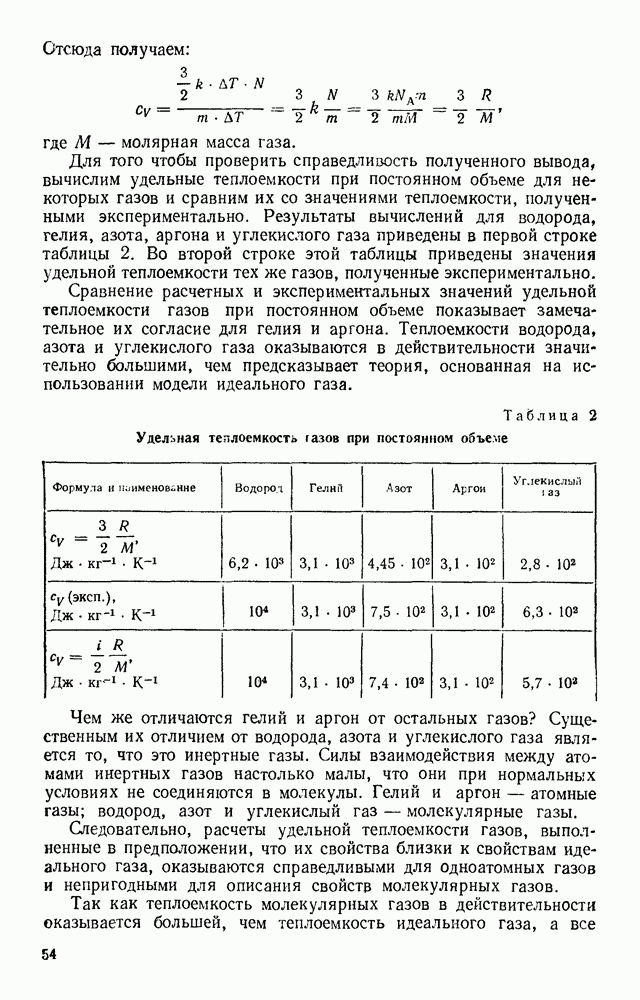
- § 21. ТЕПЛОЕМКОСТЬ ГАЗОВ
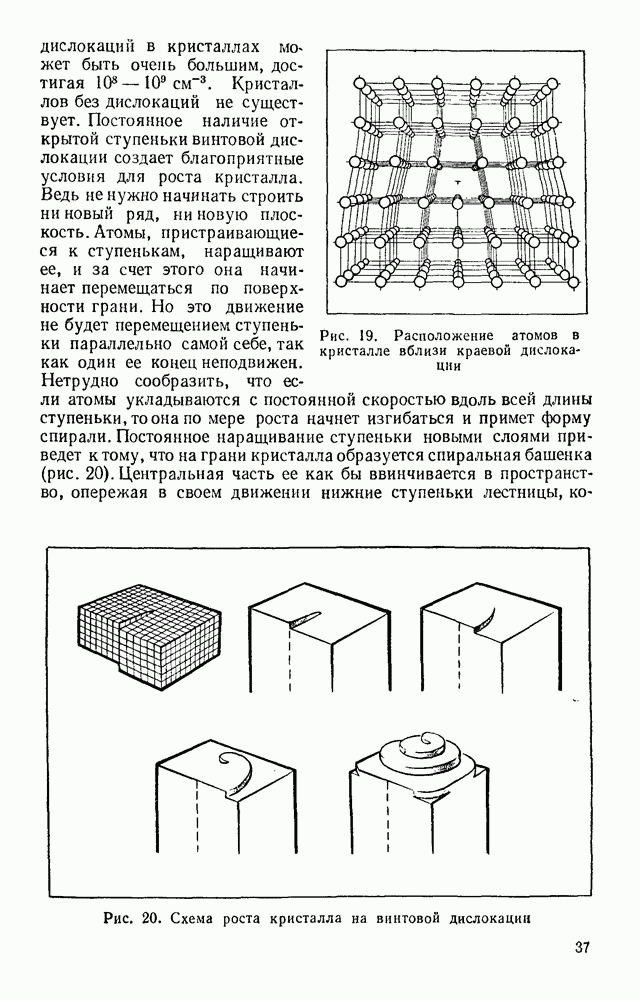
- § 22. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛ И ЖИДКОСТЕЙ
- § 23. ПОТРЕБЛЕНИЕ ЭНЕРГИИ
- § 24. ТЕПЛОВЫЕ ДВИГАТЕЛИ
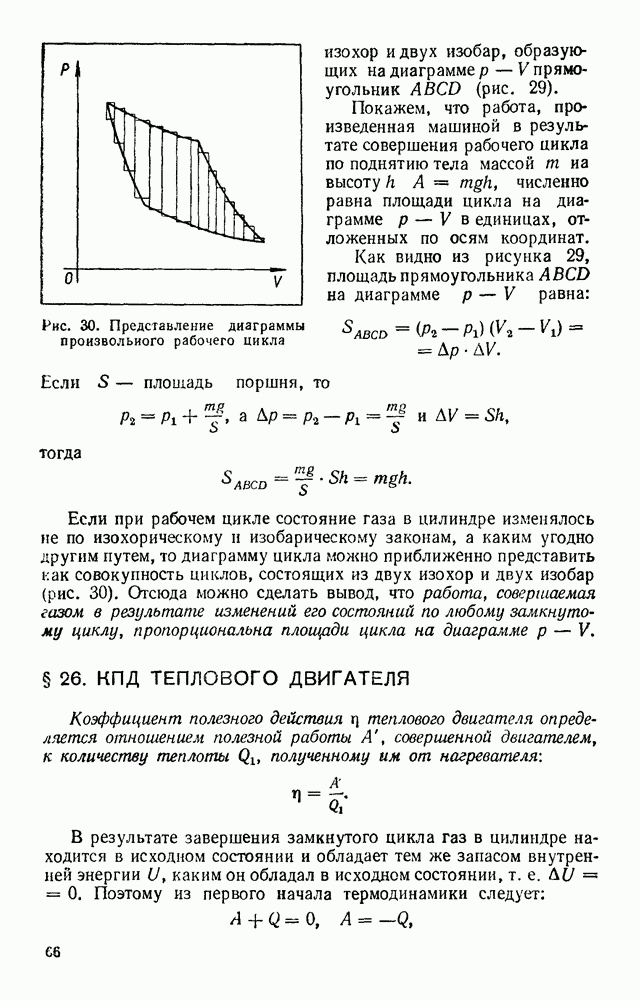
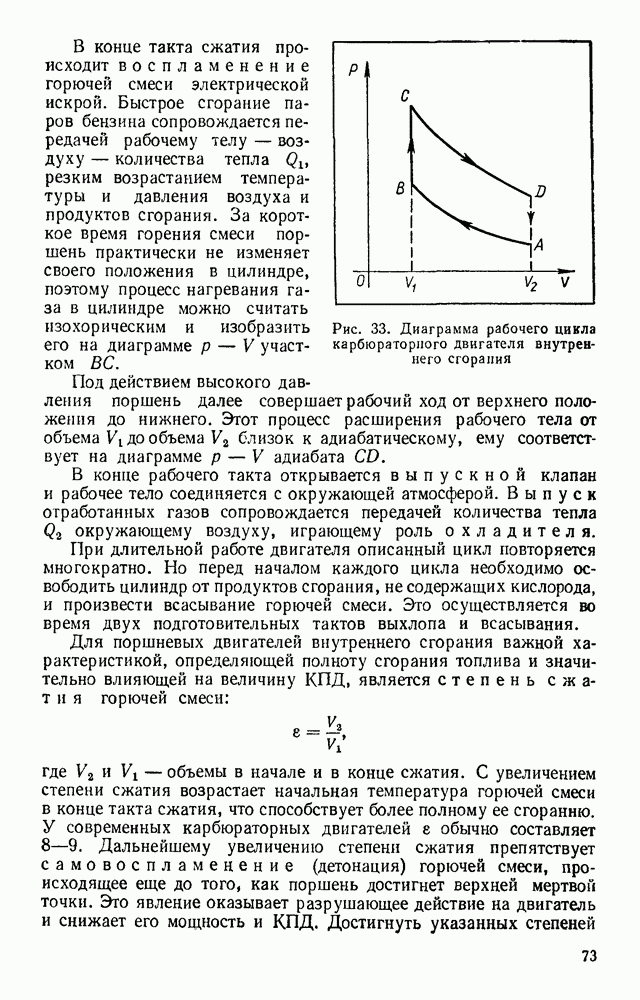
- § 25. РАБОЧИЙ ЦИКЛ ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 26. КПД ТЕПЛОВОГО ДВИГАТЕЛЯ
- § 27. ПАРОВАЯ МАШИНА
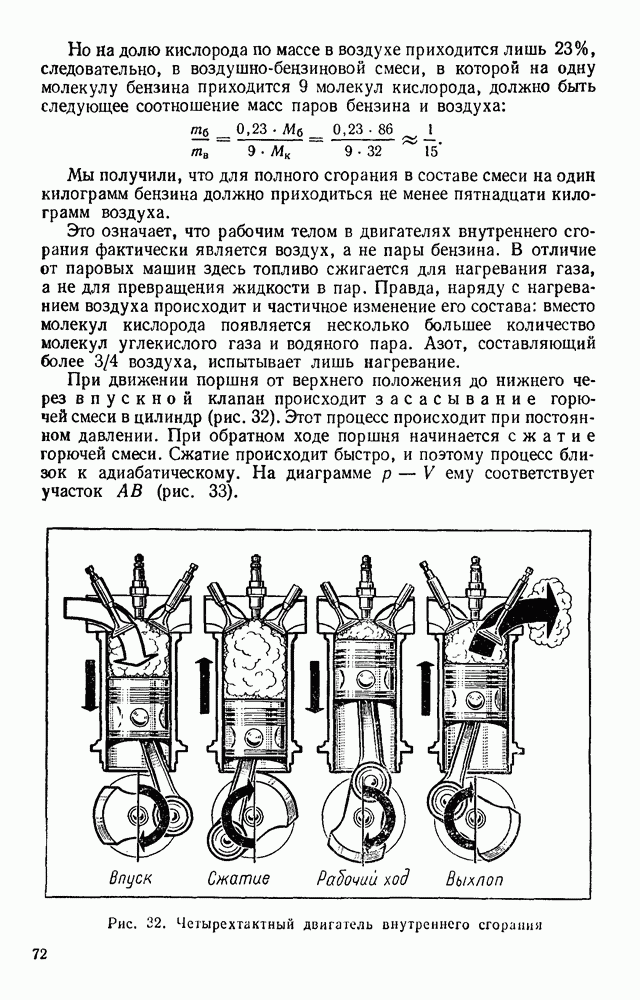
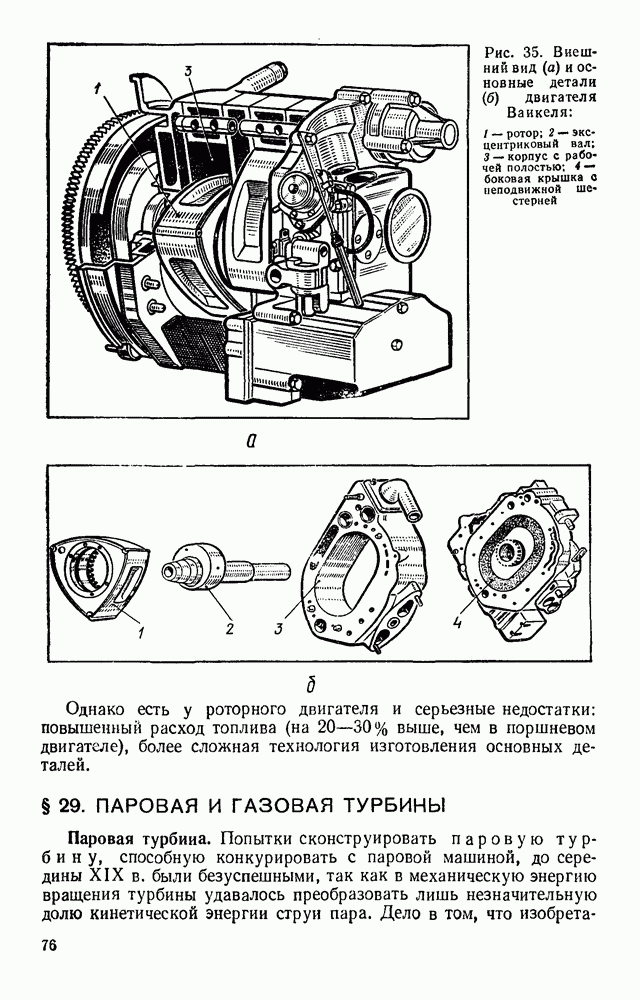
- § 28. ДВИГАТЕЛЬ ВНУТРЕННЕГО СГОРАНИЯ
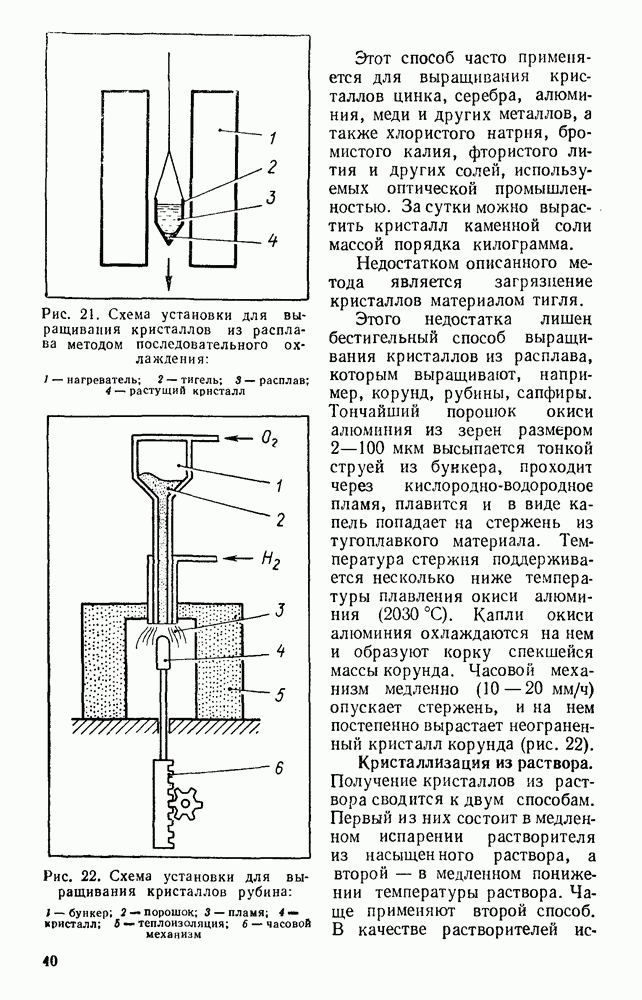
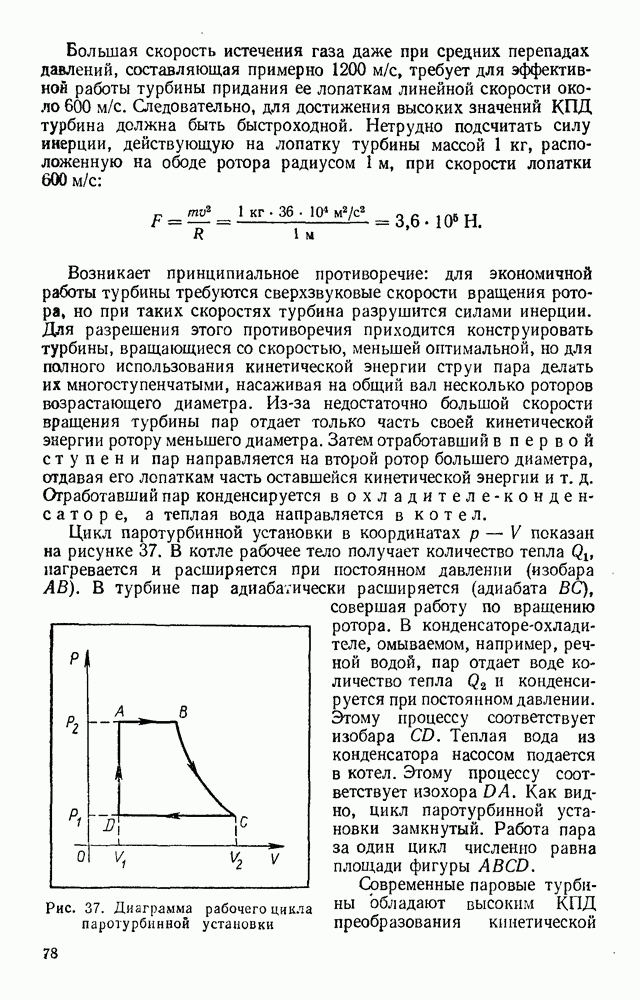
- § 29. ПАРОВАЯ И ГАЗОВАЯ ТУРБИНЫ
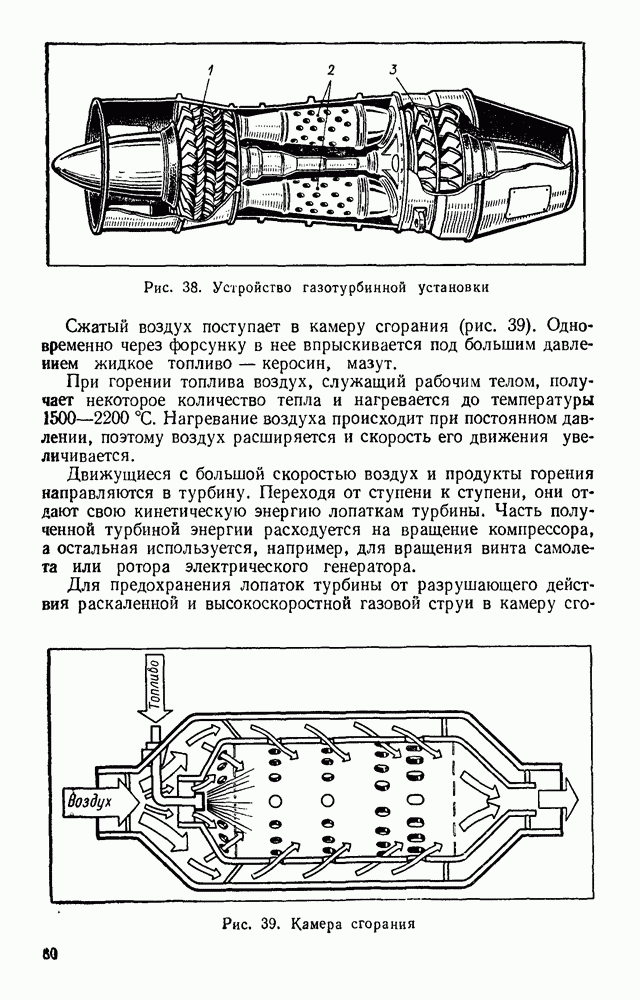
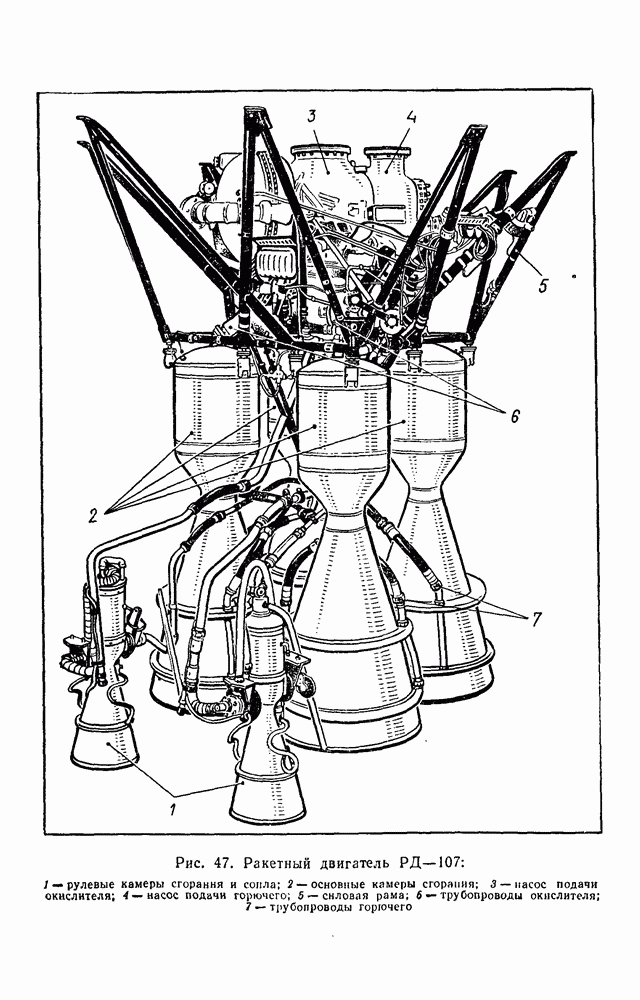
- § 30. РЕАКТИВНЫЕ ДВИГАТЕЛИ
- § 31. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- ТЕРМОДИНАМИКА
- § 32. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- ЭЛЕКТРОДИНАМИКА
- Глава 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ И ЭЛЕКТРИЧЕСКИЙ ТОК
- § 34. ПОТЕНЦИАЛ
- § 35. ДИЭЛЕКТРИКИ И ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
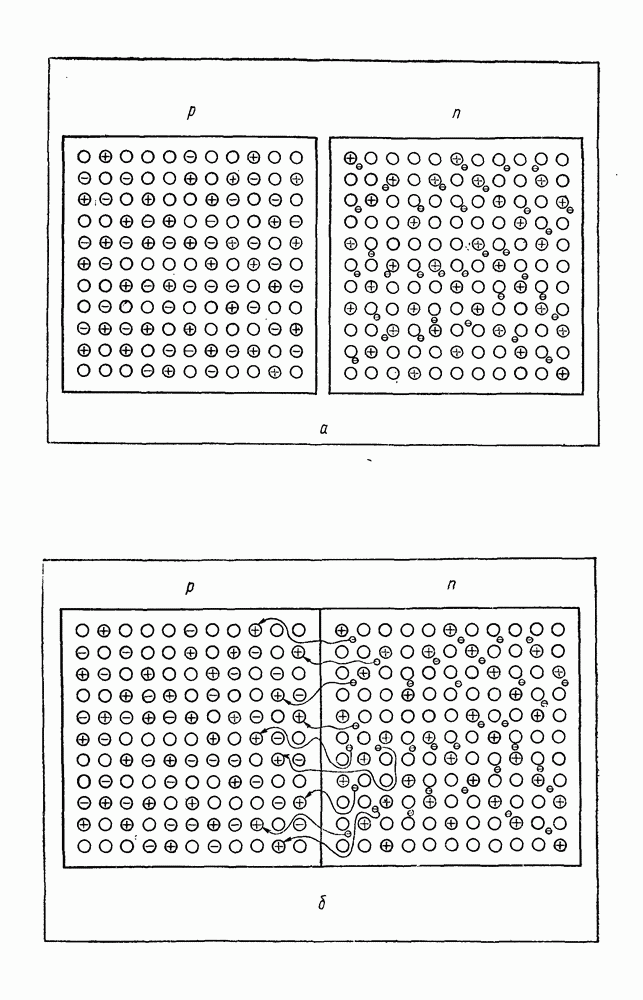
- § 36. СВОЙСТВА p-n-ПЕРЕХОДА
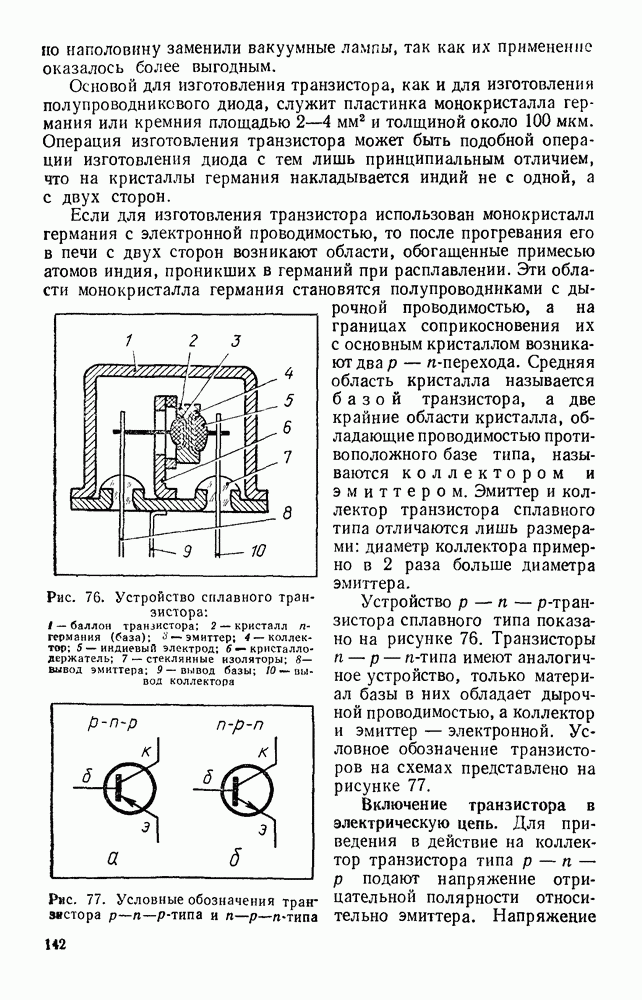
- § 37. ТРАНЗИСТОР
- Глава 4. МАГНЕТИЗМ
- § 38. МАГНИТНОЕ ВЗАИМОДЕЙСТВИЕ ДВИЖУЩИХСЯ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ
- § 39. МАГНИТНОЕ ПОЛЕ
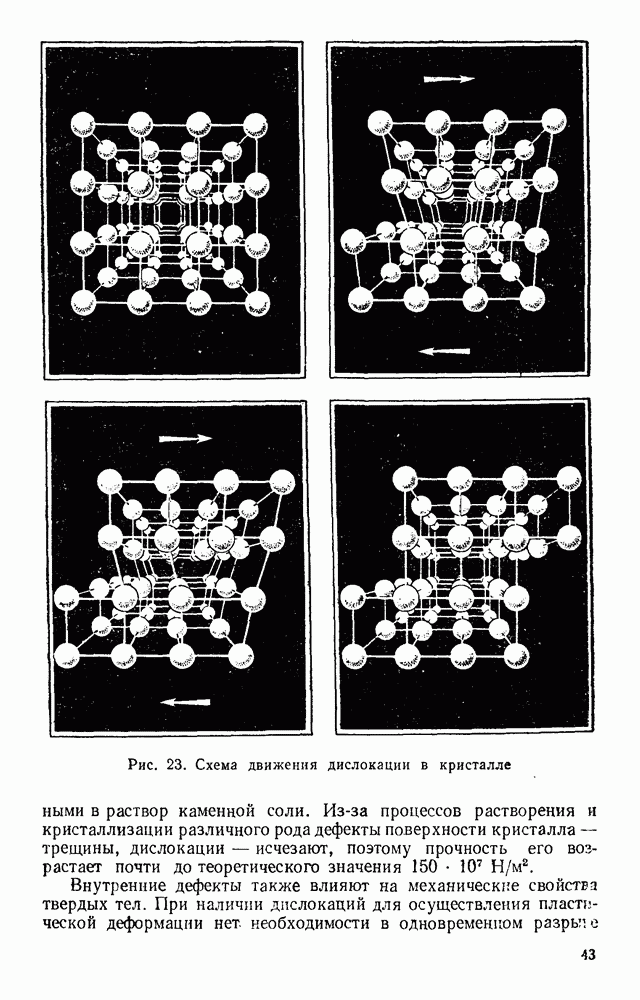
- § 40. МАГНИТНОЕ ПОЛЕ ДВИЖУЩЕГОСЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА
- § 41. МАГНИТНОЕ ПОЛЕ ТОКА В ВАКУУМЕ
- § 42. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЕСЯ ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ
- § 43. МАГНИТНАЯ ПОСТОЯННАЯ ВАКУУМА
- § 44. ЭЛЕКТРИЧЕСКИЕ ГЕНЕРАТОРЫ
- § 45. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 46. ПРАКТИКУМ ПО РЕШЕНИЮ ЗАДАЧ
- ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
- § 47. ЛАБОРАТОРНЫЕ И ПРАКТИЧЕСКИЕ ЗАДАНИЯ
- Глава 5. ФИЗИЧЕСНИЙ ПРАКТИКУМ
- ЛАБОРАТОРНАЯ РАБОТА № 2. ОПРЕДЕЛЕНИЕ МОЛЯРНОЙ МАССЫ ГАЗА
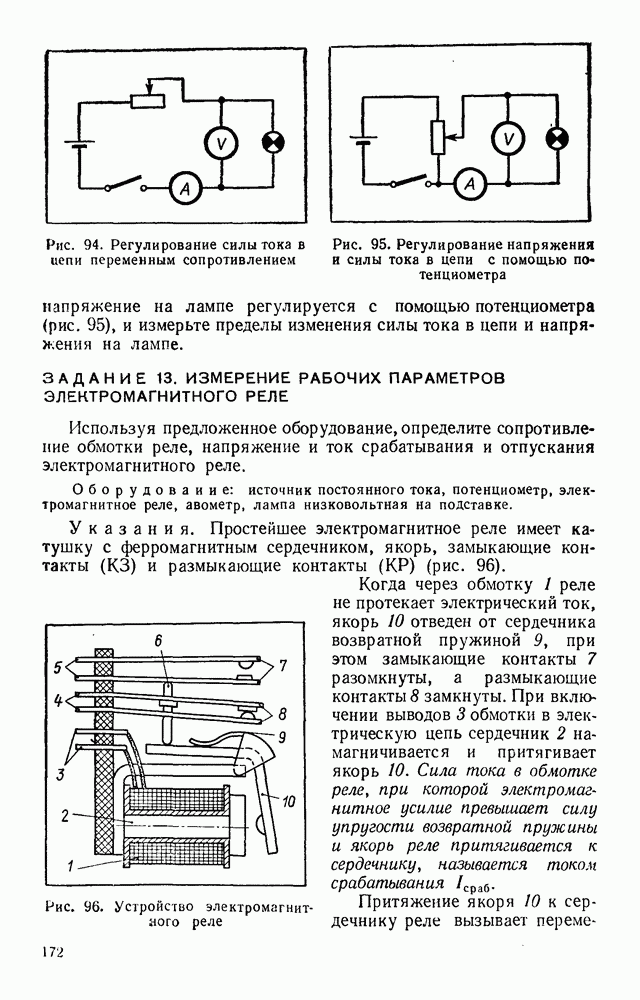
- ЛАБОРАТОРНАЯ РАБОТА № 3. ОПРЕДЕЛЕНИЕ СКОРОСТИ РОСТА КРИСТАЛЛОВ
- ЛАБОРАТОРНАЯ РАБОТА № 4. ОПРЕДЕЛЕНИЕ ТВЕРДОСТИ СТАЛИ ДО И ПОСЛЕ ЗАКАЛКИ
- ЛАБОРАТОРНАЯ РАБОТА № 6. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ХОЛОДИЛЬНИКА
- ЛАБОРАТОРНАЯ РАБОТА № 6. ПОВЕРКА ЭЛЕКТРОИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
- ЛАБОРАТОРНАЯ РАБОТА № 7. ИЗУЧЕНИЕ ЭЛЕКТРОННОГО ОСЦИЛЛОГРАФА
- ЛАБОРАТОРНАЯ РАБОТА № 8. РАСЧЕТ И ИСПЫТАНИЕ СХЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ С ФОТОРЕЗИСТОРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 9. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА УСИЛЕНИЯ ТРАНЗИСТОРА ПО ТОКУ В СХЕМЕ С ОБЩИМ ЭМИТТЕРОМ
- ЛАБОРАТОРНАЯ РАБОТА № 10. ИЗМЕРЕНИЕ МАГНИТНОГО ПОТОКА ПОСТОЯННОГО МАГНИТА
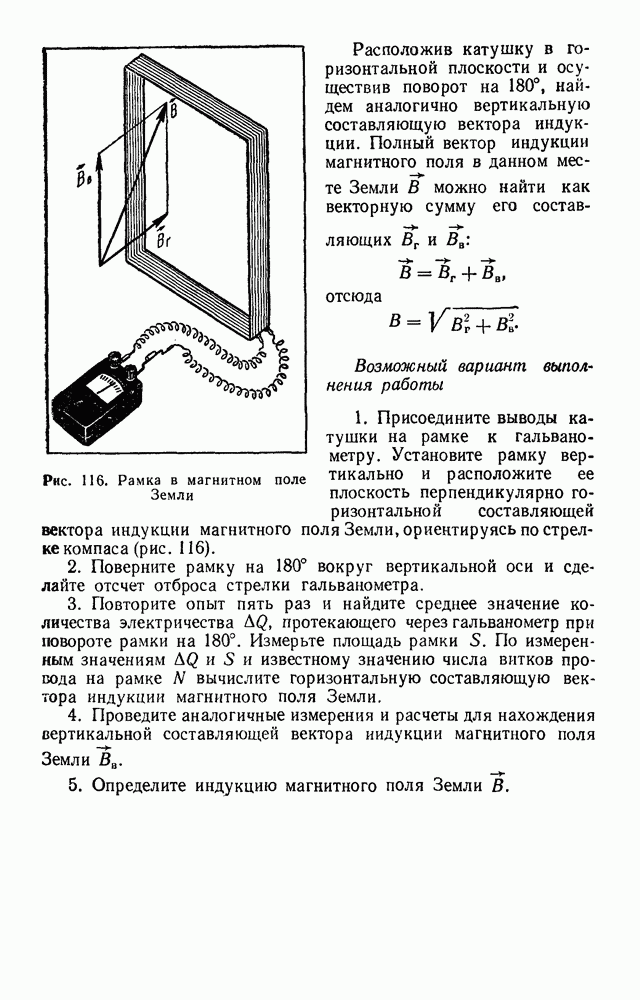
- ЛАБОРАТОРНАЯ РАБОТА № 11. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ
- ОТВЕТЫ К ЗАДАЧАМ