| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Число степеней свободы сигнала.
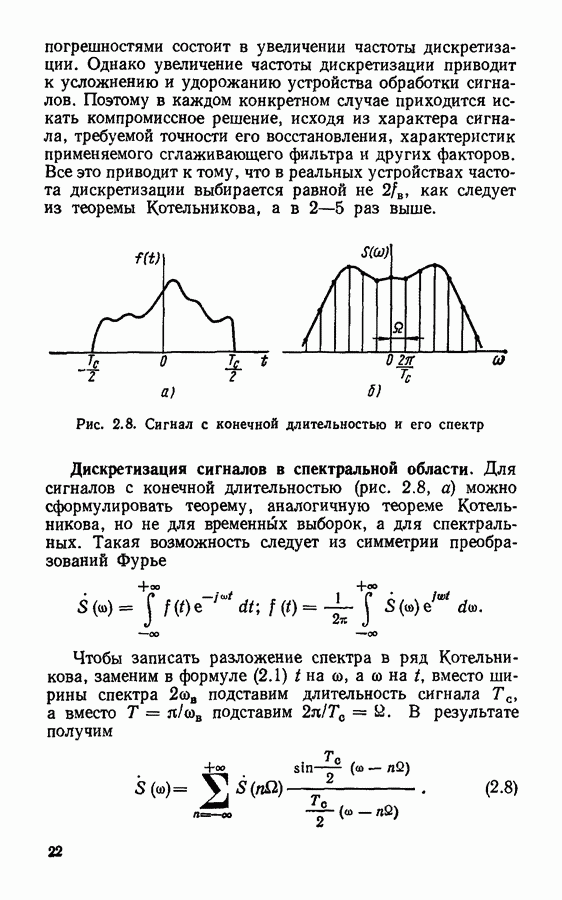
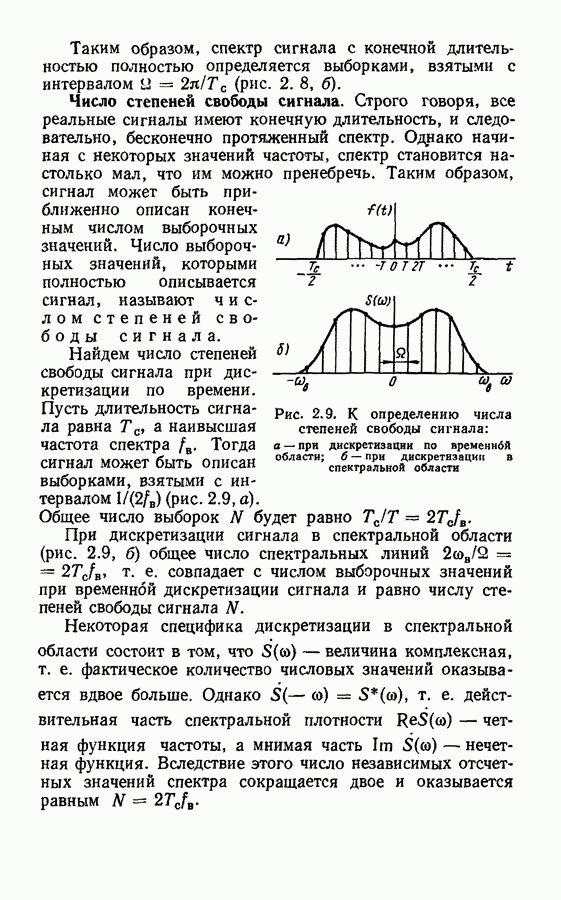
Строго говоря, все реальные сигналы имеют конечную длительность, и следовательно, бесконечно протяженный спектр. Однако начиная с некоторых значений частоты, спектр становится настолько мал, что им можно пренебречь. Таким образом, сигнал может быть приближенно описан конечным числом выборочных значений. Число выборочных значений, которыми полностью описывается сигнал, называют числом степеней свободы сигнала.

Рис. 2.9. К определению числа степеней свободы сигнала: а — при дискретизации по временнбй области;  при дискретизации в спектральной области
при дискретизации в спектральной области
Найдем число степеней свободы сигнала при дискретизации по времени. Пусть длительность сигнала равна  а наивысшая частота спектра
а наивысшая частота спектра  Тогда сигнал может быть описан выборками, взятыми с интервалом
Тогда сигнал может быть описан выборками, взятыми с интервалом  (рис. 2.9, а). Общее число выборок
(рис. 2.9, а). Общее число выборок  будет равно
будет равно 
При дискретизации сигнала в спектральной области (рис. 2.9, б) общее число спектральных линий 
т. е. совпадает с числом выборочных значений при временнбй дискретизации сигнала и равно числу степеней свободы сигнала  .
.
Некоторая специфика дискретизации в спектральной области состоит в том, что  величина комплексная, т. е. фактическое количество числовых значений оказывается вдвое больше. Однако
величина комплексная, т. е. фактическое количество числовых значений оказывается вдвое больше. Однако  т. е. действительная часть спектральной плотности
т. е. действительная часть спектральной плотности  четная функция частоты, а мнимая часть
четная функция частоты, а мнимая часть  нечетная функция. Вследствие этого число независимых отсчетных значений спектра сокращается двое и оказывается равным
нечетная функция. Вследствие этого число независимых отсчетных значений спектра сокращается двое и оказывается равным 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
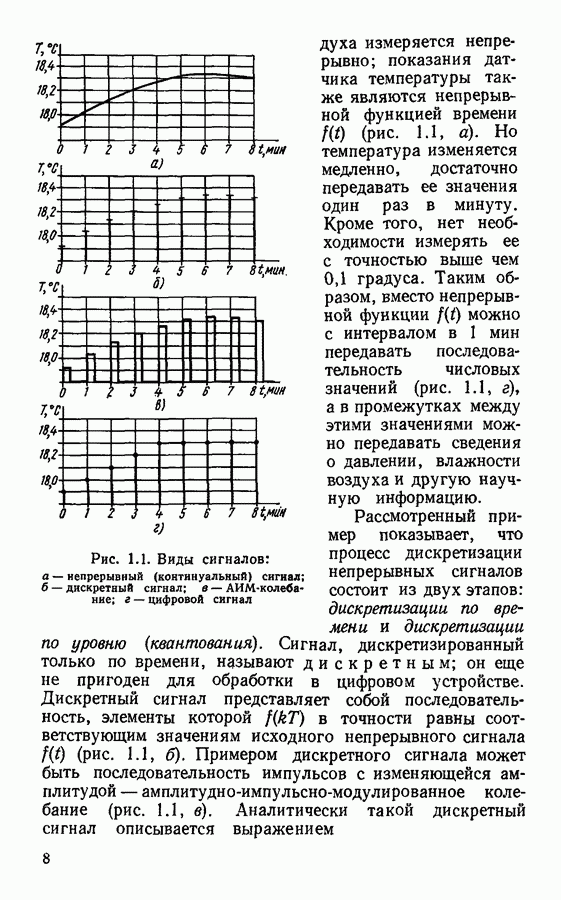
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
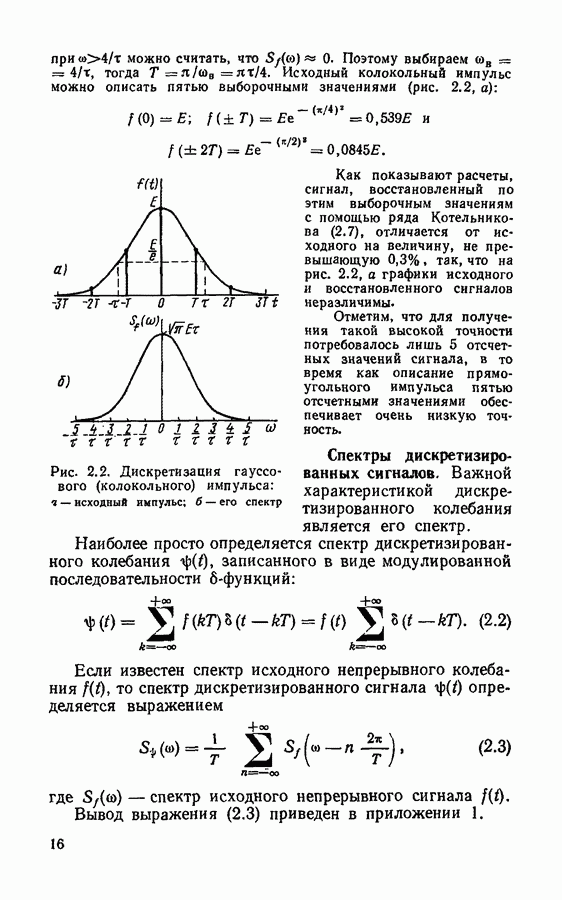
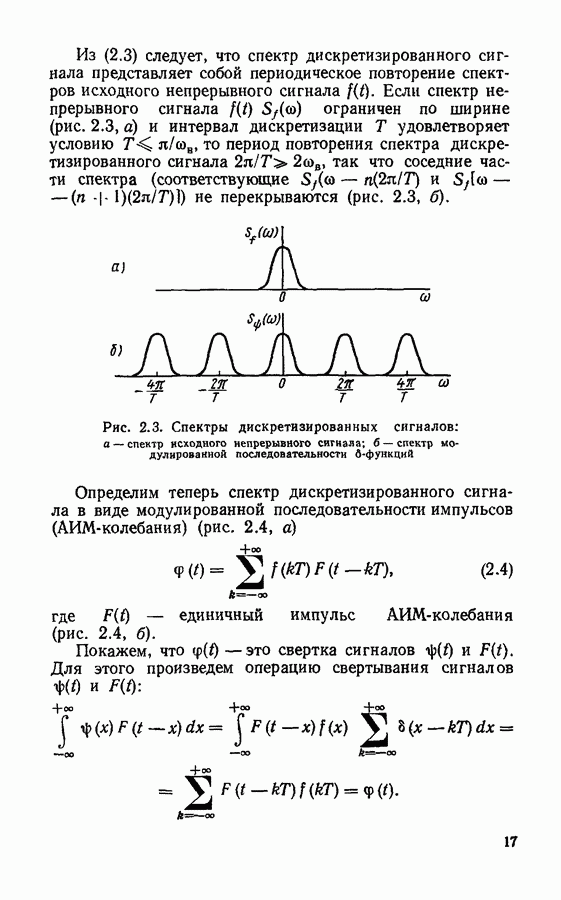
- Спектры дискретизированных сигналов.
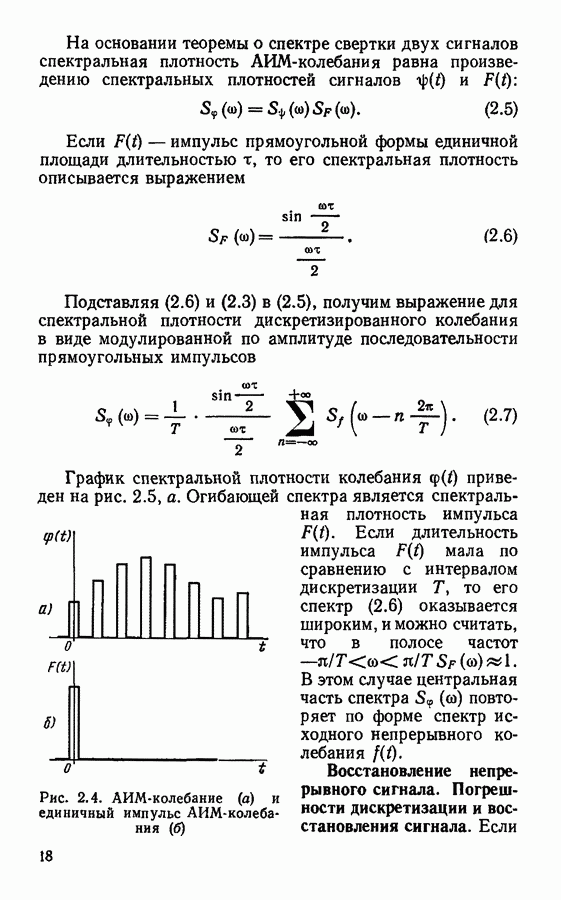
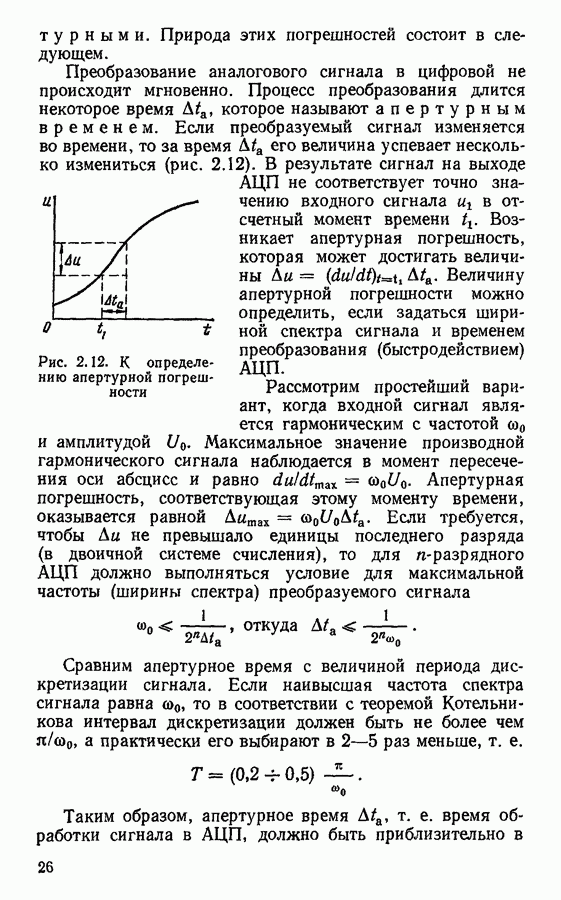
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
- Дискретизация сигналов в спектральной области.
- Число степеней свободы сигнала.
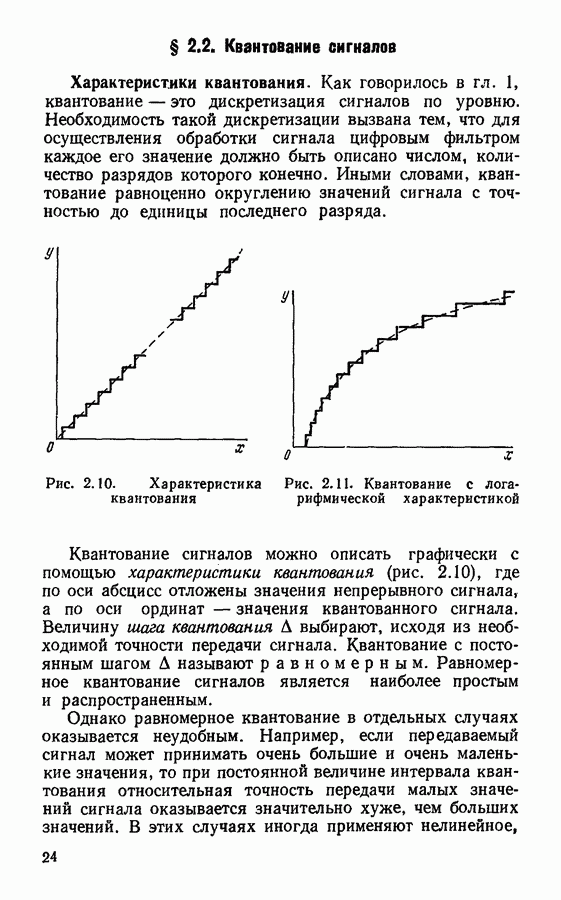
- § 2.2. Квантование сигналов
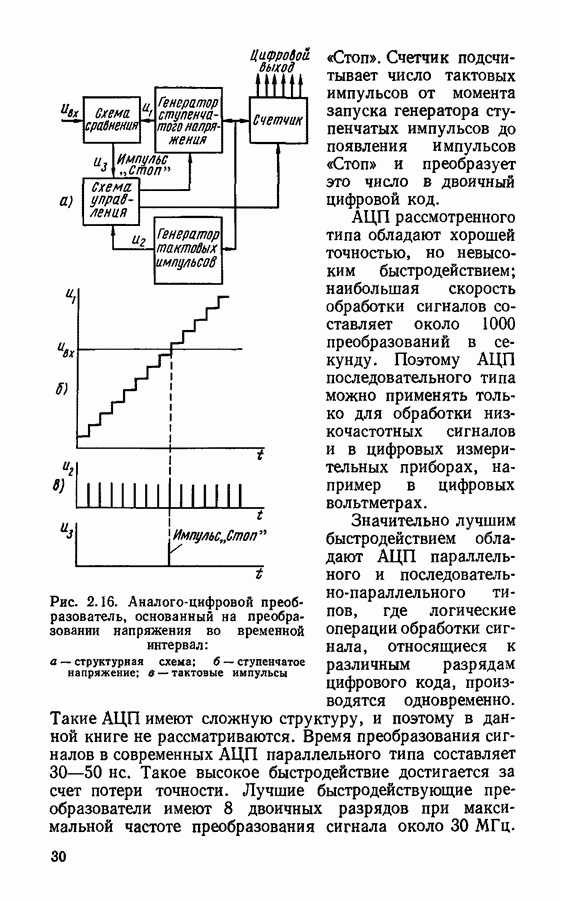
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
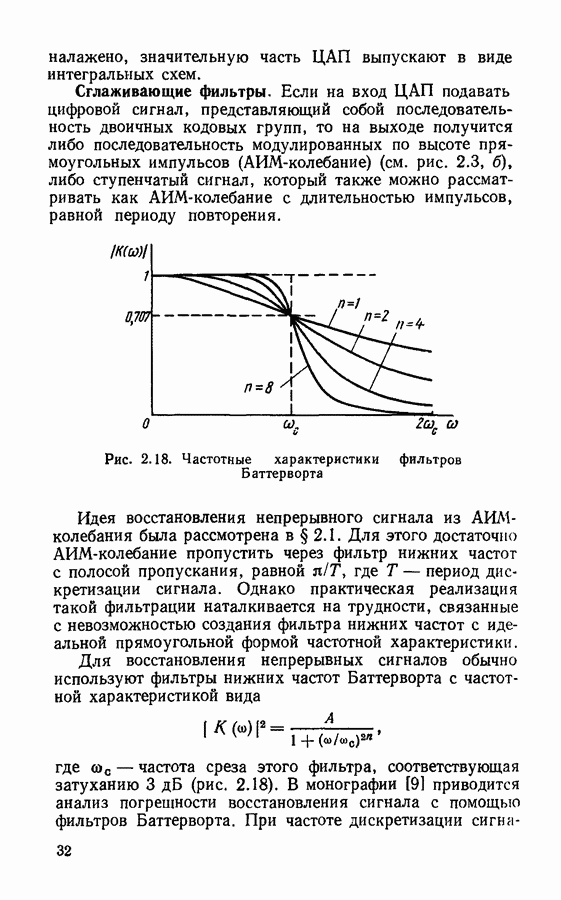
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
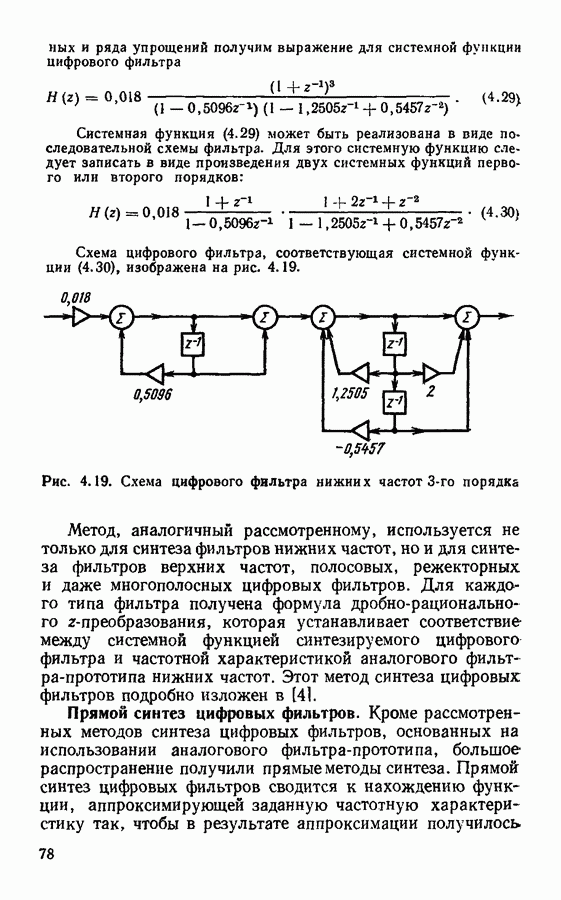
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
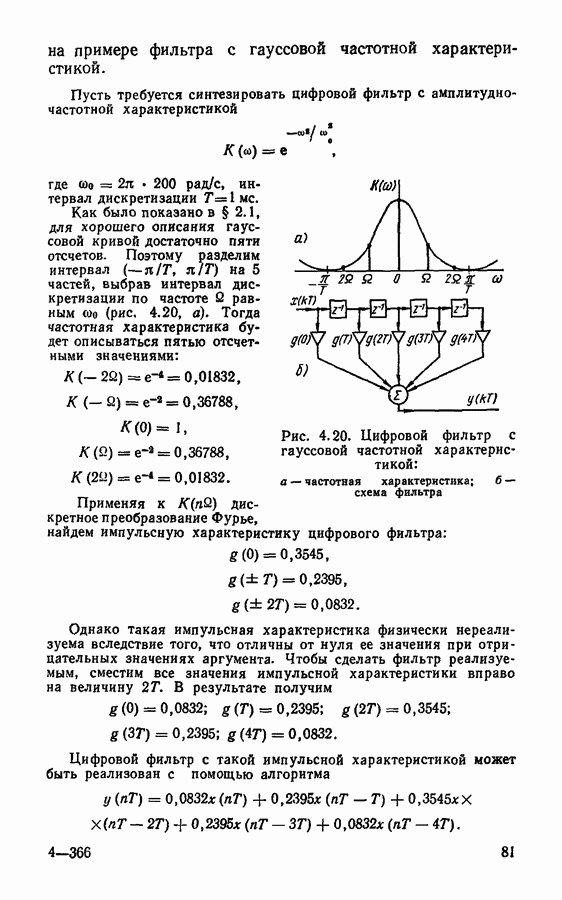
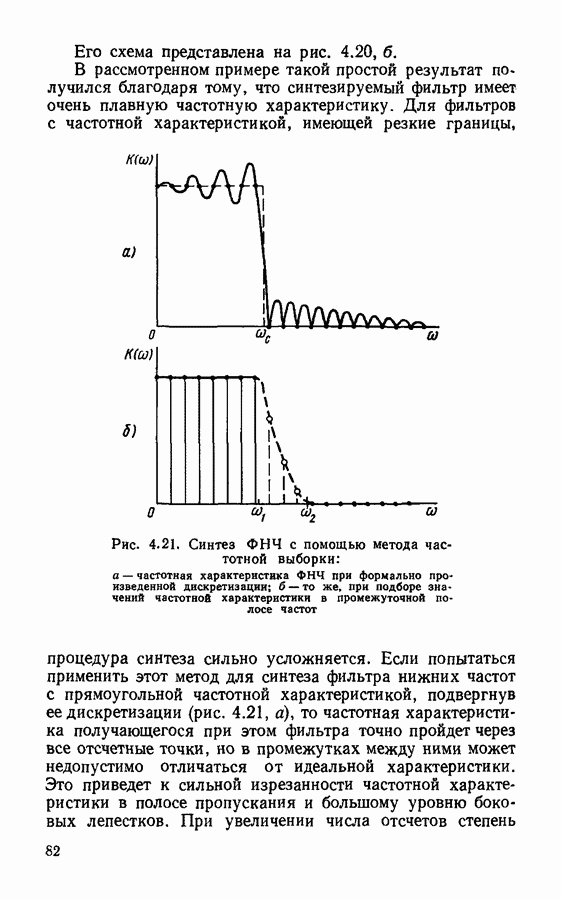
- Прямой синтез цифровых фильтров.
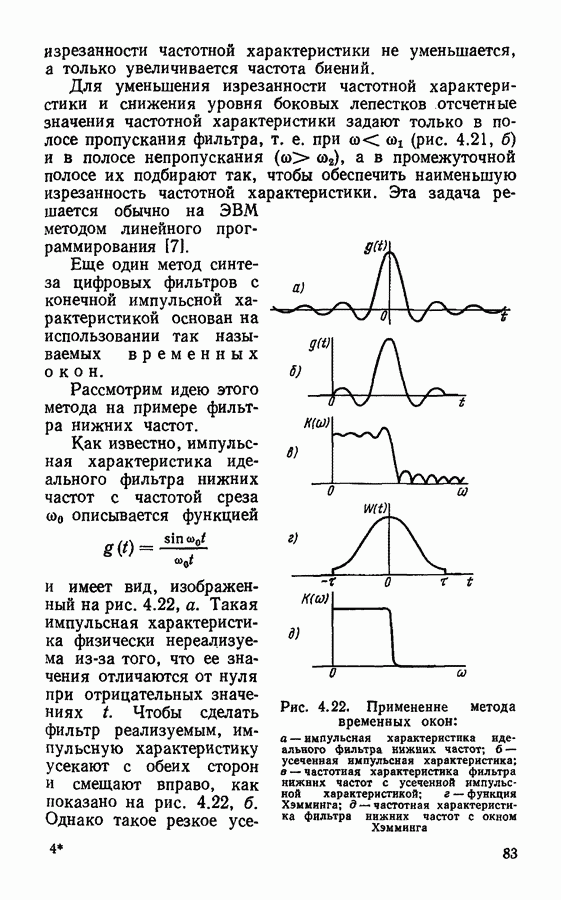
- Методы синтеза фильтров с конечной импульсной характеристикой.
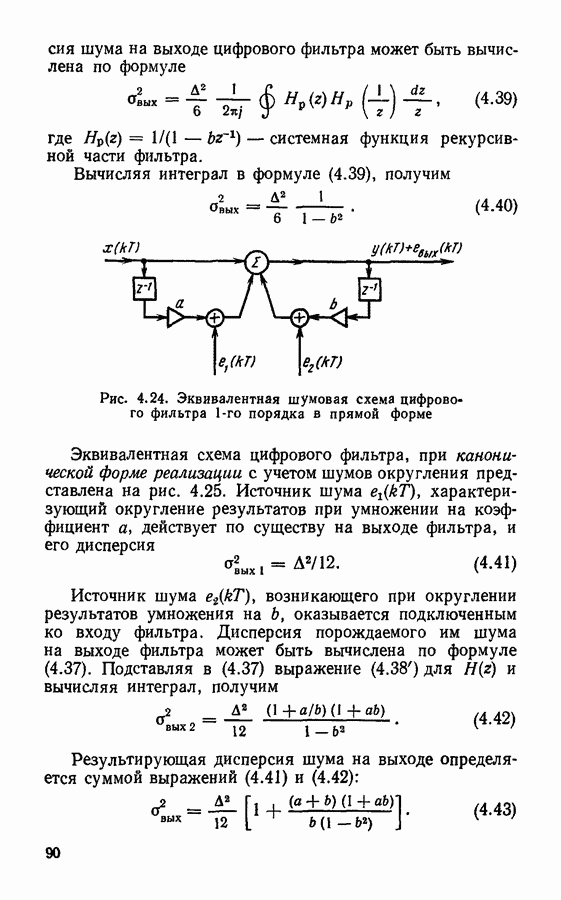
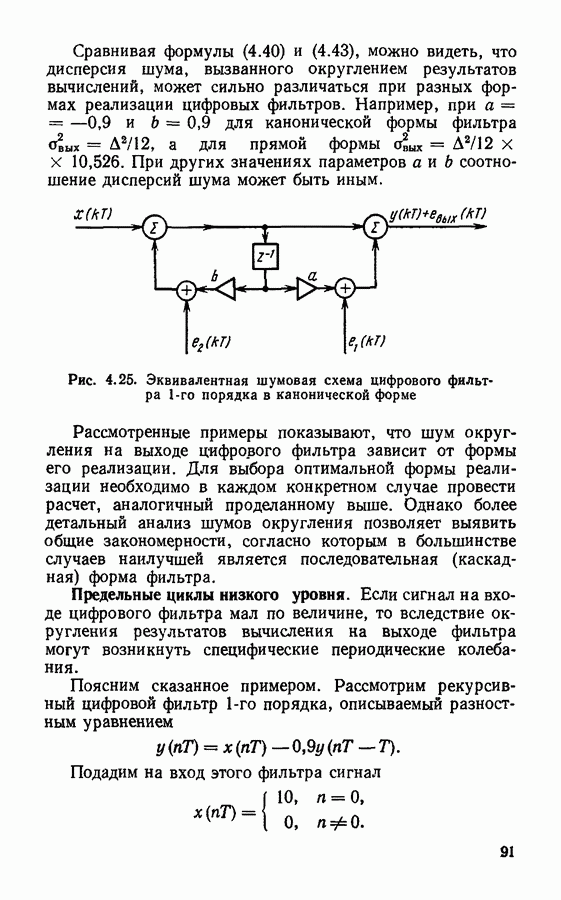
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА