| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
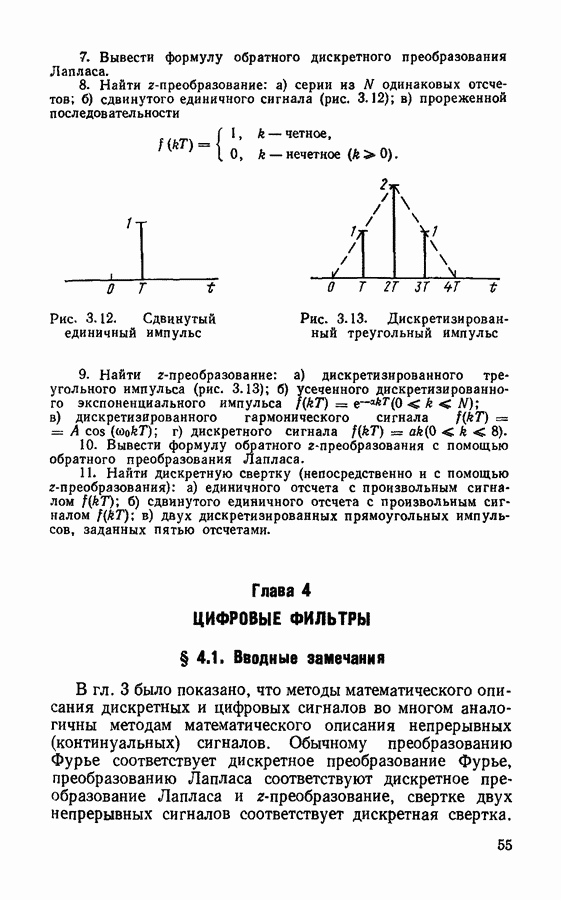
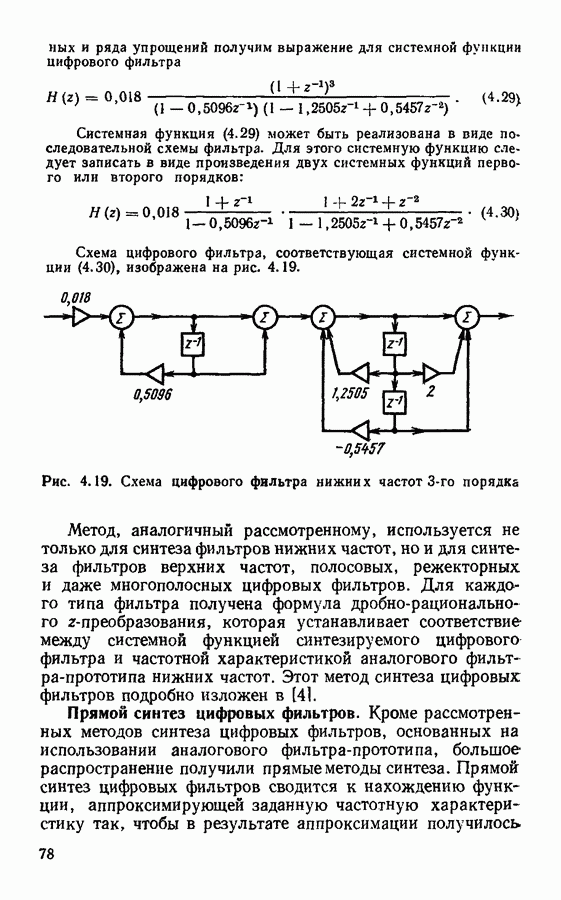
§ 3.6. Обратное z-преобразование
Обратное  -преобразование позволяет определить значения дискретного сигнала по виду функции
-преобразование позволяет определить значения дискретного сигнала по виду функции  Для нахождения формулы обратного
Для нахождения формулы обратного  -преобразования можно воспользоваться обратным преобразованием Лапласа, но легче получить ее из формулы прямого
-преобразования можно воспользоваться обратным преобразованием Лапласа, но легче получить ее из формулы прямого  -преобразования.
-преобразования.
Запишем еще раз прямое  -преобразование
-преобразование

Умножим обе части этого выражения на  проинтегрируем по окружности с радиусом, превышающим радиус сходимости
проинтегрируем по окружности с радиусом, превышающим радиус сходимости  ряда для
ряда для  и поменяем местами суммирование и интегрирование:
и поменяем местами суммирование и интегрирование:

Вычислим интеграл в правой части выражения (3.21)

Такой результат объясняется тем, что значение интеграла по замкнутому контуру в комплексной плоскости равно произведению  на сумму вычетов подынтегральной функции; единственный вычет при
на сумму вычетов подынтегральной функции; единственный вычет при  получается только при
получается только при  когда
когда 
Следовательно,

Получившееся выражение представляет собой формулу обратного  -преобразования, но надо только уточнить форму контура интегрирования. Для этого положим
-преобразования, но надо только уточнить форму контура интегрирования. Для этого положим  Тогда
Тогда  Применим обратное
Применим обратное  -преобразование к этой формуле:
-преобразование к этой формуле:


Рис. 3.9. Возможные контуры интегрирования при вычислении обратного  -преобразования
-преобразования
Подынтегральная функция имеет единственный полюс при  Интегрировать можно вдоль любого контура, охватывающего точку
Интегрировать можно вдоль любого контура, охватывающего точку  (рис. 3.9), но удобнее вдоль окружности радиуса
(рис. 3.9), но удобнее вдоль окружности радиуса 
Для сигналов, абсолютное значение которых убывает во времени,  потому в качестве контура интегрирования можно использовать окружность радиуса
потому в качестве контура интегрирования можно использовать окружность радиуса 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
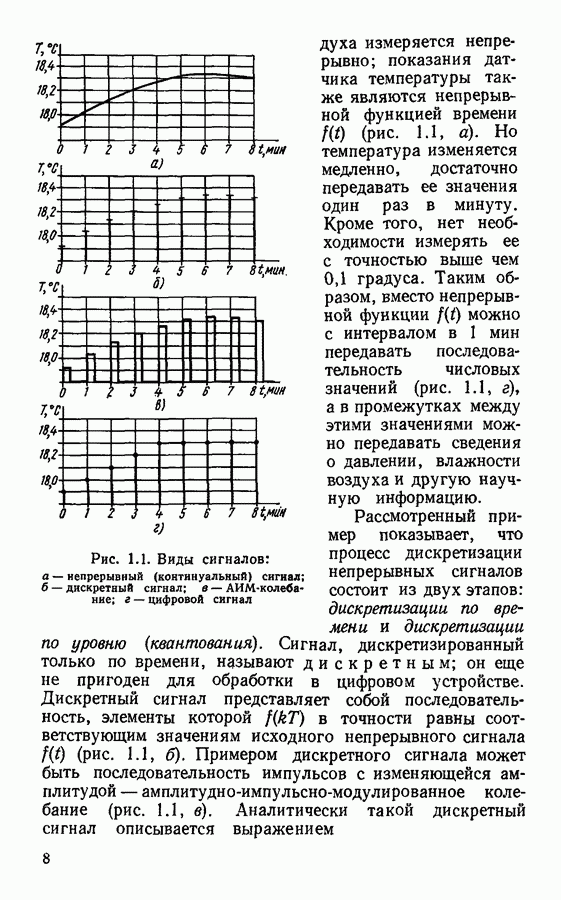
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
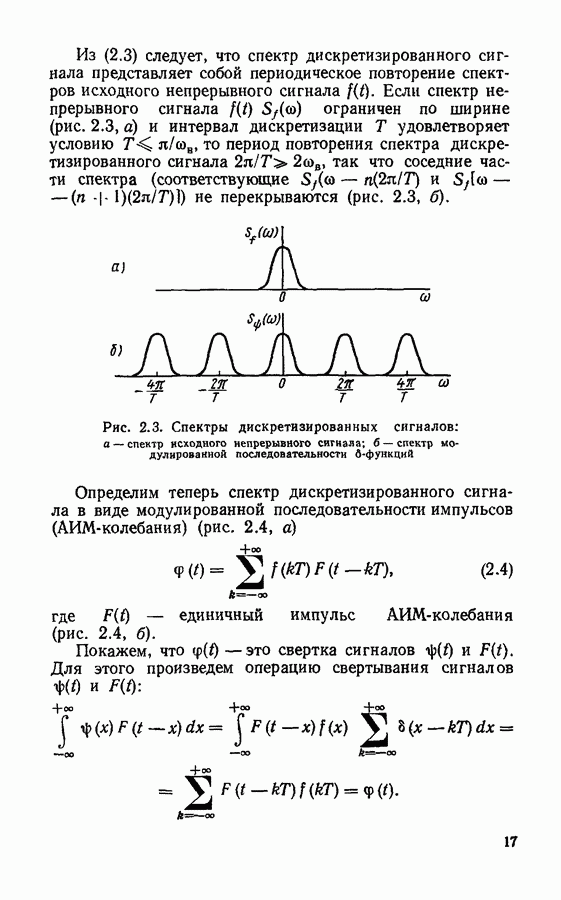
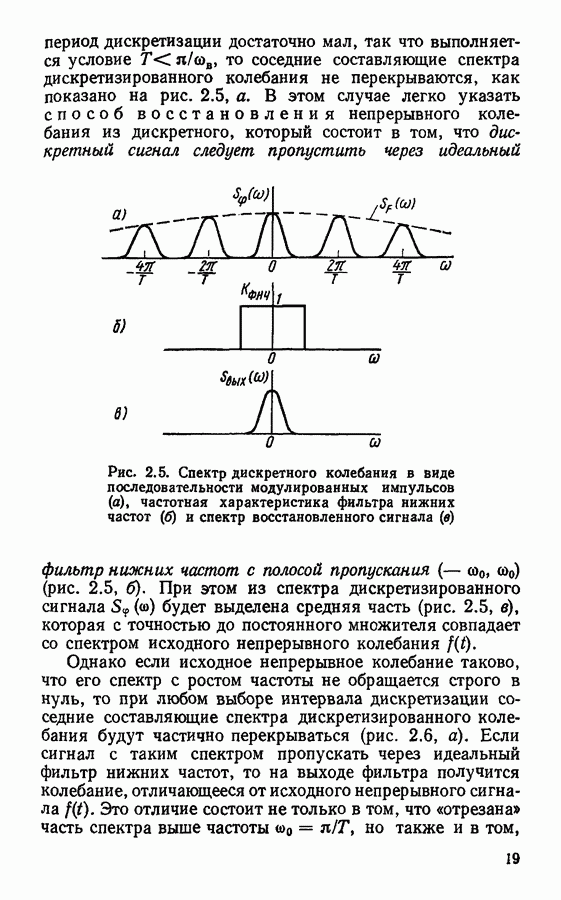
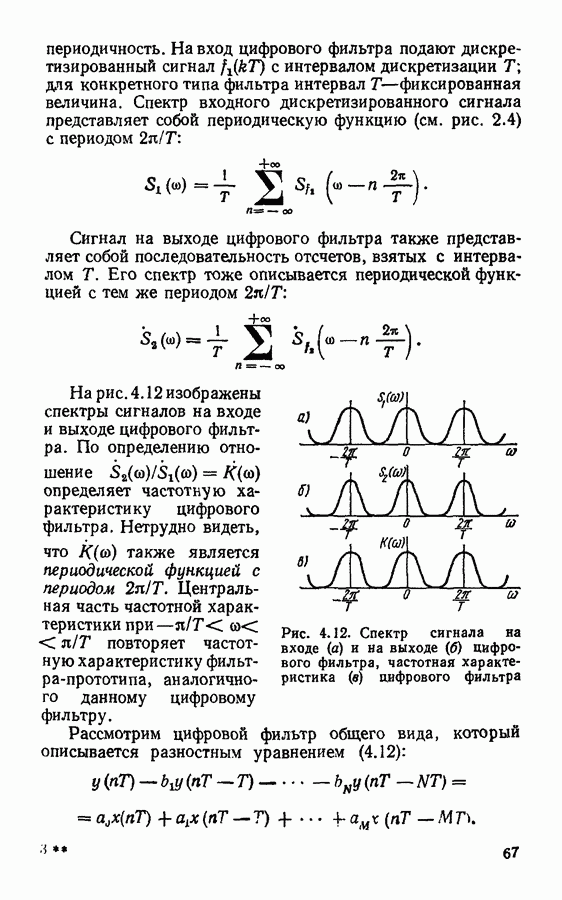
- Спектры дискретизированных сигналов.
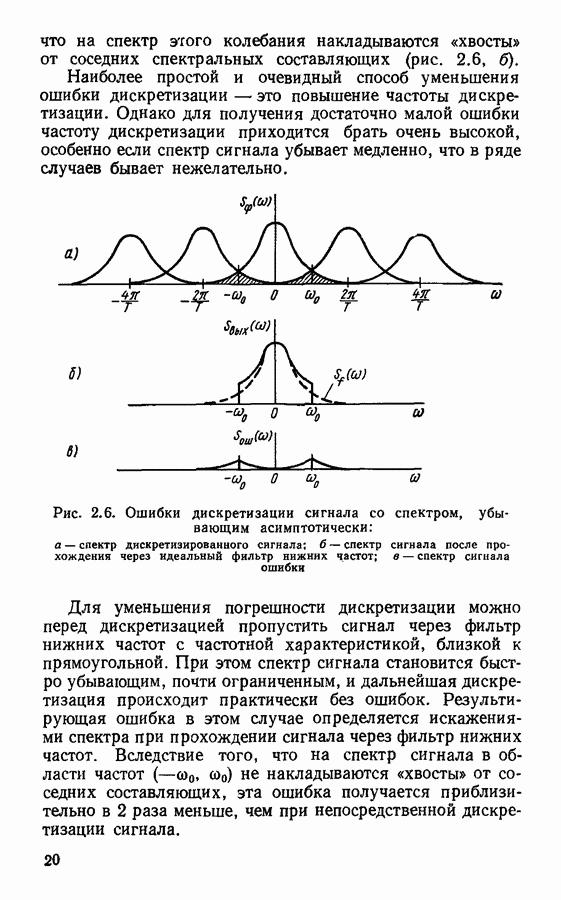
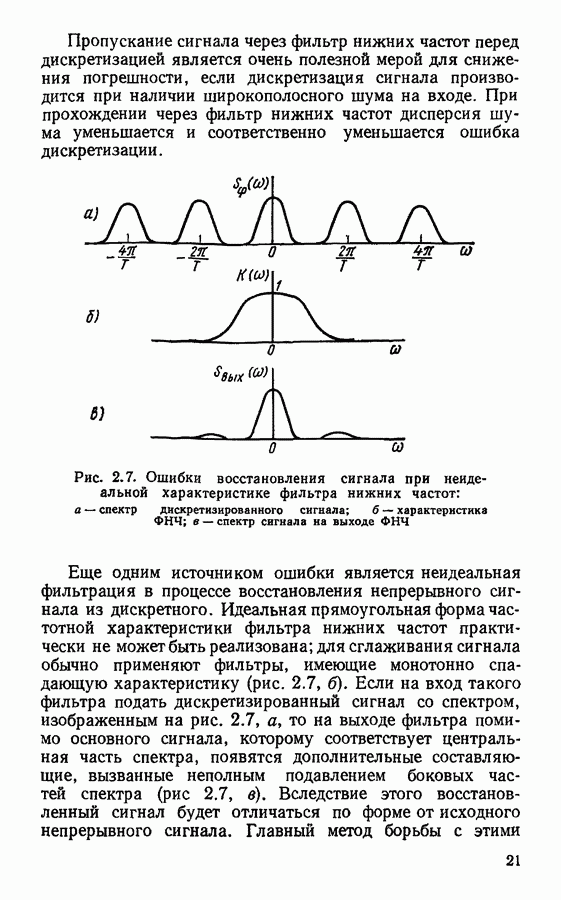
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
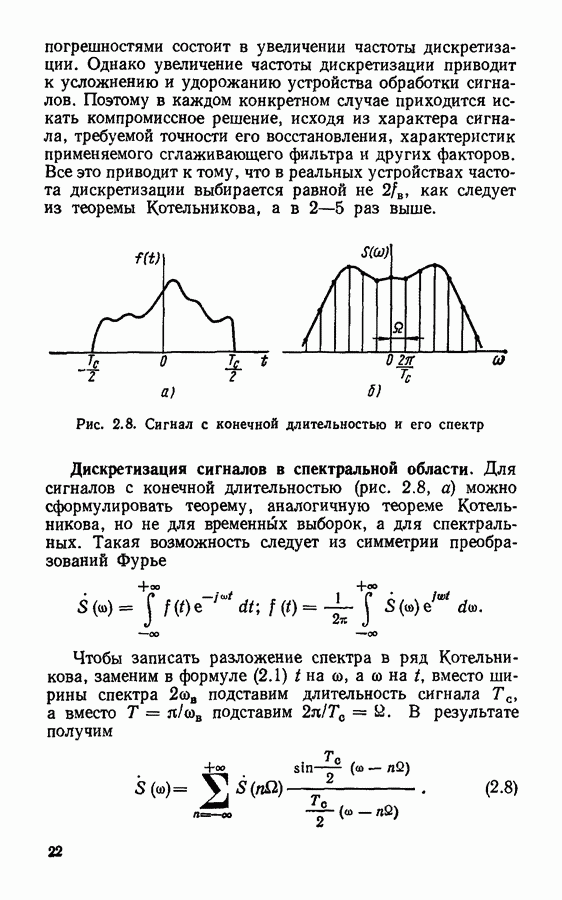
- Дискретизация сигналов в спектральной области.
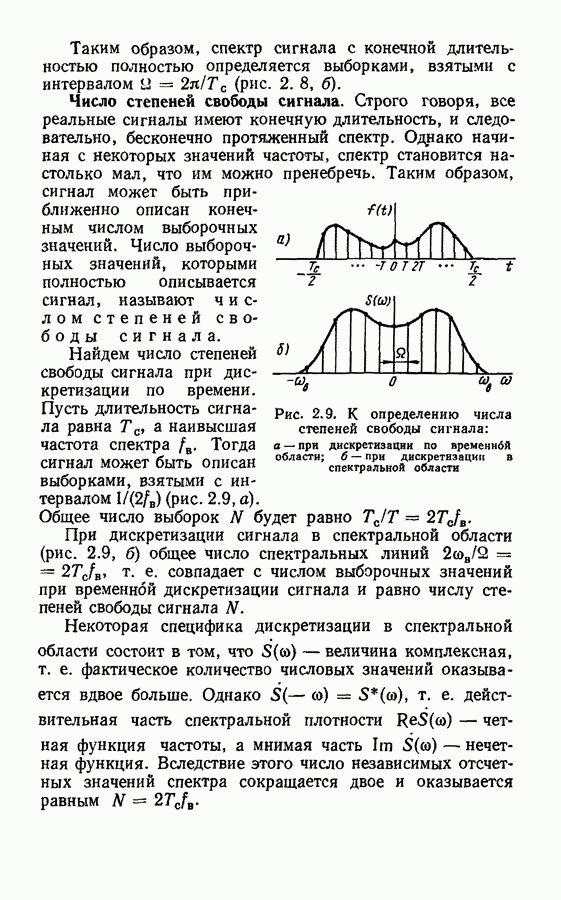
- Число степеней свободы сигнала.
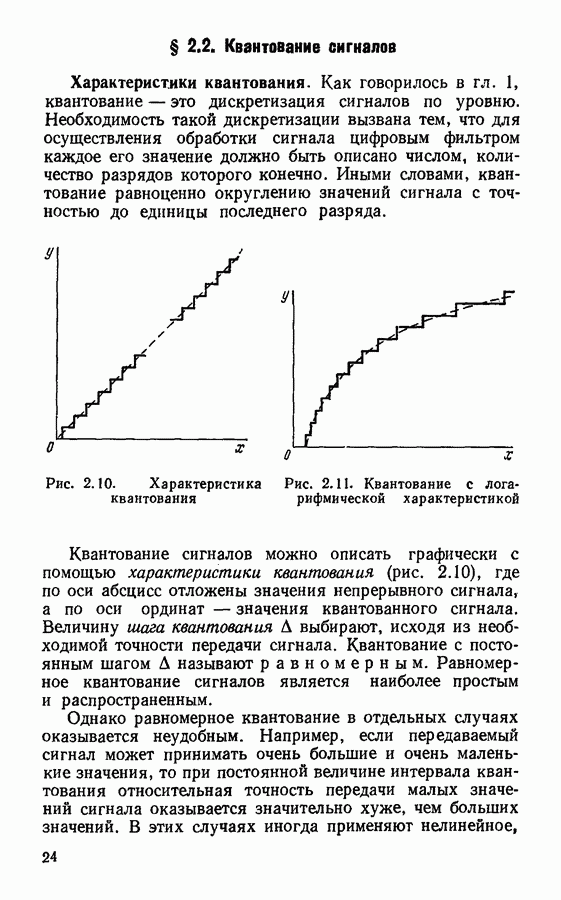
- § 2.2. Квантование сигналов
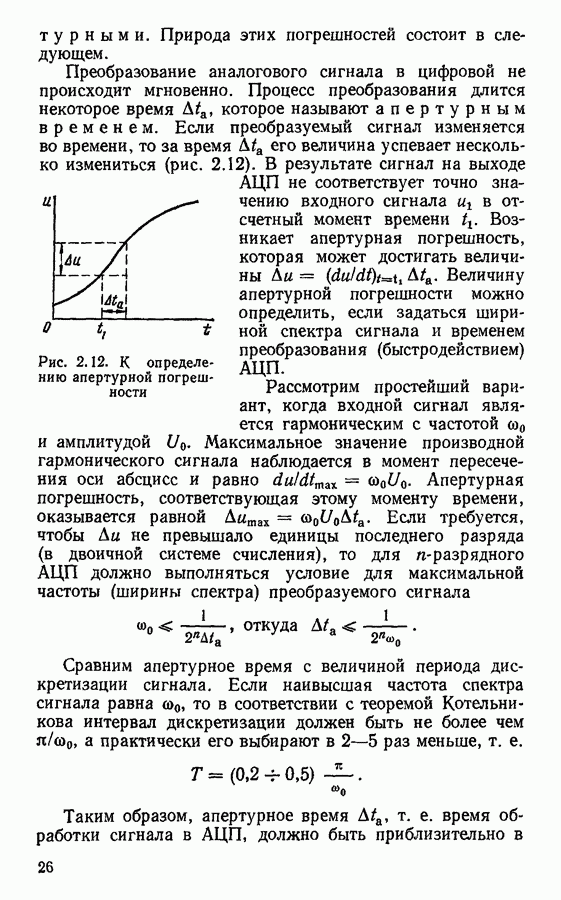
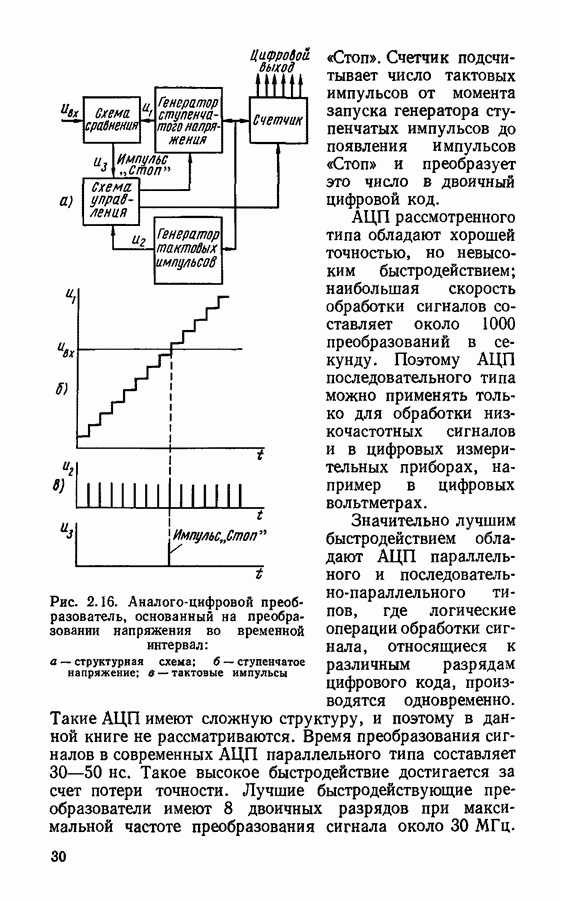
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
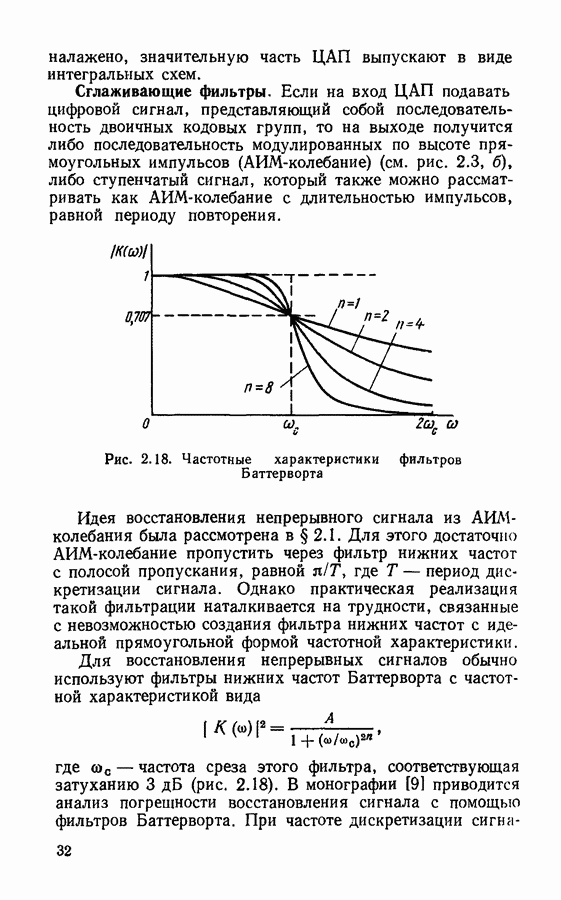
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
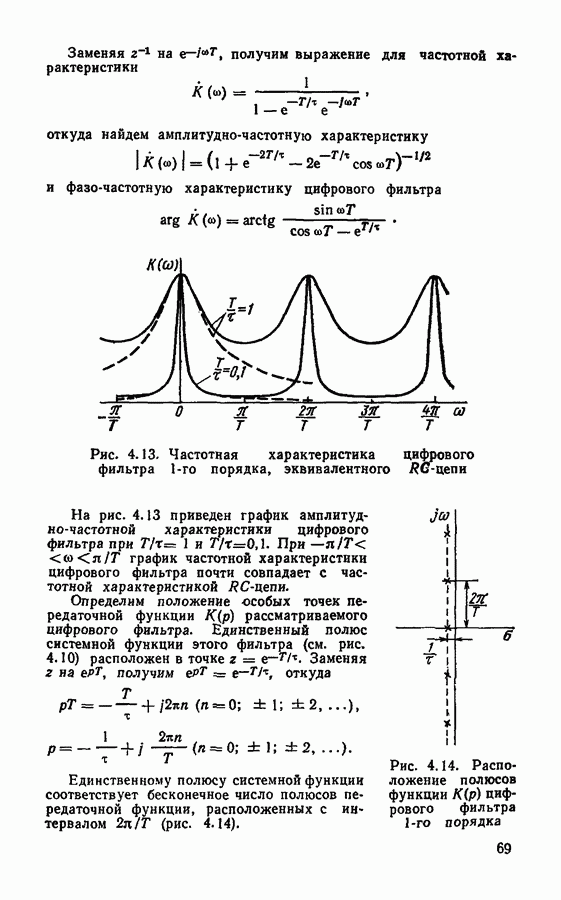
- § 4.3. Частотные характеристики цифровых фильтров
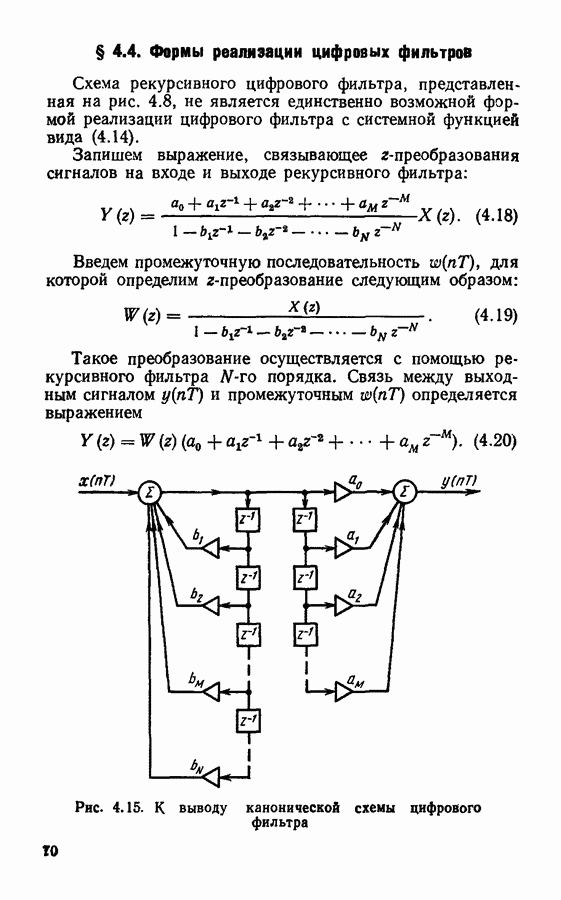
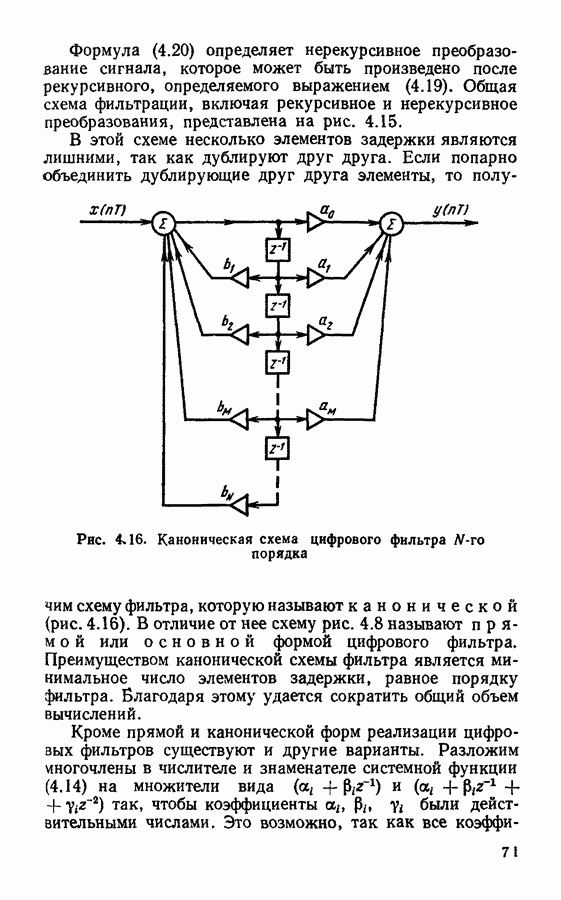
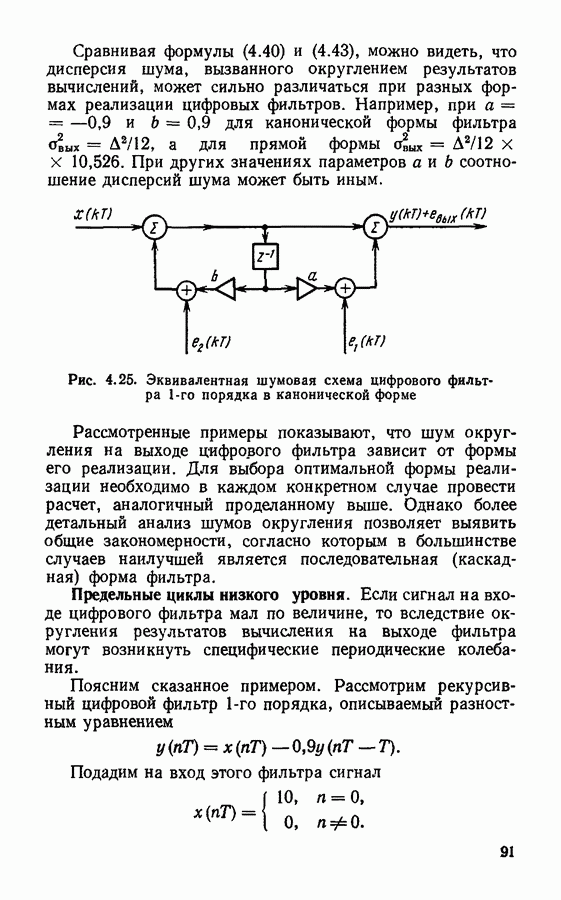
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
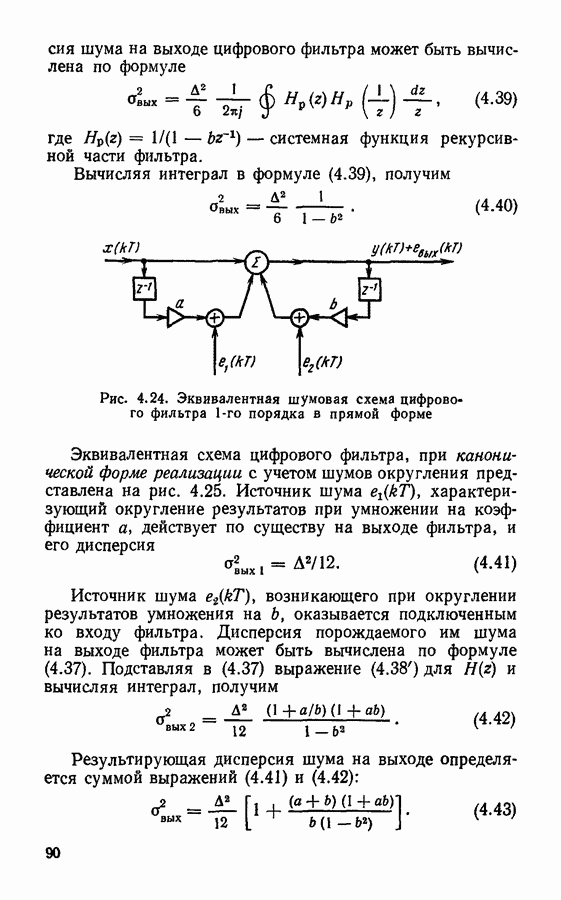
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА