| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
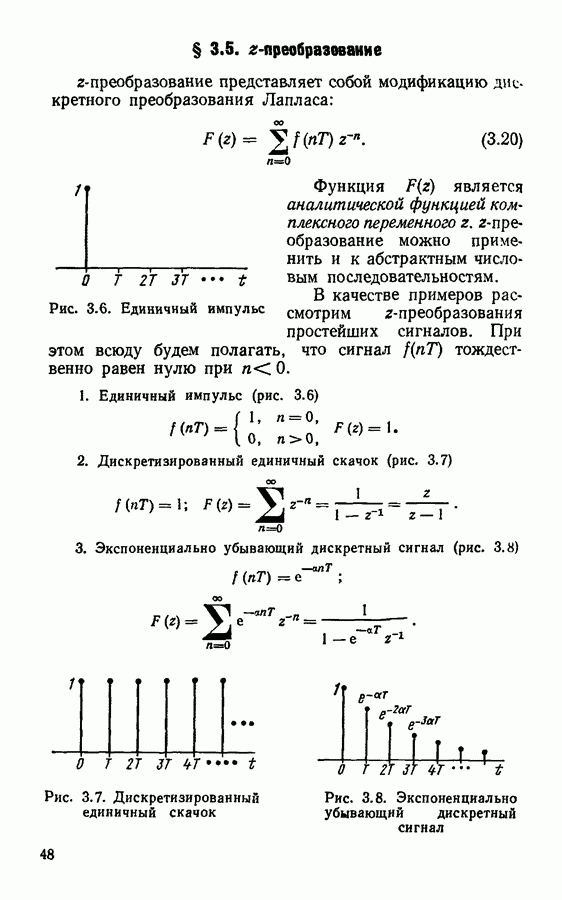
§ 3.7. Основные свойства z-преобразования
Для  -преобразования справедливы некоторые теоремы, аналогичные теоремам о спектрах непрерывных сигналов. Главная из них — теорема о свертке.
-преобразования справедливы некоторые теоремы, аналогичные теоремам о спектрах непрерывных сигналов. Главная из них — теорема о свертке.
Теорема о свертке. В теории непрерывных сигналов эта теорема формулируется следующим образом. Пусть заданы два непрерывных сигнала  и их свертка
и их свертка

Тогда спектральная плотность свертки  связана со спектральными плотностями
связана со спектральными плотностями  сигналов
сигналов  соотношением
соотношением

Для дискретных сигналов  по аналогии с непрерывными сигналами вводится дискретная свертка, которая определяется выражением
по аналогии с непрерывными сигналами вводится дискретная свертка, которая определяется выражением

или

Запишем для дискретных сигналов  их
их  -преобразования
-преобразования

Применим  -преобразование к формуле свертки (3.25)
-преобразование к формуле свертки (3.25)

Преобразуем правую часть этого выражения так, что бы получить произведение  -преобразований. Для этого нужно, в частности, чтобы
-преобразований. Для этого нужно, в частности, чтобы  умножалось на
умножалось на  на
на  Сгруппируем соответствующим образом степени
Сгруппируем соответствующим образом степени 

При  поэтому можно во второй сумме верхний предел суммирования сделать равным
поэтому можно во второй сумме верхний предел суммирования сделать равным  Далее обозначим
Далее обозначим  и получим
и получим

Нижний предел  можно заменить на
можно заменить на  так как при
так как при  все
все  . В результате получим
. В результате получим

т.е.

Выражение (3.26) аналогично формуле (3.23), описывающей теорему о свертке для обычных непрерывных сигналов.
В качестве примера рассмотрим дискретную свертку двух простых сигналов:  имеющего два ненулевых отсчета
имеющего два ненулевых отсчета  состоящего из трех отсчетов
состоящего из трех отсчетов  Непосредственный подсчет по формуле (3.24) приводит к следующему результату:
Непосредственный подсчет по формуле (3.24) приводит к следующему результату:

Сигнал  являющийся сверткой
являющийся сверткой  и
и  изображен на рис. 3.10, в.
изображен на рис. 3.10, в.

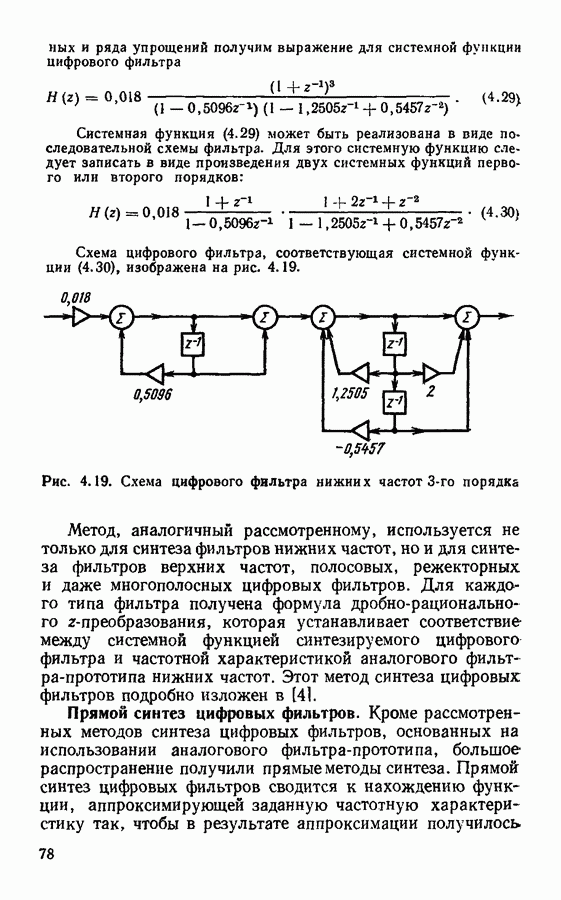
Рис. 3.10. Дискретная свертка двух сигналов
Найдем  -преобразования сигналов
-преобразования сигналов 

Перемножая выражения для  нетрудно убедиться в справедливости выражения (3.26).
нетрудно убедиться в справедливости выражения (3.26).

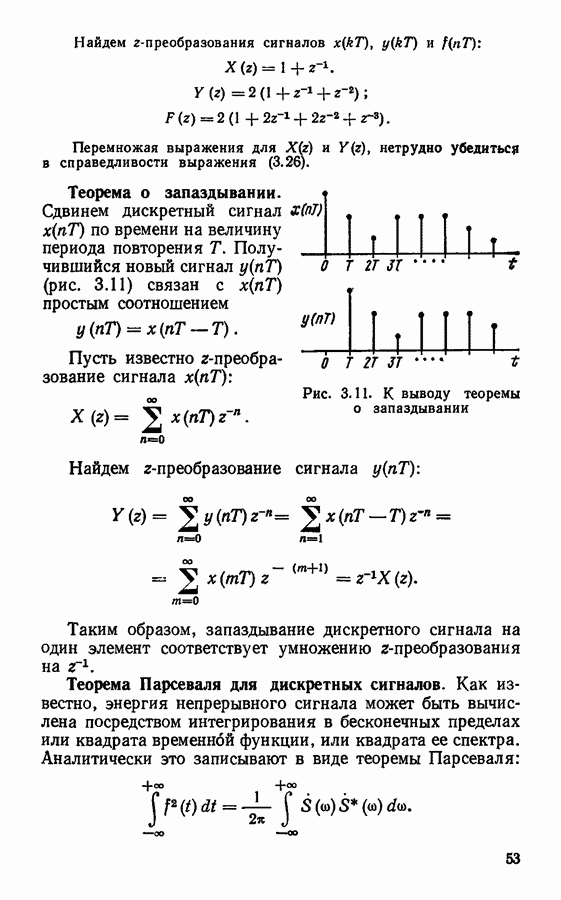
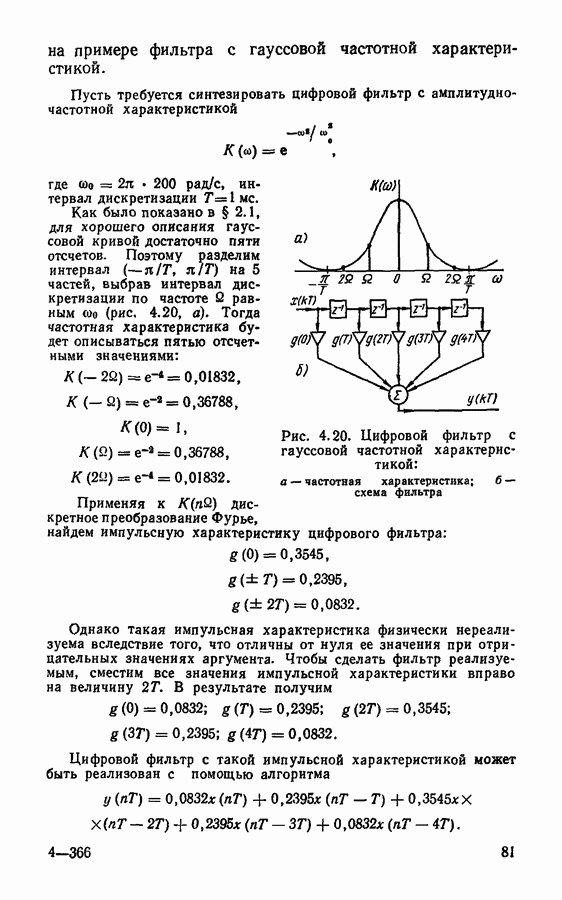
Рис. 3.11. К выводу теоремы о запаздывании
Теорема о запаздывании. Сдвинем дискретный сигнал  по времени на величину периода повторения
по времени на величину периода повторения  Получившийся новый сигнал
Получившийся новый сигнал  (рис. 3.11) связан с
(рис. 3.11) связан с  простым соотношением
простым соотношением

Пусть известно  -преобразование сигнала
-преобразование сигнала 

Найдем  -преобразование сигнала
-преобразование сигнала 

Таким образом, запаздывание дискретного сигнала на один элемент соответствует умножению  -преобразования на
-преобразования на 
Теорема Парсеваля для дискретных сигналов. Как известно, энергия непрерывного сигнала может быть вычислена посредством интегрирования в бесконечных пределах или квадрата временнбй функции, или квадрата ее спектра. Аналитически это записывают в виде теоремы Парсеваля:

Аналогичное соотношение можно получить для дискретных сигналов.
Пусть дискретный сигнал  представляет собой убывающую последовательность, так что все полюсы его
представляет собой убывающую последовательность, так что все полюсы его  -преобразования
-преобразования  находятся внутри единичной окружности в плоскости
находятся внутри единичной окружности в плоскости  Для вывода теоремы Парсеваля умножим
Для вывода теоремы Парсеваля умножим  на
на  и найдем величину этого произведения:
и найдем величину этого произведения:

Умножим обе части равенства (3.27) и  и проинтегрируем по замкнутому контуру
и проинтегрируем по замкнутому контуру  который должен располагаться в области сходимости как
который должен располагаться в области сходимости как  так и
так и  Поскольку последовательность
Поскольку последовательность  является убывающей, в качестве контура интегрирования
является убывающей, в качестве контура интегрирования  можно принять окружность
можно принять окружность  При интегрировании двойной суммы в правой части равенства (3.27) все члены окажутся равными нулю, кроме членов, соответствующих
При интегрировании двойной суммы в правой части равенства (3.27) все члены окажутся равными нулю, кроме членов, соответствующих  . В результате получим
. В результате получим

Выражение (3.28) является записью теоремы Парсеваля для дискретных сигналов.
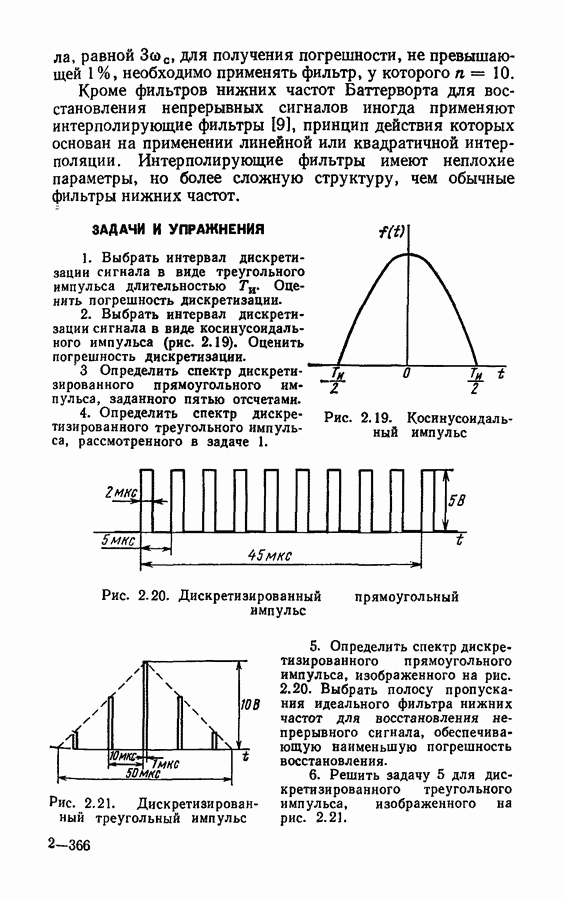
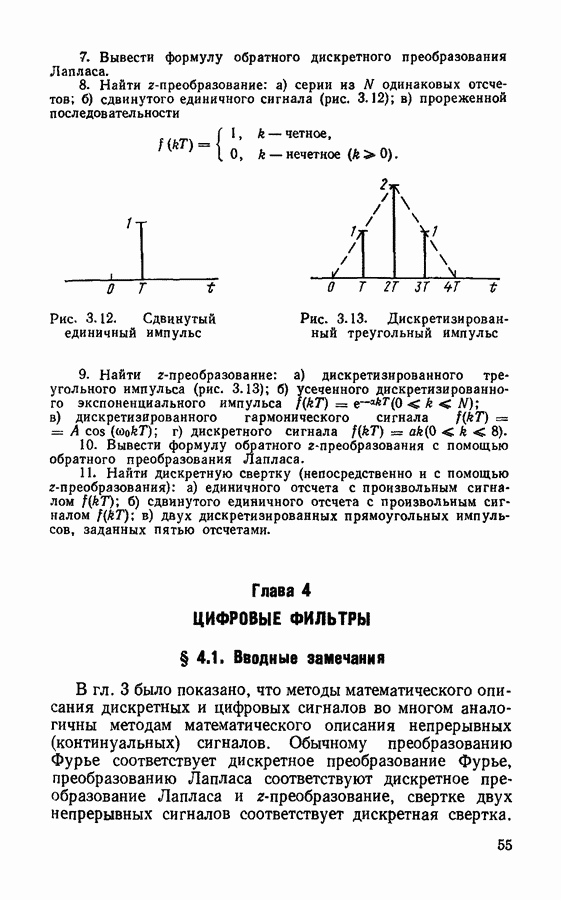
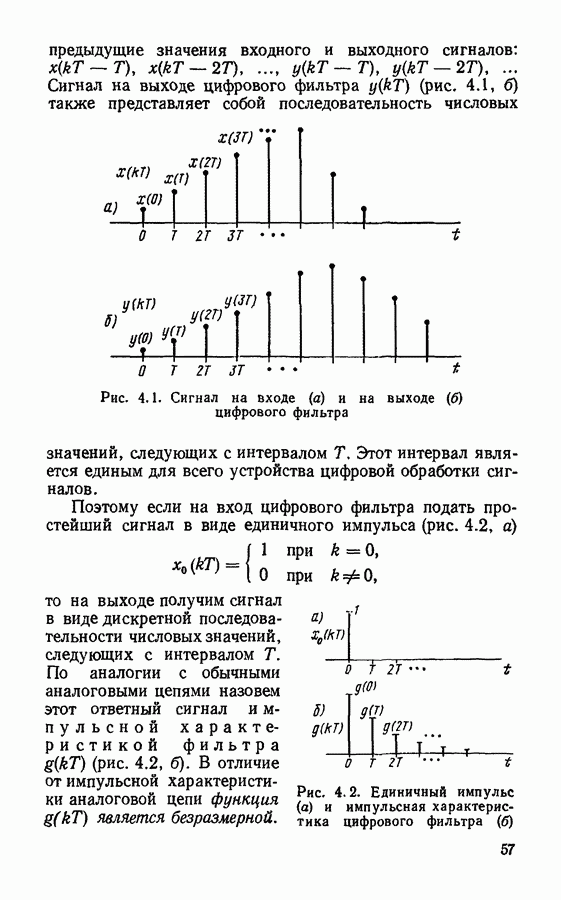
ЗАДАЧИ И УПРАЖНЕНИЯ
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
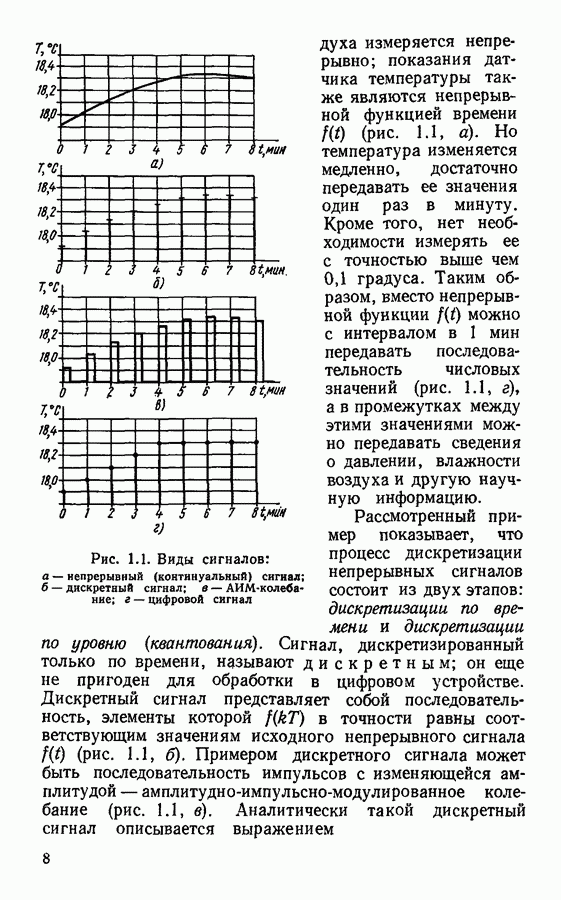
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
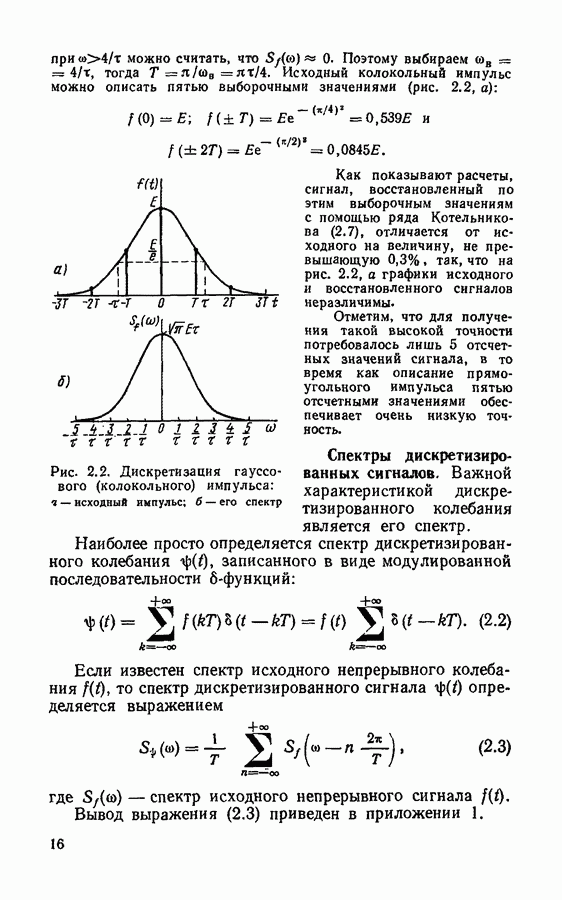
- § 2.1. Основы дискретизации непрерывных сигналов
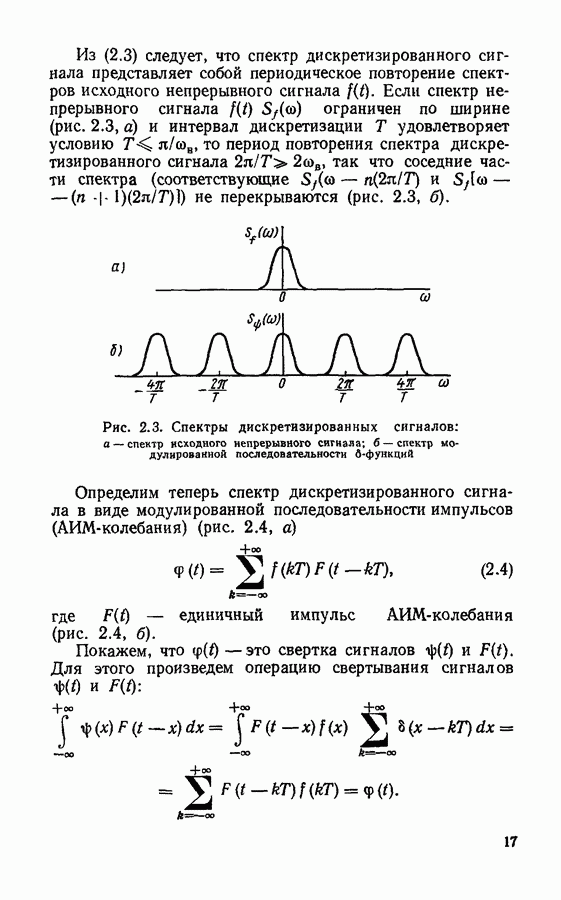
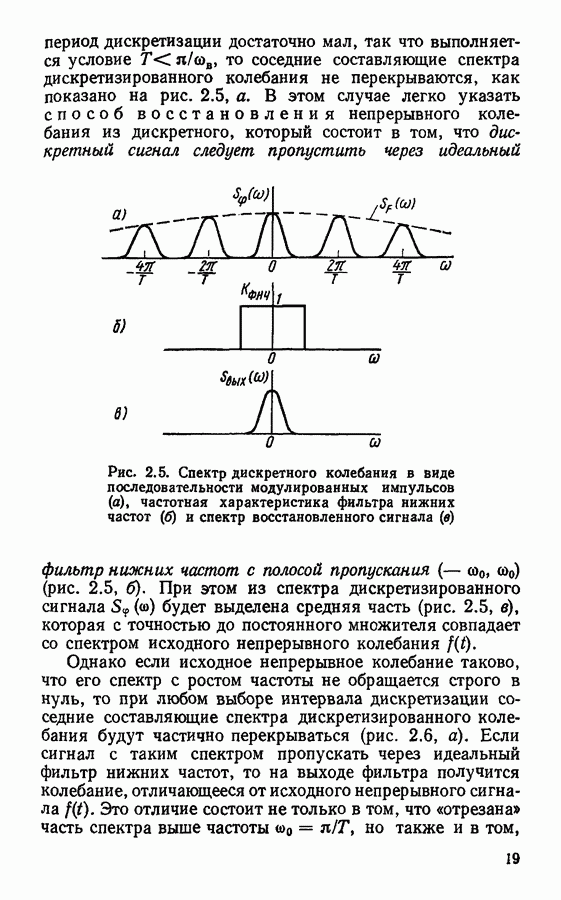
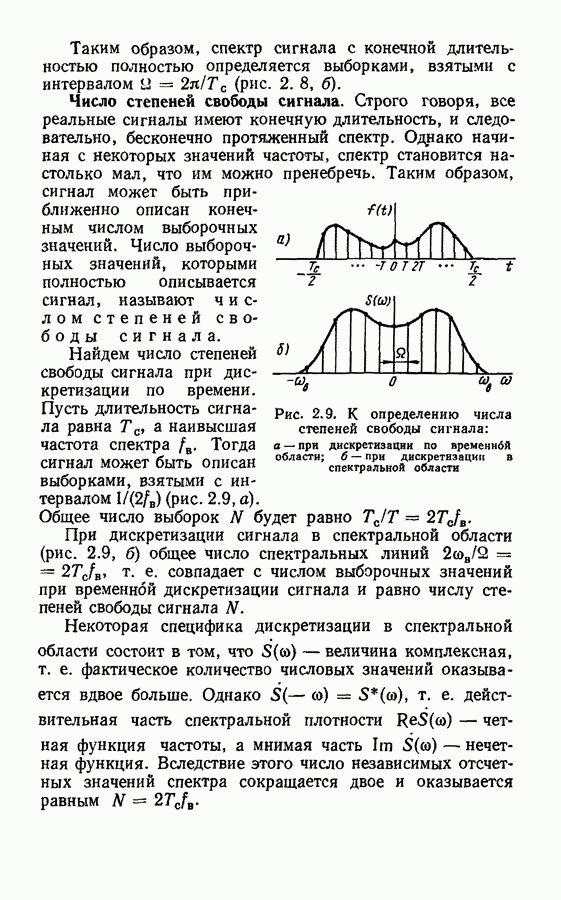
- Спектры дискретизированных сигналов.
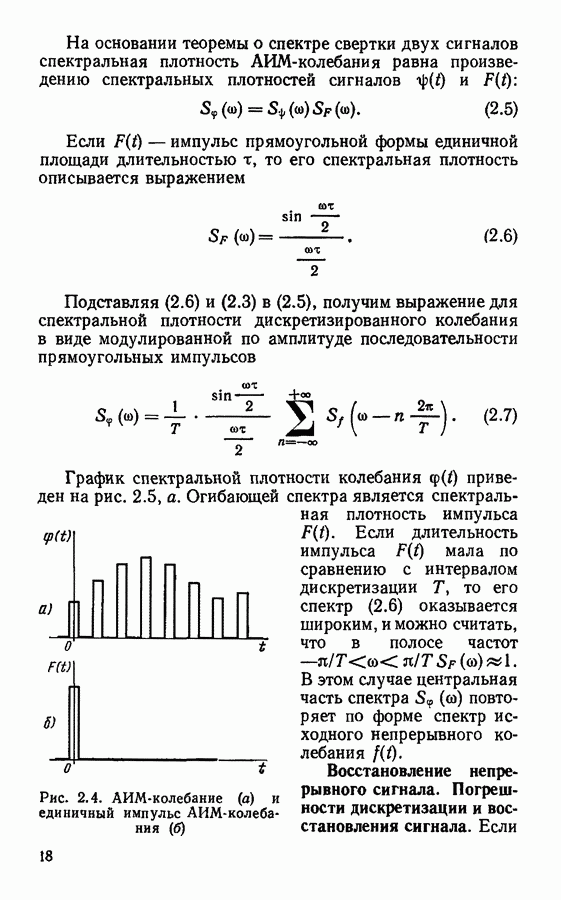
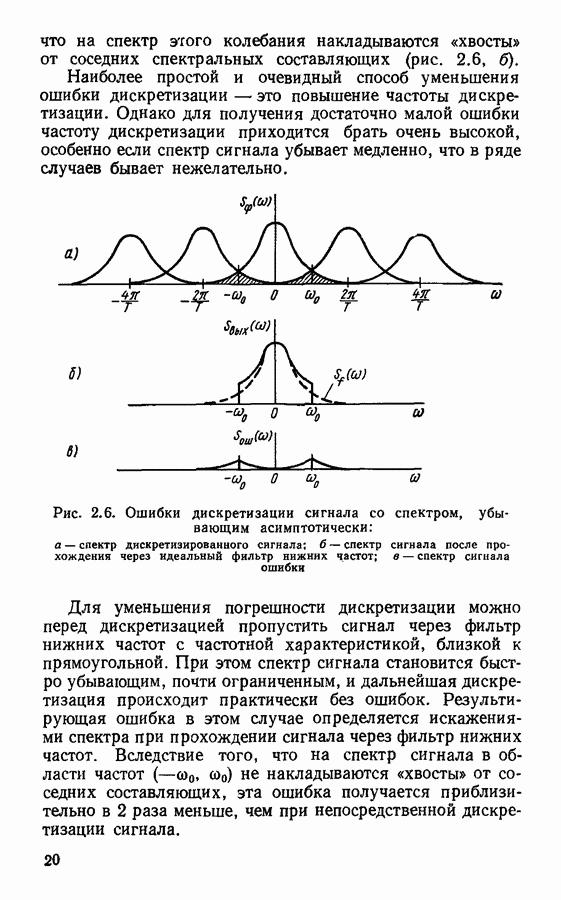
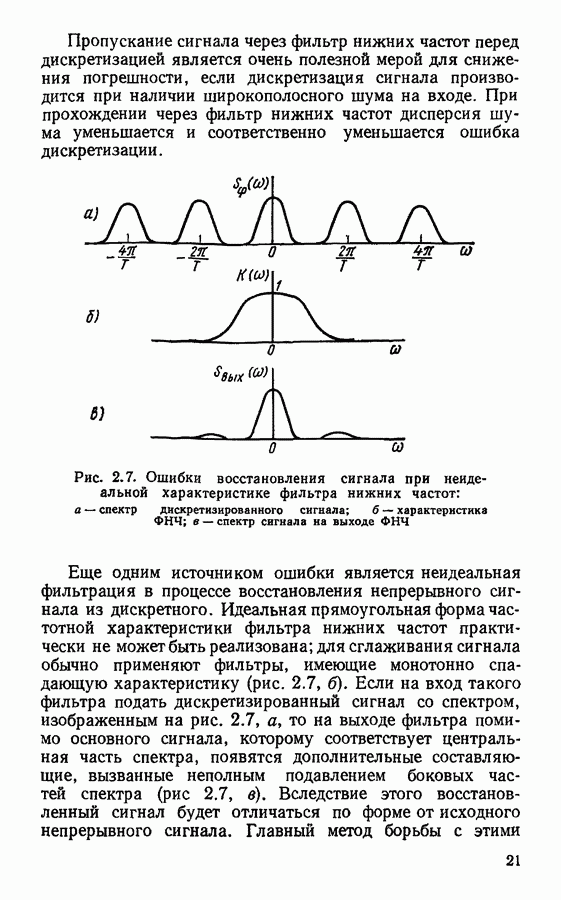
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
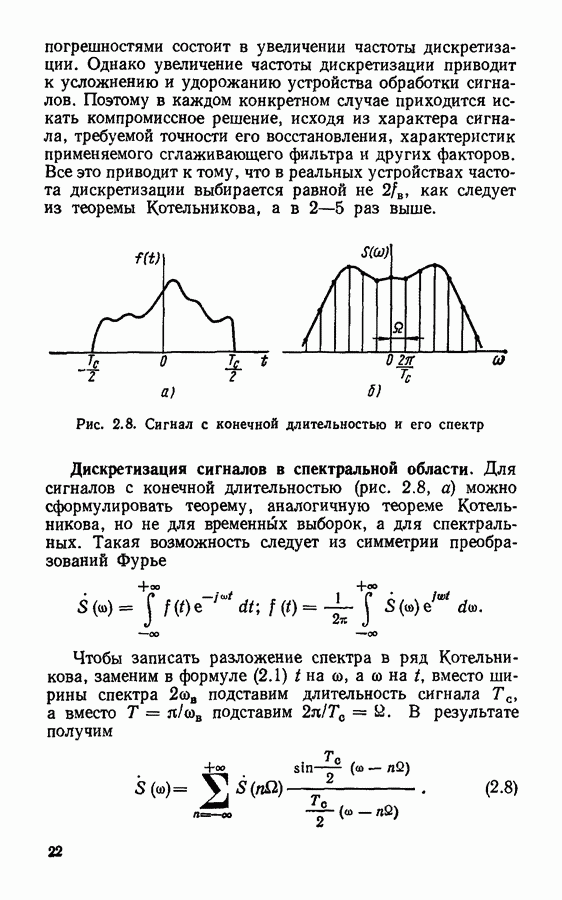
- Дискретизация сигналов в спектральной области.
- Число степеней свободы сигнала.
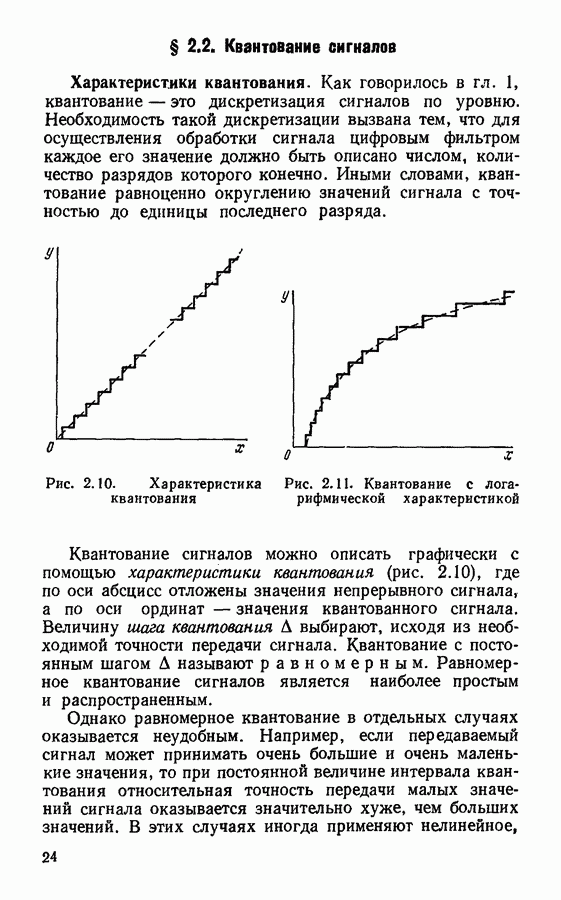
- § 2.2. Квантование сигналов
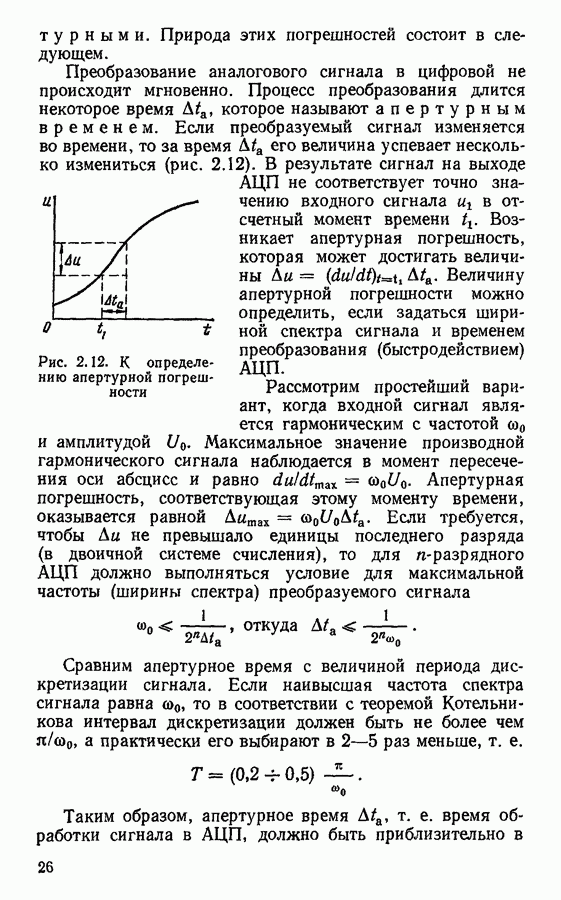
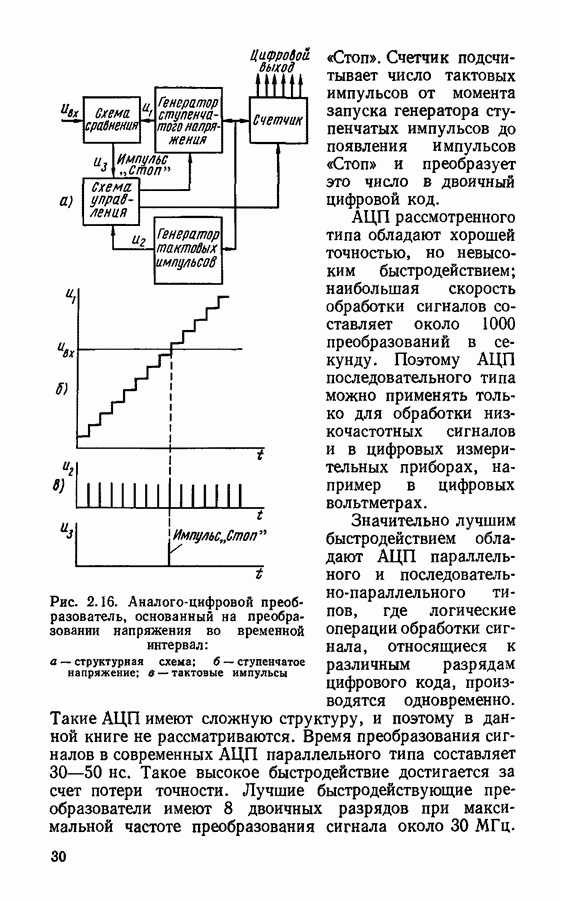
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
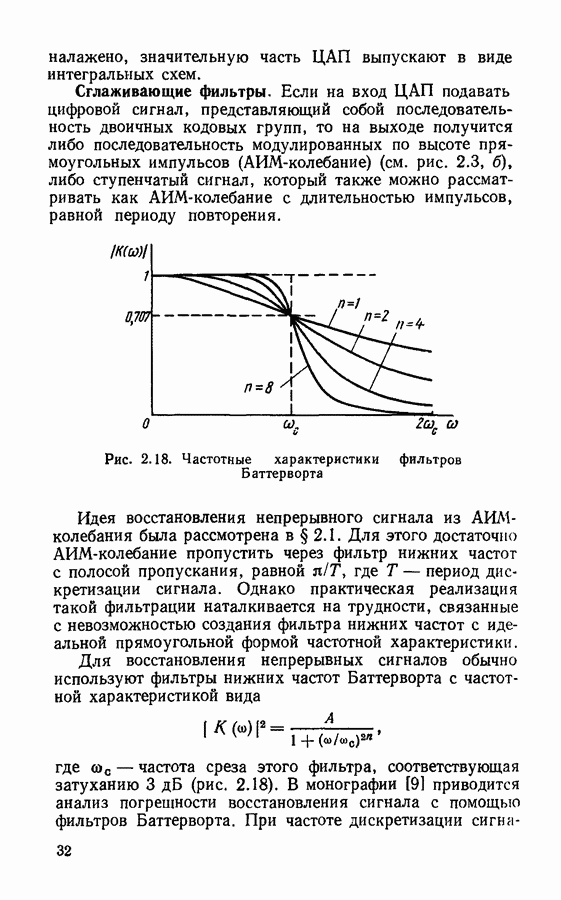
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
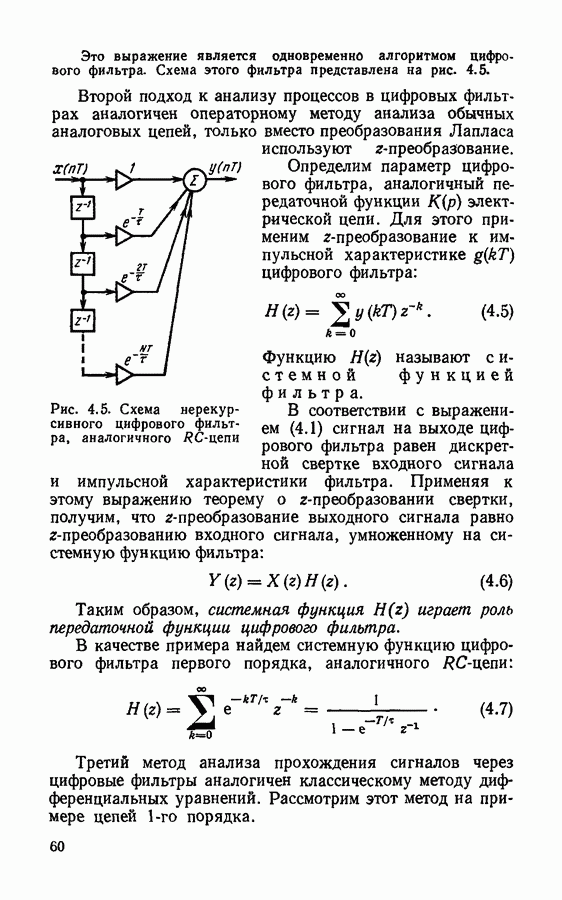
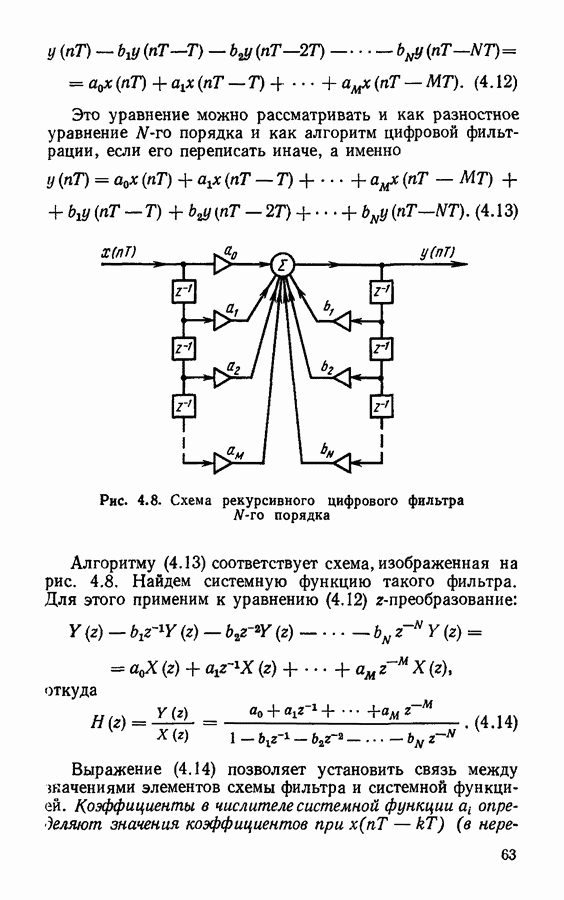
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
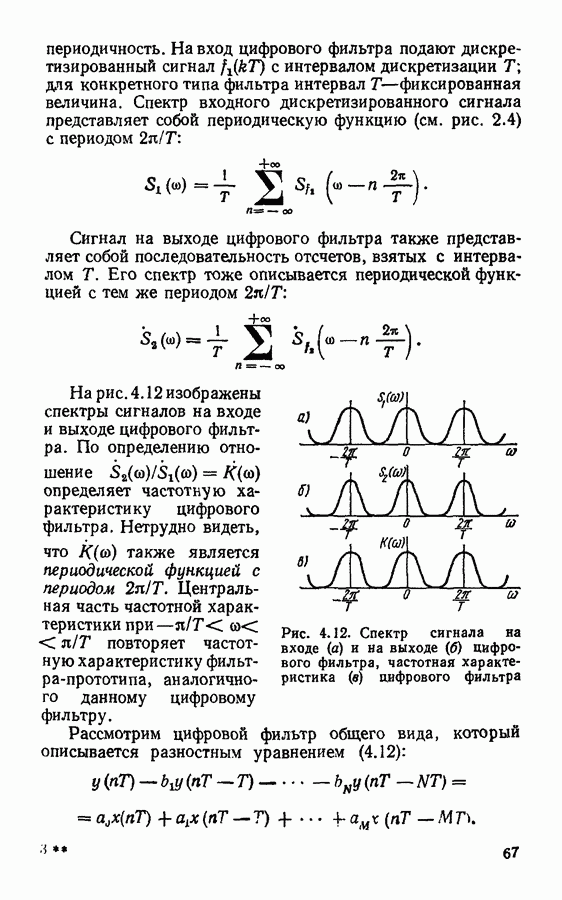
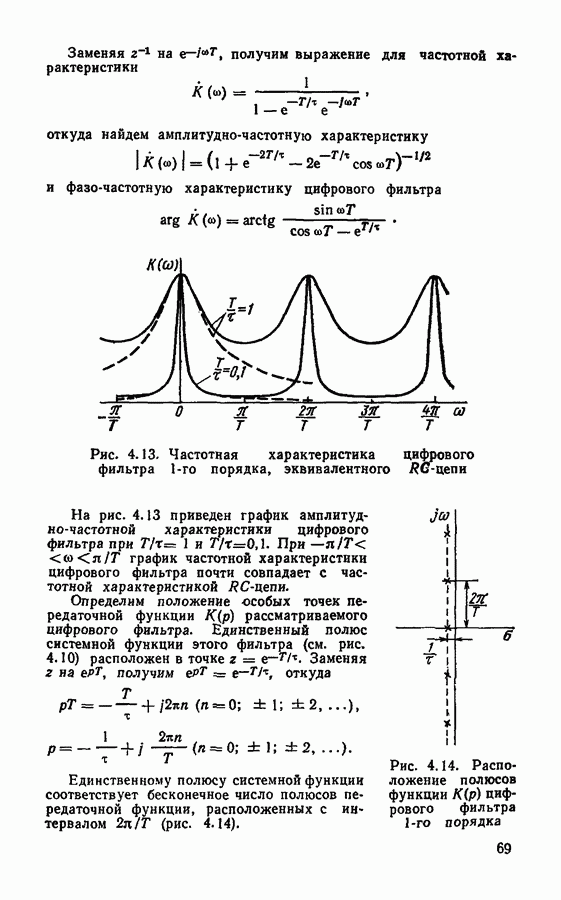
- § 4.3. Частотные характеристики цифровых фильтров
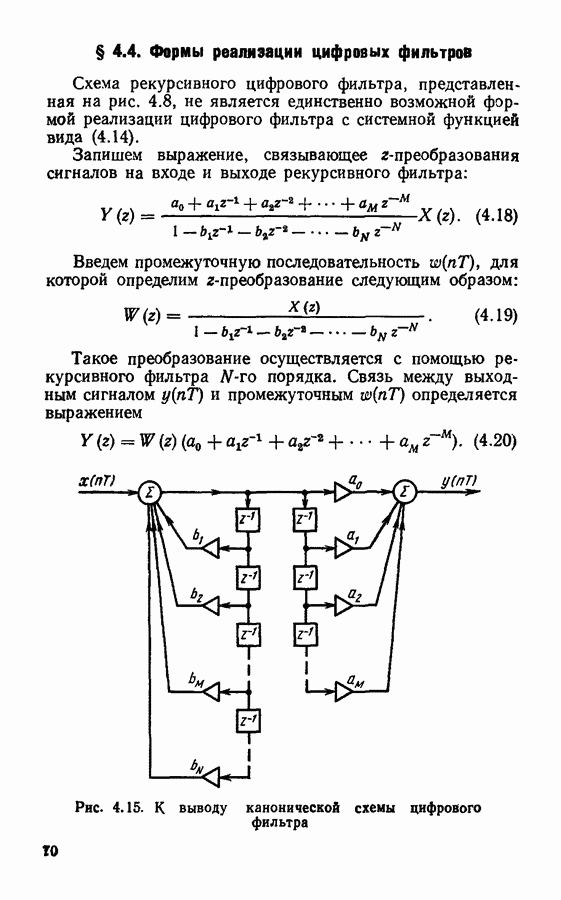
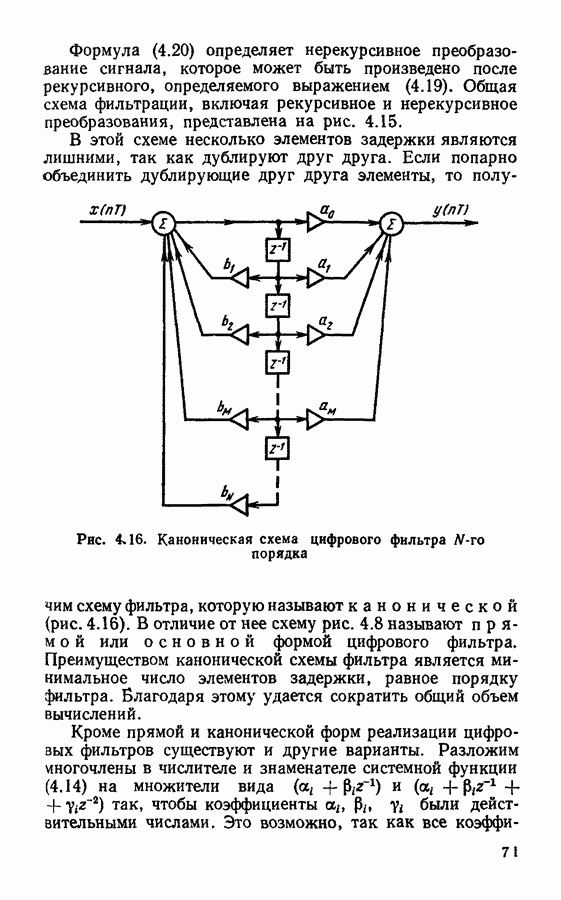
- § 4.4. Формы реализации цифровых фильтров
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
- Методы синтеза фильтров с конечной импульсной характеристикой.
- § 4.6. Эффекты квантования в цифровых фильтрах
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
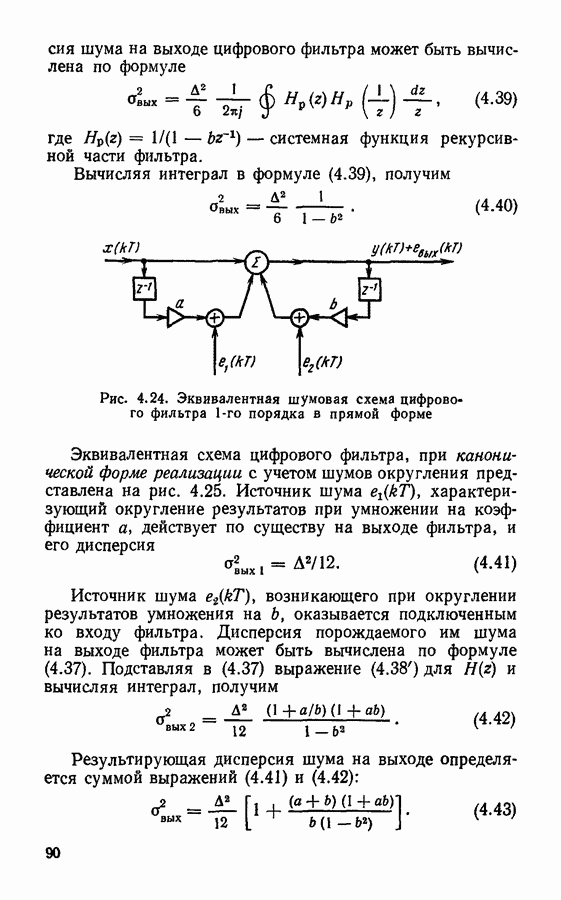
- Ошибки, вызванные квантованием результатов вычислений.
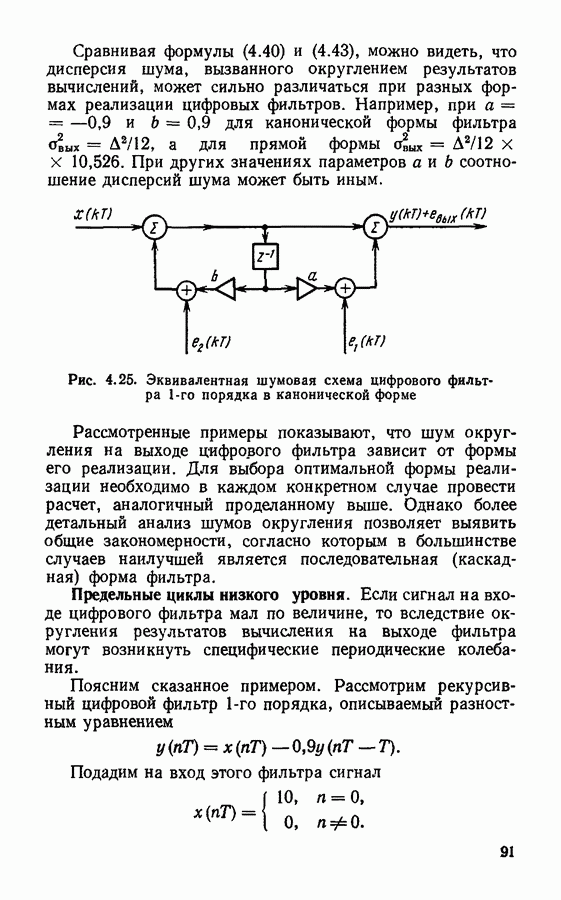
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА