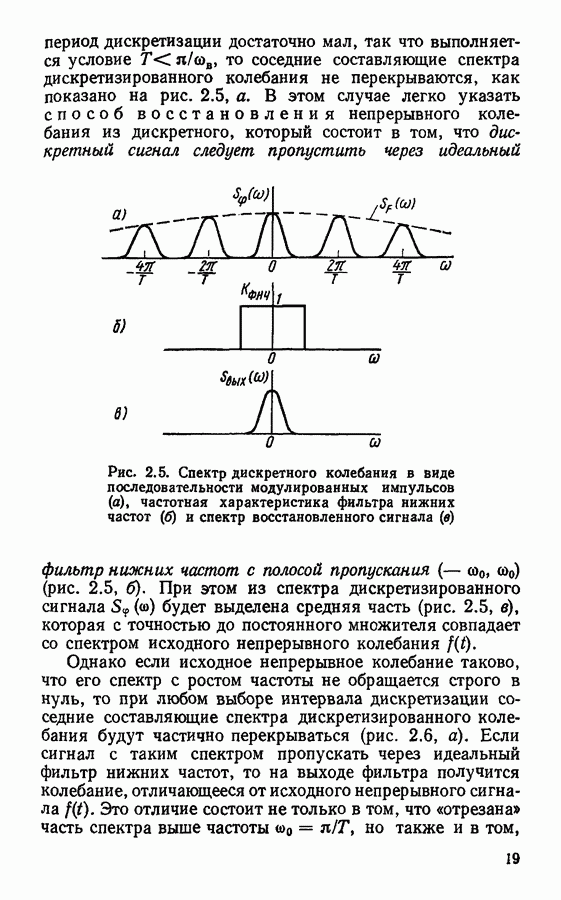
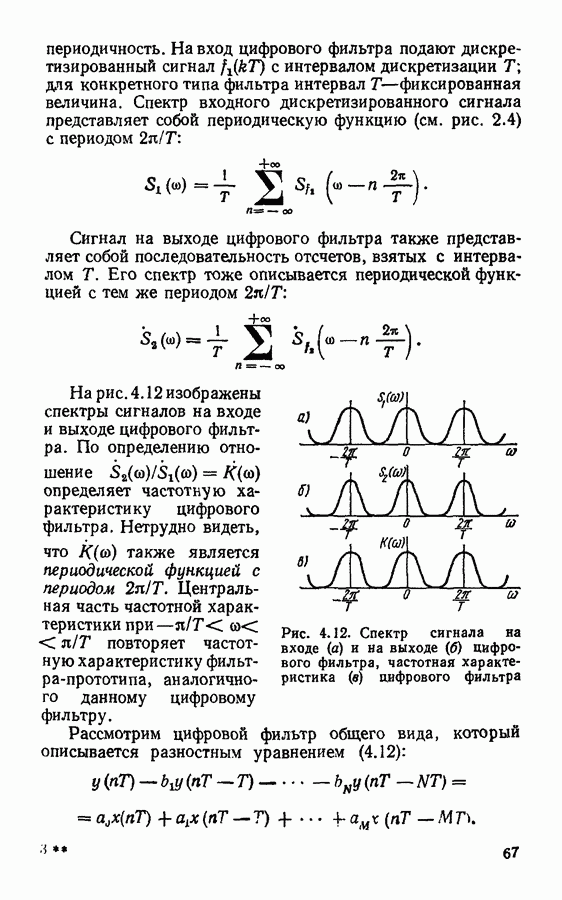
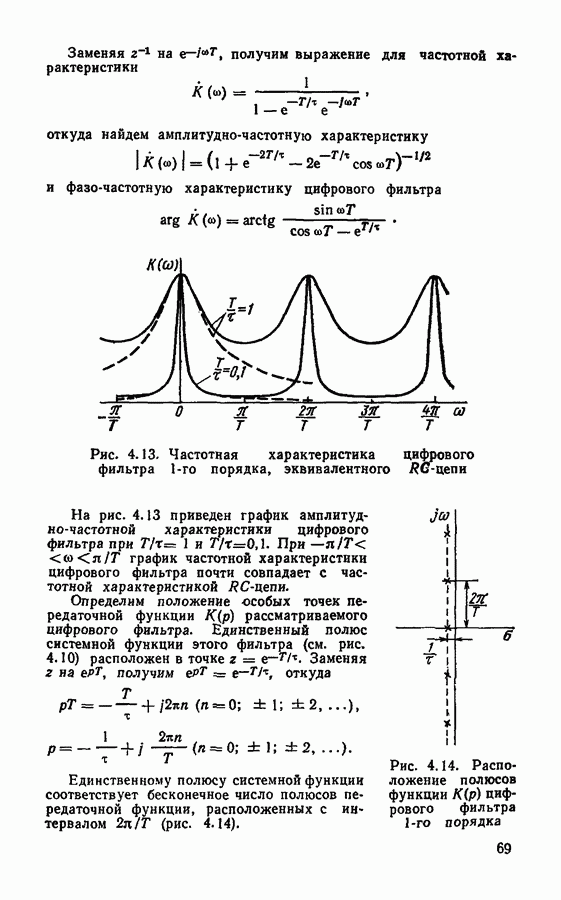
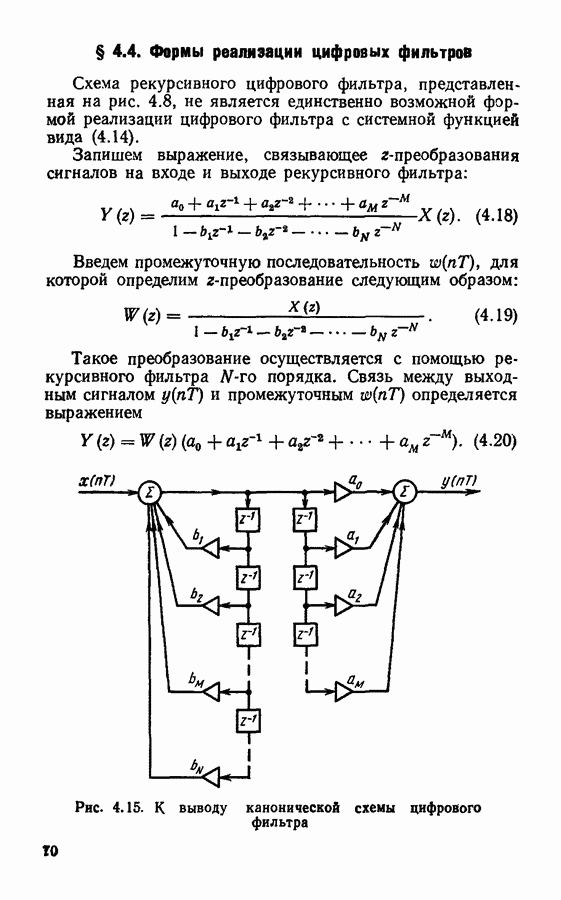
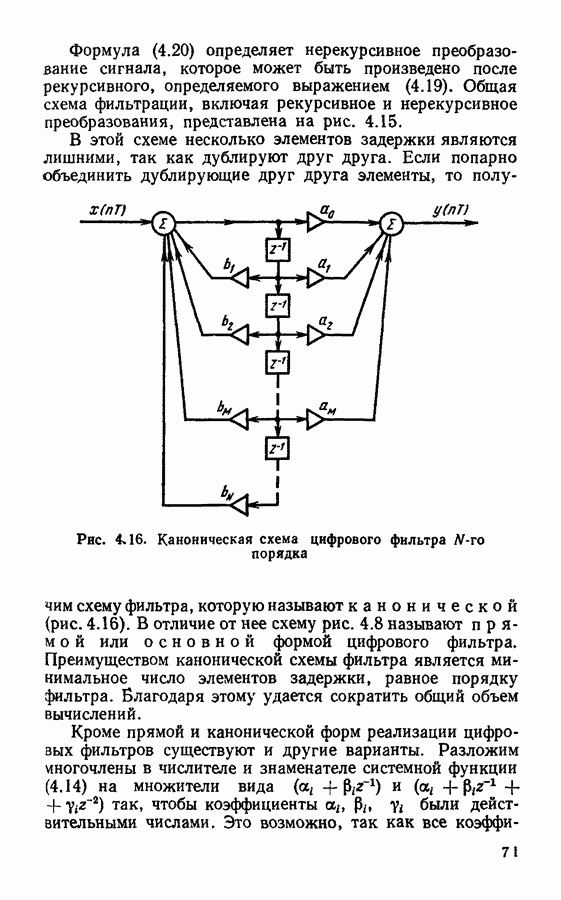
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
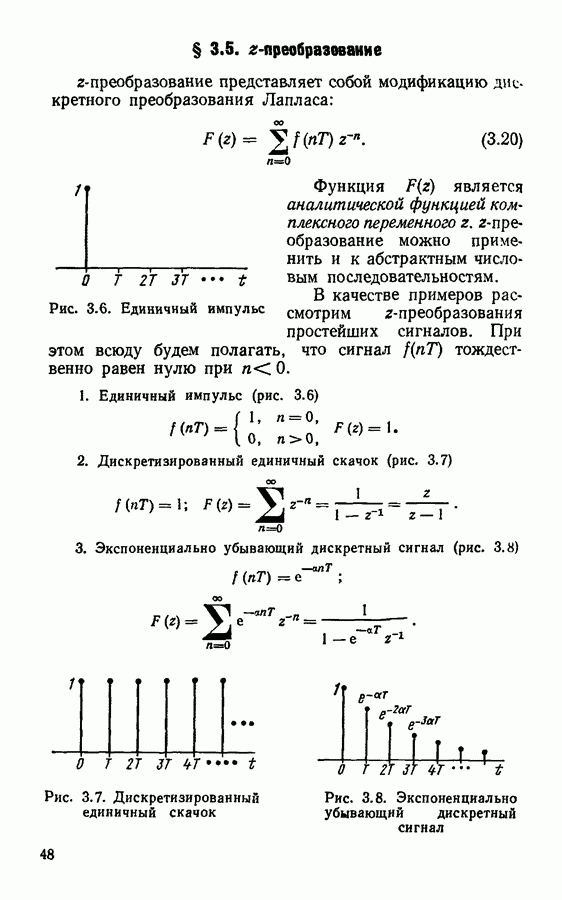
Дискретное преобразование Фурье. Ниже приводятся программы дискретного преобразования Фурье (ДПФ). Программы быстрого преобразования Фурье рассматривать не будем, так как детальное рассмотрение этого вопроса выходит за рамки курса «Радиотехнические цепи и сигналы». Кроме того, при решении простейших учебных задач мы будем рассматривать сигналы с малым числом степеней свободы, для которых применение быстрого преобразования Фурье нецелесообразно.
Главная трудность в программировании ДПФ — запись арифметических действий над комплексными числами. Чтобы обойти эту трудность, имеет смысл ограничиться вычислением ДПФ симметричных сигналов, описываемых четной функцией времени. При этом формула ДПФ значительно упрощается:

Соответствующая ей программа имеет вид

Исходный сигнал в этой программе задается центральным значением  и массивом
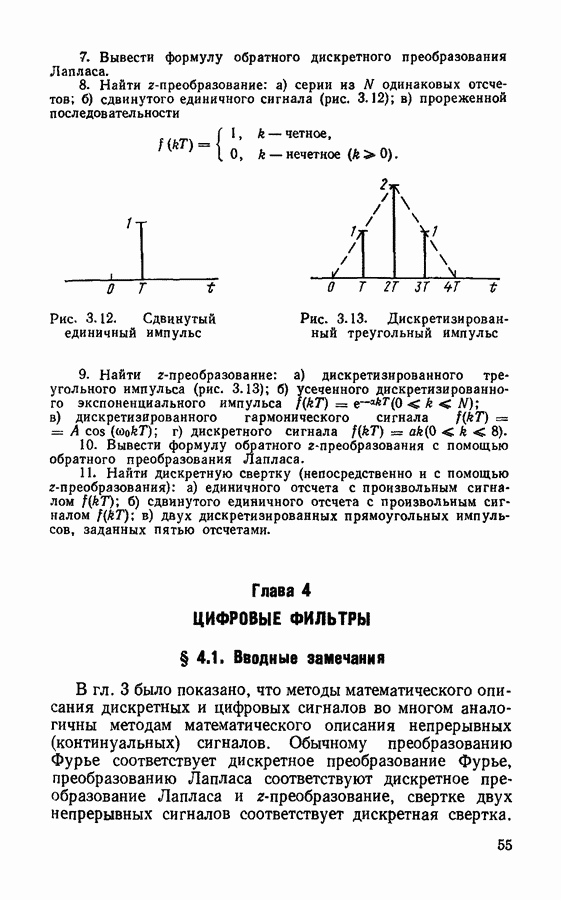
и массивом  который описывает правую половину сигнала при
который описывает правую половину сигнала при  число элементов в массиве
число элементов в массиве  где
где  число степеней свободы сигнала, т. е. общее число задаваемых выборок сигнала.
число степеней свободы сигнала, т. е. общее число задаваемых выборок сигнала.
Спектральная плотность симметричного сигнала описывается также действительной четной функцией, поэтому для вычисления обратного ДПФ используется формула, аналогичная формуле прямого ДПФ (П2.1):

В силу идентичности выражений  программа вычисления обратного ДПФ оказывается аналогичной записанной ранее программе прямого ДПФ:
программа вычисления обратного ДПФ оказывается аналогичной записанной ранее программе прямого ДПФ:

Для демонстрации действия алгоритма дискретного преобразования Фурье целесообразно вычислить ДПФ для какого-нибудь симметричного сигнала с числом степеней свободы 11 или 13 и затем, применив обратное ДПФ, убедиться в том, что получается тот же результат.
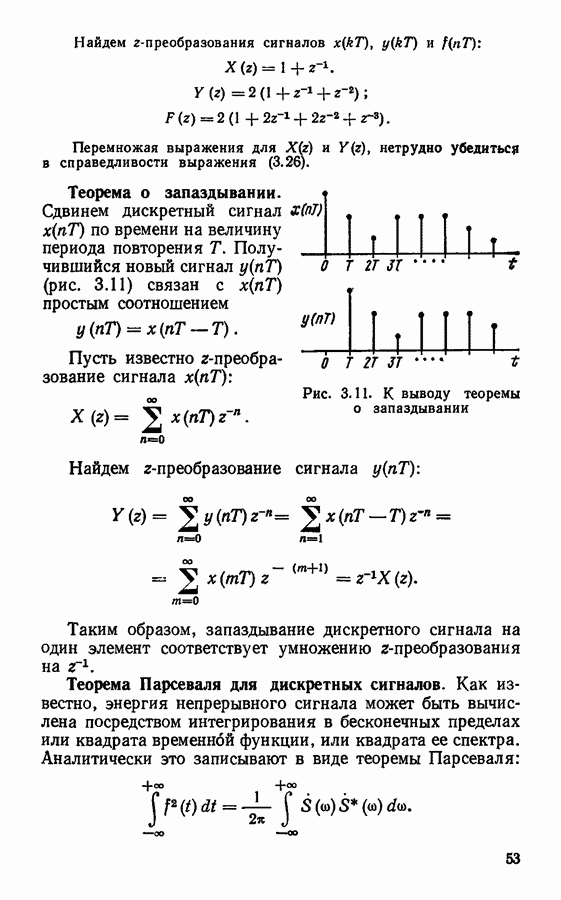
Вычисление дискретной свертки. Для записи программы вычисления дискретной свертки можно воспользоваться формулой (3.24), в которой нижний предел суммирования следует взять равным 1. При этом программа будет иметь вид

Чтобы все члены суммы могли быть вычислены, размер  исходных массивов
исходных массивов  должен быть равен сумме числа отсчетов сигналов
должен быть равен сумме числа отсчетов сигналов  Например, при вычислении свертки двух дискретизированных прямоугольных импульсов:
Например, при вычислении свертки двух дискретизированных прямоугольных импульсов:  заданного 3 отсчетами и
заданного 3 отсчетами и  заданного 5 отсчетами, размер массивов должен быть принят равным 8. При этом программу вычисления свертки можно записать в виде
заданного 5 отсчетами, размер массивов должен быть принят равным 8. При этом программу вычисления свертки можно записать в виде

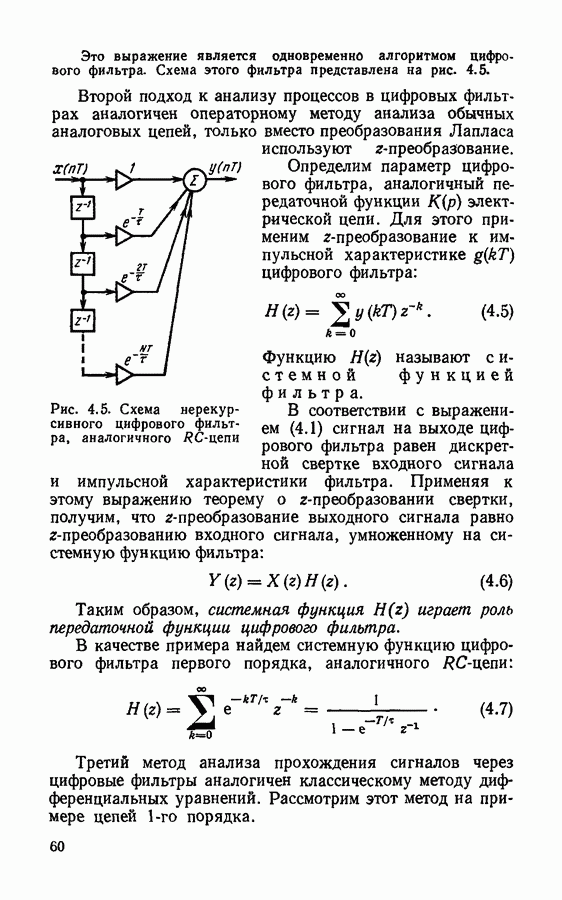
Программы цифровой фильтрации. В качестве первого примера программы цифровой фильтрации можно рассмотреть цифровой фильтр  порядка, эквивалентный
порядка, эквивалентный  -цепи, и сравнить алгоритмы этого фильтра в рекурсивной и нерекурсивной реализациях. Такой фильтр был подробно рассмотрен в гл. 4. Его алгоритм в нерекурсивной реализации имеет вид
-цепи, и сравнить алгоритмы этого фильтра в рекурсивной и нерекурсивной реализациях. Такой фильтр был подробно рассмотрен в гл. 4. Его алгоритм в нерекурсивной реализации имеет вид

где
Обозначим  и положим для определенности
и положим для определенности  входной сигнал возьмем в виде дискретизированного прямоугольного импульса, заданного 5 отсчетами. Тогда программу цифровой фильтрации можно записать в виде
входной сигнал возьмем в виде дискретизированного прямоугольного импульса, заданного 5 отсчетами. Тогда программу цифровой фильтрации можно записать в виде

Длина массивов  выбрана равной 20, что достаточно для получения наглядного представления о характере выходного сигнала. В результате расчета по данной программе получается следующий результат:
выбрана равной 20, что достаточно для получения наглядного представления о характере выходного сигнала. В результате расчета по данной программе получается следующий результат:

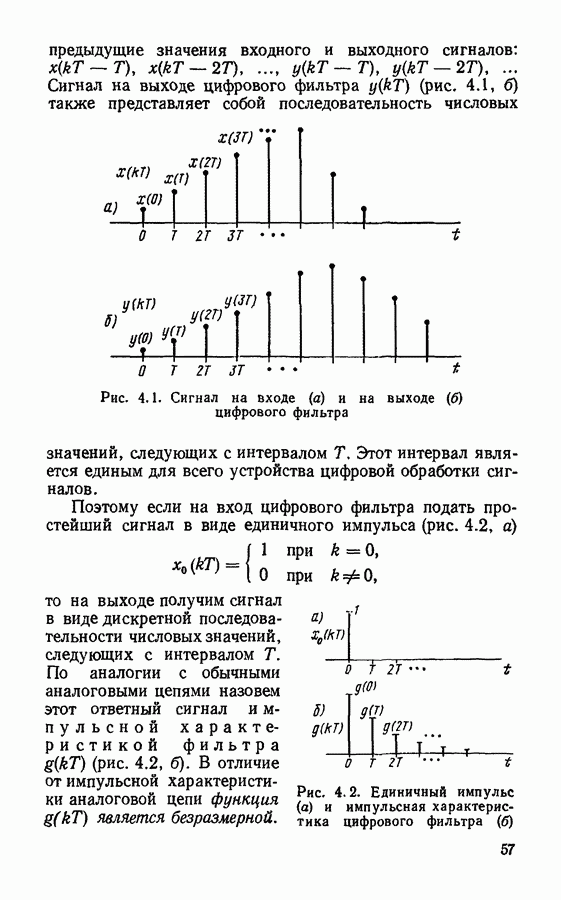
Построив график этого сигнала (рис.  нетрудно убедиться, что он повторяет вид сигнала на выходе
нетрудно убедиться, что он повторяет вид сигнала на выходе  -цепи при воздействии на ее вход прямоугольного импульса.
-цепи при воздействии на ее вход прямоугольного импульса.
Рассмотрим теперь алгоритм этого же фильтра в рекурсивной реализации


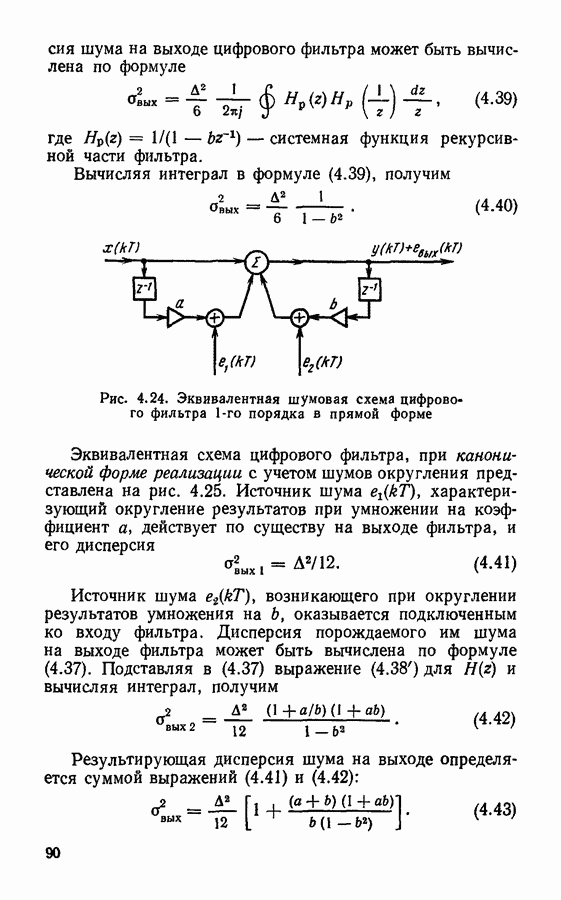
Рис.  Сигнал на выходе цифрового фильтра 1-го порядка
Сигнал на выходе цифрового фильтра 1-го порядка
Обозначая, как и раньше,  запишем программу фильтрации (для того же сигнала на входе)
запишем программу фильтрации (для того же сигнала на входе)

Сравнительный расчет с помощью этих двух программ очень нагляден; время обработки сигнала рекурсивным фильтром оказывается значительно меньше, чем нерекурсивным.
Кроме рассмотренного решения задачи моделирования фильтра 1-го порядка учащимся полезно поупражняться в составлении и реализации нескольких простых программ цифровых фильтров с заданной импульсной характеристикой или системной функцией.
Например, рассмотрим цифровой фильтр с импульсной характеристикой

Этой импульсной характеристике соответствует системная функция

Алгоритм фильтра имеет вид

Этому алгоритму соответствует программа цифровой фильтрации

Записанный в программе этого фильтра входной сигнал очень прост: он имеет лишь два ненулевых отсчета,
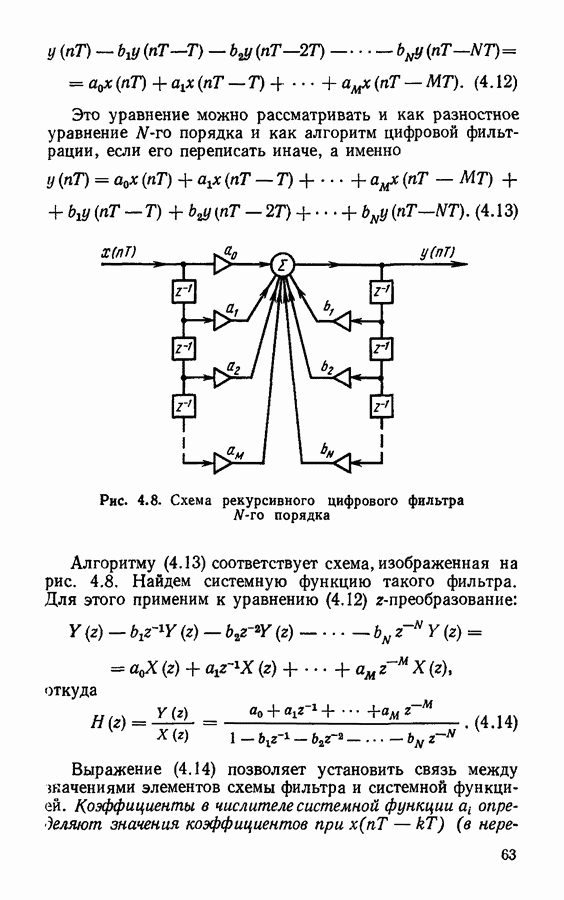
В заключение рассмотрим программу цифрового фильтра, согласованного с сигналом в виде последовательности 5 одинаковых отсчетов (см. задачу 10 к гл. 4). Импульсная характеристика такого фильтра имеет вид

На основании импульсной характеристики можем сразу записать алгоритм фильтра в нерекурсивной реализации и составить программу фильтра:

В качестве входного сигнала здесь взята последовательность 5 одинаковых отсчетов.
Для определения алгоритма рекурсивного фильтра сначала найдем системную функцию

Этой системной функции соответствует алгоритм фильтрации

Запишем программу, соответствующую этому алгоритму:

Обработка сигнала  из 5 единичных отсчетов по этим двум программам приводит к одинаковому результату
из 5 единичных отсчетов по этим двум программам приводит к одинаковому результату

ОТВЕТЫ К ЗАДАЧАМ И УПРАЖНЕНИЯМ
(см. скан)
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОБЩЕЕ ПОНЯТИЕ О ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ
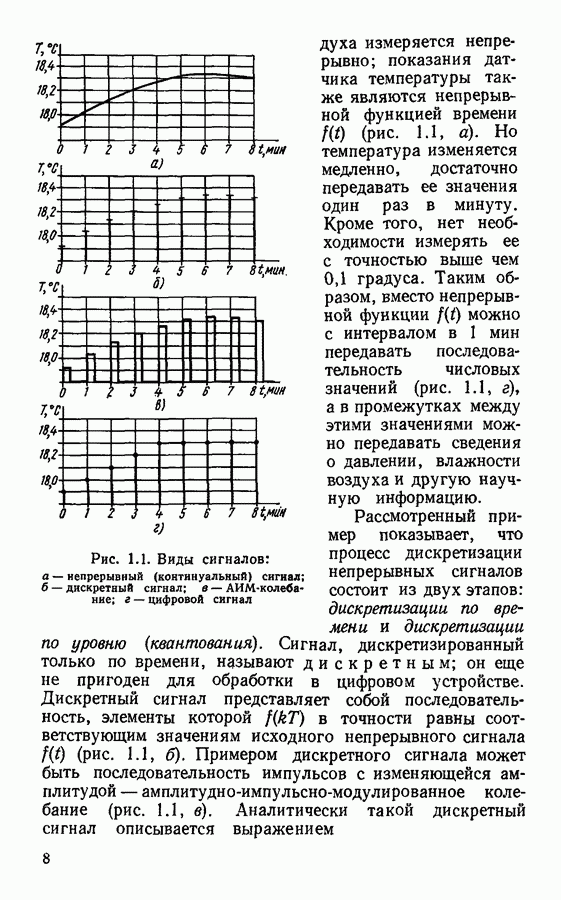
- § 1.1. Дискретные и цифровые сигналы
- § 1.2. Дискретные и цифровые фильтры
- § 1.3. Преимущества и недостатки цифровой обработки сигналов
- Глава 2. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ
- § 2.1. Основы дискретизации непрерывных сигналов
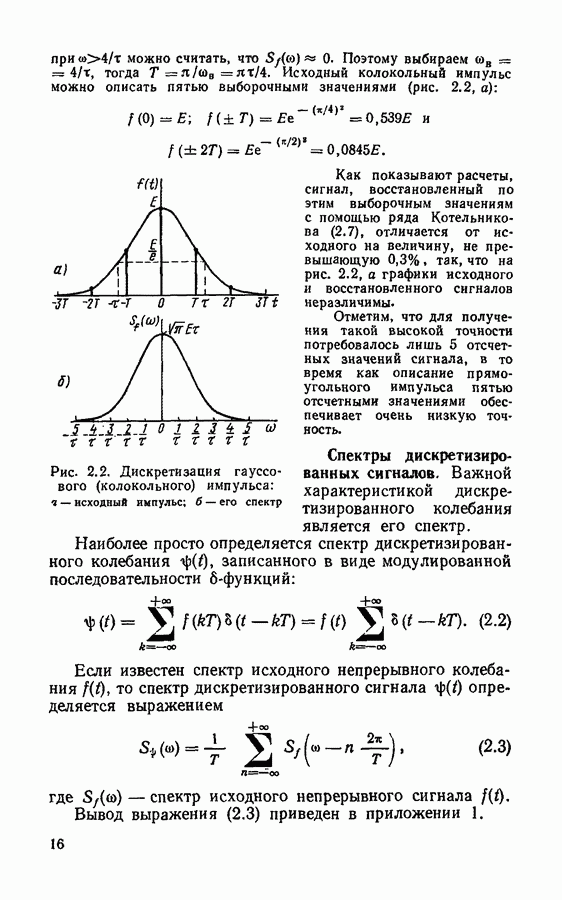
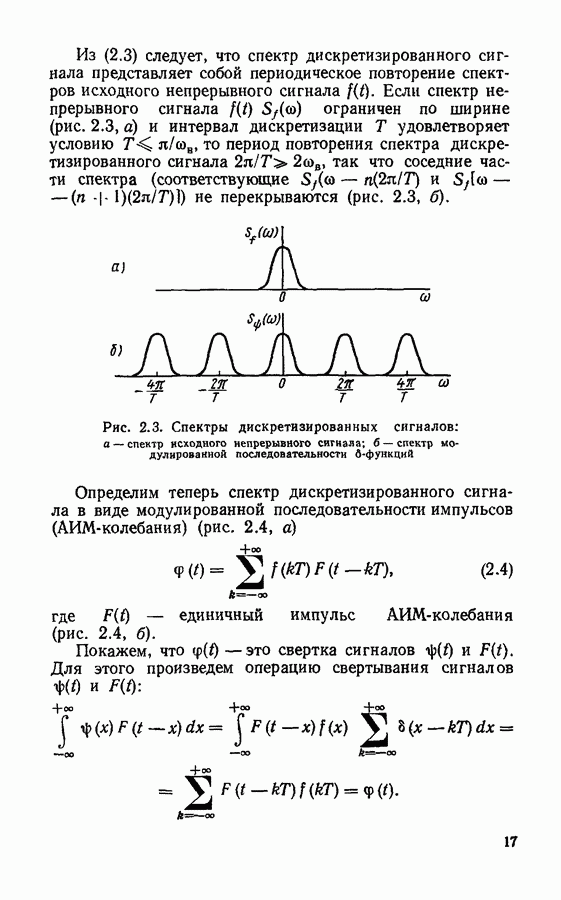
- Спектры дискретизированных сигналов.
- Восстановление непрерывного сигнала. Погрешности дискретизации и восстановления сигнала.
- Дискретизация сигналов в спектральной области.
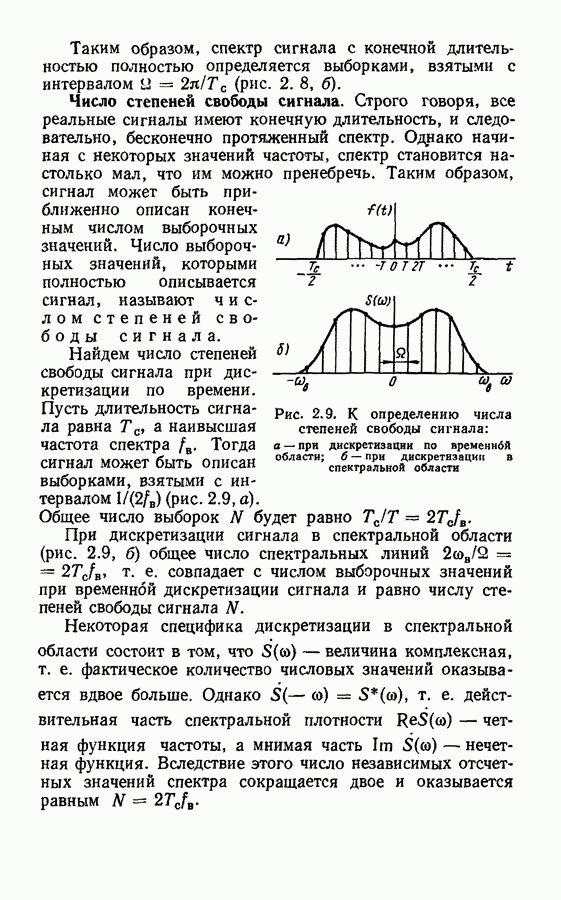
- Число степеней свободы сигнала.
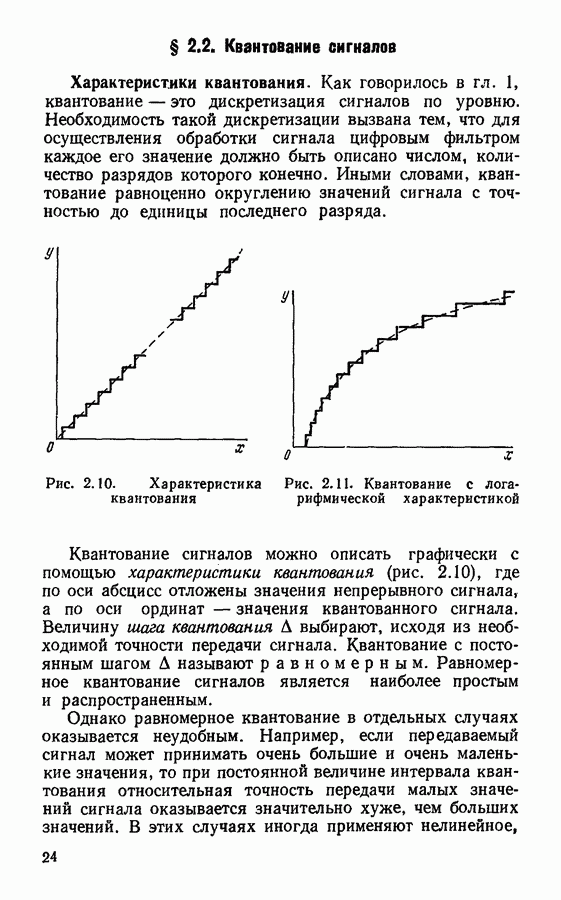
- § 2.2. Квантование сигналов
- Аналого-цифровое преобразование.
- § 2.3. Устройства для дискретизации, квантования и восстановления непрерывных сигналов
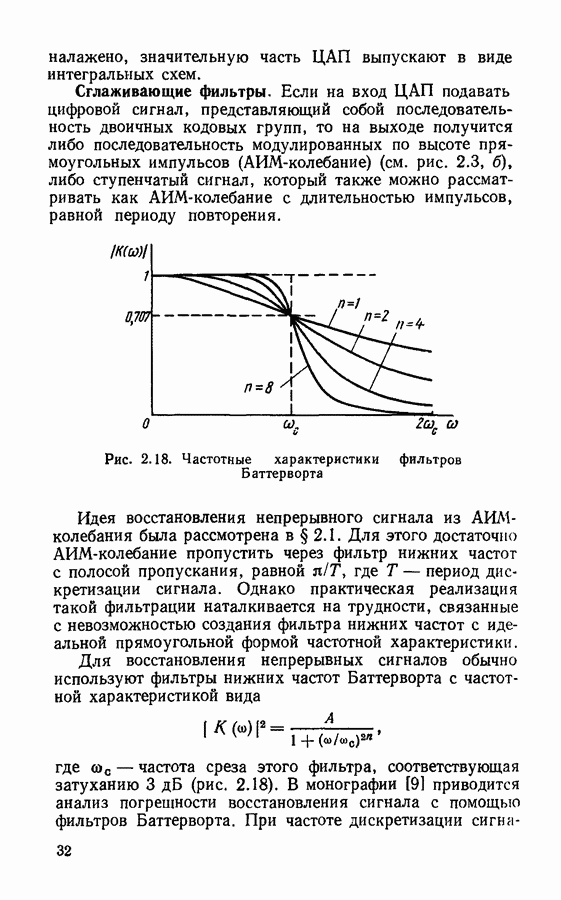
- Сглаживающие фильтры.
- Глава 3. ПРЕОБРАЗОВАНИЯ ДИСКРЕТНЫХ СИГНАЛОВ
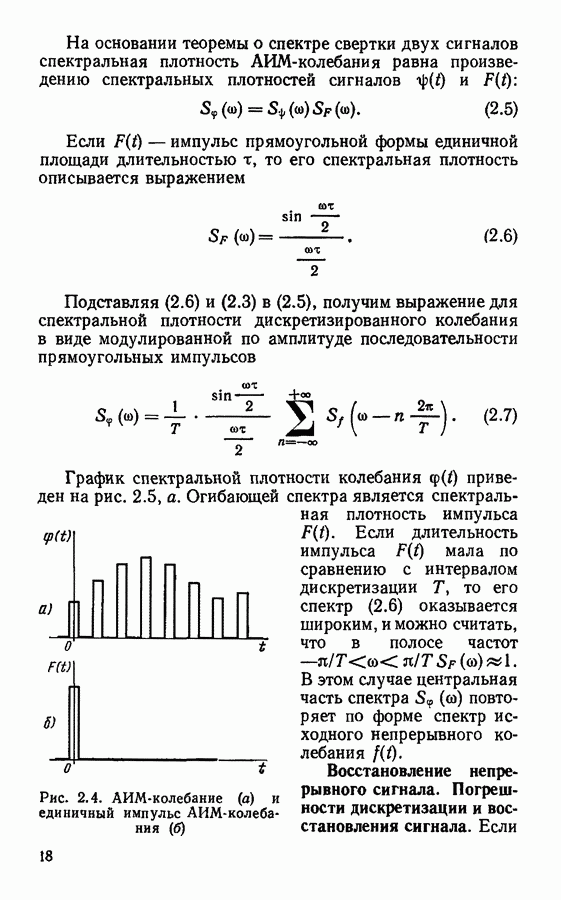
- § 3.2. Дискретное преобразование Фурье
- § 3.3. Быстрое преобразование Фурье
- § 3.4. Дискретное преобразование Лапласа
- § 3.5. z-преобразование
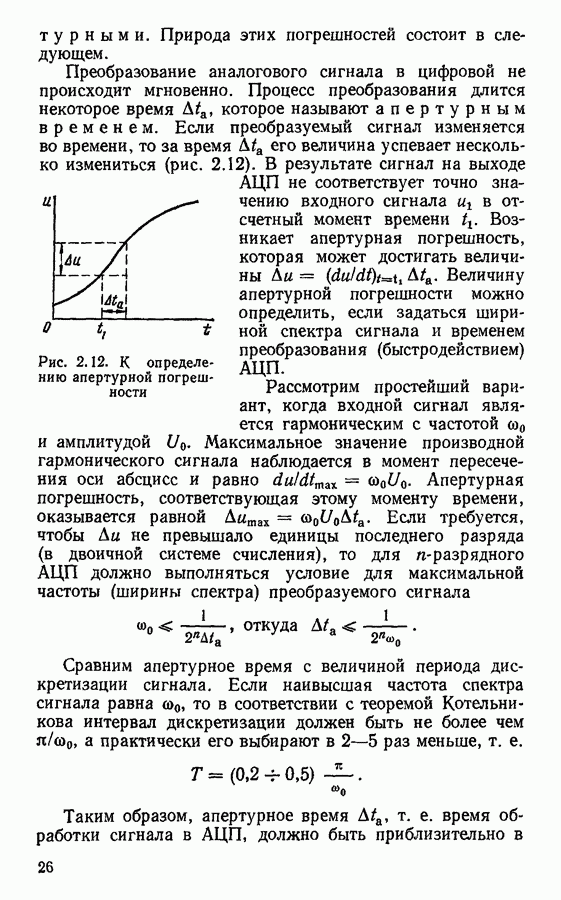
- § 3.6. Обратное z-преобразование
- § 3.7. Основные свойства z-преобразования
- Глава 4. ЦИФРОВЫЕ ФИЛЬТРЫ
- § 4.2. Важнейшие характеристики цифровых фильтров
- § 4.3. Частотные характеристики цифровых фильтров
- § 4.4. Формы реализации цифровых фильтров
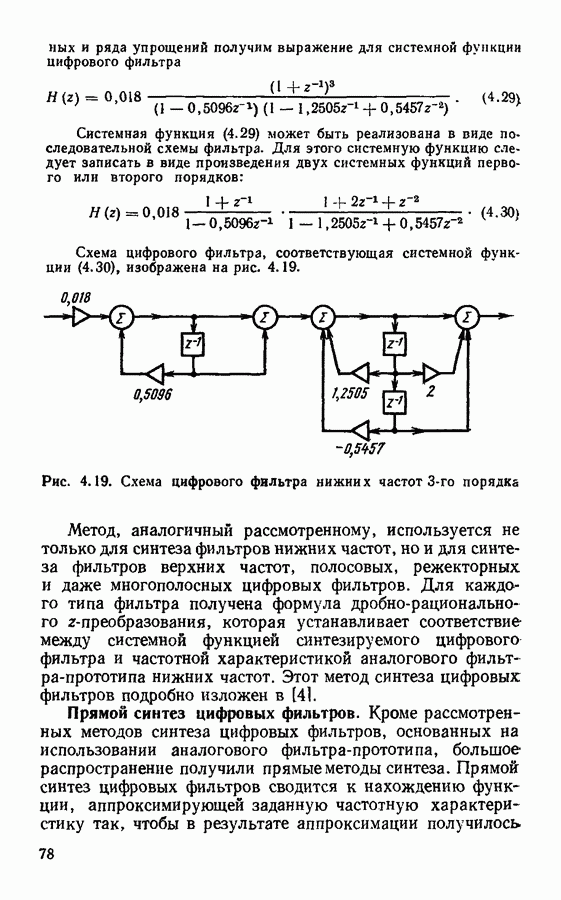
- § 4.5. Основы синтеза цифровых фильтров
- Прямой синтез цифровых фильтров.
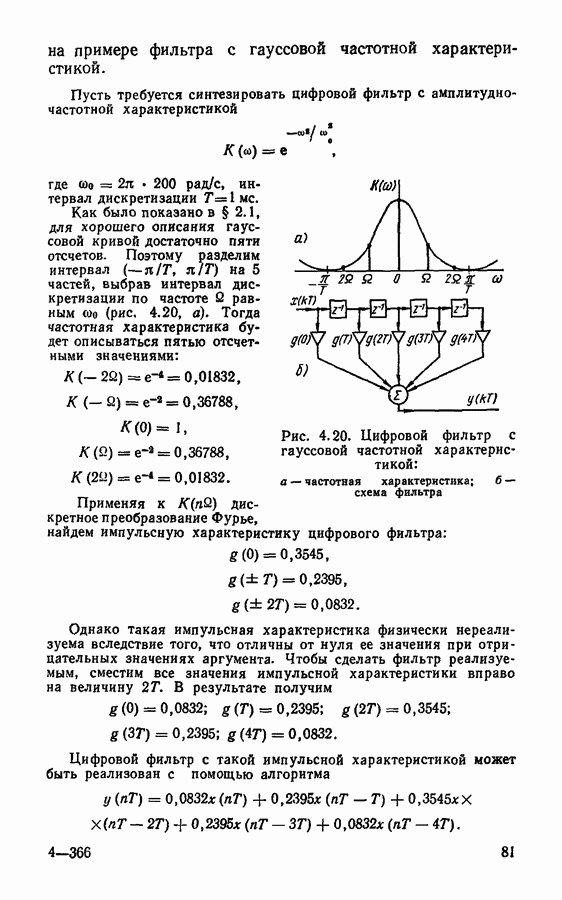
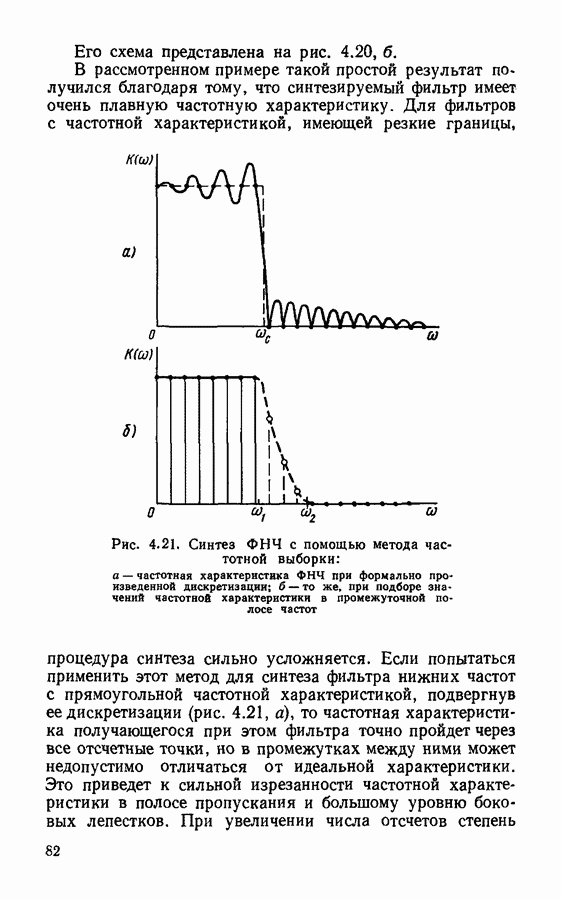
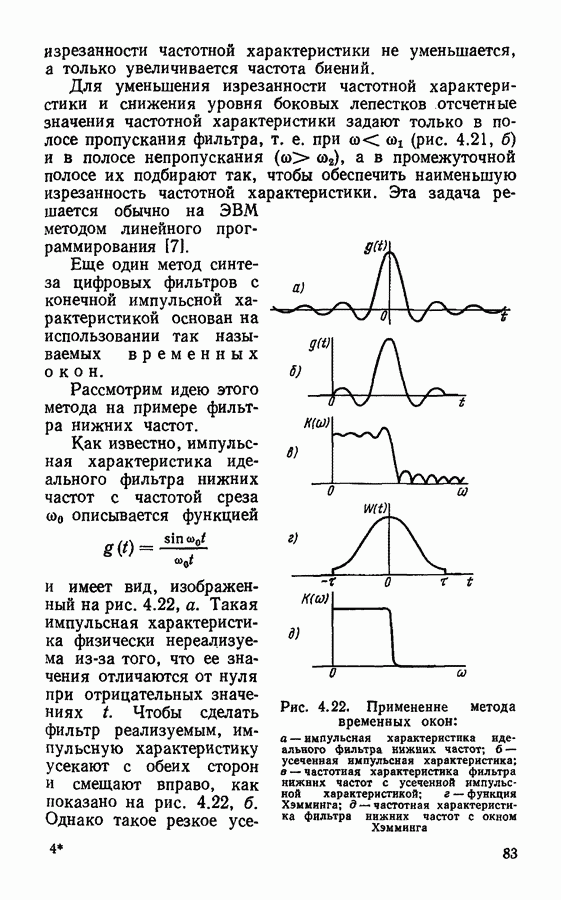
- Методы синтеза фильтров с конечной импульсной характеристикой.
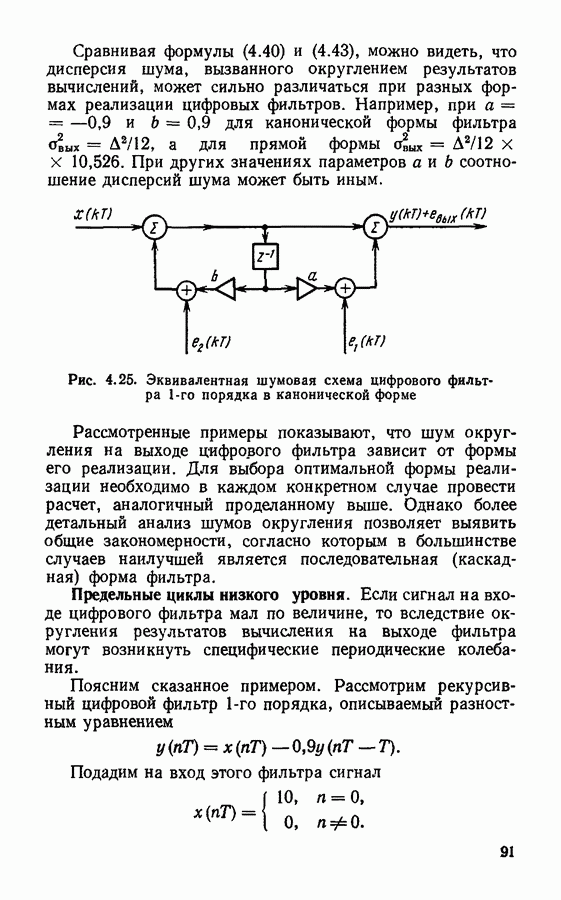
- § 4.6. Эффекты квантования в цифровых фильтрах
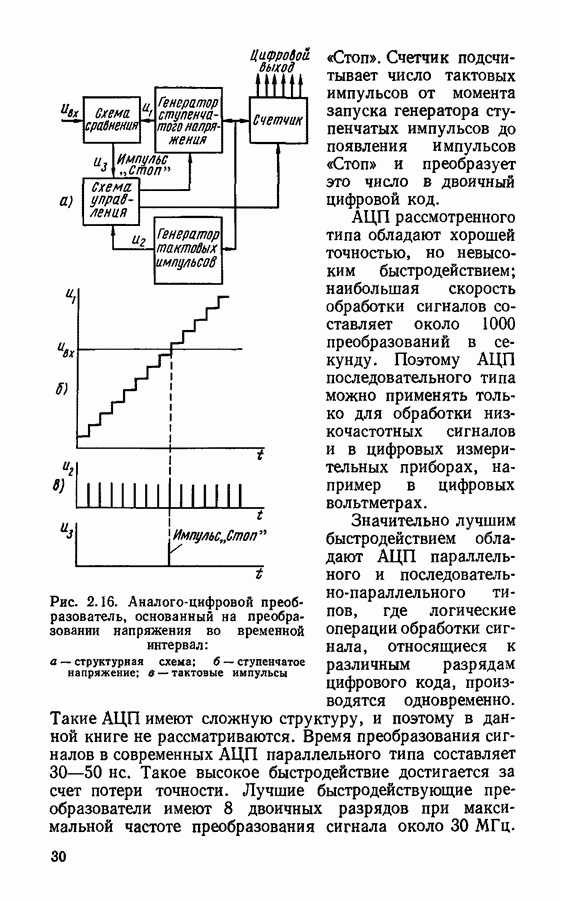
- Ошибки, вызываемые неточными значениями постоянных параметров фильтра.
- Ошибки, вызванные квантованием результатов вычислений.
- Предельные циклы низкого уровня.
- § 4.7. Вопросы реализации и применения цифровых фильтров
- ПРИЛОЖЕНИЯ
- Приложение 1. Вывод формулы спектральной плотности дискретизированного сигнала
- Приложение 2. Примеры программ реализации некоторых алгоритмов на ЭЦВМ «МИР»
- ЛИТЕРАТУРА